Гравитационные силы. Закон всемирного тяготения. Сила тяжести

Согласно законам Ньютона, движение тела с ускорением возможно только под действием силы. Т.к. падающие тела движутся с ускорением, направленным вниз, то на них действует сила притяжения к Земле. Но не только Земля обладает свойством действовать на все тела силой притяжения. Исаак Ньютон предположил, что между всеми телами действуют силы притяжения. Эти силы называются силами всемирного тяготенияилигравитационнымисилами.

Распространив установленные закономерности – зависимость силы притяжения тел к Земле от расстояний между телами и от масс взаимодействующих тел, полученные в результате наблюдений,– Ньютон открыл в 1682 г. закон всемирного тяготения:Все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:

.

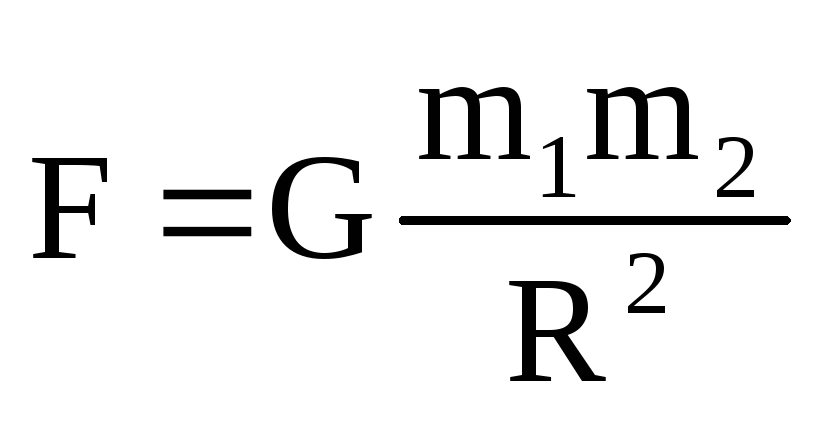Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела. Коэффициент пропорциональности Gназываетсягравитационной постоянной (постоянной всемирного тяготения)и равна

.

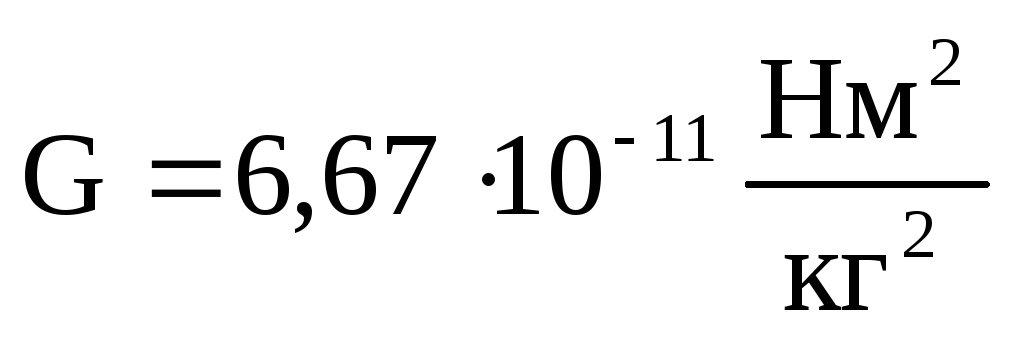Силой тяжестиназывается сила притяжения, действующая со стороны Земли на все тела:

.

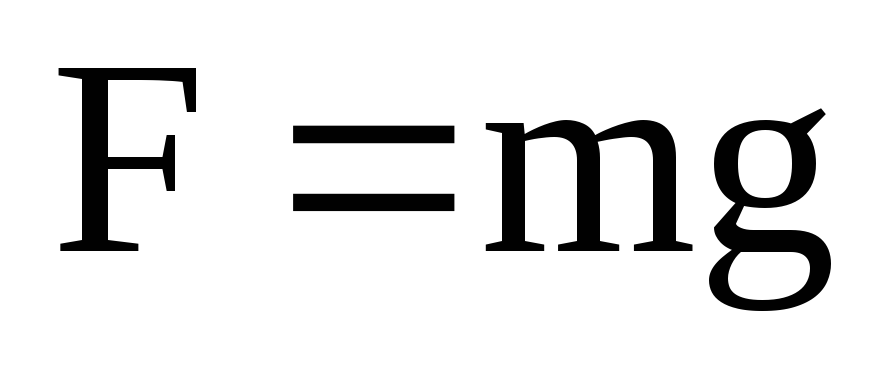Пусть

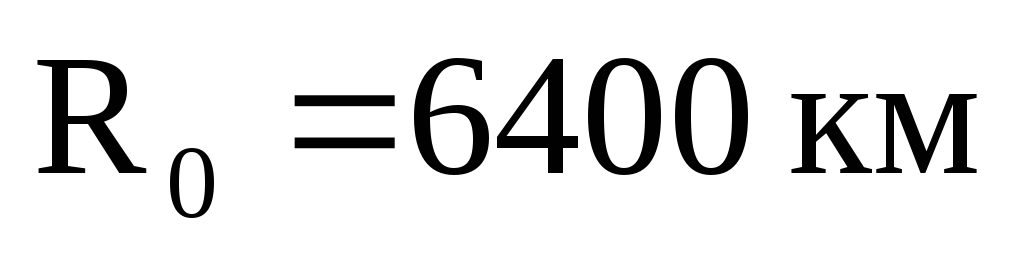– масса Земли, а– радиус Земли. Рассмотрим зависимость ускорения свободного падения от высоты подъема над поверхностью Земли:

Вес тела. Невесомость

Вес тела – сила, с которой тело давит на опору или подвес вследствие притяжения этого тела к земле. Вес тела приложен к опоре (подвесу). Величина веса тела зависит от того, как движется тело с опорой (подвесом).

Вес тела, т.е. сила, с которой тело действует на опору, и сила упругости, с которой опора действует на тело, в соответствие с третьим законом Ньютона равны по абсолютному значению и противоположны по направлению.

Если тело находится в покое на горизонтальной опоре или равномерно движется, на него действуют только сила тяжести и сила упругости со стороны опоры, следовательно вес тела равен силе тяжести (но эти силы приложены к разным телам):

.

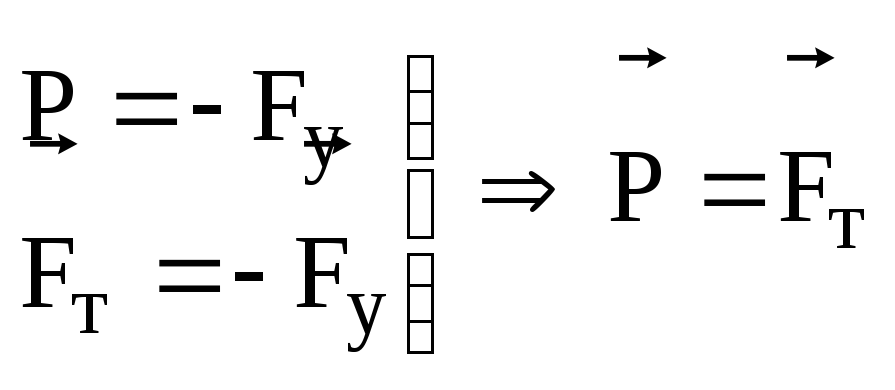При ускоренном движении вес тела не будет равен силе тяжести. Рассмотрим движение тела массой mпод действием сил тяжести и упругости с ускорением. По 2-му закону Ньютона:

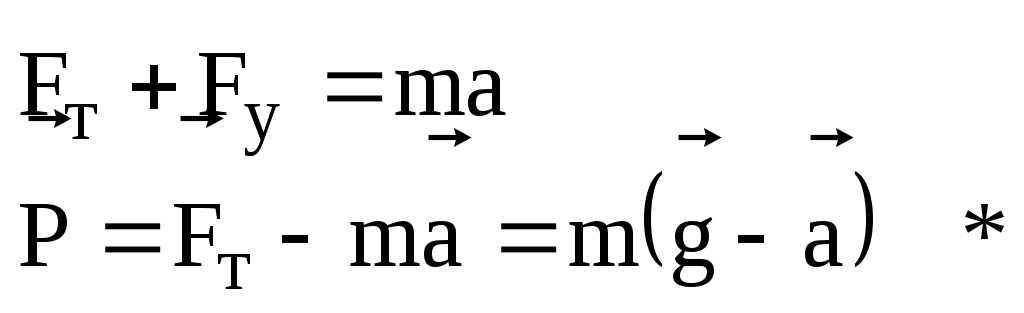
Если ускорение тела направлено вниз, то вес тела меньше силы тяжести; если ускорение тела направлено вверх, то все тела больше силы тяжести.

Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой.

Если тело свободно падает, то из формулы * следует, что вес тела равен нулю. Исчезновение веса при движении опоры с ускорением свободного падения называется невесомостью.

Состояние невесомости наблюдается в самолете или космическом корабле при движении их с ускорением свободного падения независимо от скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением; поэтому в корабле наблюдается явление невесомости.

Движение тела под действием сил тяжести. Движение искусственных спутников. Первая космическая скорость

Если модуль перемещения тела много меньше расстояния до центра Земли, то можно считать силу всемирного тяготения во время движения постоянной, а движение тела равноускоренным. Самый простой случай движения тела под действием силы тяжести – свободное падение с нулевой начальной скоростью. В этом случае тело движется с ускорением свободного падения к центру Земли. Если есть начальная скорость, направленная не по вертикали, то тело движется по криволинейной траектории (параболе, если не учитывать сопротивление воздуха).

При некоторой начальной скорости тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии атмосферы может двигаться по окружности вокруг Земли, не падая на нее и не удаляясь от нее. Такая скорость называется первой космической скоростью, а тело, движущееся таким образом –искусственным спутником Земли (ИСЗ).

Определим первую космическую скорость для Земли. Если тело под действием силы тяжести движется вокруг Земли равномерно по окружности, то ускорение свободного падения является его центростремительным ускорением:

.

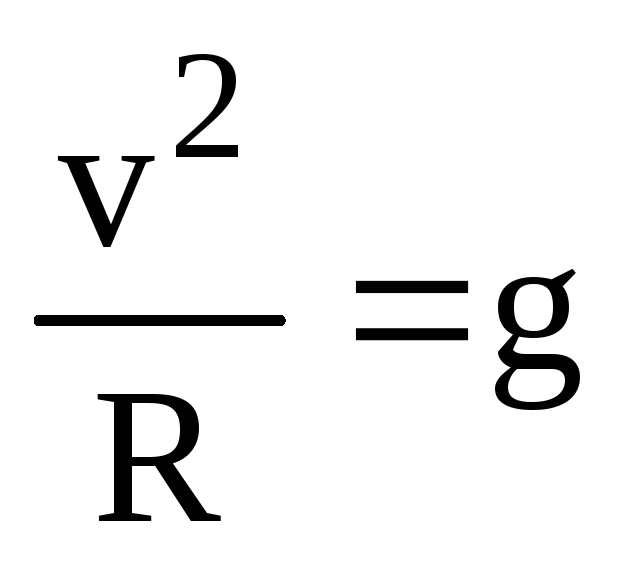Отсюда первая космическая скорость равна

.

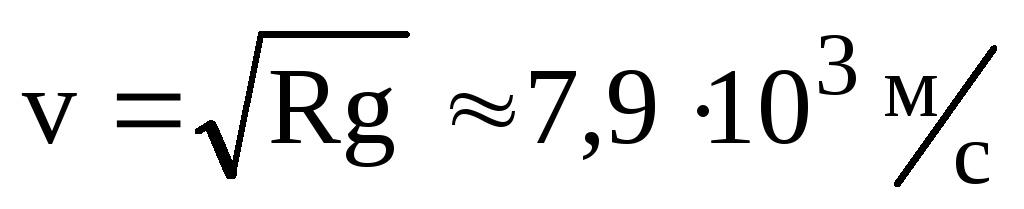Первая космическая скорость для любого небесного тела определяется таким же образом. Ускорение свободного падения на расстоянии R от центра небесного тела можно найти, воспользовавшись вторым законом Ньютона и законом всемирного тяготения:

.

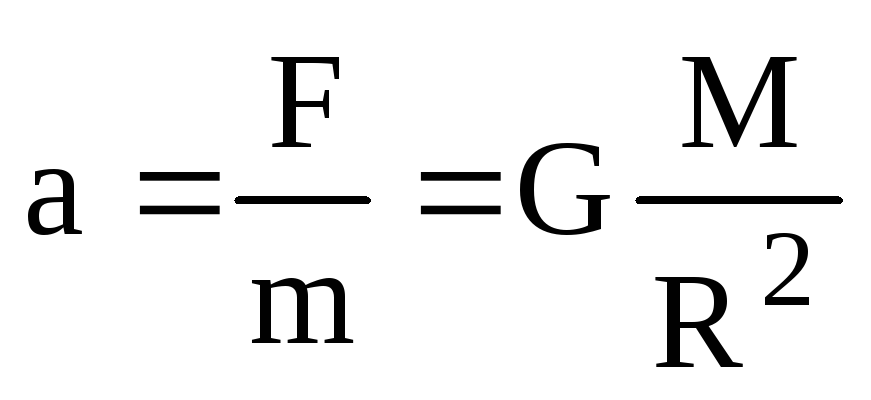
Следовательно, первая космическая скорость на расстоянии R от центра небесного тела массойM равна

.

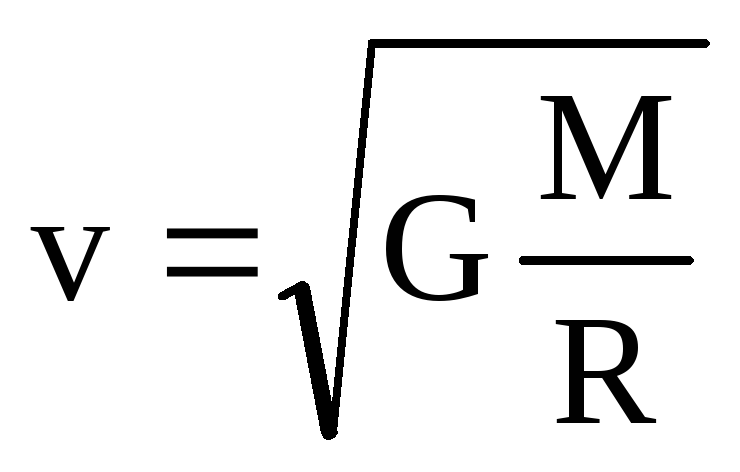Для запуска на околоземную орбиту ИСЗ необходимо сначала вывести за пределы атмосферы. Поэтому космические корабли стартуют вертикально. На высоте 200 – 300 км от поверхности Земли, где атмосфера разрежена и почти не влияет на движение ИСЗ, ракета делает поворот и сообщает ИСЗ первую космическую скорость в направлении, перпендикулярном вертикали.

Закон всемирного тяготения. Примеры силы тяготения в повседневной жизни и в космосе

При изучении школьного курса физики важной темой раздела механики является Закон всемирного тяготения. В данной статье подробнее рассмотрим, что он собой представляет, и с помощью какой математической формулы описывается, а также приведем примеры силы тяготения в повседневной жизни человека и космических масштабах.

Кто открыл Закон всемирного тяготения

Прежде чем приводить примеры силы всемирного тяготения, расскажем кратко, кому приписывают ее открытие.

С давних времен люди наблюдали за звездами и планетами и знали, что они движутся по определенным траекториям. Кроме того, любой человек, не обладающий специальными знаниями, понимал, что как бы далеко и высоко он не бросал камень или другой предмет, тот всегда падал на землю. Но ни один из людей даже не догадывался, что процессами на Земле и небесными телами управляет один и тот же природный закон.

В 1687 году сэр Исаак Ньютон опубликовал научный труд, в котором впервые изложил математическую формулировку Закона всемирного тяготения. Конечно же, Ньютон не самостоятельно пришел к этой формулировке, что признавал лично. Он использовал некоторые идеи своих современников (например, существование обратной пропорциональности от квадрата расстояния силы притяжения между телами), а также накопленный экспериментальный опыт о траекториях движения планет (три закона Кеплера). Гений Ньютона проявил себя в том, что проанализировав весь имеющийся опыт, ученый смог его оформить в виде стройной и практически пригодной теории.

Формула силы тяготения

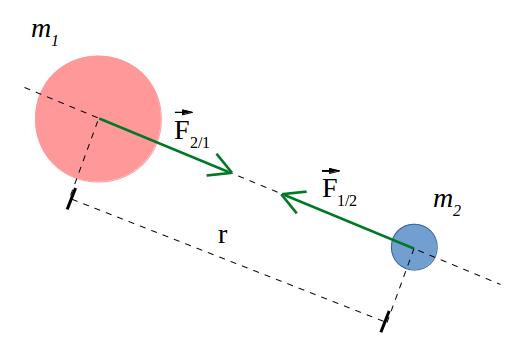
Кратко сформулировать Закон всемирного тяготения можно так: между всеми телами во Вселенной существует сила притяжения, которая обратно пропорциональна квадрату дистанции между их центрами масс и прямо пропорциональна произведению самих масс тел. Для двух тел с массами m₁ и m₂, которые друг от друга находятся на расстоянии r, изучаемый закон запишется в виде:

F = G*m₁*m₂/r².

Здесь величина G — это постоянная гравитации.

Силу притяжения можно рассчитывать по этой формуле во всех случаях, если расстояния между телами достаточно велики по сравнению с их размерами. В противном случае, а также в условиях сильной гравитации вблизи массивных космических объектов (нейтронных звезд, черных дыр) следует использовать разработанную Эйнштейном теорию относительности. Последняя рассматривает гравитацию как результат искажения пространства-времени. В классическом же законе Ньютона гравитация — это результат взаимодействия тел с некоторым энергетическим полем, подобно электрическому или магнитному полям.

Проявление силы тяготения: примеры из повседневной жизни

Во-первых, в качестве таких примеров можно назвать любые падения тел с некоторой высоты. Например, листа или знаменитого яблока с дерева, падение камня, капель дождя, явления горных обвалов и оползней. Во всех этих случаях тела стремятся к центру нашей планеты.

Во-вторых, когда учитель просит учащихся: «Приведите примеры силы тяготения», то им также следует вспомнить о существовании у всех тел веса. Когда телефон лежит на столе или когда человек взвешивается на весах, в этих случаях тело давит на опору. Вес тела — это яркий пример проявления силы тяготения, который совместно с реакцией опоры образует пару уравновешивающих друг друга сил.

Если формулу из предыдущего пункта использовать для земных условий (подставить в нее массу планеты и ее радиус), то можно получить следующее выражение:

F = m*g

Именно его используют при решении задач с силой тяжести. Здесь g — это ускорение, сообщаемое всем телам независимо от их массы при свободном падении. Если бы не существовало сопротивления воздуха, то тяжелый камень и легкое перышко падали бы за одно и то же время с одинаковой высоты.

Тяготение во Вселенной

Каждый знает, что Земля вместе с другими планетами вращается вокруг Солнца. В свою очередь, Солнце, находясь в одном из рукавов спиральной галактики Млечный путь, вращается вместе с сотнями миллионов звезд вокруг ее центра. Сами галактики также приближаются друг к другу в так называемых местных скоплениях. Если вернуться назад в масштабах, то следует вспомнить спутники, которые вращаются вокруг своих планет, астероиды, которые на эти планеты падают или пролетают рядом. Все перечисленные случаи можно вспомнить, если учитель просит школьников: «Приведите примеры силы тяготения».

Отметим, что в последние десятилетия вопрос главной силы в космическом масштабе поставлен под сомнение. В локальном космосе ею без сомнения является сила гравитации. Однако, рассматривая вопрос на уровне галактики, в игру вступает иная, пока еще неизвестная сила, связанная с темной материей. Последняя проявляет себя в виде антигравитации.

Сила всемирного тяготения — Libtime

1. Главная
2. Физика
3. Сила всемирного тяготения

Елена Голец03 Август 2017 4399 Сила всемирного тяготения — не только самая загадочная из сил природы, но и самая могучая.

Человек на пути прогресса

Исторически получилось, что человек по мере своего движения вперед по пути прогресса овладевал все более могучими силами природы. Он начинал, когда у него ничего не было, кроме палки, зажатой в кулаке, и собственных физических сил. Но он был мудр, и он привлек на службу себе физическую силу животных, сделав их домашними. Лошадь ускорила его бег, верблюд сделал проходимыми пустыни, слон — болотистые джунгли. Но физические силы даже самых сильных животных неизмеримо малы перед силами природы. Первой человек подчинил себе стихию огня, но лишь в самых ослабленных его вариантах. Вначале — в течение многих веков — использовал он в качестве горючего только дерево — очень малоэнергоемкий вид топлива. Несколько позже этого источника энергии научился он использовать энергию ветра, человек поднял в воздух белое крыло паруса — и легкое судно птицей полетело по волнам. Парусник на волнах. Он подставил порывам ветра лопасти ветряной мельницы — и завращались тяжелые камни жерновов, застучали песты крупорушек. Но каждому ясно, что энергия воздушных струй далеко не принадлежит к числу концентрированных. К тому же и парус, и ветряк боялись ударов ветра: шторм рвал паруса и топил корабли, буря ломала крылья и переворачивала мельницы. Еще позже человек начал покорение текущей воды. Колесо водяной мельницы — не только самое примитивное из устройств, способных превращать энергию воды во вращательное движение, но и самое маломощное по сравнению с разнообразными турбинами. Человек шел все вперед по лестнице прогресса и нуждался все в больших количествах энергии. Он начал использовать новые виды топлива — уже переход на сжигание каменного угля поднял энергоемкость килограмма горючего с 2500 ккал до 7000 ккал — почти в три раза. Потом пришла пора нефти и газа. Снова в полтора-два раза выросло энергосодержание каждого килограмма ископаемого топлива. На смену паровым машинам пришли паровые турбины; мельничные колеса заменялись гидравлическими турбинами. Далее протянул человек руку к расщепляющемуся атому урана. Однако первое применение нового вида энергии имело трагические последствия — ядерное пламя Хиросимы 1945 года испепелило в течение считанных минут 70 тысяч человеческих сердец. В 1954 году вступила в строй первая в мире советская атомная электростанция, превращавшая мощь урана в сияющую силу электрического тока. И надо отметить, что килограмм урана содержит в себе в два миллиона раз больше энергии, чем килограмм лучшей нефти. Это был принципиально новый огонь, который можно было бы назвать физическим, ибо именно физики изучили процессы, приводящие к рождению столь баснословных количеств энергии. Уран — не единственное ядерное горючее. Уже используется более могучий вид горючего — изотопы водорода. К сожалению, человек еще не смог подчинить себе водородно-гелиевое ядерное пламя. Он умеет на мгновение зажигать его всесжигающий костер, поджигая реакцию в водородной бомбе вспышкой уранового взрыва. Но все ближе и ближе видится ученым и водородный реактор, который будет рождать электрический ток в результате слияния ядер изотопов водорода в ядра гелия. Опять почти в десять раз возрастет количество энергии, которое сможет взять человек от каждого килограмма топлива. Но разве этот шаг будет последним в грядущей истории власти человечества над силами природы? Нет! Впереди — овладение гравитационным видом энергии. Она еще более расчетливо упакована природой, чем даже энергия водородно-гелиевого синтеза. Сегодня это самый концентрированный вид энергии, о каком может хотя бы догадываться человек. Ничего дальше пока не видно там, за передним краем науки. И хотя убежденно можно сказать, что будут работать для человека электростанции, перерабатывающие гравитационную энергию в электрический ток (а может быть, в струю газа, вылетающего из сопла реактивного двигателя, или же в запланированные превращения вездесущих атомов кремния и кислорода в атомы сверхредких металлов), мы ничего пока не можем сказать о деталях такой электростанции (ракетного двигателя, физического реактора).

Сила всемирного тяготения у истоков рождения Галактик

Сила всемирного тяготения стоит у истоков рождения Галактик из дозвездного вещества, как в том убежден академик В. А. Амбарцумян. Она же гасит звезды, отгоревшие свой срок, истратившие отпущенное им при рождении звездное горючее. Многие физики объясняют вмешательством все

Закон всемирного тяготения сила тяжести и напряженность гравитационного поля

В статье вы узнаете про закон всемирного тяготения Ньютона, а также что такое напряженность гравитационного поля, движение тела в гравитационном поле, как вычислять центр массы материальных тел и теоремы Паппуса.

Закон всемирного тяготения Ньютона гласит, что каждое тело во вселенной притягивает другое тело с силой, прямо пропорциональной произведению масс обоих тел (M и m) и обратно пропорциональной квадрату расстояния r между центрами масс обоих тел. Эта сила всегда действует по прямой линии, соединяющей оба центра масс.

G- это универсальная гравитационная постоянная величины

Сила гравитации действует между небесными телами огромной массы, а также между телами с незначительными массами в космическом масштабе, хотя в последнем случае она незаметно мала.

Напряженность гравитационного поля

Напряженность гравитационного поля представляет собой отношение силы F, действующей на тело, к массе m тела, помещенного в поле. Значение и направление напряженности гравитационного поля определяется вектором g :

Формула напряженности гравитационного поля

Напряженность гравитационного поля g является основным параметром, характеризующим это поле. На каждое тело действует сила тяготения, которое равняется массе тела умноженное на напряженность гравитационного поля:

Когда мы определяем вес тела около Земли, М — это масса Земли, а r — это расстояние от центра массы тела до центра Земли.

Движение тела в гравитационном поле, наклонная проекция

Первую космическую скорость называют минимальной скоростью, которой должно обладать тело с массой m, чтобы оно могло двигаться вокруг Земли после стабильной орбиты с радиусом г. На этой орбите будет баланс центростремительной силы тяжести и центробежной силы инерции.

Таким образом, для орбиты, расположенной в точке h над Землей с радиусом R, первая космическая скорость равна

Вторая космическая скорость (скорость выхода) — это минимальная скорость, которая позволяет телу с массой m достигать бесконечного расстояния от Земли. Кинетическая энергия, которая должна быть отдана телу для этой цели, должна быть равна потенциальной энергии тела на поверхности Земли.

Следовательно, вторая космическая скорость

Вторая космическая скорость

По аналогии мы определяем обе космические скорости для любого другого небесного тела.

Пример:

Предоставление тела с массой m начальной скорости v направленной под углом φ, означает, что это тело будет одновременно иметь горизонтальную начальную скорость v*cos φ и вертикальную начальную скорость v*sin φ, как показано на рисунке выше. Анализируя движения тела в наклонной проекции, мы предполагаем следующие предположения: 1. гравитационное ускорение g (значение вектора гравитационного поля g) является постоянным по всей траектории движения тела, и поэтому скорость в вертикальном направлении v_y подвержена постоянным изменениям и по истечении времени t равна:

Мы опускаем сопротивление воздуха, и поэтому скорость тела в горизонтальном направлении vx постоянна, и тело летит в этом направлении, пока оно находится в воздухе.

В точке, где тело достигает максимальной высоты, его скорость равна нулю 

Исходя из этого, мы получаем время полета тела t от места его выброса для достижения наибольшей высоты

Время полета тела

Время падения тела с максимальной высоты до начальной точки совпадает со временем его подъема. Это означает, что время пребывания тела в воздухе и, следовательно, время его полета в горизонтальном направлении

Простым умножением постоянной горизонтальной скорости на время, в течение которого тело находится в воздухе, мы получаем диапазон проекции под углом x _max :

Потому что этот максимальный диапазон

Интересный результат мы получаем после применения свойств функции синуса:

 После учета этого свойства симметрии, мы находим, что максимальный диапазон также выражается формулой 

то есть

Диапазоны x _max при съемке на ровной дорожке и крутой дорожке одинаковы, но поскольку в обоих случаях вертикальные составляющие скорости различны, v _o sin φ и v ₀ sin (90º — φ), то максимальные высоты y _max будут в обоих случаях разные. Максимальная высота для пути y _max1 получается простым интегрированием

Подставляя время вознесения тела

мы получаем

Аналогично для крутого пути мы получаем

Соотношение обеих максимальных высот будет

Для φ = 45º обе высоты, конечно, одинаковы. Наконец, мы находим уравнение следа тела в угловом виде. Сначала мы определим координаты x и y тела, как функцию времени, потому что

после простой интеграции мы находим это

Стандартная процедура нахождения пути тела состоит в том, чтобы исключить время из этих уравнений. У нас есть первое уравнение

Подставив это выражение во второе из уравнений и после простого преобразования, мы обнаружим, что путь тела описывается уравнением

Это уравнение перевернутой параболы, как показано на правом рисунке. Фактический курс снаряда так называемый баллистическая кривая, форма, которой зависит от величины сопротивления воздуха, то есть от давления, влажности и ветра, а также от формы самого снаряда. Диапазон баллистической кривой намного меньше, чем диапазон, определяемый идеальной параболической дорожкой.

Центр массы материальных тел

В поисках центра масс C массы M погружаем тело в систему отсчета x, y, z и вырезаем элемент объема dV = dx dy dz, который соответствует элементу массы dm = ρdV, где ρ — плотность массы

Центр массы материальных тел

С элементами массы dm мы поступаем точно так же, как и раньше, с массами m _i. Однако, поскольку массы dm бесконечно малы, сумма в формулах для координат центра масс должна быть заменена интегрированием. Интеграция осуществляется по всему объему твердого тела. В результате мы получаем полностью аналогичные выражения:

ПРИМЕРЫ СЛЕДУЮЩИХ МАТЕРИАЛОВ

Пример 1: Найти центр масс однородного стержня с массой M и длиной L.

Пример 2: Найти центр масс однородной плиты, которая имеет форму равнобедренного треугольника. Пластина имеет массу M, длину основания A и высоту H.

Пример 3: Найти центр масс однородного вращающегося конуса с радиусом основания R и высотой H.

Иногда проблема нахождения центра масс сложной массы может быть сведена к проблеме центра масс системы материальных точек, например, для ломаной кривой, образованной из стержня:

Использование теорем Паппуса для расчета центра масс материальных тел

Две теоремы Паппуса полезны для нахождения центра массы материальной массы.

1. Теорема площади поверхности: если плоская кривая с длиной L повернута на определенный угол вокруг любой оси, лежащей в той же плоскости, и не пересекает эту кривую, то площадь результирующей поверхности поворотной поверхности равна произведению длины L на длину пути S, на который прошел центр масса С этой кривой.

2. Теорема об объеме: если замкнутая плоская фигура с полем A поворачивается на определенный угол вокруг любой оси, лежащей в той же плоскости, и не пересекает эту фигуру, то объем созданного таким образом вращательного тела равен произведению поля A и длины пути S, прошедшего центр масс С этой цифры.

Второе утверждение, конечно, верно, когда мы перемещаем рассматриваемую фигуру по прямой линии, перпендикулярной к ней, но когда мы перемещаем ее по кругу или другой кривой, могут быть созданы довольно специфические тела. Однако для изогнутой дорожки внешняя часть смещается больше, а внутренняя часть меньше, и оба эффекта сбалансированы. Поэтому, если мы хотим найти положение центра масс плоской плоскости с постоянной плотностью, достаточно вспомнить, что объем, возникающий при его вращении вокруг оси, равен расстоянию, на которое центр масс умножается на поверхность панели.

Поскольку наша задача состоит в том, чтобы найти центры масс, в теоремах Паппуса мы выбираем оси вращения и углы, на которые мы поворачиваем дуги или лепестки поверхности, чтобы легко было найти подходящие площади поверхности и объем твердых тел, возникающих в результате вращений.

Например, если мы хотим найти положение центра масс прямоугольного треугольника с основанием D и высотой H, мы можем решить эту проблему следующим образом. Мы представляем себе ось, проходящую через H и вращать треугольник вокруг оси на 360. Расстояние которой центр массы x_c — координаты, это
2πx_c. Скользящая фигура была треугольником; его поле равно 1/2 HD. Расстояние, пройденное центром масс, умноженное на поле треугольника, равно объему полученной фигуры, который, конечно, равен πD²H/3. Таким образом, (2πx_c)(1/2 HD)= 1/3πD²H, то есть x_c = D/3. Аналогичным образом, вращая вокруг другой оси или ссылаясь на симметрию, мы находим, что y _c = H / 3. Действительно, центр масс каждой однородной поверхности треугольника находится в точке пересечения трех центральных линий, проведенных от вершин к центрам противоположных сторон (эта точка расположена на третьей части пути вдоль каждой медианы). Чтобы выяснить это, давайте разделим треугольник на множество небольших слоев, параллельных основанию. Следует отметить, что средняя часть делит каждый из этих слоев пополам, поэтому центр масс должен лежать на нем.

Более сложным случаем является нахождение местоположения центра масс однородного полукруга. Для полного круга центр масс, очевидно, находится в середине круга, но для полукруга проблема более сложная. Пусть r — радиус полукруга, ax _{c —} расстояние центра масс от прямой кромки. Если мы повернем полукруг вокруг этого края так, чтобы образовалась сфера, центр масс пройдет расстояние 2πx _c ; площадь поверхности πr ² /2 (так как это только половина круга). В результате чего объем равен ходу 4π R ³ /3; мы находим из этого

Гравитационное взаимодействие

Основные воздействия на природу. Все известные взаимодействия, которые тела оказывают друг на друга, делятся на четыре типа:

• гравитационные взаимодействия
• слабые взаимодействия
• электромагнитные взаимодействия
• сильные взаимодействия

Каждое из этих взаимодействий сильно отличается от других силой, которую оно создает между двумя телами. Таблица показывает относительную силу каждого из ударной силы F относительно электромагнитной силы F _E.

Тип воздействия	F / F E
гравитационные	10 -40
слабые	10 -10
электромагнитные	1
сильные	10 2

Представленный список содержит все известные в природе силы, и каждое взаимодействие между телами осуществляется одной из этих четырех сил или комбинацией нескольких из них (например, при одновременном действии силы тяжести и электромагнитных сил).

Самым слабым из этих взаимодействий является гравитационное взаимодействие, примерно слабее электромагнитного в 10 ⁴⁰ раз. Сила гравитации, созданная в этом взаимодействии, всегда привлекательна и действует между телами, обладающими массой. Значение силы тяжести описывает уже известный закон тяготения Ньютона (эта сила прямо пропорциональна произведению обеих действующих масс и обратно пропорциональна квадрату расстояния между их центрами масс).

Слабая сила, меньше, чем приблизительно 10 ¹⁰ раз происходит между лептонов (например Электроны, мюоны (μ частицы) и taonami частицы), а также несет ответственность за деградацию бета частиц и ядер.

Электромагнитное взаимодействие создает силы, ответственные за структуру атома, за химические реакции и за все электромагнитные явления в окружающем нас мире. Эти силы действуют только между заряженными частицами и могут быть как притягивающими, так и отталкивающими, что отличает их от постоянно притягивающей силы притяжения. Значение силы, генерируемой при электромагнитном взаимодействии между двумя точечными нагрузками покоя, описывает так называемые Кулоновская сила (эта сила прямо пропорциональна произведению обоих заряженных частиц и обратно пропорциональна квадрату расстояния между ними).

Сильное взаимодействие, примерно в 10²⁰ раз более сильнее, чем электромагнитное, действует только между тяжелыми частицами, называемыми адронами, которые делятся на барионы (например, протон, нейтрон) и мезоны (например, мезон π). Как мы увидим далее при обсуждении Стандартной модели, адроны имеют внутреннюю структуру и состоят из кварков, которые мы считаем фактически элементарными частицами. Каждый барион состоит из трех кварков и мезона из одного кварка и одного антикварка. Сильное взаимодействие между нуклонами (протон, нейтрон) вызывает их взаимную связь, приводящую к созданию атомного ядра. Сильные взаимодействия в атомных ядрах имеют очень короткий диапазон 10 ^-15.

Гравитация в космологии, существенное значение гравитации в эволюции звезд и поведение больших звезд.

Хотя в атомном масштабе сила гравитации ничтожно мала, когда она действует в космическом масштабе внутри массивных тел (галактик, звезд, планет), она определяет взаимные движения этих тел и в то же время является очень важным фактором в их эволюции. В определенных процессах эволюции, происходящих в очень массивных звездах, гравитационные взаимодействия порождают взрывы, мощность которых во много раз превышает мощность, генерируемую в термоядерных реакциях этих звезд.

Эволюция звезды называется последовательностью процессов, которые протекают в звезде от ее рождения до окончательного гашения. Мы предполагаем, что звезда возникает в результате конденсации межзвездного вещества, которое происходит либо случайно, либо по необъяснимым причинам. Звезда затем растет в результате гравитационного притяжения масс новой материи. В этом изначальном холодном облаке гравитационно-сжатого вещества, называемого протозвездой, растет внутреннее давление. Это повышение давления постоянно повышает температуру до уровня 5-10 × 10 ^6. При этой температуре термоядерный синтез водорода начинает образовывать гелий. Период создания протозвезды, вероятно, составляет около 50 миллионов лет. Когда начинается термоядерная реакция, гравитационное сжатие уравновешивается увеличением внутреннего давления, вызванным этой реакцией.

В типичной звезде, которой является наше Солнце, скорость сгорания водорода оценивается примерно в 10 ¹¹ кг с ^-1, с выделением энергии около 6 × 10 ²⁵ Дж с ^-1. Считается, что солнце содержать достаточное количество водорода, чтобы записать его со скоростью 10 ¹⁰ лет и что Солнце находится в середине его жизни как звезда. В конце концов, однако, период стабильности звезды подходит к концу, потому что энергии, генерируемой внутри термоядерных реакций внутри, уже недостаточно для уравновешивания гравитационного сжатия. Ядро звезд, в настоящее время содержащее в основном гелий, гравитационно разрушается до тех пор, пока температура не поднимется настолько высоко, что в окружающем ядре начинается новая фаза термоядерных реакций, состоящая из несгоревшего водорода. Энергия, полученная в этих реакциях, заставляет внешнюю оболочку звезды быстро расширяться и охлаждаться. При такой пониженной температуре, цвет раздутого в настоящее время покрытия меняется с белого на красный. Звезда в этом состоянии — красный гигант. В то же время ядро ​​звезды гравитационно сжимается, достигая температуры 10 ⁸ К, и при этой температуре гелий, образующий ядро, становится центром, в котором взрывается новый тип термоядерных реакций. Продуктом этих реакций является углерод. Звезды относительно небольшой массы быстро сжигают гелий, содержащийся в ядре, и затем ядро ​​снова разрушается гравитационно, создавая объект, который мы называем белым карликом. Внешняя оболочка, которая ранее принадлежала красному гиганту, в это время уходит в космос.

Более крупные звезды, во много раз больше Солнца, имеют достаточно гелия в ядре, чтобы позволить процессу горения продолжаться, и тогда образуются более тяжелые элементы, вплоть до железа. Поэтому железо является самым тяжелым элементом, который может быть получен в процессе горения гелия в ядре звезды. Когда в такой большой звезде гелий окончательно сгорает, происходит настоящая катастрофа в космическом масштабе. Вся масса звезды коллапсирует гравитационно, и энергия, произведенная в этом процессе, вызывает гигантский взрыв всей звезды. Это явление называется взрывом сверхновой. Мощность энергии излучения, выделяющейся при взрыве сверхновой, заставляет звезду излучать 10 ¹⁰ раз сильнее, чем средняя звезда. Это означает, что сверхновая доминирует над яркостью всей галактики, в которой она находится. При взрыве сверхновой самые тяжелые элементы, встречающиеся в природе, уже сформированы. Однако продолжительность жизни сверхновой коротка, и ее излучение исчезает через несколько лет. Остатки взрыва сверхновой завершают процесс эволюции, создавая так называемые нейтронные звезды или черные дыры.

Нейтронная звезда — это звезда, которая достигла конца своего эволюционного пути и в которой больше нет ядерного топлива. Теперь ничто не противодействует максимальному гравитационному коллапсу, и в результате звезда становится настолько сжатой, что электроны внутри нее вынуждены проникать в атомное ядро, где они соединяются с протонами и превращают их в нейтроны. Согласно принятой модели, нейтронная звезда имеет газовую оболочку толщиной в несколько метров, ниже которой находится сплошная кора толщиной около 1 км. Под корой простирается сверхтекучий слой, состоящий почти целиком из нейтронов. Сам центр такой звезды — чрезвычайно твердое ядро. Нейтронная звезда имеет диаметр, вероятно, не более 10 км, но ее масса в 1,5 раза больше массы Солнца, то есть 3 × 10 ³⁰кг. Это означает, что средняя плотность нейтронной звезды составляет около 10. ¹⁵ раз больше, чем плотность воды; это плотность, которую нельзя найти нигде во Вселенной. Считается, что пульсары — необычно правильные космические часы — это быстро вращающиеся нейтронные звезды, которые имеют очень сильные магнитные поля.

Черная дыра — это объект в космосе, созданный также гравитационным коллапсом, но в этом случае объект настолько массивен, что для него скорость выхода (вторая космическая скорость) равна скорости света. Предполагается, что появление черной дыры происходит в результате взрыва сверхновой, в которой ядро ​​материи, остающееся после взрыва, очень велико (много масс Солнца). Материал сердечника подвергается огромному гравитационному сжатию, что приводит к дальнейшему увеличению напряженности гравитационного поля. В какой-то момент это поле достигает критического значения, то есть оно становится настолько большим, что электромагнитное излучение попадает в него и больше не может распространяться в пространстве. Тогда созданный таким образом объект больше не светит, поэтому он становится черной дырой. поверхность, на котором гравитационное поле достигает этого критического значения, называется горизонтом событий. Мы не можем и никогда не сможем зарегистрировать или обнаружить что-либо, что происходит ниже горизонта событий. Мы заключаем о существовании черных дыр, основываясь на наблюдении за поведением небесных тел вблизи этих дыр. Если, например, черная дыра создает двойную систему с обычной звездой, то черная дыра высасывает вещество из этой звезды. Всасываемая материя сначала создает вращающийся диск вокруг черной дыры. Вещество в диске становится сжатым и нагретым до такой степени, что оно испускает рентгеновские лучи. Мы заключаем о существовании черных дыр, основываясь на наблюдении за поведением небесных тел вблизи этих дыр. Если, например, черная дыра создает двойную систему с обычной звездой, то черная дыра высасывает вещество из этой звезды. Всасываемая материя сначала создает вращающийся диск вокруг черной дыры. Вещество в диске становится сжатым и нагретым до такой степени, что оно испускает рентгеновские лучи. Мы заключаем о существовании черных дыр, основываясь на наблюдении за поведением небесных тел вблизи этих дыр. Если, например, черная дыра создает двойную систему с обычной звездой, то черная дыра высасывает вещество из этой звезды. Всасываемая материя сначала создает вращающийся диск вокруг черной дыры. Вещество в диске становится сжатым и нагретым до такой степени, что оно испускает рентгеновские лучи.

10 11, или сто миллиардов

Гравитационное поле влияет на поведение огромных звездных сообществ, таких как галактики. Каждая галактика — эллиптическая, спиральная или неправильная — содержит около 10 ¹¹ звезд, и все они скреплены гравитацией. Галактика, в которой находится наша Солнечная система, называется Млечный путь и представляет собой спиральную галактику, а Солнце находится на периферии этой спирали. Предполагается, что самые большие телескопы в диапазоне других галактик, число которых во Вселенной также оценивается в 10 ¹¹. Гравитационное поле также оказывает существенное влияние на ход таких гигантских событий, как галактические столкновения.

Кстати — количество нейронов (нервных клеток) в нашем мозгу совершенно случайно тоже 10 ¹¹. Каждый из этих нейронов связывается с рецепторными клетками, мышечными клетками, железистыми клетками или другими нейронами с сетью синаптических связей, число которых может достигать нескольких сотен на каждый нейрон. Фантастическая машина!

Гравитационные силы. Закон всемирного тяготения. Вес тела

Гравитационные силы. Закон всемирного тяготения. Вес тела

В природе существуют различные силы, которые характеризуют взаимодействие тел. Рассмотрим те силы, которые встречаются в механике.

Гравитационные силы. Вероятно, самой первой силой, существование которой осознал человек, являлась сила притяжения, действующая на тела со стороны Земли.

И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. Первым этот факт понял английский физик Ньютон. Анализируя законы, которым подчиняется движение планет (законы Кеплера), он пришёл к выводу, что наблюдаемые законы движения планет могут выполняться только в том случае, если между ними действует сила притяжения, прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними.

Ньютон сформулировал закон всемирного тяготения. Любые два тела притягиваются друг к другу. Сила притяжения между точечными телами направлена по прямой, их соединяющей, прямо пропорциональна массам обоих и обратно пропорциональна квадрату расстояния между ними:

Под точечными телами в данном случае понимают тела, размеры которых во много раз меньше расстояния между ними.

Силы всемирного тяготения называют гравитационными силами. Коэффициент пропорциональности G называют гравитационной постоянной. Его значение было определено экспериментально: G = 6,7 • 10¯¹¹ Н•м² / кг².

Сила тяготения действующая вблизи поверхности Земли, направлена к её центру и вычисляется по формуле:

F = m • g,

где g – ускорение свободного падения (g = 9,8 м/с²).

Роль силы тяготения в живой природе очень значительна, так как от её величины во многом зависят размеры, формы и пропорции живых существ.

Вес тела. Рассмотрим, что происходит, когда некоторый груз кладут на горизонтальную плоскость (опору). В первый момент после того, как груз опустили, он начинает двигаться вниз под действием силы тяжести (рис. 8).

Плоскость прогибается и возникает сила упругости (реакция опоры), направленная вверх. После того как сила упругости (Fу) уравновесит силу тяжести, опускание тела и прогиб опоры прекратятся.

Прогиб опоры возник под действием тела, следовательно, со стороны тела на опору действует некоторая сила (Р), которую называют весом тела (рис. 8, б). По третьему закону Ньютона вес тела равен по величине силе реакции опоры и направлен в противоположную сторону.

Р = — Fу = Fтяж.

Весом тела называют силу Р, с которой тело действует на неподвижную относительно него горизонтальную опору.

Поскольку сила тяжести (вес) приложены к опоре, она деформируется и за счёт упругости оказывает противодействие силе тяжести. Силы, развиваемые при этом со стороны опоры называются силами реакции опоры, а само явление развития противодействия — реакцией опоры. По третьему закону Ньютона сила реакции опоры равна по величине силе тяжести тела и противоположна ему по направлению.

Если человек на опоре движется с ускорением звеньев его тела, направленных от опоры, то сила реакции опоры возрастает на величину ma, где m – масса человека, а – ускорения с которыми движутся звенья его тела. Эти динамические воздействия можно фиксировать с помощью тензометрических устройств (динамограммы).

Вес не следует путать с массой тела. Масса тела характеризует его инертные свойства и не зависит ни от силы тяготения, ни от ускорения, с которым оно движется.

Вес тела характеризует силу, с которой оно действует на опору и зависит как от силы тяготения, так и от ускорения движения.

Например, на Луне вес тела примерно в 6 раз меньше, чем вес тела на Земле, Масса же в обоих случаях одинакова и определяется количеством вещества в теле.

В быту, технике, спорте вес часто указывают не в ньютонах (Н), а в килограммах силы (кгс). Переход от одной единицы к другой осуществляется по формуле: 1 кгс = 9,8 Н.

Когда опора и тело неподвижны, то масса тела равна силе тяжести этого тела. Когда же опора и тело движутся с некоторым ускорением, то в зависимости от его направления тело может испытывать или невесомость или перегрузку. Когда ускорение совпадает по направлению и равно ускорению свободного падения, вес тела будет равен нулю, поэтому возникает состояние невесомости (МКС, скоростной лифт при опускании вниз). Когда же ускорение движения опоры противоположно ускорению свободного падения, человек испытывает перегрузку (старт с поверхности Земли пилотируемого космического корабля, Скоростной лифт, поднимающийся вверх).

Силы всемирного тяготения. Закон всемирного тяготения

Вы уже знакомы с явлением всемирного тяготения из курса девятого класса. Так же мы говорили о том, что все тела, обладающие массой, притягиваются друг к другу. Из второго закона Ньютона следует, что любая равнодействующая сила равна произведению массы тела и ускорения, сообщаемого этой силой: .

Так, например, сила тяжести равна произведению массы тела и ускорения свободного падения:

Но, как мы уже выяснили, ускорение свободного падения не зависит от массы тела, из чего можно сделать вывод, что гравитационные силы сообщают ускорение, которое не зависит от массы тела!

Это поразительное свойство можно объяснить только тем, что гравитационные силы пропорциональны массе тела, на которое они действуют. А теперь, вспомним третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю, направленными по одной прямой в противоположных направлениях: .

В частности, если Земля действует на Луну с некоторой силой, то и Луна должна действовать на Землю с этой силой. Значит, гравитационная сила, возникающая между двумя телами пропорциональна массам обоих тел.

Рассмотрим теперь ускорение, с которым двигается Луна. Напомним, что любое криволинейное движение является ускоренным. Движение Луны вокруг Земли хорошо известно людям: период обращения Луны вокруг Земли составляет примерно 27,3 земных суток, а средний радиус орбиты Луны составляет 384 тыс. километров. Исходя из этого, мы можем подсчитать центростремительное ускорение Луны:

Если мы сравним теперь получившуюся величину с ускорением свободного падения на Земле, то убедимся, что ускорение Луны примерно в 3600 раз меньше, чем ускорение свободного падения на Земле:

А теперь, сравним радиус Земли с расстоянием между Землёй и Луной:

 Оказывается, что радиус Земли примерно в 60 раз меньше, чем расстояние между Землей и Луной. Заметим, что 60² — это 3600. Из этого можно заключить, что сила тяготения между двумя телами уменьшается пропорционально квадрату расстояния между этими телами.

Исходя из всего вышеперечисленного, формулировка закона всемирного тяготения такова: сила взаимного притяжения двух тел прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними.

Необходимо отметить, что если тела не являются материальными точками, то за расстояние между ними принимается расстояние между центрами тяжести этих тел. В формуле мы видим коэффициент пропорциональности, который называется гравитационной постоянной. Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массами 1 кг, если расстояние между ними составляет 1 метр.

Гравитационная постоянная является очень важной константой, поскольку именно с её помощью люди смогли вычислить массу Земли, Луны, Солнца и так далее. Но как вычислить саму гравитационную постоянную?

Впервые гравитационная постоянная была измерена Генри Кавендишем в 1798 году. С помощью крутильных весов, ему удалось определить значение гравитационной постоянной достаточно точно (оно почти совпадает с принятым сегодня значением).

Крутильные весы представляют собой следующую установку: на тонкой упругой нити подвешено лёгкое коромысло с двумя шарами на концах. Рядом закреплены два значительно более тяжёлых шара (в эксперименте Кавендиша легкие шары имели массу 775 г, а тяжёлые – 49,5 кг). В результате гравитационного взаимодействия, коромысло поворачивалось и закручивало нить. Зная упругие свойства нити, Кавендишу удалось измерить силу притяжения. Поскольку, массы шаров ему были известны, так же, как и расстояние между ними, Кавендиш смог вычислить гравитационную постоянную.

Необходимо отметить, что закон всемирного тяготения дает точный результат, в трех случаях:

1)               Если оба тела имеют форму шара и являются однородными.

2)               Если размеры тел ничтожно малы, по сравнению с расстоянием между ними.

3)               Если одно из тел обладает формой шара и его размеры многократно больше размеров второго тела любой формы.

Примеры решения задач.

Задача 1. Юпитер обладает массой и радиусом 69 911 км. Определите ускорение свободного падения на Юпитере.

Поскольку закон всемирного тяготения является одним из универсальных законов природы, он одинаково выполняется для всех тел, имеющих массу. Рассмотрим произвольное тело (масса и размеры которого ничтожно малы по сравнению с массой и размерами Юпитера).

Задача 2. Вычислите, на какой высоте над поверхностью Земли должен находиться геостационарный спутник.

На первый взгляд может показаться, что в задаче нет исходных данных. Но если мы внимательно рассмотрим ситуацию, то убедимся, что некоторые данные у нас есть. В первую очередь, — это период обращения спутника: разумеется, он должен быть равен периоду обращения Земли вокруг своей оси. И самое главное: спутник должен двигаться с постоянной скоростью, поскольку Земля тоже двигается с постоянной скоростью.

Необходимо отметить, что в задачах мы принимали орбиты планет за окружности для упрощения расчетов. В действительности, планеты Солнечной системы двигаются по эллиптическим орбитам, поэтому, когда мы говорим о расстоянии от планеты до Солнца, мы имеем ввиду средний радиус её орбиты.

Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа.  / / Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах. Поделиться:    Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах. Законы Ньютона, основные законы динамики: Первый закон Ньютона: Вариант1. Существуют такие системы отсчета, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно или покоится, если на него не действует сила, или действие внешних сил взаимно скомпенсировано. Вариант2. Существуют такие системы отсчета, называемые инерциальными, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной (в т.ч. равной 0) , если на него не действуют другие тела (или действие других тел взаимно компенсируется) Второй закон Ньютона: Сила, действующая на тело равна произведению массы тела на сообщаемое этому телу этой силой ускорение Под «силой» понимается равнодействующая всех сил: Третий закон Ньютона. Вариант 1. Тела действуют друг на друга с силами, направленными вдоль одной и той-же прямой, равными по модулю и противоположными по направлению Вариант 2. Действие равно противодействию Принцип относительности Галилея: Все механические процессы протекают одинаково во всех инерциальных системах отсчета: Закон всемирного тяготения: