Закон всемирного тяготения. Калькулятор силы притяжения, массы и расстояния онлайн.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор закона всемирного тяготения (гравитации) вычислит силу притяжения двух материальных точек, массу и расстояния между ними, а также даст подробное решение.
Единица измерения расстояния r НанометрМиллиметрСантиметрМетрДециметрКилометрДюймФутЯрдМиляМорская миляАстрономическая единицаСветовой годПарсек
Калькулятор вычисления массы материальной точки через массу второй материальной точки, силу и расстояние.
По закону всемирного тяготения масса m1 одной из материальных точек, между которыми действует сила притяжения определяется как отношение произведения силы и квадрата расстояния на произведение гравитационной постоянной и массу m2 второй материальной точки. Гравитационная постоянная G численно равна силе гравитационного притяжения между двумя телами, масса каждого тела равна 1 кг, находящимися на расстоянии 1 метра друг от друга.
Единица массы — килограмм, но также можно использовать и другие единицы, например грамм, тонна, миллиграмм и т.д.
Сила F = Ньютон (Н)Деканьютон даН (daN) × [10^1]Гектоньютон гН (hN) × [10^2]Килоньютон кН (kN) × [10^3]Меганьютон МН (MN) × [10^6]Гиганьютон ГН (GN) × [10^9]Тераньютон ТН (TN) × [10^12]Петаньютон ПН (PN) × [10^15]Эксаньютон ЭН (EN) × [10^18]Зеттаньютон ЗН (ZN) × [10^21]Иоттаньютон ИН (YN) × [10^24]Дециньютон дН (dN) × [10^-1]Сантиньютон сН (cN) × [10^-2]Миллиньютон мН (mN) × [10^-3]Микроньютон мкН (µN) × [10^-6]Наноньютон нН (nN) × [10^-9]Пиконьютон пН (pN) × [10^-12]Фемтоньютон фН (fN) × [10^-15]Аттоньютон аН (aN) × [10^-18]Зептоньютон зН (zN) × [10^-21]Иоктоньютон иН (yN) × [10^-24]
Расстояние r = НанометрМиллиметрСантиметрМетрДециметрКилометрДюймФутЯрдМиляМорская миляАстрономическая единицаСветовой годПарсек
Масса m2 = Миллиграмм мг (mg) = 10^-6 кгМикрограмм мкг (µg) = 10^-9 кгГрамм (г) = 10^-3 кгКилограмм кг (kg)Центнер ц = 10^2 кгТонна т (t) = 10^3 кг
Единица измерения массы m1 Миллиграмм мг (mg) = 10^-6 кгМикрограмм мкг (µg) = 10^-9 кгГрамм (г) = 10^-3 кгКилограмм кг (kg)Центнер ц = 10^2 кгТонна т (t) = 10^3 кг
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Работа силы тяготения. Потенциальная энергия в поле тяготения
- Подробности
- Просмотров: 638
«Физика — 10 класс»
В чём выражается гравитационное взаимодействие тел?
Как доказать наличие взаимодействия Земли и, например, учебника физики?
Как известно, сила тяжести — консервативная сила.
Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила.
Напомним, что работа консервативной силы по замкнутому контуру равна нулю.
Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения
где G — гравитационная постоянная,
М — масса Земли,
r — расстояние, на котором находится тело от центра Земли.
Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА’В’В; 3) по кривой АСВ (рис. 5.15)
1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δri = ri + 1 — ri. Среднее значение силы тяготения равно:
где r2сpi = riri + 1.
Чем меньше Δri, тем более справедливо написанное выражение r2сpi = riri + 1.
Тогда работу силы Fсpi, на малом перемещении Δri, можно записать в виде
Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:
2. При движении тела по траектории АА’В’В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА’ и В’В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31).
3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δsi равна ΔАi = FсрiΔsicosαi,..
Из рисунка видно, что Δsicosαi = — Δri, и суммарная работа опять же будет определяться по формуле (5.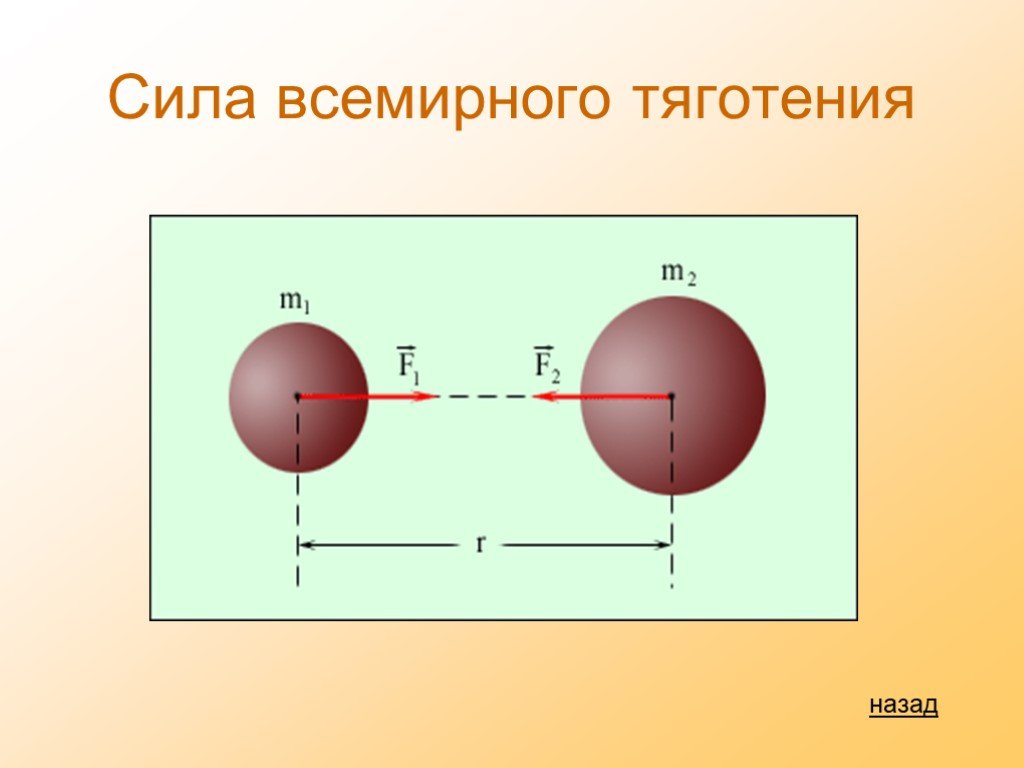
31).
Итак, можно сделать вывод, что А1 = А2 = А3, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА’В’ВА равна нулю.
Сила тяготения — консервативная сила.
Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком:
Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. ЕпВ = 0 при rВ → ∞, то следовательно,
Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:
Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид
где υ1 — скорость тела на расстоянии r1 от центра Земли, υ2 — скорость тела на расстоянии r2 от центра Земли.
Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.
Минимальную скорость, при которой тело в отсутствие сопротивления воздуха может удалиться за пределы сил земного притяжения, называют второй космической скоростью для Земли.
На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии
На поверхности Земли тело обладает и кинетической, и потенциальной энергией:
где υII — вторая космическая скорость, М3 и Я3 — соответственно масса и радиус Земли.
В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (Wп = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: Wк = 0.
Из закона сохранения энергии следует:
отсюда
Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее).
Поскольку то GM3 = gR23.
Следовательно, искомая скорость
Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в раза больше, чем первая.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Следующая страница «Примеры решения задач по теме «Закон сохранения механической энергии»»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести.
Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Самый быстрый словарь в мире | Vocabulary.com
ПЕРЕЙТИ К СОДЕРЖАНИЮ
гравитационная сила сила притяжения между всеми массами во Вселенной
гравитационное поле силовое поле, окружающее тело конечной массы
гравитационный коллапс схлопывание звезды под действием ее собственной гравитации
гравитационная масса (физика) масса тела, измеряемая его гравитационным притяжением к другим телам
гравитационные или связанные с гравитацией или вызванные ею
гравитационно по отношению к гравитации
гравитационная волна (физика) волна, которая предположительно распространяет гравитацию и движется со скоростью света
гравитационное притяжение сила притяжения между всеми массами во вселенной
гравитационная постоянная (физика) универсальная постоянная, связывающая силу с массой и расстоянием в законе тяготения Ньютона
гравитация сила притяжения между всеми массами во вселенной
задержка вращения (информатика) время, необходимое определенному блоку данных на дорожке данных для поворота вокруг головки чтения/записи
жизненная сила (биология) гипотетическая сила (не физическая или химическая), которая, по мнению Анри Бергсона, вызывает эволюцию и развитие организмов
градация происходит по ступеням
технические условия беременности
крепитационные хрипы треск, выслушиваемый при аускультации при вдохе у больных с заболеваниями органов дыхания; связанные с туберкулезом и пневмонией и застойной сердечной недостаточностью
навигационная карта карта для штурмана, показывающая преобладающие метеорологические и гидрографические и навигационные условия
Прогулочная лошадь с плантации лошадь, отличающаяся выносливостью и обученная быстрому бегу
69″>гравитационная теория (физика) теория о том, что любые две материальные частицы притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними
77″>гравитационное взаимодействие слабое взаимодействие между частицами, возникающее из-за их массы; через гравитоны
59″>обычный в соответствии с принятыми обычаями и приличиями
Концепции и приложения гравитации
Концепции и приложения гравитации
| Индекс | ||
| Гиперфизика***** Механика | Назад |
Гравитация — самая слабая из четырех фундаментальных сил, однако она является доминирующей силой во Вселенной, формирующей крупномасштабную структуру галактик, звезд и т. Это часто называют «законом всемирного тяготения», а G — постоянной всемирного тяготения. Это пример силы закона обратных квадратов. Сила всегда притягивает и действует вдоль линии, соединяющей центры масс двух масс. Силы, действующие на две массы, равны по размеру, но противоположны по направлению, подчиняясь третьему закону Ньютона. Безмассовая обменная частица, рассматриваемая как обменная сила, называется гравитоном. Согласно трактовке Эйнштейном общей теории относительности, гравитация связана с искривлением пространства-времени, а изменения в конфигурации массы могут вызывать гравитационные волны. Сила тяжести имеет ту же форму, что и закон Кулона для сил между электрическими зарядами, т. е. это сила закона обратных квадратов, которая зависит от произведения двух взаимодействующих источников. Это побудило Эйнштейна начать с электромагнитной силы и гравитации как первой попытки продемонстрировать объединение фундаментальных сил. | Index Gravity Concepts | ||
| Назад |
д. Гравитационная сила между двумя массами m 1 и m 2 дана соотношением:
Оказывается, это было неправильное начало, и что гравитация будет последней из сил, которая объединится с тремя другими силами. Электрослабое объединение (объединение электромагнитного и слабого взаимодействий) было продемонстрировано в 1983, результат, которого нельзя было ожидать во времена поисков Эйнштейна. Теперь оказывается, что общая форма сил гравитации и электромагнитных сил возникает из-за того, что каждая из них включает обменную частицу с нулевой массой, а не из-за присущей им симметрии, которая позволила бы их легко объединить.Распространенные заблуждения об оружии:Выпавшая пуля упадет на землю раньше пули, выпущенной из ружья.Как показано на иллюстрации горизонтального запуска, сила тяжести действует на обе пули одинаково, придавая им одинаковое нисходящее ускорение и заставляя их ударяться о землю в одно и то же время, если пуля выпущена горизонтально над ровной поверхностью. Пули, выпущенные из мощных винтовок, падают всего на несколько дюймов на расстоянии сотен ярдов.Выпущенная с удвоенной скоростью звука, пуля упадет более чем на 3 дюйма на 100 ярдах, а на дальности 300 ярдов она упадет примерно на 30 дюймов. Вставьте цифры в расчет падения пули, чтобы убедиться в этом. Производители боеприпасов вносят свой вклад в это заблуждение, заявляя падение своих снарядов как просто дополнительное падение, вызванное сопротивлением трения, по сравнению с идеальным снарядом без трения. | Индекс Концепции траекторий | ||
| Назад |
Если пренебречь трением воздуха, то падение пули, выпущенной горизонтально, можно рассматривать как обычную горизонтальную траекторию. Трение воздуха значительное, так что это идеализация.  |
