Урок физики № 23 в 7 классе по теме «Сила. Явление тяготения. Сила тяжести»
Цель урока: формирование первоначальных представлений о понятии «сила» как мере взаимодействия тел. Выявление природы силы тяжести.
Планируемые результаты обучения
Метапредметные: овладеть регулятивными универсальными учебными действиями на примерах гипотез о причинах изменения скорости тел (сжатой пружины, скрепки при поднесении к ней магнита, мячика) и уметь выполнять их экспериментальную проверку, применять эвристические методы при решении вопроса о причинах изменения скорости тела.
Личностные: сформировать познавательный интерес к силам в природе, творческие способности и практические умения; самостоятельно приобретать
знания о силе, деформации, законе всемирного тяготения, ценностное отношение друг к другу, к учителю, к результатам обучения; использовать экспериментальный метод исследования при изучении силы, деформации, законе всемирного тяготения; уметь самостоятельно принимать решения, обосновывать и оценивать результаты своих действий, развивать творческую инициативу.
Общие предметные: знать природу явления тяготения и понимать смысл закона всемирного тяготения; уметь пользоваться методом эмпирического исследования явления тяготения; проводить наблюдение, обнаруживать зависимость силы тяжести от массы, изменения скорости тела от приложенной силы, силы притяжения между телами от массы этих тел, делать выводы; составлять сравнительную таблицу; анализировать опыты по столкновению шаров, сжатию пружины, описывать явление всемирного тяготения.
Частные предметные: понимать и объяснять явление тяготения, смысл закона всемирного тяготения, приводить примеры действия силы, изображать силу графически и точку ее приложения, учитывать знания о всемирном тяготении в повседневной жизни.
Тип урока: урок изучения нового материала и формирования знаний, умений, навыков, возможности их применения на практике.
Формы работы учащихся: индивидуальная, фронтальная, работа в паре.
Методы обучения: проблемно-поисковый (исследовательский), наглядно-словесный, репродуктивный.
Оборудование: брусок, опора, 2-3 шара разного объема и массы, резиновая пластина, мешочки с песком, картонная полоска, шарик подвешенный на нити, трубка Ньютона.
презентация к уроку
Демонстрации. Взаимодействие шаров при столкновении. Сжатие упругого тела, действие мешочка с песком на горизонтальную опору.
Изменение скорости движения стального тела под действием магнита.
Падение шарика, подвешенного на нити. Свободное падение тел в трубке Ньютона.
Ход урока.
Организационный момент.
Работа над ошибками.
Анализ контрольной работы, разобрать типичные ошибки. Если результаты работы слабые, следует уделить внимание решению задач, вызвавших наибольшие затруднения.
Мотивация деятельности.
Слайд 1
Предлагаю обсудить притчу «Груз прошлого» и назвать тему и цель нашего урока.
Жила на свете птица вольная. Парила она в небесах, ловила мошек на обед, купалась в струйках летнего дождя в свое удовольствие. В общем, была как все птицы. Но была у нее привычка: каждый раз, когда в ее жизни происходило событие, хорошее ли, плохое, птица подбирала с земли камешек на память. И каждый день она перебирала свои камешки, весело смеясь радостным событиям прошлого и плача о грустном.
Камешки птица всегда носила с собой, летела ли она в небе, шагала ли по земле, и никогда про них не забывала.
Шли годы, и камешков у птицы вольной становилось все больше, но она все равно каждый день перебирала их, вспоминая о прошедших днях. Летать птице вольной становилось все тяжелее, и в один прекрасный день она не смогла подняться в воздух.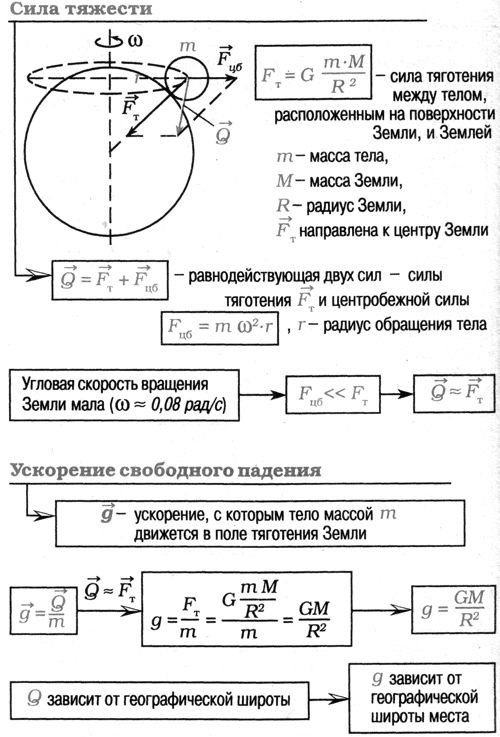 Вскоре птица, некогда бывшая вольной, даже ходить по земле не могла, не в силах сдвинуть с места свой груз. Не могла она больше ловить мошек: лишь редкий дождик давал уставшей птице необходимую влагу. Но птица мужественно терпела все невзгоды, охраняя свои драгоценные воспоминания.
Вскоре птица, некогда бывшая вольной, даже ходить по земле не могла, не в силах сдвинуть с места свой груз. Не могла она больше ловить мошек: лишь редкий дождик давал уставшей птице необходимую влагу. Но птица мужественно терпела все невзгоды, охраняя свои драгоценные воспоминания.
Прошло совсем немного времени, птица погибла от голода и жажды. И долгое время о ней напоминала лишь жалкая кучка никчемных камешков.
Измени свое отношение к прошлому: проговори застрявшие где-то слова; шагни в своих мыслях, куда не решился когда-то шагнуть, — и ты увидишь, как твоя Вселенная станет чуть ярче и добрее.
Учитель: Ребята, хочу вам напомнить, что физика неотделима от эксперимента. И так перед вами опыты. На основе показанных опытов скажите, о чем мы сегодня будем говорить на уроке.
Демонстрация опытов.
1) Неподвижный брусок. Если на неподвижный брусок, лежащий на опоре, не действуют другие тела, кроме Земли и опоры, он не изменяет своего положжения.
2) Взаимодействие шаров при столкновении. Если скорость тела изменяется, мы всегда обнаруживаем действие на него другого тела.
Ученики: о взаимодействии тел, о притяжении, о силе взаимодействия.
Учитель: Верно. Мы сегодня будем изучать силу.
Ученики формулируют тему и цели урока.
Слайд 2
Записываем тему нашего урока в тетрадь «Сила. Явления тяготения.
Сила тяжести».
Учитель. И что же нам надо узнать о силе? По какой причине тела изменяют свою скорость? После обсуждения высказанных предположений учащиеся приходят к выводу: «Проведенные опыты свидетельствуют, что причиной изменения скорости тела является действие других тел»
Слайд 3
Изучение нового материала.
Учитель. Понятие силы первоначально возникло из ощущения мышечного усилия. Чтобы поднять груз, бросить копьё, необходимо некоторое напряжение мышц, причем в различных случаях разное. Во всех случаях идет речь о взаимодействии одного тела на другое.
Чтобы поднять груз, бросить копьё, необходимо некоторое напряжение мышц, причем в различных случаях разное. Во всех случаях идет речь о взаимодействии одного тела на другое.
Учитель.
Что вы видите на рисунке? Что происходит с вагонеткой? (Она меняет свою скорость).
— Что является причиной изменения скорости вагонетки? (Действие человека).
Вывод: во всех примерах скорость тела меняется при взаимодействии его с другими телами. Часто не указывают, какое тело и как действует, а говорят, приложена сила.
Сделаем запись в тетради:
Мерой взаимодействия тел между собой является векторная величинв, называемвя силой.
Под действием другого тела может меняться скорость не всего тела, а отдельных его частей. Если руками сжать резиновый мячик, он изменит свою форму.
Демонстрация опыта.
1. Растягивание пружины. Вопрос: Что произошло с пружиной? Изменило тело скорость? Иногда под действием силы меняется скорость не всего тела, а отдельных его частей. А что же с ним произошло? (Оно изменило форму, размер).
Учитель. В таких случаях говорят, что тело дело деформируется. Деформация – это любое изменение формы и размера тела.
2. Опыт с мешочком песка.
У вас на столе полоска картона и мешочек с песком. Установите эту полоску на двух книгах, как лавочку. Поставьте на картон мешочек. Что вы увидели? (изменилась форма картона). А как называется изменение формы тела? (Деформация).
Слайд 4
Учитель. Запишите ОК. Деформация — это изменение формы и размера тела.
Примеры деформации вначале приводит учитель, а затем учащиеся, используя свой жизненный опыт.
Учитель. Сила — это количественная мера взаимодействия тел между собой.
Сила — это количественная мера взаимодействия тел между собой.
Сила — векторная величина, а это значит, что она характеризуется числовым значением и направлением. Под действием силы тело изменяет свою скорость, и наоборот, если тело изменило свою скорость, значит, на тело подействовало другое тело, т. е. сила.
Вопрос: Отчего зависит сила? От модуля, от направления, и точки приложения. Сила разная по численному значению, разная по направлению, и по точке приложения.
Итак, вывод: Сила – мера взаимодействия тел, физическая величина. А раз это МЕРА воздействия, то значит, её можно измерить.
Слайд 5
Измеряем массу в килограммах,
Время точно уж в секундах,
Ну а силу круто так
Измеряем в (Ньютонах).
Единица измерения силы: Н. Обозначение F. Сила – векторная величина.
Обозначение F. Сила – векторная величина.
Сила в 1 Н – такая сила, которая за 1 с изменяет скорость тела массой 1 кг на 1 м/с.
Кратными и дольными единицами силы являются:
1кН=1000Н
1мН=0,001Н
1МН=1000000Н
Следует обратить внимание учащихся на точку приложения силы.
Сила приложена к определенной точке тела, что всегда указывают на чертежах.
Слайд 6
Демонстрация опытов, показывающие, что все тела, подброшенные вверх, возвращаются в исходную точку (падение шарика, тела, брошенного горизонтально). Потом вместе с учащимися выясняем, что причиной изменения скорости тел является их притяжение Землей, акцентируя внимание на том, что Земля действует на все тела, находящиеся на ее поверхности и вблизи нее.
Изучение нового материала.
Луна движется вокруг Земли. Почему она не уходит прочь от нашей планеты? Ответ дает нам закон всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорционально произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.
Все тела притягиваются друг к другу с силой, прямо пропорционально произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.
Этот закон открыл великий английский ученый Исаак Ньютон.
Слайд 7
Дж. Байрон «Дон Жуан»
«Так человека яблоко сгубило,
Но яблоко его же и спасло, —
Ведь Ньютона открытие разбило
Неведенья мучительное зло.
Дорогу к новым звёздам проложило
И новый выход страждущим дало.
Уж скоро мы, природы властелины,
И на Луну пошлём свои машины»
Проблемный вопрос «Скажите, ребята, а где на Земле легче всего живётся?»
Учитель. Эта задача похожа на загадку или на задачу-шутку типа: «Почему птица летает?» (По чему? – по воздуху). Но наш вопрос не совсем такого рода. Если хорошенько подумать, то на него можно дать разумный, вполне обоснованный ответ. Какой?
Но наш вопрос не совсем такого рода. Если хорошенько подумать, то на него можно дать разумный, вполне обоснованный ответ. Какой?
Исаак Ньютон говорил, что «примеры при обучении полезнее правил». Давайте рассмотрим несколько примеров.
Выпустим камень из рук. Что вы видите? Куда падает груз? А почему? (Притяжение земли)
Перережу нить, на которой висит груз. Куда падает груз? Почему? (Притяжение земли)
Почему прыгнувший вверх человек вскоре снова оказывается внизу? (Притяжение земли) У всех явлений одна и та же причина – притяжение Земли.
Слайд 8
Учитель. Ребята, я сейчас вам прочитаю стихи, а вы выполните упражнения. У нас физминутка!
Вызывает удивление
Это сила притяженья! (руки вверх)
Как не прыгал, не старался,
Всё на землю возвращался. (прыжки)
Несмотря на малый вес
я на дерево залез, (подтянуться)
Но сучок вдруг обломился,
я в полете очутился. (покачаться)
(покачаться)
Масса есть и ускоренье
Хлоп! земное притяженье (присесть)
Физику я испытал,
Когда с дерева упал. (сесть на место)
Учитель. С понятием силы тяжести и явлением тяготения каждый знаком с раннего детства. Примеры: падение капель жидкости, падение мяча, подброшенного вверх, падение шарика после перерезания нити. Все эти тела падают вниз под действием силы тяжести. Приведите свои примеры.
Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов расположены немного ближе к центру Земли, и сила тяжести на полюсах больше, чем на экваторе.
Вопрос: Так, где же человеку легче живется? На экваторе, сила тяжести там меньше, так как ближе к центру Земли.
Слайд 9
Сила, с которой Земля притягивает к себе тело, называется силой тяжести. Она обозначается как Fт.
Если сопротивление воздуха мало, то движение тел при падении на Землю, называется свободным падением.
Таким образом, если тело движется только под действием силы тяжести – оно свободно падает.
Слайд 10
Измерения показали, что у поверхности Земли свободное падающие тело увеличивает за 1 с скорость на 9,8 м/с.
Это величина называется ускорением свободного падения.
По мере удаления тела от Земли сила тяготения уменьшается.
Закрепление пройденного материала. Решение задач.
Тест «Да-нет» ” Учитель читает вопросы, а ученик отвечает “Верно ли утверждение, определение, свойство?
1. Сила определяет меру действия одного тела на другое. (Да.)
2. Сила измеряется в Джоулях. (Нет.)
3. Сила, с которой Земля притягивает к себе все тела, называется силой тяжести. (Да.)
4. Чем больше массе тела, тем меньше его сила. (Нет.)
5. Сила тяжести всегда направлена вертикально вниз. (Да.)
Рефлексия
Слайд 10
Подведение итогов урока.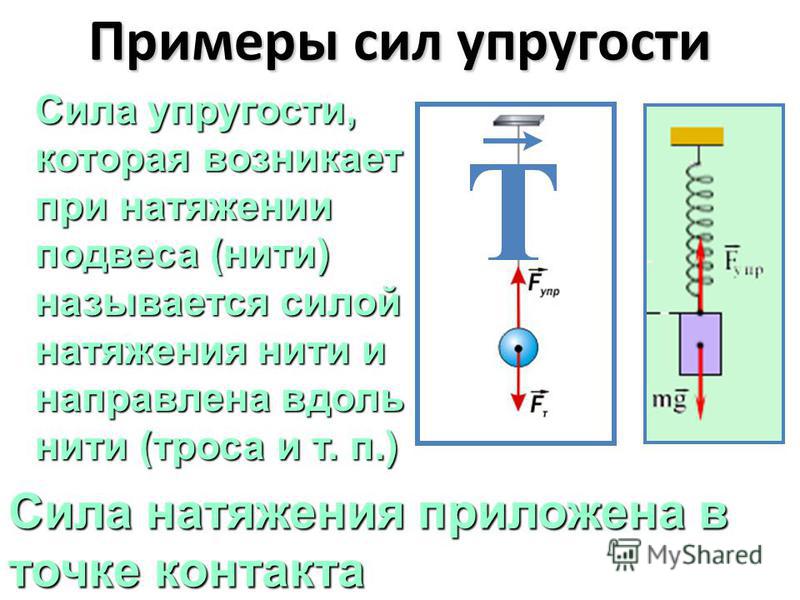 Объявление домашнего задания.
Объявление домашнего задания.
1. §24-25, упр.9.
2. ЗЛ № 285-290
3. Творческое задание:
1) Составить кроссворд, используя слова: притяжение, сила, масса, невесомость, скорость.
2) Придумать сказку о том, что было бы, если бы исчезла сила тяжести.
Список литературы:
Волков В.А., Полянский С.Е. Универсальные поурочные разработки по физике 7 класс. – М.:ВАКО, 2012
Куцакова Н. М. . Конспект открытого урока физики, проведенного 2 декабря 2013 года на краевом семинаре учителей физики в 7 классе МБОУ СОШ №14 с.Курсавка Андроповского района Ставропольского края учителем высшей категории / http://www.zavuch.info/methodlib/401/104682/
Палаева Н.П. Урок в 7 классе «Сила. Явление тяготения. Сила тяжести»/ https://nsportal.ru/shkola/fizika/library/2019/11/06/urok-v-7-klasse-sila-yavlenie-tyagoteniya-sila-tyazhesti-0
Притча «Груз прошлого» / https://poleznosti. mirtesen.ru/blog/43901640051/LISHNIY-GRUZ.-TRI-PRITCHI-O-ZHIZNI.#:~:text=Тут%20он%20увидел%20мужчину%2C%20который,были%20счастливыми%2C%20-%20ответил%20бедолага
mirtesen.ru/blog/43901640051/LISHNIY-GRUZ.-TRI-PRITCHI-O-ZHIZNI.#:~:text=Тут%20он%20увидел%20мужчину%2C%20который,были%20счастливыми%2C%20-%20ответил%20бедолага
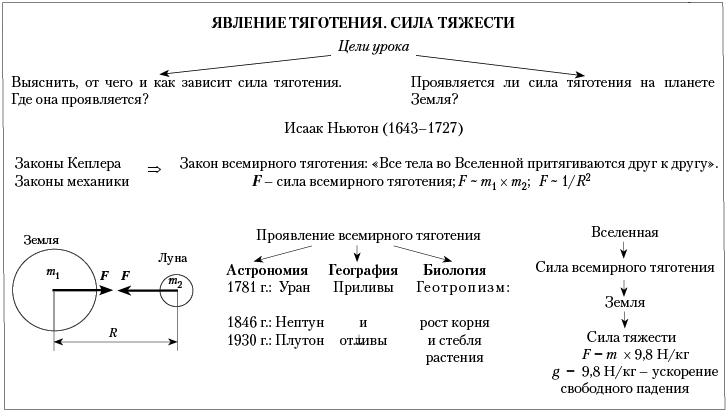
Закон всемирного тяготения
Абсолютно между всеми телами во Вселенной существуют силы притяжения или, другими словами, силы всемирного тяготения.
Тяготение, гравитация, гравитационное взаимодействие, универсальное взаимодействие между любыми видами материи. Если это взаимодействие относительно слабое и тела движутся медленно (по сравнению со скоростью света), то справедлив законвсемирноготяготения Ньютона.
Классическаятеориятяготения Ньютона (закон всемирного тяготения Ньютона) – один из универсальных законов природы, описывающий гравитационное взаимодействие в рамках классической механики.Он гласит:
| Рис. 31. |
каждые две материальные частицы притягивают друг друга с силой , прямо пропорциональной их массам и и обратно пропорциональной квадрату расстояния
 31):
31):
Здесь –гравитационная постоянная, сила направлена вдоль прямой, соединяющей эти частицы. Под «частицами» здесь подразумеваются тела, размеры которых пренебрежимо малы по сравнению с расстояниями между ними, т. е. материальные точки.
Физический смысл гравитационной постоянной: гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.
2). Сила тяжести
Сила, с которой Земля притягивает к себе тело, называется
В широком смысле: сила тяжести , действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли и центробежной силы инерции , учитывающей эффект суточного вращения Земли. Направление силы тяжести –вертикаль в данной точке земной поверхности (рис. 32). Аналогично определяется сила тяжести на любом небесном теле. Значение силы тяжести зависит от географической широты положения тела; например, на Земле сила
Значение силы тяжести зависит от географической широты положения тела; например, на Земле сила
| Рис. 32. |
тяжести на полюсе и на экваторе отличаются на 0,5% (на Луне значения силы тяжести примерно в 6 раз меньше, чем на Земле).
В узком смысле: силой тяжести называется сила , с которой Земля притягивает все находящиеся вблизи её поверхности тела:
,
где – ускорение свободного падения.
| Рис. 33. |
Сила тяжести всегда направлена вертикально вниз. Точка её приложения находится в центре тяжести тела (рис. 33).
3). Сила реакции опоры
Представим тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол, т.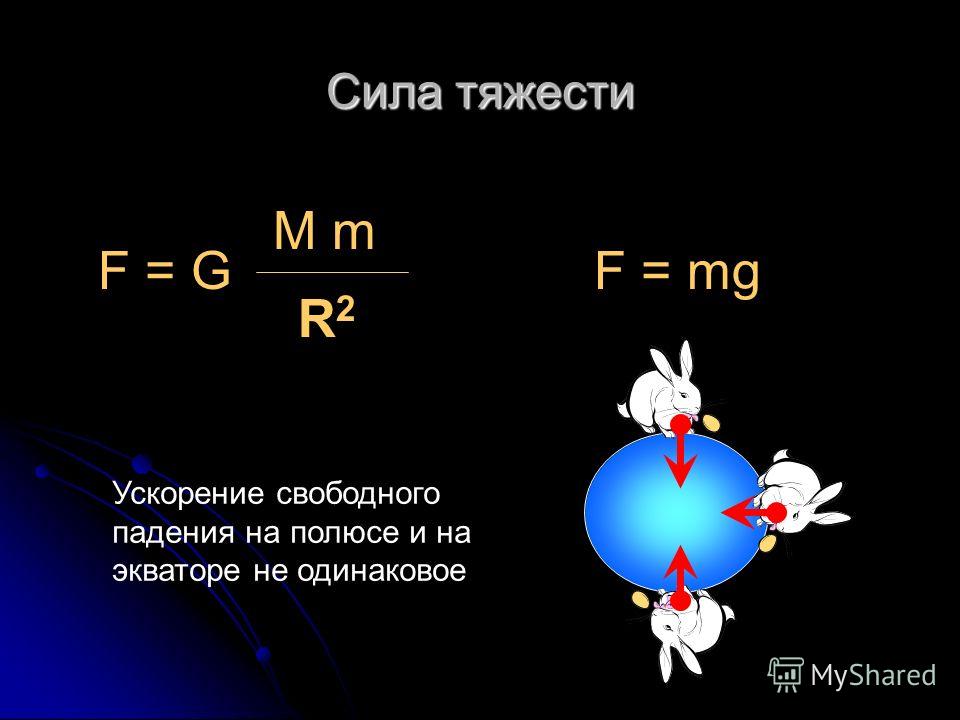
Природа этой силы объясняется на молекулярном уровне. Абсолютно любое тело на микроуровне деформирует опору, поэтому возникает реакция опоры.Специальной формулы для нахождения этой силы нет. Обозначают ее буквой но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как .Сила приложена в точке соприкосновения предмета с опорой, направлена перпендикулярно опоре
| Рис. 34. |
4). Сила трения
Тре́ние– процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. По–другому называется фрикционным взаимодействием (англ. friction). Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Сила трения– это сила, возникающая в месте соприкосновения тел и препятствующая их относительному движению.
1) Шероховатость соприкасающихся поверхностей.
2) Взаимное притяжение молекул этих поверхностей.
Принято, что сила трения прямо пропорциональна силе нормальной реакции т. е. зависит от того, насколько сильно тела прижаты друг к другу и от их материала.
Виды трения
При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:
· Трение скольжения– сила, возникающая при поступательном перемещении одного из контактирующих взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
· Трение качения – момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
· Трение покоя – сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
Рассмотрим силу трения скольжения (рис. 35).
| Рис. 35. |
Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения: , где – сила реакции опоры, a – коэффициент трения скольжения. Коэффициент зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения скольжения определяется опытным путем.
Сила трения скольжения всегда направлена противоположно движению тела. При изменении направления скорости изменяется и направление силы трения.
Сила трения начинает действовать на тело, когда его пытаются сдвинуть с места. Если внешняя сила меньше произведения то тело не будет сдвигаться – началу движения, как принято говорить, мешает сила трения покоя. Тело начнет движение только тогда, когда внешняя сила превысит максимальное значение, которое может иметь сила трения покоя
Если внешняя сила меньше произведения то тело не будет сдвигаться – началу движения, как принято говорить, мешает сила трения покоя. Тело начнет движение только тогда, когда внешняя сила превысит максимальное значение, которое может иметь сила трения покоя
Трение покоя– сила трения, препятствующая возникновению движению одного тела по поверхности другого.
В некоторых случаях трение полезно (без трения невозможно было бы ходить по земле человеку, животным, двигаться автомобилям, поездам и т.д.), в таких случаях трение усиливают. Но в других случаях трение вредно. Например, из-за него изнашиваются трущиеся детали механизмов, расходуется лишнее горючее на транспорте и т.д. Тогда с трением борются, применяя смазку («жидкостную или воздушную подушку») или заменяя скольжение на качение (поскольку
Силы трения, в отличие от гравитационных сил и сил упругости, не зависят от координат относительного расположения тел, они могут зависеть от скорости относительного движения соприкасающихся тел.
Примеры.
1). В рассматриваемом на рис.35 случае: , т.е. .
2). Рассмотрим случай тела, покоящегося на наклонной плоскости (рис.36). В этом случае: , тогда .
Рис. 36.
5). Сила упругости
Сила упругости– это сила ,возникающая в результате деформации тела и стремящаяся восстановить прежние размеры и форму тела.
Связь между силой упругости и упругой деформацией тела была установлена английским физиком Гуком.
Закон Гука
Закон Гука для одностороннего растяжения (сжатия) формулируют так:
сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела:
Рис.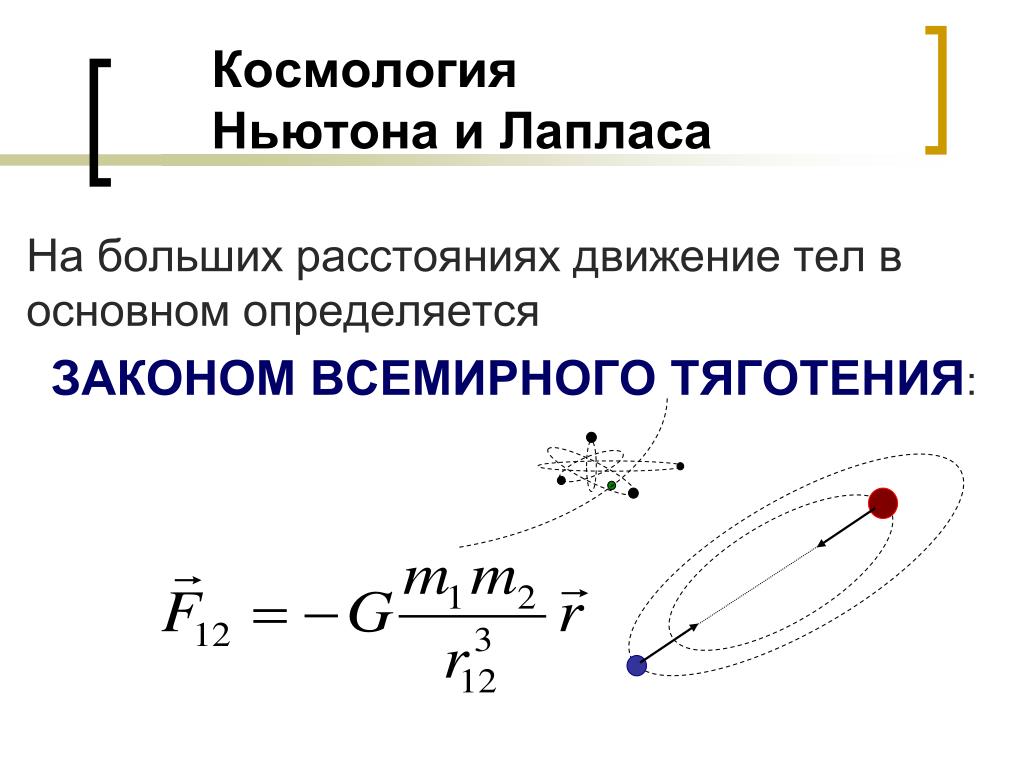 37. 37.
|
,
Сила упругости направлена противоположно деформации.
Жесткость пружинычисленно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
При последовательном соединении, например, двух пружин жесткость рассчитывается по формуле:
.
При параллельном соединении пружин их жесткость равна:
.
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Дата добавления: 2016-09-26; просмотров: 2478; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
1.2.6 Закон всемирного тяготения. Сила тяжести.
 Зависимость силы тяжести от высоты над поверхностью планеты
Зависимость силы тяжести от высоты над поверхностью планетыВидеоурок: Закон всемирного тяготения
Лекция: Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты
Закон гравитационного взаимодействия
До некоторого времени Ньютон не задумывался о том, что его предположения справедливы для всех тех, находящихся во Вселенной. Спустя некоторое время им были изучены законы Кеплера, а также законы, которых придерживаются тела, что свободно падают на поверхность Земли. Данные мысли не были зафиксированы на бумаге, а только остались заметки про яблоко, упавшее на Землю, а также о Луне, которая вращается вокруг планеты. Он считал, что
все тела рано или поздно упадут на Землю;
они падают с одинаковым ускорением;
Луна двигается по окружности с постоянным периодом;
размеры Луны практически в 60 раз меньше, чем у Земли.

В результате всего это был сделан вывод, что все тела притягиваются друг к другу. При этом, чем больше масса тела, тем с большей силой оно притягивает к себе окружающие объекты.
В результате этого был открыт закон всемирного притяжения:
Любые материальные точки притягиваются друг к другу с силой, увеличивающейся в зависимости от роста их масс, но при этом уменьшается в квадратной пропорциональности в зависимости от расстояния между этими телами.
F – сила гравитационного притяжения
m1, m2 – массы взаимодействующих тел, кг
r – расстояние между телами (центрами масс тел), м
G – коэффициент (гравитационная постоянная) ≈ 6,67*10-11 Нм2/кг2
Данный закон справедлив в том случае, когда тела можно принять за материальные точки, а вся их масса сконцентрирована в центре.
Коэффициент пропорциональности из закона всемирного тяготения был определен экспериментальным путем ученым Г. Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:
Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:
Взаимное притяжение тел объясняется гравитационным полем, подобным электрическому, которое находится вокруг всех тел.
Сила тяжести
Вокруг Земли также существует такое поле, его еще называют полем земного притяжения. Все тела, что находятся в местах его действия, притягиваются к Земле.
Сила тяжести — это равнодействующая гравитационной силы, а также центростремительной силы, направленной по оси вращения.
Именно с такой силой все планеты притягивают к себе другие тела.
Характеристика силы тяжести:
1. Точка приложения: центр масс тела.
2. Направление: к центру Земли.
3. Модуль силы определяется по формуле:
Fтяж = gmg = 9,8 м/с2 — ускорение свободного падения
m — масса тела
Так как сила тяжести — это частный случай закона гравитационного взаимодействия, то ускорение свободного падения определяется по формуле:
g — ускорение свободного падения, м/с2
G — гравитационная постоянная, Нм2/кг2
M3 — масса Земли, кг
R3 — радиус Земли
Из этого можно сделать вывод:
чем больше масса космического объекта, тем больше ускорение свободного падения;
чем больше расстояние до космического объекта, тем меньше ускорение свободного падения.

Более того, на данную величину влияет и период вращения планеты вокруг оси.
Если тело находится на некотором расстоянии от поверхности Земли, то определить ускорение можно по следующей формуле:
Если же с увеличением высоты уменьшается ускорение, то можно сделать вывод, что сила тяжести так же уменьшается.
- Вконтакте
- Сайт
Сила тяжести | Образовательная социальная сеть
Урок – презентация
на тему: « Явление тяготения. Сила тяжести»
Сила тяжести»
Цель урока: ученики должны усвоить, что такое явление тяготения и сила тяжести на уровне применения знаний в знакомой ситуации.
Задачи урока:
Образовательные:
- показать наличие тяготения между всеми телами;
- раскрыть понятие «сила тяжести»;
- показать зависимость силы тяжести от массы тела.
Воспитательные:
- показать значение явления тяготения и силы тяжести в окружающем нас мире.
Развитие мышления:
- работать над формированием умений сравнивать явления, делать выводы из наблюдения.
Основные этапы урока:
- Организационный момент.
- Проверка домашнего задания:
Слайд 1. Явление тяготения. Сила тяжести.
Слайд 4. В каких случаях говорят, что на тело действует сила?
Слайд 5. В результате чего меняется скорость вагонетки?
Слайд 6. В результате чего изменяется направление движения летящего мячика?
Что является причиной изменения формы (деформации) ракетки?
Слайд 7. Что такое сила?
Что такое сила?
Сила является мерой взаимодействия тел.
Слайд 8. От чего зависит результат действия силы на тело?
Результат действия силы на тело зависит от её модуля, направления и точки приложения.
Слайд 9. Как изображают силу на чертеже?
Чему равна сила, действующая на тележку?
III. Изучение нового материала.
Тема нашего урока «Явление тяготения. Сила тяжести».
Сегодня на уроке мы рассмотрим очень интересное явление природы – явление тяготения и силу тяжести.
Слайд 10. Почему тела падают?
Демонстрация фильма о падении шарика.
Слайд 11. В чём причина наблюдаемых явлений?
Если бросить мяч в горизонтальном направлении, то он не летит прямолинейно. Его траектория прямая линия. ПОЧЕМУ?
Слайд 12. В чём причина наблюдаемых явлений?
Искусственный спутник, запущенный с Земли, также не летит по прямой, а движется вокруг Земли. ПОЧЕМУ?
Слайд 13. В чём причина наблюдаемых явлений?
Водопад.
Слайд 14. В чём причина наблюдаемых явлений?
В чём причина наблюдаемых явлений?
Метеорный дождь.
Слайд 15. В чём причина наблюдаемых явлений?
Приливы и отливы.
Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров.
Слайд 16. В чём причина наблюдаемых явлений?
Земля и другие планеты движутся вокруг Солнца, притягиваясь к нему и друг к другу.
Слайд 17. В чём причина наблюдаемых явлений?
Полёт кометы.
Кометы – это часть Солнечной системы. Кометы движутся по вытянутым орбитам, то приближаясь к Солнцу, то удаляясь от него.
Слайд 18. Подведём итоги:
- Земля притягивает к себе все тела: дома, людей, Луну, Солнце, воду в морях и океанах и т. д.
- В свою очередь и Земля притягивается к этим телам.
- Притяжение существует не только между Землёй и телами, находящимися на ней.
- Все тела притягиваются друг к другу.
Слайд 19. Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.
Долгое время люди верили в религиозное учение о «тверди небесной», на которую бог будто бы прикрепил небесные светила. Луна и звёзды, якобы потому, и не падают на землю, что прикреплены к чему-то твёрдому наверху. Наука доказала, что никакой «небесной тверди» на самом деле нет, что Луна движется вокруг Земли, а Земля движется вокруг Солнца, следовательно и сама является небесным телом.
Вопрос о том, на чём «держатся» небесные светила, был заменён другим: почему же Луна обращается вокруг Земли, а не уходит от неё прочь? Почему Земля обращается вокруг Солнца? Что держит Луну около Земли, а Землю около Солнца?
Ответ на эти вопросы был дан после открытия одного из основных законов природы: закона всемирного тяготения.
Разгадав кроссворд, мы узнаем имя учёного, который открыл этот закон
Кроссворд:
Сила есть физическая… (величина).
Если к телу приложена сила, то тело изменяет свою… (скорость).
Основной источник получения информации в физике (наблюдение).
Сила, как и скорость является… величиной (векторной).
Изгиб, кручение, сжатие, растяжение – это … (деформация).
Сила, подобно скорости, имеет … (направление).
Ребята! Какое слово у нас получилось? Правильно, Ньютон!
Слайд 20.
Великий английский физик и математик. Исаак Ньютон открыл закон всемирного тяготения. Он разработал теорию движения небесных тел, объяснил особенности движения Луны, дал объяснение приливов и отливов. Открыл он этот закон в возрасте 23 года, но 9 лет не публиковал, т.к. в то время расстояние между Луной и Землей было измерено не точно и только после уточнения этого расстояния в 1667 году закон был опубликован.
Открытие закона было великим триумфом науки. Казалось, найдена сила, которая движет мирами.
Слайд 21. Закон всемирного тяготения.
Согласно этому закону, сила притяжения между телами тем больше, чем больше массы этих тел. Силы притяжения между телами уменьшаются, если увеличивается расстояние между ними.
Слайд 22. Динамическая пауза.
Мы в ракету дружно сели, (дети приседают)
В космос полететь хотели, (поднимаются, руки вверх)
С притяжением Земли
Мы бороться не смогли.
Шлём вам всем большой привет, (помахать рукой)
Опоздавшим места нет (быстро сесть за столы).
Слайд 23. Сила притяжения к Земле.
Для нас важное значение имеет сила притяжения тел к планете, на которой мы живём, т. е. – к Земле.
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
Движение парашютиста объясняется действием на него силы тяжести.
Слайд 24. Сила тяжести – сила, действующая на все тела со стороны Земли.
Обозначается сила тяжести – Fтяж.
Точка приложения силы тяжести – центр тела.
В каждой точке вокруг Земли сила тяжести направлена вниз, т. е. к центру планеты.
Fтяж
Демонстрация опыта: на пружину подвесили тело одной массы, а затем тело другой массы. Пружина растягивалась по-разному.
Что из этого следует?
Что сила тяжести зависит от массы тела. Во сколько раз масса одного тела, больше массы другого, во столько же раз и сила тяжести его будет больше другого.
Сила тяжести пропорциональна массе тела.
Слайд 25. Коэффициент пропорциональности между силой тяжести и массой тела.
Слайд 26. Сила тяжести на земной поверхности разная.
Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с этим сила тяжести на полюсе немного больше, чем на экваторе или на других широтах.
Слайд 27. Где сила тяжести больше: на вершине горы или у её подножия?
Сила тяжести на вершине горы несколько меньше, чем у её подножия.
IV. Закрепление:
Слайд 28. Тест:
- Что нужно сделать, чтобы увеличить силу тяготения между телами? Выберите верное утверждение.
- Сблизить оба тела
- Удалить оба тела друг от друга
- Уменьшить массы этих тел
Слайд 29. Выберите верные утверждения:
Выберите верные утверждения:
- сила тяжести увеличивается с увеличением массы тела
- сила тяжести действует на любое тело
- сила тяжести всегда направлена вниз
- сила тяжести на Земле везде одинакова
- сила тяжести уменьшается при удалении от Земли в космос
- сила тяжести измеряется в килограммах
- сила тяжести тела увеличивается, если его сжать
- сила тяжести не действует на воздушный шарик
Слайд 30. Подумайте:
- На какой из двух одинаковых по размерам брусков действует большая сила тяжести?
- Парафиновый
- Алюминиевый
- На оба бруска действует одинаковая сила тяжести
Слайд 31. Подумайте:
- На столе лежит шарик массой 400 г. Какая сила тяжести на него действует?
4000 Н
40 Н
4 Н
Слайд 32. Подумайте:
- Сила тяжести, действующая на люстру, равна 120 Н. Какова масса люстры?
12 кг
120 кг
1200 кг
Слайд 33. Подумайте:
Подумайте:
Барон Мюнхаузен, герой известной повести Р. Э. Распе, привязав конец верёвки к Луне, спускается по ней на Землю.
В чём главная физическая несуразность такого передвижения?
Герой рассказа никак не мог бы скользить по верёвке к Земле, этому препятствовала бы сила притяжения к Луне.
Слайд 34. Подумайте:
На какой шар действует большая сила тяжести?
Слайд 35. Подумайте:
Почему подниматься по лестнице значительно тяжелее, чем спускаться?
Слайд 36. Итоги урока:
● Между всеми телами Вселенной существует всемирное тяготение.
● Сила притяжения к Земле называется силой тяжести.
● Сила тяжести обозначается – Fтяж.
● Сила тяжести всегда приложена к центру тела и направлена вертикально вниз.
● Сила тяжести на полюсах Земли несколько больше силы тяжести на экваторе и на других широтах.
● Сила тяжести пропорциональна массе тела.
V. Домашнее задание: § 24, вопросы; № 291-293 (Л.), приготовить историческую справку об Исааке Ньютоне
Билет 13
1. Закон всемирного тяготения. Все тела
взаимодействуют друг с другом. Это
предположение зародилось у Ньютона в
1667 году. Ньютон понимал, что для того,
чтобы Луна вращалась вокруг Земли, а
Земля и другие планеты вокруг Солнца,
должна существовать сила, удерживающая
их на круговой орбите. Он предположил,
что сила тяжести, действующая на все
тела на Земле и сила, удерживающая
планеты на их круговых орбитах, есть
одна и та же сила. Эта сила получила
название сила всемирного тяготения или
гравитационная сила. Эта сила является
силой притяжения и действует между
всеми телами. Ньютон сформулировал закон всемирного тяготения:
две материальные точки притягиваются
друг к другу с силой прямо пропорциональной
произведению их масс и обратно
пропорциональной квадрату расстояния
между ними.
Закон всемирного тяготения. Все тела
взаимодействуют друг с другом. Это
предположение зародилось у Ньютона в
1667 году. Ньютон понимал, что для того,
чтобы Луна вращалась вокруг Земли, а
Земля и другие планеты вокруг Солнца,
должна существовать сила, удерживающая
их на круговой орбите. Он предположил,
что сила тяжести, действующая на все
тела на Земле и сила, удерживающая
планеты на их круговых орбитах, есть
одна и та же сила. Эта сила получила
название сила всемирного тяготения или
гравитационная сила. Эта сила является
силой притяжения и действует между
всеми телами. Ньютон сформулировал закон всемирного тяготения:
две материальные точки притягиваются
друг к другу с силой прямо пропорциональной
произведению их масс и обратно
пропорциональной квадрату расстояния
между ними.
Закон всемирного тяготения можно записать в векторном виде. Если сила, действующая на вторую точку со стороны первой равна F21, а радиус-вектор второй точки относительно первой равен R21, то:
Представленный вид закона всемирного
тяготения справедлив только для
гравитационного взаимодействия
материальных точек. Для тел произвольной
формы и размеров его использовать
нельзя. Вычисление гравитационной силы
в общем случае является очень непростой
задачей. Однако, есть тела, не являющиеся
материальными точками, для которых
гравитационную силу можно считать по
приведенной формуле. Это тела, обладающие
сферической симметрией, например,
имеющие форму шара. Для таких тел
приведенный закон справедлив, если под
расстоянием R понимать расстояние между центрами
тел. В частности силу тяжести, действующую
на все тела со стороны Земли можно
считать по этой формуле, так как Земля
имеет форму шара, а все остальные тела
можно считать материальными точками
по сравнению с радиусом Земли.
Для тел произвольной
формы и размеров его использовать
нельзя. Вычисление гравитационной силы
в общем случае является очень непростой
задачей. Однако, есть тела, не являющиеся
материальными точками, для которых
гравитационную силу можно считать по
приведенной формуле. Это тела, обладающие
сферической симметрией, например,
имеющие форму шара. Для таких тел
приведенный закон справедлив, если под
расстоянием R понимать расстояние между центрами
тел. В частности силу тяжести, действующую
на все тела со стороны Земли можно
считать по этой формуле, так как Земля
имеет форму шара, а все остальные тела
можно считать материальными точками
по сравнению с радиусом Земли.
Гравитационная постоянная. Коэффициент
пропорциональности G во времена Ньютона был неизвестен.
Впервые он был экспериментально измерен
английским ученым Кавендишем. Этот
коэффициент называется гравитационной
постоянной. Ее современное значение
равно .
Гравитационная постоянная является
одной из самых фундаментальных физических
констант.
Гравитационное поле.
Сила тяжести. Так как сила тяжести является гравитационной силой, то можно написать, что сила тяжести, действующая на тело массой m равна
Где МЗ и RЗ – масса и радиус Земли. С другой стороны сила тяжести равна mg, где g – ускорение свободного падения.
Ускорение свободного падения.
Значит ускорение свободного падения равно
Это формула для ускорения свободного падения на поверхности Земли. Если удаляться от поверхности Земли, то расстояние до центра Земли будет увеличиваться, а ускорение свободного падения соответственно уменьшаться. Так на высоте h над поверхностью Земли ускорение свободного падения равно:
2
. Выталкивающая сила. Рассмотрим
однородную неподвижную жидкость и
погруженное в нее тело. На поверхность
погруженного тела давит окружающаяся
жидкость. Причем, давление окружающей
жидкости зависит от глубины погружения
данной точки поверхности. Давление
жидкости увеличивается с глубиной
погружения (гидростатическое давление).
Значит, на нижнюю половину поверхности
тела жидкость будет давить больше, чем
на верхнюю половину. Значит, равнодействующая
сил давления жидкости на поверхность
погруженного в нее тела будет направлена
вверх, то есть будет выталкивать тело
из жидкости. Причем, сила давления
окружающей жидкости на поверхность
погруженного в нее тела не зависит от
материала, из которого изготовлено
тело. Мысленно вынем погруженное тело
из жидкости и заполним освободившийся
объем той же самой жидкостью. У нас
получится однородная жидкость, находящаяся
в равновесии. На объем жидкости, который
ранее занимало погруженное тело, со
стороны окружающей жидкости действуют
те же самые силы давления.
Выталкивающая сила. Рассмотрим
однородную неподвижную жидкость и
погруженное в нее тело. На поверхность
погруженного тела давит окружающаяся
жидкость. Причем, давление окружающей
жидкости зависит от глубины погружения
данной точки поверхности. Давление
жидкости увеличивается с глубиной
погружения (гидростатическое давление).
Значит, на нижнюю половину поверхности
тела жидкость будет давить больше, чем
на верхнюю половину. Значит, равнодействующая
сил давления жидкости на поверхность
погруженного в нее тела будет направлена
вверх, то есть будет выталкивать тело
из жидкости. Причем, сила давления
окружающей жидкости на поверхность
погруженного в нее тела не зависит от
материала, из которого изготовлено
тело. Мысленно вынем погруженное тело
из жидкости и заполним освободившийся
объем той же самой жидкостью. У нас
получится однородная жидкость, находящаяся
в равновесии. На объем жидкости, который
ранее занимало погруженное тело, со
стороны окружающей жидкости действуют
те же самые силы давления. При этом этот
объем жидкости находится в равновесии.
Это значит, что равнодействующая сил
давления окружающей жидкости полностью
компенсируется силой тяжести выделенного
объема жидкости. А это значит, что на
тело, погруженное в жидкость, действует
равнодействующая сил давления окружающей
жидкости, равная силе тяжести этой
жидкости в погруженном объеме тела. Эта
сила называется силой Архимеда.
При этом этот
объем жидкости находится в равновесии.
Это значит, что равнодействующая сил
давления окружающей жидкости полностью
компенсируется силой тяжести выделенного
объема жидкости. А это значит, что на
тело, погруженное в жидкость, действует
равнодействующая сил давления окружающей
жидкости, равная силе тяжести этой
жидкости в погруженном объеме тела. Эта
сила называется силой Архимеда.
Закон Архимеда. Теперь можно сформулировать закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная силе тяжести жидкости в объеме погруженной части тела.
Здесь ρж – плотность жидкости; Vпог – объем погруженной части тела.
Плавание тел. Если тело опустить в
жидкость, то оно либо плавает на ее
поверхности, либо тонет. Это зависит от
соотношения плотностей тела и жидкости.
Если плотность тела меньше, чем плотность
жидкости, то тело плавает на ее поверхности.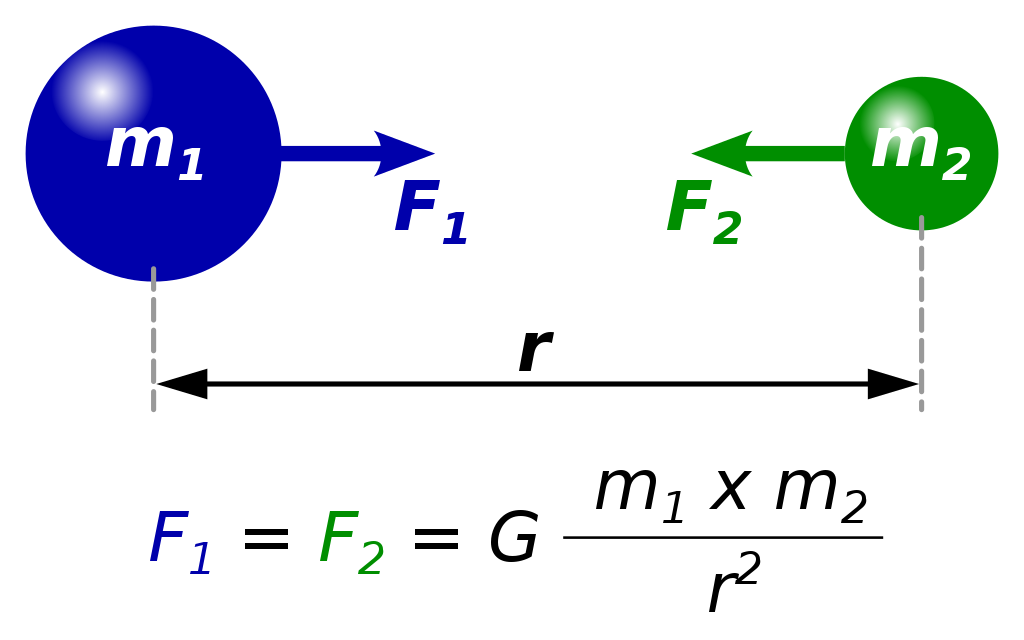 При этом тело частично погружено в
жидкость и его сила тяжести уравновешивается
силой Архимеда:
При этом тело частично погружено в
жидкость и его сила тяжести уравновешивается
силой Архимеда:
Это уравнение называется условием плавания тела. Если плотность тела больше плотности жидкости, то тело тонет. При этом оно либо давит на дно сосуда, либо натягивает нить подвеса. Эта сила называется весом тела. Вес тела погруженного в жидкость равен разнице силы тяжести и силы Архимеда:
Заметим, что если тело плавает на поверхности жидкости, то его вес равен нулю.
Воздушные шары.
Точка приложения силы Архимеда. Сила Архимеда, как и любая другая сила, имеет точку своего приложения. Точкой приложения силы Архимеда является центр тяжести жидкости в погруженном объеме тела.
У
стойчивость
плавания. Рассмотрим
устойчивость плавания тел на поверхности
жидкости. Пусть на поверхности жидкости
плавает однородный стержень, плотность
которого меньше плотности жидкости. Имеется два положения равновесия
плавания стержня: вертикальное и
горизонтальное. Сила тяжести приложена
в центре тяжести стержня, а сила Архимеда
в центре тяжести погруженной части
стержня. Если стержень находится в
строго вертикальном, или в строго
горизонтальном положении, то эти две
силы направлены вдоль одной прямой и
компенсируют друг друга. Однако, при
случайных колебаниях поверхности воды,
эти положения равновесия могут нарушиться
и стержень отклонится в сторону. При
этом возникнет момент силы тяжести и
силы Архимеда. Из рисунка вино, что при
отклонении стержня от вертикального
положения этот момент сил будет
опрокидывать стержень, а при отклонении
от горизонтального положения будет
возвращать его в исходное положение.
Значит, вертикальное положение плавания
стержня будет неустойчивым, а горизонтальное
– устойчивым.
Имеется два положения равновесия
плавания стержня: вертикальное и
горизонтальное. Сила тяжести приложена
в центре тяжести стержня, а сила Архимеда
в центре тяжести погруженной части
стержня. Если стержень находится в
строго вертикальном, или в строго
горизонтальном положении, то эти две
силы направлены вдоль одной прямой и
компенсируют друг друга. Однако, при
случайных колебаниях поверхности воды,
эти положения равновесия могут нарушиться
и стержень отклонится в сторону. При
этом возникнет момент силы тяжести и
силы Архимеда. Из рисунка вино, что при
отклонении стержня от вертикального
положения этот момент сил будет
опрокидывать стержень, а при отклонении
от горизонтального положения будет
возвращать его в исходное положение.
Значит, вертикальное положение плавания
стержня будет неустойчивым, а горизонтальное
– устойчивым.
В
опросы
устойчивости плавания очень важны при
проектировании судов. Рассмотрим
корабль, отклонившийся от вертикального
положения. Пусть ось ОО1 – ось симметрии корабля. Точка приложения
силы тяжести находится на оси ОО1,
а силы Архимеда в центре тяжести
погруженного объема корабля. Точка
пересечения линии действия выталкивающей
силы с осью ОО1 (точка N)
называется метацентром. Если метацентр
находится выше точки приложения силы
тяжести, то положение корабля устойчивое,
а если ниже, то неустойчивое.
Точка приложения
силы тяжести находится на оси ОО1,
а силы Архимеда в центре тяжести
погруженного объема корабля. Точка
пересечения линии действия выталкивающей
силы с осью ОО1 (точка N)
называется метацентром. Если метацентр
находится выше точки приложения силы
тяжести, то положение корабля устойчивое,
а если ниже, то неустойчивое.
Презентация по физике на тему Гравитационное взаимодействие. Сила всемирного тяготения доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по физике на тему Гравитационное взаимодействие. Сила всемирного тяготения, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Сила всемирного тяготения, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
внимание
Вследствие чего, согласно легенде, упало яблоко так заинтересовавшее И.Ньютона ?
Благодаря чему Земля удерживается на околосолнечной орбите ?
Что общего между обращением Луны вокруг Земли и свободным падением тел на Землю ?
В результате какого взаимодействия притягиваются тела имеющие массу ?
Гравитационное взаимодействие.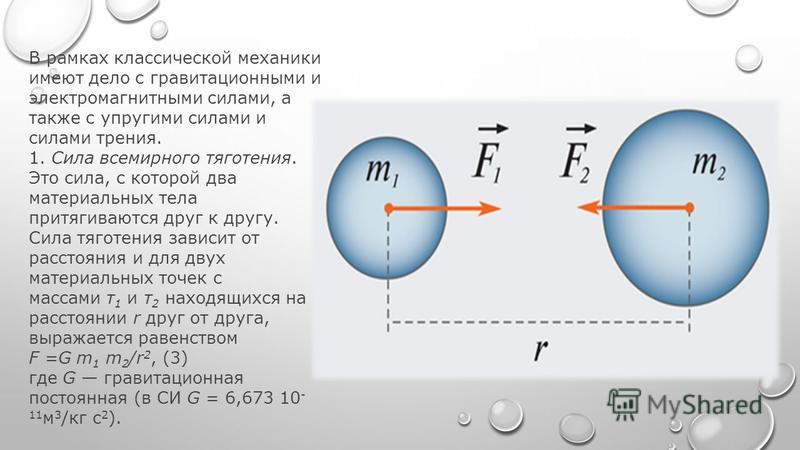 Закон всемирного тяготения
Закон всемирного тяготения
Формирование понятий
Хахулина С.Б., учитель физики
МОУ «Гимназия №7 «Ступени» г. В. Уфалей
План
1.Формирование понятия «гравитация».
2.Формирование понятия «сила всемирного тяготения»:
3.Конкретизация понятий.
4.Самоконтроль.
5.Самооценка.
а) абстрагирование понятия
б) моделирование понятия
Между какими телами проявляется данное взаимодействие?
1. Между любыми телами
2. Между заряженными телами
3. Между телами имеющими массу
4. Между большими телами
Используйте данную информацию для определения понятия «Гравитационное взаимодействие»
план
Определение понятия «Гравитационное взаимодействие»
Ближайший
родо-видовой
признак
Качественная
характеристика
Количественная
характеристика
Понятие
Гравитационное взаимодействие – это физ. явление, которое
явление, которое
заключается в действии
притяжения тел, имеющих массу.
Какой величиной в физике характеризуется любое действие ?
Какой величиной можно охарактеризовать данное взаимодействие ?
Силой
тяжести
Силой
упругости
Силой
трения
Силой всемирного тяготения
план
Прочти
От каких величин зависит модуль силы всемирного тяготения?
1. F ~ m1·m2
2. F ~ 1/r²
3. F= Gm1·m2/r²
Крутильные весы
Кавендиша
Приведите примеры
установленных зависемостей
план
Справка
Составте модель понятия «Сила всемирного тяготения» и дайте ее определение.
Сила всемирного тяготения
действие притяжения тел имеющих массу
направление
вдоль одной линии
к центру тела
модуль
F=Gm1·m2/r²
точка приложения
приложена
к центру тела
Сила всемирного тяготения – это физ. величина, характеризующая действие при-
величина, характеризующая действие при-
тяжения тел, имеющих массу, численно равная произ-
ведению гравитационной постоянной на отношение
произведения масс взаимодействующих тел к квадрату
расстояния между ними, направленная вдоль линии к
центру тела, приложенная к центру тела.
план
Вопросы для самоконтроля.
1. Какое действие характеризует сила всемирного
тяготения ?
2. Чем обьяснить различное количество спутников у планет Солнечной системы?
3. Почему поворачивалось коромысло в крутильных весах Кавендиша ?
4. Как изменится сила всемирного тяготения, если
массы обоих тел увеличить в два раза ?
5. Как изменится сила всемирного тяготения, дейст-
вующая со стороны Земли на искусственный спутник,
при запуске его с поверхности Земли на расстояние двух радиусов Земли ?
план
Самооценка
2. различным гравитационным взаимодействием, а значит и
различным гравитационным взаимодействием, а значит и
разной силой всемирного тяготения.
массивный шар притягивал к себе один из шариков в результате
гравитационного взаимодействия.
4. увеличится в четыре раза.
5. уменьшится в четыре раза.
1. действие притяжения тел имеющих массу.
В случае 5-ти правильных ответов — отметка «5»
4-х — «4» и т. д.
план
Выход
Гравитационное взаимодействие проявляется между телами,
имеющими массу. Например, частица света фотон не обладает гравитацией, т.к. не имеет массы покоя.
Благодаря гравитационному взаимодействию притягиваются даже тела, имеющие малую массу, но сила этого притяжения очень слабая. Так тела массами по 1кг. каждое, находящиеся друг от друга на расстоянии 1м. притягиваются с силой 6,67·10¯¹¹ Н . В этом и заключается физический смысл гравитационной постоянной G.
Назад
Любое действие в физике характеризуется физической величиной – силой .
Гравитационное взаимодействие характеризуется силой всемирного тяготения.
Обратно
Модуль силы всемирного тяготения прямо пропорционален произведению масс взаимодействующих тел.
Модуль силы всемирного тяготения обратно пропорционален квадрату расстояния между взаимодействующими телами.
При увеличении массы одного из взаимодействующих тел сила всемирного тяготения возрастет во столько же раз.
При увеличении расстояния между телами в n-раз сила всемирного тяготения уменьшится в n² раз.
Вернись
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
ньютоновской механики — Точка приложения, когда сила направлена вверх?
Задавать вопрос
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 243 раза
$\begingroup$
Нас учили, что точка приложения — это точка приложения силы. В контактных силах точкой приложения является точка контакта, а в силах, действующих на расстоянии, точкой приложения является центр тяжести объекта, на который действует сила.
Например, рассмотрим мяч, висящий на веревке. Сила, действующая на мяч со стороны струны, — это сила натяжения (сила контакта), а точка приложения — единственная точка контакта между струной и мячом. Поэтому, если я хочу представить силу, мне придется нарисовать восходящий вектор, где хвост вектора начинается с этой точки приложения.
Сила, действующая на мяч со стороны струны, — это сила натяжения (сила контакта), а точка приложения — единственная точка контакта между струной и мячом. Поэтому, если я хочу представить силу, мне придется нарисовать восходящий вектор, где хвост вектора начинается с этой точки приложения.
Теперь рассмотрим пример падения мяча под действием своего веса. Сила здесь — это вес, который представляет собой силу, действующую на расстоянии. Точкой приложения в данном случае является центр тяжести мяча, который математически является центром сферы. Поэтому, если я хочу представить вес силы, я нарисую нисходящий вектор, где хвост вектора начинается из центра этой сферы.
Теперь возникает путаница, когда речь заходит о силе тяги Архимеда вверх. Мы знаем, что сила является контактной силой, но в этом случае точкой приложения является точка приложения сил, действующих на расстоянии, то есть центр тяжести.
Я запутался, как же так?
Ньютоновская механика векторов сил плавучести
$\endgroup$
$\begingroup$
В случае плавучести результирующая восходящая сила создается за счет перепада давления снаружи объекта.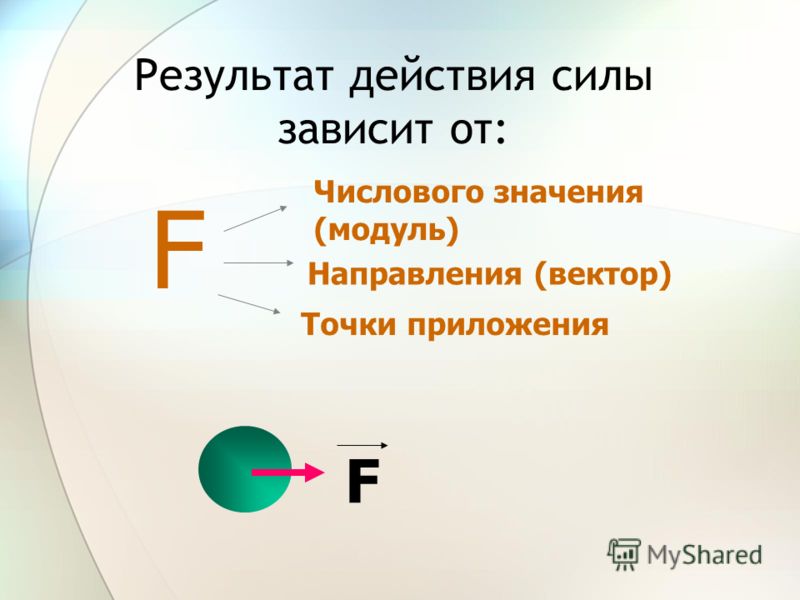 Везде, где окружающая жидкость соприкасается с объектом, давление жидкости создает силу на объект.
Везде, где окружающая жидкость соприкасается с объектом, давление жидкости создает силу на объект.
Поскольку мы предполагаем, что объект является жестким, мы можем суммировать все эти отдельные давления и найти, что они эквивалентны направленной вверх силе, действующей на линию через некоторую точку (не обязательно через центр тяжести). Если объект недостаточно жесткий, это упрощение может не сработать. Вместо этого объект может разрушиться или деформироваться.
То же самое и с гравитацией. В действительности каждая часть объекта притягивается всем остальным вокруг него. Но если предположить, что твердый объект находится в почти постоянном гравитационном поле, результирующая сила эквивалентна $mg$, действующей через центр масс.
$\endgroup$
5
$\begingroup$
Утверждение, что «…у сил, действующих на расстоянии, точкой приложения является центр тяжести объекта» технически неверно. (Хотел бы я иметь копию этого учебника, чтобы посмотреть, объясняет ли автор это чрезмерное упрощение где-нибудь еще.) Автор имеет в виду, что сумма индивидуальных сил, действующих на все частицы объекта, может быть математически смоделирована9.0043, как если бы было единой силой, действующей на центр тяжести.
(Хотел бы я иметь копию этого учебника, чтобы посмотреть, объясняет ли автор это чрезмерное упрощение где-нибудь еще.) Автор имеет в виду, что сумма индивидуальных сил, действующих на все частицы объекта, может быть математически смоделирована9.0043, как если бы было единой силой, действующей на центр тяжести.
Чтобы понять, почему исходное утверждение не может быть верным, рассмотрим, что у некоторых объектов центр тяжести находится за пределами реального объекта. (Для примеров см. https://www.quora.com/What-are-examples-of-when-the-center-of-gravity-of-a-body-is-outside-the-body или слайд 4 на эта страница: https://www.slideshare.net/ElviIdiosolo/center-of-gravity-40049394.Если бы сила буквально действовала только в центре тяжести, то сила действовала бы на пустое пространство и эти тела не подвергаться влиянию силы (например, силы тяжести) вообще.0003
Итак, как уже упоминал BowlOfRed, выталкивающая сила действительно действует везде, где окружающая жидкость соприкасается с объектом.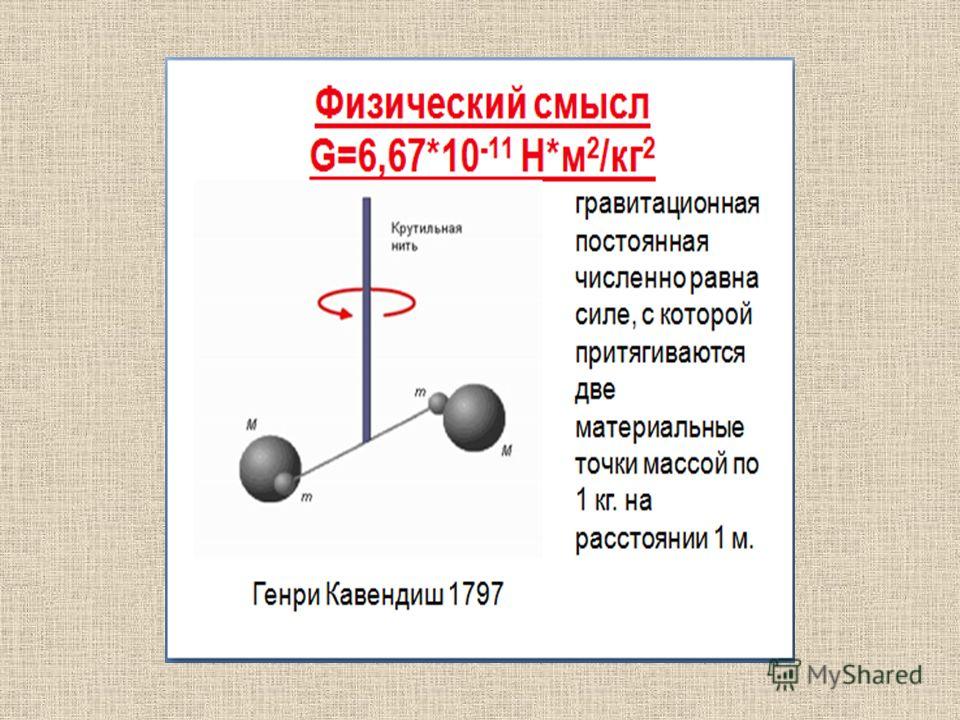 Но на ваших диаграммах вы можете смоделировать это так, как если бы была единственная сила, действующая в одной точке.
Но на ваших диаграммах вы можете смоделировать это так, как если бы была единственная сила, действующая в одной точке.
Между прочим, даже контактные силы (на твердом теле) можно смоделировать так, как если бы сумма векторов была одной силой, действующей в одной точке объекта. Так что, по моему скромному мнению, различие между контактными силами и силами, действующими на расстоянии — по крайней мере, в случае твердых тел и векторных диаграмм — на самом деле не нужно и только добавляет путаницы.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
гравитация | Определение, физика и факты
гравитационная линза
Посмотреть все медиа
- Ключевые люди:
- Кип Торн Исаак Ньютон Галилео Джон Арчибальд Уиллер Саймон Стевин
- Похожие темы:
- супергравитация масса точка Лагранжа Радиус Шварцшильда гравитационная аномалия
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
гравитация , также называемая гравитацией , в механике универсальная сила притяжения, действующая между всей материей. Это, безусловно, самая слабая из известных сил в природе, и поэтому она не играет никакой роли в определении внутренних свойств повседневного вещества. С другой стороны, благодаря своему большому охвату и универсальному действию он контролирует траектории тел в Солнечной системе и других местах во Вселенной, а также структуру и эволюцию звезд, галактик и всего космоса. На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
Понять концепцию гравитационной силы, используя теорию гравитации Ньютона
Посмотреть все видео к этой статье Работы Исаака Ньютона и Альберта Эйнштейна доминируют в развитии теории гравитации. Классическая теория силы тяготения Ньютона господствовала с его 9 лет.0043 Principia , опубликованной в 1687 году, до работы Эйнштейна в начале 20 века. Теории Ньютона достаточно даже сегодня для всех приложений, кроме самых точных. Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Запуск космических аппаратов и развитие исследований на них привели к значительному улучшению измерений гравитации вокруг Земли, других планет и Луны, а также в экспериментах по изучению природы гравитации.
Развитие теории гравитации
Ранние концепции
Ньютон утверждал, что движения небесных тел и свободное падение объектов на Земле определяются одной и той же силой. Классические греческие философы, с другой стороны, не считали, что небесные тела подвержены влиянию гравитации, поскольку наблюдалось, что тела следуют постоянно повторяющимся ненисходящим траекториям в небе. Таким образом, Аристотель считал, что каждое небесное тело следует определенному «естественному» движению, не подверженному влиянию внешних причин или факторов. Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Тест «Британника»
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Немецкий астроном XVII века Иоганн Кеплер принял аргумент Николая Коперника (который восходит к Аристарху Самосскому) о том, что планеты вращаются вокруг Солнца, а не Земли. Используя улучшенные измерения движения планет, сделанные датским астрономом Тихо Браге в 16 веке, Кеплер описал планетарные орбиты с помощью простых геометрических и арифметических соотношений. Три количественных закона движения планет Кеплера таковы:
Используя улучшенные измерения движения планет, сделанные датским астрономом Тихо Браге в 16 веке, Кеплер описал планетарные орбиты с помощью простых геометрических и арифметических соотношений. Три количественных закона движения планет Кеплера таковы:
Планеты описывают эллиптические орбиты, один из фокусов которых занимает Солнце (фокус — это одна из двух точек внутри эллипса; любой луч, исходящий из одной из них, отражается от стороны эллипса и проходит через другой фокус) .
Линия, соединяющая планету с Солнцем, заметает равные площади за равные промежутки времени.
Квадрат периода обращения планеты пропорционален кубу ее среднего расстояния от Солнца.
В этот же период итальянский астроном и естествоиспытатель Галилео Галилей добился успехов в понимании «естественного» движения и простого ускоренного движения земных объектов. Он понял, что тела, на которые не действуют силы, продолжают двигаться бесконечно и что сила необходима для изменения движения, а не для поддержания постоянного движения.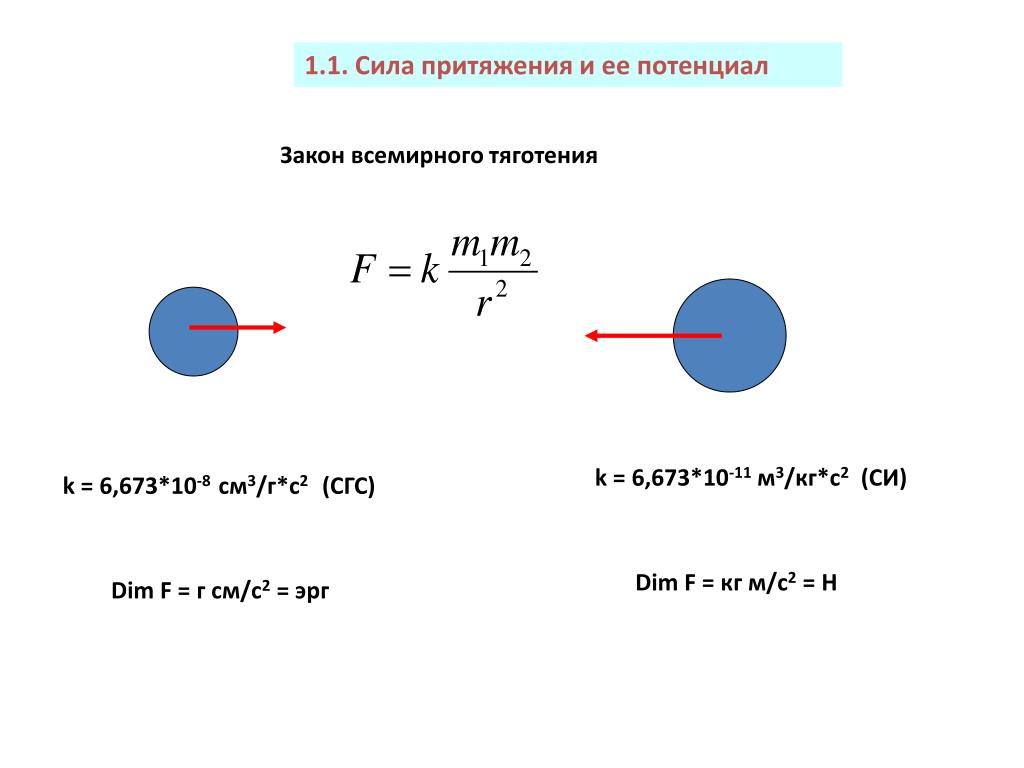 Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
2.2: Точечные силы как векторы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50573
- Джейкоб Мур и участники
- Университет штата Пенсильвания Мон-Альто через карту механики
Точечная сила — это любая сила, где точка приложения считается одиночной точкой . В действительности большинство сил технически представляют собой поверхностные силы, когда сила прикладывается к площади, но когда площадь достаточно мала (по сравнению с анализируемыми телами), ее часто можно аппроксимировать точечной силой. Поскольку точечные силы могут быть представлены в виде одного вектора (а не поля векторов для распределенных сил), с ними гораздо проще работать в инженерном анализе. По этой причине точечные силы используются вместо распределенных сил в инженерном анализе, когда это возможно. Ниже приведены некоторые примеры того, где уместно использовать точечные силы.
В действительности большинство сил технически представляют собой поверхностные силы, когда сила прикладывается к площади, но когда площадь достаточно мала (по сравнению с анализируемыми телами), ее часто можно аппроксимировать точечной силой. Поскольку точечные силы могут быть представлены в виде одного вектора (а не поля векторов для распределенных сил), с ними гораздо проще работать в инженерном анализе. По этой причине точечные силы используются вместо распределенных сил в инженерном анализе, когда это возможно. Ниже приведены некоторые примеры того, где уместно использовать точечные силы.
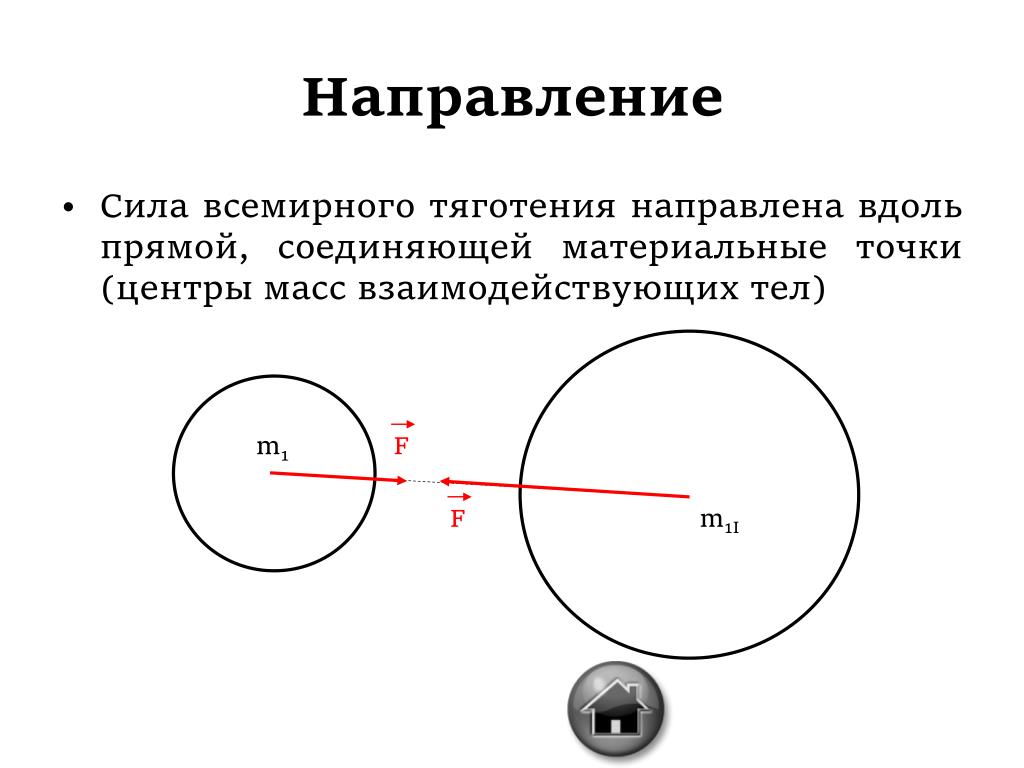 Рисунок \(\PageIndex{4}\): Гравитационная сила и нормальные силы, действующие на каждую ножку этого стола, могут быть аппроксимированы точечными силами. Адаптировано из изображения Public Domain от Seahen.
Рисунок \(\PageIndex{4}\): Гравитационная сила и нормальные силы, действующие на каждую ножку этого стола, могут быть аппроксимированы точечными силами. Адаптировано из изображения Public Domain от Seahen.В дополнение к величине, направлению и точке приложения точечной силы, другим важным термином для понимания является линия действия силы. Линия действия силы – это линия, вдоль которой действует сила. Зная направление и точку приложения, можно найти линию действия, но этот термин будет важен при обсуждении действующих сил и в принципе трансмиссивности.
Рисунок \(\PageIndex{5}\): Линия действия точечной силы — это линия, вдоль которой действует сила.Представление вектора силы:
Когда векторы рисуются для формирования диаграмм свободного тела, величина и направление обычно задаются в одном из двух форматов: форма ).
В любом формате нам потребуются два значения для полного определения вектора силы в 2D-системе (либо величина и отдельный угол, либо величина в каждой из двух координатных осей), и три значения для полного определения вектора силы в трехмерная система (либо величина и два угла, либо величина в каждой из трех координатных осей).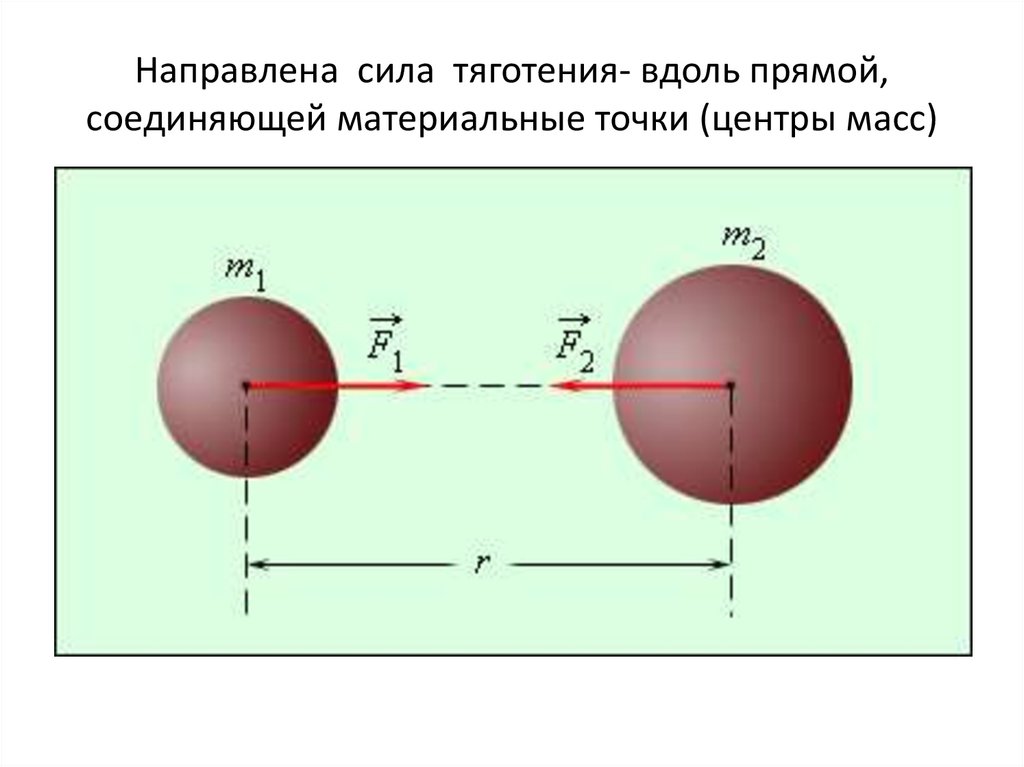 Ниже приведены некоторые примеры векторов силы в обоих представлениях.
Ниже приведены некоторые примеры векторов силы в обоих представлениях.
Изменение форм вектора силы:
Поскольку две разные формы вектора эквивалентны, мы можем переключаться между представлениями без изменения задачи. Часто в инженерных задачах сначала будет легче записать силу в виде величины и угла, но позже анализ будет проще, если силы будут записаны в виде компонентов. Чтобы переключиться с формы величины и направления на форму компонента, вы будете использовать прямоугольные треугольники и тригонометрию для определения компонента общей величины в каждом направлении. Это простая векторная декомпозиция, и дополнительную информацию об этом процессе можно увидеть на странице векторной декомпозиции. Чтобы переключиться обратно с формы компонента на форму величины и направления, вы просто используете процесс, обратный этому начальному процессу.
Чтобы переключиться обратно с формы компонента на форму величины и направления, вы просто используете процесс, обратный этому начальному процессу.
Пример \(\PageIndex{1}\)
Сила натяжения коробки ниже представлена в форме величины и направления. Перерисуйте диаграмму с силой натяжения, представленной в компонентной форме.
- Раствор
- Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/ZERURXWnlDg.
Пример \(\PageIndex{2}\)
Показанная ниже сила, действующая на консольную балку, представлена в виде компонента. Перерисуйте диаграмму с силой, заданной в виде величины и направления.
Перерисуйте диаграмму с силой, заданной в виде величины и направления.
- Раствор
- Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/M3UjDfZzRHY.
Пример \(\PageIndex{3}\)
Сила, показанная ниже, представлена в форме величины и направления. Перерисуйте диаграмму с вектором силы, заданным в компонентной форме.
- Раствор
- Видео \(\PageIndex{4}\): Рабочее решение примера проблемы \(\PageIndex{3}\), представленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/DroNv0TxnyA.
Эта страница под названием 2.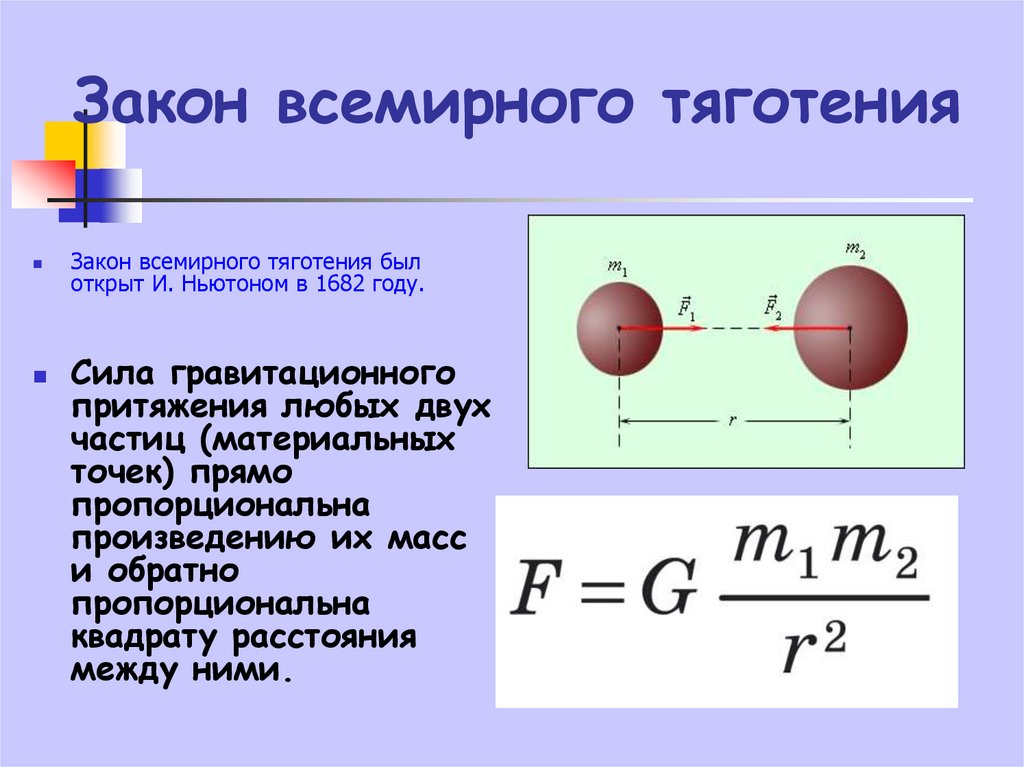 2: Point Forces as Vectors распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
2: Point Forces as Vectors распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джейкоб Мур и авторы
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Метки
- место применения
- источник@http://mechanicsmap.
 psu.edu
psu.edu
Гравитационные поля | IOPSpark
В этом эпизоде учащиеся оценят изменения в способах накопления энергии при движении тела в гравитационном поле. Они уже видели эту концепцию для однородного гравитационного поля в форме
изменение энергии, накапливаемой гравитацией, или изменение гравитационной потенциальной энергии = m x g x Δh
где Δh = изменение высоты, но это будет обобщено на неоднородные поля вокруг точечных или сферических масс. Затем они познакомятся с концепцией гравитационного потенциала и его использованием, прежде чем, наконец, установить связь между той скоростью, с которой гравитационный потенциал меняется от места к месту, и напряженностью поля.
Обратите внимание, что упоминание о бесконечности часто заставляет студентов биться в голове и ломать голову над кажущимися парадоксами, такими как «Если гравитационное поле бесконечно по протяженности, что значит быть на бесконечности там, где поле равно нулю?» Лучше подходить к этому прагматично; под бесконечностью мы на самом деле подразумеваем такое расстояние от всех масс во Вселенной, которое нам необходимо, чтобы сделать гравитационные силы незначительными в любом контексте, на который мы смотрим.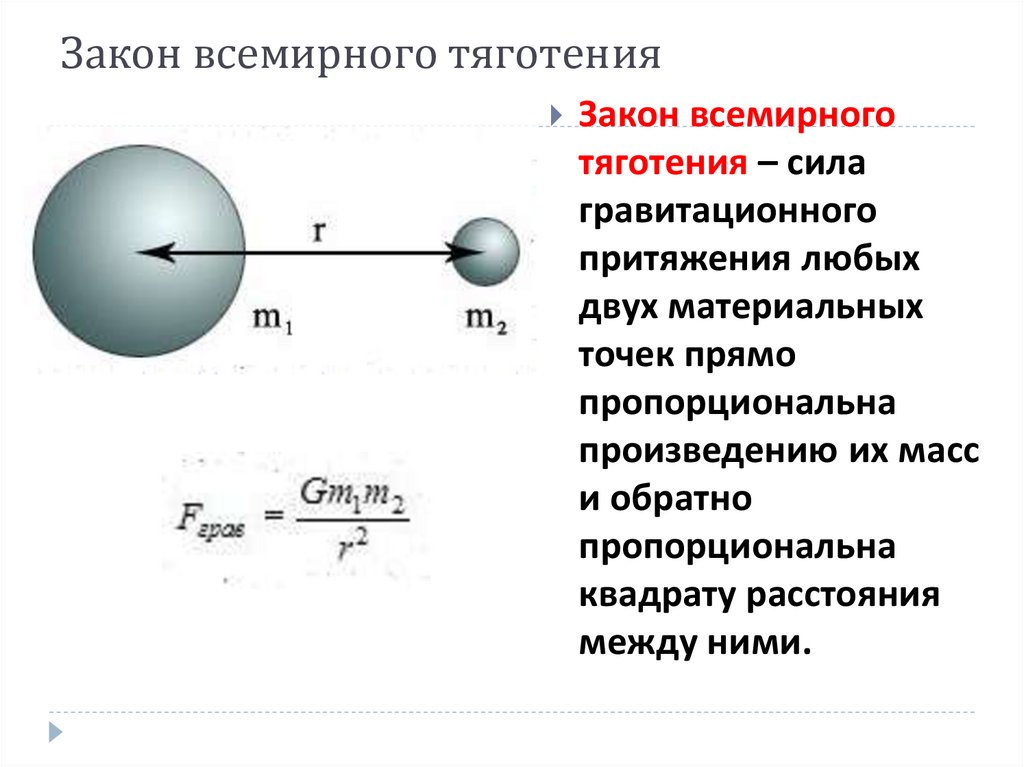
Это довольно длинный эпизод, и на него стоит потратить время, чтобы получить хорошее представление об этих идеях. Они будут важны снова с электрическими полями.
Резюме урока
Обсуждение: Работа и энергия
В этом уроке используется то, что учащиеся уже должны знать о работе и энергии.
Что такое работа? (Работа совершается, когда точка приложения силы перемещается на некоторое расстояние в направлении силы. В отсутствие сил трения эта проделанная работа запасается в виде энергии тела, на которое действовала сила.)
Если я подниму предмет с пола над головой (покажу!), выполнил ли я над ним работу? (Да. Я приложил направленную вверх силу к объекту, который сам тоже двинулся вверх.)
Что случилось с работой, которую я проделал над объектом? (Она хранится в виде энергии объекта. Мы говорим, что энергия хранится гравитационно. «Гравитационно», потому что мы должны совершать работу против гравитации, чтобы поднять объект. Если у вас есть что-то хрупкое (но безопасное и дешевое!), они действительно увидеть, как эта энергия реализуется.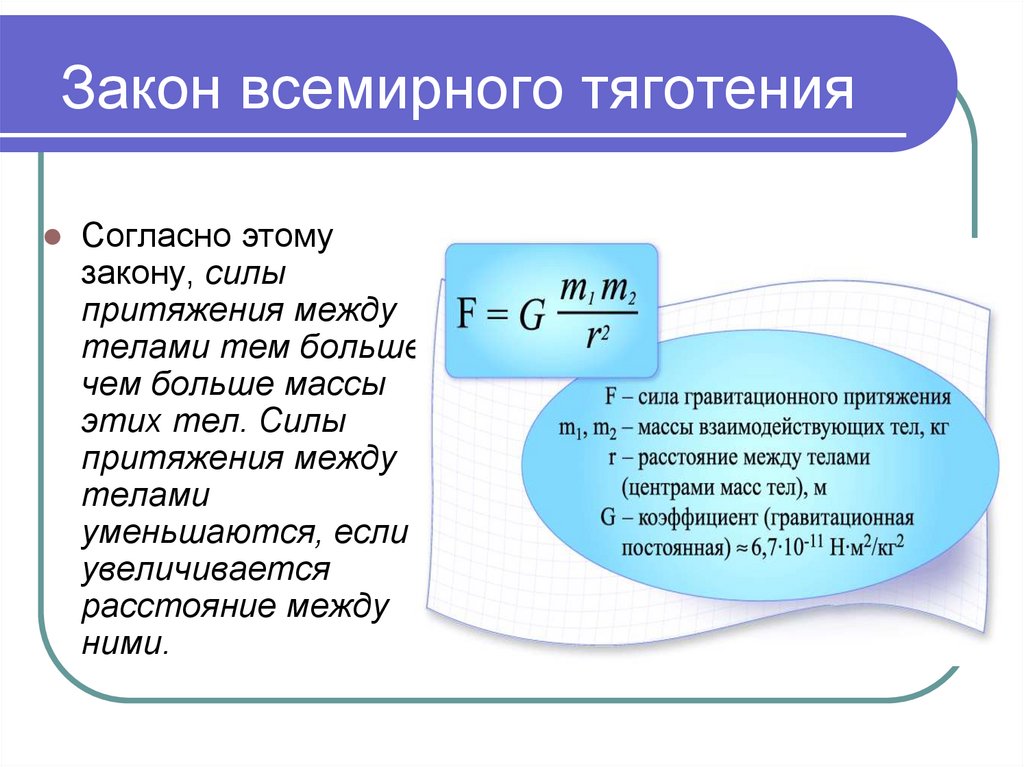 )
)
Рабочие примеры: Энергия в постоянном поле
Теперь учащиеся уже встречались с этими идеями на уровне до 16 лет в форме:
Изменение E G = m g h .
Сейчас также стоит пересмотреть это с несколькими примерами работы.
Эпизод 404-1: Энергия в постоянном поле (Word, 26 КБ)
Обсуждение: Энергия в неоднородном поле
Теперь вы можете распространить эти идеи на энергию в неоднородном поле.
Все предыдущие примеры включали изменения в энергии, накопленной гравитацией вблизи поверхности Земли. В чем была бы проблема, если бы мы захотели использовать то же уравнение для расчета изменений энергии, хранящейся в гравитации, скажем, для ракеты, запущенной на Луну? (Напряженность гравитационного поля не постоянна – значение г меняется.)
Поэтому нам нужен другой способ расчета изменений энергии, накапливаемой гравитацией в неоднородных полях. Полная трактовка того, как мы приходим к этой формуле, требует исчисления вне программы, которое на самом деле было бы доступно более способным учащимся.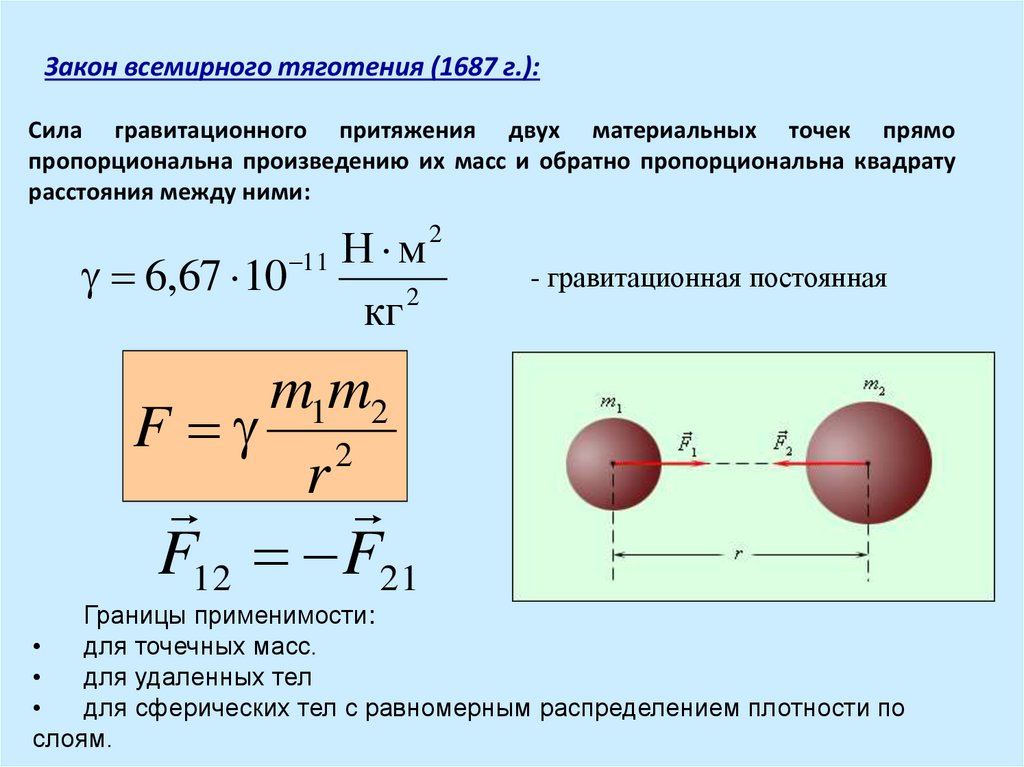 Мы находим, что мы можем вычислить энергию массы м на расстоянии r от (точечной или сферической) массы M По:
Мы находим, что мы можем вычислить энергию массы м на расстоянии r от (точечной или сферической) массы M По:
E G = — G M M R
. объекта, тем больше энергии запасено в гравитационном поле. (Поскольку что-то должно было сделать больше работы против гравитации, чтобы вы туда попали). Таким образом, когда вы находитесь бесконечно далеко, вы обладаете настолько высокой энергией по отношению к нему, насколько это возможно. Мы решили (произвольно) сделать значение энергии всех тел на бесконечности равным нулю. Затем, поскольку это наивысшее значение энергии, все реальные значения энергии, хранящиеся гравитационно (ближе, чем бесконечность), должны быть отрицательными. Поэтому знак минус в уравнении равен вместо опционально; она всегда должна быть включена, и все значения энергии, запасенной в гравитационном поле, отрицательны. (Это не тот случай, когда мы приходим к электрическим полям, потому что они тоже могут быть отталкивающими).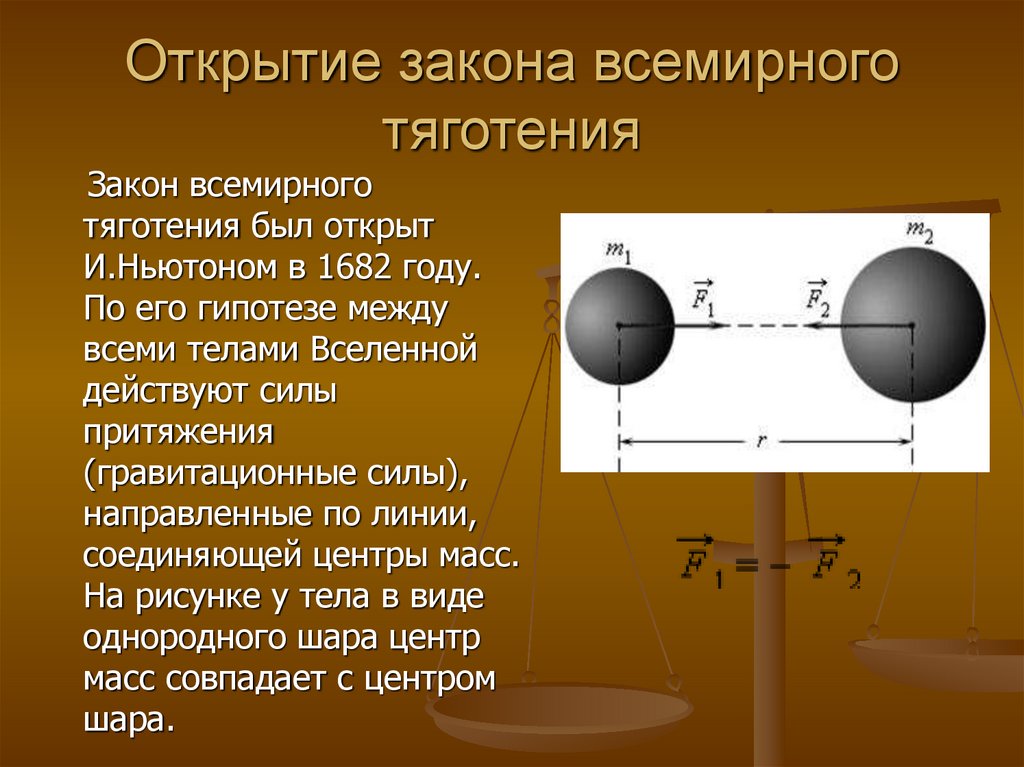
Изменение энергии. Определив точку, относительно которой измеряется вся энергия, мы можем теперь говорить о абсолютных значениях энергии, а не просто об изменениях. Эта точка находится в бесконечности (см. примечание 1 выше).
Обсуждение: Потенциал
Вес объекта в гравитационном поле Земли зависит от массы объекта (а также от массы Земли). Однако, как мы уже видели, напряженность поля в точке не зависит от помещенного в нее объекта (поскольку она определяется как сила, приходящаяся на единицу массы объекта). Таким образом, мы можем думать о напряженности поля как о свойстве поля в точке, а не о конкретном объекте, размещенном там.
Точно так же энергия, накопленная в гравитационном поле при перемещении тела относительно Земли, зависит от массы объекта (а также массы Земли) и расстояния между ними.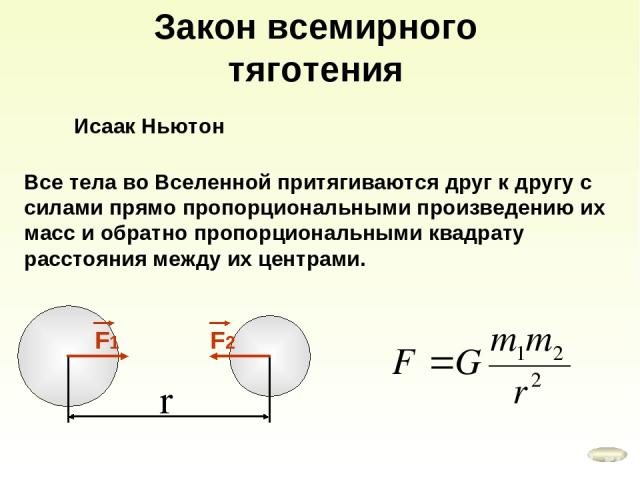 Как, по-вашему, можно получить величину, связанную с энергией поля в точке, которая не зависит от помещенного в нее предмета? (Рассматривая энергию, запасенную на единицу массы объекта, тем самым устраняя зависимость от массы объекта так же, как мы делали это с напряженностью поля.)
Как, по-вашему, можно получить величину, связанную с энергией поля в точке, которая не зависит от помещенного в нее предмета? (Рассматривая энергию, запасенную на единицу массы объекта, тем самым устраняя зависимость от массы объекта так же, как мы делали это с напряженностью поля.)
Мы определяем потенциал в точке поля как энергию на единицу массы , хранящуюся при размещении 1 кг в этой точке поля. Мы можем получить уравнения для потенциала, используя это определение. Для поля из -за (точечной или сферической) массы м , мы имеем:
E G = — G M M R
и SO SO OLTER и SO OLTER и SO OLTER и SO OLTER и SO OLTER и SO OLTER и SO SO OTME , определяется как:V = − G M r
Несколько замечаний:
- Это относится только к полю, обусловленному массой (точечной или сферической) M.

- В измеряется в Дж кг -1 . Он следует закону обратной пропорциональности (1 r ), а не обратному квадрату (1 r 2 ).
- Как и в уравнении для энергии, знак минус обязателен. Все реальные потенциалы отрицательны, а ноль потенциала находится на бесконечности (поскольку все объекты не хранят гравитационную энергию на бесконечности).
- Потенциал, как и напряженность поля, является свойством поля в точке и не зависит от помещенного в нее объекта. Два объекта с разными массами в одной и той же точке поля подвержены действию одного и того же потенциала, но имеют разные энергии.
- Для однородных полей (например, близких к поверхности Земли) мы можем использовать
изменение потенциала = г ч
(с момента изменения E G = м г ч а также потенциал = E G м ).
(К потенциалу мы снова вернемся, когда будем изучать электрические поля.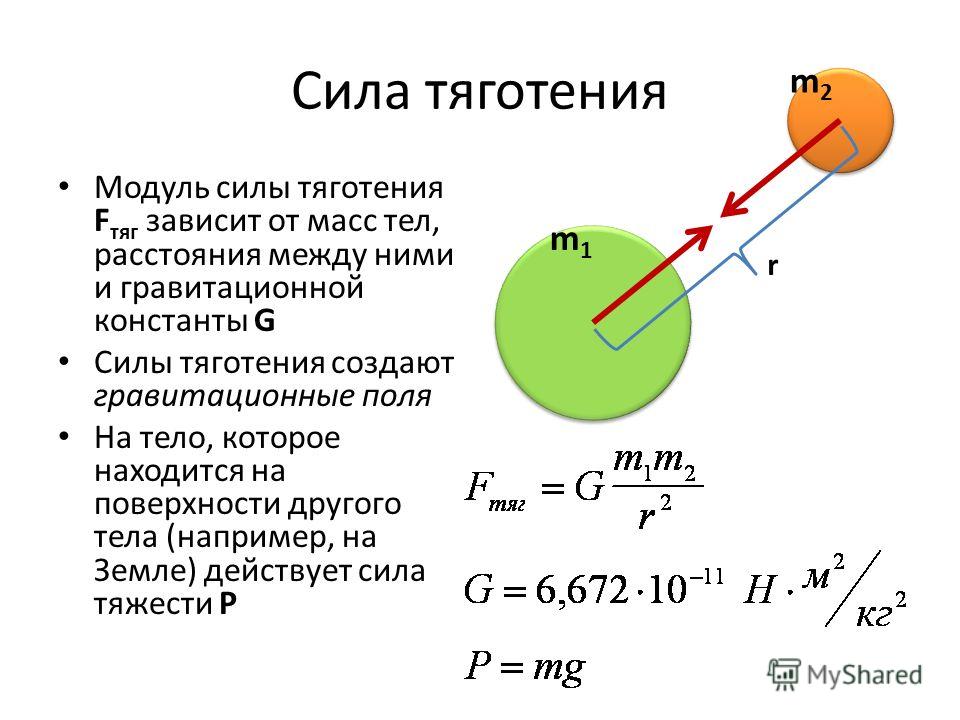 Там разность потенциалов (или разность потенциалов, pds) — это то, что мы часто называем напряжением.)
Там разность потенциалов (или разность потенциалов, pds) — это то, что мы часто называем напряжением.)
Примеры работы: Энергия и потенциал
Эпизод 404-2: Энергия и потенциал (Word, 30 КБ)
Вопросы учащихся
Эти вопросы относятся к космическому кораблю, путешествующему с Луны на Землю.
Вы можете пропустить вопросы с 3 по 5 включительно, если ваши учащиеся не рассмотрели тему импульса.
Эпизод 404-3: Гравитационное поле между Землей и Луной (Word, 74 КБ)
Упражнение с электронными таблицами
Вы можете расширить упражнение с электронными таблицами из Эпизода 402, включив идею гравитационного потенциала.
Эпизод 402-3: Данные миссии «Аполлон-11» (Word, 85 КБ)
Эпизод 404-4: Анализ данных «Аполлон-11», гравитационный потенциал (Word, 29)KB)
Обсуждение: Эквипотенциалы, градиент потенциала и напряженность поля
Эквипотенциалы соединяют точки с равным потенциалом. Они очень просты в случаях однородных полей (близких к поверхности Земли) и радиальных полей (для точечных и сферических масс):
На каком расстоянии друг от друга расположены эквипотенциальные линии на первой диаграмме? (Поскольку изменение потенциала для постоянного поля равно просто г ч (где ч — изменение высоты), мы имеем г ч = 9,8 Дж кг -1 }.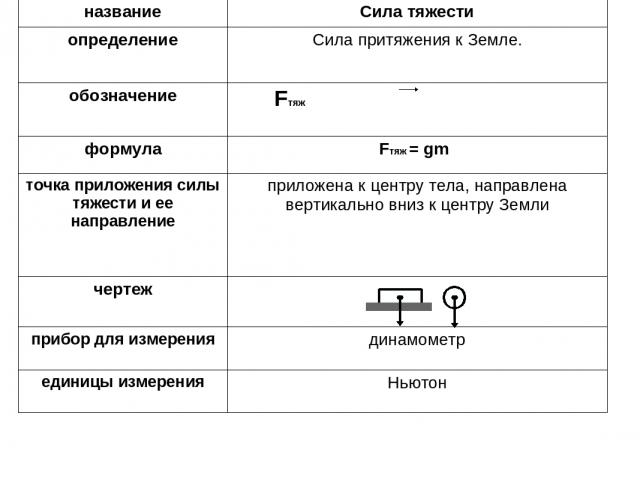 Следовательно, ч = 1 м — линии на расстоянии 1 м друг от друга.)
Следовательно, ч = 1 м — линии на расстоянии 1 м друг от друга.)
Какие формы являются эквипотенциальными в реальном мире? (Эквипотенциалы — это поверхности, а не линии в реальном трехмерном мире (т. е. горизонтальные плоскости, а не линии, близкие к поверхности Земли, и концентрические сферы, а не концентрические окружности вокруг точки/сферической массы), но мы можем зафиксировать только часть их на бумаге.)
Эквипотенциалы всегда перпендикулярны силовым линиям. Диаграммы эквипотенциальных линий дают нам информацию о гравитационном поле почти так же, как контурные карты дают нам информацию о географических высотах.
Что означает на контурной карте, если контуры расположены очень близко друг к другу? (На контурной карте контуры могут быть отмечены, скажем, с интервалом 5 м. Поэтому, если они расположены близко друг к другу, это означает, что земля, на которой они лежат, должна быть очень крутой.)
Как вы думаете, что это? значит, если эквипотенциальные поверхности расположены близко друг к другу? (Обоснованно предположить, что это означает, что гравитационное поле там очень сильное. Это было бы правильно — если эквипотенциалы расположены близко друг к другу, необходимо совершить большую работу на относительно коротком расстоянии, чтобы переместить массу из одной точки в другую. другая против поля, т. е. поле очень сильное. Следовательно, на приведенном выше рисунке эквипотенциалов вокруг точечных или сферических масс эквипотенциальные поверхности отдаляются все дальше и дальше по мере уменьшения напряженности поля с расстоянием.)
Это было бы правильно — если эквипотенциалы расположены близко друг к другу, необходимо совершить большую работу на относительно коротком расстоянии, чтобы переместить массу из одной точки в другую. другая против поля, т. е. поле очень сильное. Следовательно, на приведенном выше рисунке эквипотенциалов вокруг точечных или сферических масс эквипотенциальные поверхности отдаляются все дальше и дальше по мере уменьшения напряженности поля с расстоянием.)
На самом деле напряженность поля определяется отрицательным значением градиента потенциала: ввести как:
g = - изменение потенциалаизменение расстояния.
Упражнение с электронными таблицами: градиент потенциала и напряженность поля
В этом упражнении учащиеся будут обрабатывать (рассчитывать) необработанные данные об изменении потенциала в зависимости от высоты над поверхностью Земли. В конце они рассчитают изменение потенциала на метр (т. е. градиент потенциала), сравнит его с напряженностью поля и обнаружат, что они равны.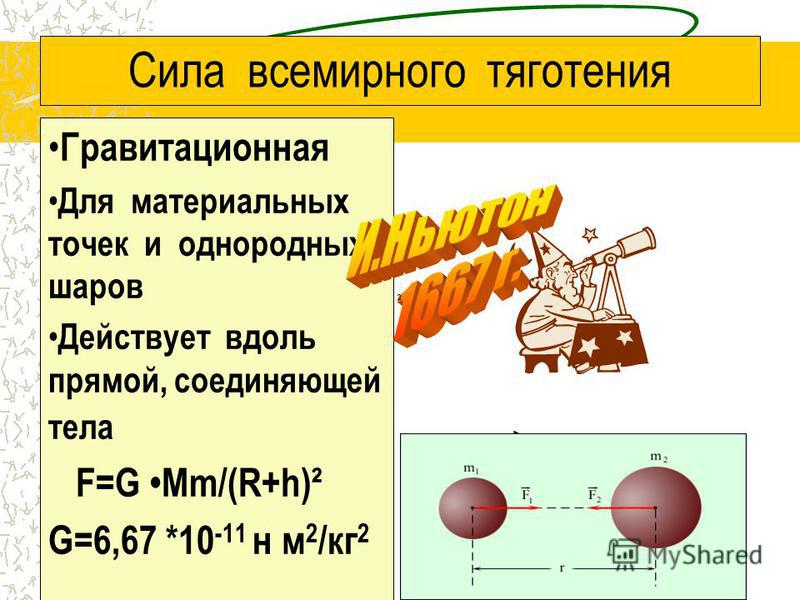 Когда они рассчитывают изменение потенциала между, скажем, 200 км и 300 км и делят его на расстояние в 100 км, чтобы получить напряженность поля, они на самом деле получают средняя напряженность поля на расстоянии от 200 км до 300 км, что, вероятно, будет очень близко к полю на расстоянии 250 км (хотя и не совсем, потому что изменение потенциала нелинейно). Следовательно, напряженность поля на листе 2 указана на расстоянии 50 км, 150 км и т. д.
Когда они рассчитывают изменение потенциала между, скажем, 200 км и 300 км и делят его на расстояние в 100 км, чтобы получить напряженность поля, они на самом деле получают средняя напряженность поля на расстоянии от 200 км до 300 км, что, вероятно, будет очень близко к полю на расстоянии 250 км (хотя и не совсем, потому что изменение потенциала нелинейно). Следовательно, напряженность поля на листе 2 указана на расстоянии 50 км, 150 км и т. д.
Ожидается, что они уже использовали электронные таблицы раньше, и их просят выполнить некоторые довольно простые манипуляции с электронными таблицами.
Эпизод 404-5: Потенциальный градиент и напряженность поля (Word, 28 КБ)
Эпизод 404-6: Файл Excel градиент потенциала и напряженность поля
(Word, 53 КБ)
Скачать этот выпуск
Эпизод 404 — Гравитационная потенциальная энергия.doc
183_notes:gravitation [Проекты и практики по физике]
Разделы 3.1, 3.2, 3.3 и 3. 4 в Материи и взаимодействиях (4-е издание)
4 в Материи и взаимодействиях (4-е издание)
Непостоянная сила: ньютоновская гравитация
Ранее вы читали о силе гравитации вблизи поверхности Земли. Эта сила была постоянной и всегда был направлен «вниз» (точнее к центру Земли). В этих заметках вы прочтете о ньютоновской формулировке силы тяготения, которая (в его время) помогла объяснить движение Солнечной системы, включая то, почему Солнце находится в центре Солнечной системы.
Видео-лекция
Сила гравитации
Используя ряд эмпирических наблюдений (Тихо Браге и Иоганна Кеплера) за движением различных астрономических объектов, Исаак Ньютон смог разработать эмпирическую формулу взаимодействия этих объектов, которая могла бы предсказать будущее (и объяснить прошлое) движение. этих объектов. Эта формула стала известна как универсальный закон всемирного тяготения Ньютона. Мы будем называть его Модель гравитационной силы 1) .
Ньютон обнаружил, что взаимодействие между двумя объектами с массой является притягивающим, прямо пропорциональным произведению их масс, обратно пропорциональным квадрату их разделения и направленным вдоль линии между их центрами. На рисунке справа показана сила, с которой планета 2 воздействует на планету 1.
На рисунке справа показана сила, с которой планета 2 воздействует на планету 1.
Для ясности рассмотрим вектор ($\vec{r}$) , который указывает от планеты 2 к планете 1 . Если положение планеты 1 относительно начала координат равно $\vec{r}_1$, а положение планеты 2 относительно того же начала координат равно $\vec{r}_2$, то это относительное положение или вектор разделения может математически представить так:
$$\vec{r} = \vec{r}_1 — \vec{r}_2$$
Вектор разделения представлен черной стрелкой на рисунке справа. Длина этого вектора разделения ($|\vec{r}|$) равна тому, насколько далеко друг от друга находятся две планеты. Единичный вектор, который указывает от планеты 2 к планете 1, определяется выражением 9.2}$.
Почему минус?
Сила гравитации является силой притяжения . То есть два объекта, которые взаимодействуют гравитационно , притягиваются друг к другу. В формуле гравитационной силы используется вектор разделения ($\vec{r}$), который указывает от объекта, на который действует сила, к объекту, на который действует сила. Например, на рисунке выше $m_2$ действует с силой на $m_1$, поэтому вектор разделения указывает от $m_2$ до $m_1$ (черная стрелка на рисунке выше).
Например, на рисунке выше $m_2$ действует с силой на $m_1$, поэтому вектор разделения указывает от $m_2$ до $m_1$ (черная стрелка на рисунке выше).
Но сила, которую испытывает $m_1$, направлена на $m_2$; он притягивается к $m_2$. Знак минус гарантирует, что сила (красная стрелка на рисунке выше) указывает в этом направлении.
Третий закон Ньютона
Сила притяжения Земли к Луне имеет ту же величину, что и сила притяжения Луны к Земле.
Гравитационная сила представляет собой первый пример 3-го закона Ньютона, который вы, возможно, слышали в разговорной речи как «На каждое действие есть равное и противоположное противодействие». К сожалению, это просторечие — ужасно неточное определение, которое довольно часто применяется неправильно, даже Разрушителями мифов!
Третий закон Ньютона следует из идеи о том, что сила количественно определяет взаимодействие между двумя объектами. Вы также можете думать об этом как об эмпирическом факте, вытекающем из нашего определения силы. То есть мы наблюдаем, когда один объект действует на другой объект с силой, второй объект оказывает на первый объект силу того же размера, но противоположного направления.
То есть мы наблюдаем, когда один объект действует на другой объект с силой, второй объект оказывает на первый объект силу того же размера, но противоположного направления.
Чтобы быть более конкретным, вы можете подумать о гравитационном взаимодействии между Землей и Луной (показано на рисунке ниже). Величина этих гравитационных сил одинакова (см. уравнение выше), но направление вектора каждой из них всегда указывает прямо на другой объект.
Мы найдем другие примеры пар 3-го закона Ньютона, когда вы узнаете о контактных взаимодействиях. Когда мы обсуждаем контактные взаимодействия, оказывается, что они являются результатом электростатической силы.
Если силы одинаковой величины, почему движение не одинаково?
Движение систем регулируется принципом импульса. В этом случае вам может быть полезно подумать об ускорении системы, которое говорит вам, как изменяется скорость системы. В то время как Земля и Луна испытывают гравитационную силу одинакового размера, небольшая масса Луны (по сравнению с Землей) приводит к гораздо большему ускорению Луны, и это изменение скорости Луны велико (по сравнению с Землей). 92}$$
92}$$
Таким образом, ускорение, которое испытала бы Земля из-за одного человека, составляет около 0,000000000000000000000001*$g$! Это значение невероятно маленькое ; мы часто пренебрегаем изменениями в движении Земли из-за объектов, которые не являются астрономически большими. В этих заметках векторное ускорение за счет гравитационных взаимодействий рассчитывается в явном виде.
(Подробнее) Современные гравитационные модели
Ньютоновская модель силы тяготения долгие годы считалась одной из самых простых и объяснительных моделей. С тех пор мы сделали наблюдения, которые больше не соответствуют модели Ньютона (например, гравитационное линзирование). Наша лучшая модель гравитации, которой продолжают соответствовать наблюдения, называется «общая теория относительности» (ОТО) и была разработана Альбертом Эйнштейном. Хотя эта модель дает нам гораздо лучшие предсказания и объяснения множества наблюдений, мы по-прежнему используем ньютоновскую модель силы тяготения по двум причинам: (1) он может дать разумные предсказания для многих случаев , и (2) математика, используемая в ОТО, достаточно сложна, поэтому вам потребуется больше знаний в области физики и математики, чтобы глубже понять ее использование.
Примеры
Расчет гравитационной силы
Пример видео: гравитационная сила и кинематические уравнения на Луне
1)
Мы называем этот «закон» моделью, поскольку, как и все физические формулы, его предсказательная сила ограничена. Ньютон был невероятно разочарован тем, что движение Меркурия нельзя было предсказать по его «закону». Фактически пришлось разрабатывать новую модель.
Значение Силы
Сила — это толчок или притяжение объекта в результате взаимодействия объекта с другим объектом. Всякий раз, когда происходит взаимодействие между двумя объектами, на каждый из объектов действует сила. Когда взаимодействие прекращается, два объекта больше не испытывают силы. Силы только существуют в результате взаимодействия.
Контакт против сил действия на расстоянии
Для простоты все силы (взаимодействия) между объектами можно разделить на две широкие категории:
- контактные силы и
- силы, возникающие в результате действия на расстоянии
Контактные силы — это те виды сил, которые возникают, когда два взаимодействующих объекта воспринимаются как физически контактирующие друг с другом. Примеры контактных сил включают силы трения, силы растяжения, нормальные силы, силы сопротивления воздуха и приложенные силы. Эти специфические силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.
Примеры контактных сил включают силы трения, силы растяжения, нормальные силы, силы сопротивления воздуха и приложенные силы. Эти специфические силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.
Силы действия на расстоянии — это такие типы сил, которые возникают, даже когда два взаимодействующих объекта не находятся в физическом контакте друг с другом, но способны оказывать толчок или тягу, несмотря на их физическое разделение. Примеры сил действия на расстоянии включают гравитационные силы. Например, Солнце и планеты притягивают друг друга, несмотря на их большое пространственное разделение. Даже когда ваши ноги отрываются от земли и вы больше не находитесь в физическом контакте с землей, между вами и Землей существует гравитационное притяжение. Электрические силы – это силы действия на расстоянии. Например, протоны в ядре атома и электроны вне ядра испытывают электрическое притяжение друг к другу, несмотря на их небольшое пространственное разделение. А магнитные силы — это силы действия на расстоянии. Например, два магнита могут оказывать магнитное притяжение друг на друга, даже если их разделяет расстояние в несколько сантиметров. Эти специфические силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.
А магнитные силы — это силы действия на расстоянии. Например, два магнита могут оказывать магнитное притяжение друг на друга, даже если их разделяет расстояние в несколько сантиметров. Эти специфические силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.
Примеры контактных сил и сил действия на расстоянии перечислены в таблице ниже.
Сила – это величина, которая измеряется с использованием стандартной метрической единицы, известной как Ньютон . Ньютон обозначается буквой «Н». Сказать «10,0 Н» означает 10,0 ньютонов силы. Один ньютон — это сила, необходимая для придания массе 1 кг ускорения 1 м/с/с. Таким образом, можно установить следующую единицу эквивалентности:
Ньютон обозначается буквой «Н». Сказать «10,0 Н» означает 10,0 ньютонов силы. Один ньютон — это сила, необходимая для придания массе 1 кг ускорения 1 м/с/с. Таким образом, можно установить следующую единицу эквивалентности:
Сила является векторной величиной. Как вы узнали из предыдущего модуля, векторная величина — это величина, которая имеет как величину, так и направление. Чтобы полностью описать силу, действующую на объект, вы должны описать как величину (размер или числовое значение), так и направление. Таким образом, 10 Ньютонов не является полным описанием силы, действующей на объект. Напротив, 10 Ньютонов вниз — это полное описание силы, действующей на объект; даны как величина (10 ньютонов), так и направление (вниз).
Поскольку сила — это вектор, имеющий направление, обычно силу представляют с помощью диаграмм, на которых сила представлена стрелкой. Такие векторные диаграммы были введены в более раннем разделе и используются на протяжении всего изучения физики. Размер стрелки отражает величину силы, а направление стрелки показывает направление, в котором действует сила. (Такие диаграммы называются диаграммами свободного тела и обсуждаются далее в этом уроке.) Более того, поскольку силы являются векторами, действие одной силы на объект часто компенсируется действием другой силы. Например, эффект направленной вверх силы в 20 ньютонов, действующей на книгу, равен отменяет под действием направленной вниз силы в 20 ньютонов, действующей на книгу. В таких случаях говорят, что две отдельные силы уравновешивают друг друга ; не было бы неуравновешенной силы, действующей на книгу.
Такие векторные диаграммы были введены в более раннем разделе и используются на протяжении всего изучения физики. Размер стрелки отражает величину силы, а направление стрелки показывает направление, в котором действует сила. (Такие диаграммы называются диаграммами свободного тела и обсуждаются далее в этом уроке.) Более того, поскольку силы являются векторами, действие одной силы на объект часто компенсируется действием другой силы. Например, эффект направленной вверх силы в 20 ньютонов, действующей на книгу, равен отменяет под действием направленной вниз силы в 20 ньютонов, действующей на книгу. В таких случаях говорят, что две отдельные силы уравновешивают друг друга ; не было бы неуравновешенной силы, действующей на книгу.
Можно представить себе и другие ситуации, в которых две отдельные векторные силы компенсируют друг друга («уравновешивают»), но существует третья отдельная сила, которая не уравновешивается другой силой. Например, представьте книгу, скользящую по шероховатой поверхности стола слева направо.




 psu.edu
psu.edu