Физические основы механики

Представим себе диск, равномерно вращающийся с угловой скоростью . Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).

Рис. 8.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском

Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины оказывается равной произведению массы шарика на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)

где — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К’, в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:

Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции

направленной от центра диска 0′ по радиус-вектору .

Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:

Здесь — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.

Видео 8.4. Центробежная сила инерции: подвешенные шарики

При произвольном положении начала отсчета на оси вращения, радиус-вектор некоторой материальной точки всегда можно представить в виде

где _парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор на оси вращения) составляющая радиус вектора , а — перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы

учитывая, что векторное произведение и скалярное произведение равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде

Таким образом, в общем случае, при произвольном выборе начала отсчета на оси вращения, для любого положения материальной точки, действующую на неё центробежную силу инерции, можно записать в виде

Видео 8. 5. «Поразительное» поведение цепи — и здесь не обошлось без центробежной силы инерции. Цепь легкая, почти без трения между звеньями

Видео 8.6. «Поразительное» поведение цепи 2. Цепь тяжелая, с большим трением между звеньями

Пример. Сосуд с жидкостью вращается с угловой скоростью вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.

Рис. 8.4. Форма поверхности вращающейся жидкости

Задачу решаем в системе отсчета, вращающейся вместе с жидкостью. В этой системе жидкость неподвижна, но кроме силы тяжести на нее действует центробежная сила инерции. Поверхность жидкости симметрична относительно оси вращения. Рассмотрим сечение этой поверхности какой-нибудь вертикальной плоскостью, содержащей ось вращения, которую мы примем за ось .

Возьмем на поверхности элемент жидкости массой , расположенный в точке с координатой . На него действует сила тяжести и центробежная сила инерции (здесь координата есть расстояние от оси вращения, а и — единичные орты).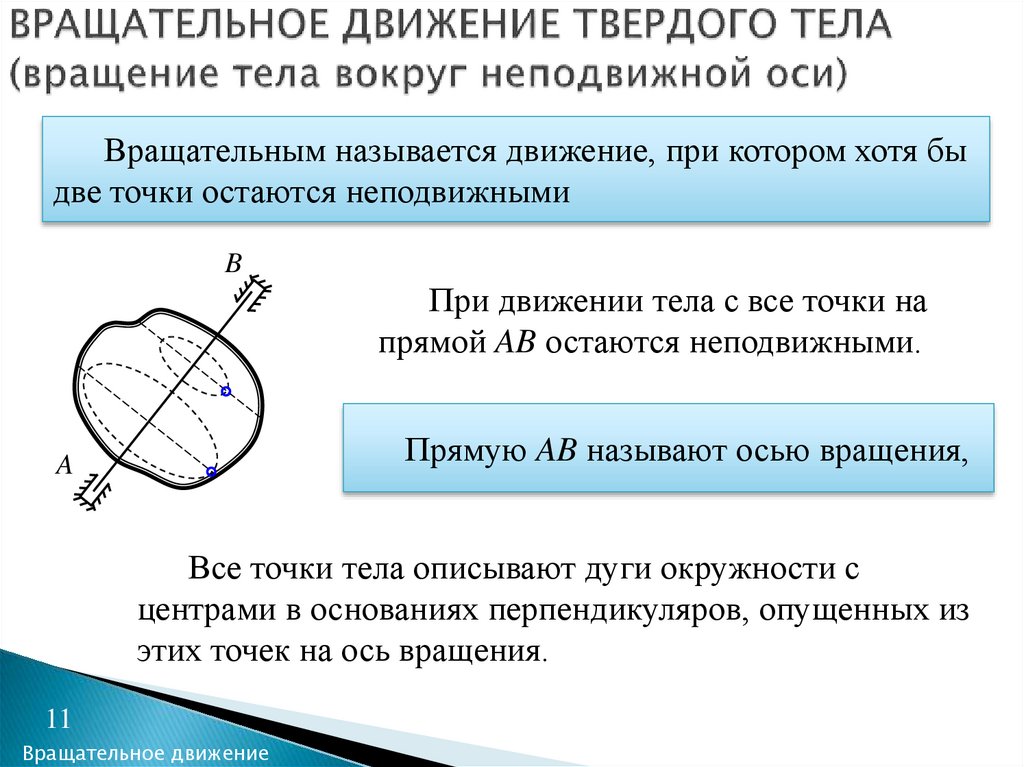

Результирующая этих сил наклонена к вертикали под углом таким, что

Поверхность жидкости, описываемая функцией , всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений

то есть как производную. Получаем уравнение

которое легко интегрируется:

Это уравнение, как известно, описывает параболу. Вращение этой параболы задает параболоид вращения. Таким образом, поверхность вращающейся жидкости принимает форму параболоида вращения. При имеем , то есть плоскую горизонтальную поверхность.

Видео 8.7. Циркулярная «пила» из бумаги – неожиданное применение центробежной силы инерции

Видео 8.8. Сила Кориолиса: траектория движения шарика по вращающейся платформе

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.–— стр.349–353 (§66): детально обсуждается вес тел и проблема взвешивания на Земле.

Центробежная сила • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения.

Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)

Стороннему наблюдателю, однако, всё будет представляться иначе. Когда машина закладывает вираж, наблюдатель сочтет, что вы просто продолжаете прямолинейное движение, как это и делало бы любое тело, на которое не оказывает действия никакая внешняя сила; а автомобиль отклоняется от прямолинейной траектории. Такому наблюдателю покажется, что это не вас прижимает к дверце машины, а, наоборот, дверца машины начинает давить на вас.

Впрочем, никаких противоречий между этими двумя точками зрения нет. В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.

Поскольку не все наблюдатели видят действие этой силы, физики часто называют центробежную силу фиктивной силой или псевдосилой. Однако мне кажется, что такая интерпретация может вводить в заблуждение. В конце концов, едва ли можно назвать фиктивной силу, которая ощутимо придавливает вас к дверце автомобиля. Просто всё дело в том, что, продолжая двигаться по инерции, ваше тело стремится сохранить прямолинейное направление движения, в то время как автомобиль от него уклоняется и из-за этого давит на вас.

Чтобы проиллюстрировать эквивалентность двух описаний центробежной силы, давайте немного поупражняемся в математике. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v²/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv²/r.

Теперь обобщим сказанное: любое тело, движущееся по криволинейной траектории, — будь то пассажир в машине на вираже, мяч на веревочке, который вы раскручиваете над головой, или Земля на орбите вокруг Солнца — испытывает на себе действие силы, которая обусловлена давлением дверцы автомобиля, натяжением веревки или гравитационным притяжением Солнца. Назовем эту силу F. С точки зрения того, кто находится во вращающейся системе отсчета, тело не движется. Это означает, что внутренняя сила F уравновешивается внешней центробежной силой:

    F = mv²/r

Однако с точки зрения наблюдателя, находящегося вне вращающейся системы отсчета, тело (вы, мяч, Земля) движется равноускоренно под воздействием внешней силы. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:

    F = ma = mv²/r

Но тем самым мы получили в точности уравнение для наблюдателя, находящегося во вращающейся системе отсчета. Значит, оба наблюдателя приходят к идентичным результатам относительно величины действующей силы, хотя и исходят из разных предпосылок.

Это очень важная иллюстрация того, что представляет собою механика как наука. Наблюдатели, находящиеся в различных системах отсчета, могут описывать происходящие явления совершенно по-разному. Однако, сколь бы принципиальными ни были различия в подходах к описанию наблюдаемых ими явлений, уравнения, их описывающие, окажутся идентичными. А это — не что иное, как принцип инвариантности законов природы, лежащий в основе теории относительности.

Награда за вращательную кинематику

Крутящий момент

Крутящий момент (τ) — это сила, которая заставляет объект вращаться. Если вы думаете об использовании гаечного ключа для затягивания болта, то чем ближе к болту вы прикладываете усилие, тем труднее повернуть ключ, а чем дальше от болта вы прикладываете усилие, тем легче поворачивать ключ. . Это связано с тем, что вы создаете больший крутящий момент, когда прикладываете силу на большем расстоянии от оси вращения.

Давайте рассмотрим пример гаечного ключа, поворачивающего болт. Сила приложена на расстоянии от оси вращения. Назовите это расстояние r. Когда вы прикладываете силы в 90 градусов к воображаемой линии, идущей от оси вращения к точке приложения силы (известной как линия действия), вы получаете максимальный крутящий момент. По мере того, как угол, под которым прикладывается сила, уменьшается (θ), уменьшается и крутящий момент, заставляющий болт поворачиваться. Следовательно, вы можете рассчитать приложенный крутящий момент как:

В некоторых случаях физики называют rsinθ плечом рычага или плечом момента системы. Плечо рычага — это перпендикулярное расстояние от оси вращения до точки приложения силы. С другой стороны, вы можете думать о крутящем моменте как о компоненте силы, перпендикулярной рычагу, умноженной на расстояние r. Единицами крутящего момента являются единицы силы × расстояние или ньютон-метры (Н·м).

 

 

Вопрос: Пиратский капитан берет штурвал и поворачивает штурвал своего корабля, прикладывая к спице колеса силу в 20 ньютонов. Если он приложит силу в радиусе 0,2 м от оси вращения под углом 80° к линии действия, какой крутящий момент он приложит к колесу?

Ответ:

 

 

 

 

Вопрос: Механик затягивает выступы на шине, прилагая крутящий момент 110 Н·м под углом 90° к линии действия. Какая сила приложена, если длина ключа 0,4 м?

Ответ:

Вопрос: Какой длины должен быть ключ, если механик способен приложить усилие только 200 Н?

Ответ:

 

Объекты, которые не имеют вращательного ускорения или имеют нулевой чистый крутящий момент, называются вращательно-равновесными. Это означает, что любой чистый положительный (против часовой стрелки) крутящий момент уравновешивается равным чистым отрицательным крутящим моментом (по часовой стрелке).

 

Момент инерции

Ранее инерционная масса объекта (его поступательная инерция) определялась как способность этого объекта сопротивляться линейному ускорению. Точно так же вращательная инерция объекта или момент инерции описывает сопротивление объекта вращательному ускорению. Символ момента инерции объекта — I.

Объекты, большая часть массы которых находится вблизи оси вращения, имеют небольшую инерцию вращения, в то время как объекты, масса которых находится дальше от оси вращения, имеют большую инерцию вращения.

Для обычных объектов вы можете найти формулу их момента инерции. Для более сложных объектов момент инерции можно рассчитать, взяв сумму всех отдельных частиц массы, составляющих объект, умноженную на квадрат их радиуса от оси вращения. Это может быть довольно обременительно с использованием алгебры, и поэтому обычно предоставляется курсам, основанным на исчислении, или числовым приближениям с использованием вычислительных систем.

 

Вопрос: Рассчитайте момент инерции твердого шара массой 10 кг и радиусом 0,2 м.

Ответ:

 

Вопрос: Рассчитайте момент инерции полого шара массой 10 кг и радиусом 0,2 м.

Ответ:

 

Второй закон Ньютона для вращения

В главе о динамике вы узнали о силах, заставляющих объекты ускоряться. Чем больше результирующая сила, тем больше линейное (или поступательное) ускорение, и чем больше масса объекта, тем меньше поступательное ускорение.

 

Вращательный эквивалент этого закона, второй закон Ньютона для вращения, связывает крутящий момент объекта с его результирующим угловым ускорением. Чем больше чистый крутящий момент, тем больше ускорение вращения, и чем больше инерция вращения, тем меньше ускорение вращения:

 

Вопрос: Какое угловое ускорение испытывает однородный сплошной диск массой 2 кг и радиусом 0,1 м при приложении к нему крутящего момента 10 Н·м? Предположим, что диск вращается вокруг своего центра.

Ответ:

 

Вопрос: Кругосветка на детской площадке с моментом инерции 100 кг·м ² начинается в состоянии покоя и ускоряется силой 150 Н в радиусе 1 м от его центра. Если эту силу приложить под углом 90° от линии действия в течение 0,5 секунды, какова конечная скорость вращения Round-A-Bout?

Ответ: Начните с создания таблицы кинематики вращения:

Поскольку вы знаете только два элемента на столе, вы должны найти третий, прежде чем решать это с помощью уравнений кинематики вращения. Поскольку вам дан момент инерции Round-A-Bout, а также приложенная сила, вы можете найти угловое ускорение, используя 2-й закон Ньютона для вращательного движения.

Теперь, используя свою кинематику вращения, определите конечную угловую скорость кругового движения.

Расчет эффективной силы (простое вращение)

Расчет эффективной силы (простое вращение)

Далее: Расчет эффективной силы Вверх: Вращающаяся система координат Предыдущая: Вращающаяся система координат Содержание

Расчет эффективной силы (простое вращение)

Чтобы рассчитать эффективная сила простым способом мы будем использовать системы координат вращающегося стола и рассчитать силу при когда две системы координат совпадают. Силы из-за вращения не зависят от времени, так что это все еще общее. Лучше всего будет работать с преобразование из вращающейся (заштрихованной) системы отсчета в инерциальную .

Это последнее уравнение является важным. На самом деле это верно для производной по времени любого вектора, а не только . Пока это верно только при совпадении осей координат, как при но, поскольку это верно для любого вектора, мы можем применить его к .

Таким образом, в производной по времени от . также не зависит от вращения и считается постоянным, поэтому мы имеем и у нас есть для общего вектора (в ) куда — вектор угловой скорости вращающейся системы координат в неподвижной системе.

Чтобы получить ускорение (и силы), возьмите вторую производную по времени.

Это дает нам фактическую силу плюс действующую силу во вращающейся системе. Три члена — это реальная сила, центробежная сила , а сила Кориолиса . Центробежная сила находится в плоскости вращения и параллельна . Сила Кориолиса перпендикулярна как скорости, так и .

Теперь пойдем вернуться к первому эксперименту . Сначала мы можем вычислить скорость во вращающейся раме при . (Оси координат соответствуют .)

Это вполне соответствует пути, нарисованному на диаграмме.

Теперь мы можем вычислить действующая сила во вращающейся раме .

Это также согласуется с направлением ускорения, показанным на диаграмме при . Потребуются некоторые усилия, чтобы интегрировать уравнения, чтобы получить точный путь. Это легче сделать, просто преобразовав путь.

Эта задача является иллюстративной, но на самом деле это не обычный тип задач, когда мы знаем положение и скорость вращающегося тела.