9.2: Трение и тяга

Одна из наиболее важных основ, которую ученики должны изучить перед тем, как приступить к проектированию ходовой части, это трение.

ТРЕНИЕ — это сила, сопротивляющаяся движению, когда две поверхности притираются друг к другу. Это исключительно противодействующая сила, возникающая, когда две поверхности находятся в контакте друг с другом и под действием силы, заставляющей их скользить друг относительно друга. Если на объект не воздействует сила, провоцирующая его к попытке движения, трение также отсутствует. Отсутствие воздействующей силы означает отсутствие противодействующей силы.

Существуют два типа трения: статическое трение и кинетическое трение.

Статическое трение представляет собой силу трения, действующую между двумя объектами, которые НЕ перемещаются друг относительно друга. Для того, чтобы сдвинуть что-либо, требуется предварительное усилие. Если значение силы, пытающейся сдвинуть объект, меньшее значения силы статического трения, объект не сможет сдвинуться с места.

Кинетическое трение — это сила трения, действующая между двумя поверхностями, перемещающимися (скользящими) друг относительно друга.

Как только объект преодолел статическое трение и начал движение, он попадает под воздействие кинетического трения, сопротивляющегося движению.

На графике выше показана обратная взаимосвязь между приложенной силой и трением. С увеличением приложенной силы, противодействующая сила трения также увеличивается. Вплоть до момента, когда объект сдвинется с места, на него действует статическое трение. Как только значение приложенной силы превысит максимальное статическое трение, масса начнет двигаться. Сразу после начала движения объект окажется под действием кинетического трения. Статическое трение больше кинетического трения, поэтому если масса уже сдвинулась, для дальнейшего скольжения ей потребуется меньше силы.

Оба типа трения можно имитировать, уперев ладонь одной руки в ладонь другой руки и попробовав подвигать ими скользящим движением. Этому движению будет противодействовать текстура кожи и величина приложенной силы. Чем плотнее ладони прижаты друг к другу, тем сложнее ими двигать. Это статическое трение.

По мере увеличения скользящей силы, руки начинают скользить и двигаться друг относительно друга. Это кинетическое трение. Можно заметить, что как только руки преодолели статическое трение, двигать ими стало проще.

Существует два фактора, определяющих максимальную силу трения, возникающую между двумя поверхностями: «цепкость» поверхностей (известная как коэффициент трения поверхностей), а также плотность прижатия поверхностей друг к другу (известная как нормальная сила).

Максимальная сила трения (Ff) между двумя поверхностями равна коэффициенту трения (Cf) этих поверхностей, умноженному на нормальную силу (N), удерживающую поверхности вместе.

Максимальная сила трения = (Коэффициент трения) х (Нормальная сила)

Ff = Cf x N

КОЭФФИЦИЕНТ ТРЕНИЯ:

Как уже говорилось выше, коэффициент трения является постоянной величиной, отражающей «цепкость» двух поверхностей, скользящих друг относительно друга. Необходимо обратить внимание на то, что это трение не одной скользящей поверхности, а двух. Например, покрышка сама по себе НЕ ОБЛАДАЕТ коэффициентом трения, но покрышка, скользящая по мостовой, ОБЛАДАЕТ коэффициентом трения.

Коэффициент трения скользких объектов чрезмерно мал, тогда как коэффициент трения липких объектов — очень велик. Эта постоянная величина определяется для пары поверхностей (не для единственной поверхности). Каждая пара материалов обладает коэффициентами статического и кинетического трения.

При этом нельзя путать чистое трение с действительно липкими поверхностями, такими как, например, изолента или покрытия с большим коэффициентом трения, связывающиеся с другими поверхностями. Подобные поверхности, соединяясь, должны выглядеть как одна. Например, изолента сопротивляется скольжению даже в том случае, когда нормальная сила отсутствует или имеет отрицательное значение.

НОРМАЛЬНАЯ СИЛА:

Сила, прижимающая две скользящие поверхности друг к другу, называется нормальной силой. Действие нормальной силы всегда направлено перпендикулярно двум поверхностям (в противном случае эта сила может действовать как нормальная сила лишь частично). Зачастую нормальная сила, воздействующая на две поверхности, является массой одного объекта, располагающегося сверху на другом объекте. В этом случае действие нормальной силы спровоцировано гравитацией.

Как показано на схеме выше, если объект лежит на наклонной поверхности, гравитация действует на две скользящие поверхности не под прямым углом. В этом случае, только часть массы объекта действует как нормальная сила.

ТЯГА:

ТЯГА может быть определена как трение между ведущим колесом и поверхностью, по которой оно катится. Это количество силы, которое колесо прикладывает к поверхности перед тем, как соскользнуть. Колесо обладает разной тягой на различных поверхностях. Как описывалось выше, значение коэффициента трения определяется для любых двух поверхностей.

Из Блока 7 и схемы, представленной выше, видно, что колесо прикладывает силу к поверхности под действием крутящего момента. Тем не менее, если бы колесо катилось по льду, оно просто проскальзывало бы, не двигаясь с места. Трение, возникающее между колесом и поверхностью земли, необходимо для создания линейного движения. Это тяговое усилие, или сила тяги.

Необходимо обратить внимание на то, что сила тяги равна силе трения между колесом и поверхностью. Если колесо катится по поверхности, а не скользит, сила тяги равна статическому трению. Если приложенная сила превышает максимальное статическое трение, колесо начинает скользить, и теперь сила тяги равна максимальному кинетическому трению.

Увеличение тяги:

Так как тяга зависит от трения между поверхностью и колесом, чтобы увеличить ее значение, необходимо увеличить трение. Как говорилось выше, трение между объектами зависит от коэффициента трения между ними (в данном случае, между колесом и поверхностью, по которой оно катится) и нормальной силы (массы робота, прижимающей колеса к поверхности). Чтобы увеличить тягу, увеличить либо коэффициент трения (сцепление колес), либо нормальную силу, действующую на колеса (массу робота).

 

Сборка толкающего робота:

Чтобы собрать робота, способного толкать или тянуть с большой силой, необходимо включить в конструкцию два элемента: колеса повышенной проходимости и значительный крутящий момент для приведения их в движение. Трение — это противодействующая сила. Если нет приложенной силы, сила трения также отсутствует. Чтобы увеличить тягу, к колесам необходимо приложить крутящий момент, достаточный для достижения максимального статического трения колес.

Автомобиль может обладать огромной тягой, но при малых размерах двигателя он не сможет толкать или тянуть что либо. Поэтому маленькие автомобили не могут тянуть за собой трейлеры или катера на прицепах.

Трение в системе VEX:

В системе проектирования VEX Robotics Design System используется множество элементов, которые могут применяться для получения трения, включая различные типы колес. Каждый из них обладает характеристиками, необходимыми для использования на различных поверхностях. Для проектировщика очень важно экспериментальным путем определить тип колес, требуемый для каждой отдельной задачи.

Трение между колесами и поверхностью пола — не единственный вид трения, применяемый в конструкции робота VEX. Существует также трение, притормаживающее вращающиеся компоненты робота и уменьшающее количество мощности на выходе электромотора. В системе проектирования VEX Robotics Design System есть ряд частей, предназначенных для уменьшения трения. Использовать соединения типа «металл к металлу» в подвижных системах не рекомендуется. Пластиковые части, например, опорные блоки, прокладки и шайбы, позволяют снизить значение трения в точках контакта подвижных частей.

Сила тяги

Сила тяги: определение

Определение 1

Силой тяги называют силу, прикладываемую к телу для поддержании его в постоянном движении.

Прекращение действия силы тяги приводит к остановке вследствие трения, вязкости окружающей среды и других противодействующих движению сил.

Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).

Величина ускорения обратнопропорциональна массе тела (чем оно массивнее, тем труднее его вывести из состояния инерции) и прямопропорциональна интенсивности приложенной силы. Таким образом:

$F = m \cdot a$,

где:

• $F$ — сила,
• $m$ — масса,
• $a$ — ускорение.

Замечание 1

Эта формула отражает Второй закон Ньютона.

Формулы для расчета

В качестве примера силы тяги, выводящей тело из состояния покоя, можно рассмотреть спортсмена, поднимающего штангу. В исходном состоянии штанга находится в состоянии инерции (остается неподвижной). Когда спортсмен отрывает ее от земли, его мышцы должны сокращаться с такой силой, чтобы она превысила вес штанги, т.е. силу, с которой ее притягивает гравитационное поле Земли. Если штангисту удастся оторвать штангу от пола — значит она переместится вверх на некоторое расстояние, т.е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:

$F_м$ > $F_т$, т.е. $F_м$ >$ m \cdot g$,

где $F_м$ — сила мышц (в данном случае сила тяги), $F_т$ — сила тяжести (гравитация), $m$ — масса, $g$ — ускорение свободного падения.

Состояние движения по инерции следует отличать от равномерного движения, когда сила тяги уравновешивается противодействующими силами. Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:

$F = m \cdot \frac{v}{t}$

Здесь ускорение выражено как частное от деления скорости на время разгона.

Силу тяги можно также выразить через мощность — способность некоторого источника энергии совершать работу. Чем мощность выше — тем за меньшее время этот источник разовьет силу, способную разогнать тело массой $m$ до требуемой скорости $v$. Работа же прямопропорциональна силе, которая ее совершила:

$A = F \cdot s$,

где $s$ — расстояние, на которое сила переместила данное тело.

Поскольку расстояние можно выразить через скорость и время,

$s = v \cdot t$,

а мощность есть работа, выполняемая в единицу времени

$N = \frac{A}{t}$

можно составить уравнения:

$\frac{A}{t} = \frac{F \cdot v \cdot t}{t} \implies N = F \cdot v \implies F = \frac{N}{v}$

Пример 1

Вычислить силу тяги автомобиля, движущегося с ускорением $3 м/с^2$, если его масса составляет 1,5 тонны, а сила трения — 10% от силы тяжести.

Рассмотрим силу тяги как сумму двух сил:

1. разгоняющей автомобиль с заданным ускорением: $F_1 = m \cdot a$, где $m$ — масса, $a$ — ускорение;
2. преодолевающей силу трения: $F_2 = \mu \cdot m \cdot g$, где $\mu$ — коэффициент силы трения, $g$ — ускорение свободного падения.

Подставив числовые значения в формулу

$F = F_1 + F_2 = m \cdot a + \mu \cdot m \cdot g$

получим, попутно переведя тонны в единицы СИ килограммы,

$F = 1500 \cdot 3 + 0,1 \cdot 9,8 \cdot 1500 = 1500 \cdot (3 + 0,98) = 5970$

Ответ: 5970 ньютонов.

Формула силы тяги | Все формулы

Силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):

Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (F_T) войдет в уравнение:

где a – ускорение, с которым движется автомобиль.

Единицы измерения силы тяги

Основной единицей измерения силы в системе СИ является: [F_T]=Н

В СГС: [F_T]=дин

В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.

Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют на транспорт делить на две части, при этом одни силы называть силами тяги , а другие — силами сопротивления  . Это делается для того, чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:

Примеры решения задач

Пример

Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна =0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?

Решение. Сделаем рисунок.

В качестве основы для решения задачи используем второй закон Ньютона:

Спроектируем уравнение (1.1) на оси X и Y:

По условию задачи:

Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:

Переведем массу в систему СИ m=1т=10³ кг, проведем вычисления:

Ответ. F_T=2,98 кН

определение, формулы для вычисления и примеры из реальной жизни

Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.

Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:

• силы трения (покоя, качения, скольжения),
• сопротивления воздуха (газа),
• сопротивления воды и др.

Первый и второй законы Ньютона

Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.

Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.

Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).

Примеры из жизни

Насколько вы сильны?

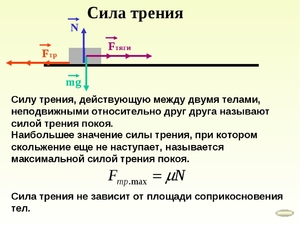
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.

Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.

Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.

Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).

Насколько силён ваш автомобиль?

Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.

Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).

Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.

Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н ~ 2,94 кН (килоньютона).

Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)~0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).

Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:

• человека,
• лошади,
• паровоза,
• автомобиля,
• космической ракеты и всех прочих видов техники.

Видео

В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.

Решите легенькую задачку по динамике…физики, пожалуйста!!(ответ есть)

Так как движение равномерное, то сила тяги, по модулю= силе трения. Сила трения вычисляется по формуле: Fтр=м*N. (м (мю) — коэффициент трения, N-сила реакции опоры, для горизонтально движущегося тела=силе тяжести. ( по модулю) N=m*g. Подставим и выразим коэф. трения. Fтр=м*m*g. м=Fтр / m*g. ( m=200г=0,2кг, g=10м/c^2) м=0,6 / 0,2*10=0,3.

Динамометр показывет векторную сумму всех сил действующих на брусок. Так как на брусок действуют две силы — сила тяжести и сила трения — и они направлены в противоположные стороны, то их разность и составляет 0, 6 Н. Найдем силу тяжестти, предварительно переведем 200 г. в кг (200 г . = 0,2 кг) , сила тяжести равна 0, 2 *9, 8 = 1, 96 Н. Тогда сила трения равна 1, 96 — 0, 6- 1, 36(Н) Ответ: 1, 36 Н

Сила трения равна произведению коэффициента трения на силу нормальной реакции опоры. Эта сила в свою очередь равна произведению массы тела на ускорение св. падения. В задаче 2Н. Если брусок равномерно тянут с силой тяги 0,6 Н, то по 2-му закону Ньютона сила трения тоже равна 0,6Н. Таким образом, чтобы найти коэффициент трения, надо силу трения 0,6Н разделить на силу нормальной реакции опоры 2Н. Ответ: 0,3.

вот именно, ты правильно решил, а тем кто отнимает силу тяжести от силы трения прошу не позорить себя и своего учителя физики

Так как движение равномерное, то сила тяги, по модулю= силе трения. Сила трения вычисляется по формуле: Fтр=м*N. (м (мю) — коэффициент трения, N-сила реакции опоры, для горизонтально движущегося тела=силе тяжести. ( по модулю) N=m*g. Подставим и выразим коэф. трения. Fтр=м*m*g. м=Fтр / m*g. ( m=200г=0,2кг, g=10м/c^2) м=0,6 / 0,2*10=0,3.

если равнодействующая всех сил равна нулю например сила тяги и сила трения то их общая работа равна 0?

Ну почему? Вон когда машина зстряла в грязи и жмут на газ изо всех сил — то вообще-то и мотор сгореть может) А при нулевой работе о не сгорит…

Отнюдь, и работа совершается против сил трения, и уходит на нагрев по большей части. Как найти? Да по классической формуле, S*Fтр

Если их сила равна нуля: то они отдают свою силу движущейся системе, Т. относительности, и принципиальная С. энергии.

Нет. Работа не обязана равняться нулю. Машина движется равномерно по шоссе. Сила тяги (она же сила трения покоя) равна силе сопротивления движению. Но работа сила тяги рана нулю, а работа силы сопротивления отрицательная.

Нет, конечно, и даже механическая. Силы могут «развратить и заколебать» тело (шутка)! Вы определение механической работы гляньте — в ней перемещение ТОЧКИ ПРИЛОЖЕНИЯ силы фигурирует, а не перемещение тела. <a rel=»nofollow» href=»http://www.femto.com.ua/articles/part_2/3206.html» target=»_blank»>http://www.femto.com.ua/articles/part_2/3206.html</a> А кто вам сказал, что движение обязано быть поступательным?

Да, равна нулю за исключением некоторых хитрых случаев. Работа нескольких сил равна сумме их работ. Работа отрицательной тоже бывает.

не работа, а результат работы

Иногда ноль в результате — это тоже работа, если нужно что то остановить например.

Работа ИСО для внешнего наблюдателя =1, для внутреннего=0

Общая сила, возникающая при взаимодействии между собой двух противоборствующих друг другу, равных по их силам сил, не равна при этом 0!!! Потому что внутри реальных физических сил, подчиняющихся законам физики, всегда существуют микро-колебания атомов внутри их физической среды, и эти колебания не имеют равнодействующие их силы воздействий внутри этих тел, а имеют их направленными в общем целом, асимметрично-симметричным образом!!! А при оказании на них, на эти тела, воздействия какой-нибудь дополнительной, сторонней физической силы, допустим силы упругого давления оказываемого на них, на их структуру снаружи, внутренние микро-колебания атомов физической среды этих тел, по этой причине ускоряются, и начинают содержать в себе большую энергию, и двигаться с меньшей их амплитудой, но при этом так же асимметрично-симметричным их образом, во внутренней физической структуре этих тел, и если посмотреть на эти колебания в очень супер мощный микроскоп, то можно увидеть в него то, как эти тела микро-вибрируют во внешних видимых их очертаниях, по причине этих их микро-колебаний атомов их структуры, нарушить же закон сохранения импульса этим телам не позволяет (наверное) при этом в случае их гигантского размера, их этот гигантский размер, собой пропорционально уравнивающий (чем он у них будет больше, тем и более от этого сильнее), между собой асимметрично-симметричные множественные атомные колебания в физической структуре этих тел, так как они относительно инертностно-инерционных сил, а так же и по причине усиления, своей собственной равнодействующей их общих сил, из-за увеличения их общего количества, и количества их микро-колебаний от этого, они уменьшают их общую асимметричность в их общих взаимодействиях и движении, относительно друг друга!!! И наоборот, по этой причине, если эти тела, будут их размером очень маленькими, буквально иметь количество молекул в их физическом теле, допустим в несколько сотен, всего лишь их количеством, то эти микроскопические тела, по этой причине, должны предположительно, мочь из-за этих их микро-колебаний атомов их структуры, и сильно усиливающейся асимметрии в их направлениях движения, относительно друг друга, как нарушать этим сегодняшний физический закон сохранения импульса, так и мочь по этой причине, хаотически двигаться сами, за счёт своих этих микро-колебаний атомов их среды, в пространстве, подобно тому, как движутся в пространстве Броуновские частицы, а то есть, совершать в этом пространстве за счёт этого, свои молекулярно-диффузионные движения!!!

Если сила тяги равна силе сопротивления, то работа равна той теплоте, которая выделяется при преодолении сил сопротивления плюс кинетическая энергия, которую приобрело тело при разгоне.

1-й закон. Результирующая сила 0, значит и суммарная работа 0. Движущие силы совершают работу (+А), силы сопротивления (-А).

Есть два пути (ДД — Диалектический дуализм) ответа на этот вопрос: короткий и длинный. Как известно, «нормальные герои всегда идут в обход» (смотреть «Айболит 66») — длинный путь ведущий в болото, то есть по сути ошибочный, и короткий — философский. Силы в природе в свободном состоянии не существуют, следовательно это терминологически определенное различимое явление в результате некоего взаимодействия. Отсюда простой вывод: РАБОТА ЕСТЬ МЕРА ЯВЛЕНИЯ СИЛЫ ЧЕРЕЗ ПЕРЕМЕЩЕНИЕ В ПРОСТРАНСТВЕ В РЕЗУЛЬТАТЕ ВЗАИМОДЕЙСТВИЯ МИНИМУМ ДВУХ ЧЕГО ЛИБО. В соответствии с постановленным выводом и с учетом предоставленной в вопросе информации, необходимо вопрос сформулировать в корректной форме: ПРИ КАКИХ УСЛОВИЯХ ОБЩАЯ РАБОТА СИЛ ТЯГИ И ТРЕНИЯ РАВНА НУЛЮ? То ответ появляется сам собой: — ПРИ ОТСУТСТВИИ ЭНЕРГИИ ДОСТАТОЧНОЙ ДЛЯ ПЕРЕМЕЩЕНИЯ. УРОК, КОТОРЫЙ НАДЛЕЖИТ ВСЕМ ИЗВЛЕЧЬ ИЗ ЭТОГО ЗАМЕЧАТЕЛЬНОГО ВОПРОСА: — зрить нужно в корень и не поддаваться на провокации.

В такой постановке вопроса механическая работа равна нулю, т. к. A=F*S*cos(фи). Раз F=0, то и А=0. В некоторых приведенных примера рассматривается не механическая работа, а изменение энергии с участием тепла и т. п. Чел устает просто стоя неподвижно на месте.

Если равнодействующая всех сил равна нулю, то тело находится в состоянии покоя или равномерного прямолинейного движения.

Перемещение это преобразование или изменение как модус с убеждением в необходимости первотолчка, в котором имеют место противоречия пространства и времени, устойчивости и изменчивости. Процессы, связанные с трансформацией предметов, появлением новых качественных положений и состояний. Проще говоря — движение субстанции с ускорением. Разберитесь с определением что означает сила тяги.

Чтобы работа была равна 0, достаточно также чтобы и путь был равен 0. А лучше пить кофе 🙂 Вчера было Благовещенье