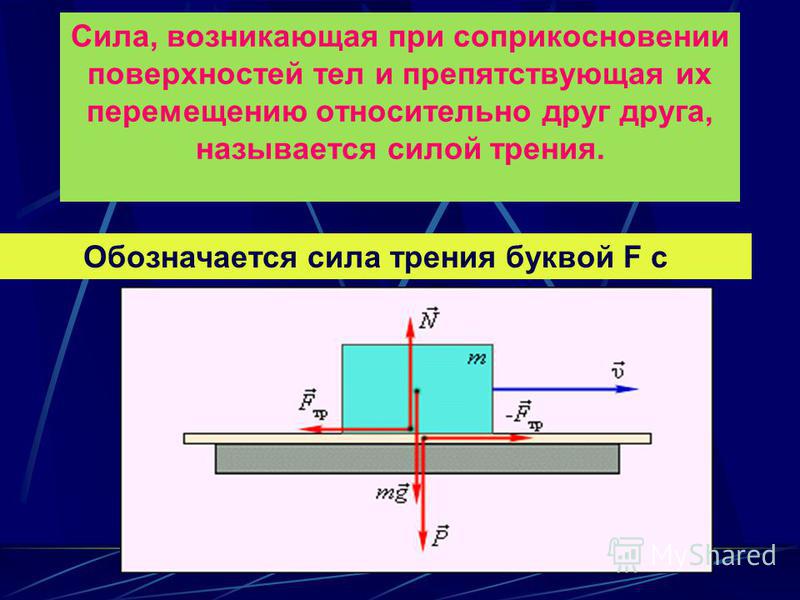
Билет 15. Сила трения.
Силы трения, как и
силы упругости, имеют электромагнитную
природу, т.е. в основе сил трения лежат
электрические силы взаимодействия
молекул. Главная особенность сил трения,
отличающая их от гравитационных сил и
сил упругости, состоит в том, что они
зависят от скорости движения тел
относительно друг друга. Сила трения
покоя – сила, действующая на данное
тело со стороны соприкасающегося с ним
другого тела вдоль поверхности
соприкосновения тел в случае, когда
тела покоятся относительно друг друга.
Сила трения покоя по модулю равна и
направлена противоположно силе,
приложенной к телу параллельно поверхности
соприкосновения его с другим телом.
Если параллельно этой поверхности не
действуют никакие силы, то сила трения
покоя равна нулю. Максимальное значение
силы трения, при котором скольжение еще
не наступает, называется максимальной
силой трения покоя. Если действующая
на покоящееся тело сила хотя бы немного
превышает максимальную силу трения
покоя, то тело начинает скользить.
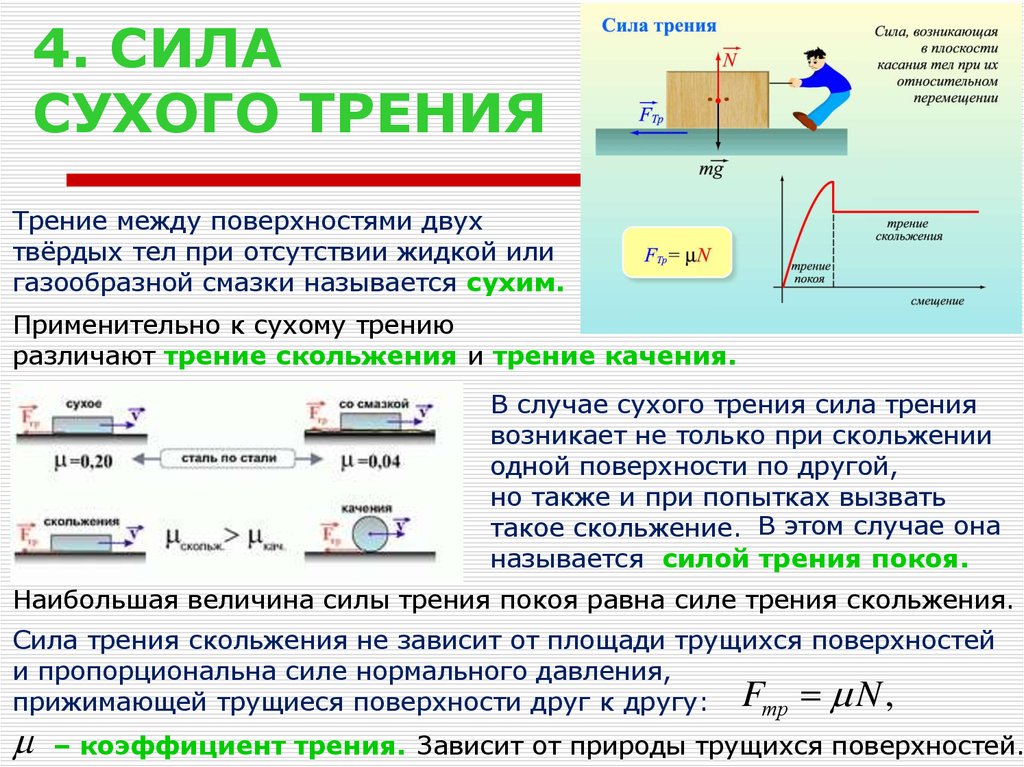
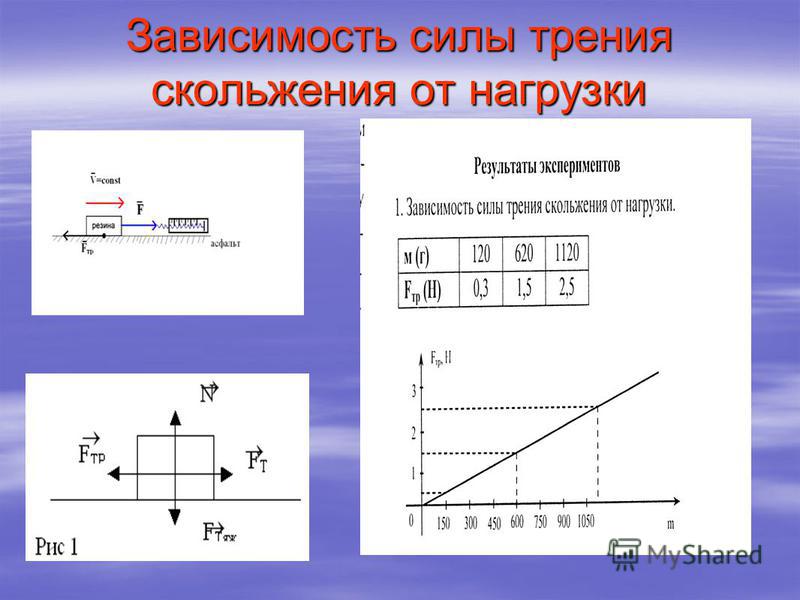
Когда тело скользит по поверхности другого тела, на него действует сила трения – сила трения скольжения. Согласно второму закону Ньютона при равномерном движении бруска равнодействующая всех сил, приложенных к нему равна нулю. Сила трения скольжения зависит от силы реакции опоры, от материала соприкасающихся тел и состояния их поверхности. Сила трения скольжения всегда направлена противоположно относительной скорости соприкасающихся тел. Модуль силы трения скольжения зависит и от модуля относительной скорости соприкасающихся тел.
Силы трения действуют
между всеми без исключения телами. Сила
трения во всех случаях препятствует
относительному движению соприкасающихся
тел. При некоторых условиях силы трения
делают это движение тел просто невозможным. Но роль сил трения – не только тормозить
движение тел. В ряде практически очень
важных случаев движение не могло бы
возникнуть без действия сил трения. На
использовании трения покоя основана
ременная и фрикционная передача вращения
от одного шкива к другому. Трение покоя
полезно и во многих других случаях. Не
будь трения, мы ничего не могли бы взять
в руками. Все предметы выскальзывали
из рук. Трение скольжения, как и трение
покоя, тоже может быть полезным и вредным.
Полезно, например, трение скольжения в
тормозных системах сухопутного
транспорта, трение скрипичного смычка
о струны. Однако во многих случаях трение
скольжения вредно. У всех машин из-за
трения скольжения происходит нагревание
и износ деталей, уменьшается коэффициент
полезного действия. Трение – явление,
сопровождающее нас везде и повсюду.
Но роль сил трения – не только тормозить
движение тел. В ряде практически очень
важных случаев движение не могло бы
возникнуть без действия сил трения. На
использовании трения покоя основана
ременная и фрикционная передача вращения
от одного шкива к другому. Трение покоя
полезно и во многих других случаях. Не
будь трения, мы ничего не могли бы взять
в руками. Все предметы выскальзывали
из рук. Трение скольжения, как и трение
покоя, тоже может быть полезным и вредным.
Полезно, например, трение скольжения в
тормозных системах сухопутного
транспорта, трение скрипичного смычка
о струны. Однако во многих случаях трение
скольжения вредно. У всех машин из-за
трения скольжения происходит нагревание
и износ деталей, уменьшается коэффициент
полезного действия. Трение – явление,
сопровождающее нас везде и повсюду.
Импульс материальной
точки – величина, равная произведению
массы точки на ее скорость. Импульс –
величина векторная. Т.к. m>0,
то импульс имеет тоже направление, что
и скорость.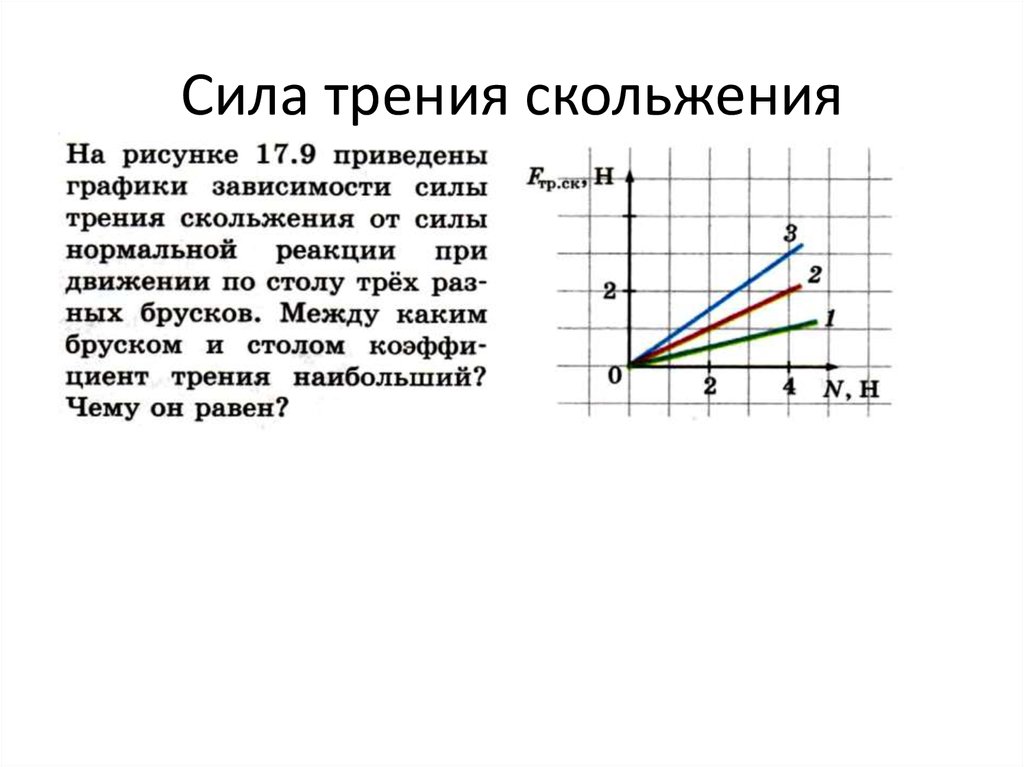
Если сумма внешних
сил, действующих на систему, равна нулю,
то равно нулю и изменение импульса
системы. Это означает, что, какой бы
интервал времени мы не взяли, суммарный
импульс в начале этого интервала и в
его конце один и тот же. Импульс системы
остается неизменным, т.е. сохраняется.
Закон сохранения импульса формулируется
так: если сумма внешних сил, действующих
на тела системы, равна нулю, то импульс
системы сохраняется. Тела могут только
обмениваться импульсами, суммарное же
значение импульса не изменяется.
Сохраняется векторная сумма импульсов,
а не сумма их модулей.
|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Наука, Ответственность, Мысли… Тивикова С. Обратная связь Отправить сообщение с сайта Партнёры |
|
Сухое трение скольжения
¶Экспериментальные объективы
Введение.
Трение — это сила, которая замедляет относительное движение любого тела при скольжении по другому телу. Сила трения, действующая на тело, параллельна поверхности, по которой скользит тело, и направлена против направления движения. Явление трения довольно сложное, особенно на микроскопическом уровне, поскольку оно зависит от природы материалов обеих контактирующих поверхностей. Сила трения зависит от шероховатости или неровностей обеих поверхностей. На макроскопическом уровне природа этой силы может быть описана простым эмпирическим законом, впервые данным Леонардо да Винчи:
Величина силы трения между несмазанными сухими поверхностями, скользящими одна по другой, пропорциональна нормальной силе, прижимающей поверхности друг к другу, и не зависит от (макроскопической) площади контакта и относительной скорости.
.{\rm nd}\) в этом перпендикулярном направлении, мы можем заключить, что величина нагрузки равна Нормальной силе \((F_N)\) поверхности, давящей на объект. Поэтому мы можем написать, что 9{\rm nd}\) Закон движения. По мере увеличения приложенной силы сила трения остается равной приложенной силе до тех пор, пока не произойдет движение. При этом максимальном значении приложенной силы сила трения также максимальна и равна
\begin{уравнение*} F_f = \mu_s F_N \end{уравнение*}
, где нижний индекс \(s\) обозначает статическое (неподвижное) трение, а \(\mu_s\) — коэффициент статического трения . Это уравнение можно использовать только в этой максимальной статической точке, также называемой точкой надвигающегося движения. В тот момент, когда приложенная сила становится больше максимальной \(f_s\text{,}\), тело приходит в движение, и этому движению противодействует сила трения, называемая кинетической (скользящей) силой трения и определяемая выражением
\begin{уравнение*} F_f = \mu_k F_N \end{уравнение*}
, где нижний индекс \(k\) обозначает кинетическое (подвижное) трение, а \(\mu_k\) — коэффициент кинетического трения .
В общем, \(\mu_k \lt \mu_s\text{;}\), то есть для преодоления статического трения требуется больше усилий, чем для преодоления кинетического трения. Коэффициенты трения обычно меньше единицы, но могут быть и больше единицы, и они зависят от природы обеих поверхностей.
Рассмотрим систему, состоящую из блока на горизонтальной поверхности, который тянут горизонтально веревкой, соединенной с подвешенным грузом. Мы можем использовать \(M\) — это масса блока на горизонтальной поверхности, а \(m\) — масса висящего блока. Сила, ускоряющая систему вперед, равна \(mg\text{.}\) Сила трения зависит от нормальной силы блока \(\mu_k (Mg)\text{.}\) Тогда вся система ускоряется с постоянным ускорением, так что второй закон Ньютона дает:
\begin{уравнение} (мг) + [-(\mu_kMg)] = (M+m)a \text{.}\label{eq-Newton-second}\tag{9.0.1} \end{уравнение}
Отсюда можно найти \(\mu_k\), что даст:
\begin{уравнение} \mu_k = \frac{ mg — (M+m) a }{ Mg}\text{.}\label{eq-Newton-mu}\tag{9.
0.2} \end{equation}
(пересмотрено: 11 октября 2017 г.)
Версию в формате PDF можно найти по адресу Friction.pdf (176 КБ)
Информацию об авторских правах и лицензии можно найти здесь.
Ньютоновская механика — Как трение зависит от скорости?
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 3к раз
$\begingroup$
Если тело в вакууме покоится на плоской поверхности (скорость равна $0$), то силы трения на него не действуют. Если тело имеет скорость, то на него действует сила трения. Это указывает на то, что сила трения является функцией скорости. Что это за отношения?
Тоже из-за ускорения? Производные положения более высокого порядка?
- ньютоновская механика
- силы
- трение
- сопротивление
$\endgroup$
1
$\begingroup$
Понимание взаимосвязи между сопротивлением , которое представляет собой силу трения в контексте жидкостей, и скоростью относительного движения проще, чем понимание взаимосвязи в контексте трения между поверхностями повседневных твердых предметов.
Закон трения покоя, о котором идет речь в вопросе, в лучшем случае полуэмпирический закон . Давайте попробуем понять это утверждение, повторив мысленный эксперимент в сочетании с эмпирическими знаниями об этом явлении, которое элегантно описано в лекции на веб-странице, ссылка на которую приведена в этом ответе.
Если мы возьмем брусок с известным весом $W$ и поместим его на наклонную поверхность, мы сможем довольно легко изменить угол наклона $\theta$. При определенном наклоне мы наблюдаем, что блок скользит вниз по склону со скоростью , приблизительно равной 9.0080 равномерная скорость. Используя первый и второй законы Ньютона, описывающие силы, и наши знания тригонометрии, мы можем определить коэффициент трения как $\mu := \frac{W \sin{\theta}}{W \cos{\theta} } = \tan{\theta}$.
Понятно, что провести реальный эксперимент, который ведет себя таким идеальным образом, чрезвычайно сложно, но мы можем наблюдать такое поведение на некоторых временных интервалах движения блока по склону.
Однако даже если мы сможем провести такой тонкий эксперимент, он не полностью описывает лежащее в его основе явление. Например, рассмотрим металлический блок, сделанный из одного элемента (наиболее чистого, насколько это возможно), помещенный на наклонную поверхность, построенную таким же образом в вакуум , при этом обе контактирующие поверхности имеют одинаковую шероховатость. В этом случае мы можем заметить, что блок и наклон сплавляют вместе. По сути, наш анзац для закона может полуэмпирически описать поведение множества поверхностей с примесями и различной шероховатостью, которые находятся в непосредственном контакте, но не способен точно предсказать для обычных поверхностей. Точно так же проверка того, что коэффициент трения не зависит от относительной скорости между поверхностями, является сложной задачей, требующей деликатных экспериментов, и в настоящее время на нее нет полного ответа.
$\endgroup$
$\begingroup$
Ответ на ваш вопрос: это зависит от обстоятельств.


 К., зав. каф. начального образования НИРО
К., зав. каф. начального образования НИРО Лаборатория знаний» объявляет о проведении конкурса методических разработок «Урок информатики в основной школе». Руководит конкурсом Организационный комитет (далее — Оргкомитет), состоящий из представителей Российской академии образования, Федерального института развития образования, методистов издательства.
Лаборатория знаний» объявляет о проведении конкурса методических разработок «Урок информатики в основной школе». Руководит конкурсом Организационный комитет (далее — Оргкомитет), состоящий из представителей Российской академии образования, Федерального института развития образования, методистов издательства. Г.
Г. А.
А.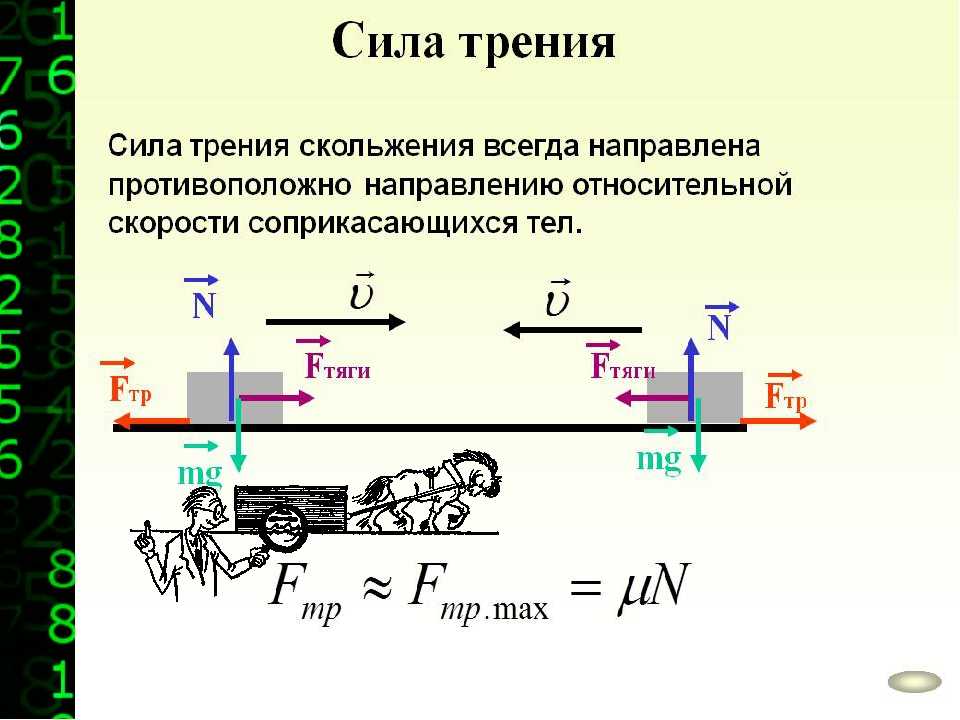
 В. Ломакович
В. Ломакович В.)
В.)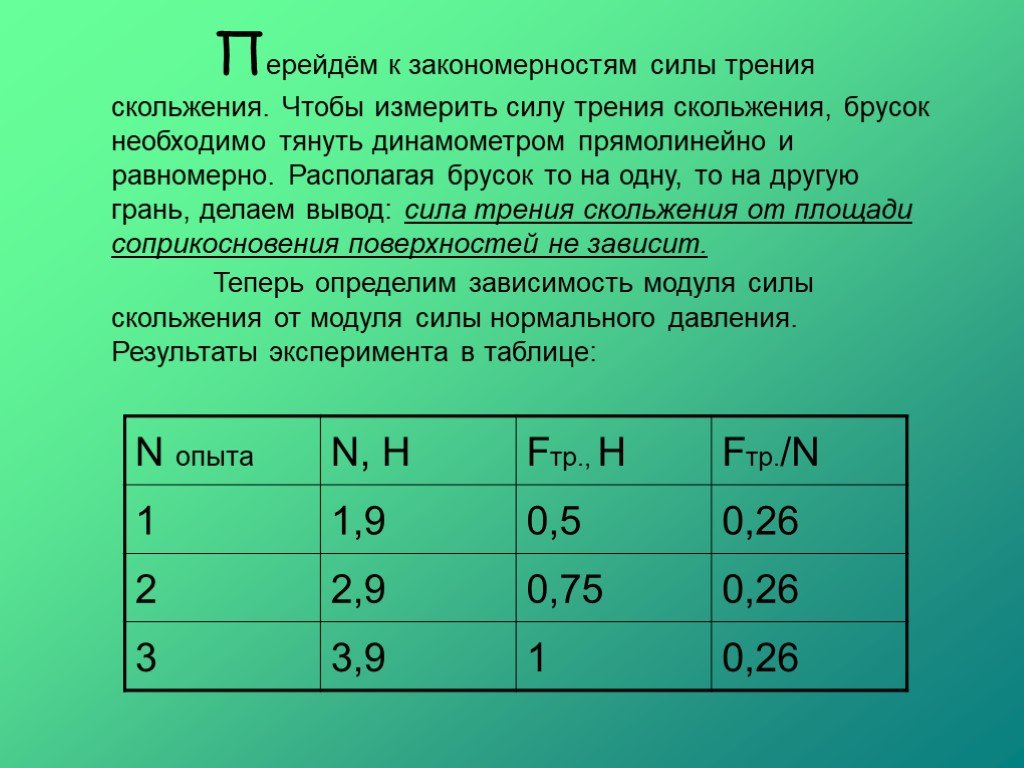
 В.
В.
 С. <br> Якушина Е.В.
С. <br> Якушина Е.В. Запись вебинаров.
Запись вебинаров.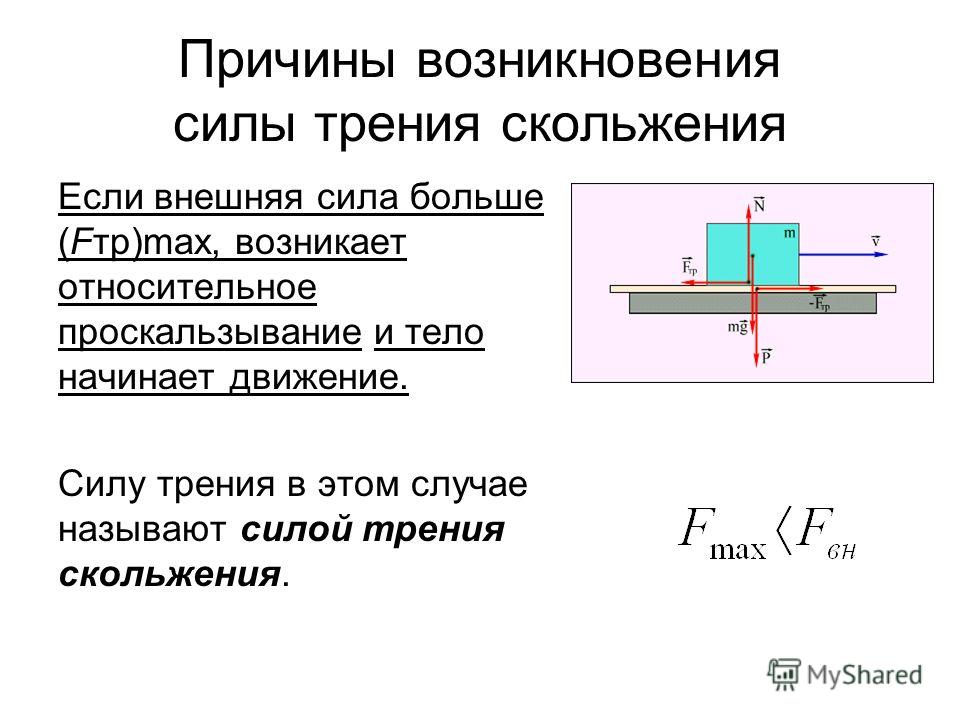
 {\rm nd}\) в этом перпендикулярном направлении, мы можем заключить, что величина нагрузки равна Нормальной силе \((F_N)\) поверхности, давящей на объект. Поэтому мы можем написать, что 9{\rm nd}\) Закон движения. По мере увеличения приложенной силы сила трения остается равной приложенной силе до тех пор, пока не произойдет движение. При этом максимальном значении приложенной силы сила трения также максимальна и равна
{\rm nd}\) в этом перпендикулярном направлении, мы можем заключить, что величина нагрузки равна Нормальной силе \((F_N)\) поверхности, давящей на объект. Поэтому мы можем написать, что 9{\rm nd}\) Закон движения. По мере увеличения приложенной силы сила трения остается равной приложенной силе до тех пор, пока не произойдет движение. При этом максимальном значении приложенной силы сила трения также максимальна и равна В общем, \(\mu_k \lt \mu_s\text{;}\), то есть для преодоления статического трения требуется больше усилий, чем для преодоления кинетического трения. Коэффициенты трения обычно меньше единицы, но могут быть и больше единицы, и они зависят от природы обеих поверхностей.
В общем, \(\mu_k \lt \mu_s\text{;}\), то есть для преодоления статического трения требуется больше усилий, чем для преодоления кинетического трения. Коэффициенты трения обычно меньше единицы, но могут быть и больше единицы, и они зависят от природы обеих поверхностей.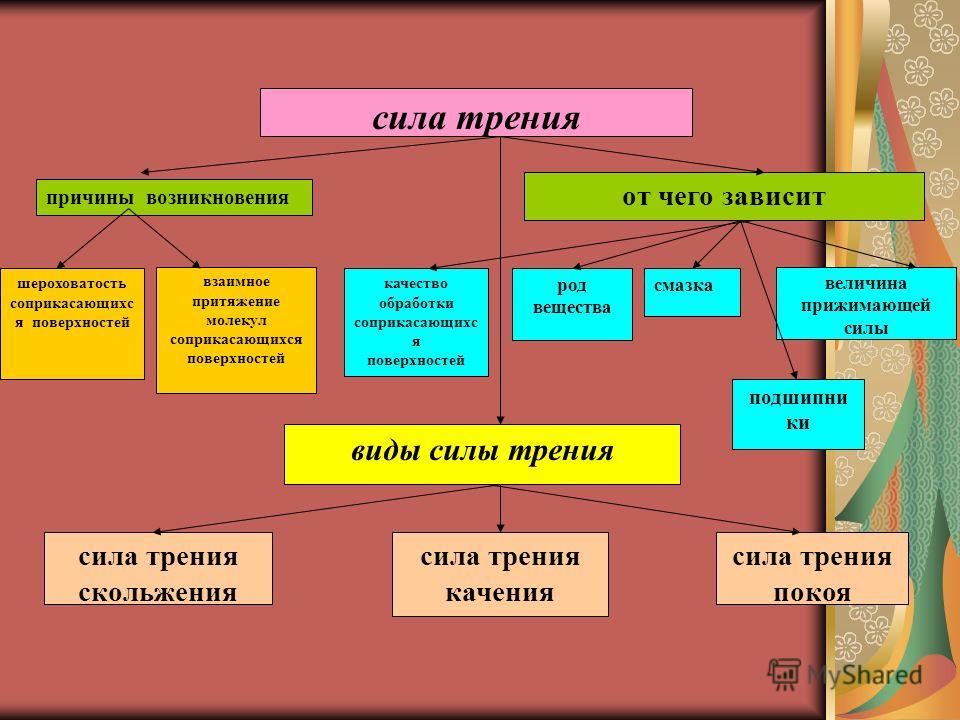 0.2}
\end{equation}
0.2}
\end{equation} Закон трения покоя, о котором идет речь в вопросе, в лучшем случае полуэмпирический закон . Давайте попробуем понять это утверждение, повторив мысленный эксперимент в сочетании с эмпирическими знаниями об этом явлении, которое элегантно описано в лекции на веб-странице, ссылка на которую приведена в этом ответе.
Закон трения покоя, о котором идет речь в вопросе, в лучшем случае полуэмпирический закон . Давайте попробуем понять это утверждение, повторив мысленный эксперимент в сочетании с эмпирическими знаниями об этом явлении, которое элегантно описано в лекции на веб-странице, ссылка на которую приведена в этом ответе. Однако даже если мы сможем провести такой тонкий эксперимент, он не полностью описывает лежащее в его основе явление. Например, рассмотрим металлический блок, сделанный из одного элемента (наиболее чистого, насколько это возможно), помещенный на наклонную поверхность, построенную таким же образом в вакуум , при этом обе контактирующие поверхности имеют одинаковую шероховатость. В этом случае мы можем заметить, что блок и наклон сплавляют вместе. По сути, наш анзац для закона может полуэмпирически описать поведение множества поверхностей с примесями и различной шероховатостью, которые находятся в непосредственном контакте, но не способен точно предсказать для обычных поверхностей. Точно так же проверка того, что коэффициент трения не зависит от относительной скорости между поверхностями, является сложной задачей, требующей деликатных экспериментов, и в настоящее время на нее нет полного ответа.
Однако даже если мы сможем провести такой тонкий эксперимент, он не полностью описывает лежащее в его основе явление. Например, рассмотрим металлический блок, сделанный из одного элемента (наиболее чистого, насколько это возможно), помещенный на наклонную поверхность, построенную таким же образом в вакуум , при этом обе контактирующие поверхности имеют одинаковую шероховатость. В этом случае мы можем заметить, что блок и наклон сплавляют вместе. По сути, наш анзац для закона может полуэмпирически описать поведение множества поверхностей с примесями и различной шероховатостью, которые находятся в непосредственном контакте, но не способен точно предсказать для обычных поверхностей. Точно так же проверка того, что коэффициент трения не зависит от относительной скорости между поверхностями, является сложной задачей, требующей деликатных экспериментов, и в настоящее время на нее нет полного ответа.