Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. 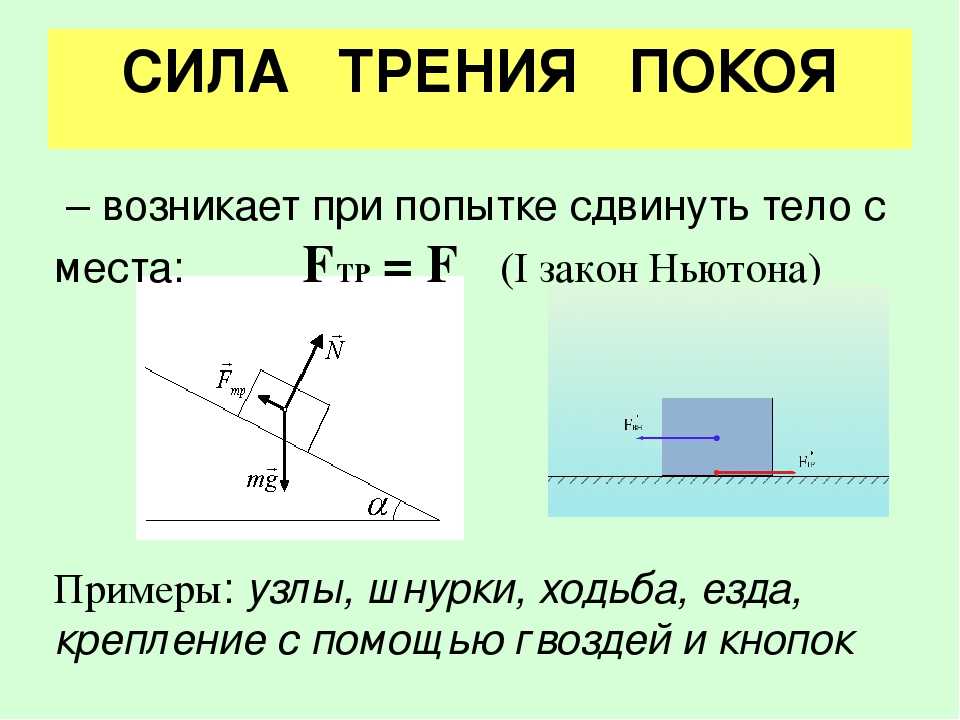СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. 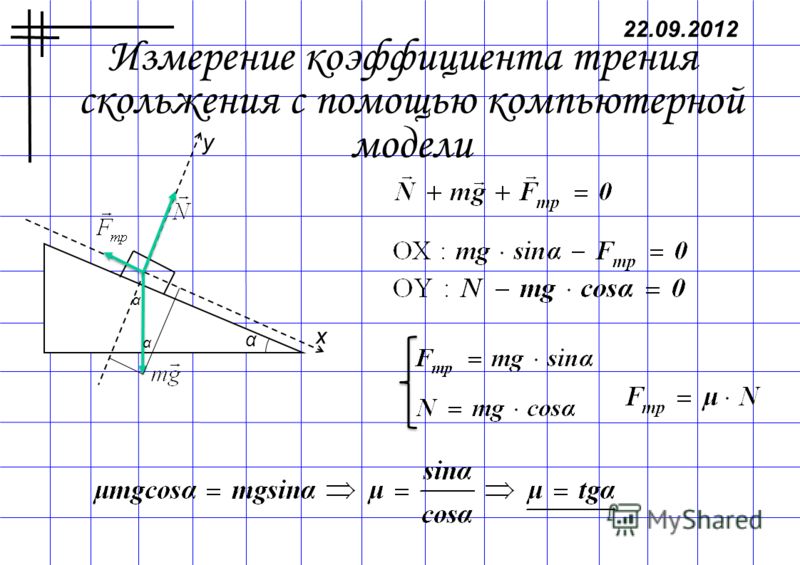ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Сила тяжести. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R0 – StudyWay

Целью данной статьи является подготовка к ЕГЭ по физике, мы займёмся изучением вышеперечисленных тем раздела динамики.

Сила тяжести. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R0

Силой тяжести является сила притяжения тел к нашей планете. 3 = 3 кг.

Далее находим вес воды: Р = 3 кг * 9,8 Н / кг = 29,4 Н.

Ответ: вес воды равен 29,4 Н

Сделаем выводы по данной теме:

– Ускорение свободного падения зависит от массы космического объекта;

– Ускорение свободного падения будет меньше, если расстояние до объекта будет большим.

Переходим к рассмотрению второй темы. Тема, касающаяся движения небесных тел, а также космической скорости обычно встречается в задании № 24 ЕГЭ по физике, сначала рассмотрим определения темы, далее – перейдём к решению задач.

Движение небесных тел и их искусственных спутников. Первая космическая скорость. Вторая космическая скорость.

Искусственным спутником Земли является космический аппарат, который вращается вокруг нашей планеты по орбите, называемой гелиоцентрической.

Для того, чтобы осуществлять движение по орбите вокруг планеты, у спутника должна быть определённая скорость, которая равна либо больше первой космической скорости. Спутник летает на большом расстоянии, обычно оно составляет сотни тысяч километров. Период вращения спутника по орбите составляет от нескольких часов до нескольких лет. Особое внимание уделяют спутникам, находящимся на геостационарной орбите. Это обусловлено тем, что они вращаются на протяжении одних суток.

Первой космической скорость (её также называют круговой с) является скорость, необходимую для объекта, не имеющего двигатель. Такой вид скорости является минимальным, при ней движущееся в горизонтальном направлении тело, не будет падать, оно будет продолжать движение по орбите.

Формула для определения этой скорости: U1 = √G * (M / R).

Второй космической скоростью (её также называют параболической либо скоростью убегания) является минимальная скорость, необходимая для объекта. Считают, что после того, как тело приобретёт эту скорость, оно перестаёт получать негравитационное ускорение.

Формула для нахождения данной скорости = √2G * (M / R).

Решим задачи по этой теме. 12 м.

В ходе подготовке к экзамену рекомендуем просмотреть демонстрационные варианты ЕГЭ по физике, так вы сможете понять примерную формулировку и тему заданий.

Сила трения. Сухое трение. Сила трения покоя. Коэффициент трения.

Переходим к рассмотрению следующей темы – сила трения, сухое трение.

Трение определяют как один из видов взаимодействия среди тел.

Внешним является трение, в ходе которого тела взаимодействуют с помощью своих поверхностей.

Внутренним трением называют движущиеся жидкости и газы.

У силы трения существуют определённые характеристики:

– Направление силы трения – противоположная сторона равнодействующей силы;

– Точкой приложения силы трения располагается на плоскости поверхностей, которые соприкасаются;

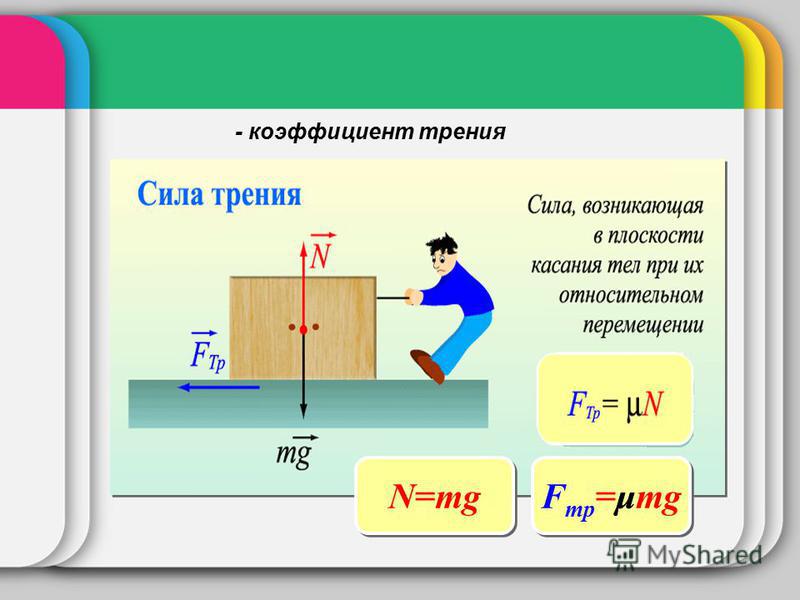
– Существует определённая формула, по которой находят модуль силы трения: F mp = μN, здесь: F mp – является силой трения скольжения, μ – коэффициентом трения, N – силой реакции опоры.

N – рассматривают, как силу, реагирующую с опорой на вес тела, а также одну из видов сил. Коэффициент трения находят в соответствующих таблицах.

Сила трения скольжения.

Сухим трением является взаимодействие, которое возникает при касании тел, при этом, между данными телами не должно быть газов и жидкостей.

Существуют несколько видов сухого трения:

– Скольжение;

– Покоя;

– Качения.

Силой трения покоя называют силу, препятствующую движению тел. Эту силу принять считать наибольшей.

Сила трения скольжения появляется в момент преодоления силы покоя. При этом коэффициенты силы трения должны уменьшаться. Для беспрепятственного скольжения следует полировать поверхность. Следует иметь в виду, что при полном устранении неровностей поверхности, коэффициент трения будет возрастать (это происходит по причине сближения молекул тела).

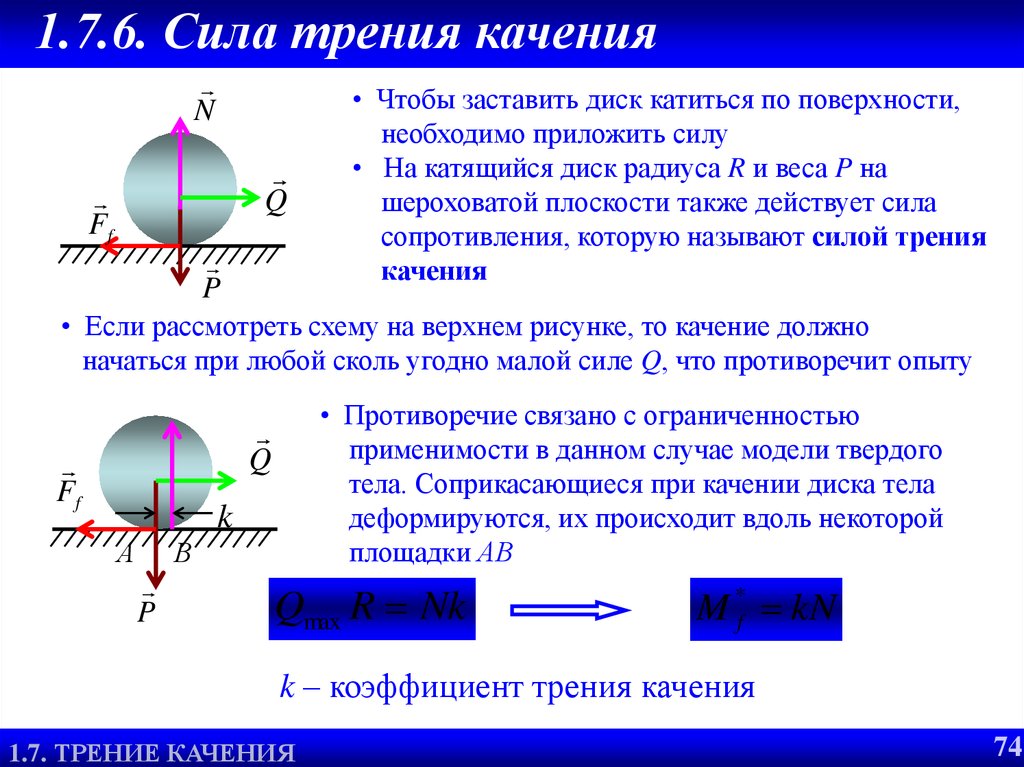
Сила трения качения является наиболее малой по сравнению с другими видами сил. Примером является тумба на колёсах, её горазда легче передвинуть, чем тумбу на опоре.

Существует определённый коэффициент трения. Им является характеристика трения в качестве давления.

Коэффициент трения находят по формуле: F tr = μN.

Коэффициент не имеет зависимости от площадей поверхностей, которые соприкасаются.

В некоторых случаях коэффициент трения заменяют углом трения.

Рассмотрим задачу по данной теме.

Бревно, у которого масса составляет пять килограммов, скользит по поверхности, являющейся горизонтальной. Известно, что сила трения скольжения = 20Н.

Найти: силу трения, при условии, что масса бревна будет меньше в два раза.

Решение: F mp = μN. N = mg. N1 = mg / 2 = N / 2, далее: F mp1 = F mp / 2 = 20 Н / 2 = 10 Н.

Ответ: сила трения равна 10 Н.

Рассмотрим ещё одну небольшую тему, встречающую в разделе динамики ЕГЭ по физике, это тема давления.

Давление

Давлением называют силу, которая приходится на определённую площадь поверхности.

Давление измеряется в Паскалях. 5 Па, или 760 миллиметров ртутного столба.

Таким образом, мы завершили рассмотрение тем из раздела динамики, встречающиеся в КИМах ЕГЭ по физике, изучили основные определения, характеристики, а также решили задачи.

6.6: Центростремительная сила — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4001

• OpenStax
• OpenStax

Цели обучения

• Объясните уравнение для центростремительного ускорения
• Применить второй закон Ньютона для получения уравнения центростремительной силы
• Использовать концепции кругового движения при решении задач, связанных с законами движения Ньютона

В книге «Движение в двух и трех измерениях» мы рассмотрели основные понятия кругового движения.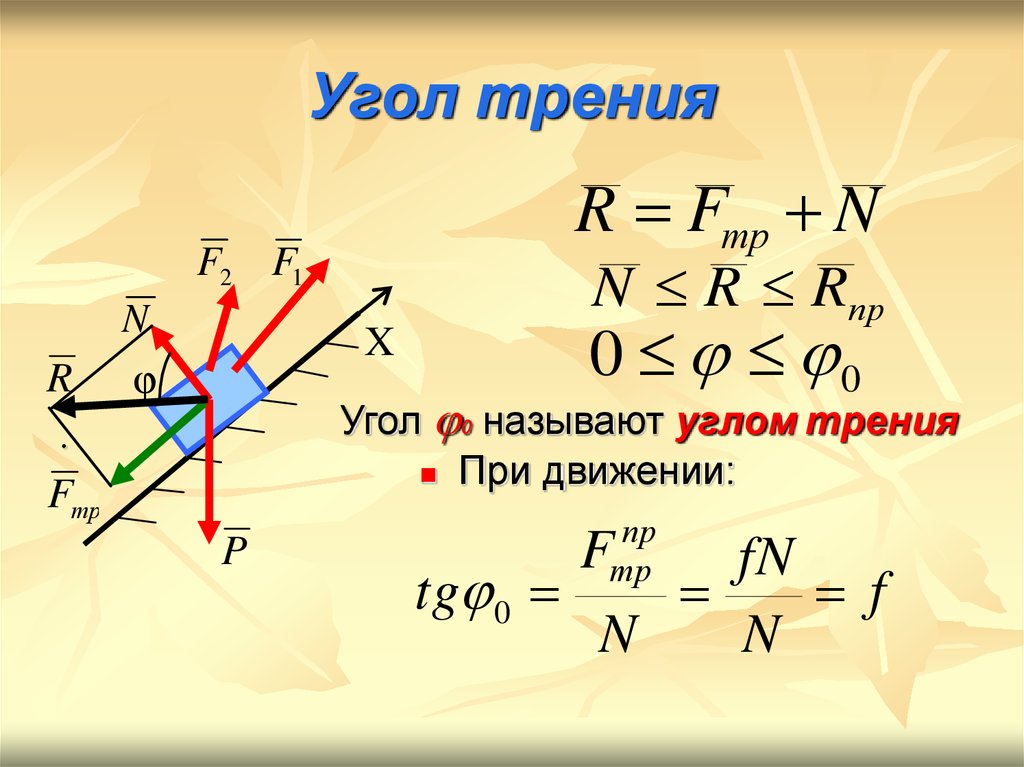 Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это направленное по центру ускорение, называемое центростремительным ускорением, определяется формулой 9{2} \ldotp\]

Угловая скорость показывает скорость, с которой объект вращается по кривой, в рад/с. Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.

Ускорение должно создаваться силой. Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется

центростремительная сила . Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: F _net = ma. Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a _c . Таким образом, величина центростремительной силы F _c равна

\[F_{c} = ma_{c} \ldotp\]

Подставляя выражения для центростремительного ускорения a 9{2}}{F_{c}} \ldotp\]

Это означает, что при данной массе и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую, как на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): Сила трения дополняет центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше F _c , тем меньше радиус кривизны r и тем острее кривая. Вторая кривая имеет тот же v, но большую F _c дает меньшее значение r′.

Пример \(\PageIndex{1}\): Какой коэффициент трения нужен автомобилям на плоской кривой?

1. Рассчитайте центростремительную силу, действующую на автомобиль массой 900,0 кг, который движется по кривой радиусом 500,0 м со скоростью 25,00 м/с.
2. Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от скольжения (рисунок \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): Этот автомобиль на ровном месте удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой. Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части. 9{2}}{(500,0\; м)} = 1125\; N \ldotp$$

На рисунке \(\PageIndex{2}\) показаны силы, действующие на автомобиль на кривой без уклона (на ровной поверхности). {2}}{(500,0\; м)(9{2})} = 0,13 \ldotp$$(Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)

Значение

Коэффициент трения, показанный на рисунке \(\PageIndex{2b}\), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение является реактивной силой, которая может принимать значение меньше, но не больше, чем \(\mu_{s}\)N. Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, а это означает, что в этом примере не имеет значения, насколько сильно загружена машина для преодоления поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.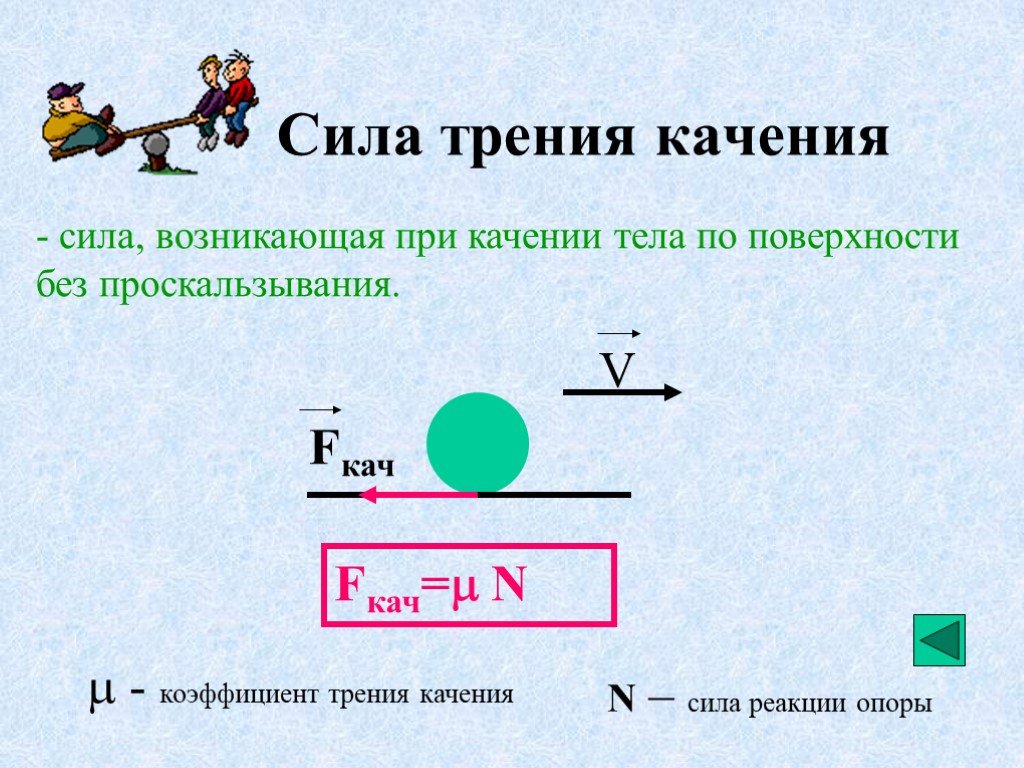

Упражнение \(\PageIndex{1}\)

Автомобиль, движущийся со скоростью 96,8 км/ч, движется по кривой окружности радиусом 182,9 м по ровной проселочной дороге. Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?

Кривые с виражами

Теперь рассмотрим кривых с виражами , где наклон дороги помогает вам преодолевать кривую (рис. \(\PageIndex{3}\)). Чем больше угол θ, тем быстрее вы сможете пройти кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол \(\theta\) таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для \(\theta\) для идеально изогнутой кривой и рассмотрим пример, связанный с ним.

Рисунок \(\PageIndex{3}\): Автомобиль на этой кривой с наклоном удаляется и поворачивает влево.

Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. {2}}{г}\). Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть 9{2}}{r} \ldotp\]

Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны друг другу. в направлении. Из рисунка \(\PageIndex{3}\) мы видим, что вертикальная составляющая нормальной силы равна N cos \(\theta\), а единственная другая вертикальная сила — это вес автомобиля. Они должны быть равны по величине; таким образом,

\[N \cos \theta = mg \ldotp\]

Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить желаемое выражение для \(\theta\). Решение второго уравнения относительно N = \(\frac{mg}{(\cos \theta)}\) и подстановка его в первое дает 9{2}}{rg}\right) \ldotp \label{6.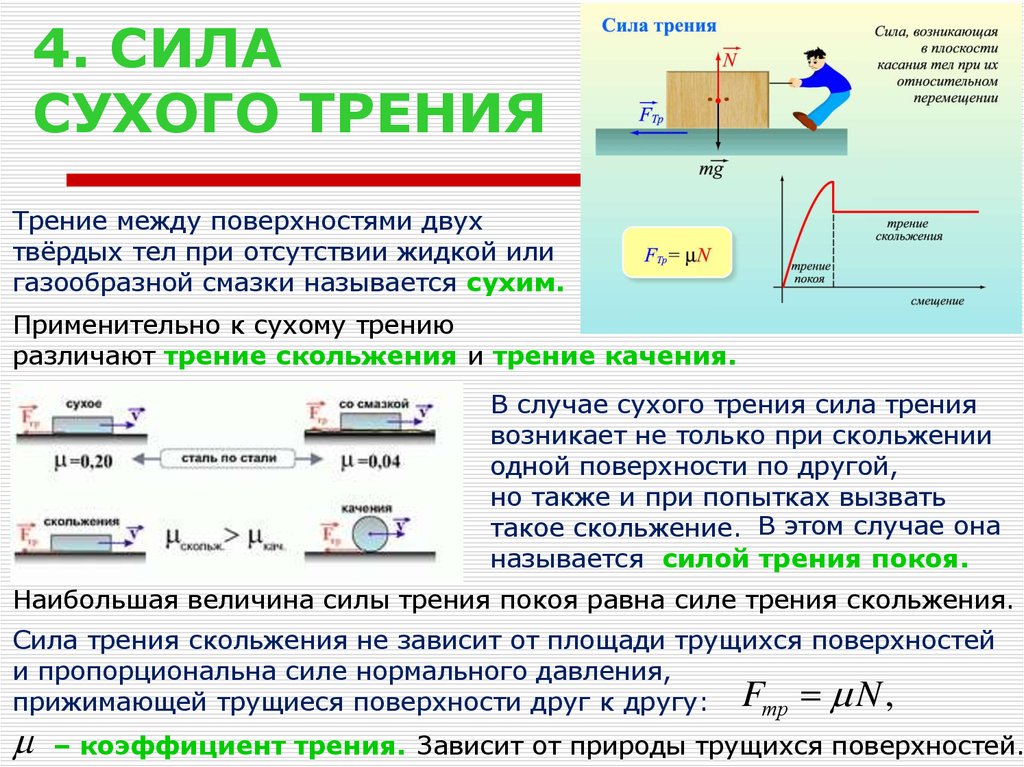 4}\]

Это выражение можно понять, рассмотрев зависимость \(\theta\) от v и r. Большое значение \(\theta\) получается при большом v и малом r. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что \(\theta\) не зависит от массы транспортного средства.

Пример \(\PageIndex{2}\): Какова идеальная скорость для прохождения крутого крутого поворота?

Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые. Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Для иллюстрации рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с наклоном 31,0°, если бы на дороге не было трения.

Стратегия

Прежде всего заметим, что все члены выражения для идеального угла кривой с креном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость появилась в левой части, а затем подставить известные величины.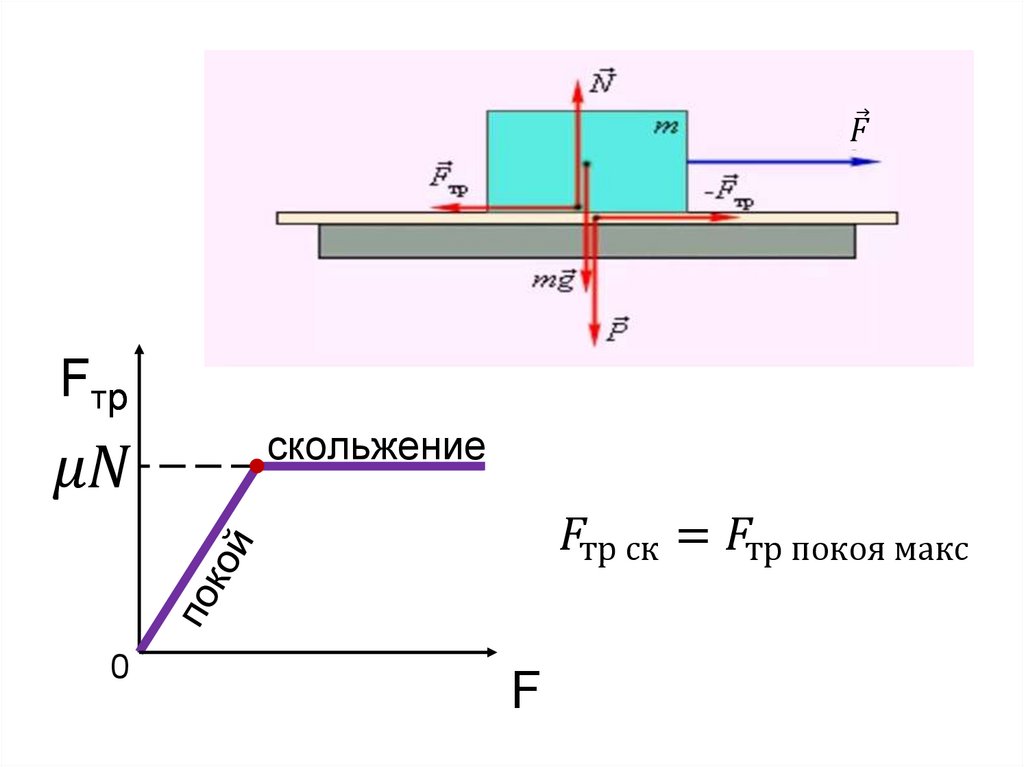 9{2})(0,609)} = 24,4\; м/с \ldotp\]

Значение

Это примерно 165 км/ч, что соответствует очень крутому виражу и довольно резкому повороту. Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.

Самолеты также делают повороты по крену. Подъемная сила из-за силы воздуха, действующей на крыло, действует под прямым углом к ​​крылу. Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет его. Угол крена, показанный на рисунке \(\PageIndex{4}\), определяется как \(\theta\). Мы анализируем силы так же, как рассматривали случай, когда автомобиль огибает кривую с креном.

Рисунок \(\PageIndex{4}\): В повороте с креном горизонтальная составляющая подъемной силы неуравновешена и ускоряет самолет. Нормальная составляющая подъемной силы уравновешивает вес самолета. Угол крена определяется как \(\theta\). Сравните векторную диаграмму с диаграммой, показанной на рис. 6.22.

Моделирование

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с координатами, скоростью и ускорением жука, используя векторы или графики.

Примечание

Круговое движение требует силы, так называемой центростремительной силы, которая направлена ​​к оси вращения. Эта упрощенная модель карусели демонстрирует эту силу.

Силы инерции и неинерциальные (ускоренные) системы отсчета: сила Кориолиса

Что имеют в виду взлет реактивного самолета, поворот на автомобиле, катание на карусели и круговое движение тропического циклона? общий? Каждая проявляет силы инерции — силы, которые просто кажутся возникающими из-за движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете в реактивном самолете вас как будто вдавливают обратно в сиденье, когда самолет ускоряется на взлетно-посадочной полосе. Тем не менее, физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более частый случай возникает, когда вы делаете крутой поворот на автомобиле, например, вправо (рис. \(\PageIndex{5}\)). Вы чувствуете, как будто вас отбрасывает (то есть вынуждает) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не в том, что на вас действует сила слева.

Рисунок \(\PageIndex{5}\): (a) Водитель автомобиля чувствует себя вынужденным сместиться влево относительно автомобиля, когда он поворачивает направо. Это сила инерции, возникающая из-за использования автомобиля в качестве системы отсчета. б) В земной системе отсчета водитель движется прямолинейно, подчиняясь первому закону Ньютона, а машина движется вправо. Слева на водителя относительно Земли силы нет. Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.

Мы можем согласовать эти точки зрения, изучив используемые системы отсчета. Давайте сосредоточимся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Машина неинерциальная система отсчета , потому что она ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, представляет собой инерционную силу , не имеющую физического происхождения (она обусловлена ​​исключительно инерцией пассажира, а не какой-либо физической причиной, такой как напряжение, трение или гравитация).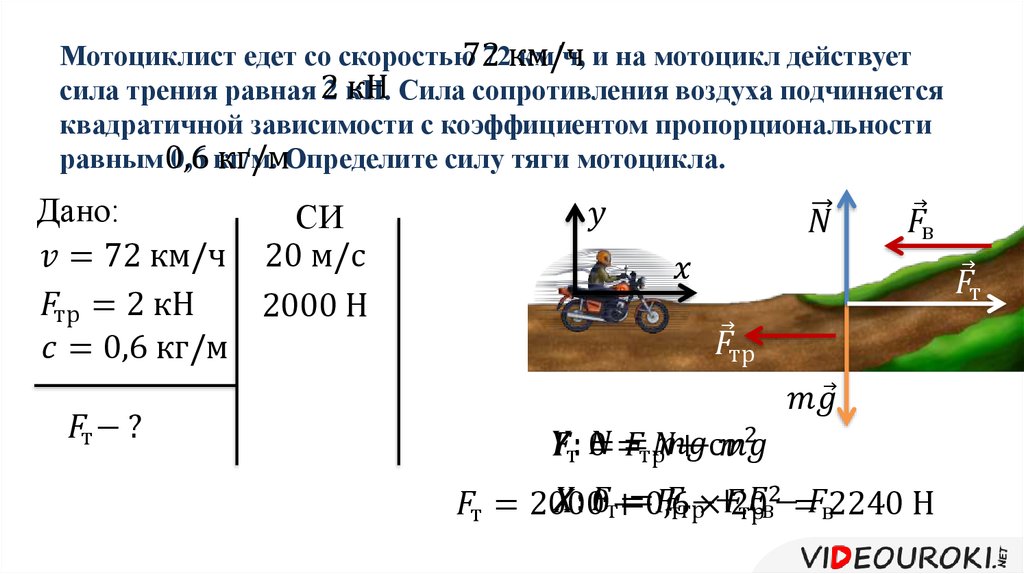 Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.

Физик выберет любую систему отсчета, наиболее удобную для анализируемой ситуации. Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.

Теперь давайте мысленно прокатимся на карусели, а именно на быстро вращающейся карусели для игровой площадки (рис. \(\PageIndex{6}\)). Вы принимаете карусель за систему отсчета, потому что вращаетесь вместе. При вращении в этой неинерциальной системе отсчета вы чувствуете силу инерции, которая стремится сбить вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.

Рисунок \(\PageIndex{6}\): (a) Всадник на карусели чувствует, как будто его сбрасывают. Эту силу инерции иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. (b) В инерциальной системе отсчета и в соответствии с законами Ньютона его увлекает инерция (незаштрихованный всадник имеет F _net = 0 и движется прямолинейно). Сила F _{центростремительная} необходима, чтобы вызвать движение по окружности.

Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах (рис. \(\PageIndex{7}\)). Как упоминалось ранее в этой главе, центрифуга вращает образец очень быстро. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.

Рисунок \(\PageIndex{7}\): Центрифуги используют инерцию для выполнения своей задачи. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет седиментацию. В конечном итоге частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для того, чтобы заставить их двигаться по окружности постоянного радиуса.

Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета. Например, что, если вы отодвинете мяч прямо от центра карусели, как показано на рисунке \(\PageIndex{8}\)? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой 9.0052 Сила Кориолиса , которая заставляет мяч искривляться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.

Рисунок \(\PageIndex{8}\): Глядя вниз на вращение карусели против часовой стрелки, мы видим, что мяч, скользящий прямо к краю, движется по кривой вправо. Человек двигает мяч к точке B, начиная с точки A.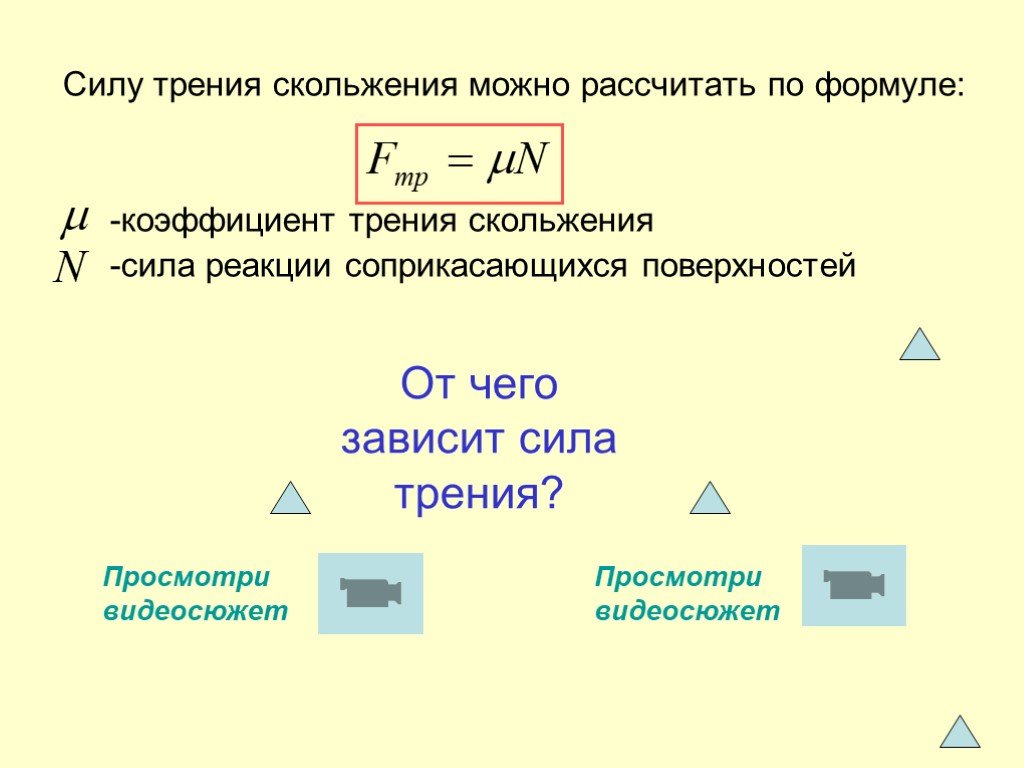 Обе точки поворачиваются к заштрихованным позициям (A’ и B’), показанным во времени, когда мяч следует по кривой траектории во вращающейся системе отсчета и по прямой траектории в системе Земли. .

До сих пор мы считали Землю инерциальной системой отсчета, практически не беспокоясь о последствиях ее вращения. Однако такие эффекты существуют, например, при вращении погодных систем. Большинство последствий вращения Земли можно качественно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на рисунке \(\PageIndex{8}\). Как и на карусели, любое движение в Северном полушарии Земли вызывает действие силы Кориолиса вправо. Как раз обратное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли невелика, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как ветры, она оказывает существенное влияние.

Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке.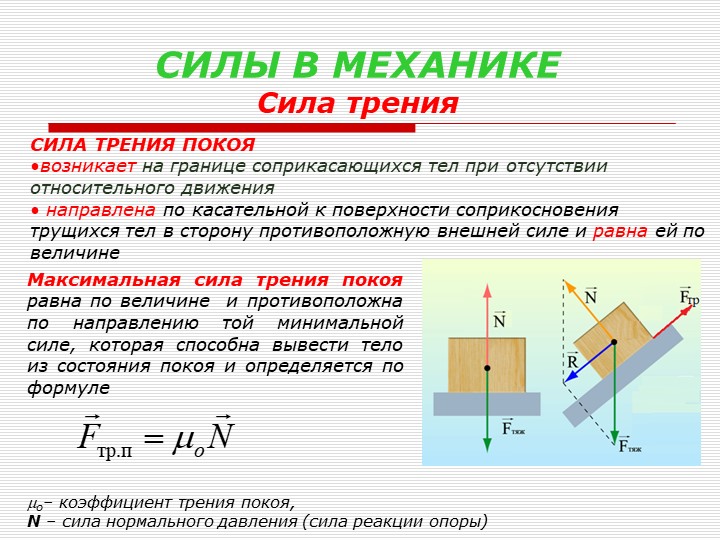 (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, которые представляют собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) Рисунок \(\PageIndex{9}\) помогает показать, как эти вращения происходить. Воздух течет к любой области низкого давления, а тропические циклоны содержат особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.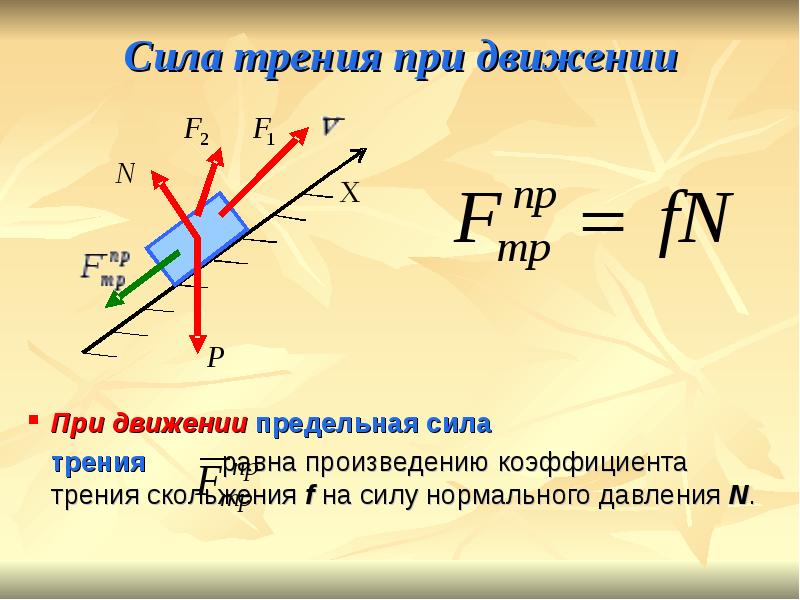

Рисунок \(\PageIndex{9}\): (a) Вращение этого урагана в Северном полушарии против часовой стрелки является основным следствием действия силы Кориолиса. (b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)

Вращение тропических циклонов и траекторию мяча на карусели с таким же успехом можно объяснить инерцией и вращением системы под ними. Когда используются неинерциальные системы отсчета, необходимо изобрести силы инерции, такие как сила Кориолиса, чтобы объяснить кривую траекторию. Не существует идентифицируемого физического источника этих сил инерции. В инерциальной системе отсчета инерция объясняет траекторию, и ни одна сила не имеет идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но точка зрения в инерциальной системе отсчета является самой простой в том смысле, что все силы имеют происхождение и объяснения.

---

Эта страница под названием 6.6: Centripetal Force распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. изогнутая кривая
   2. центростремительная сила
   3. Сила Кориолиса
   4. идеальное банковское дело
   5. сила инерции
   6. неинерциальная система отсчета
   7. источник@https://openstax. org/details/books/university-physics-volume-1

6.3 Центростремительная сила – College Physics: OpenStax

Глава 6 Равномерное круговое движение и гравитация

Резюме

• Расчет коэффициента трения автомобильной шины.
• Рассчитайте идеальную скорость и угол поворота автомобиля.

Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. .

Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительной силой . Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны.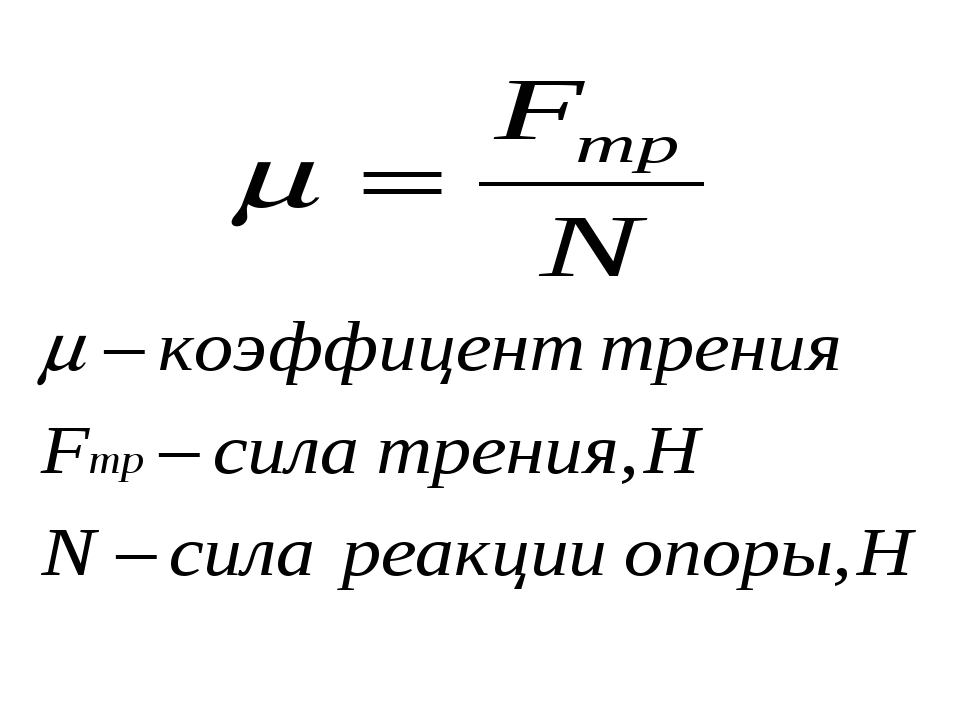 2}{\textbf{F}_{\textbf{c}}}}.[/latex]

Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть узкую кривую.

Рис. 1. Сила трения дополняет центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше F _c , тем меньше радиус кривизны r и тем острее кривая. Вторая кривая имеет те же v , но больший F _c дает меньший r’ .

Пример 1: Какой коэффициент трения нужен шинам Care на ровном повороте?

(a) Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 500 м со скоростью 25,0 м/с.

(b) Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от скольжения (см.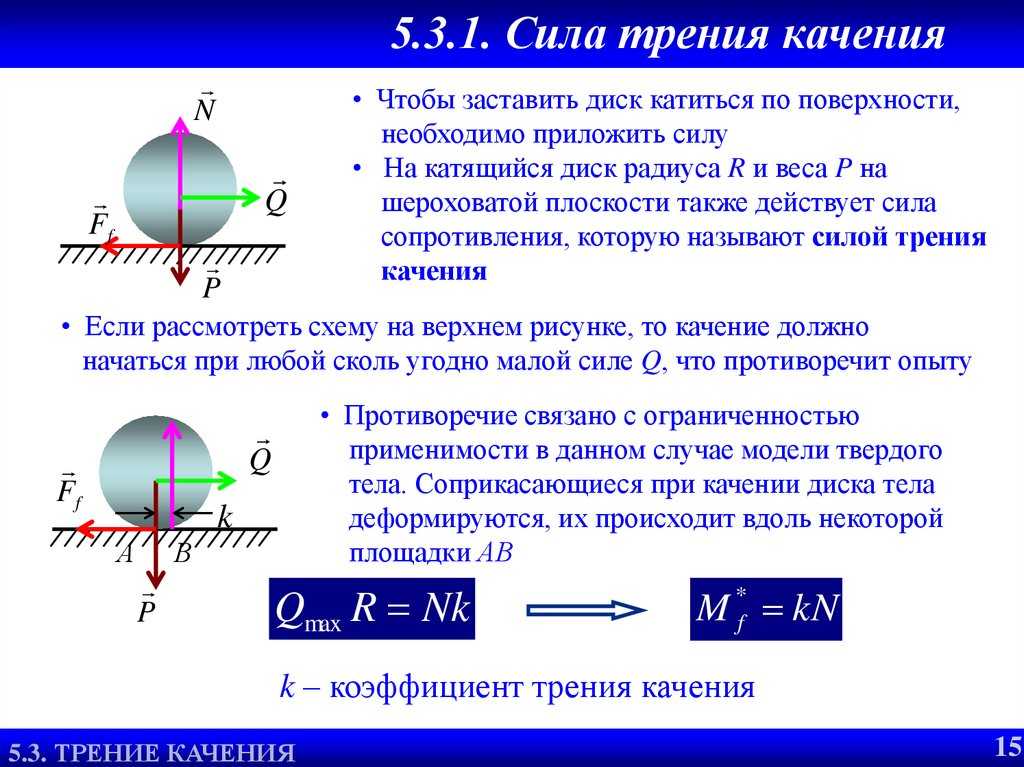 рис. 2). 92}{(500\textbf{ m})}}[/latex][latex]\boldsymbol{=\:1125\textbf{ N}}.[/latex]

Стратегия для (b)

Рисунок 2 показаны силы, действующие на автомобиль на кривой без наклона (на ровной поверхности). Трение направлено влево, удерживая автомобиль от скольжения, и, поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) равно [латекс]\boldsymbol{\mu _{\textbf{s}}\textbf{N}},[/latex],где[латекс]\ boldsymbol{\mu _{\textbf{s}}}[/latex] — статический коэффициент трения, а N — нормальная сила. Нормальная сила равна весу автомобиля на ровной поверхности, так что[latex]\boldsymbol{\textbf{N}=mg}.[/latex]Таким образом, центростремительная сила в этой ситуации равна 92} \end{array}[/latex][latex]\rbrace[/latex], потому что[latex]\boldsymbol{m},\:\boldsymbol{v},[/latex]and[latex]\boldsymbol{ r}[/latex] даны. Коэффициент трения, найденный в части (b), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль по-прежнему будет преодолевать кривую, если коэффициент больше 0,13, потому что статическое трение является реактивной силой, которая может принимать значение меньше, но не больше, чем[латекс]\boldsymbol{\mu _{\textbf{s}} N}.[/latex]Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, подразумевая, что в этом примере не имеет значения, насколько сильно загружена машина для прохождения поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как будет показано ниже.

Рисунок 2. Этот автомобиль на ровном месте удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой. Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части.

Давайте теперь рассмотрим кривых с уклоном , где уклон дороги помогает вам преодолевать кривую. См. рис. 3. Чем больше угол [латекс]\жирныйсимвол{\тета},[/латекс], тем быстрее вы сможете пройти по кривой. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол [латекс]\жирныйсимвол{\тета}[/латекс] таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для[латекс]\жирныйсимвол{\тета}[/латекс]для идеально изогнутой кривой и рассмотрим пример, связанный с ним.

Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. Составляющие нормальной силы N в горизонтальном и вертикальном направлениях должны быть равны центростремительной силе и весу автомобиля соответственно. В случаях, когда силы не параллельны, удобнее всего рассматривать составляющие вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.

На рис. 3 показана диаграмма свободного кузова автомобиля на кривой без трения. Если угол[латекс]\жирныйсимвол{\тета}[/латекс]идеален для скорости и радиуса, то чистая внешняя сила будет равна необходимой центростремительной силе. Единственными двумя внешними силами, действующими на автомобиль, являются его вес[latex]\textbf{w}[/latex] и нормальная сила дороги[latex]\textbf{N}.[/latex](Поверхность без трения может только прилагают силу, перпендикулярную поверхности, то есть нормальную силу.) Эти две силы должны складываться, чтобы получить результирующую внешнюю силу, горизонтальную по отношению к центру кривизны и имеющую величину [латекс] \boldsymbol{\textbf{mv}^ 2/\textbf{r}}. [/latex]Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, т. е. 92}{г}}.[/латекс]

Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению. Из рисунка видно, что вертикальная составляющая нормальной силы равна [латекс]\жирный символ{N\textbf{cos}\theta},[/латекс], а единственная другая вертикальная сила — это вес автомобиля. Они должны быть равны по величине; таким образом,

[латекс]\boldsymbol{N\textbf{cos} \;\theta=mg}.[/latex] 92}{rg})}[/latex][latex]\textbf{(кривая с идеальным наклоном, без трения).}[/latex]

Это выражение можно понять, рассмотрев, как [латекс]\жирныйсимвол{\тета}[/латекс]зависит от [латекс]\жирныйсимвол{v}[/латекс]и [латекс]\жирныйсимвол{г}.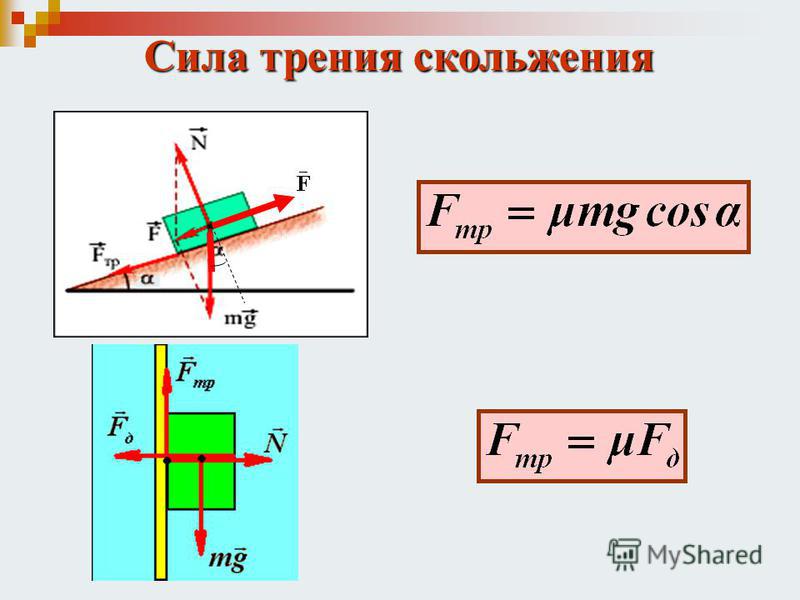 [/латекс] Большой [латекс]\boldsymbol{\theta}[/latex] будет получен для большого [латекс]\boldsymbol{v}[/latex]и маленького [латекс]\boldsymbol{r}.[/latex]Это то есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что [латекс]\жирныйсимвол{\тета}[/латекс] не зависит от массы транспортного средства.

Рисунок 3. Автомобиль на этой кривой с наклоном удаляется и поворачивает влево.

Пример 2. Какова идеальная скорость для прохождения крутого крутого виража?

Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые. Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100 м с креном 65,0°, если дорога не имеет трения. 9{1/2}} \\ \boldsymbol{} & = & \boldsymbol{45.8}\textbf{ м/с.} \end{array}[/latex]

Обсуждение

Это примерно 165 км /h, что соответствует очень крутой и довольно крутой кривой. Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.

Вычисления, подобные приведенным в предыдущих примерах, можно выполнить для множества интересных ситуаций, в которых задействована центростремительная сила — некоторые из них представлены в задачах и упражнениях этой главы.

ДОМАШНИЙ ЭКСПЕРИМЕНТ

Попросите друга или родственника помахать клюшкой для гольфа или теннисной ракеткой. Проведите соответствующие измерения, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном темпе.

ИССЛЕДОВАНИЯ PHET: ГРАВИТАЦИЯ И ОРБИТЫ

Переместите Солнце, Землю, Луну и космическую станцию, чтобы увидеть, как это влияет на их гравитационные силы и орбитальные траектории.