Сложение и вычитание векторов — презентация онлайн
Похожие презентации:
Сложение и вычитание векторов. Законы сложения
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение векторов. Правило треугольника
Векторы в пространстве. (10-11 класс)
Векторы в пространстве
Векторы на плоскости и в пространстве. Основные понятия
Какая запись является верной?
В
450
С
А
AВ > BC;
AВ > BC
AC = BC ;
AC = BC
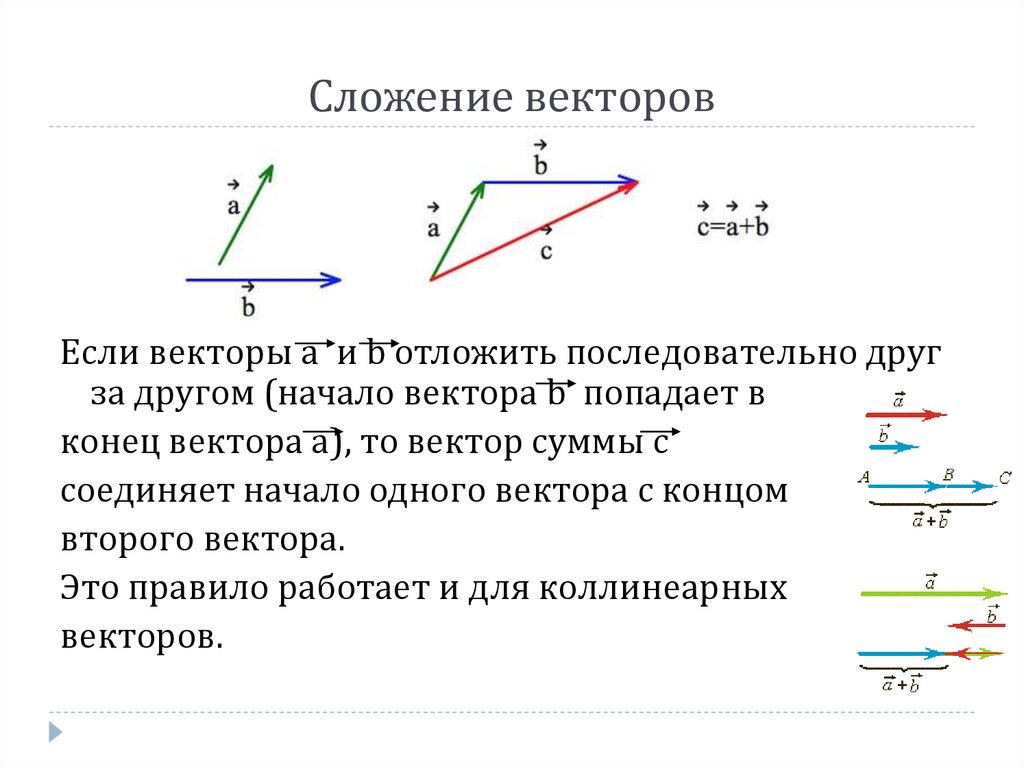
Сложение векторов. Правило треугольника.
АВ + ВС = АС
С
!
a+b
b
А
a
b
a
В
Для любого нулевого вектора
справедливо равенство
a+0=a
!
Докажем, что если при сложении векторов точку А
заменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
С
А
В1
a
А1
параллелограмм
ВСС1В1 –
параллелограмм
АСС1А1 –
параллелограмм
b
С1
Правило треугольника.

АВ + ВС = АС
АS + SС =
АО + ОР = АР
NM + ML = NL
MN + NR = MR
RP + PR = RR = 0
MK + KM = MM = 0
ZK + KZ =
MK + OM = OM + MK
DE + KD = KD + DE =
= OK
АС
ZZ = 0
= KE
Правило треугольника.
АС = АВ + ВС
из ОВN
ON = OB + ВN
OB = ON + NВ
из ASR
AS = AR + RS
RA = RS + SA
из XKH
XH = XK + KH
KX = KH + HX
из АMD
MD = MA + AD
AD = AM + MD
из FPO
OP = OF + FP
FO = FP + PO
По правилу треугольника складываются и
коллинеарные векторы, хотя при их сложении
b
a+b
a
b
a
b
a+b
a
f
c
c+ f
Законы сложения векторов
Теорема
Для любых векторов
1
2
a, b, c
a+b=b+a
справедливы равенства:
!
переместительный закон
(a + b) + c = a + (b + c)
сочетательный закон
!
11
12
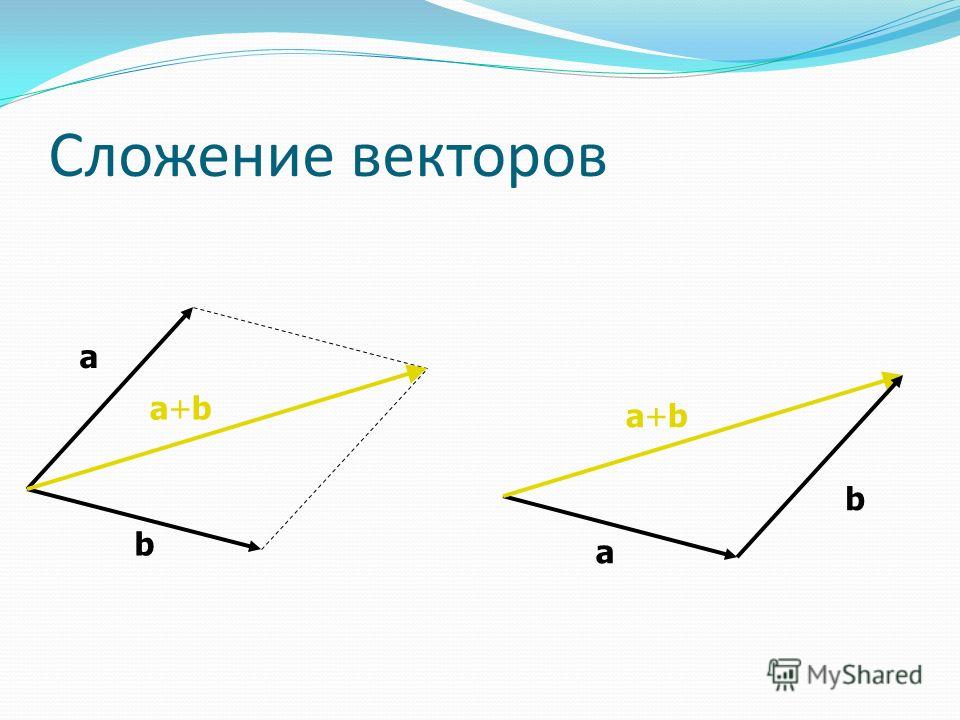
Чтобы применить
правило
параллелограмма,
надо отложить
векторы от одной
точки, как стрелки
часов.
1
10
2
3
9
4
8
7
6
5
Сложение векторов. Правило параллелограмма.
11
10
12
a
8
a
b
2
a+b
9
1
3
4
7
6
5
Сложение векторов.
Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
Правило многоугольника можно сформулировать также
следующим образом: если А1, А2, …, Аn – произвольные
точки плоскости, то А1А2 + А2А3 + … + Аn-1An = А1An
А6
А7
А1
А4
А5
А3
А2
!
Если начало первого вектора совпадает с концом
последнего вектора, то сумма данных векторов равна
1
2
3
4
5
нулевому вектору.
a +a +a +a +a
=0
a3
a3
a5
a2
a4
a4
a1
a2
a1
a5
a1 называется противоположным
вектору a, если векторы a и a1 имеют равные
длины и противоположно направлены.
a1
a
А
-b
a1
-b, противоположный вектору b
Вектор
b
a = a1 ; a
А
Вектор ВА, противоположный
вектору АВ
ВА = – АВ
В
В
a + (-a) = 0
№ 766 На рисунке изображены векторы
a, b, c, d
ХУ.
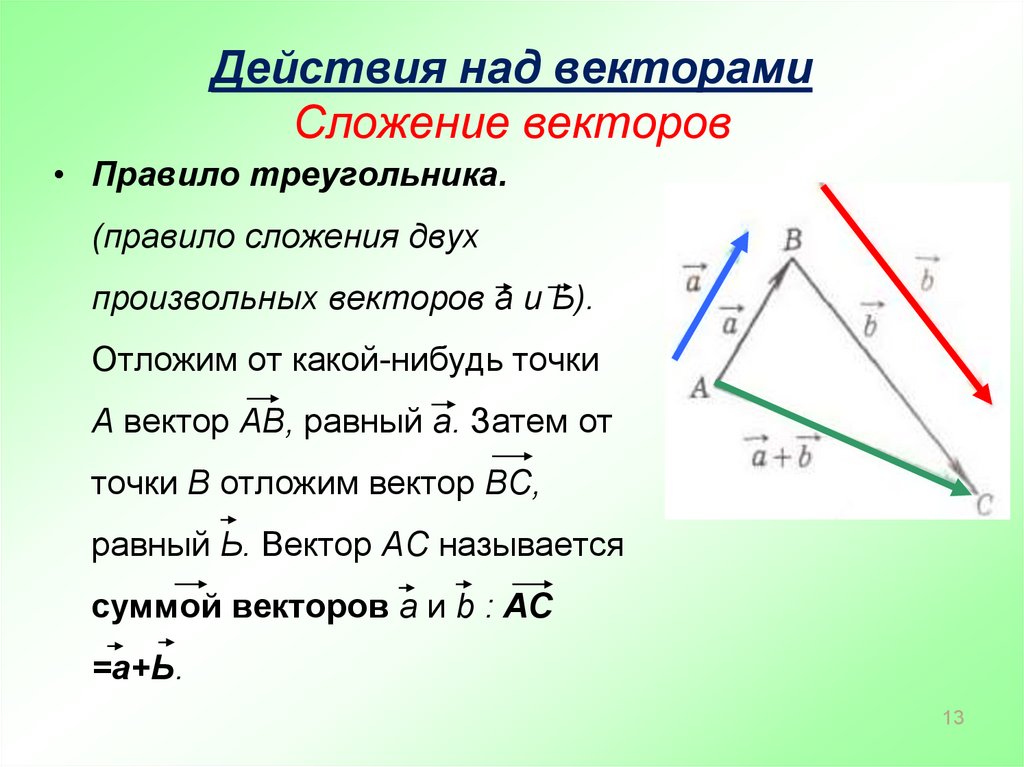 Представьте вектор ХУ в виде суммы остальных или им
Представьте вектор ХУ в виде суммы остальных или импротивоположных векторов.
–b
–a
c
Х
d
–a–b+c+d=
ХУ
У
Вычитание векторов.
a – b = a +(–b)
-b
b
-b
a
a
a- b
MF — SF =
MF + FS = MS
RO — RM = RO + MR = MR + RO = MO
MD — SD =
MD + DS = MS
RO — AO = RO + OA = RA
RO — RO = RO + OR = RR = 0
— OS — ST =
SO + TS = TS + SO = TO
1.Упростите выражение
MN+XY=MX
а) MX
в) NY
б) MY
г) YM
19
2.Найдите вектор х :
АВ + х = АК
а) ВК
в) КК
б) КВ
г) СК
20
3.Найдите вектор a+b,
используя правило треугольника :
b
а)
в)
a
a
a+b
a+b
b
б)
г)
a
a+b
b
a
a+b
b
21
4.Найдите вектор a+b,
используя правило параллелограмма:
а)
в)
a
a
a+b
a+b
b
b
б)
г)
a
a+b
b
a
a+b
22
23. Ответы:
12
3
4
Б
А
Г
Б
За верно выполненные 2 задания – оценка «3»
3 задания – оценка «4»
4 задания – оценка «5»
23
№ 768 Точки М и N – середины сторон АВ и АС
треугольника АВС.
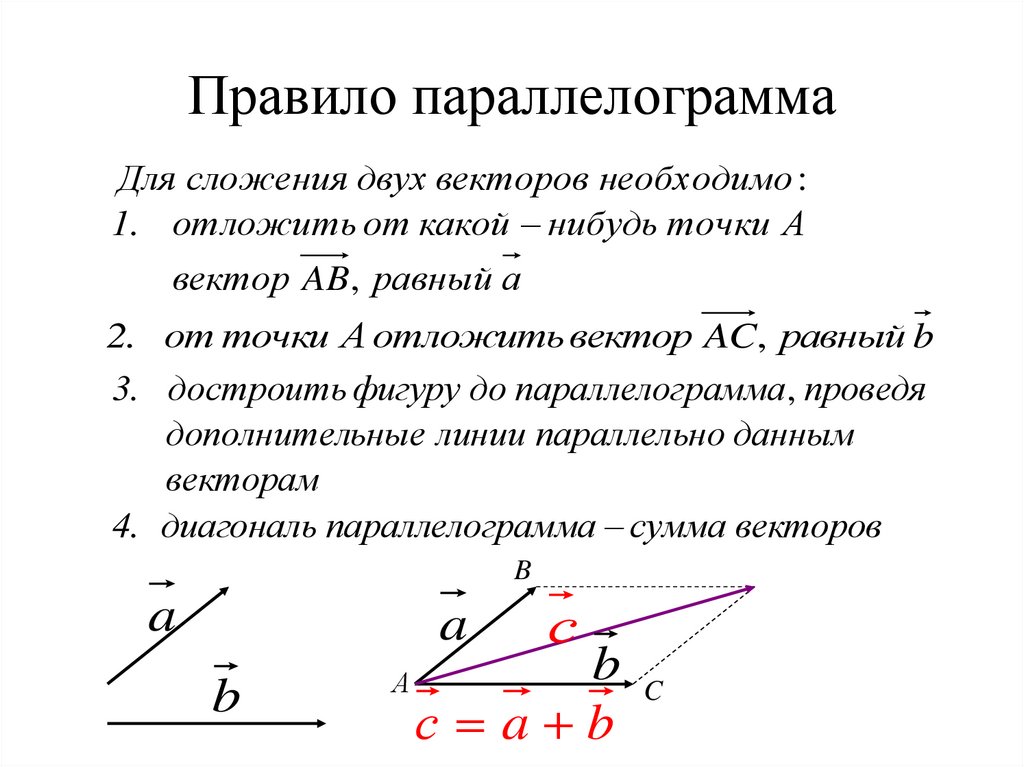 Выразите векторы ВМ, NC, MN, BN
Выразите векторы ВМ, NC, MN, BNчерез векторы
a = АМ
и
b = АN
В
М
a
ВМ =
-a
NC =
b
из AMN
MN = MA + AN =
А
b
N
С
-a + b
из ABN
BN = BA + AN =
-a-a + b
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
B
C
5
О
А
(
4
)
3
D
= АС – DC – OD = АС + CD + DO = АО
АО 5 2,5
2
АВ + ВС =
АS + SС =
АО + ОР =
NM + ML =
MN + NR =
RP + PR =
MK + KM =
ZK + KZ =
MK + OM =
DE + KD =
из ОВN
из ASR
из XKH
из АMD
из FPO
AS =
из ОВN
из ASR
RA =
XH =
из XKH
KX =
ON =
MD =
OP =
из АMD
из FPO
OB =
AD =
FO =
English Русский Правила
Векторы — что это, определение и ответ
ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
Вектор – отрезок, у которого есть начало и конец, то есть указано его направление.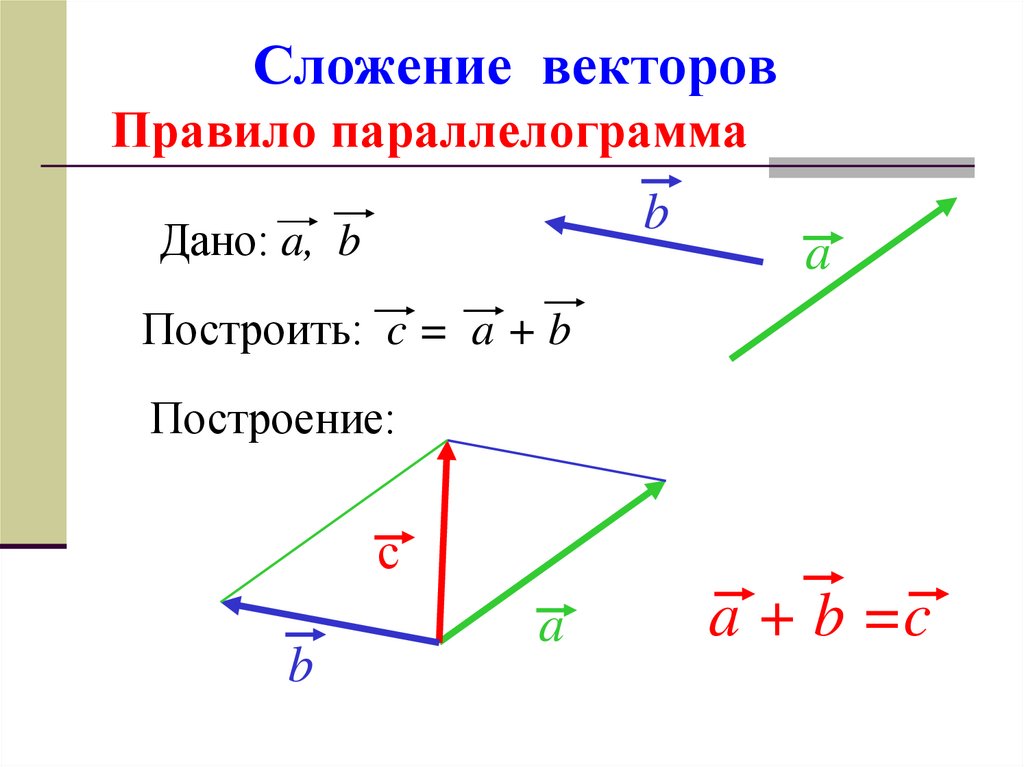
Вектор обозначается через точки начала и конца вектора, например \(\overrightarrow{АВ}\) (первая буква – начало вектора, вторая – конец) или, если мы хотим обозначить вектор без указания точек, пишем просто \(\overrightarrow{a}\).
Точка тоже может быть вектором, в таком случае вектор называют нулевым, т.к. его началом и концом является одна и та же точка. Обозначаем нулевой вектор как, например, \(\overrightarrow{\text{MM}}\) или \(\overrightarrow{0}\).
Длина или модуль вектора – это длина отрезка (как если бы у него не было направления).
Длина вектора \(\overrightarrow{АВ}\) обозначается как \(\left| \overrightarrow{АВ} \right|\), длина вектора \(\overrightarrow{a}\ \)как \(\left| \overrightarrow{a} \right|\), а длина нулевого вектора всегда равна нулю:
\(\left| \overrightarrow{АВ} \right| = 7\)
\(\left| \overrightarrow{a} \right| = 3\)
\(\left| \overrightarrow{\text{MM}} \right| = \left| \overrightarrow{0} \right| = 0\)
РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Коллинеарные векторы – это векторы, которые лежат на параллельных прямых или на одной прямой.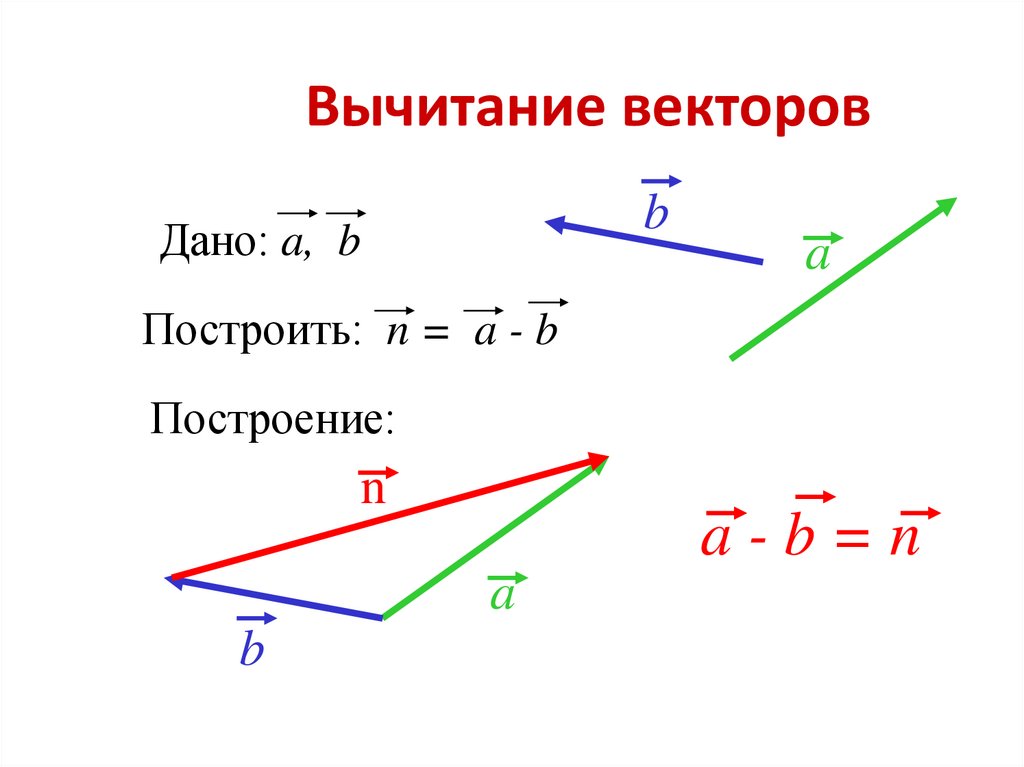 Нулевой вектор коллинеарен любому вектору.
Нулевой вектор коллинеарен любому вектору.
Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону.
Обозначается как \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) сонаправлен вектору \(\overrightarrow{b}\))
Противоположно направленные векторы – это коллинеарные векторы, которые направлены в противоположные стороны.
Обозначаются как \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) противоположно напрвлен вектору \(\overrightarrow{b}\))
Равные векторы – это сонаправленные векторы, у которых равны длины, т.е. у них одинаковые и направление, и длина.
Например:
\(\overrightarrow{АВ}\) и \(\overrightarrow{a}\) – коллинеарны, при этом противоположно направлены, т.к. лежат параллельных прямых и направлены в разные стороны:
\(\overrightarrow{АВ} \uparrow \downarrow \overrightarrow{a}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – коллинеарны, при этом сонаправлены, т.
 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:
\(\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – равны, т.к. сонаправлены (из п.2) и равны по модулю:
\(\left. \ \frac{\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}}{\overrightarrow{\left| \text{CD} \right|} = 5 = \left| \overrightarrow{b} \right|} \right\} \Longrightarrow \overrightarrow{\text{CD}} = \overrightarrow{b}\)
\(\overrightarrow{М}\) коллинеарен всем векторам, и может являться им как сонаправленным, так и противоположно направленным, т.к. \(\overrightarrow{М} = \overrightarrow{0}\).
СВОЙСТВА НЕНУЛЕВЫХ КОЛЛИНЕАРНЫХ ВЕКТОРОВ:
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{b} \upuparrows c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{b} \upuparrows c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
\ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) и \(\overrightarrow{b} \uparrow \downarrow c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}} \right\} \Longrightarrow \overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}\), то \(\overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ТОЧКИ:
Говорят, что вектор отложен от точки, если она является его началом. Например, \(\overrightarrow{АВ}\) отложен от точки А, \(\left| \text{CD} \right|\) отложен от точки С и так далее.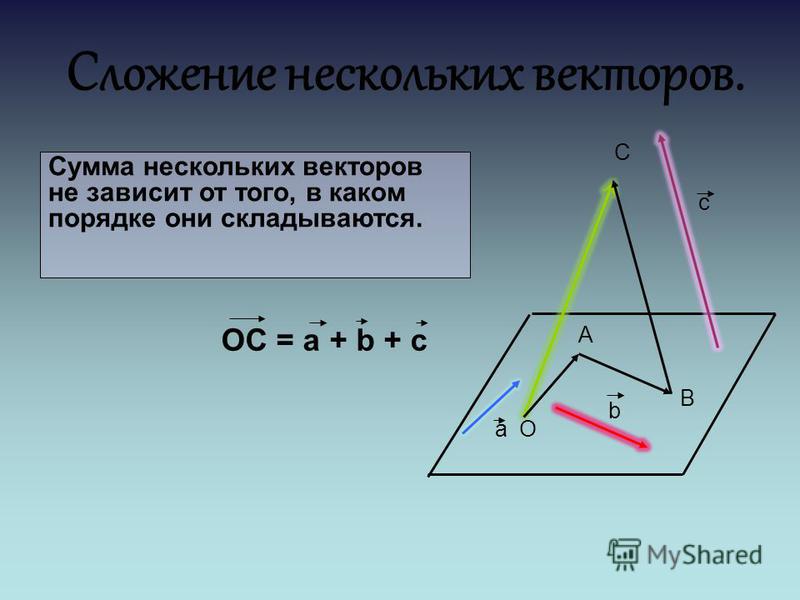 Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
От любой точки можно отложить вектор, равный данному и при том только один.
Например, возьмем точку М и два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Мы можем отложить от точки М вектора, равные \(\overrightarrow{a}\) и \(\overrightarrow{b}\) всего один раз. Делается это параллельным переносом:
Таким образом \(\overrightarrow{a} = \overrightarrow{a’}\), и \(\overrightarrow{b} = \overrightarrow{b’}\), при этом \(\overrightarrow{a’}\ и\ \overrightarrow{b’}\) отложены от точки М.
СЛОЖЕНИЕ ВЕКТОРОВ:
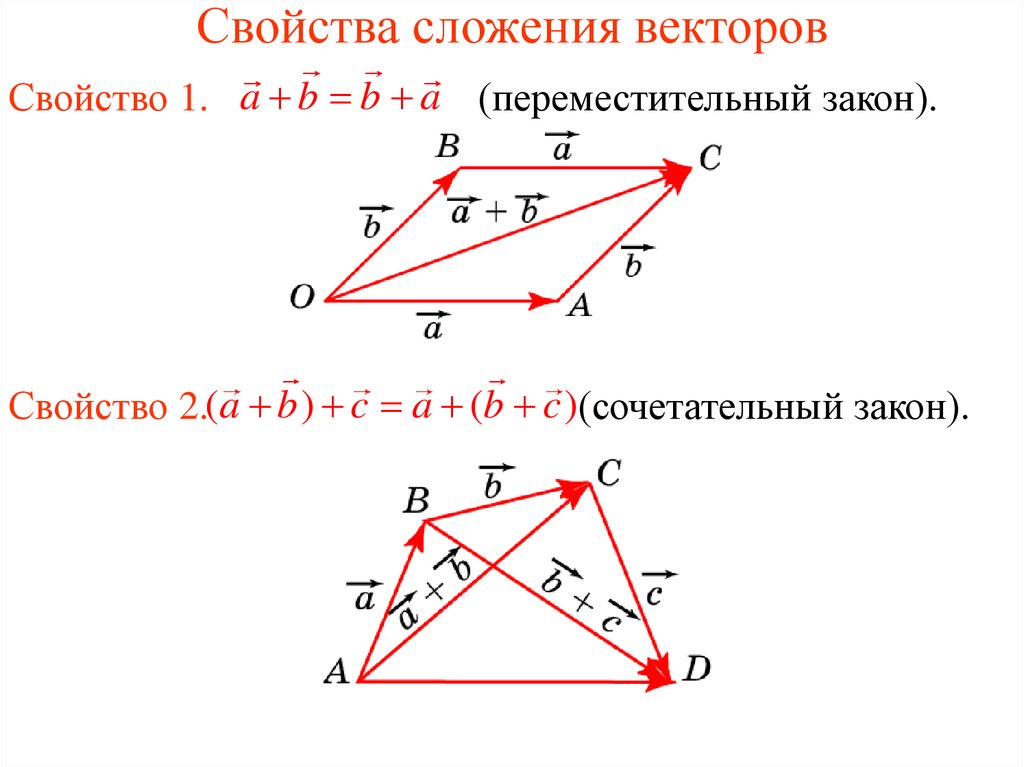
При сложении векторов нужно учитывать их направления, поэтому проще всего складывать вектора визуально. Существуют два самых простых способа сложить два вектора – это правило треугольника и правило параллелограмма.
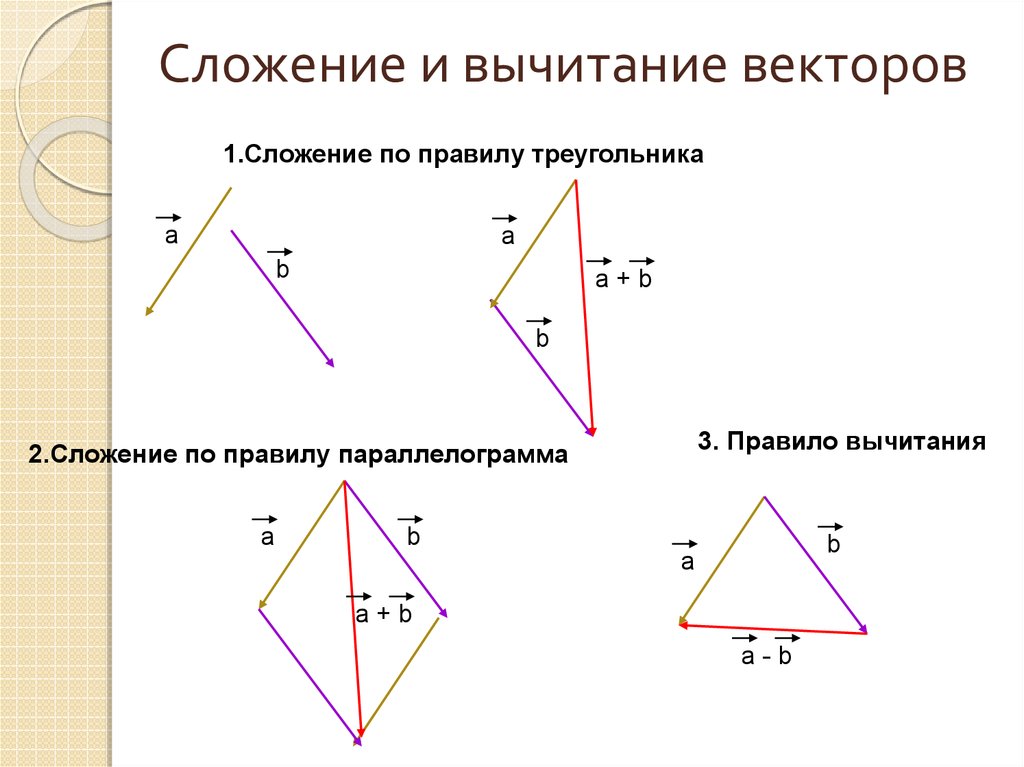
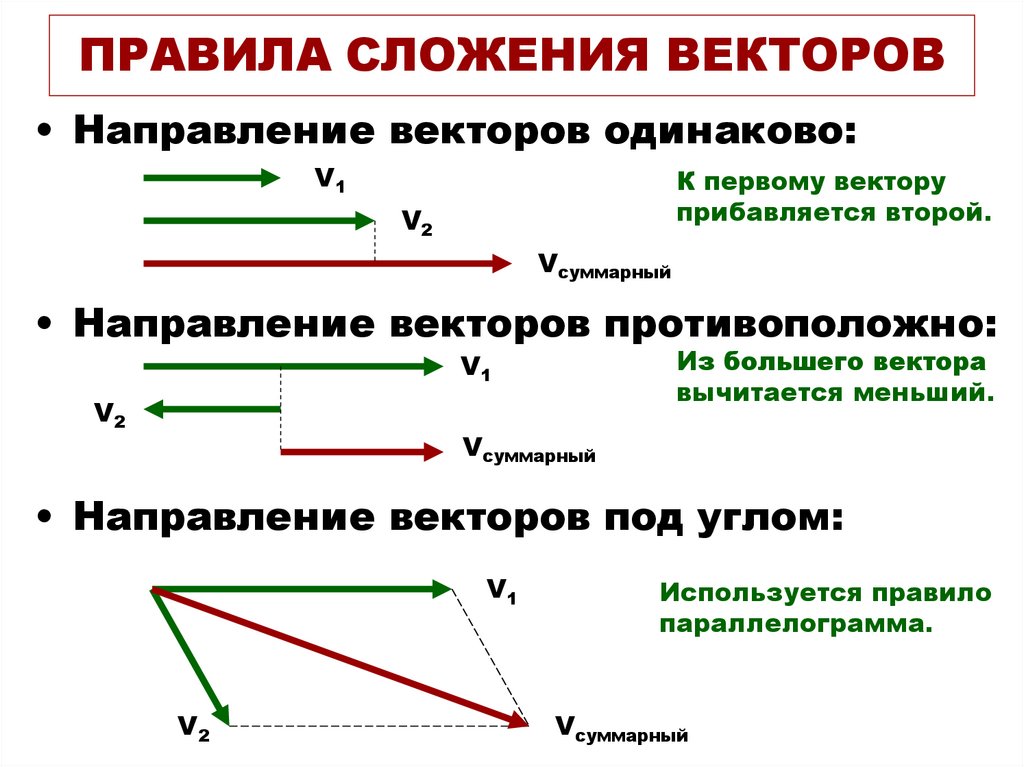
ПРАВИЛО ТРЕУГОЛЬНИКА
Если нужно найти сумму двух векторов, по правилу треугольника нужно:
Параллельным переносом перенести начало одного вектора в конец другого.

Пусть эти векторы будут сторонами треугольника, тогда третья его сторона – их сумма.
Обозначить направление получившегося вектора суммы – от начала первого вектора в конец второго (стрелка к стрелке).
Пример №1:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:
Перенесем вектор \(\overrightarrow{b}\) так, чтобы он начинался там, где заканчивается вектор \(\overrightarrow{a}\).
Соединим эти векторы в треугольник, третьей стороной которой будет вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
Направление вектора \(\overrightarrow{c}\) будет идти от начала \(\overrightarrow{a}\) до конца \(\overrightarrow{b}\) (стрелка к стрелке)
ПРАВИЛО ПАРАЛЛЕЛОГРАММА:
Если нужно найти сумму двух векторов, по правилу параллелограмма нужно:
Параллельным переносом перенести начала этих векторов в одну точку.

Пусть эти векторы будут сторонами параллелограмма, тогда диагональ этого параллелограмма – их сумма.
Обозначить направление получившегося вектора суммы – от начала векторов в противоположный конец параллелограмма (по диагонали).
Пример №2:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:
Перенесем оба вектора параллельным переносом так, чтобы они начинались из одной точки.
Представим, что они являются сторонами параллелограмма.
Диагональ этого параллелограмма, которая начинается в точке начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – это вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ:
Переместительное свойство:
\(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)
Сочетательное свойство:
\((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)
СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ:
Чтобы сложить несколько векторов, нужно ставить их друг за другом, сохраняя их направление (используя параллельный перенос), тогда их суммой будет являться вектор, начала которого – это начало первого вектора, а конец – конец последнего вектора (как в правиле треугольника).
Пример №3:
Найдите сумму векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\):
Поставим эти векторы как бы по порядку сохраняя их длину и направление. По переместительному свойству неважно, в каком порядке мы будем располагать вектора. Соединим их, например, в таком порядке — \(\overrightarrow{d}\), \(\overrightarrow{e}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{a}\).
Проведем вектор их суммы от начала первого вектора в конец второго:
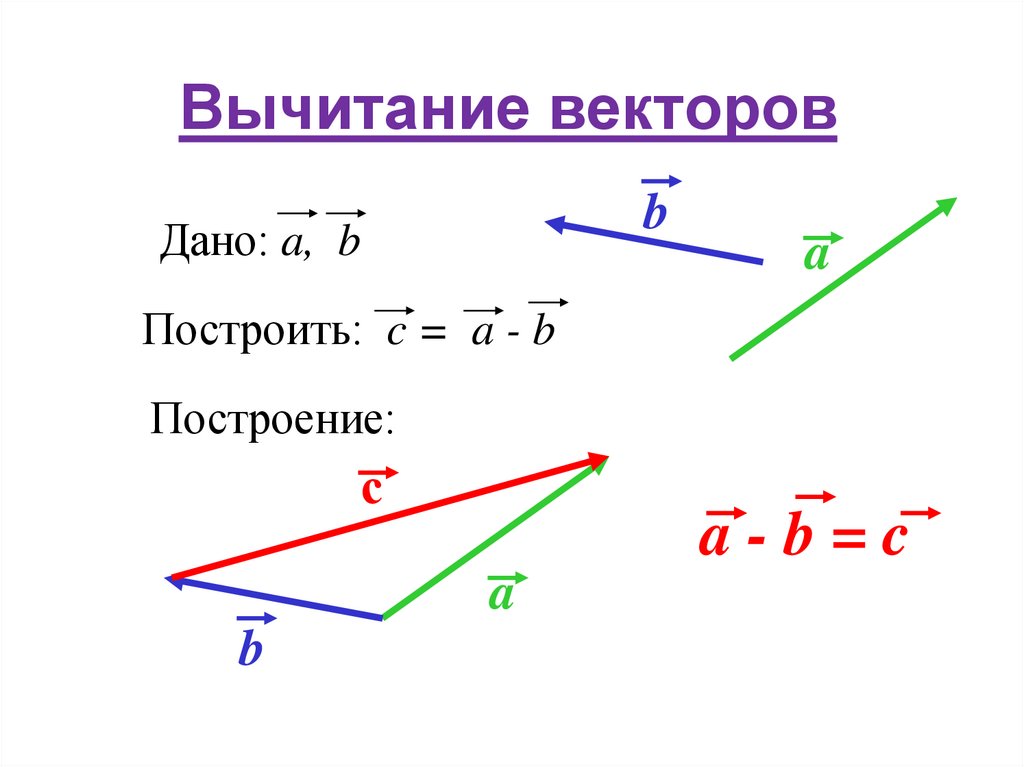
ВЫЧИТАНИЕ ВЕКТОРОВ:
Вычесть вектор – это то же самое, что прибавить отрицательный вектор:
\(\overrightarrow{a}\ –\ \overrightarrow{b} = \overrightarrow{a} + (–\overrightarrow{b})\)
То есть и при вычитании можно использовать правила сложения. Главное – найти противоположный вектор.
Главное – найти противоположный вектор.
Само словосочетание «противоположный вектор» говорит о том, что такие вектора направлены в разные стороны.
Значит вычесть вектор – значит прибавить вектор с противоположным ему направлением.
Мы можем проверить это свойство алгебраически. Мы знаем, что противоположные числа в сумме дают 0:
\(a + (–a) = a\ –\ a = 0\)
Тогда и сумма противоположных векторов дадут 0 (т.е. если мы «пойдем» от начала до конца \(\overrightarrow{a}\) и обратно по –\(\overrightarrow{a}\), то мы вернемся снова в начало \(\overrightarrow{a}\)):
Значит и для векторов справедливо это свойство:
\(\overrightarrow{a}\ + (–\ \overrightarrow{a}) = 0\)
Пример №4:
Найдите \(\overrightarrow{f} = \overrightarrow{a}\ –\ \overrightarrow{b} + \overrightarrow{c}\ –\ \overrightarrow{d}\ –\ \overrightarrow{e}\), если
Можем использовать сложение векторов, если мы найдем отрицательные векторы.
 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
Теперь сложим все векторы, учитывая отрицательные:
ПРОИЗВЕДЕНИЕ ВЕКТОРА И ЧИСЛА:
Произведением ненулевого вектора и числа является вектор, коллинеарный данному, длина которого равна произведению длины данного вектора и числа:
\(k \bullet \overrightarrow{a} = \overrightarrow{\text{ka}}\)
где k – это число, при этом:
\(\overrightarrow{a} \upuparrows \overrightarrow{\text{ka}}\) при \(k > 0\)
\(\overrightarrow{a} \uparrow \downarrow \overrightarrow{\text{ka}}\) при \(k < 0\)
Произведением любого вектора на ноль является нулевой вектор.
Пример №5:
Найдите 5\(\overrightarrow{a}\) и –2\(\overrightarrow{a}\) , если:
1.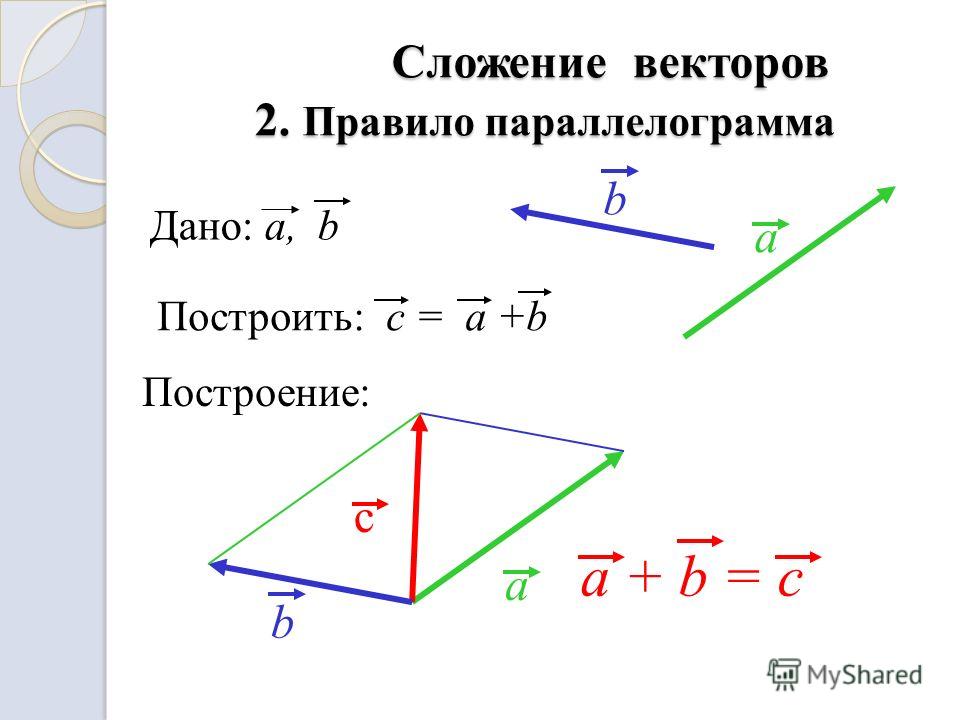 Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
\(5\overrightarrow{a} = \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a}\):
\(5\overrightarrow{a} \upuparrows \overrightarrow{a}\), т.к 5 > 0
2. Аналогично поступим и с отрицательным числом, только теперь уже складываем противоположные векторы:
\(–2\overrightarrow{a} \uparrow \downarrow \overrightarrow{a}\), т.к –2 < 0
СВОЙСТВА ПРОИЗВЕДЕНИЯ ВЕКТОРА И ЧИСЛА:
Сочетательное свойство:
\(kl \bullet \overrightarrow{a} = k(l\overrightarrow{a}) \)
Распределительный закон:
\(\overrightarrow{a}(k + l) = k\overrightarrow{a} + l\overrightarrow{a}\)
и
\(k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}\)
ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ:
Используя векторы и связанные с ними свойства можно решать различные геометрические задачи.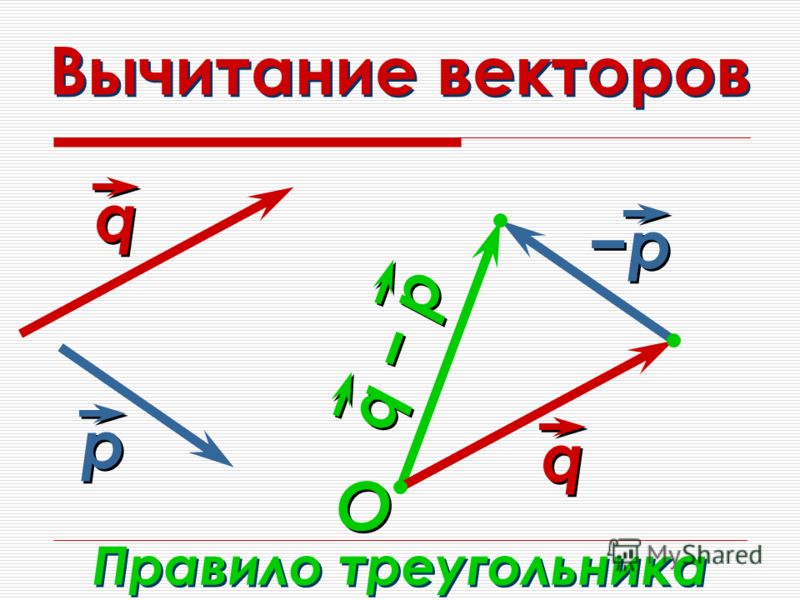
Пример №6:
Точка С – середина отрезка АВ, О – произвольная точка на плоскости. Докажите, что
\(ОС = \frac{1}{2}(АО + ОВ)\)
По правилу треугольника:
\(\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{АС}\)
\(\overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС}\)
Сложим два этих выражения, получим:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
При этом \(\overrightarrow{АС}\) и \(\overrightarrow{ВС}\) – противоположные векторы, т.к. равны по модулю (точка С середина АВ), и имеют противоположное направление, значит:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + 0\)
\(ОС = \frac{1}{2}(АО + ОВ)\)
Что и требовалось доказать.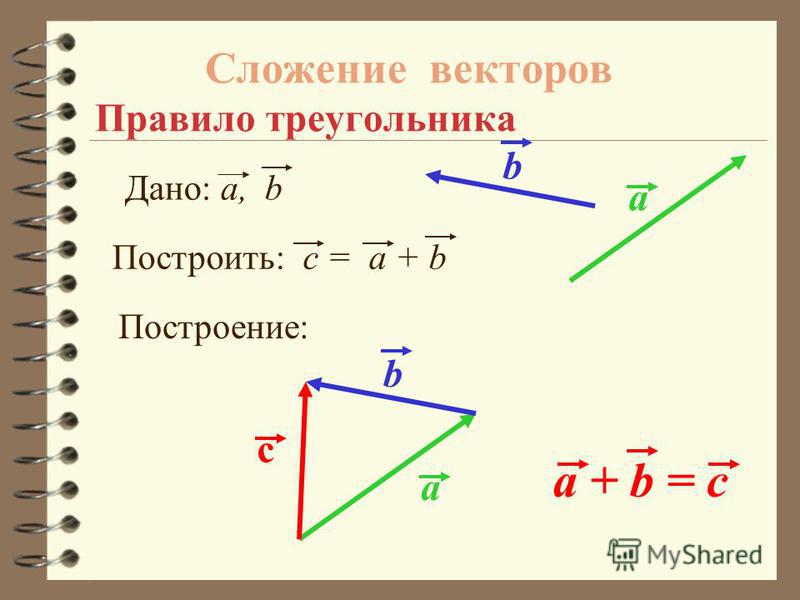
Пример №7:
ABCD – трапеция. Точки M и N середины оснований BC и AD соответственно. Точка О – точка пересечения прямых AB и CD. Докажите, что О, M и N лежат на одной прямой.
Треугольники OAD и OBC подобны по двум углам:
\(\left. \ \frac{\angle\text{OBC} = \angle OAD\ как\ соответствующие\ углы}{\angle O\ — \ общий} \right\}\Delta\text{OAD}\sim\text{ΔOBC}\)
\(\frac{\text{OA}}{\text{OB}} = \frac{\text{OD}}{\text{OC}} = k\)
При этом соответствующие стороны коллинеарны, значит можем выразить их как произведение числа и вектора:
\(\overrightarrow{\text{OA}} \upuparrows \overrightarrow{\text{OB}} \Longrightarrow \overrightarrow{\text{OA}} = k\overrightarrow{\text{OB}}\)
\(\overrightarrow{\text{OD}} \upuparrows \overrightarrow{\text{OC}} \Longrightarrow \overrightarrow{\text{OD}} = k\overrightarrow{\text{OC}}\)
В данной задаче можем выразить \(\overrightarrow{\text{OM}}\) и \(\overrightarrow{ON}\) как
\(\overrightarrow{\text{OM}} = \frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}(\overrightarrow{\text{OA}} + \overrightarrow{\text{OD}})\)
т.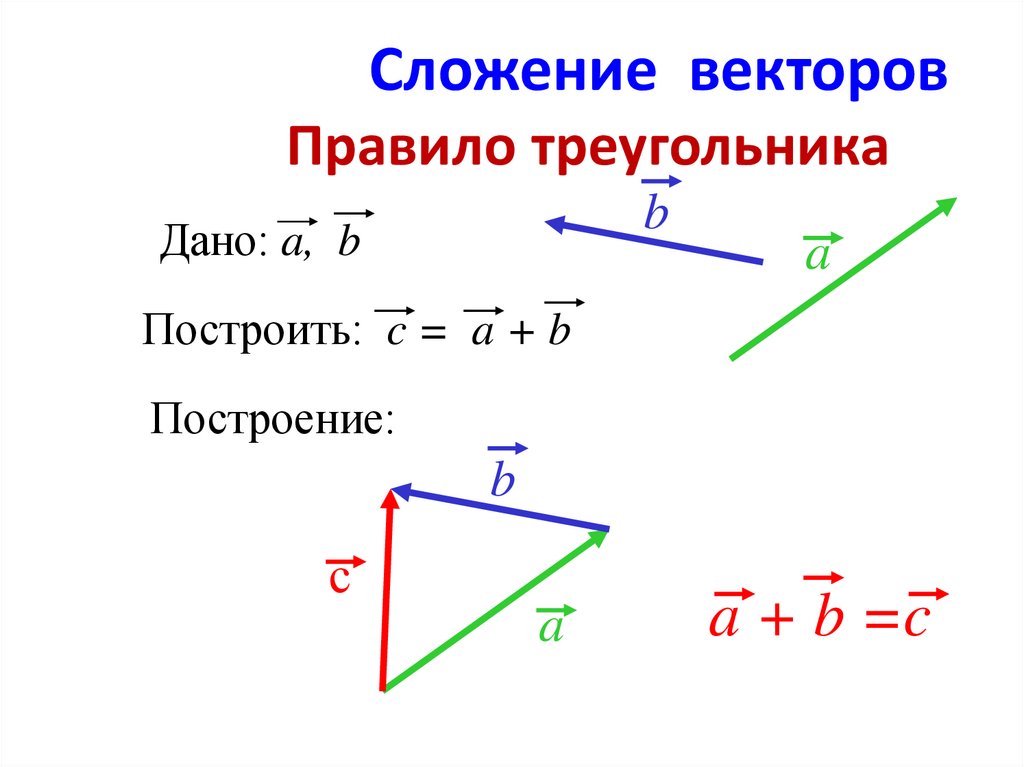 к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
Соединим выразим вектор \(\overrightarrow{\text{ON}}\) через \(\overrightarrow{\text{OA}}\) и \(\overrightarrow{\text{OD}}\) из пункта 3:
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OD}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( k\overrightarrow{\text{OB}} + k\overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}k\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = k(\frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)) = k\overrightarrow{\text{OM}}\)
Если вектор \(\overrightarrow{\text{ON}}\) можно представить как произведение числа k с вектором \(\overrightarrow{\text{OM}}\), значит \(\overrightarrow{\text{ON}}\) и \(\overrightarrow{\text{OM}}\) коллинеарны, а значит лежат на одной прямой (они не могут быть параллельны, т.
 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).
Что и требовалось доказать.
3.3 Сложение и вычитание векторов: аналитические методы
Сложение векторов с использованием аналитических методов
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рис. 3.30, на котором векторы размера AA 12{A} {} и размера BB 12{B} {} складываются для получения результирующего размера RR 12{R} {} .
Рис. 3.30 Векторы размера AA 12{A} {} и размера BB 12{B} {} представляют собой два участка пути, а размер RR 12{R} {} является результирующим или полным смещением. Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.
Если AA и BB представляют собой два этапа ходьбы (два перемещения), то RR представляет собой общее перемещение. Человек, совершающий прогулку, оказывается на вершине RR. Есть много способов попасть в одну и ту же точку. В частности, человек мог пройти сначала в направлении x , а затем в направлении y .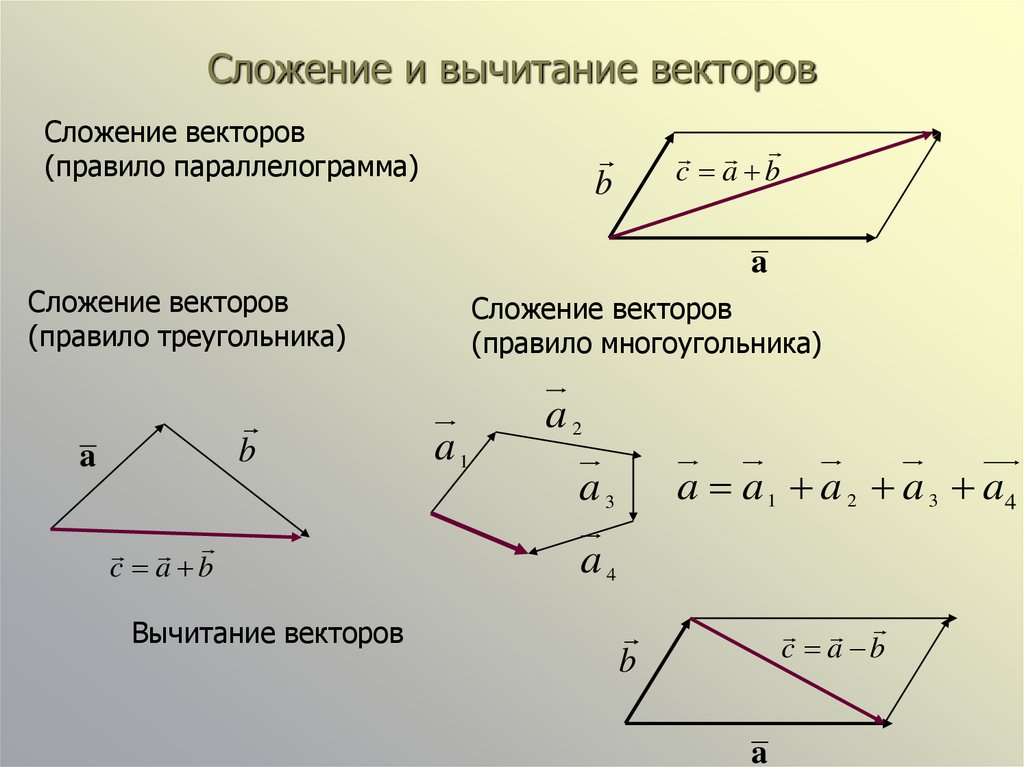
Шаг 1. 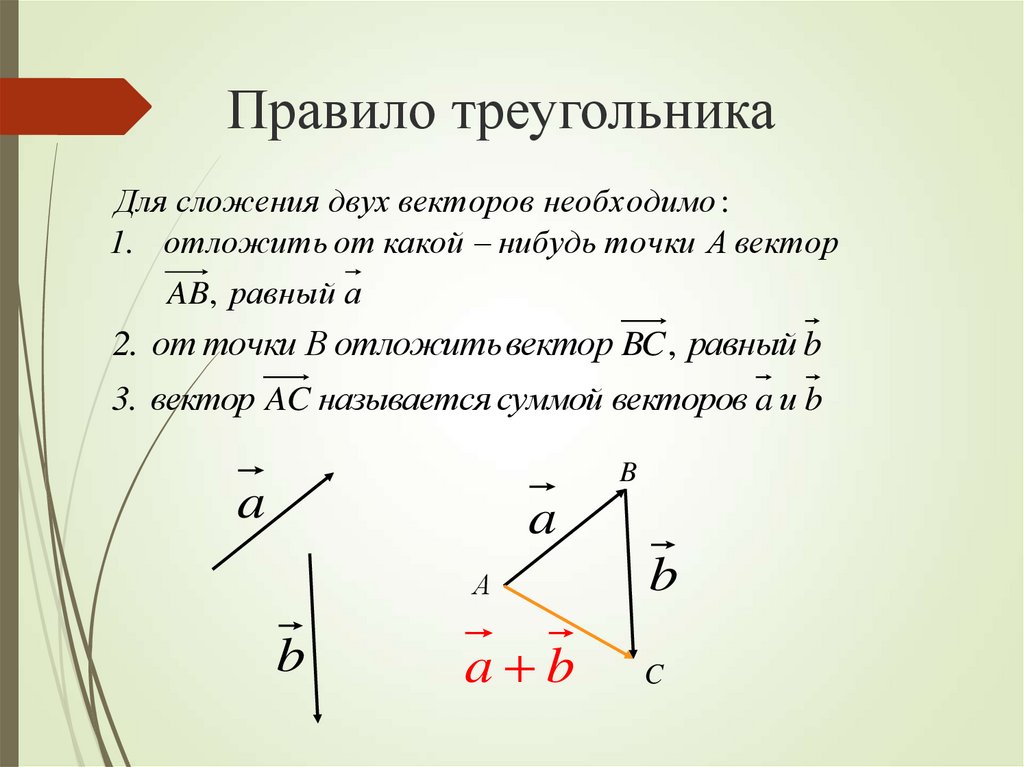 На рис. 3.31 эти компоненты
Размер AxAx 12 {A rSub { размер 8 {x} } } {},
AyAy размер 12 {A rSub { размер 8 {y} } } {},
BxBx размер 12{B rSub { размер 8{x} } } {}, и
ByBy size 12{B rSub { size 8{y} } } {}. Углы, которые составляют векторы размера AA 12{A} {} и размера BB 12{B} {} с
На рис. 3.31 эти компоненты
Размер AxAx 12 {A rSub { размер 8 {x} } } {},
AyAy размер 12 {A rSub { размер 8 {y} } } {},
BxBx размер 12{B rSub { размер 8{x} } } {}, и
ByBy size 12{B rSub { size 8{y} } } {}. Углы, которые составляют векторы размера AA 12{A} {} и размера BB 12{B} {} с
Рисунок 3.31. Чтобы добавить векторы размера AA 12{A} {} и размера BB 12{B} {}, сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы AxAx size 12{A rSub { size 8{x} } } {}, AyAy size 12{A rSub { size 8{y} } } {}, BxBx size 12{B rSub { size 8{x } } } {} и ByBy size 12{B rSub { size 8{y} } } {} показаны на изображении.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси 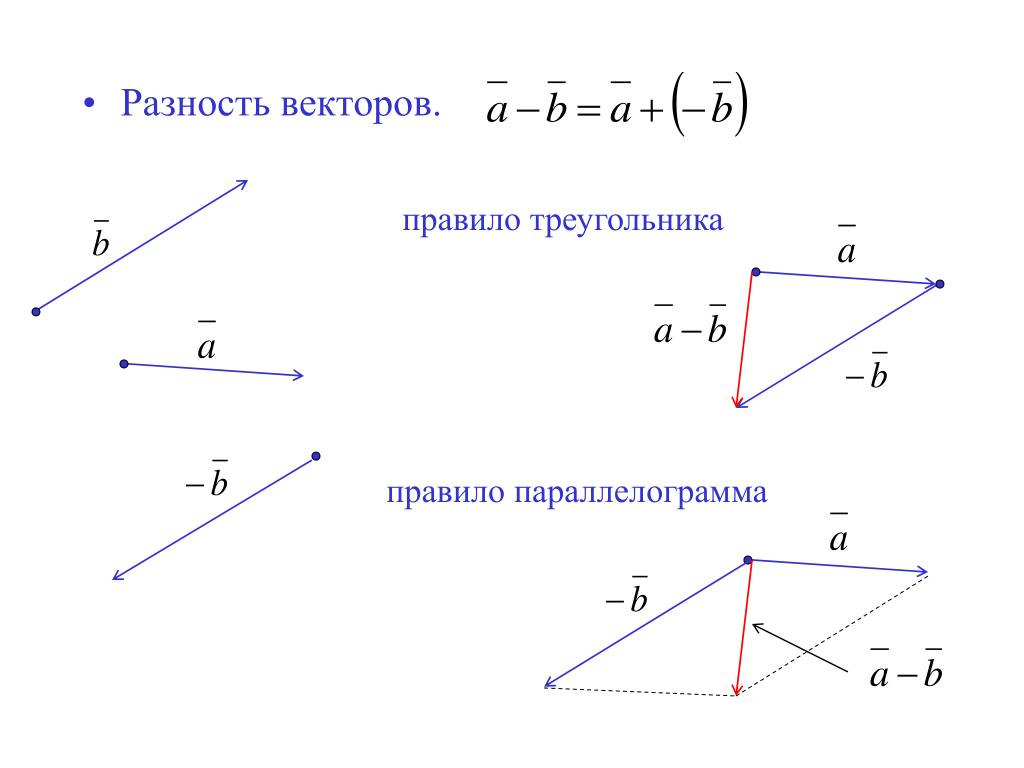 То есть, как показано на рисунке 3.32,
То есть, как показано на рисунке 3.32,
3.12 Rx=Ax+BxRx=Ax+Bx размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8 {x} } } {}
и
3.13 Ry=Ay+By.Ry=Ay+By. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}
Рисунок 3.32. Величина векторов AxAx размера 12{A rSub { size 8{x} } } {} и BxBx размера 12{B rSub { size 8{x} } } {} складывается для получения величины RxRx размера 12{ R rSub { size 8{x} } } {} результирующего вектора в горизонтальном направлении. Аналогично, величины векторов AyAy size 12{A rSub { size 8{y} } } {} и ByBy size 12{B rSub { size 8{y} } } {} в сумме дают величину RyRy size 12{R rSub { size 8{y} } } {} результирующего вектора в вертикальном направлении.
Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси y . Например, пройти 9 кварталов на восток можно двумя этапами: первые три квартала на восток и вторые шесть кварталов на восток, всего девять, потому что они идут в одном направлении. Таким образом, разложение векторов на компоненты вдоль общих осей облегчает их добавление. Теперь, когда компоненты размера RR 12{R} {} известны, можно найти его величину и направление.
То же самое верно для компонентов вдоль оси y . Например, пройти 9 кварталов на восток можно двумя этапами: первые три квартала на восток и вторые шесть кварталов на восток, всего девять, потому что они идут в одном направлении. Таким образом, разложение векторов на компоненты вдоль общих осей облегчает их добавление. Теперь, когда компоненты размера RR 12{R} {} известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину RR size 12{R } {} результанта, используйте теорему Пифагора.
3.14 R=Rx2+Ry2.R=Rx2+Ry2. размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup { размер 8{2} } } «.»} {}
Шаг 4. Чтобы получить направление равнодействующей
3,15 θ=tan-1(Ry/Rx). θ=tan-1(Ry/Rx). size 12{θ=»tan» rSup { size 8{- 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «.»} {}
θ=tan-1(Ry/Rx). size 12{θ=»tan» rSup { size 8{- 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «.»} {}
В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.
Пример 3.3 Добавление векторов с использованием аналитических методов
Добавьте вектор размера AA 12{A} {} к вектору размера BB 12{B} {}, показанному на рисунке 3.33, используя перпендикулярные компоненты вдоль x — и и -оси. Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор AA размера 12{A} {} представляет первый этап ходьбы, в котором человек проходит 53,0 м53,0 м размера 12{«53» «.» «0 м»} {} в направлении 20,0º20,0º размер 12{«20» «.» 0º } {} к северу от востока. Вектор BB размером 12{B} {} представляет собой вторую ветвь водоизмещением 34,0 м34,0 м размером 12{«34» «.» «0 м»} {} в направлении 63,0º63,0º размер 12{«63» «.» 0º } {} к северу от востока.
Вектор BB размером 12{B} {} представляет собой вторую ветвь водоизмещением 34,0 м34,0 м размером 12{«34» «.» «0 м»} {} в направлении 63,0º63,0º размер 12{«63» «.» 0º } {} к северу от востока.
Рис. 3.33 Вектор AA размера 12{A} {} имеет величину 53,0 м53,0 м размера 12{«53» «.» «0 м»} {} и направление 20,0º20,0º размер 12{«20» «.» 0 { size 12{ circ } } } {} к северу от оси x . Вектор BB размера 12{B} {} имеет звездную величину 34,0 м34,0 м размера 12{«34» «.» «0 м»} {} и направление 63,0º63,0º размер 12{«63» «.» 0° } {} к северу от оси x . Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.
Стратегия
Компоненты размера AA 12{A} {} и BB размера 12{B} {} вдоль осей x — и y — представляют собой ходьбу строго на восток и строго на север, чтобы добраться до одного и того же конечная точка. После обнаружения они объединяются для получения результирующего.
После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты Размер AA 12{A} {} и BB размер 12{B} {} вдоль x — и y -оси. Обратите внимание, что A=53,0 мА=53,0 м размер 12{«A» «=» «53,0 м»} {}, θA=20,0ºθA=20,0º размер 12{«θ» «subA» «=» «20,0°» } {}, B=34,0 mB=34,0 м размер 12{«B» «=» «34,0» «м»} {} и θB=63,0ºθB=63,0º размер 12{θ rSub {размер 8{B} } } {}. Мы находим x -компоненты, используя Ax=AcosθAx=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}, что дает
3,16 Ax=AcosθA=(53,0 m)(cos 20,0º)=(53,0 м)(0,940)=49,8 мAx=AcosθA=(53,0 м)(cos 20,0º)=(53,0 м)(0,940)=49,8 malignl { stack {
size 12{A rSub { size 8{x} } =A»cos»θ rSub {size 8{A}} = \(«53» «. 0″ m» \) \( «cos»»20″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «53» «.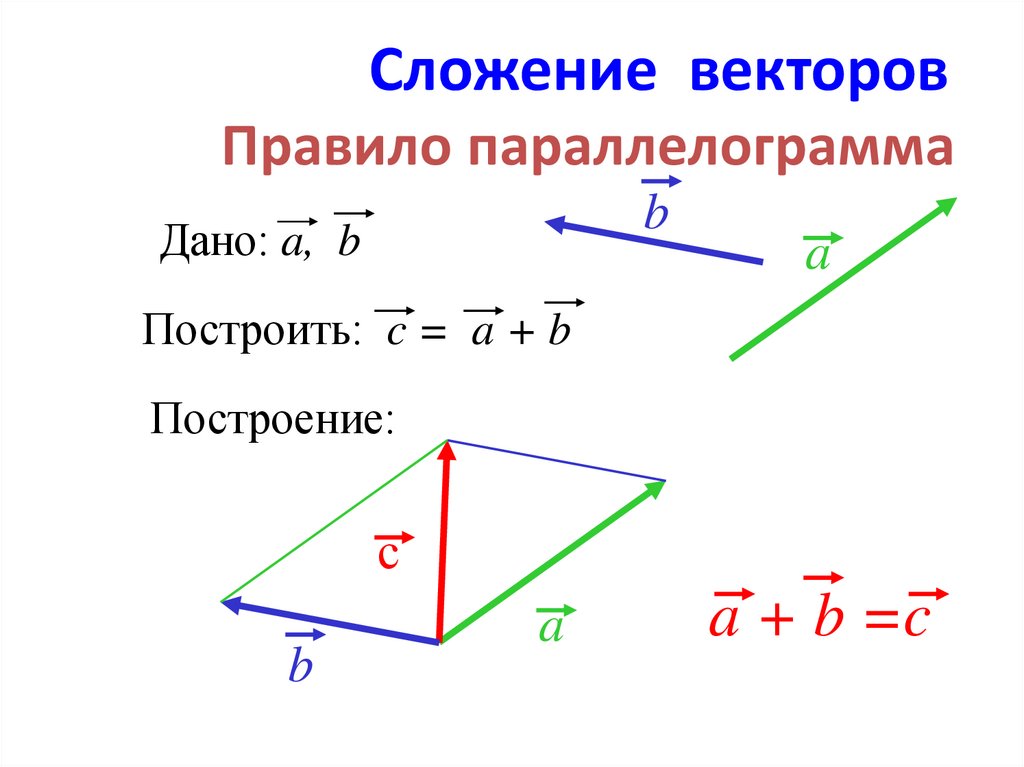 » 0″ м» \) \( 0 «.» «940» \) = «49» «.» 8″ м» {}
} } {}
» 0″ м» \) \( 0 «.» «940» \) = «49» «.» 8″ м» {}
} } {}
и
3,17 Bx=BcosθB=(34,0 м)(cos 63,0°)=(34,0 м)(0,454)=15,4 м.Bx=BcosθB=(34,0 м)(cos 63,0°)=( 34,0 м)(0,454)=15,4 м.alignl { stack { размер 12{B rSub { размер 8{x} } =B»cos»θ rSub { размер 8{B}} = \(«34» «. 0″ m» \) \( «cos»»63″ » .» 0 { размер 12 { круг } } \) } {} # » «= \( «34» «. 0″ м» \) \( 0 «.» «454» \) =»15″ «.» 4 «м» {} } } {}
Аналогично, y -компоненты находятся с использованием Ay=AsinθAAy=AsinθA size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A} } } { }.
3,18 Ay=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 мAy=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 malignl { куча { size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A}} = \(«53» «.» 0″ m» \) \( «sin»»20″ » .» 0 { размер 12 { круг } } \) } {} # » «= \(«53» «. 0″ м» \) \( 0 «.» «342» \) =»18″ «.» 1 «м» {} } } {}
и
3,19 By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891)=30,3 м.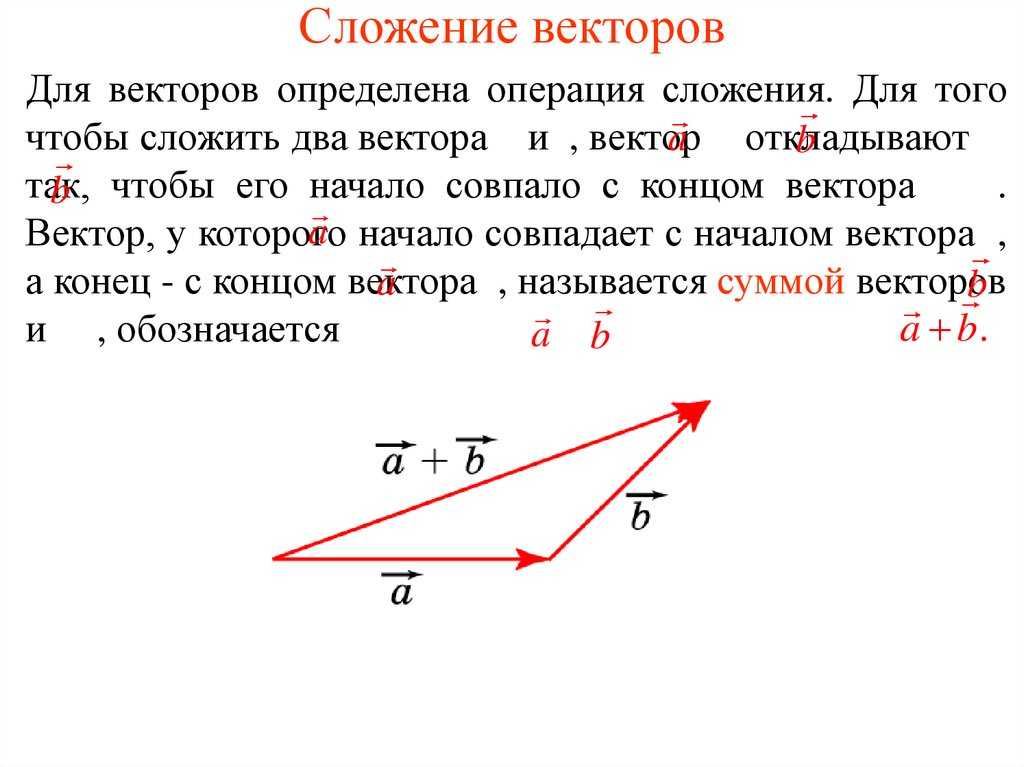 By=BsinθB=(34,0 м)(sin 63,0º)=( 34,0 м)(0,891)=30,3 м.alignl {стек {
size 12{B rSub { size 8{y} } =B»sin»θ rSub { size 8{B}} = \(«34» «. 0″ m» \) \( «sin»»63″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «34» «.» 0″ м» \) \( 0 «.» «891» \)=»30″ «.» 3″ м» «.» {}
} } {}
By=BsinθB=(34,0 м)(sin 63,0º)=( 34,0 м)(0,891)=30,3 м.alignl {стек {
size 12{B rSub { size 8{y} } =B»sin»θ rSub { size 8{B}} = \(«34» «. 0″ m» \) \( «sin»»63″ » .» 0 { размер 12 { круг } } \) } {} #
» «= \( «34» «.» 0″ м» \) \( 0 «.» «891» \)=»30″ «.» 3″ м» «.» {}
} } {}
Таким образом, x — и y -компоненты равнодействующей равны
3,20 Rx=Ax+Bx=49,8 m+15,4 m=Ax=65,2 mRx= +15,4 м=65,2 м размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8{x} } =»49″ «.» 8″ м»+»15″ «.» 4″ м»=»65″ «.» 2″ м»} {}
и
3,21 Ry=Ay+By=18,1 м+30,3 м=48,4 м. Ry=Ay+By=18,1 м+30,3 м=48,4 м. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y}} =»18″ «.» 1″ м»+»30″ «.» 3″ м»=»48″ «.» 4″ м.»} {}
Теперь мы можем найти величину равнодействующей по теореме Пифагора
3,22 R=Rx2+Ry2=(65,2)2+(48,4)2 mR=Rx2+Ry2=(65,2)2+(48,4)2 m размер 12 {R = sqrt {R rSub { размер 8 {x} } rSup { размер 8 {2} } +R rSub { размер 8 {y} } rSup { размер 8 {2} } } = sqrt { \ («65 » «. » 2 \) rSup { size 8{2} } + \( «48» «.» 4 \) rSup { size 8{2} } } » m»} {}
» 2 \) rSup { size 8{2} } + \( «48» «.» 4 \) rSup { size 8{2} } } » m»} {}
так что
3.23 R =81,2 м.R=81,2 м. size 12{R =»81.2″ «m.»} {}
Наконец, мы находим направление равнодействующей
3,24 θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2).θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2). size 12{θ=»tan» rSup { size 8{ — 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «=+»»tan» rSup { size 8{ — 1} } \(«48» «.» 4/»65″ «.» 2 \) «.»} {}
Таким образом,
3,25 θ=tan−1(0,742)=36,6º. θ=тангенс-1(0,742)=36,6º. size 12{θ=»tan» rSup { size 8{ — 1} } \( 0 «.» «742» \) =»36″ «.» 6 {размер 12{круг}} «.»} {}
Рисунок 3.34 Используя аналитические методы, мы видим, что величина RR размера 12{R} {} составляет 81,2 м81,2 м размера 12{«81» «.» «2 м»} {} и его направление 36,6º36,6º размер 12{«36» «.» 6°} {} к северу от востока.
Обсуждение
В этом примере показано сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A−B≡A+(–B)A−B≡A+(–B) размер 12{A – B эквивалент A+ \(- B \)} {}. Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты –B–B – минусы компонентов Размер каретки 12{B} {}. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R size 12{A- полужирный «B = R»} {} равны
3,26 Rx=Ax+(–Bx )Rx=Ax+(–Bx) размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +-B rSub { размер 8{x} } } {}
и
3,27 Ry=Ay+(–By)Ry=Ay+(–By) размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +-B rSub { размер 8{y} } } {}
, а в остальном метод, описанный выше, идентичен методу сложения (см.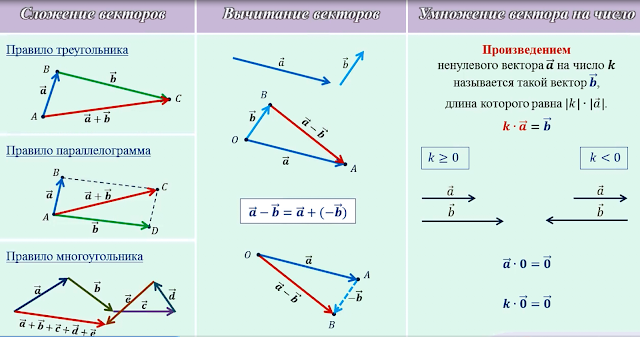 рис. 3.35).
рис. 3.35).
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль Projectile Motion — один из многих, в котором использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
Рисунок 3.35 Вычитание двух векторов, показанных на рисунке 3.30. Компоненты –B–B размера 12{B} {} являются негативами компонентов размера BB 12{B} {}. Метод вычитания такой же, как и для сложения.
Исследования PhET: сложение векторов
Узнайте, как складывать векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Рисунок 3.36 Сложение векторов
Графические методы — физика колледжа
Глава 3 Двумерная кинематика
Резюме
- Понимание правил сложения, вычитания и умножения векторов.

- Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.
А вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]{D},[/латекс], а его направление — [латекс]{\тета}.[/латекс]
2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]{D},[/латекс], а его направление — [латекс]{\тета}.[/латекс]
ВЕКТОРОВ В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором [latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]{F},[/латекс], а направление переменной будет задано углом [латекс]{\тета}.[/латекс ]
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 o к северу от востока.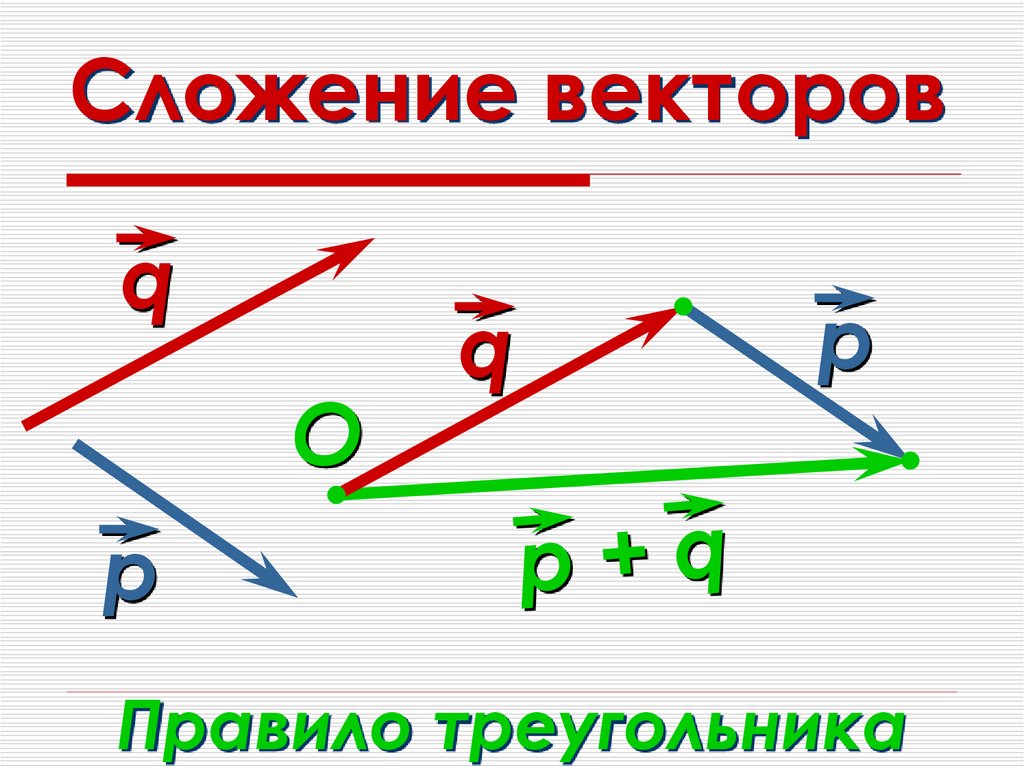 Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . Используя транспортир, начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере величина D вектора составляет 10,3 единицы, а направление θ равно 29.1 o к северу от востока.
Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . Используя транспортир, начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере величина D вектора составляет 10,3 единицы, а направление θ равно 29.1 o к северу от востока.Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а головка (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2.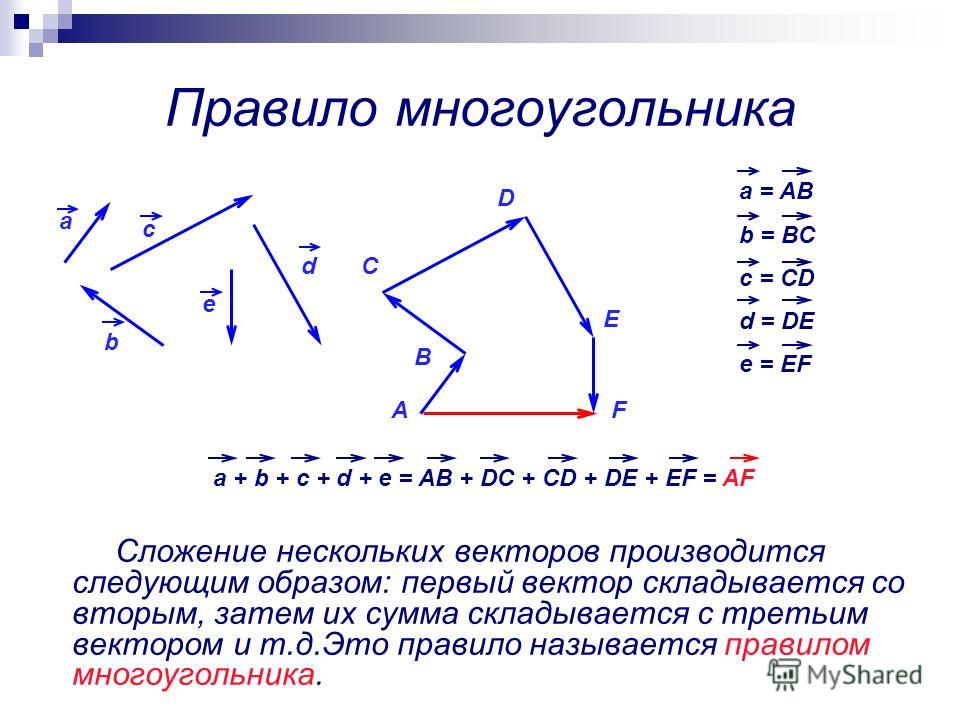 (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, составляет 29,1 0 .
(a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, составляет 29,1 0 .Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рис. 5. Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7.Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла. )
)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9o}[/latex] к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически стрелкой, обозначив первый [latex]\textbf{A},[/latex], второй [latex]\textbf{B},[/latex] и третий [latex]\text{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого [latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рис. 8.
8. (2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9.(3) Нарисуйте результирующий вектор, [латекс]\textbf{R}.[/латекс]
Рисунок 10.(4) Используйте линейку для измерения величины [латекс]\ textbf{R},[/latex] и транспортир для измерения направления [latex]\textbf{R}.[/latex] Несмотря на то, что направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9o}[/latex] к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[latex]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это справедливо и для сложения обычных чисел — вы получите тот же результат, если вы добавите, например, [латекс]{2+3}[/латекс] или [латекс]{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс] из [латекс]\текстбф{А},[/латекс], записанного [латекс]{\текстбф{А}-\текстбф{В }}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0243 отрицательный вектора [latex]\textbf{B}[/latex] определяется как [latex]{-\textbf{B}};[/latex], то есть графически отрицательный элемент любого вектора имеет той же величины, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]{-\textbf{B}},[/latex ] но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]{-\textbf{B}},[/latex ] но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора [latex]\textbf{B}[/latex] из вектора [latex]\textbf{A}[/latex] просто определяется как сложение [latex]{-\ textbf{B}}[/latex] в [latex]\textbf{A}.[/latex] Обратите внимание, что вычитание векторов — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
[латекс]{\textbf{A}-\textbf{B}=\textbf{A}+(-\textbf{B})}.[/latex]
Это аналогично вычитанию скаляров (где, например, [латекс]{5-2=5+(-2)}[/латекс] ). o}[/латекс] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
o}[/латекс] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап пути с помощью вектора [latex]\textbf{A},[/latex] и второй этап пути с помощью вектора [latex] \textbf{B}.[/latex] Док находится в месте [latex]{\textbf{A}\:+\:\textbf{B}}.[/latex] Если женщина по ошибке путешествует в напротив 9o}[/latex] к югу от востока. Мы представляем это как [латекс]{-\textbf{B}},[/латекс], как показано ниже. Вектор [latex]{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [latex]{\textbf{A}+(-\textbf{B})},[/latex] или [latex]{\textbf{A}-\textbf{B}} .[/latex]
Рисунок 15. Мы выполним сложение векторов, чтобы сравнить местоположение дока, [latex]{\textbf{A}+\textbf{B}},[/latex] с местоположением в которую по ошибке прибывает женщина, [латекс]{\textbf{A}+(-\textbf{B})}. [/latex]
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex]\textbf{A}[/latex] и [latex]{-\textbf{B}}.[ /latex]
(2) Разместите векторы «голова к хвосту».
(3) Нарисуйте результирующий вектор [latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.к югу от востока. 9o}[/latex] к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли [латекс]{3 \times 27,5\text{ м}},[/latex] или 82,5 м, в направлении [латекс]{66. o}[/латекс] к северу от востока. Это пример умножения вектора на положительное число 9.0107 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
o}[/латекс] к северу от востока. Это пример умножения вектора на положительное число 9.0107 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение на него вектора изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор [latex]\textbf{A}[/latex] умножается на скаляр [latex]{c},[/latex]
- модуль вектора становится абсолютным значением [latex]{cA},[/latex]
- , если [latex]{c}[/latex] положительный, направление вектора не меняется,
- , если [latex]{c}[/latex] имеет отрицательное значение, направление меняется на противоположное.
В нашем случае [latex]{c=3}[/latex] и [latex]{\textbf{A}=27,5\text{m}}.[/latex] Во многих случаях векторы умножаются на скаляры. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает в себя определение перпендикулярных компонентов одного вектора, например, x – и y -компоненты, или компонентов север-юг и восток-запад. 9o}[/latex] к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0107 заставляет в Главе 4 Динамика: Законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0107 заставляет в Главе 4 Динамика: Законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод сложения векторов [latex]\textbf{A}[/latex] и [latex]\textbf{B}[/latex] включает в себя рисование векторов на графике и их сложение с использованием прямой метод хвоста.
 Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно. - графический метод вычитания вектора [latex]\textbf{B}[/latex] из [latex]\textbf{A}[/latex] включает добавление противоположного вектора [latex]\textbf{B},[/latex] ] который определяется как [latex]{-\textbf{B}}.[/latex] В этом случае [latex]{\textbf{A}-\textbf{B}=\textbf{A}+(-\ textbf{B})=\textbf{R}}.[/latex] Затем обычным образом применяется метод сложения головы к хвосту для получения результирующего вектора [latex]\textbf{R}.[/ латекс]
- Сложение векторов коммутативно , такое что [латекс]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора.



 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону: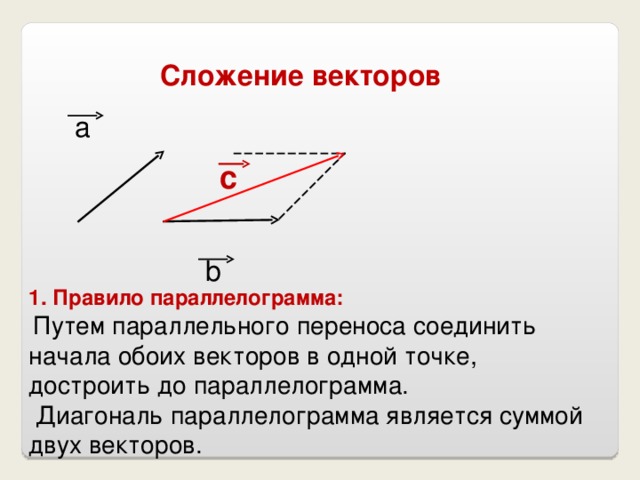
 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие: к. уже пересекаются в точке О).
к. уже пересекаются в точке О).
 Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.