Самоиндукция и взаимоиндукция
25.25.По катушке индуктивностьюL=0,03 мГн течет токI=0,6 А. При размыкании цепи сила тока изменяется практически до нуля за времяΔt=120 мкс. Определить среднюю ЭДС самоиндукции <i>, возникающую в контуре.
25.26. Спомощью реостата равномерно увеличивают силу тока в катушке наΔI=0,1 А в 1 с. ИндуктивностьLкатушки равна 0,01 Гн. Найти среднее значение ЭДС самоиндукции <i>.
25.27.ИндуктивностьLкатушки равна 2 мГн. Ток частотойυ=50 Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю ЭДС самоиндукции <i>, возникающую за интервал времениΔt, в течение которого ток в катушке изменяется от минимального до максимального значения. Амплитудное значение силы токаI0=10 А.
25.
25.29.На картонный каркас длинойl=50 см и площадьюSсечения, равной 4 см2, намотан в один слой провод диаметромd=0,2 мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Вычислить индуктивностьLполучившегося соленоида.
25. 31.Сколько витков проволоки
диаметромd=0,4 мм с
изоляцией ничтожной толщины нужно
намотать на картонный цилиндр диаметромD=2 см, чтобы получить
однослойную катушку с индуктивностьюL=lмГн?
Витки вплотную прилегают друг к другу.
31.Сколько витков проволоки
диаметромd=0,4 мм с
изоляцией ничтожной толщины нужно
намотать на картонный цилиндр диаметромD=2 см, чтобы получить
однослойную катушку с индуктивностьюL=lмГн?
Витки вплотную прилегают друг к другу.
25.32.Катушка, намотанная на немагнитный цилиндрический каркас, имеет
25.33.Определить индуктивностьLдвухпроводной линии на участке длинойl=1 км. РадиусRпровода равен 1 мм, расстояниеd между осевыми линиями равно 0,4 м.
Указание.Учесть только внутренний
магнитный поток, т.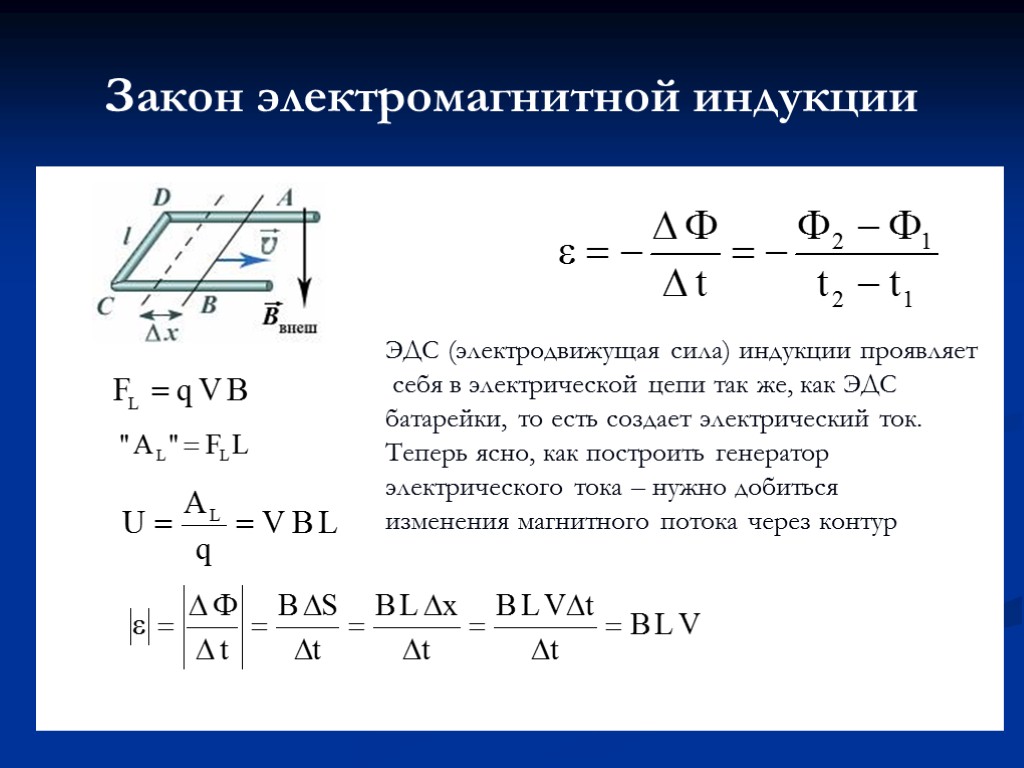
25.34.Соленоид индуктивностьюL=4 мГн содержитN=600 витков. Определить магнитный поток Ф, если сила токаI, протекающего по обмотке, равна 12 А.
25.35.ИндуктивностьLкатушки без сердечника равна 0,02 Гн. Какое потокосцепление ψ создается, когда по обмотке течет токI= 5 А?
25.36.Длинный прямой соленоид, намотанный на немагнитный каркас, имеетN=1000 витков и индуктивность
25.37.Соленоид, площадьSсечения которого равна 5 см2, содержитN=1200 витков. ИндукцияВмагнитного поля внутри соленоида при силе токаI=2 А равна 0,01 Тл. Определить индуктивностьLсоленоида.
25.38.Соленоид содержитN=1000
витков. ПлощадьSсечения сердечника равна 10 см2.
По обмотке течет ток, создающий поле с
индукцией В==1,5 Тл. Найти среднюю ЭДС
индукции <ei>,
возникающей в соленоиде, если ток
уменьшится до нуля за время
ПлощадьSсечения сердечника равна 10 см2.
По обмотке течет ток, создающий поле с
индукцией В==1,5 Тл. Найти среднюю ЭДС
индукции <ei>,
возникающей в соленоиде, если ток
уменьшится до нуля за время
25.39.Обмотка соленоида с железным сердечником содержитN=500 витков. Длинаl сердечника равна 50 см. Как и во сколько раз изменится индуктивностьLсоленоида, если сила тока, протекающего по обмотке, возрастет отI1=0,lА доI2=1 А (см. рис. 24.1).
25.40.Две катушки расположены на небольшом расстоянии одна от другой. Когда сила тока в первой катушке изменяется с быстротой5 А/с, во второй катушке возникает ЭДС индукцииei=0,1 В. Определить коэффициентМвзаимной индукции катушек.
 Средний диаметр <D>
тороида равен 8 см, диаметрd витков равен 2 см. На тороид намотана
вторичная обмотка, имеющаяN2=100
витков. При замыкании первичной обмотки
в ней в течениеt=1 мс
устанавливается сила токаI=3
А. Найти среднюю ЭДС индукции <ei>,
возникающей на вторичной обмотке.
Средний диаметр <D>
тороида равен 8 см, диаметрd витков равен 2 см. На тороид намотана
вторичная обмотка, имеющаяN2=100
витков. При замыкании первичной обмотки
в ней в течениеt=1 мс
устанавливается сила токаI=3
А. Найти среднюю ЭДС индукции <ei>,
возникающей на вторичной обмотке.Самоиндукция. Энергия магнитного поля
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Φ = LI. |
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
1 Гн = 1 Вб / 1 А. |
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой:
B = μ0 I n, |
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.
Магнитный поток, пронизывающий все N витков соленоида, равен
Φ = B S N = μ0 n2 S l I. |
Следовательно, индуктивность соленоида равна
L = μ0 n2 S l = μ0 n2 V, |
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз; поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
Lμ = μ L = μ0 μ n2 V. |
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Рисунок 1.21.1. Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает |
Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2 R Δt.
Ток в цепи равен
Выражение для ΔQ можно записать в виде
ΔQ = –L I ΔI = –Φ (I) ΔI. |
В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I0 до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I0 до 0. Это дает
Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ (I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.
Рисунок 1. Вычисление энергии магнитного поля |
Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина
равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей. Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 12Следующая ⇒ Рассчитаем энергию однородного магнитного поля длинного соленоида, индуктивность которого определяется по формуле . .
Учитывая, что напряженность поля внутри бесконечно длинного соленоида H = nI, получаем . (4.15) Выразим энергию магнитного поля через индукцию : (4.16) или (4.17)
Е д и н и ц а — Дж (джоуль). Магнитное поле соленоида однородно и сосредоточено внутри него. Энергия магнитного поля, заключенная в единице объёме соленоида называется объёмной плотностью энергии и определяется по формуле (4.18) Е д и н и ц а w — (джоуль на кубический метр). В случае неоднородного магнитного поля энергия определяется по формуле
.
Магнитные свойства вещества Всякое вещество является магнетиком, т.е. способно под действием внешнего магнитного поля намагничиваться. Магнитная индукция внутри магнетика зависит от магнитной проницаемости вещества : , (4. где -вектор магнитной индукции внешнего магнитного поля. Магнитная проницаемость у всех веществ различна. Она может быть как больше, так и меньше единицы. Различают диамагнетики ( < 1), парамагнетики ( > 1), ферромагнетики ( >> 1). Магнитная проницаемость парамагнетиков и диамагнетиков не зависит от индукции B (напряженности H) внешнего магнитного поля. У ферромагнетиков зависит от внешнего магнитного поля, т.е. между B и H существует нелинейная зависимость. График зависимости магнитной индукции B некоторых ферромагнетиков от напряженности H внешнего магнитного поля представлен на рис. 4.3.
Рис. 4.3 Вопросы для самоконтроля 1. Запишите выражение и сформулируйте основной закон электромагнитной индукции (закон Фарадея – Ленца). 2. Что называется явлением самоиндукции? 3. Напишите выражение для э.д.с. самоиндукции. 4. Что такое индуктивность контура (соленоида) и от чего она зависит? 5. 6. Каков физический смысл индуктивности? 7. Запишите выражение для определения индуктивности соленоида. 8. Запишите закон изменения силы тока в цепи, содержащей последовательно включённые R и L при включении и выключении источника постоянного тока. Постройте график и поясните его. 9. Дайте определение явления взаимной индукции, напишите формулу определения ЭДС взаимной индукции. 10. От чего зависит взаимная индуктивность? В каких единицах измеряется? По какой формуле определяется взаимная индуктивность двух контуров? 11. Как рассчитывается энергия и плотность энергии магнитного поля? 12. Действие каких электрических приборов основано на явлении взаимной индукции? Примеры решения задач Задача 1.При скорости изменения силы тока в соленоиде, равной 50 А/с, на его концах возникает ЭДС самоиндукции В. Определить индуктивность L cоленоида.
Дано: Решение. А/с Индуктивность соленоида связана с ЭДС самоиндукции и скоростью изменения силы В тока в его обмотке соотношением . L — ? Вынося постоянную величину L за знак приращения, получим . Опустив знак «минус» в этом равенстве (направление э.д.с. в данном случае несущественно) и выразив интересующую нас величину – индуктивность, получим ; (мГн). Ответ:L = 1,6 мГн.
Задача 2.Катушка имеет сопротивление R = 10 Ом и индуктивность L = 0,1 Гн. Через сколько времени после выключения в катушке возникнет ток, равный половине установившегося?
Дано: Решение. R = 10 Ом При выключении тока в катушке он не мгновенно L = 0,1 Гн становится равным нулю. При убывании тока в катушке возникает ЭДС самоиндукции, пре- пятствующая убыванию тока. t — ? Возникает экстраток размыкания. , где — установившийся ток в катушке (в начальный момент времени ), I – ток в момент времени t, R – сопротивление катушки, L – её индуктивность. Тогда ; , отсюда
Вычислим : .
Ответ:t = c.
Задача 3.Источник тока замкнули на катушку с сопротивлением R = 10 Ом и индуктивностью L = 1 Гн. Через сколько времени сила тока замыкания достигает 0,9 предельного значения.
Дано: Решение. R = 10 Ом Закон изменения силы тока при замыкании цепи L = 1 Гн имеет вид: I = 0,9∙I , t -? т.к. , то 0,9 , отсюда . Логарифмируем это выражение: ; => .
Вычислим: (с).
Ответ:t = 0,23 с.
Задача 4. На железный стержень длиной = 50 см и сечением = 2 см2 намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Дано: Решение = 50 см = 0,5 м Энергия магнитного поля соленоида S = 2 см2 = 2 .10-4 м2 = 20 . I = 0,5 А Индуктивность соленоида , — ? где = 4p · 10-7 . Магнитная проницаемость сердечника соленоида: , где В – индукция магнитного поля внутри соленоида, Н – напряженность. Подставив в формулу энергии индуктивность L и магнитную проницаемость , получим расчетную формулу: , где . Найдем напряженность Н: Н = 2 .103. 0,5 = 103 ( ). Индукцию В можно найти из графика зависимости В от Н (см. рис. 4.3). При Н = 103 индукция равна : В = 1,3 Тл. Вычислим энергию магнитного поля, подставив числовые значения в расчетную формулу. = 0,065 (Дж).
Ответ: = 0,065 Дж. Задача 5.Индуктивность L соленоида длиной ℓ = 60 см и площадью поперечного сечения S = 4 см² равна 4 Гн. При какой силе тока I объёмная плотность энергии магнитного поля внутри соленоида составляет 2 Дж/м³?
Дано: Решение. L = 4 Гн Энергия магнитного поля внутри соленоида ℓ = 60 см = 0,6 м , S = 4 см² = 4 м² где I – сила тока. = 2 Дж/м³ I -? Объёмная плотность энергии , откуда , где V = ℓS — объём соленоида, тогда , отсюда ; (А).
Ответ:I = 1,55 A.
Задача 6. На один немагнитный сердечник намотаны две катушки, имеющие индуктивности L1 = 0,2 Гн и L2 = 0,8 Гн. Дано: Решение L1 = 0,2 Гн ; ; L2 = 0,8 Гн . I = 0,3 A — индуктивность 1-ой катушки (4.20) — индуктивность 2-ой катушки (4.21) R2 = 600 Ом — взаимная индуктивность. (4.22) I2 — ? Из (4.20) выразим , из (4.21) выразим , подставим в (4.22) и получим , откуда .
Тогда . . Подставляя числовые значения, находим:
(А). Ответ: I2 = 0,2 А.
Задачи для самостоятельного решения Самоиндукция Задача 4.1.При помощи реостатаравномерно увеличивают силу тока в катушке на А в секунду. Индуктивность катушки Гн. Найти среднее значение ЭДС самоиндукции. Ответ: =1 мВ.
Задача 4.2.В соленоиде без сердечника, содержащем N = 1000 витков, при увеличении силы тока магнитный поток увеличился на = 1 мВб. Определить среднюю ЭДС самоиндукции , возникающую в соленоиде, если изменение силы тока произошло за время = 0,1 с. Ответ: =10 В.
Задача 4.3.Если сила тока, проходящего в некотором соленоиде, изменяется на = 40 А/с, то на концах соленоида возникает среднее значение ЭДС самоиндукции < > = 0,1 В. Найти индуктивность соленоида. Ответ:L = 2,5 мГн.
Задача 4.4.Катушка длиной ℓ = 50 см и диаметром d = 5 см содержит N = 200 витков. По катушке течёт ток I = 1 А. Определить: 1) индуктивность катушки L; 2) магнитный поток , пронизывающий площадь её поперечного сечения. Ответ:1) L = 197 мкГн; 2) Ф = 986 нВб.
Задача 4.5.Длинный соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см². Определить магнитную индукцию поля B внутри соленоида, если сила тока I, протекающего по его обмотке, равна 6 А. Ответ:B = 0,02 Тл.
Задача 4.6.Определить, сколько витков проволоки N, вплотную прилегающих друг к другу, диаметром d = 0,5 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром D = 1,5 см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн. Ответ:N = 225 витков.
Задача 4.7.По соленоиду течёт ток I = 2 А. Магнитный поток пронизывающий поперечное сечение соленоида, равен 4 Вб. Определить индуктивность соленоида L, если он имеет N = 800 витков. Ответ:L =1,6 мГн.
Задача 4.8. Обмотка соленоида с железным сердечником содержит N = 500 витков. Длина сердечника равна 50 см. Как и во сколько раз изменится индуктивность L соленоида, если сила тока, протекающего по обмотке, возрастет от А до А. Зави- симость B = f(H) дана на рис.4.3. Ответ: —уменьшится в 6,5 раза.
Задача 4.9.Две длинные катушки намотаны на общий сердечник, причём индуктивность этих катушек L = 0,64 Гн и 0,04 Гн. Определить, во сколько раз число витков первой катушки больше, чем второй. Ответ: = 4 .
Задача 4.10.По катушке, индуктивность которой L = 0,03 Гн, течет ток силой I =0,6 А. При размыкании цепи сила тока изменяется практически до нуля за время = 120 мс. Определить среднюю ЭДС самоиндукции < >, возникающую в контуре. Ответ: < > =0,15 В.
Задача 4. Ответ:L =6,28 мГн.
Задача 4.12.Соленоид, площадь сечения которого равна S = 5 см , содержит N = 1200 витков. Индукция В магнитного поля внутри соленоида при силе тока I =2 А равна 0,01 Тл. Определить индуктивность соленоида L. Ответ:L = 3 мГн. Взаимная индукция Задача 4.13.Две катушки намотаны на один общий сердечник. Определить их взаимную индуктивность, если при скорости изменения силы тока в первой катушке А/с во второй катушке индуцируется ЭДС В. Ответ:M =0,1 Гн.
Задача 4.14.Две катушки намотаны на один сердечник. Ответ:I2 = 0,1 А.
Задача 4.15.Две катушки расположены на небольшом расстоянии одна от другой. Когда сила тока в первой катушке изменяется с быстротой , во второй катушке возникает ЭДС индукции В. Определить коэффициент взаимной индуктивности катушек М. Ответ:M = 0,02 Гн.
Задача 4.16.На соленоид с немагнитным сердечником длиной = 0,2 м и площадью поперечного сечения S = 3 ∙ 10-3 м² надет проволочный виток. Число витков соленоида N = 320. Какая средняя ЭДС взаимоиндукции < > возникнет в витке, если ток соленоида I = 3 А выключить в течение Δt = 0,001 с. Ответ:< >=0,018 В.
Задача 4.17.Два соленоида (L = 0,64 Гн, L = 1 Гн) одинаковой длины и практически равных сечений вставлены один в другой. Определить взаимную индуктивность М соленоидов. Ответ:М= 0,8 Гн. Энергия, объемная плотность энергии Задача 4.18.Сила тока I в обмотке соленоида, содержащей N = 1500 витков, равна 5 А. Магнитный поток через поперечное сечение соленоида составляет 200 мкВб. Определить энергию магнитного поля в соленоиде. Ответ: =0,75 Дж.
Задача 4.19.Обмотка электромагнита, находясь под постоянным напряжением, имеет сопротивление R = 15 Ом и индуктивность L = 0,3 Гн. Определить время t, за которое в обмотке выделится количество теплоты Q, равное энергии магнитного поля в сердечнике. Ответ: ∆t = 0,01 с.
Задача 4.20.Соленоид без сердечника с однослойной обмоткой из проволоки диаметром d = 0,5 мм имеет длину ℓ = 0,4 м и поперечное сечение S = 50 см². Какой ток I течёт по обмотке при напряжении U = 10 В, если за время t = 0,5 мс в обмотке выделяется количество теплоты Q, равное энергии поля внутри соленоида? (Поле считать однородным). Ответ:I = 995 мА. Задача 4.21.По соленоиду длиной = 0,5 м, имеющему число витков N = 250, течет ток силой I = 5 А. Площадь поперечного сечения S = 25 см . В соленоид вставлен железный сердечник. Найти энергию магнитного поля соленоида. Зависимость B = f(H) дана на рис. 4.3. Ответ: =2,18 Дж.
Задача 4.22.Индуктивность соленоида при длине = 1 м и площади поперечного сечения S = 20 см² равна 0,4 мГн. Определить силу тока I в соленоиде, при которой объёмная плотность энергии магнитного поля внутри соленоида равна 0,1 Дж/м³. Ответ:I = 1 А.
Задача 4.23.Тороид с воздушным сердечником содержит N = 20 витков на 1 см. Определить объёмную плотность энергии в тороиде, если по его обмотке протекает ток I = 3 А. Ответ: =22,6 Дж/м³.
Задача 4.24.Определить объёмную плотность энергии магнитного поля в стальном сердечнике, если индукция В магнит- ного поля равна 0,5 Тл ( см. рис. 4.3). Ответ: =25 Дж/м .
Задача 4.25.При некоторой силе тока I объемная плотность энергии магнитного поля соленоида (без сердечника) равна 0,2 Дж/м . Во сколько раз увеличится плотность энергии поля при той же силе тока, если соленоид будет иметь железный сердечник (рис. 4.3)? Ответ:В 1600 раз. Токи при замыкании и размыкании цепи Задача 4. Ответ:R = 322 мОм.
Задача 4.27.Определить, через сколько времени t сила тока замыкания I достигнет 0,95 предельного значения, если источник тока замыкают на катушку сопротивлением R = 12 Ом и индуктивностью L = 0,5 Гн. Ответ:t = 125 мс.
Задача 4.28.Имеется катушка индуктивностью L = 0,1 Гн и сопротивлением R = 0,8 Ом. Определить, во сколько раз уменьшится сила тока I в катушке через 30 мс, если источник тока отключить и катушку замкнуть накоротко. Ответ: . Задача 4.29.Определить силу тока I в цепи через 0,01 с после её размыкания. Сопротивление цепи R = 20 Ом, индуктивность L = 0,1 Гн. Ответ:I =6,75 А. Задача 4.30.Электрическую цепь сопротивлением R = 10 Ом и индуктивность L = 1 Гн разомкнули. Через сколько времени сила тока уменьшится до 0,001 первоначального значения? Ответ:t = 0,69 с.
ГЛАВА 5. ⇐ Предыдущая3456789101112Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
XII.
 ИНДУКЦИЯ. САМОИНДУКЦИЯ. ВЗАИМНАЯ ИНДУКЦИЯ — МегаЛекции
ИНДУКЦИЯ. САМОИНДУКЦИЯ. ВЗАИМНАЯ ИНДУКЦИЯ — МегаЛекции1) Магнитная индукция B поля между полюсами двухполюсного генератора равна 0,8Тл. Ротор имеет N=100 витков площадью S=400см2. Определить частоту n вращения якоря, если максимальное значение ЭДС индукции εi=200В.
2) Прямой провод длиной l=40см движется в однородном магнитном поле со скоростью V=5м/с перпендикулярно линиям индукции. Разность потенциалов U между концами провода равна 0,6В. Вычислить индукцию B магнитного поля.
3) Катушка радиусом r=5см с числом витков N=20 и сопротивлением R=7Ом находится в однородном магнитном поле с индукцией В=6Тл. Ось катушки направлена вдоль линий поля. Концы катушки замкнуты. Какой заряд пройдет через катушку, если повернуть ее на угол α=60о?
4) Обмотка тороида с немагнитным сердечником имеет N1=251 виток. Средний диаметр <D> тороида равен 8см, диаметр d витков равен 2см. На тороид намотана вторичная обмотка, имеющая N2=100 витков. При замыкании первичной обмотки в ней в течение t=1мс устанавливается сила тока I=3А. Найти среднюю ЭДС индукции <εi>, возникающей на вторичной обмотке.
На тороид намотана вторичная обмотка, имеющая N2=100 витков. При замыкании первичной обмотки в ней в течение t=1мс устанавливается сила тока I=3А. Найти среднюю ЭДС индукции <εi>, возникающей на вторичной обмотке.
5) Обмотка соленоида с железным сердечником содержит N=500 витков. Длина l сердечника равна 50см. Как и во сколько раз изменится индукция B соленоида, если сила тока, протекающего по обмотке, возрастет от I1=0,1А до I2=1А.
6) Индуктивность L катушки равна 2мГн. Ток частотой n=50Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю ЭДС самоиндукции <εi>, возникающую за интервал времени Dt, в течение которого ток в катушке изменяется от минимального до максимального значения. Амплитудное значение силы тока I0=10А.
7) Соленоид содержит N=1000 витков. Площадь S сечения сердечника равна 10см2. По обмотке течет ток, создающий поле с индукцией B=1,5Тл. Найти среднюю ЭДС индукции <εi>, возникающей в соленоиде, если ток уменьшится до нуля за время t=500мкс.
Площадь S сечения сердечника равна 10см2. По обмотке течет ток, создающий поле с индукцией B=1,5Тл. Найти среднюю ЭДС индукции <εi>, возникающей в соленоиде, если ток уменьшится до нуля за время t=500мкс.
8) Катушка, намотанная на немагнитный цилиндрический каркас, имеет N1=750 витков и индуктивность L1=25мГн. Чтобы увеличить индуктивность катушки до L2=36мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить число N2 витков катушки после перемотки.
9) Две катушки имеют взаимную индуктивность 5 мГн. В первой катушке ток изменяется по закону . Найти наибольшее значение ЭДС, индуцируемой во второй катушке.
10) Соленоид содержит N=800 витков. Сечение сердечника (из немагнитного материала) S=10см2. По обмотке течет ток, создающий поле с индукцией B=8мТл. Определить среднее значение ЭДС <εs> самоиндукции, которая возникает на зажимах соленоида, если сила тока уменьшается практически до нуля за время Dt=0,8мс.
Определить среднее значение ЭДС <εs> самоиндукции, которая возникает на зажимах соленоида, если сила тока уменьшается практически до нуля за время Dt=0,8мс.
11) Соленоид диаметром d=4см, имеющий N=500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1мТл/с. Ось соленоида составляет с вектором магнитной индукции угол a=45о. Определить ЭДС индукции, возникающей в соленоиде.
12) В магнитное поле, изменяющееся по закону B=B0coswt (B0=0,1Тл, w=4с -1), помещена квадратная рамка со стороной a=50см, причем нормаль к рамке образует с направлением поля угол a=45о. Определить ЭДС индукции, возникающую в рамке в момент времени t=5с.
13) В однородное магнитное поле с индукцией B=0,3Тл помещена прямоугольная рамка с подвижной стороной, длина которой l=15см. Определить ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью V=10м/с.
14) В однородном магнитном поле (B=0,1Тл) вращается с постоянной угловой скоростью w=50с -1 вокруг вертикальной оси стержень длиной l=0,4м. Определить максимальную ЭДС индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнитной индукции.
15) В однородном магнитном поле (B=0,2Тл) равномерно с частотой n=600мин -1 вращается рамка, содержащая N=1200 витков, плотно прилегающих друг к другу. Площадь рамки S=100см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определить максимальную ЭДС, индуцируемую в рамке.
16) Магнитная индукция B поля между полюсами двухполюсного генератора равна 1Тл. Ротор имеет 140 витков (площадь каждого витка S=500см2). Определить частоту вращения якоря, если максимальное значение ЭДС индукции равно 220В.
17) В однородном магнитном поле (B=0,2Тл) равномерно вращается прямоугольная рамка, содержащая N=200 витков, плотно прилегающих друг к другу. Площадь рамки S=100см2. Определить частоту вращения рамки, если максимальная ЭДС, индуцируемая в ней, εimax=12,6В.
Площадь рамки S=100см2. Определить частоту вращения рамки, если максимальная ЭДС, индуцируемая в ней, εimax=12,6В.
18) Две катушки намотаны на один общий сердечник. Определить их взаимную индуктивность, если в первой катушке ток изменяется по закону , а во второй катушке в момент времени t=2c индуцируется ЭДС εi2=0,3В.
19) Проводник длиной 15см помещен в магнитное поле с индукцией 2Тл перпендикулярно силовым линиям поля. Концы проводника замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи 0,5Ом. Какую мощность необходимо затратить, чтобы двигать проводник перпендикулярно к линиям индукции и к проводнику со скоростью 10м/с.
20) Металлический стержень массой 100г и длиной 1м подвешен за середину к пружине с жесткостью 10Н/м. Стержень совершает гармонические колебания с амплитудой 10см в однородном магнитном поле с индукцией 0,01Тл, направленном перпендикулярно плоскости колебаний. Найти максимальную разность потенциалов на концах стержня.
Найти максимальную разность потенциалов на концах стержня.
21) Два параллельных идеально проводящих рельса расположены на расстоянии 1м друг от друга в плоскости, перпендикулярной магнитному полю с индукцией 1Тл. Рельсы соединены проводниками с сопротивлениями 0,5Ом и 1,5Ом, движущимися в одном направлении со скоростями 3м/с и 2м/с. Найти ток в цепи.
22) Проволочное кольцо радиусом r=7см и сопротивлением R=10Ом расположено в однородном магнитном поле, индукция которого В=5Тл. Вектор магнитной индукции перпендикулярен плоскости кольца. Определите величину заряда, который потечет по кольцу, если кольцо повернуть относительно одного из диаметров на угол p.
23) Проводящая рамка в форме равностороннего треугольника со стороной 10см может вращаться вокруг одной из своих сторон. Рамка помещена в однородное магнитное поле, линии индукции которого перпендикулярны оси вращения рамки и параллельны ее плоскости. При повороте рамки на некоторый угол по ней протек заряд 10мкКл. Определить угол, на который была повернута рамка, если индукция магнитного поля 8мТл, сопротивление рамки 3Ом.
При повороте рамки на некоторый угол по ней протек заряд 10мкКл. Определить угол, на который была повернута рамка, если индукция магнитного поля 8мТл, сопротивление рамки 3Ом.
24) В однородном магнитном поле с индукцией 0,1Тл расположен плоский проволочный виток так, что его плоскость перпендикулярна линиям индукции. Виток замкнут на гальванометр. При повороте витка через гальванометр протек заряд 9,5•10 -6Кл. На какой угол повернули виток? Площадь витка 10см2, сопротивление витка 2Ом.
25) Из двух одинаковых кусков проволоки изготовлены два контура – круглый и квадратный. Оба контура помещены в одной плоскости в однородное магнитное поле, изменяющееся со временем. В круговом контуре индуцируется постоянный ток 0,4А. Найдите силу тока в квадратном контуре.
26) По сверхпроводящему проводу, имеющему форму кольца радиусом r=8см, идет ток. Индукция магнитного поля в центре кольца равна Во=6мТл. Проводу придают форму кольца, радиусом r/2 «на ножке». Какова теперь магнитная индукция в центре уменьшенного кольца?
Проводу придают форму кольца, радиусом r/2 «на ножке». Какова теперь магнитная индукция в центре уменьшенного кольца?
27) Сверхпроводящее кольцо с током перекручивают, превращая его в «восьмерку» из двух одинаковых колец. Затем «восьмерку» складывают так, что получается одно «двойное» кольцо. Как изменится магнитная индукция в центре кольца по сравнению с первоначальной?
28) Катушка радиусом 3см с числом витков N=1000 помещают в однородное магнитное поле (ось катушки параллельна линиям поля). Индукция поля изменяется с постоянной скоростью 10мТл/с. Какой заряд будет на конденсаторе, подключенном к концам катушки? Емкость конденсатора 20мкФ.
29) Катушка радиусом 3см с числом витков N=1000 помещают в однородное магнитное поле (ось катушки параллельна линиям поля). Индукция поля изменяется с постоянной скоростью 10мТл/с. Катушка замыкается накоротко. Найти выделяющуюся в ней тепловую мощность, если сопротивление катушки 16Ом.
30) Металлический диск радиусом 10см расположен в однородном магнитном поле, перпендикулярном плоскости диска. Диск вращается с угловой скоростью 500рад/с. Два скользящих контакта (один на оси диска, другой на его цилиндрической поверхности) соединены через резистор, сопротивлением 10Ом. Какая мощность выделяется в резисторе, если индукция магнитного поля 0,5Тл?
Воспользуйтесь поиском по сайту:
5. 1. Соленоид диаметром d = 4 см, имеющий N = 500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол α = 45°. Определить э. д. с. индукции, возникающей в соленоиде. Ответ: 444 мкВ. 5. 2. В магнитное поле, изменяющееся по закону В = B0·cosωt (В0 = 0,1 Тл, ω = 4с-1), помещена квадратная рамка со стороной d = 50 см, причем нормаль к рамке образует с направлением поля угол α = 45°. 5. 3. Кольцо из алюминиевого провода (ρ = 26 нОм·м) помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца D = 30см, диаметр провода d = 2 мм. Определить скорость изменения магнитного поля, если ток в кольце I = 1 А. Ответ: 0,11 Тл/с. 5. 4. Плоскость проволочного витка площадью S = 100 см2 и сопротивлением R = 5 Ом, находящегося в однородном магнитном поле напряженностью Н = 10 кА/м, перпендикулярна линиям магнитной индукции. При повороте витка в магнитном поле отсчет гальванометра, замкнутого на виток, составляет Q = 12,6 мКл. Определить угол поворота витка. Ответ: 60°. 5. 5. В однородное магнитное поле с индукцией В = 0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 см. Определить э. д. с. индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью υ = 10 м/с. 5. 6. В катушке длиной l = 0,5 м, диаметром d = 5 см и числом витков N = 1500 ток равномерно увеличивается на 0,2 А за одну секунду. На катушку надето кольцо из медной проволоки (ρ = 17 нОм·м) площадью сечения SK= 3 мм2. Определить силу тока в кольце. Ответ: 0,166 мА. 5. 7. Катушка диаметром d = 2 см, содержащая один слой плотно прилегающих друг к другу N = 500 витков алюминиевого провода сечением S =1 мм2, помещена в магнитное поле. Ось катушки параллельна линиям индукции. Магнитная индукция поля равномерно изменяется со скоростью 1 мТл/с. Определить тепловую мощность, выделяющуюся в катушке, если ее концы замкнуть накоротко. Удельное сопротивление алюминия ρ = 26 нОм·м. Ответ: 30,2 мкВт. 5. 8. В однородном магнитном поле (B = 0,1 Тл) вращается с постоянной угловой скоростью (ω = 50 с-1) вокруг вертикальной оси стержень длиной l = 0,4 м. 5. 9. В однородном магнитном поле с индукцией В = 0,02 Тл равномерно вращается вокруг вертикальной оси горизонтальный стержень длиной l = 0,5 м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определить число оборотов в секунду, при котором на концах стержня возникает разность потенциалов U = 0,1 В. Ответ: 6,37 с-1 . 5. 10.В однородном магнитном поле (В = 0,2 Тл) равномерно с частотой n = 600 мин-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определить максимальную э. д. с., индуцируемую в рамке. Ответ: 151 В. 5. 11.Магнитная индукция В поля между полюсами двухполюсного генератора равна 1 Тл. 5. 12.В однородном магнитном поле (В = 0,2 Тл) равномерно вращается прямоугольная рамка, содержащая N = 200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Определить частоту вращения рамки, если максимальная э.д.с., индуцируемая в ней, (Ei)max= 12,6 В. Ответ: 5 с-1 . 5. 13.В однородном магнитном поле равномерно вращается прямоугольная рамка с частотой n = 600 мин-1. Амплитуда индуцируемой в рамке э. д. с. E0 = 38 В. Определить максимальный магнитный поток через рамку. Ответ: 47,7 мВб. 5. 14.Катушка длиной l = 50 см и диаметром d=5 см содержит N = 200 витков. По катушке течет ток I = 1А. 5. 15.Длинный соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см2. Определить магнитную индукцию поля внутри соленоида, если сила тока, протекающего по его обмотке, равна 6 А. Ответ: 0,02 Тл. 5. 16.Две длинные катушки намотаны на общий сердечник, причем индуктивности этих катушек L1 = 0,64 Гн и L2 = 0,04 Гн. Определить, во сколько раз число витков первой катушки больше, чем второй. Ответ: В 4 раза. 5. 17.Определить, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром d = 0,5 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром D = 1,5см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн? Ответ: 225. 5. 18. 5. 19.Сверхпроводящий соленоид длиной l = 10 см и площадью поперечного сечения S = 3 см2, содержащий N = 1000 витков, может быть подключен к источнику э. д. с. Е = 12 В. Определить силу тока через 0,01с после замыкания ключа. Ответ: 31,8 А. 5. 20.Через катушку, индуктивность L которой равна 200 мГн, протекает ток, изменяющийся по закону I = 2cos3t. Определить: 1) закон изменения э. д. с. самоиндукции; 2) максимальное значение э. д. с. самоиндукции. Ответ: Es = 1,2sin3t B; 2) 1,2 В. 5. 21.В соленоиде без сердечника, содержащем N=1000 витков, при увеличении силы тока магнитный поток увеличился на 1 мВб. Определить среднюю э. 5. 22.Имеется катушка индуктивностью L = 0,1 Гн и сопротивлением R = 0,8 Ом. Определить, во сколько раз уменьшится сила тока в катушке через t = 30 мс, если источник тока отключить и катушку замкнуть накоротко. Ответ: В 1,27 раза. 5. 23.Определить, через какое время сила тока замыкания достигнет 0,95 предельного значения, если источник тока замыкают на катушку сопротивлением R = 12 Ом и индуктивностью 0,5 Гн. Ответ: 125 мс. 5. 24.Катушку индуктивностью L = 0,6 Гн подключают к источнику тока. Определить сопротивление катушки, если за время t = 3 с сила тока через катушку достигает 80% предельного значения. Ответ: 322 мОм. 5. 25.Бесконечно длинный соленоид длиной l = 0,8 м имеет однослойную обмотку из алюминиевого провода массой m = 400г. Определить время релаксации τ для этого соленоида. 5. 26.Соленоид диаметром d = 3 см имеет однослойную обмотку из плотно прилегающих друг к другу витков· алюминиевого провода (ρ’ = 26 нОм·м) диаметром d1 = 0,3мм. По соленоиду течет ток I0 = 0,5 А. Определить количество электричества Q, протекающее по соленоиду, если его концы закоротить. Ответ: 42,7 мкКл. 5. 27.Две катушки намотаны на один общий сердечник. Определить их взаимную индуктивность, если при скорости изменения силы тока в первой катушке dI1/dt = 3 А/с во второй катушке индуцируется э.д с. E2 = 0,3 В. Ответ: 0,1 Гн. 5. 28.Два соленоида L1 = 0,64 Гн, L2 = 1 Гн одинаковой длины и равного сечения вставлены один в другой. Определить взаимную индуктивность соленоидов. Ответ: 0,8 Гн. 5. 5. 30.Автотрансформатор, понижающий напряжение с U1 = 6 кВ до U2 = 220 В, содержит в первичной обмотке N1 = 2000 витков. Сопротивление вторичной обмотки R2 = 1 Ом. Сопротивление внешней цепи (в сети пониженного напряжения) R = 12 Oм. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке трансформатора. Ответ: 79. 5. 31.Трансформатор, понижающий напряжение с 220 до 12 В, содержит в первичной обмотке N1= 2000 витков. Сопротивление вторичной обмотки R2 = 0,15 Ом. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке, если во внешнюю цепь (в сети пониженного напряжения) передают мощность P = 20 Вт. 5. 32.Сила тока I в обмотке соленоида, содержащего W = 1500 витков, равна 5 А. Магнитный поток Ф через поперечное сечение соленоида составляет 200 мкВб. Определить энергию магнитного поля в соленоиде. Ответ: 0,75 Дж. 5. 33.Обмотка электромагнита, находясь под постоянным напряжением, имеет сопротивление R =15 Ом и индуктивность L = 0,3 Гн. Определить время, за которое в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике. Ответ: 0,01 с. 5. 34.Соленоид без сердечника с однослойной обмоткой из проволоки диаметром d = 0,5 мм имеет длину l = 0,4 м и поперечное сечение S = 50 см2. Какой ток течет по обмотке при напряжении U = 10 В, если за время t = 0,5 мс в обмотке выделяется количество теплоты, равное энергии поля внутри соленоида? Поле считать однородным. Ответ: 995 мА. 5. 35.Индуктивность соленоида при длине 1 м и площади поперечного сечения 20 см2 равна 0,4 мГн. 5. 36.Две катушки расположены на небольшом расстоянии одна от другой. Когда сила тока в первой катушке изменяется с быстротой ∆I/∆t = 5 А/с, во второй катушке возникает э.д.с. индукции 0,1 В. Определить коэффициент М взаимной индукции катушек. Ответ: 20 мГн. 5. 37.Тороид с воздушным сердечником содержит 20 витков на 1 см. Определить объемную плотность энергии в тороиде, если по его обмотке протекает ток 3 А. Ответ: 22,6 Дж/м3 .
1234 |
Сила тока в катушке увеличилась в 2 раза как изменится магнитный поток
Электромагнит своими руками (инструкция). Собери электромагнит своими руками Как создать электромагнит в домашних условиях
В этом видео уроке канал «Э+М» рассказал о том, что такое электромагнит. Также показал, как сделать его руками с напряжением питания 12 вольт и поставил серию опытов с его использованием. Показал, как увеличить эффективность.
Также показал, как сделать его руками с напряжением питания 12 вольт и поставил серию опытов с его использованием. Показал, как увеличить эффективность.
Для начала немного теории истории. В начале 19 века датский физик Эрстед обнаружил связь между электричеством и магнетизмом. Ток, проходящий через проводник, находящийся рядом с компасом, отклоняет его стрелку в сторону проводника.
Это свидетельствует о наличии магнитного поля вокруг проводника. Также выяснилось, что если в намотать проводник в катушку, его магнитные свойства усилится.
В катушке с проводом, так называемом соленоиде, образуются магнитные линии, такие же, как и в постоянном магните.
В зависимости от того, какой стороной понесем катушку к компасу, он будет отклоняться в ту или иную сторону. Так как в катушке образовались два полюса: северный и южный. Можно изменить направление электрического тока, когда поменяются полюса.
Для эксперимента автор канала намотал 2 одинаковые катушки. Первая катушка 260 витков, сопротивление 7 ом. 2 в два раза больше. 520 витков, сопротивление 15 ом. Питание будет осуществляться от источника постоянного тока. Напряжение 12 вольт.
2 в два раза больше. 520 витков, сопротивление 15 ом. Питание будет осуществляться от источника постоянного тока. Напряжение 12 вольт.
В данном случае это компьютерный блок питания. Также подойдет свинцовый аккумулятор.
Катушка не может справиться с этой нагрузкой. Попробуем провести тот же опыт со второй катушкой. Ток здесь составляет 0,7 ампера. Это в 2 раза меньше, чем у 1. При том же напряжении 12 вольт. Она также не может притянуть рубль.
Что можно сделать, чтобы увеличить магнитные свойства нашей катушки? Попробуем ставить железный сердечник. Для этого используем болт. Теперь он выступит в качестве магнитопровода. Последний способствует прохождению магнитного потока через себя, увеличивает соответствующие свойства соленоида.
Теперь наша конструкция превратилась в электромагнит. Он уже с легкостью справляется с рублем. Ток остался таким же, 1,4 ампера.
Поэкспериментируем дальше и посмотрим, сколько таких предметов может притянуть магнитная катушка. Электромагнит нагрелся, значит его сопротивление увеличилось. Чем больше сопротивление, тем меньше ток. Тем меньше магнитное поле катушка создаёт.
Электромагнит нагрелся, значит его сопротивление увеличилось. Чем больше сопротивление, тем меньше ток. Тем меньше магнитное поле катушка создаёт.
Дадим а полностью остыть электромагниту и повторим экспериментов. В этот раз нагрузкой станут 12 монет. Как видим, нижние монеты при снижении тока начали сами отпадает.
Сколько не пытался ведущий экспериментировать, удалось поднять не более такой нагрузки.
Проведем тот же опыт со второй катушкой. У него два раза больше витков. Посмотрим, сильнее ли она, чем предыдущая.Смотрите продолжение о электромагните на 12 вольт на видео с 6 минуты.
izobreteniya.net
Как сделать самодельный электромагнит
В этом видеоролике канала Креосан показано, как сделать самостоятельно электрический магнит. Нужно взять трансформатор от микроволновки, распилить его и достать обмотки. Также подойдут и другие трансформаторы. Но мощные и доступные только в микроволновках.
Нам понадобится первичная обмотка. Мы его только включили в сеть, а он уже начинает вибрировать. Что же будет, когда он будет притягивать железо? Настало время испытать electromagnet. На него можно подавать 12, 24, 36, 48, 110, 220 вольт. При этом может быть постоянный и переменный ток.
Что же будет, когда он будет притягивать железо? Настало время испытать electromagnet. На него можно подавать 12, 24, 36, 48, 110, 220 вольт. При этом может быть постоянный и переменный ток.
Включаем аккумулятор от ноутбука и посмотрим, на что способен самодельный электромагнит при напряжении 12 вольт. Берем орешек и при участии электромагнита плющим его дверью. Как видите, с орешком он легко расправился. Попробуем поднять что-то потяжелее.
Например крышку от канализационного люка.
Есть идея простого измерителя пульсаций.
Простейший электромагнит за 5 минут
Далее. Еще один канал (HM Show) выпустил ролик по той же теме.Он показал, как сделать простой электромагнит за 5 минут. Для изготовления устройства своими руками понадобится стальной стержень, медная проволока и любой изолирующий материал.
Для начала изолируем стальной стержень строительным скотчем, излишки материала отрезаем. Необходимо намотать медную проволоку на изолирующий материал так, чтобы было как можно меньше воздушных зазоров.
От этого зависит сила магнита, также от толщины медной проволоки, количества витков и силы ток. Данные показатели нужно подбирать экспериментально.
После того, как намотали проволоку, обмотать её изолирующим материалом.
Что такое катушка индуктивности
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Самоиндукция
Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток L — индуктивность контура I — сила тока в контуре |
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.
Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
- первая лампа загорится практически сразу,
- вторая лампа загорится с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.
ЭДС самоиндукции ξis — ЭДС самоиндукции ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность |
Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.
Катушка индуктивности в цепи постоянного тока.
И, в первую очередь, разберемся, что происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? Однозначно нет. Ведь постоянный ток можно «включать/выключать», и как раз в моменты переключения и происходят все ключевые процессы. Давайте рассмотрим цепь:
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна.
Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна.
А далее произойдет следующее — поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот, будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
На первом графике мы видим входное напряжение цепи — изначально цепь разомкнута, но при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый).
График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции, в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является как раз индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Важный (!) нюанс заключается в том, что напряжение на катушке при описанных переходных процессах может достигнуть весьма значительных величин. Это, в свою очередь, легко может привести к выходу из строя тех или иных компонентов, входящих в состав цепи. Например, при управлении индуктивной нагрузкой при помощи ключа на транзисторе явление возникновения ЭДС самоиндукции с впечатляющей вероятностью приведет к выходу транзистора из строя. Для защиты от этого параллельно индуктивной нагрузке ставят защитный диод, но сегодня речь не об этом, поэтому для данного аспекта я опубликую отдельный материал с рассмотрением основных нюансов.
Магнитный поток
Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.
Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.
Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению:
- модуля вектора магнитной индукции B,
- площади поверхности S, которую пронизывает поток,
- и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).
Магнитный поток Ф — магнитный поток B — магнитная индукция S — площадь пронизываемой поверхности n — вектор нормали (перпендикуляр к поверхности) |
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента — катушка индуктивности, в первую очередь, представляет из себя не что иное, как катушку. То есть некоторое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием — витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность. {-7}\medspace\frac{Гн}{м}
{-7}\medspace\frac{Гн}{м}
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения), индуктивность будет увеличиваться. А при увеличении длины — уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины.
С устройством катушки индуктивности разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока.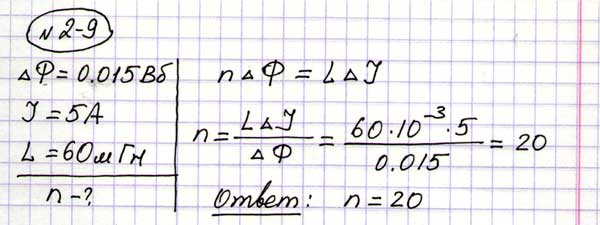 Для этого мы рассмотрим две схемы — в одной будем пропускать через катушку постоянный ток, а в другой -переменный.
Для этого мы рассмотрим две схемы — в одной будем пропускать через катушку постоянный ток, а в другой -переменный.
Индуктивность
Индуктивность — это способность катушки, контура или проводника с током накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
Как работает катушка
Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.
Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.
При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.
Задачка раз
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.
Решение
За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:
Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.
Задачка два
По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?
Решение
При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.
Отсюда индуктивность катушки равна:
Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:
Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.
Задания
Задание №1
На рисунке 10 дана схема устройства электрического звонка. На ней буквами обозначено: ЭМ — дугообразный электромагнит, Я — железная пластинка — якорь, М — молоточек, З — звонковая чаша, К — контактная пружина, касающаяся винта В. Рассмотрите схему звонка и объясните, как он действует.
Рисунок 10. Устройство электрического звонка
Когда мы подаем на это устройство питание, по проводам начинает течь ток. Он течет и по проводам в катушках дугообразного электромагнита (ЭМ).
Возникает магнитное поле. Катушки начинают действовать как магниты и притягивают к себе якорь (так как он железный).
К якорю прикреплен молоточек (М). При притяжении якоря к электромагниту он ударяется о звонковую чашу (З).
Также якорь соединен с контактной пластиной (К). При притяжении к электромагниту он тянет ее за собой и электрическая цепь размыкается — винт (В) перестает касаться пластины, тока нет.
Тут же пропадает и магнитное поле катушек.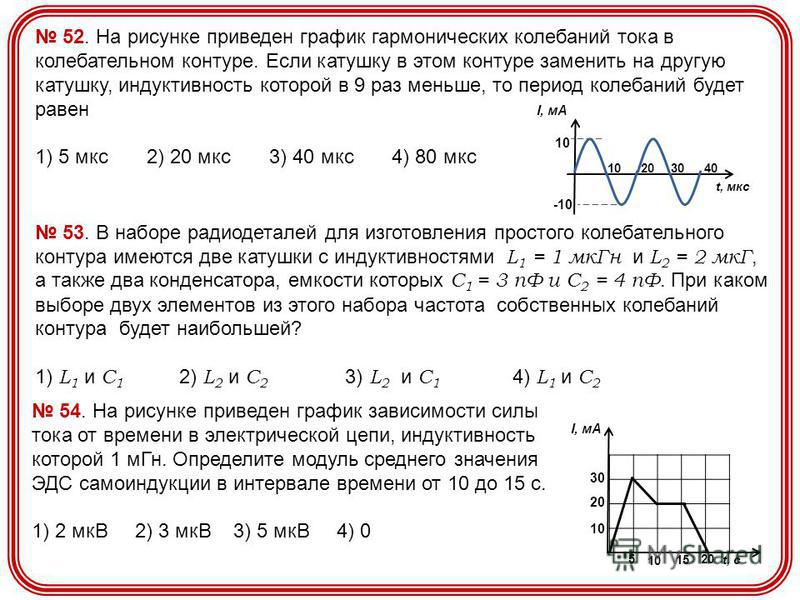 Якорь возвращается на прежнее место и цепь снова замыкается. Снова по проводам течет ток, возникает магнитное поле, и якорь притягивается к электромагниту.
Якорь возвращается на прежнее место и цепь снова замыкается. Снова по проводам течет ток, возникает магнитное поле, и якорь притягивается к электромагниту.
Получается, что молоточек совершает мелкие быстрые удары по звонковой чаше. Каждый удар происходит при возникновении магнитного поля. Так будет происходить до тех пор, пока звонок не будет отключен от источника питания.
Задание №2
На рисунке 11 показана схема простейшей телеграфной установки, позволяющей передавать телеграммы со станции A на станцию B. На схеме цифрами обозначено: 1 — ключ, 2 — электромагнит, 3 — якорь, 4 — пружина, 5 — колесико смазанное краской.По схеме объясните устройство установки.
Рисунок 11. Устройство простейшей телеграфной установки
Когда на станции A замыкается ключ, по проводам начинает идти электрический ток. На станции B вокруг катушки возникает магнитное поле, она начинает вести себя как магнит.
Катушка притягивает к себе якорь, и другой его конец прижимает ленту к колесику с краской. Пока лента прижата к колесику, на ней остается след.
Пока лента прижата к колесику, на ней остается след.
Когда на станции A размыкают ключ, якорь возвращается в исходное положение. Он больше не прижимает ленту к колесику с краской — на ней не остается следов.
С помощью такой установки, находясь далеко друг от друга, можно выбивать на ленте, замыкая и размыкая ключ, символы азбуки Морзе — точки и тире.
Задание №3
В мощных электрических двигателях, применяемых в прокатных станах, шахтных подъемниках, насосах, сила тока достигает нескольких тысяч ампер. Так как в последовательно соединенных проводниках сила тока одинакова, то такая же сила тока будет во всех соединительных проводах этой цепи. Это очень неудобно, особенно если потребитель тока находится на большом расстоянии от пульта управления, где включается ток. Такие цепи можно включать при помощи специального устройства — электромагнитного реле (рисунок 12), приводя его в действие малой силой тока. На схеме обозначено: 1 — электромагнит, 2 — якорь, 3 — контакты рабочей цепи, 4 — пружина, 5 — электродвигатель, 6 — контакты цепи электродвигателя.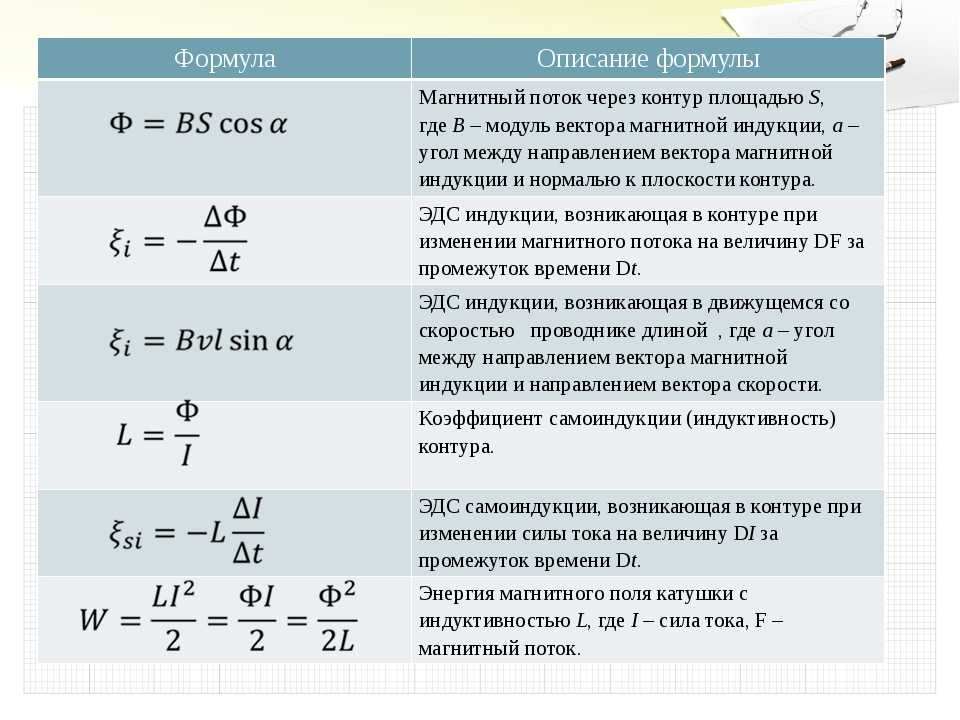 Объясните как действует прибор.
Объясните как действует прибор.
Рисунок 12. Использование электромагнитного реле
При замыкании ключа, в катушке электромагнита 1 возникает электрический ток. Также возникает и магнитное поле. Из-за этого электромагнит начинает притягивать к себе якорь 2.
Когда якорь притянулся к катушке, его правый конец опускается на контакты 3. Цепь оказывается замкнутой. Теперь по цепи, в которой находится электродвигатель тоже течет ток. Двигатель начинает работать.
Смысл такой установки в том, что малой силой тока с помощью использования электромагнита в устройстве реле, можно запускать электродвигатель большой мощности, находящийся на большом расстоянии от места включения тока.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В — магнитное поле, Вб
I — сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Применение электромагнитов
Рассмотрим несколько примеров применения электромагнитов.
На рисунке 8 изображен дугообразный электромагнит. Он удерживает железную пластину (якорь) с подвешенным грузом.
Рисунок 8. Дугообразный электромагнит
Такие установки широко используются на заводах для перемещения различных изделий из металлов, сбора металлической стружки.
На рисунке 9 изображен в разрезе магнитный сепаратор для зерна.
Рисунок 9. Магнитный сепаратор для зерна
Принцип его работы очень прост. В собранное зерно добавляют очень мелкие железные опилки. Они не прилипают к гладким зернам злаков, но прилипают к зернам сорняков.
В собранное зерно добавляют очень мелкие железные опилки. Они не прилипают к гладким зернам злаков, но прилипают к зернам сорняков.
Из бункера 1 зерна с опилками высыпаются на вращающийся барабан 2. Внутри него находится мощный электромагнит 5. Он притягивает железные опилки, а вместе с ними и зерна сорняков. Так сепаратор очищает зерно.
Электромагниты также применяются во многих других устройствах. Некоторые из них мы рассмотрим ниже в данном уроке в разделе “Задания”.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Энергия соленоида с током формула
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результате Л1 загорается позже, чем Л2.
цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результате Л1 загорается позже, чем Л2.
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает.
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике (B
I), следовательно магнитный поток пропорционален силе тока (Ф
I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
При изменении тока в катушке от 0 до 5 А за 0,5 с среднее индуцированное ЭДС в катушке 1 вольт. Собственная индуктивность катушки составляет 1. 0,1 Гн 2, 0,2 Гн 3, 0,4 Гн 4, 1,5 Гн. Физика электромагнитной индукции Практические вопросы NEET, MCQ, вопросы прошлого года (PYQ), вопросы NCERT, банк вопросов, класс 11 и класс 12 вопросов и PDF-файлы с ответами
Выберите набор вопросов:
Рекомендуемые MCQ — 104 вопроса Рекомендуемые PYQ (строго на основе NCERT) NCERT Решающие примеры на основе MCQS NCERT на основе упражнений MCQS Padma Shri H C Verma (объективные упражнения) MCQS прошлый год (2019 Ontaind -NTTA -NTA -QQS).
 MCQ прошлого года (2016 — 2018) MCQ прошлого года (2006 — 2015)
MCQ прошлого года (2016 — 2018) MCQ прошлого года (2006 — 2015) в катушке 1 вольт. Индуктивность катушки
1. 0.1H
2. 0.2H
3. 0.4H
4. 1.5H
Q197:
89
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Собственная индуктивность |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокопроизводительные книги NEET MCQ для 11 th Physics & Chemistry
Магнитный поток, связанный с катушкой, изменяется со временем -6t+5, где ϕ в веберах, а t – в секундах. Индуцированный ток равен нулю при:
Индуцированный ток равен нулю при:
1. T = 0
2. T = 1,5 S
3. T = 3 S
4. T = 5 S
Q198:
9099
%от NCERT
- 9 9099
%. (1)
(2)
(3)
(4)
Подтема: Закон Фарадея и Закон Ленца |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокодоходные книги NEET MCQ для 11 th Physics & Chemistry
Дроссельная катушка Kirchoff’s 9009
0 2. Self-induction
Self-induction
3. Mutual induction
4. All of these
Q199:
59
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Собственная индуктивность |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокодоходные книги NEET MCQ для 11 th Физика и химия
Утверждение28: Самоиндукция называется индуктивностью электричества.
Причина: Благодаря собственной индуктивности катушка сопротивляется любому изменению тока, проходящего через нее.
1. И Утверждение, и Основание верны, и основанием является правильное объяснение утверждения.
2. И Утверждение, и Причина верны, но причина не в правильном объяснении утверждения.
3. Утверждение является истинным утверждением, но Причина ложна.
4. И Утверждение, и Причина являются ложными утверждениями.
Q200:
86
% От NCERT
(1)
(2)0009
(3)
(4)
Подтема: Самоиндукция |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями Видео/текстовые решения через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Утверждение: Когда кусок неметалла и металл падают с одной высоты вблизи поверхности земли неметаллический кусок достигнет земли первым.
Причина: Наведенный ток в металле уменьшит ускорение.
1. И Утверждение, и Основание верны, и основанием является правильное объяснение утверждения.
2. И Утверждение, и Причина верны, но причина не в правильном объяснении утверждения.
3. Утверждение является истинным утверждением, но Причина ложна.
4. И Утверждение, и Причина являются ложными утверждениями.
Q201:
85
% From NCERT
(1)
(2)
(3)
(4)
Subtopic: Motional ЭДС |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокодоходные книги NEET MCQ за 11 th Физика и химия
Утверждение: Потери в железе минимизируются за счет использования многослойного сердечника.
Причина: Ламинирование сердечника ограничивает вихревые токи.
1. И Утверждение, и Основание верны, и основанием является правильное объяснение утверждения.
2. И Утверждение, и Причина верны, но причина не в правильном объяснении утверждения.
3. Утверждение является истинным утверждением, но Причина ложна.
4. И Утверждение, и Причина являются ложными утверждениями.
Q202:
89
% From NCERT
(1)
(2)
(3)
(4)
Subtopic: Eddy Текущий |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста с помощью Telegram Bot
Высокодоходные книги NEET MCQ для 11 th Физика и химия
Утверждение28: неиндуцированное электрическое поле.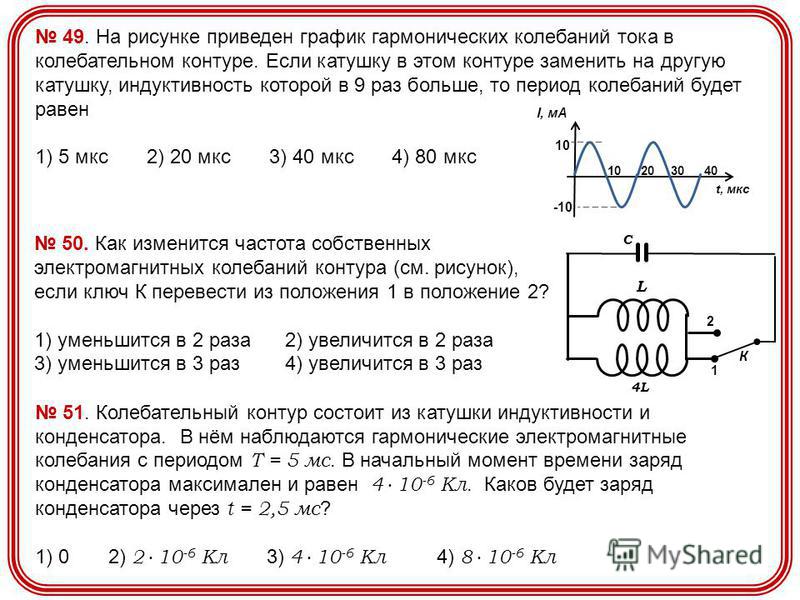
Причина: Работа, совершенная на замкнутом пути в индуцированном электрическом поле, отлична от нуля.
1. И Утверждение, и Основание верны, и основанием является правильное объяснение утверждения.
2. И Утверждение, и Причина верны, но причина не в правильном объяснении утверждения.
3. Утверждение является истинным утверждением, но Причина ложна.
4. И Утверждение, и Причина являются ложными утверждениями.
Q203:
71
% От NCERT
(1)
(2)0009
(3)
(4)
Подтема: ЭДС движения |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с Интернет Видео/Текст Решения через Telegram Bot
High Yield NEET MCQ Books for 11 th Физика и химия
Утверждение: Закон Ленца соответствует закону сохранения энергии.
Причина: Количество механической энергии, потерянной против ЭДС индукции или тока, равно электрической энергии, вновь появляющейся в цепи.
1. И Утверждение, и Основание верны, и основанием является правильное объяснение утверждения.
2. И Утверждение, и Причина верны, но причина не в правильном объяснении утверждения.
3. Утверждение является истинным утверждением, но Причина ложна.
4. И Утверждение, и Причина являются ложными утверждениями.
Q204:
88
% From NCERT
(1)
(2)
(3)
(4)
Subtopic: Faraday’s Закон и Закон Ленца |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для видео/текста через Telegram Bot
Высокодоходные книги NEET MCQ за 11 th Физика и химия
Утверждение: Зависимое от времени магнитное поле порождает электрическое поле.
Причина: Направление электрического поля, создаваемого переменным во времени магнитным полем, не подчиняется закону Ленца.
1. И утверждение, и причина верны, и причина есть правильное объяснение утверждения.
2. И утверждение, и причина верны, но причина не является правильным объяснением утверждения.
3. Утверждение является истинным утверждением, но причина ложна.
4. И утверждение, и причина являются ложными утверждениями.
Q205:
62
% From NCERT
(1)
(2)
(3)
(4)
Subtopic: Faraday’s Закон и Закон Ленца |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги NEETprep MCQ с онлайн-решениями для видео/текста через Telegram Bot
High Yield NEET MCQ Books for 11 th Physics & Chemistry
Утверждение: если ток, проходящий через индуктор, меняется со временем ( ) как t2, ЭДС индукции будет изменяться по прямой линии.
Причина: ЭДС через индуктор определяется как E=-Ldldt.
1. И утверждение, и причина верны, и причина есть правильное объяснение утверждения.
2. И утверждение, и причина верны, но причина не является правильным объяснением утверждения.
3. Утверждение является истинным утверждением, но причина ложна.
4. И утверждение, и причина являются ложными утверждениями.
Q206:
75
% От NCERT
(1)
- 5 (9)
(3)
(4)
Подтема: Собственная индуктивность |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию в курсе ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн Видео/текстовые решения через Telegram Bot
Высокие книги NEET MCQ для 110102 TH Physics & Chemistry
Выбор вопросов:
Рекомендуемые MCQ — 104 Вопросы 9000 9000. (СТРОГО на основе NCERT) Решенные примеры NCERT на основе MCQ NCERT Упражнения на основе MCQ Упражнения CMC Verma Shriive0003 Прошлый год (2019 год. 23, задача 3 (задачи и упражнения)
Вопрос
Согласно рис. 23.57(а), как направлен ток, индуцируемый в катушке 2: (а) Если ток в катушке 1 увеличивается? б) Если ток в катушке 1 уменьшится? в) Если ток в катушке 1 постоянен? Подробно покажите, как вы выполняете шаги, описанные в стратегии решения проблем для закона Ленца.
Вопрос Изображение
Рис. 23.57 (a) Катушки лежат в одной плоскости. (b) Провод находится в плоскости катушкиВопрос от OpenStax лицензирован под лицензией СС BY 4.0.
Окончательный ответ
- Наведенный ток против часовой стрелки
- Наведенный ток по часовой стрелке
- Индуктивный ток отсутствует, так как магнитный поток через катушку 2 не изменяется, поскольку магнитное поле, создаваемое постоянным током в катушке 1, постоянно.
Видеорешение
Зарегистрируйтесь для просмотра видеорешения!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
8 голосов со средней оценкой 4,9.
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. В этом вопросе мы рассматриваем ток в катушке один и влияние этого тока на индуцированный ток во второй катушке. Итак, для части А мы скажем, что ток в катушке один увеличивается. Итак, вопрос: «Какого направления будет индуцированный ток во второй катушке?» В части B ток в первой катушке уменьшается, и на что это влияет, а в части C ток в первой катушке остается постоянным. Итак, связь происходит за счет магнитного поля, создаваемого этим током. И магнитное поле, когда оно изменяется внутри катушки два, это изменяющееся магнитное поле будет индуцировать ЭДС, а величина ЭДС — это скорость изменения потока, и тогда эта ЭДС вызовет ток. Потому что ток будет равен ЭДС индукции во второй катушке, деленной на любое сопротивление, которое имеет этот провод. Теперь площадь этой катушки остается постоянной. Итак, когда мы говорим об изменении потока, на самом деле мы просто говорим об изменении напряженности поля, потому что площадь не… мы не сжимаем и не растягиваем петлю. И поэтому эта напряженность поля будет меняться в результате изменения тока в катушке. Итак, если вы посмотрите на этот участок провода и возьмете его правой рукой, а большой палец укажет вверх, вы получите силовые линии, идущие на страницу во второй катушке.
Итак, вопрос: «Какого направления будет индуцированный ток во второй катушке?» В части B ток в первой катушке уменьшается, и на что это влияет, а в части C ток в первой катушке остается постоянным. Итак, связь происходит за счет магнитного поля, создаваемого этим током. И магнитное поле, когда оно изменяется внутри катушки два, это изменяющееся магнитное поле будет индуцировать ЭДС, а величина ЭДС — это скорость изменения потока, и тогда эта ЭДС вызовет ток. Потому что ток будет равен ЭДС индукции во второй катушке, деленной на любое сопротивление, которое имеет этот провод. Теперь площадь этой катушки остается постоянной. Итак, когда мы говорим об изменении потока, на самом деле мы просто говорим об изменении напряженности поля, потому что площадь не… мы не сжимаем и не растягиваем петлю. И поэтому эта напряженность поля будет меняться в результате изменения тока в катушке. Итак, если вы посмотрите на этот участок провода и возьмете его правой рукой, а большой палец укажет вверх, вы получите силовые линии, идущие на страницу во второй катушке.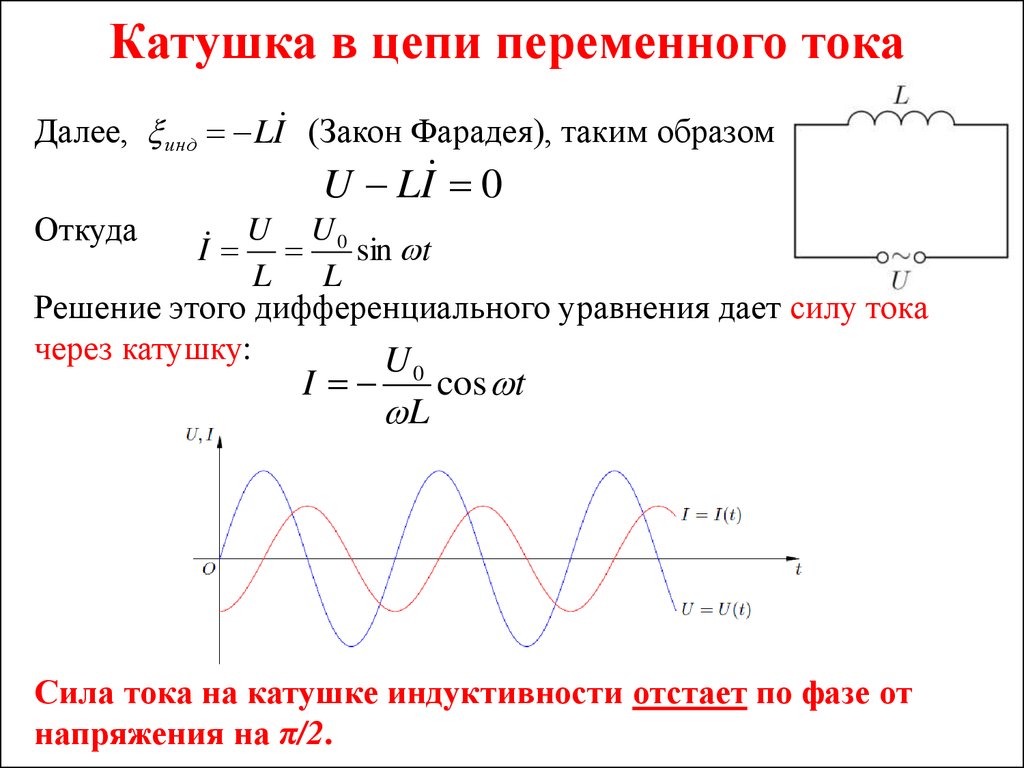 И по мере того, как текущий увеличивается, вы получите дополнительные строки поля, идущие на страницу здесь. И закон Ленца гласит, что ток, индуцируемый во второй катушке, создаст магнитное поле, противодействующее любым происходящим изменениям. Таким образом, изменение заключается в том, что вы получаете больше силовых линий на странице, и поэтому индуцированный ток должен создавать магнитное поле внутри катушки с силовыми линиями, выходящими из страницы, чтобы противодействовать этому увеличению внутрь из-за увеличения тока в странице. катушка одна. Таким образом, чтобы линии поля выходили из страницы здесь, индуцированный ток должен быть в этом направлении. Потому что, если вы возьмете второй виток правой рукой, а ваши пальцы укажут в сторону от страницы в середине петли витка два, вы обнаружите, что ваш большой палец направлен вверх с правой стороны, или он направлен вниз с левой стороны. И поэтому ток должен идти в направлении против часовой стрелки, чтобы создать магнитное поле внутри, выходящее из страницы, чтобы противодействовать усиленному магнитному полю, идущему в страницу из-за тока катушки один.
И по мере того, как текущий увеличивается, вы получите дополнительные строки поля, идущие на страницу здесь. И закон Ленца гласит, что ток, индуцируемый во второй катушке, создаст магнитное поле, противодействующее любым происходящим изменениям. Таким образом, изменение заключается в том, что вы получаете больше силовых линий на странице, и поэтому индуцированный ток должен создавать магнитное поле внутри катушки с силовыми линиями, выходящими из страницы, чтобы противодействовать этому увеличению внутрь из-за увеличения тока в странице. катушка одна. Таким образом, чтобы линии поля выходили из страницы здесь, индуцированный ток должен быть в этом направлении. Потому что, если вы возьмете второй виток правой рукой, а ваши пальцы укажут в сторону от страницы в середине петли витка два, вы обнаружите, что ваш большой палец направлен вверх с правой стороны, или он направлен вниз с левой стороны. И поэтому ток должен идти в направлении против часовой стрелки, чтобы создать магнитное поле внутри, выходящее из страницы, чтобы противодействовать усиленному магнитному полю, идущему в страницу из-за тока катушки один. Итак, это отвечает на часть А. А затем на часть Б, предположим, что ток в катушке один уменьшается. Итак, изначально у вас будет, скажем, четыре строки поля, идущие на страницу. А потом, через какое-то время, на страницу идут только две строки поля, оно уменьшилось. Таким образом, индуцированный ток всегда препятствует изменению, и поэтому он захочет создать магнитное поле, проникающее в страницу, чтобы заменить те, которые были только что потеряны. Потому что не хочет никаких изменений. Изначально их было четыре, а потом, допустим, два исчезают, потому что происходит уменьшение тока в катушке один. Итак, магнитное поле меньше при наличии двух катушек. Таким образом, индуцированный ток второй катушки будет противодействовать этому изменению и заменить то, что было потеряно. Хорошо. Таким образом, чтобы линии магнитного поля попали на страницу здесь, внутри катушки, ток должен идти по часовой стрелке. И вы можете понять это, схватив вторую катушку правой рукой и указав пальцами на страницу в середине катушки, а ваш большой палец будет указывать влево внизу или вправо вверху.
Итак, это отвечает на часть А. А затем на часть Б, предположим, что ток в катушке один уменьшается. Итак, изначально у вас будет, скажем, четыре строки поля, идущие на страницу. А потом, через какое-то время, на страницу идут только две строки поля, оно уменьшилось. Таким образом, индуцированный ток всегда препятствует изменению, и поэтому он захочет создать магнитное поле, проникающее в страницу, чтобы заменить те, которые были только что потеряны. Потому что не хочет никаких изменений. Изначально их было четыре, а потом, допустим, два исчезают, потому что происходит уменьшение тока в катушке один. Итак, магнитное поле меньше при наличии двух катушек. Таким образом, индуцированный ток второй катушки будет противодействовать этому изменению и заменить то, что было потеряно. Хорошо. Таким образом, чтобы линии магнитного поля попали на страницу здесь, внутри катушки, ток должен идти по часовой стрелке. И вы можете понять это, схватив вторую катушку правой рукой и указав пальцами на страницу в середине катушки, а ваш большой палец будет указывать влево внизу или вправо вверху. И так это по часовой стрелке. Итак, я рисую то, что индуцировано зеленым цветом, а линии магнитного поля, вызванные катушкой, — красным, просто чтобы различать их. Итак, против часовой стрелки — это ответ для части B, как показано здесь. Затем, в части C, это говорит нам, что ток в катушке один постоянный. Итак, есть магнитное поле в присутствии катушки два, внутри катушки два из-за тока катушки один. Но это магнитное поле не меняется. И площадь катушки не меняется. Другими словами, поток не меняется. Таким образом, без изменения потока этот числитель равен нулю. Конечная напряженность магнитного поля и начальная напряженность магнитного поля за счет тока катушки одинакова. Так что эта разница равна нулю. ЭДС индукции отсутствует, а значит, и индукционный ток отсутствует. Таким образом, ток во второй катушке равен нулю, когда ток в первой катушке постоянен.
И так это по часовой стрелке. Итак, я рисую то, что индуцировано зеленым цветом, а линии магнитного поля, вызванные катушкой, — красным, просто чтобы различать их. Итак, против часовой стрелки — это ответ для части B, как показано здесь. Затем, в части C, это говорит нам, что ток в катушке один постоянный. Итак, есть магнитное поле в присутствии катушки два, внутри катушки два из-за тока катушки один. Но это магнитное поле не меняется. И площадь катушки не меняется. Другими словами, поток не меняется. Таким образом, без изменения потока этот числитель равен нулю. Конечная напряженность магнитного поля и начальная напряженность магнитного поля за счет тока катушки одинакова. Так что эта разница равна нулю. ЭДС индукции отсутствует, а значит, и индукционный ток отсутствует. Таким образом, ток во второй катушке равен нулю, когда ток в первой катушке постоянен.
Гл. 13 задач — University Physics Volume 2
Проблемы
13.
 1
Закон Фарадея
1
Закон Фарадея24.
Катушка из 50 витков диаметром 15 см. Катушка помещена в пространственно однородное магнитное поле величиной 0,50 Тл так, что лицевая сторона катушки и магнитное поле перпендикулярны. Найти величину ЭДС индукции в катушке, если магнитное поле сводится к нулю равномерно за 0,10 с (а), 1,0 с (б) и 60 с (в).
25.
Повторите расчет времени предыдущей задачи 0,1 с с плоскостью катушки, образующей угол (a) 30°, 30°, (b) 60°, 60° и (c) 90°90° с магнитное поле.
26.
Квадратная петля со стороной 6,0 см изготовлена из медной проволоки радиусом 1,0 мм. Если магнитное поле, перпендикулярное петле, изменяется со скоростью 5,0 мТл/с, какова сила тока в петле?
27.
Магнитное поле через круглую петлю радиусом 10,0 см изменяется со временем, как показано ниже. Поле перпендикулярно петле. Постройте величину ЭДС индукции в контуре как функцию времени.
Постройте величину ЭДС индукции в контуре как функцию времени.
28.
На прилагаемом рисунке показана одновитковая прямоугольная катушка с сопротивлением 2,0–2,0 Ом. Магнитное поле во всех точках внутри катушки изменяется по закону B=B0e-αt, B=B0e-αt, где B0=0,25TB0=0,25T и α=200Hz.α=200Hz. Какой ток индуцируется в катушке при (а) t=0,001st=0,001 с, (б) 0,002 с, (в) 2,0 с?
29.
Как изменились бы ответы на предыдущую задачу, если бы катушка состояла из 20 близко расположенных витков?
30.
Длинный соленоид с n=10n=10 витков на сантиметр имеет площадь поперечного сечения 5,0 см25,0 см2 и пропускает ток 0,25 А. Катушка с пятью витками окружает соленоид. При выключении тока через соленоид он уменьшается до нуля за 0,050 с. Чему равна средняя ЭДС индукции в катушке?
31.
Прямоугольная проволочная петля длиной a и шириной b лежит в плоскости xy , как показано ниже. ), где B→(t)B→(t) в теслах. Определить ЭДС индукции в контуре как функцию времени.
), где B→(t)B→(t) в теслах. Определить ЭДС индукции в контуре как функцию времени.
32.
Магнитное поле, перпендикулярное одиночной проволочной петле диаметром 10,0 см, уменьшается с 0,50 Тл до нуля. Провод изготовлен из меди и имеет диаметр 2,0 мм и длину 1,0 см. Какой заряд проходит по проводу при изменении поля?
13.2 Закон Ленца
33.
Одновитковый круговой виток провода радиусом 50 мм лежит в плоскости, перпендикулярной пространственно-однородному магнитному полю. В течение интервала времени 0,10 с величина поля равномерно возрастает от 200 до 300 мТл. а) Определить ЭДС индукции в контуре. б) Если магнитное поле направлено за пределы страницы, каково направление тока, индуцируемого в петле?
34.
При первом включении магнитного поля поток через 20-витковую петлю изменяется со временем в соответствии с формулой в секундах, а петля находится в плоскости страницы с единичной нормалью, направленной наружу. а) Как зависит ЭДС, индуцируемая в петле, от времени? Как направлен индукционный ток при t = 0 (б), 0,10 (в), 1,0 (г) и 2,0 с (д)?
а) Как зависит ЭДС, индуцируемая в петле, от времени? Как направлен индукционный ток при t = 0 (б), 0,10 (в), 1,0 (г) и 2,0 с (д)?
35.
Магнитный поток через петлю, показанную на прилагаемом рисунке, изменяется со временем согласно формуле Φm=2,00e−3tsin(120πt), Φm=2,00e−3tsin(120πt), где ΦmΦm выражено в веберах. Каковы направление и величина тока через резистор 5,00 Ом5,00 Ом при (а) t=0t=0; (b) t=2,17×10-2 с, t=2,17×10-2 с и (c) t=3,00 с?t=3,00 с?
36.
Используйте закон Ленца для определения направления индукционного тока в каждом случае.
13.3 ЭДС движения
37.
Автомобиль с радиоантенной длиной 1,0 м движется со скоростью 100,0 км/ч в месте, где горизонтальное магнитное поле Земли составляет 5,5×10-5 Тл.5,5×10-5 Тл. Какова максимально возможная ЭДС, индуцируемая в антенне из-за этого движения?
38.
Показанная ниже прямоугольная петля из N витков движется вправо с постоянной скоростью v→v→, покидая полюса большого электромагнита. (a) Предполагая, что магнитное поле однородно между сторонами полюсов и пренебрежимо мало в других местах, определите ЭДС индукции в контуре. б) Каков источник работы, производящий эту ЭДС?
39.
Предположим, что магнитное поле предыдущей задачи колеблется со временем в соответствии с B=B0sinωt.B=B0sinωt. Какая же ЭДС индуцируется в петле, когда ее задняя сторона находится на расстоянии d от правого края области магнитного поля?
40.
Катушка из 1000 витков занимает площадь 25см225см2. Он поворачивается за 0,010 с из положения, в котором его плоскость перпендикулярна магнитному полю Земли, в положение, в котором его плоскость параллельна полю. Если напряженность поля 6,0×10-5 Тл, 6,0×10-5 Тл, какова средняя ЭДС, индуцируемая в катушке?
41.
В схеме, показанной на прилагаемом рисунке, стержень скользит по направляющим рельсам с постоянной скоростью v→.v→. Скорость находится в одной плоскости с рельсами и направлена под углом θθ к ним. Однородное магнитное поле B→B→ направлено за пределы страницы. Какая ЭДС индуцируется в стержне?
42.
Стержень, показанный на прилагаемом рисунке, движется через однородное магнитное поле напряженностью B=0,50TB=0,50T с постоянной скоростью v=8,0м/с.v=8,0м/с. Чему равна разность потенциалов между концами стержня? Какой конец стержня имеет более высокий потенциал?
43.
Стержень длиной 25 см движется со скоростью 5,0 м/с в плоскости, перпендикулярной магнитному полю напряженностью 0,25 Тл. Стержень, вектор скорости и вектор магнитного поля взаимно перпендикулярны, как показано на прилагаемом рисунке. Вычислите (а) магнитную силу, действующую на электрон в стержне, (б) электрическое поле в стержне и (в) разность потенциалов между концами стержня. г) Какова скорость стержня, если разность потенциалов равна 1,0 В?
г) Какова скорость стержня, если разность потенциалов равна 1,0 В?
44.
На прилагаемом рисунке рельсы, соединительный концевой элемент и стержень имеют сопротивление на единицу длины 2,0 Ом/см. 2,0 Ом/см. Стержень движется влево со скоростью v=3,0 м/с. v=3,0 м/с. Если B=0,75TB=0,75T везде в регионе, какова сила тока в цепи (a) при a=8,0cm?a=8,0cm? б) когда а=5,0 см? а=5,0 см? Укажите также смысл текущего потока.
45.
Стержень, показанный ниже, движется вправо по рельсам практически с нулевым сопротивлением со скоростью v=3,0 м/с. v=3,0 м/с. Если B=0,75TB=0,75T везде в регионе, каков ток через резистор 5,0 Ом5,0 Ом? Ток циркулирует по часовой или против часовой стрелки?
46.
Ниже показан проводящий стержень, который скользит по металлическим рельсам. Аппарат находится в однородном магнитном поле напряженностью 0,25 Тл, которое находится непосредственно в странице. Стержень тянется вправо с постоянной скоростью 5,0 м/с под действием силы F→.F→. Единственное значительное сопротивление в цепи исходит от показанного резистора 2,0 Ом2,0 Ом. а) Чему равна ЭДС индукции в цепи? б) Чему равен индукционный ток? Он вращается по часовой стрелке или против часовой стрелки? (c) Какова величина F→F→? (d) Какова выходная мощность F→F→ и мощность, рассеиваемая на резисторе?
Стержень тянется вправо с постоянной скоростью 5,0 м/с под действием силы F→.F→. Единственное значительное сопротивление в цепи исходит от показанного резистора 2,0 Ом2,0 Ом. а) Чему равна ЭДС индукции в цепи? б) Чему равен индукционный ток? Он вращается по часовой стрелке или против часовой стрелки? (c) Какова величина F→F→? (d) Какова выходная мощность F→F→ и мощность, рассеиваемая на резисторе?
13,4 Наведенные электрические поля
47.
Рассчитайте наведенное электрическое поле в 50-витковой катушке диаметром 15 см, помещенной в пространственно однородное магнитное поле величиной 0,50 Тл, так что поверхность катушки и магнитное поле перпендикулярны. Это магнитное поле уменьшается до нуля за 0,10 секунды. Предположим, что магнитное поле цилиндрически симметрично относительно центральной оси катушки.
48.
Магнитное поле через круглую петлю радиусом 10,0 см меняется со временем, как показано на прилагаемом рисунке. Поле перпендикулярно петле. Предполагая цилиндрическую симметрию по отношению к центральной оси петли, начертите зависимость индуцированного электрического поля в петле от времени.
Поле перпендикулярно петле. Предполагая цилиндрическую симметрию по отношению к центральной оси петли, начертите зависимость индуцированного электрического поля в петле от времени.
49.
Ток I через длинный соленоид с n оборотов на метр и радиусом R изменяется со временем, как указано dI / дт . Рассчитайте индуцированное электрическое поле как функцию расстояния r от центральной оси соленоида.
50.
Рассчитайте электрическое поле, индуцированное как внутри, так и снаружи соленоида из предыдущей задачи, если I=I0sinωt.I=I0sinωt.
51.
В области радиусом R имеется пространственно однородное магнитное поле B→.B→. (См. ниже.) При t=0t=0, B=1,0T, B=1,0T, после чего уменьшается с постоянной скоростью до нуля за 30 с. (а) Каково электрическое поле в областях, где r≤Rr≤R и r≥Rr≥R в течение этого 30-секундного интервала? (b) Предположим, что R=10,0 см R=10,0 см. Какую работу совершает электрическое поле над протоном, если его пронести один раз по часовой стрелке по круговой траектории радиусом 5,0 см? в) Какую работу совершает электрическое поле над протоном, который один раз пролетает против часовой стрелки по круговой траектории любого радиуса r≥Rr≥R? (г) В момент, когда B=0,50TB=0,50T, протон входит в магнитное поле на A , двигаясь со скоростью v→v→(v=5,0×106 м/с)(v=5,0×106 м/с), как показано. Каковы электрические и магнитные силы, действующие на протон в этот момент?
ниже.) При t=0t=0, B=1,0T, B=1,0T, после чего уменьшается с постоянной скоростью до нуля за 30 с. (а) Каково электрическое поле в областях, где r≤Rr≤R и r≥Rr≥R в течение этого 30-секундного интервала? (b) Предположим, что R=10,0 см R=10,0 см. Какую работу совершает электрическое поле над протоном, если его пронести один раз по часовой стрелке по круговой траектории радиусом 5,0 см? в) Какую работу совершает электрическое поле над протоном, который один раз пролетает против часовой стрелки по круговой траектории любого радиуса r≥Rr≥R? (г) В момент, когда B=0,50TB=0,50T, протон входит в магнитное поле на A , двигаясь со скоростью v→v→(v=5,0×106 м/с)(v=5,0×106 м/с), как показано. Каковы электрические и магнитные силы, действующие на протон в этот момент?
52.
Магнитное поле во всех точках цилиндрической области, поперечное сечение которой указано на прилагаемом рисунке, начинается с 1,0 Тл и равномерно уменьшается до нуля за 20 с. Каково электрическое поле (как по величине, так и по направлению) в зависимости от 90 794 r 90 795 , расстояния от геометрического центра области?
Каково электрическое поле (как по величине, так и по направлению) в зависимости от 90 794 r 90 795 , расстояния от геометрического центра области?
53.
Ток в длинном соленоиде с 20 витками на сантиметр радиуса 3 см изменяется со временем со скоростью 2 А/с. Круглая петля из проволоки радиусом 5 см и сопротивлением 2 Ом 2 Ом окружает соленоид. Найдите электрический ток, индуцируемый в петле.
54.
Ток в длинном соленоиде радиусом 3 см и 20 витками/см изменяется во времени со скоростью 2 А/с. Найти электрическое поле на расстоянии 4 см от центра соленоида.
13,6 Электрические генераторы и обратная ЭДС
55.
Разработайте петлю с током, которая при вращении в однородном магнитном поле напряженностью 0,10 Тл будет создавать ЭДС ε=ε0sinωt,ε=ε0sinωt, где ε0=110Вε0=110В и ω=120πрад/с.ω=120πрад/с .
56.
Плоская квадратная катушка из 20 витков со сторонами длиной 15,0 см вращается в магнитном поле напряженностью 0,050 Тл. Если максимальная ЭДС, создаваемая в катушке, составляет 30,0 мВ, какова угловая скорость катушки?
57.
Прямоугольная катушка из 50 витков размерами 0,15 м × 0,40 м 0,15 м × 0,40 м вращается в однородном магнитном поле величиной 0,75 Тл со скоростью 3600 об/мин. а) Определите ЭДС индукции в катушке как функцию времени. (b) Если катушка подключена к резистору 1000 Ом 1000 Ом, какова зависимость мощности от времени, необходимая для того, чтобы катушка вращалась со скоростью 3600 об/мин? (c) Ответьте на часть (b), если катушка подключена к резистору 2000 Ом.
58.
Квадратная катушка якоря генератора переменного тока имеет 200 витков и имеет длину стороны 20,0 см. Когда он вращается со скоростью 3600 об/мин, его пиковое выходное напряжение составляет 120 В. а) Какова частота выходного напряжения? б) Какова сила магнитного поля, в котором вращается катушка?
59.
Флип-катушка — относительно простое устройство, используемое для измерения магнитного поля. Он состоит из круглой катушки из 90 794 Н 90 795 витков, намотанной тонкой проводящей проволокой. Катушка присоединена к баллистическому гальванометру, устройству, измеряющему общий заряд, прошедший через нее. Катушка помещена в магнитное поле B→B→ так, что ее поверхность перпендикулярна полю. Затем его переворачивают на 180°, 180° и измеряют общий заряд Q , протекающий через гальванометр. а) Если общее сопротивление катушки и гальванометра равно R , какая связь между B и Q ? Поскольку катушка очень маленькая, можно предположить, что B→B→ по ней однородно. б) Как определить, перпендикулярно ли магнитное поле поверхности катушки?
60.
Перекидная катушка из предыдущей задачи имеет радиус 3,0 см и намотана 40 витками медного провода. Суммарное сопротивление катушки и баллистического гальванометра составляет 0,20 Ом.0,20 Ом. Когда катушку переворачивают на 180°180° в магнитном поле B→,B→, изменение составляет 0,090 С проходит через баллистический гальванометр. (a) Если предположить, что B→B→ и поверхность катушки изначально перпендикулярны, каково магнитное поле? б) Если катушку перевернуть на 90°, 90°, каково будет показание гальванометра?
Суммарное сопротивление катушки и баллистического гальванометра составляет 0,20 Ом.0,20 Ом. Когда катушку переворачивают на 180°180° в магнитном поле B→,B→, изменение составляет 0,090 С проходит через баллистический гальванометр. (a) Если предположить, что B→B→ и поверхность катушки изначально перпендикулярны, каково магнитное поле? б) Если катушку перевернуть на 90°, 90°, каково будет показание гальванометра?
61.
Двигатель с последовательным возбуждением на 120 В имеет сопротивление возбуждения 80 Ом и сопротивление якоря 10 Ом. При работе на полной скорости создается противо-ЭДС 75 В. а) Какой первоначальный ток потребляет двигатель? Когда двигатель работает на полной скорости, где (b) ток, потребляемый двигателем, (c) выходная мощность источника, (d) выходная мощность двигателя и (e) мощность, рассеиваемая в два сопротивления?
62.
Небольшой двигатель постоянного тока с последовательным возбуждением питается от 12-вольтового автомобильного аккумулятора. При нормальной нагрузке двигатель потребляет 4,0 А, а когда якорь зажат так, что он не может вращаться, двигатель потребляет 24 А. Чему равна противо-ЭДС при нормальной работе двигателя?
При нормальной нагрузке двигатель потребляет 4,0 А, а когда якорь зажат так, что он не может вращаться, двигатель потребляет 24 А. Чему равна противо-ЭДС при нормальной работе двигателя?
Электромагнитная индукция 1, поля и эффекты
описание | Закон Фарадея | Закон Ленца |
Уравнение Неймана | Правило RH Флемминга | Металлический стержень ЭДС |
Описание явления
Быстро меняющееся магнитное поле вызывает протекание электрического тока в замкнутой цепи.
На приведенной выше диаграмме стержневой магнит падает вертикально через катушку, соединенную с гальванометром с центральным нулем.
График зависимости ЭДС катушки от времени показывает, что:
Когда первый полюс (S) падает через катушку, ЭДС увеличивается до уровня, а затем уменьшается.
Когда середина магнита проходит через катушку, ЭДС минимальна. Силовые линии не пересекаются катушкой.
Максимальная ЭДС достигается, когда второй полюс (N) проходит через катушку. Это когда скорость разрезания силовых линий самая высокая, потому что магнит падает быстрее. В результате большей скорости период высокого ЭДС короче.
NB В результате изменения направления поля, когда полюса падают через катушку, направление индуцированного тока также меняется на противоположное.
Значит, ЭДС тоже обратная (ЭДС прямо пропорциональна току).
вернуться к началу
Закон Фарадея
Рассмотрим катушки разного размера, когда один и тот же магнит вводится в корпус каждой катушки с одинаковой скоростью.
Установлено, что
Так ЭДС индукции E прямо пропорциональна числу витков N ,
Теперь рассмотрим только одну катушку и по очереди введем три магнита. Магниты имеют разную силу и вводятся в катушку с одинаковой скоростью.
Магниты имеют разную силу и вводятся в катушку с одинаковой скоростью.
Путем измерения максимальной ЭДС и магнитного потока для каждого магнита установлено, что
ЭДС индукции So E прямо пропорциональна потоку φ ,
Закон Фарадея просто гласит:
ЭДС индукции в замкнутой цепи прямо пропорциональна потокосцеплению.
Потокосцепление Nφ является произведением потока φ и числа витков N на катушке.
Мы это видели,
Следовательно,
вернуться к началу
Закон Ленца
Направление ЭДС индукции таково, что индуцированный ток препятствует изменению
производство.
Таким образом, когда южный магнитный полюс перемещается к катушке в цепи, лицевая сторона катушки представляет собой южный полюс.
Индуцированный ток противодействует изменению, вызвавшему его, пытаясь предотвратить попадание южного полюса в катушку (отталкивая его).
Точно так же, когда южный полюс вытягивается из катушки в цепи, лицевая сторона катушки представляет собой северный полюс.
Индуцированный ток противодействует изменению, вызвавшему его, пытаясь предотвратить выход южного полюса из катушки (притягивая его).
НБ
1.) как направление тока изменяется направлением магнита.
2.) на каждой стороне катушки, как линия, проведенная между концами стрелок (серого цвета), образует
‘ N ‘ и ‘ S ‘ с указанием полярности катушек. |
вернуться к началу
Уравнение Неймана
Это сочетает в себе пропорциональности в законе Фарадея с направлением индуцированного тока из закона Ленца.
Благодаря постоянству используемых единиц (СИ) нет необходимости в константе пропорциональности.
Знак минус соответствует закону Ленца, указывающему на противоположный характер индуцированной ЭДС и скорости обрезания потокосцепления.
Уравнение можно изменить, включив в него скорость резки флюса dφ/dt , взяв количество витков N выход из дифференциала.
вернуться к началу
Правило правой руки Флемминга
Правило описывает результирующее направленное движение индуцированного тока для проводника, движущегося под прямым углом к направлению поля.
Три количества ПОЛЕ , ТОК И ДВИЖЕНИЕ находятся под прямым углом друг к другу.
Правой рукой расположите указательный, указательный и большой пальцы так, чтобы образовать оси x, y, z.
Выделенные буквы в словах помогут вам запомнить три величины.
F первый палец — F направление поля
se C второй палец — C текущее направление
чт M b — M исп. |
вернуться к началу
ЭДС, индуцированная металлическим стержнем
Для ЭДС индукции E изготавливается по длине L металлического стержня, магнитное поле B , скорость v и большая ось стержня должны быть взаимно расположены справа углами друг к другу.
Происхождение E = BLv :
Рассмотрим металлический стержень длиной л .
Если стержень движется со скоростью 91 103 90 227 v 90 228 90 795 под прямым углом к его длине, то площадь 91 103 90 227 A 90 228 90 795, заметаемая в секунду, определяется как:
Общий поток φ , проходящий через эту площадь в секунду, является произведением площади A и плотности потока B .
Замена области A ,
В этом случае, поскольку общий поток φ относится к 1 секунде, мы можем написать:
, где dφ/dt — скорость резки флюса.
Следовательно,
По определению, ЭДС ( E ) равна скорости резания флюса,
Следовательно,
наверх
Патент США на индукционное устройство для приготовления пищи с ферритовой опорой катушки Патент (Патент № 4,629,843, выдан 16 декабря 1986 г.)
ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ
Настоящее изобретение относится к устройству электромагнитного индукционного нагревателя, которое иногда называют керамической плитой и используют в качестве индукционной горелки.
Известный индукционный нагреватель или индукционная горелка показаны на РИС. 1, на котором цифра 1 — плоская опора катушки из жаропрочного изоляционного материала, 2 — катушка, установленная на этой опоре 1, 3 — корпус, 4 — накладка из термостойкой изоляции, 5 — нагрузка, например, кастрюля для приготовления пищи. Катушка 2 изготовлена из литцендрата.
Катушка 2 изготовлена из литцендрата.
Когда на катушку 2 подается питание высокой частоты (например, 20-40 кГц), нагрузка 5 нагревается за счет потерь на вихревые токи и/или потерь на индукцию поля электромагнитного потока, создаваемого катушкой 2.
Однако, известная индукционная горелка имеет следующий недостаток.
Поскольку опора катушки 1 изготовлена из термостойкого изоляционного материала, электромагнитное поле, создаваемое катушкой 2, просачивается за опору 1. Поток рассеяния равен действующему переднему полю. Так как некоторые электронные устройства, такие как высокочастотный источник питания (не показан), смонтированы в корпусе, то это устройство также нагревается потоком от самой катушки 2.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Целью настоящего изобретения является преодоление недостатков и ограничений известной горелки индукционного нагревателя путем создания новой и улучшенной горелки индукционного нагревателя.
Также целью настоящего изобретения является создание горелки индукционного нагревателя, которая нагревает только нагрузку на передней поверхности, но не нагревает расположенные под ней устройства.
Вышеупомянутые и другие задачи достигаются с помощью горелки индукционного нагревателя, состоящей из корпуса, опоры катушки, установленной в корпусе, катушки, расположенной на верхней плоскости опоры катушки и питаемой высокочастотной мощностью, изоляционной пластины, закрывающей кожух для обеспечения опоры для нагрузки, при этом указанная опора катушки представляет собой, по существу, плоский диск, изготовленный из смеси термостойкой изоляционной смолы и ферритового порошка, так что массовая доля ферритового порошка находится в диапазоне от 75% до 85%.
Предпочтительно указанная опора катушки имеет множество продольных ферритовых ребер, проходящих радиально на нижней плоскости опоры катушки.
Еще предпочтительно, чтобы указанная опора катушки имела точку Кюри выше 150°С. C.
C.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Вышеупомянутые и другие цели, признаки и сопутствующие преимущества настоящего изобретения будут оценены по мере того, как они станут лучше понятны с помощью следующего описания и прилагаемых чертежей, на которых:
РИС. 1 представляет собой поперечное сечение известной горелки индукционного нагревателя,
. Фиг. 2 представляет собой вид снизу индукционной катушки,
. Фиг. 3 представляет собой поперечное сечение по линии А1-А1 на фиг. 2,
РИС. 4 представляет собой вид снизу индукционной катушки согласно настоящему изобретению,
. Фиг. 5 — поперечное сечение по линии А2-А2 на фиг. 4,
РИС. 6 представляет собой вид снизу другого варианта горелки индукционного нагревателя в соответствии с настоящим изобретением,
РИС. 7 представляет собой поперечное сечение по линии А3-А3 на фиг. 6,
РИС. 8 представляет собой принципиальную схему датчика температуры, установленного в настоящей горелке индукционного нагревателя,
. Фиг. 9 представляет собой вид снизу еще одного варианта осуществления горелки индукционного нагревателя в соответствии с настоящим изобретением,
Фиг. 9 представляет собой вид снизу еще одного варианта осуществления горелки индукционного нагревателя в соответствии с настоящим изобретением,
. Фиг. 10 представляет собой поперечное сечение по линии А4-А4 на фиг. 9,
РИС. 11 показана кривая плотности потока индукционного нагревателя диапазона
. На фиг. 12 — вид снизу модификации фиг. 9,
РИС. 13 представляет собой поперечное сечение по линии А5-А5 на фиг. 12,
РИС. 14 представляет собой другую модификацию фиг. 12 и
РИС. 15 представляет собой еще одну модификацию фиг. 12.
ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ВОПЛОЩЕНИЯ
РИС. 4 представляет собой вид снизу опоры катушки по настоящему изобретению, а на фиг. 5 — поперечное сечение по линии А2-А2 на фиг. 4. Фигуры на фиг. 4 и 5 такие же, как на фиг. 1-3 показывают те же элементы, что и на фиг. 1-3. Опора 1 катушки согласно настоящему изобретению изготовлена из сложного ферритового материала, который представляет собой смесь термостойкой изоляционной смолы и спеченного ферритового порошка, вместо термостойкой изоляционной смолы предшествующего уровня техники. Термостойкая смола согласно настоящему изобретению представляет собой, например, ненасыщенную полиэфирную смолу или фенольную смолу.
Термостойкая смола согласно настоящему изобретению представляет собой, например, ненасыщенную полиэфирную смолу или фенольную смолу.
Отношение порошка спеченного феррита к смеси изоляционной смолы предпочтительно составляет от 75% до 85% по массе. Если отношение спеченного ферритового порошка к общей массе смеси выше этого значения, механическая прочность и/или термическая стабильность опоры катушки нарушается. Если доля ферритового порошка ниже этой цифры, то магнитных характеристик опоры катушки будет недостаточно для обеспечения эффекта настоящего изобретения.
Предпочтительно опора 1А катушки имеет множество ребер 12, каждое из которых расположено на задней поверхности опоры 1А в радиальном направлении того же с некоторыми угловыми интервалами. Следует отметить, что толщина опоры должна быть как можно больше, чтобы предотвратить поток рассеяния и повысить механическую прочность, однако толстая опора имеет тот недостаток, что общий вес опоры катушки увеличивается. , а затем стоимость производства того же увеличивается. Наличие множества ребер 13 увеличивает механическую прочность опоры без увеличения ее толщины и увеличивает эффект магнитного экрана опоры. В предпочтительном варианте длина t 1 участков сектора, где нет ребра, составляет t 1 =3,5 мм, а длина t 2 ребер составляет t 2 =5 мм. , и этот вариант осуществления имеет тот же эффект, что и опора катушки, которая не имеет ребра, но имеет одинаковую толщину 5-7 мм в отношении механической прочности и магнитных характеристик. Предпочтительно длина t 1 больше 2 мм, а ширина ребра больше 5 мм. Ребро может быть выполнено за одно целое с самой опорой катушки, в качестве альтернативы к опоре катушки прикреплено отдельное ребро. Ребро выполнено либо из того же материала, что и сама опора катушки, либо из феррита, не содержащего смолы.
Наличие множества ребер 13 увеличивает механическую прочность опоры без увеличения ее толщины и увеличивает эффект магнитного экрана опоры. В предпочтительном варианте длина t 1 участков сектора, где нет ребра, составляет t 1 =3,5 мм, а длина t 2 ребер составляет t 2 =5 мм. , и этот вариант осуществления имеет тот же эффект, что и опора катушки, которая не имеет ребра, но имеет одинаковую толщину 5-7 мм в отношении механической прочности и магнитных характеристик. Предпочтительно длина t 1 больше 2 мм, а ширина ребра больше 5 мм. Ребро может быть выполнено за одно целое с самой опорой катушки, в качестве альтернативы к опоре катушки прикреплено отдельное ребро. Ребро выполнено либо из того же материала, что и сама опора катушки, либо из феррита, не содержащего смолы.
Предпочтительно количество ребер равно или больше 5, а еще предпочтительно находится в диапазоне от 6 до 8. Если количество ребер меньше 4, это не может обеспечить достаточную механическую прочность и магнитное экранирование.
Еще предпочтительнее опора катушки 1А имеет множество отверстий 20 вблизи внутренней стороны диска. Эти отверстия предназначены для выравнивания магнитного потока между внешней и внутренней сторонами путем существенного уменьшения магнитной проницаемости опоры 1А во внутренней части диска.
Далее описывается предпочтительная физическая природа опоры катушки.
Следует отметить, что ферромагнитный материал, такой как феррит, теряет ферромагнитную природу при высокой температуре выше точки Кюри, которая определяется каждым ферромагнитным материалом. Когда опора катушки теряет ферромагнитную природу, индуктивность катушки значительно уменьшается, а затем частота и/или ток, подаваемый на катушку, сильно изменяются, поскольку катушка образует резонансный контур с внешним конденсатором (не показан), связанным с источником питания, таким образом ухудшается нагревательная способность горелки. Когда пища готовится на масле на настоящей горелке, змеевик и/или опора змеевика нагреваются даже до 140-150°С. С. через 30-60 минут.
С. через 30-60 минут.
Соответственно, предпочтительно, чтобы точка Кюри опоры катушки была выше 150°С. C., а еще предпочтительно выше 180°C. C. Когда опора катушки имеет точку Кюри Т с, указанную на этой фигуре, почти все приготовление осуществляется при температуре ниже этой точки Кюри.
Что касается сопротивления изоляции опоры катушки, предпочтительно, чтобы собственное сопротивление опоры катушки было выше 1×10 4 Ом·см. Когда опора катушки имеет собственное сопротивление этой цифры, дополнительный процесс изоляции катушки и опоры катушки не требуется, и, следовательно, процесс изготовления катушки очень упрощается.
Кроме того, предпочтительно, чтобы начальная проницаемость опоры катушки при комнатной температуре на частоте 1 кГц была выше 7 (μi ≥ 7), чтобы катушка имела достаточную индуктивность для нагрева.
Вообще говоря, ферритовый материал с высокой точкой Кюри имеет высокое сопротивление изоляции, но низкую начальную магнитную проницаемость и низкий уровень насыщения потока. Таким образом, указанная выше предпочтительная природа феррита достигается за счет объединения множества исходных ферритов, а указанное предпочтительное сопротивление изоляции достигается за счет природы самого феррита без покрытия опоры катушки пленкой изоляционной смолы. Исходные ферриты выбирают из феррита Ni-Zn, феррита Mn-Zn и феррита Cu-Mg. Комбинация выполняется таким образом, что феррит с высокой начальной проницаемостью, низкой точкой Кюри и низким внутренним сопротивлением комбинируется с другим ферритом с низкой начальной проницаемостью, высокой точкой Кюри и высоким собственным сопротивлением.
Таким образом, указанная выше предпочтительная природа феррита достигается за счет объединения множества исходных ферритов, а указанное предпочтительное сопротивление изоляции достигается за счет природы самого феррита без покрытия опоры катушки пленкой изоляционной смолы. Исходные ферриты выбирают из феррита Ni-Zn, феррита Mn-Zn и феррита Cu-Mg. Комбинация выполняется таким образом, что феррит с высокой начальной проницаемостью, низкой точкой Кюри и низким внутренним сопротивлением комбинируется с другим ферритом с низкой начальной проницаемостью, высокой точкой Кюри и высоким собственным сопротивлением.
В варианте осуществления настоящего изобретения первый феррит А, который имеет высокую начальную магнитную проницаемость и высокий уровень потока насыщения, но низкую точку Кюри Tc 80°-120°C. C. и низким собственным сопротивлением менее 104 Ом·см сочетается со вторым ферритом B, имеющим высокое собственное сопротивление (1×106 -1×1012 Ом-см). см) и высокой точкой Кюри (Т с =200°С). Соотношение комбинаций (весовое соотношение) первого феррита А и второго феррита В (А:В) находится в диапазоне от 60:40 до 70:30.
Соотношение комбинаций (весовое соотношение) первого феррита А и второго феррита В (А:В) находится в диапазоне от 60:40 до 70:30.
Состав этого смешанного феррита;
Fe2O3: 52-62 мол. %
MnO: 23-27 мол. %
ZnO: 10-20 мол. %
MgO: 10-20 мол. %
CuO -8 мол.%
NiO: 15-24 мол.%
И результирующая точка Кюри равна Tc=180°С. C., а собственное сопротивление составляет от 1×10 7 до 1×10 8 Ом·см.
Соответственно, смешанный феррит с точкой Кюри Tc выше 150°С. C., а собственное сопротивление выше 1×10 4 Ом·см получают основные составы Fe 2 O 3 ; 54-62 мол. %, MNo; 23-33 мол.%, ZnO; 9-20 мол.%, а добавки MgO, CuO и NiO более 0,1 мол.% каждой.
Далее описывается другой вариант опоры катушки согласно настоящему изобретению в соответствии с фиг. с 6 по 8.
На РИС. 6 опора катушки 1В изготовлена из смеси изоляционной смолы и ферритового порошка с массовой долей феррита 75-85%, как и в случае фиг. 4. Материал опоры катушки 1В имеет такую природу, что точка Кюри Тс выше 150°С. C., а собственное сопротивление выше 10 4 Ом·см, как в случае на фиг. 4. Особенность варианта осуществления по фиг. 6-8, является наличие множества ребер с 8а по 8h, каждое из которых прикреплено к круглой опоре 1В катушки. Ребра изготовлены из самого феррита, так что проницаемость опоры катушки существенно увеличивается, хотя базовая пластина изготовлена из смеси изоляционной смолы и ферритового порошка. В варианте осуществления по фиг. 6, опорная пластина опоры 1В катушки имеет множество радиальных пазов, в которые вставлено ребро (8а-8h). Точка Кюри каждого ребра отличается от точки Кюри других ребер, поэтому сами ребра действуют как термометр.
C., а собственное сопротивление выше 10 4 Ом·см, как в случае на фиг. 4. Особенность варианта осуществления по фиг. 6-8, является наличие множества ребер с 8а по 8h, каждое из которых прикреплено к круглой опоре 1В катушки. Ребра изготовлены из самого феррита, так что проницаемость опоры катушки существенно увеличивается, хотя базовая пластина изготовлена из смеси изоляционной смолы и ферритового порошка. В варианте осуществления по фиг. 6, опорная пластина опоры 1В катушки имеет множество радиальных пазов, в которые вставлено ребро (8а-8h). Точка Кюри каждого ребра отличается от точки Кюри других ребер, поэтому сами ребра действуют как термометр.
РИС. 8 показано расположение термометра. На фиг. 8 цифра 9 обозначает средство обнаружения для обнаружения магнитной природы соответствующего ребра 8. Средство обнаружения 8 электрически связано с регулятором тока катушки 10, который регулирует ток в катушке 2. Средство обнаружения 9 обнаруживает тот факт, что ребро 8, расположенное близко к средству 9, теряет ферромагнитную природу из-за высокой температуры выше точки Кюри. Затем устройство 10 управления током катушки, которое включает в себя схему инвертора, регулирует ток в катушке 2 так, чтобы температура катушки была ниже допустимого верхнего предела. Обычно допустимая верхняя температура горелки находится в пределах 100°С. С. и 250°С. C. Следовательно, если точка Кюри ребер 8a-8h на фиг. 6 отличаются друг от друга и распределяются в пределах 100-250°. C., мощность, подаваемая на катушку 2 регулятором 10 тока катушки, регулируется в соответствии с мгновенной температурой каждого ребра.
Затем устройство 10 управления током катушки, которое включает в себя схему инвертора, регулирует ток в катушке 2 так, чтобы температура катушки была ниже допустимого верхнего предела. Обычно допустимая верхняя температура горелки находится в пределах 100°С. С. и 250°С. C. Следовательно, если точка Кюри ребер 8a-8h на фиг. 6 отличаются друг от друга и распределяются в пределах 100-250°. C., мощность, подаваемая на катушку 2 регулятором 10 тока катушки, регулируется в соответствии с мгновенной температурой каждого ребра.
Другой вариант осуществления описан в соответствии с фиг. 9-11, на которых ФИГ. 9 представляет собой вид снизу опоры 1С катушки, фиг. 10 — поперечное сечение по линии А4-А4 на фиг. 9 и фиг. 11 – кривая плотности потока. Опора катушки 1C на фиг. 9 изготовлен из того же материала, что и в предыдущих вариантах, то есть опора катушки 1C изготовлена из смеси изоляционной смолы и ферритового порошка с весовым соотношением феррита 75-85%, а материал опора катушки 1C имеет такую природу, что точка Кюри Tc выше 150°С. C., а собственное сопротивление выше 10 4 Ом·см. Кроме того, опора 1С катушки имеет множество радиальных ребер 12, изготовленных из ферритового материала. Эти ребра могут иметь точку Кюри, отличающуюся друг от друга, как в случае предыдущего варианта осуществления.
C., а собственное сопротивление выше 10 4 Ом·см. Кроме того, опора 1С катушки имеет множество радиальных ребер 12, изготовленных из ферритового материала. Эти ребра могут иметь точку Кюри, отличающуюся друг от друга, как в случае предыдущего варианта осуществления.
Особенность фиг. 9, это наличие множества отверстий 20, которые располагаются во внутренней области диска 1С, а не в центральной окружности (а). Эта центральная окружность (а) является центром длины (А) между окружностью 71 центрального отверстия 7 и внешней окружностью. Эти отверстия 20 функционируют так, что проницаемость внутренней части диска 1С существенно меньше, чем проницаемость внешней части диска.
Когда магнитная проницаемость диска 1C одинакова, магнитный поток, создаваемый катушкой 2, является плотным во внутренней части диска и не является плотным в выходной части. Пунктирная кривая L1 на фиг. 11 показан магнитный поток при постоянной проницаемости диска. Кривая L2 на фиг. 11 показан магнитный поток при наличии отверстий 20. На фиг. 11 по горизонтальной оси показана длина в радиальном направлении, по вертикальной оси показана плотность потока, а по вертикальной оси показан коэффициент потока. Как видно на фиг. 11, когда предусмотрены отверстия 20, поток во внутренней части диска не такой высокий, как в случае, когда отверстия не предусмотрены. Отверстия 20 имеют еще одно преимущество, заключающееся в том, что обеспечивается охлаждающий эффект за счет вентиляции через отверстия. Кроме того, вариант осуществления по фиг. 9Преимущество заключается в том, что обеспечивается равномерный нагрев для приготовления пищи, а изменение нагрузки на источник питания уменьшается независимо от того, кладется ли пища на внутреннюю часть диска или на внешнюю часть диска.
На фиг. 11 по горизонтальной оси показана длина в радиальном направлении, по вертикальной оси показана плотность потока, а по вертикальной оси показан коэффициент потока. Как видно на фиг. 11, когда предусмотрены отверстия 20, поток во внутренней части диска не такой высокий, как в случае, когда отверстия не предусмотрены. Отверстия 20 имеют еще одно преимущество, заключающееся в том, что обеспечивается охлаждающий эффект за счет вентиляции через отверстия. Кроме того, вариант осуществления по фиг. 9Преимущество заключается в том, что обеспечивается равномерный нагрев для приготовления пищи, а изменение нагрузки на источник питания уменьшается независимо от того, кладется ли пища на внутреннюю часть диска или на внешнюю часть диска.
РИС. 12 и 13 показывают модификацию фиг. с 9 по 11. Особенность фиг. 12 и 13 — форма отверстий. Хотя отверстия 20 на фиг. 9 круглые, отверстия на фиг. 12 имеют форму сектора.
РИС. 14 показана другая модификация отверстий в виде тонких линейных щелей.
РИС. 15 показана еще одна модификация отверстий, в которой отверстия имеют форму эллипса.
Из вышеизложенного становится очевидным, что найдена новая улучшенная холодная электрическая горелка. Разумеется, следует понимать, что раскрытые варианты осуществления являются просто иллюстративными и не предназначены для ограничения объема изобретения. Поэтому следует сделать ссылку на прилагаемую формулу изобретения, а не на описание, которое указывает объем изобретения.
Электродинамометрические приборы – амперметр, вольтметр и ваттметр
Электродинамометр представляет собой прибор передающего типа. Прибор переносного типа можно откалибровать с помощью источника постоянного тока, а затем использовать без модификации для измерения переменного тока. Это требует, чтобы приборы передающего типа имели одинаковую точность как для постоянного, так и для переменного тока .
Эти приборы также называются Приборы электродинамического или динамометрического типа .
Электродинамический прибор представляет собой прибор с подвижной катушкой, в котором рабочее поле создается не постоянным магнитом, а другой неподвижной катушкой. Этот прибор может использоваться как амперметр или вольтметр, но обычно используется как ваттметр.
Электродинамический инструмент или инструмент динамометрического типа представляет собой инструмент с подвижной катушкой, но магнитное поле, в котором движется катушка, обеспечивается двумя неподвижными катушками, а не постоянными магнитами (например, инструменты PMMC).
Показана принципиальная схема электродинамического прибора и практического измерителя.
Электродинамометр или электродинамический приборСостоит из двух неподвижных катушек, расположенных симметрично. Он будет иметь крутящий момент в одном направлении в течение одной половины цикла и такой же эффект в противоположном направлении в течение другой половины цикла.
Если бы, однако, мы меняли направление потока каждый раз, когда ток через подвижную катушку меняется на противоположное, то однонаправленный крутящий момент создавался бы как для положительной, так и для отрицательной половины цикла. В электродинамических приборах поле можно заставить реверсировать одновременно с током в подвижной катушке, если неподвижную катушку соединить последовательно с подвижной катушкой.
В электродинамических приборах поле можно заставить реверсировать одновременно с током в подвижной катушке, если неподвижную катушку соединить последовательно с подвижной катушкой.
1. Управляющий крутящий момент
Управляющий крутящий момент обеспечивается двумя управляющими пружинами. Эти пружины действуют как провода к движущейся катушке.
2. Демпфирование
В этих приборах используется воздушное демпфирование, обеспечиваемое парой алюминиевых лопастей, прикрепленных к шпинделю в нижней части. Эти лопасти движутся в секторной камере.
Содержание
Принцип работы электродинамометрических приборов
Мы можем получить представление о принципе работы электродинамометрического прибора, взяв прибор с подвижной катушкой на постоянном магните и рассмотрев, как он будет вести себя на переменном токе.
Он будет иметь крутящий момент в одном направлении в течение одной половины цикла и такой же эффект в противоположном направлении в течение другой половины цикла.
Если бы частота была очень низкой, стрелка качалась бы вперед и назад вокруг нулевой точки. Однако для обычного измерителя инерция настолько велика, что на промышленных частотах стрелка не уходит далеко ни в ту, ни в другую сторону, а просто остается (слегка вибрирует) около нуля.
Если бы, однако, мы меняли направление потока поля каждый раз, когда ток через подвижную катушку меняется на противоположное, крутящий момент создавался бы в одном и том же направлении для обеих половин цикла.
Поле можно изменить на обратное одновременно с током в подвижной катушке, если катушка возбуждения подключена последовательно с подвижной катушкой.
Почему приборы PMMC нельзя использовать для измерения переменного тока?
Теперь давайте обсудим, почему приборы PMMC нельзя использовать для измерений переменного тока.
Прибор PMMC нельзя использовать при переменном токе или напряжении. Если на эти инструменты подается переменный ток, будет развиваться переменный крутящий момент. Из-за момента инерции движущейся системы стрелка не будет следовать за быстро меняющимся переменным крутящим моментом и не будет показывать никаких показаний.
Из-за момента инерции движущейся системы стрелка не будет следовать за быстро меняющимся переменным крутящим моментом и не будет показывать никаких показаний.
Чтобы прибор мог считывать величины переменного тока, магнитное поле в воздушном зазоре должно изменяться вместе с изменением тока. Этот принцип используется в приборе электродинамометрического типа.
Вместо постоянного магнита прибор электродинамометрического типа использует измеряемый ток для создания необходимого магнитного поля.
Конструкция инструментов для электродинамометрии
В этом разделе вы узнаете, как изготавливаются следующие части инструментов для электродинамометрии.
- Фиксированная катушка
- Подвижная катушка
- Управление
- Подвижная система
- Демпфирование
- Экранирование
- Футляры и весы
1. Фиксированные катушки:
Фиксированные катушки:
Поле создается фиксированной катушкой. Эта катушка разделена на две секции, чтобы обеспечить более однородное поле вблизи центра и обеспечить прохождение стержня инструмента.
Прибор, показанный на рисунке миллиамперметром, или может стать вольтметром путем добавления последовательного сопротивления. Фиксированные катушки намотаны тонкой проволокой для таких применений.
Катушки возбуждения (фиксированные) обычно наматывают толстым проводом, по которому течет основной ток в амперметрах и ваттметрах.
Провод скрученный там, где это необходимо для уменьшения потерь на вихревые токи в проводниках. Катушки обычно покрывают лаком и запекают, чтобы сформировать прочную сборку.
Затем они прижимаются к опорам катушки. Это делает конструкцию жесткой, чтобы не было смещения или изменения размеров, которые могли бы повлиять на калибровку. Монтажные опоры предпочтительно изготавливаются из керамики, так как металлические детали могут ослабить поле неподвижной катушки из-за вихревых токов.
2. Подвижная катушка
Одноэлементный прибор имеет одну подвижную катушку. Подвижная катушка намотана либо как самоподдерживающаяся катушка, либо на неметаллическом каркасе.
Металлический каркас использовать нельзя, так как переменным полем в нем будут индуцироваться вихревые токи. Для подвижной катушки используется легкая, но жесткая конструкция. Следует отметить, что и неподвижные, и подвижные катушки имеют воздушный сердечник.
3. Управление
Управляющий момент обеспечивается двумя пружинами управления. Эти пружины действуют как провода к движущейся катушке.
4. Подвижная система
Подвижная катушка установлена на алюминиевом шпинделе. Подвижная система также несет противовесы и указатель ферменного типа. Иногда можно использовать суспензию, если требуется высокая чувствительность.
5. Демпфирование
В этих приборах используется демпфирование воздушным трением, которое обеспечивается парой алюминиевых лопастей, прикрепленных к шпинделю в нижней части. Эти лопасти перемещаются в секторных камерах.
Эти лопасти перемещаются в секторных камерах.
6. Экранирование
Поле, создаваемое неподвижными катушками, несколько слабее, чем в других типах приборов. Оно составляет примерно от 0,005 до 0,006 Втб/м 2 .
При измерении постоянного тока даже магнитное поле Земли может повлиять на показания. Таким образом, необходимо защитить электродинамометрический прибор от влияния блуждающих магнитных полей. Электродинамометрические приборы с воздушным сердечником защищают от внешних магнитных полей, заключая их в корпус из сплава с высокой проницаемостью.
7. Футляры и весы
Стандартные лабораторные инструменты обычно хранятся в полированных деревянных футлярах. Эти корпуса сконструированы таким образом, чтобы оставаться стабильными по размерам в течение длительных периодов времени.
Стекло с некоторым покрытием. проводящий материал для полного устранения электростатических эффектов. Корпус поддерживается пахотными выравнивающими винтами. Также имеется спиртовой уровень, чтобы обеспечить правильное выравнивание.
Также имеется спиртовой уровень, чтобы обеспечить правильное выравнивание.
Уравнение крутящего момента электродинамометрических инструментов
Let,
i 1 = мгновенное значение тока в неподвижных катушках, (А)
i 2 = мгновенное значение тока в подвижных катушках, (А) 7 118043 91 = самоиндукция неподвижной катушки, (Гн)
L 2 = самоиндукция подвижной катушки, (Гн)
M = взаимная индуктивность между неподвижной и подвижной катушкой (Гн)
9
9 Потокосцепление катушки 1,
ψ 1 = L 1 i 1 + Mi 2Flux linkage of Coil 2, ψ 2 = L 2 i 2 + Mi 1
Electrical input energy = e 1 i 1 dt + e 2 i 2 dt = i 1 dψ 1 + i 2 dψ 2
As e 1 = d ψ 1 /dt и e 1 = dψ 2 /dt
Electrical input energy = i 1 d( L 1 i 1 + Mi 2 )+ i 2 d(L 2 i 2 + Mi 1 )
Энергия, хранящаяся в магнитном поле = ½ I 1 2 L 1 + ½ I 2 2 L 2 9188 + +
+58 +858 +
858 +
858 +
858 +
858 +
8 +58 +858 2 L 2 +
+ + +58 .
Изменение накопленной энергии = d( ½ i 1 2 L 1 + ½ I 2 2 L 2 + I 1 I 2 M)
от Принципной консервации
от Принципной консервации
от Принципной природы. Изменение запасенной энергии + механическая энергия
Механическая энергия может быть получена путем вычитания приведенных выше уравнений
Следовательно, механическая энергия = ½ i 1 2 дл 1 + ½ i 2 2 3 DL 2 + I 1 I 2 DM
СЕЙЧАС, СЕМПАНА L 1 и L 2 ARE AT SINT dL 2 оба равны нулю.
Следовательно, механическая энергия = i 1 i 2 дМ
Предположим, что T i — мгновенный отклоняющий момент, а dθ — изменение, тогда — изменение0009
Механическая энергия = работа = T I Dθ
Таким образом, мы имеем
T I Dθ = I 1 I 2 DM 999999999958 2 DM
9999999999999999891857 18
588 2 DM 2 DM 2 DM I 2 DM 1 i 2 (dM/dθ)
1.
 Работа на постоянном токе крутящий момент T d = I 1 I 2 (dM/dθ)
Работа на постоянном токе крутящий момент T d = I 1 I 2 (dM/dθ) Это показывает, что отклоняющий момент в целом зависит от произведения тока I 1 и I 2 и скорости изменения взаимной индуктивности.
Этот отклоняющий момент отклоняет подвижную катушку в такое положение, при котором управляющий момент пружины равен отклоняющему моменту. Предположим, что θ — окончательное устойчивое отклонение.
Таким образом, управляющий крутящий момент T c = kθ где k = жесткость пружины (Н-м/рад)
At final steady position T d = T c
I 1 I 2 (dM/dθ) = kθ
Deflection, θ = (I 1 I 2 /k)(dM/dθ)
Если две катушки соединены последовательно для измерения тока, два тока I 1 и I 2 равны.
Скажем, I 1 = I 2 = I
Таким образом, отклонение стрелки равно θ = (I 2 /k)(dM/dθ)
Для использования постоянного тока отклонение , таким образом, пропорционально квадрату тока и, следовательно, шкала неоднородна и скучена на концах.
2. Работа от сети переменного тока
Пусть i 1 и i 2 будут мгновенными значениями тока, проходящего через катушки. Следовательно, мгновенный отклоняющий момент равен:
T i = i 1 i 2 (dM/dθ)
Если две катушки соединены последовательно для измерения тока, то два мгновенных тока i 1 и i 2 равны.
, скажем, I 1 = I 2 = I
Таким образом, мгновенный крутящий момент на указателе составляет T I = I 2 (DM/Dθ)
9999999999957. , мгновенный крутящий момент пропорционален квадрату мгновенного тока. Поскольку количество я 2 всегда положительный, ток меняется, а также меняется мгновенный крутящий момент. Но движущаяся система в силу своей инерции не может следовать таким быстрым изменениям мгновенного момента и реагирует только на средний момент.
Средний отклоняющий момент за полный цикл определяется по формуле:
где T — период времени для одного полного цикла.
В конечном устойчивом положении T d = T C
Таким образом, отклонение стрелки составляет
Таким образом, прогиб является функцией среднего квадрата тока.
Если стрелочная шкала откалибрована по квадратному корню из этого значения, т. е. квадратному корню из среднего квадрата текущего значения, то этим прибором может быть непосредственно измерено среднеквадратичное значение величины переменного тока.
3. Синусоидальный ток
Если токи i 1 и i 2 синусоидальны и смещены на фазовый угол j, т. е.
i 1 = i m1 sin ωt and i 2 = I m1 sin(wt – j)
The average deflecting torque
где I 1 и I 2 — действующие значения токов, протекающих через катушки.
В равновесии T d = T c
Как и в случае измерения переменного тока, при синусоидальном токе также отклонение является функцией среднего квадрата тока .
Если стрелочная шкала откалибрована по квадратному корню из этого значения, т. е. квадратному корню из среднего квадрата текущего значения, то этим прибором может быть непосредственно измерено среднеквадратичное значение переменной величины.
Типы электродинамометрических инструментов
В этом разделе вы познакомитесь с тремя типами электродинамических инструментов.
- Электродинамический амперметр
- Электродинамический вольтметр
- Электродинамический ваттметр
1. Электродинамический амперметр
В электродинамическом амперметре неподвижная и подвижная катушки соединены последовательно , как показано на рисунке. Шунт подключен к подвижной катушке для ограничения тока.
Отношение реактивного сопротивления к сопротивлению шунта и подвижной катушки сохраняется почти одинаковым для независимости показаний счетчика от частоты питания.
Поскольку токи катушек одинаковы, отклоняющий момент пропорционален среднеквадратичному значению тока. Таким образом, весы откалиброваны для считывания среднеквадратичного значения .
2. Вольтметр электродинамический
Электродинамический прибор можно использовать в качестве вольтметра, подключив последовательно с катушкой прибора большое неиндуктивное сопротивление (R) с низкотемпературным коэффициентом.
Электродинамометрический вольтметр3. Электродинамический ваттметр
Электродинамический ваттметр состоит из двух неподвижных катушек «а» и «б», расположенных симметрично друг другу и создающих однородное магнитное поле. Они соединены последовательно с нагрузкой и называются токовыми катушками (CC) .
Электродинамометрический ваттметр Две фиксированные катушки могут быть соединены последовательно или параллельно для получения двух различных значений тока. Катушки тока проводят ток полной нагрузки или часть тока полной нагрузки. Таким образом, ток в токовых катушках пропорционален току нагрузки.
Катушки тока проводят ток полной нагрузки или часть тока полной нагрузки. Таким образом, ток в токовых катушках пропорционален току нагрузки.
Подвижная катушка «с», последовательно соединенная с высоким неиндуктивным сопротивлением R v , подключена к источнику питания. Таким образом, ток, протекающий в подвижной катушке, пропорционален напряжению питания и практически совпадает по фазе с ним. Подвижная катушка также называется катушкой напряжения или катушкой давления (PC) .
Катушка напряжения установлена на поворотном шпинделе , на котором установлен указатель , стрелка переместилась по калиброванной шкале.
Две спиральные пружины используются для обеспечения управляющего крутящего момента и подачи тока в подвижную катушку и из нее. Демпфирование обеспечивается трением воздуха .
Видео ниже объясняет работу электродинамометрического ваттметра.
4. Уравнение крутящего момента
Выведем уравнение крутящего момента электродинамометрического прибора.
Пусть, i f = ток в неподвижной катушке
i m = current in the moving coil
i = load current
v = load voltage
T in = instantaneous value of the deflecting torque
p = instantaneous power
T in α i f i m
Since i f α i and i m α v
T in α vi α p
Таким образом, мгновенное значение отклоняющего момента пропорционально мгновенной мощности. Благодаря инерции подвижной системы стрелка считывает среднюю мощность.
В цепях постоянного тока мощность определяется произведением напряжения и тока, поэтому крутящий момент прямо пропорционален мощности. Таким образом, прибор показывает мощность.
Таким образом, прибор показывает мощность.
Для переменного тока прибор показывает среднюю мощность . Это можно доказать следующим образом:
T in α vi
Средний отклоняющий момент × средняя мощность
Пусть, v = V m sin d
I = I m sin (θ – Ф) 9000 значение V м sin d × I m sin (θ – Ф) α VI cos θ
Если T d – средний крутящий момент, то
T d α VI cos θ α истинная мощность = kP
, где P — действительная мощность, а k — постоянная.
для контроля пружины T C = K S θ 1
, где T C — Control Corpe, K S — это ул. отклонения указателя.
For steady deflection,
T c = T d
k s θ 1 = kP
θ 1 = ( k/k s )P
θ 1 α P
Следовательно, и в случае переменного тока отклонение пропорционально истинной мощности в цепи. Таким образом, шкала электродинамометрического ваттметра однородна.
Таким образом, шкала электродинамометрического ваттметра однородна.
Преимущества приборов электродинамометрического типа
Преимущества приборов электродинамометрического типа
- Они могут быть использованы для измерений как переменного, так и постоянного тока.
- Эти приборы свободны от вихретоковых и гистерезисных ошибок .
- Электродинамометрические приборы очень полезны для точного измерения среднеквадратичных значений напряжения независимо от формы сигнала.
- Из-за прецизионного класса точности и одинаковой калибровки для измерений переменного и постоянного тока эти приборы полезны в качестве измерительных приборов и калибровочных приборов .
Недостатки приборов электродинамометрического типа
Преимущества приборов электродинамометрического типа:
- Поскольку прибор имеет квадратичную характеристику, шкала неравномерна .

- Эти инструменты имеют малое отношение крутящего момента к весу , поэтому погрешность трения значительна.
- Дороже, чем инструменты с подвижной катушкой с постоянными магнитами (PMMC) и с подвижным железом (MI).
- Надлежащее экранирование механизмов от паразитных магнитных полей необходим.
- Потребляемая мощность сравнительно выше из-за его конструкции.
Ошибки в приборах электродинамометра
Различные ошибки в приборах электродинамометра:
- Отношение крутящего момента к весу
- Ошибки частоты
- Вихретоковые ошибки
- Ошибка рассеянного магнитного поля
- Ошибка температуры
1. Отношение крутящего момента к весу
Чтобы иметь приемлемый отклоняющий момент, м.д.с. подвижной катушки должно быть достаточно большим. Таким образом, mmf = NI , следовательно, ток через подвижную катушку должен быть высоким или число витков должно быть большим.
Ток нельзя делать очень большим, т. к. это может привести к чрезмерному заживлению пружин. Следовательно, большое количество витков является единственным вариантом, но это увеличивает вес катушки.
Это утяжеляет систему, снижая отношение крутящего момента к весу. Это может привести к фрикционным ошибкам при считывании.
2. Ошибки частоты
Изменения частоты вызывают изменение собственной индуктивности подвижной и неподвижной катушек. Это вызывает ошибку в чтении. Ошибка частоты может быть уменьшена за счет одинаковых постоянных времени как для цепей с фиксированной, так и с подвижной катушкой.
3. Вихретоковые ошибки
В металлических частях прибора возникают вихревые токи. Вихревые токи взаимодействуют с током прибора, вызывая изменение отклоняющего момента, вызывая ошибку.
Следовательно, металлических деталей должно быть как можно меньше. Кроме того, удельное сопротивление используемых металлических деталей должно быть высоким, чтобы уменьшить вихревые токи.
4. Ошибка рассеянного магнитного поля
Как и в инструментах с подвижным железом, рабочее поле в электродинамометрическом инструменте очень слабое.
Следовательно, внешнее магнитное поле может взаимодействовать с рабочим полем, вызывая изменение отклонения и вызывая ошибку. Чтобы уменьшить влияние рассеянного магнитного поля, для приборов необходимо использовать экраны.
5. Температурная ошибка
Температурные ошибки вызваны самонагревом катушки, что вызывает изменение сопротивления катушки. Таким образом, в точном приборе можно использовать термокомпенсирующие резисторы для устранения температурных погрешностей.
Ассортимент электродинамометрических приборов
Ассортимент электродинамометрических амперметров и вольтметров приведен ниже.
Диапазон амперметра
- Для фиксированной и подвижной катушек последовательно – 200 мА
- Шунтированная подвижная катушка – 30 A
Диапазон вольтметра – до 750 В
Сравнение различных типов приборов
Сравнение приборов типа PMMC, подвижного железа и электродинамометрических приборов представлено в таблице
| Управление | Демпфирование | Пригодность | Приложение | |
| ЧВК | Весна | Вихревой поток | DC | Широко используется для измерения постоянного тока и напряжения в цепях с низким и средним импедансом. |




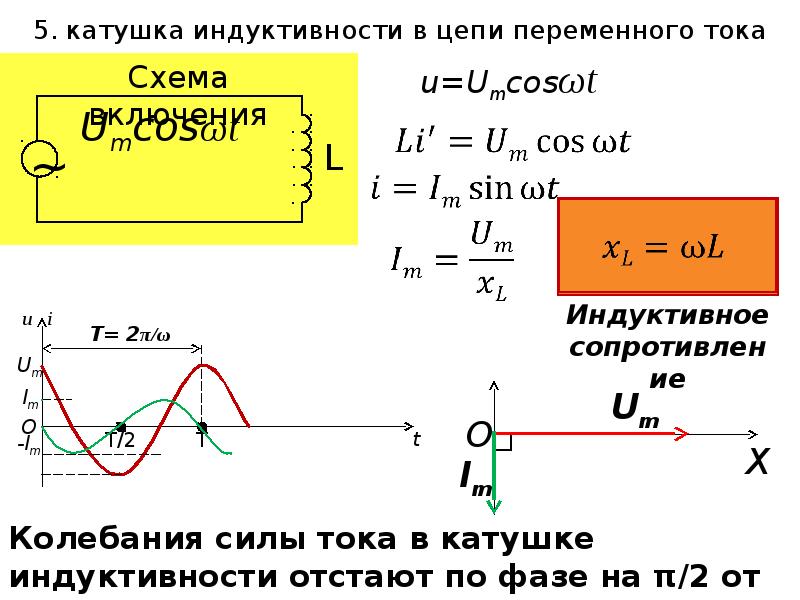 21.2.
21.2.

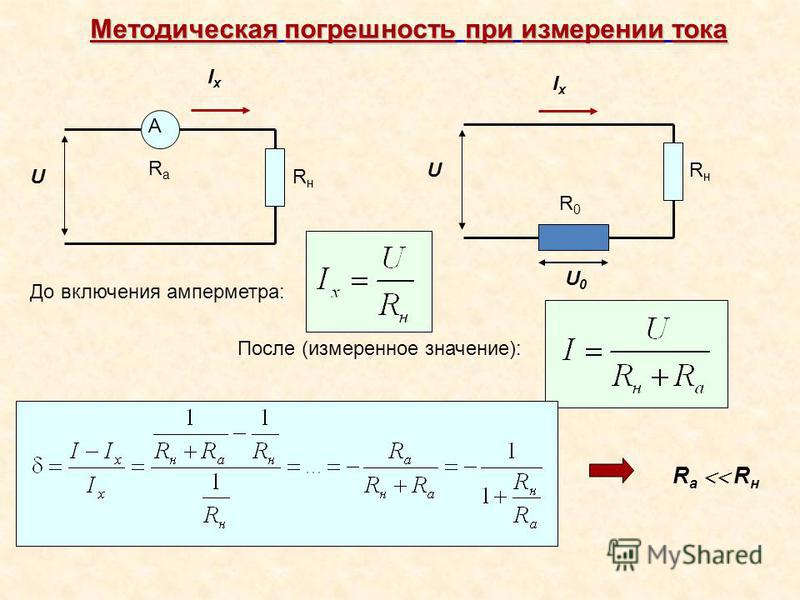 19)
19) Назовите единицу индуктивности.
Назовите единицу индуктивности.
 Этот ток будет изменятся по закону
Этот ток будет изменятся по закону Определить энергию магнитного поля в сердечнике соленоида, если сила тока в обмотке = 0,5 А.
Определить энергию магнитного поля в сердечнике соленоида, если сила тока в обмотке = 0,5 А.
 Какой ток потечет во второй катушке, если ток I1 = 0,3 А в первой катушке выключить в течение = 0,001 с. Сопротивление второй катушки R2 = 600 Ом.
Какой ток потечет во второй катушке, если ток I1 = 0,3 А в первой катушке выключить в течение = 0,001 с. Сопротивление второй катушки R2 = 600 Ом.


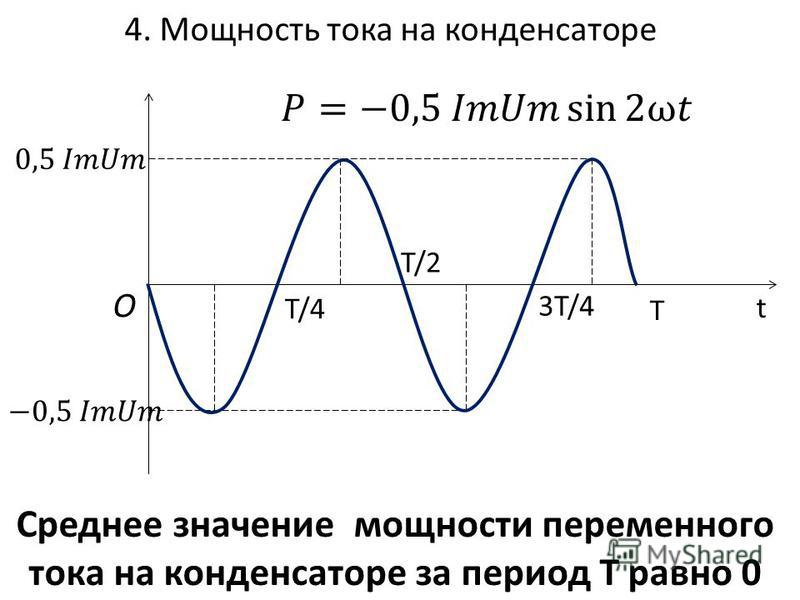 11.На картонный каркас длиной = 50 см и площадью сечения S = 4 см ,намотан в один слой провод диаметромd =0,2 мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Вычислить индуктивность L получившегося соленоида.
11.На картонный каркас длиной = 50 см и площадью сечения S = 4 см ,намотан в один слой провод диаметромd =0,2 мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Вычислить индуктивность L получившегося соленоида. Индуктивность первой катушки L1= 0,12 Гн, второй — Гн. Сопротивление второй катушки R2 = 300 Ом. Определить силу тока I2 во второй катушке, если за время с силу тока в первой катушке уменьшить от I1 = 0,5 А до нуля.
Индуктивность первой катушки L1= 0,12 Гн, второй — Гн. Сопротивление второй катушки R2 = 300 Ом. Определить силу тока I2 во второй катушке, если за время с силу тока в первой катушке уменьшить от I1 = 0,5 А до нуля.


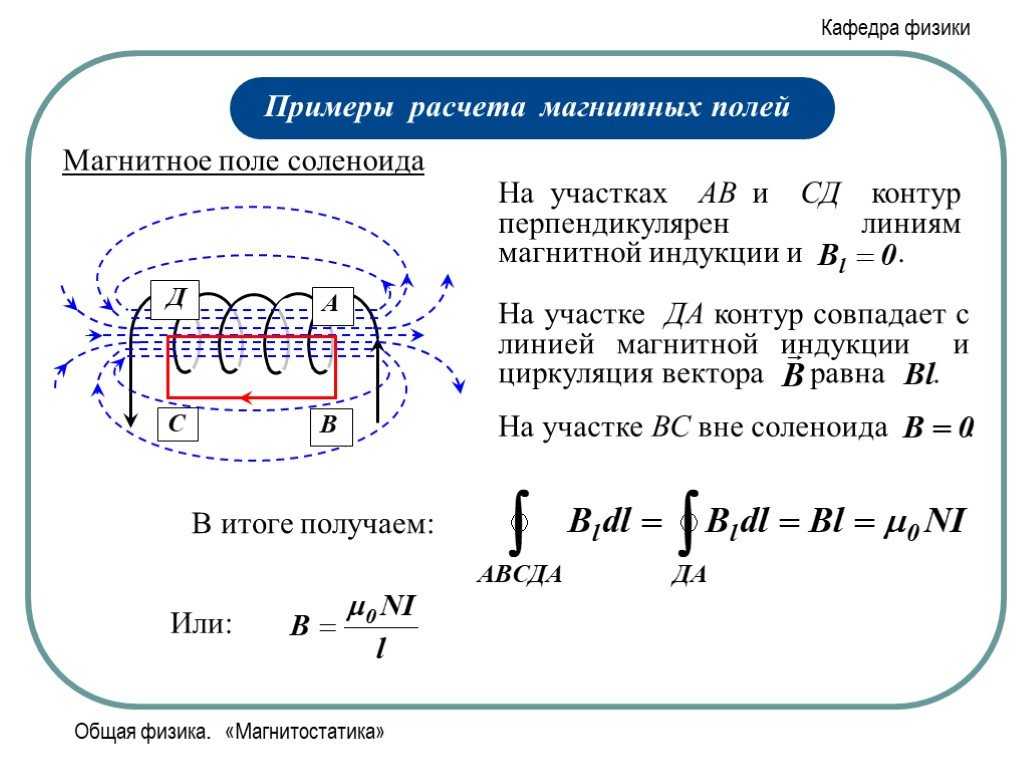 26.Катушку индуктивностью L = 0,6 Гн подключают к источнику тока. Определить сопротивление катушки R, если за время t = 3 с сила тока I через катушку достигает 80% предельного значения.
26.Катушку индуктивностью L = 0,6 Гн подключают к источнику тока. Определить сопротивление катушки R, если за время t = 3 с сила тока I через катушку достигает 80% предельного значения.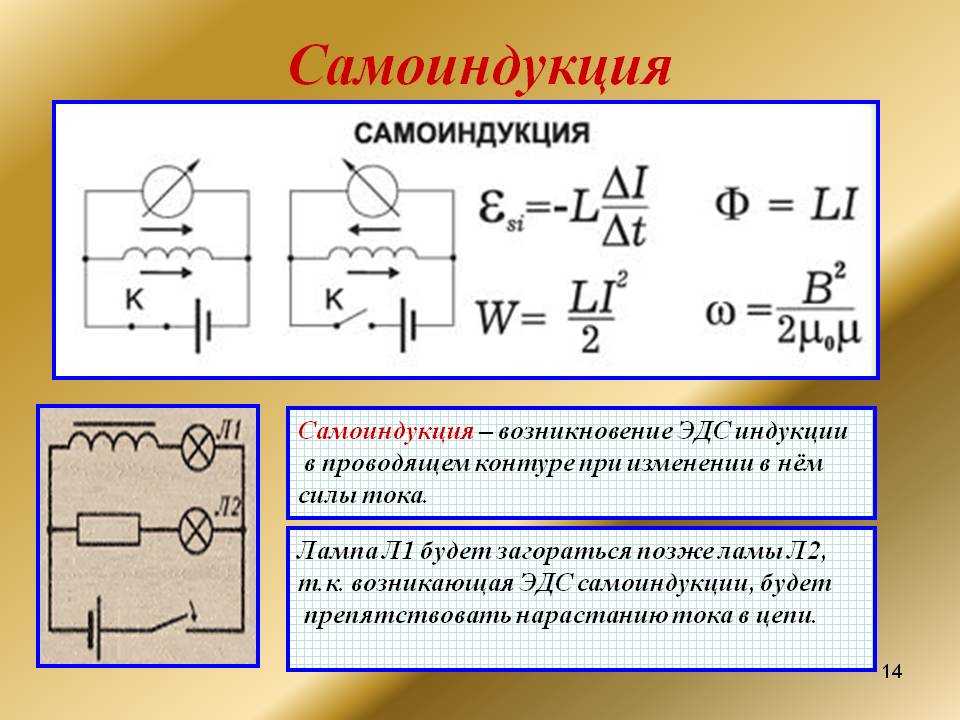 До размыкания в цепи шёл ток А.
До размыкания в цепи шёл ток А. Определить э. д. с. индукции, возникающую в рамке в момент времени t = 5 с. Ответ: 64 мВ.
Определить э. д. с. индукции, возникающую в рамке в момент времени t = 5 с. Ответ: 64 мВ.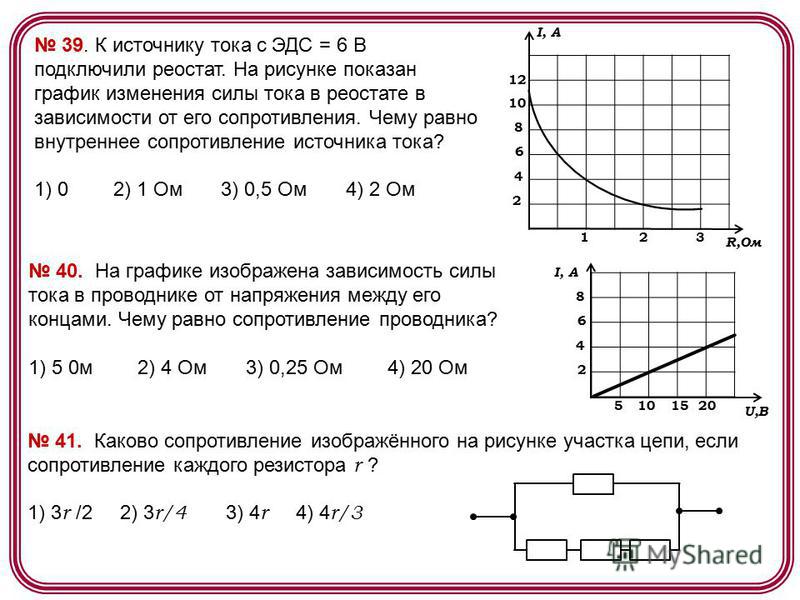 Ответ: 0,45 В.
Ответ: 0,45 В.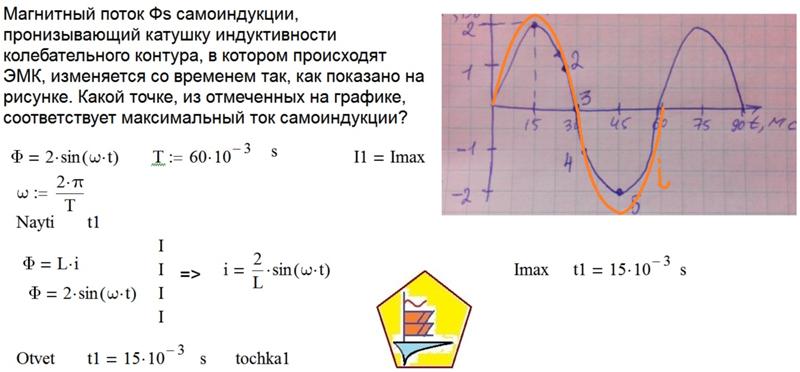 Определить э. д. с. индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Ответ: 0,4 В.
Определить э. д. с. индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Ответ: 0,4 В.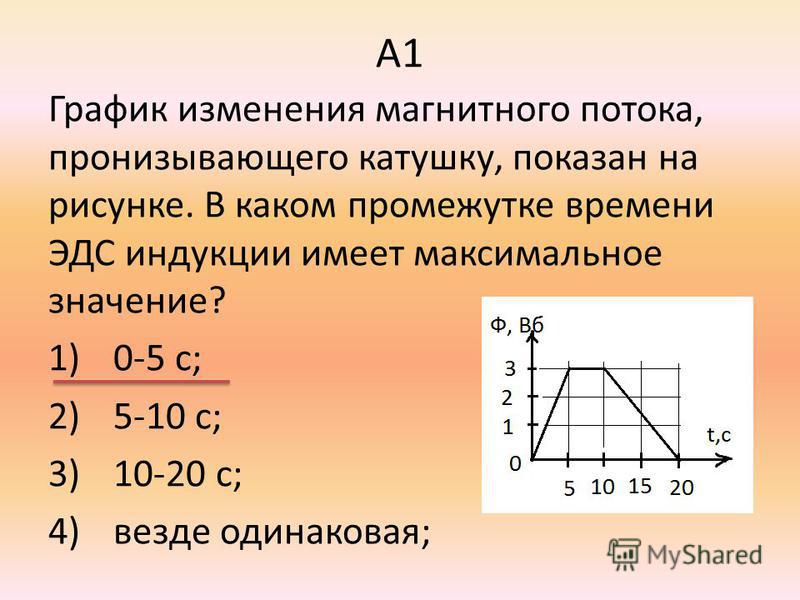 Ротор имеет 140 витков (площадь каждого витка S = 500 см2). Определить частоту вращения якоря, если максимальное значение э.д.с. индукции равно 220 В. Ответ: 5 с-1.
Ротор имеет 140 витков (площадь каждого витка S = 500 см2). Определить частоту вращения якоря, если максимальное значение э.д.с. индукции равно 220 В. Ответ: 5 с-1. Определить: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь ее поперечного сечения. Ответ: 1) 197 мкГн; 2) 985 нВб.
Определить: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь ее поперечного сечения. Ответ: 1) 197 мкГн; 2) 985 нВб. Индуктивность соленоида, намотанного в один слой на немагнитный каркас, L = 1,6мГн. Длина соленоида l = 1 м, сечение S = 20 см2. Сколько витков приходится на каждый сантиметр длины соленоида? Ответ: 8 см2.
Индуктивность соленоида, намотанного в один слой на немагнитный каркас, L = 1,6мГн. Длина соленоида l = 1 м, сечение S = 20 см2. Сколько витков приходится на каждый сантиметр длины соленоида? Ответ: 8 см2. д. с. самоиндукции <Es>, возникающую в соленоиде, если изменение силы тока произошло за 0,1 с. Ответ: 1 В.
д. с. самоиндукции <Es>, возникающую в соленоиде, если изменение силы тока произошло за 0,1 с. Ответ: 1 В. Плотность и удельное сопротивление алюминия равны соответственно ρ = 2,7 г/см3 и ρ’ = 26 нОм·м. Ответ: 712 мкс.
Плотность и удельное сопротивление алюминия равны соответственно ρ = 2,7 г/см3 и ρ’ = 26 нОм·м. Ответ: 712 мкс. 29.Трансформатор с коэффициентом трансформации 0,15 понижает напряжение с 220 до 6 В. При этом сила тока во вторичной обмотке равна 6 А. Пренебрегая потерями энергии в первичной обмотке, определить сопротивление вторичной обмотки трансформатора Ответ: 4,5 Ом.
29.Трансформатор с коэффициентом трансформации 0,15 понижает напряжение с 220 до 6 В. При этом сила тока во вторичной обмотке равна 6 А. Пренебрегая потерями энергии в первичной обмотке, определить сопротивление вторичной обмотки трансформатора Ответ: 4,5 Ом. Ответ: 111.
Ответ: 111. Определить силу тока в соленоиде, при которой объемная плотность энергии магнитного поля внутри соленоида равна 0,1 Дж/м3. Ответ: 1 А.
Определить силу тока в соленоиде, при которой объемная плотность энергии магнитного поля внутри соленоида равна 0,1 Дж/м3. Ответ: 1 А.