Смешанное соединение проводников. Расчёт электрических цепей 8 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

На прошлых уроках мы рассмотрели электрические цепи только с последовательным или только с параллельным соединением проводников. Но существуют такие цепи, в которых присутствует как параллельное, так и последовательное соединение. Этот урок посвящён рассмотрению таких цепей со смешанным соединением проводников, а также расчёту различных электрических цепей.

 

 

Повторение. Факты про последовательное и параллельное соединение проводников.

 

 

1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:

 

 

2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:

 

3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:

 

4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:

 

5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:

 

6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:

 

 

Задача 1

 

 

Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.

 

Дано: ;

Найти: , , ,

Решение

Рис. 1. Иллюстрация к задаче

На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.

Проводимость участка цепи, состоящего из ламп 2 и 3, равна:

 

Следовательно, сопротивление этого участка равно:

 

Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:

 

Согласно закону Ома, сила тока всей цепи равна:

 

Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:

 

Необходимо найти силу тока на лампах 2 и 3.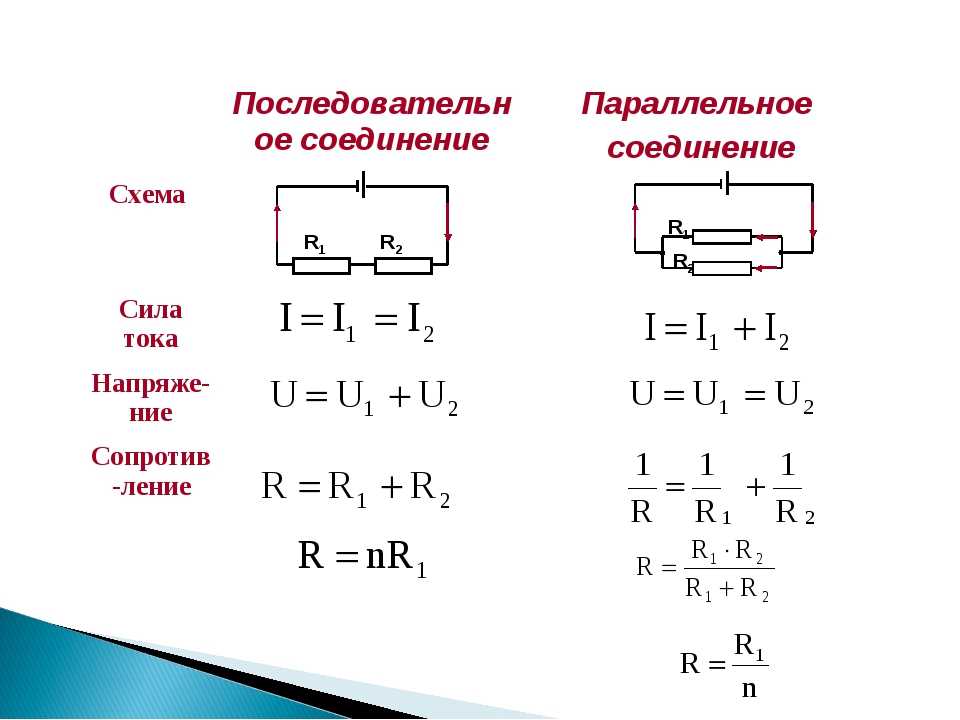 Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:

 

Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:

 

Отсюда сила тока в каждой лампе равна:

 

 

Ответ:  ;

 

Задача 2

 

 

Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.

 

Дано: ; ; ;

Найти: , ,

Решение

Рис. 2. Иллюстрация к задаче

Через резистор  течёт такой же ток, как и через весь участок (), следовательно, согласно закону Ома:

 

То есть для нахождения  нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором , другая часть с резисторами :

 

Резистор  соединён параллельно резисторам  и , следовательно:

 

Резисторы  и  соединены последовательно, поэтому:

 

 

 

Следовательно, сопротивление всей цепи равно:

 

Подставим данное значение в формулу для нахождения тока в резисторе :

 

Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:

 

Отсюда:

 

 

 

При последовательном соединении силы тока одинаковы, поэтому:

 

Получили систему уравнений:

 

Решив эту систему получим, что:

 

 

Так как  и  соединены последовательно:

 

Напряжение на резисторе  равно:

 

Ответ: ;  ;

 

Задача 3

 

 

Найдите полное сопротивление цепи (см.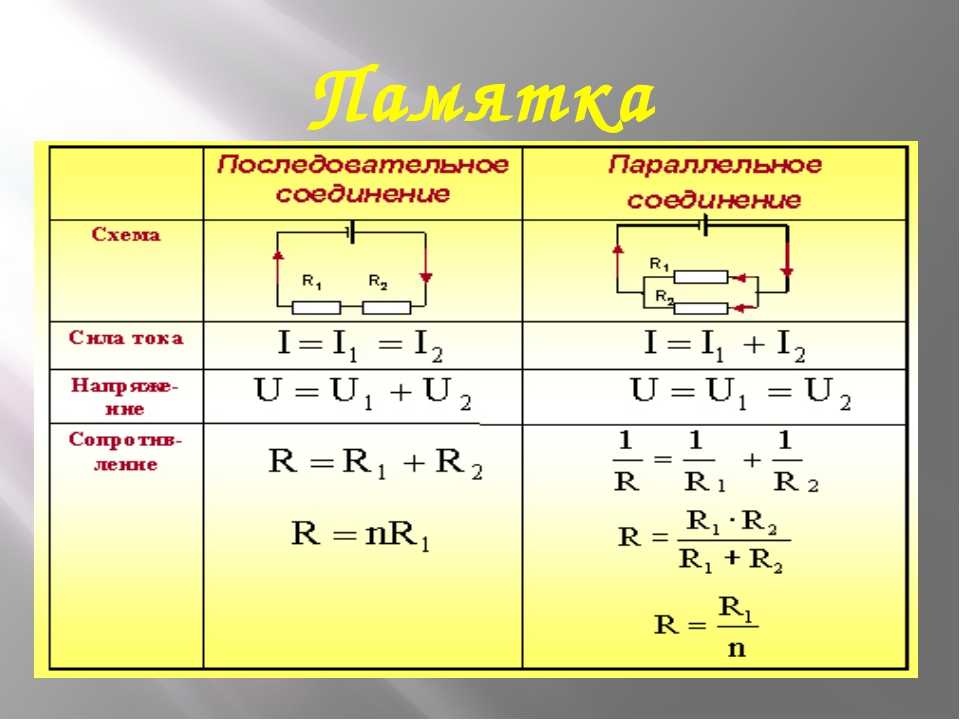 рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.

 

Дано: ; ; ;

Найти: , , , , , ;

Решение

Рис. 3. Иллюстрация к задаче

Резисторы , ,  соединены последовательно, поэтому сопротивление на этом участке равно:

 

Резистор  подключён параллельно участку с резисторами , , , поэтому сопротивление на участке с резисторами ,, ,  равно:

 

Резисторы  и  соединены с участком цепи с резисторами ,, ,  последовательно, то есть общее сопротивление цепи равно:

 

Через резистор  и   () неразветвлённой цепи течёт весь ток цепи, поэтому:

 

По закону Ома этот ток равен:

 

Общее напряжение цепи будет состоять из напряжений , так как ,,  соединены последовательно (, потому что  и  параллельны):

 

 

Согласно закону Ома:

 

Резисторы , ,  соединены последовательно, следовательно:

 

Ответ: ; ; ; 

 

---

Задача на бесконечную электрическую цепь

Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.

Рис. 4. Иллюстрация к задаче

Решение

Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов  и , не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена , тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. рис. 5) и записать для неё уравнение.

Рис. 5. Иллюстрация к задаче

 

 

Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:

 

Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи . То есть резистор с малым сопротивление  практически закоротит всю последующую бесконечную цепь.

Ответ: 

---

 

---

Задача из ЕГЭ

Сопротивление каждого резистора в цепи (см.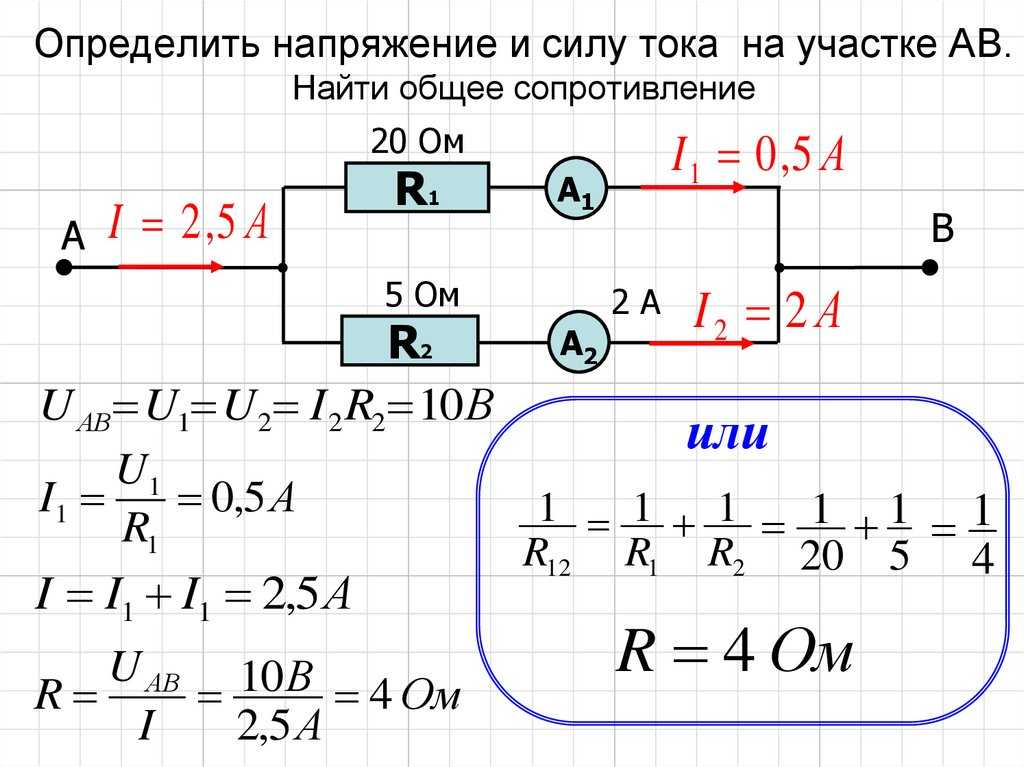 рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами A и B. Напряжение на резисторе  равно 12 В. Найти напряжение между выводами схемы на участке A–B (варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В).

Дано: ;

Найти:

Решение

Рис. 6. Иллюстрация к задаче

Резисторы  расположены последовательно, значит, силы тока на этих резисторах равны:

 

Так как, по условию, , то и напряжения на этих резисторах будут равны:

 

Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:

 

Так как участок с резисторами  соединён с участком с резисторами  параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:

 

Ответ: г) 36 В

Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.

---

 

 

Итоги урока

 

 

На этом уроке мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.

 

 

Список литературы

1. Генденштейн Л. Э, Кайдалов А. Б., Кожевников В. Б. / Под ред. Орлова В. А., Ройзена И. И. Физика 8. – М.: Мнемозина.
2. Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
3. Фадеева А. А., Засов А. В., Киселев Д. Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «school56.pips.ru» (Источник)
2. Интернет-портал «clck.ru» (Источник)
3. Интернет-портал «clck.ru» (Источник)

 

Домашнее задание

1. П. 49, стр. 117, задание 23 (5). Перышкин А. В. Физика 8. – М. : Дрофа, 2010.
2. Участок электрической цепи состоит из трех сопротивлений: ; ;  (см. рис. 7). Определите показания вольтметров  и амперметров , если амперметр  показывает силу тока 2 А.

   Рис. 7. Иллюстрация к задаче (Источник)

3. Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?

 

Цепи . Популярная физика. От архимедова рычага до квантовой механики

Допустим, что ток пропустили через проводник сопротивлением (R) в 100 Ом. Далее его пропустили через проводник сопротивлением (R’) в 50 Ом, а затем сопротивлением (R») в 30 Ом. Назовем эти этапы «сопротивлениями» и для простоты допустим, что сопротивления других проводников, помимо трех вышеназванных, маловажны и могут быть опущены.

Вышеуказанные сопротивления являются последовательными: ток должен пройти сначала первый, потом второй, а затем и третий этап сопротивления. Очевидно, что в конечном счете ток прошел через общее сопротивление в 100 + 50 + 30, или 180 Ом. Каждый раз, когда ток проходит через этапы, соединенные одной цепью, общее сопротивление будет равным сумме всех поэтапных сопротивлений.

Если в наших домашних электрических сетях ток имеет разность потенциалов в 120 вольт и мы допустим, что ток должен будет пройти только через сопротивления

R, R’ и R», то при помощи закона Ома мы сможем высчитать силу тока, проходящего через сопротивления. Общее сопротивление равно 180 Ом, и, следуя формуле I = ER, вычисляем, что сила тока равна 120 В, разделенным на 180 Ом, следовательно, ²/₃ ампера. Весь ток проходит через все сопротивления, поэтому его сила на всем протяжении системы остается неизменной.

Закон Ома может быть применен как к части системы, так и ко всей системе. Какова, к примеру, разность потенциалов на первом из трех этапов системы, обозначенном R? Его сопротивление задано как 100 Ом, а его вычисленная нами для этого участка (как и для всех остальных) сила тока равна

2/₃ ампера. По закону Ома Е = IR, так что разность потенциалов на первом участке будет равна 100 Ом умножить на ²/₃ ампера, следовательно, 66²/₃ вольта. На втором сопротивлении, обозначенном как R’ она будет равна 50 Ом умножить на ²/₃ ампера, следовательно, 33¹/₃ вольта. На третьем сопротивлении, обозначенном как R», будет равна 30 Ом умножить на ²/₃ ампера, следовательно, 20 вольт. Общая разность потенциалов будет равна 66²/₃ + 33¹/₃ + 20, следовательно, 120 вольт[103]. Общая разность потенциалов в цепи равна сумме разности потенциалов всех участков цепи.

Допустим, что к цепи добавили четвертый участок сопротивления, скажем в 60 000 000 000 000 Ом. Другие сопротивления по сравнению с этим настолько малозначительны, что их можно будет игнорировать. Сила тока будет равна 120 вольтам, поделенным на 60 триллионов Ом, следовательно — две триллионных ампера.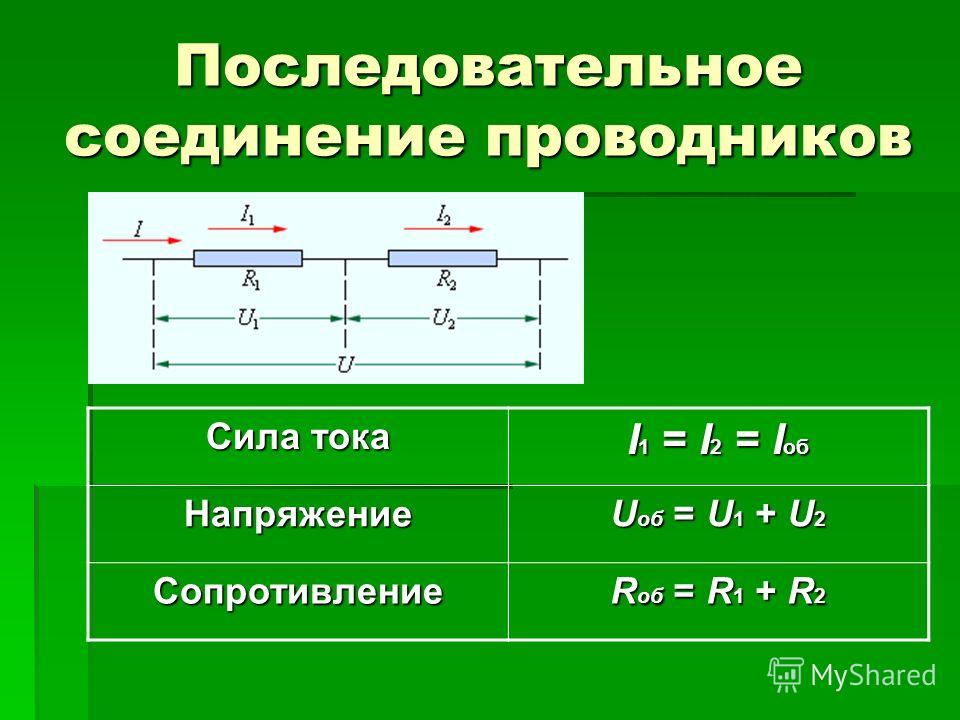 Эта сила настолько мала, что с таким же успехом можно говорить об отсутствии тока вообще.

Если два проводника разделить воздушной пробкой, то движение тока прекратится, так как у воздуха очень высокая сопротивляемость. Для непрерывного движения тока требуется, чтобы между проводниками не было значительных прослоек воздуха. Электрический ток должен передвигаться по непрерывному пласту проводящих материалов от одного полюса аккумулятора (или другого источника электричества) к другому полюсу. Электрический ток, покинув аккумулятор, должен по кругу вернуться к нему, это называется электрической цепью.

Если в последовательно соединенной цепи возникает воздушная пробка, появляется высокое сопротивление и ток практически пропадает. Такая цепь называется «разомкнутой», или «разорванной». Если же воздушная пробка устраняется, то электрический ток возобновляет свое движение и цепь называется «замкнутой»[104]. Электрические розетки в стенах не передают электрического тока, если в них не вставить штепсель, потому что между двумя «порталами» существует воздушная пробка.

Однако она исчезает, когда в розетку вставляют штепсель. Тем не менее в электрических приборах имеется своя воздушная пробка, так что сразу после подключения к электрической цепи электрический ток не поступает. Только после того как повернуть переключатель или нажать кнопку на приборе, эта вторая воздушная пробка исчезает и электрический ток начинает циркулировать.

Иногда желательно, чтобы воздушная пробка возникала мгновенно. Существуют некоторые условия, когда сила тока в той или иной цепи может возрасти до нежелательного уровня. При возрастании силы тока уровень расхода энергии и соответственно уровень нагревания возрастают пропорционально квадрату силы тока (см. уравнение 11.8). Тепло может повредить электрический прибор или положить начало пожару в доме.

Для того чтобы это предотвратить, обычно в цепи вставляют пластину низкоплавкого сплава. Устройство, содержащее подобный сплав, называется «плавким предохранителем».

В том случае, если сила тока превышает предел, указанный на предохранителе (обычно в бытовых приборах этот предел составляет 15 ампер), то уровень тепла возрастает и пластина начинает плавиться, что приводит к возникновению воздушной пробки, и цепь разрывается. Электрический ток в цепи можно возобновить только после замены предохранителя. Разумеется, если предохранитель сгорает неоднократно, то разумнее всего проверить всю цепь и выявить неполадки.

Когда в сети последовательно соединены несколько объектов, то один и тот же электрический ток, проходя в цепи первый объект, затем проходит по очереди и все остальные. Тем не менее ток может проходить из пункта А в пункт В и другими путями, которые могут быть, например, соединены отдельно тремя разными сопротивлениями

R (100 Ом), R’ (50 Ом), R” (30 Ом). Ток протекает в соответствии с разностью потенциалов между пунктами А и В, и она должна быть одной и той же независимо от того, каким путем идет электрический ток. (Например, при перемещении внутри здания с 12-го этажа на 10-й изменение гравитационного потенциала на протяжении двух этажей будет постоянной — не важно, спускаться ли на лифте, по лестнице или по веревке.)

Так как обычно эти три сопротивления на схемах изображаются параллельно, то соединение называется

параллельным. Касательно параллельной электрической цепи можно сказать, что разность потенциалов всегда постоянна на каждом ее этапе.

Достаточно легко вычислить силу тока в каждом из участков с разными сопротивлениями, так как разность потенциалов и сопротивления нам известна. Если в бытовых домашних электросетях разность потенциалов равна 120 вольт, то, значит, такова же и разность потенциалов каждого из параллельных участков. Поскольку по закону Ома I = E/R, сила тока на первом участке равна 120/100, или 1,2 ампера, на втором — 120/50, или 2,4 ампера, и на третьем — 120/30, или 4 ампера.

Видно, что существует обратная связь между силой тока и сопротивлением на объектах в параллельной цепи. Так как противоположностью сопротивления является проводимость (С= 1/R), то можно сказать, что сила тока в параллельно соединенных объектах прямо пропорциональна их проводимости.

Представим, что точки А и В соединены очень длинной, компактно смотанной проволокой, настолько компактно, что эти точки разделяют одновременно и несколько метров проволоки, и 1 см воздуха. Можно считать, что проволока и воздух являются частями параллельной цепи. Таким образом, ток может поступать или через проволоку, или через небольшой слой воздуха. Однако сопротивление воздуха гораздо больше, чем проволоки, и через воздух проходит лишь минимальное количество тока. Практически весь электрический ток проходит через проволоку.

Если же слой воздуха уменьшить, то общее сопротивление воздушной пробки между пунктами А и В понизится и в ней будет обнаруживаться ток все большей и большей силы. По пути ток выбивает электроны из атомов воздуха, повышая тем самым способность воздуха проводить электричество при помощи электронов и положительно заряженных ионов, которые электроны оставляют после себя. В результате сопротивление воздушной пробки понижается еще дальше.

В один переломный момент этот порочный круг, в котором ток создает все больше ионов, вызывающих все больший ток, приводит к тому, что через воздух проходит ток в больших количествах, с искрами и треском, которые и привлекли такое внимание к лейденской банке (см. гл. 10). Так как ток выбрал наикратчайший путь из пункта А в В, данное явление назвали коротким замыканием. По проволоке и другим предметам из пункта А в пункт В ток больше не идет, и электричество в цепи пропадает.

При коротком замыкании, когда значительная часть прежней цепи выходит из строя, происходит внезапное снижение общего сопротивления в цепи. Сопротивление в искрящейся воздушной пробке очень низкое, возможно, даже ниже, чем в проволоке и других приборах цепи. В остатке цепи сила тока значительно возрастает, что приводит к увеличенному нагреву. В лучшем случае должен выйти из строя один из предохранителей, в худшем — искры в конце концов подожгут любой воспламеняющийся предмет, находящийся поблизости, что может привести к пожару.

Для снижения вероятности коротких замыканий обычно проволоку окружают изоляционным материалом: шелком, резиной, пластмассой и т. д. У этих веществ не только сопротивление выше, чем у воздуха, но и, будучи твердыми телами, они всегда разделяют две разные проволоки (даже если эти проволоки крепко прижимают друг к другу). Однако изоляция может изнашиваться, и тогда снова появляется опасность коротких замыканий.

Возвращаясь к нашим трем участкам с разными сопротивлениями в параллельной сети, зададимся вопросом: каково же общее сопротивление системы? Известно, что общая сила тока в цепи равна сумме сил тока на каждом ее участке. В нашем примере общая сила тока в цепи будет 1,2 + 2,4 + 4,0 = 7,6 ампера. Разность потенциалов между точками А и В параллельной цепи — 120 вольт. Следуя закону Ома R = E/I, общее сопротивление будет равно 120 вольтам, поделенным на общую силу тока в 7,6 ампера. Следовательно, общее сопротивление равно 120/7,6, т. е. чуть менее 16 Ом.

Следует обратить внимание, что общее сопротивление меньше каждого из трех взятых по отдельности сопротивлений отдельных участков. Для того чтобы понять, почему так происходит, следует рассмотреть закон Ома R = E/I применительно к параллельной цепи. R обозначает общее сопротивление, I — общую силу тока, а E остается неизменной независимо от того, взят один объект или несколько. Сила тока равна сумме сил тока на каждом отдельном отрезке цепи (I, I’ и I»). Следовательно:

R_i = E/(I + I’ + I»). (Уравнение 11.9)

Обратив это выражение, получим:

1/R_i = (I + I’ + I»)/E. Уравнение (11.10)

Согласно закону Ома, I/Е должно равняться 1/R, I’/E — равняться 1/R’ и I»/Е — равняться 1/R», индивидуальным сопротивлениям объектов параллельной цепи. Таким образом:

1/R_i = 1/R + 1/R’ + 1/R». (Уравнение 11.11)

Поговорим об обратных соотношениях в уравнении 11.11. Можно сказать, к примеру, что обратное отношение общего сопротивления равняется сумме обратных отношений отдельных сопротивлений. Выходит так, что чем меньше величина, тем больше обратная ей, и наоборот. (Например, число 11 больше, чем 3, а ¹/₁₁ меньше, чем ¹/₃) Таким образом, исходя из того, что обратное соотношение общего сопротивления (1/R_i) равняется сумме обратных соотношений каждого сопротивления в отдельности и соответственно превосходит каждое из них в отдельности, общее сопротивление (R_i), как таковое, должно быть меньше каждого отдельно взятого сопротивления.

Важным свойством параллельных цепей является следующее: если в параллельной цепи произошел разрыв, то электричество исчезает только в том отрезке, где это случилось. Ток продолжает поступать из пункта А в пункт В по оставшимся отрезкам цепи. При параллельных цепях можно, например, пользоваться одной розеткой, в то время как другие остаются разомкнутыми. А если в параллельной цепи перегорает лампочка (в месте разрыва перегоревшей нити накала получается воздушная пробка), то другие лампочки продолжают гореть.

Видео с вопросами: Расчет полного тока в комбинированной цепи

Стенограмма видео

Найдите общий ток в схема показана. Дайте ответ с точностью до одной запятой место.

В этом вопросе у нас есть схема который содержит как последовательные, так и параллельные комбинации резисторов. Мы хотим рассчитать общую ток в цепи. Мы начнем с нахождения эквивалентное сопротивление цепи.

Сначала перерисуем схему чтобы мы могли более четко видеть, как все компоненты связаны. Если сравнить эту схему с показанный в вопросе, мы видим, что они эквивалентны. Резисторы 3,5 Ом и 1,8 Ом соединены последовательно друг с другом, а резистор сопротивлением 1,2 Ом включен в параллельно им обоим. Резистор 6,5 Ом подключен последовательно к параллельной комбинации трех других резисторов. Мы также пометили резисторы 𝑅 один к 𝑅 четырем, чтобы упростить наши расчеты. Чтобы найти эквивалентное сопротивление схемы, нам просто нужно вычислить общее сопротивление, обеспечиваемое этим комбинация резисторов.

Первый шаг расчета эквивалентное сопротивление цепи заключается в том, чтобы найти эквивалентное сопротивление резисторы 𝑅 один и 𝑅 два, которые соединены последовательно. Напомним, что для любого числа резисторы последовательно, общее сопротивление, 𝑅 общее, равно 𝑅 один плюс 𝑅 два плюс точка точка точка плюс 𝑅 под 𝑁. Можем заменить резисторы 𝑅 один и 𝑅 два с эквивалентным резистором 𝑅 сабвуфер 𝐴 с сопротивлением 𝑅 сабвуфер 𝐴 равен 𝑅 одному плюс 𝑅 два. Подставляя значения для резисторов 𝑅 один равен 3,5 Ом и 𝑅 два равен 1,8 Ом, находим, что 𝑅 sub 𝐴 равно 𝑅 один плюс 𝑅 два равно 3,5 Ом плюс 1,8 Ом равно 5,3 Ом. Теперь мы можем видеть два резистора 𝑅 sub 𝐴 и 𝑅 три, которые соединены параллельно.

Напомним, что для любого количества резисторов, соединенных параллельно, общее сопротивление, 𝑅 total, равно обратной величине количество один больше 𝑅 один плюс один больше 𝑅 два плюс и так далее плюс один больше 𝑅 саб 𝑁. Итак, мы можем заменить резисторы 𝑅 sub 𝐴 и 𝑅 три с эквивалентным резистором 𝑅 sub 𝐵 ​​с сопротивлением, заданным 𝑅 sub 𝐵 ​​равно обратному количеству на единицу больше 𝑅 sub 𝐴 плюс единица больше 𝑅 три. Подставив значения 𝑅 sub 𝐴 равно 5,3 Ом, а 𝑅 three равно 1,2 Ом, мы находим, что 𝑅 sub 𝐵 ​​равно количество, обратное числу один на 𝑅 под 𝐴 плюс один на 𝑅 три равно обратно величине один больше 5,3 Ом плюс один больше 1,2 Ом, что к трем десятичных разрядов, 0,978 Ом.

Наконец, у нас есть два резистора 𝑅 сабвуферы 𝐵 и 𝑅 четыре соединены последовательно. Мы можем заменить эти два резистора с эквивалентным резистором 𝑅 sub 𝐶 равно 𝑅 sub 𝐵 ​​плюс 𝑅 четыре. Подставляя значения 𝑅 sub 𝐵 ​​равно 0,978 Ом, а 𝑅 четыре равно 6,5 Ом, мы получаем 𝑅 sub 𝐶 равно 0,978 Ом плюс 6,5 Ом равно 7,478 Ом. Резистор 𝑅 sub 𝐶 имеет эквивалентное сопротивление четырех резисторов, первоначально показанных в вопросе. Теперь мы можем использовать закон Ома для одиночный резистор 𝑅 sub 𝐶, чтобы найти значение тока.

Напомним, что закон Ома может быть записывается как 𝑉 равно 𝐼 умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, а 𝑅 — сопротивление. Здесь нам интересно найти ток, поэтому нам нужно изменить это уравнение, чтобы сделать 𝐼 субъектом. Для этого мы просто делим оба сторон на 𝑅, чтобы 𝐼 равнялось 𝑉 больше 𝑅. Нам дана клетка, которая обеспечивает разность потенциалов 14 вольт в цепи. Подставляя это значение и значение сопротивления, которое мы только что рассчитали, мы можем использовать закон Ома, чтобы найти, что ток через одиночный резистор 𝑅 sub 𝐶 равен 𝐼 равен 𝑉, деленный на 𝑅 sub 𝐶 равно 14 вольт, деленное на 7,478 Ом, равно 1,87204 и т. д. ампер.

Ток везде одинаковый последовательная цепь, поэтому ток, который мы рассчитали через одиночный резистор, равен равно полному току через эквивалентную цепь. Поскольку эквивалентная схема имеет того же полного сопротивления, что и исходная цепь, которую нам дали, этот ток должен также равен полному току в исходной цепи.

Последнее, что нам нужно сделать этот вопрос должен дать ответ до одного десятичного знака. Мы возьмем числа перед десятичного знака и два числа после запятой, чтобы получить 1,87 ампер. Затем смотрим на второе число после запятой, чтобы увидеть, нужно ли нам округлить в меньшую или большую сторону. Мы видим, что второе число после десятичный знак равен семи, поэтому мы можем округлить это число, что дает ответ 1,9ампер. Следовательно, полный ток через цепь 1,9 ампера.

Определение полного тока | PVEducation

Обзор

1. Суммарный ток можно определить только в предположении, что он постоянен на расстоянии от солнечного элемента, если нет контакта для ввода или вывода носителей и если элемент работает в установившемся режиме.
2. Ток в области I и II известен, но переменная расстояния для этих двух областей различна. Поэтому мы должны принять это во внимание, прежде чем вычислять общий ток.
3. Суммарный ток = ток на краях обедненной области (ток в области I и области II после учета разницы переменных расстояния).

Чтобы найти полный ток, заметим, что ОБЩИЙ ток в устройстве должен быть постоянным, не зависящим от расстояния до тех пор, пока нет контакта, который может извлекать или вводить носители, и пока устройство находится в установившемся режиме. Это можно показать с помощью:

 

вверх)

Поскольку каждый электрон генерирует отверстие, и каждый рекомбинирующий электрон также использует отверстие, U _N = U _P и G _N = G _P G _P . производная от J _T равна 0, а J _T является константой. Физически уравнение непрерывности утверждает, что общее количество электронов и дырок в полупроводнике не может измениться (в стационарном состоянии), и, следовательно, общий ток также не может измениться. Поэтому, если мы найдем J _T в любом месте устройства, мы нашли его повсюду в устройстве. Полный ток удобнее всего находить на краях областей обеднения. Поскольку мы знаем токи в Областях I и III, для расчета полного тока нам нужно сделать две вещи. (1) Учтите тот факт, что переменная расстояния x не одинакова в области I и области III, и (2) найдите ток на краях обедненной области.

Сделать переменную расстояния одинаковой

В наших решениях переменная расстояния x в приведенных выше уравнениях обычно не одинакова для разных областей устройства. Как правило, мы определяем x в области I (здесь область p-типа с током неосновных электронных носителей) как расстояние от края обедненной области и увеличивающееся далее в область I. Другая переменная расстояния x определяется как ноль. на другом краю области обеднения и увеличивается в область III (здесь материал n-типа с током неосновных носителей дырок). Используя эти определения, уравнения переноса имеют вид:

и

Поскольку x = — x ‘ — Вт ,

и тогда ток становится или

Раньше ток в области истощения был равен нулю и мы заявили

количество свободных носителей было небольшим, поэтому рекомбинацией в обедненной области также можно было пренебречь.