Смешанное соединение проводников. Расчёт электрических цепей 8 класс онлайн-подготовка на Ростелеком Лицей
Введение
На прошлых уроках мы рассмотрели электрические цепи только с последовательным или только с параллельным соединением проводников. Но существуют такие цепи, в которых присутствует как параллельное, так и последовательное соединение. Этот урок посвящён рассмотрению таких цепей со смешанным соединением проводников, а также расчёту различных электрических цепей.
Повторение. Факты про последовательное и параллельное соединение проводников.
1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:
2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:
3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:
4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:
5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:
6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:
Задача 1
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.
Дано: ;
Найти: , , ,
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.
Проводимость участка цепи, состоящего из ламп 2 и 3, равна:
Следовательно, сопротивление этого участка равно:
Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:
Согласно закону Ома, сила тока всей цепи равна:
Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:
Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:
Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:
Отсюда сила тока в каждой лампе равна:
Ответ: ;
Задача 2
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.
Дано: ; ; ;
Найти: , ,
Решение
Рис. 2. Иллюстрация к задаче
Через резистор течёт такой же ток, как и через весь участок (), следовательно, согласно закону Ома:
То есть для нахождения нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором , другая часть с резисторами :
Резистор соединён параллельно резисторам и , следовательно:
Резисторы и соединены последовательно, поэтому:
Следовательно, сопротивление всей цепи равно:
Подставим данное значение в формулу для нахождения тока в резисторе :
Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:
Отсюда:
При последовательном соединении силы тока одинаковы, поэтому:
Получили систему уравнений:
Решив эту систему получим, что:
Так как и соединены последовательно:
Напряжение на резисторе равно:
Ответ: ; ;
Задача 3
Найдите полное сопротивление цепи (см.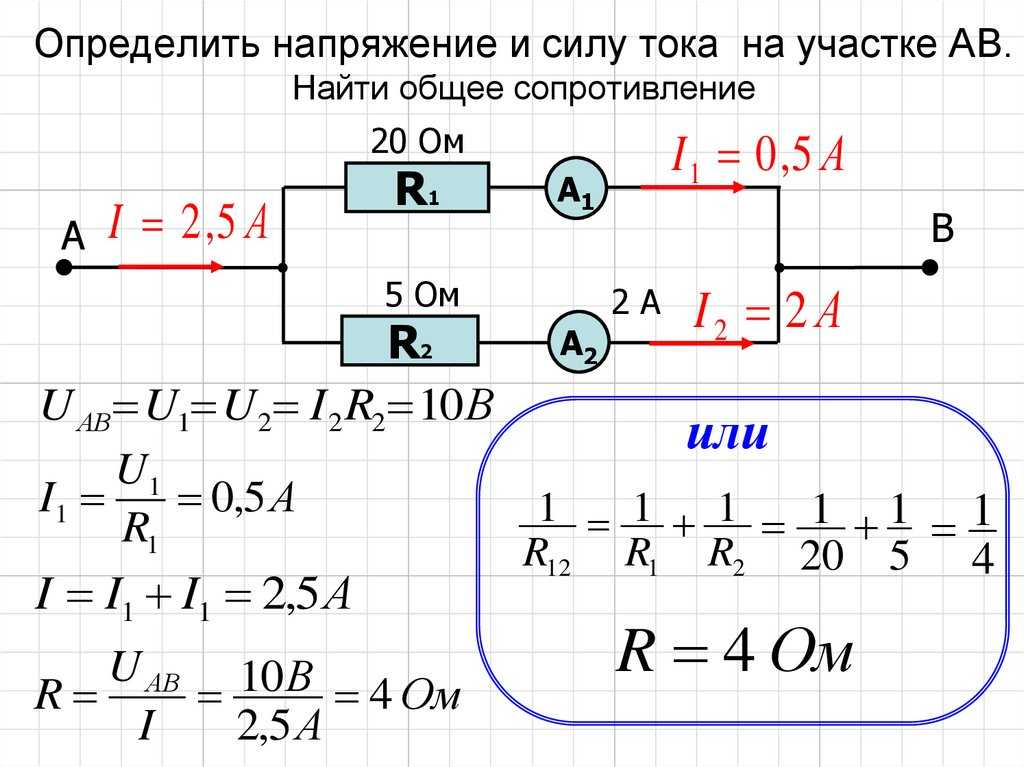 рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.
Дано: ; ; ;
Найти: , , , , , ;
Решение
Рис. 3. Иллюстрация к задаче
Резисторы , , соединены последовательно, поэтому сопротивление на этом участке равно:
Резистор подключён параллельно участку с резисторами , , , поэтому сопротивление на участке с резисторами ,, , равно:
Резисторы и соединены с участком цепи с резисторами ,, , последовательно, то есть общее сопротивление цепи равно:
Через резистор и () неразветвлённой цепи течёт весь ток цепи, поэтому:
По закону Ома этот ток равен:
Общее напряжение цепи будет состоять из напряжений , так как ,, соединены последовательно (, потому что и параллельны):
Согласно закону Ома:
Резисторы , , соединены последовательно, следовательно:
Ответ: ; ; ;
Задача на бесконечную электрическую цепь
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.
Рис. 4. Иллюстрация к задаче
Решение
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов и , не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена , тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. рис. 5) и записать для неё уравнение.
Рис. 5. Иллюстрация к задаче
Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:
Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи . То есть резистор с малым сопротивление практически закоротит всю последующую бесконечную цепь.
Ответ:
Задача из ЕГЭ
Сопротивление каждого резистора в цепи (см. рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами A и B. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B (варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В).
рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами A и B. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B (варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В).
Дано: ;
Найти:
Решение
Рис. 6. Иллюстрация к задаче
Резисторы расположены последовательно, значит, силы тока на этих резисторах равны:
Так как, по условию, , то и напряжения на этих резисторах будут равны:
Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:
Так как участок с резисторами соединён с участком с резисторами параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:
Ответ: г) 36 В
Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.
Итоги урока
На этом уроке мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.
Список литературы
- Генденштейн Л. Э, Кайдалов А. Б., Кожевников В. Б. / Под ред. Орлова В. А., Ройзена И. И. Физика 8. – М.: Мнемозина.
- Перышкин А. В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А. А., Засов А. В., Киселев Д. Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «school56.pips.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
Домашнее задание
- П. 49, стр. 117, задание 23 (5). Перышкин А. В. Физика 8. – М.

- Участок электрической цепи состоит из трех сопротивлений: ; ; (см. рис. 7). Определите показания вольтметров и амперметров , если амперметр показывает силу тока 2 А.
Рис. 7. Иллюстрация к задаче (Источник)
-
Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?
Электрические схемы. Соединение проводников — Умскул Учебник
На этой странице вы узнаете- Нужен ли блендер, чтобы попить чай?
- Куда идет ток?
- Когда “сопротивление бесполезно”?
Всем приготовиться к погружению в мир электрических соединений и схем. Сопротивление бесполезно!
Условное обозначение элементов электрической цепиЕсть история о том, как одного физика-теоретика током ударило. Конечно, в теории он был силен, но знать — одно, а применять знания в жизни — совсем другое дело. Вот и получилось у него всякое, странное. Не советуем повторять: опасно для жизни!
Вот и получилось у него всякое, странное. Не советуем повторять: опасно для жизни!
А с чего вся история началась?
Когда мы говорим об электрических приборах, мы понимаем, что сам по себе прибор работать не будет. Его нужно подключить, к источнику тока. А если схема сложная, в которой несколько приборов? И как изобразить цепь на рисунке? Всеми этими вопросами задался наш герой.
Для решения умные люди придумали условные обозначения, которые уже много лет используются в электромире:
Итак, наш физик-теоретик решил по схеме собрать гирлянду. Всё как положено. Лампочки подобрал все одинаковые. И даже соединения между ними учел.
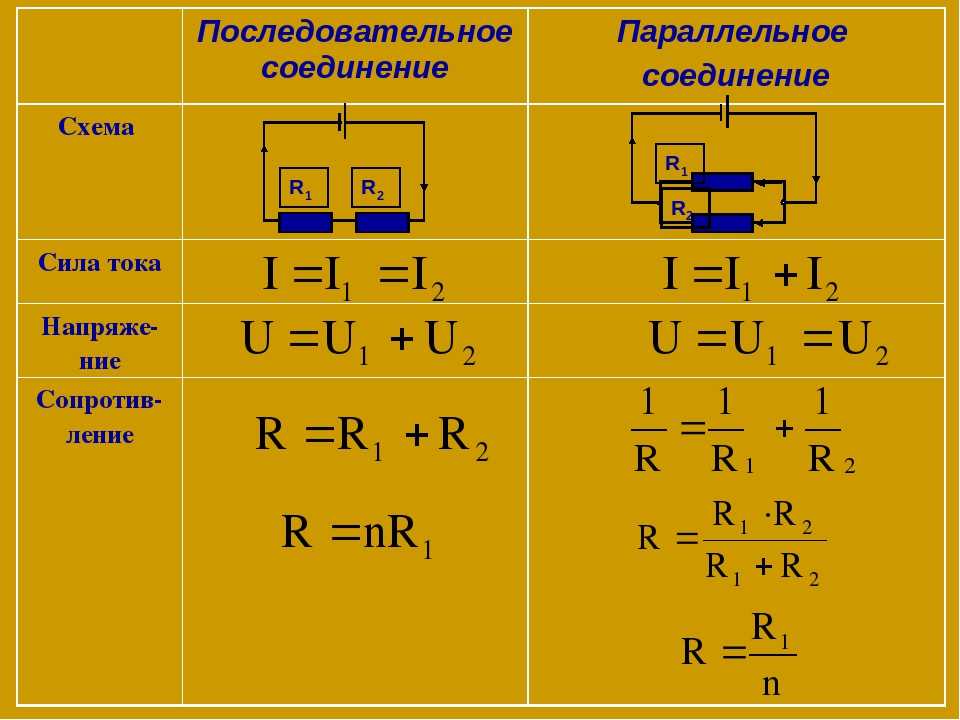
Соединения проводниковПроводники в электрических цепях могут соединяться последовательно и параллельно. Давайте разберем, чем отличаются эти два вида соединений и чем они полезны.
| Последовательное соединение | Параллельное соединение |
Соединение проводников без разветвлений, когда конец одного проводника соединен с началом другого. | Соединение, в котором начала и концы проводников соединены вместе. |
| R1 и R2 — сопротивления проводников, R— общее сопротивление, I1 и I2— сила тока на каждом проводнике, I — общая сила тока, U1 и U2 — напряжение на каждом проводнике, U — общее напряжение цепи. | R1 и R2 — сопротивления проводников, R— общее сопротивление, I1 и I2— сила тока на каждом проводнике, I — общая сила тока, U1 и U2 — напряжение на каждом проводнике, U — общее напряжение цепи. |
Схема последовательного соединения проводников. | Схема параллельного соединения проводников. |
| I1 = I2 = I Сила тока, протекающего через каждый проводник, одна и та же (I = const). | I = I1 + I2 Сила тока, протекающего в неразветвлённой части цепи, равна сумме сил токов, протекающих по каждому из проводников.  |
| U1 = IR1, U2 = IR2; U = U1 + U2 Общее напряжение равно сумме напряжений на отдельных участках цепи. | U1 = I1R1, U2 = I2R2; U = U1 = U2 Напряжение на каждом из проводников одинаково (U = const). |
| R = R1 + R2 Общее сопротивление цепи равно сумме сопротивлений отдельных участков. | \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\) Проводимость равна сумме проводимостей каждого из проводников. |
| \(\frac{U_1}{U_2} = \frac{R_1}{R_2}\) | \(\frac{I_1}{I_2} = \frac{R_2}{R_1}\) |
| Если все сопротивления одинаковы, то: R = nr и U = nu, где r и u — соответственно сопротивление одного элемента и напряжение на нём, | Если все сопротивления одинаковы, то: \(R = \frac{r}{n}\) и U = u, где r и u — соответственно сопротивление одного элемента и напряжение на нём, |
| Общее сопротивление цепи больше наибольшего сопротивления, входящего в эту цепь. | Общее сопротивление цепи меньше наименьшего сопротивления, входящего в эту цепь. |
| Количество теплоты, выделяемое на каждом проводнике, пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_1}{R_2}\) | Количество теплоты, выделяемое на каждом проводнике, обратно пропорционально их сопротивлениям \(\frac{Q_1}{Q_2} = \frac{R_2}{R_1}\) |
| Мощность, выделяемая в проводниках, пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_1}{R_2}\) | Мощность, выделяемая в проводниках, обратно пропорциональна их сопротивлению \(\frac{P_1}{P_2} = \frac{R_2}{R_1}\) |
При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.
Важно учитывать, какие приборы, как подключать. Например, елочная гирлянда является примером последовательного соединения. Если одна лампочка перегорит, то вся гирлянда работать перестанет. Это, кстати, относится к недостаткам такого вида соединения. Наш физик-теоритк был в курсе этой особенности.
Тогда зачем такое соединение нужно?
Когда необходимо целенаправленно подключить какой-то один прибор. Например, карманный фонарик. Он будет работать только тогда, когда включена кнопка.
А вот в люстре лучше использовать параллельное соединение. И когда одна лампочка перегорит, все остальные по-прежнему будут светить.
| Нужен ли блендер, чтобы попить чай? Бытовые приборы на кухне соединены параллельно. Это значит, что чайник может спокойно работать без микроволновки. И чтобы поджарить тосты, блендер включать необязательно. Но если все эти приборы соединить последовательно, защитный выключатель может не выдержать, и произойдет перегрузка. |
Задачи на комбинированное соединение проводников удобно решать, используя эквивалентные схемы.
Смешанное (комбинированное) соединение проводниковКомбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.
| Куда идет ток? Ток не любит напрягаться. Поэтому ток течёт по пути наименьшего сопротивления. |
Рассмотрим пример задачи.
Вопрос: Каким будет сопротивление участка цепи (см. рисунок), если ключ К замкнуть? Каждый из резисторов имеет сопротивление 2R.
Ответ: если ключ К замкнуть, то сопротивление станет равным нулю.
| Когда “Сопротивление бесполезно”? После замыкания ключа участок схемы окажется закороченным; ток пойдёт через ключ, минуя резисторы. |
Что же произошло к нашим физиком-теоретиком? Он даже соединения источников учел. Только забыл он самое главное правило: сначала собери схему, а только потом подключи ее к источнику.
Вот он подключил один конец провода с лампочками к источнику, другой конец взял в руку… И навсегда запомнил технику безопасности при работе c электричеством: не стоит человеку становиться звеном цепи, подключенной к источнику.
Источники тока соединяют между собой для совместного питания всей цепи.
| Последовательное соединение | Параллельное соединение | |
| Схема | ||
| Эквивалентное внутреннее сопротивление | rэ = r1 + r2 | \(\frac{1}{r_э} = \frac{1}{r_1} + \frac{1}{r_2}\) |
| Эквивалентное ЭДС | \(\varepsilon_э = \pm \varepsilon_1 \pm \varepsilon_2\) знаки зависят от направления подключения источников | \(\frac{\varepsilon_э}{r_э} = \pm \frac{\varepsilon_1}{r_1} \pm \frac{\varepsilon_2}{r_2}\) знаки зависят от направления подключения источников |
| Закон Ома для полной цепи | \(I = \frac{\varepsilon_э}{r_э + R}\) | \(I = \frac{\varepsilon_э}{r_э + R}\) |
| Закон Ома для n одинаковых источников | \(I = \frac{n \varepsilon}{R + nr}\) | \(I = \frac{\varepsilon}{R + rn}\) |
Чем отличаются понятия “соединения резисторов” и “соединения источников тока”? Пример резистора — чайник, простой проводник электрического тока. Если чайник подключить параллельно, это никак не повлияет на работу всей цепи. А источник тока — это розетка. Она дает “питание” всей цепи. Без источника тока не будет работать ни один прибор.
Если чайник подключить параллельно, это никак не повлияет на работу всей цепи. А источник тока — это розетка. Она дает “питание” всей цепи. Без источника тока не будет работать ни один прибор.
Важно запомнить правила подключения амперметра и вольтметра. Это необходимо для того, что приборы не перегорели и показывали корректные значения при измерении.
| Амперметр | Вольтметр |
| Амперметр подключается последовательно участку цепи. Соблюдаем полярность: “+” амперметра подключают к “+” источника тока, а “−” подключают к “−” источника тока. | Вольтметр подключается параллельно участку цепи. Соблюдаем полярность: “+” вольтметра подключают к “+” источника тока, а “−” подключают к “−” источника тока. |
Шунт — проводник, присоединяемый параллельно амперметру для увеличения предела его измерений. \(R_ш = \frac{R_A}{n — 1}\), где Rш — сопротивление шунта, | Добавочное сопротивление — проводник, присоединяемый последовательно с вольтметром для увеличения предела его измерений. Rд = RV(n-1), где Rд — добавочное сопротивление, |
Научиться читать электрические схемы важно для любителей электроники. Ведь если правильно ее прочитать, можно спаять что-то интересное, например, карманный фонарик.
Фактчек- Проводники в электрических цепях могут соединяться последовательно и параллельно.
- При последовательном соединении проводников общее сопротивление участка цепи увеличивается, при параллельном соединении — уменьшается.

- Комбинированным называется соединение, при котором некоторые проводники соединены последовательно, а некоторые — параллельно.
- При подключении приборов обязательно нужно учитывать их полярность.
Задание 1.
Какие существуют соединения проводников?
- Последовательное
- Параллельное
- Смешанное
- Все варианты верны
Задание 2.
При последовательном соединении проводников общее сопротивление участка цепи:
- Увеличивается
- Уменьшается
- Не изменяется
Задание 3.
При параллельном соединении проводников общее сопротивление участка цепи:
- Увеличивается
- Уменьшается
- Не изменяется
Задание 4.
Как подключается амперметр в цепи?
- Последовательно
- Параллельно
- Не имеет значения
Задание 5.
Как подключается вольтметр в цепи?
- Последовательно
- Параллельно
- Не имеет значения
Ответы: 1. — 4; 2. — 1; 3. — 2; 4. — 1; 5. — 2
Цепи . Популярная физика. От архимедова рычага до квантовой механики
Допустим, что ток пропустили через проводник сопротивлением (R) в 100 Ом. Далее его пропустили через проводник сопротивлением (R’) в 50 Ом, а затем сопротивлением (R») в 30 Ом. Назовем эти этапы «сопротивлениями» и для простоты допустим, что сопротивления других проводников, помимо трех вышеназванных, маловажны и могут быть опущены.
Вышеуказанные сопротивления являются последовательными: ток должен пройти сначала первый, потом второй, а затем и третий этап сопротивления. Очевидно, что в конечном счете ток прошел через общее сопротивление в 100 + 50 + 30, или 180 Ом. Каждый раз, когда ток проходит через этапы, соединенные одной цепью, общее сопротивление будет равным сумме всех поэтапных сопротивлений.
Если в наших домашних электрических сетях ток имеет разность потенциалов в 120 вольт и мы допустим, что ток должен будет пройти только через сопротивления
Закон Ома может быть применен как к части системы, так и ко всей системе. Какова, к примеру, разность потенциалов на первом из трех этапов системы, обозначенном R? Его сопротивление задано как 100 Ом, а его вычисленная нами для этого участка (как и для всех остальных) сила тока равна  На втором сопротивлении, обозначенном как R’ она будет равна 50 Ом умножить на 2/3 ампера, следовательно, 331/3 вольта. На третьем сопротивлении, обозначенном как R», будет равна 30 Ом умножить на 2/3
На втором сопротивлении, обозначенном как R’ она будет равна 50 Ом умножить на 2/3 ампера, следовательно, 331/3 вольта. На третьем сопротивлении, обозначенном как R», будет равна 30 Ом умножить на 2/3
Допустим, что к цепи добавили четвертый участок сопротивления, скажем в 60 000 000 000 000 Ом. Другие сопротивления по сравнению с этим настолько малозначительны, что их можно будет игнорировать. Сила тока будет равна 120 вольтам, поделенным на 60 триллионов Ом, следовательно — две триллионных ампера. Эта сила настолько мала, что с таким же успехом можно говорить об отсутствии тока вообще.
Если два проводника разделить воздушной пробкой, то движение тока прекратится, так как у воздуха очень высокая сопротивляемость.
Если в последовательно соединенной цепи возникает воздушная пробка, появляется высокое сопротивление и ток практически пропадает. Такая цепь называется «разомкнутой», или «разорванной». Если же воздушная пробка устраняется, то электрический ток возобновляет свое движение и цепь называется «замкнутой»[104]. Электрические розетки в стенах не передают электрического тока, если в них не вставить штепсель, потому что между двумя «порталами» существует воздушная пробка. Однако она исчезает, когда в розетку вставляют штепсель. Тем не менее в электрических приборах имеется своя воздушная пробка, так что сразу после подключения к электрической цепи электрический ток не поступает.
Иногда желательно, чтобы воздушная пробка возникала мгновенно. Существуют некоторые условия, когда сила тока в той или иной цепи может возрасти до нежелательного уровня. При возрастании силы тока уровень расхода энергии и соответственно уровень нагревания возрастают пропорционально квадрату силы тока (см. уравнение 11.8). Тепло может повредить электрический прибор или положить начало пожару в доме.
Для того чтобы это предотвратить, обычно в цепи вставляют пластину низкоплавкого сплава. Устройство, содержащее подобный сплав, называется «плавким предохранителем».
 Электрический ток в цепи можно возобновить только после замены предохранителя. Разумеется, если предохранитель сгорает неоднократно, то разумнее всего проверить всю цепь и выявить неполадки.
Электрический ток в цепи можно возобновить только после замены предохранителя. Разумеется, если предохранитель сгорает неоднократно, то разумнее всего проверить всю цепь и выявить неполадки.Когда в сети последовательно соединены несколько объектов, то один и тот же электрический ток, проходя в цепи первый объект, затем проходит по очереди и все остальные. Тем не менее ток может проходить из пункта А в пункт В и другими путями, которые могут быть, например, соединены отдельно тремя разными сопротивлениями
Так как обычно эти три сопротивления на схемах изображаются параллельно, то соединение называется  Касательно параллельной электрической цепи можно сказать, что разность потенциалов всегда постоянна на каждом ее этапе.
Касательно параллельной электрической цепи можно сказать, что разность потенциалов всегда постоянна на каждом ее этапе.
Достаточно легко вычислить силу тока в каждом из участков с разными сопротивлениями, так как разность потенциалов и сопротивления нам известна. Если в бытовых домашних электросетях разность потенциалов равна 120 вольт, то, значит, такова же и разность потенциалов каждого из параллельных участков. Поскольку по закону Ома I = E/R, сила тока на первом участке равна 120/100, или 1,2 ампера, на втором — 120/50, или 2,4 ампера, и на третьем — 120/30, или 4 ампера.
Видно, что существует обратная связь между силой тока и сопротивлением на объектах в параллельной цепи. Так как противоположностью сопротивления является проводимость (С= 1/R), то можно сказать, что сила тока в параллельно соединенных объектах прямо пропорциональна их проводимости.
Представим, что точки А и В соединены очень длинной, компактно смотанной проволокой, настолько компактно, что эти точки разделяют одновременно и несколько метров проволоки, и 1 см воздуха. Можно считать, что проволока и воздух являются частями параллельной цепи. Таким образом, ток может поступать или через проволоку, или через небольшой слой воздуха. Однако сопротивление воздуха гораздо больше, чем проволоки, и через воздух проходит лишь минимальное количество тока. Практически весь электрический ток проходит через проволоку.
Можно считать, что проволока и воздух являются частями параллельной цепи. Таким образом, ток может поступать или через проволоку, или через небольшой слой воздуха. Однако сопротивление воздуха гораздо больше, чем проволоки, и через воздух проходит лишь минимальное количество тока. Практически весь электрический ток проходит через проволоку.
Если же слой воздуха уменьшить, то общее сопротивление воздушной пробки между пунктами А и В понизится и в ней будет обнаруживаться ток все большей и большей силы. По пути ток выбивает электроны из атомов воздуха, повышая тем самым способность воздуха проводить электричество при помощи электронов и положительно заряженных ионов, которые электроны оставляют после себя. В результате сопротивление воздушной пробки понижается еще дальше.
В один переломный момент этот порочный круг, в котором ток создает все больше ионов, вызывающих все больший ток, приводит к тому, что через воздух проходит ток в больших количествах, с искрами и треском, которые и привлекли такое внимание к лейденской банке (см. гл. 10). Так как ток выбрал наикратчайший путь из пункта А в В, данное явление назвали коротким замыканием. По проволоке и другим предметам из пункта А в пункт В ток больше не идет, и электричество в цепи пропадает.
гл. 10). Так как ток выбрал наикратчайший путь из пункта А в В, данное явление назвали коротким замыканием. По проволоке и другим предметам из пункта А в пункт В ток больше не идет, и электричество в цепи пропадает.
При коротком замыкании, когда значительная часть прежней цепи выходит из строя, происходит внезапное снижение общего сопротивления в цепи. Сопротивление в искрящейся воздушной пробке очень низкое, возможно, даже ниже, чем в проволоке и других приборах цепи. В остатке цепи сила тока значительно возрастает, что приводит к увеличенному нагреву. В лучшем случае должен выйти из строя один из предохранителей, в худшем — искры в конце концов подожгут любой воспламеняющийся предмет, находящийся поблизости, что может привести к пожару.
Для снижения вероятности коротких замыканий обычно проволоку окружают изоляционным материалом: шелком, резиной, пластмассой и т. д. У этих веществ не только сопротивление выше, чем у воздуха, но и, будучи твердыми телами, они всегда разделяют две разные проволоки (даже если эти проволоки крепко прижимают друг к другу). Однако изоляция может изнашиваться, и тогда снова появляется опасность коротких замыканий.
Однако изоляция может изнашиваться, и тогда снова появляется опасность коротких замыканий.
Возвращаясь к нашим трем участкам с разными сопротивлениями в параллельной сети, зададимся вопросом: каково же общее сопротивление системы? Известно, что общая сила тока в цепи равна сумме сил тока на каждом ее участке. В нашем примере общая сила тока в цепи будет 1,2 + 2,4 + 4,0 = 7,6 ампера. Разность потенциалов между точками А и В параллельной цепи — 120 вольт. Следуя закону Ома R = E/I, общее сопротивление будет равно 120 вольтам, поделенным на общую силу тока в 7,6 ампера. Следовательно, общее сопротивление равно 120/7,6, т. е. чуть менее 16 Ом.
Следует обратить внимание, что общее сопротивление меньше каждого из трех взятых по отдельности сопротивлений отдельных участков. Для того чтобы понять, почему так происходит, следует рассмотреть закон Ома R = E/I применительно к параллельной цепи. R обозначает общее сопротивление, I — общую силу тока, а E остается неизменной независимо от того, взят один объект или несколько. Сила тока равна сумме сил тока на каждом отдельном отрезке цепи (I, I’ и I»). Следовательно:
Сила тока равна сумме сил тока на каждом отдельном отрезке цепи (I, I’ и I»). Следовательно:
Ri = E/(I + I’ + I»). (Уравнение 11.9)
Обратив это выражение, получим:
1/Ri = (I + I’ + I»)/E. Уравнение (11.10)
Согласно закону Ома, I/Е должно равняться 1/R, I’/E — равняться 1/R’ и I»/Е — равняться 1/R», индивидуальным сопротивлениям объектов параллельной цепи. Таким образом:
1/Ri = 1/R + 1/R’ + 1/R». (Уравнение 11.11)
Поговорим об обратных соотношениях в уравнении 11.11. Можно сказать, к примеру, что обратное отношение общего сопротивления равняется сумме обратных отношений отдельных сопротивлений. Выходит так, что чем меньше величина, тем больше обратная ей, и наоборот. (Например, число 11 больше, чем 3, а 1/11 меньше, чем 1/3) Таким образом, исходя из того, что обратное соотношение общего сопротивления (1/Ri) равняется сумме обратных соотношений каждого сопротивления в отдельности и соответственно превосходит каждое из них в отдельности, общее сопротивление (Ri), как таковое, должно быть меньше каждого отдельно взятого сопротивления.
Важным свойством параллельных цепей является следующее: если в параллельной цепи произошел разрыв, то электричество исчезает только в том отрезке, где это случилось. Ток продолжает поступать из пункта А в пункт В по оставшимся отрезкам цепи. При параллельных цепях можно, например, пользоваться одной розеткой, в то время как другие остаются разомкнутыми. А если в параллельной цепи перегорает лампочка (в месте разрыва перегоревшей нити накала получается воздушная пробка), то другие лампочки продолжают гореть.
Видео с вопросами: Расчет полного тока в комбинированной цепи
Стенограмма видео
Найдите общий ток в схема показана. Дайте ответ с точностью до одной запятой место.
В этом вопросе у нас есть схема
который содержит как последовательные, так и параллельные комбинации резисторов. Мы хотим рассчитать общую
ток в цепи. Мы начнем с нахождения
эквивалентное сопротивление цепи.
Мы хотим рассчитать общую
ток в цепи. Мы начнем с нахождения
эквивалентное сопротивление цепи.
Сначала перерисуем схему чтобы мы могли более четко видеть, как все компоненты связаны. Если сравнить эту схему с показанный в вопросе, мы видим, что они эквивалентны. Резисторы 3,5 Ом и 1,8 Ом соединены последовательно друг с другом, а резистор сопротивлением 1,2 Ом включен в параллельно им обоим. Резистор 6,5 Ом подключен последовательно к параллельной комбинации трех других резисторов. Мы также пометили резисторы 𝑅 один к 𝑅 четырем, чтобы упростить наши расчеты. Чтобы найти эквивалентное сопротивление схемы, нам просто нужно вычислить общее сопротивление, обеспечиваемое этим комбинация резисторов.
Первый шаг расчета
эквивалентное сопротивление цепи заключается в том, чтобы найти эквивалентное сопротивление
резисторы 𝑅 один и 𝑅 два, которые соединены последовательно. Напомним, что для любого числа
резисторы последовательно, общее сопротивление, 𝑅 общее, равно 𝑅 один плюс 𝑅 два плюс
точка точка точка плюс 𝑅 под 𝑁. Можем заменить резисторы 𝑅 один и
𝑅 два с эквивалентным резистором 𝑅 сабвуфер 𝐴 с сопротивлением 𝑅 сабвуфер 𝐴 равен 𝑅 одному
плюс 𝑅 два. Подставляя значения для
резисторов 𝑅 один равен 3,5 Ом и 𝑅 два равен 1,8 Ом, находим, что 𝑅 sub 𝐴
равно 𝑅 один плюс 𝑅 два равно 3,5 Ом плюс 1,8 Ом равно 5,3 Ом. Теперь мы можем видеть два резистора 𝑅 sub
𝐴 и 𝑅 три, которые соединены параллельно.
Напомним, что для любого числа
резисторы последовательно, общее сопротивление, 𝑅 общее, равно 𝑅 один плюс 𝑅 два плюс
точка точка точка плюс 𝑅 под 𝑁. Можем заменить резисторы 𝑅 один и
𝑅 два с эквивалентным резистором 𝑅 сабвуфер 𝐴 с сопротивлением 𝑅 сабвуфер 𝐴 равен 𝑅 одному
плюс 𝑅 два. Подставляя значения для
резисторов 𝑅 один равен 3,5 Ом и 𝑅 два равен 1,8 Ом, находим, что 𝑅 sub 𝐴
равно 𝑅 один плюс 𝑅 два равно 3,5 Ом плюс 1,8 Ом равно 5,3 Ом. Теперь мы можем видеть два резистора 𝑅 sub
𝐴 и 𝑅 три, которые соединены параллельно.
Напомним, что для любого количества
резисторов, соединенных параллельно, общее сопротивление, 𝑅 total, равно обратной величине
количество один больше 𝑅 один плюс один больше 𝑅 два плюс и так далее плюс один больше 𝑅 саб
𝑁. Итак, мы можем заменить резисторы 𝑅 sub
𝐴 и 𝑅 три с эквивалентным резистором 𝑅 sub 𝐵 с сопротивлением, заданным 𝑅
sub 𝐵 равно обратному количеству на единицу больше 𝑅 sub 𝐴 плюс единица больше 𝑅
три. Подставив значения 𝑅
sub 𝐴 равно 5,3 Ом, а 𝑅 three равно 1,2 Ом, мы находим, что 𝑅 sub 𝐵 равно
количество, обратное числу один на 𝑅 под 𝐴 плюс один на 𝑅 три равно
обратно величине один больше 5,3 Ом плюс один больше 1,2 Ом, что к трем
десятичных разрядов, 0,978 Ом.
Подставив значения 𝑅
sub 𝐴 равно 5,3 Ом, а 𝑅 three равно 1,2 Ом, мы находим, что 𝑅 sub 𝐵 равно
количество, обратное числу один на 𝑅 под 𝐴 плюс один на 𝑅 три равно
обратно величине один больше 5,3 Ом плюс один больше 1,2 Ом, что к трем
десятичных разрядов, 0,978 Ом.
Наконец, у нас есть два резистора 𝑅 сабвуферы 𝐵 и 𝑅 четыре соединены последовательно. Мы можем заменить эти два резистора с эквивалентным резистором 𝑅 sub 𝐶 равно 𝑅 sub 𝐵 плюс 𝑅 четыре. Подставляя значения 𝑅 sub 𝐵 равно 0,978 Ом, а 𝑅 четыре равно 6,5 Ом, мы получаем 𝑅 sub 𝐶 равно 0,978 Ом плюс 6,5 Ом равно 7,478 Ом. Резистор 𝑅 sub 𝐶 имеет эквивалентное сопротивление четырех резисторов, первоначально показанных в вопросе. Теперь мы можем использовать закон Ома для одиночный резистор 𝑅 sub 𝐶, чтобы найти значение тока.
Напомним, что закон Ома может быть
записывается как 𝑉 равно 𝐼 умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 —
ток, а 𝑅 — сопротивление. Здесь нам интересно найти
ток, поэтому нам нужно изменить это уравнение, чтобы сделать 𝐼 субъектом. Для этого мы просто делим оба
сторон на 𝑅, чтобы 𝐼 равнялось 𝑉 больше 𝑅. Нам дана клетка, которая
обеспечивает разность потенциалов 14 вольт в цепи. Подставляя это значение и
значение сопротивления, которое мы только что рассчитали, мы можем использовать закон Ома, чтобы найти, что
ток через одиночный резистор 𝑅 sub 𝐶 равен 𝐼 равен 𝑉, деленный на
𝑅 sub 𝐶 равно 14 вольт, деленное на 7,478 Ом, равно 1,87204 и т. д.
ампер.
Здесь нам интересно найти
ток, поэтому нам нужно изменить это уравнение, чтобы сделать 𝐼 субъектом. Для этого мы просто делим оба
сторон на 𝑅, чтобы 𝐼 равнялось 𝑉 больше 𝑅. Нам дана клетка, которая
обеспечивает разность потенциалов 14 вольт в цепи. Подставляя это значение и
значение сопротивления, которое мы только что рассчитали, мы можем использовать закон Ома, чтобы найти, что
ток через одиночный резистор 𝑅 sub 𝐶 равен 𝐼 равен 𝑉, деленный на
𝑅 sub 𝐶 равно 14 вольт, деленное на 7,478 Ом, равно 1,87204 и т. д.
ампер.
Ток везде одинаковый
последовательная цепь, поэтому ток, который мы рассчитали через одиночный резистор, равен
равно полному току через эквивалентную цепь. Поскольку эквивалентная схема имеет
того же полного сопротивления, что и исходная цепь, которую нам дали, этот ток должен
также равен полному току в исходной цепи.
Последнее, что нам нужно сделать этот вопрос должен дать ответ до одного десятичного знака. Мы возьмем числа перед десятичного знака и два числа после запятой, чтобы получить 1,87 ампер. Затем смотрим на второе число после запятой, чтобы увидеть, нужно ли нам округлить в меньшую или большую сторону. Мы видим, что второе число после десятичный знак равен семи, поэтому мы можем округлить это число, что дает ответ 1,9ампер. Следовательно, полный ток через цепь 1,9 ампера.
Как рассчитать текущие активы
Когда дело доходит до вашего бизнеса, необходимо следить за своими финансами. И чтобы знать, в каком вы положении в финансовом отношении, поймите, как рассчитать определенные цифры, такие как текущие активы. Узнайте, как рассчитать текущие активы для вашего бизнеса и как использовать их для оценки финансов вашей компании.
Что такое оборотные средства?
Прежде чем вы сможете погрузиться в поиск текущих активов, вам нужно узнать, что такое текущие активы. Вот краткое изложение.
Вот краткое изложение.
Оборотные активы — это объекты ценности, которые ваш бизнес планирует использовать или конвертировать в денежные средства в течение одного года и которые считаются краткосрочными инвестициями. Предприятия продают, потребляют и используют эти активы в ходе своей повседневной деятельности. Несколько примеров оборотных активов включают:
- Денежные средства и их эквиваленты
- Дебиторская задолженность
- Товарно-материальные запасы
- Предоплата расходов
- Краткосрочные инвестиции
- Ценные бумаги, обращающиеся на рынке (например, акции)
Некоторые из ваших текущих активов могут считаться ликвидными. Ликвидные активы — это активы, которые можно быстро превратить в наличные деньги, например акции.
Текущие активы помогают поддерживать бесперебойную работу вашего бизнеса. Вы можете использовать их для оплаты ежедневных операционных расходов и других краткосрочных финансовых обязательств. Не говоря уже о том, что поиск текущих активов может помочь вам получить представление о денежных потоках и ликвидности вашего бизнеса.
Не говоря уже о том, что поиск текущих активов может помочь вам получить представление о денежных потоках и ликвидности вашего бизнеса.
Как рассчитать оборотные средства
Если вы знаете, что ищете, вычислить оборотные средства несложно. Чтобы найти оборотные активы для вашего бизнеса, используйте формулу оборотных активов:
Оборотные активы = Денежные средства + Денежные эквиваленты + Товарно-материальные запасы + Дебиторская задолженность + Рыночные ценные бумаги + Предоплаченные расходы + Другие ликвидные активы
Да, рассчитать оборотные активы так же просто так как делаю небольшое дополнение. Пока вы знаете, каковы ваши текущие активы, вы в золоте.
Используйте свой балансовый отчет, чтобы найти суммы, необходимые для расчета общих текущих активов.
Лучший способ оценить свои текущие активы — сравнить их с текущими обязательствами. Как правило, наличие большего количества текущих активов, чем текущих обязательств, является положительным признаком, поскольку это показывает хорошую краткосрочную ликвидность. Однако иметь слишком много оборотных средств не всегда хорошо. «Хорошая» сумма текущих активов также может варьироваться в зависимости от отрасли и целей вашего бизнеса.
Однако иметь слишком много оборотных средств не всегда хорошо. «Хорошая» сумма текущих активов также может варьироваться в зависимости от отрасли и целей вашего бизнеса.
После расчета текущих активов вы можете использовать полученные результаты для расчета других коэффициентов малого бизнеса, таких как:
- Коэффициент текущей ликвидности (Оборотные активы / Текущие обязательства)
- Коэффициент быстрой ликвидности = [(Оборотные активы – Запасы + Предоплаченные расходы) / Текущие обязательства]
- Чистый оборотный капитал = (Оборотные активы – Текущие обязательства)
Хотите посмотреть как ваш бизнес стоит в финансовом отношении?
Загрузите наш БЕСПЛАТНЫЙ технический документ, Используйте финансовые отчеты для оценки состояния вашего бизнеса , чтобы узнать о финансовых отчетах, которые вам необходимо собрать для своих расчетов.
Получите мое бесплатное руководство!
Расчет оборотных средств: пример
Теперь, когда вы знаете, как найти общую сумму оборотных средств, давайте рассмотрим ее расчет в действии.
Скажите, что у вашей компании есть следующие текущие активы:
- Денежные средства: 6 000 долл. США
- Инвентаризация: 500 долл. США
- Дебиторская задолженность: 1 000 долл. США
- . Напоминаем, что используйте следующую формулу, чтобы найти свои общие текущие активы:
Текущие активы = Денежные средства + Денежные эквиваленты + Товарно-материальные запасы + Дебиторская задолженность + Рыночные ценные бумаги + Предоплаченные расходы + Другие ликвидные активы 11 700 долларов.
Допустим, ваши текущие обязательства равны 8000 долларов. В вашем случае наличие большего количества текущих активов, чем текущих обязательств, показывает, что у вас есть достаточный объем текущих активов.
Использование оборотных средств
Опять же, ваши текущие активы могут многое рассказать вам о том, насколько здоровы финансы вашего бизнеса. Имейте в виду следующее при поиске и использовании текущих активов для оценки вашего финансового состояния:
- Текущие активы включают только активы, которые вы можете превратить в наличные деньги в течение одного года, или краткосрочные инвестиции
- Средние текущие активы могут варьироваться в зависимости от вашего бизнеса отрасль и цели
- Как правило, ваш бизнес должен иметь соотношение оборотных активов к текущим обязательствам не менее 1:1
- Во многих случаях вы хотите, чтобы оборотные активы превышали текущие обязательства, но бывает так, что оборотных активов слишком много
- Коэффициент оборотных активов не должен превышать 2.
 Коэффициент выше 2 показывает, что вы недостаточное инвестирование активов
Коэффициент выше 2 показывает, что вы недостаточное инвестирование активов
Наличие здорового баланса между текущими активами и текущими обязательствами может помочь вам, когда речь идет о:
- достижении целей
- подаче заявки на финансирование бизнеса
- сборе средств
Короче говоря, вы можете использовать свои текущие активы для мониторинга финансов вашего бизнеса и выявления проблемных областей для внесения корректировок и улучшений.
Это не юридическая консультация; Для большей информации, пожалуйста нажмите сюда.
Алфавит Итого Текущие обязательства 2010-2022 | ГУГЛ
Суммарные текущие обязательства в алфавитном порядке с 2010 по 2022 год. Общие текущие обязательства могут быть определены как сумма всех обязательств, классифицированных как краткосрочные, со сроком погашения менее одного года.
- Сумма текущих обязательств Alphabet за квартал, закончившийся 30 июня 2022 г.
 , составила 61,354 млрд долларов , что на 10,07% больше по сравнению с прошлым годом.
, составила 61,354 млрд долларов , что на 10,07% больше по сравнению с прошлым годом. - Общие краткосрочные обязательства Alphabet на 2021 год составили 64,254 миллиарда долларов , что на 13,06% больше по сравнению с 2020 годом.
- Общие текущие обязательства Alphabet на 2020 год составили 56,834 млрд долларов , что на 25,68% больше по сравнению с 2019 годом.
- Сумма краткосрочных обязательств по алфавиту за 2019 годбыли 45,221 млрд долларов , что на 30,62% больше по сравнению с 2018 годом.
Алфавит Сумма годовых текущих обязательств
(в миллионах долларов США)2021 64 254 долл. США 2020 56 834 долл. США 2019 45 221 $ 2018 34 620 долл.  США
США2017 24 183 долл. США 2016 $16 756 2015 $19 310 2014 $16 779 2013 $15 908 2012 14 337 долларов 2011 8 913 $ 2010 9 996 долл. США 2009 2747 долларов Алфавит Квартальные Итого Краткосрочные обязательства
(в миллионах долларов США)30.06.2022 61 354 долл. США 31.03.2022 61 948 долларов 31.12.2021 64 254 $ 30.  09.2021
09.202161 782 $ 30.06.2021 55 741 $ 31.03.2021 $55 453 2020-12-31 56 834 долл. США 30.09.2020 48 200 долларов США 2020-06-30 43 658 долларов 31.03.2020 40 189 долларов 31.12.2019 45 221 $ 30.09.2019 39 224 $ 30.06.2019 37 000 долларов США 31.03.2019 $34 910 2018-12-31 34 620 долларов 30.09.2018 31 301 $ 30.06.2018 29 903 $ 31.  03.2018
03.201825 394 $ 2017-12-31 24 183 долл. США 30.09.2017 20 693 долл. США 30.06.2017 $18 685 31.03.2017 15 256 долларов США 2016-12-31 $16 756 30.09.2016 $14 323 30.06.2016 17 341 $ 31.03.2016 17 684 долл. США 2015-12-31 $19 310 30.09.2015 18 457 долларов 30.06.2015 17 362 долл. США 31.03.2015 $14 336 2014-12-31 $16 779 30.  09.2014
09.201417 920 долларов США 30.06.2014 $17 097 31.03.2014 16 270 долларов США 31.12.2013 $15 908 30.09.2013 14 475 долларов 30.06.2013 $15 329 31.03.2013 13 252 долл. США 31.12.2012 14 337 долларов 30.09.2012 14 434 долл. США 30.06.2012 14 028 долларов 31.03.2012 9 742 $ 2011-12-31 8 913 $ 30.09.2011 8 888 $ 30.06.2011 7 798 $ 31.  03.2011
03.20119 332 $ 2010-12-31 9 996 долл. США 30.09.2010 8 530 долларов 30.06.2010 5 747 долл. США 31.03.2010 2 922 $ 31.12.2009 2747 долларов 30 сентября 2009 г. 2 322 долл. США 30.06.2009 2001 $ 31 марта 2009 г. 2184 $ Сектор Промышленность Рыночная капитализация Доход Компьютеры и технологии Интернет-услуги $1323.053B 257,637 млрд долларов Alphabet превратился из поставщика поисковых систем в облачные вычисления, потоковую передачу видео и музыки на основе рекламы, автономные транспортные средства, поставщиков медицинских услуг и многое другое. 




 Что может привести к возгоранию. И не будет нам ни чая, ни взбитого теста для блинчиков, ни тостов.
Что может привести к возгоранию. И не будет нам ни чая, ни взбитого теста для блинчиков, ни тостов. Сопротивление участка станет равным нулю, как показано на рисунке:
Сопротивление участка станет равным нулю, как показано на рисунке: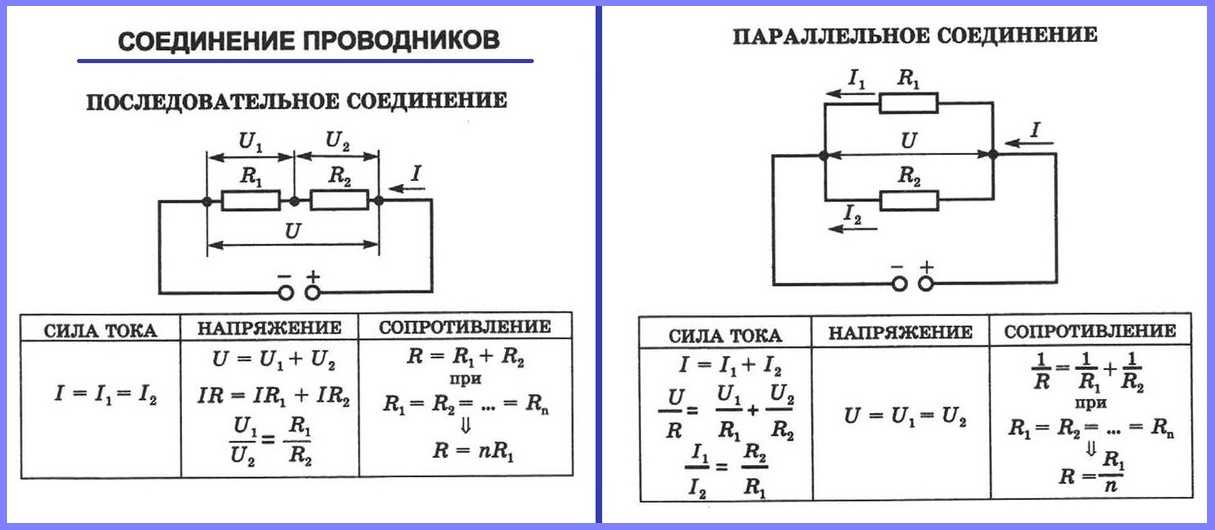
 Коэффициент выше 2 показывает, что вы недостаточное инвестирование активов
Коэффициент выше 2 показывает, что вы недостаточное инвестирование активов , составила 61,354 млрд долларов , что на 10,07% больше по сравнению с прошлым годом.
, составила 61,354 млрд долларов , что на 10,07% больше по сравнению с прошлым годом. США
США 09.2021
09.2021 03.2018
03.2018 09.2014
09.2014 03.2011
03.2011