формула, единица измерения, определение простыми словами, прибор, какой буквой обозначается
Электричеством пользуются все и постоянно, поэтому знание его природы необходимо каждому. Разбираемся, каким прибором измеряется сила тока и какой буквой она обозначается. Наш эксперт поможет окончательно разобраться и сделать понятным физический смысл явления
Борис Михеев
Автор КП
Николай Герасимов
Старший преподаватель в Домашней школе по физике «ИнтернетУрок»
Электрический ток, текущий по проводу, можно сравнить с водой, текущей по шлангу. Струя воды может обладать как огромной силой, способной, например, сбить человека с ног, так и силой очень маленькой, как при капельном поливе, где её хватает лишь на то, чтобы капелька жидкости покинула шланг. Так вот, электрический ток тоже обладает силой.
Определение силы тока простыми словами
Сила тока – это упорядоченное движение заряженных частиц. Её величина может проявляться, например, в яркости лампы. Ток в мощном прожекторе обладает большой силой и совершает большую работу, что проявляется в том, что его лампа даёт много света. Лампа же ночника светит слабо, и в этом случае говорят, что сила тока маленькая.
Её величина может проявляться, например, в яркости лампы. Ток в мощном прожекторе обладает большой силой и совершает большую работу, что проявляется в том, что его лампа даёт много света. Лампа же ночника светит слабо, и в этом случае говорят, что сила тока маленькая.
Природа силы тока
Если посмотреть на определение силы тока, то можно выделить два условия, необходимые для его возникновения: наличие свободных зарядов и электрического поля, которое заставит двигаться все эти заряды в одну сторону, то есть упорядоченно. Например, в металлах такими свободными зарядами являются свободные электроны, которые очень плохо притягиваются к ядрам, и даже теплового движения достаточно, чтобы разорвать их связь. Таким образом, электрический ток имеет электромагнитную природу.
В ТЕМУ
Формула силы тока
I = N/t
Где:
I — собственно сила тока, Амперы;
N — количество электронов;
t — период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды.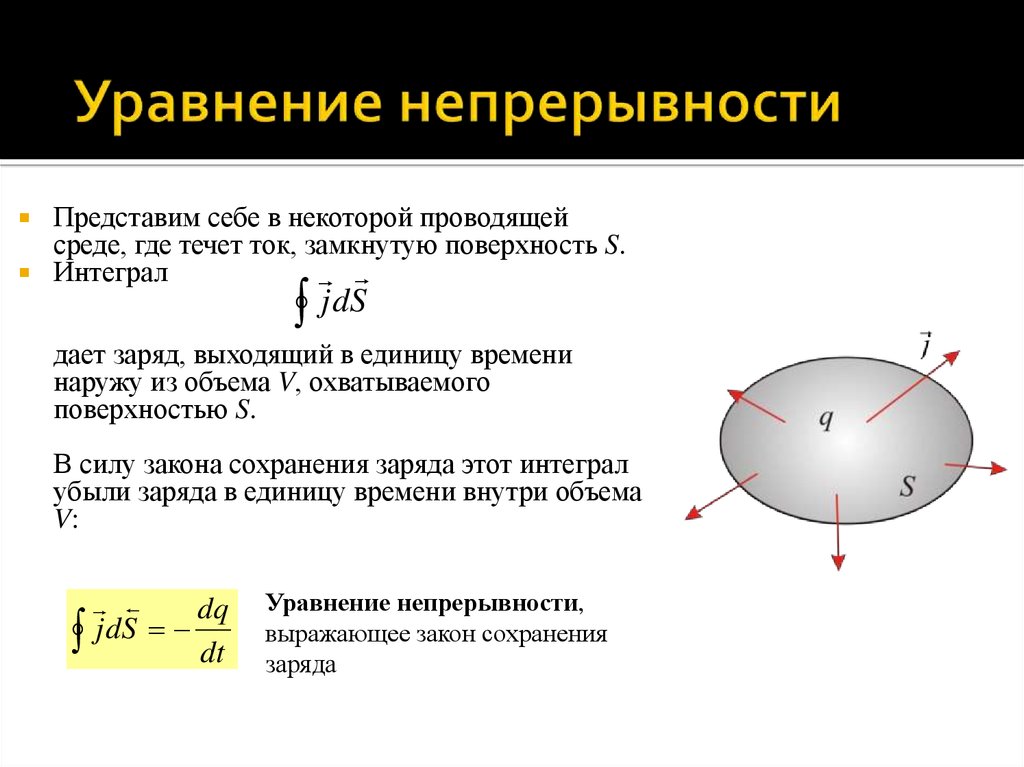
Электромобиль — один из современных примеров использования электричества в нашей жизни. Фото: Pixabay.com
Единица измерения силы тока
Единица измерения силы тока – Ампер, одна из основных единиц системы СИ ⓘ.
Международная система единиц, СИ (Le Système International d’Unités — SI) — система единиц физических величин, современный вариант метрической системы.
Прибор для измерения силы тока
Приборы для измерения силы тока называются амперметры. Приборы для измерения малых токов порядка миллиампер (одна тысячная часть от ампера) или микроампер (одна миллионная часть от ампера) называются миллиамперметры и микроамперметры соответственно. Для измерения больших токов порядка килоампер (тысячи ампер) используют приборы, которые называются килоамперметры.
Популярные вопросы и ответы
На вопросы читателей отвечает Николай Герасимов, старший преподаватель в Домашней школе по физике «ИнтернетУрок»
Какой буквой обозначается сила тока?
Сила тока обозначается буквой I.
Какова сила тока в проводнике?
Токи, с которыми мы можем встретиться, могут быть от нескольких миллиампер до сотен тысяч ампер. Например, токи, текущие по проводам в наших домах, редко превышают значения в 10 ампер. Однако стоит сразу отметить, что ток силой несколько десятков миллиампер вызывает неприятные ощущения, а ток силой 0,1 А (Ампера) может быть смертельным для человека. Все мы пользуемся зарядными устройствами для мобильных телефонов, ток в которых может достигать 1-2 А, поэтому нужно быть аккуратными при зарядке телефонов и обязательно соблюдать меры предосторожности.
Как измерить силу тока мультиметром?
Сегодня электрики нередко используют мультиметры – приборы, которые позволяют измерять силу тока, напряжение, сопротивление, электроёмкость конденсаторов и так далее. Для измерения силы тока нужно правильно подключить провода и выставить соответствующий режим работы. В разных приборах могут быть различные способы включения, но сектор для измерения силы тока обычно обозначен буквой «А», а начинать нужно с режима для измерения максимального тока, иначе прибор может сгореть. Также следует помнить, что амперметр нельзя подсоединять к источнику тока без потребителей, например электрической лампы. То есть ни в коем случае нельзя щупы мультиметра, работающего в режиме амперметра, присоединять непосредственно к клеммам электрической розетки.
Также следует помнить, что амперметр нельзя подсоединять к источнику тока без потребителей, например электрической лампы. То есть ни в коем случае нельзя щупы мультиметра, работающего в режиме амперметра, присоединять непосредственно к клеммам электрической розетки.
Фото на обложке: shutterstock.com
Презентация по физике по теме Сила тока, напряжение и электрическое сопротивление доклад, проект
План ответа о физической величине:
Формула. Физический смысл величины.
Определение величины.
Единицы измерения. Определение единицы измерения.
Прибор для измерения физической величины.
Правило работы с этим прибором.
Сила тока.
Физический смысл:
Если
Сила тока – это физическая скалярная величина, характеризующая электрический ток и численно равная электрическому заряду прошедшему через поперечное сечение проводника за 1 секунду.
Единицы измерения силы тока
За единицу силы тока принимают силу тока, при которой отрезки таких параллельных проводников длиной 1метр взаимодействуют с силой
Прибор для измерения силы тока называется Амперметр.
Правило работы с прибором:
Соблюдение полярности.
Амперметр всегда соединяется последовательно с тем участком ,на котором измеряется сила тока.
Нельзя включать прибор в цепь с большим током, чем он рассчитан.
Электрическое напряжение
Физический смысл:
Если
Электрическое напряжение – это физическая скалярная величина, характеризующая действие электрического поля на заряженные частицы и численно равная работе этого поля по перемещению единичного электрического заряда.
1 Вольт- это такое электрическое напряжение,
при котором электрическое поле перемещая заряд в 1Кулон совершает работу в 1Джоуль.
Единицы измерения электрического напряжения
Прибор для измерения силы тока называется Вольтметр.
Правило работы с прибором:
Соблюдение полярности.
Вольтметр всегда соединяется параллельно тому участку ,на котором измеряется напряжение.
Нельзя включать прибор в цепь с большим напряжением, чем рассчитан данный прибор.
Зависимость силы тока от напряжения
Во сколько раз увеличивается напряжение , приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нём.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.
Электрическое сопротивление проводников.
Это физическая скалярная величина, характеризующая способность проводника препятствовать (сопротивляться) прохождению электрического тока.
Обозначается буквой R
Единицы сопротивления
1Ом –это сопротивление такого проводника, в котором при напряжении на концах 1Вольт сила тока равна 1Амперу.
Применяют и другие единицы
сопротивления: миллиом (мОм),
килиом (кОм), мегаом(МОм).
1мОм=0,001.Ом
1кОм=1000.Ом
1МОм=1000000.Ом
Омметр – это измерительный прибор специализированного назначения, предназначенный для определения сопротивления электрического тока.
Омметр – это прибор непосредственного отсчета. Его основная функция – определение активных сопротивлений электрического тока. Как правило, омметр преобразует переменный ток в постоянный и производит измерения.
Причиной электрического сопротивления проводника является взаимодействие электронов с ионами кристаллической решетки металлов.
Можно предположить, что сопротивление зависит от:
— длины проводника,
— площади поперечного сечения проводника,
Чем проводник длиннее, тем больше его сопротивление
Чем площадь поперечного сечения проводника больше, тем сопротивление проводника меньше
Сопротивление зависит от вещества проводника
R ~ l
R ~ ρ
Физический смысл:
Если
то
Удельное сопротивление вещества — физическая скалярная величина,
характеризующая способность вещества препятствовать прохождению электрического тока и численно равная сопротивлению проводника длинной 1 м, площадью поперечного сечения проводника 1 мм2.
Единица измерения
удельного сопротивления вещества
Удельное электрическое сопротивление некоторых веществ,
(при t = 20 C0 )
Выберите
— обозначение,
— единицу измерения,
— формулу для расчета
— прибор для измерения
характеристик тока по вариантам:
I вариант – сила тока;
II вариант – напряжение;
III вариант – сопротивление.
А
В
Ом
Дж
Калориметр
Н
Динамометр
R
U
Q
F
I
Вольтметр
Омметр
Амперметр
I вариант
Максимальный балл — 4
А
Калориметр
Максимальный балл — 4
Q
F
В
Амперметр
R
Динамометр
I
Ом
Вольтметр
Дж
II вариант
Н
U
Омметр
А
В
Ом
Дж
Калориметр
Н
Динамометр
R
U
Q
F
I
Вольтметр
Омметр
Амперметр
III вариант
Максимальный балл — 4
Критерии оценивания:
5 баллов — оценка «5»;
4 балла – оценка «4»;
3 балла – оценка «3».
Основные характеристики тока
Сила тока – I, [A];
Напряжение – U, [B];
Сопротивление — R, [Ом]
Эти величины связаны между собой!
КАК?
Закон Ома для участка цепи
Ломмель Эуген
Корнелиус Йозеф
…Ом вырвал у природы так долго
скрываемую тайну и передал ее
в руки современников»
Схема опыта
V
Зависимость силы тока от напряжения
Сила тока прямо пропорциональна напряжению
I, А
0,2
0,8
0,6
0,4
0
U, B
1
2
3
4
Линейная зависимость или
прямая пропорциональность
I ~ U
2В
0,4 А
3В
0,6 А
4В
0,8 А
Зависимость силы тока от сопротивления
Сила тока обратно пропорциональна сопротивлению
I,А
R,Ом
1
График – ветвь гиперболы
обратная пропорциональность
R, Ом
4 Ом
2 Ом
1 Ом
5 В
5 В
5 В
1 А
2 А
4 А
4
2
2
4
1
0
U — const
1 . I ~ U – прямая зависимость
I ~ U – прямая зависимость
2 . – обратная зависимость
Георг Симон Ом (1789–1854)
Закон Ома для участка цепи
1827 год
Формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Закон Ома для участка цепи
Магический треугольник:
Зависимость силы тока от сопротивления
на участке АВ выражена графиками 1 и 2.
В каком случае проводник АВ находился под
большим напряжением?
На рисунке изображены графики зависимости силы тока от напряжения для двух проводников А и В.
Какой из этих проводников обладает большим сопротивлением?
I вариант
II вариант
V
А
I=5A
R=22Ом
V
А
U=6B
R=2Ом
1. По данным приведенным на
По данным приведенным на
рисунке определите показания
вольтметра.
1. По данным приведенным на
рисунке определите показания
амперметра.
2. Лампа рассчитана на
напряжение 6В и силу тока 4 А.
Каково сопротивление лампы?
2. Лампа рассчитана на
напряжение 127 В, имеет
сопротивление 254 Ом.
Вычислите силу тока в лампе.
U = 110 B;
I = 0,5 A.
I = 3A;
R = 1,5 Ом.
природа электрических явлений, основные отличия их друг от друга
Физические проявления
Физически ощутить проявления электричества человеку можно только опосредованно. Если попробовать на язык батарейку — можно почувствовать пощипывание. Это следствие протекания малого тока через организм. Чувствительная слизистая языка уже ощущает это раздражение. Можно увидеть искры статического электричества между двумя заряженными объектами, например, синтетическими тканями, или в школьном опыте с динамо-машиной. Все это следствие накопления заряда или потенциального напряжения.
Все это следствие накопления заряда или потенциального напряжения.
Чтобы узнать, что такое сила тока, нужно определиться с понятием заряда. Как известно, вся материя в мире состоит из атомов. Атомы, в свою очередь, состоят из протонов, нейтронов и электронов. Среди этих частиц нейтрально заряжены только нейтроны. Протоны и электроны обладают потенциальной энергией — электрическим зарядом, который, в частности, и держит атомы в цельном состоянии.
Протоны и нейтроны находятся в ядре атома. Электроны же, напротив, располагаются далеко от ядра и движутся вокруг него по орбитам, сходным с орбитами планет солнечной системы. Чем дальше находится электрон от ядра, тем меньше его связь с центром атома, и тем проще он может потеряться. В различных материалах электроны ведут себя по-разному.
В металлах они слабо связаны с ядром и свободно перемещаются внутри вещества. Однако их общее количество в предмете с нейтральным зарядом всегда должно соответствовать количеству протонов.
Если электроны вследствие каких-то действий покидают вещество, они уносят с собой заряд. Соответственно, заряд, оставшийся в протонах вещества, будет накоплен этим веществом. Электроны могут унести заряд в случаях:
- Трения двух веществ друг о друга.
- Воздействия ультрафиолета или радиации.
- Быстрого перепада температур.
Таким образом, между предметами возникает разность потенциалов, или напряжение, способное вызвать искру. А искра — это уже проявление электрического тока. Заряды разного знака всегда притягиваются друг к другу. Если электроны перешли с одного материала на другой, то один материал накопил положительный заряд, а другой — отрицательный.
При их сближении электроны притянутся к положительно заряженному телу — и возникнет искра. То есть электроток — это движение заряженных ча
Сбор нагрузок.
Когда расчетная схема определена, когда принято решение, что же будет работать в нашей конструкции, а что «сидеть на шее», следует как можно тщательней разобраться с тем, что же воздействует на нашу конструкцию. И здесь мы впервые сталкиваемся с понятием «нагрузка». Нагрузка– это любое внешнее воздействие, которое влияет на нашу конструкцию. Список нагрузок не так уж велик:
И здесь мы впервые сталкиваемся с понятием «нагрузка». Нагрузка– это любое внешнее воздействие, которое влияет на нашу конструкцию. Список нагрузок не так уж велик:
- Нагрузка от собственного веса (да, даже под своим собственным весом неправильно рассчитанная конструкция может сломаться) и от веса других элементов, материалов.
- Нагрузка от веса людей, мебели, оборудования – в общем всего того, что может быть, может не быть, но важно это учесть и не просчитаться.
- Нагрузка от снега.
- Нагрузка от ветра.
- Нагрузка от температурных воздействий (под действием температур материалы расширяются вплоть до разрушения, это явление также можно выразить в виде нагрузки).
- Сейсмическая нагрузка.
Как видите, всё это (ну, за исключением собственного веса) приходит извне, но оказывает значительное влияние на любую конструкцию. Причем каждая нагрузка может располагаться в пространстве произвольным образом по отношению к объекту расчета – и перпендикулярно, и под углом, и вдоль оси. Нагрузки могут сочетаться между собой, могут исключать друг друга. В общем, вариантов масса, но все это нам нужно свести в единую систему, найти наихудший вариант и запроектировать такую конструкцию, которая этот наихудший вариант сможет на собственных плечах вынести. Каким же приемом пользуются в расчете, чтобы перевести нагрузки в удобоваримый формат? Ведь нагрузок может быть масса, но глядя на них, не сразу возможно понять, плохо или хорошо они воздействуют на конструкцию. Именно для прояснения картины с нагрузками в алгоритме расчета присутствует следующий, очень важный шаг.
Нагрузки могут сочетаться между собой, могут исключать друг друга. В общем, вариантов масса, но все это нам нужно свести в единую систему, найти наихудший вариант и запроектировать такую конструкцию, которая этот наихудший вариант сможет на собственных плечах вынести. Каким же приемом пользуются в расчете, чтобы перевести нагрузки в удобоваримый формат? Ведь нагрузок может быть масса, но глядя на них, не сразу возможно понять, плохо или хорошо они воздействуют на конструкцию. Именно для прояснения картины с нагрузками в алгоритме расчета присутствует следующий, очень важный шаг.
Аналогия с гидравликой
Слово ток имеет происхождение от слова течение. Соответственно, можно провести аналогию течения жидкости с электрическим током. Протекание жидкости возможно из одного места в другое, только если возникает сила, заставляющая ее сделать это. В самом простом случае — это разница уровней жидкости. То есть потенциальная энергия, заставляющая жидкое вещество течь от более высокого уровня к более низкому.
Аналогом разности уровней жидкости будет разность потенциалов или напряжение. Аналогом силы тока будет напор потока воды, создаваемый этой разностью уровней. Примеры потоков жидкости:
- Водопад.
- Поток, создаваемый водонапорной башней.
- Реки, текущие туда, где есть наклон территории.
Везде вода течет туда, где уровень меньше, а электроток — от большего напряжения к меньшему.
Определение
Током называется процесс, когда под воздействием электрического поля начинается упорядоченное движение заряженных частиц. Частицами могут выступать самые разные элементы, все зависит от конкретного случая. Если мы говорим о проводниках, то частицами в данной ситуации являются электроны. Изучая электричество, люди стали понимать, что возможности тока позволяют использовать его в самых разных областях, включая медицину. Ведь электрические заряды помогают реанимировать больных, восстанавливать работу сердца. Кроме того, ток применяют в лечении таких сложных заболеваний, как эпилепсия или болезнь Паркинсона. В быту же электрический ток просто незаменим, ведь с его помощью в наших квартирах и домах горит свет, работают электроприборы.
В быту же электрический ток просто незаменим, ведь с его помощью в наших квартирах и домах горит свет, работают электроприборы.
Напряжение – понятие куда более сложное, нежели ток. Единичные положительные заряды перемещаются из разных точек: из низкого потенциала в высокий. И напряжением называется энергия, затрачиваемая на это перемещение. Для простоты понимания часто приводят пример с течением воды между двумя банками: ток – это сам поток воды, а напряжение показывает разницу уровней в двух банках. Соответственно, течение будет до тех пор, пока уровни не сравнятся.
Связь величин законом Ома
Электротехнические величины также зависят и от материала, в котором протекает . Эти параметры определяются электросопротивлением вещества. Сопротивление бывает как бесконечно большим у диэлектриков, так и падать практически до нуля в условиях сверхпроводимости. Оно зависит от формы проводника (его длины и сечения) и вещества, из которого он изготовлен.
В обычных условиях сопротивление определяется по закону Ома как отношение напряжения к силе тока на участке цепи.
То есть разность потенциалов можно найти как произведение силы тока на сопротивление. Знать, чем отличается сила тока от напряжения очень важно для электротехнических расчетов. На этом базируются все основы функционирования электрических цепей.
Мощность ток напряжение, расчёты для однофазной сети 220 В
Сила тока I (в амперах, А) подсчитывается по формуле:
P – электрическая полная нагрузка (обязательно указывается в техническом паспорте устройства), Вт (ватт)
U – напряжение электрической сети, В (вольт)
Ниже в таблице представлены величины нагрузки типичных бытовых электроприборов и потребляемый ими ток (для напряжения 220 В).
| Электроприбор | Потребляемая мощность, Вт | Сила тока, А |
| Стиральная машина | 2000 – 2500 | 9,0 – 11,4 |
| Джакузи | 2000 – 2500 | 9,0 – 11,4 |
| Электроподогрев пола | 800 – 1400 | 3,6 – 6,4 |
| Стационарная электрическая плита | 4500 – 8500 | 20,5 – 38,6 |
| СВЧ печь | 900 – 1300 | 4,1 – 5,9 |
| Посудомоечная машина | 2000 — 2500 | 9,0 – 11,4 |
| Морозильники, холодильники | 140 — 300 | 0,6 – 1,4 |
| Мясорубка с электроприводом | 1100 — 1200 | 5,0 — 5,5 |
| Электрочайник | 1850 – 2000 | 8,4 – 9,0 |
| Электрическая кофеварка | 6з0 — 1200 | 3,0 – 5,5 |
| Соковыжималка | 240 — 360 | 1,1 – 1,6 |
| Тостер | 640 — 1100 | 2,9 — 5,0 |
| Миксер | 250 — 400 | 1,1 – 1,8 |
| Фен | 400 — 1600 | 1,8 – 7,3 |
| Утюг | 900 — 1700 | 4,1 – 7,7 |
| Пылесос | 680 — 1400 | 3,1 – 6,4 |
| Вентилятор | 250 — 400 | 1,0 – 1,8 |
| Телевизор | 125 — 180 | 0,6 – 0,8 |
| Радиоаппаратура | 70 — 100 | 0,3 – 0,5 |
| Приборы освещения | 20 — 100 | 0,1 – 0,4 |
Различные потребители электроэнергии подключаются через соответствующие автоматы к электросчётчику и далее общему автомату, который должен быть рассчитан на нагрузку приборов, которыми будет оборудована квартира. Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Постоянный и переменный
Сила тока и напряжение могут быть как постоянными, так и переменными. Постоянство величины говорит о ее неизменности во времени. Напротив, переменные величины периодически изменяют свое значение во времени. Если напряжение питания окажется переменным, то и сила тока, генерируемая им, будет переменной величиной. Это значит, что оба этих значения будут то увеличиваться, то уменьшаться. Форма сигнала может быть различной:
- Синусоидальный сигнал (плавное возрастание — убывание).
- Меандр (прямоугольный, треугольный сигнал), когда значение резко претерпевает изменение.
- Пульсирующий сигнал, изменяющийся то плавно, то резко, согласно некоторому закону.
Вне зависимости от того, постоянным или переменным является ток, его главное отличие от напряжения — то, что ток — это движение носителей заряда, а напряжение — причина этого движения.
Мощность ток напряжение, расчёты для трёхфазной сети 380 В
При трёхфазном электроснабжении сила тока I (в амперах, А) вычисляется по формуле:
где P -потребляемая мощность, Вт;
U — напряжение в сети, В,
так как напряжение при трёхфазной схеме электроснабжения 380 В, формула примет вид:
I = P /657, 4.
Сечение жил в питающем кабеле при различной нагрузке при трёхфазной схеме напряжением 380 В для скрытой проводки представлена в таблице.
| Сечение жилы провода, мм 2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 2250 | ||
| 0,75 | 0,98 | 10 | 3800 | ||
| 1,00 | 1,13 | 14 | 5300 | ||
| 1,50 | 1,38 | 15 | 5700 | 10 | 3800 |
| 2,00 | 1,60 | 19 | 7200 | 14 | 5300 |
| 2,50 | 1,78 | 21 | 7900 | 16 | 6000 |
| 4,00 | 2,26 | 27 | 10000 | 21 | 7900 |
| 6,00 | 2,76 | 34 | 12000 | 26 | 9800 |
| 10,00 | 3,57 | 50 | 19000 | 38 | 14000 |
| 16,00 | 4,51 | 80 | 30000 | 55 | 20000 |
| 25,00 | 5,64 | 100 | 38000 | 65 | 24000 |
Для расчёта тока в цепях питания нагрузки, характеризующейся большой реактивной полной мощностью, что характерно применению электроснабжения в промышленности:
- электрические двигатели
- дроссели приборов освещения
- сварочные трансформаторы
- индукционные печи
В мощных приборах и оборудовании, доля реактивной нагрузки выше и поэтому для таких приборов в расчетах коэффициент мощности принимают равным 0,8.
На практике принято считать, что при подсчёте электрических нагрузок для бытовых целей запас мощности принимают 5%. В случае расчёта электрических сетей для промышленного производства запас мощности принимают 20%.
Хочется написать ответ на этот вопрос, чтобы расставить все точки над «i». При расчете любых конструкций всплывают оба эти термина. Причем как нагрузки могут быть и в виде сил, и в виде моментов, так и усилия.
Как же не запутаться в этих понятиях и выполнить расчет с пониманием?
Давайте рассмотрим алгоритм любого расчета.
Формула силы тока
Формула для чайников будет выглядеть вот так:
где
I — собственно сила тока, Амперы
N — количество электронов
t — период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:
где
Δq — это заряд за какой-то определенный промежуток времени, Кулон
Δt — тот самый промежуток времени, секунды
I — сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10-19 Кулон. Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока — это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время. Измеряется как Кулон/секунда. Чтобы сэкономить время и по другим морально-эстетическим нормам, Кулон/секунду договорились называть Ампером, в честь французского ученого-физика.
Выполнение расчета для определения усилий.
Усилия – это именно те данные, которые помогают инженеру понять, как же чувствует себя конструкция под воздействием всей совокупности нагрузок. Если нагрузки (внешние силы) – это то, что влияет на схему извне, то усилия – это то, что чувствует каждый элемент расчетной схемы непосредственно на своей шкуре. Человек стал вам на ногу – это нагрузка, приложенная к вашей ноге как к конструкции; вы почувствовали давление веса этого человека, оно вызывает в вас определенные напряжения, деформации – это усилие в вашей ноге.
Если нагрузки (внешние силы) – это то, что влияет на схему извне, то усилия – это то, что чувствует каждый элемент расчетной схемы непосредственно на своей шкуре. Человек стал вам на ногу – это нагрузка, приложенная к вашей ноге как к конструкции; вы почувствовали давление веса этого человека, оно вызывает в вас определенные напряжения, деформации – это усилие в вашей ноге.
Один очень опытный конструктор говорил мне, что при проверке решений других инженеров он представляет себя на месте конструкции. И иногда обнаруживает, что кто-то прицепил значительную нагрузку не на туловище, руки или ноги (в общем, не на выносливые элементы), а подвесил к уху или носу, а то и за волосы попытался зацепиться. Это шутки, но очень глубокие. Если научиться представлять работу конструкции: представлять в виде образов возникающие в ней усилия от всех нагрузок, представлять ее деформации от этих усилий, можно значительно облегчить себе жизнь, да и жизнь конструкции тоже.
Видов усилий не так уж и много, все они собраны в двух понятиях – силы и моменты. Усилие в виде силы всегда прямое, оно либо сжимает, либо растягивает, либо пытается перерезать. Усилие в виде момента пытается изогнуть или закрутить. Если взять стержень (балку, колонну), его «самочувствие» очень просто описать несколькими значениями:
Усилие в виде силы всегда прямое, оно либо сжимает, либо растягивает, либо пытается перерезать. Усилие в виде момента пытается изогнуть или закрутить. Если взять стержень (балку, колонну), его «самочувствие» очень просто описать несколькими значениями:
- продольной силой N, которая либо сжимает, либо растягивает вдоль оси;
- поперечной силой Q, которая пытается срезать стержень поперек сечения (как мы ножом режем морковку) или хотя бы помочь потерять ему устойчивость;
- изгибающим моментом M, который стремится согнуть стержень, искривить его;
- крутящим моментом Т, который пытается скрутить стержень так, как мы выкручиваем мокрое полотенце.
Все это усилия, полученные в результате расчета конструкции (взяты в типовом примере Лиры).
Получается, что нагрузки – это исходные данные для расчета, а усилия – результат. Отчего же тогда возникает путаница в понятиях? Думаю потому, что найденные усилия – это результат не окончательный, а промежуточный. С учетом этих усилий идет дальнейшая проверка несущей способности сечения, рассчитывается и подбирается армирование. И в этом дальнейшем расчете усилия становятся уже на место исходных данных. И у нас вырисовывается следующий этап.
С учетом этих усилий идет дальнейшая проверка несущей способности сечения, рассчитывается и подбирается армирование. И в этом дальнейшем расчете усилия становятся уже на место исходных данных. И у нас вырисовывается следующий этап.
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
От чего зависит ток
Поскольку токовая сила является скалярной величиной, имеющей положительный и отрицательный заряд, то зависит она от мощности заряда, концентрации сосредоточенных в заряде частиц, скорости их движения и площади проводника. Стоит также указать, что зависит она от значения сопротивления с напряжением, величиной магнитного поля, числом катушечных витков, мощностью работы ротора, диаметром проводника и параметром генераторной установки.
Стоит также указать, что зависит она от значения сопротивления с напряжением, величиной магнитного поля, числом катушечных витков, мощностью работы ротора, диаметром проводника и параметром генераторной установки.
Зависимости электротока от сопротивления и напряжения
В чем она измеряется и как посчитать
Сила тока измеряется в амперах – обозначение 1 А. Ампер – одна из семи основных единиц.
1А = 1Кл/c, где Кл (или С) – это кулон, единица измерения количества электрического заряда.
Сила тока обозначается символом I (согласно первой букве французского Intensite´ du courant).
Величина ее определяется по формуле I=qn Vср S cos a, где:
- q – сумма зарядов;
- n – концентрация частиц;
- Vср – средняя скорость их упорядоченного движения;
- S – площадь проводника;
- a – угол между вектором направления движения и вектором нормали (перпендикуляра) к поверхности проводника.
Ампер – единица измерения силы электрического тока.

Электричество
Электричество – это природное явление, подтверждающее существование, взаимодействие и движение электрических зарядов. Электричество впервые было обнаружено еще в VII веке до н.э. греческим философом Фалесом. Фалес обратил внимание на то, что если кусочек янтаря потереть о шерсть, он начинает притягивать к себе легкие предметы. Янтарь на древнегреческом – электрон.
Вот так и представляю себе, сидит Фалес, трет кусок янтаря о свой гиматий (это шерстяная верхняя одежда у древних греков), а затем с озадаченным видом смотрит, как к янтарю притягиваются волосы, обрывки ниток, перья и клочки бумаги.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 13 из 37Следующая ⇒
Сила Ампера в квантовой теории электрического тока имеет гравитационную природу. Рассмотрим механизм её возникновения. Выделение энергии проводником на участке цепи — потребителе тока связано с потреблением внешней энергии от источника тока. При выходе из проводника, гравитон уносит с собой импульс движения
, (7) где — импульс выхода гравитона из проводника, — масса гравитона, — скорость выхода гравитона из проводника. При выходе нескольких электронов из проводника образуется реактивная сила , направленная противоположно направлению выхода гравитонов из проводника. Процесс выхода гравитонов из проводника и его беспорядочное перемещение в результате реакции на выход гравитонов можно наблюдать в специально поставленном эксперименте, при токах порядка А. При прохождении по проводнику тока выделяется количество гравитонов . Рис. 2. При отсутствии внешнего магнитного поля происходит равномерное распределение выхода гравитонов из проводника.
Гравитоны, обладая массой, отличной от нуля, при выходе из проводника приобретают импульс. Этот импульс, в соответствии с третьим законом Ньютона, противоположен импульсу, получаемому проводником. Общий импульс гравитонов равен:
, (8) где — суммарный импульс выхода всех гравитонов. Совсем другая картина получается, если проводник с током находится во внешнем магнитном поле. Внешнее магнитное поле будет затруднять возникновение магнитного поля проводника с одной стороны проводника, и усиливать с другой стороны. В результате этого процесса магнитное поле проводника деформируется (рис. Рис. 3. Внешнее магнитное поле искажает распределение выхода гравитонов из проводника и образует силу Ампера (участок цепи – потребителя тока).
Для описания влияния магнитного поля на выход гравитонов, нужно ввести коэффициент искажения гравитационного поля проводника с током . Равнодействующую силу импульсов выходящих гравитонов в этом случае можно описать формулой: , (9) где — равнодействующая сила импульсов выходящих гравитонов. — сумма импульсов всех гравитонов. — искажение симметрии выхода гравитонов, связанное с воздействием на проводник внешнего магнитного поля. В соответствии с третьим законом Ньютона равнодействующая сила выхода гравитонов уравновешивается силой Ампера
, (10)
И окончательно силу Ампера в квантовой теории электрического тока можно определить по формуле: (11) Сила Ампера зависит как от количества выделившихся гравитонов (величины электрического тока), так и от асимметричности их выхода из проводника (от напряжённости внешнего магнитного поля). Направление силы Ампера в квантовой физической модели электрического тока совпадает с эмпирическим правилом для определения силы Ампера на участке цепи — потребителе тока. «Правило левой руки определяет направление силы, которая действует на находящийся в магнитном поле проводник с током. Если ладонь левой руки расположить так, чтобы вытянутые пальцы были направлены по току, а силовые линии магнитного поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник». [6] Из квантового механизма возникновения силы Ампера видно, что на участке цепи – источнике тока сила Ампера меняет своё направление (рис. 4). Это отражено в эмпирическом правиле правой руки. «Правило правой руки определяет направление индукционного тока в проводнике, движущемся в магнитном поле. Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый палец направить по движениюпроводника, то 4 вытянутых пальца укажут направление индукционного тока». Рис. 4. Внешнее магнитное поле искажает распределение входа гравитонов в проводник и образует силу Ампера (участок цепи – источника тока).
Квантовая теория электрического тока позволяет достаточно просто объяснить одновременное существование правил левой руки и правой руки изменением направления потока энергии в полной цепи электрического тока. В случае работы электрической машины в качестве генератора гравитоны поглощаются проводником с током. В случае работы электрической машины в качестве двигателя гравитоны излучаются. Квантовая теория электрического тока впервые позволила дать объяснение силы Ампера с позиций близкодействия. Квантовая теория электрического тока не противоречит классической электродинамике, а только её дополняет. Силу Ампера в классической электродинамике определяет формулы (1) и (4), в квантовой теории — формула (11). В формуле (11) сомножитель соответствует току в формуле (1) или сомножителю в формуле (4). В формуле (11) соответствует В вформуле (1) и (4). Запись силы Ампера в квантовой теории может быть различна, но смысл силы Ампера как гравитационной силы отличает её от классической электродинамики.
ЛИТЕРАТУРА
1. Фейнмановские лекции по физике. М., Изд. Мир, 1976. 2. Королев Ф.А. Курс физики. Оптика, атомная и ядерная физика: Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. 2-е изд., перераб. М.: Просвещение, 1974. 3. Трофимова Т. И. Курс Физики. «Высшая школа». М.,1997. 4. Ландау Л. Д., Лифшиц Е.М., Квантовая механика. Нерелятивистская теория, 3 изд., М., 1974. 5. Дрюков В.М. Илюхина Н.И. Проектирование новых физических технологий. Вопросыоборонной техники. Научно — технический сборник. № 1-2. М:, Н.Т.Ц. «Информтехника»1995. 6. Советский энциклопедический словарь. М., «Советская энциклопедия.» 1985. 7. Дрюков В.М. Илюхина Н.И. Квантовая физическая модель электрического тока. 8. Дрюков В.М. О чём молчат физики. Тула 2004.
⇐ Предыдущая891011121314151617Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Закон ома физический смысл. Школьная энциклопедия
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.
Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.
Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.
Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.
Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.
Этот круг также, как и треугольник можно назвать магическим.
Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Закон Ома для участка цепи
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
I=12 В/6 Ом=2 А
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.
Чем больше ток – тем больше столкновений – тем больше нагрев.
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
R провод =ρ(L/S)
Где ρ – удельное сопротивление в Ом*мм 2 /м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
U эл =I*R элемента
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Закон Ома для полной цепи
Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:
- напряжение, если это источник ЭДС;
- силу тока, если это источник тока;
Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:
I=ε/(R+r)
Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.
На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.
Закон Ома в дифференциальной и интегральной форме
Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.
Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.
В интегральной форме:
Закон Ома для переменного тока
При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R a и реактивное сопротивление X (или R r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
- Ток в цепи с индуктивностью не может измениться мгновенно.
- Напряжение в цепи с ёмкостью не может измениться мгновенно.
Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.
X L и X C – это реактивные составляющие нагрузки.
В связи с этим вводится величина cosФ:
Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.
Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
При этом сопротивление представляют в комплексной форме:
Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.
Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».
Как запомнить закон Ома
Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:
Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.
Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.
Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:
Вот как это работает:
Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.
Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома». И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.
Нравится(0 ) Не нравится(0 )
Такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома . В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой , и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно
Все в этом мире живет и происходит по своим законам. Маугли, писателя Киплинга, жил по закону джунглей, люди живут по своим писаным законам, так и в физике электрического тока существуют свои законы и один из этих законов называется “закон Ома“. Это очень важный закон, один из основополагающих законов в физике электрического тока, и ты обязан его знать и понимать, если хочешь разбираться в электрике и электронике. Я же постараюсь помочь тебе и объясню для тебя, закон Ома простыми словами .
Это очень важный закон, один из основополагающих законов в физике электрического тока, и ты обязан его знать и понимать, если хочешь разбираться в электрике и электронике. Я же постараюсь помочь тебе и объясню для тебя, закон Ома простыми словами .
Впервые, закон открыл и описал в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость. В честь этого самого Георга Ома и назван закон.
Теперь давай выведем определение закона Ома.
Величина тока на участке цепи, прямо пропорциональна напряжению приложенному к этому участку цепи и обратно пропорциональна его сопротивлению.
Теперь разберем эту абракадабру по частям. Часть первая — Величина тока на участке цепи, прямо пропорциональна напряжению приложенному к этому участку цепи. В принципе все понятно и логично, чем выше напряжение подключенное к цепи, тем больше ток. Вторая часть закона — и обратно пропорциональна его сопротивлению. Это означает что чем больше сопротивление на участке, тем меньше ток.
Вторая часть закона — и обратно пропорциональна его сопротивлению. Это означает что чем больше сопротивление на участке, тем меньше ток.
Формула закона Ома
В этой формуле — I — Сила тока (Ампер), U — Напряжение (Вольт), R — Сопротивление (Ом-).
Прикладываю к этому объяснению шуточный рисунок ты мог видеть его и раньше на других сайтах, это очень хороший “рисунок — пример” многие его используют на страницах своих сайтов.
Как найти силу тока, что такое сила тока — это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
I=U/R — формула тока
U = IR — формула напряжения
Сопротивление — если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.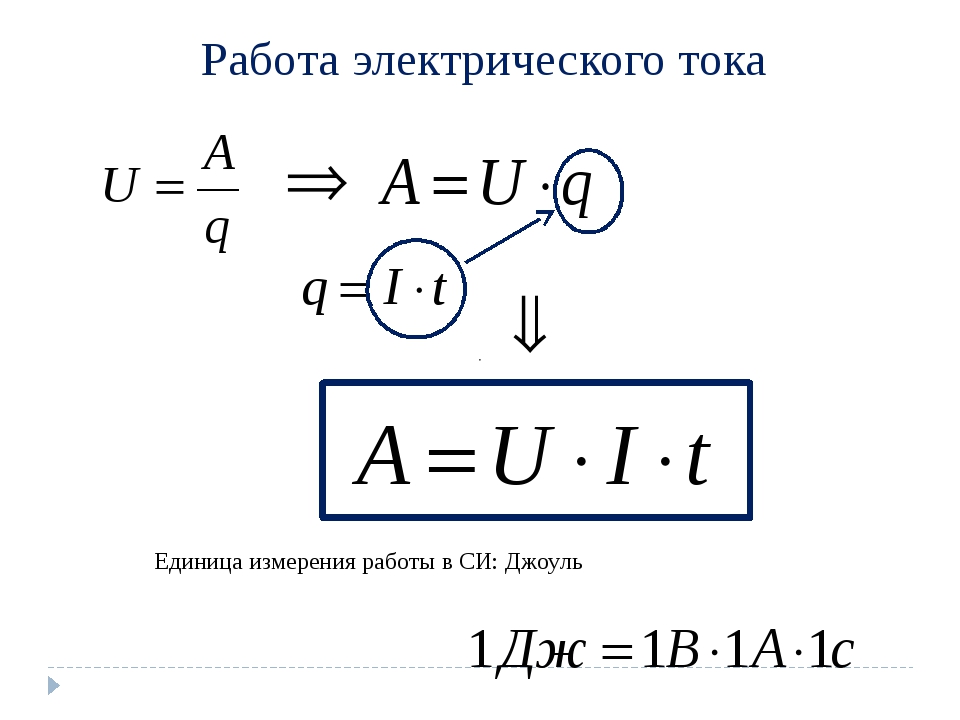
R = U/I — формула сопротивления
Для удобства пользования формулой можно применить такую “фишку “.
Закрывая пальцем на треугольнике, значение, которое нужно определить, видим действие, которое нужно выполнить. Например — если тебе нужно определить значение сопротивления, закроем — R
Теперь ты видишь, какое действие нужно выполнить? Правильно, напряжение U разделить на силу тока I .
Формулы, которые тебе обязательно пригодятся.
Я рассказал тебе очень кратко и простым языком о законе Ома , но этого вполне достаточно, чтобы ты смог самостоятельно на первых парах производить расчеты для своих будущих электронных шедевров!
Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.
В популярной форме этот закон можно сформулировать следующим образом: чем выше напряжение при одном и том же сопротивлении, тем выше сила тока и в то же время чем выше сопротивление при одном и том же напряжении, тем ниже сила тока.
Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.
Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи
записывается следующей формулой:
Поэтому закон Ома для участка цепи
записывается следующей формулой:
I = U/R.
Магический треугольник
Любой участок или элемент электрической цепи можно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
Как использовать треугольник Ома: закрываем искомую величину — два других символа дадут формулу для её вычисления. Кстати, законом Ома называется только одна формула из треугольника – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют.
Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:
ампер = вольт/ом
Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килоомах и мегаомах соответственно.
Другие статьи про электричество в простом и доступном изложении:
Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.
Рис 1. Применение закона Ома для участка цепи
Приведем пример расчета тока по закону Ома . Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.
Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения
U = IR
Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению
. Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.
Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.
Напряжение на участке цепи часто называют падением напряжения
. Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны.
Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.
Умножив I = 0,005 А на R -10000 Ом, получим напряжение,равное 5 0 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В
В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.
Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.
По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.
Сопротивление всегда представляет собой отношение напряжения к току. Если напряжение увеличить или уменьшить в несколько раз, то ток увеличится или уменьшится в такое же число раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.
Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит оттока и напряжения. Известно, что оно зависит от длины, площади сечения и материала проводника. По внешнему виду формула для определения сопротивления напоминает формулу для расчета тока, но между ними имеется принципиальная разница.
Ток в данном участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. А сопротивление данного участка цепи является величиной постоянной, не зависящей от изменения напряжения и тока, но равной отношению этих величин.
Когда один и тот же ток проходит в двух участках цепи, а напряжения, приложенные к ним, различны, то ясно, что участок, к которому приложено большее напряжение, имеет соответственно большее сопротивление.
А если под действием одного и того же напряжения в двух разных участках цепи проходит различный ток, то меньший ток всегда будет на том участке, который имеет большее сопротивление. Все это вытекает из основной формулировки закона Ома для участка цепи, т. е. из того, что ток тем больше, чем больше напряжение и чем меньше сопротивление.
Расчет сопротивления с помощью закона Ома для участка цепи покажем на следующем примере. Пусть требуется найти сопротивление участка, через который при напряжении 40 В проходит ток 50 мА. Выразив ток в амперах, получим I = 0,05 А. Разделим 40 на 0,05 и найдем, что сопротивление составляет 800 Ом.
Закон Ома можно наглядно представить в виде так называемой вольт-амперной характеристики
. Как известно, прямая пропорциональная зависимость между двумя величинами представляет собой прямую линию, проходящую через начало координат. Такую зависимость принято называть линейной
.
Такую зависимость принято называть линейной
.
На рис. 2
показан в качестве примера график закона Ома для участка цепи с сопротивлением 100 Ом. По горизонтальной оси отложено напряжение в вольтах, а по вертикальной оси — ток в амперах. Масштаб тока и напряжения может быть выбран каким угодно. Прямая линия проведена так, что для любой ее точки отношение напряжения к току равно 100 Ом. Например, если U = 50 В, то I
= 0,5 А и R = 50: 0,5 = 100 Ом.
Рис. 2 . Закон Ома (вольт-амперная характеристика)
График закона Ома для отрицательных значений тока и напряжения имеет такой же вид. Это говорит о том, что ток в цепи проходит одинаково в обоих направлениях. Чем больше сопротивление, тем меньше получается ток при данном напряжении и тем более полого идет прямая.
Приборы, у которых вольт-амперная характеристика является прямой линией, проходящей через начало координат, т. е. сопротивление остается постоянным при изменении напряжения или тока, называются линейными приборами
. Применяют также термины линейные цепи, линейные сопротивления.
Применяют также термины линейные цепи, линейные сопротивления.
Существуют также приборы, у которых сопротивление изменяется при изменении напряжения или тока. Тогда зависимость между током и напряжением выражается не по закону Ома, а более сложно. Для таких приборов вольт-амперная характеристика не будет прямой линией, проходящей через начало координат, а является либо кривой, либо ломаной линией. Эти приборы называются нелинейными .
Мнемоническая диаграмма для закона Ома
В чем измеряется работа. Физический смысл работы
Прежде чем раскрывать тему «В чём измеряется работа», необходимо сделать небольшое отступление. Всё в этом мире подчиняется законам физики. Каждый процесс или явление можно объяснить на основе тех или иных законов физики. Для каждой измеряемой величины существует единица, в которой её принято измерять. Единицы измерения являются неизменными и имеют единое значение во всём мире.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-1-768×451. .jpg 1024w»>
.jpg 1024w»>
Система международных единиц
Причиной этого является следующее. В тысяча девятьсот шестидесятом году на одиннадцатой генеральной конференции по мерам и весам была принята система измерений, которая признана во всём мире. Эта система получила наименование Le Système International d’Unités, SI (СИ система интернационал). Эта система стала базовой для определений принятых во всём мире единиц измерения и их соотношения.
Физические термины и терминология
В физике единица измерения работы силы называется Дж (Джоуль), в честь английского учёного физика Джеймса Джоуля, сделавшего большой вклад в развитие раздела термодинамики в физике. Один Джоуль равен работе, совершаемой силой в один Н (Ньютон), при перемещении её приложения на один М (метр) в направлении действия силы. Один Н (Ньютон) равен силе, массой в один кг (килограмм), при ускорении в один м/с2 (метр в секунду) в направлении силы.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-2-2-210×140. jpg 210w»>
jpg 210w»>
Формула нахождения работы
К сведению. В физике всё взаимосвязано, выполнение любой работы связано с выполнением дополнительных действий. В качестве примера можно взять бытовой вентилятор. При включении вентилятора в сеть лопасти вентилятора начинают вращаться. Вращающиеся лопасти воздействуют на поток воздуха, придавая ему направленное движение. Это является результатом работы. Но для выполнения работы необходимо воздействие других сторонних сил, без которых выполнение действия невозможно. К ним относятся сила электрического тока, мощность, напряжение и многие другие взаимосвязанные значения.
Электрический ток, по своей сути, – это упорядоченное движение электронов в проводнике в единицу времени. В основе электрического тока лежит положительно или отрицательно заряжённые частицы. Они носят название электрических зарядов. Обозначается буквами C, q, Кл (Кулон), названо в честь французского учёного и изобретателя Шарля Кулона. В системе СИ является единицей измерения количества заряженных электронов. 1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.
1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-3-768×486..jpg 848w»>
Формула нахождения электрического заряда
Сила электрического тока обозначается буквой А (ампер). Ампер – это единица в физике, характеризующая измерение работы силы, которая затрачивается для перемещения зарядов по проводнику. По своей сути, электрический ток – это упорядоченное движение электронов в проводнике под воздействием электромагнитного поля. Под проводником подразумевается материал или расплав солей (электролит), имеющий небольшую сопротивляемость прохождению электронов. На силу электрического тока влияют две физические величины: напряжение и сопротивление. Они будут рассмотрены ниже. Сила тока всегда прямо пропорциональна по напряжению и обратно пропорциональна по сопротивлению.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-4-768×552..jpg 800w»>
Формула нахождения силы тока
Как было сказано выше, электрический ток – это упорядоченное движение электронов в проводнике. Но есть один нюанс: для их движения нужно определённое воздействие. Это воздействие создаётся путём создания разности потенциалов. Электрический заряд может быть положительным или отрицательным. Положительные заряды всегда стремятся к отрицательным зарядам. Это необходимо для равновесия системы. Разница между количеством положительно и отрицательно заряжённых частиц называется электрическим напряжением.
Gif?.gif 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-5-768×499.gif 768w»>
Формула нахождения напряжения
Мощность – это количество энергии, затрачиваемое на выполнение работы в один Дж (Джоуль) за промежуток времени в одну секунду. Единицей измерения в физике обозначается как Вт (Ватт), в системе СИ W (Watt). Так как рассматривается мощность электрическая, то здесь она является значением затраченной электрической энергии на выполнение определённого действия в промежуток времени.
Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/risunok-6-120×74..jpg 750w»>
Формула нахождения электрической мощности
В заключение следует отметить, что единица измерения работы является скалярной величиной, имеет взаимосвязь со всеми разделами физики и может рассматриваться со стороны не только электродинамики или теплотехники, но и других разделов. В статье кратко рассмотрено значение, характеризующее единицу измерения работы силы.
Видео
Если на тело действует сила, то эта сила совершает работу по перемещению этого тела. Прежде чем дать определение работе при криволинейном движении материальной точки, рассмотрим частные случаи:
В этом случае механическая работа A равна:
A = F s cos =
,
или A = Fcos × s = F S × s ,
где F S – проекция силы на перемещение.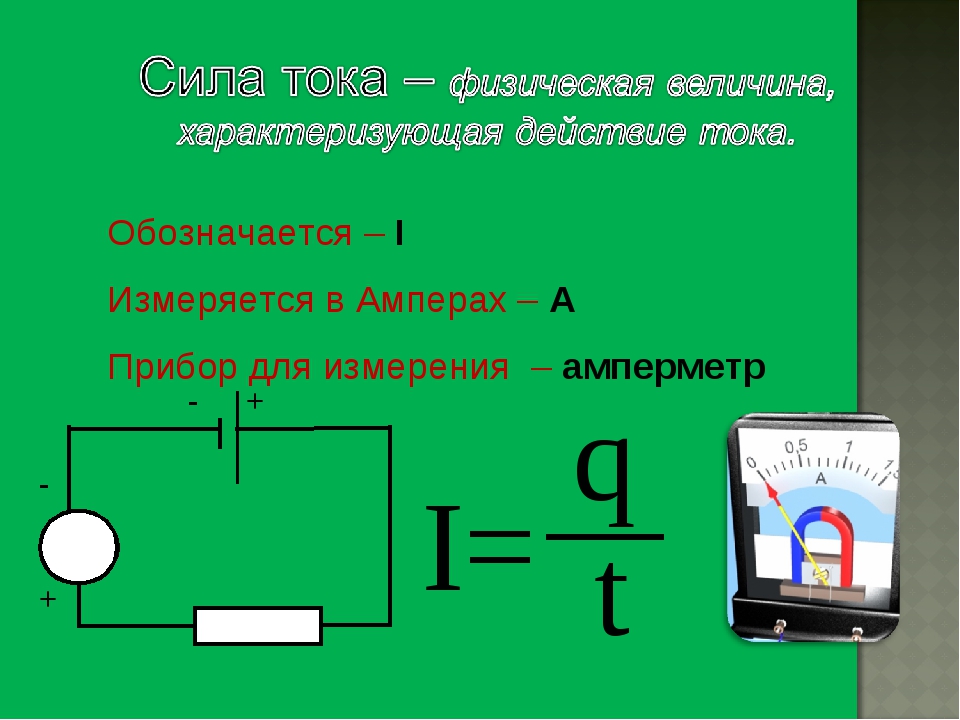 В данном случае F s = const ,
и геометрический смысл работы A – это площадь прямоугольника,
построенного в координатах F S , , s .
В данном случае F s = const ,
и геометрический смысл работы A – это площадь прямоугольника,
построенного в координатах F S , , s .
Построим график
проекции силы на направление перемещения F S как функции перемещения s.
Полное перемещение представим как сумму
n
малых перемещений
.
Для малого i -ого
перемещения
работа равна
или площади заштрихованной трапеции
на рисунке.
Полная механическая работа по перемещению из точки 1 в точку 2 будет равна:
.
Величина, стоящая
под интегралом будет представлять
элементарную работу по бесконечно
малому перемещению
:
– элементарная работа.
Разбиваем траекторию движения материальной точки на бесконечно малые перемещения и работу силы по перемещению материальной точки из точки 1 в точку 2 определяем как криволинейный интеграл:
–работа при
криволинейном движении.
Пример 1: Работа
силы тяжести
при криволинейном движении материальной
точки.
.
Далее как постоянную величину можно вынести за знак интеграла, а интеграл согласно рисунку будет представлять полное перемещение . .
Если обозначить высоту точки 1 от поверхности Земли через , а высоту точки 2 через , то
Мы видим, что в
данном случае работа определяется
положением материальной точки в начальный
и конечный момент времени и не зависит
от формы траектории или пути. Работа
силы тяжести по замкнутому пути равна
нулю:
.
Силы, работа которых на замкнутом пути равна нулю, называется консервативными .
Пример 2 : Работа силы трения.
Это пример неконсервативной силы. Чтобы показать это достаточно рассмотреть элементарную работу силы трения:
,
т.е. работа силы
трения всегда отрицательная величина
и на замкнутом пути не может быть равной
нулю. Работа, совершаемая в единицу
времени, называется мощностью .
Если за время
Работа, совершаемая в единицу
времени, называется мощностью .
Если за время
совершается работа
,
то мощность равна
–механическая мощность .
Взяв
в виде
,
получим для мощности выражение:
.
В СИ единицей
работы является джоуль:
=
1 Дж = 1 Н1
м, а единицей мощности является ватт: 1
Вт = 1 Дж/с.
Механическая энергия.
Энергия является общей количественной мерой движения взаимодействия всех видов материи. Энергия не исчезает и не возникает из нечего: она лишь может переходить из одной формы в другую. Понятие энергии связывает воедино все явления в природе. В соответствии с различными формами движения материи рассматривают разные виды энергии – механическую, внутреннюю, электромагнитную, ядерную и др.
Понятия энергии и работы тесно связаны друг с другом. Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Другими словами работа – это количественная мера изменения энергии:
.
Энергия также как и работа в СИ измеряется в джоулях: [E ]=1 Дж.
Механическая энергия бывает двух видов – кинетическая и потенциальная.
Кинетическая
энергия (или энергия
движения) определяется массами и
скоростями рассматриваемых тел.
Рассмотрим материальную точку, движущуюся
под действием силы
.
Работа этой силы увеличивает кинетическую
энергию материальной точки
.
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
При вычислении
использован
второй закон Ньютона
,
а также
— модуль скорости материальной точки.
Тогда
можно представить в виде:
—
— кинетическая энергия движущейся материальной точки .
Умножив и разделив
это выражение на
,
и учитывая, что
,
получим
—
— связь между импульсом и кинетической энергией движущейся материальной точки .
Потенциальная
энергия (или
энергия положения тел) определяется
действием на тело консервативных сил
и зависит только от положения тела.
Мы видели, что
работу силы тяжести
при криволинейном движении материальной
точки
можно представить в виде разности
значений функции
,
взятых в точке 1 и в точке 2 :
.
Оказывается, что
всегда, когда силы консервативны, работу
этих сил на пути 1
2 можно представить в виде:
.
Функция , которая зависит только от положения тела – называется потенциальной энергией .
Тогда для элементарной работы получим
–работа равна убыли потенциальной энергии .
Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.
Величину , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:
–полная механическая энергия тела .
В заключении
заметим, что используя второй закон
Ньютона
,
дифференциал кинетической энергии
можно представить в виде:
.
Дифференциал
потенциальной энергии
,
как указывали выше, равен:
.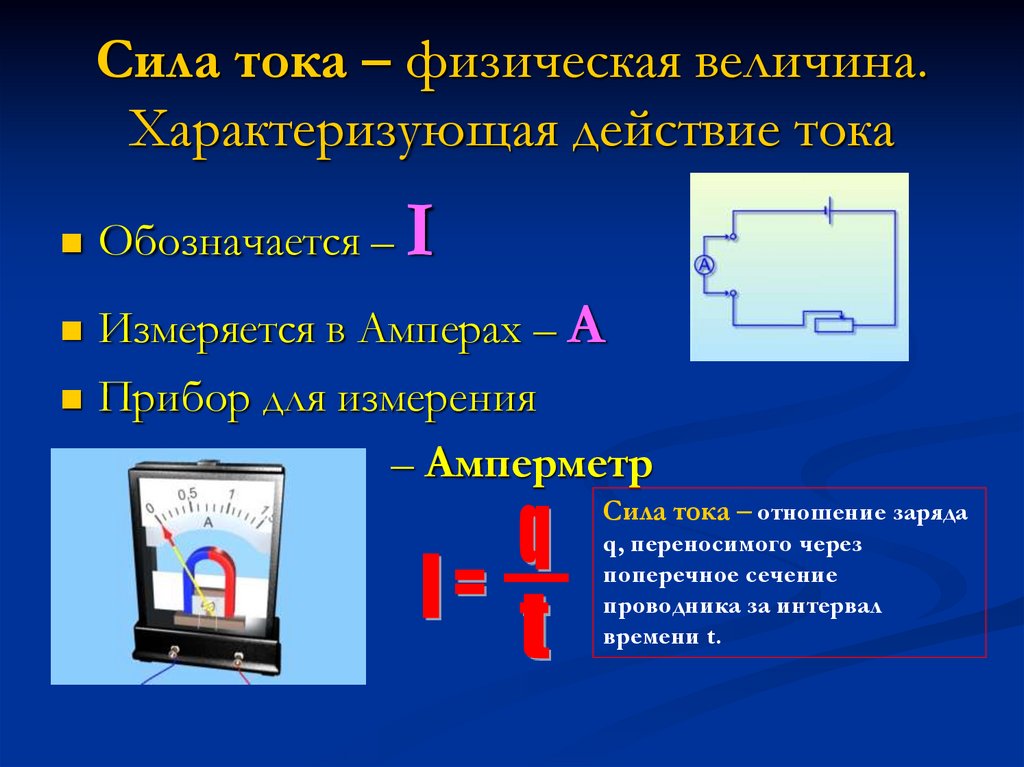
Таким образом, если сила – консервативная сила и отсутствуют другие внешние силы, то , т.е. в этом случае полная механическая энергия тела сохраняется.
Механическая работа. Единицы работы.
В обыденной жизни под понятием «работа» мы понимаем всё.
В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа .
Рассмотрим примеры механической работы.
Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули при этом увеличивается.
Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.
Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.
Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.
Итак, механическая работа совершается, только когда на тело действует сила, и оно движется .
Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.
Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути .
Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:
работа = сила × путь
где А — работа, F — сила и s — пройденный путь.
За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.
Единица работы — джоуль (Дж ) названа в честь английского ученого Джоуля. Таким образом,
1 Дж = 1Н · м.
Используется также килоджоули (кДж ) .
1 кДж = 1000 Дж.
Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.
Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.
Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.
Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:
В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.
Пример . Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м3 на высоту 20 м. Плотность гранита 2500 кг/м 3 .
Дано :
ρ = 2500 кг/м 3
Решение :
где F -сила, которую нужно приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, т. е. F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, т. е. путь равен высоте подъема.
Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, т. е. F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, т. е. путь равен высоте подъема.
Итак, m = 2500 кг/м3 · 0,5 м3 = 1250 кг.
F = 9,8 Н/кг · 1250 кг ≈ 12 250 Н.
A = 12 250 Н · 20 м = 245 000 Дж = 245 кДж.
Ответ : А =245 кДж.
Рычаги.Мощность.Энергия
На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10-12 ч, трактор же с многолемешным плугом (лемех — часть плуга, подрезающая пласт земли снизу и передающая его на отвал; многолемешный — много лемехов), эту работу выполнит на 40-50 мин.
Ясно, что подъемный кран ту же работу совершает быстрее, чем рабочий, а трактор — быстрее чем лошадь. Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.
Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.
Мощность равна отношению работы ко времени, за которое она была совершена.
Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа. мощность = работа/время.
где N — мощность, A — работа, t — время выполненной работы.
Мощность — величина постоянная, когда за каждую секунду совершается одинаковая работа, в других случаях отношение A/t определяет среднюю мощность:
N ср = A/t . За единицу мощности приняли такую мощность, при которой в 1 с совершается работа в Дж.
Эта единица называется ваттом (Вт ) в честь еще одного английского ученого Уатта.
1 ватт = 1 джоуль/ 1 секунда , или 1 Вт = 1 Дж/с.
Ватт (джоуль в секунду) — Вт (1 Дж/с).
В технике широко используется более крупные единицы мощности — киловатт (кВт ), мегаватт (МВт ) .
1 МВт = 1 000 000 Вт
1 кВт = 1000 Вт
1 мВт = 0,001 Вт
1 Вт = 0,000001 МВт
1 Вт = 0,001 кВт
1 Вт = 1000 мВт
Пример . Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 м3 в минуту.
Дано :
ρ = 1000 кг/м3
Решение :
Масса падающей воды: m = ρV ,
m = 1000 кг/м3 · 120 м3 = 120 000 кг (12 · 104 кг).
Сила тяжести, действующая на воду:
F = 9.8 м/с2 · 120 000 кг ≈ 1 200 000 Н (12 · 105 Н)
Работа, совершаемая потоком в минуту:
А — 1 200 000 Н · 25 м = 30 000 000 Дж (3 · 107 Дж).
Мощность потока: N = A/t,
N = 30 000 000 Дж / 60 с = 500 000 Вт = 0,5 МВт.
Ответ : N = 0.5 МВт.
Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до сотен тысяч киловатт (водяные и паровые турбины).
Таблица 5.
Мощность некоторых двигателей, кВт.
На каждом двигателе имеется табличка (паспорт двигателя), на которой указаны некоторые данные о двигателе, в том числе и его мощность.
Мощность человека при нормальный условиях работы в среднем равна 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и еще бóльшую.
Из формулы N = A/t следует, что
Чтобы вычислить работу, необходимо мощность умножить на время, в течение которого совершалась эта работа.
Пример. Двигатель комнатного вентилятора имеет мощность 35 Вт. Какую работу он совершает за 10 мин?
Запишем условие задачи и решим ее.
Дано :
Решение :
A = 35 Вт * 600с = 21 000 Вт* с = 21 000 Дж = 21 кДж.
Ответ A = 21 кДж.
Простые механизмы.
С незапамятных времен человек использует для совершения механической работы различные приспособления.
Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно сдвинуть руками, можно сдвинуть с помощью достаточно длинной палки — рычага.
На данный момент считается, что с помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.
Во многих случаях, вместо того, чтобы поднимать тяжелый груз на некоторую высоту, его можно вкатывать или втаскивать на ту же высоту по наклонной плоскости или поднимать с помощью блоков.
Приспособления, служащие для преобразования силы, называются механизмами .
К простым механизмам относятся: рычаги и его разновидности — блок, ворот; наклонная плоскость и ее разновидности — клин, винт . В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, т. е. увеличить силу, действующую на тело, в несколько раз.
Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручивают и штампуют большие листы стали или вытягивают тончайшие нити, из которых делаются потом ткани. Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.
Рычаг. Равновесие сил на рычаге.
Рассмотрим самый простой и распространенный механизм — рычаг.
Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.
На рисунках показано, как рабочий для поднятия груза в качестве рычага, использует лом. В первом случае рабочий с силой F нажимает на конец лома B , во втором — приподнимает конец B .
Рабочему нужно преодолеть вес груза P — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О . Сила F , с которой рабочий действует на рычаг, меньше силы P , таким образом, рабочий получает выигрыш в силе . При помощи рычага можно поднять такой тяжелый груз, который своими силами поднять нельзя.
На рисунке изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В . На другом рисунке показана схема этого рычага. Обе силы F 1 и F 2, действующие на рычаг, направлены в одну сторону.
На другом рисунке показана схема этого рычага. Обе силы F 1 и F 2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы. На рисунке показано, что ОА — плечо силы F 1; ОВ — плечо силы F 2 . Силы, действующие на рычаг могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F 1 вращает рычаг по ходу часовой стрелки, а сила F 2 вращает его против часовой стрелки.
Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы, зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу, или как направлена.
К рычагу (см рис.) по обе стороны от точки опоры подвешиваются различные грузы так, что каждый раз рычаг оставался в равновесии. Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н . При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.
На основании таких опытов было установлено условие (правило) равновесия рычага.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Это правило можно записать в виде формулы:
F 1/F 2 = l2/ l1 ,
где F 1 и F2 — силы, действующие на рычаг, l 1 и l2 , — плечи этих сил (см. рис.).
Правило равновесия рычага было установлено Архимедом около 287 — 212 гг. до н. э. (но ведь в прошлом параграфе говорилось, что рычаги использовались египтянами? Или тут важную роль играет слово «установлено»?)
Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага бóльшую силу. Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.
Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.
Пример . С помощью рычага рабочий поднимает плиту массой 240 кг (см рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?
Запишем условие задачи, и решим ее.
Дано :
Решение :
По правилу равновесия рычага F1/F2 = l2/l1, откуда F1 = F2 l2/l1, где F2 = Р — вес камня. Вес камня asd = gm, F = 9,8 Н · 240 кг ≈ 2400 Н
Тогда, F1 = 2400 Н · 0,6/2,4 = 600 Н.
Ответ : F1 = 600 Н.
В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес камня (l 1 : l2 = 2,4 м: 0,6 м = 4).
Применяя правило рычага, можно меньшей силой уравновесить бóльшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Момент силы.
Вам уже известно правило равновесия рычага:
F 1 / F2 = l 2 / l1 ,
Пользуясь свойством пропорции (произведение ее крайних членов, равно произведению ее средних членов), запишем его в таком виде:
F 1l 1 = F2 l2 .
В левой части равенства стоит произведение силы F 1 на ее плечо l 1, а в правой — произведение силы F 2 на ее плечо l 2 .
Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы ; он обозначается буквой М. Значит,
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов , можно записать в виде формулы:
М1 = М2
Действительно, в рассмотренном нами опыте, (§ 56) действующие силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 давления рычага, т. е. моменты этих сил одинаковы при равновесии рычага.
е. моменты этих сил одинаковы при равновесии рычага.
Момент силы, как и всякая физическая величина, может быть измерена. За единицу момента силы принимается момент силы в 1 Н, плечо которой ровно 1 м.
Эта единица называется ньютон-метр (Н · м ).
Момент силы характеризует действие силы, и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила. Гайку, лучше отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка вóрота, и т. д.
Рычаги в технике, быту и природе.
Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.
Выигрыш в силе мы имеем при работе с ножницами. Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F 1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F 2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.
Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F 1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F 2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.
Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.
Примеры применения рычагов — это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.
На принципе рычага основано действие и рычажных весов (рис.). Учебные весы, изображенные на рисунке 48 (с. 42), действуют как равноплечий рычаг . В десятичных весах плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.
Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.
Рычаги встречаются также в разных частях тела животных и человека. Это, например, руки, ноги, челюсти. Много рычагов можно найти в теле насекомых (прочитав книгу про насекомых и строение их тела), птиц, в строении растений.
Применение закона равновесия рычага к блоку.
Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускается веревка, трос или цепь.
Неподвижным блоком называется такой блок, ось которого закреплена, и при подъеме грузов не поднимается и не опускается (рис).
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис): ОА = ОВ = r . Такой блок не дает выигрыша в силе. (F 1 = F 2), но позволяет менять направление действие силы. Подвижный блок — это блок. ось которого поднимается и опускается вместе с грузом (рис.). На рисунке показан соответствующий ему рычаг: О — точка опоры рычага, ОА — плечо силы Р и ОВ — плечо силы F . Так как плечо ОВ в 2 раза больше плеча ОА , то сила F в 2 раза меньше силы Р :
F = P/2 .
Таким образом, подвижный блок дает выигрыш в силе в 2 раза .
Это можно доказать и пользуясь понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р , а, значит, сама сила F в 2 раза меньше силы Р .
При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р , а, значит, сама сила F в 2 раза меньше силы Р .
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.). Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы. Например, позволяет поднимать груз, стоя на земле. Это пригождается многим людям или рабочим. Тем не менее, он даёт выигрыш в силе в 2 раза больше обычного!
Равенство работ при использовании простых механизмов. «Золотое правило» механики.
Рассмотренные нами простые механизмы применяются при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Естественно, возникает вопрос: давая выигрыш в силе или пути, не дают ли простые механизмы выигрыша в работе? Ответ на поставленный вопрос можно получить из опыта.
Уравновесив на рычаге две какие-нибудь разные по модулю силы F 1 и F 2 (рис. ), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F 2 проходит больший путь s 2 , а точка приложения большей силы F 1 — меньший путь s 1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F 2 проходит больший путь s 2 , а точка приложения большей силы F 1 — меньший путь s 1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
s 1 / s 2 = F 2 / F 1.
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.
Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:
F 1 s 1 = F 2 s 2, т. е. А 1 = А 2.
Итак, при использовании рычага выигрыша в работе не получится.
Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Действуя же силой на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проигрываем в силе.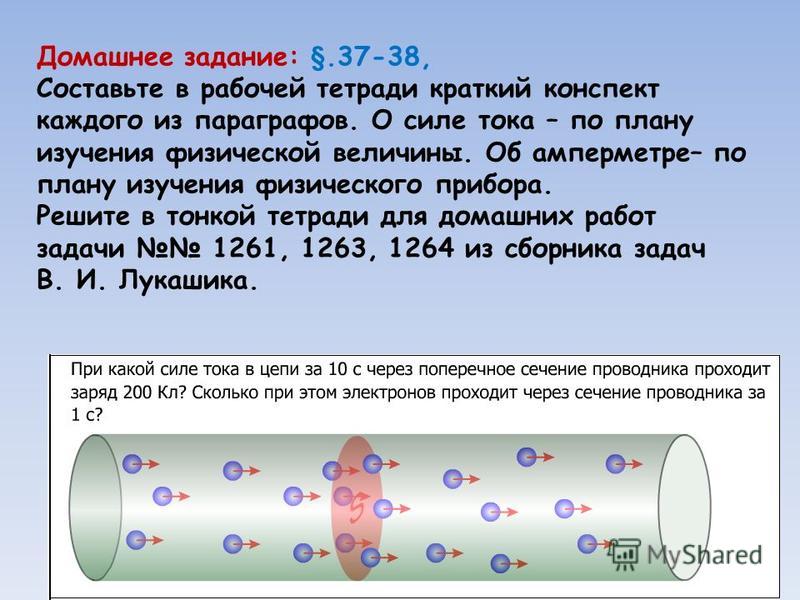
Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я переверну Землю!».
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали бы точку опоры (которая должна была бы быть вне Земли) и рычаг нужной длины.
Для подъема земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например, со скоростью 1 м/с, потребовались бы миллионы лет!
Не дает выигрыша в работе и неподвижный блок, в чем легко убедиться на опыте (см. рис.). Пути, проходимые точками приложения сил F и F , одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис.), переместить на высоту 2h.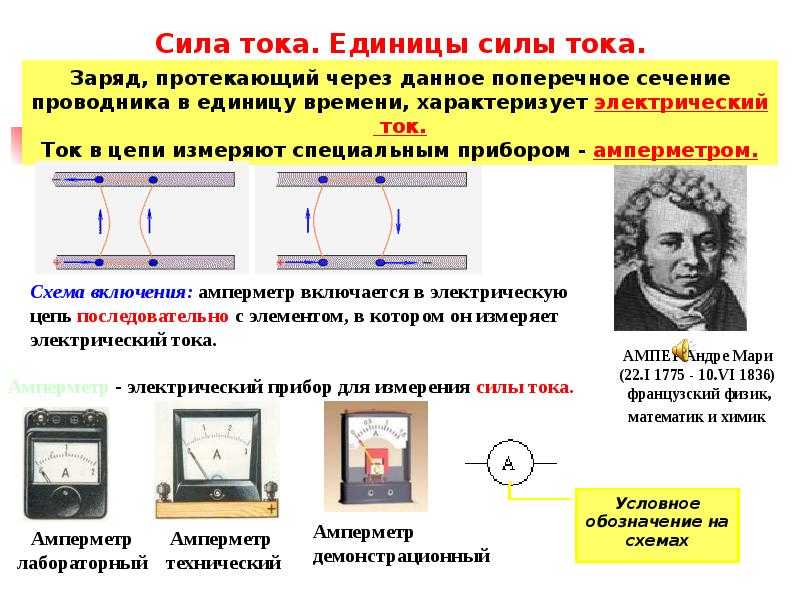
Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок, на дает выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не дает выигрыш в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.
Уже древним ученым было известно правило, применимое ко всем механизмом: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.
Коэффициент полезного действия механизма.
Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. в этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной ), равна полезной работе по подъему грузов или преодоления какого — либо сопротивления.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.
Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по определению силы трения в оси блока.
Какой мы механизм мы не взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Значит, обозначив полезную работу буквой Ап, полную(затраченную) работу буквой Аз, можно записать:
Ап
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД = Ап / Аз.
КПД обычно выражается в процентах и обозначается греческой буквой η, читается он как «эта»:
η = Ап / Аз · 100%.
Пример : На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложена сила 250 Н. Груз подняли на высоту h2 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h3 = 0,4 м.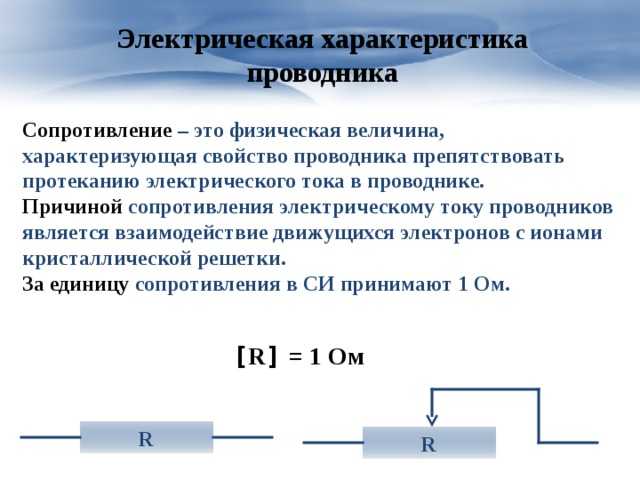 Найти КПД рычага.
Найти КПД рычага.
Запишем условие задачи и решим ее.
Дано :
Решение :
η = Ап / Аз · 100%.
Полная (затраченная) работа Аз = Fh3.
Полезная работа Ап = Рh2
Р = 9,8 · 100 кг ≈ 1000 Н.
Ап = 1000 Н · 0,08 = 80 Дж.
Аз = 250 Н · 0,4 м = 100 Дж.
η = 80 Дж/100 Дж · 100% = 80%.
Ответ : η = 80%.
Но «золотое правило» выполняется и в этом случае. Часть полезной работы — 20% ее-расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.
КПД любого механизма всегда меньше 100%. Конструируя механизмы, люди стремятся увеличить их КПД. Для этого уменьшаются трение в осях механизмов и их вес.
Энергия.
На заводах и фабриках, станки и машины приводятся в движения с помощью электродвигателей, которые расходуют при этом электрическую энергию (отсюда и название).
Сжатая пружина (рис), распрямляясь, совершить работу, поднять на высоту груз, или заставить двигаться тележку. Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю). Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа. Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, говорится, что они обладают энергией. Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергия выражается в системе СИ в тех же единицах, что и работу, т. е. в джоулях . Чем большую работу может совершить тело, тем большей энергией оно обладает. При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии. Потенциальная и кинетическая энергия.Потенциальной (от лат. Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия зависит от взаимного положения его и Земли. и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Е п, поскольку Е = А , а работа, как мы знаем, равна произведению силы на путь, то А = Fh , где F — сила тяжести. Значит, и потенциальная энергия Еп равна: Е = Fh, или Е = gmh, где g — ускорение свободного падения, m — масса тела, h — высота, на которую поднято тело. Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Потенциальную энергию молота копра (рис.) используют в строительстве для совершению работы по забиванию свай. Открывая дверь с пружиной, совершается работа по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь. Энергию сжатых и раскрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр. Потенциальной энергией обладает всякое упругое деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д. Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией. Кинетическая энергия тела обозначается буквой Е к. Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер. От чего зависит кинетическая энергия? Обратимся к опыту (см. рис.). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он продвигает брусок, т. е. совершает большую работу. Значит, кинетическая энергия тела зависит от его скорости. За счет скорости большой кинетической энергией обладает летящая пуля. Кинетическая энергия тела зависит и от его массы. Еще раз проделаем наш опыт, но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, т. е. будет совершена бóльшая работа. Значит, и кинетическая энергия второго шарика, больше, чем первого. Чем больше масса тела и скорость, с которой он движется, тем больше его кинетическая энергия. Для того чтобы определить кинетическую энергию тела, применяется формула: Ек = mv^2 /2, где m — масса тела, v — скорость движения тела. Кинетическую энергию тел используют в технике. Удерживаемая плотиной вода обладает, как было уже сказано, большой потенциальной энергией. При падении с плотины вода движется и имеет такую же большую кинетическую энергию. Она приводит в движение турбину, соединенную с генератором электрического тока. За счет кинетической энергии воды вырабатывается электрическая энергия. Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций. Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива. Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией. Мы познакомились с двумя видами механической энергии. Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики. Превращение одного вида механической энергии в другой. Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображенном на рисунке. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.) Поднявшись вверх, диск снова падает, а затем снова поднимается. В этом опыте при движении диска вниз его потенциальная энергия превращается в кинетическую, а при движении вверх кинетическая превращается в потенциальную. Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту. Если поднять над стальной плитой стальной шарик (рис) и выпустить его из рук, он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик, примут свою первоначальную форму. Шарик отскочит от плиты, а их потенциальная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а значит, и его кинетическая энергия уменьшаются, потенциальная энергия увеличивается. отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся его кинетическая энергия вновь превратится в потенциальную. Явления природы обычно сопровождается превращением одного вида энергии в другой. Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы. |
«Работа» — Примеры механической работы. Задача. Груз не сдвинулся с места, проделанный путь равен 0. Кто прошел больший путь. Мешок с картошкой перетащили на 2м. Джеймс Прескотт Джоуль. Какую работу нужно совершить, чтобы положить гантель на стол. Формула для расчета работы. Внутренняя энергия газа не зависит от занимаемого им объема.
«Энергия и работа» — Потенциальная энергия. Пороховые газы действуют всего на расстоянии 1м. Пример действия кинетической энергии. Формы энергии. Пример действия потенциальной энергии. Из вертикально поставленной пушки длинной 1м вылетает ядро весом 1кг. Пример действия тепловой энергии. Как произвести килограммометр работы.
«Физика «Мощность, энергия, работа»» — Работа. Работа равна скалярному произведению. Человек перемещает санки. Сумма кинетической и потенциальной энергий. Работа, мощность, энергия. Человек в хорошей физической форме. Понятие мощности. Скорость движения после неупругого удара. Электроновольт. Работа, совершаемая консервативной силой. Кинетическая энергия.
Сумма кинетической и потенциальной энергий. Работа, мощность, энергия. Человек в хорошей физической форме. Понятие мощности. Скорость движения после неупругого удара. Электроновольт. Работа, совершаемая консервативной силой. Кинетическая энергия.
«Механическая работа физика» — Единица работы – джоуль (Дж). Значения слова «работа». Механическая работа. Понятие работы в физике. 1 МДж =1 000 000Дж. Движение по инерции. За единицу работы принимают работу, совершаемую силой в 1Н, на пути, равном 1м. 1 кДж =1000Дж. Единицы работы. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.
«Задачи на работу и мощность» — Условие. При последовательном соединении токи одинаковы. КПД кипятильника 80%. Параллельное соединение. Формулы работы и мощности электрического тока. Кипятильник с КПД 80% изготовлен из нихромовой проволоки. Выразили длину проволоки из формулы. На каком резисторе выделяется большая тепловая мощность.
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Определение 1
Работа А, совершаемая постоянной силой F → , — это физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α , располагаемого между векторами силы F → и перемещением s → .
Данное определение рассматривается на рисунке 1 . 18 . 1 .
Формула работы записывается как,
A = F s cos α .
Работа – это скалярная величина. Это дает возможность быть положительной при (0 ° ≤ α
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1 . 18 . 1 . Работа силы F → : A = F s cos α = F s s
При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:
A = ∑ ∆ A i = ∑ F s i ∆ s i .
Данная сумма работы вычисляется из предела (Δ s i → 0) , после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s (x) рисунка 1 . 18 . 2 .
Рисунок 1 . 18 . 2 . Графическое определение работы Δ A i = F s i Δ s i .
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 1 . 18 . 3 .
Рисунок 1 . 18 . 3 . Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.
F → у п р = — F →
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
Рисунок 1 . 18 . 4 . Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
Формула примет вид
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.
Определение 2
Если на тело действует несколько сил, то формула общей работы будет выглядеть, как сумма всех работ, совершаемых над ним. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Рисунок 1 . 18 . 5 . Модель механической работы.
Определение мощности
Определение 3
Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
Определение 4
Система С И использует в качестве единицы мощности ватт (В т) , равняющийся мощности силы, которая совершает работу в 1 Д ж за время 1 с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
определение силы тока| Словарь определений английского языка
adj
1 настоящего времени; в процессе
текущие события
2 самые последние; актуальный
текущий номер журнала
3 общеизвестный, практикуемый или общепринятый; широко распространенный
ходячий слух
4 обращающийся и действительный в настоящее время
текущие монеты
n
5 (особенно воды или воздуха) постоянный, обычно естественный поток
6 масса воздуха, водоема и т. д., который имеет постоянный поток в определенном направлении
7 скорость потока такой массы
8 (Также называется) электрический ток (Физика)
а поток электрического заряда через проводник
b скорость потока этого заряда. Обычно измеряется в амперах., (Символ) I
Обычно измеряется в амперах., (Символ) I
9 общая тенденция или дрейф
течения мнений
(C13: от старофранцузского corant, буквально: бег, от corre к бегу, от латинского currere)
♦ в настоящее время adv
♦ ток п
переменный ток AC Сравнить → постоянный ток
Cromwell Current
N Экваториальное Тихоокеанское теч, текущий на восток от Гавайских островов на Галапагосские острова
(C20: назван в честь Т. Кромвеля (1922–58), океанический океан США)
текущий счет
n
1 счет в банке или строительном кооперативе, по которому в любое время могут быть выписаны чеки, (название в США) расчетный счет (название в Канаде) текущий счет счет операций с капиталом → 1
оборотные средства
pl n денежные средства и операционные активы, которые могут быть конвертированы в денежные средства в течение года, (также называемые) оборотные средства Сравнить →
основные средства
учет по текущей стоимости
n метод учета, при котором активы оцениваются по их текущей восстановительной стоимости, а не по их первоначальной стоимости. Он часто используется во время высокой инфляции
Он часто используется во время высокой инфляции
Сравнить →
учет исторической стоимости
плотность тока
n отношение электрического тока, протекающего в определенной точке проводника, к площади поперечного сечения проводника, взятой перпендикулярно току, протекающему в этой точке. Измеряется в амперах на квадратный метр., (символ) Дж
Выход по току
n (Физика) отношение фактической массы вещества, выделившегося из электролита при прохождении тока, к теоретической массе, выделившейся по закону Фарадея
current expenses
pl n noncapital and usually recurrent expenditures necessary for the operation of a business
current liabilities
pl n business liabilities maturing within a year
dark current
n остаточный ток, создаваемый фотоэлектрическим устройством, когда он не освещен
постоянный ток
n постоянный электрический ток, протекающий только в одном направлении без существенного изменения величины, (аббревиатура) DC Сравнить →
переменный ток
вихревой ток
n электрический ток, индуцируемый переменным магнитным полем в массивном проводнике, таком как сердечник электромагнита, трансформатор и т. д., (также называется) ток Фуко
д., (также называется) ток Фуко
электрический ток
n другое название →
текущий →
8
ток Фуко
n другое название для →
вихревое течение
Течение Гумбольдта
n холодное океаническое течение в южной части Тихого океана, текущее на север вдоль побережий Чили и Перу, (также называемое) Перуанское течение
Японское течение
n теплое океаническое течение, текущее на северо-восток от восточного побережья Японии в сторону северной части Тихого океана, (также называемое) Куросио
Лабрадорское течение
n холодное океаническое течение, текущее на юг от побережья Лабрадора и встречающееся с теплым Гольфстримом, вызывающее густые туманы у Ньюфаундлендского течения
n другое имя для → Humboldt Current
устройство защитного отключения
adv
n устройство отключения цепи, устанавливаемое в электрическом оборудовании для защиты оператора от поражения электрическим током, (сокращение) УЗО
термоэмиссионный ток
n электрический ток, возникающий между двумя электродами в результате испускания электронов в результате термоэлектронной эмиссии
мутное течение
n вихревая масса воды и взвешенных веществ, поднятая цунами, штормом, разливом реки и т.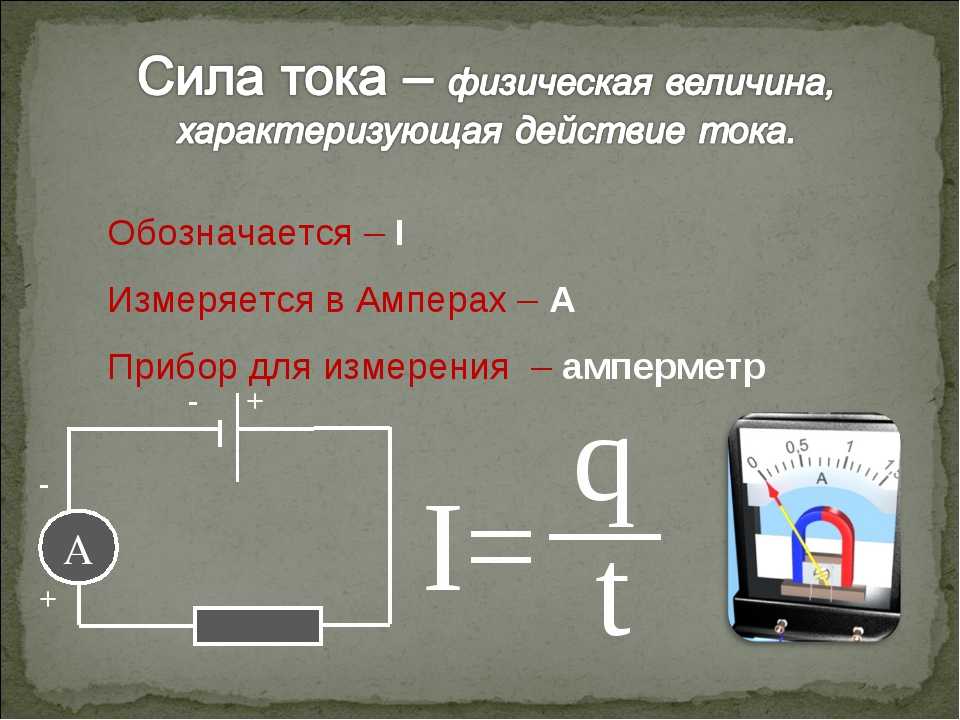 д.
д.
Мышечная сила: польза, упражнения002
и др. Под выносливостью понимается способность мышцы выдерживать повторяющиеся сокращения, преодолевая сопротивление, в течение длительного периода времени. Чтобы увеличить мышечную выносливость, вы должны заниматься деятельностью, которая нагружает ваши мышцы больше, чем обычно, например, приседаниями, отжиманиями или прыжками.
Мышечная сила связана с вашей способностью передвигать и поднимать предметы. Он измеряется тем, какую силу вы можете приложить и какой вес вы можете поднять за короткий промежуток времени.
Примеры упражнений, которые развивают мышечную силу и мощь, включают силовые тренировки, такие как поднятие тяжестей, упражнения с собственным весом и упражнения с эспандером. Бег, езда на велосипеде и восхождение на холмы также являются вариантами.
Читайте дальше, чтобы узнать больше о разнице между мышечной силой и мышечной выносливостью, а также о преимуществах мышечной силы, предостережениях и упражнениях.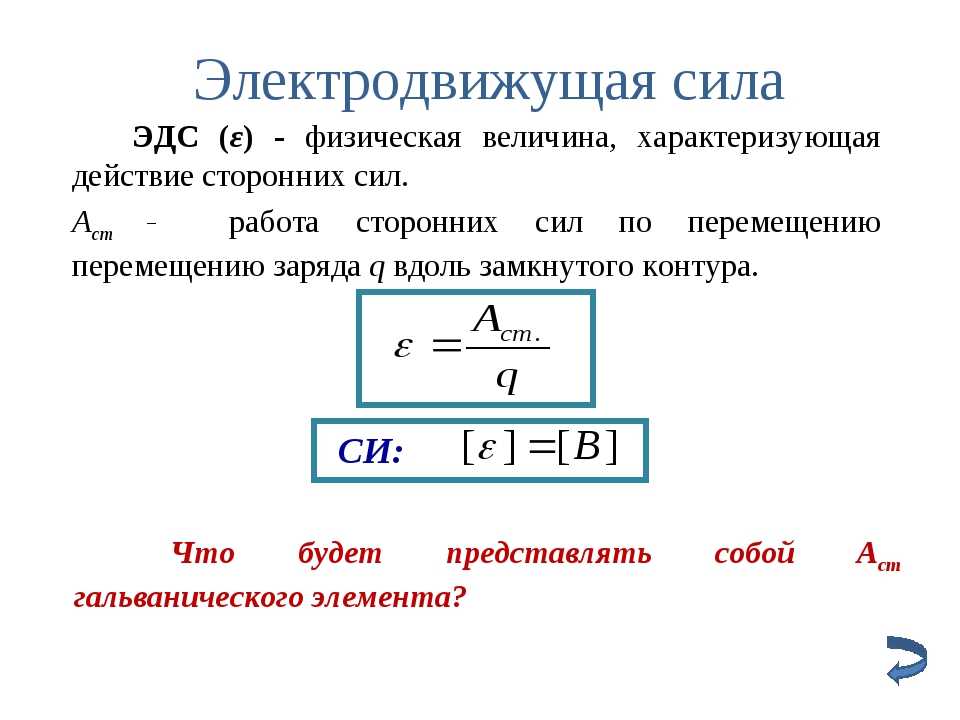
Несмотря на то, что мышечная сила и мышечная выносливость в чем-то схожи, у них есть несколько ключевых отличий. Мышечная сила определяется тем, какую силу вы можете приложить или какой вес вы можете поднять. Для наращивания мышечной силы используются более тяжелые веса для меньшего количества повторений.
Мышечная выносливость относится к способности мышцы выдерживать повторяющиеся сокращения вопреки сопротивлению в течение продолжительного периода времени.
К видам деятельности, повышающим мышечную выносливость, относятся бег на длинные дистанции, езда на велосипеде или плавание, а также круговые тренировки и упражнения с собственным весом. Вы можете улучшить мышечную силу и выносливость, выполняя повторяющиеся движения до изнеможения.
Мышечная сила улучшает общее состояние здоровья и повышает спортивную активность.
- Сильное тело позволяет выполнять движения и действия, требующие силы, без усталости.
- Мышечная сила помогает поддерживать здоровый вес тела за счет сжигания калорий и улучшения состава тела, то есть соотношения жира и мышц.

- Наращивание силы также может повысить настроение и уровень энергии, способствуя здоровому сну. Это может повысить уверенность в себе, дать чувство выполненного долга и позволить вам добавить более сложные или напряженные занятия в свою физическую форму.
- Развитие мышечной силы помогает укрепить крепкие и здоровые мышцы и кости. Это помогает выработать хорошую осанку и облегчить боль в спине.
- У вас будет больше стабильности, баланса и гибкости, что снизит вероятность травм и падений.
Чтобы нарастить мышечную силу, размер и мощность, выполняйте упражнения и упражнения, которые заставляют вас работать с мышцами сильнее, чем обычно.
Поскольку вы сосредоточены на том, чтобы стать сильнее, вы можете попробовать интенсифицировать упражнения, используя более тяжелые веса и увеличивая сопротивление тела, даже если это означает, что вы делаете меньше повторений.
Выполняйте эти упражнения по крайней мере два раза в неделю. Если у вас нет времени на более длительную сессию, сделайте несколько подходов в течение дня.
Посмотрите это видео, чтобы продемонстрировать некоторые из следующих упражнений.
Приседания
Сядьте на стул во время приседания, чтобы упростить это упражнение. Чтобы увеличить интенсивность, держите гантели или штангу на уровне груди.
Поделиться на Pinterest
Чтобы сделать
- Встаньте, поставив ноги немного шире, чем расстояние между бедрами.
- Медленно согните колени, чтобы присесть.
- Сделайте паузу в этом положении, прежде чем вернуться в исходное положение.
- Сделайте от 2 до 3 подходов по 8–12 повторений.
Сгибание рук на бицепс
Для этого упражнения вам понадобятся гантели или штанга.
Поделиться на Pinterest
Чтобы сделать
- Встаньте, ноги на ширине плеч, колени слегка согнуты.
- Положите руки вдоль туловища ладонями вверх.
- Подтяните локти к телу, медленно поднимая вес.
- Сделайте паузу, а затем медленно опустите руки в исходное положение.

- Сделайте от 2 до 3 подходов по 8–12 повторений.
Модифицированные отжимания
Когда вы освоите форму этого упражнения, попробуйте выполнять стандартные отжимания с поднятыми коленями и вытянутыми ступнями позади себя.
Поделиться на Pinterest
Чтобы сделать это
- Из положения на столе поднимите ноги от пола.
- Держите голову, шею и позвоночник на одной линии, медленно опуская тело к полу.
- Медленно вернитесь в исходное положение.
- Сделайте от 2 до 3 подходов по 8–12 повторений.
Планка для предплечий
Этот вариант планки — хороший вариант, если у вас есть проблемы с запястьями.
Поделиться на Pinterest
Чтобы сделать это
- Из положения на столе вытяните ступни и ноги.
- Встаньте на предплечья, положив локти под плечи и вытянув руки.
- Выровняйте шею, позвоночник и бедра так, чтобы они образовывали прямую линию с телом.
- Удерживайте это положение до 1 минуты.

- Сделайте это 2-3 раза.
Скручивания брюшного пресса
Это упражнение нацелено на спину и кор для улучшения устойчивости и хорошей осанки.
Поделиться на Pinterest
Чтобы сделать это
- Лягте на спину, сцепив пальцы у основания черепа.
- Согните колени, чтобы ступни оказались ближе к пояснице.
- Медленно оторвите голову и лопатки от пола.
- Сделайте паузу на несколько счетов, прежде чем опуститься в исходное положение.
- Сделайте от 2 до 3 подходов по 8–12 повторений.
Прыжки с трамплина
Это кардиоупражнение поможет увеличить частоту сердечных сокращений и накачать кровь, а также укрепит нижнюю часть тела.
Поделиться на Pinterest
Чтобы сделать
- Встаньте, ноги на ширине плеч, руки вдоль туловища.
- Подпрыгните и расставьте ноги как можно дальше.
- Одновременно поднимите руки над головой, чтобы хлопнуть в ладоши.

- Вернитесь в исходное положение.
- Сделайте от 2 до 3 подходов по 15–30 прыжков.
Соблюдайте осторожность при начале программы укрепляющих упражнений, если вы новичок в упражнениях или у вас есть какие-либо травмы или проблемы со здоровьем. Вот несколько советов, которые помогут вам избежать травм:
- Начните медленно и постепенно увеличивайте интенсивность и продолжительность тренировок в течение нескольких недель.
- Прислушивайтесь к своему телу и остановитесь, если вам нужен перерыв или если вы почувствуете боль.
- Разрешить 1 день восстановления между работой с различными группами мышц.
- Всегда используйте правильную форму и технику, чтобы получать максимальную пользу от тренировок.
- Используйте устойчивые, контролируемые движения, особенно если вы поднимаете тяжести.
- Дайте себе время на отдых между подходами.
- Будьте осторожны при проработке любой части тела, которая может вызвать боль или травму.
 Это может касаться шеи, плеч, спины и суставов, таких как запястья, колени и лодыжки.
Это может касаться шеи, плеч, спины и суставов, таких как запястья, колени и лодыжки. - Избегайте одышки или задержки дыхания, поскольку это может привести к повышению артериального давления. Для каждого движения делайте выдох при подъеме и вдох при опускании.
Если это возможно, поговорите с личным тренером, чтобы составить программу упражнений, если вы новичок в фитнесе или просто хотите узнать мнение эксперта. Ваш тренер поможет вам создать и поддерживать мотивацию, необходимую для того, чтобы придерживаться режима тренировок и получать желаемые результаты.
Работа с профессионалом гарантирует правильное и эффективное выполнение упражнений. Они помогут вам оставаться на правильном пути, следить за тем, чтобы вы использовали правильную технику, и улучшать упражнения по мере их улучшения.
Если нет возможности работать с профессионалом, найдите партнера по обучению. Вы можете помочь друг другу сохранить мотивацию и убедиться, что вы оба используете правильную технику.
Заставляя мышцы работать больше, чем обычно, на регулярной основе, вы можете увеличить мышечную силу.
Чтобы не сбиться с пути и достичь поставленных целей в фитнесе, важно, чтобы вы разработали режим, который вам нравится. Меняйте его так часто, как вам нравится, чтобы не скучать и нацеливаться на разные группы мышц.
Наряду с упражнениями с отягощениями и сопротивлением увеличьте свои обычные занятия, такие как подъем по лестнице или переноска тяжелых сумок, чтобы развить мышечную силу и выносливость.
Включите больше этих повседневных задач в свой распорядок дня, чтобы вы могли наслаждаться преимуществами сильного тела.
17.2 Текущий | Электрические цепи
Предыдущий 17.1 Разность потенциалов и ЭДС | Следующий 17. |
17.2 Текущий (ESAFD)
Поток заряда (ESAFE)
Когда мы говорим о токе, мы говорим о том, сколько зарядов проходит мимо фиксированной точки цепи за одну секунду. Подумайте о зарядах, переносимых батареей по цепи, в проводах есть заряды, но если их нет. это батарея, которую они не будут двигаться.
Когда один заряд перемещается, заряды рядом с ним также перемещаются. Они сохраняют расстояние, как если бы у вас была трубка с шариками. как на этой картинке или посмотрел на поезд и его вагоны.
Если вы втолкнете один шарик в трубу, один должен выйти с другой стороны, если локомотив поезда перемещает все вагоны движутся немедленно, потому что они соединены. Это похоже на заряды в проводах цепи.
Идея состоит в том, что если батарея начала управлять зарядом в цепи, все заряды начинают двигаться
мгновенно.
Бенджамин Франклин сделал предположение о направлении потока заряда при натирании гладкого воска грубой шерстью. Он считал, что заряды перетекают от воска к шерсти (то есть от положительного к отрицательному), что было противоположно к реальному направлению. Из-за этого говорят, что электроны имеют 90 501 отрицательный заряд 90 502 и, следовательно, объекты, которые Бен Франклин назвал «отрицательным» (имея в виду недостаток заряда) действительно наличие избытка электронов. К тому времени, когда было обнаружено истинное направление потока электронов, условность «положительного» и «отрицательный» уже был настолько хорошо принят в научном мире, что не было предпринято никаких усилий, чтобы Измени это.
Медная проволока
Фотография на Flickr.com
- Текущий
Ток — это скорость, с которой заряды перемещаются мимо фиксированной точки в цепи.
 Единицы тока
ампер (А), который определяется как один кулон в секунду.
Единицы тока
ампер (А), который определяется как один кулон в секунду.Количество: Текущий (I) Название единицы: ампер Обозначение единицы измерения: A
9{-1}$}\)).
\[I = \frac{Q}{\Delta t}\]Когда в цепи течет ток, мы показываем это на диаграмме, добавляя стрелки. Стрелки показывают направление течь в цепи. Условно мы говорим, что заряд течет от положительной клеммы батареи к отрицательный терминал.
Если напряжение достаточно высокое, ток может проходить почти через все. В примере с плазменным шаром на слева создается напряжение, достаточно высокое, чтобы заряд протекал через газ в шаре. напряжение очень высокое, но результирующий ток очень низкий. Это делает его безопасным для прикосновения.
временный текстАмперметр (ESAFF)
Амперметр — это прибор, используемый для измерения скорости электрического тока в цепи. Так как один
заинтересован в измерении тока, протекающего через компонент цепи, амперметр должен быть подключен
в серии с измеряемым компонентом цепи.
Так как один
заинтересован в измерении тока, протекающего через компонент цепи, амперметр должен быть подключен
в серии с измеряемым компонентом цепи.
Амперметр
Построение схем
Построить схемы для измерения ЭДС и разности потенциалов на клеммах аккумулятора. Некоторые общие элементы (компоненты), встречающиеся в электрических цепях, включают лампочки, аккумуляторы, соединительные провода, переключатели, резисторы, вольтметры и амперметры. О многих из них вы уже узнали. Ниже приведен таблица с предметами и их обозначениями:
Компонент | Символ | Применение |
лампочка | светится, когда через него проходит заряд | |
батарея | обеспечивает энергию для заряда для перемещения | |
переключатель | позволяет разомкнуть или замкнуть цепь | |
резистор | сопротивляется потоку заряда | |
ИЛИ | ||
вольтметр | измеряет разность потенциалов | |
амперметр | измеряет ток в цепи | |
соединительный провод | соединяет элементы схемы вместе |
Поэкспериментируйте с различными комбинациями компонентов в цепях.
В таблице ниже приведены сведения об использовании каждого из рассмотренных нами измерительных приборов и о том, как это должно быть. подключен к компоненту цепи.
Аккумулятор не производит одинакового тока независимо от того, что к нему подключено. В то время как напряжение, создаваемое батареей, является постоянным, количество подаваемого тока зависит от того, что находится в схема.
Инструмент | Измеряемое количество | Правильное соединение |
Вольтметр | Напряжение | Параллельно |
Амперметр | Текущий | В серии |
Использование счетчиков
Если возможно, подключите счетчики к цепям, чтобы привыкнуть к использованию счетчиков для измерения электрических величин. Если
счетчики имеют более одной шкалы, всегда подключайтесь к первой, чтобы счетчик не был поврежден
необходимости измерять значения, выходящие за его пределы.
Если
счетчики имеют более одной шкалы, всегда подключайтесь к первой, чтобы счетчик не был поврежден
необходимости измерять значения, выходящие за его пределы.
Рабочий пример 1: расчет тока I
Количество заряда, равное \(\text{45}\) \(\text{C}\), проходит мимо точки цепи в \(\text{1}\) \(\text{секунда}\), какова сила тока в цепи?
Проанализируйте вопрос
Нам дают количество заряда и время и просят рассчитать ток. Мы знаем, что ток скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому у нас есть вся необходимая информация. У нас есть уже в правильных единицах. 9{-1}$} \\ Я & = \текст{45}\текст{А} \конец{выравнивание*}
Укажите окончательный результат
Текущий результат равен \(\text{45}\) \(\text{A}\).
Рабочий пример 2: расчет тока II
Количество заряда, равное \(\text{53}\) \(\text{C}\), перемещается мимо фиксированной точки цепи в \(\text{2}\) \(\text{s}\), какова сила тока в цепи?
Проанализируйте вопрос
Нам дают количество заряда и время и просят рассчитать ток. Мы знаем, что ток
скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому у нас есть вся необходимая информация. У нас есть
уже в правильных единицах. 9{-1}$} \\
I & = \text{26,5}\text{ А}
\конец{выравнивание*}
Мы знаем, что ток
скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому у нас есть вся необходимая информация. У нас есть
уже в правильных единицах. 9{-1}$} \\
I & = \text{26,5}\text{ А}
\конец{выравнивание*}
Укажите окончательный результат
Текущий результат равен \(\text{26,5}\) \(\text{A}\).
Рабочий пример 3: расчет тока III
95 электронов проходят мимо фиксированной точки цепи за одну десятую секунды, какова сила тока в цепи? схема?
Проанализируйте вопрос
Нам дано количество заряженных частиц, которые проходят мимо фиксированной точки, и время, за которое это происходит. Мы знаем
что ток — это скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому мы должны определить
обвинение. В предыдущей главе мы узнали, что заряд, переносимый электроном, равен \(\text{1,6} \times
\текст{10}^{-\текст{19{-\text{16}}\) \(\text{A}\).
Предыдущий 17.1 Разность потенциалов и ЭДС | Оглавление | Следующий 17.3 Сопротивление |
Напряженность магнитного поля [Encyclopedia Magnetica]
Содержание
Напряженность магнитного поля
Плотность магнитного потока B
Трудность с определением
Аналог электрических цепей
Электрическая цепь
Магнитная цепь
H из-за электрического тока
H из-за M и B
Уравнения Максвелла
H в электромагнитных волнах
Определение H с силой
Поколение H
Соленоид
Катушка Гельмгольца
Магнитопровод с малым зазором
Поле размагничивания
Измерение H
Энергия и плотность энергии
Петля гистерезиса и потери мощности
Модели петли B-H
Коэрцитивная сила
См.
 также
такжеКаталожные номера
Напряженность магнитного поля H — физическая величина, используемая в качестве одной из основных мер напряженности магнитного поля. Единицей напряженности магнитного поля является ампер на метр или А/м .
Электрический ток $I$ создает напряженность магнитного поля $H$, величина которой не зависит от типа однородной изотропной окружающей среды (магнитная или немагнитная)
С инженерной точки зрения напряженность магнитного поля $H$ можно рассматривать как возбуждение, а плотность магнитного потока $B$ как реакцию среды. Это соглашение об именах определено в системе единиц СИ.
С точки зрения теоретической физики поле $H$ определяется как векторная разность между плотностью потока $B$ и намагниченностью $M$. Поле H иногда называют «вспомогательным» или просто «полем H».
Поле H иногда называют «вспомогательным» или просто «полем H».
Эти два подхода идентичны в смысле рассматриваемых физических величин (с одними и теми же физическими единицами А/м), но называются разными именами, и разные акценты делаются на их значении и использовании при выводе некоторых уравнений.
Магнитное поле является векторным полем в пространстве и представляет собой разновидность энергии, полное количественное определение которой требует знания векторных полей как напряженности магнитного поля $H$, так и плотности потока $B$ (или других связанных с ними величин, таких как намагниченность M или поляризация J ). В вакууме векторы $H$ и $B$ в каждой точке ориентированы в одном направлении и прямо пропорциональны проницаемости свободного пространства, но в других средах они могут быть несовмещены (особенно в неоднородных или анизотропных материалах).
Требование двух величин аналогично, например, электричеству. Для полной количественной оценки эффектов электричества требуются как электрическое напряжение $V$, так и электрический ток $I$. количество передаваемой энергии.
Для полной количественной оценки эффектов электричества требуются как электрическое напряжение $V$, так и электрический ток $I$. количество передаваемой энергии.
Название напряженность магнитного поля и символ $H$ определены Международного бюро мер и весов (BIPM) как одна из когерентных производных физических единиц. Поэтому, строго говоря, другие имена, такие как напряженность магнитного поля или магнитное поле (или даже просто поле ), которые можно встретить в повседневном техническом жаргоне , неверны, если используются при ссылке на конкретное значение H в A/ м.
В литературе используется много других названий, обозначающих одно и то же количество:
напряженность магнитного поля H
магнитное поле Н
поле H
поле H’
Напряженность H-поля
H-поле
напряженность поля намагничивания H
напряженность поля намагничивания H
сила намагничивания H
магнитная сила H
интенсивность магнитной силы H
вспомогательное поле H
и, возможно, несколько других.

| → → → Полезная страница? Поддержите нас! → → → | PayPal | ← ← ← Помогите нам с всего $0,10 в месяц? Давай… ← ← ← |
Плотность магнитного потока B
| См. отдельную статью по : Плотность магнитного потока |
| См. отдельную статью о : Путаница между B и H |
Иллюстрация напряженности магнитного поля H , плотности потока B , намагниченности M и поляризация J в ферромагнетике
Плотность магнитного потока B является отдельной физической величиной с разными физическими единицами в системе СИ. H и B взаимосвязаны таким образом, что:
| \vec{M}) $$ | (Т) |
| где: $µ_0$ — абсолютная проницаемость вакуума (Гн/м), $µ_r$ — относительная проницаемость материала (безразмерная), $µ = µ_0 · µ_r$ — абсолютная проницаемость материала (Гн/м), $ J$ — магнитная поляризация (Тл), $M$ — намагниченность (А/м) | |
Намагниченность М представляет собой ориентацию субатомных магнитных дипольных моментов на единицу объема, а магнитная поляризация Дж равна М в масштабе проницаемости вакуума.
В общем случае все три вектора B , H и J (или B , H и M ) могут указывать в разных направлениях (как показано на рисунке для анизотропного материала) , но всегда так, что векторная сумма в приведенном выше уравнении выполняется.
Для одноосного намагничивания уравнение можно упростить до скалярной формы, которая широко используется в технических приложениях:
| $$B = µ_0 · µ_r · H = µ · H $$ | (T) |
Относительная магнитная проницаемость $μ_r$ является показателем качества магнитомягких материалов и имеет значения, значительно превышающие единицу.
Для магнитотвердых материалов $µ_r \приблизительно$ 1, и это гораздо менее важный параметр.
Для немагнитных материалов также $µ_r \приблизительно$ 1, но такое, что парамагнетики слабо притягиваются к любой полярности магнитного поля ($µ_r$ чуть больше единицы), а диамагнетики всегда слабо отталкиваются ($µ_r$ чуть меньше единство). В зависимости от точки зрения сверхпроводники можно отнести к идеальным диамагнетикам, для которых $µ_r$ = 0, а значит, они достаточно сильно отталкиваются от магнитного поля, достаточного для магнитной левитации.
В зависимости от точки зрения сверхпроводники можно отнести к идеальным диамагнетикам, для которых $µ_r$ = 0, а значит, они достаточно сильно отталкиваются от магнитного поля, достаточного для магнитной левитации.
Трудность с определением
Трудно дать краткое определение такой базовой величине, как магнитное поле, но разные авторы дают хотя бы описательный вариант. То же самое относится к напряженности магнитного поля , а также к другой базовой величине — плотности магнитного потока .
В таблице ниже приведены некоторые примеры определений $H$, данных в литературе (приведены точные цитаты).
| Публикация | Определение магнитного поля | Определение напряженности магнитного поля $H$ | Определение плотности магнитного потока $B$74 |
|---|---|---|---|
Р. Фейнман, Р. Лейтон, М. Сэндс Фейнман, Р. Лейтон, М. Сэндс Фейнмановские лекции по физике | Во-первых, мы должны несколько расширить наши представления об электрическом и магнитном векторах, E и 5 92$ в качестве нового числа 1/μ 0 | Мы можем записать силу F, действующую на заряд q, движущийся со скоростью v, как $$\mathbf{F} = q(\mathbf{E} + \mathbf {v} × \mathbf{B})$$ Мы называем E электрическим полем, а B магнитным полем в месте расположения заряда. | |
| Ричард М. Бозорт Ферромагнетизм | Магнит будет притягивать кусок железа, даже если они не соприкасаются, и считается, что это действие на расстоянии вызвано магнитным полем , или силовое поле. | Напряженность силового поля, напряженность магнитного поля или намагничивающая сила H могут быть определены с точки зрения магнитных полюсов: в одном сантиметре от единичного полюса напряженность поля равна одной эрстеде. | Фарадей показал, что некоторые свойства магнетизма можно уподобить потоку, и представил бесконечные линии индукции , которые представляют направление и своей концентрацией поток в любой точке. […] Общее количество линий, пересекающих данную область под прямым углом, является потоком в этой области. Поток на единицу ар – это плотность потока, или магнитная индукция и обозначается символом B. |
| Дэвид С. Джайлс Введение в магнетизм и магнитные материалы | Одной из самых фундаментальных идей в магнетизме является концепция магнитного поля. Когда поле генерируется в объеме пространства, это означает, что происходит изменение энергии этого объема и, кроме того, существует градиент энергии, так что создается сила, которую можно обнаружить по ускорению электрического заряда, движущегося в нем. поле, силой, действующей на проводник с током, крутящим моментом на магнитном диполе, таком как стержневой магнит, или даже переориентацией спинов электронов внутри определенных типов атомов. | Существует несколько способов определения напряженности магнитного поля H. В соответствии с развитыми здесь идеями мы хотим подчеркнуть связь между магнитным полем H и генерирующим электрическим током. […] Самое простое определение следующее. Ампер на метр — это напряженность поля, создаваемого бесконечно длинным соленоидом, содержащим 90 502 n 90 501 витков на метр катушки и пропускающим ток 1 90 502 / n 90 501 ампер. | Когда магнитное поле H создается в среде током, в соответствии с законом Ампера реакция среды представляет собой ее магнитную индукцию B, также иногда называемую плотностью потока. |
| Магнитное поле , Британская энциклопедия | Магнитное поле, область вблизи магнитного поля, электрического тока или изменяющегося электрического поля, в которой наблюдаются магнитные силы. | Магнитное поле H можно рассматривать как магнитное поле, создаваемое протеканием тока в проводах […] | […] магнитное поле B [можно рассматривать] как полное магнитное поле, включая также вклад, вносимый магнитными свойствами материалов в поле. |
| Э. М. Перселл, Д. Дж. Morin, Электричество и магнетизм | Это взаимодействие токов и других движущихся зарядов можно описать, введя магнитное поле. […] Мы предлагаем продолжать называть $\mathbf{B}$ магнитным полем. | Если мы теперь определим векторную функцию $\mathbf{H}(x, y, z)$ в каждой точке пространства соотношением $$ \mathbf{H} \equiv \frac{\mathbf{ B}}{µ_0} — \mathbf{M} $$ […] Что касается $\mathbf{H}$, хотя для него придуманы и другие названия, мы будем называть его полем $\mathbf{H} $, или даже магнитного поля $\mathbf{H}$. | […] на любую движущуюся заряженную частицу, оказавшуюся в этом поле, действует сила […], определяемая выражением $$ \mathbf{F} = q·\mathbf{E} + q·\mathbf{v} × \mathbf{B} $$ […] Мы возьмем уравнение в качестве определения $\mathbf{B}$. |
Аналог электрических цепей
Электрическая цепь
На фундаментальном уровне все электричество связано с наличием и движением электрических зарядов, поэтому знания их положения было бы достаточно для полной количественной оценки всех электрических эффектов, включая электрическое поле. Однако на практике гораздо проще оперировать непосредственно измеряемыми величинами, такими как ток $I$ и напряжение $V$.
Однако на практике гораздо проще оперировать непосредственно измеряемыми величинами, такими как ток $I$ и напряжение $V$.
С макроскопической точки зрения, значения $I$ и $V$ необходимы для полной количественной оценки влияния электричества в электрических цепях. В цепях постоянного тока пропорциональность между $V$ и $I$ определяется электрическим сопротивлением $R$ данной среды (согласно закону Ома), таким что $V = R·I$.
Произведение $V$ и $I$ пропорционально мощности $P$ и энергии $E$ в данной электрической цепи.
Магнитная цепь
По аналогии и напряженность магнитного поля $H$, и плотность магнитного потока $B$ (или их представление другими связанными переменными) необходимы для количественной оценки эффектов магнетизма в магнитных цепях. Соотношение между $H$ и $B$ диктуется магнитной проницаемостью $µ$ данной среды.
Все эффекты магнитного поля также связаны с движением и внутренними свойствами электрических зарядов. Зная эти свойства (например, спиновой магнитный момент) и детали движения зарядов (с учетом релятивистских эффектов), можно было бы полностью описать магнитное поле. Однако на практике гораздо проще, особенно с инженерной точки зрения, использовать непосредственно измеряемые величины, такие как $H$ и $B$, для количественного определения мощности и энергии в данной магнитной цепи.
Однако на практике гораздо проще, особенно с инженерной точки зрения, использовать непосредственно измеряемые величины, такие как $H$ и $B$, для количественного определения мощности и энергии в данной магнитной цепи.
Произведение $H$ и $B$ в стационарных условиях является мерой удельной энергии в Дж/м 3 , запасенной в магнитном поле, содержащемся в данной среде. Произведение $B·H$ (количество накопленной энергии) используется, например, для классификации постоянных магнитов.
Н за счет электрического тока
Амплитуда напряженности магнитного поля $H$ уменьшается по мере удаления от проводника с электрическим током $I$
Ориентация Прочность на магнитное поле $ H $ Vector с уважением к текущим $ I $.
С макроскопической точки зрения поля можно рассматривать как усредненные по некоторому объему материала, а их величины можно связать с измеряемыми сигналами, такими как ток или напряжение. Поэтому этот подход широко используется в технике.
Поэтому этот подход широко используется в технике.
$H$ всегда генерируется вокруг электрического тока $I$, который может быть сплошным проводником с током или просто движущимся электрическим зарядом (также в свободном пространстве). Направление вектора $H$ перпендикулярно направлению порождающего его тока $I$, и предполагается, что направления векторов подчиняются правилу правой руки. Можно сказать, что H «циркулирует» вокруг текущего I .
Без других источников магнитного поля и в однородной и изотропной среде напряженность генерируемого магнитного поля $H$ зависит только от величины и направления электрического тока $I$ и задействованных физических размеров (например, длины и диаметра проводника и т. д.). .) поэтому по закону Ампера пропорциональность определяется длиной магнитного пути $l$:
| $$ \int_C \vec{H} · d \vec{l} = I $$ | (A) |
| где: C — замкнутый путь, по которому вычисляется интеграл, $dl$ — бесконечно малый фрагмент длины магнитного пути (м), $I$ — ток (А) | |
В линейной изотропной среде значения из разных источников объединяются и могут быть вычислены из суперпозиции источников. Для простых геометрических случаев значение $H$ можно вычислить аналитически, а для очень сложных систем можно выполнить расчет, например, с помощью конечно-элементного моделирования.
Для простых геометрических случаев значение $H$ можно вычислить аналитически, а для очень сложных систем можно выполнить расчет, например, с помощью конечно-элементного моделирования.
Связь между $H$ и $I$ часто показывается с помощью закона Био-Савара или закона Ампера. Часто (но не всегда ) оба они задаются с переменной плотности потока $B$, так что автоматически учитывается проницаемость среды.
Во многих примерах, приводимых в литературе, имеется неявное предположение (обычно не оговариваемое), что вывод ведется для вакуума, а не для произвольной среды с другой магнитной проницаемостью . Когда проницаемость $μ_0$ приведена в уравнениях с обеих сторон, то $H$ пропорциональна только $I$ и это верно для любой однородной изотропной среды с любой проницаемостью, даже нелинейной.
Ситуация несколько иная для анизотропной или прерывистой среды. Они могут вызывать дополнительные источники магнитного поля, так как возбужденная среда может генерировать новые магнитные полюса, которые необходимо учитывать для точного описания распределения $H$. Например, полюсные наконечники в электромагните влияют на $H$, распределение которого больше не определяется только катушками с электрическим током.
Например, полюсные наконечники в электромагните влияют на $H$, распределение которого больше не определяется только катушками с электрическим током.
H due to M and B
H , B , M , and J in a paramagnet
Микроскопическая точка зрения часто используется в теоретической физике.
Каждый атом реагирует на приложенное извне магнитное поле B некоторой намагниченностью M , которая определяется как векторная сумма магнитных моментов на данный объем. «Вспомогательное» магнитное поле H тогда определяется как разность векторов между приложенным магнитным полем B и намагниченностью M :
| $$\vec{H} = \frac{\vec{B}} {μ_0} — \vec{M}$$ | (А/м) |
| где: $μ_0$ — абсолютная проницаемость вакуума (Гн/м) | |
Для возбуждения постоянным током в немагнитных или магнитных, но изотропных материалах B и H векторы параллельны. Для ферромагнитных (и других упорядоченных структур) анизотропия кристалла или формы может вводить значительный угол между двумя векторами.
Для ферромагнитных (и других упорядоченных структур) анизотропия кристалла или формы может вводить значительный угол между двумя векторами.
Уравнения Максвелла
Уравнения Максвелла обычно даются относительно плотности магнитного потока B , потому что в такой форме они справедливы при более общих условиях.
Однако при определенных условиях их также можно выразить по отношению к H . Этот подход широко используется в численных расчетах, таких как моделирование методом конечных элементов (МКЭ), где прямая связь между электрическим током (выражаемым плотностью тока J ) и H используется с помощью закона Ампера как для решений, так и для формулировок граничных условий.
| Пример обозначения, используемого в документации по МКЭ (после ссылки ) | |
|---|---|
| $$ \nabla · \mathbf{D} = ρ$$ | $$ \nabla · \mathbf{B} = 0$$ |
| $$ \nabla \times \mathbf{E} = — \frac {\partial \mathbf{B}}{\partial t}$$ | $$ \nabla \times \mathbf{H} = \mathbf{J} + \frac {\partial \mathbf{D}}{\partial t} $$ |
H в электромагнитных волнах
В вакууме при отсутствии зарядов и токов уравнения Максвелла упрощаются, и их можно записать либо относительно плотности магнитного потока B (как показано в таблице ниже), либо напряженности магнитного поля H . Это можно сделать из-за линейности вакуума (или другой немагнитной среды), в котором нет свободных зарядов, поэтому нет дополнительных электрических токов, которые приходится учитывать. Формат с B действителен при более общих условиях.
Это можно сделать из-за линейности вакуума (или другой немагнитной среды), в котором нет свободных зарядов, поэтому нет дополнительных электрических токов, которые приходится учитывать. Формат с B действителен при более общих условиях.
| Уравнения Максвелла в вакууме (в дифференциальной форме) | |||
|---|---|---|---|
| магнитное поле, представленное H | магнитное поле, представленное B | ||
| $$ \text{div} \mathbf{E} = 0$$ | $$ \text{div} \mathbf{H} = 0$$ | $$ \text{div} \mathbf{ Е} = 0$$ | $$ \text{div} \mathbf{B} = 0$$ |
| $$ \text{curl} \mathbf{E} = — \mu_0 · \frac {\partial \mathbf{H}}{\partial t}$$ | $$ \text{curl} \mathbf{ H} = \epsilon_0 · \frac {\partial \mathbf{E}}{\partial t} $$ | $$ \text{curl} \mathbf{E} = — \frac {\partial \mathbf{B} }{\partial t}$$ | $$ \text{curl} \mathbf{B} = \mu_0 · \epsilon_0 · \frac {\ partial \mathbf{E}}{\partial t} $$ |
В вакууме две записи с B или H точно эквивалентны, причем последний весьма популярен для анализа излучения антенн. Например, используя вектор Пойнтинга, который представляет мощность как произведение электрического поля E в В/м и магнитного поля H в А/м, результатом будет В·А/м 2 или Вт/м м 2 (удельная мощность).
Например, используя вектор Пойнтинга, который представляет мощность как произведение электрического поля E в В/м и магнитного поля H в А/м, результатом будет В·А/м 2 или Вт/м м 2 (удельная мощность).
Определение H с силой
В литературе показано, что напряженность магнитного поля в данной точке пространства можно определить как механическую силу, действующую на единичный полюс в данной точке. Однако для расчета силы требуется $B$, что зависит от свойств среды. Действительно, в первоначальном эксперименте, проведенном Био и Саваром, использовались физические силы, действующие на провода.
Силы, действующие на два намагниченных тела, будут разными, если их поместить в кислород (парамагнитный) или в воду (диамагнитный). Эта разница будет прямо пропорциональна относительной проницаемости вовлеченных сред. Однако $H$, создаваемый вокруг провода, будет одинаковым (пока среда однородна и изотропна).
Величина магнитной силы (силы Лоренца) всегда пропорциональна плотности потока $B$.
Поколение H
Известные значения H получены с использованием упомянутых выше законов Ампера или Био-Савара. Если можно пренебречь релятивистскими эффектами, то пропорциональность точно прямая такая, что мгновенным значениям напряженности магнитного поля $H$ соответствуют мгновенные значения приложенного тока $I$:
| $$ H(t) = c · I(t) $$ | (А/м) |
| где: $c$ — коэффициент пропорциональности данного контура (1/м) | |
При определенных условиях генерируемое магнитное поле может быть рассчитано настолько точно, что его можно использовать для калибровки других датчиков или определения значений, как это рекомендовано BIPM.
Двумя типичными устройствами, которые можно использовать для получения известных значений H , являются соленоид и катушка Гельмгольца. Их можно использовать даже в комбинированной установке, в которой внешние катушки Гельмгольца компенсируют магнитное поле Земли (или другие нежелательные источники), а внутренний соленоид создает точно известное магнитное поле.
Их можно использовать даже в комбинированной установке, в которой внешние катушки Гельмгольца компенсируют магнитное поле Земли (или другие нежелательные источники), а внутренний соленоид создает точно известное магнитное поле.
Соленоид
Соленоид часто используется в качестве источника известного значения напряженности магнитного поля H , которую можно рассчитать для его геометрического центра (черная точка)
| См. также основной артикул: Соленоид |
В бесконечно длинном однородном соленоиде величина Н на его оси зависит только от величины тока в катушке и числа витков на единицу длины. 92}} \приблизительно \frac{N·I}{l} $$
Если толщина проволоки в соленоиде значительна или имеется много слоев катушки, в уравнении требуются дополнительные поправочные члены.
Катушка Гельмгольца
| См. также основную статью: Катушка Гельмгольца |
Другим широко используемым источником H является катушка Гельмгольца . Устройство состоит из двух одинаковых катушек, напоминающих круговые токовые петли, расположенных параллельно на одной оси и разделенных точно радиусом окружности.
Для двух катушек, каждая с радиусом r и числом витков каждая N , каждая , значение магнитного поля в геометрическом центре можно рассчитать как: 93}}{2·r} \приблизительно \frac{0,35777·N_{всего}·I}{r} $$
Также используются формы, отличные от круглых (например, квадратные), но за счет однородности полученного распределения поля.
Катушка Гельмгольца является точным источником магнитного поля в ее геометрическом центре (черная точка)
Путь движущихся электронов, изогнутый в окружность магнитным полем, создаваемым внешней катушкой Гельмгольца (красная круглая форма на заднем плане) М. Бялек, Wikimedia Commons, CC-BY-SA-3.0
Набор из трех больших ортогональных катушек Гельмгольца, используемых для компенсации магнитного поля Земли в 3D
Магнитопровод с малым зазором
Закон Ампера связывает интеграл вокруг замкнутого пути с током, протекающим по такому пути.
Это соотношение широко используется в технике с использованием понятия магнитодвижущей силы (произведение тока и витков катушки, выраженное в ампер-витках). Для простой магнитной цепи с одним воздушным зазором можно написать, что:
Для простой магнитной цепи с одним воздушным зазором можно написать, что:
| $$ N·I = H_{core}·l_{core} + H_{gap}·l_{gap} $$ | (A-витки) ≡ (A) |
| где: $N$ — число витков обмотки (безразмерное), $I$ — ток (А), $H_{core}$ — H в сердечнике (А/м), $l_{ core}$ — длина жилы (м), $H_{gap}$ — H в воздушном зазоре (А/м), $l_{gap}$ — длина воздушного зазора (м) | |
В магнитопроводе с относительно небольшим воздушным зазором значение плотности магнитного потока таково, что $B_{зазор} \ приблизительно B_{сердечник}$. Однако значение H требуется для поддержки некоторого значения B масштабируется обратной величиной относительной проницаемости. Следовательно, для магнитного материала с большой магнитной проницаемостью приводит к условию $H_{core} \ll H_{gap}$, а также к $H_{core}·l_{core} \ll H_{gap}·l_{gap }$, поэтому существенными являются только члены, относящиеся к воздушному зазору. Это позволяет упростить уравнение следующим образом:
Это позволяет упростить уравнение следующим образом:
| $$ H_{пробел} \приблизительно \frac{N·I}{l_{пробел}} $$ | (А/м) |
| где: $N$ — число витков обмотки (безразмерное), $I$ — ток (А), $l_{зазор}$ — длина воздушного зазора (м) | |
Однако для более сложных магнитных цепей необходимо учитывать такие эффекты, как окантовка потока или магнитная энергия, хранящаяся в материале, и это можно сделать с помощью численных методов, таких как моделирование методом конечных элементов.
Добавление воздушного зазора позволяет накапливать в нем энергию. Петля B-H «срезается», расширяя операцию до более высоких Н . Эти эффекты широко используются, например, в обратноходовых трансформаторах.
Магнитная цепь с магнитным путем и воздушным зазором
больший электромет с электрометом с большими электрометражными сетями; разработано с помощью упрощенного уравнения0501 H
Поле размагничивания
Упрощенное изображение намагничивания в $M$$ поле $M_d
Магнитное поле создается не только электрическими токами, но и магнитными моментами, которые могут запасать магнитную энергию, например, путем выравнивания за счет ранее примененного процесса намагничивания. Совокупность таких собственных магнитных моментов составляет намагниченность $M$ и становится источником магнитного поля, как это имеет место в постоянных магнитах. Если создаются магнитные полюса, то линии магнитного поля ($H$) обычно предполагаются направленными от северного к южному полюсу.
Совокупность таких собственных магнитных моментов составляет намагниченность $M$ и становится источником магнитного поля, как это имеет место в постоянных магнитах. Если создаются магнитные полюса, то линии магнитного поля ($H$) обычно предполагаются направленными от северного к южному полюсу.
Силовые линии магнитного поля будут замыкаться через среду, окружающую магнит, а также через сам магнит в направлении, противоположном намагниченности $M$, уменьшая тем самым эффективную намагниченность тела, поэтому этот эффект называется поле размагничивания $H_d$.
Эффект можно количественно оценить с помощью безразмерного коэффициента размагничивания $N_d$, который пропорционален намагниченности и зависит от размеров тела, так что для очень длинных конструкций или для магнитно-замкнутых цепей $N_d=0$ и для тонкие плоские структуры бесконечных размеров, намагниченные перпендикулярно поверхности $N_d=1$.
Значение коэффициента размагничивания можно вычислить аналитически для эллипсоидов и других очень простых геометрических фигур, а также для сферы $N_d=1/3$.
| $$H_d = — N_d·M $$ | (А/м) |
| где: $N_d$ — коэффициент размагничивания (безразмерный), $M$ — намагниченность (А/м) | |
Размагничивающее поле $H_d$ в намагниченном однородно намагниченном теле $M$
На рисунке показан постоянный магнит, намагниченный однородным M (или J ), окруженный вакуумом. Силовые линии магнитного поля показаны отдельно для каждого поля: M , H и B , что представляет собой векторную сумму M и H .
Размагничивающее поле H d направлено в противоположную сторону, но оно неоднородно, так как некоторый магнитный поток замыкается и снаружи тела (где M = 0 и J = 0).
В результате внутри тела B также неоднородно и по величине B < J .
Вне тела силовые линии B и H имеют одинаковую форму, поскольку в вакууме две векторные величины отличаются только на скалярную константу вакуумной проницаемости μ 0 (оба M и J равны нулю).
На этом рисунке также видно, что на границе двух сред с разными значениями проницаемости для H сохраняется тангенциальная составляющая H t , а для B сохраняется нормальная составляющая B t .
Измерение H
Значение H не может быть измерено напрямую, но получено другими способами.
В некоторых магнитных измерительных системах пропорциональность току используется явно, как, например, в таких устройствах, как рамка Эпштейна, однолистовой тестер или тороидальный образец. Измеряемая величина представляет собой ток (например, с помощью шунтирующего резистора), и H вычисляется из него.
В некоторых других случаях можно использовать принцип, согласно которому тангенциальная составляющая H не изменяется на границе раздела двух материалов. Следовательно, измеряя тангенциальную составляющую магнитного поля прямо у поверхности образца, можно узнать о поле непосредственно под поверхностью. Однако такое измерение основано на допущении, что зависимость B-H внутри датчика является линейной, поскольку работа сенсорной катушки основана на законе индукции Фарадея, в котором измеренным значением является плотность магнитного потока В . Обычно это достигается за счет использования немагнитного материала в качестве каркаса, на который наматывается H-катушка. Сигнал в катушке индуцируется пропорционально B в H-катушке, но благодаря линейности его можно пересчитать для извлечения информации о H . Другие детекторы, такие как потенциометр Роговского-Чаттока или датчик Холла, также могут использоваться для обнаружения тангенциальной составляющей H , но они также измеряют количество B , которое затем можно пересчитать и выразить как Н .
Следовательно, измеряя тангенциальную составляющую магнитного поля прямо у поверхности образца, можно узнать о поле непосредственно под поверхностью. Однако такое измерение основано на допущении, что зависимость B-H внутри датчика является линейной, поскольку работа сенсорной катушки основана на законе индукции Фарадея, в котором измеренным значением является плотность магнитного потока В . Обычно это достигается за счет использования немагнитного материала в качестве каркаса, на который наматывается H-катушка. Сигнал в катушке индуцируется пропорционально B в H-катушке, но благодаря линейности его можно пересчитать для извлечения информации о H . Другие детекторы, такие как потенциометр Роговского-Чаттока или датчик Холла, также могут использоваться для обнаружения тангенциальной составляющей H , но они также измеряют количество B , которое затем можно пересчитать и выразить как Н .
На границе двух материалов (с разными магнитными проницаемостями $μ_1$ и $μ_2$) тангенциальная составляющая H не меняется, поэтому: $H_{t1} = H_{t2 }$
Flat H-coil made with PCB tracks
Simple wire-wound H-coil
Энергия и плотность энергии
Плотность энергии $E_d$ запасенной в магнитном поле энергии в данном материале можно рассчитать как:
| $$E_d = \int H · дБ $$ | (Дж/м 3 ) |
который для материала с линейными характеристиками, включая высокоэнергетические постоянные магниты, можно упростить до:
| $$E_d = \frac{H·B}{2} $$ | (Дж/м 3 ) |
Следует отметить, что последнее приведенное выше уравнение охватывает как приложенное поле, так и реакцию материала на намагничивание (независимо от того, какая величина считается «основной», B или H ).
Однако в немагнитных материалах, для которых $µ_r$ ≈ 1, можно записать, что:
| $$B = μ_0 · H $$ | (Т) | и | $$\frac{B}{μ_0} = H $$ | (А/м) |
Следовательно, замена может быть сделана таким образом, чтобы исключить одну из переменных, сделав плотность энергии пропорциональной квадрату либо только B , либо только H . В зависимости от публикации используются обе формы, часто не указывает неявное предположение о том, что $μ_r$ ≈ 1. Эти две формы эквивалентны, хотя выражение с B кажется более популярным. Если предположение $µ_r$ ≈ 1 сделать невозможно, то энергия пропорциональна произведению $B·H$, или уравнение должно включать также относительную магнитную проницаемость $µ_r$. 92}{2} $$
Hysteresis loop and power loss
In ferromagnets the power or energy loss is proportional to the area of the B-H loop
Магнитомягкие материалы используются для преобразования энергии в режимах переменного или импульсного намагничивания. Энергетическая эффективность магнитной цепи зависит от мощности, теряемой в данном магнитном материале.
9T \left(\frac{dB}{dt} · H \right) dt $$
Энергетическая эффективность магнитной цепи зависит от мощности, теряемой в данном магнитном материале.
9T \left(\frac{dB}{dt} · H \right) dt $$
Удельные потери мощности являются важным показателем качества для магнитомягких материалов и, например, являются основой для классификации электротехнических сталей.
Из-за условий эксплуатации такие петли B-H измеряются в условиях синусоидального напряжения, что также обеспечивает синусоидальность В . Форма волны H может сильно искажаться, особенно когда материал работает близко к насыщению. Этот эффект отвечает, например, за пусковой ток в трансформаторах.
Модели петли B-H
Существует несколько аналитических, статистических и численных моделей, которые используются для математического описания траекторий петли B-H с целью «предсказания» поведения материала при заранее определенных или произвольных условиях намагничивания. Общие магнитные потери можно рассчитать, потому что реальные петли BH представляют такие полные потери, а модели пытаются представить нелинейные траектории таких петель.
Общие магнитные потери можно рассчитать, потому что реальные петли BH представляют такие полные потери, а модели пытаются представить нелинейные траектории таких петель.
Такие модели, как Джайлс-Атертон или Прейзак, используют H в качестве независимой переменной, представляющей приложенное возбуждение, как это продиктовано схемным законом Ампера.
Coercivity
In high-energy magnets there are two values of coercivity: J H c and B H c
Коэрцитивная сила H c определяется как точка, в которой петля гистерезиса пересекает горизонтальную ось ( B или J или M = 0), измеренная для данного материала. Значения коэрцитивной силы используются для широкой классификации магнитных материалов на: мягкие ( H c < 1 кА/м), жесткие ( H c > 100 кА/м) и полужесткие (1 кА < H c < 100 кА/м).
Коэрцитивная сила связана с количеством энергии, необходимой для намагничивания (и размагничивания) данного магнитного материала. Магнитомягкие материалы имеют узкую петлю B-H, они легко намагничиваются и поэтому имеют низкие значения коэрцитивной силы.
В высокоэнергетических постоянных магнитах значения коэрцитивной силы очень велики (широкая петля гистерезиса), и из-за значительных различий между значениями плотности магнитного потока B и магнитной поляризации Дж можно выделить два значения коэрцитивной силы: J H c и B H c . Для таких магнитов почти прямая линия, идущая от точки коэрцитивной силы B H c до точки остаточной намагниченности B r обозначает условия работы магнетика в данной магнитной цепи. Приложение магнитного поля, превышающего коэрцитивную силу, может навсегда размагнитить даже высокоэнергетический магнит. Для магнитов с более низкой энергией размагничивание может произойти даже в полях ниже коэрцитивной силы.
Для магнитов с более низкой энергией размагничивание может произойти даже в полях ниже коэрцитивной силы.
В магнитомягких материалах при нормальных рабочих условиях (значительно ниже насыщения) $B \приблизительно J$ и, следовательно, только одно значение коэрцитивной силы H c измеряется (потому что J H c ≈ B H c ).
См. также
Магнитное поле
Плотность магнитного потока B
Путаница между B и H
Ссылки
1) , 1) , 1) Майкл Мэнсфилд, Колм О’Салливан, Понимание физики, John Wiley & Sons, 2010, ISBN 9780470746387, с. 407
2) , 2) , 2) Encyclopaedia Britannica, Magnetism, {дата обращения: 02.05.2021}
3) , 3) , 3) , 3) , 3) , 3) , 3) , 3) , 3) Дэвид Джайлс, Введение в магнетизм и магнитные материалы, Чепмен и Холл, 1991, ISBN 9780412386404, с. 1-13
1-13
4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) Зурек С., Характеристика магнитомягких материалов при намагничивании вращением, CRC Press, 2019, ISBN 97803678
5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) Славомир Туманьски, Справочник по магнитным измерениям, CRC Press / Taylor & Francis, Boca Raton, FL, 2011, ISBN 9780367864958
6) , 6) , 6) , 6) , 6) , 6) , 6) , 6) , 6) E.M. Purcell, D.J. Morin, Electricity and magnetism, 3rd edition, Cambridge University Press, 2013, ISBN 9781107014022
7) R Murugeshan, Electricity and Magnetism, S Chand Publishing, 2019, ISBN 9352837347
8) , 8) , 8) Ричард Фейнман, Роберт Лейтон, Мэтью Сэндс, Ферромагнетизм, Фейнмановские лекции по физике, Vol. II, Калифорнийский технологический институт, {дата обращения: 16 мая 2021 г.}
II, Калифорнийский технологический институт, {дата обращения: 16 мая 2021 г.}
9) , 9) Мэри Энн Уайт, Физические свойства материалов, второе издание, CRC Press, 2011, ISBN 9781439866511, с. 359
10) СИ Брошюра: Международная система единиц (СИ) [8-е издание, 2006; обновлено в 2014 г.], Раздел 2.2: Производные единицы СИ, {по состоянию на 15 июня 2016 г.}
11) Рональд Т. Меррилл, М. В. МакЭлхинни, Филлип Л. Макфадден (редактор), Магнитное поле Земли: палеомагнетизм, ядро и глубокая мантия, том 63 серии международных геофизических исследований, ISBN 9780124
12) D. Poljak, M. Cvetković, Human interaction with electromagnetic fields, Computational models in dosimetry, Academic Press, Elsevier, 2019, ISBN 9780128164433
13) Magnetic Field (H- Филд), Antenna-Theory.com, {дата обращения: 05 мая 2021 г.}
14) , 14) Райнер Хильзингер, Вернер Родевальд, Магнитные материалы, основы, продукты, свойства, приложения, VAC Vacuumschmelze, Publicis, 2013, ISBN 9783895783524
15) , 15) , 15) Сильванус П. Томпсон, Электромагнит, The Telegraphic Journal and Electrical Review, Vol. XXVII, 4 июля — 26 декабря 1890 г., стр. 372-377
Томпсон, Электромагнит, The Telegraphic Journal and Electrical Review, Vol. XXVII, 4 июля — 26 декабря 1890 г., стр. 372-377
16) Р Муругашан, Электричество и магнетизм, S Chand Publishing, 2019, ISBN 9352837347
17) Ричард М. Бозорт, Ферромагнетизм, IEEE Press, 2003, ISBN 0780310322, с. 1-3
18) Магнитное поле, Британская энциклопедия онлайн, {дата обращения: 07.03.2020}
19) На момент написания этой статьи не было отдельной записи под названием «напряженность магнитного поля» {проверено 7 марта 2020 г.}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г.}.
20) На момент написания этой статьи не было отдельной записи под названием «плотность магнитного потока» {дата обращения: 07.03.2020}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г. }.
}.
21) Марки неодима, NdFeB-Info.com, {дата обращения: 28.06.2016}
22) , 22) MIT OpenCourseWare, Закон Био-Савара и Закон Ампера, Глава 9
23) Уравнения Максвелла, Британская энциклопедия. Encyclopdia Britannica Online, {доступ 28 июня 2016 г.}
24) , 24) , 24) Дэвид Дж. Гриффитс, Введение в электродинамику, 4-е изд., Пирсон, Бостон, 2013, ISBN 0321856562
25) , 25) Введение в электромагнетизм поля, Мультифизическая энциклопедия, COMSOL, {дата обращения: 25 июня 2021 г.}
26) AC/DC ModuleUser’s Guide, COMSOL 5.4, {дата обращения: 25.06.2021}
27) Дэвид Микер, Метод конечных элементов Magnetics: Documentation, {дата обращения: 2025-09060
28) Электромагнетизм, мультифизическое обучение и создание сетей, http://www.multiphysics. us, {дата обращения: 25.06.2021}
us, {дата обращения: 25.06.2021}
29) ANSYS Maxwell Magnetic Field Formulation, Application Brief , 2013, {дата обращения: 25 июня 2021}
30) , 30) Ray Kwok, Maxwell Equations, Государственный университет Сан-Хосе, Калифорния, США, www.sjsu.edu, {дата обращения: 22 июня 2021 г.}
31) Candace Suriano, et al., Antenna Основы, Interference Technology, 3 мая 2007 г., {доступ 22 апреля 2021 г.}
32) Жан-Батист Био и Феликс Савар. Обратите внимание на магнетизм де ла пайл де Вольта. Анна. хим.физ., 15:222–223, 1820
33) , 33) Брошюра SI – 9-е издание (2019 г.) – Приложение 2, 20 мая 2019 г., {по состоянию на 27 июня 2021 г.}
34) , 34) , 34) Фаусто Фиорилло, Измерение и определение характеристик магнитных материалов, Academic Press, 2005, ISBN 9780122572517
35) , 35) , 35) А. Козловски, Р. Рыгал и С. Зурек, Большой электромагнит постоянного тока для полупромышленной термомагнитной обработки нанокристаллической ленты, IEEE Transactions on Magnetics, 50 (4), стр. 1-4, 2014 г., № ст. . 8000404, ДОИ 10.1109/Tmag.2013.2288322
Козловски, Р. Рыгал и С. Зурек, Большой электромагнит постоянного тока для полупромышленной термомагнитной обработки нанокристаллической ленты, IEEE Transactions on Magnetics, 50 (4), стр. 1-4, 2014 г., № ст. . 8000404, ДОИ 10.1109/Tmag.2013.2288322
36) E.R. Dobbs, Basic Electromagnetism, Springer Science & Business Medi 4431545263
38) Ji-Yeon Shim, Bong-Yong Kang, Распределение электромагнитной силы квадратной рабочей катушки для высокоскоростной магнитно-импульсной сварки с использованием FEM, Материаловедение и приложения, Vol. 4 (12), 2013, стр. 856-862. doi: 10.4236/msa.2013.412109
39) Б.Д. Каллити, К.Д. Грэм, Введение в магнитные материалы, 2-е издание, Wiley, IEEE Press, 2009, ISBN 9780471477419
40) , 40) Arnold Magnetic Technologies, TECHNotes, The Vocabulary of Magnetism, 2016, {доступ 2021-05-02}
Магнитное поле, Counter
Тренировки с отягощениями — польза для здоровья
Тренировки с отягощениями (также называемые силовыми тренировками или силовыми тренировками) — это использование сопротивления мышечным сокращениям для наращивания силы, анаэробной выносливости и размера скелетных мышц.
Тренировка с отягощениями основана на том принципе, что мышцы тела будут работать, чтобы преодолеть силу сопротивления, когда от них потребуется это сделать. Когда вы регулярно и последовательно выполняете силовые тренировки, ваши мышцы становятся сильнее.
Комплексная фитнес-программа включает силовые тренировки для улучшения функции суставов, плотности костей, силы мышц, сухожилий и связок, а также аэробные упражнения для улучшения состояния сердца и легких, упражнения на гибкость и равновесие. Австралийские рекомендации по физической активности и малоподвижному образу жизни рекомендуют взрослым заниматься укреплением мышц не менее двух дней в неделю.
Меняйте свою прогрессивную программу тренировок с отягощениями каждые шесть-восемь недель, чтобы поддерживать прогресс.
Переменные, которые могут повлиять на ваши результаты, включают:
- Наборы.
- Повторы.
- Проведены учения.
- Интенсивность (используемые веса).
- Частота сеансов.

- Отдых между подходами.
Если вы измените свою программу тренировок с отягощениями за счет количества повторений и подходов, выполняемых упражнений и используемых весов, вы сохраните достигнутый прирост силы.
Примеры тренировок с отягощениями
Существует множество способов укрепить мышцы дома или в тренажерном зале.
Различные типы тренировок с отягощениями включают:
- Свободные веса – классические силовые тренажеры, такие как гантели, штанги и гири.
- Медицинские мячи или мешки с песком – утяжеленные мячи или мешки.
- Грузовые тренажеры – устройства с регулируемыми сиденьями и ручками, прикрепленными либо к грузу, либо к гидравлике.
- Эластичные ленты, похожие на гигантские резиновые ленты, обеспечивают сопротивление при растяжении. Они портативны и могут быть адаптированы к большинству тренировок. Ленты обеспечивают постоянное сопротивление на протяжении всего движения.
- Подвесное оборудование – тренажер, использующий гравитацию и вес тела пользователя для выполнения различных упражнений.

- Вес собственного тела – можно использовать для приседаний, отжиманий и подтягиваний. Использовать вес собственного тела удобно, особенно в путешествии или на работе.
Польза для здоровья от тренировок с отягощениями
Польза для физического и психического здоровья, которую можно получить с помощью тренировок с отягощениями, включает:
- Улучшение мышечной силы и тонуса — для защиты суставов от травм.
- Сохранение гибкости и баланса, которые помогут вам оставаться независимыми в старости.
- Управление весом и увеличение соотношения мышечной массы к жиру — по мере набора мышечной массы ваше тело сжигает больше килоджоулей в состоянии покоя.
- Может помочь уменьшить или предотвратить снижение когнитивных функций у пожилых людей.
- Повышенная выносливость — по мере того, как вы становитесь сильнее, вы не так быстро устаете.
- Профилактика или контроль хронических состояний, таких как диабет, болезни сердца, артрит, боли в спине, депрессия и ожирение.

- Лечение боли.
- Улучшенная подвижность и баланс.
- Улучшение осанки.
- Снижение риска травм.
- Увеличение плотности и прочности костей и снижение риска остеопороза.
- Улучшение самочувствия – тренировки с отягощениями могут повысить вашу уверенность в себе, улучшить внешний вид тела и настроение.
- Улучшение сна и предотвращение бессонницы.
- Повышение самооценки.
- Повышенная производительность повседневных задач.
Основные принципы тренировки с отягощениями
Тренировка с отягощениями состоит из различных компонентов. Основные принципы включают:
- Программа – ваша общая фитнес-программа состоит из различных типов упражнений, таких как аэробные тренировки, тренировки на гибкость, силовые тренировки и упражнения на равновесие.
- Вес – различные веса или другие виды сопротивления, например, 3-килограммовый ручной вес или фиксированный вес, вес тела или резиновая лента будут использоваться для различных упражнений во время силовой тренировки.

- Упражнение – конкретное движение, например подъем на носки, предназначенное для укрепления определенной мышцы или группы мышц.
- Повторения или повторения — относится к тому, сколько раз вы непрерывно повторяете каждое упражнение в подходе.
- Сет – это группа повторений, выполняемых без отдыха, например, два подхода приседаний по 15 повторений означают, что вы делаете 15 приседаний, затем даете мышцам отдых, прежде чем делать еще 15 приседаний.
- Отдых – отдыхать нужно между подходами. Периоды отдыха варьируются в зависимости от интенсивности выполняемых упражнений.
- Разнообразие — изменение режима тренировок, например, регулярное введение новых упражнений, бросает вызов вашим мышцам и заставляет их адаптироваться и укрепляться.
- Принцип прогрессивной перегрузки — чтобы продолжать получать пользу, силовые тренировки должны выполняться до такой степени, что вам будет трудно сделать еще одно повторение.
 Цель состоит в том, чтобы использовать соответствующий вес или силу сопротивления, которые бросят вам вызов, сохраняя при этом хорошую технику. Кроме того, регулярная корректировка тренировочных переменных, таких как частота, продолжительность, упражнения для каждой группы мышц, количество упражнений для каждой группы мышц, наборы и повторения, помогают убедиться, что вы прогрессируете и совершенствуетесь.
Цель состоит в том, чтобы использовать соответствующий вес или силу сопротивления, которые бросят вам вызов, сохраняя при этом хорошую технику. Кроме того, регулярная корректировка тренировочных переменных, таких как частота, продолжительность, упражнения для каждой группы мышц, количество упражнений для каждой группы мышц, наборы и повторения, помогают убедиться, что вы прогрессируете и совершенствуетесь. - Восстановление – мышцам нужно время для восстановления и адаптации после тренировки. Хорошим практическим правилом является отдых группы мышц до 48 часов, прежде чем снова работать с той же группой мышц.
Тренировки с отягощениями для начинающих
Скрининг перед тренировкой используется для выявления людей с заболеваниями, которые могут подвергать их повышенному риску возникновения проблем со здоровьем во время физической активности. Это фильтр или защитная сетка, помогающая решить, перевешивают ли потенциальные преимущества упражнений риски для вас.
Распечатайте копию инструмента AUSactive для скрининга взрослых перед тренировкой и обсудите его со своим врачом, специалистом по медицинскому обслуживанию или специалистом по физическим упражнениям.
В Австралийских рекомендациях по физической активности и малоподвижному образу жизни рекомендуется заниматься силовыми тренировками не менее двух дней в неделю. Эти упражнения должны задействовать все основные группы мышц вашего тела (ноги, бедра, спина, грудь, корпус, плечи и руки).
Начало тренировки с отягощениями
Важно обращать внимание на безопасность и форму, чтобы снизить риск получения травмы. Зарегистрированный специалист AUSactive может помочь вам разработать безопасную и эффективную программу.
Для начала типичная программа силовых тренировок для начинающих включает:
- От восьми до десяти упражнений, которые задействуют основные группы мышц тела и выполняются два-три раза в неделю.
- Начиная с одного подхода каждого упражнения, включающего всего восемь повторений (повторений), не чаще двух раз в неделю.

Ваша цель — постепенно увеличить количество подходов до двух-трех подходов в каждом упражнении, состоящих из восьми-двенадцати повторений, каждый второй или третий день. Как только вы сможете с комфортом выполнить 12 повторений в упражнении, вам следует подумать о дальнейшем прогрессе.
Разминка перед тренировкой с отягощениями
Разогрейте тело перед началом силовых упражнений. Начните с легких аэробных упражнений (таких как ходьба, езда на велосипеде или гребля) в течение примерно пяти минут в дополнение к нескольким динамическим растяжкам. Динамическая растяжка включает в себя медленные контролируемые движения по всему диапазону движений.
Усовершенствованные тренировки с отягощениями
Чтобы получить максимальную отдачу от тренировок с отягощениями, постепенно увеличивайте интенсивность тренировок в соответствии с вашим опытом и тренировочными целями. Это может означать увеличение веса, изменение продолжительности сокращения (время, в течение которого вы удерживаете вес, уменьшая время отдыха или увеличивая объем тренировки). 0008
0008
После того, как вы регулярно занимаетесь тренировками с отягощениями в течение четырех-шести недель, вы можете постепенно увеличивать интенсивность тренировок по мере адаптации мышц.
Исследования показывают, что наблюдение и инструктаж специалистов могут улучшить ваши результаты, поскольку они гарантируют, что вы будете практиковать правильную технику и следовать принципам безопасности. Если вы испытываете какой-либо дискомфорт или боль, обратитесь к медицинскому работнику, прежде чем продолжить свою программу.
Повторяющийся максимум (ПМ) и тренировка с отягощениями
Наилучший способ развития мышечной силы заключается в том, чтобы мышца сокращалась до своего максимального потенциала в любой момент времени – максимальное произвольное сокращение (МПС). В тренировках с отягощениями MVC измеряется термином XRM, где RM — это максимальное количество повторений, которые можно выполнить с заданным сопротивлением или весом. Х — это количество раз, которое можно поднять определенный вес до того, как мышцы устанут.
Это диапазон RM, который определяет тип улучшения мышц. Оптимальный диапазон для увеличения мышечной силы — 8–12 ПМ для новичков и 2–6 ПМ для более продвинутых.
Например, формула 7ПМ означает, что человек может поднять вес (скажем, 50 кг) семь раз, прежде чем мышцы устанут слишком долго. Более высокие веса означают более низкий RM — например, тот же человек может поднять вес 65 кг, но менее семи раз.
Меньшие веса обычно приводят к более высокому RM — например, один и тот же человек может поднять вес 35 кг примерно 12 раз, прежде чем наступит мышечная усталость. Принципы MVC могут помочь вам получить максимальную пользу от тренировок. Хорошее эмпирическое правило состоит в том, чтобы увеличивать вес от 2 до 10 процентов только после того, как вы сможете с комфортом выполнить два повторения сверх максимума.
Применение MVC для достижения целей продвинутой тренировки с отягощениями
Принципы силовой тренировки включают манипулирование количеством повторений (повторений), наборов, темпом, упражнениями и усилием для перегрузки группы мышц и получения желаемого изменения силы, выносливости , размер или форма.
Конкретные комбинации повторений, подходов, упражнений, сопротивления и силы определяют тип развития мышц, которого вы достигаете. Общие рекомендации по использованию линейки RM включают:
- Мышечная сила: 1–5 повторных повторений за подход, выполняется взрывным образом.
- Мышечная сила: 1–6 RM в подходе, под контролем.
- Размер мышц (гипертрофия): 6–12 повторных повторений в подходе, контролируемо.
- Мышечная выносливость: 12–15 или более повторных повторений в подходе, контролируемая.
Восстановление мышц во время интенсивных тренировок с отягощениями
Мышцам требуется время для восстановления и роста после тренировки. Недостаточное время для восстановления мышц означает, что они не станут больше и сильнее. Хорошее эмпирическое правило — давать группе мышц отдых не менее 48 часов.
Когда у вас будет достаточный опыт в тренировках с отягощениями и при поддержке квалифицированного специалиста в области здравоохранения или физических упражнений, вы можете подумать о сплит-программе. Например, вы можете тренировать верхнюю часть тела по понедельникам и пятницам, а нижнюю — по средам и воскресеньям.
Например, вы можете тренировать верхнюю часть тела по понедельникам и пятницам, а нижнюю — по средам и воскресеньям.
Увеличение силы за счет продвинутых тренировок с отягощениями
У большинства начинающих наблюдается быстрый рост силы, за которым следует плато или выравнивание силы. После этого прирост мышечной силы и размера с трудом зарабатывается.
Когда вы начинаете тренироваться с отягощениями, большая часть первоначального прироста силы связана с феноменом, называемым нейронной адаптацией. Это означает, что нервы, обслуживающие мышцы, меняют свое поведение. Считается, что нервы возбуждаются чаще (вызывая усиление сокращения мышц), и для выполнения сокращения задействуется больше двигательных единиц (двигательная единица — это нервная клетка и связанные с ней мышечные волокна). Это означает, что вы становитесь сильнее, но мышцы остаются прежнего размера — вы достигли плато.
Со временем мышечные клетки реагируют на непрерывную тренировку с отягощениями, увеличиваясь в размерах (гипертрофия), поэтому не расстраивайтесь, достигнув плато — на самом деле это обнадеживающий признак того, что рост мышц вскоре последует. Различные методы могут помочь вам сократить период плато.
Различные методы могут помочь вам сократить период плато.
Варьируя тренировки, вы сможете преодолеть плато. Теория вариативности заключается в том, что вы можете стимулировать рост и силу своих мышц, подвергая их различным нагрузкам. Мышцы будут реагировать размером и силой, поскольку они вынуждены адаптироваться.
Проконсультируйтесь с инструктором тренажерного зала или личным тренером, но рекомендации включают:
- Увеличьте количество повторений.
- Увеличьте время тренировки на 10 или 15 минут.
- Увеличьте частоту тренировок, помня о том, что каждой мышце требуется не менее 48 часов на восстановление. Когда вы станете более опытным, вы можете рассмотреть возможность разделения частей тела на разные дни недели — например, грудь, плечи и трицепсы на первой тренировке, спина, бицепсы и мышцы живота на второй тренировке и ноги на третьей тренировке.
- Переключитесь на другие упражнения — например, сосредоточьтесь на упражнениях, которые задействуют несколько групп мышц и которые носят функциональный или специфический характер, то есть связаны с повседневной деятельностью или спортивными потребностями.

- Увеличьте вес примерно на 5-10 процентов.
- Комбинируйте другие виды деятельности, такие как плавание или бег.
- Меняйте тренировку примерно каждые четыре-восемь недель, чтобы ваши мышцы оставались в тонусе.
Где получить помощь
- Ваш врач общей практики.
- Физиотерапевт.
- Аккредитованный физиотерапевт.
- Зарегистрированный специалист в Австралии.
- AUSactive Тел. 1300 211 311.
Преимущества силовых и силовых тренировок
Если бы вы знали, что определенный тип упражнений может принести пользу вашему сердцу, улучшить равновесие, укрепить кости и мышцы и помочь вам похудеть или сохранить вес, разве вы не хотите начать? Что ж, исследования показывают, что силовые тренировки могут дать все эти преимущества и даже больше.
Силовые тренировки, также известные как силовые тренировки или тренировки с отягощениями, — это физическая активность, предназначенная для улучшения мышечной силы и физической формы путем тренировки определенных мышц или групп мышц с внешним сопротивлением, включая свободные веса, силовые тренажеры или собственный вес тела, в зависимости от в Американскую кардиологическую ассоциацию.
«Основной принцип заключается в том, чтобы приложить нагрузку и перегрузить мышцы, чтобы они адаптировались и стали сильнее», — объясняет Нил Пайр, CSCS, сертифицированный ACSM физиолог и менеджер по работе с клиентами в The Gym at Englewood в Энглвуде, Нью-Джерси. .
Всем важно знать, что силовые тренировки — это не только бодибилдеры, поднимающие тяжести в тренажерном зале. Регулярные силовые тренировки или тренировки с отягощениями полезны для людей всех возрастов и уровней физической подготовки, поскольку они помогают предотвратить естественную потерю мышечной массы, которая происходит с возрастом (медицинский термин для этой потери — саркопения). Он также может быть полезен людям с хроническими заболеваниями, такими как ожирение, артрит или болезни сердца.
По своей сути силовые тренировки основаны на функциональных движениях — поднятии, толкании, подтягивании — для наращивания мышечной массы и координации, необходимых для повседневной деятельности, — объясняет Рамона Браганса, знаменитый личный тренер из Лос-Анджелеса, сертифицированный Канадской организация фитнес-образования Canfitpro.
«Некоторых людей словосочетание «силовые тренировки» пугает, но оно повышает вашу способность безопасно и эффективно двигаться в жизни, — говорит она. Например: ваша способность что-то поднять и поставить на полку, отнести продукты в дверь, наклониться и поднять что-то или встать после того, как вы упали. «Чтобы встать с пола, вам нужно задействовать мышцы верхней части тела, пресса, ног и ягодиц», — говорит Браганса.
СВЯЗАННЫЕ: Все, что вам нужно знать о том, как быть в хорошей физической форме
Руководство по физической активности для американцев от Министерства здравоохранения и социальных служб США (HHS) рекомендует детям и подросткам в возрасте от 6 до 17 лет включать силовые тренировки в свои ежедневные 60-минутные физические нагрузки три дня в неделю. Взрослые должны стремиться выполнять умеренные или интенсивные силовые тренировки, направленные на все группы мышц, два дня в неделю.
И вам нужно отдыхать между силовыми тренировками.
СВЯЗАННЫЕ: Все, что вам нужно знать об отдыхе и восстановлении
«Вы не поправляетесь во время тренировок; вы поправляетесь в промежутках», — говорит Пире. «Вы должны дать себе день между силовыми тренировками, чтобы позволить вашему телу восстановиться и восстановить мышечную ткань после подъема или сопротивления».
Как силовые тренировки помогают вашему здоровью
Помимо хорошо разрекламированного (и часто рекламируемого в Instagram) преимущества повышения тонуса и четкости ваших мышц, как помогают силовые тренировки? Вот лишь некоторые из многих способов:
1. Силовые тренировки делают вас сильнее и выносливее Это преимущество очевидно, но его не следует упускать из виду. «Мышечная сила имеет решающее значение для того, чтобы вам было легче делать то, что вам нужно делать изо дня в день», — говорит Пире, — особенно когда мы становимся старше и естественным образом начинаем терять мышечную массу.
Силовые тренировки также называют тренировками с отягощениями, поскольку они включают в себя укрепление и повышение тонуса мышц путем их сокращения против силы сопротивления. Согласно Энциклопедии поведенческой медицины, существует два типа тренировок с отягощениями:
- Изометрическое сопротивление включает в себя сокращение мышц относительно неподвижного объекта, например, от пола при отжимании.
- Изотоническая силовая тренировка включает в себя сокращение мышц посредством различных движений, как при поднятии тяжестей.
2.
Силовые тренировки защищают здоровье костей и мышечную массуПримерно в возрасте 30 лет мы начинаем терять от 3 до 5 процентов сухой мышечной массы за десять лет из-за старения, отмечает Harvard Health Publishing.
Согласно исследованию, опубликованному в октябре 2017 г. в Journal of Bone and Mineral Research , всего 30 минут высокоинтенсивных силовых и ударных тренировок два раза в неделю улучшают функциональные показатели, а также плотность, структуру и упругость костей. силы у женщин в постменопаузе с низкой костной массой — и это не имело негативных последствий.
в Journal of Bone and Mineral Research , всего 30 минут высокоинтенсивных силовых и ударных тренировок два раза в неделю улучшают функциональные показатели, а также плотность, структуру и упругость костей. силы у женщин в постменопаузе с низкой костной массой — и это не имело негативных последствий.
Аналогичным образом, в рекомендациях по физической активности HHS отмечается, что для всех занятия по укреплению мышц помогают сохранить или увеличить мышечную массу, силу и мощность, которые необходимы для здоровья костей, суставов и мышц с возрастом.
3. Силовые тренировки помогают организму эффективно сжигать калорииВсе упражнения помогают повысить метаболизм (скорость сжигания калорий в состоянии покоя в течение дня).
Как при аэробных нагрузках, так и при силовых тренировках ваше тело продолжает сжигать калории после силовых тренировок, возвращаясь в более спокойное состояние (с точки зрения затрачиваемой энергии). По данным Американского совета по физическим упражнениям, это процесс, называемый «избыточным потреблением кислорода после тренировки».0008
По данным Американского совета по физическим упражнениям, это процесс, называемый «избыточным потреблением кислорода после тренировки».0008
Но когда вы выполняете силовые, силовые или силовые тренировки, ваше тело требует больше энергии в зависимости от того, сколько энергии вы прилагаете (это означает, что чем больше вы работаете, тем больше энергии требуется). Таким образом, вы можете усилить этот эффект в зависимости от количества энергии, которую вы вкладываете в тренировку. Это означает, что во время тренировки сжигается больше калорий, а также калорий после тренировки, пока ваше тело восстанавливается до состояния покоя.
4. Силовые тренировки помогают снизить вес навсегда Поскольку силовые тренировки повышают избыточное потребление кислорода после тренировки, они также могут помочь тренирующимся ускорить потерю веса больше, чем если бы вы занимались только аэробными упражнениями, говорит Пайр. «[Упражнения с сопротивлением или укрепляющие упражнения] поддерживают ваш метаболизм активным после тренировки гораздо дольше, чем после аэробной тренировки».
Это потому, что мышечная ткань в целом более активна. «Если у вас больше мышечной массы, вы будете сжигать больше калорий — даже во сне, чем если бы у вас не было этой лишней мышечной массы», — добавляет он.
Исследование, опубликованное в журнале Obesity в ноябре 2017 года, показало, что по сравнению с людьми, сидящими на диете, которые не занимались физическими упражнениями, и теми, кто выполнял только аэробные упражнения, люди, сидящие на диете, которые выполняли силовые упражнения четыре раза в неделю в течение 18 месяцев, потеряли больше всего жира. (около 18 фунтов по сравнению с 10 фунтами для тех, кто не занимается спортом, и 16 фунтами для тех, кто занимается аэробикой).
Возможно, вы даже сможете дополнительно уменьшить жировые отложения, особенно если силовые тренировки сочетаются с уменьшением калорий с помощью диеты. Люди, которые следовали комбинированным тренировкам с отягощениями всего тела и диете в течение четырех месяцев, уменьшали свою жировую массу, улучшая при этом мышечную массу лучше, чем только тренировки с отягощениями или диета, пришли к выводу небольшое исследование, опубликованное в январе 2018 года в журнале 9. 0501 Международный журнал спортивного питания и метаболизма при физических нагрузках .
0501 Международный журнал спортивного питания и метаболизма при физических нагрузках .
Силовые тренировки также улучшают баланс, координацию и осанку, согласно прошлым исследованиям.
В одном обзоре, опубликованном в журнале Aging Clinical and Experimental Research в ноябре 2017 года, сделан вывод о том, что хотя бы одна тренировка с отягощениями в неделю — отдельно или в рамках программы с несколькими различными типами тренировок — приводит к увеличению до 37 процентов. мышечной силы, увеличение мышечной массы на 7,5% и увеличение функциональных возможностей на 58% (связанное с риском падений) у ослабленных пожилых людей.
«Баланс зависит от силы мышц, удерживающих вас на ногах», — отмечает Пире. «Чем сильнее эти мышцы, тем лучше ваш баланс».
6. Силовые тренировки могут помочь в лечении хронических заболеваний
Исследования показали, что силовые тренировки могут также помочь облегчить симптомы у людей со многими хроническими заболеваниями, включая нервно-мышечные расстройства, ВИЧ, хроническую обструктивную болезнь легких и некоторые виды рака, среди прочих .
По данным Центров по контролю и профилактике заболеваний и исследованию, опубликованному в июне 2017 года в журнале Diabetes Therapy , для более чем 30 миллионов американцев с диабетом 2 типа силовые тренировки наряду с другими изменениями в здоровом образе жизни могут помочь улучшить контроль уровня глюкозы.
А исследование, опубликованное в 2019 году в Frontiers in Psychology , показало, что регулярные тренировки с отягощениями также могут помочь предотвратить хронические проблемы с подвижностью, болезни сердца, диабет 2 типа и рак.
7. Силовые тренировки повышают уровень энергии и улучшают настроение
Согласно метаанализу 33 клинических испытаний, силовые тренировки являются законным вариантом лечения (или дополнительным лечением) для подавления симптомов депрессии. опубликовано в журнале JAMA Psychiatry в июне 2018 года.
«Все упражнения улучшают настроение, потому что повышают уровень эндорфинов», — говорит Пире. Но что касается силовых тренировок, дополнительные исследования, в которых изучались нейрохимические и нервно-мышечные реакции на такие тренировки, дают дополнительные доказательства того, что они оказывают положительное влияние на мозг, добавляет он.
Согласно исследованию, опубликованному в выпуске Brazilian Journal of Psychology за январь–февраль 2019 года, силовые тренировки также могут помочь вам лучше спать.
И все мы знаем, что хороший ночной сон может значительно улучшить настроение.
8. Силовые тренировки полезны для здоровья сердечно-сосудистой системы По данным HHS, наряду с аэробными упражнениями упражнения по укреплению мышц помогают снизить кровяное давление и снизить риск гипертонии и сердечных заболеваний.
СВЯЗАННЫЕ: Силовые тренировки снижают риск сердечно-сосудистых заболеваний и диабета, независимо от того, сколько кардио вы делаете Тренировки с отягощениями для вашей рутины у вас есть много вариантов, отмечает Пире. Вам определенно не нужен абонемент в спортзал или дорогие силовые тренажеры, добавляет он. «Приседания на стуле дома, отжимания, планки или другие движения, требующие использования веса собственного тела в качестве сопротивления, могут быть очень эффективными. Чем больше интенсивности, объема и разнообразия вы можете применить к своему телу, тем сильнее отклик», — говорит он.
Браганса соглашается, добавляя, что продолжая бросать себе вызов, добавляя свободные веса или используя тренажеры в тренажерном зале, или изменяя темп выполнения упражнений, вы поможете смешивать вещи, чтобы создать адаптацию, необходимую вашему телу для наращивания силы.
СВЯЗАННЫЕ: Упражнения с собственным весом для каждой части тела
Если у вас есть какие-либо проблемы со здоровьем, спросите своего врача, какой тип силовых тренировок лучше всего соответствует вашим потребностям и способностям. Вы также можете поработать с экспертом по фитнесу, чтобы разработать программу силовых тренировок, которая будет безопасной и эффективной для вас.
Вы также можете поработать с экспертом по фитнесу, чтобы разработать программу силовых тренировок, которая будет безопасной и эффективной для вас.
Даже найм тренера на один-три занятия может помочь вам освоить правильную форму силовых упражнений и создать всестороннюю программу, подходящую для вашего тела, целей и других рисков для здоровья, говорит Браганса.
Дополнительные отчеты Джилл Вальдбизер, Никол Натале и Джессика Мигала .
Редакционные источники и проверка фактов
- Тренировочные упражнения на силу и сопротивление. Американская Ассоциация Сердца. 19 апреля, 2018.
- Сантилли В., Бернетти А., Мангон М. и др. Клиническое определение саркопении. Клинические случаи минеральной и костной плотности . Сентябрь–декабрь 2014 г.
- Рекомендации по физической активности для американцев: второе издание. Министерство здравоохранения и социальных служб США. 2018.
- Ремо А. Изометрически-изотонические упражнения.
 Энциклопедия поведенческой медицины . 2013.
Энциклопедия поведенческой медицины . 2013. - Сохраните мышечную массу. Издательство Harvard Health Publishing. Февраль 2016.
- Watson SL, Weeks BK, Weis LJ, et al. Высокоинтенсивные тренировки с отягощениями и ударами улучшают минеральную плотность костей и физическую функцию у женщин в постменопаузе с остеопенией и остеопорозом: рандомизированное контролируемое исследование LIFTMOR. Журнал исследований костей и минералов . 4 октября 2017 г.
- Миллер Т., Малл С., Арагон А.А. Тренировки с отягощениями в сочетании с диетой уменьшают жировые отложения, сохраняя мышечную массу независимо от уровня метаболизма в состоянии покоя. Международный журнал спортивного питания и метаболизма при физических нагрузках . Январь 2018 г.
- Биверс К.М., Амброзиус В.Т., Реески В.Дж. и др. Влияние типа упражнений во время преднамеренной потери веса на состав тела у пожилых людей с ожирением. Ожирение . 25 ноября 2017 г.
- Кадоре Э.
 Л., Родригес-Маньяс Л., Синклер А., Искьердо М. Влияние различных упражнений на риск падений, походку и равновесие у физически ослабленных пожилых людей: систематический обзор. Исследование омоложения . Апрель 2013 г.
Л., Родригес-Маньяс Л., Синклер А., Искьердо М. Влияние различных упражнений на риск падений, походку и равновесие у физически ослабленных пожилых людей: систематический обзор. Исследование омоложения . Апрель 2013 г. - Лопес П., Пинто Р.С., Радаэлли Р. и др. Преимущества тренировок с отягощениями для пожилых людей с физическими недостатками: систематический обзор. Клинические и экспериментальные исследования старения . Ноябрь 2017 г.
- Диабет 2 типа. Центры по контролю и профилактике заболеваний. 30 мая 2019 г.
- Ли Дж., Ким Д., Ким С. Тренировки с отягощениями для гликемического контроля, мышечной силы и безжировой массы тела у старых пациентов с диабетом 2 типа: метаанализ. Терапия диабета. Июнь 2017 г.
- Gordon BR, McDowell CP, Hallgren Mats, et al. Связь эффективности тренировок с отягощениями с депрессивными симптомами. JAMA Психиатрия . Июнь 2018 г.
- Стикленд, Дж. К., и Смит, Массачусетс. Анксиолитические эффекты упражнений с отягощениями.
 Границы психологии . 2014.
Границы психологии . 2014. - D’Aurea CVR, Poyares D, Passos GS, et al. Влияние тренировок с отягощениями и растяжек на хроническую бессонницу. Бразильский журнал психиатрии . Январь–февраль 2019 г.
- McCall P. 7 Что нужно знать об избыточном потреблении кислорода после тренировки (EPOC). Американский совет по физическим упражнениям. 28 августа 2014 г.
- Чикколо Дж.Т., Карр Л.Дж., Крупель К.Л., Лонгвал Дж.Л. Роль силовых тренировок в профилактике и лечении хронических заболеваний. Американский журнал медицины образа жизни . 15 декабря 2009 г.
- Маклеод Дж. К., Стоукс Т., Филлипс С. М. Тренировки с отягощениями как основная мера противодействия возрастным хроническим заболеваниям. Границы физиологии . 6 июня 2019 г.
Скрыть
Стоит ли тренироваться, если вы поститесь?
Если вы один из многих людей, которые время от времени воздерживаются от еды по религиозным или медицинским причинам, вам также необходимо скорректировать график тренировок, эксперты. ..
..
от Lauren Bedosky


 То есть разность потенциалов можно найти как произведение силы тока на сопротивление. Знать, чем отличается сила тока от напряжения очень важно для электротехнических расчетов. На этом базируются все основы функционирования электрических цепей.
То есть разность потенциалов можно найти как произведение силы тока на сопротивление. Знать, чем отличается сила тока от напряжения очень важно для электротехнических расчетов. На этом базируются все основы функционирования электрических цепей.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 При больших токах без внешнего магнитного поля, происходит равномерное распределение выхода гравитонов во все стороны, и реакции проводника на выход гравитонов нет.
При больших токах без внешнего магнитного поля, происходит равномерное распределение выхода гравитонов во все стороны, и реакции проводника на выход гравитонов нет. 3). Поскольку каждому кванту магнитного поля соответствует квант гравитационного поля, происходит искажение гравитационного поля проводника. В результате этого процесса возникает сила Ампера .
3). Поскольку каждому кванту магнитного поля соответствует квант гравитационного поля, происходит искажение гравитационного поля проводника. В результате этого процесса возникает сила Ампера .
 [6]
[6]
 Тула, 1997.
Тула, 1997. Обратная связь — 161.97.168.212 (0.011 с.)
Обратная связь — 161.97.168.212 (0.011 с.)
 потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.
потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.  Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.
Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.





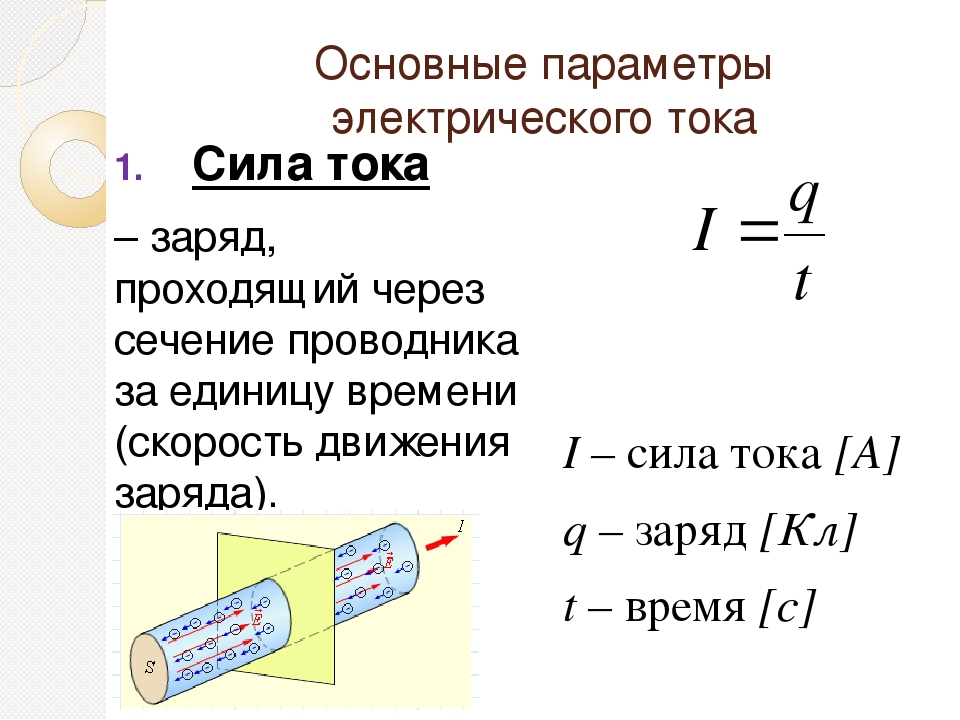


 Это может касаться шеи, плеч, спины и суставов, таких как запястья, колени и лодыжки.
Это может касаться шеи, плеч, спины и суставов, таких как запястья, колени и лодыжки. 3 Сопротивление
3 Сопротивление Единицы тока
ампер (А), который определяется как один кулон в секунду.
Единицы тока
ампер (А), который определяется как один кулон в секунду.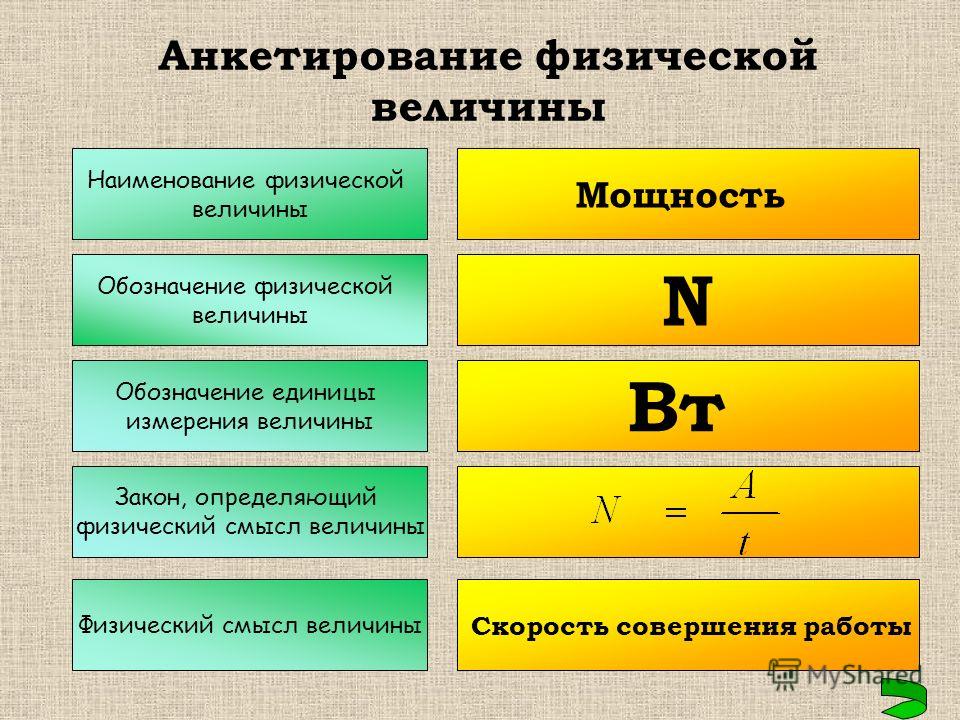 также
также