2=2gl{\cos \alpha \ }\left(2.9\right).\]

Подставим результат (2.9) в формулу (2.7), получили:

\[N=m\frac{2gl{cos \alpha \ }}{l}+mg{\cos \alpha \ }\ \left(2.10\right).\]

Приравниваем по условию силу натяжения нити к силе тяжести, выражаем величину угла:

\[mg=m\frac{2gl{cos \alpha \ }}{l}+mg{\cos \alpha \ }\to 1=3{cos \alpha \to \alpha =arc{\cos \frac{1}{3}\ }\ }.\]

Ответ. 1) $N=3mg$. 2) $\alpha =arc{\cos \frac{1}{3}\ }$

   

формула, как найти, куда направлена

Сила натяжения нити — формулировка

Определение

Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

• создание строительного отвеса;
• установка растяжек для фиксации радиоантенн;
• поведение арматуры внутри напряженного бетона;
• устройство корабельного такелажа.

Как определить силу, формулы

Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

С неподвижно закрепленным верхним концом

Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:

\(F=F_{тяж}=m*g\)

где m – это масса тела, а g представляет собой ускорение свободного падения.

Если нить под углом

В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.  

\(F_n=m*g*cos(a)\)

где а равен углу отклонения.

Формула с учетом ускорения и массы

В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:

\(F=F_{тяж}+m*a\)

Сила натяжения во вращающейся системе

Описание

Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:

• приближение к земле приводит к увеличению силы;
• во время удаления от земли сила слабеет.

Формула расчета

Рассчитать силу натяжения в условиях вращающейся системы можно так:

\(F=\frac{m\times \nu ^{2}}{r}\)

Обозначение, единица измерения

Существуют определенные стандарты для написания формулы силы натяжения.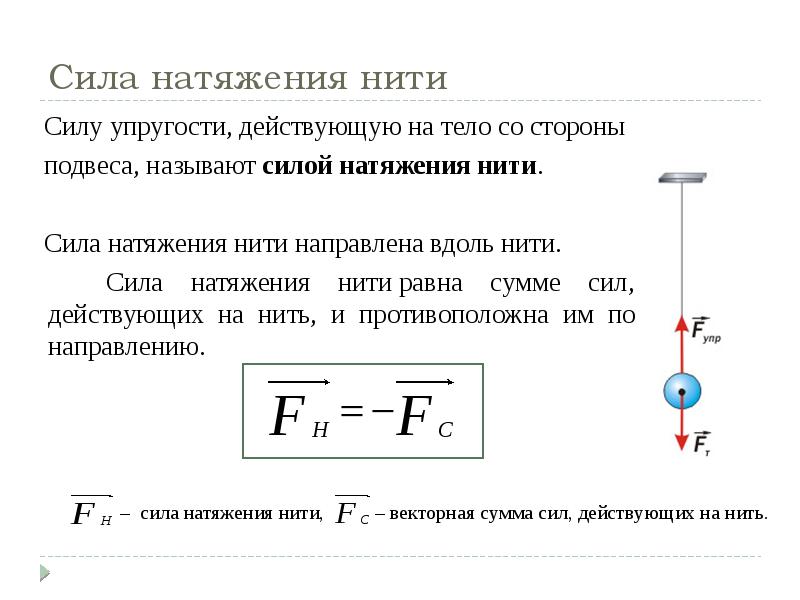 {2}}\)

Примеры решения задач

Задание 1

На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.

Решение

Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.

Источник: webmath.ru

\(\bar{T}+m\bar{g}=m\bar{a}\)

\(\bar{T}\) является силой натяжения нити.

Проекция уравнения будет иметь следующий вид:

\(T – mg = ma\)

Данное выражение позволяет рассчитать ускорение:

\(a=\frac{T-mg}{m}\)

Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления

\(a=\frac{4400-4*9,8}{400}\)

Ответ: a = 1. 2\)

Задание 2

На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.

Решение

Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:

\(\bar{T}+m\bar{g}=m\bar{a}\)

Источник: webmath.ru

Проекции данной формулы по осям определяются следующим образом:

X:  \(T sin α = ma = mω2R\)

Y:  \(-mg + T cos α = 0\)

Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:

\(T=\frac{mg}{\cos \alpha }\)

Анализ рисунка позволяет вывести следующее уравнение:

\(\sin \alpha = \frac{R}{l}\rightarrow \cos \alpha = \sqrt{1-\left(\frac{R}{l} \right)^{2}}\)

Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:

\(T=\frac{mg}{\sqrt{1-\left(\frac{R}{l} \right)^{2}}}= \frac{mgl}{\sqrt{l^{2}-R^{2}}}\)

Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:

\(T=\frac{0,1*9,8*5}{\sqrt{5^{2}-3^{2}}}=1,225\left(H \right)\)

Ответ: Т=1,225 H

Вес тела.

Сила реакции опоры. Сила натяжения нити | LAMPA

Многие из вас пользуются или пользовались обычной проводной компьютерной мышкой. Если такая проводная мышка рядом с вами, то посмотрите на нее (а если ее нет рядом — то представьте). Мы знаем, что, как и на все тела на Земле, на нее действует сила тяжести Fтяготения=m⋅gF_{тяготения}=m\cdot gFтяготения​=m⋅g.

Почему же она не падает вниз, а находится в состоянии покоя? Мы помним из 1-го закона Ньютона, что в инерциальных системах тело может находиться в состоянии покоя, если на него не действуют никакие силы (не наш случай) или действие всех сил скомпенсировано. Значит, что-то компенсирует действие силы тяжести. Но что? Мы забыли, что мышка лежит на столе. Мышка, на которую действует сила тяжести m⋅g⃗m\cdot\vec{g}m⋅g⃗​, в свою очередь давит на стол с силой, которую называют вес тела. Обычно вес тела обозначается P⃗\vec{P}P⃗. Но из 3-го закона Ньютона мы знаем: с какой силой мышка давит на стол (мышка→\rightarrow→стол), с точно такой же по величине силой стол давит на мышку (стол→\rightarrow→мышка). Сила, с которой стол давит на мышку, называется силой реакции опоры. Чаще всего она обозначается N⃗\vec{N}N⃗. Из 3-го закона Ньютона следует, что N⃗=−P⃗.\vec{N}=-\vec{P}{.}N⃗=−P⃗.

Заметьте, что сил три:

• на тело действует сила тяжести m⋅g⃗m\cdot\vec{g}m⋅g⃗​
• из-за действия силы тяжести на мышку мышка давит на стол с силой P⃗\vec{P}P⃗ (вес тела)
• и уже стол «отвечает» мышке на ее давление силой реакции опоры N⃗\vec{N}N⃗.

Важно помнить, что хотя силы N⃗\vec{N}N⃗ и P⃗\vec{P}P⃗ связаны друг с другом и равны по модулю, но приложены они к разным телам. Еще раз:

• вес тела P⃗\vec{P}P⃗ приложен к опоре (столу) со стороны мышки
• сила реакции опоры N⃗\vec{N}N⃗ приложена к мышке со стороны стола как «ответ» стола на действие мышки.

Давайте посмотрим, насколько хорошо вы усвоили разницу между весом P⃗\vec{P}P⃗ и силой реакции опоры N⃗\vec{N}N⃗. Попробуйте решить классическую задачу.

Сила натяжения | Динамика | Физика

Вообразите себе большой ящик, наполненный новенькими айфонами. Кто-то (я, например) привязывает к такому ящику крепкую веревку и зовет двух своих друзей, чтобы начать тащить его в неизвестном направлении.

Неважно откуда этот ящик взялся и почему именно я его нашел. Главное тут другое. Ящик изначально покоился, а затем начал двигаться. Его скорость изменилась, и это означает, что на него подействовали с какой-то силой. Что же это за сила? Сила натяжения.

Сила натяжения – это сила, с которой действует на тело веревка, нить, кабель, трос или нечто подобное. Обозначается обычно так: \vec{T}. Измеряется в ньютонах, как и любая другая сила.

Теперь важный вопрос: куда направлена эта сила? Иногда ее направляют по веревке к телу. Это неверно. С помощью веревки тянут, а не толкают. Поэтому сила натяжения направлена по веревке от тела.

Так, а как можно вычислить величину этой силы? Для начала нужно сказать вот о чем: в задачах часто говорится о том, что веревка, которую используют для перемещения предмета, – невесомая, подразумевая под этим, что у нее нет массы.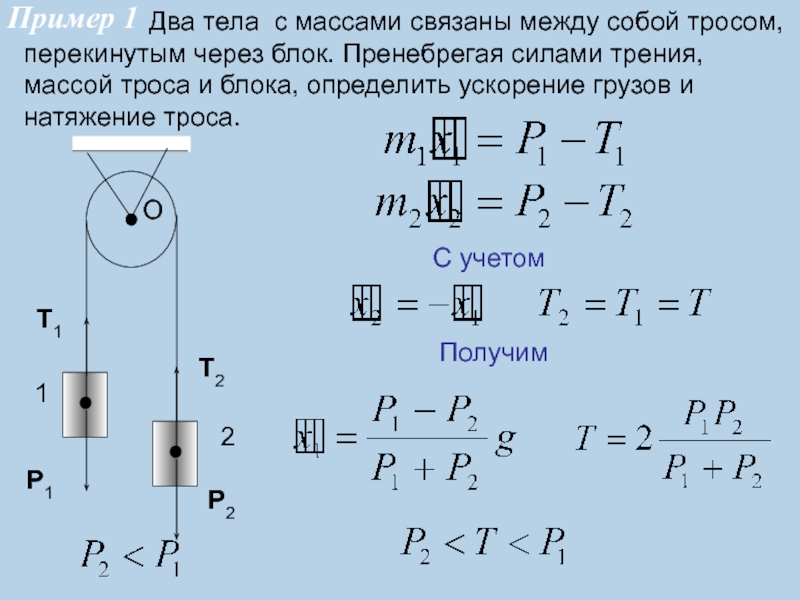 И тут можно удивленно поднять брови, задавая вопрос: «Как это нет массы?»

Хорошо, давайте представим, что у веревки есть масса, что она тяжелая, как канат, по которому заставляют лазить детей на физкультуре (ладно, не только детей). Веревки тем хороши, что позволяют передать силу на некоторое расстояние. Если сам трос будет тяжелым, его натяжение будет неодинаковым. В нашем случае правый конец веревки будет натянут гораздо сильнее, чем левый. Это связано с тем, что часть «исходной» силы, направленной на перемещение предмета, пойдет на то, чтобы растянуть в достаточной степени сам канат. В общем, чтобы упростить себе жизнь, мы предполагаем, что трос достаточно легкий и его массой можно пренебречь. В таком случае сила, с которой я и мои друзья тянут за правый конец веревки, будет равна силе, с которой левый конец веревки тянет ящик.

Итак, предположим, что наш ящик движется вправо с ускорением \vec{a}. Его масса равна m, а коэффициент трения скольжения равен \mu_с.

Как же мы можем найти величину силы натяжения? С помощью второго закона Ньютона. Причем использовать его следует для оси x:

\vec{a}_x=\dfrac{\varSigma\vec{F}_x}{m}

Вдоль этой оси на тело будут действовать две силы – сила натяжения и сила трения скольжения:

a=\dfrac{T-F_с}{m}

Силу трения скольжения мы можем выразить через силу реакции опоры:

a=\dfrac{T-\mu_сN}{m}

А силу реакции опоры мы можем выразить через силу тяжести:

a=\dfrac{T-\mu_сmg}{m}

Отсюда нетрудно найти модуль силы натяжения:

T=ma+\mu_сmg

Немного усложним задачу.

Очень вероятно, что в Тольятти просто так не получится протащить ящик с айфонами по улицам города. Скорее всего, кто-то обязательно накинет свою собственную веревку и начнет тащить в другом направлении.

Как изменится значение силы \vec{T_1}? Давайте посмотрим:

a=\dfrac{T_1-F_с-\textcolor{#E12020}{T_2}}{m}

a=\dfrac{T_1-\mu_сN-\textcolor{#E12020}{T_2}}{m}

a=\dfrac{T_1-\mu_сmg-\textcolor{#E12020}{T_2}}{m}

T_1=ma+\mu_сmg+\textcolor{#E12020}{T_2}

Все логично. Чтобы сохранить прежнее ускорение ящика, нужно компенсировать воздействие силы \vec{T_2}, поэтому мне и моим друзьям придется тянуть с большей силой.

Конвертер поверхностного натяжения • Гидравлика и гидромеханика — жидкости • Определения единиц • Онлайн-конвертеры единиц измерения

Гидравлика и гидромеханика — жидкости

Гидравлика — наука о законах движения и равновесии жидкостей и способах приложения этих законов к решению задач инженерной практики. Гидравлика характеризуется особым подходом к изучению явлений течения жидкостей; она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях. Гидромеханика — прикладная наука (раздел механики сплошных сред) изучающая равновесие и движение жидкости. Гидромеханика подразделяется на гидростатику, изучающую жидкость в равновесии, а также гидродинамику, изучающую движение жидкости.

Конвертер поверхностного натяжения

Поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Поверхностное натяжение определяют также как силу, действующую на единицу длины линии, которая ограничивает поверхность жидкости. Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения.

Коэффициент поверхностного натяжения измеряется в единицах силы на единицу длины (например, ньютон на метр, Н/м) или в единицах энергии на единицу поверхности (например, джоуль на квадратный метр, Дж/м²).

Использование конвертера «Конвертер поверхностного натяжения»

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Пользуйтесь конвертером для преобразования нескольких сотен единиц в 76 категориях или несколько тысяч пар единиц, включая метрические, британские и американские единицы. Вы сможете перевести единицы измерения длины, площади, объема, ускорения, силы, массы, потока, плотности, удельного объема, мощности, давления, напряжения, температуры, времени, момента, скорости, вязкости, электромагнитные и другие.
Примечание. В связи с ограниченной точностью преобразования возможны ошибки округления. В этом конвертере целые числа считаются точными до 15 знаков, а максимальное количество цифр после десятичной запятой или точки равно 10.

Для представления очень больших и очень малых чисел в этом калькуляторе используется компьютерная экспоненциальная запись, являющаяся альтернативной формой нормализованной экспоненциальной (научной) записи, в которой числа записываются в форме a · 10^x. », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Канал Конвертера единиц TranslatorsCafe.com на YouTube

Путеводитель по толщине струн для электрогитары

     В настоящее время выпускается такое количество разных струн для электрогитары, что у любого неподготовленного человека при визите в крупный музыкальный магазин может случится нервный срыв из-за тщетных попыток выбрать себе подходящие струны среди сотен разноцветных коробочек с кучей непонятных цифр на них.

 

Выясним что же означают эти загадочные циферки на примере струн Ernie Ball 2223 Nickel Super Slinky 9-42.

Нас интересует только 6 цифр слева: 9-11-16-24-32-42. 

Это ничто иное, как обозначение толщины струн в наборе. А крайние числа 9 и 42 это толщина 1-й и 6-й струны. Обычно этими двумя цифрами для простоты и указывается калибр. То есть, вы можете прийти в магазин, просто сказать 9-42 и любой продавец сразу же поймёт, что вам требуется.

Поскольку первые серийные струны для электрогитары запустили в массовое производство на территории США, толщину струн указывают в тысячных долях дюйма. Например цифра 9 означает, что струна №1 имеет толщину 0.009 американского дюйма, 42 – 0.042 дюйма и т.п.

Самая педантичная компания в мире D’Addario указывает также толщину струн в общепринятой метрической системе в миллиметрах, и даже силу натяжения каждой струны в американских фунтах и килограммах. На эту тему было написано очень дотошное и подробное руководство.

Но это большая редкость для производителей струн и вряд ли имеет практический смысл, так как сила натяжения — величина очень относительная и может значительно отличатся на разных типах гитар с различной мензурой и системой крепления струн.

 

Струны для электрогитары для начинающих.

 

8-38 – прекрасный выбор для начинающих и всех тех, у кого еще не выросли каменные мозоли. 

Даже некоторые скоростные технари-виртуозы играют на таком калибре, ведь чем тоньше струна, тем меньше у неё амплитуда колебания и можно добиться более четкой и быстрой игры.

9-42 – это один из самых популярных калибров. Разумное соотношение между натяжением и мощностью звучания особенно на фендеровской мензуре 25.5”. Часто именно этот калибр ставится с завода на электрогитары компании Fender.

9-46 – переходной гибридный набор между 9-42 и 10-46. Можно и риффы поиграть неплохо и выдать яркие соло не особо напрягаясь. Неплохо подойдёт для установки на гитары с системой Floyd Rose (также  как и 9-42).  Многие великие виртуозы играют именно на этом калибре, например Джо Сатриани.

9,5-44 – крайне интересный гибрид от D’Addario. Если вам слишком мягко на 9-42 и слишком жёстко на 10-46 возможно это будет панацеей.

                   

Обычные струны для гитары.

 

10-38 — самый загадочный калибр для электрогитары на сегодняшний день от компании GHS.

10-46 – легендарная десятка, которая перевернула весь гитарный мир (подробнее см. статью про компанию Ernie Ball). Золотая середина в мире гитарных калибров — это наиболее популярный и универсальный набор в наше время. Большинство профессионалов выбирают именно его.

Мощные басы вкупе с прозрачными верхами и оптимальное натяжение.

10-48 – любимый набор Дэвида Гилмора для стратокастера.

10,5-50 — на гибсон Дэвид предпочитает ставить потолще.

10-52 – ещё один гибрид. Выдаёт отличный мощный саунд, но для новичков вряд ли подойдет. Рекомендуется опытным гитаристам, которые уже знают, чего хотят в этой жизни.

Это мой любимый набор для телекастера, хотя он отлично становится практически на любую гитару. Можно спокойно опускать строй на пол-тона и не терять в натяжении и мощности звука (для игры например многих оригинальных композиций 80-90х годов). Можно играть в Дроп Ре или сделать Open G и валить кантри – всё зависит только от вашей фантазии.

10-54 – легендарный Б.Б. Кинг использовал на своей «Люсиль» именно такой калибр.

10-60 — оригинальный набор для игры в дропе от великого и ужасного Закка Вайлда.

       

 

Струны для профессионалов.

 

11-48 – базовый набор 11 от Ernie Ball. Органично подходит на гитары с мензурой 24.75″, тогда по натяжению получится практически как 10-46 на стратокастере.

11-49 – примерно тоже самое в версиях Elixir и D’addario.

11-50 – GHS решила тоже хоть чем-то выделится и поэтому сделала в своём наборе 6-тую струну еще толще.

В принципе какой-то смысл в этом есть.

11-52 – а у нас всё равно будет толще! Сказали маркетологи Dean Markley и выиграли эту бессмысленную гонку.  Ну и порадуемся за них. Хорошие басы еще никому не вредили.

11-54 – этот калибр с утолщёнными толстыми струнами изобретён относительно недавно в 90-х годах компанией Ernie Ball. Оптимизирован под пониженные строи типа Дроп Ре.

11-70 – еще один подарочек любителям изощрённого садомазо от мистера Вайлда.

Билет в закрытый клуб «у меня тоже гриф скрутило штопором».

                     

 

Как научится играть джаз.

 

12-52 – для начала купить этот набор. Прекрасный тёплый и мощный звук и максимальное неудобство при игре, особенно если вы начинающий. Правда современные любители маткора и прочего джента научились опускать строй и совмещать очень жирный звук с полноценной возможностью игры.

Для игры в стандартном строе лучше ставить на электрогитары с короткой мензурой 24.75” например на джазовые полу-акустики.

12-54 — неплохой вариант от D’Addario.

12-56 – название Not Even Slinky говорит само за себя. Действительно никакими Slinky тут и не пахнет.

Для дроп До или Си.

12-60 – все члены правления компании Cleartone тоже очень любят собираться холодными зимними вечерами и рубить в дропе.

12-68 — для электрогитар баритонов с мензурой 27”. На обычную гитару ставить не очень рекомендуется.

                       

 

Струны для пониженных строев.

 

13-56 – основная целевая аудитория: лесные великаны из сказок Толкиена. Так как затраченные калории для колебания этих мостовых канатов плохо сочетаются с размером денежного вознаграждения среднестатистического джазмена в стране Украина. Только для ОЧЕНЬ пониженных строёв.

13-62 — Light и баритон это, казалось бы взаимоисключающие понятия. В D’Addario не согласны.

13-65 — хорошая попытка DR, но нас этим не удивишь.

13-70 – а вот с этим наборчиком точно не соскучишся. Для Дроп До или Си.

13-72 – версия Ernie Ball для баритона. Можно также попробовать в Дроп Ля. Только очень осторожно.

14-55 — ходят слухи что на них играл сам George Benson.  Такие струны обычно идут с плоской обмоткой и стоят как пол-гитары. Потому что это Thomastik, а не какая-то хрень с китайской толкучки.

14-68 — только на баритон.

14-80 – Адский Ад. Используется для изгнания Сатаны. Чтоб поставить данный набор на гитару, вам скорее всего придётся растачивать свой бедный колок. Так как большинство производителей колков делают отверстие не более 0,068-0,070 дюймов. Наконец существует вполне вероятный риск деформации и складывания грифа, особенно на бюджетных инструментах. Стоят ли все эти мучения, чтоб всё-таки поиграть 10 минут в Дропе Ля/Соль решать только Вам.

                     

 

Моя гитара семиструнная…

 

9-52, 10-56, 11-58 — это наиболее популярные наборы для 7-ми струнной электро гитары.

Просто добавление толстой струны к готовым наборам для 6-ти струнок и дело в шляпе.

Но существует и масса других вариаций.

9-53, 9-64, 10-64, 10-70, 11-70 — особенно на этом поприще отличилась компания Labella.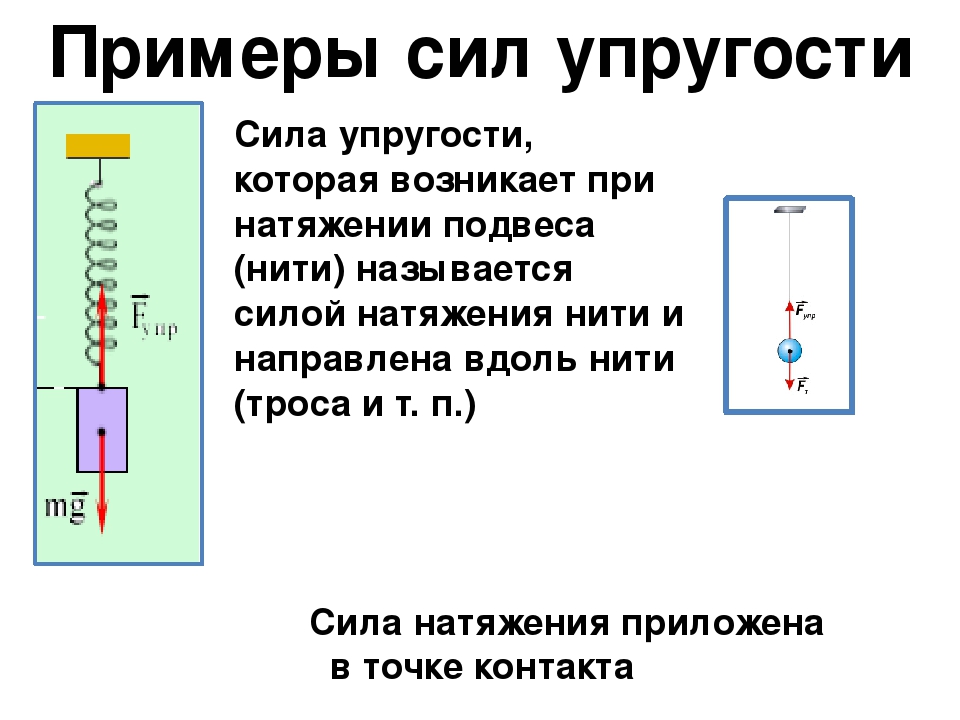

9-58, 9-62, 10-60, 11-64, 13-74 — и её главный конкурент GHS.

9-54, 10-59, 11-65 – самый крупный производитель струн в США D’Addario нервно курит в углу, также как и Dean Markley.

10-62 – очень интересный гибрид от Ernie Ball. И не простой — а с супер-навивкой из сплава кобальт.

У такого сплава гораздо лучше магнитное взаимодействие со звукоснимателями, в результате звучание становится значительно жирнее, что имеет первостепенную важность в любом тяжёлом стиле музыки.

                          

 

Сегодня ты играешь джаз, а завтра…все играют джент!

 

9-65 — наш победитель в номинации «самый бесполезный и дурацкий набор для 8-ми струнки».

9-80 — если выкинуть девятку может выйдет что-то толковое.

10-74 — наконец можно начинать валить джент прямо сейчас.

10-75 — дж-дж-дж!

10-76 — маловато перегруза, надо добавить.

10-80 — а что будет если опустить 8-мую струну?

11-80 — наконец-то DR удалось сделать что-то полезное!

11-85 — дальнейшее чтение может серьёзно повредить вашей психике.  мы вас предупредили…

9-90 — а это точно для игры на гитаре??

9-105 — все басисты плачут и идут домой.

         

 

А если на вашей гитаре струн больше девяти – значит вас обманули и подсунули ситар.

Примите наши искренние соболезнования.

Исключение составляют редкие 12-ти струнные электрогитары для которых существует всего пара видов наборов с крайне запутанной системой калибровки.

Например 8-8, 10-10, 14-8, 24w-11, 32-17, 40-22 или 10-10, 13-13 ,17-08, 26-12, 36-18, 46-26.

Такой выбор калибров связан с тем, что некоторые струны настраивают в октавы, а некоторые просто дублируют друг друга. В результате получается красивый эффект задержки типа Chorus.

Единственное что можно утверждать наверняка — если вы смогли самостоятельно настроить 12-ти струнную гитару, то вам совершенно незачем читать подобные статьи: рискуете опоздать нв свой собственный концерт.

(с) При копировании ссылка на источник guitarstrings.com.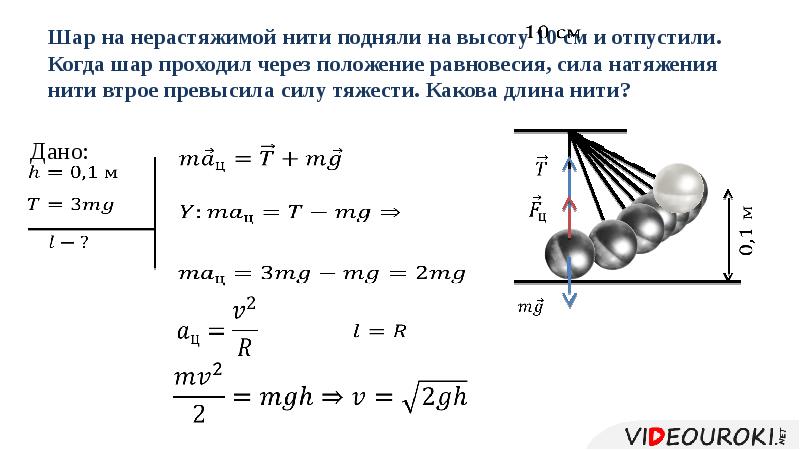 ua обязательна.

Самые читаемые

Натяжение струн: все, что необходимо знать

Главная — О нас — Статьи и обзоры — Натяжение струн: все, что необходимо знать

Сегодня музыка пестрит поражающим воображение разнообразием видов, стилей и подстилей, а также техник игры на инструментах. В XXI веке однозначно нельзя выработать какие-то четкие формулы и точные решения для музыкальных жанров с точки зрения стремления получить идеальное звучание . И причины тому достаточно просты: каждый музыкант имеет свой особый стиль игры на гитаре – а в рамках данной статьи мы будет говорить именно о гитаристах – свои собственные предпочтения в области формирования звучания инструмента и группы в целом.

Когда мы говорим о вкусах гитаристов, наибольшие споры обычно вызывает выбор определенной толщины струн. От чего же он зависит?

Предпочтения музыкантов по выбору калибра струн во многом формируются из трех факторов:

• Строй, в котором играет гитарист;
• Особенности инструмента, в частности, величина его мензуры;
• Сила пальцев музыканта, от которой зависит комфорт при игре на комплектах разной толщины (сравните пальцы Джимми Пэйджа, который был фанатом «восьмерок» и SRV, который играл на комплектах .013-.056/.058).

 

И если сила пальцев – параметр сугубо индивидуальный, то составить определенные рекомендации и выявить зависимость между силой натяжения струны, ее строем и мензурой инструмента вполне возможно. Именно об этом мы сегодня и поговорим.

 

Натяжение струн в истории гитаростроения

Как ни странно, но жестких стандартов толщины/силы натяжения струн не было почти до середины прошлого века! Лишь в конце 30-х годов 20 века Джон Д’Аддарио (John D’Addario) ввел на своем производстве стандартизацию калибров струн и их разделение, выпустив на рынок три типа комплектов для акустической гитары: с легким, нормальным и сильным натяжением.

Почти до самого конца 20 века – если быть точнее, то где-то до середины 80-х годов – подобных стандартизированных комплектов было достаточно для удовлетворения потребностей всех музыкантов. Периодически по специальным заказам крупные производители выпускали и новые наборы: чаще всего они представляли собой гибриды из существующих струн, которые использовали для открытых строев и строев с понижением. В конце концов, к 90-м годам такие предложения стали очень многочисленными – музыканты все чаще применяли нестандартные музыкальные решения, выходили за рамки музыкальных трендов и старались по-максимуму использовать все возможности гитары в популярных музыкальных стилях. Все это привело к резко возросшей популярности открытых настроек гитары (open tuning), более частому применению вариаций пониженного строя, когда шестая струна настраивается на тон ниже традиционной ноты (drop tuning), разработке гитар-баритонов, а также нетрадиционных инструментов с 7-ю и 5-ю струнами. Такой скачок в музыкальной индустрии способствовал тому, что на рынке стали все чаще появляться необычные наборы струн, музыканты стали искать свой любимый «калибр» и свой звук – и такие крупные производители, как D’Addario, дали гитаристам возможность это сделать.

 

Теоретические аспекты натяжения струн

Ежегодно службы по работе с клиентами крупнейших музыкальных брендов получают тысячи писем с просьбой решить их проблемы с выбором наиболее подходящего набора струн.

В качестве ремарки: далее мы будем рассказывать про максимально точный подбор струн под свои предпочтения на примере товаров компании D’Addario. Если вы не уверены, что хотите заниматься столь кропотливыми и тщательными расчетами натяжения струн либо вы не имеете большого опыта в выборе струн или играли всего на 1-2 различных калибрах, обратитесь к нашей обзорной статье «Какие струны лучше подойдут под определенный строй?». В ней обобщенно описаны рекомендации крупнейших производителей струн по выбору оптимального комплекта для стандартного и пониженных строев гитары.

Для помощи в выборе струн компания ДиАддарио создала великолепный Онлайн-помощник по натяжению струн – в нем собраны все необходимые данные для выбора отдельных струн под желаемый строй. 2)/386.4

 

Как натяжение влияет на ощущения музыканта?

Как ни странно, но непосредственно толщина струны не оказывает влияние на натяжение:  значение имеет в первую очередь ее масса, а также длина мензуры и величина частота, на которую данная струна настроена. Изготовители применяют самые неожиданные технологии технологии и материалы (никель, фосфор, нейлон и др.) для того, чтобы добиваться разного натяжения даже при равном диаметре керна и обмотки – и даже, порой, при использовании одинаковых материалов.

Немного о мензуре. Она представляет собой расстояние от верхнего порожка, расположенного в районе головы грифа, до места перегиба струны на бридже. Чем она длиннее – тем выше будет натяжение при прочих равных условиях. В качестве примера: первая струна с толщиной .009 на Stratocaster (мензура 25.5 дюймов) будет казаться более натянутой и жесткой, чем на Gibson Les Paul (мензура 24.75 дюймов) при условии, что обе настроены в Ми или любую другую одинаковую по высоте ноту. Поэтому в общем случае на гитару с меньшей мензурой рекомендуют струны потолще.

Приведем самые распространенные длины мензур для современных инструментов:

Большинство гитар – 24.75”, 25.5”

7- и 8-струнные электрогитары – 26.5”, 27”, 29”

Бас – 30”, 32”, 34” или 36”

Мандолина и Мандола – 13 7/8” и 15 7/8”, соответственно

Банджо – 26 ¼”

 

ВНИМАНИЕ! Перед тем, как начинать расчет натяжения и толщины струн, убедитесь, что ваша гитара правильно отстроена. Проверьте правильность настройки расстояния от струн до грифа, далее – мензуры, в самом конце – отстройте струны по высоте звучания.

 

Как измерить натяжение струны

Натяжение струн выражается в фунтах: натяжение по таблице в 12.2 фунта означает, что она тянет c силой, равной воздействию гравитации на тело массой 12.2 фунта. Если вы на данный момент ощущаете комфортное натяжение струн и планируете изменить строй всех струн – просто изучите руководство, ссылку на которое мы давали выше, и приобретите набор с таким калибром, который обеспечит идентичное натяжение в измененном строе.

Настало время привести конкретный пример!

Итак, допустим, на вашей гитаре установлен набор струн D’Addario EXL140 (10-13-17-30-42-52). Ниже приведена таблица с детализацией модели каждой струны в наборе, ее диаметра и натяжения для стандартного строя. Предположим, что вы хотите сохранить то же натяжение, но начать играть в Drop D строе (ebgDAD) – теперь по таблице необходимо лишь определить требуемый калибр шестой струны.

1. Находим в руководстве на странице 6 свой тип струн: XL Nickelplated Steel (серия XL, сталь с никелированной обмоткой), находим струну с калибром .052 и ноту E (Ми), получаем силу натяжения ~22 фунта (обозначены красным цветом).

2. Ищем в таблице ноту D (Ре) и схожее натяжение (обозначены зеленым цветом) – получаем, что наиболее похожими по натяжению будут струны с калибром .056 (20.9 фунтов, натяжение будет незначительно слабее) или .059 (23.3 фунта – натяжение будет немного сильнее).

Таким образом, для Drop D в данном случае оптимальным будет набор 10-13-17-30-42-56/59.

 

Используя подобную методику, вы сможете заменять любую струну в наборе на ту, с которой вам будет комфортнее играть. Купить струны поштучно вы можете в наших разделах одиночных струн:

Обратите внимание, что приведенная информация актуальна только для продукции от D’Addario. На всякий случай дублируем ссылку на Онлайн руководство по натяжению струн.

Сила растяжения — обзор

7.2.2 Простая арматура

Растягивающая сила ( Н ) или среднее напряжение сцепления (τ¯) и проскальзывания на обоих концах плоской арматуры ( S _l и S _f ) измеряются во время испытания на выдергивание, а экспериментальные кривые показаны на рис. 7-7 (a). Распределения по длине связи нормального напряжения ( σ _s ), рассчитанного напряжения сцепления ( τ ) и скольжения арматуры изменяются, как показано на рис.7-7 (б), когда нагрузка (натяжение) увеличивается.

РИС. 7-7. Результаты испытания на вырыв плоской арматуры: (а) кривые τ — S , (б) распределения напряжения и скольжения

После того, как образец нагружен, связь в конце нагружения арматуры вскоре вышел из строя, и измеряется относительное скольжение ( S _l ) между арматурой и прилегающим бетоном. Между тем, только часть арматуры около конца нагружения несет напряжение ( σ _s > 0), и распределение напряжения связи также ограничено в этой части.Относительное скольжение происходит только в пределах зоны от точки пика напряжения сцепления до конца нагружения арматуры, другая часть арматуры все еще прилипает и не скользит. Зона растяжения арматуры постепенно увеличивается, и точка пика распределения напряжений сцепления смещается к свободному концу арматуры по мере увеличения нагрузки (или τ¯). Затем зона скольжения арматуры расширяется, и скольжение в конце загрузки ( S _l ) ускоряется.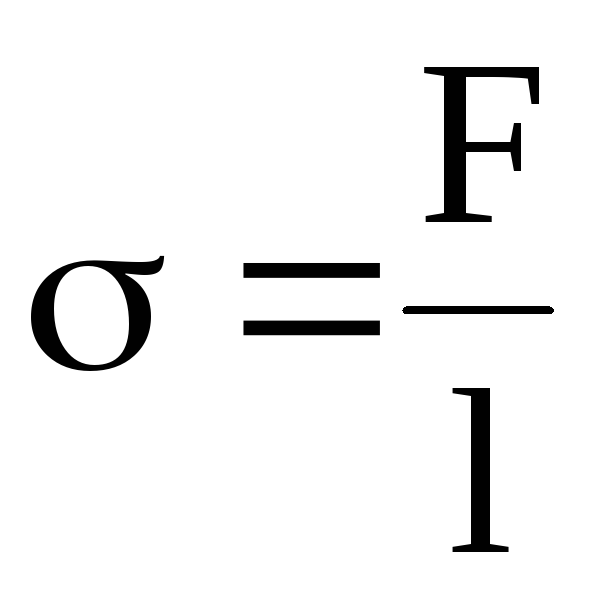

При увеличении нагрузки и достижении τ¯ / τu = 0,4∼0,6 зоны растяжения и скольжения арматуры постепенно расширяются, и скольжение в конце нагружения ( S _l ) явно ускоряется и τ — S _l становится кривой, но свободный конец арматуры по-прежнему не проскальзывает. Распределенная длина напряжения связи ( τ ) распределяется, точка его пика быстро перемещается, а форма кривой изменяется от наклона вправо к наклону влево.Когда τ¯ / τu≈0,8, свободный конец арматуры начинает проскальзывать, связь около конца нагружения серьезно повреждается, и напряжение связи там уменьшается, так что приближается к равномерному нормальному напряжению арматуры.

Когда скольжение на свободном конце арматуры достигает S _f = 0,1–0,2 мм, нагрузка образца достигает максимума Н _u и предела прочности сцепления ( τ _и , Ур. 7-2) получается. После этого проскальзывания арматуры ( S _l и S _f ) быстро увеличиваются, натяжение переносится трением и остаточным взаимодействием на периферии арматуры, затем соседний бетон разрушается, и его сопротивление уменьшается, и образуется нисходящая ветвь кривой τ¯ − S. Наконец, арматура постепенно вытягивается из образца, и некоторые бетонные отходы адсорбируются на его периферии.

Процесс вытягивания арматуры, описанный выше, происходит только для образца с более короткой длиной соединения. Если длина скрепления арматуры достаточно велика, она не будет вытягиваться даже после того, как ее нагружающий конец будет уступен, когда образец нагружен до Н _u = A _s ж _л . Минимальная длина соединения арматуры, необходимая для этого, называется длиной анкерного крепления ( l _a ) [2-1], которая необходима для обеспечения полного использования прочности арматуры на разрыв в конструкции. Согласно условию равновесия, длину анкеровки можно рассчитать по формуле

(7-3) la = fy4τud⌽,

, где τ _u — средний предел прочности сцепления арматуры.

Что такое растягивающая сила [Использование, формула и единицы]

Растягивающая сила:

Растягивающая сила определяется как растягивающая сила, действующая на материал, и состоит из двух частей, которые являются специфическими: управляемое давление и пластическая деформация. .

Это означает, что углерод, сталкиваясь с растягивающим усилием, находится под действием растягивающего усилия, и растягивающее усилие пытается его растянуть. В момент, когда к углю прикладывается растягивающая сила, он создает давление, соответствующее приложенной растягивающей силе, увеличивая площадь поперечного сечения и увеличивая длину.

Пояснение:

Деформация пластической деформации ε обозначается как ε = ΔL / L. В случае приложения сжимающей растягивающей силы к бетону деформация сжатия передается как ε = — ΔL / L. В соответствии с законом Гука связь между тревогой выражается как σ = Eε, где σ — напряжение, E — модуль Юнга и ε — деформация.

При принятии растягивающего усилия материал расширяется в подшипнике ступицы (продольная деформация), сжимаясь поперечно (поперечное перенапряжение) материаловедение.

• Напряжение определяется как: Напряжение (σ) = Растягивающая сила (F) / Площадь (A)
• Деформация определяется как: Деформация (ε) = Длинное удлинение (ΔL) / Длина (L)

Единицы:

Единицы Нм-2

Единицы СИ Паскаль

Формула размеров ML-1T2

Модель: Ниже приведены важные модели, которые можно использовать:

• Соединительные стойки
• Звенья подъемника

Контраст между растягивающим напряжением и прочностью на растяжение:

прочности на разрыв характеризуются как сила растяжения на единицу площади, которая связана с растяжением и обозначается σ. Уравнение имеет следующий вид: σ = F / A

Где

• σ — сговорчивое давление
• F — действующая растягивающая сила

An — зона Эластичность характеризуется как мера пластичного давления, которое материал может выдержать раньше. нарушение и подразумевается под s.

Уравнение: s = P / a

Где

• s — упругость
• P — сила натяжения, необходимая для разрушения, — площадь поперечного сечения.

Исследование характеристик сжатия и упругости:

Цемент и керамика обычно имеют гораздо более высокие характеристики сжатия бетона, чем жесткость.Композиционные материалы, например, композитное волокно на основе стекловолокна и эпоксидной смолы, обычно имеют более высокую жесткость, чем характеристики сжатия.

Металлы трудно испытать образец, разочаровавшись в давлении по сравнению с давлением. Под давлением сталь шипит от сжимания / разрушения / сдвига под 45 градусов, что совершенно отличается (хотя и вызывает большее беспокойство), чем деформация, которая падает плоско из-за недостатков или сужения.

Свойства пластичного растягивающего усилия:

В момент, когда пластичное растягивающее усилие следует за материалом, можно определить сопутствующие гибкие важные свойства:

• Модуль упругого растягивающего усилия: это твердость материала и, кроме того, известен как модуль универсальности.
• Характеризуется степенью беспокойства, когда скручивание полностью универсально. Для количественной оценки универсального модуля упругости используется изгиб деформации под давлением.
• Предельное послушное давление (UTS): характеризуется как наибольшее давление, которое материал может выдержать при приложении растягивающего усилия. В момент, когда материалы проталкиваются через UTS, они ломаются / выходят из строя.
• Модификация прочности: характеризуется как пропорция между гибким давлением и многократной модой Юнга материала.
• Напряжение разрушения: характеризуется как наибольшее давление, о котором известно о точке разделения, прежде чем она отделяется, и обозначается как σf.
• Метод смещения для определения предела текучести используется, когда исследуемый материал не показывает эффективно распознаваемую штифту из прямой гибкой области на диаграмме. К этому классу относятся многие металлы и большинство пластмасс. Противовес указывается в процентах от плотности. На весах проводится линия с таким же наклоном, как и в Моде эластичности.Давление как стимул при схождении линии баланса с линией прямого гибкого района затем используется для расчета уровня доходности методом смещения.
• Модуль упругости определяется при проверке растягивающего усилия путем вычисления абсолютной зоны под изгибом давления / плотности до точки разочарования / разрушения.
• Инженерное напряжение и плотность — это пропорция относительной нагрузки к площади нереформированного поперечного сечения, в то время как Истинное напряжение и давление — это пропорция относящейся растягивающей силы к быстрой области поперечного сечения.Подлинное напряжение и деформация рассчитываются для уменьшенной области в контрольном примере, поскольку при пластическом скручивании происходит растягивающее напряжение и предел прочности при растяжении, предел прочности. Для большинства применений, включая низкие уровни плотности (менее 5%), инженерное напряжение и предел прочности при растяжении являются достаточно точными. При более значительном изменении скорости деформации максимальные включенные оценки, отображаемые при истинном напряжении и деформации, становятся фундаментальными.

Повседневные модели жизни:

Несколько реальных случаев растягивающего типа растягивающего напряжения-деформации, обычно используемых:

• Натягивание веревки в игре с возвратно-поступательной растягивающей силой (жизнь ).
• Транспортное средство, буксирующее другое транспортное средство с помощью натяжения цепи.
• Протягивание каната в колодце, связанное со сроком службы шкива.
• Взвешивание органических продуктов или овощей с использованием старых измерительных весов, в которых нагрузки используются с одной стороны, а органические продукты или овощи сохраняются с односторонним натяжением.
• Овощ из измельчителя органических продуктов, используемых на кухне.
• Рабочие веревки используют для вытягивания прочного материала, имеющего предел прочности на разрыв колесной тележки.
• Бумажный ротатор, используемый для улучшения самочувствия.
• Весовые мероприятия в центре прочности на растяжение, предел прочности при растяжении, растягивающее напряжение.
• Кран подъемная сила натяжения вещей.
• Whirligig, Колониальные детские игры прочность, прочность на разрыв.

Вопрос: Как проверить предел прочности при растяжении?

Эластичность — важная часть давления, которое, как ожидается, разрушит сталь за счет частичного расширения до ее первоначальной формы и размера.Напряжение — это растягивающая сила, приложенная сжимающая сила растягивающее напряжение, разделенное площадью поперечного сечения металла.

Под эластичностью также понимается чрезвычайная жесткость. Жесткость оценивается с помощью податливых контрольных приборов и испытаний конкретных материалов.

Образец для испытаний на вязкость также можно использовать для определения предела текучести, который представляет собой давление, которое, как ожидается, будет постоянно приводить к скручиванию стали.

Нетрудно изготовить базовое устройство для проверки податливости и использовать его для проверки жесткости обычных металлов.Присоединитесь к застежке исследовательского центра на лабораторном стенде.

Растягивающая нагрузка Пятна остаются на ровной, устойчивой поверхности. Присоедините металлическую проволочную чеканку длиной 16 м к застежке. Используйте отверстия по бокам пластикового стаканчика.

Протяните немного веревки через эти отверстия и привяжите замки веревки к нижнему концу веревки, проверьте натяжение.

Найдите измерительную линейку рядом с проводом. Запишите основную длину проволоки для прочности на разрыв.Включите по очереди большую часть охарактеризованного веса. После включения каждой массы запишите длину проволоки.

Используйте натяжение штангенциркуля для определения толщины проволоки после каждого расширения массы.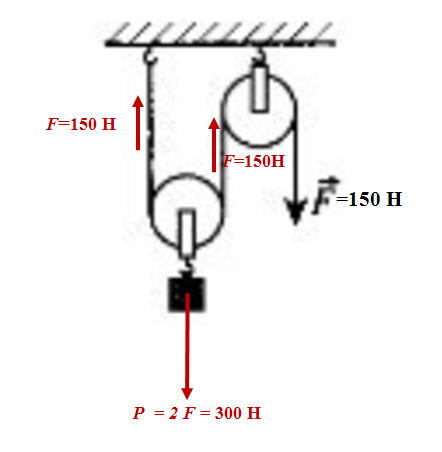

Сделайте таблицу, показывающую общую массу в стакане, соответствующую длину проволоки и толщину проволоки. Продолжайте включать массы, пока не порвется проволока. Разделение оценок толщины, оцененных штангенциркулем по двум наукам.

Возвести результат в квадрат и увеличить на число «пи».Это обеспечивает зону поперечного сечения провода в каждой точке анализа. Обратите внимание на эти качества. Увеличивайте общую массу в чаше на каждом этапе испытания в зависимости от качества гравитационного поля Земли.

Эти качества говорят о сжимающей и растягивающей силе проволоки. Обратите внимание на такие качества, как предел прочности при растяжении, напряжение при растяжении, предел прочности при растяжении, прочность, предел прочности при растяжении, сила сжатия.

Разделение податливой растягивающей силы, оцененной незадолго до разрыва проволоки, в зоне ее поперечного сечения незадолго до разрыва проволоки.

Это значение говорит об окончательной жесткости материалов, которые вы испытываете по модулю молодости.

Зачем проводить испытания на пластичность?

Многие свойства физики материалов на растяжение могут быть продиктованы использованием испытаний на пластичность. Испытание на податливое растяжение дает информацию о качестве и гибкости металлов при одноосных податливых растягивающих и сжимающих усилиях.

Жесткость металла — главное в его способности безупречно выдерживать тягучие нагрузки.Это важный фактор в цикле обработки металлов давлением, поскольку хрупкие металлы неизбежно ломаются.

Проверка эластичности обычно используется для выбора испытания материалов для приложения, для контроля качества и для прогнозирования реакции материала на различные виды энергии растяжения.

WMT & R дает несколько видов испытаний на растяжение, выполненных с нормализованными или повторными данными. Подходящие испытания можно проводить при комнатной температуре, повышенных температурах (от -452 до 2200 ° F), с набором примеров типов, установок и регулируемых контрольных устройств.

Напряжение при растяжении, сжатии, сдвиге и скручивании

Условия механических свойств

Кредит: Рон Редвинг

Как мы видим на приведенном выше рисунке, существует довольно много терминов материалов, которые используются при описании свойств материалов. В этом уроке мы собираемся дать определение вышеуказанным терминам. Оказывается, что многие из перечисленных выше терминов связаны с кривой зависимости напряжения от деформации материала. Что такое стресс и напряжение и как они связаны?

Возьмем цилиндр и напрягаем его.Чтобы подчеркнуть это, я бы зафиксировал один конец цилиндра и потянул за другой конец, как показано на рисунке ниже.

Растягивающее напряжение

Кредит: Каллистер

Согласно третьему закону Ньютона, цилиндр будет испытывать силу, направленную вниз на нижнюю поверхность цилиндра, и равную и противоположную силу на верхнюю поверхность цилиндра. Мой цилиндр имеет исходную длину I _o и площадь поверхности A _o . Когда я натягиваю материал с силой F, цилиндр удлиняется, и в результате получается длина l.Напряжение σ определяется как сила, деленная на начальную площадь поверхности σ = F / A _o . Это растягивающее напряжение называется растягивающим напряжением . Напряжение — это результат этого стресса. Деформация ε определяется как изменение длины, деленное на исходную длину, ε = ΔI / I _o . Прежде чем мы продолжим рассмотрение стресса и деформации, давайте определим некоторые другие типы стресса.

Если вместо того, чтобы тянуть наш материал, мы толкаем или сжимаем наш цилиндр, мы вводим сжимающее напряжение .Это показано на следующем рисунке:

Напряжение сжатия

Кредит: Каллистер

Если вместо приложения силы, перпендикулярной поверхности, мы прикладываем параллельные, но противоположные силы к двум поверхностям, мы прикладываем напряжение сдвига . Это показано на следующем рисунке:

Напряжение сдвига

Кредит: Каллистер

Напряжение, связанное с сдвигом, составляет напряжение скручивания . Если мы удерживаем один конец нашего цилиндра неподвижным и скручиваем другой конец, как показано на рисунке ниже, мы прикладываем скручивающее (или скручивающее) напряжение.

Торсионное напряжение

Кредит: Каллистер

Приложение «Напряжение и деформация — сопротивление материалов для энергетики»

напряжение-деформация

Цели обучения

После завершения этой главы вы сможете:

• Определите нормальное напряжение и напряжение сдвига и деформацию и обсудите взаимосвязь между расчетным напряжением, пределом текучести и предельным напряжением
• Расчетные элементы при нагрузках на растяжение, сжатие и сдвиг
• Определение деформации элементов при растяжении и сжатии

Механическое напряжение

В этом разделе обсуждается влияние механических нагрузок (сил), действующих на элементы.В следующей главе мы рассмотрим влияние тепловых нагрузок (тепловое расширение).

Нормальные, растягивающие и сжимающие напряжения

Растяжение или сжатие в элементе создают нормальные напряжения; они называются «нормальными», потому что поперечное сечение, которое выдерживает нагрузку, перпендикулярно (перпендикулярно) направлению приложенных сил. И растягивающие, и сжимающие напряжения рассчитываются по формуле:

Если элемент имеет переменное поперечное сечение, площадь, которая должна использоваться в расчетах, является минимальной площадью поперечного сечения; это даст вам максимальное напряжение в элементе, что в конечном итоге будет определять дизайн.

При сдвиге площадь поперечного сечения, которая сопротивляется нагрузке, параллельна направлению приложенных сил. В дополнение к этому, при оценке площади сдвига вы должны учитывать, сколько поперечных сечений вносит вклад в общую прочность сборки.

Например, если вы считаете, что штифт дверной петли подвергается действию сдвигающей нагрузки, вы должны подсчитать, сколько поперечных сечений выдерживает эту нагрузку.

Формула для расчета напряжения сдвига та же:

При штамповке область, которая сопротивляется сдвигу, имеет форму цилиндра для круглого отверстия (представьте себе формочку для печенья).Следовательно, площадь сдвига будет найдена путем умножения длины окружности формы на толщину пластины.

Обратите внимание:

Глядя на цифры из учебника, вы заметите, что указаны две силы. Это не означает, что сила, которую вы используете в формуле, равна (2 × Сила P), но просто указывает, что одна сила — это сила действия, а вторая — реакция.

Деформация и модуль упругости

Элемент при растяжении или сжатии будет упруго деформироваться пропорционально, помимо других параметров, исходной длине.Деформация, также называемая единичной деформацией, является безразмерным параметром, выражаемым как:

Если вы решили использовать отрицательное значение для деформации сжатия (уменьшение длины), вы также должны выразить эквивалентное напряжение сжатия как отрицательное значение.

Модуль упругости

Кривая напряжение-деформация построена в результате испытания на растяжение. В упругой области графика деформация прямо пропорциональна нагрузке. Разделив нагрузку на площадь поперечного сечения (константу) и деформацию на исходную длину (константа), можно получить графическое представление зависимости деформации от деформации.Стресс. Постоянное соотношение напряжения и деформации — это модуль Юнга или модуль упругости, свойство каждого материала.

Упругая деформация

Объединение двух приведенных выше соотношений для деформации и модуля упругости приводит к единой формуле для упругой деформации при растяжении или сжатии.

Это соотношение применимо к элементам с однородным поперечным сечением из однородного материала, подверженным растягивающим или сжимающим нагрузкам, которые приводят к напряжениям ниже пропорционального предела (прямая линия на кривой σ-ε).

Расчетное напряжение и коэффициенты запаса прочности

Эти темы были рассмотрены в 1 ^st год «Сопротивление материалов» и представлены здесь в виде краткого обзора.

Стержни, подвергающиеся чрезмерному напряжению, могут выйти из строя из-за разрушения, когда фактическое рабочее напряжение превышает предельное напряжение, или из-за чрезмерной деформации, которая в таком случае становится неработоспособной. Рассмотрим тяжелую линию конденсата, которая прогибается сверх допустимого предела, и, хотя она не ломается, во фланцевых соединениях на концах линий будут возникать утечки из-за углового перемещения.

Расчетное напряжение σ _d — это максимальный уровень фактического / рабочего напряжения, который считается приемлемым с точки зрения безопасности. Расчетное напряжение определяется по:

Коэффициент безопасности выбирается проектировщиком на основе опыта, суждений И руководящих принципов / правил соответствующих норм и стандартов, на основе нескольких критериев, таких как риск травм, точность проектных данных, вероятность, отраслевые стандарты и, что не менее важно, стоимость. . Стандарты коэффициентов безопасности были установлены инженерами-строителями на основе точных оценок и многолетнего опыта.Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:

Дизайнерские шкафы

При решении задач ученики могут столкнуться с разными сценариями. Хотя теоретические концепции одинаковы, пути к окончательным ответам могут быть разными, в зависимости от каждого подхода.

1. Оценка безопасности конструкции / конструкции
   1. Дано: величина и распределение нагрузок, свойства материала, форма и размеры элемента
   2. Найдите: фактическое напряжение и сравните с расчетным напряжением; в качестве альтернативы найдите коэффициент запаса прочности и решите, приемлем ли он в соответствии с применимыми стандартами
2. Выбор подходящего материала
   1. Дано: величина и распределение нагрузок, форма и размеры стержня
   2. Найдите: какой тип или марка материала обеспечит прочность (предел текучести или предельную) большую, чем требуется, с учетом выбранного или указанного коэффициента безопасности
3. Определение формы и размеров поперечного сечения элемента
   1. Дано: величина и распределение нагрузок, свойства материала
   2. Найдите: форму и размеры элемента таким образом, чтобы фактическая площадь поперечного сечения была больше требуемого минимума.
4. Оценка максимально допустимой нагрузки на компонент
   1. Дано: тип и распределение нагрузки, свойства материала, форма и размеры элемента
   2. Найти: максимальная величина нагрузки, которая приводит к приемлемому напряжению

Стержни из двух разных материалов

Бывают случаи, когда стержень при нормальных напряжениях изготавливается из двух (или более) материалов. Одна из целей таких задач — найти напряжение в каждом компоненте.

Например, у вас может быть короткая колонна, сделанная из стальной трубы, заполненной бетоном, как на рисунке. Учитывая общую нагрузку, свойства материалов и геометрические размеры, мы должны найти индивидуальное напряжение в каждом компоненте.

И стальная труба, и бетонный стержень работают вместе, поддерживая нагрузку, поэтому мы должны найти дополнительные отношения, которые объединяют две проблемы в одну. Обычно ищем:

• соотношение, которое описывает распределение силы между двумя материалами
• соотношение, которое коррелирует деформации каждого материала

Для этой конкретной проблемы мы можем сказать, что:

Уравнение 1: Общая нагрузка P = нагрузка, поддерживаемая сталью P _сталь + нагрузка, поддерживаемая бетоном P _бетон

, следовательно, P = напряжение _сталь × площадь _сталь + напряжение _бетон × площадь _бетон

Уравнение 2: деформации обоих материалов одинаковы

поэтому Деформация _сталь = Деформация _бетон

Учитывая, что модуль упругости = напряжение / деформация, уравнение (2) дает соотношение между напряжением и упругостью обоих материалов

Подстановка этого последнего соотношения в уравнение (1) и решение для напряжения _бетон приводит к следующему соотношению

Далее можно найти Stress _{, сталь} .

Обратите внимание, что в зависимости от проблемы исходные два отношения могут отличаться, поэтому каждый раз может потребоваться полный пошаговый вывод.

Разумные ответы

При решении обычных задач «напряжение — деформация», особенно в системе СИ, вы должны суметь оценить, являются ли ваши ответы разумными или нет.

Пример: Пруток из углеродистой стали A 36 длиной 1 м и диаметром 20 мм (свойства материалов в приложении B, таблица B2) выдерживает нагрузку 6 тонн.Оцените напряжение и деформацию штанги.

Обратите внимание, что обычно нагрузки выражаются в кН, площади поперечного сечения 10 ^-3 м ² и результирующие напряжения в МПа.

Кроме того, поскольку модули упругости выражены в ГПа, деформация (безразмерная) будет в диапазоне 10 ^-3 . Этот стержень будет растягиваться на 0,9 мм при данной нагрузке.

Назначенные задачи

При решении этих вопросов необходимо использовать приложения учебника.Это ценные справочные материалы по свойствам материалов, геометрическим размерам и т. Д.

Задача 1: Конденсатопровод номинальным диаметром 152 мм, изготовленный из трубы из углеродистой стали сортамента 40, поддерживается подвесами для стержней с резьбой, расположенными на расстоянии 2,5 м от центра к центру. Подвески изготовлены из углеродистой стали, длиной 50 см, диаметром основания 12 мм. Рассчитайте напряжение и деформацию в подвесках. Для материала подвесов используйте E = 200 ГПа.

Задача 2: Зажимная скоба со штифтом 1/2 дюйма используется в подъемной машине для магазинов.Если штифт изготовлен из стали A36, определите максимальную безопасную нагрузку, используя коэффициент безопасности 2,5, основанный на пределе текучести.

Проблема 3: Котел поддерживается на нескольких коротких стойках, как показано на рисунке, изготовленных из серого чугуна класса 35. Каждая колонна выдерживает нагрузку 50 тонн. Требуемый коэффициент запаса прочности для этой конструкции равен 3. Безопасны ли колонны?

Используйте следующие размеры: A = 30 мм, B = 80 мм, C = 50 мм, D = 140 мм

Проблема 4: Натяжной элемент в ферме крыши подвергается нагрузке в 25 тысяч фунтов.Конструкция требует использования уголка L2x2x1 / 4 с поперечным сечением 0,944 дюйма ² . Для строительных конструкций Американский институт стальных конструкций рекомендует использовать расчетное напряжение 0,60 × S _y . Используя таблицу B2 приложения B, укажите подходящий стальной материал.

Задача 5: Гидравлический цилиндр рулевой тяги, показанный на рисунке, изготовлен из 6-дюймовой трубы из нержавеющей стали Schedule 40 и длиной 15 дюймов. Шесть стяжных шпилек представляют собой шпильки с резьбой 1 / 2-13 UNC с диаметром впадины 0.4822 дюйма и шаг резьбы 13 TPI. При сборке цилиндра требуется усилие зажима, эквивалентное одному полному обороту гайки из положения затяжки вручную.

Определите напряжение в цилиндре и стяжных шпильках. Также рассчитайте деформацию в каждом компоненте, используя модуль упругости E _ss = 28 × 10 ⁶ фунтов на квадратный дюйм и стержень E = 30 × 10 ⁶ фунтов на квадратный дюйм.

Задача 6: Предложите одно улучшение для этой главы.

Эксперимент по испытанию на растяжение | Материаловедение и инженерия

Одним из широко используемых и признанных свойств материала является его прочность. Но что означает слово «сила»? «Сила» может иметь много значений, поэтому позвольте Давайте подробнее рассмотрим, что подразумевается под прочностью материала. Мы будем смотреть в очень простом эксперименте, который дает много информации о силе или механическое поведение материала, называемое испытанием на растяжение.

Основная идея испытания на растяжение заключается в размещении образца материала между двумя креплениями. так называемые «захваты», которые зажимают материал. Материал имеет известные размеры, например длину. и площадь поперечного сечения. Затем мы начинаем прикладывать вес к материалу, захваченному за один конец, а другой конец закреплен. Мы продолжаем увеличивать вес (часто называемый нагрузку или силу), одновременно измеряя изменение длины образца.

Испытание на растяжение

Очень упрощенный тест можно сделать дома.

Если у вас есть способ подвесить один конец какого-либо материала к твердой точке, которая не двигаться, то на другой конец можно повесить гири.

Измерьте изменение длины при добавлении веса, пока деталь не начнет растягиваться и наконец ломается.

Результатом этого теста является график зависимости нагрузки (веса) от смещения. (количество растянутых). Поскольку вес, необходимый для растяжения материала, зависит от по размеру материала (и, конечно, свойствам материала), сравнение между материалами может быть очень сложно. Умение провести правильное сравнение может быть очень важно для тех, кто занимается проектированием конструкций, в которых материал должен выдерживать определенные силы.

Площадь поперечного сечения

Нам нужен способ напрямую сравнивать различные материалы, чтобы определить «прочность» мы сообщаем независимо от размера материала. Мы можем сделать это, просто разделив нагрузка, приложенная к материалу (вес или сила) начальным поперечным сечением область.Мы также делим величину его перемещения (смещение) на начальную длину материал. Это создает то, что ученые-материаловеды называют инженерным стрессом (нагрузка деленная на начальную площадь поперечного сечения) и инженерной деформации (смещения деленное на исходную длину). Глядя на инженерный отклик на напряжение-деформацию материал, мы можем сравнивать прочность различных материалов, независимо от их размеры.

Чтобы использовать реакцию «напряжение-деформация» для проектирования конструкций, мы можем разделить нагрузку мы хотим с помощью инженерного напряжения определить площадь поперечного сечения, необходимую для уметь удерживать этот груз. Например, стальная проволока 4340 диаметром 1/8 дюйма может удерживать маленькая машина. Опять же, не всегда все так просто. Нам нужно понять разные значения «силы» или инженерного напряжения.

Теперь все становится сложнее. Давайте посмотрим, что подразумевается под разными значения прочности, а также посмотрите на другие важные свойства, которые мы можем получить с помощью этого простого контрольная работа. Самый простой способ — изучить график зависимости инженерного напряжения от инженерного. штамм. Ниже показан график испытания на растяжение обычного стального резьбового стержня. являясь хорошим примером общего испытания металла на растяжение.Единицы техники напряжение составляет тысяч фунтов на квадратный дюйм , что означает тысячу фунтов на квадратный дюйм. Обратите внимание на ссылку на область в единицы. Единицы измерения деформации, конечно, безразмерны, поскольку мы делим расстояние по расстоянию.

Местоположение графика 1: эластичная область

Давайте обсудим некоторые важные области графика.Во-первых, точка на графике цифра 1 обозначает конец упругой области кривой. До этого точка, материал растягивается эластично или обратимо.

Все материалы состоят из набора атомов. Эластичность можно лучше понять посредством изображения атомы связаны пружинами.Когда мы натягиваем материал, пружины между атомами удлиняется, и материал удлиняется. Эластичная часть кривая — прямая линия. Прямая линия означает, что материал вернется до первоначальной формы после снятия нагрузки.

Расположение графика 2: 0.Предел текучести смещения 2%

Следующая часть интересующей кривой — это точка 2. В этой точке кривая имеет начал наклоняться или больше не является линейным. Эта точка известна как смещение 0,2%. предел текучести. Это указывает на прочность материала, когда он начинает постоянно изменить форму.Он определяется как значение напряжения, при котором линия того же наклон как начальная часть (упругая область) кривой, которая смещена деформацией 0,2% или значение 0,002 деформации пересекает кривую.

В нашем примере предел текучести смещения 0,2% составляет 88 тыс. Фунтов на кв. Дюйм.

Это очень важный аспект силы.Это в основном говорит нам о количестве стресса мы можем нанести до того, как материал начнет постоянно менять форму, надев его путь к возможной неудаче. Те, кто проектирует детали, которые используются в стрессовых ситуациях, должны убедитесь, что напряжение или сила со стороны детали никогда не превышают этого значения.

Местоположение графика 3: Максимальное выдерживаемое напряжение

По мере продвижения от точки 2 нагрузка или «напряжение» на материал увеличивается, пока мы не достигают максимального приложенного напряжения, при этом материал деформируется или меняет форму равномерно по всей длине колеи.Когда мы достигаем точки 3, мы можем определить растяжение прочность или максимальное напряжение (или нагрузка), которую может выдержать материал. Это не очень полезный свойство, так как материал в этот момент необратимо деформировался. После того, как мы достигнем в этот момент напряжение начинает резко снижаться. Это соответствует локализованному деформация, которая наблюдается по заметному «сужению» или уменьшению диаметра и соответствующее поперечное сечение образца в очень маленькой области.Если мы выпустим нагрузка в этой области, материал будет немного пружинить, но все равно пострадает постоянное изменение формы.

Местоположение графика 4: Отказ или перелом

Наконец, следуя кривой, мы в конечном итоге достигаем точки, где материал разрывается. или терпит неудачу.Здесь интересна конечная степень изменения формы материала. Это «пластичность» материала. Определяется пересечением линии номер 4, имеющий такой же наклон, что и линейный участок кривой, с деформацией ось.

Наш пример показывает деформацию 0.15. Изменение длины на 15% — это величина «пластичности».

Когда образец раскалывается или ломается, нагрузка снимается. Следовательно, атомы упруго растянутые вернутся в свои ненагруженные позиции. Другая информация о механическом реакцию материала также можно получить из испытания на излом.

Испытания на растяжение — композиты

Если тянуть за материал до тех пор, пока он не разорвется, можно найти много информации о различная прочность и механическое поведение материала.В этом виртуальном эксперименте мы исследуем поведение при растяжении трех различных композитных волокнистых материалов. У них схожее использование, но очень разные свойства.

Процедура

Материал захватывается с обоих концов устройством, которое медленно тянет в продольном направлении. на кусок, пока он не сломается.Сила тяги называется нагрузкой, которая наносится на график против изменения длины или смещения материала. Нагрузка преобразуется в напряжение значение, а смещение преобразуется в значение деформации.

О материалах

Материалом для испытаний являются композиты из стекловолокна, кевлара® и углеродного волокна.Композиты представляют собой комбинации двух или более отдельных материалов с целью производства материал с уникальными свойствами, которых нет ни в одном материале.

Все эти композиты используют эпоксидную смолу в качестве матрицы, которая «склеивает» ткань, как композиция. волокон соответствующих материалов.

Эпоксидные смолы — это термореактивные сетчатые полимеры, которые очень твердые и прочные, но не хрупкая сторона.

Все ткани имеют одинаковый «вес», который является мерой размера или веса ткани. квадратного двора.Пример волокнистого материала из стекловолокна показан выше. оставил. Кевлар очень похож, за исключением того, что он имеет желтый цвет. Углерод имеет черный цвет цвет. Образцы, используемые в этом случае, представляют собой плоские прутки, вырезанные из более крупного материала с использованием водоструйная пила. Три образца показаны внизу слева.

Свойства материала

Свойства материала	Стекловолокно	Кевлар®	Углеродное волокно
Плотность	P	E	E
Предел прочности	F	G	E
Прочность на сжатие	G	P	E
Жесткость	F	G	F
Сопротивление усталости	G-E	E	G
Сопротивление истиранию	F	E	F
Шлифование / обработка	E	P	E
Электропроводность	P	P	E
Термостойкость	E	F	E
Влагостойкость	G	F	G
Совместимость смол	E	F	E
Стоимость	E	F	P

P = плохо, G = хорошо, F = удовлетворительно, E = отлично

Эксперимент

Описание: Устройство тянет за каждый конец материала, пока он не сломается.

Стекловолокно 00:00
Кевлар 01:10
Углеродное волокно 03:09

Видео продолжительностью 5 минут 5 секунд без звука.

Исполнительный продюсер Эд Лайтила
Ведущий Стивен Форселл
Видеограф Бритта Лундберг

Окончательные данные

Исходные данные для стекловолокна

Смещение увеличивается от нуля до немногим более 5 мм.Нагрузка увеличивается почти линейно от 0 до примерно 12 кН перед почти вертикальным падением.

Исправленные данные для стекловолокна

Инженерное напряжение увеличивается от нуля до примерно 0.10. Инженерное напряжение возрастает. линейно от нуля до примерно 170 МПа, предел прочности. Модуль составляет 1,7 ГПа.

Исправленные данные для кевлара

Инженерное напряжение увеличивается от нуля до примерно 0.11. Инженерное напряжение возрастает. линейно от нуля до примерно 265 МПа, предел прочности. Модуль составляет 2,3 ГПа.

Исправленные данные для углеродного волокна

Инженерное напряжение увеличивается от нуля до примерно 0.10. Инженерное напряжение возрастает. линейно от нуля до примерно 580 МПа, предел прочности. Модуль составляет 5,7 ГПа.

Выводы

Композитный материал из углеродного волокна имеет гораздо более высокий предел прочности и модуль упругости. эластичнее, чем другие материалы.Обратите внимание, что все они ломаются «хрупко», так как кривая является линейной до тех пор, пока она не разорвется или не сломается без изгиба кривой при высокие нагрузки. Следовательно, при этом не происходит постоянного изменения первоначальной формы. тест, и, следовательно, никакой пластичности.

Виртуальные примеры

Вы видели эксперименты с композитными материалами.Сравните композитный материал Кривые напряжения-деформации с кривыми для полимера и стали.

Сталь для испытаний на растяжение

Стальной образец с шейкой имеет непрерывную зависимость между напряжением и деформацией.Стресс увеличивается почти вертикально, затем постепенно опускается.

Полимер для испытаний на растяжение

Образец растягивающегося полимера имеет разрывную зависимость напряжения от деформации.В напряжение увеличивается почти вертикально, затем падает и неравномерно увеличивается.

Фото галерея

Ниже представлены оптические фотографии разбитых или расколотых образцов, а также крупные планы. поверхности излома, снятые с помощью растрового электронного микроскопа.Изучение этих поверхности излома также являются очень важной частью материаловедения и инженерии, что делает это областью специализации.

Механические испытания — Испытания на растяжение, часть 1

Механические испытания проводятся для получения данных, которые могут использоваться для целей проектирования или как часть процедуры соединения материалов или схемы приемки оператора.Самая важная функция может заключаться в предоставлении проектных данных, поскольку важно, чтобы предельные значения, которые конструкция может выдерживать без сбоев, были известны.

Рис.1. Типовая машина для испытания на растяжение

Однако неадекватный контроль свойств материала со стороны поставщика или некомпетентные процедуры соединения и операторы не менее важны для поставки продукта, безопасного в использовании. Примером этой двойной роли механических испытаний является испытание на растяжение, которое может использоваться либо для определения предела текучести стали для использования в расчетах конструкции, либо для обеспечения того, чтобы сталь соответствовала требованиям к прочности, указанным в спецификации материала.

Щелкните здесь, чтобы увидеть наши последние подкасты по технической инженерии на YouTube .

Механические испытания также можно разделить на количественных или качественных испытаний. Количественный тест — это тест, который предоставляет данные, которые будут использоваться для целей проектирования, качественный тест, результаты которого будут использоваться для сравнений — твердость или тесты Шарпи-V — например, в качестве теста «годен / не годен», например тест на изгиб.

Данные о механических свойствах получены в результате относительно небольшого количества стандартных испытаний, и они будут рассмотрены в следующих нескольких статьях.Они будут включать испытания на растяжение и ударную вязкость, испытания, используемые для процедуры сварки и утверждения сварщика, а также испытания, используемые для определения эксплуатационных свойств.

Испытание на растяжение

Как упоминалось ранее, испытание на растяжение используется для получения информации, которая будет использоваться в расчетах конструкции, или для демонстрации того, что материал соответствует требованиям соответствующей спецификации — следовательно, это может быть количественное или качественное испытание.

Испытание проводится путем захвата концов соответствующим образом подготовленного стандартизованного испытательного образца в машине для испытания на растяжение и последующего приложения постоянно увеличивающейся одноосной нагрузки до тех пор, пока не произойдет отказ.Образцы для испытаний стандартизированы для обеспечения воспроизводимости и сопоставимости результатов, как показано на Рис. 2 .

Рис.2. Образцы на растяжение стандартной формы

Образцы считаются пропорциональными , когда длина , L ₀ , связана с исходной площадью поперечного сечения, A ₀ , выраженной как L ₀ = k√A ₀ . Константа k составляет 5,65 в спецификациях EN и 5 в кодах ASME. Это дает измерительную длину примерно в 5 раз больше диаметра образца и 4 раза диаметр образца соответственно — хотя эта разница может не быть технически значимой, это важно при заявлении о соответствии спецификациям.

Рис.3. Кривая напряжения / деформации

Измеряются как нагрузка (напряжение), так и растяжение (деформация) испытательного образца, и на основе этих данных строится инженерная кривая напряжения / деформации , Рис.3 . По этой кривой мы можем определить:

a) предел прочности при растяжении , также известный как предел прочности при растяжении , нагрузка при разрушении, деленная на исходную площадь поперечного сечения, где предел прочности на растяжение (U.T.S.), σ _max = P _max / A ₀ , где P _max = максимальная нагрузка, A ₀ = исходная площадь поперечного сечения. В спецификациях EN этот параметр также обозначается как «R _m »;

b) предел текучести (YP), напряжение, при котором деформация изменяется с упругой на пластическую, т.е. ниже предела текучести, разгрузка образца означает, что он возвращается к своей исходной длине, выше предела текучести возникла остаточная пластическая деформация, YP или σ _y = P _yp / A ₀ , где P _yp = нагрузка в пределе текучести.В спецификациях EN этот параметр также обозначается как «R _e »;

c) Повторно собрав сломанный образец, мы также можем измерить относительное удлинение , El%, насколько испытательный образец растянулся при разрыве, где El% = (L _f — L ₀ / L _o ) x100 где L _f = измерительная длина до разрыва, а L ₀ = исходная измерительная длина. В спецификациях EN этот параметр также обозначается как «A» ( Fig. 4a ).

d) уменьшение площади на процентов, насколько образец сузился или уменьшился в диаметре в точке разрушения, где R = A% = (A ₀ — A _f / A ₀ ) x 100 где A _f = площадь поперечного сечения в месте разрушения. В спецификациях EN этот параметр также обозначается как «Z» ( Fig. 4b ).

Рис.4: а) Расчет относительного удлинения, б) Расчет процентного уменьшения площади

(a) и (b) являются мерой прочности материала, (c) и (d) указывают на пластичность или способность материала деформироваться без разрушения.

Наклон упругой части кривой, по существу прямая линия, дает Модуль упругости Юнга , меру того, насколько конструкция будет упруго деформироваться при нагрузке.

Низкий модуль упругости означает, что конструкция будет гибкой, а высокий модуль — жесткой и негибкой.

Для получения наиболее точной кривой напряжения / деформации к образцу должен быть прикреплен экстензометр для измерения удлинения измерительной длины.Менее точный метод — это измерение движения траверсы натяжной машины.

Кривая напряжения-деформации на рисунке 3 показывает материал с хорошо выраженным пределом текучести, но только отожженная углеродистая сталь демонстрирует такое поведение. Металлы, упрочненные легированием, термообработкой или холодной обработкой, не обладают ярко выраженной текучестью, и необходимо найти другой метод определения «предела текучести».

Это делается путем измерения предела текучести ( предел текучести со смещением в американской терминологии), напряжения, необходимого для создания небольшой заданной величины пластической деформации в испытательном образце.

Предел текучести измеряется путем проведения линии, параллельной упругой части кривой напряжения / деформации при заданной деформации, эта деформация представляет собой процент от исходной калибровочной длины, следовательно, — 0,2%, 1% — (см. ). Рис.5 ).

Рис.5. Определение предела текучести

Например, 0,2% предела текучести можно измерить, используя 0,2 мм остаточной деформации в образце с измерительной длиной 100 мм.Таким образом, испытательная прочность не является фиксированной характеристикой материала, например пределом текучести, а будет зависеть от заданной пластической деформации. Поэтому важно, чтобы при рассмотрении прочности доказательства всегда указывалось процентное значение. В большинстве спецификаций стали используется деформация 0,2%, R _P0,2 в спецификациях EN.

Некоторые материалы, такие как отожженная медь, серый чугун и пластмассы, не имеют прямолинейного упругого участка на кривой напряжения / деформации.В этом случае обычная практика, аналогичная методу определения предела текучести, заключается в определении «предела текучести» как напряжения, вызывающего определенную остаточную деформацию.

Часть 2 этой серии по механическим испытаниям будет охватывать испытания на растяжение, одобренные для процедуры сварки.

Эту статью подготовил Gene Mathers .

Механические свойства материалов | MechaniCalc

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения.Пожалуйста, включите JavaScript.

---

Механические свойства материала влияют на его поведение при нагрузке. Модуль упругости материала влияет на то, насколько он прогибается под нагрузкой, а прочность материала определяет напряжения, которые он может выдержать до разрушения. Пластичность материала также играет важную роль в определении того, когда материал сломается, когда он будет нагружен за пределы его предела упругости. Поскольку каждая механическая система подвергается нагрузкам во время работы, важно понимать, как ведут себя материалы, из которых состоят эти механические системы.

На этой странице описаны механические свойства материалов, которые имеют отношение к проектированию и анализу механических систем.

Содержание

Напряжение и деформация

Взаимосвязь между напряжением и деформацией в материале определяется путем испытания образца материала на растяжение или сжатие. В этом испытании к испытательному образцу прикладывают постоянно увеличивающуюся осевую силу и измеряют прогиб при увеличении нагрузки.Эти значения могут быть нанесены на график в виде кривой нагрузки-прогиба. Прогиб испытуемого образца зависит как от модуля упругости материала, так и от геометрии образца (площади и длины). Поскольку нас интересует поведение материала безотносительно к геометрии, полезно обобщить данные, чтобы устранить влияние геометрии. Это делается путем преобразования значений нагрузки в значения напряжения и преобразования значений прогиба в значения деформации:

Напряжение:
Штамм:

В уравнении для напряжения P — нагрузка, а A ₀ — исходная площадь поперечного сечения испытуемого образца.В уравнении для деформации L — текущая длина образца, а L ₀ — исходная длина.

Кривая напряжения-деформации

Значения напряжения и деформации, определенные в результате испытания на растяжение, можно построить как кривую «напряжение-деформация» , как показано ниже:

На диаграмме выше есть несколько интересных мест:

• P: Это предел пропорциональности , который представляет максимальное значение напряжения, при котором кривая напряжения-деформации является линейной.
• E: Это предел упругости , который представляет собой максимальное значение напряжения, при котором нет постоянного смещения. Несмотря на то, что кривая не является линейной между пределом пропорциональности и пределом упругости, материал все еще остается эластичным в этой области, и если нагрузка снимается в этой точке или ниже, образец вернется к своей исходной длине.
• Y: Это предел текучести , который представляет значение напряжения, выше которого деформация начнет быстро увеличиваться.Напряжение в пределе текучести называется пределом текучести , S _ty . Для материалов без четко определенного предела текучести он обычно определяется с использованием метода смещения 0,2% , в котором проводится линия, параллельная линейному участку кривой, которая пересекает ось x при значении деформации 0,002. Точка, в которой линия пересекает кривую напряжения-деформации, обозначается как предел текучести.
• U: Эта точка соответствует пределу прочности , S _tu , который является максимальным значением напряжения на диаграмме «напряжение-деформация».Предел прочности также называют пределом прочности на разрыв . После достижения предельного напряжения образцы из пластичных материалов будут демонстрировать сужение , при котором площадь поперечного сечения в локализованной области образца значительно уменьшается.
• F: Это точка излома или точка излома , которая является точкой, в которой материал выходит из строя и разделяется на две части.

Кривые «напряжение-деформация» обычно необходимы при анализе сконструированного компонента.Однако данные «напряжение-деформация» не всегда могут быть легко доступны. В этом случае довольно просто аппроксимировать кривую деформации материала, используя уравнение Рамберга-Осгуда.

Истинное напряжение и деформация

Инженеры обычно работают с инженерным напряжением , которое представляет собой силу, деленную на исходную площадь образца перед нагрузкой: σ = P / A ₀ . Однако по мере загрузки материала площадь уменьшается. Истинное напряжение ,, — это значение напряжения в материале с учетом фактической площади образца.Поскольку площадь уменьшается по мере нагружения материала, истинное напряжение выше, чем инженерное напряжение.

На рисунке ниже показана инженерная кривая напряжения-деформации в сравнении с истинной кривой напряжения-деформации. Поскольку инженерное напряжение рассчитывается как сила, деленная на исходную площадь (которая является постоянной), инженерная кривая напряжения-деформации имеет ту же форму, что и кривая нагрузки-прогиба. Инженерная кривая напряжения-деформации падает после достижения предела прочности, потому что сила, которую может выдержать материал, падает, когда он начинает сужаться.Однако значение напряжения на истинной кривой напряжения-деформации всегда увеличивается по мере увеличения деформации. Это связано с тем, что при расчете истинного напряжения используется мгновенное значение площади. Даже когда сила, поддерживаемая материалом, падает, уменьшение площади образца перевешивает уменьшение силы, и напряжение продолжает расти.

Следует отметить, что инженерное напряжение и истинное напряжение практически одинаковы в линейно-упругой области кривой напряжения-деформации.Поскольку инженеры обычно работают в этой линейно-упругой области (редко проектируют конструкцию, которая предназначена для работы за пределами предела упругости), допустимо работать с инженерным напряжением, а не с истинным напряжением.

Техническая деформация — это изменение длины, деленное на исходную длину: ε = ΔL / L ₀ . Вместо того, чтобы просто рассчитывать одно значение ΔL, примите во внимание, что изменение длины делится на множество небольших приращений, ΔL _j .Деформация также рассчитывается с небольшими приращениями: ε _j = ΔL _j / L _j , где ΔL _j — изменение длины для приращения, а L _j — длина в начале приращение. Когда эти приращения становятся бесконечно малыми, сумма деформаций приближается к истинной деформации:

Если предположить, что объем постоянный на протяжении всего прогиба, то истинное напряжение и деформацию можно рассчитать как:

Истинное напряжение:
Истинный штамм:

где и — истинные напряжения и деформации, а σ и ε — инженерные напряжения и деформации.

Закон Гука

Ниже предела пропорциональности кривой напряжение-деформация зависимость между напряжением и деформацией является линейной. Наклон этого линейного участка кривой напряжения-деформации представляет собой модуль упругости , E, также называемый модулем упругости и модулем упругости . Закон Гука выражает взаимосвязь между модулем упругости, напряжением и деформацией в материале в линейной области:

σ = E ε

где σ — величина напряжения, а ε — величина деформации.

Закон Гука при сдвиге

Закон Гука также имеет форму, касающуюся касательных напряжений и деформаций:

τ = G γ

где τ — значение напряжения сдвига, γ — значение деформации сдвига, G — модуль упругости при сдвиге. Модуль упругости и модуль сдвига связаны соотношением:

где ν — коэффициент Пуассона.

Более подробную информацию о законе Гука можно найти здесь.

Коэффициент Пуассона

Когда к материалу прилагается нагрузка, он удлиняется, и площадь поперечного сечения уменьшается.Это уменьшение площади поперечного сечения называется боковой деформацией и связано с осевой деформацией коэффициентом Пуассона , ν. Для круглого образца это уменьшение площади реализуется как уменьшение диаметра, а коэффициент Пуассона рассчитывается как:

Коэффициент Пуассона

применяется только в упругой области кривой зависимости напряжения от деформации и обычно составляет около 0,3 для большинства металлов. Теоретический максимальный предел коэффициента Пуассона составляет 0,5.

---

---

Деформационное упрочнение

После того, как материал поддается пластической деформации, он начинает подвергаться высокой скорости пластической деформации.Когда материал поддается, он начинает деформироваться, что увеличивает прочность материала. На приведенных ниже кривых «напряжение-деформация» видно, что прочность материала увеличивается между пределом текучести Y и пределом прочности в точке U. Это увеличение прочности является результатом деформационного упрочнения.

Пластичный материал на рисунке ниже все еще способен выдерживать нагрузку даже после достижения предельной прочности. Однако после достижения предела прочности в точке U увеличение прочности за счет деформационного упрочнения опережает снижение несущей способности из-за уменьшения площади поперечного сечения.Между пределом прочности в точке U и точкой разрушения F инженерная прочность материала уменьшается и возникает образование шейки.

На приведенной ниже кривой напряжение-деформация для хрупкого материала показана очень небольшая область деформационного упрочнения между пределом текучести Y и пределом прочности U. Однако обратите внимание, что хрупкий материал на самом деле может вообще не проявлять никаких свойств текучести или деформационного упрочнения. — в этом случае материал выйдет из строя на линейном участке кривой.Это чаще встречается в таких материалах, как керамика или бетон.

Поскольку область деформационного упрочнения возникает между пределом текучести и пределом прочности, отношение предела прочности к пределу текучести иногда используется как мера степени деформационного упрочнения материала. Это соотношение представляет собой коэффициент деформационного упрочнения :

Коэффициент деформационного упрочнения = S _tu / S _ty

Согласно Доулингу, типичные значения коэффициента деформационного упрочнения в металлах составляют примерно от 1.2 к 1.4.

Если материал нагружен сверх предела упругости, он подвергнется остаточной деформации. После разгрузки материала упругая деформация восстановится (вернется к нулю), но пластическая деформация останется.

На рисунке ниже показана кривая напряжения-деформации материала, который был нагружен за пределом текучести, Y. При первом нагружении материала напряжение и деформация следовали кривой OY-Y ‘, а затем нагрузка была снята после напряжение достигло точки Y ‘.Поскольку материал был нагружен за пределом упругости, восстанавливается только упругая часть деформации — теперь в материале есть некоторая постоянная деформация. Если материал будет загружен снова, он будет следовать линии O’-Y’-F, где O’-Y ‘- предыдущая линия разгрузки. Точка Y ‘- это новый предел текучести. Обратите внимание, что линия O’-Y ‘является линейной с наклоном, равным модулю упругости, а точка Y’ имеет более высокое значение напряжения, чем точка Y. Следовательно, теперь материал имеет более высокий предел текучести, чем был ранее, что является результатом деформационного упрочнения, произошедшего при нагружении материала сверх предела упругости.

Благодаря деформационному упрочнению материал теперь имеет большую эластичную область и более высокий предел текучести, но его пластичность была снижена (деформация между точками Y’-F меньше, чем деформация между точками Y-F).

Упругая и пластическая деформация

До предела упругости деформация материала также является упругой и будет восстанавливаться при снятии нагрузки, так что материал возвращается к своей исходной длине. Однако, если материал нагружен сверх предела упругости, в материале будет возникать остаточная деформация, которую также называют пластической деформацией.

На рисунке выше в материале присутствуют как упругие, так и пластические деформации. Если нагрузка снимается в указанной точке (σ, ε), напряжение и деформация в материале будут следовать линии разгрузки, как показано. Упругая деформация и пластическая деформация указаны на рисунке и рассчитываются как:

Упругая деформация:	ε e = σ / E
Пластиковая деформация:	ε p = ε — ε e

где σ — напряжение в указанной точке, ε — деформация в указанной точке, а E — модуль упругости.

Пластичность

Пластичность — это показатель того, сколько пластической деформации может выдержать материал до того, как он сломается. Пластичный материал может выдерживать большие деформации даже после того, как он начал деформироваться. Общие меры пластичности включают удлинение на процентов и уменьшение площади на , как описано в этом разделе.

После разрушения образца во время испытания на растяжение измеряется окончательная длина образца и рассчитывается пластическая деформация при разрыве, также известная как деформация при разрыве :

где L _f — конечная длина образца после разрыва, а L _o — начальная длина образца.Важно отметить, что после разрушения образца упругая деформация, которая существовала, когда образец находился под нагрузкой, восстанавливается, поэтому измеренная разница между конечной и начальной длинами дает пластическую деформацию при разрушении. Это показано на рисунке ниже:

На рисунке видно, что пластическая деформация при разрушении ε _f — это деформация, остающаяся в материале после восстановления упругой деформации. Предел деформации, ε _u , представляет собой полную деформацию при разрушении (пластическая деформация плюс упругая деформация).

Относительное удлинение % рассчитывается исходя из пластической деформации при разрушении по формуле

Относительное удлинение в процентах — это обычно предоставляемое свойство материала, поэтому пластическая деформация при разрушении обычно рассчитывается как процентное удлинение:

ε _f = eL / 100%

Предел деформации учитывает как пластическую, так и упругую деформацию при разрушении:

ε _u = ε _f & plus; S _tu / E

Еще одним важным свойством материала, которое можно измерить во время испытания на растяжение, является уменьшение площади , которое рассчитывается по формуле:

Помните, что относительное удлинение и уменьшение площади составляют пластиковые компоненты осевой деформации и поперечной деформации соответственно.

Пластичные и хрупкие материалы

Пластичный материал может выдерживать большие деформации даже после того, как он начал деформироваться, тогда как хрупкий материал может выдерживать небольшую пластическую деформацию или вообще не выдерживать ее. На рисунке ниже показаны типичные кривые зависимости напряжения от деформации для пластичного и хрупкого материала.

На рисунке выше видно, что пластичный материал значительно деформируется до точки разрушения F. Существует длинная область между пределом текучести в точке Y и пределом прочности в точке U, где материал подвергается деформационному упрочнению.Также существует длинная область между пределом прочности в точке U и точкой разрушения F, в которой площадь поперечного сечения материала быстро уменьшается и возникает образование шейки.

На рисунке выше видно, что хрупкий материал разрушается вскоре после достижения предела текучести. Кроме того, предел прочности совпадает с точкой разрушения. В этом случае шейки не происходит.

Поскольку площадь под кривой зависимости напряжения от деформации для пластичного материала выше, чем площадь под кривой зависимости напряжения от деформации для хрупкого материала, пластичный материал имеет более высокий модуль вязкости — он может поглощать гораздо больше энергии деформации перед тем, как перерывы.Кроме того, поскольку пластичный материал сильно деформируется перед тем, как сломаться, его прогиб перед разрушением будет очень высоким. Таким образом, будет визуально очевидно, что сбой неизбежен, и можно предпринять действия для разрешения ситуации до того, как произойдет катастрофа.

Типичная кривая напряжения-деформации для хрупкого материала показана ниже. Эта кривая показывает напряжение и деформацию как для растягивающей, так и для сжимающей нагрузки. Обратите внимание на то, что материал намного более устойчив к сжатию, чем к растяжению, как с точки зрения напряжения, которое он может выдержать, так и с точки зрения деформации перед разрушением.Это типично для хрупкого материала.

Энергия деформации

Когда к материалу прикладывается сила, он деформируется и накапливает потенциальную энергию, как пружина. Энергия деформации (то есть количество потенциальной энергии, накопленной из-за деформации) равна работе, затрачиваемой на деформацию материала. Полная энергия деформации соответствует площади под кривой прогиба нагрузки и имеет единицы дюйм-фунт-сила в обычных единицах США и Н-м в единицах СИ.Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах упругости, то вся энергия деформации может быть восстановлена.

Энергия деформации рассчитывается как:

Общая форма:	U = Работа = ∫ F dL	(площадь под кривой нагрузки-прогиб)
В пределах эластичности:		(площадь под кривой нагрузки-прогиб)
		(потенциальная энергия пружины)

Обратите внимание, что есть два уравнения для энергии деформации в пределах упругого предела.Первое уравнение основано на площади под кривой прогиба нагрузки. Второе уравнение основано на уравнении для потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.

Плотность энергии деформации

Иногда удобнее работать с плотностью энергии деформации , которая представляет собой энергию деформации на единицу объема. Это равно площади под диаграммой растяжения:

где пределы в приведенном выше интеграле — от деформации от 0 до ε _app , которая представляет собой деформацию, существующую в загружаемом материале.

Обратите внимание, что единицы измерения плотности энергии деформации — фунты на квадратный дюйм в обычных единицах США и Па в единицах СИ.

Модуль упругости

Модуль упругости представляет собой количество энергии деформации на единицу объема (т.е. плотность энергии деформации), которую материал может поглотить без остаточной деформации. Модуль упругости рассчитывается как площадь под кривой зависимости напряжения от деформации до предела упругости. Однако, поскольку предел упругости и предел текучести обычно очень близки, упругость может быть аппроксимирована как площадь под кривой зависимости напряжения от деформации до предела текучести.Поскольку кривая напряжения-деформации почти линейна до предела упругости, эта область имеет треугольную форму.

Модуль упругости рассчитывается как:

	общая форма
	треугольная форма

где σ _el и ε _el — напряжение и деформация на пределе упругости, S _ty — предел текучести при растяжении, а E — модуль упругости.

Обратите внимание, что единицы модуля упругости такие же, как и единицы плотности энергии деформации: фунты на квадратный дюйм в обычных единицах США и Па в единицах СИ.

Модуль упругости

Модуль ударной вязкости — это количество энергии деформации на единицу объема (то есть плотность энергии деформации), которую материал может поглотить непосредственно перед разрушением. Модуль ударной вязкости рассчитывается как площадь под кривой зависимости напряжения от деформации до точки разрушения.

Точный расчет общей площади под кривой зависимости напряжения от деформации для определения модуля ударной вязкости в некоторой степени затруднен. Однако можно сделать грубое приближение, разделив кривую зависимости напряжения от деформации на треугольное и прямоугольное сечения, как показано на рисунке ниже. Высота секций равна среднему значению предела текучести и предела прочности.

Модуль ударной вязкости можно приблизительно рассчитать как:

где S _ty — предел текучести при растяжении, S _tu — предел прочности при растяжении, ε _y — деформация при текучести, ε _u — предельная деформация (общая деформация при разрушении), а E — модуль упругости.

Более точный расчет модуля ударной вязкости может быть выполнен с помощью уравнения Рамберга-Осгуда для аппроксимации кривой напряжения-деформации и последующего интегрирования площади под кривой.

Следует отметить, насколько сильно площадь под пластическим участком кривой зависимости напряжения от деформации (то есть прямоугольный участок) влияет на ударную вязкость материала. Поскольку пластичный материал может выдерживать гораздо большую пластическую деформацию, чем хрупкий материал, пластичный материал, следовательно, будет иметь более высокий модуль ударной вязкости, чем хрупкий материал с тем же пределом текучести.Несмотря на то, что конструкции обычно предназначены для удержания напряжений в упругой области, пластичный материал с более высоким модулем ударной вязкости лучше подходит для приложений, в которых может произойти случайная перегрузка.

Обратите внимание, что единицы модуля ударной вязкости такие же, как единицы плотности энергии деформации: фунты на квадратный дюйм в обычных единицах США и Па в единицах СИ.

---

---

Аппроксимация кривой напряжения-деформации

Кривые напряжения-деформации для материалов обычно необходимы; однако без репрезентативных данных испытаний необходимо приблизить кривую.Уравнение Рамберга-Осгуда можно использовать для аппроксимации кривой напряжения-деформации для материала, зная только предел текучести, предел прочности, модуль упругости и относительное удлинение материала (все из которых являются общими и легко доступными свойствами).

Уравнение Рамберга-Осгуда для полной деформации (упругой и пластической) как функции напряжения:

где σ — величина напряжения, E — модуль упругости материала, S _ty — предел текучести материала при растяжении, а n — показатель деформационного упрочнения материала, который может быть рассчитан на основе известных свойств материала как показано далее в этом разделе. ^{(Примечание 1)}

Объяснение вывода уравнения Рамберга-Осгуда дается в следующих разделах.

Уравнение Рамберга-Осгуда

Рамберг и Осгуд предложили соотношение, которое часто используется для аппроксимации кривой напряжения-деформации для материала. Эта зависимость является экспоненциальной и используется для описания пластической деформации материала. Кривая напряжения-деформации в пластической области может быть аппроксимирована следующим образом:

σ = H ε p n

& xrArr;

где в приведенном выше уравнении ε _p — пластическая деформация, H — коэффициент прочности с теми же единицами измерения, что и напряжение, и n — показатель деформационного упрочнения и не имеет единиц измерения.

Упругая деформация материала прямо пропорциональна напряжению:

σ = E ε e

& xrArr;

ε e = σ / E

где в приведенном выше уравнении ε _e — упругая деформация, а E — модуль упругости.

Полная деформация в материале складывается из упругой деформации и пластической деформации:

ε = ε e & plus; ε п

& xrArr;

Определение констант для Ramberg-Osgood

Чтобы уравнение Рамберга-Осгуда было полезным, необходимо знать значения констант n и H.Здесь обсуждается, как определить константы для экспоненциального уравнения.

Константы находятся:

где в приведенных выше уравнениях (σ ₁ , ε ₁ ) и (σ ₂ , ε ₂ ) соответствуют двум точкам в пределах пластической области кривой напряжения-деформации. Теперь задача состоит в том, чтобы найти эти две точки, чтобы можно было вычислить константы.

Если известны предел текучести (S _ty ), предел прочности (S _tu ), модуль упругости (E) и пластическая деформация при разрушении (ε _f ) для материала, то тогда две точки в пластической области могут быть определены (точки текучести и предела), и по этим точкам может быть рассчитана кривая пластической области.Помните, что пластическая деформация при разрушении может быть рассчитана из относительного удлинения, eL, по формуле ε _f = eL / 100%. К счастью, все эти свойства общеизвестны для материала.

Важно отметить, что уравнение кривой пластической области, σ = H ε _p ⁿ , зависит от пластической деформации, поэтому нам нужно будет определить значения пластической деформации для двух представляющих интерес точек. Пластическую деформацию можно рассчитать из общей деформации, используя:

ε _p = ε — ε _e = ε — σ / E

где в приведенном выше уравнении ε — полная деформация, а ε _e — упругая деформация.

Приведенная ниже таблица используется для определения предела текучести и предельного значения:

	Напряжение, σ	Полная деформация, ε	Упругая деформация, ε e	Пластическая деформация, ε p
Предел текучести:	S ty	S ty / E + 0,002	S ty / E	0,002
Конечная точка:	С ту	S tu / E + ε f	S tu / E	ε f

Обратите внимание, что при определении деформации в пределе текучести пластическая деформация 0.002 предполагалось. Это соответствует методу смещения 0,2%, как описано ранее. Это предположение необходимо для того, чтобы поместить предел текучести в пластический участок кривой. Из приведенной выше таблицы можно увидеть, что предел текучести и предел прочности в пластической области определяются по формуле:

•	Предел текучести:	(S ty , 0,002)
•	Конечная точка:	(S tu , ε f )

По двум точкам в пластической области кривой можно вычислить константы n и H для уравнения Рамберга-Осгуда.Показатель деформационного упрочнения n рассчитывается как: ^{(Примечание 1)}

Значение H рассчитывается с использованием предела текучести (S _ty , 0,002) в качестве точки отсчета, хотя подойдет любая точка:

Теперь, когда константы n и H определены, уравнение для полной деформации как функции напряжения известно:

Приведенное выше уравнение можно упростить, подставив выражение для H. Окончательное уравнение для полной деформации как функции напряжения:

---

Банкноты

Примечание 1: Показатель деформационного упрочнения в уравнении Рамберга-Осгуда

Показатель деформационного упрочнения, обозначенный n, не следует путать с параметром Рамберга-Осгуда, который также обозначается n.Эти два параметра являются взаимными, что только усугубляет путаницу. Мы используем показатель деформационного упрочнения в уравнении Рамберга-Осгуда, а не параметр Рамберга-Осгуда. Причина, по которой мы используем показатель деформационного упрочнения, заключается в том, что это общее свойство материала, которое полезно вне контекста уравнения Рамберга-Осгуда.

---

Подпишитесь, чтобы получать обновления о последних улучшениях:

---

Список литературы

Общие ссылки:

1. Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е изд.
2. Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы для деформации, разрушения и усталости», 3-е изд.