Период (сигнала) — это… Что такое Период (сигнала)?
- Период (сигнала)
- 1. Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала
Употребляется в документе:
ОСТ 45.159-2000Отраслевая система обеспечения единства измерений. Термины и определения
Телекоммуникационный словарь. 2013.
- Переходный режим работы электротехнического изделия (электротехнического устройства, электрооборудования)
- Период (электрического тока)
Смотреть что такое «Период (сигнала)» в других словарях:
период (сигнала) — Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала (ОСТ 45.159 2000.1 Термины и определения (Минсвязи России)). [http://www.iks media.ru/glossary/index.html?glossid=2400324]… … Справочник технического переводчика
период дискретизации сигнала электросвязи — Интервал дискретизации сигнала электросвязи по времени при равномерной дискретизации этого сигнала по времени. [ГОСТ 22670 77] Тематики сети передачи данных Синонимы период дискретизации EN sampling period … Справочник технического переводчика
период периодического сигнала — период Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала. Обозначение T [ГОСТ 16465 70] Тематики сигналы радиотехнические измерительные Обобщающие термины характеристики… … Справочник технического переводчика
период Найквиста — Временно интервал между двумя соседними отсчетами входного сигнала с ограниченным спектром. При дискретизации с частотой Найквиста период равен T=1/2F, где F верхняя частота спектра. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский… … Справочник технического переводчика
период проверки — Интервал времени, в течение которого проводится проверка наличия полезного сигнала на входе [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики… … Справочник технического переводчика
период — 2.18 период: Продолжительность времени. Источник: ГОСТ ИСО 8601 2001: Система стандартов по информации, библиотечному и издательскому делу. Представлен … Словарь-справочник терминов нормативно-технической документации
период измерений — 3.3 период измерений: Интервал времени, в течение которого осуществляют непрерывный сбор данных о вибрации здания. Источник: ГОСТ Р 52892 2007: Вибрация и удар. Вибрация зданий. Измерение вибрации и оценка ее воздействия на конструкцию … Словарь-справочник терминов нормативно-технической документации
Период дискретизации сигнала электросвязи — 31. Период дискретизации сигнала электросвязи Период дискретизации Sampling period Интервал дискретизации сигнала электросвязи по времени при равномерной дискретизации этого сигнала по времени Источник: ГОСТ 22670 77: Сеть связи цифровая… … Словарь-справочник терминов нормативно-технической документации
Период периодического сигнала — 17. Период периодического сигнала Период Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Формы и характеристики электрических сигналов
Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.
Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.
С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.
- Однополярные сигналы — это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.
- Двухполярные сигналы — эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.
Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:
- Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.
- Частота — это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, (). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
- Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.
Периодические сигналы
Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.
Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.
Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1 секунда для совершения полного цикла, имеет период равный одной секунде. Аналогично, для синусоидального сигнала, которому требуется 5 секунд для совершения полного цикла, имеет период равный 5 секундам, и так далее.
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.
Синусоидальный сигнал
Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то (T = ).
Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.
Соотношения между периодом сигнала и его частотой:
Гц
c
Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц
| Префикс | Определение | Запись | Период |
| Кило | тысяча | кГц | 1 мс |
| Мега | миллион | МГц | 1 мкс |
| Гига | миллиард | ГГц | 1 нс |
| Тера | триллион | ТГц | 1 пс |
Меандр
Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.
Для меандра, время заполнения равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
Гц
Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.
Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.
Прямоугольный сигнал
Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.
На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.
Отношение периода повторения сигнала , к длительности положительного импульса , называют скважностью:
Величину обратную скважности называют коэффициентом заполнения (duty cycle):
Пример расчета
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
Гц
Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».
Треугольные сигналы
Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями. Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.
В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.
Пилообразный сигнал
Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.
Импульсы и запускающие сигналы (триггеры)
Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал. Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения. Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.
Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
Я рассмотрел здесь только основные виды электрических сигналов. Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например:
- Амплитудно-модулированный сигнал
- Частотно-модулированный сигнал
- Фазо-модулированный сигнал
- Фазо-частотно-модулированный сигнал
- Фазо-кодо-манипулированный сигнал
Подробно я вернусь к ним в своих последующих публикациях.
Еще по этой теме
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Меандр (радиотехника) — Википедия
Материал из Википедии — свободной энциклопедии
Меа́ндр (по названию геометрического орнамента в виде ломаной линии) — периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Меандр может быть знакопеременным (двухполярным) или однополярным. Во втором случае длительность импульса и длительность паузы между импульсами равны, то есть в этом случае меандр — периодический сигнал прямоугольной формы, имеющий скважность 2 (или коэффициент заполнения 0,5).
Математически меандр можно описать многими разными способами, например, через функцию сигнум:
- x(t)=sgn(sin(t)).{\displaystyle \ x(t)=\operatorname {sgn}(\sin(t)).}
Или через функции Хевисайда h(t){\displaystyle h(t)}:
- x(t)=∑n=−∞+∞(h[t−nT+12]−h[t−nT−12]).{\displaystyle \ x(t)=\sum _{n=-\infty }^{+\infty }\left(h\left[t-nT+{1 \over 2}\right]-h\left[t-nT-{1 \over 2}\right]\right).}
Для того, чтобы скважность равнялась 2 необходимо положить T=2.{\displaystyle T=2.}
И многими другими способами.
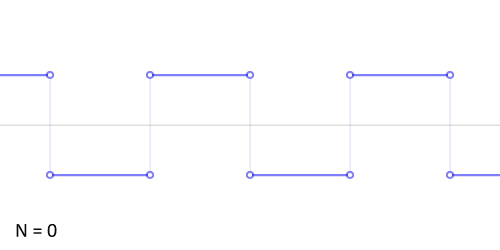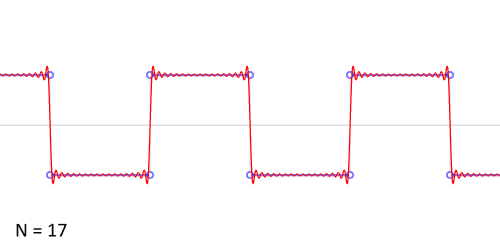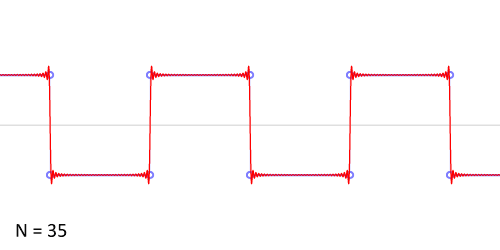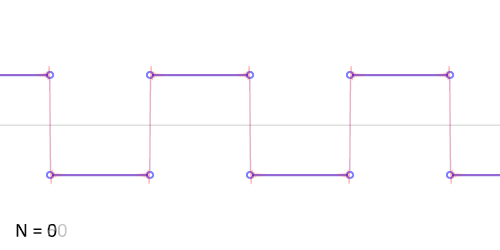 Синтез меандра из набора гармоник периодического сигнала. Чем больше число гармоник, тем ближе к идеальной форма сигнала. Выбросы на фронтах обусловлены неравномерной сходимостью ряда Фурье в точках разрыва.
Синтез меандра из набора гармоник периодического сигнала. Чем больше число гармоник, тем ближе к идеальной форма сигнала. Выбросы на фронтах обусловлены неравномерной сходимостью ряда Фурье в точках разрыва.Разложение меандра с нарастающим фронтом при t=0{\displaystyle t=0} в ряд Фурье дает:
- xмеандр(t)=4π∑k=1∞sin(2π(2k−1)ft)2k−1==4π(sin(2πft)+13sin(6πft)+15sin(10πft)+…).{\displaystyle {\begin{aligned}x_{\text{меандр}}(t)&={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}
Примечательно, что в спектре меандра отсутствуют чётные гармонические составляющие (гармоники). Амплитуда нечетных гармоник обратно пропорциональна их частоте с нулевым сдвигом фазы.
Прямоугольные сигналы в радиотехнике и электронике[править | править код]
Истинный меандр с нулевой длительностью фронтов физически нереализуем.[источник не указан 594 дня] В радиотехнике и электронике меандром обычно называют сигналы со скважностью 2 и длительностями фронтов много меньших периода повторения сигнала.
Сигнал приближённо такого вида (с ненулевой длительностью фронтов и спадов) генерируется различными автогенераторами, например, мультивибраторами, выполненными на транзисторах, логических элементах, операционных усилителях). Также сигналы такого типа обычно присутствуют практически во всех цифровых схемах, например, двоичный триггер со счетным входом, переключаемый периодическими импульсами даёт на выходе меандр.
Форма сигнала
Изменения тока или напряжения во времени можно представить в виде различных линий, или графиков. Постоянный ток, как неизменяющийся во времени, изображается прямой линией (рис. 3.1(а)), а переменный ток — самыми различными кривыми. Форма кривой переменного тока отражает периодические изменения значения тока от максимального к минимальному, затем опять к максимальному и т. д. (рис. 3.1(б)). Несколько таких кривых показано на рис. 3.2.
Рис. 3.1. График постоянного (а) и переменного (б) токов
Цикл
Повторяющаяся часть сигнала переменного тока называется циклом сигнала. Так, на кривых, изображенных на рис. 3.2, точка А является началом цикла, а точка В — его концом и началом следующего цикла.
Частота
Количество циклов сигнала в единицу времени называется частотой сигнала. Единица измерения частоты — герц (Гц). Например, если цикл изменения сигнала повторяется один раз в секунду, то частота сигнала равна 1 Гц, если 10 раз — 10 Гц (рис. 3.3).
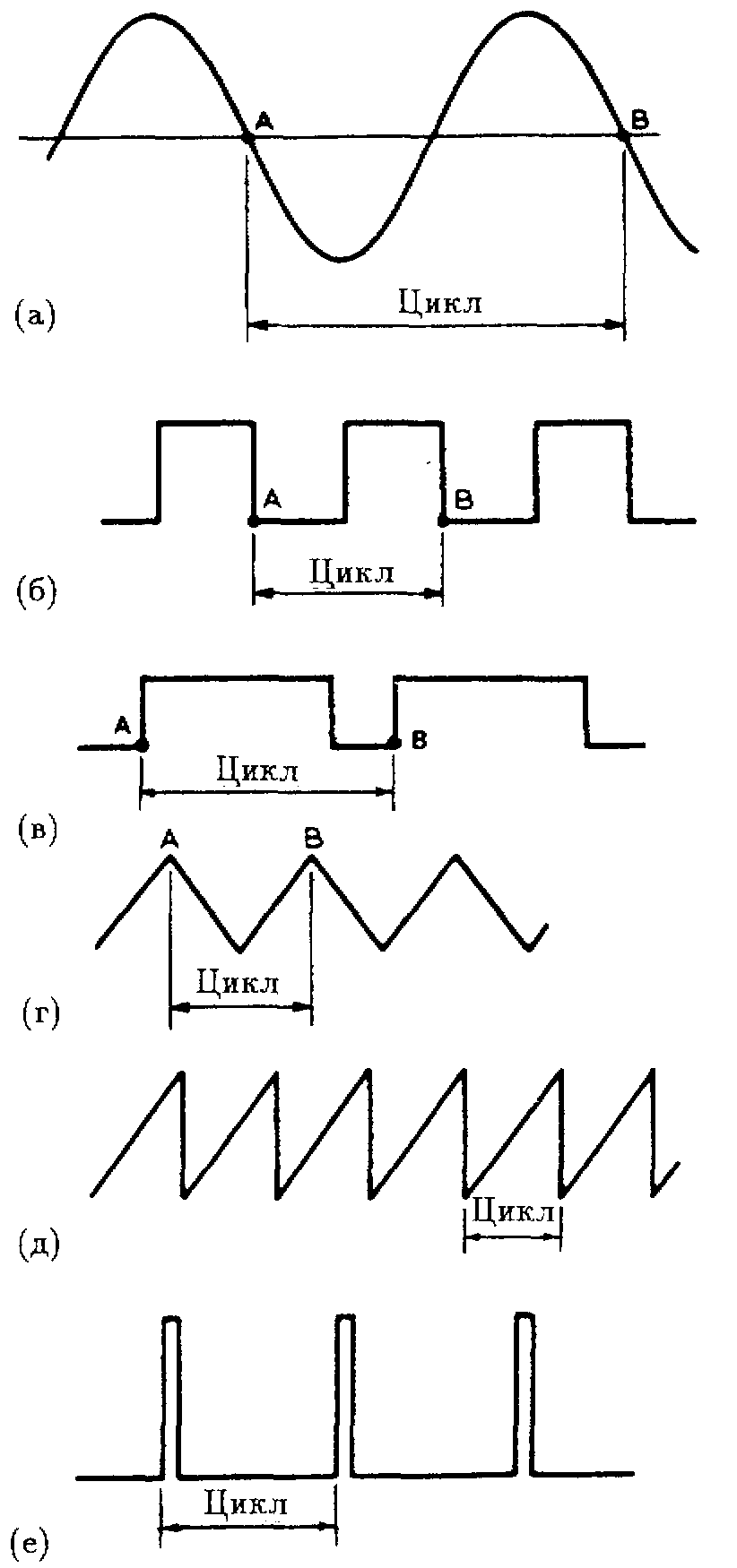
Рис. 3.2. Типы кривых переменного тока: синусоида (а), меандр (б), прямоугольный (в), треугольный (г), пилообразный (д), импульсы (е).
Длительность периода
Время, за которое завершается полный цикл изменения сигнала, называется длительностью его периода Т или просто периодом. Например, если сигнал проходит все изменения за одну секунду, то его период равен 1 если за половину секунды, то период равен 0,5 с.
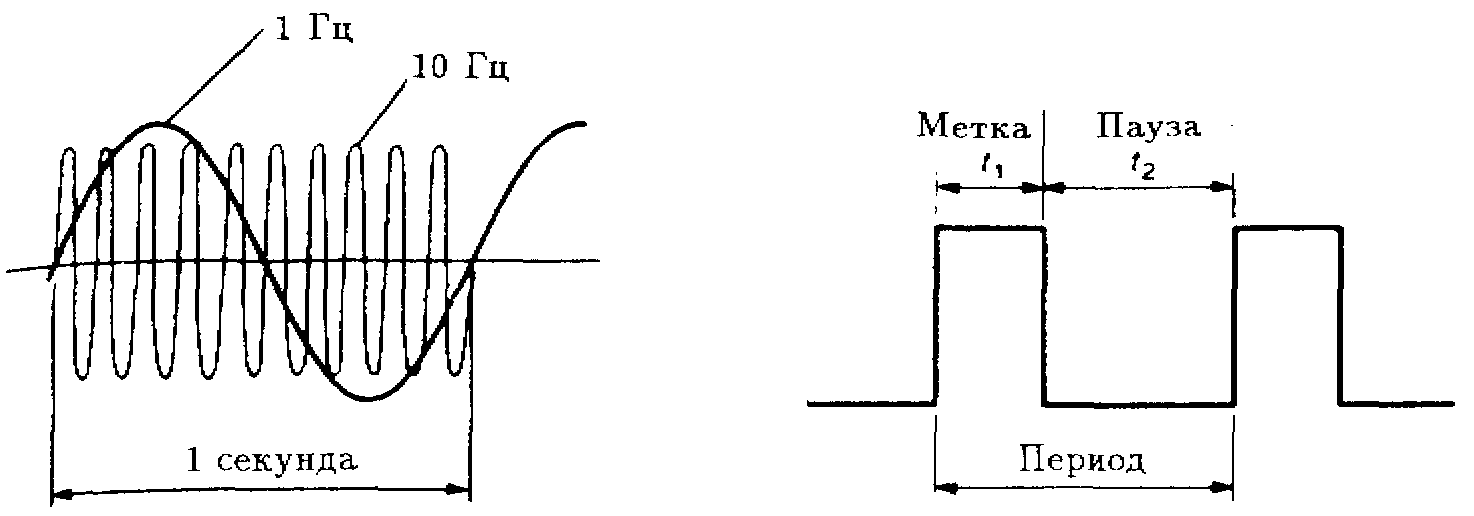
Рис. 3.3. Сигналы различных частот. Рис. 3.4. Коэффициент заполнения меньше 1.
Метка и пауза
Один период прямоугольного сигнала можно разделить на метку (Mark) и паузу (Space) (рис. 3.4). Отношение длительности метки к длительности паузы называется коэффициентом заполнения. Если длительность метки t1, а длительность паузы t2, то
Длительность метки t1
Коэффициент заполнения = ————————————— = —
Длительность паузы t2
Поскольку сигнал совершает полный цикл изменения за один период, то
Период = t1 + t2.
Если коэффициент заполнения равен 1, то
Длительность метки t1 = Длительность паузы t2.
Это можно записать иначе:
Период = 2 * Длительность паузы = 2 * Длительность метки.
Единицы измерения частоты ƒ:
герц, Гц; килогерц, кГц; мегагерц, МГц.
Единицы измерения периода Т:
секунда,с;
миллисекунда, мс = 1/1000 с = 10-3 с
микросекунда, мкс = 1/1000 мс = 10-3 мс = 10-6 с
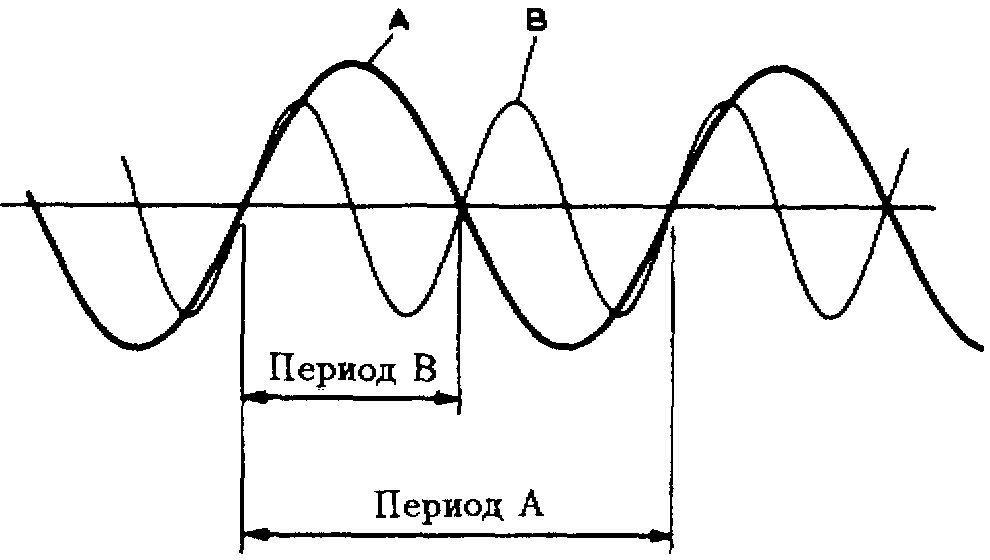
Рис.3.5.
Соотношение между частотой и периодом
Рассмотрим графики сигналов на рис. 3.5. Сигнал В имеет частоту выше, чем сигнал А, но период сигнала В составляет половину периода сигнала А. При увеличении частоты сигнала его период уменьшается, наоборот.
Следующая таблица содержит соотношения единиц измерения частоты и периода. Будет полезно, если вы ее запомните.
|
Частота f |
1 Гц |
1 кГц |
1 МГц |
|
Период Т |
1 с |
1 мс |
1 мкс |
Звуковые волны
Звуковые волны возникают в воздухе, например, когда кто-нибудь говорит или при работе громкоговорителя или пневматической дрели, при настройке по камертону и т. д. Звуковые волны изменяют давление воздуха, и воздух необходим им для распространения.
Интенсивность звуковых волн характеризуется громкостью, тон характеризует их частоту. При изменении частоты изменяется тон звука.
Звуковые частоты
Диапазон звуковых частот, которые воспринимаются ухом человека, называется диапазоном аудиочастот. Он простирается от 20 Гц до 20 кГц. Звуки частотой ниже 20 Гц и выше 20 кГц человек не слышит. На основе этого создан специальный свисток для подзыва собаки. Частота звукового сигнала этого свистка превышает 20 кГц, поэтому собаки, имеющие более широкий частотный диапазон чувствительности уха, слышат его, а человек — нет.
Чистые и инструментальные тоны
Чистым тоном называется простое синусоидальное колебание, содержащее одну частоту (рис. 3.2(а)). Инструментальный тон представляет собой сложное колебание, состоящее из ряда синусоидальных колебаний разной частоты (рис. 3.1(б)). Такие звуковые колебания возникают, когда звучит речь или музыка.
Гармоники
При сложении нескольких различных по частоте синусоидальных колебаний возникает сложное колебание. И наоборот, сложный сигнал можно разложить на ряд входящих в него чистых синусоидальных колебаний. Среди этих простых синусоидальных колебаний различают основную, или первую, гармонику и набор гармоник. Таким образом, любой сложный сигнал может быть разложен на следующие компоненты:
1. Первая, или основная, гармоника. Простое синусоидальное колебание, имеющее тот же период, что и исходное сложное колебание.
2. Набор гармоник. Простые синусоидальные колебания, частоты ко¬торых кратны частоте основной гармоники. Например, если частота первой гармоники равна 100 Гц, то
частота 2-й гармоники = 2 * 100 = 200 Гц;
частота 4-й гармоники = 4 * 100 = 400 Гц и т. д.
Чем больше номер гармоники, т. е. чем выше ее частота, тем меньше ее амплитуда. Поэтому высшими гармониками обычно пренебрегают.
Высота тона
Высота тона звуковой волны указывает, в какой части диапазона звуковых частот находится ее частота.
Звуки высокой тональности занимают верхнюю половину диапазона аудиочастот, а звуки низкой тональности — нижнюю половину. Женские голоса обычно имеют более высокую тональность, чем мужские. Барабан издает низкие звуки, а флейта — очень высокие, В сложном колебании частота основной гармоники определяет тональность сигнала.
Качество звука
Качество звука определяется числом гармоник инструментального сигнала, которые воспроизводятся аппаратурой без искажения.
Примеры некоторых сложных сигналов
1. Основная гармоника + 3-я гармоника (рис. 3.6).
2. Основная гармоника + 2-я гармоника (рис. 3.7).
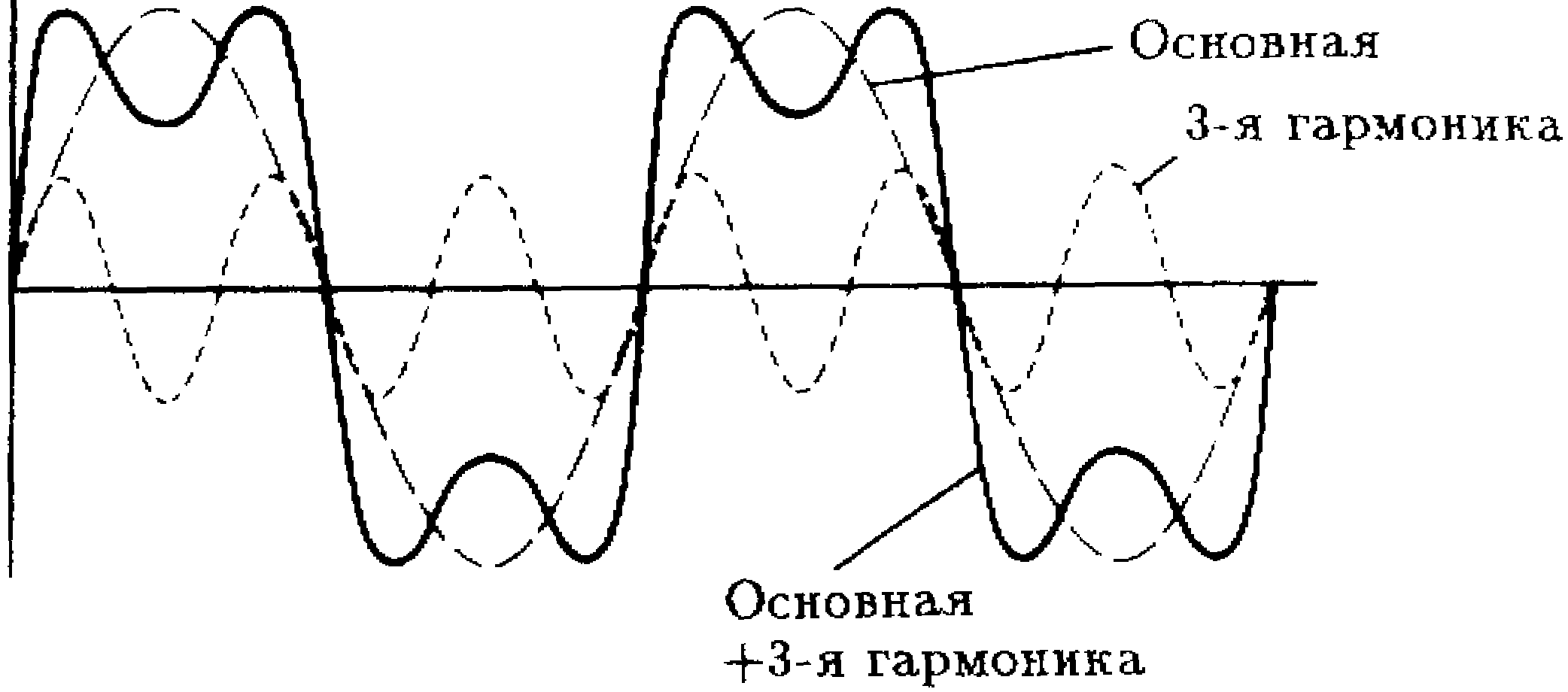
Рис. 3.6. Основная гармоника + 3-я гармоника (аппроксимация прямоугольного сигнала).
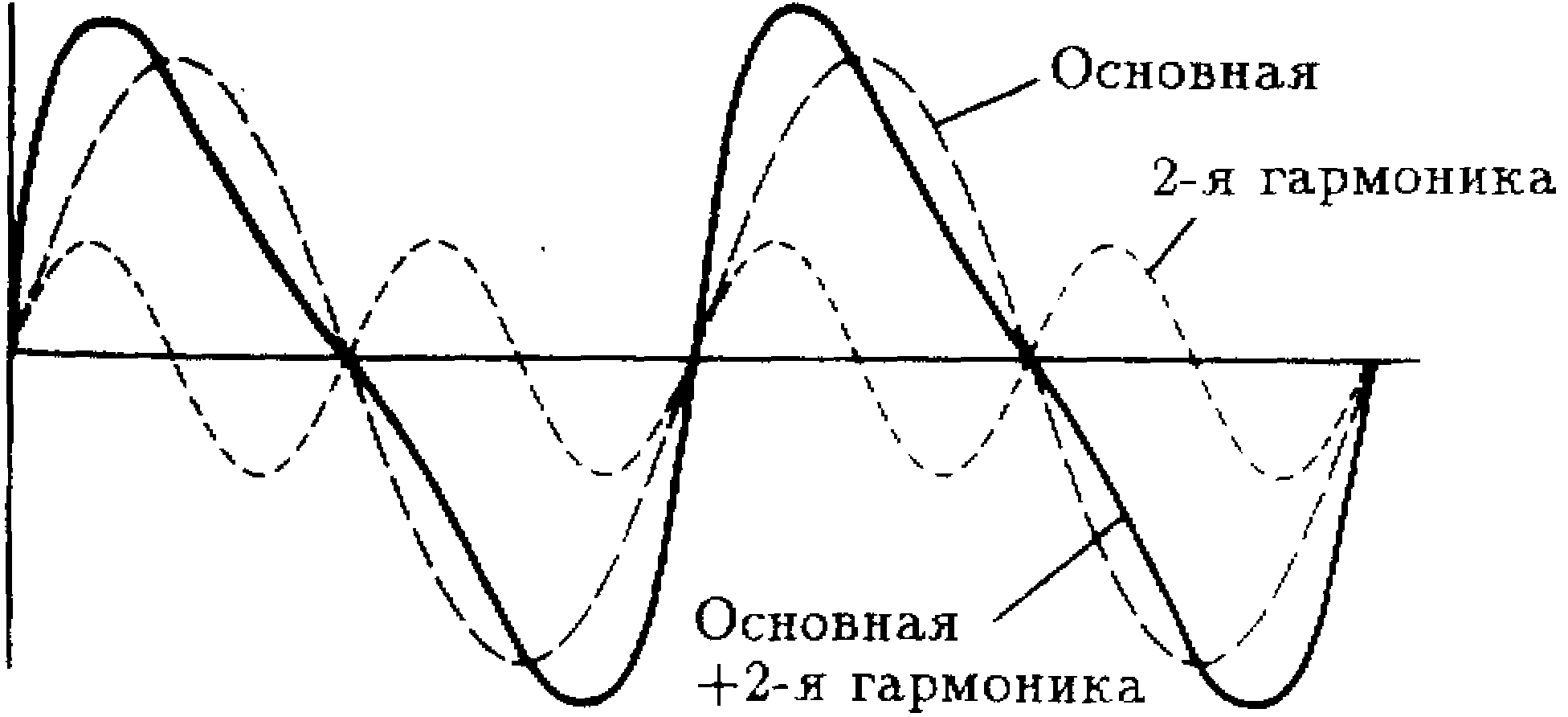
Рис. 3.7. Основная гармоника + 2-я гармоника (аппроксимация пилообразного сигнала).
Гармонические составляющие прямоугольного сигнала
Прямоугольный сигнал содержит основную гармонику плюс бесконечное множество нечетных гармоник. Например, прямоугольный сигнал частотой 1 кГц состоит из
основной гармоники 1 кГц;
3-й гармоники 3*1 = 3 кГц;
5-й гармоники 5*1 = 5 кГц;
7-й гармоники 7*1 = 7 кГц и т. д.
Заметим, что сложные колебания, содержащие только нечетные гармоники, имеют круто нарастающие фронты и резко спадающие срезы. Чем больше нечетных гармоник содержит сигнал, тем ближе его форма к форме прямоугольного сигнала.
Гармонические составляющие пилообразного сигнала
Пилообразный сигнал содержит основную гармонику плюс бесконечное множество четных гармоник. Например, пилообразный сигнал частотой 1 кГц состоит из
основной гармоники 1 кГц;
2-й гармоники 2*1 = 2 кГц;
4-й гармоники 4*1 = 4 кГц;
6-й гармоники 6*1 = 6 кГц и т. д.
В этом видео рассказывается о различных видах электрических сигналов:
Добавить комментарий
период (сигнала) — это… Что такое период (сигнала)?
- период (сигнала)
период (сигнала)
Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала (ОСТ 45.159-2000.1 Термины и определения (Минсвязи России)).
[http://www.iks-media.ru/glossary/index.html?glossid=2400324]Тематики
- электросвязь, основные понятия
Справочник технического переводчика. – Интент. 2009-2013.
- расширенный простой протокол передачи электронной почты
Смотреть что такое «период (сигнала)» в других словарях:
Период (сигнала) — 1. Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала Употребляется в документе: ОСТ 45.159 2000 Отраслевая система обеспечения единства измерений. Термины и определения … Телекоммуникационный словарь
период дискретизации сигнала электросвязи — Интервал дискретизации сигнала электросвязи по времени при равномерной дискретизации этого сигнала по времени. [ГОСТ 22670 77] Тематики сети передачи данных Синонимы период дискретизации EN sampling period … Справочник технического переводчика
период периодического сигнала — период Параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала. Обозначение T [ГОСТ 16465 70] Тематики сигналы радиотехнические измерительные Обобщающие термины характеристики… … Справочник технического переводчика
период основного тона — Период вокализованного речевого сигнала, частота которого лежит ниже рабочей частоты стандартного телефонного канала 300 3400 Гц. Для мужского голоса период основного тона равен 6,2 8,3 мс, для женского и детских голосов – от 3,3 до 4,5 мс. [Л.М … Справочник технического переводчика
период Найквиста — Временно интервал между двумя соседними отсчетами входного сигнала с ограниченным спектром. При дискретизации с частотой Найквиста период равен T=1/2F, где F верхняя частота спектра. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский… … Справочник технического переводчика
период проверки — Интервал времени, в течение которого проводится проверка наличия полезного сигнала на входе [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики… … Справочник технического переводчика
период — 2.18 период: Продолжительность времени. Источник: ГОСТ ИСО 8601 2001: Система стандартов по информации, библиотечному и издательскому делу. Представлен … Словарь-справочник терминов нормативно-технической документации
период измерений — 3.3 период измерений: Интервал времени, в течение которого осуществляют непрерывный сбор данных о вибрации здания. Источник: ГОСТ Р 52892 2007: Вибрация и удар. Вибрация зданий. Измерение вибрации и оценка ее воздействия на конструкцию … Словарь-справочник терминов нормативно-технической документации
Период дискретизации сигнала электросвязи — 31. Период дискретизации сигнала электросвязи Период дискретизации Sampling period Интервал дискретизации сигнала электросвязи по времени при равномерной дискретизации этого сигнала по времени Источник: ГОСТ 22670 77: Сеть связи цифровая… … Словарь-справочник терминов нормативно-технической документации
Период периодического сигнала — 17. Период периодического сигнала Период Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
2.4 Периодические сигналы
Периодическими называются сигналы, бесконечно повторяющиеся по своей форме, то есть отвечающие условию:
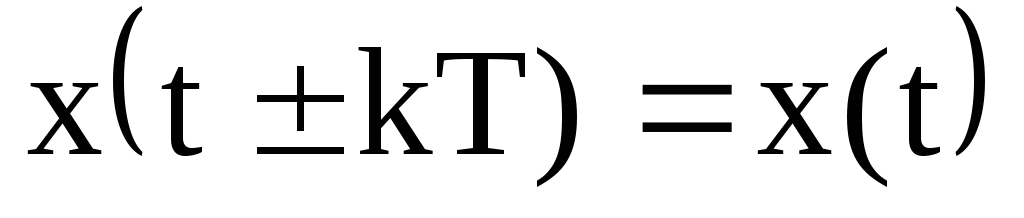 ,
,
где T – период повторения сигнала (основной период),
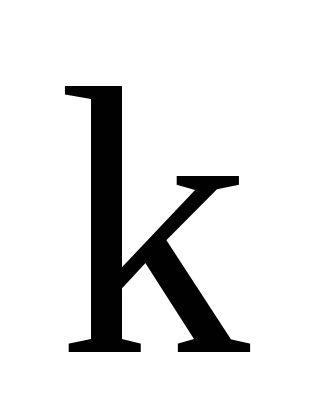 —
любое целое число.
—
любое целое число.
Уже из этого определения видно, что периодические сигналы весьма похожи на гармонические сигналы, хотя бы тем, что они бесконечно повторяются во времени. Поэтому при анализе периодических сигналов их удобно представлять в виде суммы чистых гармоник или комплексных экспонент с частотами, образующими арифметическую прогрессию:
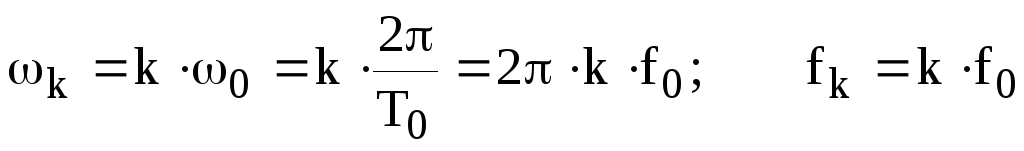
 .
.
Такое представление периодических сигналов впервые предложил и обосновал французский математик Жан – Батист — Жозеф, барон де Фурье, между прочим, член Петербургской Академии наук. Разложение периодического сигнала в ряд Фурье возможно при соблюдении ряда условий (условия Дирихле):
число разрывов сигнала первого рода (скачков) должно быть конечным,
н
 е
должно быть разрывов второго рода
(уходящих в бесконечности ветвей),
е
должно быть разрывов второго рода
(уходящих в бесконечности ветвей),должно быть конечным число экстремумов сигнала (максимумов и минимумов).
Ряд Фурье можно использовать и для представления в виде суммы гармонических колебаний любого финитного сигнала, то есть сигнала конечной длительности Т. За пределами интервала времени [0; T] финитный сигнал равен нулю, хотя его представление в виде ряда Фурье означает его периодическое продолжение за границы этого интервала.
Так же как и простое гармоническое колебание, периодический сигнал, отвечающий условиям Дирихле, может быть представлен в одной из трех форм.
а). Синусно-косинусное
представление периодического сигнала x(t)
с периодом 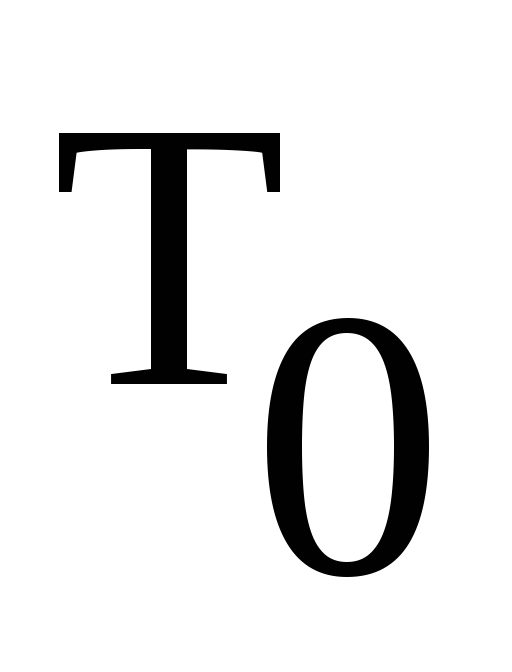 и основной частотой
и основной частотой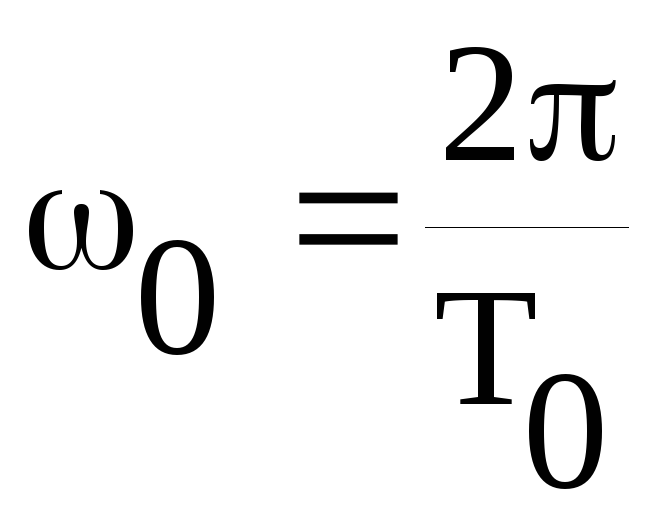 имеет вид:
имеет вид:
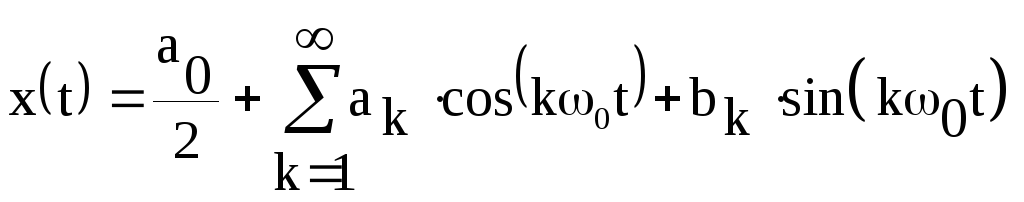 .
.
Колебания
с кратными частотами 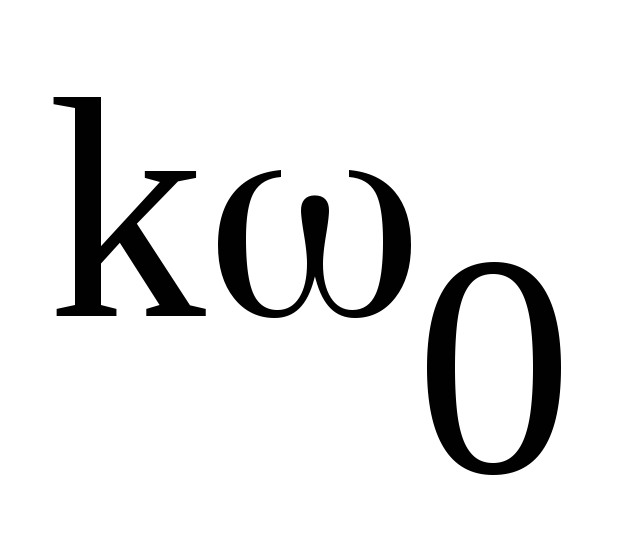 называются высшими гармониками. Колебание
с частотой
называются высшими гармониками. Колебание
с частотой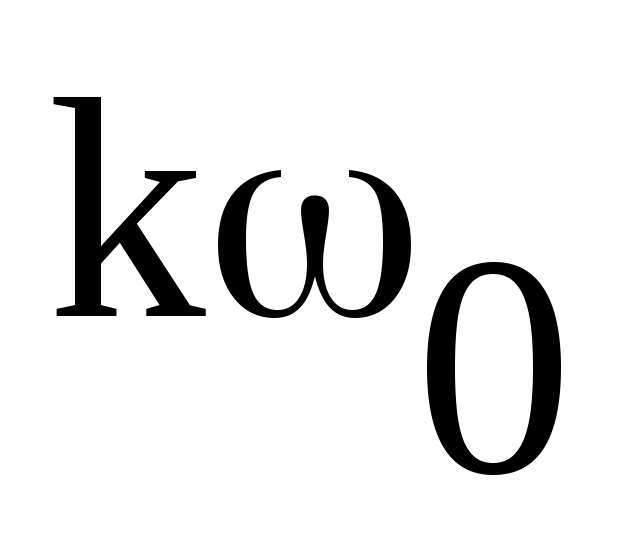 являетсяk-ой
гармоникой. Коэффициенты ряда определяются
по формулам:
являетсяk-ой
гармоникой. Коэффициенты ряда определяются
по формулам:
 ,
,
которые
позволяют вычислить амплитуды квадратурных
составляющих каждой  гармоники.
гармоники.
Константа  рассчитывается по обычной для коэффициента
рассчитывается по обычной для коэффициента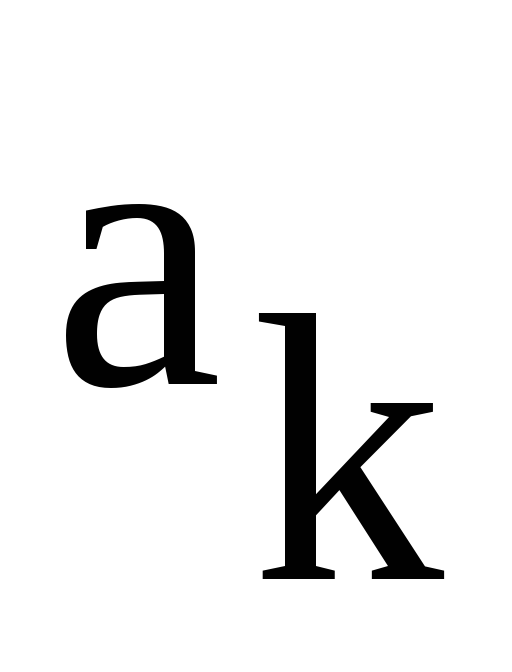 формуле, которая приk=0
значительно упрощается:
формуле, которая приk=0
значительно упрощается:
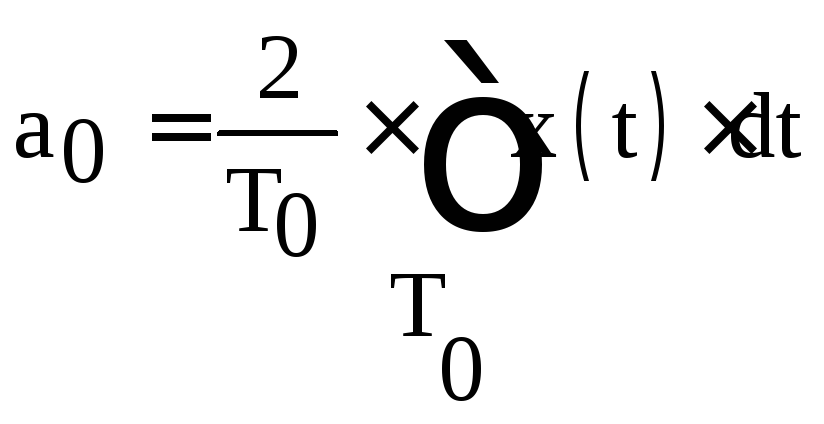 .
.
Таким
образом, член ряда 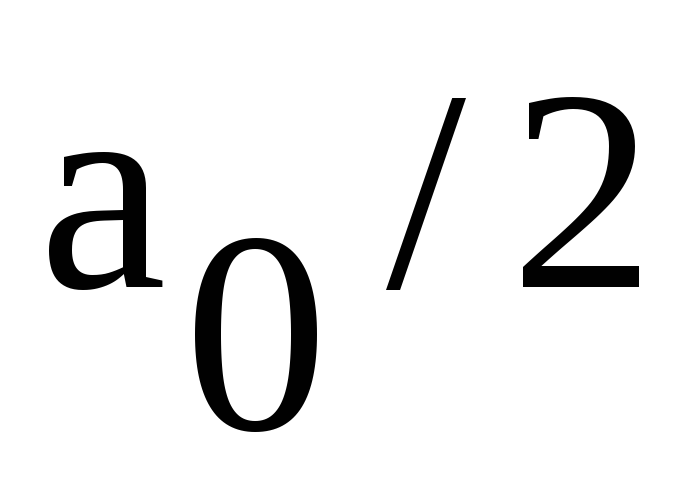 — это просто среднее значение сигнала
за период.
— это просто среднее значение сигнала
за период.
Если
x(t)
– четная функция, то все коэффициенты 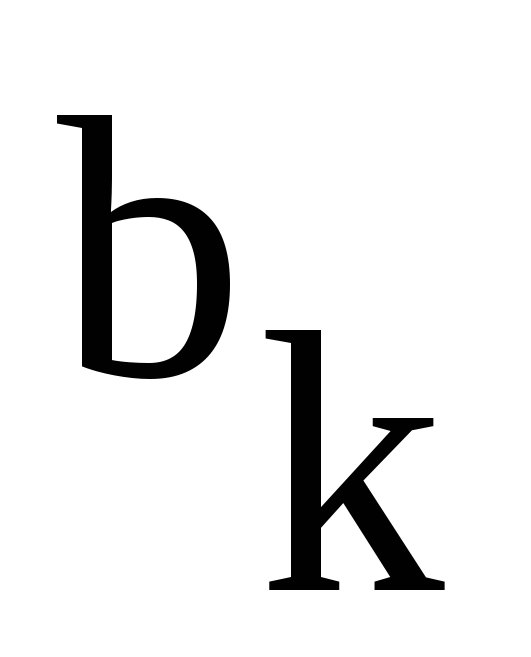 обращаются в нуль и в выражении для ряда
Фурье присутствуют только косинусные
слагаемые. Если жеx(t)
– нечетная функция, то все коэффициенты
обращаются в нуль и в выражении для ряда
Фурье присутствуют только косинусные
слагаемые. Если жеx(t)
– нечетная функция, то все коэффициенты 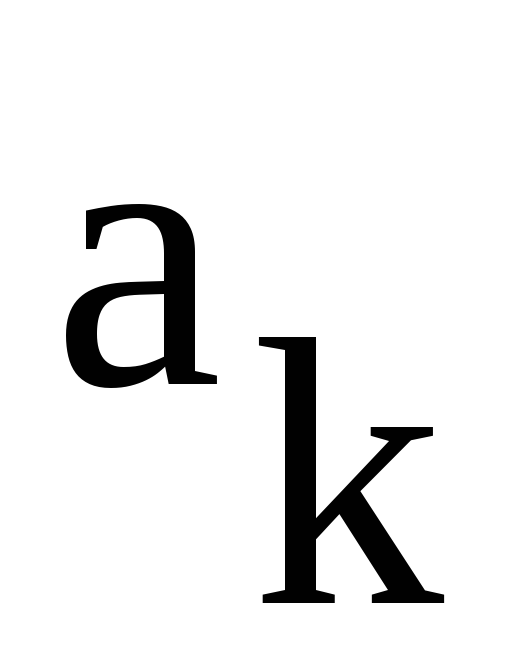 ,
в том числе и
,
в том числе и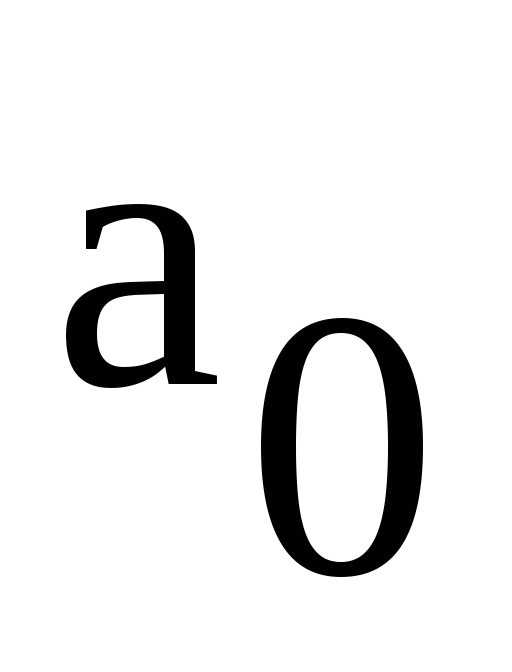 ,
равны нулю и ряд Фурье содержит только
синусные слагаемые.
,
равны нулю и ряд Фурье содержит только
синусные слагаемые.
Пример.
П оследовательность
прямоугольных импульсов (видеоимпульсов)x(t),
изображенная на рис. 2.9, является четной
последовательностью и поэтому ряд Фурье
для неё содержит только косинусные
члены:
оследовательность
прямоугольных импульсов (видеоимпульсов)x(t),
изображенная на рис. 2.9, является четной
последовательностью и поэтому ряд Фурье
для неё содержит только косинусные
члены:
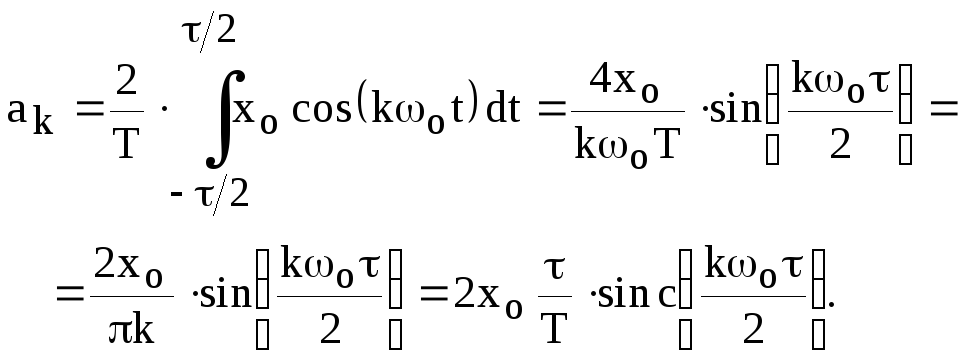
В полученном выражении
полученном выражении
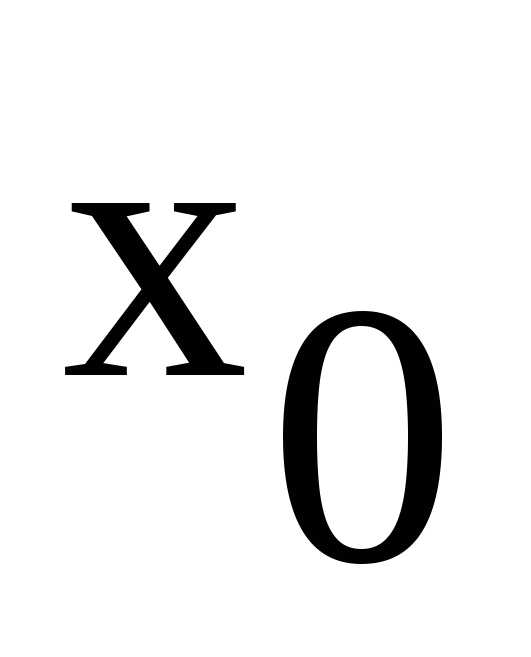 — амплитуда импульсов,
— амплитуда импульсов,
 — период их следования,
— период их следования,
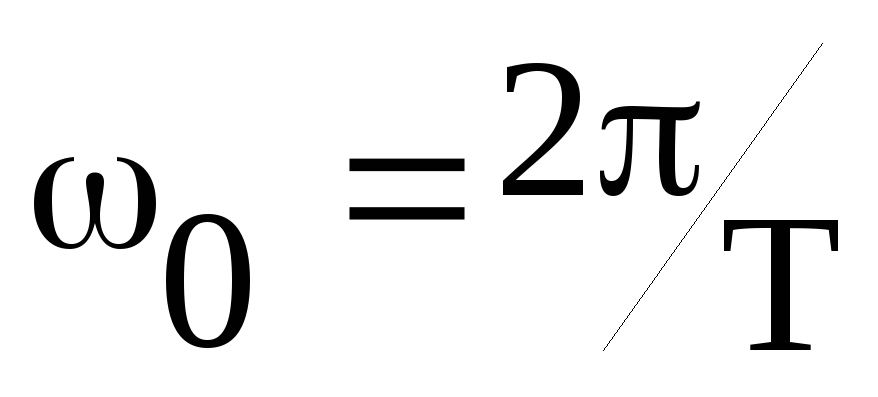 —
основная частота (соответствует амплитуде
первой гармоники),
—
основная частота (соответствует амплитуде
первой гармоники),
τ – длительность импульсов.
Здесь
нам впервые встречается интересная
функция 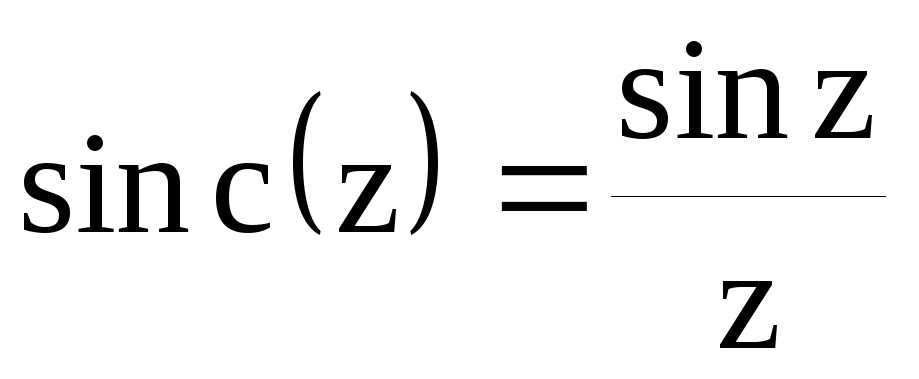 .
.
График этой функции изображен на рис. 2.10. В дальнейшем нам придется очень часто использовать эту функцию, которая представляет собой затухающую синусоиду, амплитуда которой уменьшается во времени по гиперболическому закону. В нуле эта функция обращается в единицу, поскольку:
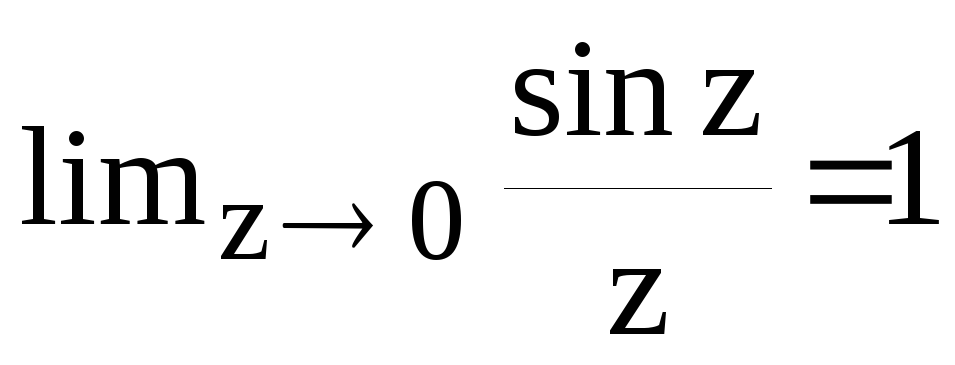 .
.
Ряд Фурье для последовательности прямоугольных импульсов приобретает теперь следующий вид:
 .
.
Отношение
периода следования импульсов к их
длительности называется скважностью
импульсов  .
С учетом скважности выражение для ряда
Фурье последовательности прямоугольных
импульсов приобретает законченный вид:
.
С учетом скважности выражение для ряда
Фурье последовательности прямоугольных
импульсов приобретает законченный вид:
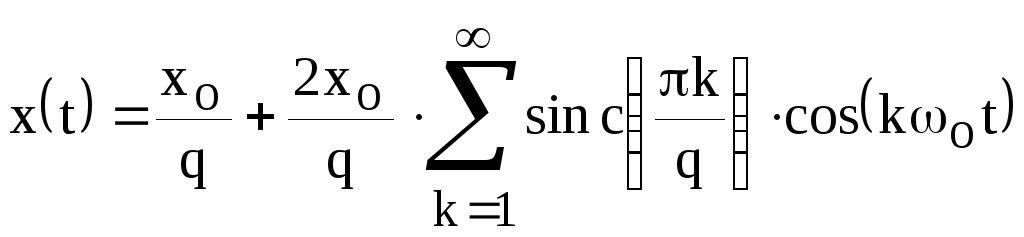 .
.
При q=2 последовательность прямоугольных импульсов превращается в меандр. При этом ширина импульсов равна половине периода их следования.
Н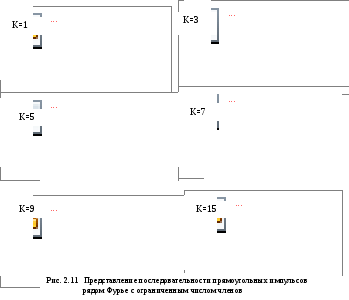 а
рис. 2.11 построены графики, иллюстрирующие
представление исходной последовательности
прямоугольных импульсов при Т = 0,01 с, τ
= 0,008 с и
а
рис. 2.11 построены графики, иллюстрирующие
представление исходной последовательности
прямоугольных импульсов при Т = 0,01 с, τ
= 0,008 с и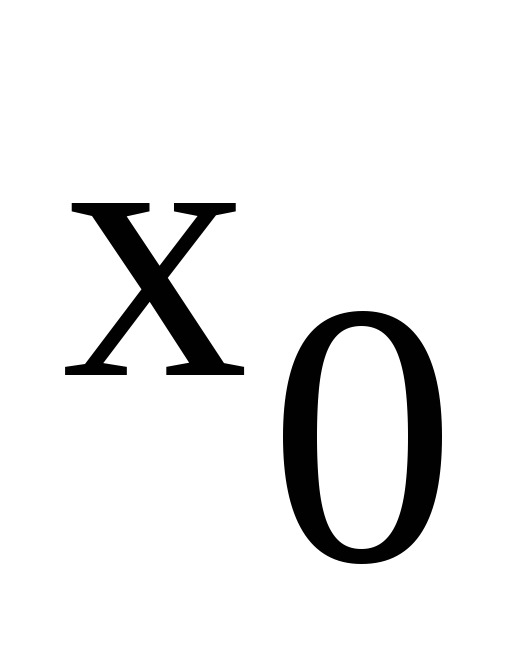 =
1В в виде ряда Фурье при использовании
К = 1, 3, 5, 7, 9 и 15 гармоник. На приведенных
рисунках хорошо видно, как с ростом
числа членов разложения последовательности
в ряд Фурье получаемая конечная сумма
всё более приближается к исходной
последовательности.
=
1В в виде ряда Фурье при использовании
К = 1, 3, 5, 7, 9 и 15 гармоник. На приведенных
рисунках хорошо видно, как с ростом
числа членов разложения последовательности
в ряд Фурье получаемая конечная сумма
всё более приближается к исходной
последовательности.
б) Вещественное представление ряда Фурье получается путем записи отдельных гармоник в вещественной форме:
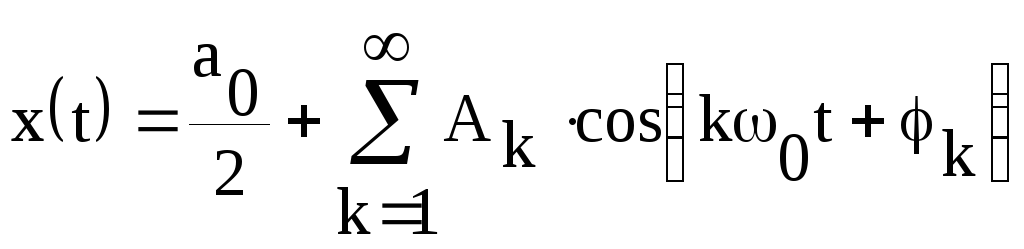 ,
,
где 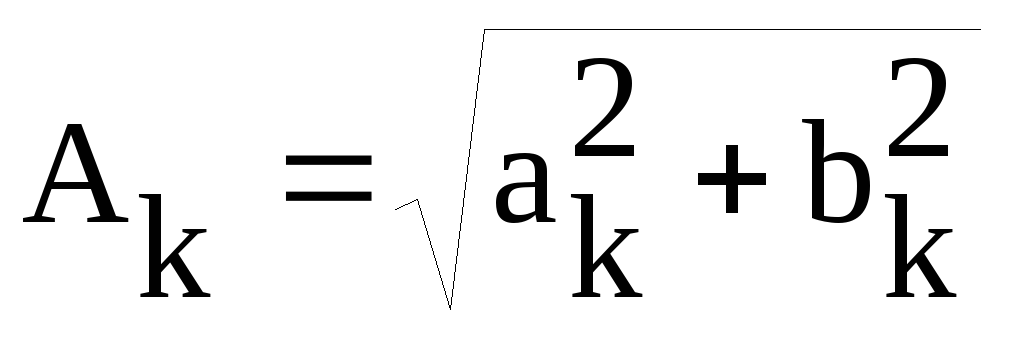 —
амплитудаk-той
гармоники,
—
амплитудаk-той
гармоники,
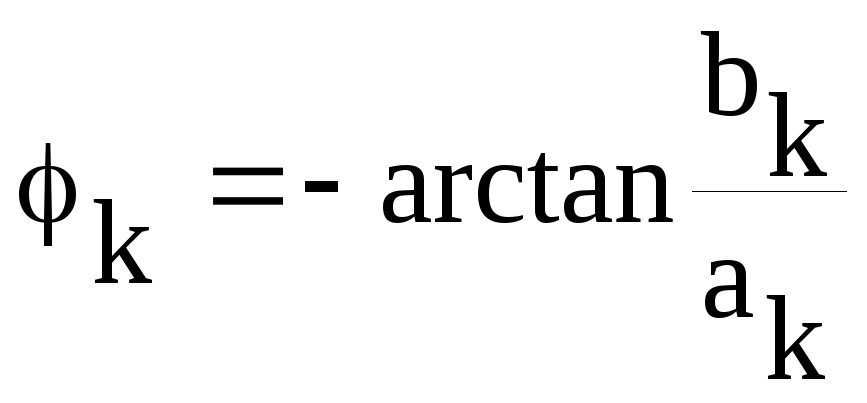 —
фаза k-той
гармоники.
—
фаза k-той
гармоники.
Такая форма записи предпочтительнее предыдущей, поскольку под знаком суммирования остается только один член разложения.
Совокупность
амплитуд гармонических составляющих 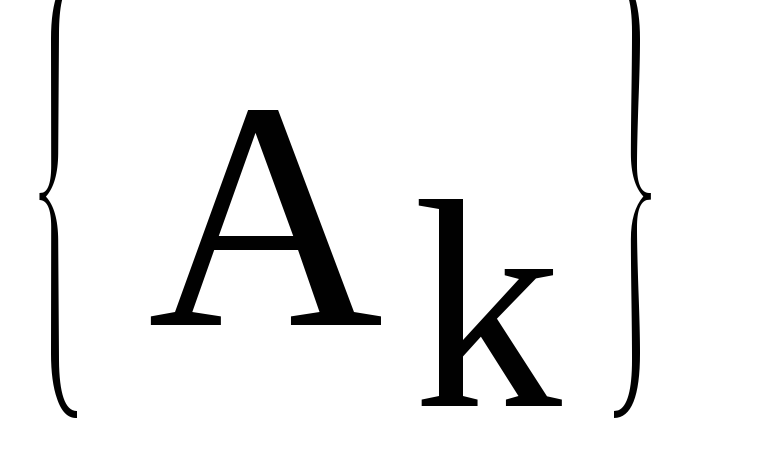 периодического сигнала образует егоамплитудный
спектр, а
совокупность фаз
периодического сигнала образует егоамплитудный
спектр, а
совокупность фаз 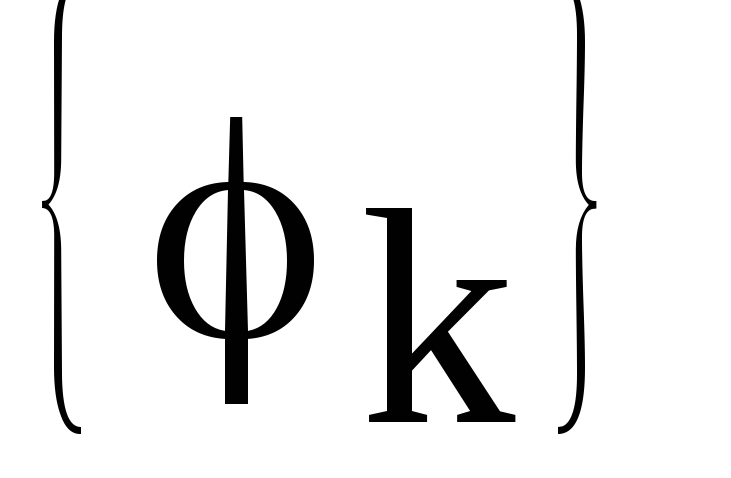 –фазовый
спектр сигнала.
–фазовый
спектр сигнала.
В рассмотренном ранее примере последовательность прямоугольных импульсов содержала только косинусные члены, поэтому ее представление в виде
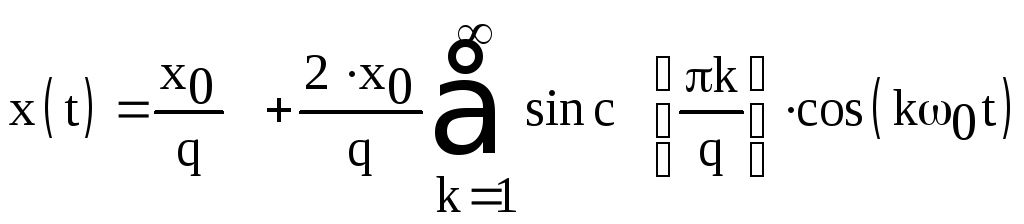
является, по сути, вещественным представлением. Амплитудный и фазовый спектры этой последовательности (рис. 2.9) определяются совокупностью амплитуд и фаз отдельных гармонических составляющих:
— амплитудный спектр

 ,
,
— фазовый спектр
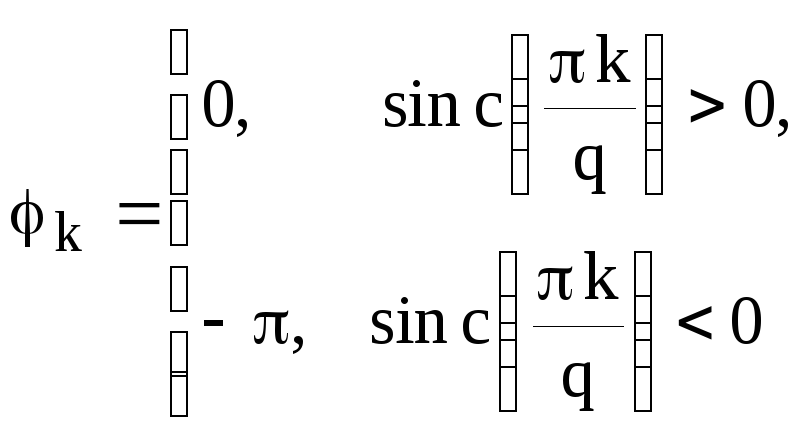 .
.
Спектры
сигнала 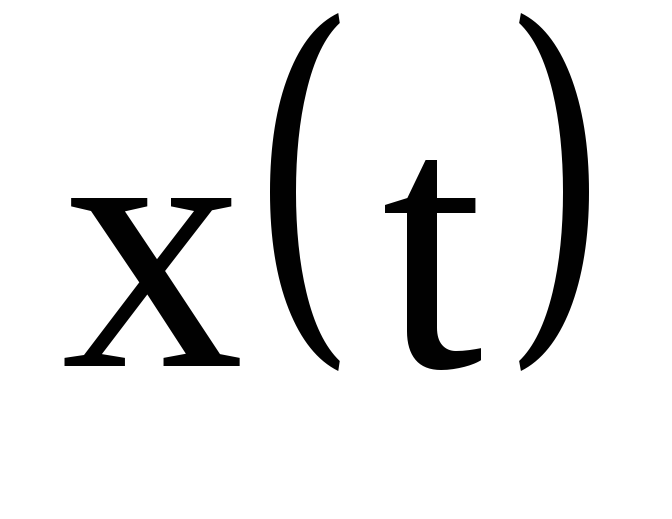 в виде последовательности видеоимпульсовc
параметрами
представлены на рис. 2.12, причем ось
абсцисс проградуирована в номерах
гармоник. Гармоники с номерами, кратными
скважности импульсовq
(если q
– целое), имеют нулевую амплитуду,
амплитудный спектр обращается в нуль.
в виде последовательности видеоимпульсовc
параметрами
представлены на рис. 2.12, причем ось
абсцисс проградуирована в номерах
гармоник. Гармоники с номерами, кратными
скважности импульсовq
(если q
– целое), имеют нулевую амплитуду,
амплитудный спектр обращается в нуль.
Амплитудный спектр имеет ярко выраженный лепестковый характер. Для таких спектров в качестве ширины спектра (эффективная ширина спектра) принимают обычно ширину первого лепестка, равную скважности импульсов. На рис. 2.12 эффективная ширина спектра равна 11 гармоникам.
Поскольку
расстояние между линиями спектра в
единицах частоты равно 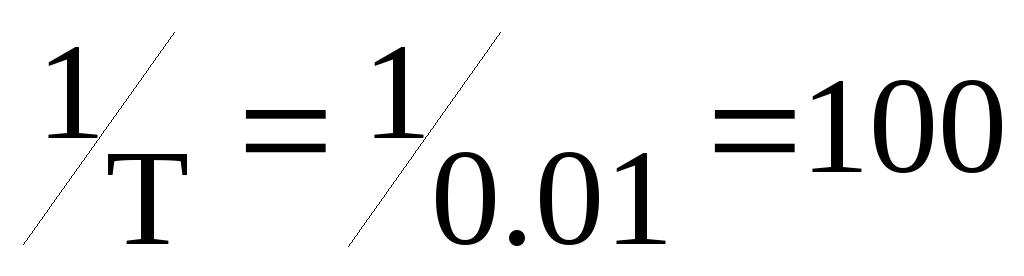 Гц, то эффективная ширина спектра
последовательности прямоугольных
импульсов с такой частотой составляет
1100 Гц =1.1 кГц. Отсюда вытекает одна общая
закономерность, справедливая для
последовательности импульсов любой
формы:чем
короче импульсы по сравнению с шириной
их следования, тем протяженнее амплитудный
спектр этой последовательности.
Гц, то эффективная ширина спектра
последовательности прямоугольных
импульсов с такой частотой составляет
1100 Гц =1.1 кГц. Отсюда вытекает одна общая
закономерность, справедливая для
последовательности импульсов любой
формы:чем
короче импульсы по сравнению с шириной
их следования, тем протяженнее амплитудный
спектр этой последовательности.
в) Комплексное представление ряда Фурье имеет наибольшее распространение в теории и практике преобразования сигналов. Оно получается из вещественного представления заменой косинуса через комплексные экспоненты в соответствии с формулами Эйлера:
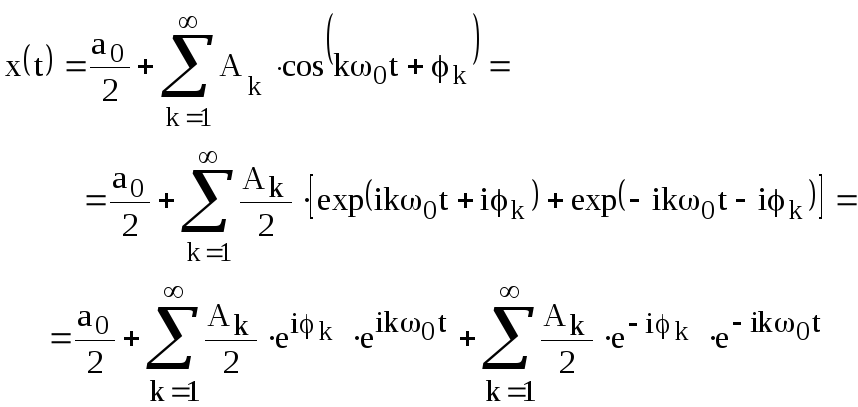
Будем рассматривать экспоненты со знаком минус в показателе в качестве членов ряда с отрицательными номерами k. Свободный член ряда – это член с номером k=0. Теперь ряд Фурье можно записать в более компактной форме – комплексной форме представления:
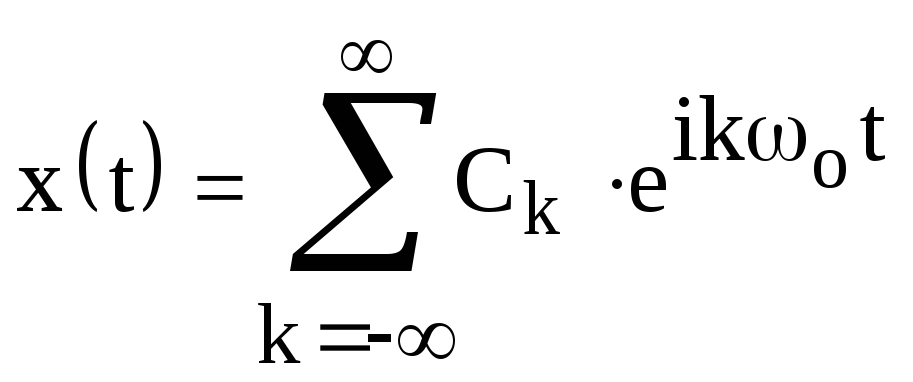 .
.
Коэффициенты
этого ряда 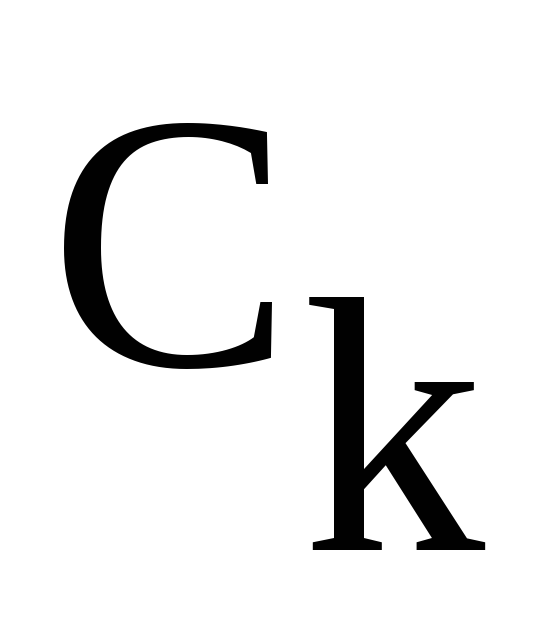 являются комплексными величинами. Они
связаны с амплитудами
являются комплексными величинами. Они
связаны с амплитудами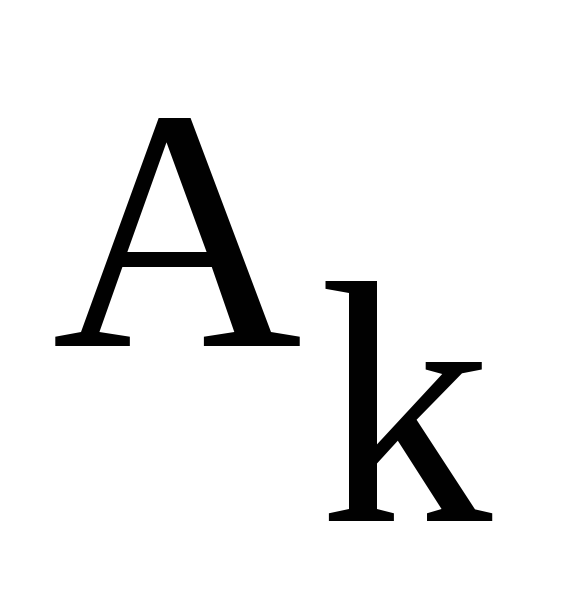 и фазами
и фазами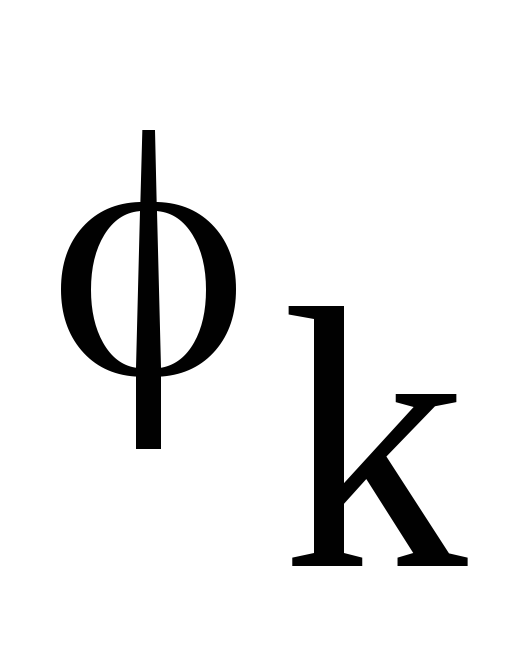 отдельных гармоник, фигурирующих в
вещественном представлении ряда Фурье,
следующими соотношениями:
отдельных гармоник, фигурирующих в
вещественном представлении ряда Фурье,
следующими соотношениями:
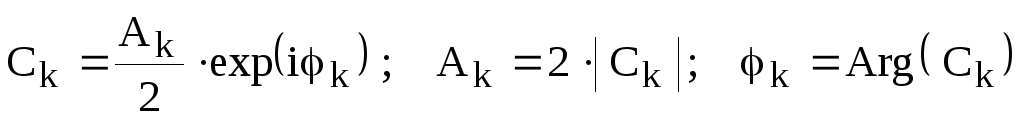 .
.
Не более сложно найти и соотношения с коэффициентами синусно-косинусного представления ряда Фурье:
 .
.
Совокупность
комплексных амплитуд 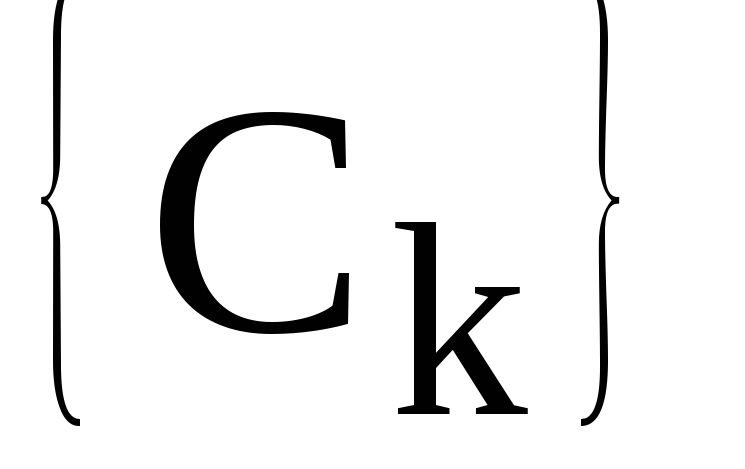 образуеткомплексный
спектр периодического сигнала x(t),
который содержит в себе и амплитудный,
и фазовый спектры. Взаимно однозначное
соответствие между периодическим
сигналом x(t)
и его комплексным спектром выражается
формулами соответствия:
образуеткомплексный
спектр периодического сигнала x(t),
который содержит в себе и амплитудный,
и фазовый спектры. Взаимно однозначное
соответствие между периодическим
сигналом x(t)
и его комплексным спектром выражается
формулами соответствия:
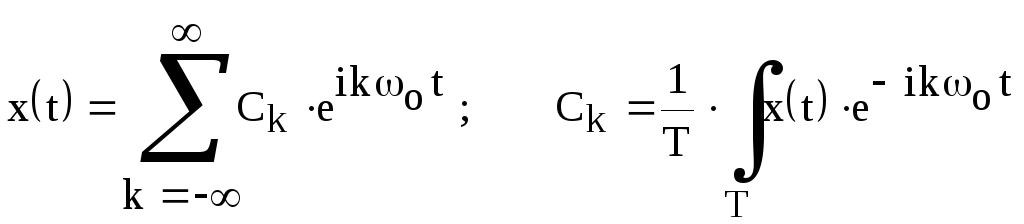
Если
функция x(t)
является четной, то амплитуды  будут чисто вещественными, в случае
нечетностиx(t)
они будут чисто мнимыми. Если сигнал
x(t)
вещественный, то амплитудный, фазовый
и комплексный спектры обладают следующими
свойствами симметрии:
будут чисто вещественными, в случае
нечетностиx(t)
они будут чисто мнимыми. Если сигнал
x(t)
вещественный, то амплитудный, фазовый
и комплексный спектры обладают следующими
свойствами симметрии:
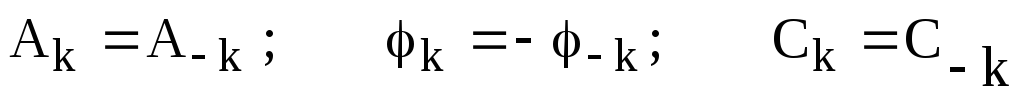 ,
,
то
есть спектральные амплитуды 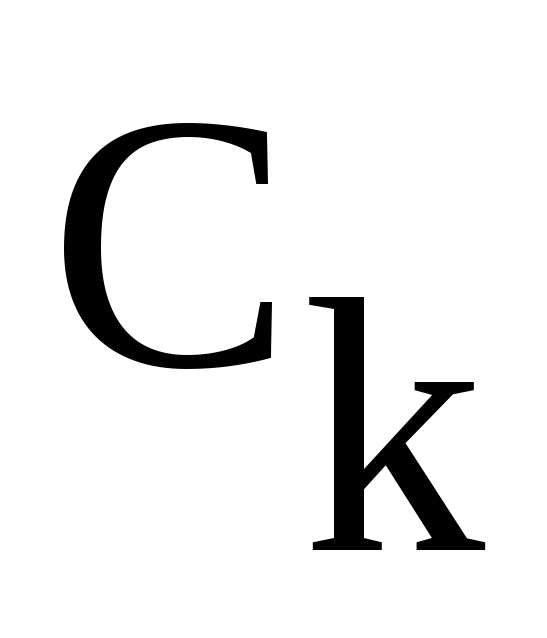 и
и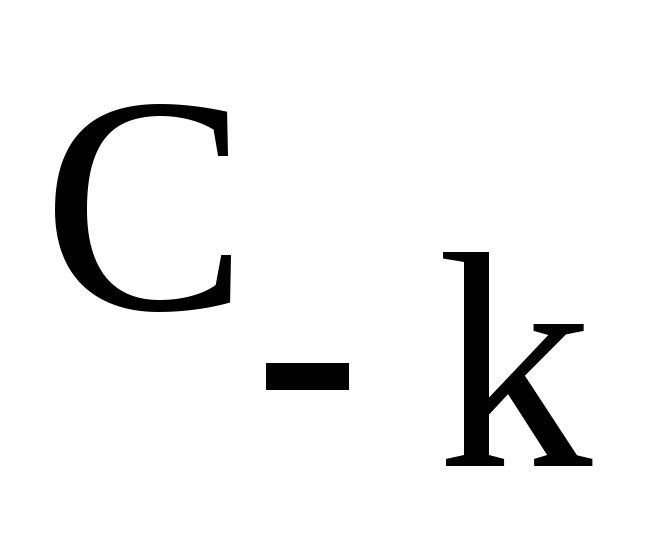 являются комплексно сопряженными
выражениями. Поэтому
являются комплексно сопряженными
выражениями. Поэтому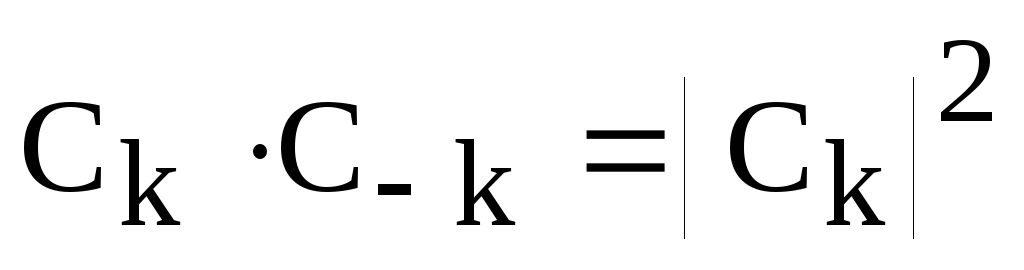 и, следовательно
и, следовательно
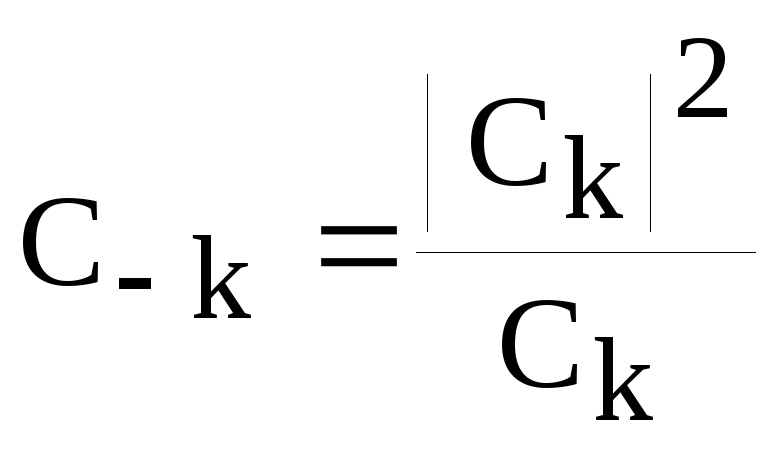 .
.
При работе в среде Mat Cad для представления периодического сигнала в виде конечного ряда Фурье лучше пользоваться развернутым выражением:
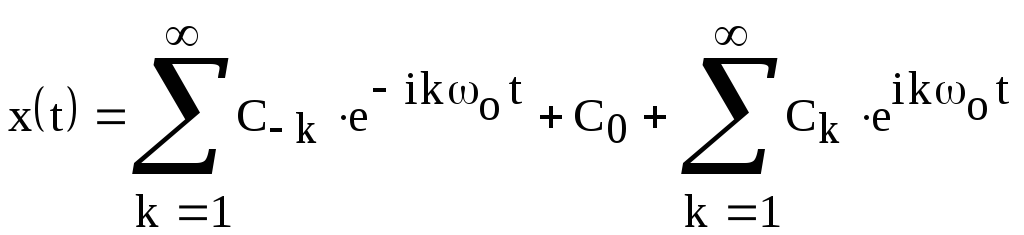 .
.
Пример.
Врезультате однополупериодного выпрямления синусоидально изменяющегося напряжения частотой 50 Гц получается периодический сигнал с периодом следования импульсовT=0.02 с, построение которого представлено на рис. 2-13.
Комплексный
спектр сигнала 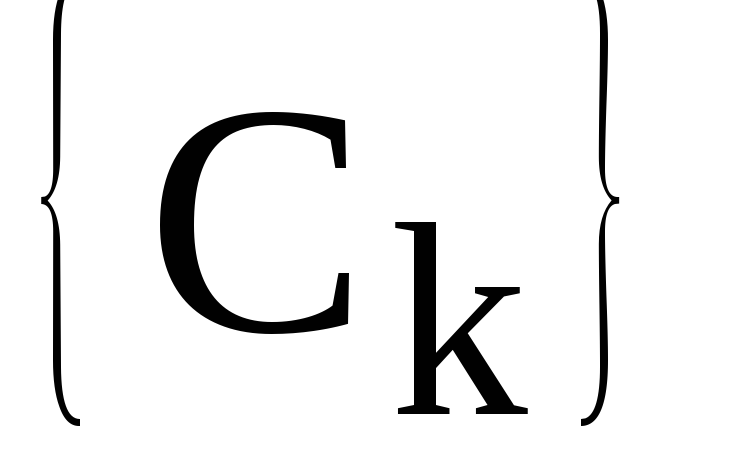 разбивается на два спектра: — амплитудный
спектр
разбивается на два спектра: — амплитудный
спектр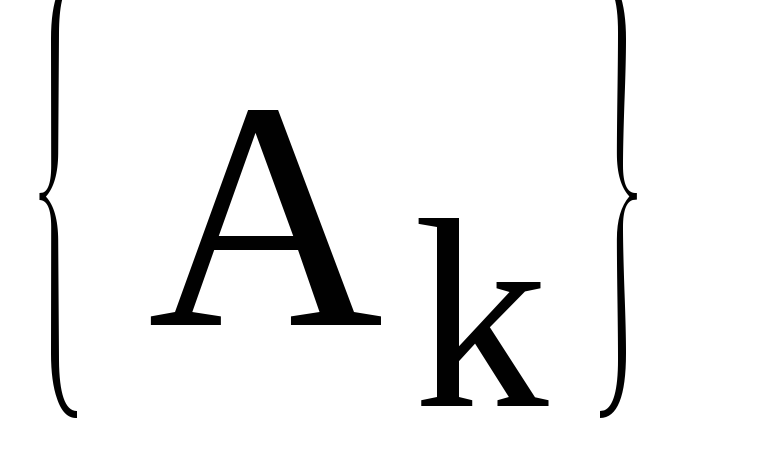 и фазовый спектр
и фазовый спектр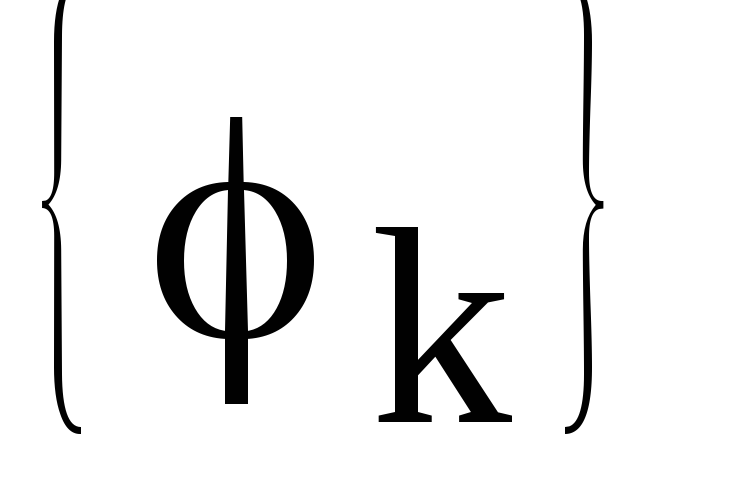 .
Оба эти спектра изображены на рис. 2.13 и
2.14 в функции номеров гармоник. Фазовый
спектр в этом примере представлен в
радианах.
.
Оба эти спектра изображены на рис. 2.13 и
2.14 в функции номеров гармоник. Фазовый
спектр в этом примере представлен в
радианах.
А мплитудный
спектр ясно показывает, что наибольшую
роль в формировании исходного сигнала
играют только первые две гармоники, так
что сигнал состоит практически из двух
синусоидальных колебаний с частотами
100 Гц и 200 Гц и постоянной составляющей,
равной среднему значению сигнала. Более
высокие гармоники имеют лишь незначительные
амплитуды и могут только в малом изменить
форму сигнала.
мплитудный
спектр ясно показывает, что наибольшую
роль в формировании исходного сигнала
играют только первые две гармоники, так
что сигнал состоит практически из двух
синусоидальных колебаний с частотами
100 Гц и 200 Гц и постоянной составляющей,
равной среднему значению сигнала. Более
высокие гармоники имеют лишь незначительные
амплитуды и могут только в малом изменить
форму сигнала.
Д
 ействительно,
как видно по рис. 2.15, где представлена
сумма, с учетом фазовых соотношений,
только среднего значения сигнала
(нулевая гармоника), первой и второй
гармоник, полученный в таком виде сигнал
мало отличается от исходного сигнала,
представленного на рис. 2.13.
ействительно,
как видно по рис. 2.15, где представлена
сумма, с учетом фазовых соотношений,
только среднего значения сигнала
(нулевая гармоника), первой и второй
гармоник, полученный в таком виде сигнал
мало отличается от исходного сигнала,
представленного на рис. 2.13.
Поскольку периодический сигнал представляется рядом Фурье в виде суммы гармонических колебаний, то и его мощность должна равняться сумме мощностей гармоник, равных половинам квадратов соответствующих амплитуд. Это соотношение известно как теорема де Парсеваля для периодических сигналов:
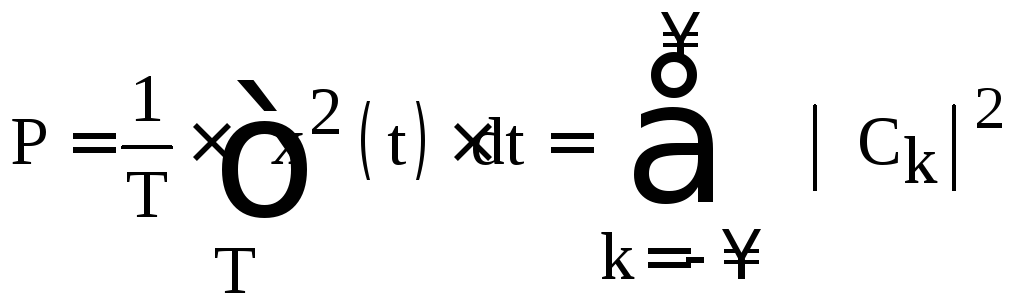 .
.
Данное равенство означает, что мощность периодического сигнала равна сумме квадратов модулей комплексных амплитуд его разложения в ряд Фурье.
Если
в выражении для ряда Фурье мы ограничиваемся
суммой конечного числа K
членов разложения, то мы получаем сигнал 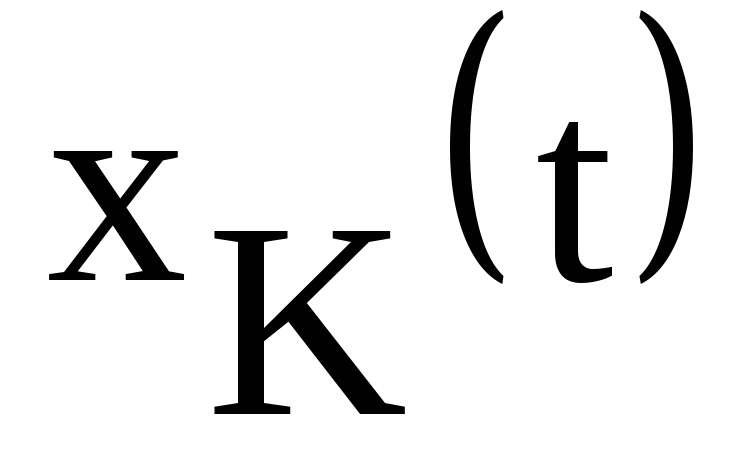 ,
несколько отличный от исходного сигналаx(t).
Меру приближения исходного сигнала
x(t)
конечной суммой
,
несколько отличный от исходного сигналаx(t).
Меру приближения исходного сигнала
x(t)
конечной суммой 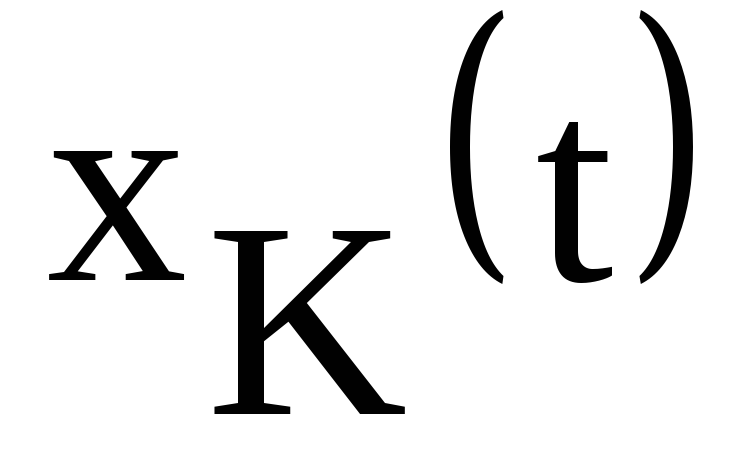 можно характеризовать средней
квадратической погрешностью, равной
корню квадратному из дисперсии, то есть
мощности неучтенных гармоник:
можно характеризовать средней
квадратической погрешностью, равной
корню квадратному из дисперсии, то есть
мощности неучтенных гармоник:
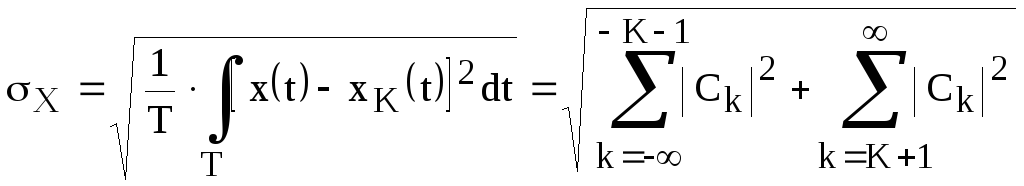 .
.
Интересно то, что с ростом числа K членов разложения средняя квадратическая погрешность воспроизведения исходного сигнала конечным рядом Фурье всегда только уменьшается.
Нотная запись музыкальных произведений – это запись мгновенных амплитудных спектров звуковых колебаний, разделенных паузами между нотами. Соотношение между нотами и соответствующими им частотами чистых гармоник имеет следующий вид
О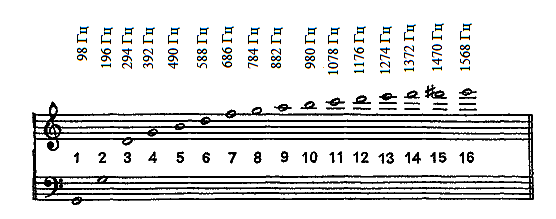 днако
каждая нота, взятая на соответствующем
музыкальном инструменте, создает звук,
амплитудный спектр которого, кроме
основной частоты (смотри рисунок),
содержит и ряд других частот. Совокупность
этих дополнительных частот (спектр)
характеризуется тембром данного
музыкального инструмента, отличным от
любого другого инструмента. Взятие
аккорда приводит к еще большему усложнению
спектра, соответствующему содержанию
аккорда. При игре оркестра амплитудные
спектры различных музыкальных инструментов
накладываются друг на друга, образуя
то, что мы называем исполнением
музыкального произведения.
днако
каждая нота, взятая на соответствующем
музыкальном инструменте, создает звук,
амплитудный спектр которого, кроме
основной частоты (смотри рисунок),
содержит и ряд других частот. Совокупность
этих дополнительных частот (спектр)
характеризуется тембром данного
музыкального инструмента, отличным от
любого другого инструмента. Взятие
аккорда приводит к еще большему усложнению
спектра, соответствующему содержанию
аккорда. При игре оркестра амплитудные
спектры различных музыкальных инструментов
накладываются друг на друга, образуя
то, что мы называем исполнением
музыкального произведения.
Картину постоянной смены спектра прослушиваемого музыкального фрагмента можно наблюдать и на экране проигрывателя Windows Media при выборе частотной диаграммы. Каждая, вновь взятая комбинация нот приводит к изменению структуры спектра и мощности звучания, что наглядно отображается частотной диаграммой.
Читать онлайн Введение в электронику страница 86

Рис. 30-5.Формирование сигнала пилообразной формы методом сложения его частотных составляющих.
Осциллограф выводит на экран временные характеристики сигналов. Анализатор спектра (рис. 30-6) выводит на экран частотные характеристики сигнала. Анализ частотных характеристик может быть использован для определения влияния цепей на форму сигнала.

Рис. 30-6. Анализатор спектра.
Периодические сигналы — это сигналы, повторяющиеся через определенные промежутки времени. Период сигнала измеряется интервалом времени от любой точки цикла до такой же точки следующего цикла (рис. 30-7).

Рис. 30-7.Период сигнала.
Длительность импульса — это длина импульса по оси времени.

Рис. 30-8.Длительность импульса сигнала.
Скважность — это отношение длительности импульса к его периоду. Скважность может быть представлена как процентное отношение времени существования импульса в течение каждого периода к периоду.

Все импульсы имеют время нарастания и время спада. Время нарастания — это время, требуемое для увеличения импульса от 10 % до 90 % от величины максимальной амплитуды. Время спада — это время, за которое импульс уменьшается от 90 % до 10 % от величины максимальной амплитуды (рис. 30-9).

Рис. 30-9.Время нарастания импульса и время спада импульса измеряются на уровнях 10 % и 90 % от максимальной амплитуды сигнала.
Форма отрицательных и положительных выбросов и «звон», т. е. возникновение высокочастотных затухающих колебаний, показаны на рис. 30–10.

Рис. 30–10.Положительный выброс, отрицательный выброс и «звон».
Положительный выброс наблюдается, когда передний фронт импульса превышает его максимальное значение. Отрицательный выброс имеет место, когда задний фронт импульса превышает его минимальное значение. Оба эти явления наблюдаются при возникновении затухающих колебаний (при ударном возбуждении), и известны, как «звон». Явления эти нежелательны, но существуют вследствие несовершенства цепей.
30-1. Вопросы
1. Дайте определение концепции частотных характеристик.
2. Как конструируются следующие колебания согласно концепции частотных характеристик?
а. Прямоугольные колебания
б. Пилообразные колебания.
3. Что такое периодическое колебание?
4. Что такое скважность?
5. Нарисуйте примеры положительного выброса, отрицательного выброса и «звона» в применении к реальному сигналу.
30-2. ЦЕПИ ФОРМИРОВАНИЯ СИГНАЛА
RC цепь может изменять форму сложных сигналов так, что выходная форма будет совсем не похожа на входную. Величина искажения определяется постоянной времени RC цепи. Тип искажения определяется выходной компонентой, включенной параллельно выходу. Если параллельно выходу включен резистор, то цепь называется дифференцирующей. Дифференцирующая цепь используется в цепях синхронизации, для получения узких импульсов из прямоугольных, а также для получения переключающих импульсов и меток. Если параллельно выходу включен конденсатор, то цепь называется интегрирующей. Интегрирующая цепь используется в цепях формирования сигналов в радио, телевидении, радиолокаторах и в компьютерах.
На рис. 30–11 изображена дифференцирующая цепь.

Рис. 30–11.Дифференцирующая цепь.
Напомним, что сложные сигналы состоят из основной частоты и большого числа гармоник. Когда сложный сигнал поступает на дифференцирующую цепь, она влияет на каждую частоту по разному. Отношение емкостного сопротивления (Хс) к R для каждой гармоники различно. Это приводит к тому, что каждая гармоника сдвигается по фазе и уменьшается по амплитуде в разной степени. В результате исходная форма сигнала искажается. На рис. 30–12 показано, что происходит с сигналом прямоугольной фор- мы, прошедшим дифференцирующую цепь. На рис. 30–13 показано влияние различных постоянных времени RC цепи.

Рис. 30–12. Преобразование сигнала прямоугольной формы на выходе дифференцирующей цепи.

Рис. 30–13. Влияние различных постоянных времени на форму выходного сигнала дифференцирующей цепи.
Интегрирующая цепь подобна дифференцирующей, за исключением того, что параллельно выходу включен конденсатор (рис. 30–14). На рис. 30–15 показано, как изменяется форма прямоугольного сигнала, прошедшего интегрирующую цепь. Интегрирующая цепь искажает сигнал не так, как дифференцирующая.

Рис. 30–14.Интегрирующая цепь.

Рис. 30–15.Преобразование сигнала прямоугольной формы на выходе интегрирующей цепи.
На рис. 30–16 показано влияние различных постоянных времени RC цепи.

Рис. 30–16.Влияние различных постоянных времени на форму выходного сигнала интегрирующей цепи.
Другим типом цепи, изменяющим форму сигнала, является ограничитель сигнала (рис. 30–17). Цепь ограничения может быть использована для обрезания пиков приложенного сигнала, для получения прямоугольного сигнала из синусоидального, для удаления положительных или отрицательных частей сигнала или для поддержания амплитуды входного сигнала на постоянном уровне. Диод смещен в прямом направлении и проводит ток в течение положительного полупериода входного сигнала. В течение отрицательного полупериода входного сигнала диод смещен в обратном направлении и ток не проводит. На рис. 30–17 показана форма сигнала на входе ограничителя: отрицательная часть входного сигнала обрезана. Цепь является, по существу, однополупериодным выпрямителем.

Рис. 30–17.Последовательный диодный ограничитель.

Рис. 30–18.Выходной сигнал при перемене полярности диода в цепи ограничителя.
Используя напряжение смещения можно регулировать величину обрезаемого сигнала. На рис. 30–19 изображен последовательный ограничитель со смещением. Диод не может проводить до тех пор, пока входной сигнал не превысит напряжение смещения.

Рис. 30–19.Последовательный диодный ограничитель со смещением.
На рис. 30–20 показан выходной сигнал, полученный в результате перемены полярности диода и напряжения смещения в последовательном ограничителе.

Рис. 30–20. Выходной сигнал при перемене полярности диода и источника смещения в смещенном последовательном диодном ограничителе.
Цепь параллельного ограничения выполняет те же функции, что и последовательный ограничитель (рис. 30–21). Разница состоит в том, что диод включен параллельно выходу. Эта цепь обрезает отрицательную часть входного сигнала.


 е
должно быть разрывов второго рода
(уходящих в бесконечности ветвей),
е
должно быть разрывов второго рода
(уходящих в бесконечности ветвей),