Сила лоренца википедия: Сила Лоренца — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Сила Лоренца — Википедия

Материал из Википедии — свободной энциклопедии

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v {\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E {\displaystyle \mathbf {E} } и магнитного B {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F = q ( E + [ v × B ] ) . {\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца

[3].

Уравнение (единицы СИ)

Заряженная частица

$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$

Сила F {\displaystyle \mathbf {F} } , действующая на частицу с электрическим зарядом q {\displaystyle q} , движущуюся со скоростью v {\displaystyle \mathbf {v} } , во внешнем электрическом E {\displaystyle \mathbf {E} } и магнитном B {\displaystyle \mathbf {B} } полях, такова:

F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где × {\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F ( r , t , q ) = q E ( r , t ) + q r ˙ × B ( r , t ) , {\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r {\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t {\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

d F = d q ( E + v × B ) , {\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где d F {\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент d q {\displaystyle dq} .

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

F μ = q F ν μ u ν , {\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

где F μ {\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q {\displaystyle q} — заряд частицы, F ν μ {\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, u ν {\displaystyle u_{\nu }} — 4-скорость.

Частные случаи

$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r {\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
m v 2 r = \| q \| c v B ⇒ r = c m \| q \| ⋅ v B {\displaystyle {mv^{2} \over r}={\|q\| \over c}vB\Rightarrow r={cm \over \|q\|}\cdot {v \over B}}	m v 2 r = \| q \| v B ⇒ r = m \| q \| ⋅ v B {\displaystyle {mv^{2} \over r}=\|q\|vB\Rightarrow r={m \over \|q\|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ } , намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ } :

СГС	СИ
ω = \| q \| B m c {\displaystyle \omega ={\|q\|B \over mc}}	ω = \| q \| B m {\displaystyle \omega ={\|q\|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B {\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ } , то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ } :

СГС	СИ
r = m c \| q \| ⋅ v sin ⁡ α B {\displaystyle r={mc \over \|q\|}\cdot {v\sin \alpha \over B}} , h = 2 π B ⋅ m c \| q \| ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {mc \over \|q\|}\cdot v\cos \alpha }	r = m \| q \| ⋅ v sin ⁡ α B {\displaystyle r={m \over \|q\|}\cdot {v\sin \alpha \over B}} , h = 2 π B ⋅ m \| q \| ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {m \over \|q\|}\cdot v\cos \alpha }

Использование

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$

Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

См. также

Примечания

↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренца — Википедия
Материал из Википедии — свободной энциклопедии
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v {\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E {\displaystyle \mathbf {E} } и магнитного B {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:
F = q ( E + [ v × B ] ) . {\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца

[3].
Уравнение (единицы СИ)
Заряженная частица
$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$
Сила F {\displaystyle \mathbf {F} } , действующая на частицу с электрическим зарядом q {\displaystyle q} , движущуюся со скоростью v {\displaystyle \mathbf {v} } , во внешнем электрическом E {\displaystyle \mathbf {E} } и магнитном B {\displaystyle \mathbf {B} } полях, такова:

F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где × {\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
F ( r , t , q ) = q E ( r , t ) + q r ˙ × B ( r , t ) , {\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r {\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t {\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
d F = d q ( E + v × B ) , {\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где d F {\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент d q {\displaystyle dq} .
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
F μ = q F ν μ u ν , {\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
где F μ {\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q {\displaystyle q} — заряд частицы, F ν μ {\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, u ν {\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r {\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
СГС СИ
m v 2 r = | q | c v B ⇒ r = c m | q | ⋅ v B {\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}
m v 2 r = | q | v B ⇒ r = m | q | ⋅ v B {\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ } , намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ } :
СГС СИ
ω = | q | B m c {\displaystyle \omega ={|q|B \over mc}}
ω = | q | B m {\displaystyle \omega ={|q|B \over m}}
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B {\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ } , то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ } :
СГС СИ
r = m c | q | ⋅ v sin ⁡ α B {\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m c | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }
r = m | q | ⋅ v sin ⁡ α B {\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$ Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
См. также
Примечания
↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренца — Википедия. Что такое Сила Лоренца
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v {\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E {\displaystyle \mathbf {E} } и магнитного B {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:
F = q ( E + [ v × B ] ) . {\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].
Уравнение (единицы СИ)
Заряженная частица
$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$
Сила F {\displaystyle \mathbf {F} } , действующая на частицу с электрическим зарядом q {\displaystyle q} , движущуюся со скоростью v {\displaystyle \mathbf {v} } , во внешнем электрическом E {\displaystyle \mathbf {E} } и магнитном B {\displaystyle \mathbf {B} } полях, такова:
F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}
где × {\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
F ( r , t , q ) = q E ( r , t ) + q r ˙ × B ( r , t ) , {\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}
где r {\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t {\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
d F = d q ( E + v × B ) , {\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}
где d F {\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент d q {\displaystyle dq} .
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
F μ = q F ν μ u ν , {\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
где F μ {\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q {\displaystyle q} — заряд частицы, F ν μ {\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, u ν {\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r {\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
СГС СИ
m v 2 r = | q | c v B ⇒ r = c m | q | ⋅ v B {\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}
m v 2 r = | q | v B ⇒ r = m | q | ⋅ v B {\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ } , намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ } :
СГС СИ
ω = | q | B m c {\displaystyle \omega ={|q|B \over mc}}
ω = | q | B m {\displaystyle \omega ={|q|B \over m}}
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B {\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ } , то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ } :
СГС СИ
r = m c | q | ⋅ v sin ⁡ α B {\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m c | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }
r = m | q | ⋅ v sin ⁡ α B {\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$ Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
См. также
Примечания
↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Сила Лоренца — Википедия. Что такое Сила Лоренца
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v {\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E {\displaystyle \mathbf {E} } и магнитного B {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:
F = q ( E + [ v × B ] ) . {\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].
Уравнение (единицы СИ)
Заряженная частица
$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$
Сила F {\displaystyle \mathbf {F} } , действующая на частицу с электрическим зарядом q {\displaystyle q} , движущуюся со скоростью v {\displaystyle \mathbf {v} } , во внешнем электрическом E {\displaystyle \mathbf {E} } и магнитном B {\displaystyle \mathbf {B} } полях, такова:
F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}
где × {\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
F ( r , t , q ) = q E ( r , t ) + q r ˙ × B ( r , t ) , {\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}
где r {\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t {\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
d F = d q ( E + v × B ) , {\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}
где d F {\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент d q {\displaystyle dq} .
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
F μ = q F ν μ u ν , {\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
где F μ {\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q {\displaystyle q} — заряд частицы, F ν μ {\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, u ν {\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r {\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
СГС СИ
m v 2 r = | q | c v B ⇒ r = c m | q | ⋅ v B {\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}
m v 2 r = | q | v B ⇒ r = m | q | ⋅ v B {\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ } , намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ } :
СГС СИ
ω = | q | B m c {\displaystyle \omega ={|q|B \over mc}}
ω = | q | B m {\displaystyle \omega ={|q|B \over m}}
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B {\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ } , то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ } :
СГС СИ
r = m c | q | ⋅ v sin ⁡ α B {\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m c | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }
r = m | q | ⋅ v sin ⁡ α B {\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$ Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
См. также
Примечания
↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Сила Лоренца — Википедия
Материал из Википедии — свободной энциклопедии
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v {\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E {\displaystyle \mathbf {E} } и магнитного B {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:
F = q ( E + [ v × B ] ) . {\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].
Уравнение (единицы СИ)
Заряженная частица
$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$
Сила F {\displaystyle \mathbf {F} } , действующая на частицу с электрическим зарядом q {\displaystyle q} , движущуюся со скоростью v {\displaystyle \mathbf {v} } , во внешнем электрическом E {\displaystyle \mathbf {E} } и магнитном B {\displaystyle \mathbf {B} } полях, такова:
F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}
где × {\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
F ( r , t , q ) = q E ( r , t ) + q r ˙ × B ( r , t ) , {\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}
где r {\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t {\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
d F = d q ( E + v × B ) , {\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}
где d F {\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент d q {\displaystyle dq} .
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
F μ = q F ν μ u ν , {\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
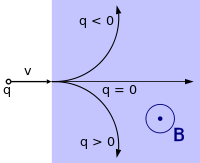где F μ {\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q {\displaystyle q} — заряд частицы, F ν μ {\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, u ν {\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r {\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
СГС СИ
m v 2 r = | q | c v B ⇒ r = c m | q | ⋅ v B {\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}
m v 2 r = | q | v B ⇒ r = m | q | ⋅ v B {\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ } , намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ } :
СГС СИ
ω = | q | B m c {\displaystyle \omega ={|q|B \over mc}}
ω = | q | B m {\displaystyle \omega ={|q|B \over m}}
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B {\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ } , то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ } :
СГС СИ
r = m c | q | ⋅ v sin ⁡ α B {\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m c | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }
r = m | q | ⋅ v sin ⁡ α B {\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}} ,
h = 2 π B ⋅ m | q | ⋅ v cos ⁡ α {\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$ Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
См. также
Примечания
↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Сила Лоренца — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью <math>\mathbf{v}</math> заряд <math>q\ </math> лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического <math>\mathbf{E}</math> и магнитного <math>\mathbf{B}</math> полей. В Международной системе единиц (СИ) выражается как:
<math>\mathbf{F}=q\left(\mathbf{E}+[\mathbf{v}\times\mathbf{B}]\right)</math>
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].
Уравнение (единицы СИ)
Заряженная частица
Сила F, действующая на частицу с электрическим зарядом q, движущуюся со скоростью v, во внешнем электрическом E и магнитном B полях, такова:
<math>\mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B})</math>
где × — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
<math>\mathbf{F}(\mathbf{r},t,q) = q \mathbf{E}(\mathbf{r},t) + q \mathbf{\dot{r}} \times \mathbf{B}(\mathbf{r},t) ,</math>
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
<math>d\mathbf{F} = dq\left(\mathbf{E} + \mathbf{v} \times \mathbf{B}\right)</math>
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
<math>\mathcal{F}^\mu = qF^{\nu \mu} u_\nu</math>, где <math>\mathcal{F}^\mu</math> — 4-сила, q — заряд частицы, <math>F^{\nu \mu}</math> — тензор электромагнитного поля, <math>u_\nu</math> — 4-скорость.
Частные случаи
В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса <math>r</math> (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
СГС СИ
<math>{mv^2\over r} = {|q|\over c}vB\Rightarrow r = {cm\over |q|}\cdot{v\over B}</math>
<math>{mv^2\over r} = |q|vB\Rightarrow r = {m\over |q|}\cdot{v\over B}</math>
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости <math>v\ </math>, намного меньшей скорости света, круговая частота <math>\omega\ </math> не зависит от <math>v\ </math>:
СГС СИ
<math>\omega ={|q|B\over mc}</math>
<math>\omega = {|q|B\over m}</math>
Если заряженная частица движется в магнитном поле так, что вектор скорости <math>v\ </math> составляет с вектором магнитной индукции <math>\mathbf{B}</math> угол <math>\alpha\ </math>, то траекторией движения частицы является винтовая линия с радиусом <math>r\ </math> и шагом винта <math>h\ </math>:
СГС СИ
<math>r = {mc\over |q|}\cdot{v\sin\alpha\over B}</math>,
<math>h = {2\pi\over B}\cdot{mc\over |q|}\cdot v\cos\alpha</math>
<math>r = {m\over |q|}\cdot{v\sin\alpha\over B}</math>,
<math>h = {2\pi\over B}\cdot{m\over |q|}\cdot v\cos\alpha</math>
Использование
См. также
Напишите отзыв о статье «Сила Лоренца»
Ссылки
[www.youtube.com/watch?v=UpC2WndKKGk Сила Лоренца, учебный фильм]
Примечания
↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. [vivovoco.astronet.ru/VV/BOOKS/HEAVISIDE/CONTENT.HTM Оливер Хевисайд]. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Отрывок, характеризующий Сила Лоренца
Когда Пьер, обежав дворами и переулками, вышел назад с своей ношей к саду Грузинского, на углу Поварской, он в первую минуту не узнал того места, с которого он пошел за ребенком: так оно было загромождено народом и вытащенными из домов пожитками. Кроме русских семей с своим добром, спасавшихся здесь от пожара, тут же было и несколько французских солдат в различных одеяниях. Пьер не обратил на них внимания. Он спешил найти семейство чиновника, с тем чтобы отдать дочь матери и идти опять спасать еще кого то. Пьеру казалось, что ему что то еще многое и поскорее нужно сделать. Разгоревшись от жара и беготни, Пьер в эту минуту еще сильнее, чем прежде, испытывал то чувство молодости, оживления и решительности, которое охватило его в то время, как он побежал спасать ребенка. Девочка затихла теперь и, держась ручонками за кафтан Пьера, сидела на его руке и, как дикий зверек, оглядывалась вокруг себя. Пьер изредка поглядывал на нее и слегка улыбался. Ему казалось, что он видел что то трогательно невинное и ангельское в этом испуганном и болезненном личике.
На прежнем месте ни чиновника, ни его жены уже не было. Пьер быстрыми шагами ходил между народом, оглядывая разные лица, попадавшиеся ему. Невольно он заметил грузинское или армянское семейство, состоявшее из красивого, с восточным типом лица, очень старого человека, одетого в новый крытый тулуп и новые сапоги, старухи такого же типа и молодой женщины. Очень молодая женщина эта показалась Пьеру совершенством восточной красоты, с ее резкими, дугами очерченными черными бровями и длинным, необыкновенно нежно румяным и красивым лицом без всякого выражения. Среди раскиданных пожитков, в толпе на площади, она, в своем богатом атласном салопе и ярко лиловом платке, накрывавшем ее голову, напоминала нежное тепличное растение, выброшенное на снег. Она сидела на узлах несколько позади старухи и неподвижно большими черными продолговатыми, с длинными ресницами, глазами смотрела в землю. Видимо, она знала свою красоту и боялась за нее. Лицо это поразило Пьера, и он, в своей поспешности, проходя вдоль забора, несколько раз оглянулся на нее. Дойдя до забора и все таки не найдя тех, кого ему было нужно, Пьер остановился, оглядываясь.
Фигура Пьера с ребенком на руках теперь была еще более замечательна, чем прежде, и около него собралось несколько человек русских мужчин и женщин.
– Или потерял кого, милый человек? Сами вы из благородных, что ли? Чей ребенок то? – спрашивали у него.
Пьер отвечал, что ребенок принадлежал женщине и черном салопе, которая сидела с детьми на этом месте, и спрашивал, не знает ли кто ее и куда она перешла.
– Ведь это Анферовы должны быть, – сказал старый дьякон, обращаясь к рябой бабе. – Господи помилуй, господи помилуй, – прибавил он привычным басом.
– Где Анферовы! – сказала баба. – Анферовы еще с утра уехали. А это либо Марьи Николавны, либо Ивановы.
– Он говорит – женщина, а Марья Николавна – барыня, – сказал дворовый человек.
– Да вы знаете ее, зубы длинные, худая, – говорил Пьер.
– И есть Марья Николавна. Они ушли в сад, как тут волки то эти налетели, – сказала баба, указывая на французских солдат.
– О, господи помилуй, – прибавил опять дьякон.
– Вы пройдите вот туда то, они там. Она и есть. Все убивалась, плакала, – сказала опять баба. – Она и есть. Вот сюда то.
Но Пьер не слушал бабу. Он уже несколько секунд, не спуская глаз, смотрел на то, что делалось в нескольких шагах от него. Он смотрел на армянское семейство и двух французских солдат, подошедших к армянам. Один из этих солдат, маленький вертлявый человечек, был одет в синюю шинель, подпоясанную веревкой. На голове его был колпак, и ноги были босые. Другой, который особенно поразил Пьера, был длинный, сутуловатый, белокурый, худой человек с медлительными движениями и идиотическим выражением лица. Этот был одет в фризовый капот, в синие штаны и большие рваные ботфорты. Маленький француз, без сапог, в синей шипели, подойдя к армянам, тотчас же, сказав что то, взялся за ноги старика, и старик тотчас же поспешно стал снимать сапоги. Другой, в капоте, остановился против красавицы армянки и молча, неподвижно, держа руки в карманах, смотрел на нее.
– Возьми, возьми ребенка, – проговорил Пьер, подавая девочку и повелительно и поспешно обращаясь к бабе. – Ты отдай им, отдай! – закричал он почти на бабу, сажая закричавшую девочку на землю, и опять оглянулся на французов и на армянское семейство. Старик уже сидел босой. Маленький француз снял с него последний сапог и похлопывал сапогами один о другой. Старик, всхлипывая, говорил что то, но Пьер только мельком видел это; все внимание его было обращено на француза в капоте, который в это время, медлительно раскачиваясь, подвинулся к молодой женщине и, вынув руки из карманов, взялся за ее шею.
Красавица армянка продолжала сидеть в том же неподвижном положении, с опущенными длинными ресницами, и как будто не видала и не чувствовала того, что делал с нею солдат.
Пока Пьер пробежал те несколько шагов, которые отделяли его от французов, длинный мародер в капоте уж рвал с шеи армянки ожерелье, которое было на ней, и молодая женщина, хватаясь руками за шею, кричала пронзительным голосом.
– Laissez cette femme! [Оставьте эту женщину!] – бешеным голосом прохрипел Пьер, схватывая длинного, сутоловатого солдата за плечи и отбрасывая его. Солдат упал, приподнялся и побежал прочь. Но товарищ его, бросив сапоги, вынул тесак и грозно надвинулся на Пьера.
– Voyons, pas de betises! [Ну, ну! Не дури!] – крикнул он.
Пьер был в том восторге бешенства, в котором он ничего не помнил и в котором силы его удесятерялись. Он бросился на босого француза и, прежде чем тот успел вынуть свой тесак, уже сбил его с ног и молотил по нем кулаками. Послышался одобрительный крик окружавшей толпы, в то же время из за угла показался конный разъезд французских уланов. Уланы рысью подъехали к Пьеру и французу и окружили их. Пьер ничего не помнил из того, что было дальше. Он помнил, что он бил кого то, его били и что под конец он почувствовал, что руки его связаны, что толпа французских солдат стоит вокруг него и обыскивает его платье.
Гендрік Антон Лоренц — Вікіпедія
Ге́ндрік Анто́н Ло́ренц
нід. Hendrik Antoon Lorentz
Ім’я при народженні нід. Hendrik Antoon Lorentz
Народився 18 липня 1853(1853-07-18)^[1]^[2]^[…]
Арнем, Гелдерланд, Нідерланди, Нідерланди^[4]^[5]
Помер 4 лютого 1928(1928-02-04)^[4]^[2]^[…] (74 роки)
Гарлем, Нідерланди, Нідерланди^[4]
Поховання Algemene Begraafplaats Kleverlaan^d
Громадянство Нідерланди
Діяльність куратор, фізик-теоретик, професор, математик, фізик, викладач університету
Alma mater Лейденський університет
Сфера інтересів фізика
Заклад Лейденський університет
Посада rector magnificus of Leiden University^d
Науковий ступінь докторський ступінь^[5]
Науковий керівник Pieter Rijke^d
Відомі учні Adriaan Fokker^d
Член Лондонське королівське товариство, Академія наук СРСР, Петербурзька академія наук, Французька академія наук, Шведська королівська академія наук, Нідерландська королівська академія наук, Американська академія мистецтв і наук, Російська академія наук, Прусська академія наук, Національна академія наук Італії^d, Баварська академія наук, Академія наук Турина^d і Національна академія наук США
Відомий завдяки: сила Лоренца
У шлюбі з Aletta Lorentz-Kaiser^d
Діти Geertruida de Haas-Lorentz^d
Нагороди Нобелівська премія з фізики (1902)
Медаль Коплі
Роботи у Вікіджерелах
Гендрік Антон Лоренц у Вікісховищі
У Вікіпедії є статті про інших людей з іменем Гендрік. У Вікіпедії є статті про інших людей із таким прізвищем: Лоренц.
Ге́ндрік Анто́н Ло́ренц (нід. Hendrik Antoon Lorentz; 18 липня 1853, Арнем — 4 лютого 1928, Гарлем, Нідерланди) — нідерландський фізик. Створив класичну електронну теорію, за допомогою якої пояснив багато електричних та оптичних явищ, в тому числі ефект Зеемана. Розробив електродинаміку рухомих середовищ. Вивів перетворення, названі його іменем. Г. Лоренц близько підійшов до створення теорії відносності. Лауреат нобелівської премії з фізики (1902, спільно з П. Зеєманом)
Нідерландський фізик народився 18 липня 1853 року в місті Арнемі, в родині дрібного підприємця, що утримував дитячі ясла. Предки Лоренца походили з прирейнської Німеччини. Головною діяльністю їх було землеробство. Жили вони в достатку, який тримався на їхній праці. Мати Лоренца, Гертруда, уроджена ван Гінкель, виросла в Ренсвуді (провінція Утрехт). ЇЇ першим чоловіком був Якоб Янссен, який рано помер. На третьому році вдівства вона вийшла заміж за Геррита Фредеріка Лоренца. Від Янсена у неї був син Гендрік Ян Якоб, а від Лоренца — двоє синів. Старшим сином Лоренца був Гендрік Антон, другий, молодший син, скоро помер.

Початкову та середню освіту Гендрік здобув у місцевій школі. У 1857 р. Гендрік і його старший брат залишилися, втративши матір, під опікою вітчима, а через 4 роки в будинку з’явилася мачуха Луберта Гупкес. До цієї жінки Гендрік на все життя зберіг найтепліші почуття. Маленький Лоренц, як здавалося, дуже відставав у розвитку. Коли його зведений брат уже пішов у школу, Гендрік міг лише із зусиллям вимовити «до побачення».

У шість років Гендріка віддали до школи, яка вважалася найкращою в Арнемі, і незабаром він став першим у своєму класі. У 1866 р. він перейшов у Вищу громадянську школу, яка тільки що відкрилася. І тут він вчився блискуче. Залучення до наук було захоплюючим; а впевненість у своїх силах породжувала наступні успіхи. Володіючи винятковою пам’яттю, Гендрік Лоренц, крім всіх шкільних справ, встиг вивчити англійську, французьку, і німецьку мови, а перед вступом до університету ще грецьку і латину (до старості він міг складати вірші з латини).
З 1870 р. продовжує навчання в Лейденському університеті, відвідує лекції відомого на той час професора астрономії Фредеріка Кайзера. І тут сталася подія, яка визначила весь подальший шлях Лоренца в науці: він познайомився з працями Джеймса Клерка Максвелла. До того часу «Трактат про електрику» був зрозумілий лише небагатьом фізикам. Більше того, коли юний Гендрік попросив паризького перекладача «Трактату…» пояснити йому фізичний зміст рівнянь Максвелла, він почув у відповідь, що «… жодного фізичного сенсу ці рівняння не мають і зрозуміти їх не можна; їх слід розглядати як чисто математичну абстракцію».
За 2 роки Лоренц дістає звання бакалавра наук із фізики та математики й повертається до Арнему учителем місцевої середньої школи. 1873 р. успішно складає екзамени на присвоєння докторського ступеня й досліджує теорію відбивання та заломлення світла, а 1875 р. захищає в Лейденському університеті докторську дисертацію з цієї проблеми. 1878 р. Лоренц переїздить з Арнема до Лейдена й працює на кафедрі теоретичної фізики університету, одній з перших у Європі, продовжуючи вивчати оптичні явища.
У 1881 р. він одружується з племінницею професора астрономії Кайзера Аллеттою Кайзер. У них народилося четверо дітей, проте одна дитина померла немовлям.
Продовжуючи працювати в університеті, Лоренц 1892 р. формулює теорію електронів, публікує роботи з розщеплення спектральних ліній у магнітному полі. 1896 р. колега Гендріка Лоренца Пітер Зеєман підтвердив його теоретичне положення про поляризацію світла. У 1900 році на Міжнародному конгресі фізиків у Парижі Лоренц виступив з доповіддю про магнітооптичні явища. Його друзями стали Больцман, Він, Пуанкаре, Рентген, Планк і інші знамениті фізики. У 1902 році Лоренц і його колега Пітер Земан стають Нобелівськими лауреатами.
… ми сподіваємося, що електронна гіпотеза, оскільки вона прийнята в різних розділах фізики, веде до загальної теорії, яка охопить багато областей фізики і хімії. Можливо, що на цьому довгому шляху вона сама повністю перебудується
— Гендрік Антон Лоренц, при врученні Нобелівської премії
.
Через чотири роки він виступив з основоположною статтею «Електромагнітні явища в системі, що рухається зі швидкістю, меншою за швидкість світла». Лоренц вивів формули, що зв’язують між собою просторові координати і моменти часу у двох різних інерційних системах відліку (Перетворення Лоренца). Вченому вдалося отримати формулу залежності маси електрона від швидкості.
Особливо потрібно відзначити участь Гендрік Лоренца в підготовці та проведенні «I Міжнародного конгресу Сольвеївських фізиків». Він відбувся у 1911 році в Брюсселі, і був присвячений проблемі «Випромінювання і кванти». У його роботі брали участь 23 фізика, головував Лоренц.
Нас не покидає відчуття, що ми перебуваємо в глухому куті; старі теорії виявляються усе менш здатними проникнути в пітьму, що оточує нас з усіх боків
— Гендрік Антон Лоренц, із вступного слова
Він ставить перед фізиками завдання створити нову механіку: «Ми будемо дуже щасливі, якщо нам вдасться хоч трохи наблизитися до тієї майбутньої механіки, про яку йде мова».
У 1912 році Лоренц подає у відставку з Лейденського університету, проте раз на тиждень читає лекції й виконує обов’язки секретаря Нідерландського наукового товариства. Через рік переїздить до Гарлема, де працює директором фізичного кабінету Тейлерівського музею. З 1923 р. входить до складу міжнародної комісії з інтелектуальної співпраці Ліги Націй, а з 1925 р. очолює її.
Лоренц любив свою країну і писав:
Я щасливий, що належу до нації, надто маленької, щоб здійснювати великі дурниці.
Він користувався величезною повагою і любов’ю, як у себе на батьківщині, так і скрізь, де його знали. Святкування п’ятдесятиріччя з дня захисту ним докторської дисертації, що почалося 11 грудня 1925 вилилося в загальнонаціональне свято.
У 1927 році, Гендрік Лоренц писав дочці, що сподівається «завершити ще кілька наукових справ», але тут же додав: «Втім, те, що є — теж добре: за плечима у мене — велика і чудова життя». Вчений зберігав інтелектуальну активність до самої смерті. Помер він 4 лютого 1928 р. у віці 75 років у Гарлемі.
Гендрік Лоренц розвинув електромагнітну теорію світла і електронну теорію матерії, а також сформулював самоузгоджену теорію електрики, магнетизму і світла. З іменем цього ученого пов’язана відома з шкільного курсу фізики сила Лоренца (це поняття він розвинув в 1895 р.) — сила, що діє на заряд, рухомий в магнітному полі.
Розвинув теорію про перетворення стану рухомого тіла, одним з результатів якої було так зване скорочення Лоренца-Фітцжеральда (Георг Фітцжеральд — ірландський фізик), що описує зменшення довжини об’єкта при поступальному русі. Отримані в рамках цієї теорії перетворення Лоренца є найважливішим внеском в розвиток теорії відносності.
Пояснив феномен, відомого як ефект Зеемана, за який отримав Нобелівську премію.
Гендрік Лоренц був почесним доктором Паризького й Кембріджського університетів, членом Лондонського королівського й Німецького фізичного товариств.
Лорентц Г. А. Теория электромагнитного поля. — — : ГТТИ, 1933. — 172 с.
Лорентц Г. А. Статистические теории в термодинамике. — — : ГТТИ, 1935. — 156 с.
Лоренц Г. А., Пуанкаре А., Эйнштейн А., Минковский Г. Принцип относительности. — — : ОНТИ НКТП СССР, 1935. — 388 с.
Лоренц Г. А. Лекции по термодинамике. — — : ГИТТЛ, 1946. — 156 с.
Лорентц Г. А. Теория электронов и ее применение к явлениям света и теплового излучения. — — : ГИТТЛ, 1956. — 472 с.
Лоренц Г. А. Старые и новые проблемы физики. — : Наука, 1970. — 370 с.
Fuerza de Lorentz — Wikipedia, la enciclopedia libre
Trayectoria bajo la fuerza de Lorentz de una partícula cargada en un campo magnético constante, según el signo de la carga eléctrica. Fuerza sobre una partícula cargada. Fuerza sobre una corriente.
En física, la fuerza de Lorentz es la fuerza ejercida por el campo electromagnético que recibe una partícula cargada o una corriente eléctrica.
Forma clásica [редактор]
Para una partícula sometida a un campo eléctrico combinado con un campo magnético, la fuerza electromagnética total o fuerza de Lorentz sobre esa partícula viene dada por:
F → знак равно q ( v → × B → + E → ) , {\ displaystyle {\ vec {F}} = q ({\ vec {v}} \ times {\ vec {B}} + {\ vec {E}}),}
донде v {\ displaystyle \ mathbf {v}} es la velocidad de la carga, E {\ displaystyle \ mathbf {E}} es el vectortensidad de campo eléctrico y B {\ displaystyle \ mathbf {B}} es el vector Inducción Magnética.La expresión siguiente está relacionada con la fuerza de Laplace o fuerza sobre un hilo dioctor por el que circa corriente:
F знак равно ∫ L я ⋅ d л × B {\ displaystyle \ mathbf {F} = \ int _ {L} I \ cdot d \ mathbf {l} \ times \ mathbf {B}}
донде L {\ Displaystyle L \,} es la продольный проводник, я {\ Displaystyle I \,} es latensidad de corriente y B {\ displaystyle \ mathbf {B}} la Inducción Magnética.A pesar de ser una conscuencia directa de ella, esta última expresión históricamente se encontró antes que la anterior, debido a que las corrientes eléctricas se manejaban antes de que estuviese Claro si la carque eléctrica era constitas caroñeñóñóíîé
Formas alternativas [редактор]
Форма интегральная [редактор]
Si los campos eléctrico E {\ displaystyle \ mathbf {E}} y magnético B {\ displaystyle \ mathbf {B}} Нет изменений в сыновьях в отношении присутствия в плотностях электрического каркаса ρ y la densidad de corriente J {\ displaystyle \ mathbf {J}} , y las dos últimas no son modificadas por dichos campos, la fuerza de Lorentz se puede expresar como:
ж знак равно ∫ V ( ρ E + J × B ) d V {\ Displaystyle \ mathbf {е} = \ int _ {V} (\ rho \ mathbf {E} + \ mathbf {J} \ times \ mathbf {B}) \ dV}
Como en general esto no es cierto, la resolución de las fuerzas resultantes Requiere el uso de consideraciones energéticas y la resolución de ecuaciones diferenciales Derivadas de las ecuaciones de Maxwell.
Forma tensorial [редактор]
En teoría de la relatividad conviene escribir las leyes físicas en forma explicitamente tenorial. Eso impla que las magnitude que se transforman vectorialmente como, por ejemplo, la velocidad o la densidad de corriente, deben ser submitadas por cuadrivectores. La fuerza de Lorentz escrita en forma explicitamente tenorial es:
ж α знак равно ∑ β знак равно 0 3 q F α β ты β {\ displaystyle f _ {\ alpha} = \ sum _ {\ beta = 0} ^ {3} qF _ {\ alpha \ beta} u ^ {\ beta} \,} (expresión tenorial relativista)
Донде:
( ж α ) , ( ж 0 , ж 1 , ж 2 , ж 3 ) знак равно ( ж → ⋅ v → / c , ж Икс , ж y , ж z ) {\ displaystyle (е _ {\ альфа}), \ quad (f_ {0}, f_ {1}, f_ {2}, f_ {3}) = ({\ vec {f}} \ cdot {\ vec {v }} / c, f_ {x}, f_ {y}, f_ {z})} сын лас компонентов дель cuadrivector fuerza.
( ты β ) , ( ты 0 , ты 1 , ты 2 , ты 3 ) знак равно γ ( c , v Икс , v y , v z ) {\ displaystyle (u ^ {\ beta}), \ quad (u_ {0}, u_ {1}, u_ {2}, u_ {3}) = \ gamma (c, v_ {x}, v_ {y} , v_ {z})} сын лас-компонентес-дель-куадривелосидад, сьендо γ знак равно 1 1 — ( v Икс 2 + v y 2 + v z 2 ) / c 2 {\ displaystyle \ gamma = {\ frac {1} {\ sqrt {1- (v_ {x} ^ {2} + v_ {y} ^ {2} + v_ {z} ^ {2}) / c ^ { 2}}}}} Эль фактор де Лоренца.
( F α β ) {\ Displaystyle (F _ {\ альфа \ бета}) \,} son las components del tensor de campo electromagnético cuyas components se relacionan con la parte eléctrica y magnética del campo así:
F знак равно ( F 00 F 01 F 02 F 03 F 01 F 11 F 12 F 13 F 02 F 21 год F 22 F 23 F 03 F 31 год F 32 F 33 ) знак равно ( 0 E Икс / c E y / c E z / c — E Икс / c 0 B z — B y — E y / c — B z 0 B Икс — E z / c B y — B Икс 0 ) {\ displaystyle \ mathbf {F} = {\ begin {pmatrix} F_ {00} & F_ {01} & F_ {02} & F_ {03} \\ F_ {01} & F_ {11} & F_ {12} & F_ {13} \ \ F_ {02} & F_ {21} & F_ {22} & F_ {23} \\ F_ {03} & F_ {31} & F_ {32} & F_ {33} \ end {pmatrix}} = {\ begin {pmatrix} 0 & E_ { x} / c & E_ {y} / c & E_ {z} / c \\ — E_ {x} / c & 0 & B_ {z} & — B_ {y} \\ — E_ {y} / c & -B_ {z} & 0 & B_ {x} \\ — E_ {z} / c & B_ {y} & — B_ {x} & 0 \ end {pmatrix}}}
Fuerza de Lorentz y tercera ley de Newton [редактор]
La fuerza magnética que se ejercen dos partículas en movimiento no Satisface el Principio de Acción-reacción o tercera ley de Newton, es decir, la fuerza ejercida por la primera partícula sobre la segunda no es igual a la poríza ejerca Partica la primera.^[1] Esto se puede comprobar por cálculo directo considerando dos cargas puntuales. La fuerza de la partícula 1 sobre la partícula 2 es, utilizando la Ley de Biot-Savart:
F 12 знак равно q 2 v 2 × B 1 знак равно μ q 2 q 1 4 π ( v 2 × ( v 1 × ( р 2 — р 1 ) ) ) d 3 {\ displaystyle \ mathbf {F} _ {12} = q_ {2} \ mathbf {v} _ {2} \ times \ mathbf {B} _ {1} = {\ frac {\ mu q_ {2} q_ { 1}} {4 \ pi}} {\ frac {\ left (\ mathbf {v} _ {2} \ times (\ mathbf {v} _ {1} \ times (\ mathbf {r} _ {2}) — \ mathbf {r} _ {1})) \ right)} {d ^ {3}}}}
Donde los р я {\ Displaystyle \ mathbf {r} _ {я}} сын лос-валорес-де-posición respectivos, v я {\ Displaystyle \ mathbf {v} _ {я}} las velocidades lineales respectivas, q _i las cargas respectivas, d la distancia entre las dos partículas y B я {\ displaystyle \ mathbf {B} _ {i}} los campos magnéticos.Análogamente la fuerza de la partícula 2 sobre la partícula 1 es:
F 21 год знак равно q 1 v 1 × B 2 знак равно μ q 2 q 1 4 π ( v 1 × ( v 2 × ( р 1 — р 2 ) ) ) d 3 {\ displaystyle \ mathbf {F} _ {21} = q_ {1} \ mathbf {v} _ {1} \ times \ mathbf {B} _ {2} = {\ frac {\ mu q_ {2} q_ { 1}} {4 \ pi}} {\ frac {\ left (\ mathbf {v} _ {1} \ times (\ mathbf {v} _ {2} \ times (\ mathbf {r} _ {1} — \ mathbf {r} _ {2})) \ right)} {d ^ {3}}}}
Empleando la Identidad а × ( б × c ) знак равно ( а ⋅ c ) б — ( а ⋅ б ) c {\ displaystyle \ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) = (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b} — (\ mathbf {a } \ cdot \ mathbf {b}) \ mathbf {c}} puede verse que la primera fuerza está en el plano formado por р 1 — р 2 {\ displaystyle \ mathbf {r} _ {1} — \ mathbf {r} _ {2}} y v 1 {\ displaystyle \ mathbf {v} _ {1}} que la segunda fuerza está en el plano formado por р 1 — р 2 {\ displaystyle \ mathbf {r} _ {1} — \ mathbf {r} _ {2}} y v 2 {\ displaystyle \ mathbf {v} _ {2}} .
Véase también [редактор]
Ссылки [редактор]
↑ Дж. Р. Тейлор, 2005, гл. 1.
Библиография [редактор]
Тейлор, Джон Роберт (2005). Классическая механика (en inglés). Книги университетских наук.
Enlaces externos [редактор]
Animaciones y simulaciones [редактировать]
.
ფაილი: Lorentz force.svg — ვიკიპედია
Deutsch: Lorentz force. Meine rechte Hand, die die Rechte-Hand-Regel erklärt. Denkt euch Vektorpfeile über a, b, c / x, y, z (der Gimp ist zu unfähig für TeX-Formatierung).
l, B, F stehen für die Formel
F → знак равно я ( л → × B → ) {\ displaystyle {\ vec {F}} = я ({\ vec {l}} \ times {\ vec {B}})} ,
die Kraft F, die auf einen stromdurchflossenen Leiter l ausgeübt wird, wenn auf ihn ein B-Feld einwirkt — ein klassischer Fall der Rechte-Hand-Regel. Английский язык: Сила Лоренца. Эта диаграмма иллюстрирует поведение заряженной частицы q , движущейся со скоростью v в магнитном поле B . Последний ориентирован за пределы страницы, на что указывает точка в круге. Частица ускоряется силой Лоренца, поведение которой определяется формулой:
F знак равно q E + q c [ v × B ] {\ displaystyle F = qE + {\ frac {q} {c}} \ left [v \ times B \ right]}
где F — вектор силы, E — электрическое поле, а c — скорость света.Символ × представляет математический оператор curl. Направление искривленного пути электрона определяется знаком его заряда, который изменяет знак v × B в формуле выше. .
Ficheru: Lorentz force.svg — Wikipedia
Deutsch: Lorentz force. Meine rechte Hand, die die Rechte-Hand-Regel erklärt. Denkt euch Vektorpfeile über a, b, c / x, y, z (der Gimp ist zu unfähig für TeX-Formatierung).
l, B, F stehen für die Formel
F → знак равно я ( л → × B → ) {\ displaystyle {\ vec {F}} = я ({\ vec {l}} \ times {\ vec {B}})} ,
die Kraft F, die auf einen stromdurchflossenen Leiter l ausgeübt wird, wenn auf ihn ein B-Feld einwirkt — ein klassischer Fall der Rechte-Hand-Regel. Английский язык: Сила Лоренца. Эта диаграмма иллюстрирует поведение заряженной частицы q , движущейся со скоростью v в магнитном поле B . Последний ориентирован за пределы страницы, на что указывает точка в круге. Частица ускоряется силой Лоренца, поведение которой определяется формулой:
F знак равно q E + q c [ v × B ] {\ displaystyle F = qE + {\ frac {q} {c}} \ left [v \ times B \ right]}
где F — вектор силы, E — электрическое поле, а c — скорость света.Символ × представляет математический оператор curl. Направление искривленного пути электрона определяется знаком его заряда, который изменяет знак v × B в формуле выше. .
Dosya: Lorentz force.svg — Vikipedi
Deutsch: Lorentz force. Meine rechte Hand, die die Rechte-Hand-Regel erklärt. Denkt euch Vektorpfeile über a, b, c / x, y, z (der Gimp ist zu unfähig für TeX-Formatierung).
l, B, F stehen für die Formel
F → знак равно я ( л → × B → ) {\ displaystyle {\ vec {F}} = я ({\ vec {l}} \ times {\ vec {B}})} ,
die Kraft F, die auf einen stromdurchflossenen Leiter l ausgeübt wird, wenn auf ihn ein B-Feld einwirkt — ein klassischer Fall der Rechte-Hand-Regel. Английский язык: Сила Лоренца. Эта диаграмма иллюстрирует поведение заряженной частицы q , движущейся со скоростью v в магнитном поле B . Последний ориентирован за пределы страницы, на что указывает точка в круге. Частица ускоряется силой Лоренца, поведение которой определяется формулой:
F знак равно q E + q c [ v × B ] {\ displaystyle F = qE + {\ frac {q} {c}} \ left [v \ times B \ right]}
где F — вектор силы, E — электрическое поле, а c — скорость света.Символ × представляет математический оператор curl. Направление искривленного пути электрона определяется знаком его заряда, который изменяет знак v × B в формуле выше. .

Ге́ндрік Анто́н Ло́ренц
нід. Hendrik Antoon Lorentz

Ім’я при народженні	нід. Hendrik Antoon Lorentz
Народився	18 липня 1853(1853-07-18)^[1]^[2]^[…] Арнем, Гелдерланд, Нідерланди, Нідерланди^[4]^[5]
Помер	4 лютого 1928(1928-02-04)^[4]^[2]^[…] (74 роки) Гарлем, Нідерланди, Нідерланди^[4]
Поховання	Algemene Begraafplaats Kleverlaan^d
Громадянство	Нідерланди
Діяльність	куратор, фізик-теоретик, професор, математик, фізик, викладач університету
Alma mater	Лейденський університет
Сфера інтересів	фізика
Заклад	Лейденський університет
Посада	rector magnificus of Leiden University^d
Науковий ступінь	докторський ступінь^[5]
Науковий керівник	Pieter Rijke^d
Відомі учні	Adriaan Fokker^d
Член	Лондонське королівське товариство, Академія наук СРСР, Петербурзька академія наук, Французька академія наук, Шведська королівська академія наук, Нідерландська королівська академія наук, Американська академія мистецтв і наук, Російська академія наук, Прусська академія наук, Національна академія наук Італії^d, Баварська академія наук, Академія наук Турина^d і Національна академія наук США
Відомий завдяки:	сила Лоренца
У шлюбі з	Aletta Lorentz-Kaiser^d
Діти	Geertruida de Haas-Lorentz^d
Нагороди	Нобелівська премія з фізики (1902) Медаль Коплі
Роботи у Вікіджерелах Гендрік Антон Лоренц у Вікісховищі

	… ми сподіваємося, що електронна гіпотеза, оскільки вона прийнята в різних розділах фізики, веде до загальної теорії, яка охопить багато областей фізики і хімії. Можливо, що на цьому довгому шляху вона сама повністю перебудується
— Гендрік Антон Лоренц, при врученні Нобелівської премії

	Нас не покидає відчуття, що ми перебуваємо в глухому куті; старі теорії виявляються усе менш здатними проникнути в пітьму, що оточує нас з усіх боків
— Гендрік Антон Лоренц, із вступного слова