Сортамент фасонных профилей: Геометрические характеристики фигур

Геометрические характеристики фигур / Геометрические характеристики простых фигур: прямоугольника, квадрата, треугольника, круга, полукруга

Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.

Геометрические характеристики прямоугольника и квадрата

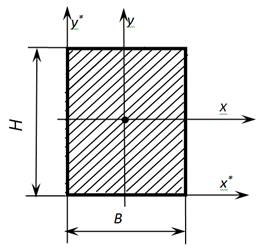
Осевые моменты инерции прямоугольника (квадрата)

Геометрические характеристики прямоугольного треугольника

Осевые моменты инерции прямоугольного треугольника

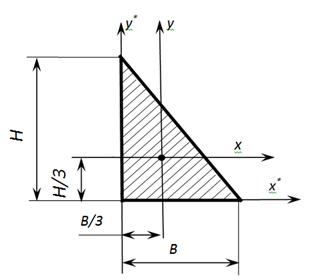
Геометрические характеристики равнобедренного треугольника

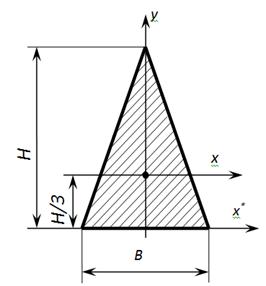
Осевые моменты инерции равнобедренного треугольника

Геометрические характеристики круга

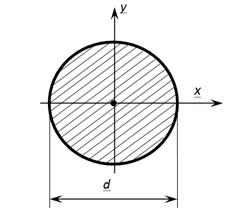
Осевые моменты инерции круга

Геометрические характеристики полукруга

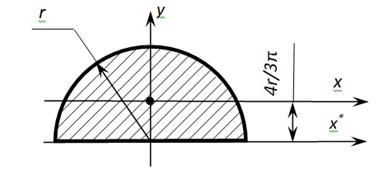
Осевые моменты инерции полукруга

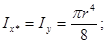
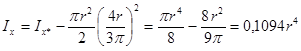
Моменти инерции некоторых простых сечений

Момент инерции прямоугольного пересечения

Розмеры прямоугольного сечения – b*h
Осевые моменты инерции
$$J_x = {b*h^3\over 12} $$
$$J_y = {h*b^3\over 12} $$
Полярный момент инерции прямоугольного сечения
$$J_p = {b*h\over 12}*(h^2-b^2) $$

Квадратное сечение

a – сторона квадрата.
Осевые моменты инерции
$$J_x = J_y = {a^4\over 12}$$
Полярный момент инерции квадрата
$$J_p = 2J_x = {a^4\over 6}$$

Момент инерции круга

Запишем
$$J_{p}= 2\,\pi \,\int_{0}^{p}{p}^{3}dp$$
Интегрируем выражение и получаем
$$J_p= \frac{\pi \,{p}^{4}}{2}$$
Полярный момент инерции круга
$$J_p=J_x+J_y=2I_x$$
Осевые моменты инерции круга

Момент инерции кругового кольца.

 
Круговое кольцо с внутренним диаметром d и внешним D

Момент инерции полукруга

Диаметр полукруга d .
Моменты инерции полукруга относительно осей y и x₁ будут равными между собою и в два раза меньшими, нежели осевой центральный момент инерции круга.
$$J_y = J_{x_1} = {\pi d^4\over 128}$$
Площадь полукруга
$$A={\pi*d^2\over 8}$$
Статический момент полукруга относительно оси x₁:
$$S_{x_1} = {d^3\over 12}$$
Находим момент инерции полукруга относительно оси x:
$$J_x = \frac{\left( 9\,{\pi }^{2}-64\right) \,{d}^{4}}{1152\,\pi } \approx 0.00686d^4$$

Момент инерции треугольника

вычислим моменты инерции для треугольника относительно центральной оси.
Центр тяжести треугольника: [math]y_o=\frac{1}{3}h[/math].

С выражения dA=b(y)*dy, а также с подобия
треугольников (2/3*h-y)/h=b(y)/b
можем получить
$$dA=\left( \frac{2\,b}{3}-\frac{b\,y}{h}\right)*dy $$
тогда
$$J_x= \int_{\frac{h}{3}}^{\frac{2\,h}{3}}{y}^{2}\,\left( \frac{2\,b}{3}-\frac{b\,y}{h}\right) dy$$

Интегрируем выражение и получаем: $$J_x=\frac{b\,{h}^{3}}{36}$$
Для равнобедренного треугольника [math]J_y=\frac{hb^3}{48}[/math]

Момент инерции двутавра и профилей

Дополнительная информация

В приложенном файле – геометрические характеристики других сечений (из справочника по сопротивлению материалов /Фесик С.П. – 1982)

---

Связанные статьи

Моменты инерции треугольника. — МегаЛекции

В расчетной практике часто встречаются сечения в виде простейших фигур (прямоугольников, кругов, треугольников и т.п.) или их комбинаций. При вычислении моментов инерции таких фигур обычно пользуются заранее выведенными формулами.

Определим осевые моменты инерции треугольника относительно трех параллельных осей z₁, z₀ и z₂, проходящих через его основание (рис. 13.5 а), центр тяжести (13.5, б) и вершину (рис. 13.5, в).

Для случая, когда ось проходит через основание треугольника (рис. 13.5, а),

 

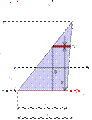
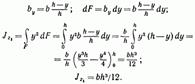
Для случая, когда ось проходит через центр тяжести треугольника параллельно его основанию (рис. 13.5, б),

 

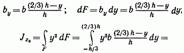
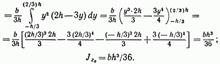
В случае, когда ось проходит через вершину треугольника параллельно его основанию (рис. 13.5, в),

 

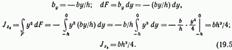
Для равнобедренного треугольника

 

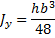
№ 15 билет.

Статически неопределимые задачи при растяжении и сжатии.

1. Статически неопределимые называются задачи, которые нельзя решить с помощью только уравнений статики. Дополнительные уравнения составляются из рассмотрения деформаций системы.

Назовем степенью статической неопределенности разность между числом неизвестных и числом независимых уравнений статики, которые можно составить для данной задачи.

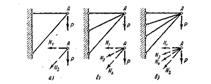На рис. 2.7 представлены системы: а) статически определимая, б) один раз статически неопределима n=3-2=1, в) два раза статически неопределима n= 4-2=2.

Для изучения свойств материалов под нагрузкой производят испытания образцов, изготовленных из этих материалов. Эти испытания проводят с целью определить числовые характеристики, позволяющие оценить прочность и пластичность материала. Такие характеристики называют механическими.

Важнейшие механические свойства реальных тел могут быть выявлены из опытов на растяжение — сжатие. Эти опыты проводят на специальных машинах

Статически неопределимые системы в отличие от статически определимых обладают рядом особенностей. Распределение нормальных сил в таких системах зависит от соотношения жесткостей отдельных стержней. При изменении температуры стержней в статически неопределимых системах возникают температурные напряжения. Кроме того, могут возникать монтажные (или начальные) напряжения в результате сборки стержневых систем, у которых отдельные стержни имеют отклонения от номинальных размеров.

Если в статически неопределимой системе необходимо провести расчет напряжений от действия внешних нагрузок, учесть изменение температуры и монтажные напряжения, то применяется принцип суперпозиции: определяются напряжения в стержнях отдельно от каждого из перечисленных выше факторов, а результирующие напряжения вычисляются как алгебраическая сумма напряжений в стержне от внешней нагрузки, температурных и монтажных напряжений.

Закон Гука при кручении.

Закон Гука при кручении записывается, как закон Гука при сдвиге:

Формула закона Гука при кручении с учетом зависимости между углом сдвига и относительным углом закручивания:

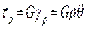
Формулировка закона Гука при кручении: касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести на расстоянии , пропорциональны относительному углу закручивания. В точках, равноудаленных от центра тяжести сечения, численные значения касательных напряжений одинаковы.

Из формулы закона Гука при кручении следует: касательные напряжения в поперечном сечении вала изменяются по линейному закону (пропорционально расстоянию от точки до центра тяжести). Касательные напряжения равны нулю в центре вала и достигают максимального значения ( ) в точках контура поперечного сечения (рис. 5.2).

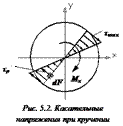
Из рис. 5.2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полые валы. Такие валы, при той же площади поперечного сечения (F), могут воспринять больший скручивающий момент.

№ 16 билет.

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

Моменты инерции простейших фигур (вывод формул для круга, прямоугольника, треугольника)

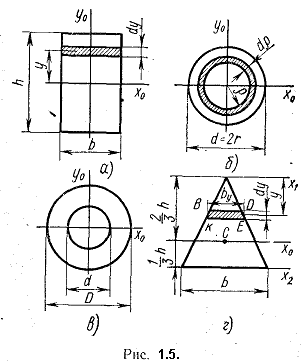
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию.

За dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда

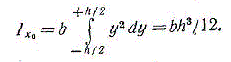
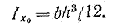(1.11)

Аналогично получим

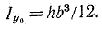    (1.12)

 

2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга

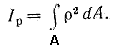
За dA принимаем площадь бесконечно тонкого кольца толщиной dp

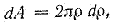
Тогда

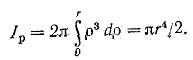
Следовательно

(1.13)

Теперь легко найдем Ixo. Действительно, для круга имеем Iр = 2Iхо = 2Iуо, откуда

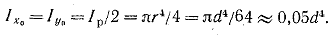(1.14)

3. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника

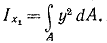
За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника:

dA = bydy,

где by — длина прямоугольника.

Легко получить из подобия треугольников

by = yb/h;

тогда 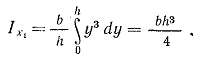(1.15)

Определим момент инерции относительно центральной оси

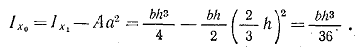(1.16)

Определим момент инерции относительно оси, проходящей через основание:

(1.17)

 

Момент — инерция — треугольник

Момент — инерция — треугольник

Cтраница 1

Момент инерции треугольника ( рис. АЛО) относительно основания уже был получен ранее ( см. выражение ( А.  [1]

Найти моменты инерции треугольника, ограниченного прямыми х у а, х — а, у а, относительно осей Оде, Оу и относительно начала координат, если плотность пропорциональна ординате точки.  [2]

Найти момент инерции треугольника относительно оси, проходящей через центр тяжести и параллельной основанию ( фиг.  [3]

Найти момент инерции треугольника с основанием b и высотой h относительно его основания.  [4]

Найти моменты инерции треугольника, ограниченного прямыми х у-а, х а, у — а, относительно осей Ох, Оу и относительно начала координат, если плотность пропорциональна ординате точки.  [5]

Найти моменты инерции треугольника с высотой h и основанием b относительно центральных осей, одна из которых параллельна основанию, а вторая совпадает с высотой.  [6]

Определить момент инерции треугольника ( рис. 2.86) относительно оси xlt проходящей через его основание.  [7]

Найти Момент инерции треугольника ABC относительно оси X, вот.  [8]

Найти момент инерции однородного треугольника с основанием а и высотой h относительно: 1) оси, содержащей его основание; 2) оси, проходящей через вершину параллельно основанию; 3) оси, проходящей через центр масс треугольника параллельно основанию.  [9]

Вычислить также момент инерции треугольника относительно основания АС.  [10]

Вычислить значения моментов инерции треугольника ( рис. 4.6) относительно оси, совпадающей с основанием треугольника, и оси, проходящей через центр тяжести треугольника параллельно его основанию.  [11]

Во сколько раз момент инерции треугольника относительно оси, проходящей вдоль его основания, меньше момента инерции относительно оси, проходящей через вершину параллельно основанию.  [12]

Найти статический момент и момент инерции треугольника с основанием а и высотой / г относительно его основания.  [13]

Найти статический момент и момент инерции треугольника с основанием а и высотой h относительно его основания.  [14]

Найти статический момент и момент инерции треугольника с основанием а и высотой / i относительно его основания.  [15]

Страницы:      1    2

MYsopromat.ru: Моменты инерции простейших фигур

В расчетной практике часто встречаются сечения в виде простейших фигур (прямоугольников, кругов, треугольников и т. п.) или их комбинаций. При вычислении моментов инерции таких фигур обычно пользуются заранее выведенными расчетными формулами. Рассмотрим некоторые из фигур.

Прямоугольник и параллелограмм (рис. 6.4). Выделим элементарную полоску площадью dF=bdy и подставим это значение dF под знак интеграла (6.5):

Рис. 6.4	Рис. 6.5

.

Следовательно, момент инерции прямоугольника и параллелограмма с основанием b и высотой h относительно центральной оси, параллельной основанию,

.

(6.16)

Моменты инерции этих фигур относительно осей, проходящих через основание, находим по формуле (6.13):

.

(6.17)

Моменты инерции прямоугольника относительно осей y_c и y вычисляются по формулам (6.16) и (6.17), где b заменяется на h, а h на b:

.	(6.18)
.	(6.19)

Треугольник с основанием b и высотой h (рис. 6.5).

Разобьем треугольник на элементарные полоски, параллельные его основанию. Площадь такой полоски

.

Тогда момент инерции треугольника относительно оси, проходящей через основание,

.

(6.20)

Подсчитывая по формулам переноса момент инерции треугольника относительно центральной оси, параллельной основанию, получаем

.

(6.21)

Круг и полукруг диаметра d (рис. 6.6). Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиуса ρ и ρ+dρ элементарное кольцо площадью dF=2πρdρ и вычислим I_y по формуле (6.7):

.

(6.22)

Рис. 6.6.

Обычно размеры круглого сечения выражают через диаметр d и подсчитывают I_p по формуле

.

(6.23)

Осевые моменты инерции круга найдем с помощью соотношения (6.8). Замечая, что в силу симметрии круга I_z=I_y, получаем для осевых моментов инерции круга выражение

.

(6.24)

Центральные оси y и z делят круг на четыре совершенно одинаковые части с равными моментами инерции относительно этих осей. Следовательно, моменты инерции круга и полукруга относительно осей y и z должны быть равны соответственно учетверенным и удвоенным моментам инерции относительно тех же осей одной четверти круга. Из сказанного следует, что моменты инерции полукруга относительно оси симметрии y и оси z, проходящей через его основание (рис. 6.2), будут одинаковы и равны половине момента инерции круга,

,

(6.25)

а моменты инерции четверти круга

.

(6.26)

    

Момент инерции — это… Что такое Момент инерции?

У этого термина существуют и другие значения, см. Момент.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

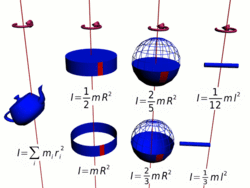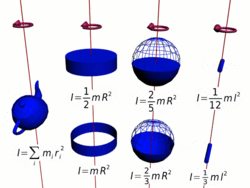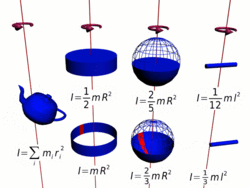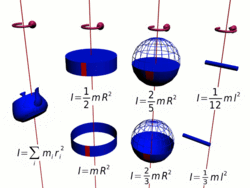Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где  — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Осевые моменты инерции некоторых тел

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы  

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы  

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Вывод формулы  

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Сплошной конус

Вывод формулы  

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Интегрируя, получим

Сплошной однородный шар

Вывод формулы  

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Тонкостенная сфера

Вывод формулы  

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Тонкий стержень (ось проходит через центр)

Вывод формулы  

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Интегрируя, получим

Тонкий стержень (ось проходит через конец)

Вывод формулы  

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Безразмерные моменты инерции планет и их спутников^[1][2]

Безразмерные моменты инерции планет и их спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. ^[3][4]

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

где  — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см⁴.

Из него выражается момент сопротивления сечения:

.

Центральный момент инерции

Центральный момент инерции (или момент инерции относительно точки O) — это величина

,

где:

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:

(1),

где  — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

,
.

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где  — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

,

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на

и произведя замены:

,

получаем канонический вид уравнения эллипсоида в координатах :

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

См. также

Примечания

Литература

• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
• Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки