404 Not Found
404 Not Found
|
|
Что такое Сила Лоренца?
Определение + формула
Сила Лоренца – сила, оказывающая воздействие на движущийся электрический заряд со стороны электромагнитного поля.
Названа она по фамилии ученого-физика, который впервые описал это явление. Зачастую, обозначение сила Лоренца применяют в формуле имея в виду лишь магнитную силу:
\[\mathrm{F}=\mathrm{q}(E+v B)\]
Где магнитная сила обозначена B, заряд частицы – q, напряжение электрополя – E, скорость движущейся частицы – v.
Сила Ампера, оказывающая воздействие на фрагмент проводника, имеющего длину Δl с определенной силой тока l, во время его нахождения в магнитном поле B, F = I ⋅ B ⋅ Δ l ⋅ sin α может быть выражена через силы, воздействующие на определенные носители заряда.
Обозначим заряд конкретного носителя как q. При этом n представляет собой значение концентрации в проводнике носителей свободного заряда.
Таким образом выражение n ⋅ q ⋅ υ ⋅ S, где S применяется для обозначения площади поперечного сечения предлагаемого проводника, а u – является модулем скорости упорядоченного перемещения носителей в представленном проводнике, будет соответствовать току, текущему в проводнике: I = q ⋅ n ⋅ υ ⋅ S
Формула 2
Формула силы Ампера выглядит следующим образом:
\[\mathrm{F}=\mathrm{q} \cdot \mathrm{n} \cdot \mathrm{S} \cdot \Delta \mathrm{l} \cdot \mathrm{u} \cdot \mathrm{B} \cdot \sin \alpha\]
Исходя из того, что переменная N, с помощью которой обозначено число носителей свободного заряда, движущихся в проводнике с площадью сечения S и длиной Δl равна произведению n ⋅ S ⋅ Δ l, мы можем говорить, что сила, действующая на каждую из заряженных частиц, равна выражению:
\[F_{Л}\] = q ⋅ υ ⋅ B ⋅ sin α.
Сила, которую мы нашли называют- силой Лоренца. Формула показывает, что значение угла α соответствует углу, образованному вектором магнитной индукции \[\vec{B}\] и скоростью \[\vec{v}\].
По принципу действия сила Лоренца имеет большое сходство с силой Ампера. Отличие состоит в том, что действие последней распространяется на весь проводник, нейтральный в электрическом смысле, а первая описывает как влияет электромагнитное поле на отдельную движущуюся заряженную частицу.
Направление силы Лоренца
Определяя направление силы Лоренца, исходим из того, что она всегда будет перпендикулярна вектору магнитной индукции. Это значит, что \[\vec{B}\] соответствует тому выделенному направлению в пространстве, вдоль которого действие магнитных сил не распространяется. Вектор силы Лоренца имеет направление перпендикулярное вектору \[\vec{v}\]. Для определения окончательного направления силы можно воспользоваться правилом левой руки.
Ладонь необходимо расположить таким образом, чтобы четыре пальца были вытянуты вдоль направления движения заряда, а положение отставленного большого пальца соответствовало вектору магнитной индукции поля.
Именно большой палец будет указывать направление силы Лоренца, которая действует на положительный заряд.
Если заряд отрицательный, направление силы станет противоположным.
Рисунок 1. Правило левой рукиНа рис. 2 можно увидеть демонстрацию взаимного расположения векторов \[\vec{v}\] и \[\vec{B}\] для положительно заряженной частицы.
Рисунок 2. Взаимное расположение векторов \[\vec{v} \vec{B}\] и \[\vec{F}_{Л}\].Модуль силы Лоренца − \[\vec{F}_{Л}\] равен площади параллелограмма, построенного на векторах \[\vec{v}\] и \[\vec{B}\], умноженной на заряд q.
Сила Лоренца имеет нормальное, то есть перпендикулярное направление относительно векторов \[vec{v}\] и \[\vec{B}\].
Работа силы Лоренца всегда имеет нулевое значение, поскольку эта сила всегда перпендикулярна скорости и движению заряда. Величина скорости не изменяется под влиянием магнитного поля, его воздействие приводит к изменению лишь направления скорости. Поэтому заряженная частица, движущаяся под воздействием силы Лоренца перпендикулярно магнитному полю, при условии его однородности, и скорости лежащей в плоскости, направленной нормально относительно вектора \[\vec{B}\] , будет иметь траекторию в виде окружности.
Радиус можно рассчитать, используя формулу:
R = m ν q B
В таких случаях магнитная сила Лоренца выступает в роли центростремительной силы. Это проиллюстрировано на рис. 3.
Рисунок 3. Круговая траектория движения заряженной частицы в условиях однородного магнитного поля.Формула 3
Период кругового движения частицы внутри однородного магнитного поля можно определить по формуле:
\[T=2 \pi R u=2 \pi m q B\]
Данное выражение подтверждает, что заряженные частицы с заданной массой m не зависят от скорости u и радиуса круговой траектории R.
Применение силы Лоренца
Формула 4 + определение
Для определения угловой скорости кругового движения заряженной частицы применяется следующая формула:
\[\omega=u R=u q B m u=q B m\]
Частота, с которой заряженная частица обращается в однородном магнитном поле именуется циклотронной. Она не зависит от скорости, с которой движется частица, а также от ее кинетической энергии.
Благодаря данному обстоятельству становится возможным применение силы Лоренца для циклотронов, если конкретнее – ускорителей тяжелых частиц, известных как ионы, протоны. Рисунок 4 демонстрирует принципиальную схему циклотрона.
Рисунок 4. Траектория движения заряженных частиц внутри вакуумной камеры циклотрона.Определение 3
Дуант — один из двух полых металлических полуцилиндров, размещенных в вакуумной камере циклотрона между двух полюсов электромагнита в качестве ускоряющего D-образного электрода.
Дуанты подвергаются воздействию переменного электрического напряжения, частота которого равна частоте циклотрона. В центре камеры происходит инжектирование заряженных частиц. Электрическое поле, создаваемое в зазоре между двух дуантов ускоряет движение частиц. Двигаясь по полуокружностям они подвергаются воздействию силы Лоренца. Рост энергии частиц приводит к увеличению радиуса полуокружностей. Электрическое поле вызывает ускорение заряженных частиц, а на заданной траектории ее удерживает магнитное поле.
Энергия за счет ускорения протонов в циклотронах может увеличиваться до 20 МэВ.
Однородные магнитные поля нашли свое применение в самых разных устройствах – в частности, в масс-спектрометрах.
Приборы делают возможным разделение изотопов – ядер, имеющих одинаковый заряд, но различную массу. Например, 20Ne, 22Ne.
Элементарный масс-спектрометр можно увидеть на рисунке 5.
Рисунок 5. Селектор скоростей и масс-спектрометр.Ионы, вылетая из источника S преодолевают несколько мелких отверстий и образуют узкий пучок. После попадания в селектор скоростей они продолжают движение в альянсе однородного электрического, образованного в промежутке между пластин плоского конденсатора и магнитного поля, формирующегося в зазоре, возникающего между разнозаряженными полюсами электромагнита. Направление начальной скорости \[\vec{v}\] заряженных частиц перпендикулярно относительно векторов \[\vec{E}\] и \[\vec{B}\].
Во время движения в зоне скрещенных электрического и магнитного полей на частица воздействует электрическая сила — \[\vec{q E}\] и магнитная сила Лоренца.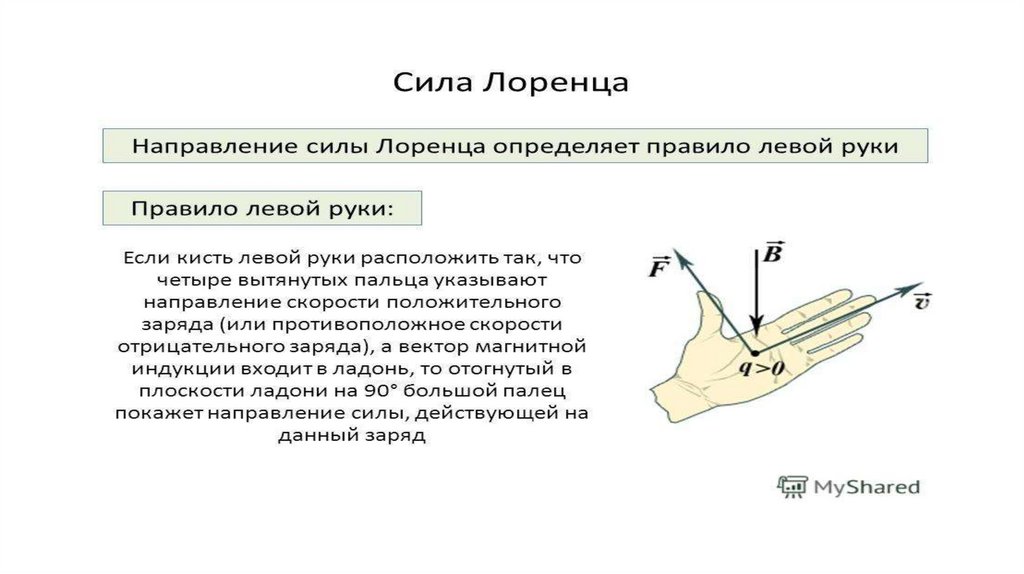
{6}\] K с практически одинаковой плотностью положительных и отрицательных зарядов. Для доведения вещества до подобного состояния используют установки типа «Токамак». Такие процедуры проводят в процессе изучения управляемых реакций термоядерного типа. Необходимо исключить попадание плазмы на стенки. Достигнуть необходимого уровня термоизоляции получается за счет формирования магнитного поля определенной конфигурации.
Траекторию движения заряженной частицы внутри магнитной «бутылки» или ловушки можно увидеть на рисунке 7.
Рисунок 7. Магнитная «бутылка». Заряженные частицы не покидают пределов магнитного поля. Для его создания применяют две круглые катушки с током.Аналогичное явление наблюдается в магнитном поле нашей планеты, которое обеспечивает надежную защиту всего живого, выступая в качестве преграды на пути потока заряженных частиц из космоса.
Магнитное поле Земли осуществляет «перехват» быстрых заряженных частиц из космического пространства. В результате происходит формирование радиационных поясов.
Внутри этих магнитных ловушек частицы стремительно перемещаются по спиралевидным траекториям в одну сторону и в другую между северным и южным магнитным полюсом. Движение совершается за доли секунды.
В полярных областях частицы могут прорываться и оказываться в верхних слоях атмосферы. Это явление известно, как «северное сияние». Размеры радиационных поясов Земли (рис.8) могут занимать как 500 км, так и десятки радиусов Земли. Считаем нелишним напомнить, что южный магнитный полюс располагается неподалеку от северного географического полюса Земли на северо-западе острова Гренландия. На сегодняшний день секреты природы земного магнетизма пока еще не раскрыты.
Рисунок 8. Радиационные пояса Земли.Практическое применение силы Лоренца. Примеры
Силу Лоренца широко используют в электродвигателя, генераторах. На ней основано функционирование электронных приборов, оказывающих воздействие на заряженные частицы – ионы, электроны. Среди таких устройств можно выделить телевизионные электронно-лучевые трубки, масс- спектрометры, МГД-генераторы.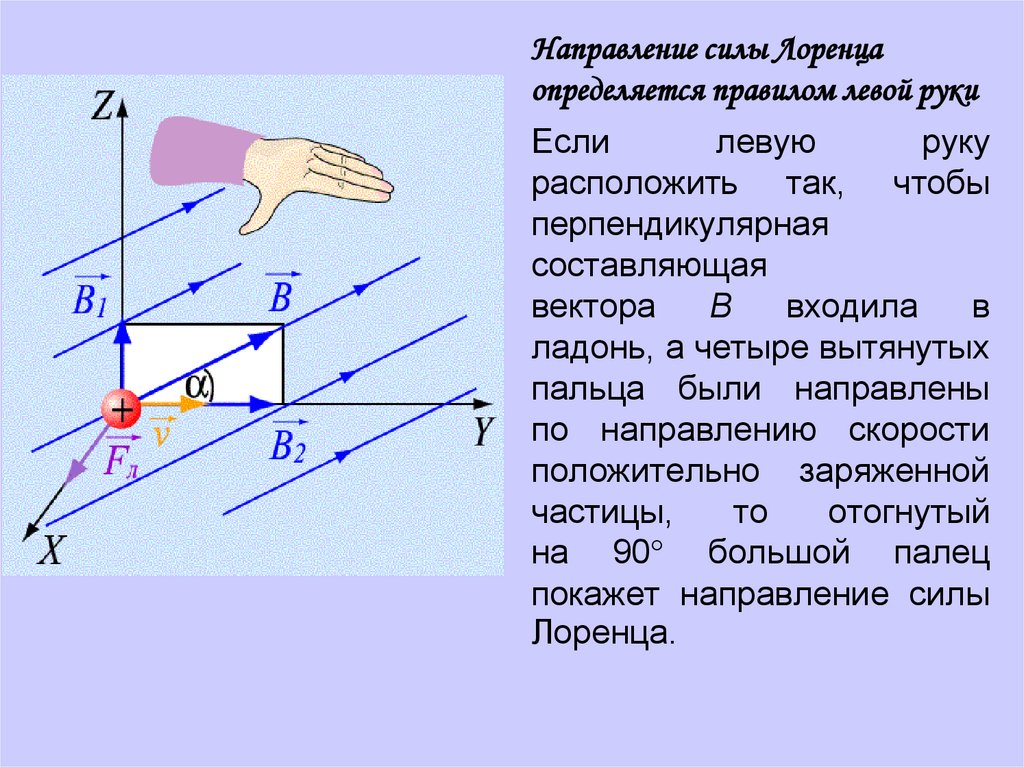
Практическое применение сила Лоренца находит в рельсотронах, циклотронах, фильтрах скорости, магнетронах. Она задает орбиту движения заряженных частиц в специальных ускорителях.
Рисунок 9. Модель движения заряженных частиц в магнитном поле.Рисунок 10. Модель масс-спектрометра.Рисунок 11. Модель селектора скоростей.Уравнения Максвелла объясняются с помощью закона силы Лоренца
Давайте сначала покажем формулу…
Формула
\[\nabla\cdot \bold{E}=\frac{\rho}{\epsilon_0} \\ \nabla\cdot \ жирный{B}=0 \\ \nabla\times \bold{E} = -\frac{\partial \bold{B}}{\partial t} \\ \nabla\times \bold{B} = \mu_0 \ жирный {j} + \mu_0\epsilon_0 \frac{\partial \bold{E}}{\partial t} \\ \bold{F}=q(\bold{E}+\bold{v}\times\bold {B})\]
Почему это основные уравнения электромагнетизма?
Потому что электромагнетизм основан на взаимодействии трех объектов: электрического поля, магнитного поля и заряда. Эти 5 формул дают полные законы взаимодействия между этими 3 объектами, поэтому они являются фундаментальными и составляют всю теорию электромагнетизма.
\(\bold{E} \Longleftrightarrow \bold{B} \\ \bold{E},\bold{B} \longleftrightarrow Q\)
примечание:
Технически уравнения, представленные выше, не являются самыми фундаментальными уравнениями электромагнетизм. Это потому, что мы записали уравнения Максвелла в их дифференцируемой форме, которая предполагает, что дискретные заряды достаточно малы, чтобы их можно было аппроксимировать континуумом зарядов. Технически, чтобы получить самые фундаментальные уравнения Максвелла в классической физике, мы должны написать: \(\iint \limits_{\partial\sigma} \bold{E}\cdot \bold{dA} = \sum \limits_\sigma \ frac{q}{\epsilon_0}\) И так далее…
Итак, просто помните, что предпосылка дифференциальной формы уравнений Максвелла состоит в том, что заряды не дискретны, а аппроксимированы континуумом. Так что $\rho\lt\infty$ всегда.
Что делает каждое уравнение по отдельности?
Закон Гаусса
$\nabla \cdot \bold{E}=\frac{\rho}{\epsilon_0}$ можно рассматривать как уравнение, определяющее влияние заряда на электрическое поле.
В нем говорится: плотность заряда $\rho$ создает расходимость величины $\frac{\rho}{\epsilon_0}$ в электрическом поле. (дивергенция просто означает, какая плотность электрического потока генерируется в этой точке, или, выражаясь более распространенным языком, сколько силовых линий исходит из этой точки на единицу объема).
Закон Гаусса для магнетизма
$\nabla \cdot \bold{B}=0$ говорит почти то же самое. Дивергенция магнитного поля всегда равна 0. Если вы думаете о поле скорости любой несжимаемой жидкости, его дивергенция также должна быть равна нулю (поскольку 0 силовая линия/жидкость исходят из определенной точки). Это определяет, как статический заряд влияет на поле $\bold{B}$: он ничего не делает с ним (однако движущийся заряд влияет на магнитное поле).
Итак, два закона Гаусса говорят нам, как заряд влияет на поля $\bold{E}$ и $\bold{B}$. И в просторечии нам говорят, что заряды создают «стоки» или «источники» в электрическом поле, но не создают «источники» и «стоки» в магнитном поле.
Они обозначают $Q_{positional}\rightarrow \bold{E},\bold{B}$ направление взаимодействия
примечание:
Чтобы быть более точным, мы можем разделить обсуждение дивергенции и завихрения $\ Полужирный{E}, \bold{B}$. Два закона Гаусса дают нам расхождение двух полей. На расхождения двух полей влияет только расположение заряда, что довольно интересно.
Закон Максвелла-Фарадея
$\nabla\times \bold{E} = -\frac{\partial \bold{B}}{\partial t}$
Обратите внимание на его отличие от закона Фарадея. Этот закон определяет, как изменение поля $\bold{B}$ влияет на поле $\bold{E}$ или, в частности, вызывает завихрение. Таким образом, он представляет собой $\bold{B}\rightarrow \bold{E}$ направление взаимодействия.
Закон Ампера
$\nabla\times \bold{B} = \mu_0 \bold{j} + \mu_0\epsilon_0 \frac{\partial \bold{E}}{\partial t}$
Это чрезвычайно похож на закон Максвелла-Фарадея. Это в значительной степени его противоположность. Он определяет, как изменение поля $\bold{E}$ влияет на поле $\bold{B}$ или приводит к искривлению поля $\bold{B}$.
Он указывает направление $\bold{E}\rightarrow \bold{B}$.
Однако это еще не все: уравнение также включает плотность тока $\bold{j}$. Таким образом, закон также определяет, как движение заряда влияет на поле $\bold{B}$. Как естественный вопрос: почему существует этот член $\bold{j}$, который, кажется, мешает гармонии уравнений Максвелла? Мы рассмотрим это в следующем посте.
Последнее, но не менее важное (на самом деле, возможно, самое важное)
Закон силы Лоренца
$\bold{F}=q(\bold{E}+\bold{v}\times\bold{B})$
Он показывает, как поле $\bold{E}$ и $\bold{B}$ влияют на заряд, поэтому он обеспечивает это направление взаимодействия $\bold{E},\bold{B}\rightarrow Q$. Это не уравнение Максвелла, потому что, в отличие от остальных четырех, оно не описывает электромагнитное поле (или $\bold{E}$ и $\bold{B}$). Вместо этого он описывает, как они влияют на заряды.
Заключение
Как мы видели, каждый закон электромагнетизма регулирует 1 из 6 направлений взаимодействия между 3 объектами: электрическое поле, магнитное поле и заряд.
\(\bold{E} \longleftrightarrow \bold{B} \\ \bold{E} \longleftrightarrow Q \\ \bold{B} \longleftrightarrow Q\) Причина, по которой существует только 5 уравнений вместо 6, заключается в том, что Закон силы Лоренца на самом деле имеет 2 компонента: отдельные компоненты $\bold{F}=q\bold{E}$ и $\bold{F}=q\bold{v}\times \bold{B}$. Таким образом, он фактически содержит 2 части информации и 2 направления взаимодействия.
электромагнетизм — Что такое $c$ в выражении силы Лоренца?
спросил
Изменено 7 лет, 7 месяцев назад
Просмотрено 591 раз
$\begingroup$
Обычное выражение силы Лоренца, с которым я знаком, таково:
$$\vec F=q(\vec E+\vec v \times \vec B)$$
В последнее время я видел несколько других версий, которые включают дополнительный множитель $1/c$:
$$\vec F =q\left(\vec E+ \frac{1}{c} \vec v \times \vec B\right)$$
Что это за $c$ и как оно включается? Я предполагаю, что другие параметры в выражении также отличаются от верхнего выражения, чтобы это соответствовало?
Пример фрагмента текста, в котором я наткнулся на этот дополнительный параметр:
- электромагнетизм
- скорость света
- единицы
- си-единицы
- единица преобразования
$\endgroup$
2
$\begingroup$
Во второй формуле $c$ — это скорость света.
В обеих формулах используется разная система единиц. В первом используется система СИ: $q$ в кулонах, $\vec{E}$ в вольтах на метр и $\vec{B}$ в теслах. Второй использует гауссовые единицы измерения: $q$ в статкулонах, $\vec{E}$ в статвольтах на сантиметр и $\vec{B}$ в гауссах (будучи статвольтами на сантиметр и гауссом размерно эквивалентны).
При работе с электромагнетизмом часто приходится сталкиваться с различными системами единиц (SI, гаусс, Хевисайд…), в которых уравнения различаются множителями $c$, $4\pi \mu_0$ и т. д. Это всегда удобно чтобы было понятно, какую систему единиц вы используете.
$\endgroup$
$\begingroup$
это зависит от системы (sI или CGS или…), в которой вы работаете. В этом нет ничего особенного. и иногда вы получаете c=1 или h=1 )постоянную Планка только для того, чтобы иметь более простые формы, которые не влияют на желаемый результат.
