Что такое Ампер
Ампе́р (обозначение: А) — единица измерения силы электрического тока в системе СИ, а также единица магнитодвижущей силы и разности магнитных потенциалов (устаревшее наименование — ампер-виток).
1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
\[ \mbox{I} = \dfrac{\mbox{q}}{\mbox{t}} \qquad \qquad \mbox{1A} = \dfrac{\mbox{1Кл}}{\mbox{1c}} \]
Одним Ампером называется сила постоянного тока, текущего в каждом из двух параллельных бесконечно длинных бесконечно малого кругового сечения проводников в вакууме на расстоянии 1 метр, и создающая силу взаимодействия между ними 2×10−7 ньютонов на каждый метр длины проводника.
Ампер назван в честь французского физика Андре Ампера.
Сила тока – это такая физическая величина, которая показывает скорость прохождения заряда q через S поперечное сечение проводника за одну секунду t.
Сила тока – пожалуй, одна из самых основополагающих характеристик электрического тока. Она обозначает заглавной буквой I латинского алфавита и равняется Δq разделить на Δt, где Δt – это время, в течение которого через сечение проводника протекает заряд Δq.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 А | декаампер | даА | daA | 10−1 А | дециампер | дА | dA |
| 102 А | гектоампер | гА | hA | 10−2 А | сантиампер | сА | cA |
| 103 А | килоампер | кА | kA | 10−3 А | миллиампер | мА | mA |
| 106 А | мегаампер | МА | MA | 10−6 А | микроампер | мкА | µA |
| 109 А | гигаампер | ГА | GA | 10−9 А | наноампер | нА | nA |
| 1012 А | тераампер | ТА | TA | 10−12 А | пикоампер | пА | pA |
| 1015 А | петаампер | ПА | PA | 10−15 А | фемтоампер | фА | fA |
| 1018 А | эксаампер | ЭА | EA | 10−18 А | аттоампер | аА | aA |
| 1021 А | зеттаампер | ЗА | ZA | 10−21 А | зептоампер | зА | zA |
| 1024 А | йоттаампер | ИА | YA | 10−24 А | йоктоампер | иА | yA |
| применять не рекомендуется | |||||||
Физическое значение данного параметра состоит в следующем:
- Элементарные частицы постоянно текут по бесконечно тонким и длинным проводникам в одном направлении;
- Цепь находится в вакууме, и потенциалы расположены параллельно друг к другу с расстоянием в один метр;
- Сила притяжения или отталкивания между ними составляет 2*10-7 Ньютона.
На практике такие условия даже в лаборатории воспроизвести невозможно, поэтому для установления эталона и тарирования измерительных приборов специалисты мерили уровень взаимодействия, возникающий между двумя катушками с большим количеством проводов минимального сечения.
Связь с другими единицами СИ
Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону.
Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.
Сокращённое русское обозначение а, международное А. Весьма малые токи (например, в радиолампах) измеряются в тысячных долях а — миллиамперах (ма или mА), а особо малые токи — в миллионных долях а — микроамперах (мка или μА). Человек начинает ощущать проходящий через его тело ток, если он не ниже 0,5 ма. Ток в 50 ма опасен для жизни человека. Квартирный ввод рассчитывается на ток силой от 5 до 20 а; ток ламп накаливания мощностью 60 вт при напряжении 127 в имеет около 0,5 а.
Ампер-час — единица количества электричества, применяемая для измерения ёмкости аккумуляторов и гальванических элементов. Сокращённое русское обозначение а-ч, международное Аh. Один а-ч равен количеству электричества, проходящему через проводник в течение 1 часа при токе в 1 ампер. 1 а-ч = 3600 кулонам (основным единицам количества электричества).
Упрощенно электрический ток можно рассматривать как течение воды по трубе, то есть протекание электрических зарядов по проводу можно сопоставить с протекание воды по трубе. Так вот, по сути, скорость этой «воды», а именно скорость зарядов в проводе, она и будет прямым образом связана с силой тока. И чем быстрее «вода» течет по «трубе», а именно чем быстрее вместе все носители заряда двигаются по поводу, тем сила тока будет больше.
Как вы думаете, большая ли это сила тока в 1 ампер? Да, это большая сила тока, но на практике можно встретить различные силы тока: и миллиамперы, и микроамперы, и амперы, и килоамперы, и все они довольно разные.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Формула силы Ампера в физике
Определение и формула силы Ампера
ОпределениеСила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: . Сила Ампера векторная величина. Ее направление определяет правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее. Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера определена законом (или формулой) Ампера:
где I – сила тока, – малый элемент длины проводника – это вектор, равный по модулю длине проводника, направленный в таком же направлении как вектор плотности тока, – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
где – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
где – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
где магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I, в однородном магнитном поле действует сила Ампера равная
Сила Ампера, которая действует н
Закон Ампера: формула, определение, применение
 Закон Ампера — один из важнейших и полезнейших законов в электротехнике, без которого немыслим научно-технический прогресс. Этот закон был впервые сформулирован в 1820 году Андре Мари Ампером. Из него следует, что два расположенные параллельно проводника, по которым проходит электрический ток, притягиваются, если направления токов совпадают, а если ток течёт в противоположных направлениях, то проводники отталкиваются. Взаимодействие здесь происходит посредством магнитного поля, которое перманентно возникает при движении заряженных частиц. Математически закон Ампера в простой форме выглядит так:
Закон Ампера — один из важнейших и полезнейших законов в электротехнике, без которого немыслим научно-технический прогресс. Этот закон был впервые сформулирован в 1820 году Андре Мари Ампером. Из него следует, что два расположенные параллельно проводника, по которым проходит электрический ток, притягиваются, если направления токов совпадают, а если ток течёт в противоположных направлениях, то проводники отталкиваются. Взаимодействие здесь происходит посредством магнитного поля, которое перманентно возникает при движении заряженных частиц. Математически закон Ампера в простой форме выглядит так:
F = BILsinα,
где F — это сила Ампера (сила, с которой проводники отталкиваются или притягиваются), где B — магнитная индукция; I — сила тока; L — длина проводника; α — угол между направлением тока и направлением магнитной индукции.
Интересное видео с уроком о силе Ампера:
Любые узлы в электротехнике, где под действием электромагнитного поля происходит движение каких-либо элементов, используют закон Ампера. Самый широко распространённый и используемый чуть-ли не во всех технических конструкциях агрегат, в основе своей работы использующий закон Ампера — это электродвигатель, либо, что конструктивно почти то же самое, генератор. 

Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др). Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеющие вращающиеся узлы основаны на эксплуатации закона Ампера. Также он находит применение во многих других видах электротехники, например, в громкоговорителях.
В громкоговорителе или динамике для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит. На него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.
Ещё одно видео о законе Ампера смотрите ниже:
Обсуждение:Закон Ампера — Википедия
ссылка на англ. вики неправильная. идет на Ampère’s circuital law, а должно на Ampère’s force law 192.84.134.230 12:50, 2 мая 2008 (UTC)
- Исправил. —gribozavr 21:08, 27 июня 2008 (UTC)
Сила Лоренца есть сила Ампера.[править код]
Для восстановления исторической справедливости, надо бы упомянуть, что сила Лоренца вышла из силы Ампера.
Сила тока равна заряду, проходящему по проводнику со скоростью V I=q∗V{\displaystyle I=q*V}
Ток электронов при увеличении заряда на обкладке конденсатора I=Qt{\displaystyle I={\frac {Q}{t}}} Этот ток путают с током по проводнику для силы Ампера. Когда силу тока пишут как I=qsek{\displaystyle I={\frac {q}{sek}}}
Формула Ампера F→A=I→×H→{\displaystyle {\vec {F}}_{A}={\vec {I}}\times {\vec {H}}}
I→=qV→{\displaystyle {\vec {I}}=q{\vec {V}}}
Отсюда сила Ампера — Лоренца FL=q[V→×H→]{\displaystyle F_{L}=q[{\vec {V}}\times {\vec {H}}]}—Михаил Певунов 16:18, 20 января 2016 (UTC)
Просьба убрать под кат довольно длинный кусок текста, который я выделил такими скобками {{{текст}}}, а то у меня не получаетсяClothclub 04:39, 6 января 2016 (UTC)
- А зачем вообще нужны эти выкладки? Википедия это не справочник и не учебник. Доказательства там совершено не нужны. Но главное, что википедия пишется по авторитетным источникам. В двух новых разделах нет ни одной ссылки. Нужны ссылки на источники. Пока это похоже на ВП:Оригинальное исследование. Alexei Kopylov 07:23, 6 января 2016 (UTC)
- Очень рад, что вы спросили. Во-первых, ссылка все-таки есть — на книгу Максвелла «Treatise on Electricity and Magnetism». Но вы правы: почти весь раздел «Закон Грассмана» я переписал из английской Википедии. Правда, та вещь, которую я доказал, там не доказывается, и это доказательство мне не удалось найти ни в одном источнике. Поэтому я его придумал самостоятельно и решил записать. Но я считаю, в случае очевидных вещей ссылки на авторитетные источники не нужны. Вам ведь не нужен авторитет, чтобы понять, что 2×2=4? Это тот же случай, просто немного более сложный и менее очевидный. Я же постарался сделать его более очевидным. Лично мне таких доказательств в Википедии никогда не хватало, и я надеюсь, что не только мне. Да, и я был бы рад, если бы кто-то озадачился и добавил эти ссылки, если он о них знает, исправил бы мои ошибки, если они есть, и т.д., а не просто бы все откатил назад. Потому что русская Википедия по сравнению с английской похожа на счастливое неведение.Clothclub 14:11, 6 января 2016 (UTC)
- Википедия — это не учебник, поэтому не удивительно, что вам не хватает доказательств в Википедии — вы видимо пытаетесь использовать ее как учебник. Доказательства в Википедии могут быть только, если они имеют самостоятельную значимость. То что вы не нашли доказательства, только ставить под сомнения их значимость. С другой стороны, есть Викиучебник в котором такие доказательства вполне уместны. Советую перенести ваши доказательства туда, а тут поставить на них ссылку при помощи Шаблон:Викиучебник. Alexei Kopylov 17:47, 6 января 2016 (UTC)
- Во-вторых информация в википедии должна быть проверяемой. Поэтому 2×2=4 можно писать без указание источника, но самостоятельно придумывать доказательства более сложных вещей — это уже типичный ВП:ОРИСС. Ваши доказательства я, например, не в состоянии проверить. Например, мне не ясно зачем интегрировать в док-ве 3-ого закона Ньютона, разве это не следует из выполнения 3-го закона для силы Лоренца? Alexei Kopylov 17:47, 6 января 2016 (UTC)
- Ваше добавления про Грассмана и оригинальный закон Ампера — очень полезно. Только всё равно надо добавить источники, иначе это не ВП:ПРОВ. Alexei Kopylov 17:47, 6 января 2016 (UTC)
- Alexei Kopylov, а что такое самостоятельная значимость? Я это не очень понимаю. Мне, например, это доказательство было нужно, а найти его я нигде не смог, хотя искал везде. Но я согласен: Википедия — не мой личный сайт, и вы можете поступить по правилам, если считаете, что я их нарушаю. Только перенесите, пожалуйста, доказательства сами, а то я не очень разбираюсь во всем этом.
- Ну, например, про разные доказательства теоремы Пифагора есть литература. Так что эти доказательства значимы даже без привязки к самой теореме. Доказательства самого Ампера или Максвела тоже могли быть значимы. Alexei Kopylov 01:44, 9 января 2016 (UTC)
- Да, и еще: Википедия, может, не учебник, но какой-то смысл в ней есть, все-таки? Какой именно? Мне кажется, я правильно уловил ее дух. Вот вы говорите, например, «разве это не следует из выполнения 3-го закона для силы Лоренца?» — вообще-то не следует. Потому что 3-й закон не выполняется для силы Лоренца. И об этом здесь не было сказано ни слова. А между тем, как раз на тех вещах, на которых теория трещит по швам, нужно сосредотачивать особое внимание (если вас, конечно, интересует истина, а не теоретические построения). В интернете не утихают споры на эту тему, и я подумал, почему бы не написать об этом здесь, чтобы любой человек с незатуманенным умом мог придти и сам во всем разобраться, провести самостоятельно все доказательства и найти истину прежде всего для самого себя. Третий закон Ньютона нарушается, когда заряды летят так, как показано здесь (http://forum.lebedev.ru/viewtopic.php?f=26&t=3706&sid=72bcdbae6a6d2dbc58203f992572d32b&start=60). Кто-то когда-то давал мне ссылку на страницу в книге Фейнмана, где он вроде бы разбирает этот эксперимент. Я скачал ту книгу, но на той странице не было объяснений. Сейчас у меня нет той книги, так что я не могу, к сожалению, ничего предоставить в подтверждение своих слов, кроме расчетов.Clothclub 20:11, 6 января 2016 (UTC)
- А что тут сложного? Кликайте сюда и копируйте свой текст в окошко. Впрочем я не знаю правил этого проекта.
- Так вы знаете или не знаете? Может, сначала выясните, прежде чем советы давать?Clothclub 02:24, 9 января 2016 (UTC)
- Про то, что 3-й закон Ньютона не выполняется для силы Лоренца, но выполняется для силы Ампера, можно написать, но только по источникам.
- Ради бога. Загляните в соседнюю статью «Сила Лоренца», где написано буквально следующее «Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется.» Доказательство, что для силы Ампера он выполняется, можно найти здесь: на этот сайт ссылается английская Википедия.Clothclub 02:24, 9 января 2016 (UTC)
- А откуда вы взяли, что «Закон взаимодействия двух элементарных электрических токов, известный как закон Ампера, на самом деле был позднее предложен Грассманом» и формулировку оригинального закон Ампера? Если вы укажите источник, то это надо оставить. Всё остальное, к сожалению, прийдется убрать. — Alexei Kopylov 01:44, 9 января 2016 (UTC)
- А что тут сложного? Кликайте сюда и копируйте свой текст в окошко. Впрочем я не знаю правил этого проекта.
- Alexei Kopylov, а что такое самостоятельная значимость? Я это не очень понимаю. Мне, например, это доказательство было нужно, а найти его я нигде не смог, хотя искал везде. Но я согласен: Википедия — не мой личный сайт, и вы можете поступить по правилам, если считаете, что я их нарушаю. Только перенесите, пожалуйста, доказательства сами, а то я не очень разбираюсь во всем этом.
- Я вижу, вы не ходили по предложенной ссылке. Учебник Матвеева А.Н. «Электричество и магнетизм.» 2005г., стр.71: «Используемая в настоящее время формула для взаимодействия элементов тока была получена в 1844 г.Грассманом ( 1809-1877) и имеет в современных обозначениях вид dF12= (m0/4*pi)*(1/r12^3)*( [I2*dl2, [I1*dl1,r12]])». Формулировка оригинального закона Ампера находится в английской Википедии. Она же может быть получена из формулы Максвелла, если подставить k=-1, о чем тоже сказано в английской википедии. Формула Максвелла есть в книге Treatise on Electricity and Magnetism.Clothclub 02:24, 9 января 2016 (UTC)
- Понятно. А зачем тогда доказывать, что 3-й закон Ньютона выполняется для силы Ампера в формулировке Грассмана, и то, что оригинальный закон Ампера эквивалентен закону Грассмана? Разве первое не следует сразу из второго? —Alexei Kopylov 01:31, 27 января 2016 (UTC)
- Вы правы, вроде бы следует. Однако в доказательстве эквивалентности я опирался на выводы, полученные в доказательстве 3-го закона Ньютона. После фразы «В таком случае для силы F12 можно записать:» следует формула, к которой в доказательстве эквивалентности фактически я свел оригинальный закон Ампера в интегральной форме, доказав, что второй интеграл (P) равен нулю. Кроме того, как я уже говорил, доказательство выполнения 3-го закона Ньютона я позаимствовал в одном английском источнике — на мой взгляд, оно может иметь и самостоятельную ценность (если говорить вашим языком). И оно более простое, чем доказательство эквивалентности. Но самое главное даже не в этом. Если вы посмотрите внимательно на формулу Максвелла в дифференциальной форме (в которой присутствует параметр k), вы заметите, что 3-й закон Ньютона для нее выполняется вообще всегда, при любом k. Поэтому непонятно, каким образом Грассман мог получить свою формулу, в которой 3-й закон в дифференциальной форме не выполняется. Точнее, это понятно: он зачем-то выбросил ту часть формулы, которая при интегрировании дает ноль. Но вот правомочность этого действия для меня сомнительна. И я все жду, что придет человек, который обратит на это внимание и допишет, как же там на самом деле все исторически сложилось, почему Грассман так поступил. И кроме того, лично мне было бы интересно, если бы кто-нибудь написал о роли Лапласа в выводе закона Ампера (имеется в виду закон Био-Савара-Лапласа), потому что история каким-то образом обо всём этом умалчивает. Я это к тому веду, что, на мой взгляд, не нужно выкидывать те части, которые вроде бы кажутся лишними. Они не лишние, поскольку позволяют посмотреть на все с разных сторон. Но, конечно, это не мне решать.Clothclub 15:22, 27 января 2016 (UTC)
- А разве закон Грассмана не есть закон Максвелла при к=1? Alexei Kopylov 19:06, 27 января 2016 (UTC)
- Да, почти. Просто прочтите написанное в статье — уверен, что вы разберетесь. Ко мне претензии маленькие: в данном случае я просто перевел английскую вики. Грассман действительно взял k=1, но еще и потерял часть формулы. Об этом в английской вики не сказано, но это очевидно (после того, как я все расписал).Clothclub 20:16, 27 января 2016 (UTC)
- Не помню, я уже просил ссылку на английский источник из которого вы взяли доказательство? Alexei Kopylov 19:10, 27 января 2016 (UTC)
- В любом случае, я ее уже приводил. Вот онаClothclub 20:16, 27 января 2016 (UTC)
- А разве закон Грассмана не есть закон Максвелла при к=1? Alexei Kopylov 19:06, 27 января 2016 (UTC)
- Вы правы, вроде бы следует. Однако в доказательстве эквивалентности я опирался на выводы, полученные в доказательстве 3-го закона Ньютона. После фразы «В таком случае для силы F12 можно записать:» следует формула, к которой в доказательстве эквивалентности фактически я свел оригинальный закон Ампера в интегральной форме, доказав, что второй интеграл (P) равен нулю. Кроме того, как я уже говорил, доказательство выполнения 3-го закона Ньютона я позаимствовал в одном английском источнике — на мой взгляд, оно может иметь и самостоятельную ценность (если говорить вашим языком). И оно более простое, чем доказательство эквивалентности. Но самое главное даже не в этом. Если вы посмотрите внимательно на формулу Максвелла в дифференциальной форме (в которой присутствует параметр k), вы заметите, что 3-й закон Ньютона для нее выполняется вообще всегда, при любом k. Поэтому непонятно, каким образом Грассман мог получить свою формулу, в которой 3-й закон в дифференциальной форме не выполняется. Точнее, это понятно: он зачем-то выбросил ту часть формулы, которая при интегрировании дает ноль. Но вот правомочность этого действия для меня сомнительна. И я все жду, что придет человек, который обратит на это внимание и допишет, как же там на самом деле все исторически сложилось, почему Грассман так поступил. И кроме того, лично мне было бы интересно, если бы кто-нибудь написал о роли Лапласа в выводе закона Ампера (имеется в виду закон Био-Савара-Лапласа), потому что история каким-то образом обо всём этом умалчивает. Я это к тому веду, что, на мой взгляд, не нужно выкидывать те части, которые вроде бы кажутся лишними. Они не лишние, поскольку позволяют посмотреть на все с разных сторон. Но, конечно, это не мне решать.Clothclub 15:22, 27 января 2016 (UTC)
- Понятно. А зачем тогда доказывать, что 3-й закон Ньютона выполняется для силы Ампера в формулировке Грассмана, и то, что оригинальный закон Ампера эквивалентен закону Грассмана? Разве первое не следует сразу из второго? —Alexei Kopylov 01:31, 27 января 2016 (UTC)
Диаметр БАКа рассчитывался для протона по этому уравнению.
q[V×H]=mpV2R{\displaystyle q[V\times H]=m_{p}{\frac {V^{2}}{R}}}
Слева центростремительная сила Лоренца, справа центробежная сила инерции.
Говорить о не выполнения третьего закона для сил инерции и Лоренца, мягко говоря, нельзя.—Михаил Певунов 17:31, 21 января 2016 (UTC)
- Михаил Певунов, каким образом у вас получилось приравнять вектор к скаляру? Так, как вы пишете, писать нельзя. И потом, почему «говорить о не выполнения третьего закона для сил инерции и Лоренца, мягко говоря, нельзя»? В частном случае он вполне может выполняться, а вот в общем — нет. Чтобы доказать последнее, достаточно единственного примера. Этот пример — заряды движутся перпендикулярно друг другу. Выше я приводил ссылку на схему.Clothclub 02:18, 22 января 2016 (UTC)
1.Если вы ознакомитесь с учебником физики, то узнаете, что работа, это скаляр, равна произведению вектора силы, на вектор перемещения. A=F→×S→{\displaystyle A={\vec {F}}\times {\vec {S}}}
Вы путаете понятие скалярной величины с модулем векторного произведения.
2. Если заряды движутся перпендикулярно друг другу, то сила Лоренца равна нулю, по определению.
3. Не вижу смысла обсуждать с вами проблемы физики. Ваши тексты сохранены по недосмотру редакции.—Михаил Певунов 14:04, 24 января 2016 (UTC)
- Михаил Певунов, вы еще и векторное произведение от скалярного не отличаете. Думаю, с учебником физики в первую очередь не мешало бы ознакомиться именно вам. Лучше пишите поменьше, чтобы не сбивать людей с толку.Clothclub 14:49, 24 января 2016 (UTC)
Статья нуждается в упрощении[править код]
Рисунок нуждается в корректировке. Круги могут ввести в заблуждение. Не понятно почему вектор Н перпендикулярен силовым линиям магнитного поля.
Надо обозначить окружность с радиусом R c центром в точке 1 и показать ее как Н1 на всей окружности. Тогда в точке 2 ,будет начало вектора Н1
Показать окружность с центром в точке 2, тогда в точке 1 будет начало вектора Н2
H→2=moI22piR{\displaystyle {\vec {H}}_{2}=m_{o}{\frac {I_{2}}{2piR}}}
Тогда перемножением векторов получаем
F1−2=I→1×H→2=moI22piR×I1=moI2I12piR{\displaystyle F_{1-2}={\vec {I}}_{1}\times {\vec {H}}_{2}=m_{o}{\frac {I_{2}}{2piR}}\times I_{1}=m_{o}{\frac {I_{2}I_{1}}{2piR}}}
- Михаил Певунов, к чему этот пустой трёп? Если вы считаете, что рисунок должен быть улучшен — хотя бы предложите свой вариант. Я не вижу, чтобы вы предложили какой-нибудь рисунок. Более того, хоть рисунок рисовал и не я, но мне он кажется удачным и лично меня вполне устраивает. Я даже думаю, если вы попытаетесь нарисовать то, о чем вы говорите, вы поймете, что ошибаетесь. Потому что вы опять начинаете приравнивать вектор к скаляру. Эта ошибка у вас и во всех нижеследующих формулах.Clothclub 02:18, 22 января 2016 (UTC)
Почему статья начинается с уравнения dF=j→×B→dV{\displaystyle dF={\vec {j}}\times {\vec {B}}dV}
Диаметр проводника у Ампера не был переменным, переменными были ток и радиус.
Автор хотел образованность свою показать, вот и показал нелепое.
Лучше бы он показал два дифференциальных уравнения.
1.dF=H→2×I→1dI{\displaystyle 1.dF={\vec {H}}_{2}\times {\vec {I}}_{1}dI}
2.dF=I→1×H→2dH{\displaystyle 2.dF={\vec {I}}_{1}\times {\vec {H}}_{2}dH}
Оба уравнения имеют одинаковое решение. Это значит, что для силы Ампера третий закон соблюдается. .—Михаил Певунов 00:29, 20 января 2016 (UTC)
И что тут то делают всякие форумные неучи.
V→2=V2{\displaystyle {\vec {V}}^{2}=V^{2}}
Произведение векторов может дать вектор, а может и скаляр, тогда определяется только модуль, без направления.
Понял?
Да?
—Михаил Певунов 17:58, 24 января 2016 (UTC)
Прошу редакцию посмотреть правильные рисунки по теме.[править код]
Щелкнуть по ссылке. Нужные кадры два первых. Когда запустится первый, щелкнуть по нему, он остановится.Затем хапустить и щелкнуть по аторому. Остальные кадры на хвост сели. Так работает Ютуб слайдов. https://you.be/71qKy0AV2xk
youtu в черном списке. Вставьте в ссылку после you буковки tu и просмотрите на любом форумном редакторе. —Михаил Певунов 15:32, 24 января 2016 (UTC)
- Он не зря в чёрном списке. По вопросам физики (и по многим другим вопросам) youtube не считается в Википедии авторитетным источником, поэтому приводить ссылки на него не нужно. Лучше всего привести ссылки на публикацию в рецензируемом журнале или учебник. — stannic(обс)(вкл)(выкл) 18:13, 24 января 2016 (UTC)
Отвечать в данной теме должен чел, имеющий физико-математическое образование. Я предлагаю посмотреть, как улучшить рисунок, а вы предлагаете мне сначала опубликовать его в платном журнале.
Я пишу, что решение уравнения вашего АИ dF=i→B→dV{\displaystyle dF={\vec {i}}{\vec {B}}dV} дает размерность I*B*метр, потому как размерность плотности тока метр-2, а объем метр3, но вы не понимаете абсурдность этой размерности.—Михаил Певунов 10:59, 25 января 2016 (UTC)
Узнали бы Ампер, Био и Савар свои законы в данной статье.[править код]
В их времена никаких векторов не было. Они собирали свои установки, наблюдали, замеряли и обнаружив закономерности, обнародовали свои законы.
Ампер замерял силовое взаимодействие двух двух параллельных прямых проводников при различных параметрах постоянного тока и на различных расстояниях между ними. Вопрос о направлении токов перед ним не стоял.
То, что силы взаимодействия направлены по кратчайшей прямой, перпендикулярно проводникам, для него было очевидным.
Также очевидным для него было, что силовое взаимодействие проводников, как и гравитационное взаимодействие, подчиняется третьему закону Ньютона. Иначе это будет не взаимодействие, что он и показал в своем законе F1.2=kI1I22piR=−F2.1=−kI2I12piR{\displaystyle F_{1.2}=k{\frac {I_{1}I_{2}}{2piR}}=-F_{2.1}=-k{\frac {I_{2}I_{1}}{2piR}}}
Ампер практически замерил силу силу взаимодействия бесконечных проводников на симметричных отрезках длиной Δ=1m{\displaystyle \Delta =1m} на расстоянии R = 1 метр при силе тока 1 ампер. Которая по современным данным равна 2*10-7 ньютон
Тогда его формула приобретает вид 2*10-7 = 2∗10−7k1∗12pi{\displaystyle 2*10^{-7}k{\frac {1*1}{2pi}}}
Отсюда магнитная постоянная k=m0=2pi∗2∗10−7=4pi∗10−7{\displaystyle k=m_{0}=2pi*2*10^{-7}=4pi*10^{-7}} Это известное выражение, но не известно откуда оно взялось. Непонятно зачем в статье формула https://upload.wikimedia.org/math/e/c/2/ec267329d3cda88fe6bca032e7b716e2.png Зачем в знаменатель и числитель умножен на 2.
Чуть раньше Био с Саваром установили, сила напряженности магнитного поля Н расстоянии R направлена перпендикулярно радиусу и и пропорциональна moI12piR=h2{\displaystyle m_{o}{\frac {I_{1}}{2piR}}=H_{1}}
А так как, эта сила должна быть пропорциональна току I2=qV→{\displaystyle I_{2}=q{\vec {V}}} то формула силы Ампера записывалась F=q∗V∗H.{\displaystyle F=q*V*H.}
И н потому что так им хотелось, а потому что такое замерялось.
То, что я тут изложил, не моя самодеятельность, а взято из учебников, но в доступном для понимания школьниками. Данная статья доступна для людей уже владеющих физикой и математикой.
А оно им надо.
Непонятно, зачем в силу Ампера вводить плотность тока i→=I→S{\displaystyle {\vec {i}}={\frac {\vec {I}}{S}}} c размерностью ампер/метр2, но тогда следует писать
dF→=i→∗S∗H→dL=I→H→dL{\displaystyle d{\vec {F}}={\vec {i}}*S*{\vec {H}}dL={\vec {I}}{\vec {H}}dL}
Уровень изложения во введении совершенно неадекватен. Весьма простое выражение для практического случая перпендикулярных проводника и силовых линий магнитного поля F=BLI, где L — длина, тщательно замаскировано значками векторов, дифференциальных форм, и т.д., и т.п. —Викидим (обс.) 22:02, 24 ноября 2018 (UTC)
Третий закон Ньютона и Грассман[править код]
Формулы-баяны, выписанные с целью доказать очевидное: третий закон Ньютона соблюдается. В этом кто-то из учёных сомневался? Если нет, то откуда формулы? —Викидим (обс.) 22:27, 2 декабря 2018 (UTC)
- Например, Сивухин в третьем томе своего курса физики пишет, что «В общем случае силы магнитного взаимодействия [двух движущихся точечных зарядов] не удовлетворяют принципу равенства действия и противодействия». И добавляет «для взаимодействий, осуществляющихся посредством полей, соблюдение принципа равенства действия и противодействия не обязательно». О том же пишет и Матвеев в своей книге «Механика и теория относительности». —VladVD (обс.) 09:16, 3 декабря 2018 (UTC)
- Спасибо! У них разве есть эти многомерные интегралы? —Викидим (обс.) 10:33, 3 декабря 2018 (UTC)
- Коли уж здесь появился специалист, как этот Грассман сумел сформулировать закон Ампера и где это описано? —Викидим (обс.) 10:38, 3 декабря 2018 (UTC)
- Доказательство того, что механическое взаимодействие замкнутых токов удовлетворяет принципу равенства действия и противодействия, имеется в книге Тамма «Основы теории электричества». На первый взгляд, это доказательство покороче, чем представленное в статье. Однако и оно содержит двойные интегралы по контурам. К тому же думаю, что после дополнения его необходимыми подробностями оно станет не менее громоздким, чем то, что содержится в статье.
- О законе Грассмана никогда ничего не слышал. Об этом законе нет ничего и в статье о Грассмане в английской ВП. —VladVD (обс.) 13:42, 3 декабря 2018 (UTC)
- Вроде бы решение очевидно тогда: раздел о третьем законе снабдить ссылкой на Тамма и пояснением, почему это вообще интересно, а раздел о Грассмане просто удалить. —Викидим (обс.) 18:17, 3 декабря 2018 (UTC)
- Мне эта статья не нравится тем, что макроскопически простое по сути (и полезное для общего понимания принципов работы многих машин) явление тщательно замаскировано за нехитрой, но объёмной, математикой, при том, что для деталей у нас уже есть Сила Лоренца. Введение хорошо бы переписать так, чтобы было понятно школьнику. —Викидим (обс.) 18:21, 3 декабря 2018 (UTC)
- Прошлое обсуждение вопроса есть, оказывается, выше в разделе с интригующим названием #Под кат. Похоже, что Грассман заимствован из англовики — но упомяну у Матвеева. Из англовики это уже ушло, а вот у нас осталось. —Викидим (обс.) 21:36, 3 декабря 2018 (UTC)
- Ссылаться на Тамма в разделе о третьем законе было бы нехорошо. У Тамма логика рассуждений и набор формул не такие, как здесь в статье.
- Есть ещё одна проблема. Дело в том, что в одних источниках (например, Сивухин) законом Ампера называют соотношение dF=I[dl,B]{\displaystyle \mathrm {d} \mathbf {F} =I[d\mathbf {l} ,B]}, а в других (например, Физическая энциклопедия) — dF21=μ0I1I24π[dr1,[dr2,r1−r2]]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {F} _{21}={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. —VladVD (обс.) 15:10, 4 декабря 2018 (UTC)
- По-моему, имеет смысл завести раздел о терминологии, выделив его из введения, тем более что надо разойтись и с силой Лоренца. Там можно разместить соображения о связи с единицами измерения (см. [1], по этой логике первая формула ближе к Лоренцу), соображения о производстве/непроизводстве работы. —Викидим (обс.) 00:20, 5 декабря 2018 (UTC)
Что такое сила Ампера? :: SYL.ru
Знания о том, что такое сила Ампера, как она относится и чем может быть полезна для людей, необходимы для тех, кто работает с током. Как для собственной безопасности, так и для работы с различной радиоэлектроникой (при конструировании рельсетронов, что довольно популярно). Но хватит ходить вокруг, приступим к выяснению того, что такое сила Ампера, особенности этой силы и где она используется. Также можно будет прочитать потенциал использования в будущем и пользу от использования сейчас.
Закон Ампера
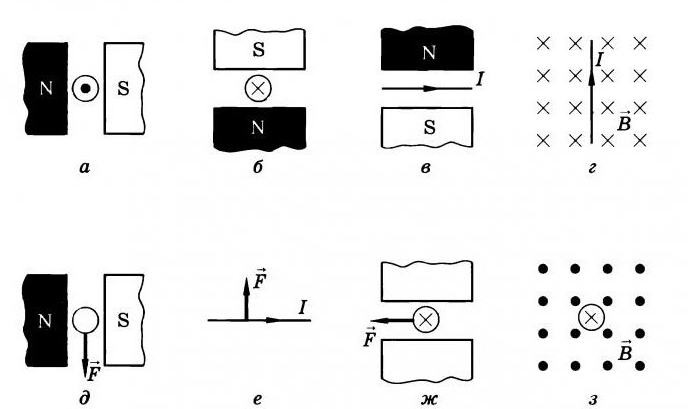 Сила Ампера является главной составляющей закона Ампера — закона о взаимодействии электрических токов. В нём говорится, что в параллельных проводниках, в которых электрические токи текут в одном направлении, возникает сила притягивания. А в тех проводниках, в которых электрические токи текут в противоположных направлениях, возникает сила отталкивания.
Сила Ампера является главной составляющей закона Ампера — закона о взаимодействии электрических токов. В нём говорится, что в параллельных проводниках, в которых электрические токи текут в одном направлении, возникает сила притягивания. А в тех проводниках, в которых электрические токи текут в противоположных направлениях, возникает сила отталкивания.Также законом Ампера называют закон, который определяет силу действия магнитного поля не небольшую часть проводника, по которой протекает ток. В данном случае она определяется как результат умножения плотности тока, который идёт по проводнику, на индукцию магнитного поля, в котором проводник находится.
Из самого закона Ампера сделаны выводы, что сила Ампера равняется нулю, если величина угла, расположенного между током и линией магнитной индукции, тоже будет равняться нулю. Другими словами, проводник для достижения нулевого значения должен быть расположен вдоль линии магнитной индукции.
А что же такое сила Ампера?
 Это сила, с которой магнитное поле влияет на часть проводника, по которому течёт ток. Сам проводник находится в магнитном поле. Сила Ампера прямо зависит от силы тока в проводнике и векторного произведения длины части проводника, множимого на магнитную индукцию.
Это сила, с которой магнитное поле влияет на часть проводника, по которому течёт ток. Сам проводник находится в магнитном поле. Сила Ампера прямо зависит от силы тока в проводнике и векторного произведения длины части проводника, множимого на магнитную индукцию.В формульном виде всё будет выглядеть так: са=ст*дчп*ми. Здесь:
- са – сила Ампера,
- ст – сила тока,
- дчп – длина части проводника,
- ми – магнитная индукция.
История открытия
Впервые его сформулировал Андре Ампер, который применил закон к постоянному току. Открыт он был в 1820 году. Этот закон в будущем имел далеко идущие последствия, ведь без него представить работу целого ряда электрических приборов просто невозможно.
Правило левой руки
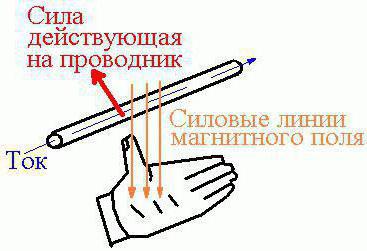
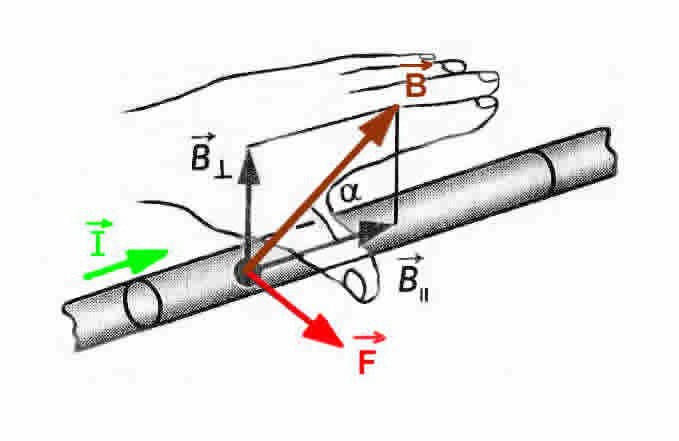 Это правило помогает запомнить направление силы Ампера. Само правило звучит так: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый по углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника. Могут возникнуть некоторые затруднения при использовании этого правила, но только если угол между током и индукцией поля слишком маленький. Для простоты применения этого правила ладонь часто располагают так, чтобы в неё входил не вектор, а модуль магнитной индукции (как изображено на картинке).
Это правило помогает запомнить направление силы Ампера. Само правило звучит так: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый по углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника. Могут возникнуть некоторые затруднения при использовании этого правила, но только если угол между током и индукцией поля слишком маленький. Для простоты применения этого правила ладонь часто располагают так, чтобы в неё входил не вектор, а модуль магнитной индукции (как изображено на картинке).Сила Ампера (при использовании двух параллельных проводников)
 Представьте два бесконечных проводника, которые расположены на определённом расстоянии. По ним протекают токи. Если токи текут в одном направлении, то проводники притягиваются. В противоположном случае они будут отталкиваться один от одного. Поля, которые создают параллельные проводники, направлены встречно друг другу. И чтобы понять, почему они реагируют именно так, вам достаточно вспомнить о том, что одноименные полюса магнитов или одноименные заряды всегда отталкиваются. Для определения стороны направления поля, созданного проводником, следует использовать правило правого винта.
Представьте два бесконечных проводника, которые расположены на определённом расстоянии. По ним протекают токи. Если токи текут в одном направлении, то проводники притягиваются. В противоположном случае они будут отталкиваться один от одного. Поля, которые создают параллельные проводники, направлены встречно друг другу. И чтобы понять, почему они реагируют именно так, вам достаточно вспомнить о том, что одноименные полюса магнитов или одноименные заряды всегда отталкиваются. Для определения стороны направления поля, созданного проводником, следует использовать правило правого винта.Применение знаний о силе Ампера
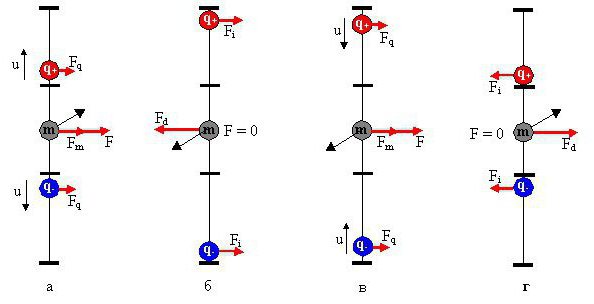 Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера:
Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера:- Любые узлы в электротехнике. Самый популярный – элементарный электродвигатель.
- Различные виды электротехники, которая формирует различные звуковые колебания с использованием постоянного магнита. Механизм действия таков, что на магнит действует электромагнитное поле, что создает расположенный рядом проводник с током, и изменение напряжения приводит к смене звуковой частоты.
- На силе Ампера построена работа электромеханических машин, в которых движение обмотки ротора происходит относительно обмотки статора.
- С помощью силы Ампера происходит электродинамический процесс сжатия плазмы, что нашло применение в токамаках и потенциально открывает огромные пути развития термоядерной энергии.
- Также с помощью электродинамического сжатия применяется электродинамический метод прессования.
Потенциал
Несмотря на уже сейчас существующее практическое применение, потенциал использования силы Ампера настолько огромен, что с трудом поддаётся описанию. Она может использоваться в сложных механизмах, которые призваны облегчить существование человека, автоматизировать его деятельность, а также усовершенствовать природные жизненные процессы.
Эксперимент
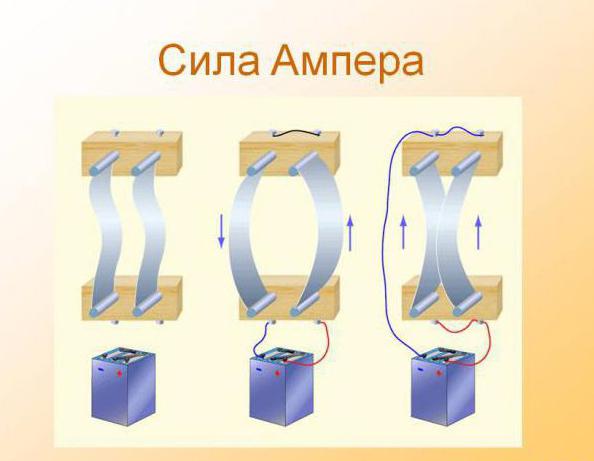
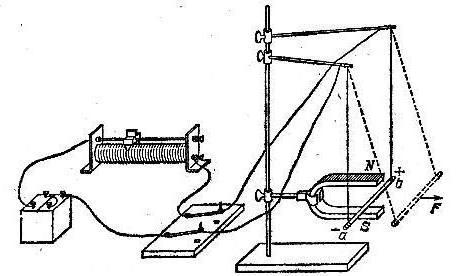 Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке. Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:
Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке. Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:- Магнитное поле действует исключительно на проводник с током.
- На проводник с током в магнитном поле действует сила, которая является следствием их взаимодействия. Именно под воздействием этой силы проводник движется в пространстве в границах магнитного поля.
- Характер взаимодействия прямо зависит от напряжения электрического тока и силовых линий магнитного поля.
- Поле не действует на проводник с током, если ток в проводнике течёт параллельно направлению линий поля.
Безопасность при работе с током
При работе с электрическим током необходимо придерживаться нескольких простых правил техники безопасности, которые позволят вам избежать негативных последствий:
- Работать с источниками питания не больше 12 Вольт.
- Не работать на воспламеняемых материалах.
- Не работать с мокрыми руками.
- Не браться за части прибора, которые находятся под напряжением.
Ампер — это… Что такое Ампер?
Ампе́р (обозначение: А) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток)[1].
Определение
Современное определение ампера было предложено Международным комитетом мер и весов в 1946 году и принято IX Генеральной конференцией по мерам и весам в 1948 году[2][3].
- Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7ньютона.
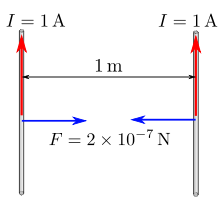 Иллюстрация к определению ампера.
Иллюстрация к определению ампера.Из определения ампера следует, что магнитная постоянная равна Гн/ м или, что то же самое, Н/А² точно. Это утверждение становится понятным, если учесть, что сила взаимодействия двух расположенных на расстоянии друг от друга параллельных проводников единичной длины, по которым текут токи и , выражается соотношением:
Магнитодвижущая сила 1 ампер (ампер-виток) — это такая магнитодвижущая сила, которую создает замкнутый контур, по которому протекает ток, равный 1 амперу.
История и перспективы
Единица измерения, принятая на 1-м Международном конгрессе электриков[4] (1881 г., Париж), названа в честь французского физика Андре Ампера. Она была первоначально определёна как одна десятая единицы тока системы СГСМ (эта единица, известная в настоящее время как абампер или био, определяла ток, создающий силу в 2 дины на сантиметр длины между двумя тонкими проводниками на расстоянии в 1 см).
В 2011 г. XXIV Генеральная конференция по мерам и весам приняла резолюцию[5], в которой предложено в будущей ревизии Международной системы единиц (СИ) продолжить переопределение основных единиц таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.
В частности, предполагается, что СИ станет системой единиц, в которой элементарный электрический заряд e равен 1,602 17X·10−19 Кл точно[6]. Результатом этого явится отмена ныне действующего определения ампера и принятие нового. Величина ампера будет установлена в соответствии с новым точным значением элементарного электрического заряда, выраженным в c .А.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 А | декаампер | даА | daA | 10−1 А | дециампер | дА | dA |
| 102 А | гектоампер | гА | hA | 10−2 А | сантиампер | сА | cA |
| 103 А | килоампер | кА | kA | 10−3 А | миллиампер | мА | mA |
| 106 А | мегаампер | МА | MA | 10−6 А | микроампер | мкА | µA |
| 109 А | гигаампер | ГА | GA | 10−9 А | наноампер | нА | nA |
| 1012 А | тераампер | ТА | TA | 10−12 А | пикоампер | пА | pA |
| 1015 А | петаампер | ПА | PA | 10−15 А | фемтоампер | фА | fA |
| 1018 А | эксаампер | ЭА | EA | 10−18 А | аттоампер | аА | aA |
| 1021 А | зеттаампер | ЗА | ZA | 10−21 А | зептоампер | зА | zA |
| 1024 А | йоттаампер | ИА | YA | 10−24 А | йоктоампер | иА | yA |
| применять не рекомендуется | |||||||
Связь с другими единицами СИ
Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону.
Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.
См. также
Примечания
Литература
- Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Вышэйшая школа, 1979. — С. 23-24. — 416 с. — 30 000 экз.
Ампер — Википедия
Ампе́р (русское обозначение: А; международное: A) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток)[1]. Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.
Определение
Современное определение ампера было предложено Международным комитетом мер и весов в 1946 году и принято IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году[2][3].
Ампер — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7ньютона.
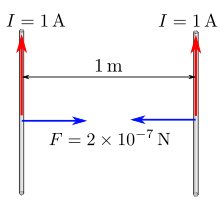 Иллюстрация к определению ампера.
Иллюстрация к определению ампера.Из определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² точно. Это утверждение становится понятным, если учесть, что сила взаимодействия двух расположенных на расстоянии d{\displaystyle d} друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}, приходящаяся на единицу длины, выражается соотношением:
- F=μ04π2I1I2d.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{d}}.}
Магнитодвижущая сила 1 ампер (ампер-виток) — это такая магнитодвижущая сила, которую создает замкнутый контур, по которому протекает ток, равный 1 амперу.
История и перспективы
Единица измерения, принятая на 1-м Международном конгрессе электриков[4] (1881 г., Париж), названа в честь французского физика Андре Ампера. Она была первоначально определена как одна десятая единицы тока системы СГСМ (эта единица, известная в настоящее время как абампер или био, определяла ток, создающий силу в 2 дины на сантиметр длины между двумя тонкими проводниками на расстоянии в 1 см).
В 2011 г. XXIV ГКМВ приняла резолюцию[5], в которой предложено в будущей ревизии Международной системы единиц (СИ) продолжить переопределение основных единиц таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.
В частности, предполагается, что СИ станет системой единиц, в которой элементарный электрический заряд e равен 1,602 17X·10−19 Кл точно[6]. Результатом этого явится отмена ныне действующего определения ампера и принятие нового. Величина ампера будет установлена в соответствии с новым точным значением элементарного электрического заряда, выраженным в c·А. В связи с этим в резолюции XXIV ГКМВ по поводу ампера сформулировано следующее положение[5]:
Ампер останется единицей силы электрического тока, но его величина будет устанавливаться фиксацией численного значения элементарного электрического заряда равным в точности 1,602 17X·10−19, когда он выражен единицей СИ c·А, что эквивалентно Кл.
XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей переопределение ампера, и наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ в том же году[7].
Кратные и дольные единицы
В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы ампера образуются с помощью стандартных приставок СИ[2]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в России тех же приставок[8].
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 А | декаампер | даА | daA | 10−1 А | дециампер | дА | dA |
| 102 А | гектоампер | гА | hA | 10−2 А | сантиампер | сА | cA |
| 103 А | килоампер | кА | kA | 10−3 А | миллиампер | мА | mA |
| 106 А | мегаампер | МА | MA | 10−6 А | микроампер | мкА | µA |
| 109 А | гигаампер | ГА | GA | 10−9 А | наноампер | нА | nA |
| 1012 А | тераампер | ТА | TA | 10−12 А | пикоампер | пА | pA |
| 1015 А | петаампер | ПА | PA | 10−15 А | фемтоампер | фА | fA |
| 1018 А | эксаампер | ЭА | EA | 10−18 А | аттоампер | аА | aA |
| 1021 А | зеттаампер | ЗА | ZA | 10−21 А | зептоампер | зА | zA |
| 1024 А | иоттаампер | ИА | YA | 10−24 А | иоктоампер | иА | yA |
| применять не рекомендуется | |||||||
Связь с другими единицами СИ
Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону.
Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.
См. также
Примечания
Литература
- Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Вышэйшая школа, 1979. — С. 23-24. — 416 с. — 30 000 экз.

