Момент силы относительно точки и оси
– для произвольной системы сил.
– для плоской системы сходящихся сил.
1.5. Момент силы относительно точки и оси
1. Алгебраический момент силы относительно точки.
Используется при рассмотрении плоской системы сил. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис.10). Плечом h силы F называют кратчайшее расстояние между этой точкой и линией действия силы. Знак зависит от направления «вращения» тела относительно точки: при «вращении» тела против часовой стрелки будем считать момент положительным МО — (+) и наоборот МО — (-).
;
.
Рис. 10
2. Векторный момент силы относительно точки.
Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю (рис.11), произведению силы на плечо силы относительно этой точки.
Рис. 11
Векторный момент силы относительно точки не меняется при скольжении силы по линии действия и равен нулю, если линия проходит через точку О.
Момент силы относительно начала координат можно выразить через проекции силы на координатные оси и координаты точки приложения силы (рис.12).
Рис. 12
3. Момент силы относительно оси.
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси
Знак определяется направлением вращения (против часовой стрелки − (+), по часовой стрелки − (−)).
Рис. 13
Замечания: а) Mz=0, если сила параллельна оси Oz.
б) Mz=0, если линия действия пересекает ось Oz.
Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
1.6. Приведение системы сил к простейшей системе
Пусть на тело действует произвольная система сил . Приведем эту систему сил к заданному центру. Выберем произвольную точку О за точку приведения
Рассмотрим одну из сил системы – F1. Добавим в точке О нулевую систему сил – (F1′, F2″). Заметим, что силы (F1, F1″) представляют пару сил, которую можно заменить вектором момента пары
Рис.14
M0 (F1), приложенным в точке О (он же равен мо-менту силы F1 относительно центра О), то есть исходная сила эквилентна силе F1′ и вектору момента пары, приложенным в той же точке.
Проведя аналогичную операцию со всеми векторами исходной системы сил, мы получим два пучка векторов, приложенных в точке O – пучок сил и пучок векторов моментов которые приводятся к эквивалентной системе двух векторов:
Главным вектором системы сил называют вектор, равный векторной сумме этих сил (вектор R). Значение главного вектора сил не зависит от выбора точки приведения.
Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки (вектор момента результирующей пары М0). Вектор М0 зависит от точки приведения О:
По проекциям сил можно найти модуль главного вектора и главного момента, а также косинусы их углов с осями координат.
Главный момент плоской системы сил перпендикулярен главному вектору.
1.7. Условия равновесия систем сил
Пространственная система сил
Если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из главного вектора и главного момента пары. Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно, чтобы выполнялось условие: ( где О – произвольная точка)
Эти условия являются векторными условиями равновесия для любой системы сил. В аналитической форме это эквивалентно условиям: Rx=Ry=Rz=0; Mx=My=Mz=0,
то есть в самом общем случае имеем шесть скалярных уравнений равновесия (уравнений статики).
Система параллельных сил
Пусть Fi параллельно оси Oz, тогда
Mz тождественно равно нулю и
.
Таким образом, имеем три уравнения равновесия
Рис.15
Плоская система сил (рис. 16)
После отбрасывания тождеств:
Термех / УМК статика.кинематика / лекции / статика / проба1
Лекция 1
1Предмет механики
2.Основные задачи статики
3.Основные понятия и определения статики твердого тела
4. Момент силы относительно центра и оси
5.Способы вычисления момента силы относительно оси
6.Алгебраический момент силы относительно центра
1.Предмет механики
Механика это наука, изучающая основные законы механического движения, т.е. законы изменения взаимного расположения материальных тел или частиц в сплошной среде с течением времени. Содержанием курса теоретической механики в техническом вузе является изучение равновесия и движения абсолютно твердых тел, материальных точек и их систем. Теоретическая механика является базой для многих обще-профессиональных дисциплин (сопротивление материалов, детали машин, теория машин и механизмов и др.), а также имеет самостоятельное мировоззренческое и методологическое значение. Иллюстрирует научный метод познания закономерностей окружающего нас мира – от наблюдения к математической модели, её анализ, получение решений и их применение в практической деятельности.
Курс теоретической механики традиционно делится на три части:
Статика изучает правила эквивалентного преобразования и условия равновесия систем сил.
Кинематика рассматривает движение тел с геометрической стороны, без учета сил, вызывающих это движение.
Динамика изучает движение тел в связи с действующими на них силами.

Основные задачи статики:
Изучение методов преобразования одних систем сил в другие, эквивалентные данным.
Установление условий равновесия систем сил.
Основные понятия и аксиомы статики
Сила мера механического воздействия одного тела на другое.
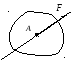
Сила задается
модулем, направлением и точкой приложения.
Обозначается большими буквами латинского
алфавита: 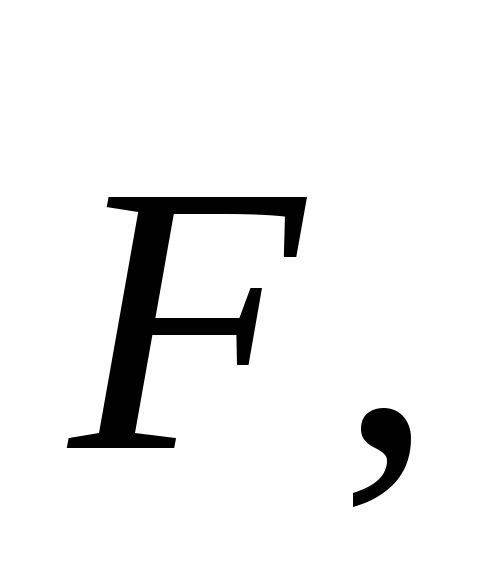
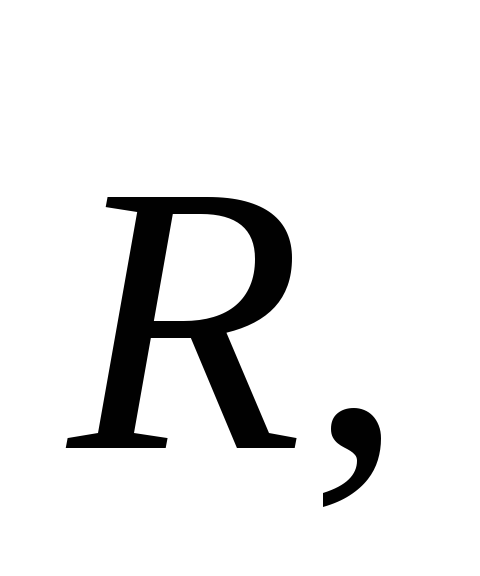
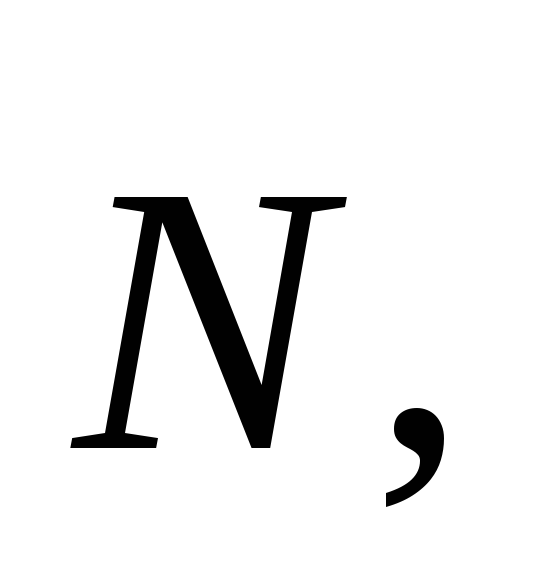

модуль силы.
модуль силы.
Аналитически силу
можно задать ее проекциями на оси
координат.: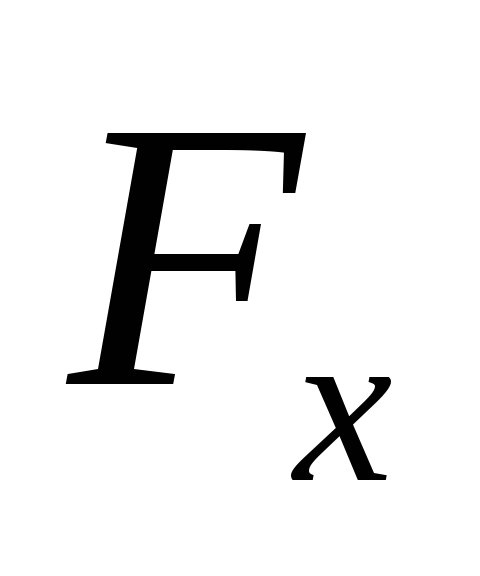 ,
,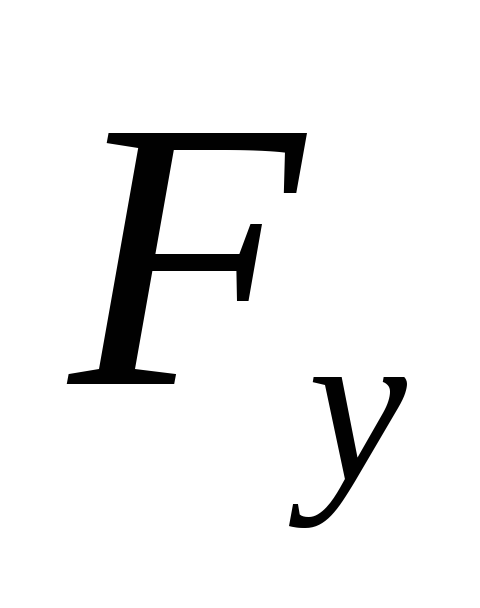
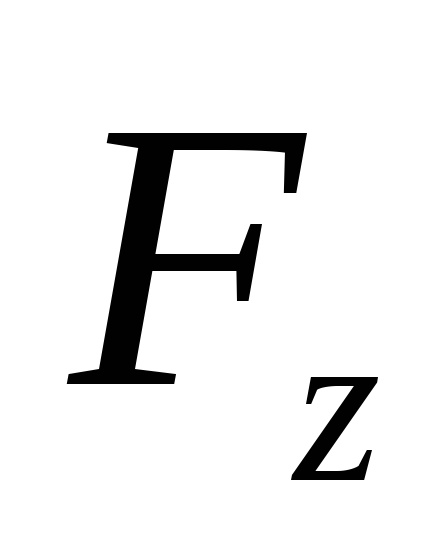 ,
а направление в пространстве
направляющими косинусами:
,
а направление в пространстве
направляющими косинусами: 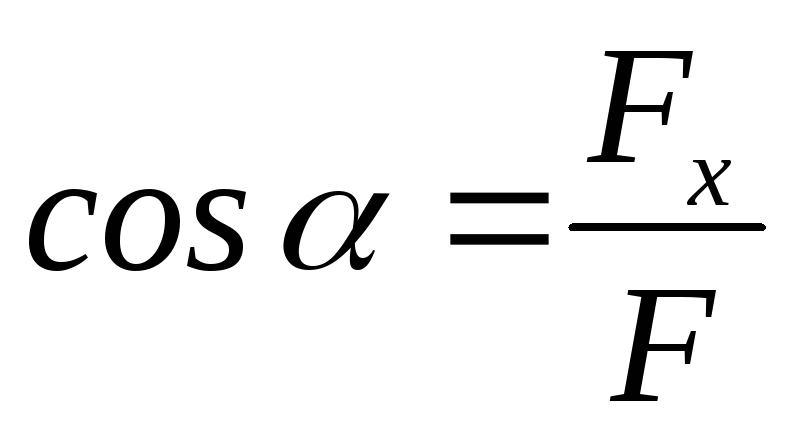 ,
, 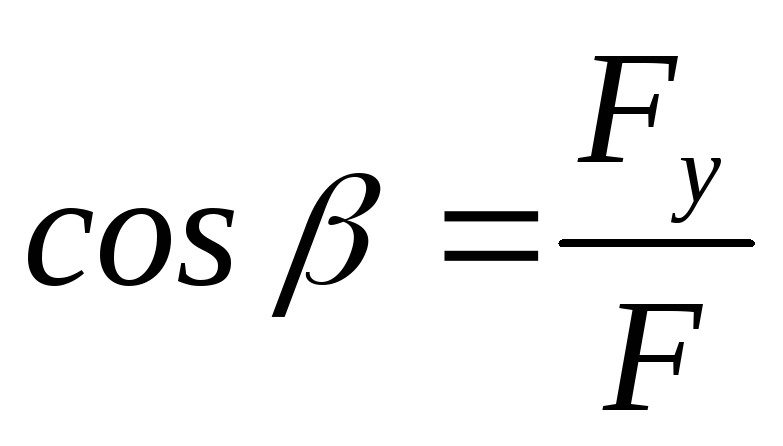 ,
, 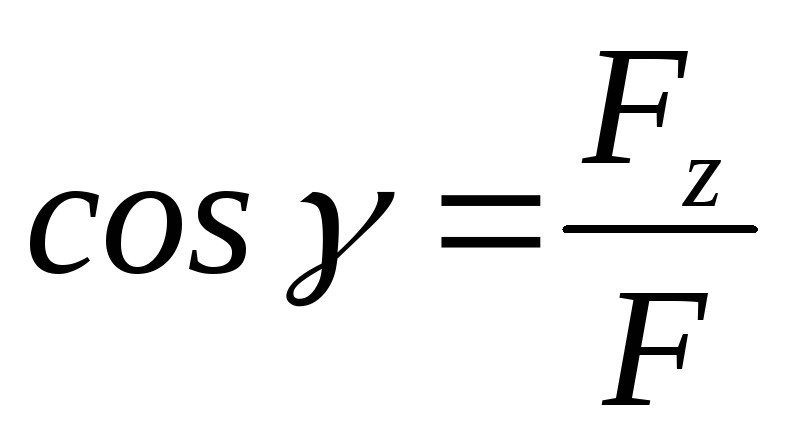 .
.
Совокупность нескольких сил, действующих на твердое тело, называется системой сил
Две системы сил эквивалентны () между собой, если, не нарушая состояния тела, одну систему сил можно заменить другой.
Сила, эквивалентная
данной системе сил, называется равнодействующей: 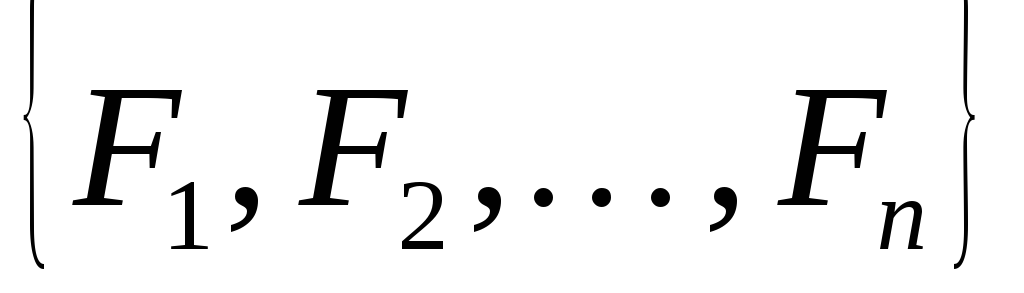
 .
Не всегда систему сил можно заменить
равнодействующей.
.
Не всегда систему сил можно заменить
равнодействующей.
Систему сил,
приложенную к свободному твердому телу,
находящемуся в равновесии, и не выводящую
его из этого состояния, называют уравновешенной
системой сил 
.
Абсолютно твердое тело тело, у которого расстояние между любыми двумя точками остается неизменным.
Момент силы относительно центра и оси
Действие силы на твердое тело, закрепленное в одной точке, заключается в стремлении повернуть его вокруг точки закрепления. Для характеристики вращательного действия силы вводится понятие момента силы относительно центра (или точки).
М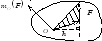 оментом
силы относительно центра называется
векторное произведение радиуса-вектора
точки приложения силы на вектор силы.
оментом
силы относительно центра называется
векторное произведение радиуса-вектора
точки приложения силы на вектор силы.

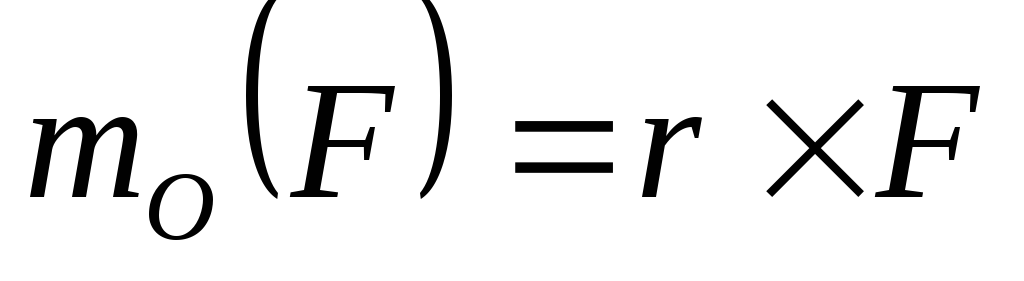
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
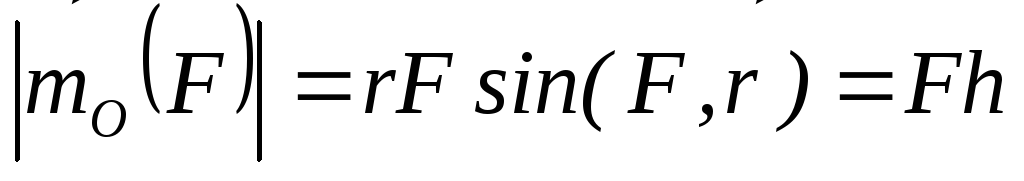 ,
,
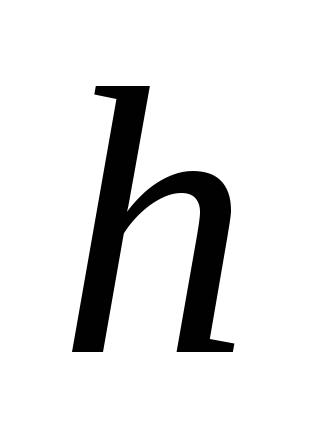 — плечо силы (кратчайшее расстояние
от центра момента до линии действия
силы). Если сила проходит через точку,
то ее момент относительно этой точки
равен нулю.
— плечо силы (кратчайшее расстояние
от центра момента до линии действия
силы). Если сила проходит через точку,
то ее момент относительно этой точки
равен нулю.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.
Алгебраическим моментом силы относительно центра называется взятое со знаком плюс или минус произведение модуля силы на плечо.
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра против хода часовой стрелки

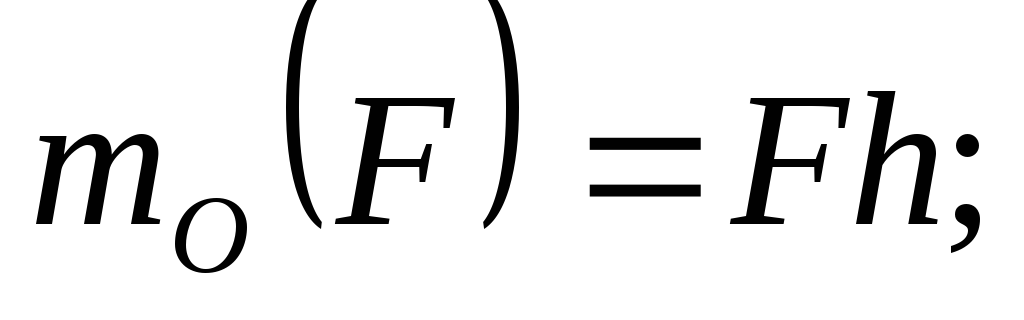

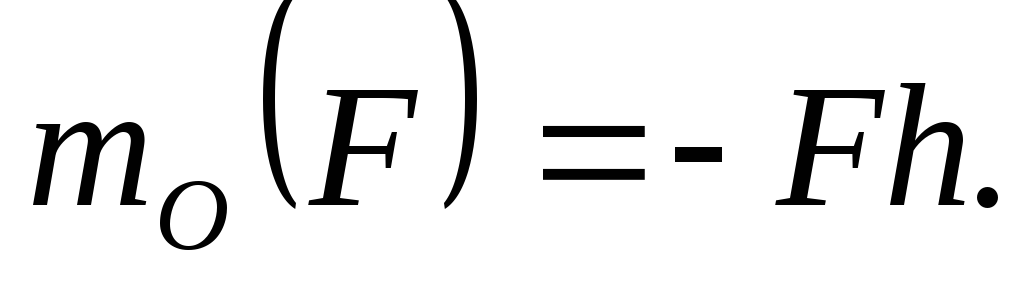
Д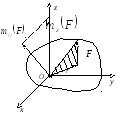 ля
характеристики вращательного действия
силы на тело, закрепленное на оси, служит момент силы относительно оси
алгебраическая величина, равная проекции
вектора момента силы относительно
произвольной точки оси на эту ось:
ля
характеристики вращательного действия
силы на тело, закрепленное на оси, служит момент силы относительно оси
алгебраическая величина, равная проекции
вектора момента силы относительно
произвольной точки оси на эту ось:
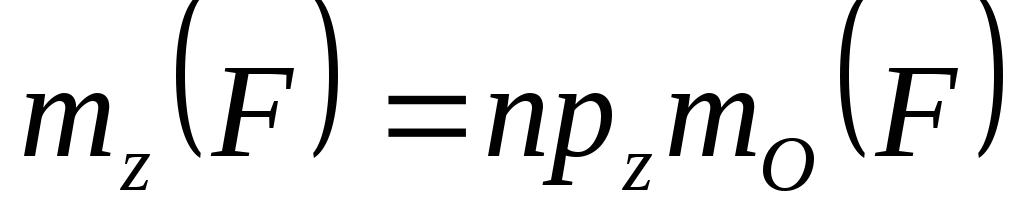 .
.
Способы вычисления момента силы
относительно оси
1. Аналитический
По правилу вычисления векторного произведения:

Откуда:
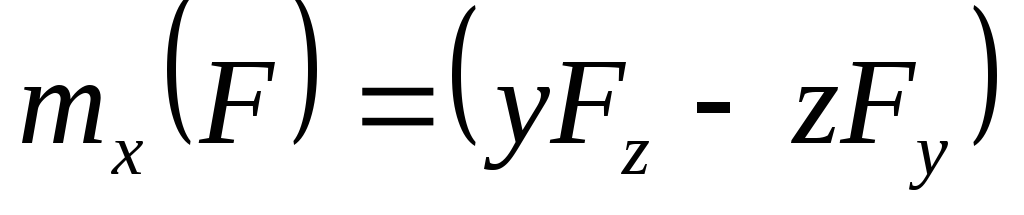 ,
,
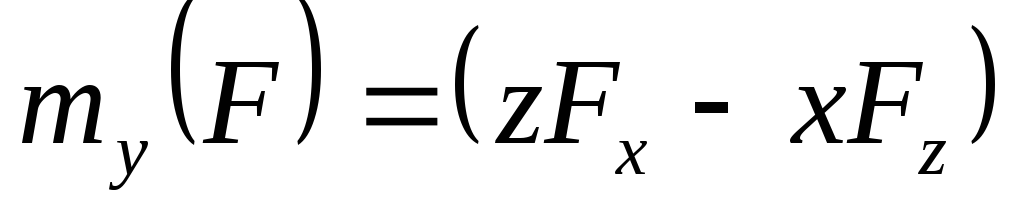 ,
,
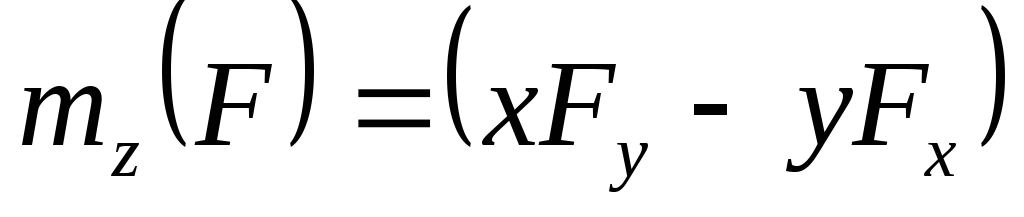 .
.
2.Геометрический
П ровести
плоскость ,
перпендикулярную данной оси (Oz),
спроектировать силу на эту плоскость
и вычислить момент проекции
ровести
плоскость ,
перпендикулярную данной оси (Oz),
спроектировать силу на эту плоскость
и вычислить момент проекции  относительно точки O
точки пересечения оси z с плоскостью .
относительно точки O
точки пересечения оси z с плоскостью .
Момент положителен, если, глядя с положительного направления оси, вращение видно происходящим против хода часовой стрелки.
Момент силы относительно оси равен нулю, если сила параллельна оси или линия действия силы пересекает ось.
31
03. Момент силы относительно точки и относительно оси
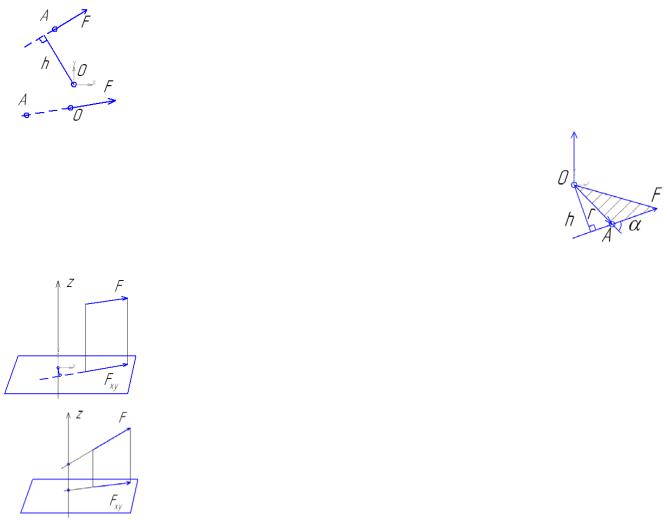
Момент силы относительно точки.
Момент силы характеризует ее вращательное действие.
Алгебраическим моментом силы относительно точки называется произведением модуля силы на плечо взятое с соответствующим знаком.
Плечом называется, длинна перпендикуляра опущенного из точки на плечо действия сил. Момент имеет знак «+» если сила стремиться совершать поворот относительно точки против часовой стрелки а «–» в противном случае.
mo(F)=±F*h
mo(F)= 0 если сила лежит на линии действия силы и плечо
равняется 0. |
|
|
|
|
| mo F = F |
|
|
| ||
Векторным моментом | сил | относительно |
| точки |
| ||||||
mo F = F = r F sin | = F m = mo(F) |
|
|
|
| ||||||
называется определенным | соотношением: |
|
|
|
|
|
| ||||
|
| α |
|
|
|
|
| ||||
Модуль вектора | момента | сил относительно | точки – это |
| |||||||
|
|
|
|
| |||||||
алгебраическим моментом силы относительно точки. |
|
|
|
| |||||||
| Момент силы относительно Оси. |
|
| ||||||||
| Моментом |
| силы | относительно | оси | называют | |||||
алгебраический момент проекции силы на плоскость | |||||||||||
перпендикулярную оси относительно точки пересечения оси с | |||||||||||
| Существует 2 ( ) | = mo Fxy = ±Fxy | h |
| |||||||
этой плоскостью. | ( ) = 0 |
|
|
|
|
| |||||
| 2. |
|
|
|
|
|
|
| |||
силы. | ( ) |
| случая при которых момент равняется 0. | ||||||||
= 0 |
|
|
|
|
|
| |||||
| 1. | OzIIF |
|
|
|
|
|
|
|
| |
если ось пересекается с линей действия
Момент силы относительно оси равен проекции векторного момента силы относительно любой точки оси на эту
точку.
Момент силы относительно точки и оси
Стр 1 из 5Следующая ⇒Основные понятия статики
Теоретическая механика — наука, изучающая общие законы механического движения и механического взаимодействия материальных тел.
Мех. движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и времени.
Мех. взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их мех. движения.
Статика — раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.
Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой (МТ). МТ обладает массой и способностью взаимодействовать с другими телами. Системой МТ или механической системой называется такая совокупность МТ, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы. Тела, расстояния между любыми точками которых остаются неизменными, называют абсолютно твердыми.
Кинематическое состояние тела — состояние покоя или движения определенного характера.
Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Изображается сила вектором. Прямая, по которой направлена сила называется, называется линией действия силы.
Совокупность нескольких сил, действующих на данное тело, называется системой сил.
Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются эквивалентными.
Сила, эквивалентная некоторой системе сил, называется равнодействующей.
Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.
Система сил, которая, будучи приложенной к твердому телу, находящемуся в состоянии покоя, не выводящая его из этого состояния, называется системой взаимно уравновешивающихся сил.
Внешними называются силы, действующие на МТ (тела) данной системы со стороны МТ (тел), не принадлежащих этой системе. Внутренними называются силы взаимодействия между МТ (телами) рассматриваемой системы.
Аксиомы статики
1) Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется равномерно прямолинейно.
2) Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны, и они направлены по одной линии прямой в противоположные стороны.
3) Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил.
Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление.
4) Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
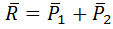
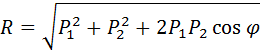
φ – угол между направлениями сил 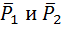
5) Аксиома равенства действия и противодействия. Всякому действию соответствует равное по величине и противоположное по направлению противодействие.
6) Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил приложенных к деформирующемуся телу сохраняется при его затвердении.
Связи и их реакции
Тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающие свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Задаваемые силы выражают действие на твердое тело других тел, вызывающих или свободных вызвать изменение его кинематического состояния. Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело.
Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил действуют реакции связей.
Теорема Пуансо
Приведение силы к заданному центру (метод Пуансо) – силу можно перенести параллельно самой себе в любую точку плоскости, если добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки.
Добавим к системе в точке A две силы, равные по величине между собой и величине заданной силы, направленные по одной прямой в противоположные стороны параллельно заданной силе.
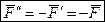 |
Кинематическое состояние не изменилось (аксиома о присоединении). Исходная сила и одна из добавленных сил противоположно направленная образуют пару сил. Момент этой пары численно равен моменту исходной силы относительно центра приведения. Во многих случаях пару сил удобно изображать дуговой стрелкой.
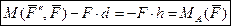 |
Центр параллельных сил
При сложении двух параллельных сил две параллельные приводятся к одной силе — равнодействующей, линия действия которой направлена параллельно линиям действия сил. Равнодействующая приложена в точке делящей прямую, на расстояния обратно пропорциональные величинам сил.
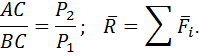
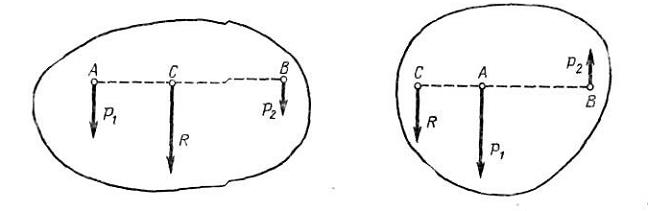
Поскольку силу можно переносить по линии ее действия, то точка приложения равнодействующей не определена. Если силы повернуть на один и тот же угол и вновь произвести сложение сил, то получим другое направление линии действия равнодействующей. Точка пересечения этих двух линий равнодействующих может рассматриваться как точка приложения равнодействующей, не изменяющая своего положения при повороте всех сил одновременно на один и тот же угол. Такая точка называется центром параллельных сил.
Теорема Вариньона
Теорема о моменте равнодействующей силы: момент равнодействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно этой точки, а момент равнодействующей силы относительно оси равен алгебраической сумме моментов составляющих сил относительно этой оси.
Определим момент равнодействующей силы 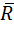 , приложенной в точке К, относительно произвольно выбранного центра приведения О:
, приложенной в точке К, относительно произвольно выбранного центра приведения О:
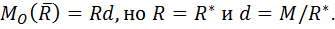
Тогда 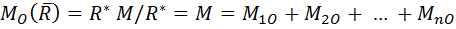 , что сформулировано в первой части теоремы.
, что сформулировано в первой части теоремы.
Проекция момента равнодействующей на произвольную ось 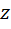 проходящую через точку O равна:
проходящую через точку O равна:
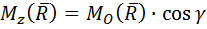
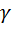 – угол между осью
– угол между осью 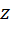 и направлением
и направлением 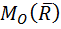 .
.
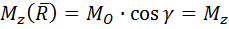
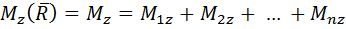 , что сформулировано во второй части теоремы.
, что сформулировано во второй части теоремы.
Фермы. Методы расчета ферм
 Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.
Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.
Способ вырезания узлов. Суть способа заключается в том, что мысленно вырезают каждый узел фермы, прикладывают к нему известные силы и реакции стержней, которые направляют от узла, т.к. неизвестно какие стержни фермы растянуты, а какие сжаты, изначально полагают, что все стержни растянуты, а затем составляются уравнения равновесия сил, приложенных к каждому узлу. Расчет фермы начинают с узлов, к которым приложено не более двух неизвестных сил для плоской фермы, и не более трех для пространственной.
Метод Риттера. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая их растянутыми. Затем составляют уравнения моментов относительно точек Риттера (точка пересечения двух из трех перерезанных стержней). Из полученных уравнений определяются усилия в стержнях.
Сила трения. Законы трения
Силы трения скольжения появляются при скольжении одного тела по поверхности другого в плоскости соприкосновения тел. Часто приходится учитывать действие этих сил при изучении равновесия тел. С этой целью используются приближенные законы трения, полученные опытным путем:
1. Сила трения возникает лишь тогда, когда приложенные к телу силы стремятся сдвинуть его или оно уже скользит по поверхности другого тела. Сила трения направлена в сторону, противоположную направлению движения или в сторону, противоположную той, в которую приложенные силы стремятся сдвинуть тело.
2. В конкретных условиях сила трения может принимать любые значения в пределах от нуля до некоторого придельного значения 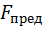 , которое достигается в состоянии относительного проскальзывания или в состоянии предельного равновесия тела.
, которое достигается в состоянии относительного проскальзывания или в состоянии предельного равновесия тела.
3. Величина предельной силы трения пропорциональна силе нормального давления N между трущимися поверхностями и не зависит от величины площади соприкасания тел:
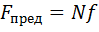 ,
,
где 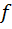 – коэффициент трения скольжения.
– коэффициент трения скольжения.
Наибольший угол, на который может отклониться линия действия силы реакции негладкой поверхности от нормали, проведенной к ней в точке контакта тел, называется углом трения скольжения. Тангенс угла скольжения равен коэффициенту трения скольжения:
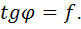
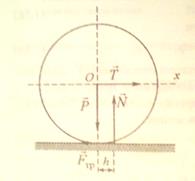 Трением качения называется сопротивление, возникающие при качении одного тела по поверхности другого. Трение качения возникает оттого, что поверхность катящегося тела и плоскость, по которой тело катится, не абсолютно тверды, а несколько деформируются вследствие давления тела на плоскость.
Трением качения называется сопротивление, возникающие при качении одного тела по поверхности другого. Трение качения возникает оттого, что поверхность катящегося тела и плоскость, по которой тело катится, не абсолютно тверды, а несколько деформируются вследствие давления тела на плоскость.
 – вес колеса и его линия действия проходит через центр О катка. Приложим в этой точке горизонтальную силу
– вес колеса и его линия действия проходит через центр О катка. Приложим в этой точке горизонтальную силу 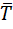 . В месте контакта катка и поверхности возникает сила трения скольжения
. В месте контакта катка и поверхности возникает сила трения скольжения 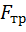 , препятствующая проскальзыванию катка.
, препятствующая проскальзыванию катка.
Под действием силы  происходит деформация в месте контакта, в результате чего нормальная реакция
происходит деформация в месте контакта, в результате чего нормальная реакция  смещается в сторону действия силы
смещается в сторону действия силы 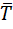 на некоторое расстояние h. Максимальная величина h=k, соответствующая предельному положению равновесия, называют трением качения.
на некоторое расстояние h. Максимальная величина h=k, соответствующая предельному положению равновесия, называют трением качения.
Значение 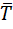 , соответствующее случаю предельного равновесия,
, соответствующее случаю предельного равновесия,
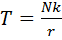 .
.
Основные понятия кинематики. Скорость точки. Ускорение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Тело, относительно которого рассматривается положение изучаемого тела, называется телом отсчета.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Скорость — векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Для характеристики движения вводится понятие средней скорости:
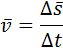
Мгновенная скорость определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt:
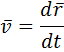
Ускорение — быстрота изменения модуля и направления скорости точки.
Среднее ускорение:
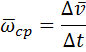
Мгновенное ускорение:
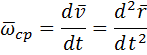
Поступательное движение тела. Задание движения. Распределение скоростей и ускорений точек тела
Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Теорема. Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести:
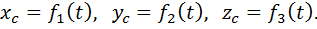
Общие для всех точек твердого тела, движущегося поступательно, скорость 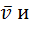 ускорение
ускорение 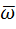 называют скоростью и ускорением поступательного движения твердого тела.
называют скоростью и ускорением поступательного движения твердого тела.
Вращательное движение. Задание движения
Вращательным называется такое движение тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.
При вращении тела угол поворота  изменяется в зависимости от времени:
изменяется в зависимости от времени:  .
.
Величина, характеризующая быстроту изменения угла поворота 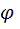 с течением времени называется угловой скоростью тела.
с течением времени называется угловой скоростью тела.
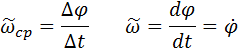
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
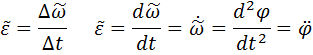
Уравнение равномерного вращения тела. Вращение тела с постоянной скоростью называется равномерным.
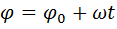
Уравнение равнопеременного вращения тела. Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением.
Основные понятия статики
Теоретическая механика — наука, изучающая общие законы механического движения и механического взаимодействия материальных тел.
Мех. движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и времени.
Мех. взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их мех. движения.
Статика — раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.
Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой (МТ). МТ обладает массой и способностью взаимодействовать с другими телами. Системой МТ или механической системой называется такая совокупность МТ, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы. Тела, расстояния между любыми точками которых остаются неизменными, называют абсолютно твердыми.
Кинематическое состояние тела — состояние покоя или движения определенного характера.
Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Изображается сила вектором. Прямая, по которой направлена сила называется, называется линией действия силы.
Совокупность нескольких сил, действующих на данное тело, называется системой сил.
Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются эквивалентными.
Сила, эквивалентная некоторой системе сил, называется равнодействующей.
Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.
Система сил, которая, будучи приложенной к твердому телу, находящемуся в состоянии покоя, не выводящая его из этого состояния, называется системой взаимно уравновешивающихся сил.
Внешними называются силы, действующие на МТ (тела) данной системы со стороны МТ (тел), не принадлежащих этой системе. Внутренними называются силы взаимодействия между МТ (телами) рассматриваемой системы.
Аксиомы статики
1) Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется равномерно прямолинейно.
2) Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны, и они направлены по одной линии прямой в противоположные стороны.
3) Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил.
Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление.
4) Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
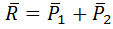
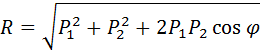
φ – угол между направлениями сил 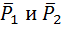
5) Аксиома равенства действия и противодействия. Всякому действию соответствует равное по величине и противоположное по направлению противодействие.
6) Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил приложенных к деформирующемуся телу сохраняется при его затвердении.
Связи и их реакции
Тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающие свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Задаваемые силы выражают действие на твердое тело других тел, вызывающих или свободных вызвать изменение его кинематического состояния. Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело.
Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил действуют реакции связей.
Момент силы относительно точки и оси
Момент силы — векторная величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы на вектор этой силы. МС характеризует вращательное действие этой силы на твердое тело.
Алгебраическим моментом силы относительно точки (центра момента) называется взятое со знаком «+» или «-» произведение величины силы на плече силы.

Плечо силы — кратчайшее расстояние от точки центра момента до линии действия силы.
Правило знаков: если сила стремится повернуть тело вокруг точки центра момента против часовой стрелки ставится знак «+», если по часовой знак «-».
Из определения следует, что момент силы относительно точки равен нулю лишь в том случае, когда плече силы равно нулю, т.е. линия действия силы проходит через точку центр момента.
Момент силы относительно оси — момент проекции силы на плоскость перпендикулярную оси взятый относительно точки пересечения оси и плоскости.
Правило знаков: если с острия оси видеть вращение плоскости под действием проекции силы против часовой стрелки ставится знак «+», если по часовой — знак «-».
Из определения следует что момент силы относительно оси равен нулю если:
1) сила пересекает ось (h=0)
2) сила параллельна оси (Fp=0)
3) сила совпадает с осью (h=0 и Fp=0)
Для вычисления момента силы относительно оси необходимо:
1) Выбрать плоскость перпендикулярную оси;
2) Спроецировать силу на эту плоскость;
3) Найти точку пересечения оси и плоскости;
4) Определить плечо относительно точки;
5) Определить знак момента.
10.2. Зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку

100
Проекция вектор-момента силы относительно точки на любую ось, проходящую через эту точку, численно равна моменту силы относительно этой оси.
Действительно, пусть к телу в точке А приложена сила Р (рис. 10. 1, г). Вектор момента силы относительно произвольно выбранной точки О направлен перпендикулярно плоскости треугольника ОАВ (см. п. 4. 2), а модуль его согласно выражению (4. 2) равен:
Мо (Р) = 2 А Оав
Момент силы относительно оси z, проходящей через точку О, в соответствии с выражением (10. 2) равняется:
Мz (Р) = 2 А Оав
Треугольник Оав является проекцией треугольника ОАВ на плоскость, перпендикулярную оси z, т.е.
А Оав = А ОАВ Соs α ,
где α — угол между плоскостями треугольников ОАВ и Оав и, следовательно, между вектором Мo (Р) и осью z.
Тогда, проектируя вектор Мo (Р) на ось z, получаем:
[Мо (Р)]z = Моz = Мо (Р) Соs α = 2 А ОАВ Соs α = 2 А Оав = Мz (Р) ,
т.е. |
|
Моz = Мо (Р) Соs α = Мz (Р) | (10. 5) |
10.3. Аналитические выражения моментов силы относительно координатных осей
Пусть в точке А с известными координатами х, у, z приложена сила Р (рис. 10. 1, д). Вектор-момент силы Мо (Р) относительно начала координат (т. О) перпендикулярен плоскости треугольника ОАВ. Проведем также радиус-вектор r точки А относительно точки О. Выразим эти вектора через их проекции на оси координат:
r = xi + yj + z k,
Р = Хi + Yj + Zk ,
Мо (Р) = Моx i + Моу j + Моz k ,
где Х, У, Z и Моx , Моу , Моz – проекции на координатные оси
соответственно силы Р и момента Мо (Р).
В соответствии с выражением (10. 5) можно записать:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мо (Р) = Мx (Р) i + Му (Р) j + Мz (Р) k | (10. 6) | |||||||||||||||
101
Принимая во внимание зависимость (4.3) и выражая векторное
произведение |
| х Р через определитель, получаем: |
|
|
|
|
|
|
| |||||||||||||||||||||||
r |
|
|
|
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| i j k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
Мо (Р) = r * Р |
| х у z | = i | у z | — j | x z | + k | x у | = | |||||||||||||||||||||||
= |
|
|
|
|
|
| Х У Z |
|
|
|
|
| У Z |
|
|
|
|
| У Z |
|
|
|
|
| Х У |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (уZ — zУ) i + (zX — xZ) j + (xY — уХ) k . | (10.7) | ||
Сравнивая выражения (10. 6) и (10. 7), получаем формулы Эйлера для | |||
определения моментов силы относительно координатных осей: |
| ||
|
|
|
|
Мx (Р) = уZ – zУ , |
| ||
Му (Р) = zX – xZ , | (10. 8) | ||
Мz (Р) = xY – уХ . |
| ||
10.4. Приведение пространственной системы сил к данному центру
Чтобы выяснить, в каком кинематическом состоянии находится твердое
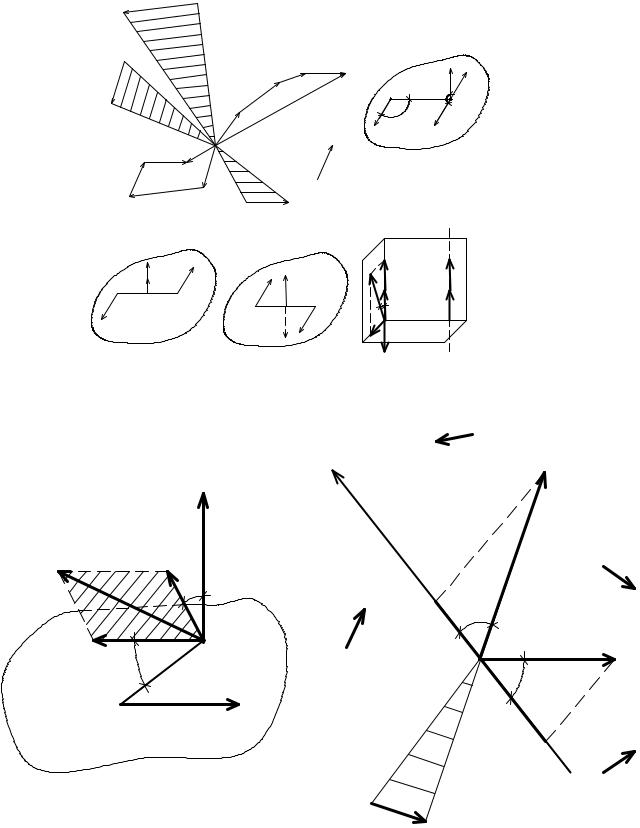
тело под действием системы сил (Р1, Р2, … , Рn ), произвольно расположенных в пространстве, ее необходимо преобразовать в более простую эквивалентную систему сил. Применяя метод Пуансо (см. п. 6. 1), приведем силы Р1, Р2, … , Рn к центру О (рис. 10. 2, а). В результате в центре О получим приведенные силы Р1′, Р2′, … , Рn′ , образующие систему сходящихся сил, и вектор-моменты М1, М2, … , Мn присоединенных пар, направленные перпендикулярно плоскостям треугольников, построенных на силе Рi (i = 1, 2 … , n) и точке О.
Геометрически суммируя вектора Рi′, а затем – вектора Мi, получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
|
| |||||
|
|
|
|
|
|
|
|
|
|
| R | ′= ∑ | Рi | ′ | , |
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| i=1 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| n | (10. 9) | ||||||
|
|
|
|
|
|
|
|
|
| М | o = ∑ | М | i . |
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| i=1 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Поскольку Рi ′ = Рi и Мi = Мo (Рi), то |
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
|
| |||||
|
|
|
|
|
|
|
|
|
|
| R | ′= ∑i=1 | Рi |
|
| , |
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
|
|
|
|
| (10. 10) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Мo = ∑i=1Мо (Рi) .
Геометрическая сумма всех сил системы называется главным вектором (R′), а геометрическая сумма вектор-моментов всех сил относительно центра приведения (т. О) – главным моментом пространственной системы сил (Мo).
P2
a.
| Mn | б. |
|
P1 | M2 |
|
|
|
|
| |
|
| A | d |
M1 | M0 | 0Е |
|
9 |
|
| P2 | ‘ |
|
|
|
|
|
|
| Pn |
|
|
|
|
|
|
|
| д. |
|
| z0 | |
|
|
|
|
|
|
| II |
в. | P | г | I | M0 | ‘ |
| M0 ‘ |
|
| ||||||
| M | P |
| M0 |
|
|
|
|
|
| aR’ |
|
|
| |
|
|
|
|
|
| R | |
|
|
|
|
|
|
| |
|
| M |
| O |
| d | A |
Рис. 10.2
a. |
|
|
|
|
|
| M0 |
R |
|
| R’ |
|
|
| a |
| Q | 9 | O |
| d | ||
|
| 0 | |
|
|
| |
|
| Е | Q1 |
|
|
|
P2
Pn | M o z | a |
| |
O | M i | |||
|
| |||
|
|
|
ai

103
Таким образом, силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору, и одной паре сил с моментом, равным главному моменту всех сил относительно центра приведения, т.е.
(Р1, Р2, … , Рn) ~ R′, Мo.
Следует отметить, что как и в случае плоской системы сил, главный вектор не зависит, а главный момент пространственной системы сил зависит от выбора центра приведения.
10.5. Возможные случаи приведения пространственной системы сил к данному центру
1. Система сил приводится к одной паре. Если окажется, что R′ = 0, а Мо≠0, то система сил приводится к одной паре сил с моментом, равным главному моменту сил, который в данном случае (при R′ = 0) не зависит от выбора центра приведения, так как вектор-момент пары сил является свободным вектором.
2. Система сил приводится к равнодействующей. Если R′ ≠ 0, а Мо = 0, то система сил приводится к равнодействующей R, равной главному вектору и приложенной в центре приведения:
n
R = R′= ∑ Рi .
i=1
Пространственная система приводится к равнодействующей и в том случае, если R′ ≠ 0 и Мо ≠ 0, но R′ Мо. При этом равнодействующая R геометрически равна главному вектору R′, но линия действия ее не проходит через центр приведения, а отстоит от него на расстоянии, равном:
Мо d = ——-
R′
Действительно, представим главный момент Мо в виде пары сил (R, R′′), действующей в одной плоскости с главным вектором R′ (рис. 10. 2, б), полагая при этом, что R = R′′ = R′ и R′′ = — R′. В результате получим:
(Мo , R′) ~ (R, R′, R′′) ,
но
(R′, R′′) ~ 0
и, следовательно,
(Мo , R′) ~ R ,
причем, равнодействующая R приложена не в центре приведения О, а в точке А, поскольку модуль главного момента равен:
Мo = М (R, R′′) = Rd = R′d ,
откуда
104
Мо
R′
В этом случае условием приведения системы сил к равнодействующей является равенство нулю скалярного произведения главного вектора и вектора главного момента сил. Действительно:
R′ . Мo = R′ Мo Соs (R′,^ Мo) ,
но |
| ′,^ |
| o) = 90° и, следовательно, |
| ||
(R | М | (10. 11) | |||||
|
|
|
| R′ . |
| o | = 0 , |
|
|
|
| М | |||
или |
| ||||||
Rх′ Мoх + Rу′ Мoу +Rz′ Мoz = 0 ,
где Rх′ , Rу′ , Rz′ и Мoх , Мoу , Мoz – проекции на оси координат
соответственно вектора R′ и Мo.
3. Если окажется, что R′ ≠ 0 , Мо ≠ 0 и α = (R′,^ Мo) ≠ 90°, то система сил приводится или к силовому винту, или к двум скрещивающимся силам (т.е. к силам, лежащим в разных плоскостях). При этом скалярное произведение
R′. Мo ≠ 0, так как в выражении (10. 11) угол (R′,^ Мo) ≠ 90° и, следовательно,
Rх′ Мoх + Rу′ Мoу +Rz′ Мoz ≠ 0 .
Рассмотрим сначала приведение системы сил к силовому винту. Силовой винт (или динама) – это совокупность силы и пары сил, действующей в плоскости, перпендикулярной силе. Различают левый силовой винт (рис. 10. 2, в) и правый силовой винт (рис. 10. 2, г).
Проведем через центр приведения О три взаимно перпендикулярные плоскости I, II, III (рис. 10. 2, д), располагая вектора R′ и Мo в плоскости I.
Разложим главный моментМo на составляющие Мo′ иМo′′ (рис. 10. 2, д):
Мo = Мo′ + Мo′′,
где
Мo′ = Мo Соs α , а Мo′′= Мo Sin α .
Представим вектор-момент М′′o в виде пары сил (R, R′′), действующих в плоскости II, принимая R = R′′ = R′ и R′′ = — R′, т.е.
М″o = Мo(R, R′′) ,
где
М″o = М (R, R′′) = R d = R′ d ,
откуда |
|
М″о | Мо Sin α |
d = ——- = ————— . | |
R′ | R′ |
Таким образом, данная система сил (Р1, Р2, … , Рn) будет эквивалентна следующим системам:
(Р1, Р2, … , Рn) ~ (R′, Мo) ~ (R′ , М″o , Мo′) ~ (R′, R′′, R, Мo′).
105
Но (R′, R′′) ~ 0, следовательно,
(Р1, Р2, … , Рn) ~ (R′, Мo)
Вектор-момент Мo′, как вектор свободный, переносим параллельно самому в точку приложения силы R и в результате получаем силовой винт в виде силы R, равной по модулю главному вектору (R = R′) и пары сил в плоскости, перпендикулярной R, с моментом, равным Мo′ = Мo Соs α.
Прямая Zо, по которой направлена сила R и вектор-момент М′o, называется
центральной осью данной системы сил. Поскольку Мo′ < Мo (катет меньше гипотенузы, см. рис. 10. 2, д), то модуль главного момента системы сил относительно любой точки, лежащей на центральной оси, имеет наименьшее одно и то же значение. Поэтому центральную ось называют также осью наименьших моментов.
Приведем теперь данную систему сил к двум скрещивающимся силам. Заменим главный момент парой сил (Q, Q1), действующей в плоскости, перпендикулярной Мo, совмещая начало одной из сил пары с центром приведения О (рис. 10. 3, а), т.е.
Мo = М (Q, Q1),
где
Мo = М (Q, Q1) = Q d = Q1 d ,
откуда
Мо
Q = Q1 = ——- . d
Складывая геометрически силы R′ и Q1, найдем их равнодействующую:
R = R′ + Q1
В результате получаем:
(Р1, Р2, … , Рn) ~ (R′, Мo) ~ (R , Q) ,
т.е. данная система сил приводится к двум силам R и Q, лежащим в разных плоскостях, или – к двум скрещивающимся силам.
4. Система сил уравновешивается.
Если R′ = 0 и Мo = 0, то пространственная система сил находится в равновесии. Другими словами, условием равновесия произвольной системы сил в пространстве является равенство нулю главного вектора и главного момента сил.
Момент силы. Момент силы относительно центра и осей
Моментом силы относительно произвольного центра в плоскости действия силы, называется произведение модуля силы на плечо.
Плечо — кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т.к. сила-скользящий вектор.
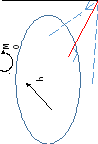
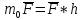
Знак момента:
По часовой-минус, против часовой-плюс;
Момент силы можно выразить как вектор. Это перпендикуляр к плоскости по правилу Буравчика.
Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.
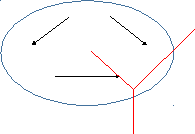
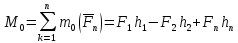
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z;
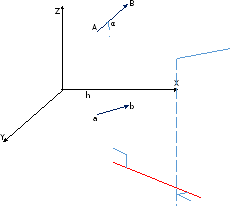
Спроецируем F на XY;
Fxy=Fcosα=ab
m0(Fxy)=mz(F), то есть mz=Fxy*h= Fcosα*h
Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости
Если сила параллельна оси или пересекает ее, то mz(F)=0
Выражение момента силы в виде векторного выражения
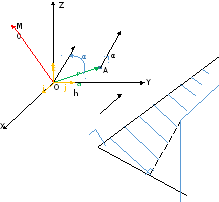
Проведем rа в точку A. Рассмотрим OA x F.
Это третий вектор mo, перпендикулярный плоскости. Модуль векторного произведения можно вычислить с помощью удвоенной площади заштрихованного треугольника.
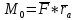 или
или 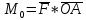
Аналитическое выражение силы относительно координатных осей.
Предположим, что с точкой О связаны оси Y и Z, X с единичными векторами i, j, k Учитывая, что:
rx=X
* Fx
; ry=Y
* Fy;
rz=Z
* Fy получим: mo(F)=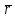 x
x 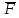 =
=
Раскроем определитель и получим:
mx=YFz — ZFy
my=ZFx — XFz
mz=XFy— YFx
Эти формулы дают возможность вычислить проекцию вектор-момента на оси, а потом и сам вектор-момент.
Теорема Вариньона о моменте равнодействующей
Если система сил имеет равнодействующую, то её момент относительно любого центра равен алгебраической сумме моментов всех сил относительно этой точки
Если приложить Q= -R , то система (Q,F1 … Fn) будет равен уравновешиваться.
Сумма моментов относительно любого центра будет равен нулю.
Аналитическое условие равновесия плоской системы сил
Это плоская система сил, линии действия которых расположены в одной плоскости
Цель расчета задач данного типа — определение реакций внешних связей. Для этого используются основные уравнения в плоской системе сил.
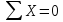
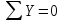
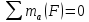
Могут использоваться 2 или 3 уравнения моментов.
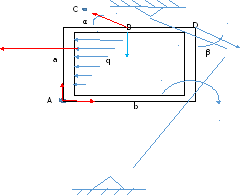 Пример
Пример
Составим уравнение суммы всех сил на ось X и Y:
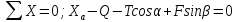
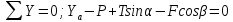
Сумма моментов всех сил относительно точки А:
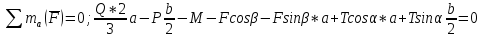
Параллельные силы
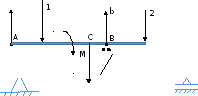

Уравнение относительно точки А:
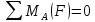
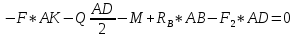
Уравнение относительно точки В:
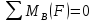
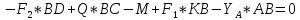
Сумма проекций сил на ось У:
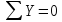
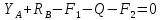
2.7. Момент силы относительно оси
Момент
силы относительно оси характеризует
вращательный эффект, создаваемый силой,
стремящейся повернуть тело вокруг
данной оси. Если рассмотреть тело,
которое может вращаться вокруг некоторой
оси z,
то можно убедиться в том, что весь
вращательный эффект, создаваемый силой 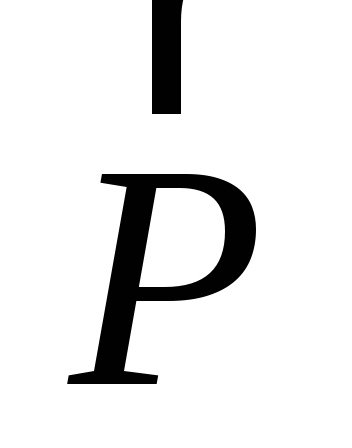 ,
будет совпадать с вращательным эффектом
ее составляющей
,
будет совпадать с вращательным эффектом
ее составляющей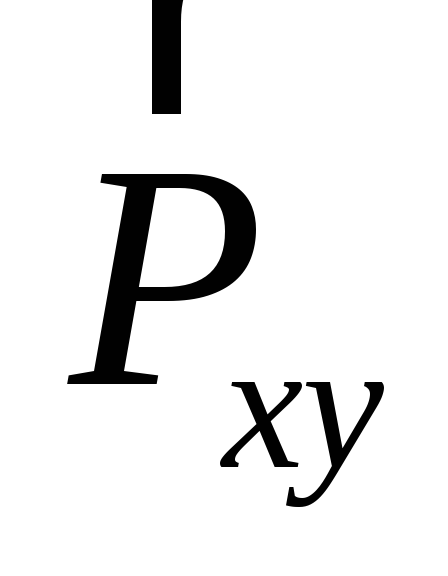 (рис.2.9).
(рис.2.9).
Моментом силы относительно оси называют скалярную величину, равную моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью
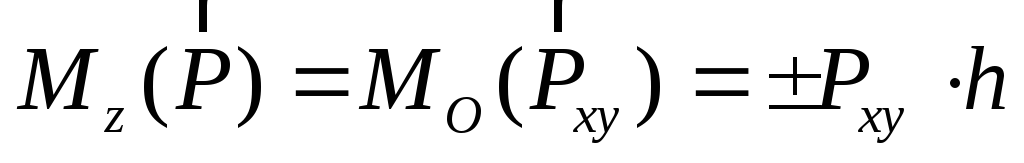 ,
(2.14)
,
(2.14)
где 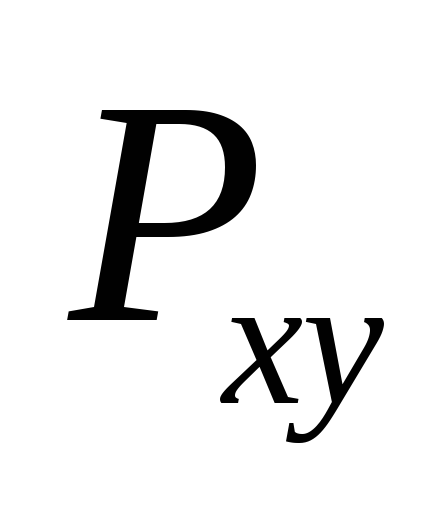 — величина проекции силы
— величина проекции силы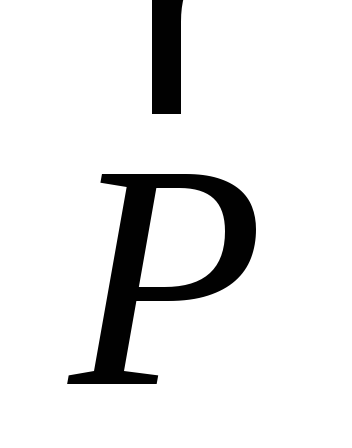 на плоскостьxOy; h – плечо силы
на плоскостьxOy; h – плечо силы 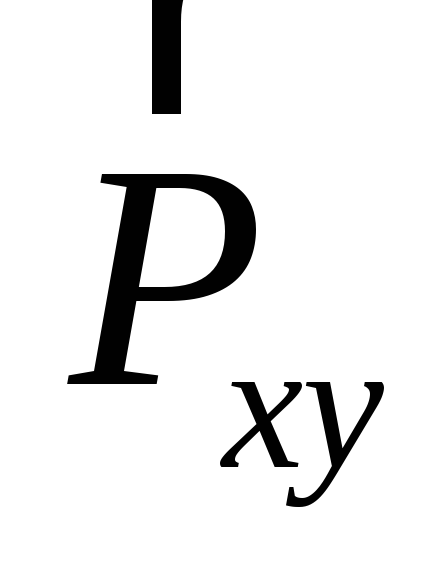 относительно точкиО.
относительно точкиО.
Чтобы найти момент силы относительно оси в соответствии с выражением (2.14), необходимо:
1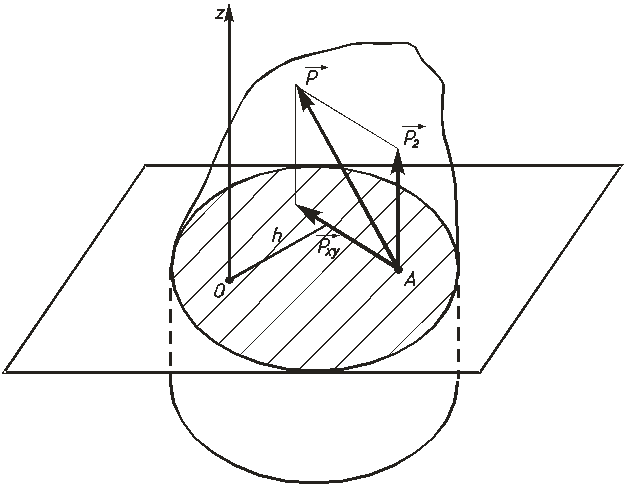 )
провести плоскость, перпендикулярную
оси;
)
провести плоскость, перпендикулярную
оси;
2) спроецировать силу на эту плоскость и вычислить величину про-екции;
3) опустить из точки пересечения оси с плоскостью перпендикуляр на направление проекции и определить его длину h;
Рисунок 2.9
4) вычислить произведение модуля проекции на величину h;
5) определить знак момента в соответствии с правилом знаков.
Момент
считается положительным,
если с положительного конца оси поворот,
производимый силой, виден происходящим
против хода часовой стрелки. Момент
силы относительно оси равен нулю, если
сила и ось принадлежат одной плоскости.
Тогда либо сила параллельна оси z (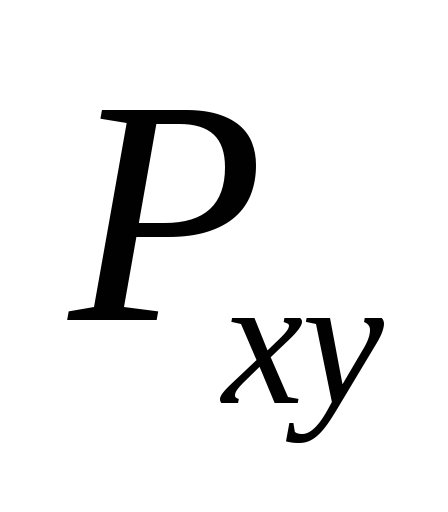 ),
либо линия действия силы пересекает
ось (h =
0).
),
либо линия действия силы пересекает
ось (h =
0).
Аналитические выражения для моментов силы относительно координатных осей представим в виде:
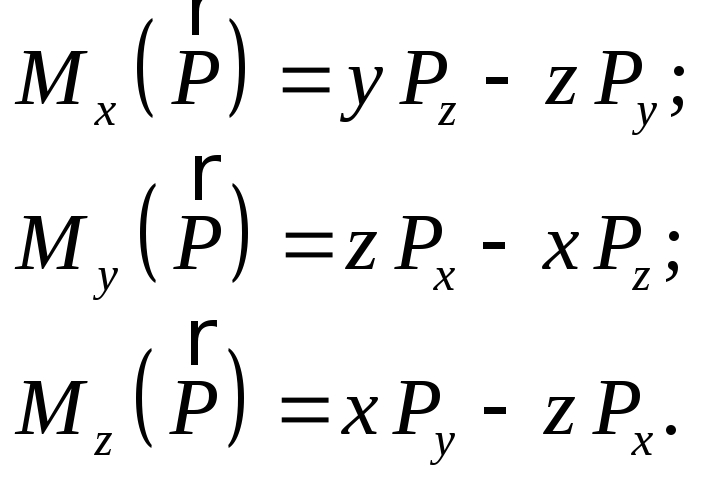 (2.15)
(2.15)
С помощью формул (2.15) можно вычислять моменты силы относительно координатных осей, зная проекции силы на эти оси и координаты точки ее приложения. Сравнивая выражения (2.13) и (2.15), можно найти связь между моментами силы относительно оси и относительно центра, лежащего на этой оси:
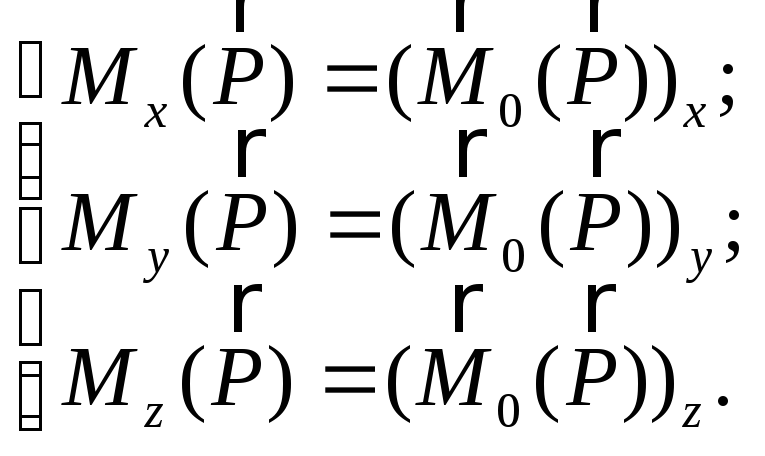 .
(2.16)
.
(2.16)
Таким образом, момент силы относительно оси – это скалярная величина, равная проекции на эту ось вектора-момента силы относительно произвольной точки оси.
2.8. Пара сил и момент пары сил
Парой сил называют систему двух сил, которые равны по модулю, параллельны, направлены в противоположные стороны, и действуют на абсолютно твердое тело (рис.2.10). Плоскость, проходящая через линии действия сил пары, называют плоскостью действия пары.
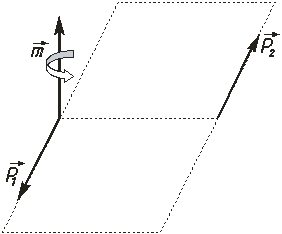
Кратчайшее
расстояние d между линиями действия сил пары называют плечом
пары. Система сил,
образующих пару, очевидно, не находится
в равновесии, так как силы пары не
направлены вдоль одной прямой. В то же
время пара сил не имеет равнодействующей.
Как видно из рис. 2.10, 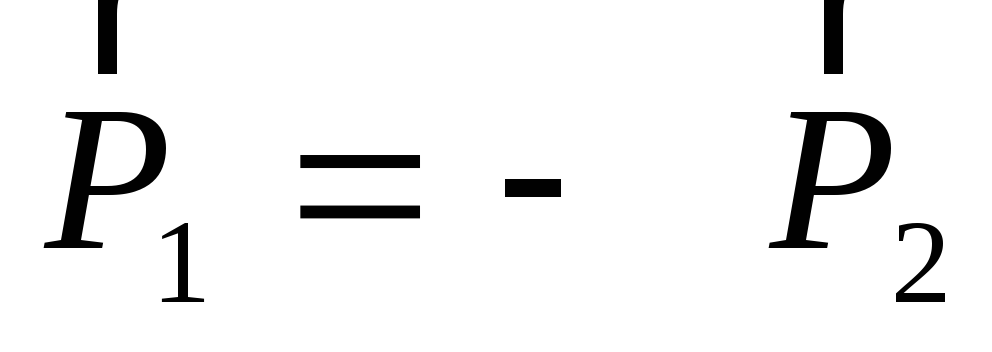 .
.
Рисунок 2.10
Пара сил, как и сила, является самостоятельным силовым фактором, поэтому свойства пары сил, как особой меры механического действия, должны быть изучены отдельно. Пара сил оказывает на тело вращательное воздействие, которое зависит от следующих факторов:
■
модуля одной из сил пары |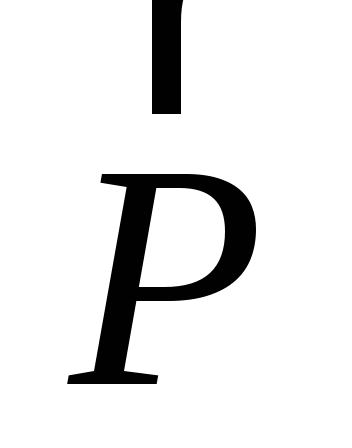 |
и длины плечаd;
|
и длины плечаd;
■ положения плоскости действия пары сил;
■ направления поворота в этой плоскости.
Для количественной характеристики вращательного эффекта, к которому сводится действие пары сил на твердое тело, вводится понятие момента пары сил. Для пар сил, лежащих в одной плоскости, достаточно алгебраического момента пары сил, который равен взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо:
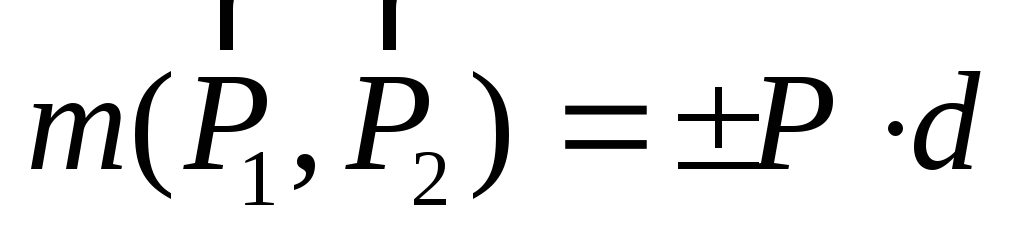 .
(2.17)
.
(2.17)
Правило знаков здесь такое же, как и для момента силы.
При рассмотрении пар сил, не лежащих в одной плоскости, необходимо задать плоскость действия пары сил. Это возможно, если изображать момент пары сил вектором, направленным перпендикулярно заданной плоскости.
Момент
пары сил –
вектор 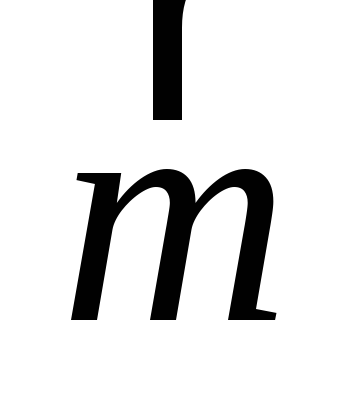 ,
равный по модулю произведению модуля
одной из сил пары на плечо, направленный
перпендикулярно плоскости действия
пары в ту сторону, откуда поворот пары
виден происходящим против хода часовой
стрелки. Следует заметить, что момент
пары сил равен моменту одной из сил пары
относительно точки приложения другой
силы. Также нетрудно показать, что момент
пары сил равен сумме моментов сил пары
относительно любого центра и может быть
приложен в любой точке.
,
равный по модулю произведению модуля
одной из сил пары на плечо, направленный
перпендикулярно плоскости действия
пары в ту сторону, откуда поворот пары
виден происходящим против хода часовой
стрелки. Следует заметить, что момент
пары сил равен моменту одной из сил пары
относительно точки приложения другой
силы. Также нетрудно показать, что момент
пары сил равен сумме моментов сил пары
относительно любого центра и может быть
приложен в любой точке.
Теорема: «Момент пары сил равен геометрической сумме моментов сил, образующих пару, относительно любого центра»:
 .
(2.18)
.
(2.18)
Таким образом, сумма моментов сил пары относительно центра не зависит от выбора этого центра и равна моменту пары сил. Так как выбор центра О произволен, то вектор-момент пары сил можно считать приложенным в любой точке, т.е. это так называемый свободный вектор (см. рис. 2.10).
Понятие момента пары сил не следует смешивать с понятием момента силы относительно центра. В отличие от момента силы, который зависит от выбора центра и приложен к этому центру, момент пары сил определяется только ее силами и плечом, а приложен он может быть в любой точке. Итак, основной характеристикой пары сил – количественной мерой ее механического действия на твердое тело является момент пары сил. Из выражения (2.18) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны друг другу, т.е. оказывают на тело одинаковое механическое действие:
если 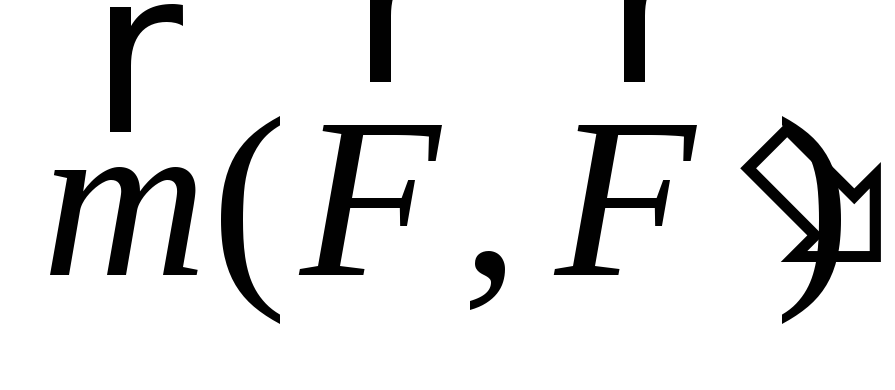 =
=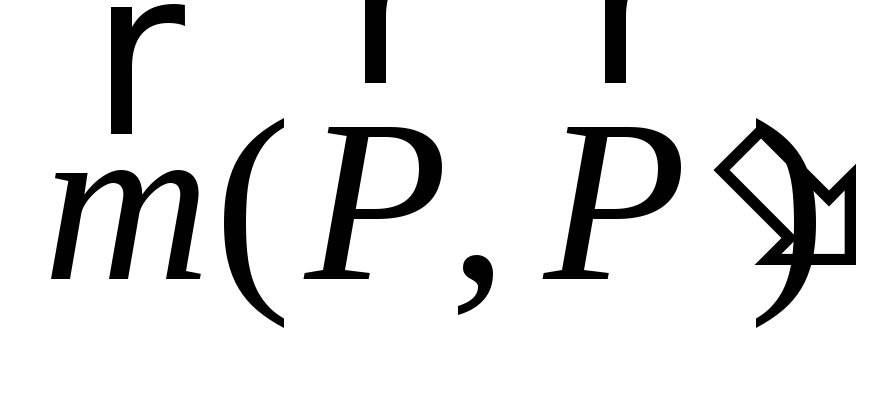 ,
то
,
то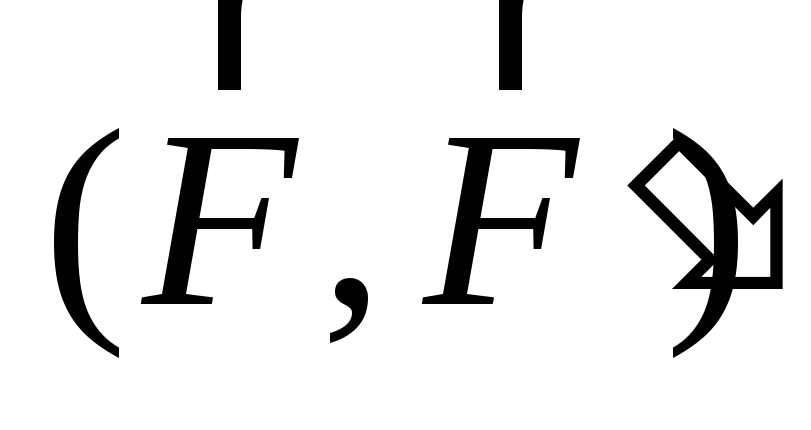 ~
~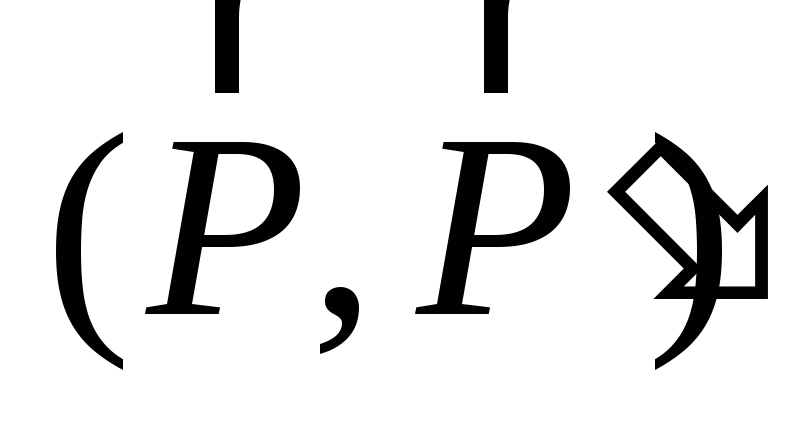 .
.
Иными
словами, две пары сил, независимо от
места их расположения в данной плоскости
(или параллельных плоскостях) и от того,
чему равны в отдельности модули сил пар
и их плечи, будут эквивалентны, если
моменты этих пар сил имеют одно и то же
значение 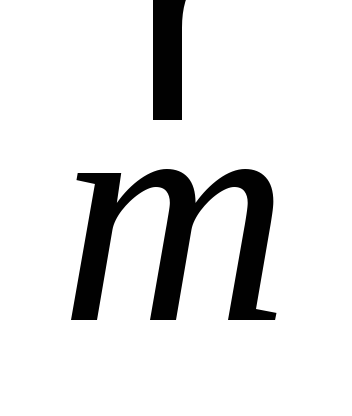 .
.
Свойства пары сил описывают следующими теоремами об эквивалентности пар сил:
■ действие пары сил на твердое тело не изменится, если пару перенести в любое место плоскости ее действия;
■ действие пары сил на твердое тело не изменится, если изменить модули сил и длину плеча так, чтобы момент пары не изменился;
■ действие пары сил на твердое тело не изменится, если пару сил перенести из плоскости ее действия в любую другую параллельную плоскость.
Отсюда следует теорема об эквивалентности пар сил: «Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу, так как путем изменения плеча, модуля сил и перемещения пары сил в плоскости ее действия или переноса этой пары в параллельную плоскость, пары сил с одинаковыми моментами могут быть преобразованы одна в другую».
На
расчетных схемах обычно вместо пары
сил изображают векторный момент 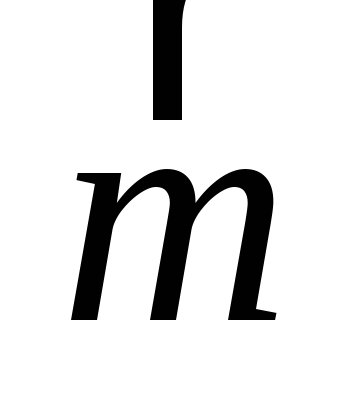 ,
полностью характеризующий ее, при этом
модуль
,
полностью характеризующий ее, при этом
модуль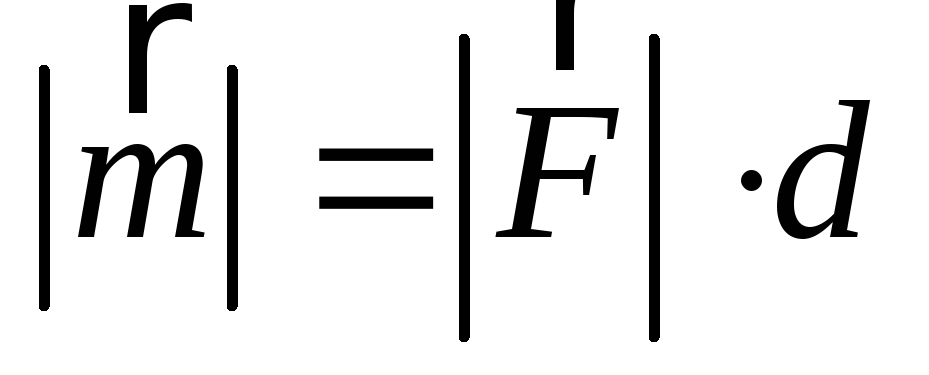 .
Направление вектора определяет плоскость
действия пары и направление поворота
в этой плоскости. Чтобы задать пары сил,
лежащих в одной плоскости, достаточно
обозначить их круговой стрелкой,
учитывающей направление поворота, и не
изображать сами силы.
.
Направление вектора определяет плоскость
действия пары и направление поворота
в этой плоскости. Чтобы задать пары сил,
лежащих в одной плоскости, достаточно
обозначить их круговой стрелкой,
учитывающей направление поворота, и не
изображать сами силы.
Сложение пар сил сводится к теореме о сложении пар: «Система пар сил, действующих на абсолютно твердое тело, эквивалентна одной паре, момент которой равен геометрической сумме моментов слагаемых пар»:
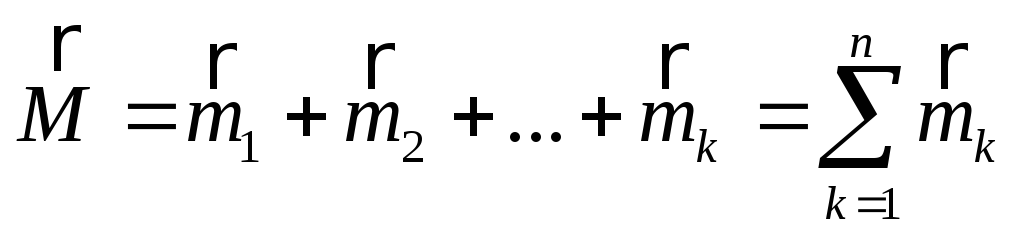 .
(2.19)
.
(2.19)
Из приведенной теоремы вытекает условие равновесия системы пар сил, согласно которому для равновесия системы пар сил, действующих на абсолютно твердое тело, необходимо и достаточно, чтобы момент результирующей пары был равен нулю
 .
(2.20)
.
(2.20)
Действительно, либо силы результирующей пары равны нулю, либо плечо этой пары равно нулю. В последнем случае силы пары направлены вдоль одной прямой и в соответствии с 1-й аксиомой статики образуют уравновешенную систему сил.
Проецируя векторное равенство (2.20) на координатные оси, получим аналитические условия равновесия системы пар сил:
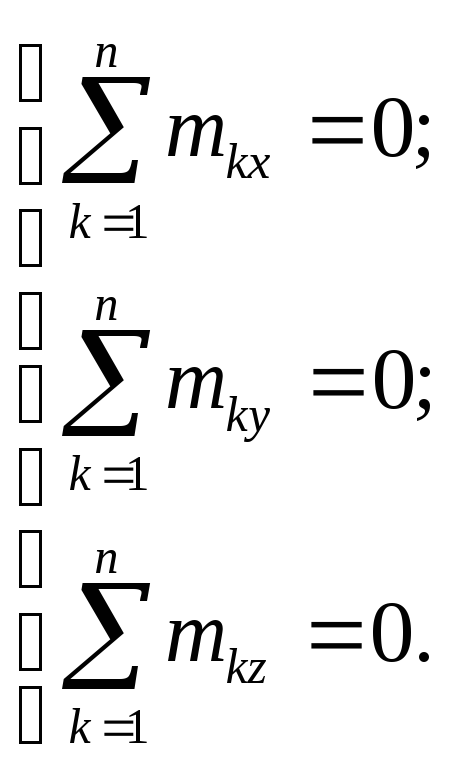 (2.21)
(2.21)
В частном случае действия на твердое тело системы пар сил, расположенных в одной плоскости, моменты этих пар, направленные по одной прямой, складываются алгебраически. Тогда теорему о сложении пар сил формулируют следующим образом: «Система пар сил, лежащих в одной плоскости, эквивалентна одной паре сил, лежащей в той же плоскости и имеющей алгебраический момент, равный алгебраической сумме моментов слагаемых пар»:
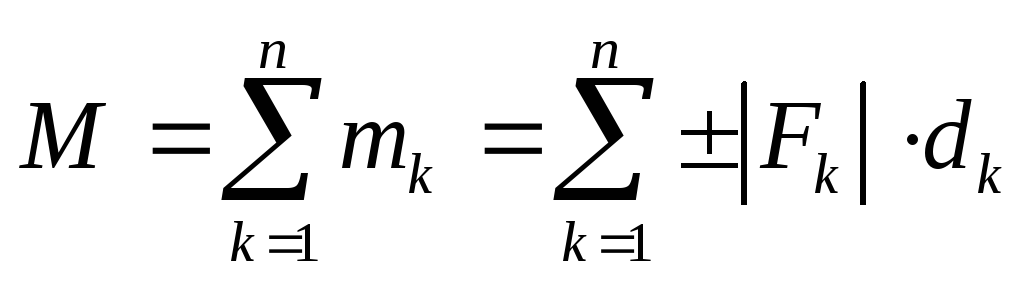 .
(2.22)
.
(2.22)
Условия равновесия плоской системы пар сил: «Для равновесия плоской системы пар сил необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю»
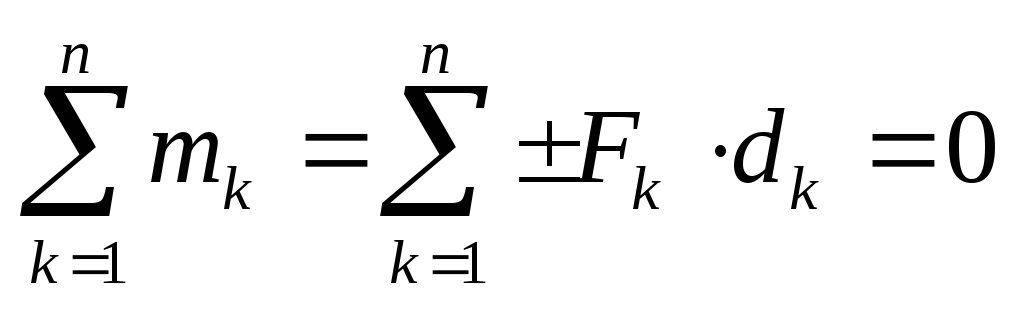 .
(2.23)
.
(2.23)

