Урок 3. магнитная индукция. действие магнитного поля на проводник с током и движущуюся заряженную частицу — Физика — 11 класс
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» — правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.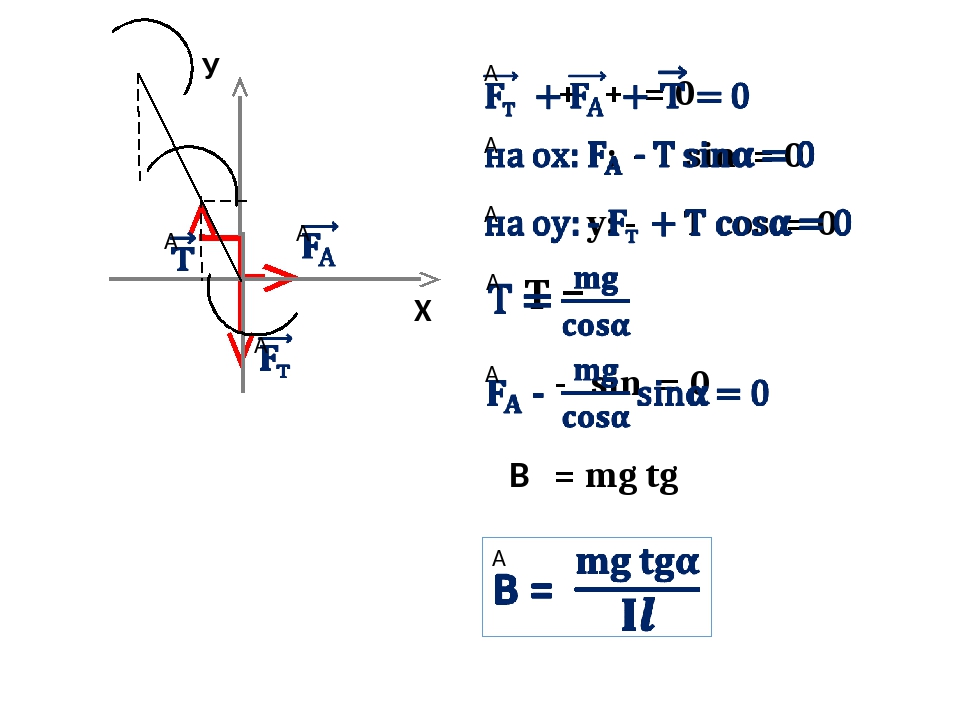
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. — М: Дрофа, 2009. – С.109 — 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).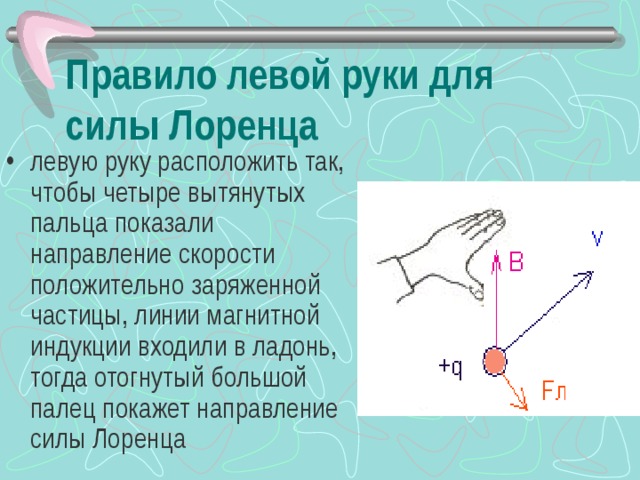
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
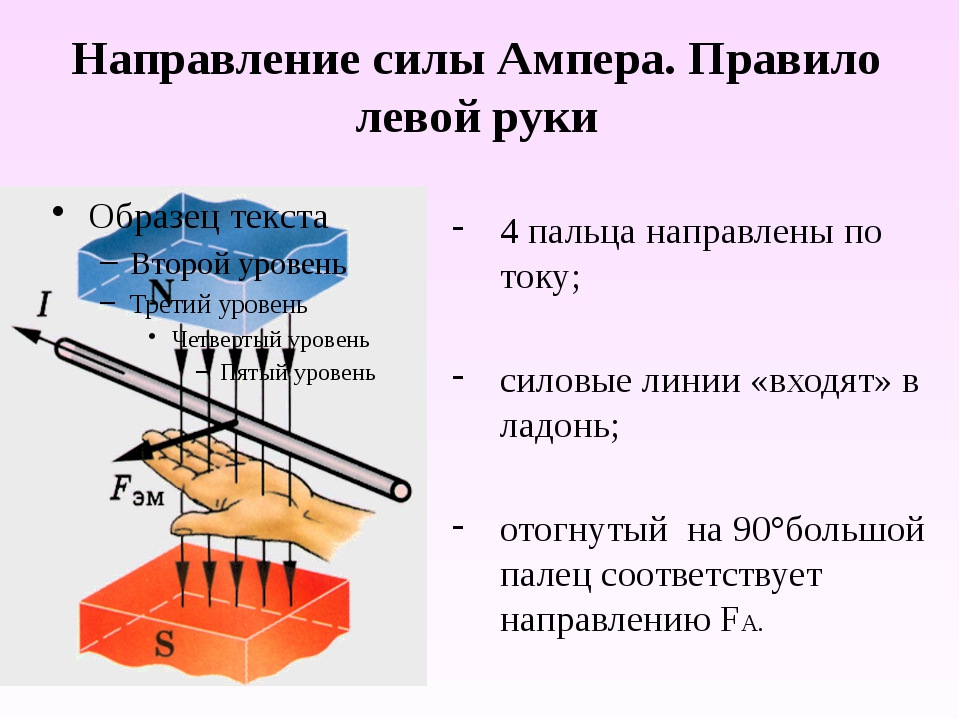
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 900 большой палец покажет направление силы Ампера.
Сила Ампера — сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.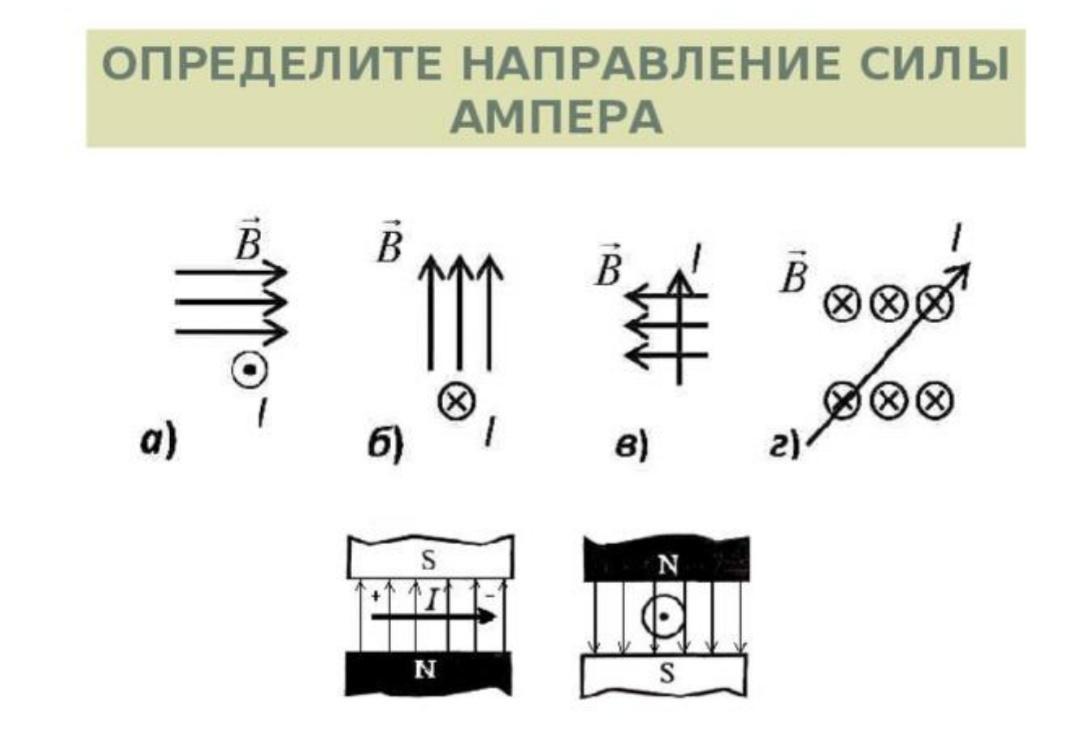
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 90
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Отсюда
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия.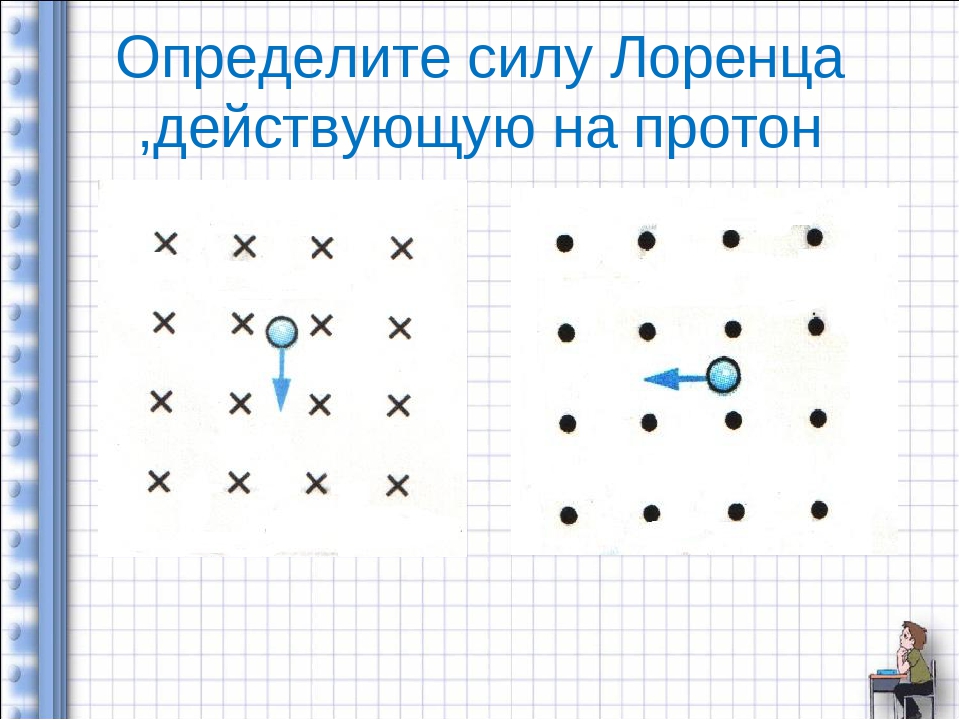
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
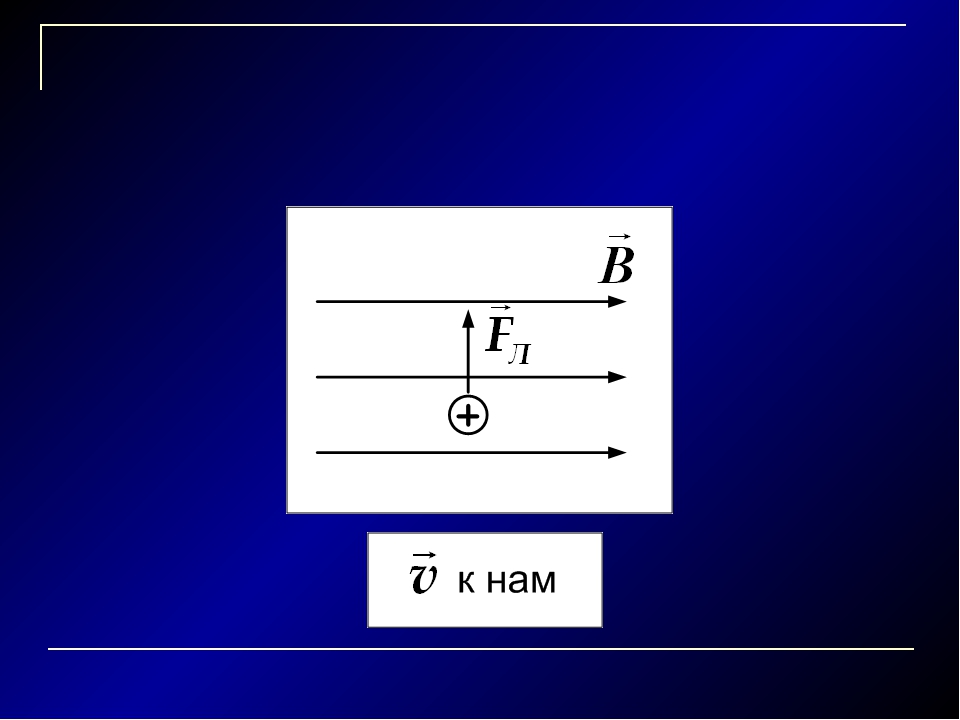
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике.
Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
— точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т. е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл.
(Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10—¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:
Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.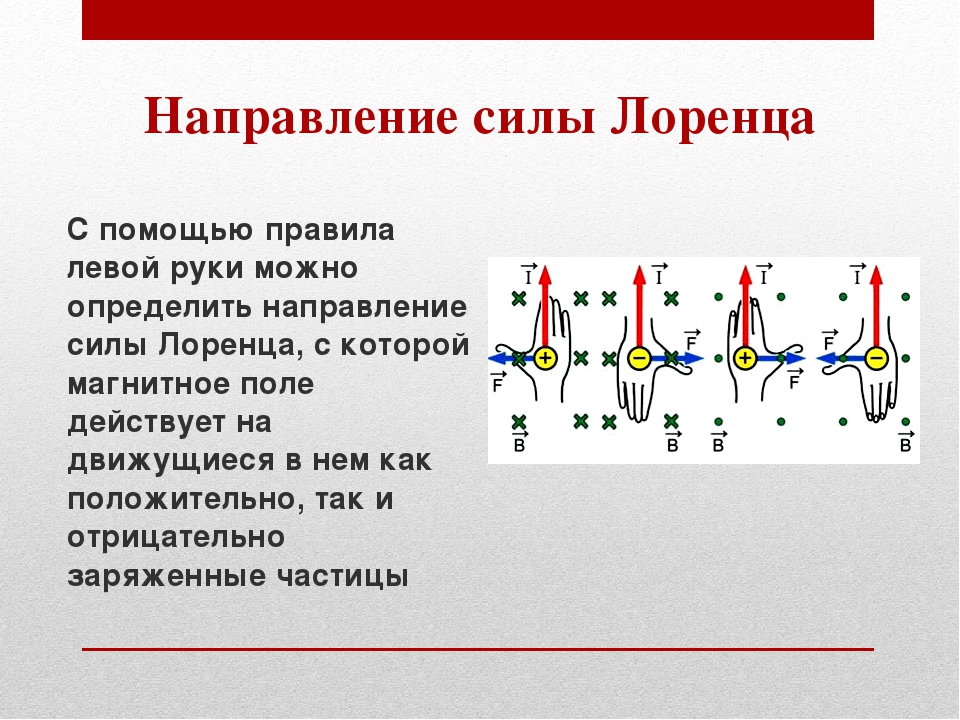
Найти: F
Решение:
Запишем формулу силы Ампера:
Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
Отсюда следует:
Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти:
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Пример решения задачи по теме «Сила Лоренца» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема: Примеры решения задач по электродинамике
Задача.
Электрон влетает в однородное магнитное поле с индукцией 10-4 Тл перпендикулярно линиям магнитной индукции. Его скорость 1,6 • 106 м/с. Определить радиус окружности, по которой движется электрон.
|
Дано: B = 10-4 Тл v = 1,6 • 106 м/с q = e = 1,6 • 10-19 Кл α = 90° |
Решение: Сила Лоренца действует под прямым углом к скорости движения электрона, не изменяя модуля его скорости. В этих условиях она сообщает электрону лишь центростремительное ускорение. Поэтому можно записать, что qvB = mv2 / R. Отсюда R = mv / qB. Подставив значения величин, получим Материал с сайта http://worldofschool. R = (9,1 • 10-31 кг • 1,6 • 106 м/с) / (1,6 • 10-19 Кл • 10-4 Тл) = 9,1 • 10-2 м. |
|
R — ? |
Ответ: электрон будет двигаться по окружности радиуса 9,1 • 10-2 м. |
ruЗадачи с решением на силу лоренца
Примеры задач сила ампера сила лоуренса
Задачи с решением на закон ампера лоренца
Графические задачи на силу лоренца и ампера решение
Сила лоренца задачи с решением
Элеком37, Сила Ампера, Сила Лоренца. Физика.
Сила Ампера. Сила Лоренца.
Сила Ампера.
Заряженные тела способны создавать кроме электрического еще один вид поля.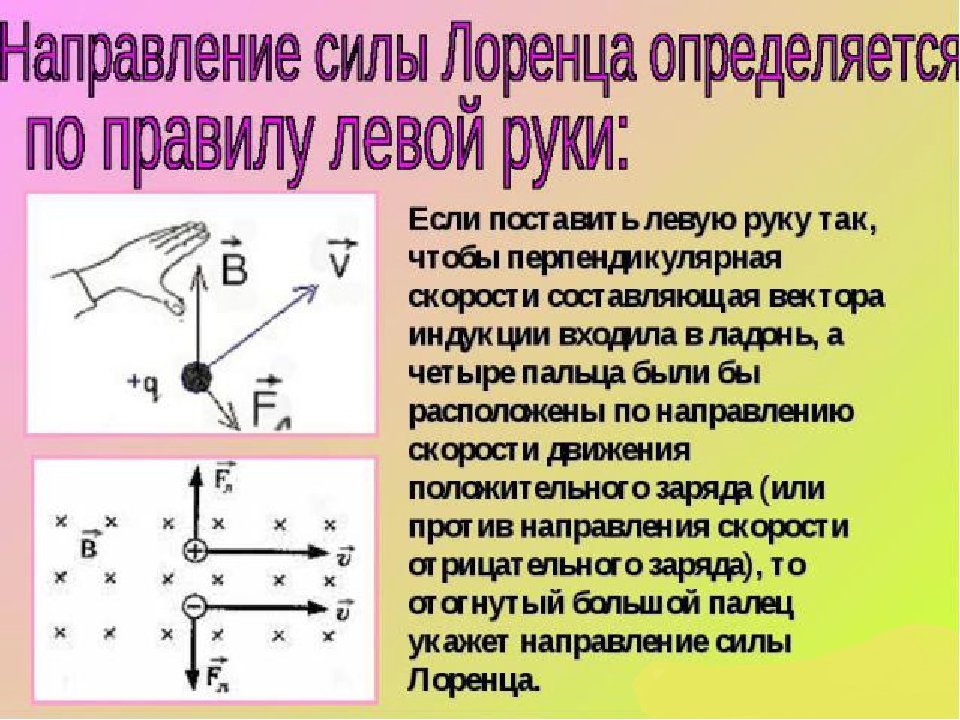
Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток,
представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью.
Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина.
Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю.
Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление,
и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:
где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца.
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции.
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера,
может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости
движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы.
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.
Другие стаьи по теме «Электричество»
Вариант 1. Сила Лоренца и сила Ампера Вариант 2.
Сила Лоренца и сила АмпераСила Лоренца и сила Ампера
Вариант 1. 1. С какой силой действует магнитное поле индукцией 1Тл на отрезок прямого провода длиной 2м, расположенного перпендикулярно линиям индукции, если по проводу течет ток 1кА? (2кН) 2. Рамка гальванометра
ПодробнееКОНТРОЛЬНАЯ РАБОТА 3 ВАРИАНТ 1
КОНТРОЛЬНАЯ РАБОТА 3 ВАРИАНТ 1 1. Три источника тока с ЭДС ξ 1 = 1,8 В, ξ 2 = 1,4 В, ξ 3 = 1,1 В соединены накоротко одноименными полюсами. Внутреннее сопротивление первого источника r 1 = 0,4 Ом, второго
ПодробнееИДЗ-4 / Вариант 1 ИДЗ-4 / Вариант 2
ИДЗ-4 / Вариант 1 1.
Сила тока в проводнике равномерно нарастает от 0 до 3 А в течение 10 с. Определить заряд, прошедший в проводнике за это время. 2. Три батареи аккумуляторов с ЭДС 12 В, 5 В и 10 В и
КОНТРОЛЬНАЯ РАБОТА 3 ВАРИАНТ 1
КОНТРОЛЬНАЯ РАБОТА 3 ВАРИАНТ 1 1. Четыре одинаковых заряда Q 1 = Q 2 = Q 3 = Q 4 = 40 кнл закреплены в вершинах квадрата со стороной а = 10 см. Определить силу F, действующую на каждый из этих зарядов
ПодробнееЗадачи. Принцип суперпозиции.
Задачи. Принцип суперпозиции. 1. В вершинах квадрата находятся одинаковые заряды Q = 0, 3 нкл каждый. Какой отрицательный заряд Q x нужно поместить в центре квадрата, чтобы сила взаимного отталкивания
ПодробнееИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 3 МАГНЕТИЗМ
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 3 МАГНЕТИЗМ 1-1.
Определить величину индукции магнитного поля, создаваемого горизонтальным отрезком проводника длиной l = 10 см с током i = 10 А в точке над ним на высоте 5 м. Найти
Контрольная работа 2 Вариант 1
Вариант 1 1. Заряды по 10 нкл расположены на расстоянии 6 см друг от друга. Найти напряженность поля и потенциал в точке, удаленной на 5 см от каждого заряда. 2. Два заряда по +2нКл каждый находятся на
ПодробнееИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 2.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ. Вариант 1 1. Два параллельных бесконечно длинных провода, по которым в одном направлении текут токи силой 60 А, расположены на расстоянии 10 см друг от друга. Определите магнитную
ПодробнееРешение задач ЕГЭ части С: Магнетизм
С1.1. Рамку с постоянным током удерживают неподвижно в поле полосового магнита (см.
рисунок). Полярность подключения источника тока к выводам рамки показана на рисунке. Как будет двигаться рамка на неподвижной
Контрольная работа 3 ЭЛЕКТРИЧЕСТВО
Кафедра физики, контрольные для заочников 1 Контрольная работа 3 ЭЛЕКТРИЧЕСТВО 1. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики
ПодробнееФизика Электромагнетизм
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ухтинский государственный технический университет Физика Электромагнетизм Контрольные
Подробнее6.12. Примеры расчётов магнитных полей
6.. Примеры расчётов магнитных полей Магнитное поле постоянного тока Пример.
Напряжённость магнитного поля Н 79,6 ка/м. Определить магнитную индукцию этого поля в вакууме В.. Магнитная индукция В связана
Тема 9. Электромагнетизм
1 Тема 9. Электромагнетизм 01. Магнитное поле создается постоянными магнитами и движущимися зарядами (токами) и изображается с помощью силовых линий линий вектора магнитной индукции. Рис. 9.1 Силовые линии
ПодробнееVIII. Электромагнетизм
VIII. Электромагнетизм 48.1. Два одинаковых круговых проволочных витка расположены в двух взаимно перпендикулярных плоскостях так, что центры витков совпадают. По виткам текут токи I 1 и I 2. Как следует
ПодробнееРешение задач по теме «Магнетизм»
Решение задач по теме «Магнетизм» Магнитное поле- это особая форма материи, которая возникает вокруг любой заряженной движущейся частицы.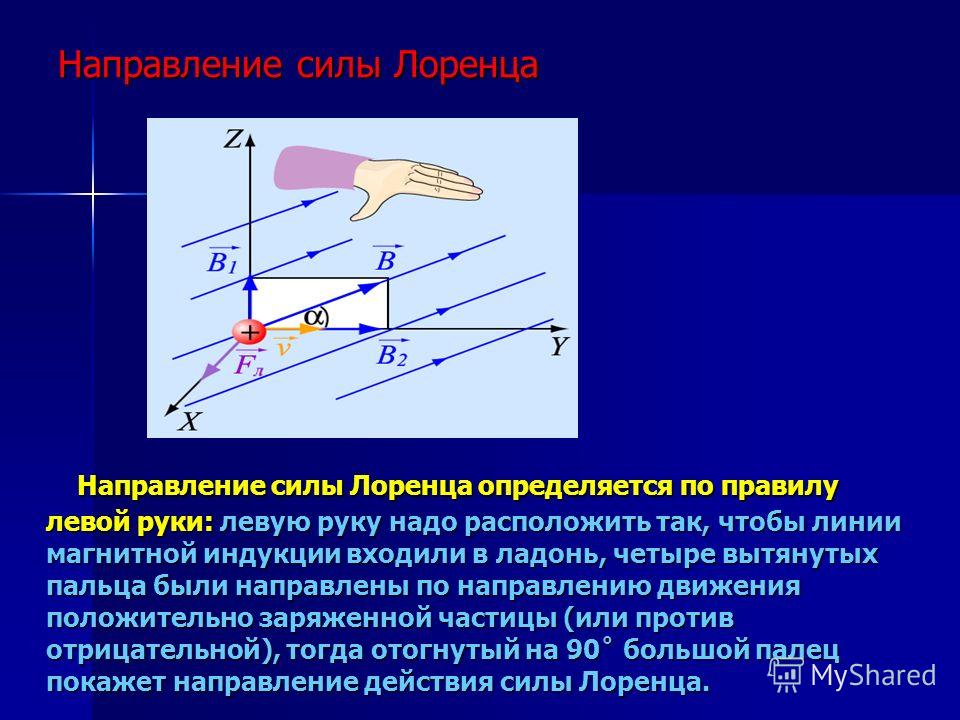
Электрический ток- это упорядоченное движение заряженных частиц
Электромагнитная индукция
Вариант 1. 1. Определить среднее значение ЭДС индукции в контуре, если магнитный поток, пронизывающий контур, изменяется от 0 до 40мВб за время 2 мс. (20В) 2. На картонный каркас длиной 50см и площадью
Подробнеепосередині між провідниками, та B
Завдання на контрольну роботу 2 з курсу «Загальна фізика» на тему «Магнетизм». 401. Два однакові круглі витки радіуса R = 15 см з ізольованого дроту мають спільний центр і розміщені у взаємно перпендикулярних
ПодробнееВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ 3
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ 3 В контрольную работу 3 включены задачи по разделам: «Электромагнетизм» и «Колебания и волны».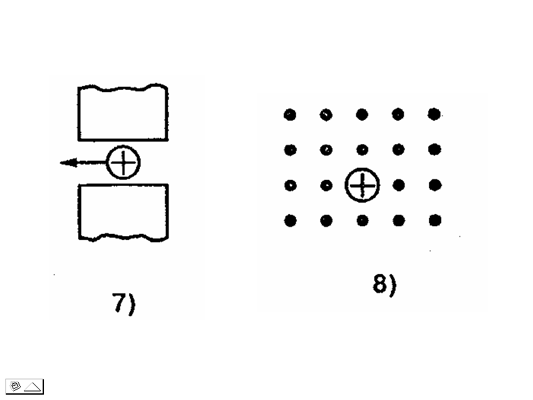
1. Решая задачи по разделу «Электромагнетизм» прежде
Ч. II. ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (СИБСТРИН) ФИЗИКА Кафедра физики Ч. II. ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК. ЭЛЕКТРОМАГНЕТИЗМ
ПодробнееПримеры решения задач
51 Примеры решения задач Задача 1. По прямому проводнику длиной l=8см течет ток I=5A. Определить магнитную индукцию B поля, создаваемого этим током, в точке А, равноудаленной от концов проводника и находящейся
ПодробнееФИЗИКА ЗАДАЧИ ДЛЯ ПОДГОТОВКИ К ОКР 2
ФИЗИКА ЗАДАЧИ ДЛЯ ПОДГОТОВКИ К ОКР 2 1.1. По мере удаления от заряда напряженность поля, создаваемого им, А) усиливается; В) не изменяется; Б) ослабевает; Г) однозначного ответа нет. 1.2. Движение каких
ПодробнееЗадание 6 для 10-х классов. ( учебный год)
Министерство образования и науки Российской Федерации Федеральная заочная физико-техническая школа при Московском физико-техническом институте (государственном университете) ФИЗИКА Магнитное поле Задание
ПодробнееВариант 1 I 3 I 1 I 2 I 4
Вариант 1 1. В некоторой системе отсчета электрические заряды q 1 и q 2 неподвижны. Наблюдатель А находится в покое, а наблюдатель В движется с постоянной скоростью. Одинакова ли по величине сила взаимодействия
ПодробнееРис. 11 расположены заряды q1 5 нкл и
Электростатика 1. Четыре одинаковых точечных заряда q 10 нкл расположены в вершинах квадрата со стороной a 10 см. Найти силу F, действующую со стороны трех зарядов на четвертый. 2. Два одинаковых положительных
ПодробнееОтложенные задания (23)
Отложенные задания (23) Виток провода находится в магнитном поле, перпендикулярном плоскости витка, и своими концами замкнут на амперметр. Магнитная индукция поля меняется с течением времени согласно графику
ПодробнееДвижение зарядов и токов в магнитном поле
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Кафедра физики Утверждаю Зав. каф. Физики Е.М. Окс 2012г. ЭЛЕКТРОМАГНЕТИЗМ Часть 2 Движение
ПодробнееЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ И манит за собой Загадочный магнит… Д. Долинин 5. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ. МАГНИТНОЕ ПОЛЕ Fa = BII sina, = qvb sina УСТНАЯ РАЗМИНКА 5.1. На какие частицы или тела действует электрическое
ПодробнееДано: СИ Решение: Ответ: F к
3-7. На шелковых нитях длиной 50 см каждая, прикрепленных к одной точке, висят два одинаково заряженных шарика массой по 0,2 г каждый. Определить заряд каждого шарика, если они отошли друг от друга на
ПодробнееЗадачи для самостоятельной работы
Задачи для самостоятельной работы Закон Кулона. Напряженность. Принцип суперпозиции для электростатического поля. Потенциал. Работа электрического поля. Связь напряженности и потенциала. 1. Расстояние
Подробнее2,5 2,5. a x, м/с 2 2,5
Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
Подробнее«Физика», осень 2017 г. Вариант 1
З А Д А Ч А 1. ствола Первый (отборочный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по общеобразовательному предмету Снаряд вылетел со скоростью «Физика», осень 217 г. 32 Вариант
ПодробнееЭлектромагнитная индукция
И. В. Яковлев Материалы по физике MthUs.ru Электромагнитная индукция Задача 1. Проволочное кольцо радиусом r находится в однородном магнитном поле, линии которого перпендикулярны плоскости кольца. Индукция
ПодробнееМагнитное поле. Тест 1
Магнитное поле. Тест 1 1. Магнитное поле: чем создается, чем обнаруживается. 1.1 Магнитное поле создается (выберите правильные варианты ответа): 1) заряженными частицами 2)!!! постоянными магнитами 3)!!!
Подробнее1. Электростатика
1. Электростатика 1.1. Расстояние d между двумя точечными зарядами Q 1 = — 180 нкл и Q 2 = 720 нкл равно 60 см. Определите точку, в которую нужно поместить третий заряд Q 3 так, чтобы система зарядов находилась
ПодробнееСБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Министерство образования Российской Федерации УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ по разделу «Электричество и магнетизм» Уфа 2004 Министерство образования
ПодробнееЗадания А13 по физике
Задания А13 по физике 1. Прямой тонкий провод длиной 1,5 м находится в однородном магнитном поле с индукцией 0,4 Тл. По проводу течет постоянный электрический ток силой 5 А. Чему может быть равна по модулю
ПодробнееКонспект урока по физике
Люгаева Алевтина Сергеевна
Преподаватель физики, астрономии, естествознания и общепрофессиональных дисциплин
ГАПОУ МО «Оленегорский горнопромышленный колледж»
г. Оленегорск Мурманской области
КОНСПЕКТ УРОКА
Тема урока: Решение задач: «Сила Ампера. Сила Лоренца».
Конспект урока рассчитан на 2 академических (учебных) часа.
Презентация к уроку: Сила Ампера. Сила Лоренца.
PPTX / 2.36 Мб
Дидактическая цель: создать условия для совершенствования знаний, умений, навыков.
Цель урока: совершенствовать навыки решения задач на применение силы Ампера и силы Лоренца; закрепить знание силы Ампера и силы Лоренца при решении задач; проверить уровень знаний, полученных при изучении данной темы.
Задачи урока:
Образовательные:
Продолжить развитие умения использовать теоретические знания при решении задач.
Продолжить формировать обобщенное умение решать задачи.
Сформировать умение решать задачи с использованием формул для расчета силы Ампера и силы Лоренца.
Проконтролировать степень усвоения знаний, умений и навыков по данной теме.
Развивающие:
Продолжить работу по формированию умения анализировать, делать выводы.
Воспитательные:
Продолжать работу по формированию внимания, усидчивости, аккуратности, доброжелательного отношения к товарищам, воспитание умения слушать мнение других.
— Совершенствовать навыки самостоятельной работы.
Личностные:
Способствовать саморазвитию и самообразованию учащихся на основе мотивации к обучению и познанию.
Формировать целостную картину мира.
Формировать осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению.
Формировать умение контролировать процесс и результат деятельности (в частности, за счет рефлексии).
Метапредметные:
Использовать основные интеллектуальные операций: постановка задачи, формулирование гипотез, анализа и синтеза, сравнения, обобщения, систематизации, выявления причинно-следственных связей, поиска аналогов, формулирования выводов для решения задач.
Организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.
Создавать, применять и преобразовывать знаково-символические средства для решения задач.
Самостоятельно планировать пути достижения целей
Предметные:
Владеть правилом левой руки, понятием Силы Ампера, Силы Лоренца.
Формировать умения решать задачи на тему «Сила Ампера. Сила Лоренца».
Использовать приобретенные знания в повседневной деятельности.
Формируемые УУД:
Личностные: Формирование мотивации изучения физики; стремление к самомовершенствованию; стремление к совершенствованию собственной речевой культуры в целом; развитие таких качеств как целеустремленность и инициативность.
Регулятивные: осуществление регулятивных действий самонаблюдения, самоконроля, самооценки в процессе коммуникативной и самостоятельной деятельности на уроке физики.
Познавательные: построение логических рассуждения, включающих анализ, синтез, установление причинно-следственныз связей, рефлексию.
Коммуникативные: планирование учебного сотрудничества, формулировка собственного мнения и позиции; способность аргументировать и координировать собственную позицию с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности; умение задавать вопросы; адекватно использовать речевые средства для решения различных коммуникативных задач.
Тип урока: урок совершенствования знаний, умений и навыков.
Оборудование, материалы: проектор, компьютер, экран, доска, Касьянов В.А. Учебник Физика 11 класс, Степанова Г.Н.Сборник задач по физике, Рымкевич А.П.Задачник по физике.
Методы обучения: словесный, репродуктивный, проблемный (решение задач), частично-поисковый, эвристическая беседа.
Формы обучения: фронтальная, индивидуальная.
Методы контроля: письменный, устный.
Межпредметные связи: математика.
Методическое и дидактическое сопровождение урока:
— Презентация в Microsoft Power Point;
— Видеоролики на тему «Опыт Ампера», «Правило левой руки», «Электродвигатель».
— Компьютер, экран, мультимедиапроектор;
— Касьянов В.А. Учебник Физика 11 класс, Степанова Г.Н.Сборник задач по физике, Рымкевич А.П.Задачник по физике.;
— Раздаточный дидактический материал (конспект урока) для студентов.
СТРУКТУРА УРОКА
№ П/П | Этапы урока | Время (мин) | Задачи этапа | Деятельность | Метод | Организационная форма | |
преподавателя | обучающихся | ||||||
1 | Организационный этап | 1 | Проверить готовность к уроку | Приветствие. Проверка готовности обучающихся к работе | Проверяют готовность своего рабочего места | Информационный | Индивидуальная |
2 | Этап подготовки обучающихся к активному и сознательному усвоению знаний (целепологание и мотивация) | 5 | Подготовить к закреплению материала | В ходе беседы помогает сформулировать тему и цель занятия. Помогает сформулировать план занятия. | Отвечают на вопросы, определяют тему и цель занятия, и как может быть построено занятие | Словесный | Фронтальная |
3 | Актуализация знаний и умений | 15 | Повторить основные понятия и формулы | Предлагает ответить на вопросы | Отвечают на вопросы преподавателя. Вспоминают основные понятия и формулы по данной теме | Словесный (с использованием мультимедийной презентации) | Фронтальная |
4 | Этап решения типовых задач по теме: «Сила Ампера. Сила Лоренца». | 32 | Отработать умения решать задачи по данной теме | Организует работу обучающихся по решению задач и контролирует ход ее решения и результат | Совместное и самостоятельное решение задач по данной теме | Практический | Индивидуальная и фронтальная |
5 | Творческое применение и добывание знаний в новой ситуации | 32 | Отработать умения решать задачи по данной теме | Организует самостоятельную работу обучающихся по решению задач и контролирует | Самостоятельное решение задач по данной теме | Практический | Индивидуальная |
6 | Этап информации обучающихся о домашнем задании | 2 | Разъяснить методику выполнения домашнего задания | Задает домашнее задание | Определяют для себя уровень домашнего задания | Информационный | Индивидуальная |
| 7 | Рефлексия, подведение итогов занятий | 3 | Осознать и оценить уровень сформированности навыков решения задач | Организует обсуждение, оценивает степень выполнения решения задач, анализирует итоги урока | Дают оценку результатов своей работы. Анализируют затруднения при решении задач | Анализ | Индивидуальная |
Ход урока:
1. Организационный момент. Приветствие. Проверка готовности обучающихся к работе
2. Этап подготовки обучающихся к активному и сознательному усвоению знаний (целепологание и мотивация) В ходе беседы помогает сформулировать тему и цель занятия. Помогает сформулировать план занятия.
3. Актуализация знаний:
Вокруг чего существует магнитное поле?
Чем характеризуется магнитное поле?
Что такое вектор магнитной индукции? Какой буквой обозначается? В каких единицах измеряется?
Сформулируйте правило буравчика?
Что такое линии магнитной индукции? Они всегда замкнуты или разомкнуты? Откуда выходят и куда входят линии магнитной индукции?
Что такое сила Ампера?
Сформулируйте закон Ампера? Формула? Как называется каждая буква в законе и в каких единицах измеряется?
Сформулируйте правило левой руки для проводника с током?
Что такое сила Лоренца? Формула? Как называется каждая буква в законе и в каких единицах измеряется?
Сформулируйте правило левой руки для заряженной частицы?
Какими формулами описывается движение частицы в магнитном поле по окружности? Из каких законов они выводятся?
4. Формирование умений.
Решение задач:
Рымкевич А.П.Задачник № 840, 841, 842
Касьянов В.А. Учебник. Физика 11 класс Стр.85 № 1,2
Вопросы к видеофильмам:
1. Опыт Ампера. https://www.youtube.com/watch?v=5HKE5TWF7nk
Описать установку действия магнитного поля на рамку с током?
Когда рамка отклоняется от положения равновесия?
Когда выталкивается рамка?
Причина отклонения рамки?
Как влияет сила тока в рамке на ее отклонение?
2.Правило левой руки. https://www.youtube.com/watch?v=ZNz5nhBKaGY
Сходство и различия правила левой руки, описанного в учебнике и описанного в видеофильме?
Когда сила Ампера не действует на проводник с током?
3. Электродвигатель. https://www.youtube.com/watch?v=rzOD8Mwlqm8
Какой закон применяется в электродвигателе?
5. Самостоятельная работа:
Степанова Г.Н.Сборник задач по физике
1 вариант № 1083, 1100, 1098, 1079, 1078 (1,3,5,7)
2 вариант № 1097, 1102, 1099, 1080, 1078 (2,4,6,8)
6. Этап информации обучающегося о домашнем задании.
Ваше домашнее задание: решить к следующему занятию контрольную работу по теме «Сила Ампера. Сила Лоренца».
7. Подведение итогов урока. Анализ результатов. Рефлексия учащихся.
Поднимите руки кто решил 5 задач? Кто 4? Кто 3? (5 задач – оценка 5, 4 задачи – оценка 4, 3 задачи – оценка 3).
Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
Перечислите в порядке убывания основные трудности, которые вы испытывали во время самостоятельной работы. Как вы их преодолевали?
Какая сегодня была тема урока?
Какая сегодня была цель урока?
Заполните карточку:
Физика задачи на направление силы ампера и лоренца. Первые 2 картинки сила ампера 3 лоренца.
Объяснение:
1.1: Вверх
1.2: Направлена влево (условие некорректно, потому что ток идет от плюса к минусу, следовательно участок не 4-1, а 1-4)
1.3: Влево
2.1: Не действует, потому что sin180° = 0 (из формулы Fa = BIlsin)
2.2: На нас ⊙
2.3: Вверх
Примечание: поиск направления силы Ампера осуществлялся по правилу левой руки, где перпендикулярная составляющая магнитной индукции входит в ладонь, сила тока идет по направлению 4—х пальцев, а сила Ампера по направлению отопыренного большого пальца
Ни в одной из данных задач по условию не требовалось найти направление силы Лоренца. Все было выполнено по условию. Если преподаватель изменил условие задачи, то должны быть данные для того чтобы найти направление силы Лоренца (скорость)
Задачи с решениями 10 — Магнитное поле и электромагнитная индукция — ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. ОТРАБОТКА ТЕМАТИЧЕСКОГО МАТЕРИАЛА — ЕГЭ 2018. Тренажёр: Физика. — ЕГЭ 2018 — Справочное издание
ЕГЭ 2018. Тренажёр: Физика
Магнитное поле и электромагнитная индукция
Задачи с решениями
1. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор индукции магнитного поля тока в центре витка? Ответ запишите словом (словами).
Решение. Направление вектора магнитной индукции можно определить по правилу буравчика. Использование этого правила применительно к току, текущему по витку, дает: в центре витка вектор магнитной индукции направлен горизонтально (вдоль оси витка) вправо.
Ответ: вправо.
2. Электрическая цепь, состоящая из четырех прямолинейных горизонтальных проводников (1-2, 2-3, 3-4, 4-1) и источника постоянного тока, находится в однородном магнитном поле, вектор магнитной индукции которого направлен вертикально вверх перпендикулярно плоскости рисунка (см. рис., вид сверху). Куда направлена (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вызванная этим полем сила Ампера, действующая на проводник 4-1?
Ответ запишите словом (словами).
Решение. Направление силы Ампера, действующей на проводник с током, можно определить по правилу левой руки. Ток в цепи течет от «+» источника к «-». Таким образом, ток на участке 4-1 течет от 1 к 4. Значит, в данном случае сила Ампера направлена горизонтально влево.
Ответ: влево.
3. По трем тонким параллельным проводникам текут одинаковые токиКак направлена (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) сила Ампера, действующая на проводник № 3 со стороны двух других (см. рис.)? Расстояния между соседними проводниками одинаковы. Ответ запишите словом (словами).
Решение. Магнитное взаимодействие проводников с током приводит к тому, что если токи имеют одинаковое направление, то проводники притягиваются, а если токи имеют противоположное направление — проводники отталкиваются. В данном случае токи во всех проводниках имеют одинаковое направление, значит, проводник № 3 притягивается и к проводнику № 1, и к проводнику № 2.
Ответ: вверх.
4. Протон влетает в область пространства, в которой создано однородное магнитное поле, вектор индукции которого направлен от нас, перпендикулярно плоскости рисунка. Куда направлена (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) сила Лоренца, действующая на протон? Ответ запишите словом (словами).
Решение. Направление силы Лоренца, действующей на заряд, движущийся в однородном магнитном поле, определяется по правилу левой руки (если заряд положительный). Заряд протона положительный, поэтому сила Лоренца направлена вверх.
Ответ: вверх.
5. Электрон влетел в однородное магнитное поле с индукцией перпендикулярно линиям магнитной индукции. Определите радиус окружности, по которой будет двигаться электрон в магнитном поле, если модуль его скорости равен 880 км/с. Отношение заряда электрона к его массе равно
Ответ: _______________ мм.
Решение. Сила Лоренца, действующая на заряд, движущийся в однородном магнитном поле, равна , где — угол между векторами(в данном случае), и направлена перпендикулярно векторам (по правилу левой руки). Эта сила сообщает электрону центростремительное ускорение — радиус окружности, по которой движется заряд. Согласно второму закону Ньютона , откуда получаем
Ответ: 5 мм.
6. Прямолинейный проводник длиной , по которому течет ток , расположен в однородном магнитном поле под углом 90° к вектору . Каков модуль индукции магнитного поля В, если сила, действующая на проводник со стороны магнитного поля, равна 0,2 Н?
Ответ: Тл.
Решение. На проводник с током в однородном магнитном поле действует сила Ампера, равная по модулю — длина проводника, I — сила тока в нем, В — модуль индукции магнитного поля, — угол между направлением вектора магнитной индукции и проводником. Тогда
Ответ: 0,5 Тл.
7. На рисунке приведен график зависимости магнитного потока через плоскость проволочного витка от времени. Определите модуль ЭДС индукции в витке в промежутке времени 1-5 с.
Ответ: __________________ В.
Решение. По закону электромагнитной индукции
Ответ: 0,25 В.
8. В колебательном контуре, приведенном на рисунке, период электромагнитных колебаний равен 2 мкс. Какой будет частота электромагнитных колебаний в контуре, если ключ К превести из положения 1 в положение 2?
Ответ: ____________________ кГц.
Решение. Период собственных электромагнитных колебаний в колебательном контуре равен (формула Томпсона). При переводе ключа в положение 2 емкость конденсатора в контуре увеличится в 4 раза, т.е. период увеличится в 2 раза и станет равным 4 мкс. Тогда частота колебаний
Ответ: 250 кГц.
9. Конденсатор колебательного контура длительное время подключен к источнику постоянного напряжения (см. рис.). В момент переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого (Т — период колебаний). Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Решение. Когда ключ находится в положении 1, ток через катушку равен 0, а конденсатор заряжен до максимального напряжения. После переключения ключа в положение 2, в контуре начнутся электромагнитные гармонические колебания. Заряд правой обкладки конденсатора вначале был положителен и максимален, затем он будет меняться с течением времени по закону . Энергия конденсатора в начальный момент также максимальна, т.к. , а период ее изменений вдвое меньше периода колебания заряда конденсатора.
Ответ: 34 или 43.
10. В таблице показано, как изменялся заряд одной из обкладок конденсатора емкостью 50 пФ в колебательном контуре с течением времени. Выберите два верных утверждения о процессах, происходящих в контуре.
1) Частота колебаний тока в контуре равна 125 кГц.
2) Период колебаний заряда конденсатора равен 4 мкс.
3) Амплитудное значение силы тока в контуре равно 2,84 мА.
4) В момент времени 4 мкс сила тока в контуре максимальна.
5) Энергия магнитного поля катушки в момент времени 6 мкс равна 40 нДж.
Ответ: ___________________ .
Решение. Период колебаний в контуре — минимальный промежуток времени, в течение которого совершается одно полное колебание. В данном случае период колебаний равен Т = 8 мкс. Частота колебаний обратна периоду . Когда заряд конденсатора максимален (по модулю), сила тока через катушку равна 0, а когда заряд конденсатора равен 0 — сила тока через катушку максимальна. Значит, в момент времени 4 мкс сила тока в контуре равна 0. Максимальная энергия конденсатора равна и равна максимальной энергии магнитного поля катушки , где — амплитуда тока через катушку, — индуктивность катушки. Максимальная энергия конденсатора в данном случае . Приравнивая друг другу максимальные энергии конденсатора и катушки, можно получить , где учтено, что (формула Томсона). Используя данные задачи, получим
Ответ: 15 (или 51).
11. На железный сердечник надеты две катушки, как показано на рисунке. По правой катушке пропускают ток, который меняется согласно приведенному графику. На основании этого графика выберите два верных утверждения.
1) В промежутке между 1 с и 2 с показания амперметра были равны 0.
2) В промежутках 0-1 с и 2-3 с направления тока в левой катушке были одинаковы.
3) В промежутке между 1 с и 2 с индукция магнитного поля в сердечнике была равна 0.
4) Все время измерений сила тока через амперметр была отлична от 0.
5) В промежутках 0-1 с и 2-3 с сила тока в левой катушке была одинаковой.
Решение. Ток в левой катушке возникает вследствие явления электромагнитной индукции. Ток, текущий в правой катушке, создает магнитное поле, которое пронизывает и левую катушку. При изменении силы тока в правой катушке, магнитный поток Ф, пронизывающий левую, изменяется, в ней возникает ЭДС индукции и появляется индукционный ток. Модуль ЭДС индукции определяется законом Фарадея . Направление индукционного тока определяется правилом Ленца и зависит от того, возрастает магнитный поток или убывает. Таким образом, ток в левой катушке тек только в те промежутки времени, когда менялась сила тока в правой катушке. В тех промежутках, когда сила тока уменьшалась, индукционный ток имел одно и то же направление, а когда сила тока возрастала, он тек в противоположном направлении.
Ответ: 15 (или 51).
электромагнетизм — Сила Лоренца относится только к силе, описанной законом Лоренца?
Итак, мой вопрос, проще говоря — что такое сила Лоренца? Относится ли это только к силе, описанной законом Лоренца (F = qvB)? Применимо ли это только для одной частицы, где сила перпендикулярна другим вовлеченным факторам?
Термин «сила Лоренца» используется в нескольких различных значениях. Да, я знаю.
До Лоренца были известны правильные формулы для расчета силы, действующей на макроскопические заряженные или токонесущие тела (Ампер, Био, Савар, Лаплас умели рассчитывать силы).Лоренц сформулировал микроскопическую теорию заряженных частиц, в которой материя состоит из таких частиц. В этой теории сила, действующая на заряженную частицу за счет электромагнитного взаимодействия, выражалась как функция:
1) плотность заряда $ \ rho $ и плотность потока электрического тока $ \ mathbf j $ (обычно называемая плотностью тока) и
2) величины, описывающие состояние электромагнитного поля $ \ mathbf d $ и $ \ mathbf h $.
Сила постулировалась как интеграл
$$ \ mathbf F = \ int_V \ rho \ mathbf d + \ mathbf j \ times \ mathbf h \, dV $$ где интегрирование производится по пространственной области, содержащей все части частицы.
Позже, в 20-м веке, это обозначение пришло в упадок, и $ \ mathbf d, \ mathbf h $ были заменены символами $ \ mathbf e, \ mathbf b $, но смысл остался прежним. Это одно из значений «силы Лоренца».
Эта теория Лоренца оказалась весьма полезной и привела к успешным моделям взаимодействия материи и электромагнитного поля (модели преломления, поглощения, эффекта Зеемана и др.). Но у этой «силы Лоренца» была существенная проблема: она не могла объяснить, как крошечные заряженные частицы ненулевого размера могут удерживаться вместе.И даже если добавить не-ЭМ силы, чтобы удерживать их вместе, любая релятивистски правильная модель такой частицы конечного размера имеет бесконечное количество степеней свободы, и с ней очень трудно работать.
Итак, люди очень скоро упростили теорию, предположив, что заряженные частицы — это просто точки. Тогда вопрос о том, как заряд может удерживаться, отпадает — нет отталкивающих частей. Согласно этой теории, формула силы постулируется равной
.$$ \ mathbf F = q \ mathbf e + q \ mathbf v \ times \ mathbf b $$ где $ q $ — заряд частицы, а $ \ mathbf e, \ mathbf b $ — внешнее электрическое и магнитное поля, действующие на эту частицу.
Наблюдения электронов в ЭМ поле (эксперименты Дж. Дж. Томсона и многие более поздние) подтверждают, что это выражение очень хорошо описывает силу, действующую на электроны во внешнем ЭМ поле. Это еще одно значение термина «сила Лоренца».
Иногда люди имеют дело с частицами, движущимися в области пространства, где электрическое поле незначительно и единственное, что имеет значение, — это магнитная сила. Затем формула упрощается до
$$ \ mathbf F = q \ mathbf v \ times \ mathbf b.
$Это также называется «силой Лоренца».
Однако, к сожалению, это еще не все.
Возвращаясь к макроскопическим явлениям, сила величины $ BIL $, действующая на провод длиной $ L $, несущий ток $ I $ в магнитном поле $ B $, также называется в некоторых учебниках и людьми «силой Лоренца». Такое использование кажется довольно распространенным, но, на мой взгляд, неверным *; Лучшее название было бы исходной терминологией, использованной до Лоренца: «магнитная сила» или «пондеромоторная сила», что примерно означает «сила, действующая на / движущаяся тяжелое вещество», в отличие от «электродвижущей силы», что примерно означает «сила, перемещающая электричество в дирижер ».
Когда два магнита отталкиваются друг от друга, является ли сила, которая заставляет их это делать, силой Лоренца? Если нет, то что это за сила и какое уравнение следует использовать для ее описания?
В макроскопической теории нет, потому что нет заряженных частиц. Сила должна называться «макроскопической магнитной силой» и может быть рассчитана как:
1) сила одного магнитного диполя на другой магнитный диполь (кулоновский подход)
2) сила одного тела, несущего токовую петлю, на другое тело, несущее токовую петлю (подход Ампера)
В микроскопической разработке второго подхода сила, действующая на любое тело с токовой петлей, является суммой сил Лоренца $ q \ mathbf e + q \ mathbf v \ times \ mathbf b $ на всех частицах, которые являются частью этого тела.
* Эта сила и формулы для нее были известны до того, как Лоренц сделал свою работу. Также это выражение взято из макроскопической теории, где сила действует на тяжелую часть тела, а не только на заряженные частицы.
электромагнетизм — Можно ли вывести выражение силы Лоренца из уравнений Максвелла?
Я удалил свой собственный ответ (который, однако, все еще можно найти в записи о редакции), потому что он имеет противоположное значение.
Рассмотрим поле скоростей $ {\ bf u} ({\ bf x}, t) $, где $ {\ bf x} $ — вектор положения, а $ t $ — время.Допустим, что $ {\ bf u} $ сохраняет магнитный поток тогда и только тогда, когда магнитный поток через каждую замкнутую кривую, каждая часть которой движется со скоростью $ {\ bf u} $, постоянен — как если бы поток двигались с такой скоростью. Тогда (как я уже сказал) закон Фарадея для фиксированного цикла $ {\ cal C} $ сводится к следующему: \ begin {уравнение} \ label {2} \ tag {2} \ oint _ {\ cal C} {\ bf E} \ cdot d {\ bf x} = — \ oint _ {\ cal C} {\ bf u} \ times {\ bf B} \ cdot d {\ bf x} \ ,. \ end {уравнение} Все идет нормально. Но затем я утверждал, что поскольку поле $ {\ bf E} $ обусловлено движущимся потоком, мы можем локализовать влияние и интерпретировать указанное выше равенство как поэлементно, получая \ begin {уравнение} \ label {4} \ tag {4} {\ bf E} = — {\ bf u} \ times {\ bf B} \ end {уравнение} как закон Фарадея для поля скоростей $ {\ bf u} $, сохраняющего магнитный поток.Точно так же для закона Максвелла-Ампера (без тока проводимости) для скорости $ {\ bf u} $, сохраняющей электрический поток смещения , я утверждал \ begin {уравнение} \ label {6} \ tag {6} {\ bf H} = {\ bf u} \ times {\ bf D} \ ,. \ end {уравнение} Вместе (4) и (6) означают, что если скорость $ {\ bf u} $ сохраняет поток (в обоих смыслах), то и $ {\ bf E} $, и $ {\ bf H} $ являются перпендикулярно $ {\ bf u} $. Это, в свою очередь, означало бы, что волна, бегущая со скоростью, сохраняющей поток в изотропной среде, называется ТЕМ.
Это значение неверно . Контрпримеры включают:
TE и TM моды прямого прямоугольного волновода без потерь; и
затухающая волна из-за полного внутреннего отражения плоской синусоидальной волны от плоской границы раздела и наложения падающей и отраженной волн; и затухающая волна, и суперпозиция являются TE для поляризации s и TM для поляризации p , но не одновременно.
В обоих случаях форма волны движется с очевидной фиксированной скоростью (скорость затухающей волны в последнем случае) без каких-либо других изменений, так что скорость сохраняет поток.
Таким образом, существование скорости, сохраняющей поток, не дает нам права интерпретировать интегральные формы законов Фарадея и Максвелла-Ампера локализованным образом.
С философской точки зрения проблема заключается в следующем: поскольку скорость, сохраняющая поток, не существует, за исключением особых случаев, поток как таковой не является каким-то «веществом», которое движется, и не становится таковым в тех случаях в что, на акциденцию , скорость, сохраняющая поток, действительно существует.И даже если мы примем предпосылку, что все мгновенное влияние является локальным, мы не сможем построить действительный физический аргумент, локализуя влияние «вещества, которое движется», если у нас физически нет «вещества, которое движется»!
Спешу добавить, что уравнения (4) и (6) по-прежнему верны, если мы возьмем $ {\ bf u} $ в качестве скорости луча , определение которой было первоначальной причиной моего интереса к этому вопросу.
Итак, с точки зрения моей первоначальной цели, проблема заключается в следующем: сохранение потока не зависит от скорости луча.3} $$ и формула для силы Лоренца $$ d \ vec {F} _2 = I_2 \ cdot d \ vec {r} _2 \ times \ vec {B} (\ vec {r} _2) $$ где $ \ vec {r} _2 $ — точка на втором проводе, а $ d \ vec {r} _2 $ — соответствующий элемент пути. Интеграл по путям по второму проводу дает вашу формулу.
Закон Био-Савара
Из $ \ def \ div {\ operatorname {div}} \ def \ rot {\ operatorname {rot}} \ def \ grad {\ operatorname {grad}} \ div (\ vec {B}) = 0 $ следует существование некоторого векторного потенциала $ \ vec {A} $ с $ \ vec {B} = \ rot \ vec {A} $.Подставляя это в закон Ампера (для устойчивого состояния)
$ \ rot (\ vec {H}) = \ vec {S}
долл. США$ \ rot (\ vec {B}) = \ mu_0 \ vec {S}
долл. СШАдает
$ \ rot (\ rot \ vec {A}) = \ mu_0 \ vec {S}
долл. СШАПо формуле $ \ rot \ rot \ vec {A} = \ vec {\ nabla} \ times (\ vec {\ nabla} \ times \ vec {A}) = \ vec {\ nabla} (\ vec {\ набла} \ cdot \ vec {A}) — (\ vec {\ nabla} \ cdot \ vec {\ nabla}) \ vec {A} = \ grad \ div \ vec {A} — \ Delta \ vec {A} $ и калибровочного условия Кулона $ \ div \ vec {A} = 0 $ получаем
$ \ Delta \ vec {A} = — \ mu_0 \ vec {S}
долл. 3} d V_1 долл. СШАДля интеграла по площади поперечного сечения провода изменениями $ r_1 $ пренебрегают и $ \ int_ {A _ {\ rm cross}} \ vec {S} d V $ устанавливается равным $ I_1 d \ vec { r} _1 $.3}.
долл. СШАПонимание основ закона силы Ампера
Закон силы Ампера был открыт Андре-Мари Ампера (которая легла в основу определения единицы электричества, Ампера). Не вдаваясь в утомительные математические уравнения, мы собираемся понять, что такое закон, как был определен Ампер и как этот закон изменения пути изменил физику в то время.
Закон силыАмпера гласит, что сила притяжения или отталкивания между двумя проводами, по которым проходят токи, пропорциональна их длине и силе тока, проходящего через них.Если токи текут в одном направлении, происходит отталкивание. Если токи текут в противоположных направлениях, происходит притяжение. Закон основан на этих двух основных понятиях электростатики:
- Закон Био-Савара гласит, что каждый токоведущий провод создает вокруг себя магнитное поле, как показано на Рис. 1 .
- Сила Лоренца относится к силе, которую каждое магнитное поле оказывает на любой электрический заряд, движущийся в его поле.
Рисунок 1: Правило большого пальца для обнаружения магнитного поля вокруг токоведущего провода
На основании закона Био-Савара и силы Лоренца существует связь между магнитным полем и электрическим зарядом / током.Именно эту связь Ампер пытался установить с помощью экспериментов. Самый простой из этих экспериментов заключался в изучении силы между двумя токоведущими проводами, как показано на Рис. 2 . Этот эксперимент и последующие теории, объясняющие его результаты, заложили основу электромагнетизма как области физики.
Рисунок 2: Магнитное поле между токоведущими проводами
Ампер, единица измерения электрического тока в системе СИ, определяется как сила электромагнетизма на единицу длины между двумя проводами бесконечной длины, имеющими незначительный диаметр и расположенными на расстоянии 1 м друг от друга в вакууме.Основное предположение здесь заключается в том, что провода находятся в свободном пространстве, то есть в нем нет вещества, которое можно было бы намагнитить. Если какая-либо материя, присутствующая в окружающей среде, намагничивается, она проявляет свою собственную магнитную силу, которую необходимо принимать во внимание, поэтому следует сделать это предположение.
Используя закон силы Ампера, можно рассчитать магнитное поле вокруг бесконечного провода, бесконечного листа, тороида, соленоида или любой другой правильной формы, как показано на Рисунках 3 и 4 ниже.
Рисунок 3: Магнитное поле вокруг соленоида Рисунок 4: Магнитное поле вокруг тороида
Закон силы Ампера оказался настолько фундаментальным законом, что после него многие физики, такие как Джеймс Клерк Максвелл, Вильгельм Вебер, Бернард Риман и т. Д.расширил его, чтобы найти базовое определение самой силы. Возвращаясь к работе Ампера, Закон силы утверждает, что сила между токоведущими проводами пропорциональна их длине и силе протекающего тока. Это означает, что чем выше ток, тем больше притяжение или отталкивание между проводами.
Статьи по теме:
Какой номинал батареи в ампер-часах (ампер-час или Ач)?
Напряжение в батарее: нам нужно, чтобы оно было постоянным
Как работает магнит?
Электромагнитная сила — Гипертекст по физике
Обсуждение
введение
Магнетизм — это сила, с которой движущиеся заряды действуют друг на друга.Это формальное определение основано на этом простом уравнении.
F B = q v × B
Напомним, что электричество (по сути) — это сила, с помощью которой заряды действуют друг на друга. Поскольку эта сила существует независимо от того, движутся ли заряды, ее иногда называют электростатической силой. Можно сказать, что магнетизм — это электродинамическая сила, но это случается редко. Комбинация электрических и магнитных сил на заряженном объекте известна как сила Лоренца .
F = q ( E + v × B )
Для большого заряда…
| F B = q | v × B | ||||
| F B = q | г x | × В = | дк | ℓ × B | |
| дт | дт | ||||
| F B = I | ℓ × B | ||||
Эта формула для магнитной силы, действующей на токоведущий провод, является основой эксперимента, который использовался для определения ампер с 1948 по 2019 год.
Ампер — это тот постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины и пренебрежимо малого круглого поперечного сечения, и помещать на расстоянии одного метра в вакууме, между этими проводниками создается сила, равная 2 × 10 −7. ньютон на метр длины
МБПМ, 1948 г.
Используя закон Ампера, мы вывели формулу для силы магнитного поля, окружающего длинный прямой провод с током…
Подставьте это выражение в формулу магнитной силы.(Поскольку два провода параллельны, поле одного встречает другой под прямым углом, и перекрестное произведение сводится к прямому умножению.) Решение для силы на единицу длины, как описано в эксперименте…
| Ф. B | = | I ℓ × B | ||
| Факс Б | = | Iℓ | мкм 0 I | |
| 2π r | ||||
| Ф Б | = | мкм 0 I 2 | ||
| ℓ | 2π r | |||
Устанавливает необычно точное значение проницаемости свободного пространства (необычно точное для физической константы).Подставьте значения для измерений, описанных в эксперименте BIPM, в последнее полученное нами уравнение…
| = | ||
| (2 × 10 -7 Н) | = | мкм 0 (1 А) 2 |
| (1 м) | 2π (1 м) |
и решите для проницаемости свободного пространства…
| мкм 0 = | 2π (1 м) (2 × 10 −7 Н) | |
| (1 м) (1 А) 2 | ||
| мкм 0 = | 4π × 10 −7 НЕТ 2 | |
Возвращение к формуле для магнитной силы на проводе с током приводит к следующему определению напряженности магнитного поля и ее единицы, тесла.
| d F B = I d ℓ × B | ⇒ | .В = | Ф Б | ⇒ | . ⎡ ⎢ ⎣ | Т = | N | ⎤ ⎥ ⎦ |
| Iℓ | Am |
Третья линейка для правой / левой руки
Электронно-лучевая трубка: цветной телевизор (цветной монитор), осциллограф,
масс-спектрометр
циклотрон
космическая погода, сияние, радиационные пояса Ван Аллена
электродвигатель
Электромагнитный рельсовый пистолет
ядерный магнитный резонанс?
Магнитная сила — AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Сила Лоренца
Сила ЛоренцаДалее: Закон Ампера Up: Не зависящие от времени уравнения Максвелла Предыдущая: Эксперименты Ампера
Сила Лоренца Поток электрического тока вниз проводящий провод в конечном итоге из-за движения электрически заряженные частицы (в большинстве случаев электроны) через проводящую среду.Поэтому кажется разумным, что сила, действующая на провод, когда он помещен в магнитное поле, действительно равнодействующая сил, действующих на эти движущиеся заряды. Разрешите нам Предположим, что это так.
Пусть будет
(равномерная) площадь поперечного сечения провода, и пусть будет числовая плотность
мобильных зарядов в проводнике. Предположим, что
у мобильных зарядов есть заряд и скорость. Мы должны предположить, что
проводник также содержит стационарные заряды с зарядовой и числовой плотностью.
(скажем), так что чистая плотность заряда в проводе равна нулю.У большинства дирижеров
подвижные заряды — это электроны, а стационарные заряды — это атомные ядра.
Величина электрического тока, протекающего по проволоке, — это просто
количество кулонов в секунду, которые проходят через заданную точку. За одну секунду
мобильный заряд перемещается на расстояние, поэтому все заряды, содержащиеся в
цилиндр площади поперечного сечения и длины обтекает заданную точку.
Таким образом, величина тока составляет. Направление
ток совпадает с направлением движения зарядов, поэтому
векторный ток
.Согласно формуле. (229) сила на единицу длины, действующая на провод, равна
| (232) |
Однако на единице длины провода есть движущиеся заряды. Итак, если предположить что на каждый заряд действует одинаковая сила магнитного поля (мы имеем нет причин предполагать иное), сила, действующая на отдельный заряд, равна
| (233) |
Мы можем объединить это с формулой.(169) дать силу, действующую на движущийся заряд со скоростью в электрическом поле и магнитном поле :
| (234) |
Это называется законом силы Лоренца , в честь голландского физика. Хендрик Антун Лоренц, который первым ее сформулировал. Электрический сила, действующая на заряженную частицу, параллельна локальному электрическому полю. Однако магнитная сила перпендикулярна как местному магнитному полю. поле и направление движения частицы.Магнитная сила не действует на неподвижная заряженная частица.
уравнение движения свободной частицы заряда и
перемещение массы в электрическом и
магнитные поля
| (235) |
согласно закону силы Лоренца. Это уравнение движения было впервые проверено в известном эксперименте, проведенном Кембриджским физиком Дж. Дж. Томпсон в 1897 году. Томпсон проводил расследование катодных лучей , тогда таинственная форма излучения, испускаемого нагретым металлический элемент, находящийся под большим отрицательным напряжением ( i.е. , катод) с учетом к другому металлическому элементу (, т. е. , анод) в откачанной трубке. Немецкие физики считали, что катодные лучи форма электромагнитного излучения, в то время как британские и французские физики подозревали что они на самом деле были потоком заряженных частиц. Томпсон смог демонстрируют, что последнее мнение было правильным. В эксперименте Томпсона катодные лучи проходили через область « скрещенных » электрических и магнитных поля (все еще в вакууме). Поля были перпендикулярны исходному траектории лучей, а также были взаимно перпендикулярны.
Разберем эксперимент Томпсона. Предположим, что
лучи изначально движутся в -направлении и подвержены влиянию
однородное электрическое поле в -направлении и однородное магнитное поле.
поле в направлении. Предположим, как это сделал Томпсон, что катод
лучи — это поток частиц массы и заряда. В
уравнение движения частиц в -направлении имеет вид
| (236) |
где — скорость частиц в -направлении.Томпсон начал свой эксперимент с только включив электрическое поле в своем аппарате, и измерение отклонение луча в -направлении после того, как он прошел расстояние через электрическое поле. Из уравнения видно движения, которое
| (237) |
где « время полета » заменено на. Эта формула только действительно, если, что предполагается. Затем Томпсон включил магнитное поле в его аппарате и отрегулировал его так, чтобы катодный луч был больше не отклоняется.Отсутствие отклонения означает, что результирующая сила, действующая на частиц в -направлении была равна нулю. Другими словами, электрические и магнитные силы точно сбалансированы. Как следует из уравнения. (236) что при правильно настроенной напряженности магнитного поля
| (238) |
Таким образом, уравнения. (237) и (238) и могут быть объединены и перегруппированы, чтобы получить отношение заряда к массе частицы в единицах измерения:
| (239) |
Используя этот метод, Томпсон сделал вывод, что катодные лучи состоят из отрицательно заряженные частицы (знак заряда виден из направление отклонения в электрическом поле) с зарядом к массе соотношение Кл / кг.Десять лет спустя, в 1908 году, американец Роберт Милликен провел свой знаменитый эксперимент с « каплей масла » и обнаружил, что мобильные электрические заряды квантуются в единицах С. Предполагая, что мобильные электрические заряды и частицы, которые составлять катодные лучи одно и то же, Эксперименты Томпсона и Милликена предполагают, что масса этих частиц составляет кг. Конечно, это масса электрон (современное значение кг), и C — заряд электрона. Таким образом, катодные лучи, по сути, являются потоки электронов, которые вылетают из нагретого катода, а затем ускоряется из-за большой разницы напряжений между катодом и анодом.
Теперь рассмотрим частицу массы и заряда, движущуюся в однородной
магнитное поле,
. В соответствии с
Уравнение (235) уравнение движения частицы можно записать:
| (240) |
Это сводится к
Здесь, называется циклотронной частотой . Приведенные выше уравнения могут быть решены, чтобы дать
а также
Согласно этим уравнениям траектория частицы представляет собой спираль ось которого параллельна магнитному полю.Радиус спираль , где постоянная скорость в плоскости, перпендикулярной магнитному полю. Частица дрейфует параллельно магнитному полю с постоянной скоростью,. Ну наконец то, частица вращается в плоскости, перпендикулярной магнитному полю на циклотроне частота.
Наконец, если частица подвергается действию силы и перемещается на расстояние
в интервале времени, то работа, совершаемая над частицей
сила
| (250) |
Подвод мощности к частице от силового поля равен
| (251) |
где — скорость частицы.Из силы Лоренца следует закон, Ур. (234), что подвод энергии к частице, движущейся в электрическом и магнитном поля
| (252) |
Обратите внимание, что заряженная частица может получать (или терять) энергию от электрического поле, но не от магнитного поля. Это потому, что магнитная сила всегда перпендикулярно направлению движения частицы и, следовательно, делает нет работы на частице [см. (250)]. Так, в ускорителях частиц магнитные поля часто используются для направления движения частиц ( e.грамм. , по кругу), но Фактическое ускорение осуществляется электрическими полями.
Далее: Закон Ампера Up: Не зависящие от времени уравнения Максвелла Предыдущая: Эксперименты Ампера Ричард Фицпатрик 2006-02-02 .
