БиоВитрум — Система Signal
Система Signal, основанная на манометрическом методе, уже более 20 лет успешно применяется в Европе для тестирования крови на стерильность.
- Уникальная однофазная многокомпонентная среда
- Объем среды – 84 мл
- Подходит для взрослых и педиатрических образцов до 10 мл
- Рост анаэробов, аэробов и грибов в 1 флаконе
- Метод детекции – манометрия
- Четкий результат по поднятию бульона с кровью в индикаторное устройство.
- Положительный результат в течение 24 часов
- Превосходная высеваемость
- Низкий уровень контаминации
- Безопасность
- Хранение при комнатной температуре
- Срок годности 2 года
Методика использования*:
- Поместите образец крови во флакон, проколов шприцом резиновую пробку флакона.
- Присоедините к флакону индикаторное устройство.
- Инкубируйте флакон при 36 ± 1°C (первые сутки встряхивая на шейкере или вручную)
- При наличии роста бактерий и в результате процесса газообразования, во флаконе изменится давление, и бульон с кровью по капилляру поступит в индикаторное устройство.
- Для дальнейшего анализа заберите материал из верхнего индикаторного устройства, сняв крышку.
|
Артикул |
Название |
Фасовка |
Описание |
|
BC0100M |
Система Signal (бутыль и приспособление индикатора роста) |
20 шт. |
20 флаконов и 20 насадок |
Скачать инструкцию к системе Signal.
*полная методика использования приведена в инструкции к системе.
Система спутниковой связи «Сигнал»
Космический сегмент системы состоит из 48 КА (по 12 КА на каждой из орбит, расположенных в 4 плоскостях). Плоскости орбит разнесены в пространстве по долготе восходящего узла на 90°. Высота орбиты каждого КА составляет 1500 км, наклонение г = 74°. Масса спутника-ретранслятора 310 кг, срок службы — не менее 6 лет. Для вывода КА на орбиту предполагается использовать ракеты-носители «Циклон» (6 КА за один пуск) или «Космос» (2 КА за один пуск). Бортовые антенные системы КА состоят из 3 антенн, которые работают диапазонах:
0,3—0,4ГГц (один луч, покрывающий всю зону)
1,5—1,6 ГГц (шесть лучей, покрывающих всю зону)
11—14 ГГц (три луча, покрывающих всю зону)
Наземный сегмент
Шлюзовые станции, работающие в диапазоне 11—14 ГГц .
Подвижные абонентские терминалы, работающие в диапазонах 0,3—0,4 и 1,5-1,6 ГГц
Стационарные абонентские терминалы коллективного пользования, работающие в диапазоне 20—30 ГГц и используемые для сопряжения с телефонными и сотовыми системами связи (на экспериментальном этапе не предусмотрены)
Центр управления полетом и связью
Командно-измерительный комплекс
На территории России после полного развертывания системы предполагается размещение 6 базовых станций (в Москве, Самаре, Екатеринбурге, Томске, Чите и Комсомольске-на-Амуре). Бортовая аппаратура КА Сигнал предназначена для сопряжения с наземной телефонной связью общего назначения и для коммутации каналов различных коммерческих сетей. С системой «Сигнал» решаются следующие задачи:
Организация персонального радиовызова абонента
Организация устойчивой телефонной связи между парами абонентов
Обеспечение контроля связи между абонентами
Поддержание канала связи между абонентами с учетом динамики орбитальной группировки
Организация связи
В системе «Сигнал» не исключается межспутниковая связь, а связь между любыми абонентами организуется через КА и шлюзовые станции.
Этой системой обеспечивается асинхронный многостанционный доступ абонентов. При этом используется модификация частотно-кодового разделения каналов в пределах одного ствола и пространственное разделение стволов в БРТК спутника-ретранслятора. Для увеличения эффективности использования полосы частот применяется относительная четырехпозиционная фазовая манипуляция. Данный вид модуляции обеспечивает удовлетворение требований по электромагнитной совместимости (ЭМС) и уменьшение влияния узкополосных помех на качество передаваемой информации. Кроме того, применение широкополосных сигналов в системе «Сигнал» позволяет с высокой точностью проводить навигационные измерения, а также определять местоположение каждого абонента системы.
Этапы создания системы
Предусмотрены следующие основные этапы создания системы:
Экспериментальный этап — вывод на орбиту двух спутников-ретрансляторов
Этап развертывания системы — ввод в строй 12 КА, а в дальнейшем доведение их числа до 24
Этап полного развертывания системы — ввод в эксплуатацию до 48 КА и необходимого числа шлюзовых станций для обеспечения зон обслуживания на территории России.
Сверхзащищенный мессенджер Signal «тайно» сохраняет историю и ключи шифрования открытым текстом
Иллюстрация thehackernews.com
Signal обрел популярность после того, как стал известен в качестве «любимого мессенджера» Эдварда Сноудена. В 2015 г. он рассказал, что ежедневно пользуется приложением Signal для связи с журналистами.
Мессенджер Signal позиционируется как особо защищённое средство обмена информацией, в котором используется сквозное шифрование, что должно исключать доступ посторонних к содержимому переписки. Однако, как выяснилось, существуют ситуации, когда всё старания по шифрованию информации Signal оказываются тщетными.
Первоначально Signal был доступен только как приложение для мобильных телефонов, но удобство требовало настольной версии, которая в результате появилась в виде расширения для Chrome. С конца октября 2017 пользователям стал доступен новый вариант автономного приложения, не зависящего от браузера. С этого же момента расширение для Chrome получило статус end-of-life, и на момент публикации данной статьи срок его поддержки истекает менее чем через месяц. Здесь и начинается грустная история.
Делай раз
Исследователь в области информационной безопасности Мэтью Сюиш поделился открытием, что один из самых защищенных крипто-мессенджеров «подложил» своим пользователям «свинью» впечатляющих размеров. Мессенджер Signal в процессе миграции от расширения для Chrome до полноценного десктопного клиента экспортирует сообщения пользователя в незашифрованные текстовые файлы.
При экспорте диалогов на диск Signal формирует отдельные папки, именованные по имени и телефонному номеру контактов. Всё содержимое диалогов хранится в формате JSON открытым текстом. Никаких предупреждений о том, что информация расшифровывается и сохраняется на диск, программа не выводит. Этот момент и является ключевым для угрозы утечки конфиденциальных данных.
Самое плохое же в этой ситуации — незашифрованные сообщения остаются на диске даже после завершения апгрейда, и удалять их придется вручную, если, конечно, пользователь вообще догадается…
Делай два
Но этого было мало! Вторую проблему в Signal Desktop выявил другой исследователь, Нэйтан Сёчи.
Нэйтан Сёчи узнал, что во время установки Signal Desktop создается зашифрованная база данных db.sqlite с архивом сообщений пользователя. Ключ шифрования для базы данных генерируется мессенджером без взаимодействия с пользователем и используется каждый раз, когда нужно прочитать базу с архивом сообщений. Кто бы мог подумать, что ключ хранится локально и открытым текстом? Этот ключ можно найти на PC в файле
Делай три, Signal синим пламенем гори!
По-видимому, на этом проблемы с Signal не заканчиваются. Например, ещё один эксперт, Кит МакКэммон указывает, что Signal Desktop плохо справляется с удалением вложений из «исчезающих» сообщений.
Using Signal Desktop? Search your local filesystem for media attached to disappearing messages. Rejoice when you find that media files are never removed.
Signal does not aim to protect against filesystem access. Which would be fine, if this were apparent to anyone at all . . .
— Keith (@kwm) October 22, 2018
Функция «исчезающих» сообщений задумывалась разработчиками Signal как дополнительный эшелон безопасности, но на деле работает она не очень ненадёжно. По заявлению МакКэммона, все вложения остаются на диске пользователей Signal даже после того, как должны были быть удалены.
Вторая сигнальная система — Википедия
Материал из Википедии — свободной энциклопедии
Вторая сигнальная система — специальный тип высшей нервной деятельности человека, система «сигналов», идущих от общей с животными первой сигнальной системы — ощущений, представлений, относящихся к окружающему миру. Речь, как вторая сигнальная система, как семиотическая система значимостей — это «идущие в кору от речевых органов есть вторые сигналы, сигналы сигналов. Они представляют собой отвлечение от действительности и допускают обобщение, что и составляет наше личное, специально человеческое, высшее мышление, создающее сперва общечеловеческий эмпиризм, а, наконец, и науку — орудие высшей ориентировки человека в окружающем мире и в самом себе». И. П. Павлов (1932).
В процессе эволюции животного мира на этапе становления и начального развития вида Homo sapiens произошло качественное видоизменение системы сигнализации, обеспечивающее активное и коллективное адаптивное приспособительное поведение, создавшее многообразные, принятые в группе системы сигнализации и языки: слово, по выражению И. П. Павлова, становится «сигналом сигналов». (см.подробнее: Знаковая система). Появление второй сигнальной системы — возникновение речи и языков, сигнальных систем человека с сородичами, где условные (произвольные) сигналы индивида приобретают определенные, принятые группой значения и значимости, преобразуются в знаки языка в прямом смысле этого слова — это один из важнейших результатов длительной эволюции социальной жизни рода Homo, передающиеся через речевую деятельность из поколения в поколение. Биопсихологические и социальные условия формирования структур мозга (неокортекса) и образования языков подвергнуты в последние полтораста лет глубокому анализу палеопсихологами Б. Ф. Поршневым, (см. его О начале человеческой истории) и антропологами. А лингвистами — лишь с открытием европейской наукой санскрита и с появлением сравнительного языкознания индоевропейских языков (см. В.фон Гумбольдт, Фердинанд де Соссюр) .
В своей работе «Проба физиологического понимания симптомологии истерии» И. П. Павлов разделяет функции сигнальных систем следующим образом:
Всю совокупность высшей нервной деятельности я представляю себе так. У высших животных, до человека включительно, первая инстанция для сложных соотношений организма с окружающей средой есть ближайшая к полушариям подкорка с её сложнейшими безусловными рефлексами (наша терминология), инстинктами, влечениями, аффектами, эмоциями (разнообразная, обычная терминология). Вызываются эти рефлексы относительно немногими безусловными внешними агентами. Отсюда — ограниченная ориентировка в окружающей среде и вместе с тем слабое приспособление.
Вторая инстанция — большие полушария… Тут возникает при помощи условной связи (ассоциации) новый принцип деятельности: сигнализация немногих, безусловных внешних агентов бесчисленной массой других агентов, постоянно вместе с тем анализируемых и синтезируемых, дающих возможность очень большой ориентировки в той же среде и тем же гораздо большего приспособления. Это составляет единственную сигнализационную систему в животном организме и первую в человеке.
В человеке прибавляется… другая система сигнализации, сигнализация первой системы — речью, её базисом или базальным компонентом — кинестетическими раздражениями речевых органов. Этим вводится новый принцип нервной деятельности — отвлечение и вместе обобщение бесчисленных сигналов предшествующей системы, в свою очередь опять же с анализированием и синтезированием этих первых обобщенных сигналов — принцип, обусловливающий безграничную ориентировку в окружающем мире и создающий высшее приспособление человека — науку, как в виде общечеловеческого эмпиризма, так и в её специализированной форме.[1]
— Павлов И.П. «Проба физиологического понимания симптомологии истерии»
В исследованиях В.с.с. в лаборатории высшей нейродинамики и психологии высших когнитивных процессов Е. И. Бойко [1] показана плодотворность учения И. П. Павлова о динамических временных связях В.с.с.[2] В развитие идей И. П. Павлова и Е. А. Бойко в школе Е. А. Бойко разработана общая когнитивистская модель целостного рече-мысле-языкового процесса, найдены решения сложнейших теоретических проблем психологии в её взаимосвязях с лингвистикой, такие как вопросы соотношения языка и речи в процессах речепроизводства и речепонимания; характер связей речи с мыслью, речи с личностью говорящего; особенности развития детской речи и др. Здесь разработаны новые методы анализа публичных выступлений (интент-анализ), позволяющий в известной мере реконструировать «картину мира» говорящего — его целевые и предметные направленности, их динамику, особенности в конфликтной ситуации, в свободных условиях общения, в публичных выступлениях и др.
Существенным резервом для дальнейших исследований остаются проблемы типологии колоссальных индивидуальных различий во взаимосвязях общего и специального типов ВНД, неокортекса и эмоционально-волевой и непроизвольной регуляции деятельности и общения, пока что слабо представленных как в физиологии ВНД [2], так и в психолингвистических исследованиях и в антропологической лингвистике.
Понятие второй сигнальной системы в современной мировой науке о мозге[править | править код]
- Шичко Г. А. Вторая сигнальная система и её физиологические механизмы. Л., Медицина, 1969;
- Бойко Е. И. Механизмы умственной деятельности. М., 1976;
- Чуприкова Н. И. Слово как фактор управления в высшей нервной деятельности человека. М., 1976;
- Ушакова Т. Н. Функциональные структуры второй сигнальной системы. М., 1979.
- Ушакова Т. Н., Павлова Н. Д., Зачесова И. А. Речь человека в общении. М., 1985;
- Ушакова Т. Н. (ред.). Современные модели психологии речии психолингвистики. М., 1990.
- Ушакова Т.Н . и др. Ведение политических дискуссий. М., 1995.
- Ушакова Т. Н. и др. Слово в действии. Интент-анализ политического дискурса. СПб., 2000.
- Ушакова Т. Н. Психология речи и языка. Психолингвистика //Психология ХХ1 века, Учебник для вузов. М., 2003.
- ИНТЕГРАТИВНАЯ ДЕЯТЕЛЬНОСТЬ МОЗГА ЧЕЛОВЕКА. ВТОРАЯ СИГНАЛЬНАЯ СИСТЕМА в учебнике для студентов медвузов «Физиология человека» под редакцией В. М. Покровского, Г. Ф. Коротько, 2007,-656 стр. 2-е перераб. изд. [3]
- Поршнев Б. Ф. О начале человеческой истории (проблемы палеопсихологии). — М.: Академический проект; Трикста, 2013. — 542 с.
- Вторая сигнальная система / Кольцова М. М. // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
Система спутниковой связи «Сигнал»
Низкоорбитальная система спутниковой связи Сигнала разработана Международным концерном космической связи (КОСС).Она предназначена для непрерывного, круглосуточного обмена информацией между подвижными абонентами в реальном масштабе времени. Скорость передачи информации до 9,6 Кбит/с. В системе все абоненты имеют возможность беспрепятственного доступа к наземным телефонным сетям общего использования, а также к различным коммерческим сетям связи. Кроме того, система позволяет осуществлять с высокой точностью определение координат абонентов.
Космический сегмент
Космический сегмент системы состоит из 48 КА (по 12 КА на каждой из орбит, расположенных в 4 плоскостях). Плоскости орбит разнесены в пространстве по долготе восходящего узла на 90°. Высота орбиты каждого КА составляет 1500 км, наклонение г = 74°. Масса спутника-ретранслятора 310 кг, срок службы — не менее 6 лет. Для вывода КА на орбиту предполагается использовать ракеты-носители «Циклон» (6 КА за один пуск) или «Космос» (2 КА за один пуск). Бортовые антенные системы КА состоят из 3 антенн, которые работают диапазонах:
0,3—0,4ГГц (один луч, покрывающий всю зону)
1,5—1,6 ГГц (шесть лучей, покрывающих всю зону)
11—14 ГГц (три луча, покрывающих всю зону)
Наземный сегмент
Наземный сегмент, как и во всех системах спутниковой связи, включает в себя:
Шлюзовые станции, работающие в диапазоне 11—14 ГГц .
Подвижные абонентские терминалы, работающие в диапазонах 0,3—0,4 и 1,5-1,6 ГГц
Стационарные абонентские терминалы коллективного пользования, работающие в диапазоне 20—30 ГГц и используемые для сопряжения с телефонными и сотовыми системами связи (на экспериментальном этапе не предусмотрены)
Центр управления полетом и связью
Командно-измерительный комплекс
На территории России после полного развертывания системы предполагается размещение 6 базовых станций (в Москве, Самаре, Екатеринбурге, Томске, Чите и Комсомольске-на-Амуре). Бортовая аппаратура КА Сигнал предназначена для сопряжения с наземной телефонной связью общего назначения и для коммутации каналов различных коммерческих сетей. С системой «Сигнал» решаются следующие задачи:
Организация персонального радиовызова абонента
Организация устойчивой телефонной связи между парами абонентов
Обеспечение контроля связи между абонентами
Поддержание канала связи между абонентами с учетом динамики орбитальной группировки
Организация связи
В системе «Сигнал» не исключается межспутниковая связь, а связь между любыми абонентами организуется через КА и шлюзовые станции.
Этой системой обеспечивается асинхронный многостанционный доступ абонентов. При этом используется модификация частотно-кодового разделения каналов в пределах одного ствола и пространственное разделение стволов в БРТК спутника-ретранслятора. Для увеличения эффективности использования полосы частот применяется относительная четырехпозиционная фазовая манипуляция. Данный вид модуляции обеспечивает удовлетворение требований по электромагнитной совместимости (ЭМС) и уменьшение влияния узкополосных помех на качество передаваемой информации. Кроме того, применение широкополосных сигналов в системе «Сигнал» позволяет с высокой точностью проводить навигационные измерения, а также определять местоположение каждого абонента системы.
Этапы создания системы
Предусмотрены следующие основные этапы создания системы:
Экспериментальный этап — вывод на орбиту двух спутников-ретрансляторов
Этап развертывания системы — ввод в строй 12 КА, а в дальнейшем доведение их числа до 24
Этап полного развертывания системы — ввод в эксплуатацию до 48 КА и необходимого числа шлюзовых станций для обеспечения зон обслуживания на территории России.
Сигналы и линейные системы.
10
Signals and linear systems. Transformations of signals in systems.
Тема 11. Преобразование формы сигналов в системах
На свете мало недостижимых вещей. Будь у нас больше настойчивости, мы могли бы отыскать путь почти к любой цели.
Франсуа де Ларошфуко.
Цель поставлена, настойчивости хватает. Осталось разработать методику оценки параметра «почти». При всей настойчивости виноделом на изготовлении шампанского из картошки не прославишься.
Юрий Овченков. Уральский геофизик, XX в.
Введение
1. Понятие систем. Линейные системы. Основные системные операции. Инвариантность систем к сдвигу. Математическая модель системы. Нерекурсивные системы. Рекурсивные системы.
2. Нерекурсивная фильтрация сигналов. Частотные характеристики фильтров. Расчет операторов нерекурсивных фильтров.
Введение
Преобразование и обработка сигналов осуществляется в системах. Понятия сигнала и системы неразрывны, так как любой сигнал существует в какой-либо системе его обращения. Система обработки сигналов может быть реализована как в материальной форме (специальное устройство, измерительный прибор и т.п.), так и программно на ЭВМ или на любом другом вычислительном устройстве. Существуют и комплексные измерительно-вычислительные системы (ИВС), которые выполняют как регистрацию и первичную обработку сигналов непосредственно в материальной форме их представления, так и преобразование сигналов в цифровую форму, и последующую программную обработку. Форма реализации систем в теоретическом плане существенного значения не имеет.
11.1. Понятие систем [1, 25]
Система любого назначения всегда имеет вход, на который подается входной сигнал или входное воздействие, в общем случае многомерное, и выход, с которого снимается обработанный выходной сигнал. Если устройство системы и внутренние операции преобразований принципиального значения не имеют, то система в целом может восприниматься как “черный ящик”, в формализованном виде. Формализованная система представляет собой определенный системный оператор (алгоритм) преобразования входного сигнала – воздействия s(t), в сигнал на выходе системы y(t) – отклик или выходную реакцию системы. Символическое обозначение операции преобразования (трансформации):
y(t) = T[s(t)].
Системный оператор T — это правило (набор правил, алгоритм) преобразования сигнала s(t) в сигнал y(t). Для общеизвестных операций преобразования сигналов применяются также расширенные символы операторов трансформации, где вторым символом и специальными индексами обозначается конкретный вид операции (как, например, TF — преобразование Фурье, TF-1 — обратное преобразование Фурье).
Входной сигнал системы может представлять собой m — мерный вектор, а выходной сигнал n — мерный вектор, при этом система будет иметь m входов и n выходов. Пример такой системы в геофизике: трехканальный гамма-спектрометр. На три входа решающего блока спектрометра поступают потоки сигналов от калиевого, радиевого и ториевого каналов амплитудного анализатора спектрометра, а на три выхода решающего блока подаются результаты количественной интерпретации входной информации — сигналы количественных содержаний калия, урана и тория в точке измерений. Системный оператор спектрометра реализует алгоритм решения системы трех линейных уравнений с тремя неизвестными.
Для детерминированных входных сигналов соотношение между выходными и входными сигналами однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса также существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, корреляционной функции и пр.), которое также определяется системным оператором.
Для полного определения системы необходимо задание характера, типа и области допустимых величин входных и выходных сигналов. Как правило, системы выполняются на сигналы одного типа по входу и выходу. По типу обработки входных сигналов они обычно подразделяются на системы непрерывного времени, в основном для аналоговых или дискретных сигналов непосредственно в процессе измерений, и цифровые системы для обработки данных, зарегистрированных на промежуточных носителях. Совокупность системного оператора Т и областей входных/выходных сигналов образует математическую модель системы.
Линейные системы. Любые преобразования сигналов сопровождаются изменением их спектра и по характеру этих изменений разделяются на два вида: линейные и нелинейные. К нелинейным относят изменения, при которых в составе спектра сигналов появляются новые гармонические составляющие. При линейных изменениях сигналов изменяются амплитуды и/или начальные фазы гармонических составляющих спектра. Оба вида изменений могут происходить как с сохранением полезной информации, так и с ее искажением. Это зависит не только от характера изменения спектра сигналов, но и от спектрального состава самой полезной информации.
Линейные системы составляют основной класс систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.
Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).
Принцип аддитивности требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:
T[a(t)+b(t)] = T[a(t)]+T[b(t)].
Принцип однородности или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:
T[c a(t)]= c T[a(t)].
Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.
Примеры.
1. Система y(t) = a2t. y(t1) = a2t1, y(t2) = a2t2, y(ct) = a2ct.
y(t1+t2) = a2(t1+t2) = a2t1+a2t2 = y(t1)+y(t2). Система аддитивна.
cy(t) = ca2t = a2ct = y(сt). Система однородна. И в целом линейна.
2. Система y(t) = at2. y(t1) = at12, y(t2) = at22, y(ct) = a(ct)2 = ac2t2.
y(t1+t2) = a(t1+t2)2 y(t1)+y(t2)= at12+at22. Система не аддитивна.
с y(t) = с at2 y(сt) = ac2t2. Система неоднородна. И в целом нелинейна.
При программной реализации линейных систем на ЭВМ особых затруднений с обеспечением линейности в разумных пределах значений входных и выходных сигналов, как правило, не возникает. При физической (аппаратной) реализации систем обработки данных диапазон входных и/или выходных сигналов, в котором обеспечивается линейность преобразования сигналов, всегда ограничен и должен быть специально оговорен в технической документации или методической инструкции.
Основные системные операции.К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:
y(t) = b x(t), y(t) = x(t-t), y(t) = a(t)+b(t).
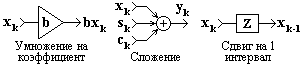
Рис. 11.1.1. Графика системных операций
Графическое отображение операций (цифровая форма) приведено на рис. 11.1.1.Отметим, что операции сложения и умножения являются линейными только для аналоговых и дискретных сигналов. В случае цифровых сигналов они линейны относительно самих цифровых сигналов, но если последние — результат операции амплитудно-цифрового преобразования, то сложение и умножение не может считаться линейным абсолютно точно по отношению к исходным сигналам.
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.
Инвариантность систем к сдвигу. Система называется инвариантной к сдвигу (инвариантной во времени, а равно и по любым другим аргументам), если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:
s(x,t) = T[a(x,t)], T[a(x-x,t-t)] = s(x-x,t-t).
Это означает, что форма выходного сигнала зависит только от входного сигнала, и не зависит от времени поступления сигнала на вход системы. Инвариантность системы к сдвигу является одним из подтверждений постоянства ее параметров.
Линейность и инвариантность к сдвигу являются независимыми свойствами систем и не определяют друг друга. Так, например, операция квадратирования сигнала (возведения в квадрат всех значений сигнала) инвариантна к сдвигу, но нелинейна.
В теории анализа и обработки данных основное место занимают системы, линейные и инвариантные к сдвигу (ЛИС — системы). Они обладают достаточно широкими практическими возможностями при относительной простоте математического аппарата. В дальнейшем, если это специально не оговаривается, будем иметь в виду именно такие системы.
Преимущество, которое отдается ЛИС — системам в методах обработки информации, базируется на возможности разложения входного сигнала любой, сколь угодно сложной формы, на составляющие простейших форм, отклик системы на которые известен и хорошо изучен, с последующим вычислением выходного сигнала в виде суммы откликов на все составляющие входного сигнала.
Другой важной особенностью ЛИС — систем является то, что любые их комбинации также являются ЛИС — системами, а любую сложную ЛИС — систему можно разложить на комбинации простых систем. Так, например, при последовательном (каскадном) соединении систем, когда выходной сигнал одной системы служит входным сигналом для второй и т.д., образуемая система в целом также является ЛИС — системой, если линейны и инвариантны к сдвигу все системы, в нее входящие, при этом по отношению к общей системной операции преобразования порядок соединения входящих в нее систем значения не имеет.
Математическая модель системы, как совокупности связанных физических, радио-, электротехнических и/или программных элементов, образующих устройство, способное воспринимать внешнее воздействие x(t) и выполнять его преобразование в некоторую выходную величину y(t), в наиболее общей описывается системой дифференциальных уравнений. Дифференциальные уравнения представляют собой универсальный инструмент задания определенной связи между сигналами входа и выхода в как в одномерных, так и в многомерных системах, и могут описывать систему, как в режиме реального времени, так и апостериорно. Так, в аналоговой одномерной линейной системе такая связь обычно выражается линейным дифференциальным уравнением
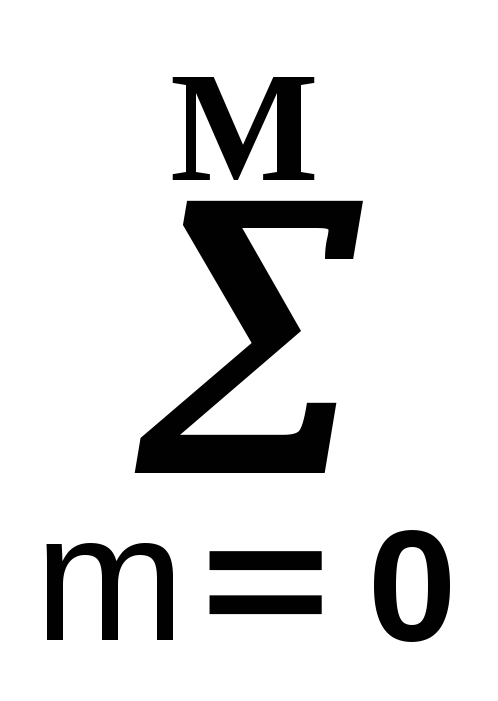 am
am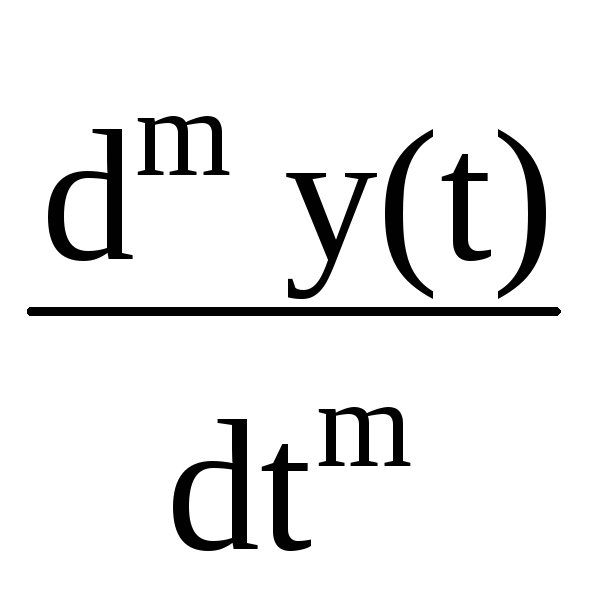 =
=  bn
bn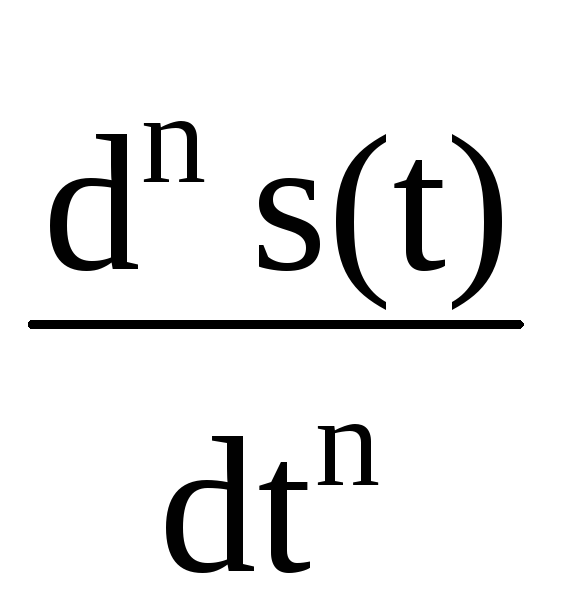 .
(11.1.1)
.
(11.1.1)
При нормировке к ао = 1, отсюда следует
y(t)
=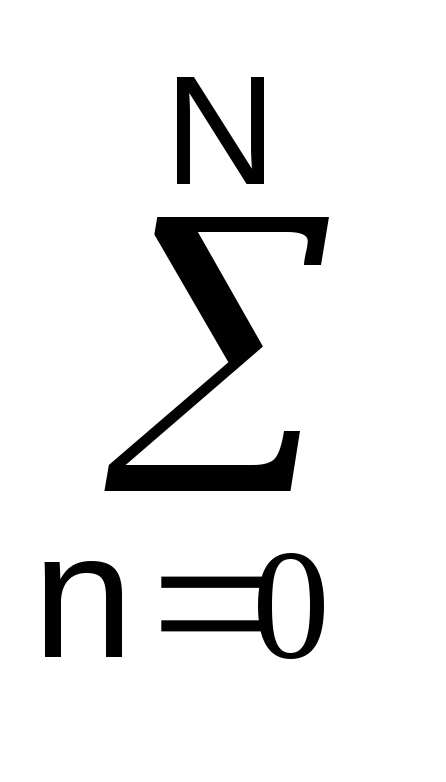 bn
bn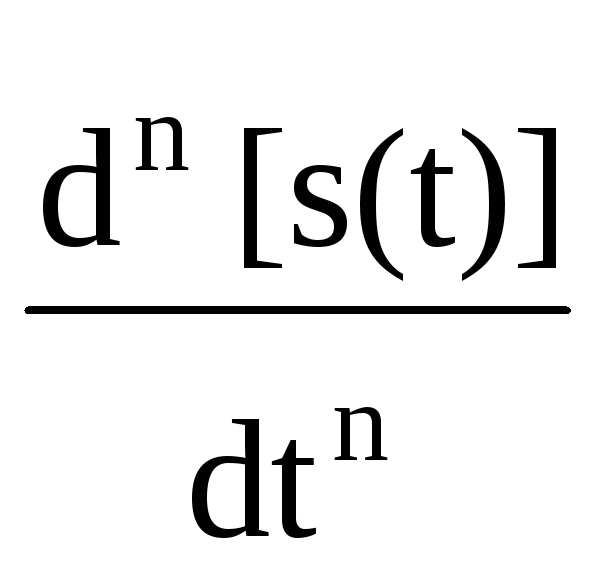 –
–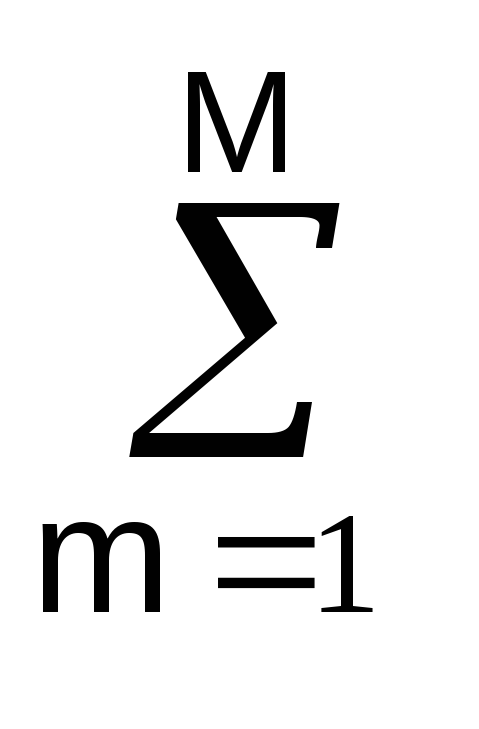 am
am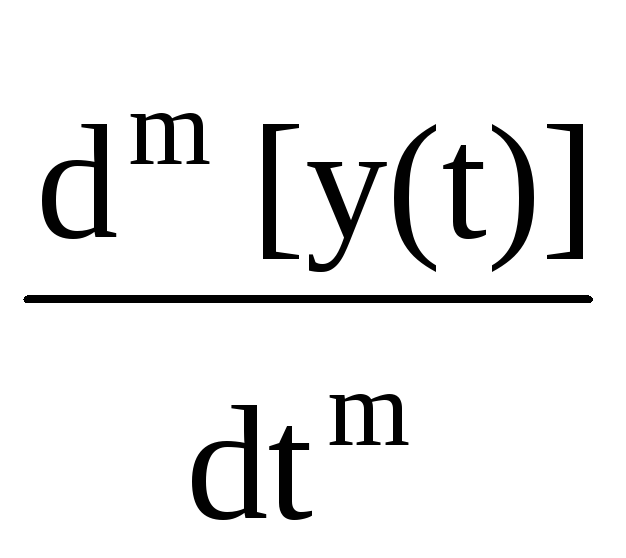 .(11.1.1′)
.(11.1.1′)
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной. Для однозначного решения уравнений (11.1.1) кроме входного сигнала s(t) должны задаваться определенные начальные условия, например, значения решения y(0) и его производной y'(0) по времени в начальный момент времени.
Аналогичная связь в цифровой системе описывается разностными уравнениями
 am y((k-m)t)
=
am y((k-m)t)
= bn s((k-n)t).
(11.1.2)
bn s((k-n)t).
(11.1.2)
y(kt)
= bn s((k-n)t)
–
bn s((k-n)t)
– am y((k-m)t).
(11.1.2′)
am y((k-m)t).
(11.1.2′)
Последнее уравнение можно рассматривать как алгоритм последовательного вычисления значений y(kt), k = 0, 1, 2, …, по значениям входного сигнала s(kt) и предыдущих вычисленных значений y(kt) при известных значениях коэффициентов am, bn и с учетом задания начальных условий — значений s(kt) и y(kt) при k < 0. Интервал дискретизации в цифровых последовательностях отсчетов обычно принимается равным 1, т.к. выполняет только роль масштабного множителя.
Нерекурсивные системы. При нулевых значениях коэффициентов am уравнение (11.1.2′) принимает вид:
y(k)
=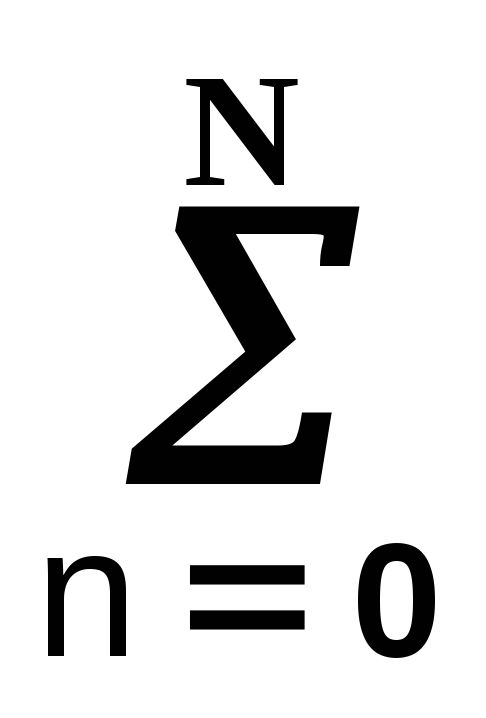 bnx(k-n).
(11.1.3)
bnx(k-n).
(11.1.3)
При установленных значениях коэффициентов bn значения выходных отсчетов свертки для любого аргумента k определяются текущим и «прошлыми» значениями входных отсчетов. Такая система называется нерекурсивной цифровой системой (НЦС). Нетрудно заметить, что уравнение (11.1.3) полностью повторяет уравнение свертки произвольного сигнала s(k) с импульсным откликом системы h(n), которое уже рассматривалось в теме динамического представления сигналов с базовой позиции «от сигнала». В данном случае, это уравнение получено в более строгой математической форме «от системы» и, как это следует из вышеизложенного, является только частным случаем системного уравнения (11.1.1). Отсюда следует также, что для НЦС импульсным откликом системы является непосредственно ядро свертки bn = hn. Но это действительно только для НЦС. Для систем, описываемых полной формой уравнений (11.1.1) и (11.1.2), импульсный отклик h(n) не равен коэффициентам bn, а зависит и от коэффициентов am, и представляет собой именно отклик системы на единичный входной сигнал.
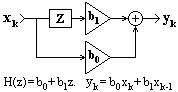
Рис. 11.1.2. Пример НЦС.
Пример простейшей НЦС приведен на рис. 11.1.2. Интервал суммирования по n получил название «окна» системы. Окно системы (11.1.3) составляет N+1 точку, система является односторонней каузальной, причинно обусловленной текущими и «прошлыми» значениями входного сигнала, выходной сигнал не опережает входного. Каузальная система может быть реализована аппаратно в реальном масштабе времени. При k<n проведение обработки входных данных возможно только при задании определенных начальных условий для точек x(-k), k=1,2,..,N. Как правило, в качестве начальных условий принимаются нулевые значения или значения отсчета х(0). Применяется также четное или нечетное продление функции x(k) на интервал отрицательных значений k. Если при обработке данных начальные интервалы массивов x(k) существенного значения не имеют, то обработку можно начинать с отсчета k=N.При обработке данных на ЭВМ ограничение по каузальности системного оператора снимается. В программном распоряжении системы могут находиться как «прошлые», так и «будущие» значения входных отсчетов, при этом уравнение (11.1.3) будет иметь вид:
y(k)
=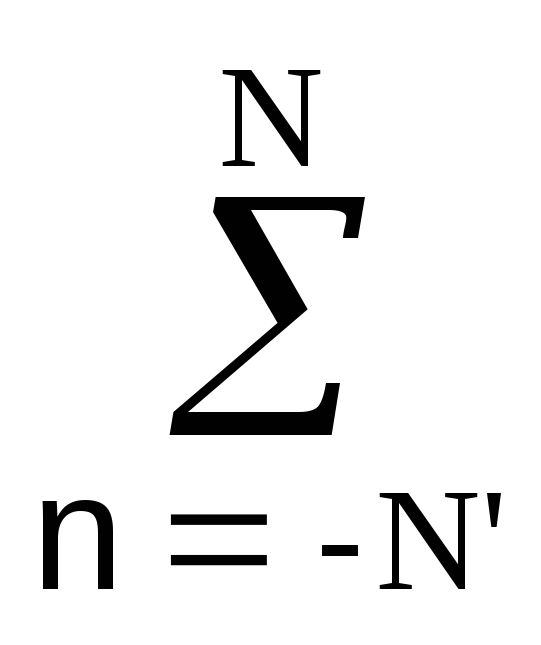 bnx(k-n).
(11.1.3′)
bnx(k-n).
(11.1.3′)
При N’ = N система называется двусторонней симметричной. Симметричные системы, в отличие от каузальных, не изменяют фазы обрабатываемых сигналов.
Описанный процесс свертки в вещественной области массива данных x(k) с нерекурсивным оператором системы bn (массивом весовых коэффициентов системы) обычно называют нерекурсивной цифровой фильтрацией данных, а саму систему, если она выполняет только данную операцию, нерекурсивным цифровым фильтром (НЦФ).
Пример. Сглаживание данных скользящим симметричным П-окном размером 5 отсчетов.
Уравнение НЦФ:
yk =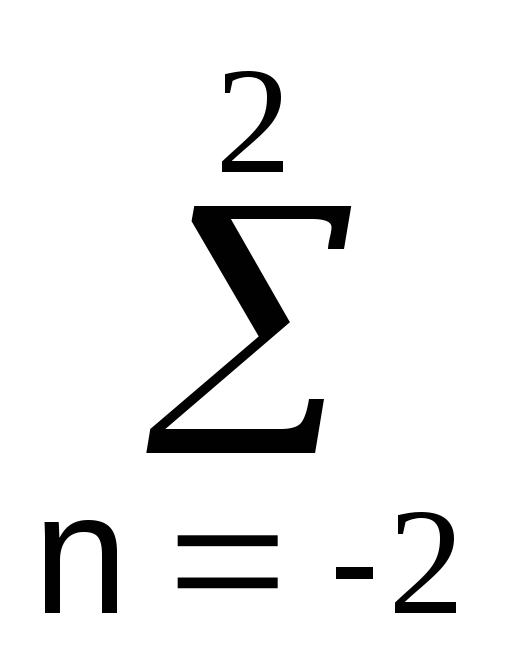 bn xk-n,
bn =
0,2. Начальные условия — нулевые.
bn xk-n,
bn =
0,2. Начальные условия — нулевые.
Входной сигнал: xk = {0,0,0,0,10,0,10,0,0,0,0}. Выходной сигнал: yk = {0,0,2,2,4, 4, 4,2,2,0,0}.
Проверьте результат (выполните фильтрацию сигнала).
Заметим: сумма коэффициентов bn сглаживающего НЦФ равна 1, при этом сумма значений выходного сигнала равна сумме значений входного сигнала. Сигнал «размазался» по аргументу.
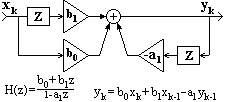
Рис. 11.1.3. Пример РЦС.
Рекурсивные системы. Системы, которые описываются полным разностным уравнением (11.1.2), принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью. Пример рекурсивной системы приведен на рис. 11.1.3. 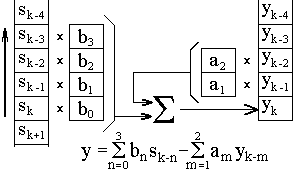
Рис. 11.1.4. Техника вычислений в РЦС.
Полное окно рекурсивной системы состоит из двух составляющих: нерекурсивной части bn,, аналогичной окну нерекурсивной системы и ограниченной в работе текущими и «прошлыми» значениями входного сигнала (при реализации на ЭВМ возможно использование и “будущих” отсчетов сигнала), и рекурсивной части am, которая работает только с «прошлыми», ранее вычисленными значениями выходного сигнала. Техника вычислений для РЦС приведена на рис. 11.1.4.Пример. Уравнение РЦС: yk= boxk+a1yk-1, при bo=a1=0.5, y-1=0. Входной сигнал: xk = {0, 10, 0, 0, 0,….}.
Расчет выходного сигнала:
уo = 0,5xo + 0,5y-1 = 0 y1 = 0,5x1 + 0,5yo = 5 y2 = 0,5x2 + 0,5y1 = 2.5 y3 = 0,5x3 + 0,5y2 = 1.25
y4 = 0,5x4 + 0,5y3 = 0.625 y5 = 0,5x5 + 0,5y4 = 0.3125 и т.д.
Выходной сигнал: yk = {0, 5, 2.5, 1.25, 0.625, 0.3125, 0.15625,…}
Из примера можно видеть, что реакция РЦС на конечный входной сигнал, в принципе, может иметь бесконечную длительность, в отличие от реакции НЦС, которая всегда ограничена количеством членов bk (окном системы).
Пример. Уравнение РЦС: yk = boxk+a1yk-1+a2yk-2, при bo=a1=a2=1. xk = {0, 1, 0, 0, 0,….}, y-1 = y-2 = 0.
Расчет выходного сигнала:
yo= xo+y-1+y-2 = 0. y1 = x1+yo+y-1 = 1. y2 = x2+y1+yo = 1. y3 = x3+y2+y1 = 2.
y4 = x4+y3+y2 = 3. y5 = x5+y4+y3 = 5. y6 = x6+y5+y4 = 8. y7 = x7+y6+y5 = 13. и т.д.
Заметим: сумма коэффициентов обратной связи ai больше 1 и выходной сигнал идет «в разнос».
Пример. Интегрирование данных по формуле трапеций.
Уравнение РЦФ: yk=(xk+xk-1)/2+yk-1, начальные условия — нулевые.
Входной сигнал: xk={0,0,2,2,8,0,4,4,0,..}.
Выполните фильтрацию. Контроль: yk= {0,0,1,3,8,12,14,18,20,20,…}.
Сигналы и линейные системы
16
Signals and linear systems. Stationary linear systems.
Тема 10. Стационарные линейные системы
Такова взаимосвязь: раз существует гадание, значит должны быть и боги; а раз существуют боги, значит должно быть и гадание.
Марк Туллий Цицерон. Римский философ и политик, I в.д.н.э.
Геология, наряду с медициной и богословием, относится к точным наукам. Есть геологический объект — должен быть сигнал. Есть сигнал — должен быть объект.
Владимир Мартынов. Мордовский геофизик Уральской школы, XX в.
Содержание
Введение.
1. Линейные системы. Общие понятия систем. Линейные системы. Основные системные операции. Инвариантность систем к сдвигу. Математическая модель системы. Нерекурсивные цифровые системы. Рекурсивные цифровые системы. Стационарные и нестационарные системы.
2. Импульсная характеристика системы. Импульсный отклик системы. Реакция системы на произвольный сигнал. Усиление постоянной составляющей сигнала. Усиление шумов. Определение импульсной реакции.
3. Передаточные функции цифровых систем. Z-преобразование. Устойчивость систем.
4. Частотные характеристики систем. Основные свойства.
5. Реакция систем на случайные сигналы. Квазидетерминированный сигнал. Математическое ожидание. Корреляционные соотношения. Спектральные соотношения. Дисперсия выходного сигнала. Функция когерентности.
6. Структурные схемы систем. Структурные схемы. Графы систем. Соединения систем. Схемы реализации систем. Обращенные формы.
Литература.
Введение
Преобразование и обработка сигналов осуществляется в системах. Понятия сигнала и системы неразрывны, так как любой сигнал существует в какой-либо системе его обращения. Система обработки сигналов может быть реализована как в материальной форме (специальное устройство, измерительный прибор и т.п.), так и программно на ЭВМ или на любом другом вычислительном устройстве. Существуют и комплексные измерительно-вычислительные системы (ИВС), которые выполняют как регистрацию и первичную обработку сигналов непосредственно в материальной форме их представления, так и преобразование сигналов в цифровую форму, и последующую программную обработку. Форма реализации систем существенного значения не имеет и определяет только их возможности при анализе и обработке сигналов. Основное внимание при рассмотрении данной темы будем уделять цифровым системам и дискретной математике их отображения и анализа, применяя аналитическую математику при рассмотрении общих вопросов, если последнее упрощает изложение и понимание теоретического материала.
10.1. Линейные системы [1, 2, 9, 14, 18, 20]
Общие понятия систем. Безотносительно к назначению и исполнению система всегда имеет вход, на который подается входной сигнал или входное воздействие, в общем случае многомерное, и выход, с которого снимается обработанный выходной сигнал. Если устройство системы и внутренние операции преобразований принципиального значения не имеют, то система в целом может восприниматься как “черный ящик”, в формализованном виде. Формализованная система представляет собой определенный системный оператор (алгоритм) преобразования входного сигнала – воздействия s(t), в сигнал на выходе системы y(t) – отклик или выходную реакцию системы. Символическое обозначение операции преобразования (трансформации):
y(t) = T[s(t)].
Системный оператор T — это правило (набор правил, алгоритм) преобразования сигнала s(t) в сигнал y(t). Для общеизвестных операций преобразования сигналов применяются также расширенные символы операторов трансформации, где вторым символом и специальными индексами обозначается конкретный вид операции (как, например, TF — преобразование Фурье, TF-1 — обратное преобразование Фурье).
Входной сигнал системы может представлять собой m — мерный вектор (m входных сигналов), а выходной сигнал n — мерный вектор, при этом система будет иметь m входов и n выходов. Пример такой системы в геофизике: трехканальный гамма-спектрометр, на три входа решающего блока которого поступают сигналы от калиевого, радиевого и ториевого каналов спектрометра, а на три выхода выводятся сигналы содержаний калия, урана и тория, при этом системный оператор реализует алгоритм решения системы трех линейных уравнений с тремя неизвестными.
Для детерминированных входных сигналов соотношение между выходными и входными сигналами однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса также существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, корреляционной функции и пр.), которое также определяется системным оператором.
Для определения системы необходимо задать характер, тип и области допустимых величин входных и выходных сигналов. Как правило, системы выполняются на сигналы одного типа по входу/выходу и подразделяются на системы непрерывного времени (аналоговые или дискретные сигналы на входе и выходе) и цифровые системы. Совокупность системного оператора Т и пространства сигналов образует математическую модель системы.
Линейные системы. Любые преобразования сигналов сопровождаются изменением их спектра и по характеру этих изменений разделяются на два вида: линейные и нелинейные. К нелинейным относят изменения, при которых в составе спектра сигналов появляются новые гармонические составляющие. При линейных изменениях сигналов изменяются амплитуды и/или начальные фазы гармонических составляющих спектра. Оба вида изменений могут происходить как с сохранением полезной информации, так и с ее искажением. Это зависит не только от характера изменения спектра сигналов, но и от спектрального состава самой полезной информации.
Линейные системы составляют основной класс систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.
Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).
Принцип аддитивности требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:
T[a(t)+b(t)] = T[a(t)]+T[b(t)].
Принцип однородности или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:
T[c a(t)]= c T[a(t)].
Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.
Примеры.
1. Система y(t) = a2t. y(t1) = a2t1, y(t2) = a2t2, y(ct) = a2ct.
y(t1+t2) = a2(t1+t2) = a2t1+a2t2 = y(t1)+y(t2). Система аддитивна.
cy(t) = ca2t = a2ct = y(сt). Система однородна. И в целом линейна.
2. Система y(t) = at2. y(t1) = at12, y(t2) = at22, y(ct) = a(ct)2 = ac2t2.
y(t1+t2) = a(t1+t2)2 y(t1)+y(t2)= at12+at22. Система не аддитивна.
с y(t) = с at2 y(сt) = ac2t2. Система неоднородна. И в целом нелинейна.
При программной реализации линейных систем на ЭВМ особых затруднений с обеспечением линейности в разумных пределах значений входных и выходных сигналов, как правило, не возникает. При физической (аппаратной) реализации систем обработки данных диапазон входных и/или выходных сигналов, в котором обеспечивается линейность преобразования сигналов, всегда ограничен и должен быть специально оговорен в технической документации или методической инструкции.
Основные системные операции. К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:

Рис. 10.1.1. Графика системных операций
y(t) = b x(t),y(t) = x(t-t),
y(t) = a(t)+b(t).
Графическое отображение операций (цифровая форма) приведено на рис. 10.1.1.
Отметим, что операции сложения и умножения являются линейными только для аналоговых и дискретных сигналов. В случае цифровых сигналов они линейны относительно самих цифровых сигналов, но если последние — результат операции амплитудно-цифрового преобразования, то сложение и умножение не может считаться линейным абсолютно точно по отношению к исходным сигналам.
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.
Инвариантность систем к сдвигу. Система называется инвариантной к сдвигу (инвариантной во времени, а равно и по любым другим аргументам), если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:
s(x,t) = T[a(x,t)], T[a(x-x,t-t)] = s(x-x,t-t).
Линейность и инвариантность к сдвигу являются независимыми свойствами систем и не определяют друг друга. Так, например, операция квадратирования сигнала (возведения в квадрат всех значений сигнала) инвариантна к сдвигу, но нелинейна.
В теории анализа и обработки данных основное место занимают системы, линейные и инвариантные к сдвигу (ЛИС — системы). Они обладают достаточно широкими практическими возможностями при относительной простоте математического аппарата. В дальнейшем, если это специально не оговаривается, будем иметь в виду именно такие системы.
Преимущество, которое отдается ЛИС — системам в методах обработки информации, базируется на возможности разложения входного сигнала любой, сколь угодно сложной формы, на составляющие простейших форм, отклик системы на которые известен и хорошо изучен, с последующим вычислением выходного сигнала в виде суммы откликов на все составляющие входного сигнала. В качестве простейших форм разложения сигналов используются, как правило, единичные импульсы и гармонические составляющие. Первая применяется при представлении сигнала в динамической форме и использует преобразование свертки, вторая — частотное представление сигнала и преобразование Фурье.
Другой важной особенностью ЛИС — систем является то, что любые их комбинации также являются ЛИС — системами, а любую сложную ЛИС — систему можно разложить на комбинации простых систем. Так, например, при последовательном (каскадном) соединении систем, когда выходной сигнал одной системы служит входным сигналом для второй и т.д., образуемая система в целом также является ЛИС — системой, если линейны и инвариантны к сдвигу все системы, в нее входящие, при этом по отношению к общей системной операции преобразования порядок соединения входящих в нее систем значения не имеет.
Математическая модель системы задает связь физических (программных) элементов, образующих техническое устройство, способное воспринимать внешнее воздействие s(t) и формировать выходную величину y(t), определенным образом зависимую от воздействия x(t). В аналитической форме эта связь в аналоговой одномерной линейной системе обычно выражается линейным дифференциальным уравнением
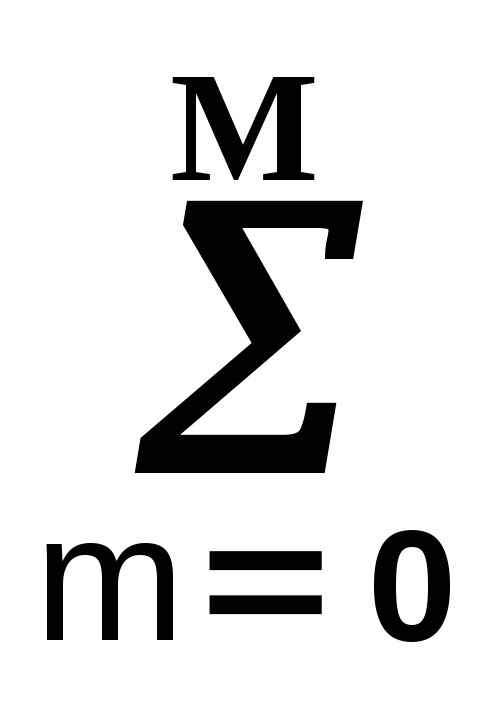 am
am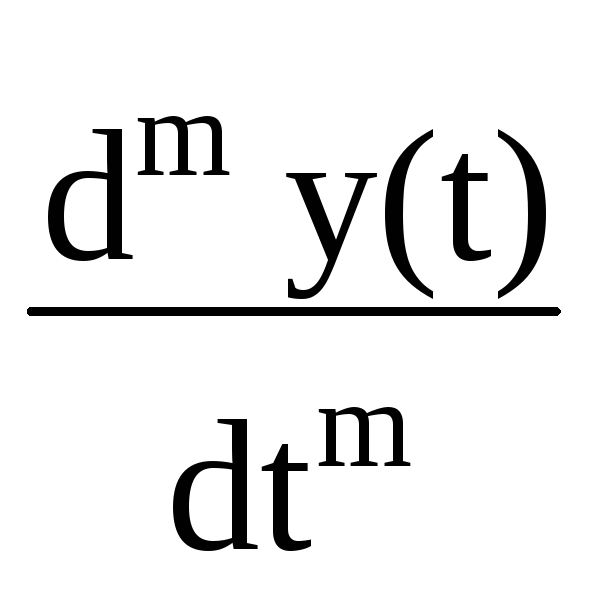 =
= 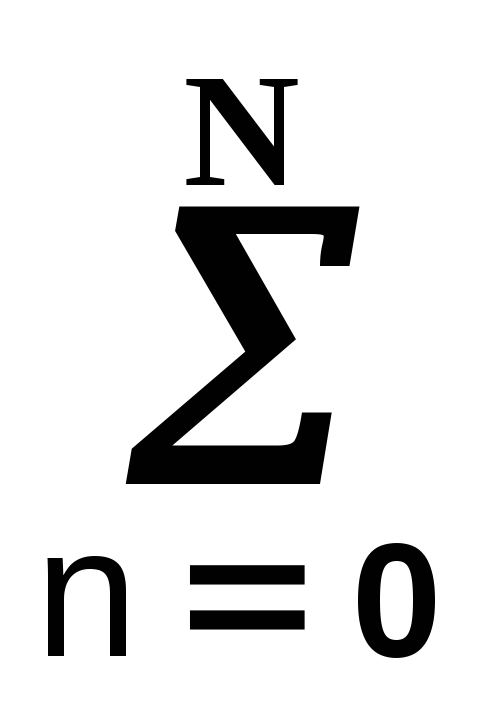 bn
bn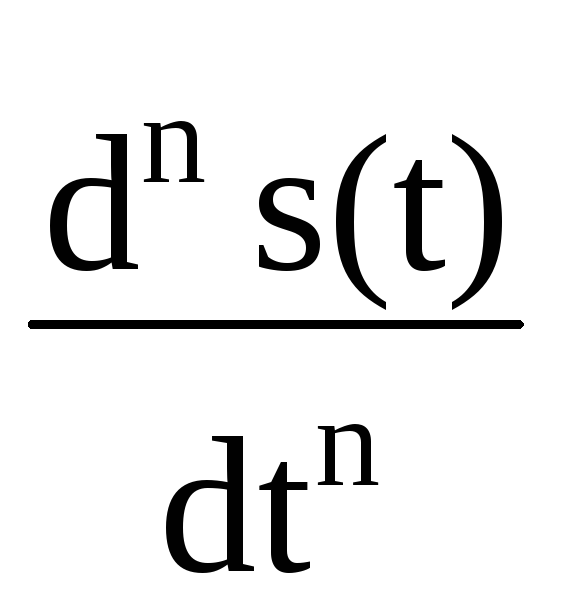 .
(10.1.1)
.
(10.1.1)
При нормировке к ао = 1, отсюда следует
y(t)
=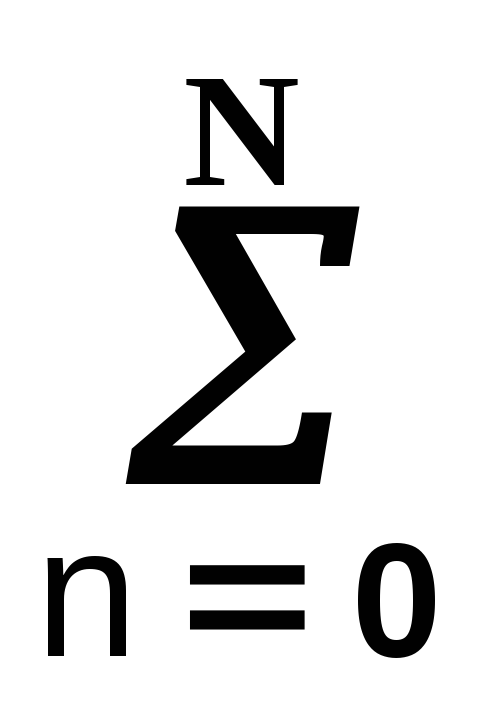 bn
bn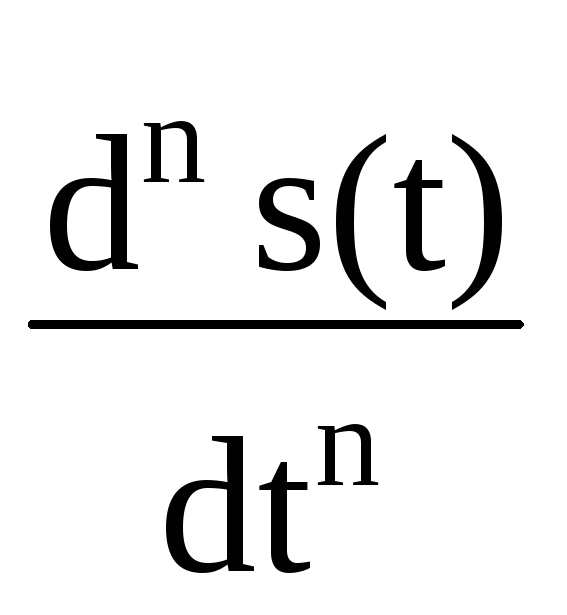 —
— am
am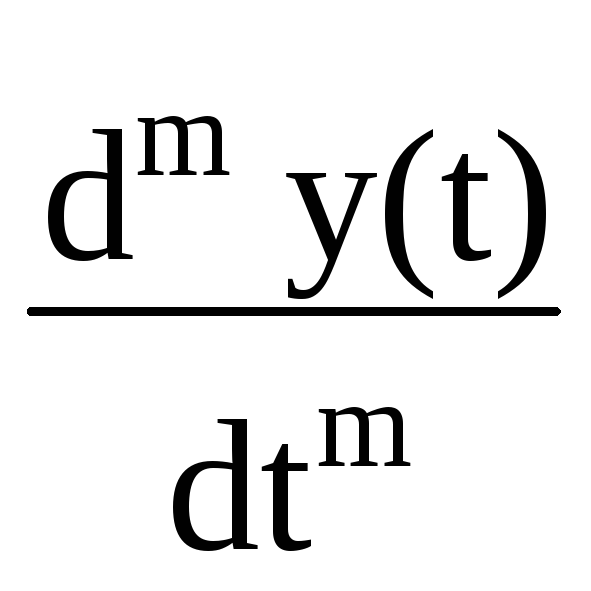 .
(10.1.1′)
.
(10.1.1′)
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной. Для однозначного решения уравнений (10.1.1) должны задаваться начальные условия: значения решения y(0) и его производных по времени в начальный (нулевой) момент времени. В физической системе эти значения определяются начальной энергией в элементах, способных ее накапливать. Входным воздействием может быть произвольный сигнал. Коэффициенты am и bn, которые определяются составом и свойствами системы, должны быть известными.
Как правило, решение уравнения (10.1.1) складывается из суммы принужденной yпр(t) и свободной yсв(t) составляющих:
y(t) = yпр(t) + ycв(t).
В устойчивых системах yсв(t) определяется параметрами системы (реакция на «ударное» воздействие – единичный «дельта-импульс» или скачок) и с течением времени затухает. Если входное воздействие достаточно гладкое и не содержит скачков (разрывов первого рода), то по истечении определенного времени затуханияyсв(t), которое обычно называют временем переходного процесса, система переходит в установившийся динамический режим, а выходной сигналy(t) определяется только значениемyпр(t) и линейно связан с входным воздействиемx(t).
Аналогичная модель в цифровой системы описывается разностными уравнениями
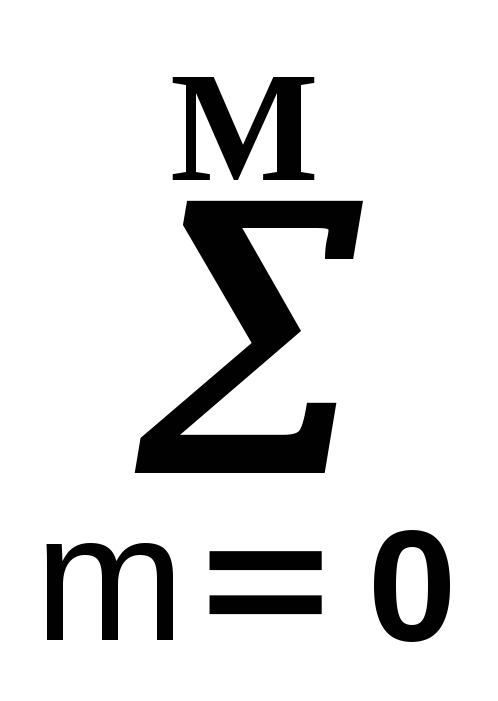 am y((k-m)t)
=
am y((k-m)t)
= 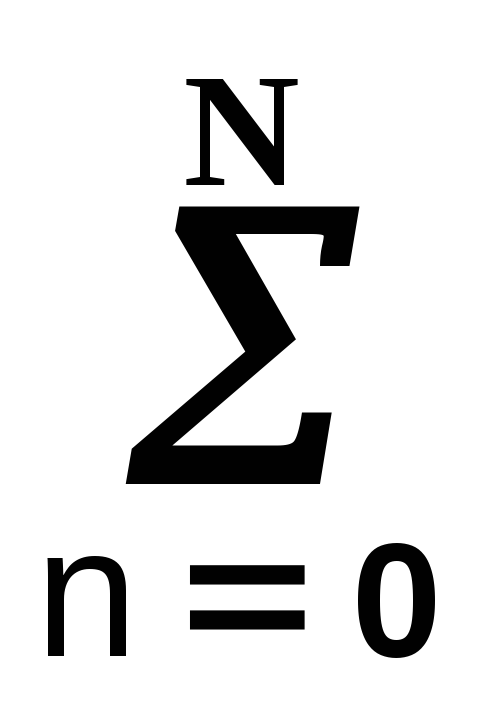 bn s((k-n)t).
(10.1.2)
bn s((k-n)t).
(10.1.2)
y(kt)
= bn s((k-n)t)
—
bn s((k-n)t)
—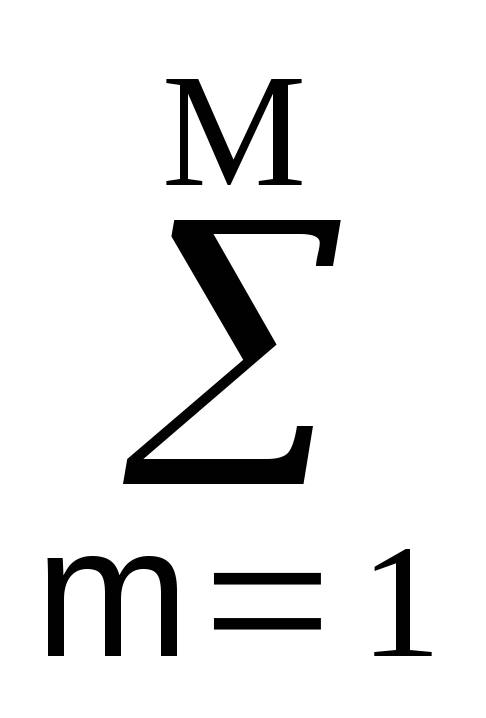 am y((k-m)t).
(10.1.2′)
am y((k-m)t).
(10.1.2′)
Последнее уравнение можно рассматривать как алгоритм последовательного вычисления значений y(kt), k = 0,1,2, …, по значениям входного сигнала s(kt) и предыдущих вычисленных значений y(kt) при известных значениях коэффициентов am, bn и с учетом задания определенных начальных условий — значений s(kt) и y(kt) при k < 0. Интервал дискретизации в цифровых последовательностях отсчетов обычно принимается равным 1, т.к. выполняет только роль масштабного множителя.
Нерекурсивные цифровые системы. При нулевых значениях коэффициентов am уравнение (10.1.2′) переходит в уравнение дискретной свертки x(k) с оператором bn:
y(k) =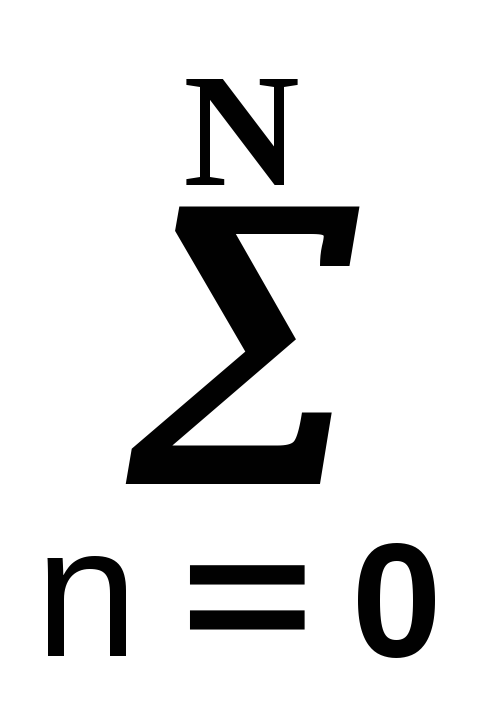 bn x(k-n).
(10.1.3)
bn x(k-n).
(10.1.3)
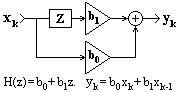
Рис. 10.1.2. Пример НЦС.
При установленных значениях коэффициентов bn значения выходных отсчетов свертки для любого аргумента k определяются текущим и «прошлыми» значениями входных отсчетов. Такая система называется нерекурсивной цифровой системой (НЦС). Пример простейшей НЦС приведен на рис. 10.1.2. Интервал суммирования по n получил название «окна» системы. Окно системы (10.1.3) составляет N+1 точку, система является односторонней каузальной, причинно обусловленной текущими и «прошлыми» значениями входного сигнала, выходной сигнал не опережает входного. Каузальная система может быть реализована аппаратно в реальном масштабе времени. При k<n проведение обработки входных данных возможно только при задании определенных начальных условий для точек x(-k), k=1,2,..,N. Как правило, в качестве начальных условий принимаются нулевые значения или значения отсчета х(0). Применяется также четное или нечетное продление функции x(k) на интервал отрицательных значений k. Если при обработке данных начальные интервалы массивов x(k) существенного значения не имеют, то обработку можно начинать с отсчета k=N.При обработке данных на ЭВМ ограничение по каузальности системного оператора снимается. В программном распоряжении системы могут находиться как «прошлые», так и «будущие» значения входных отсчетов, при этом уравнение (10.1.3) будет иметь вид:
y(k) = bn x(k-n).
(10.1.3′)
bn x(k-n).
(10.1.3′)
При N’ = N система называется двусторонней симметричной. Симметричные системы, в отличие от каузальных, не изменяют фазы обрабатываемых сигналов.
Техника выполнения свертки в координатной области не отличается от техники выполнения обычной дискретной свертки двух массивов данных.
Представим, что на одной полоске бумаги выписаны по порядку сверху вниз значения данных x(k). На второй полоске бумаги находятся записанные в обратном порядке значения коэффициентов системы bn. Для вычисления y(k) располагаем вторую полоску против первой таким образом, чтобы значение b0 совпало со значением x(k), перемножаем все значения bn с расположенными против них значениями x(k-n)и суммируем результаты перемножения. Результат суммирования является выходным значением сигнала y(k). Сдвигаем окно системы — полоску коэффициентов bk, на один отсчет последовательности x(k) вниз (по порядку возрастания номеров k) или массив x(k) сдвигаем на отсчет вверх и вычисляем аналогично следующее значение, и т.д.
Описанный процесс свертки в вещественной области массива данных x(k) с нерекурсивным оператором системы bn (массивом весовых коэффициентов системы) обычно называют нерекурсивной цифровой фильтрацией данных, а саму систему, если она выполняет только данную операцию, нерекурсивным цифровым фильтром (НЦФ).
Пример. Сглаживание данных скользящим симметричным П-окном размером 5 отсчетов.
Уравнение НЦФ:
yk =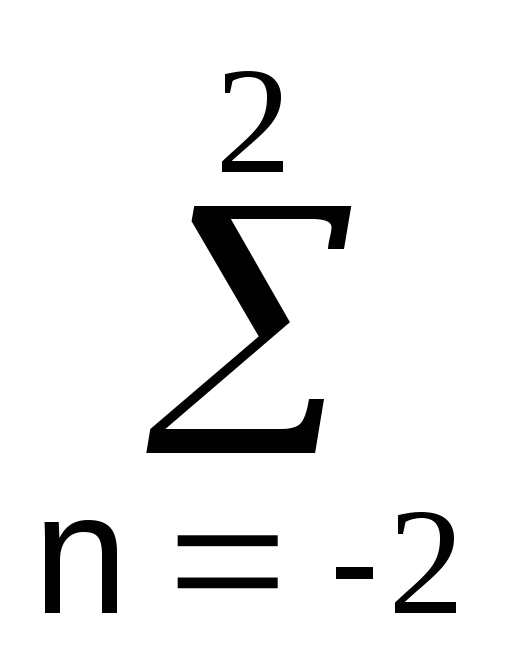 bn xk-n,
bn =
0,2. Начальные условия — нулевые.
bn xk-n,
bn =
0,2. Начальные условия — нулевые.
Входной сигнал: xk = {0,0,0,0,10,0,10,0,0,0,0}. Выходной сигнал: yk = {0,0,2,2,4, 4, 4,2,2,0,0}.
Проверьте результат (выполните фильтрацию сигнала).
Заметим: сумма коэффициентов bn сглаживающего НЦФ равна 1, при этом сумма значений выходного сигнала равна сумме значений входного сигнала. Сигнал «размазался» по аргументу.
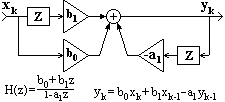
Рис. 10.1.3. Пример РЦС.
Рекурсивные цифровые системы. Системы, которые описываются полным разностным уравнением (10.1.2), принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью. Пример рекурсивной системы приведен на рис. 10.1.3. 
Рис. 10.1.4. Техника вычислений в РЦС.
Полное окно рекурсивной системы состоит из двух составляющих: нерекурсивной части bn,, аналогичной окну нерекурсивной системы и ограниченной в работе текущими и «прошлыми» значениями входного сигнала (при реализации на ЭВМ возможно использование и “будущих” отсчетов сигнала), и рекурсивной части am, которая работает только с «прошлыми», ранее вычисленными значениями выходного сигнала. Техника вычислений для РЦС приведена на рис. 10.1.4.Пример. Уравнение РЦС:yk=boxk+a1yk-1, при bo=a1=0.5, y-1=0. Входной сигнал: xk = {0, 10, 0, 0, 0,….}.
Расчет выходного сигнала:
уo= 0,5xo+ 0,5y-1 = 0 y1 = 0,5x1+ 0,5yo = 5 y2 = 0,5x2+ 0,5y1 = 2.5 y3 = 0,5x3+ 0,5y2 = 1.25
y4= 0,5x4+ 0,5y3 = 0.625 y5 = 0,5x5+ 0,5y4 = 0.3125 и т.д.
Выходной сигнал: yk = {0, 5, 2.5, 1.25, 0.625, 0.3125, 0.15625,…}
Из примера можно видеть, что реакция РЦС на конечный входной сигнал, в принципе, может иметь бесконечную длительность, в отличие от реакции НЦС, которая всегда ограничена количеством членов bk (окном системы).
Пример. Уравнение РЦС:yk=boxk+a1yk-1+a2yk-2, при bo=a1=a2=1. xk = {0, 1, 0, 0, 0,….}, y-1 = y-2 = 0.
Расчет выходного сигнала:
yo = xo+y-1+y-2 = 0. y1 = x1+yo+y-1 = 1. y2 = x2+y1+yo = 1. y3 = x3+y2+y1 = 2.
y4 = x4+y3+y2 = 3. y5 = x5+y4+y3 = 5. y6 = x6+y5+y4 = 8. y7 = x7+y6+y5 = 13. и т.д.
Заметим:сумма коэффициентов обратной связи ai больше 1 и выходной сигнал идет «в разнос».
Пример. Интегрирование данных по формуле трапеций.
Уравнение РЦФ: yk=(xk+xk-1)/2+yk-1, начальные условия — нулевые.
Входной сигнал: xk={0,0,2,2,8,0,4,4,0,..}.
Выполните фильтрацию. Контроль: yk= {0,0,1,3,8,12,14,18,20,20,…}.
Стационарные и нестационарные системы. Система считается стационарной и имеет постоянные параметры, если ее свойства (математический алгоритм оператора преобразования) в пределах заданной точности не зависят от входного и выходного сигналов и не изменяются ни во времени, ни от каких-либо других внешних факторов. Математически это означает задание системы уравнениями типа (10.1.1-2) с постоянными значениями коэффициентов aj и bi и реакция системы на какое-либо воздействие не зависит от времени (координат) его приложения. В противном случае система является нестационарной или параметрической (системой с переменными параметрами). Среди последних большое значение имеют так называемые адаптивные системы обработки данных. В этих системах производится, например, оценивание определенных параметров входных и выходных сигналов, по результатам сравнения которых осуществляется подстройка параметров преобразования (переходной характеристики системы) таким образом, чтобы обеспечить оптимальные по производительности условия обработки сигналов или минимизировать погрешность обработки.

