Момент силы — как найти? В чем измеряется? Формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.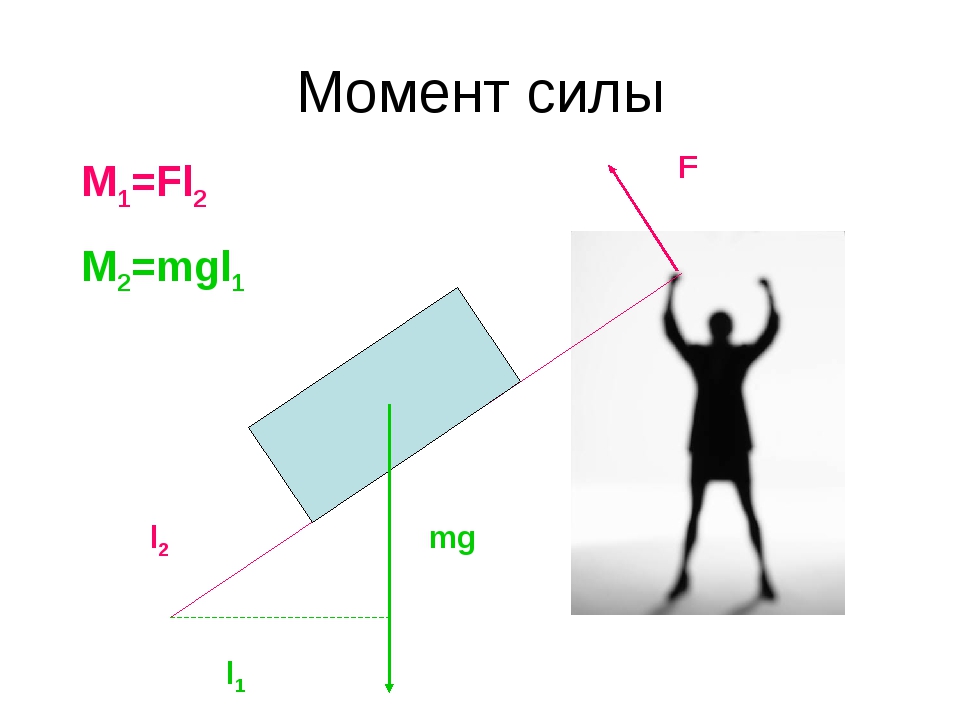
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции.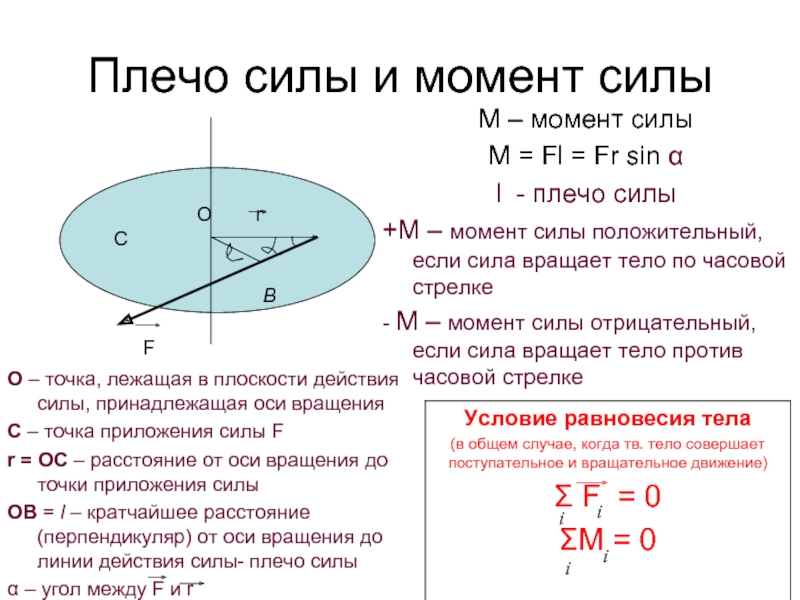 Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы M = Fl M — момент силы [Н*м] l — плечо [м] |
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МА=F×AB=F×3м
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м] |
Давайте рассмотрим этот закон на примере задач.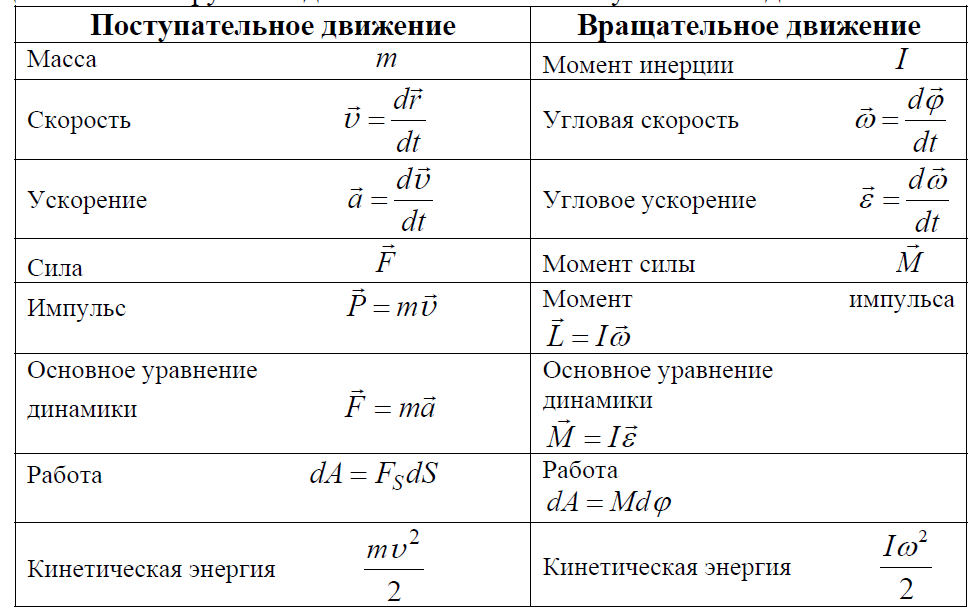
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
|OA|=FB/FA)*|OB|=30/80*80=30 см
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
4T = 4*100= 400 Н
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
mg=F*5/0,8=120*5/0,8=750Н
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
Ловите момент! Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!
Момент затяжки резьбовых соединений — Момент силы (теория) :: АвтоМотоГараж
Немного теории для полного понимания момента затяжки резьбовых соединений.
Момент силы, приложенный к гаечному ключу.
Момент силы (он же: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Но понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, т.к в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, Символ момента силы M . Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, это то же самое, что сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, это то же самое, что сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где F — сила, действующая на частицу, а r — радиус-вектор частицы.
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Посчитать: — кликни на любое число
Определения величин: наведи на любую величину
Ньютон (Н, N) — Newton.
Производная единица системы СИ, имеющая специальное название.
1 ньютон равен силе, сообщающей телу массой 1 кг. ускорение 1 м/с2 в направлении ее действия.
Названа в честь Исаака Ньютона (1643-1727)- английского физика и математика, создавшего теоретические основы механики и астрономии и открывшего закон всемирного тяготения.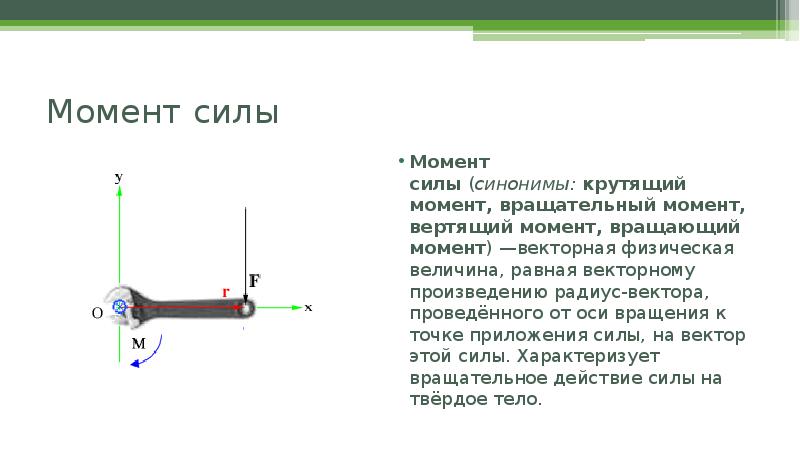
Дина (дин, dyn) — dyne.
Название происходит от греческого dýnamis — сила.
Дина — Основная единица давления системы СГС, которую в настоящее время вытеснила система СИ.
Дина равная силе, которая массе в 1 грамм сообщает ускорение 1 см/с2 и , соответственно, соотношение между диной и ньютоном (единицей силы в Международной системе единиц): 1 Дина = 0,00001 Ньютонов (точно).
Килограмм-сила (кгс или кГ, kgf или kG), kilogram-force
Единица силы системы единиц МКГСС.
Равен силе, сообщающей телу массой один килограмм, ускорение 9,80665 м/с2 (нормальное ускорение свободного падения, принятое 3-й Генеральной конференцией по мерам и весам, 1901).
1 кгс = 9,80665 ньютонов (точно).
В ряде европейских государств для килограмм-силы официально принято название килопонд (обозначается kp).
Фунт силы (lbf, иногда Lb), pound-force.
Британская единица силы.
Масса фунта-силы равна весу одного фунта.
Ускорение свободного падения в британской системе мер было равно 32,1740 футов в секунду за секунду, а после принятия международного значения нормального ускорения свободного падения (1901) равного 9,80665 м/c2, преобразовалось в 32,1740485564304 футов в секунду в секунду.
Cейчас 1 фунт силы равен 4,4482216152605 ньютонов (точно) или 0,45359237 килограмм силы (точно).
kip (килофунт силы)
Единица силы, распространенная в США с 20-го века по настоящее время и используется в основном архитекторами и инженерами. Образовано от слияния ’kilo’ + ’pound’.
1 kip равен 1000 фунтов силы или 4448,2216152605 ньютонов (точно).
Грамм-сила, pond, понд (гс или Г, p, pond, G) pond, gramm — force.
Грамм-сила — дольная единица силы в системе единиц МКГСС .
В ряде стран эту меру силы называют pond (русское ’понд’ почти никогда не используется).
1 грамм силы равен 0,001 килограмм-силы (точно) или 0,00980665 ньютонов.
Также может быть определен как сила, сообщающая массе 1 грамм ускорение, равное 980,665 см/с2.
Единицы измерения силы
Момент силы. | Поурочные планы по физике 7 класс
Момент силы.
27.02.2014 4695 0Цель: установить условие момента силы. Побуждать учащихся к преодолению трудностей в процессе умственной деятельности, воспитать интерес к физике.
Ход урока
I. Организационный момент
II. Повторение. Беседа
1.Дайте определение закону сохранения энергии?
2. В каких единицах измеряется потенциальная энергия пружины?
3 Что такое кинетическая энергия?
III. Изучение нового материала
На практике часто встречаются случаи, когда тело не
может двигаться свободно в любом направлении, а движения его ограничены
какими-либо другими твердыми телами.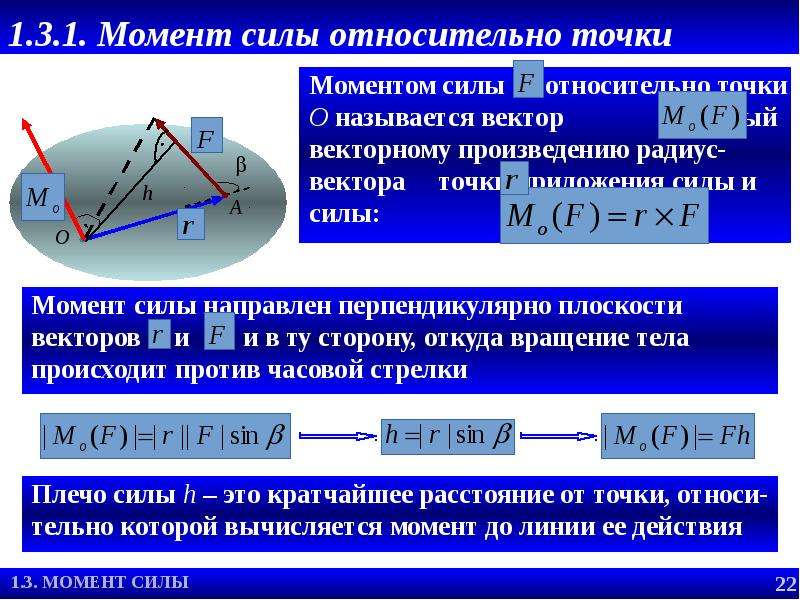 Эти тела называют в механике жесткими
связями. Важным примером движения, ограниченного жесткой связью, является
вращение тела вокруг жесткой оси или, как говорят, вращения тела, закрепленного
на оси.
Эти тела называют в механике жесткими
связями. Важным примером движения, ограниченного жесткой связью, является
вращение тела вокруг жесткой оси или, как говорят, вращения тела, закрепленного
на оси.
Например, пропеллер самолета, колодезный журавль, дверь на петлях. Представим себе рулевое колесо корабля или «баранку» автомобильного руля. Прилагая усилия вдоль радиуса, мы будем только пытаться согнуть ось, но не сможем повернуть колесо. Для поворота необходимо приложить усилие вдоль его обода, т.е. перпендикулярно радиусу. Из сказанного следует, что при выявлении условий равновесия тела, закрепленного на оси, можно не рассматривать силу со стороны оси, т.к. она не может вызвать вращение тела.
Эксперимент 1
Для равновесия необходимо, во-первых, чтобы силы, действуя в отдельности, поворачивали тело в противоположные стороны .
Эксперимент 2
Уменьшим расстояние от центра вращения до линии действия
силы. Что видим? Для того чтобы тело находилось в равновесии потребуется
большая сила .
Оказывается, что для равновесия тела закрепленного на оси, существуют не только величины сил, но и расстояние между точками их приложения и осью вращения, как для обычного рычага.
Если обозначить величины сил через F1 и F2, длины радиусов, проведенных в точки их приложения, через , и 12, тог условие равновесия выразится равенством:
Если силы не перпендикулярны радиусу точек приложения, то такое соотношение должно выполнятся для проекций этих сил на направления, перпендикулярные к радиусам.
Произведение Fa называют моментом силы относительно равной оси, или просто моментом силы.
Для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю.
В случае произвольного числа внешних сил условия равновесия твердого тела запишутся в виде:
F, + F2 + F3 + … — 0
IV. Закрепление изученного
Закрепление изученного
1. Что называют плечом силы?
2. Что называют моментом силы? Какая формула выражает смысл этого понятия?
3. Какова единица измерения момента силы в системе СИ?
4. Какую роль играет момент силы во вращательном движении?
5. Как определяется знак момента силы?
6. Чему равен момент силы, проходящий через ось вращения?
7. Сформулируйте и запищите условие равновесия тела с закрепленной осью вращения.
V. Решение задач
1. Длина горизонтально установленного рычага с грузами весом 2,5 Н и 4 Н на концах равна 52 см. Найти плечи сил тяжести грузов и силу давления рычага на точечную опору. Массу самого рычага не учитывать.
Домашняя работа
§ 69
Перевод единиц измерения крутящего момента. Конвертер величин
Калькулятор момента силы преобразует вашу единицу крутящего момента в другие единицы измерения:
- введите свое значение крутящего момента в текстовое поле;
- нажмите кнопку Вычислить, чтобы увидеть результаты в таблице.

В физике крутящий момент (его часто называют моментом или моментом силы) можно неофициально считать «вращающей» или «угловой силой», которая вызывает изменение вращательного движения. Эта сила определяется линейной силой, умноженной на радиус.
Крутящий момент, момент или момент силы — это единица силы для вращения объекта вокруг оси, точки опоры или оси вращения. Так же, как сила тяги, крутящий момент можно рассматривать как поворот объекта. Математически крутящий момент определяется как перекрестное произведение вектора расстояния между рычагом и рычагом вектора силы, который имеет тенденцию вызывать вращение.
Пример. Крутящий момент — это приложение силы с помощью рычага, вращающегося вокруг оси. Проще говоря, крутящий момент — это мера силы поворота на объект, такой как болт или маховик. Хорошим примером крутящего момента в действии является гаечный ключ. Головка гаечного ключа захватывает болт и прилагает к нему давление. Если вы продолжаете оказывать давление, гаечный ключ в конечном итоге будет вращаться вокруг болта. Чем дальше от болта вы прикладываете давление, тем больший крутящий момент у вас будет.
Головка гаечного ключа захватывает болт и прилагает к нему давление. Если вы продолжаете оказывать давление, гаечный ключ в конечном итоге будет вращаться вокруг болта. Чем дальше от болта вы прикладываете давление, тем больший крутящий момент у вас будет.
Единицы измерения
Единица СИ для крутящего момента — ньютон-метр (Н·м). Заметим, что Джоуль, который также находят как 1 Н·м, для крутящего момента не применяется. В американских единицах измерения она измеряется в фунтах на фут (ft · lbf) (также известных как «фунты футов»). 1 Н·м = 0,74 фунт сила-фут. Символом крутящего момента является греческая буква тау (τ).
М = Fp (520.1) где М — момент силы F — действующая сила р — плечо действия силы Одним из самых наглядных и действенных устройств, демонстрирующих действие момента силы, является гвоздодер (фомка). Рисунок 520.1. Силы и плечи сил на примере гвоздодера. Итак на рисунке 5210.1 мы можем наблюдать: 1 — фомку (гвоздодер), 2 — вытаскиваемый из доски гвоздь, 3 — доску, из которой данный гвоздь вытаскивается, 4 — лагу или балку перекрытия, к которой гвоздем крепилась доска, 5 — руку, пытающуюся вытащить гвоздь (скорее всего это ваша рука в перчатке), а также точку О, являющуюся точкой опоры фомки, показанную на рисунке 520.1 красным цветом (данная точка цифрового обозначения на рисунке не имеет). Таким образом извлечение гвоздя из доски и лаги (рис. 520.1.а)) с точки зрения физики может рассматриваться, как приложение силы F2 (сила, с которой вы давите на фомку) на расстоянии р2 от точки опоры О (на рисунке 520.1. б) показана красным цветом). При этом сила F1 — это сила сцепления гвоздя с древесиной, а расстояние р1 — это расстояние от оси гвоздя до точки опоры О. Если рассматривать ситуацию статического равновесия системы, то момент силы F2, приложенной на расстоянии р2 от точки опоры О, равен моменту силы F1, приложенной на расстоянии р1 от точки опоры О (рис. 520.1.г)). Другими словами, чем больше расстояние, на котором можно приложить силу, тем меньше будет значение этой силы по сравнению с противодействующей (рис. 520.1.в)). Именно это и имел в виду Архимед, описывая чудесные свойства рычага. Само собой при вытаскивании гвоздя статическое равновесие системы нас не интересует, а потому, чтобы вытащить этот самый гвоздь, достаточно приложить силу F2, имеющую немного большее значение, чем F1p1/p2. Вот в принципе и все, что я хотел сказать по поводу момента силы. Возможно вам известны другие, более наглядные примеры, описывающие момент силы, но я таких не знаю. | А еще у Вас есть уникальная возможность помочь автору материально. После успешного завершения перевода откроется страница с благодарностью и адресом электронной почты. Если вы хотите задать вопрос, пожалуйста, воспользуйтесь этим адресом. Спасибо. Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору» Для терминалов номер Яндекс Кошелька 410012390761783 Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630 |
Мощность и крутящий момент — что это?
ЧТО ТАКОЕ ЛОШАДИНАЯ СИЛА?
— У тебя сколько сил? — такой вопрос слышал любой, кто хоть немного касался мира автомобилей. Никому даже пояснять не надо, какие силы на самом деле имеются в виду — лошадиные. Именно в них мы привыкли оценивать мощность мотора, одну из важнейших потребительских характеристик машины.
Никому даже пояснять не надо, какие силы на самом деле имеются в виду — лошадиные. Именно в них мы привыкли оценивать мощность мотора, одну из важнейших потребительских характеристик машины.
Уже и гужевого транспорта практически не осталось даже в деревнях, а эта единица измерения живёт и здравствует больше ста лет. А ведь лошадиная сила — величина, по сути, нелегальная. Она не входит в международную систему единиц (полагаю, многие со школы помнят, что называется она СИ) и потому не имеет официального статуса. Более того, Международная организация законодательной метрологии требует как можно скорее изъять лошадиную силу из обращения, а директива ЕС 80/181/EEC от 1 января 2010 прямо обязует автопроизводителей использовать традиционные «л.с.» только как вспомогательную величину для обозначения мощности.
Но не зря считается, что привычка — вторая натура. Ведь говорим же мы в обиходе «ксерокс» вместо копир и обзываем клейкую ленту «скотчем». Вот и непризнанные «л.с.» сейчас используют не только обыватели, но и едва ли не все автомобильные компании. Какое им дело до рекомендательных директив? Раз покупателю удобнее — пусть так и будет. Да что там производители — даже государство на поводу идёт. Если кто забыл, в России транспортный налог и тариф ОСАГО именно от лошадиных сил высчитываются, как и стоимость эвакуации неправильно припаркованного транспорта в Москве.
Какое им дело до рекомендательных директив? Раз покупателю удобнее — пусть так и будет. Да что там производители — даже государство на поводу идёт. Если кто забыл, в России транспортный налог и тариф ОСАГО именно от лошадиных сил высчитываются, как и стоимость эвакуации неправильно припаркованного транспорта в Москве.
Лошадиная сила родилась в эпоху промышленной революции, когда потребовалось оценить, насколько эффективно механизмы заменяют животную тягу. По наследству от стационарных двигателей эта условная единица измерения мощности со временем перешла и на автомобили.
И никто бы к этому не придирался, если не одно весомое «но». Задуманная, чтобы упростить нам жизнь, лошадиная сила на самом деле вносит путаницу. Ведь появилась она в эпоху промышленной революции как совершенно условная величина, которая не то что к автомобильному мотору, даже к лошади имеет достаточно опосредованное отношение. Смысл этой единицы в следующем — 1 л.с. достаточно, чтобы поднять груз массой 75 кг на высоту 1 метр за 1 секунду. Фактически, это сильно усреднённый показатель производительности одной кобылы. И не более того.
Фактически, это сильно усреднённый показатель производительности одной кобылы. И не более того.
Иными словами, новая единица измерения очень пригодилась промышленникам, добывавшим, к примеру, уголь из шахт, и производителям соответствующего оборудования. С её помощью было проще оценить преимущество механизмов над животной силой. А поскольку приводились станки уже паровыми, а позднее и керосиновыми двигателями, то «л.с.» перешли по наследству и к самобеглым экипажам.
Джеймс Уатт — шотландский инженер, изобретатель, учёный, живший в XVIII — начале XIX века. Именно он ввёл в обращение как «нелегальную» сейчас лошадиную силу, так и официальную единицу измерения мощности, которую назвали его именем.
По иронии судьбы изобрёл лошадиную силу человек, именем которого названа официальная единица измерения мощности — Джеймс Уатт. А поскольку ватт (а точнее, применительно к могучим машинам, киловатт — кВт) к началу XIX века тоже активно входил в оборот, пришлось две величины как-то приводить друг к другу.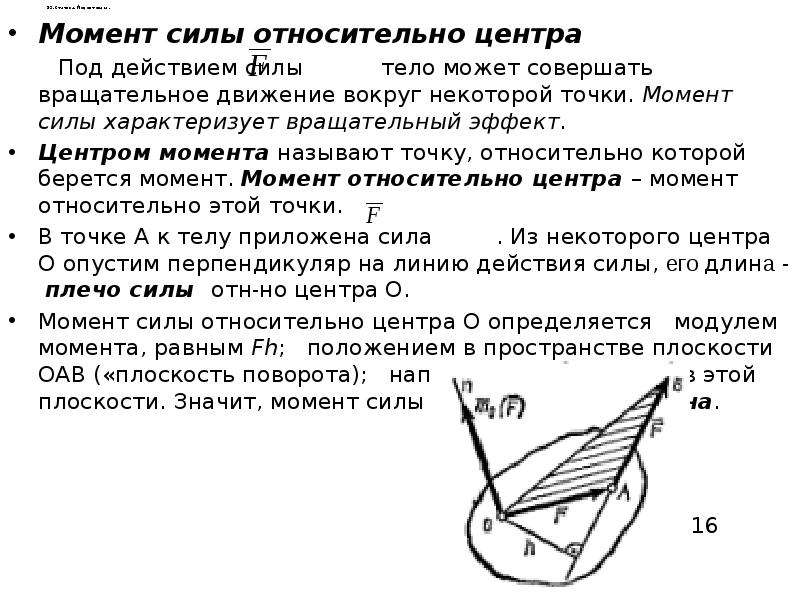
Вот здесь-то и возникли ключевые разногласия. Например, в России и большинстве других европейских стран приняли так называемую метрическую лошадиную силу, которая равна 735,49875 Вт или, что сейчас нам более привычно, 1 кВт = 1,36 л.с. Такие «л.с.» чаще всего обозначают PS (от немецкого Pferdestärke), но есть и другие варианты — cv, hk, pk, ks, ch… При этом в Великобритании и ряде её бывших колоний решили пойти своим путём, организовав «имперскую» систему измерений с её фунтами, футами и прочими прелестями, в которой механическая (или, по-другому, индикаторная) лошадиная сила составляла уже 745,69987158227022 Вт. А дальше — пошло-поехало. К примеру, в США придумали даже электрическую (746 Вт) и котловую (9809,5 Вт) лошадиные силы.
Вот и получается, что один и тот же автомобиль с одним и тем же двигателем в разных странах на бумаге может иметь разную мощность. Возьмём, например, популярный у нас кроссовер Kia Sportage — в России или Германии по паспорту его двухлитровый турбодизель в двух вариантах развивает 136 или 184 л. с., а в Англии — 134 и 181 «лошадку». Хотя на самом деле отдача мотора в международных единицах составляет ровно 100 и 135 кВт — причём в любой точке земного шара. Но, согласитесь, звучит непривычно. Да и цифры уже не такие впечатляющие. Поэтому автопроизводители и не спешат переходить на официальную единицу измерения, объясняя это маркетингом и традициями. Это как же? У конкурентов будет 136 сил, а у нас всего 100 каких-то кВт? Нет, так не пойдёт…
с., а в Англии — 134 и 181 «лошадку». Хотя на самом деле отдача мотора в международных единицах составляет ровно 100 и 135 кВт — причём в любой точке земного шара. Но, согласитесь, звучит непривычно. Да и цифры уже не такие впечатляющие. Поэтому автопроизводители и не спешат переходить на официальную единицу измерения, объясняя это маркетингом и традициями. Это как же? У конкурентов будет 136 сил, а у нас всего 100 каких-то кВт? Нет, так не пойдёт…
КАК ИЗМЕРЯЮТ МОЩНОСТЬ?
Впрочем, «мощностные» хитрости игрой с единицами измерения не ограничиваются. До последнего времени её не только обозначали, но даже измеряли по-разному. В частности, в Америке долгое время (до начала 1970-х годов) автопроизводители практиковали стендовые испытания двигателей, раздетых до гола — без навески вроде генератора, компрессора кондиционера, насоса системы охлаждения и с прямоточной трубой вместо многочисленных глушителей. Само собой, сбросивший оковы мотор легко выдавал процентов на 10-20 больше «л. с.», так необходимых менеджерам по продажам. Ведь в тонкости методики испытаний мало кто из покупателей вдавался.
с.», так необходимых менеджерам по продажам. Ведь в тонкости методики испытаний мало кто из покупателей вдавался.
Другая крайность (но гораздо более приближенная к реальности) — снятие показателей прямо с колёс автомобиля, на беговых барабанах. Так поступают гоночные команды, тюнинговые мастерские и прочие коллективы, которым важно знать отдачу мотора с учётом всех возможных потерь, и трансмиссионных в том числе.
Мощность также зависит от того, как её измерять. Одно дело крутить на стенде «голый» мотор без навесного оборудования и совсем другое — снимать показания с колёс, на беговых барабанах, с учётом трансмиссионных потерь. Современные методики предлагают компромиссный вариант — стендовые испытания двигателя с необходимой для его автономной работы навеской.
Но в итоге за образец в различных методиках вроде европейских ECE, DIN или американских SAE приняли компромиссный вариант. Когда двигатель устанавливают на стенде, но со всей необходимой для бесперебойного функционирования навеской, включая стандартный выпускной тракт.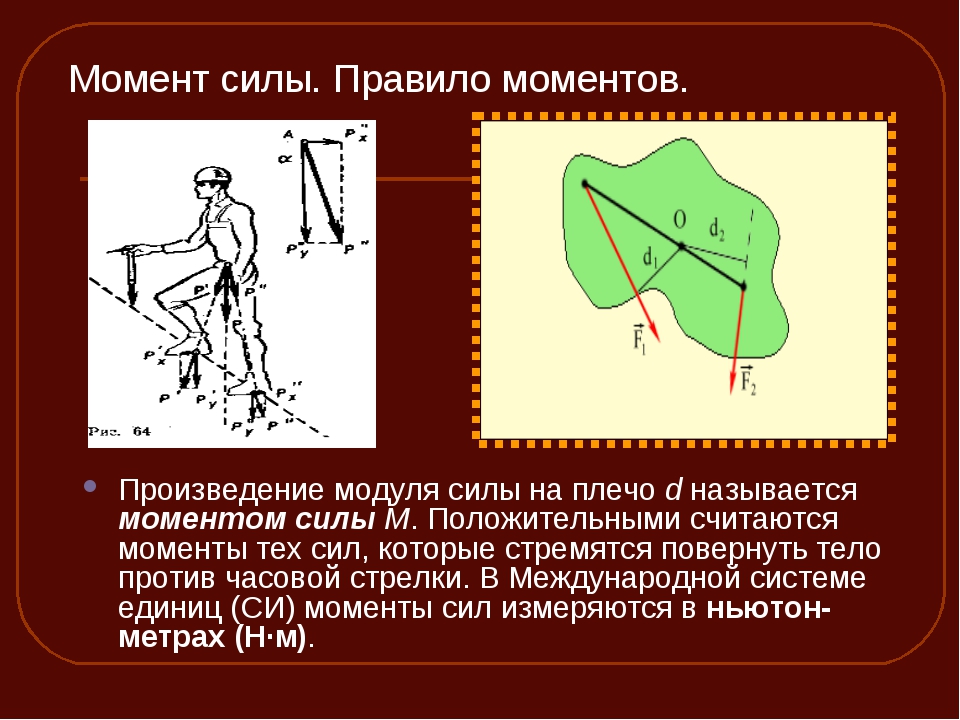 Снять можно только оборудование, относящееся к другим системам машины (к примеру, компрессор пневмоподвески или насос гидроусилителя руля). То есть тестируют мотор ровно в том виде, в котором он фактически стоит под капотом автомобиля.
Снять можно только оборудование, относящееся к другим системам машины (к примеру, компрессор пневмоподвески или насос гидроусилителя руля). То есть тестируют мотор ровно в том виде, в котором он фактически стоит под капотом автомобиля.
Это позволяет исключить из финального результата «качество» трансмиссии и определить мощность на коленвале с учётом потерь на привод основных навесных агрегатов. Так, если говорить о Европе, то эту процедуру регламентирует директива 80/1269/EEC, впервые принятая ещё в 1980 году и с тех пор регулярно обновляемая.
ЧТО ТАКОЕ КРУТЯЩИЙ МОМЕНТ?
Но если мощность, как говорят в Америке, помогает автомобили продавать, то двигает их вперёд крутящий момент. Измеряют его в ньютон-метрах (Н∙м), однако у большинства водителей до сих пор нет чёткого представления об этой характеристике мотора. В лучшем случае обыватели знают одно — чем выше крутящий момент, тем лучше. Почти как с мощностью, не правда ли? Вот только чем тогда «Н∙м» отличаются от «л. с.».?
с.».?
На самом деле, это связанные величины. Более того, мощность — производная от крутящего момента и оборотов мотора. И рассматривать их по отдельности просто нельзя. Знайте — чтобы получить мощность в ваттах необходимо крутящий момент в ньютон-метрах умножить на текущее число оборотов коленвала и коэффициент 0,1047. Хотите привычные лошадиные силы? Нет проблем! Делите результат на 1000 (таким образом получатся киловатты) и умножайте на коэффициент 1,36.
Чтобы обеспечить дизелю (на фото слева) высокую степень сжатия, инженеры вынуждены делать его длинноходным (это когда ход поршня превышает диаметр цилиндра). Поэтому у таких моторов крутящий момент конструктивно получается большим, но предельное число оборотов приходится ограничивать ради повышения ресурса. Разработчикам бензиновых агрегатов, наоборот, проще получить высокую мощность — детали здесь не такие массивные, степень сжатия меньше, так что двигатель можно сделать короткоходным и высокооборотным. Впрочем, в последнее время различие между дизелями и бензиновыми агрегатами постепенно стирается — они становятся всё более похожими как по конструкции, так и по характеристикам.
Выражаясь техническим языком, мощность показывает, сколько работы способен выполнить мотор за единицу времени. А вот крутящий момент характеризует потенциал двигателя к совершению этой самой работы. Показывает сопротивление, которое он может преодолеть. Например, если машина упрётся колёсами в высокий бордюр и не сможет тронуться с места, мощность будет нулевой, так как никакой работы мотор не совершает — движения нет, но крутящий момент при этом развивается. Ведь за то мгновение, пока движок не заглохнет от натуги, в цилиндрах сгорает рабочая смесь, газы давят на поршни, а шатуны стараются привести во вращение коленвал. Иными словами, момент без мощности существовать может, а мощность без момента — нет. То есть именно «Н∙м» являются основой «продукцией» двигателя, которую он производит, превращая тепловую энергию в механическую.
Если проводить аналогии с человеком, «Н∙м» отражают его силу, а «л.с.» — выносливость. Именно поэтому тихоходные дизельные двигатели в силу своих конструктивных особенностей у нас, как правило, тяжелоатлеты — при прочих равных условиях они могут тащить на себе больше и легче преодолевают сопротивление на колёсах, пусть и не так проворно.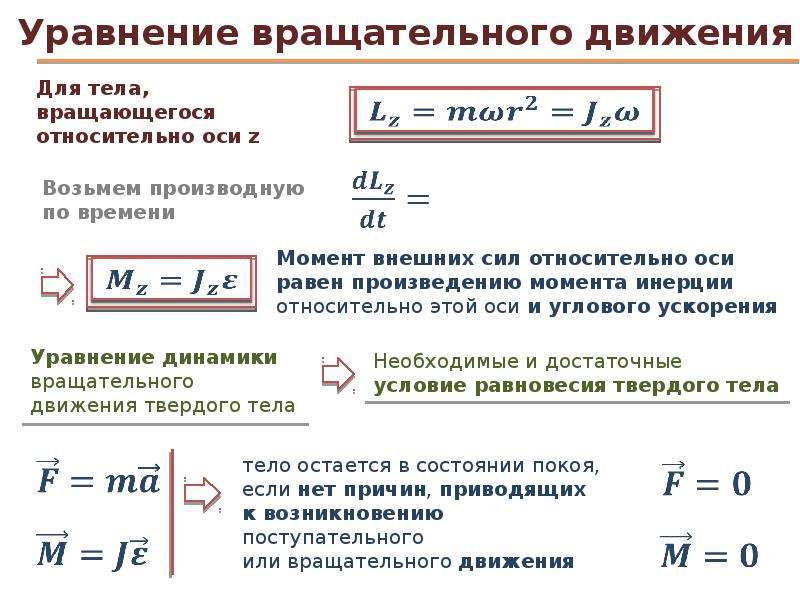 А вот быстроходные бензиновые моторы скорее относятся к бегунам — нагрузку держат хуже, зато перемещаются быстрее. В общем, действует простое правило рычага — выигрываем в силе, проигрываем в расстоянии или скорости. И наоборот.
А вот быстроходные бензиновые моторы скорее относятся к бегунам — нагрузку держат хуже, зато перемещаются быстрее. В общем, действует простое правило рычага — выигрываем в силе, проигрываем в расстоянии или скорости. И наоборот.
Так называемая внешняя скоростная характеристика двигателя отражает зависимость мощности и крутящего момента от оборотов коленвала при полностью открытом дросселе. По идее, чем раньше наступает пик тяги и позже — мощности, тем проще мотору адаптироваться к нагрузкам, его рабочий диапазон увеличивается, что позволяет водителю или электронике реже переключать передачи и почём зря не жечь топливо. На этих графиках видно, что бензиновый двухлитровый турбомотор (справа) выигрывает по этому показателю у турбодизеля аналогичного объёма, но уступает ему в абсолютной величине крутящего момента.
Как это выражается на практике? В первую очередь, надо понять, что именно кривые крутящего момента и мощности (вместе, а не по отдельности!) на так называемой внешней скоростной характеристике двигателя будут раскрывать его истинные возможности. Чем раньше достигается пик тяги и позже пик мощности, тем лучше мотор приспособлен к своим задачам. Возьмём простой пример — автомобиль движется по ровной дороге и вдруг начинается подъём.
Чем раньше достигается пик тяги и позже пик мощности, тем лучше мотор приспособлен к своим задачам. Возьмём простой пример — автомобиль движется по ровной дороге и вдруг начинается подъём.
Сопротивление на колёсах возрастает, так что при неизменной подаче топлива обороты станут падать. Но если характеристика двигателя грамотная, крутящий момент при этом наоборот начнёт расти. То есть мотор сам приспособится к увеличению нагрузки и не потребует от водителя или электроники перейти на передачу пониже. Перевал пройден, начинается спуск. Машина пошла на разгон — высокая тяга здесь уже не так важна, критичным становится другой фактор — мотор должен успевать её вырабатывать. То есть на первый план выходит мощность. Которую можно регулировать не только передаточными числами в трансмиссии, а повышением оборотов двигателя.
Здесь уместно вспомнить гоночные автомобильные или мотоциклетные моторы. В силу относительно небольших рабочих объёмов, они не могут развить рекордный крутящий момент, зато способность раскручиваться до 15 тысяч об/мин и выше позволяет им выдавать фантастическую мощность. К примеру, если условный двигатель при 4000 об/мин обеспечивает 250 Н∙м и, соответственно, примерно 143 л.с., то при 18000 об/мин он мог бы выдать уже 640,76 л.с. Впечатляет, не правда ли? Другое дело, что «гражданскими» технологиями это не всегда получается добиться.
К примеру, если условный двигатель при 4000 об/мин обеспечивает 250 Н∙м и, соответственно, примерно 143 л.с., то при 18000 об/мин он мог бы выдать уже 640,76 л.с. Впечатляет, не правда ли? Другое дело, что «гражданскими» технологиями это не всегда получается добиться.
И, кстати, в этом плане близкую к идеальной характеристику имеют электродвигатели. Они развивают максимальные «ньютон-метры» прямо со старта, а потом кривая крутящего момента плавно падает с ростом оборотов. График мощности при этом прогрессивно возрастает.
Современные моторы «Формулы 1» имеют скромный объём 1,6 л и относительно невысокий крутящий момент. Но за счёт турбонаддува, а главное — способности раскручиваться до 15000 об/мин, выдают порядка 600 л.с. Кроме того, инженеры грамотно интегрировали в силовой агрегат электродвигатель, который в определённых режимах может добавлять ещё 160 «лошадок». Так что гибридные технологии могут работать не только на экономичность.
Думаю, вы уже поняли — в характеристиках автомобиля важны не только максимальные значения мощности и крутящего момента, но и их зависимость от оборотов. Вот почему журналисты так любят повторять слово «полка» — когда, допустим, мотор выдаёт пик тяги не в одной точке, а в диапазоне от 1500 до 4500 об/мин. Ведь если есть запас крутящего момента, мощности тоже, скорее всего, будет хватать.
Вот почему журналисты так любят повторять слово «полка» — когда, допустим, мотор выдаёт пик тяги не в одной точке, а в диапазоне от 1500 до 4500 об/мин. Ведь если есть запас крутящего момента, мощности тоже, скорее всего, будет хватать.
Но всё же лучший показатель «качества» (назовём его так) отдачи автомобильного двигателя — его эластичность, то есть способность набирать обороты под нагрузкой. Она выражается, например, в разгоне от 60 до 100 км/ч на четвёртой передаче или с 80 до 120 км/ч на пятой — это стандартные тесты в автомобильной индустрии. И может случиться так, что какой-нибудь современный турбомотор с высокой тягой на малых оборотах и широченной полкой момента даёт ощущение отличной динамики в городе, но на трассе при обгоне окажется хуже древнего атмосферника с более выгодной характеристикой не только момента, но и мощности…
Так что пусть в последнее время разница между дизельными и бензиновыми агрегатами становится всё более расплывчатой, пусть развиваются альтернативные моторы, но извечный союз мощности, крутящего момента и оборотов двигателя останется актуальным. Всегда.
Всегда.
Что важнее — крутящий момент или лошадиные силы?
Обычно при оценке характеристик того или иного автомобиля в первую очередь мы обращаем внимание на мощность двигателя или количество лошадиных сил. Но не менее важной характеристикой является крутящий момент. Давайте разберемся, в чем разница между ними.Появившаяся задолго до первого механического транспортного средства «лошадиная сила» условна, так как определяет относительный уровень производительности среднестатистической лошади путем определения работы, необходимой для поднятия 75–килограммового груза на один метр за одну секунду.
Шотландский инженер Джеймс Уатт ввел новую единицу измерения мощности в лошадиную силу, но в системе СИ единицу мощности назвали уже в его честь — ватт (Вт). 1 киловатт (кВт) равен 1,36 л. с. Но в обычной жизни лошадиные силы оказались как-то ближе к народу, поэтому мы получаем письма с налогом за количество лошадиных сил в наших автомобилях, а не за киловатт и хвастаемся друзьям именно количеством«лошадей». Лошадиная сила остается очень популярной внесистемной единицей измерения мощности для транспортных средств. Кстати, типичная лошадь имеет предельную мощность порядка 13–15 лошадиных сил, как это ни забавно. Во всяком случае, на диностенде в режиме 5–минутной нагрузки она может выдать примерно столько. А тягловые тяжеловесы способны выдать даже в даже за 25 сил на такой отрезок времени.
Лошадиная сила остается очень популярной внесистемной единицей измерения мощности для транспортных средств. Кстати, типичная лошадь имеет предельную мощность порядка 13–15 лошадиных сил, как это ни забавно. Во всяком случае, на диностенде в режиме 5–минутной нагрузки она может выдать примерно столько. А тягловые тяжеловесы способны выдать даже в даже за 25 сил на такой отрезок времени.
А сам автомобиль тянет вперед не сама мощность, а крутящий момент, выдаваемый силовым агрегатом. И именно с ним мы сталкиваемся каждый день в обычной жизни чаще. Например, открывая крышку пластиковой бутылки, вы используете именно крутящий момент, именуемый также моментом силы или вращательным моментом. Ведь вряд ли вы проверяете, как быстро открутили крышку?
Крутящий момент измеряется в ньютон-метрах (Н·м). И он тесно связан с мощностью, ведь для двигателя с вращающимся валом мощность на любых оборотах легко рассчитать, зная момент. И наоборот, зная мощность, можно подсчитать момент. Упрощенная формула его расчета выглядит так:
P = M x 9549 x N
и, соответственно:
M = P х 9549 / N,
где P — это мощность двигателя в киловаттах (кВт), а N — это количество оборотов коленчатого вала в минуту.
Мощность демонстрирует количество работы, которое выполняет двигатель за промежуток времени, а крутящий момент отражает способность силового агрегата эту работу совершить. Например, ускорение машины в каждый момент времени при постоянном передаточном отношении трансмиссии пропорционально крутящему моменту. А вот время разгона с одной скорости до другой, именно мощности двигателя в этом диапазоне оборотов, иначе говоря, проделанной работе. В общем-то, всем изучавшим физику в школе это покажется очевидным, но, к сожалению, не все помнят или не соотносят знания теоретического курса и примеры из реальной жизни.
Уверен, многие автолюбители даже не обращают внимание на значение крутящего момента в списке технических характеристик автомобиля и на обороты, при которых он достигается. А ведь чем выше крутящий момент и с чем более низких оборотов он достигается, тем приятнее и «эластичнее» ощущается двигатель, тем выше его реальная мощность на промежуточных режимах. Именно поэтому дизельные двигатели с турбонаддувом зачастую кажутся более приятными в обращении, чем более форсированные атмосферные бензиновые, которые необходимо «крутить» в отсечку ради достижения максимальной динамики разгона. И именно по этой причине тот, кто вкусил радости хорошего двигателя с турбонаддувом, уже не очень хочет пересаживаться на атмосферные, которые даже при схожей мощности «едут» ощутимо хуже.
И именно по этой причине тот, кто вкусил радости хорошего двигателя с турбонаддувом, уже не очень хочет пересаживаться на атмосферные, которые даже при схожей мощности «едут» ощутимо хуже.
Почему же такое внимание уделяется именно максимальной мощности? Дело в том, что владельца машины редко волнует максимальное ускорение автомобиля на скорости 20 или 30 километров в час, как физическая величина. Его, скорее всего, интересует динамика разгона в диапазоне 0–100, 80–120 или 100–200, а не абстрактное ускорение. А в этом случае речь идет о приращении кинетической энергии автомобиля, а значит, о проделанной двигателем работе. Которая зависит именно от мощности. В случае с идеальной трансмиссией проделанная работа будет прямо пропорциональна максимальной мощности мотора.
Вот только машин с идеальными трансмиссиями не бывает, если это не карьерные самосвалы с электропередачей, а значит, важна не только максимальная мощность, но и мощность во всем диапазоне оборотов, в котором вынужденно будет работать двигатель при таком разгоне.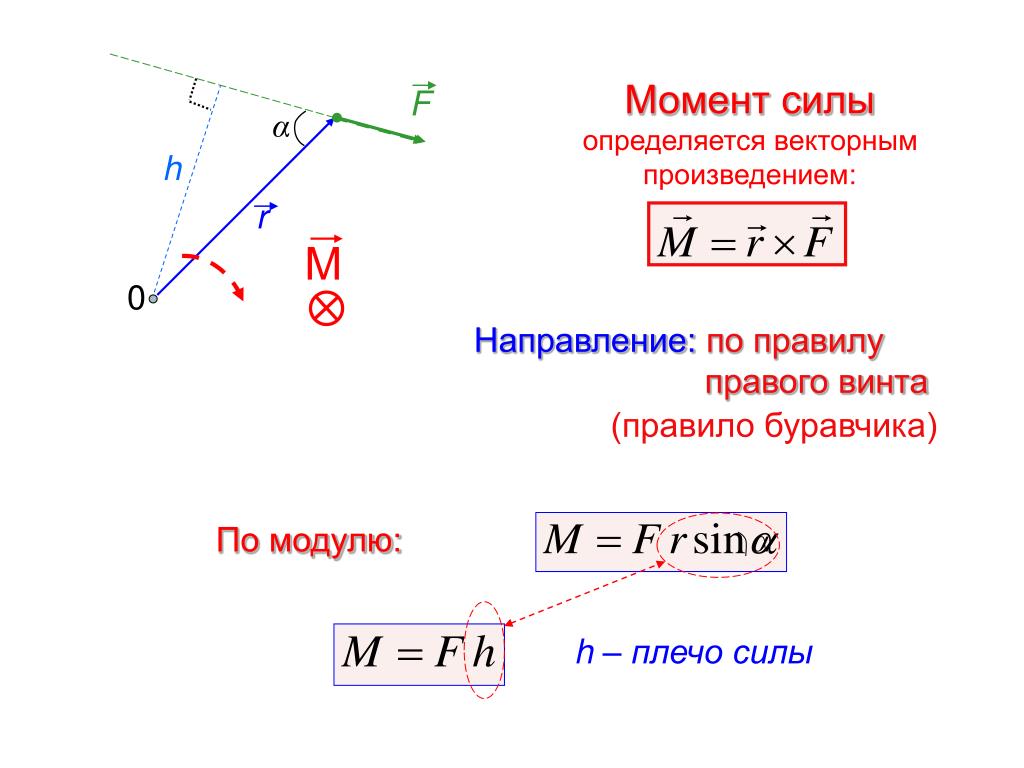 Оценить ее можно по графику внешней скоростной характеристики автомобиля, так называемой ВСХ, зная передаточное отношение трансмиссии на каждой передаче и предельные обороты мотора. А косвенно понять, насколько мощным будет мотор на промежуточных оборотах, позволяют именно данные по максимальному крутящему моменту и оборотам, при которых он достигается. Ведь чем выше момент на всех оборотах ниже максимальной мощности, тем ближе мощность на этих оборотах к максимально возможной и тем большую работу сможет проделать двигатель. Сложно? Тогда просто используйте эмпирическое правило, упомянутое выше.
Оценить ее можно по графику внешней скоростной характеристики автомобиля, так называемой ВСХ, зная передаточное отношение трансмиссии на каждой передаче и предельные обороты мотора. А косвенно понять, насколько мощным будет мотор на промежуточных оборотах, позволяют именно данные по максимальному крутящему моменту и оборотам, при которых он достигается. Ведь чем выше момент на всех оборотах ниже максимальной мощности, тем ближе мощность на этих оборотах к максимально возможной и тем большую работу сможет проделать двигатель. Сложно? Тогда просто используйте эмпирическое правило, упомянутое выше.
Главное, помните, что мощность и крутящий момент — зависящие друг от друга величины, поэтому всегда важно и то, и другое.
Конвертер момента силы • Механика • Определения единиц измерения • Онлайн-конвертеры единиц
Механика
Механика — это раздел физики, изучающий поведение физических тел при воздействии сил или смещений и последующее воздействие тел на окружающую их среду.
Преобразователь момента силы
Момент силы (также называемый крутящим моментом или просто моментом) — это тенденция силы к скручиванию или вращению объекта. Момент — это произведение силы и плеча момента.Плечо момента — это перпендикулярное расстояние от точки вращения до линии действия силы. Момент можно рассматривать как меру стремления силы вызывать вращение вокруг воображаемой оси через точку.
В системе СИ момент силы измеряется в ньютон-метре (Н · м). Один ньютон-метр равен крутящему моменту, возникающему в результате силы в один ньютон, приложенной перпендикулярно к плечу момента длиной один метр. В CGS момент силы измеряется в грамм-сила-сантиметр (гс · см).
Использование преобразователя момента силы
Этот онлайн-преобразователь единиц измерения позволяет быстро и точно преобразовывать многие единицы измерения из одной системы в другую. Страница преобразования единиц представляет собой решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеренными в различных единицах. », то есть « умножить на десять в степени ».Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
», то есть « умножить на десять в степени ».Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
Мы прилагаем все усилия, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.
Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом!
TranslatorsCafe.com Конвертер единиц YouTube канал
Эффект поворота — Момент силы — CCEA — Редакция GCSE Physics (Single Science) — CCEA
Сила может заставить объект повернуться вокруг оси.
Поворачивающий эффект силы называется моментом 0.0.0.1:0.1.0.$0.$1.$1.$1″> силы .
Моменты вращаются вокруг оси по часовой стрелке или против часовой стрелки.
Момент против часовой стрелки действует вниз слева, а момент по часовой стрелке действует вниз справаРасчет момента силы
Величина момента силы может быть рассчитана с помощью уравнения:
момент силы = сила F x расстояние по перпендикуляру от оси d
момент = F xd
- сила F измеряется в ньютонах (Н) 1gbjh3su3fy.0.0.0.1:0.1.0.$0.$2.$4.$1″> расстояние d измеряется в метрах (м)
- момент измеряется в ньютон-метрах (Нм)
Расстояние по перпендикуляру от шарнира до усилия d = 0.50 м.
Сила F = 10 Н
Момент = Fd
Момент = 10 Н x 0,50 м
Момент = 5 Нм
Это момент по часовой стрелке.
Сила будет вращать объект по часовой стрелке вокруг оси вращения.
Важно помнить, что расстояние d — это перпендикулярное расстояние от оси до линии действия силы (см. Диаграмму).
К дверной ручке на расстоянии 12 см от петли прикладывается усилие 15 Н.
Рассчитайте момент силы.
Перпендикулярное расстояние от оси до усилия d = 12 см = 0,12 м.
Усилие поворота F = 15 Н.
Момент = Fd.
Момент = 15 Н x 0,12 м.
Момент = 1,8 Нм.
1gbjh3su3fy.0.0.0.1:0.1.0.$0.$3.$0.3.$5″> Момент силы 1,8 Нм.Вопрос
- Вопрос
К гаечному ключу прикладывают усилие 40 Н для поворота гайки.
Перпендикулярное расстояние составляет 30 см.
Рассчитайте момент силы.
- Показать ответ
Перпендикулярное расстояние от оси до усилия d = 30 см = 0,30 м.
Усилие поворота F = 40 Н.

Момент = Fd.
Момент = 40 Н x 0,30 м.
Момент = 12 Нм.
Момент 12 Нм. Это момент по часовой стрелке.
Моменты — Моменты, рычаги и шестерни — AQA — Редакция GCSE Physics (Single Science) — AQA
Джонни Нельсон представляет анимированное объяснение моментов, рычагов и шестерен. повернуть.Момент — это поворачивающий эффект силы. Моменты действуют относительно точки по часовой стрелке или против часовой стрелки. Выбранной точкой может быть любая точка на объекте, но обычно выбирается точка поворота, также известная как точка опоры.
Момент против часовой стрелки действует вниз слева, а момент по часовой стрелке действует вниз справа 0.0.0.1:0.1.0.$0.$1.$3″> Величину момента можно рассчитать с помощью уравнения:момент силы = сила × расстояние
\ [M = F ~ d \]
Это когда:
- момент ( M ) измеряется в ньютон-метрах (Нм)
- сила ( F ) измеряется в ньютонах (Н)
- расстояние ( d ) измеряется в метрах (м)
Важно помнить, что расстояние ( d ) — это перпендикулярное расстояние от оси до линии действия силы (см. диаграмму).
диаграмму).
Пример
Сила 15 Н прикладывается к дверной ручке на расстоянии 12 см от оси. Рассчитайте момент силы.
Сначала преобразуйте сантиметры в метры:
12 см = 12 ÷ 100 = 0,12 м
Затем рассчитайте, используя значения, указанные в вопросе:
\ [M = F ~ d \]
\ [M = 15 \ раз 0,12 \]
\ [M = 1,8 ~ Нм \]
- Вопрос bkt24olmps.0.0.0.1:0.1.0.$0.$1.$19.1″>
- Показать ответ
\ [M = F ~ d \]
\ [30 ~ cm = 0,30 ~ m \]
\ [M = 40 \ times 0,30 \]
\ [M = 12 ~ Нм \]
К гаечному ключу прикладывают усилие 40 Н для поворота гайки.Расстояние по перпендикуляру — 30 см. Рассчитайте момент силы.
Механическая карта — момент около точки
Момент силы — это тенденция некоторых сил вызывать вращение. Любой простой способ визуализировать концепцию — это поставить коробку на гладкую поверхность. Если бы вы приложили силу к центру коробки, она просто скользила бы по поверхности, не вращаясь.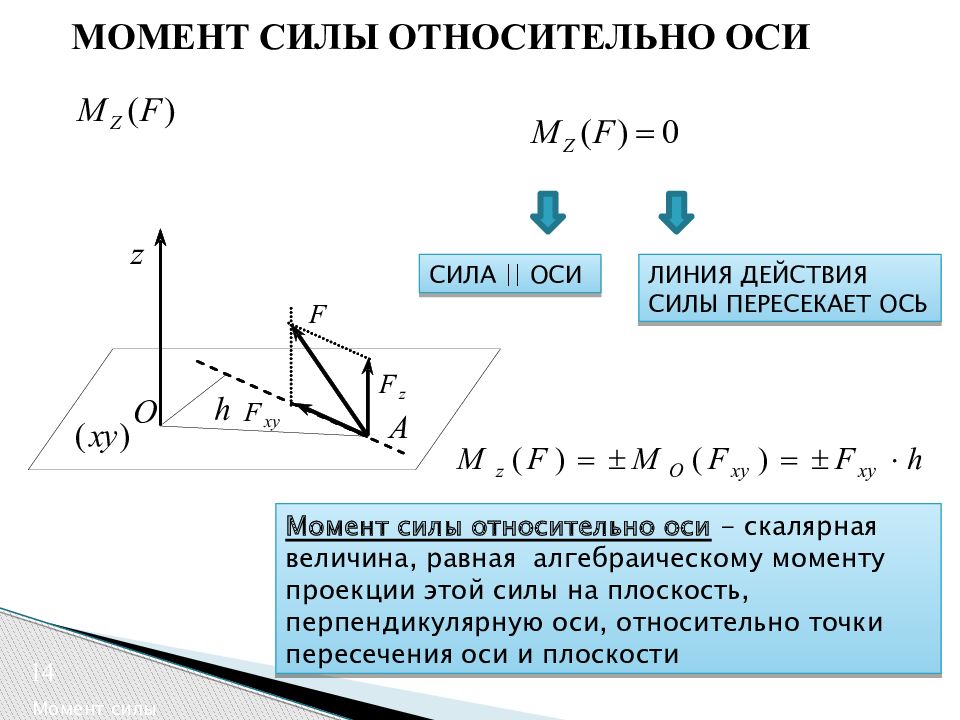 Если вместо этого вы нажмете на одну сторону коробки, она начнет вращаться при движении. Несмотря на то, что силы имеют одинаковую величину и одинаковое направление, они вызывают разные реакции. Это связано с тем, что нецентральная сила имеет другую точку приложения и оказывает момент вокруг центра коробки, тогда как сила в центре коробки не оказывает момента вокруг центральной точки коробки.
Если вместо этого вы нажмете на одну сторону коробки, она начнет вращаться при движении. Несмотря на то, что силы имеют одинаковую величину и одинаковое направление, они вызывают разные реакции. Это связано с тем, что нецентральная сила имеет другую точку приложения и оказывает момент вокруг центра коробки, тогда как сила в центре коробки не оказывает момента вокруг центральной точки коробки.
Как и силы, моменты имеют величину (степень вращения, которую он может вызвать) и направление (ось, вокруг которой будет вращаться тело). Определение величины и направления этих моментов относительно данной точки является важным шагом в анализе систем твердых тел (твердых тел, в которых силы не действуют одновременно). Приведенный ниже скалярный метод — самый простой способ сделать это в простых двумерных задачах, в то время как альтернативные векторные методы лучше всего работают в более сложных трехмерных системах.
Скалярный метод в двух измерениях
Обсуждая, как вычислить момент силы относительно точки с помощью скалярных величин, мы начнем с примера силы, действующей на простой рычаг, как показано ниже. В этом простом рычаге на конце рычага действует сила на расстоянии d от центра вращения рычага (точка A), где сила имеет величину F.
Величина момента силы F относительно точки A на этом рычаге будет равна величине силы, умноженной на расстояние d.При использовании скалярных величин величина момента будет равна расстоянию по перпендикуляру между линией действия силы и точкой, в которой мы принимаем момент.
Чтобы определить знак момента, мы определяем, какой тип вращения вызовет сила. В этом случае мы можем видеть, что сила заставит рычаг вращаться против часовой стрелки вокруг точки A. Вращения против часовой стрелки вызваны положительными моментами, тогда как вращение по часовой стрелке вызвано отрицательными моментами.
Еще один важный фактор, о котором следует помнить, — это то, что величина d — это перпендикулярное расстояние от силы до точки, в которой мы принимаем момент.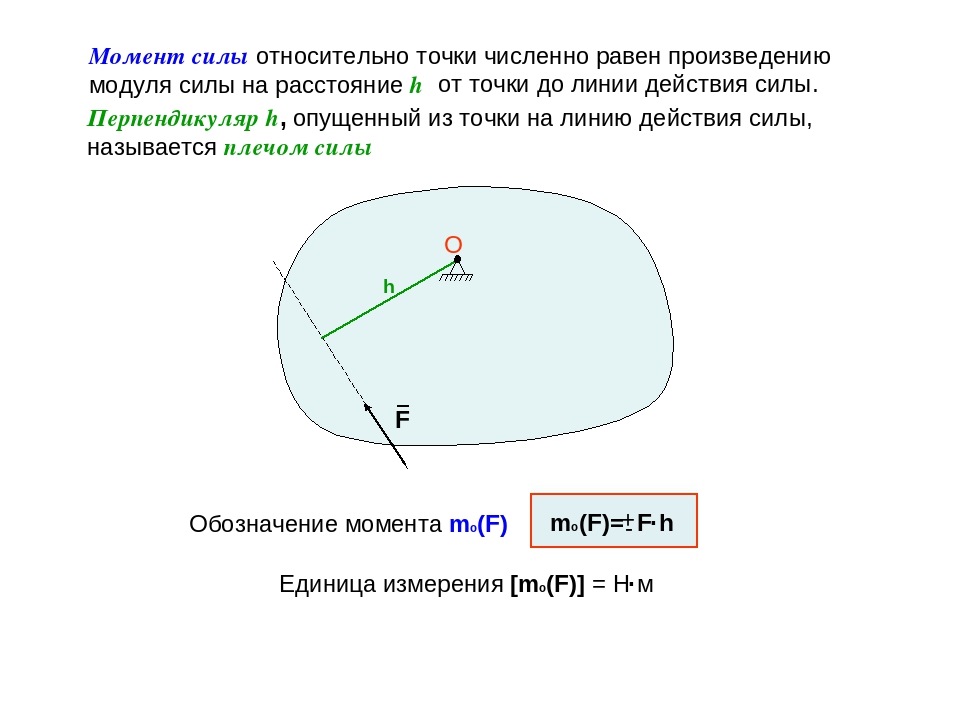 Мы могли бы измерить расстояние от точки A до головы вектора силы, или хвоста вектора силы, или действительно любой точки вдоль линии действия силы F. Однако расстояние, которое нам нужно использовать для вычисления скалярного момента, равно кратчайшее расстояние между точкой и линией действия силы. Это всегда будет линия, перпендикулярная линии действия силы, идущая в точку, о которой мы принимаем момент.
Мы могли бы измерить расстояние от точки A до головы вектора силы, или хвоста вектора силы, или действительно любой точки вдоль линии действия силы F. Однако расстояние, которое нам нужно использовать для вычисления скалярного момента, равно кратчайшее расстояние между точкой и линией действия силы. Это всегда будет линия, перпендикулярная линии действия силы, идущая в точку, о которой мы принимаем момент.
Скалярный метод в трех измерениях
Для трехмерных скалярных вычислений мы все равно найдем величину момента тем же способом, умножив величину силы на перпендикулярное расстояние между точкой и линией действия силы.Это перпендикулярное расстояние снова является минимальным расстоянием между точкой и линией действия силы. В некоторых случаях найти это расстояние может быть очень сложно.
Еще одним сложным фактором в трехмерных скалярных задачах является определение оси вращения, поскольку теперь это более сложно, чем просто «по часовой стрелке или против часовой стрелки». Ось вращения будет линией, проходящей через точку, в которой мы принимаем момент, которая перпендикулярна как вектору силы, так и вектору перпендикулярного смещения (вектор, идущий от точки, в которой мы принимаем момент, до точки приложения сила.Хотя это возможно в любой ситуации, это становится очень трудным, если векторы силы или смещения не лежат в одном из трех координатных направлений.
Для дальнейшего определения направления вектора момента (который будет действовать вдоль установленной линии для оси вращения) воспользуемся правилом правой руки в измененной форме. Оберните пальцы правой руки вокруг оси вращения, согнув кончики пальцев в направлении вращения тела. Если вы сделаете это, ваш большой палец должен указывать вдоль линии в направлении вектора момента.Это важный последний шаг, потому что мы можем вращаться по часовой стрелке или против часовой стрелки вокруг любой заданной оси вращения. Имея вектор конечного момента, мы знали не только ось вращения, но и то, как тело будет вращаться вокруг этой оси.
Что такое момент и как его рассчитать?
Когда я обучаю своих студентов-физиков, я хочу, чтобы они понимали основы концепции, а не только то, как подставить числа в уравнение. Когда я изучал физику, мне хотелось, чтобы мои учителя больше обращались к приложениям из реальной жизни, к вещам, которые мы уже знаем о мире, чтобы помочь нам действительно понять это .
Я надеюсь, что этот пример понравится всем моим друзьям-заядлым лыжникам.
Когда я был молод и учился кататься на лыжах, меня пугали кресельные канатные дороги (до сих пор немного). Свисать высоко на открытом воздухе было страшно. Когда канатная дорога была заполнена, когда я сидел на ней со всей семьей — все казалось сбалансированным, меня там благополучно зажали. Но если бы я был на кресельном подъемнике один, если бы я сел на один край, кресельный подъемник сильно наклонился бы в эту сторону.
Или, если бы я (легкий ребенок) сидел с моим папой (намного тяжелее ребенка), кресельная канатная дорога перевернулась бы на его сторону.
За годы езды на кресельной канатной дороге я понял, как удержать кресельную канатную дорогу в равновесии. Если бы я был один, я бы сел посередине. Если бы я был с отцом, он мог бы сидеть немного смещен от центра с одной стороны, а я мог бы сидеть полностью до одного края с другой стороны. Это позволит кресельной канатной дороге оставаться в горизонтальном положении.
Замечали ли вы это, когда сидели на кресельной канатной дороге с кем-то намного легче или тяжелее вас?
Вот несколько правил сидения на кресельной канатной дороге — подумайте, имеют ли они для вас смысл.
- Сидя в одиночестве посередине, кресельный подъемник будет горизонтальным.
- Более тяжелый человек наклонит кресельную канатную дорогу больше, чем легкий, если сидит на одинаковом расстоянии от центра.
- Есть способ достичь равновесия двумя людьми разного веса, сидящими на расчетном расстоянии от центра.
Эта фундаментальная физическая концепция называется моментом .
МОМЕНТ силы — это мера ее тенденции заставить тело вращаться вокруг определенной точки или оси.
Когда я сижу на кресельной канатной дороге, я создаю момент, который заставляет кресельную канатную дорогу вращаться вокруг оси.
Момент равен приложенной силе, умноженной на расстояние от оси поворота:
Момент = Сила x Расстояние
Попробуем на примере
Ребенок весом 60 фунтов сидит в 2 футах от центра кресельного подъемника. На каком расстоянии от центра на противоположной стороне кресельного подъемника должен сидеть ее отец (который весит 180 фунтов), чтобы кресельная канатная дорога была горизонтальной («сбалансированной»)?
Сначала вычислите момент, вызванный ребенком:
ПРИМЕЧАНИЕ: Кресельный подъемник можно смоделировать как невесомую балку
Момент = Сила x Расстояние
(60 фунтов) (2 фута) = 120 фут-фунтов
Когда ребенок сидит слева от точки поворота, в какую сторону наклоняется кресельная канатная дорога?
Она заставляет кресельный подъемник поворачиваться на против часовой стрелки .
Моменты против часовой стрелки считаются отрицательными значениями.Для того, чтобы кресельная канатная дорога находилась в равновесии, момент, действующий на ось со стороны Отца, должен быть равен и противоположен ребенку.
Ребенок создал момент -120 фут-фунт, поэтому ее отцу необходимо создать момент +120 фут-фунт.
120 фут-фунтов = (180 фунтов) (x фут)
x = ⅔ футов = 8 дюймов.
С какой стороны от точки поворота должен сидеть отец, чтобы уравновесить ребенка
Правая сторона!
Когда Отец сидит с правой стороны, он заставляет канатную дорогу опускаться на по часовой стрелке .
Моменты по часовой стрелке считаются положительными значениями.Когда Отец сидит на расстоянии 8 дюймов слева от оси вращения, он создает вокруг оси момент -120 фут-фунт. Равный и противоположный момент ребенку. Следовательно, кресельная канатная дорога находится в равновесии.
Какие еще приложения из реальной жизни вы можете придумать для работы с моментами?- Если гайку трудно открутить коротким гаечным ключом, поможет более длинный гаечный ключ. Это связано с тем, что момент на гайке будет больше, когда такая же сила будет приложена дальше от оси.
- Попробуйте толкнуть дверь как можно ближе к точке петли. Чем ближе к точке шарнира, тем сильнее приходится нажимать. Если дверца очень тяжелая, толкните дверцу прямо у самого дальнего от петли края. Это еще одно реальное применение момента.
Физика может показаться абстрактной и запутанной, когда вы рисуете пучки и диаграммы свободного тела. Но физика везде. Когда вы изучаете новую концепцию физики, попросите своих преподавателей привести примеры из реальной жизни и объяснить, как теория применяется на практике!
Вы хотите пообщаться с репетитором физики в Кембридже или Нью-Йорке?
Хотите узнать больше по теме?
Крутящий момент (момент)
Силу можно рассматривать как толчок или тянуть в определенном направлении.Когда к объекту прикладывается сила, результирующее движение объекта зависит от того, где сила приложена и как объект ограничен. Если объект не ограничен и сила приложена через центр гравитации, объект движется в чистом виде перевод, как описано Ньютоном законы движения. Если объект ограничен (или закреплен) в каком-то месте, называемом опорная , объект вращается насчет стержня, но не переводит.Усилие передается через шарнир а детали вращения зависят от расстояния от приложенное усилие к оси. Если объект не ограничен и сила приложена в некотором расстояние от центра тяжести, объект как переводит и вращается вокруг центра тяжести. Детали вращения зависят от расстояния от приложенная сила к центру тяжести. Движение летающих объектов описанный этим третьим типом движения; сочетание перевода и вращения.M называется крутящий момент или момент . Крутящий момент также является векторной величиной и производит вращение. так же, как сила производит перевод. А именно объект на покой или вращение с постоянной угловой скоростью, будет продолжать делать это пока он не подвергнется внешнему крутящему моменту. Крутящий момент вызывает изменение в угловой скорости, которая называется угловым ускорением.
Расстояние L , используемое для определения крутящего момента T , является расстоянием от шарнир p к силе, но измеряется перпендикулярно к направление силы.На рисунке показаны четыре примера крутящих моментов, чтобы проиллюстрировать основные принципы, регулирующие крутящие моменты. В каждом примере синий груз W воздействует на красную полосу, которая называется рука.
В примере 1 сила (вес) приложена перпендикулярно к руке. В этом случае перпендикулярное расстояние — это длина бар и крутящий момент равен произведению длины и силы.
Т = F * L
В примере 2 к руке приложено такое же усилие, но сила теперь действует прямо через вращаться.В этом случае расстояние от оси перпендикулярно силе равно нулю. Значит, и в этом случае крутящий момент также равен нулю. Представьте себе распашную дверь. Если вы нажмете край двери, в сторону петли, дверь не двигается потому что крутящий момент равен нулю.
Пример 3 представляет собой общий случай, когда сила прилагается. под некоторым углом a к рука. Перпендикулярное расстояние определяется выражением тригонометрия как длина плеча (L), умноженная на косинус (cos) угла.Тогда крутящий момент определяется по формуле:
Т = F * L * cos (а)
Примеры 1 и 2 могут быть получены из этой общей формулы, так как косинус 0 градусов составляет 1,0 (Пример 1), а косинус 90 градусов равен 0,0 (Пример 2).
В примере 4 точка поворота была перемещена с конца полосы на место около середины бара. Вес добавлен с обеих сторон оси. Справа один груз W создает силу F1 , действующую на расстоянии L1 от оси.Это создает крутящий момент T1 , равный произведение силы и расстояния.
Т1 = F1 * L1
Слева от два шарнирных груза W создают усилие F2 на расстоянии L2 . Это производит крутящий момент T2 в направлении, противоположном T1, поскольку расстояние находится в противоположном направлении.
Т2 = F2 * L2
Если бы система находилась в равновесии , или сбалансирован, крутящие моменты будут равны, и никакой полезный крутящий момент не будет действовать на систему.
T1 = T2 или T1 — T2 = 0
F1 * L1 = F2 * L2
Если система не находится в равновесии или неуравновешена, стержень вращается. вокруг оси в направлении большего крутящего момента. Если F2 = 2 * F1, какова связь между L1 и L2, чтобы сбалансировать систему? Если F2 = 2 * F1, и L1 = L2, в каком направлении будет вращаться система?
Авиационные инженеры используют крутящий момент, создаваемый аэродинамическими поверхностями. для стабилизации и управления самолетом.В самолетах рули производят аэродинамические силы. Эти силы действуют на некотором расстоянии от самолет cg и поэтому заставить летательный аппарат вращаться. В лифты производят момент качки, руль направления момент рыскания, и элероны производят момент качения. Возможность варьировать количество сила и момент позволяют пилоту маневрировать или обрезать самолет. На модельных ракетах плавники используются для создания крутящего момента вокруг ракеты центр гравитации предоставлять стабильность во время автономного полета.На воздушных змеях аэродинамические и весовые силы производить крутящий момент вокруг уздечка. Расстояние от точки уздечки и величина сил оказывает сильное влияние на представление воздушного змея.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Момент силы — Вопросы и ответы по инженерной механике
Этот набор вопросов и ответов по инженерной механике с множественным выбором (MCQ) посвящен теме «Момент силы — 1».
1. Определите наименьшую силу, приложенную к точке R, которая создает такой же момент около P, как и сила 75Н.
a) 37,5N
b) 112,5N
c) 60N
d) 0N
Просмотреть ответ
Ответ: a
Объяснение: поскольку мы знаем, что момент — это перекрестное произведение расстояния и силы, которую мы попытаемся применить тут то же самое. Мы видим, что расстояние по перпендикуляру равно 3м. Таким образом мы получаем расстояние. А значит, умножьте его на силу, момент = 112,5 Нм. Потому что нужно брать составляющую силы, перпендикулярную расстоянию.
2. Что измеряет момент силы?
a) Тенденция вращения тела вдоль любой оси
b) Момент инерции тела относительно любой оси
c) Момент пары, создаваемый единственной силой, действующей на тело
d) Вся работа выполняется на тело силой
Посмотреть ответ
Ответ: a
Объяснение: Момент силы измеряет тенденцию вращения тела вдоль любой оси, будь то центральная ось тела или какая-либо внешняя ось.Момент пары создается двумя силами, а не одной силой. Общая проделанная работа — это скалярное произведение силы и расстояния, а не крест.
3. Если автомобиль движется вперед, каково направление момента момента, вызванного вращением шин?
a) Он направлен внутрь, то есть в направлении внутрь автомобиля
b) Он направлен наружу, то есть в направлении снаружи автомобиля
c) Он движется вперед, то есть в направлении вперед движения автомобиля
d) Он движется назад, т.е.е. направление движения автомобиля — назад.
Посмотреть ответ
Ответ: a
Пояснение: когда вы сгибаете запястье в том направлении, в котором движутся шины, вы обнаружите, что большой палец указывает наружу. Это снаружи кузова машины. Это явление наблюдается и в сезон дождей. Когда автомобили едут по дорогам, вода моментально выбрасывается из шин.
4. Тенденцию вращения тела вдоль любой оси также называют ___________
a) Момент инерции
b) Момент пары
c) Крутящий момент
d) Сила
Посмотреть ответ
Ответ: c
Пояснение: Тенденция вращения тела по любой оси также называется крутящим моментом.Это момент силы, действующей перпендикулярно направлению оси вращения. Если ось и сила встречаются в любой точке, то сила не прикладывает никакого момента.
5. Момент силы — это произведение силы на перпендикулярное расстояние оси и точки действия силы.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: a
Объяснение: Момент — это произведение силы, приложенной к телу, и перпендикулярного расстояния от точки действия силы до оси, вокруг которой тело вращается.То есть момент является перекрестным произведением силы и расстояния между осью и точкой действия.
6. Определить момент около точки Т.
a) 0 Нм
b) 350 Нм
c) 100 Нм
d) 200 Нм
Посмотреть ответ
Ответ: a
Объяснение: Поскольку мы знаем, что момент — это перекрестное произведение расстояния и силы, мы попытаемся применить то же самое здесь. Мы видим, что перпендикулярное расстояние равно 0м. Таким образом мы получаем расстояние.И, следовательно, умножьте его на силу 0x50.
7. Ось момента находится в направлении, перпендикулярном плоскости силы и расстояния.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: a
Объяснение: Ось момента всегда перпендикулярна плоскостям силы и расстоянию до оси и точки действия силы на тело. Это означает, что момент — это перекрестное произведение силы на расстояние между осью и точкой действия силы.
8. Найдите момент по Т.
а) 1200 Нм
б) 600 Нм
в) 0 Нм
г) 1400 Нм
Посмотреть ответ
Ответ: б
Объяснение: Поскольку мы знаем, что момент — это произведение расстояния и силы, мы попытаемся применить то же самое здесь. Но здесь мы имеем ряд составляющих сил, действующих на точку T. Таким образом, добавление всех моментов, вызванных всеми силами, даст нам значение 600 Нм.
9. Если вы узнаете направление момента, вызванного силой, приложенной к телу, с помощью запястья и сгибания его в направлении вращения, то что из следующего неверно?
a) Большой палец представляет направление силы
b) Большой палец представляет направление момента
c) Пальцы представляют направление силы
d) Направление, в котором вы сгибаете запястье, — к направлению расстояние от точки приложения силы до оси вращения.
Посмотреть ответ
Ответ: b
Пояснение: Согнутая рука олицетворяет разные вещи. Направление оси момента задается большим пальцем. Направление силы задается пальцами. Как мы кладем пальцы на силу и сгибаемся в направлении вращения тела вокруг оси.
10. Ось момента, сила и перпендикулярное расстояние в момент расчета силы лежат в ____________
a) Две плоскости, перпендикулярные друг другу
b) Одна плоскость в направлении силы
c) Одна плоскость в направление перпендикулярного расстояния
d) Одна линия в направлении силы
Просмотр Ответ
Ответ: a
Пояснение: Ось момента, сила и перпендикулярное расстояние лежат в трехмерной декартовой системе координат.Он не лежит на одном плане. И не в одну строчку. Ни в сторону силы. Таким образом, все они лежат в плоскостях, перпендикулярных друг другу.
11. Если на этой странице вращение происходит по часовой стрелке, предположим, тогда в каком направлении будет выступать большой палец, если вы согнете руку в том же направлении вращения?
a) Он будет указывать в направлении, перпендикулярном плоскости бумаги и к вам
b) Он будет указывать в направлении, перпендикулярном плоскости бумаги и от вас
c) Он будет указывать в направлении, параллельном плоскости бумаги. плоскость бумаги и направо
d) Он будет указывать в направлении, параллельном плоскости бумаги и влево.
Посмотреть ответ
Ответ: b
Пояснение: Поскольку скручивание дает направление, перпендикулярное бумаге.Но это действительно зависит от направления вращения. В этом примере значение по часовой стрелке. Таким образом, большой палец входит в бумагу. То есть уходит от зрителя. Итак, ответ.
12. Что из следующего верно?
a) Полный момент различных сил, действующих на тело, является векторной суммой всех моментов
b) Полный момент различных сил, действующих на тело, является алгебраической суммой всех моментов
c) Суммарный момент различных сил, действующих на тело всегда равен нулю
d) Суммарный момент различных сил, действующих на тело, представляет собой векторную сумму всех моментов, перпендикулярных друг другу сил.
Посмотреть ответ
Ответ: a
Объяснение: Момент — это векторная величина.Таким образом, значение полного момента, вызванного различными силами, действующими на тело, является векторной суммой всех векторов. Кроме того, моменты не перпендикулярны друг другу, если не указано иное. Таким образом, предположения нельзя принимать за актуальность момента.
13. Определить момент около точки R.
a) 0Nm
b) 350Nm
c) 100Nm
d) 200Nm
Посмотреть ответ
Ответ: c
Объяснение: Поскольку мы знаем, что момент — это перекрестное произведение расстояния и силы, мы попытаемся применить то же самое здесь.Мы видим, что расстояние по перпендикуляру равно 7м. Таким образом мы получаем расстояние. И, следовательно, умножьте это на силу, 7 × 50.
14. Найдите момент по Q.
а) 1200 Нм
б) 600 Нм
в) 0 Нм
г) 1400 Нм
Посмотреть ответ
Ответ: а
Объяснение: Поскольку мы знаем, что момент — это перекрестное произведение расстояния и силы, мы попытаемся применить то же самое здесь. Но здесь мы имеем ряд составляющих сил, действующих на точку T. Таким образом, сложив все моменты, вызванные всеми силами, мы получим значение 1200 Нм.
15. Определить момент силы по точке P.
a) 110 Нм
b) 112,5 Нм
c) 60 Нм
d) 0 Нм
Посмотреть ответ
Ответ: b
Объяснение: Поскольку мы знаем, что момент — это перекрестное произведение расстояния и силы, мы попытаемся применить то же самое. Мы видим, что расстояние по перпендикуляру составляет 1,5 (3cos60). Таким образом мы получаем расстояние. И, следовательно, умножьте это на силу, 75 × 1,5.



 Рассмотрим ситуацию, возникающую при выдергивании гвоздя, более детально:
Рассмотрим ситуацию, возникающую при выдергивании гвоздя, более детально:

