Виды шумов, отношение сигнал/шум, Статистическая обработка сигнала, Корреляционная функция
Рассмотрены 3 темы по основам цифровой обработки сигналов: виды шумов, отношение сигнал/шум, статистическая обработка сигнала, корреляционная функция.
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- Виды шумов, отношение сигнал/шум,
- Статистическая обработка сигнала,
- Корреляционная функция.
Виды шумов, отношение сигнал/шум.
В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.
Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.
Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.
Также в качестве меры разброса употребляется среднеквадратичное отклонение
На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.
В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.
В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.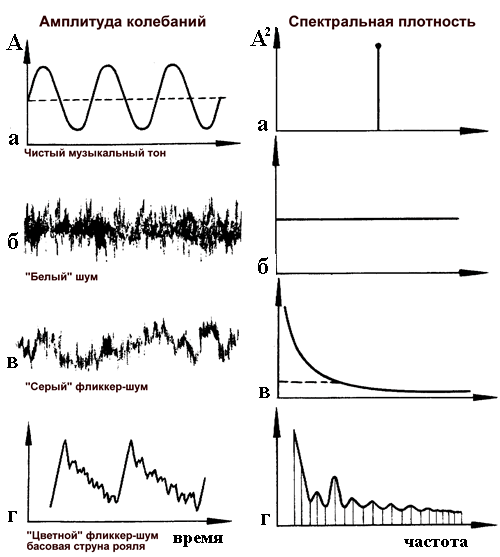
Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.
Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения. При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.
Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.
Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.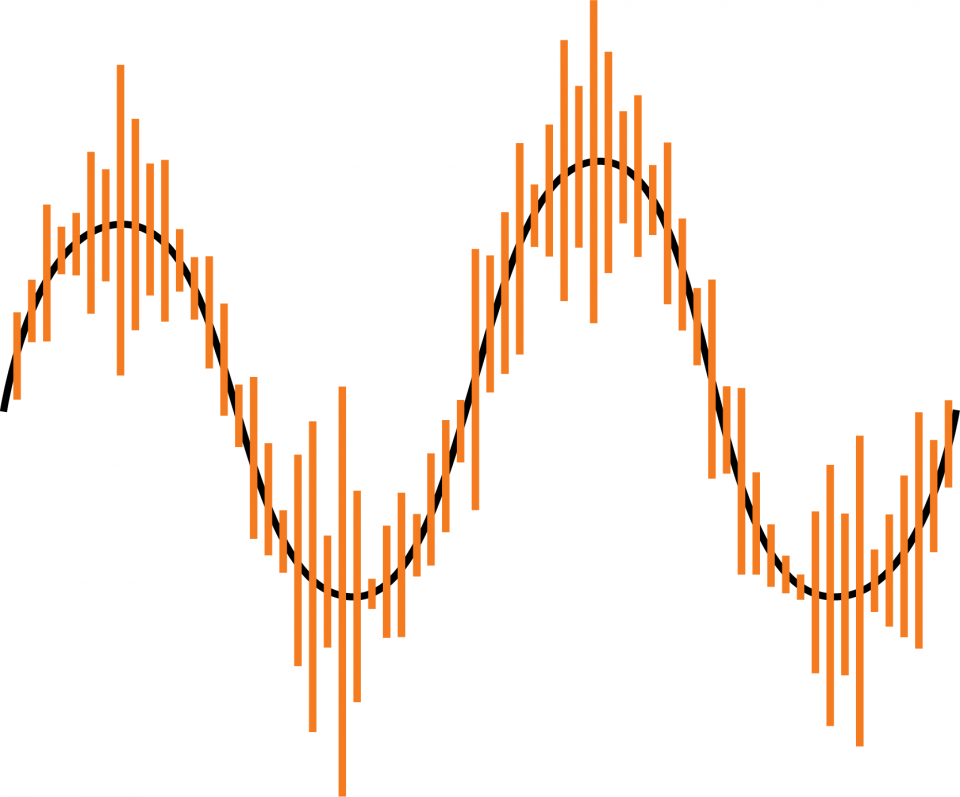
Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.
Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.
А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.
Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот.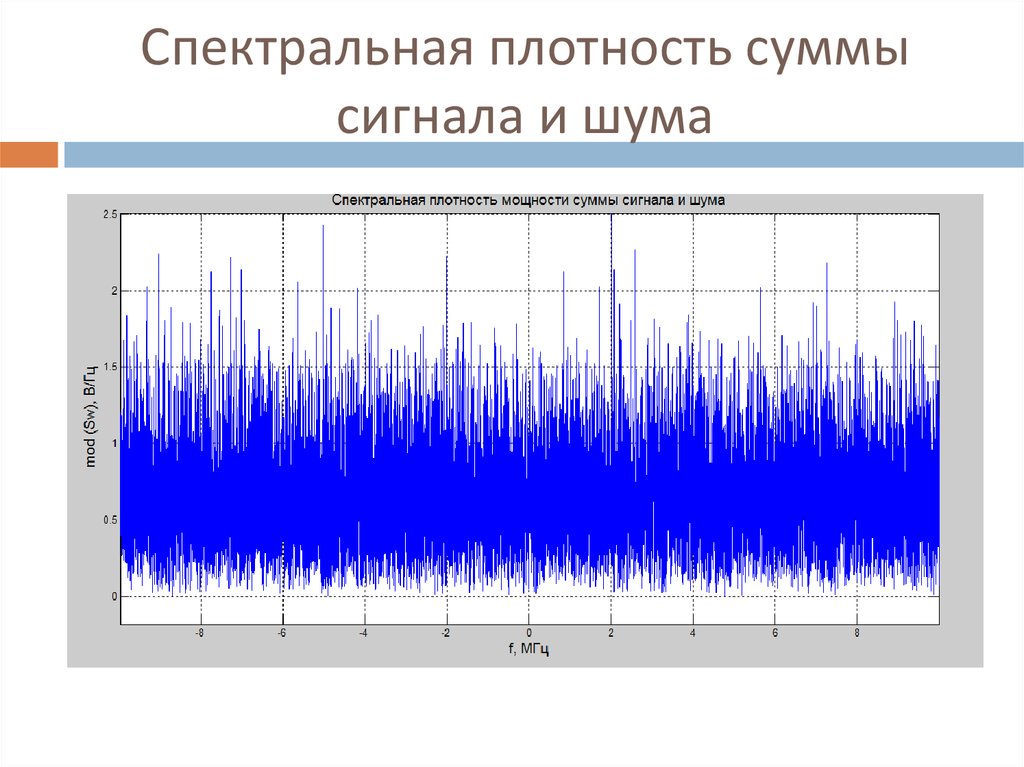
В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.
Слуйчайный процесс, у которого область частот заполнена равномерно, называется
Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности. В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.
Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.
Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления. К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.
Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.
- У него равномерная спектральная плотность мощности, поэтому он белый.
- Нормальное распределение, поэтому он Гауссовский.
- С полезным сигналом он суммируется, поэтому он аддитивный.
- И статистически он от сигнала независим.
На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.
Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных. Шум в подобных системах, конечно же, является нежелательным явлением.
Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.
Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.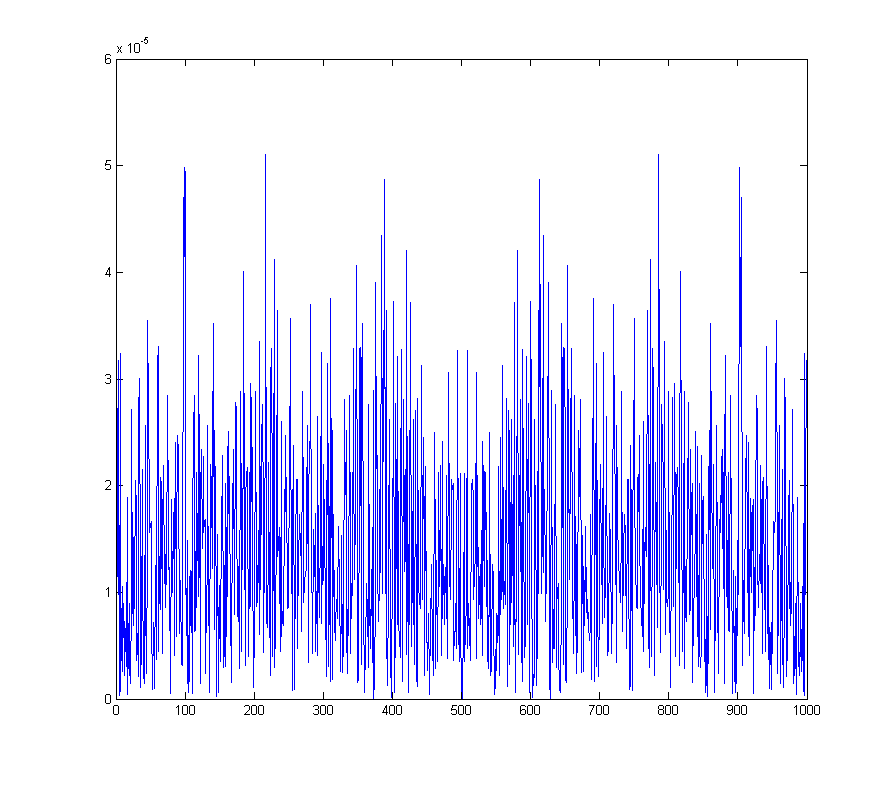
Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.
Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.
Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.
Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума.
Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному.
Теперь мы генерируем большое число зашумлённых сигналов. Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.
Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.
В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.
Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.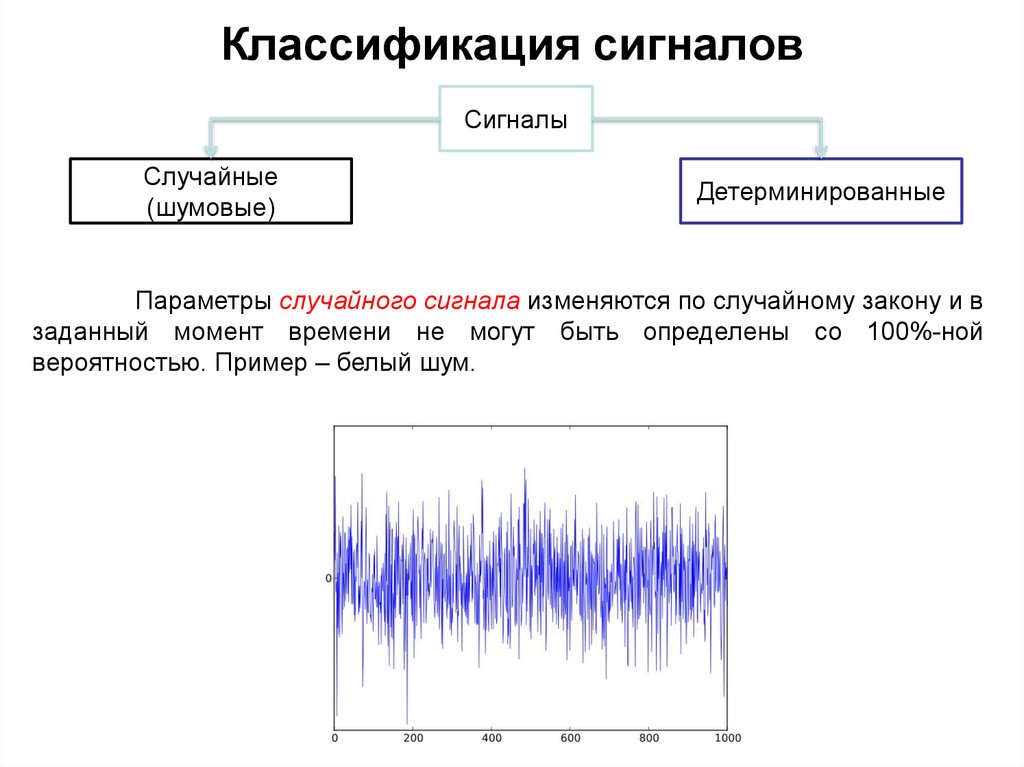
Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.
В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.
Наверх
Статистическая обработка сигнала.
В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.
У любого сигнала, непрерывного и дискретного, можно определить среднее значение.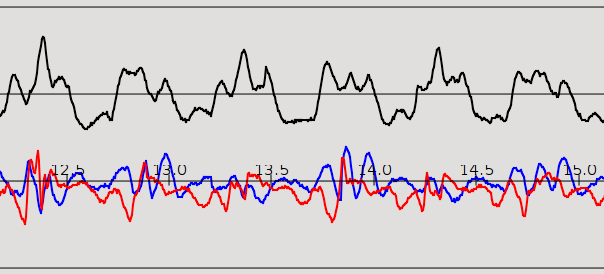
Оно может вычисляться по-разному.
Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.
Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.
То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.
Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.
Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.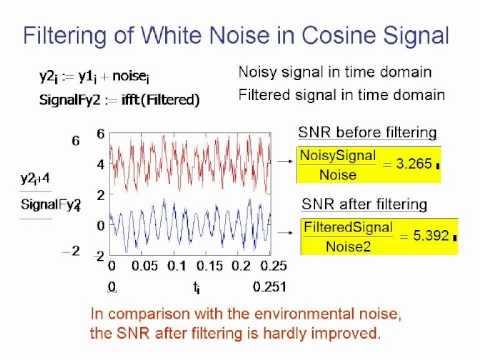
Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».
При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.
Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.
Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего.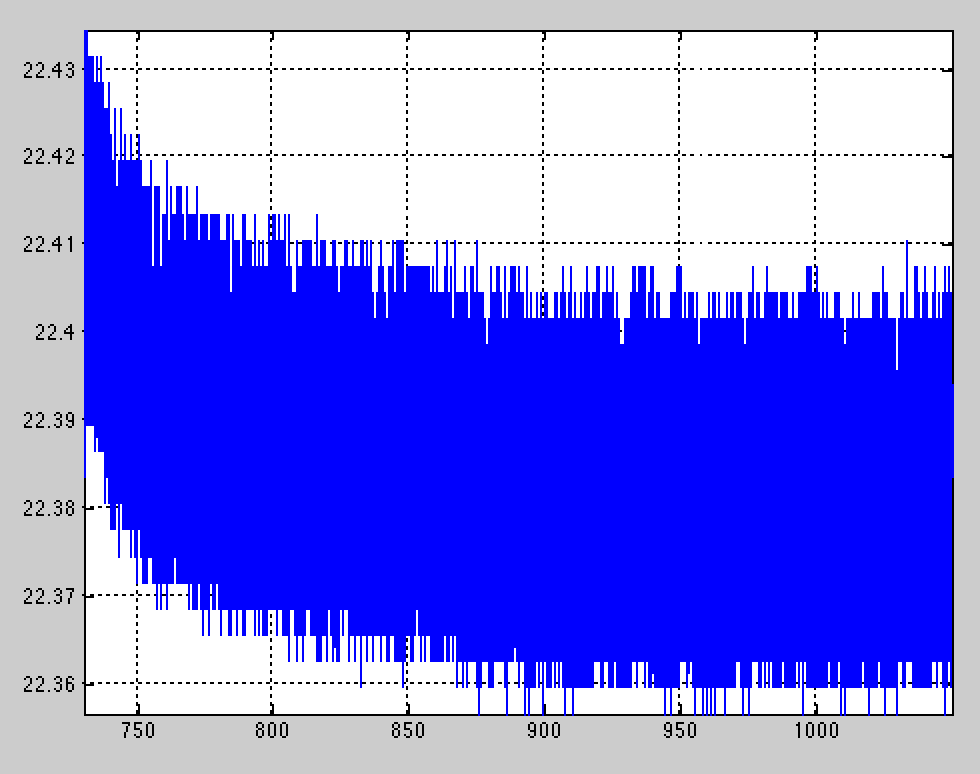
Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.
Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.
Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.
Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми.
В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.
Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего.
Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.
Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.
А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах. Также можно построить Q-зубцы на том же самом графике.
Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.
Наверх
Корреляционная функция.
Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.
Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.
Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.
В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.
При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.
Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.
В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией.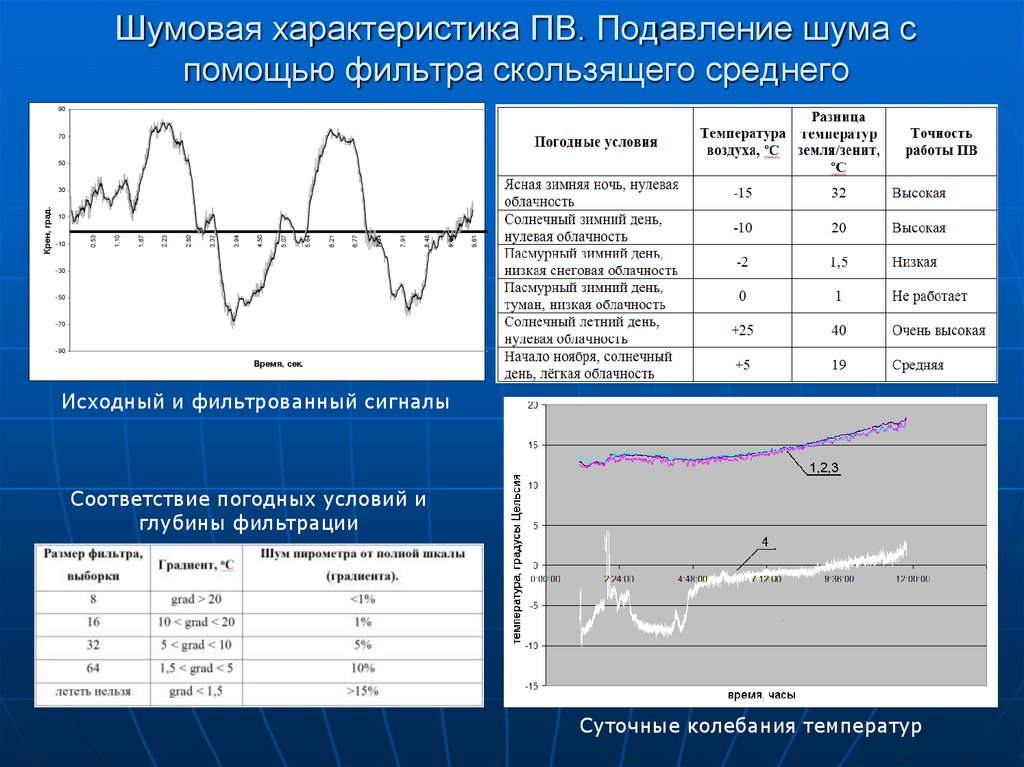
Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.
Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный.
В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.
Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.
Автокорреляционная функция прямоугольного импульса имеет форму треугольника.
Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.
Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов
А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.
Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.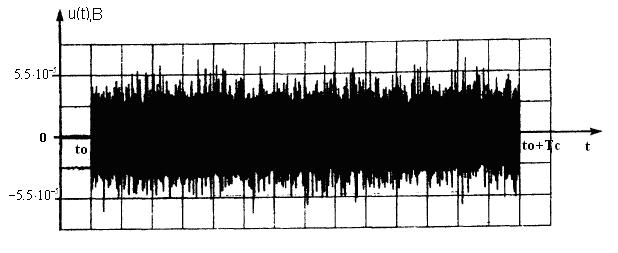
А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.
Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти.
Область, которую мы выделили, обозначена на графике двумя пунктирными линиями.
Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.
В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале.
Теперь давайте добавим шум к исходному сигналу и к фрагментам.
Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.
Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале.
Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.
Измерение оптического отношения сигнал/шум в когерентных системах с использованием передачи с поляризационным мультиплексированием, метод Viavi SCorM
Измерение оптического отношения сигнал/шум OSNR (Optical Signal-to-Noise-Ratio) в работающих системах DWDM (Dense Wavelength Division Multiplexing), где не просто применяется высокоплотное мультиплексирование по длине волны, а используется передача с поляризационным мультиплексированием (Pol-Mux), представляет собой сложную задачу. В этой статье предлагается новый метод определения OSNR на основе анализа корреляционной зависимости между спектральными компонентами сигнала в оптическом диапазоне.
Введение
В современных высокоскоростных системах DWDM когерентное детектирование с цифровой обработкой сигнала и использование поляризационного мультиплексирования Pol-Mux стали стандартным решением.
Качество модулированных оптических сигналов, передаваемых в волоконно-оптических системах на большие расстояния, обычно характеризуют параметром OSNR – оптическим отношением сигнал/шум.
Телекоммуникационные стандарты описывают несколько методов измерения OSNR в системах DWDM, однако до сего момента для систем, использующих в сетевой топологии поляризационное мультиплексирование Pol-Mux и перестраиваемые оптические мультиплексоры ввода-вывода ROADM, не существовало универсального метода измерения внутриполосного значения OSNR в работающих системах, без перерыва связи. 100-гигабитные и более производительные системы передачи задействуют при кодировании сигналов все возможные физические параметры – длину волны, амплитуду, фазу, состояние поляризации. Для выделения шума и расчета значения OSNR не остается какого-либо независимого физического показателя.
Определение OSNR дополнительно осложняется тем, что передаваемые сигналы могут в значительной степени искажаться из-за хроматической дисперсии CD (Chromatic Dispersion) и поляризационной модовой дисперсии PMD (Polarization Mode Dispersion).
В этой статье мы рассмотрим новый метод, предложенный компания Viavi. Он основан на измерении спектральной корреляции, который позволяет определять внутриполосное значение OSNR в когерентных системах прямо в ходе работы систем.
Измерение оптического отношения сигнал/шум
Значение OSNR измеряется оптическими анализаторами спектра OSA (Optical Spectrum Analyzer). По определению оптическое отношение сигнал/шум – это частное от деления оптической мощности цифрового информационного сигнала Pсигнала на мощность оптического шума Pшума, вносимого в сигналы оптическими усилителями EDFA. В значении Pсигнала учтена полная мощность сигнала, передаваемого внутри полосы пропускания канала Bканала (ширина полосы обычно составляет 50 ГГц). Мощность шума нормируется относительно измерительной полосы Bшума= 0.1 нм. Расчет значения OSNR производится по формуле:
Традиционный метод определения OSNR по стандарту IEC 61280-2-9
Чаще всего для определения отношения OSNR используется интерполяция или внеполосный метод, описанный в стандарте IEC 61280-2-9.
Эта методика предусматривает измерение мощности шума за пределами оптического канала и основывается на предположении о том, что сигнал имеет ограниченную оптическую полосу пропускания, в то время как для шума характерно широкополосное распределение.
Из этого предположения следует, что внеполосное измерение шума, выполненное на частотах вне оптических каналов (PNL для левой точки и PNR для правой, см. рис. 1), можно интерполировать и таким путем рассчитать мощность шума PN внутри оптического канала.
Рис. 1: Метод определения OSNR по стандарту IEC 61280-2-9
Для типовых систем с простыми оптическими сегментами от точки к точке, обслуживающими приложения до 10 Гбит/с, описанный метод дает вполне точные значения OSNR.
Методы определения OSNR для оптических сетей с ячеистой структурой
Если сетевая топология усложняется и становится динамически переконфигурируемой, построенной на ячеистой архитектуре, стандартным решением будет использование перестраиваемых оптических мультиплексоров ввода-вывода ROADM.
Для разделения индивидуальных каналов ввода и вывода мультиплексоры ROADM используют демультиплексирование. Демультиплексорные схемы построены на оптических фильтрах, которые пропускают оптический сигнал, относящийся к конкретному каналу, но подавляют оптическую мощность на частотах за его пределами. В результате в среде, использующей мультиплексоры ROADM, нет широкополосного шума от усилителей EDFA. Характеристики шума на разных частотах меняются в зависимости от работы фильтров, поэтому параметры шума за пределами и внутри оптического канала в этом случае нельзя считать связанными общей зависимостью. Использованная ранее формула перестает быть корректной.
Приведенный далее график иллюстрирует эффекты, накладываемые на параметры шума в результате фильтрации, выполняемой устройствами ROADM.
Рис. 2: Влияние фильтрации на профиль шума в среде, использующей перестраиваемые оптические мультиплексоры ввода-вывода ROADM
В системах, основанных на перестраиваемых мультиплексорах ROADM, внеполосное измерение мощности шума по стандарту IEC на частотах между оптическими каналами не позволит получить корректное значение OSNR.
В таких системах для определения отношения OSNR необходимо измерять опорное значение шума внутри спектрального диапазона сигнала – нужно проводить внутриполосное измерение OSNR. Для общепринятых оптических сигналов, использующих одиночную поляризацию – амплитудную или OOK-модуляцию (On-Off-Key, бинарный формат модуляции с двумя значениями амплитуды сигнала, соответствующими включенному и выключенному состоянию передатчика) – и обеспечивающих пропускную способность 2.5 Гбит/с, 10 Гбит/с, а иногда и 40 Гбит/с, применяются методы поляризационного подавления. Если исходить из того, что передаваемый сигнал поляризован, а шум – нет, то поляризационный фильтр позволит подавить поляризованный сигнал и измерить неполяризованный шум внутри оптического канала, чтобы получить таким путем внутриполосное значение OSNR.
Сложности с измерениями в высокоскоростных системах, использующих поляризационное мультиплексирование
В когерентных системах, обеспечивающих 100-гигабитную пропускную способность и выше, используется передача с поляризационным мультиплексированием Pol-Mux.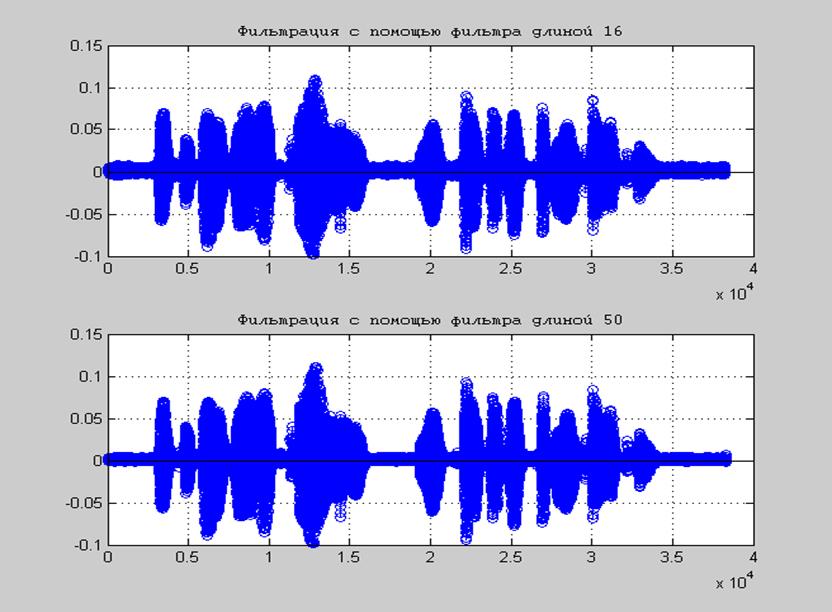
Эта технология предусматривает одновременную передачу сигналов на одной и той же длине волны во встречных направлениях, однако излучение отличается поляризацией – волны используют взаимно ортогональные плоскости поляризации. Измерительным прибором (например, оптическим анализатором спектра) такое излучение воспринимается как неполяризованное. Поэтому для отделения сигнала от шума и определения внутриполосного значения OSNR в этом случае нельзя применить поляризационный фильтр и технологию поляризационного подавления.
Хотя для определения внутриполосного OSNR в сигналах Pol-Mux было предложено несколько методов, на практике они работают только в том случае, если оптические сигналы подаются с заранее известной битовой скоростью, типом модуляции и/или формой сигнала. Следовательно, такие методы могут быть пригодны для мониторинга параметра OSNR только в части телекоммуникационных систем. Их нельзя использовать как общую методику тестирования, пригодную для любых случаев. Более того, часть методов заведомо непригодна для определения внутриполосного значения OSNR в сигналах, которые существенно искажены вследствие хроматической дисперсии CD и поляризационной модовой дисперсии PMD.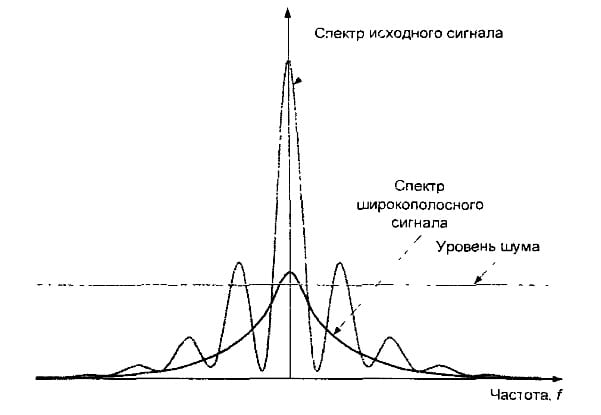
Для проведения измерений внутриполосного OSNR при помощи типового спектрального анализа мощности оптических сигналов был разработан метод сравнения спектральных форм. К сожалению, для таких измерений характерны большие ошибки, в которые вносят свой вклад и спектральные фильтры мультиплексоров ROADM, и пульсация при передаче, и уровень воспроизводимости результатов, который может обеспечить оптический анализатор спектра OSA. Методы измерений во временной области требуют применения высокоскоростных фотоприемников, охватывающих всю полосу пропускания, используемую при передаче на скорости 100 Гбит/с или выше. На практике такое решение применить невозможно, поскольку точки мониторинга не могут обеспечить мощность, достаточную для таких высокоскоростных фотоприемников. Единственный известный в телекоммуникационной отрасли метод для измерения внутриполосного значения OSNR предусматривает временное отключение канала – метод On/Off. Этот метод нельзя применять «по живому», в ходе работы системы, поскольку для измерения шума в канале полезный сигнал приходится отключать.
В итоге можно констатировать, что до сего момента в телекоммуникационной отрасли не существовало коммерчески доступного способа измерения внутриполосного оптического отношения сигнал/шум в когерентных системах с использованием поляризационного мультиплексирования Pol-Mux – метода, который можно было бы применять в работающих системах.
Измерение корреляции – новый шаг в технологии измерений
В высокоскоростных когерентных системах, использующих мультиплексоры ROADM, привычные физические параметры – частоту, мощность, состояние поляризации – нельзя использовать для отделения модулированного сигнала от шума, вносимого усилителем, и последующего измерения внутриполосного значения OSNR. Необходим какой-то другой параметр, позволяющий выделить сигнал на фоне шума.
Как оказалось, для этой цели можно использовать корреляцию между замерами, выполненными внутри оптического канала, и такое решение дает вполне надежные результаты. Корреляционный анализ позволяет статистически оценить зависимость между двумя численными переменными – например, результатами замеров амплитуды оптического сигнала.
Полученную корреляционную зависимость можно использовать для расчета отношения OSNR, основываясь на том факте, что замеры дискретных модулированных сигналов заведомо должны коррелировать между собой, в то время как параметры белого шума по определению ни с чем не коррелируют.
Корреляционные свойства дискретных модулированных сигналов
Коэффициент корреляции Corr – безразмерный статистический показатель, характеризующий взаимную зависимость двух переменных. Значение коэффициента может варьироваться от 0 (взаимной зависимости между переменными нет) до 1 (полное совпадение = измерения идентичны).
На рис. 3 показан пример двоичного модулированного сигнала, на который накладывается белый шум.
Рис. 3: Измерения для определения корреляционной зависимости
Методика основана на сравнении замеров чистого сигнала (показан серым цветом) и чистого шума (показан оранжевым цветом) и определении корреляции между результатами.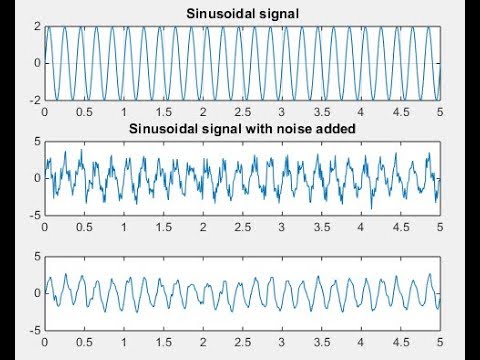
Точки замеров должны отстоять друг от друга на расстояние заведомо меньше, чем продолжительность двоичного импульса TB.
Корреляция сигнала:
Замеры, соответствующие сигналу (желтые отрезки) показывают высокую степень соответствия дискретным состояниям «1» или «0». Коэффициент корреляции равен единице: Corr = 1.
Корреляция шума:
Когда замеры соответствуют белому шуму (синие отрезки), вероятность того, что они окажутся одинаковыми, очень низка. Коэффициент корреляции в этом случае равен нулю: Corr = 0.
Смесь полезного сигнала и шума будет характеризоваться коэффициентом корреляции от 0 до 1, и поскольку этот параметр характеризует взаимную зависимость между сигналом и шумом, его можно использовать как основу для определения оптического отношения сигнал/шум OSNR.
Это пример рассуждений, справедливых для измерений во временной области. Как уже упоминалось ранее, методы измерений во временной области требуют применения очень высокоскоростных фотоприемников, которые на практике не смогут работать в точках мониторинга системы. Преобразование Фурье позволяет применить корреляционный анализ в частотной области, где выполнять измерения гораздо проще.
Метод спектральной корреляции (
SCorM), предложенный компанией ViaviКомпания Viavi разработала новый метод спектральной корреляции, его сокращенное обозначение – SCorM, на него в США выдан патент US20160164599 A1. Метод применяется в частотной области, для его реализации нет нужды использовать высокоскоростные фотоприемники и функцию CDR (Clock and Data Recovery) для корректной синхронизации и распознавания сигналов. Методика основана на оценке корреляционной зависимости между компонентами сигнала в пределах оптического спектра канала передачи и том факте, что спектральные компоненты модулированных сигналов демонстрируют высокую корреляцию, в то время как для спектральных компонентов шума никакой корреляции нет. Значение OSNR можно рассчитать на основе оценки корреляционных зависимостей между спектральными компонентами на предварительно заданных парах отстоящих друг от друга длин волн.
Компоненты имеют зависимость от времени, анализ охватывает оптический амплитудный спектр сигнала, и определенная сложность состоит в том, чтобы проанализировать и сравнить между собой весьма узкие интервалы частот в оптическом канале, причем в сигнале содержатся как компоненты сигнала, демонстрирующие высокую корреляцию, так и компоненты шума с нулевым уровнем корреляции. Ширина полосы при измерении должна быть гораздо меньше, чем при передаче целевого сигнала. В стандартных системах DWDM ширина обычно не превышает 50 ГГц. Для оценки корреляции спектральных компонентов необходимо использовать два независимо настраиваемых фотоприемника, обладающих сверхвысокой разрешающей способностью в диапазоне менее 50 МГц. Такая чувствительность более чем в 100 раз выше, чем у наиболее продвинутых оптических анализаторов спектра, основанных на технологиях оптики свободного пространства FSO (Free Space Optics). Столь высокого разрешения можно добиться только при использовании схем на основе когерентных детекторов, по принципам работы сходных с высокоскоростными когерентными фотоприемниками.
Рис. 4: Анализ спектральной корреляции компонентов сигнала
На рис. 4 показан спектр 100-гигабитного сигнала с поляризационным мультиплексированием Pol-Mux (квадратурная фазовая манипуляция PM-QPSK). Спектральные плотности SPL и SPR отображают измерения спектральных компонентов внутри оптического канала, содержащих как целевой сигнал, так и шум.
Коэффициент корреляции Corr можно выразить в виде функции от параметров SPL и SPR; он может принимать значения между 0 и 1.
Через коэффициент корреляции Corr может быть рассчитано внутриполосное значение отношения OSNR (OSNRC):
Близкие к нулю значения коэффициента корреляции Corr приводят к низким значениям отношения OSNR, близкие к единице – к высоким.
Оптический анализатор спектра OSA-710 компании Viavi для сетей с поляризационным мультиплексированием Pol-Mux, основанный на применении метода SCorM
Оптический анализатор спектра Viavi Pol-Mux OSA-710 – это первый измерительный прибор, основанный на методике SCorM.
Он позволяет определять внутриполосное отношение OSNR в работающих системах при передаче сигналов с использованием как одиночной поляризации – амплитудной или OOK-модуляции (On-Off-Key) – так и сигналов с когерентной фазовой модуляцией xPSK и квадратурной амплитудной модуляцией xQAM в сетях с поляризационным мультиплексированием Pol-Mux на основе топологии ROADM. Метод нечувствителен к значительным искажениям сигнала из-за хроматической дисперсии CD и поляризационной модовой дисперсии PMD, не требует предварительной калибровки с использованием эталонного оптического сигнала, свободного от шумов.
Оптический анализатор спектра OSA включает в себя два независимо настраиваемых когерентных приемника, обладающих продвинутыми возможностями цифровой обработки сигналов. Это позволяет работать со всеми параметрами сигнала, включая амплитуду, частоту, фазу и поляризацию, независимо от используемого вида модуляции. Настройки прибора позволяют анализировать символьную или битовую скорость передачи, измерять в работающих системах хроматическую дисперсию в каждом канале.
Стандартные измерения спектра выполняются со сверхвысоким разрешением – ширина полосы в C-диапазоне составляет 20 МГц. На рис. 5 показано принципиальное строение анализатора Viavi Pol-Mux OSA-710.
Рис. 5: Принципиальная схема анализатора OSA-710, тестовая платформа MTS/T-BERD-8000 с анализатором OSA-710
Результаты измерений
Далее приведены результаты измерений, выполненных прибором Viavi Pol-Mux OSA-710: внутриполосное оптическое отношение сигнал/шум OSNR было определено в работающих системах, передающих 100- и 200-гигабитные когерентные сигналы. Для сравнения также было выполнено измерение OSNR с отключением канала – применялся метод On/Off.
На рис. 6 показано соотношение между внутриполосными значениями OSNR (шкала OSNRC), определенными по методу SCorM, разработанному компанией Viavi, и используемыми для сопоставления измерениями OSNR по методу On/Off (шкала OSNROn/Off). Измерения проводились в оптическом сегменте длиной 400 км, по которому передавался 100-гигабитный сигнал с символьной скоростью 28 ГБод (использовалось поляризационное мультиплексирование, квадратурная фазовая манипуляция PM-QPSK).
Рис. 6: Сопоставление результатов определения OSNR разными методами в 100-гигабитной системе
Анализ показывает, что полученные по разным методикам значения отличаются не более чем на ±1 дБ – столь высокая воспроизводимость результатов обеспечена в диапазоне измерения OSNR между 10 и 22 дБ.
Методика SCorM, разработанная компанией Viavi, может применяться также для найквистовских импульсов – измерения обеспечивают получение корректных результатов.
На рис. 7 показано сопоставление результатов измерения OSNR, полученных в 200-гигабитной системе с передачей сигналов по Найквисту, квадратурная амплитудная модуляция 16 QAM (шкала OSNRC), и значений OSNR, определенных по методу On/Off (шкала OSNROn/Off).
Рис. 7: Сопоставление результатов измерения OSNR разными методами при использовании найквистовских импульсов
Заключение
Оптическое отношение сигнал/шум OSNR по-прежнему остается основным параметром, характеризующим качество передачи модулированных оптических сигналов.
В этой статье компания Viavi показала, что обычно используемые методики измерения OSNR нельзя применять в высокоскоростных когерентных системах, основанных на сетевой топологии ROADM. Разработанный компанией Viavi прибор Pol-Mux OSA-710 – первый оптический анализатор спектра, основанный на новейшей методике определения спектральной корреляции и ее применении для получения внутриполосного значения OSNR. Новая методика позволяет оценивать хроматическую дисперсию для каждого канала при передаче когерентных сигналов со скоростями 40, 100, 200 и 400 Гбит/с в сетях, использующих мультиплексирование Pol-Mux, причем измерения производятся в работающих системах, без отключения. Разработанный метод может применяться независимо от вида модуляции и скорости передачи данных. На его использование не влияют значительные искажения сигналов из-за хроматической и поляризационной модовой дисперсии, ему не препятствует спектральная фильтрация, выполняемая мультиплексорами ROADM.
Метод SCorM, предложенный компанией Viavi, представляет собой первый и единственный на сегодня способ измерения внутриполосного значения OSNR в работающих когерентных системах с поляризационным мультиплексированием Pol-Mux.
Оптический анализатор спектра Viavi Pol-Mux OSA-710 существенно упростит выполнение измерений в оптических системах при их монтаже, вводе в эксплуатацию и обслуживании, позволит свести к минимуму периоды простоя и количество человеко-часов, затрачиваемых на устранение неисправностей.
Видео
Приборы и инструменты для работы с ВОЛС
Материал подготовлен
техническими специалистами компании “СвязКомплект”.
Подпишитесь на рассылку новых материалов!
Имя
E-mail *
Согласие на отправку персональных данных *
* — Обязательное для заполнения
См.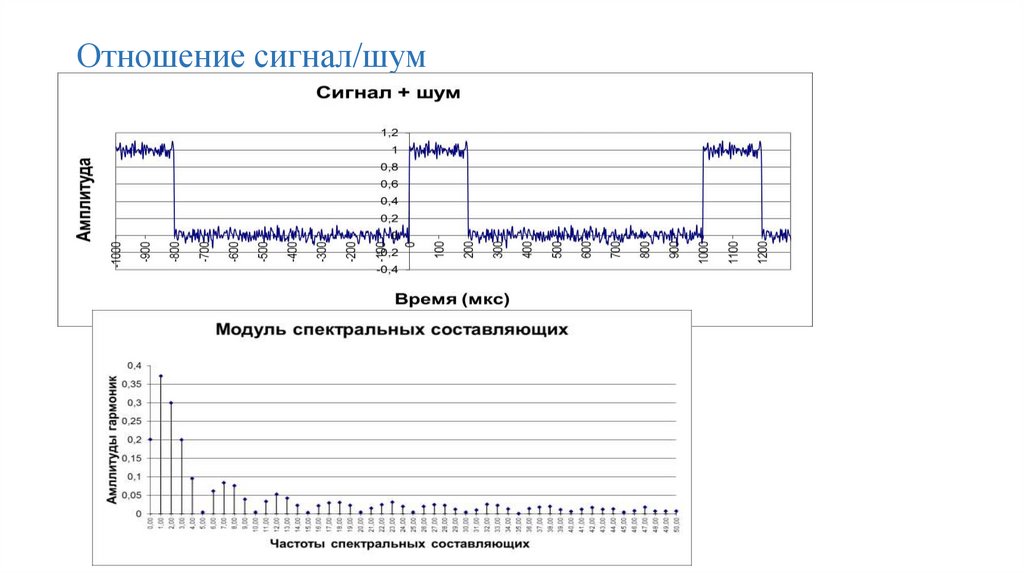
также:
Duke University Press — Signal and Noise
« Signal and Noise — увлекательная работа, которая должна вызвать значительный интерес у ученых, занимающихся исследованиями африканской культуры, городской истории и медиа». — Брайан Хохман, Каллалу
« Сигнал и шум прочно укоренился в поджанре современной антропологии, занимающемся отношениями между медиа и религиозными и культурными образами, и известен своими теоретическими интересами. Отличие книги в этом отношении заключается в том, что в ней инфраструктурные технологии выдвигаются на первый план как составляющие повседневной жизни в Кано, как в колониальном контексте, так и в эпоху транснационализации медиа». — Акинвуми Адесокан, 9 лет0003 Исследования в области африканской литературы
«[A] увлекательная историческая этнография». — Обзор ISIM
«Работа Брайана Ларкина « Сигнал и шум » знаменует собой важное вмешательство в область исследований кино и медиа, поскольку в ней делается акцент на давнем акценте на единстве кинематографической артикуляции и произношения в пользу изучения влияния кино на инфраструктуру и восприятие в четко определенный культурный контекст.
. . . Это важная книга, которая бросает вызов прежним представлениям читателей об отношениях между кино и СМИ и глубоко погружается в контекст нигерийской истории и городской культуры». — Питер Дж. Блум, 9 лет.0003 Киножурнал
«Ларкин демонстрирует устрашающую эрудицию и применяет эти знания в серии часто очень стимулированных теоретических междометий». — Чарльз Эмблер, Journal of African History
«Эта книга дает редкую информацию о внедрении многих технологий, включая радио и кино, в Африку в колониальный период». — Маргарет Кэссиди, Media International Australia
«Это редкая книга. Наполненный анекдотами Ларкина и наблюдениями Кано и написанный ясно, его академические инновации и аргументы легко усваиваются. И картинки! Почти каждая глава снабжена визуальным сопровождением из коллекции Ларкина постеров к нигерийским фильмам, радиорекламы и фотографий с мест. Любой, кто интересуется средствами массовой информации, нигерийским кино и видео, историей и судьбой постколонии или неформальной, но глобальной экономикой современной городской жизни, оценит идеи Ларкина».
— Закари Хукер, 9 лет.0003 Бидун
«Впечатляющее исследование. . . . Исследование открывает дверь в более широкий анализ того, как различные части городского общества, начиная с колониальных времен и до самого недавнего времени, договариваются о технических и экономических изменениях, создают смысл, развивают способы выживания и сопротивления, а также местные культурные стили. простая адаптация к новым технологическим проектам». — Тило Грец, Социальная антропология
«Настоящая интеллектуальная демонстрация силы, сигнал и шум должны оказать большое влияние на то, как мы понимаем Африку в современный период».
— Кеннет В. Харроу, Обзор африканских исследований
«Ларкин разработал обширное исследование медиакультур в Нигерии. Обладая языковыми навыками и тонким пониманием местных мусульманских религиозных обычаев и традиций, Ларкин предлагает яркий рассказ о появлении современной нигерийской медиа-инфраструктуры. . . . Сигнал и шум вдохновляет на новые взгляды на то, что такое медиатехнологии, как они по-разному появлялись в разных частях мира и как местные и национальные нигерийские деятели боролись с силами глобальной медиаэкономики».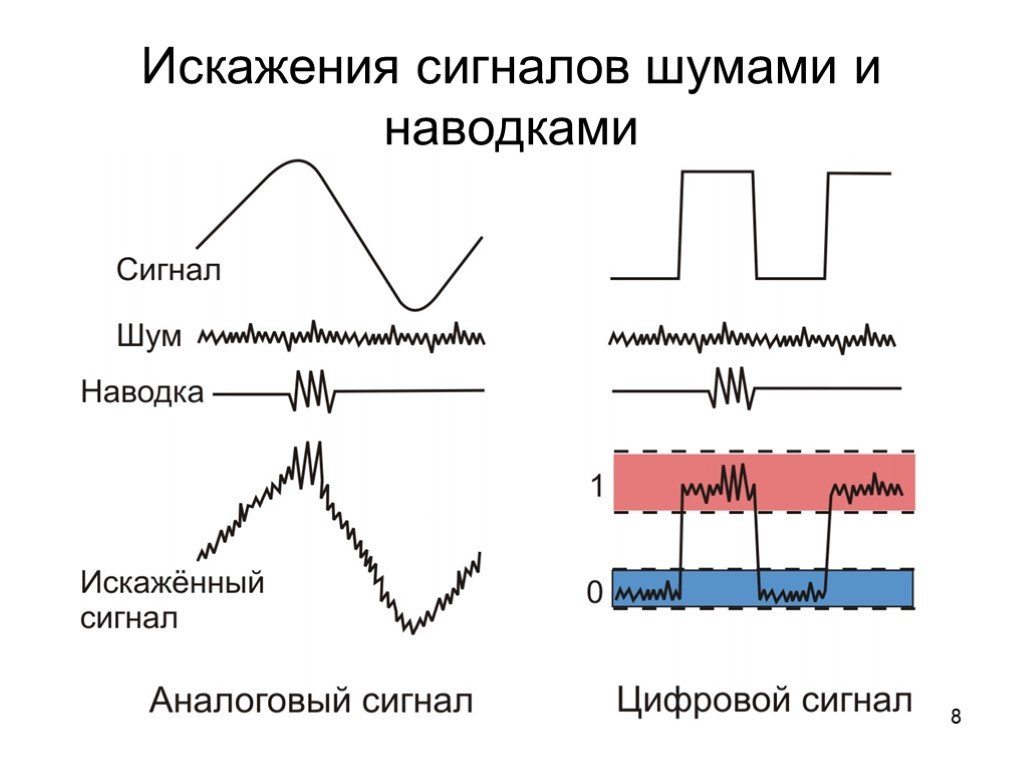
— Лиза Паркс, 9 лет0003 Киножурнал
«Работа Ларкина впечатляет своей теоретической и аналитической глубиной, богатыми эмпирическими деталями, а также проницательными наблюдениями и резюме о кино и современности в городской Нигерии. Эта работа является в такой же степени коммуникативным проектом развития, как и антропологическим исследованием или проектом киноисследований. . . . [Эта] книга является отличным чтением для студентов и ученых по ряду дисциплин и поддисциплин, включая международное общение и общение в целях развития». — Суджата Сосале, 9 лет.0003 Global Media Journal
«Эта проницательная, очень вдохновляющая и хорошо написанная книга исследует, как медиатехнологии вошли в общество северной Нигерии в 20-м веке, и как их первоначальная связь с колониальным правлением, а также их материальные качества и культурные возможности, которые они открыли, изменили общественные и социальные жизнь порой неожиданным образом. . . . [A] Высокоинновационное исследование колониальной и постколониальной городской культуры в Африке.
Это также делает его весьма желанным вкладом в исследования современности и постколониальности, в области средств массовой информации и общественной культуры, а также в анализ глобальных форм и потребления средств массовой информации. Он очарует широкий круг читателей, предоставив стимулирующие аналитические выводы о месте СМИ в городской жизни». — Доротея Э. Шульц, 9 лет.0003 Американский этнолог
«Эта долгожданная книга является прекрасным вкладом в несколько областей: медиа-исследования, культурологические исследования, африканистика, антропология и анализ глобализации. Брайан Ларкин пишет красноречиво и страстно, и он заставляет нас переосмыслить наши представления о работе транснациональных медиа и формировании идентичности». — Пурнима Манкекар, автор книги Screening Culture, Viewing Politics
«Эта вдумчивая, научная и оригинальная книга связывает транснациональный трафик медиаформ с логикой колониального государства и уязвимостью крупных городов Африки.
Это спровоцирует новое мышление среди африканистов, урбанистов, антропологов и всех, кто изучает глобализирующиеся медиапроцессы. Брайан Ларкин — крупный новый голос в изучении медиа как живой инфраструктуры в мире неравномерной связи».
— Арджун Аппадураи, автор книги «Страх перед малыми числами: очерк географии гнева»
Снижение уровня шума на практике
Сигнальный шум в промышленной среде может вызвать сбои в работе систем управления технологическими процессами. Этот электрический шум может внедряться в аналоговые или цифровые сигналы и обманывать управляющее оборудование, заставляя думать, что переменная процесса отличается от того, чем она является на самом деле. Это недопонимание между оборудованием управления технологическим процессом, как и все виды недопонимания, может привести к любому количеству непредвиденных, непредвиденных последствий. Как скажет вам любой инженер-электрик, ни одна система не может продолжать нормально функционировать без надлежащей связи.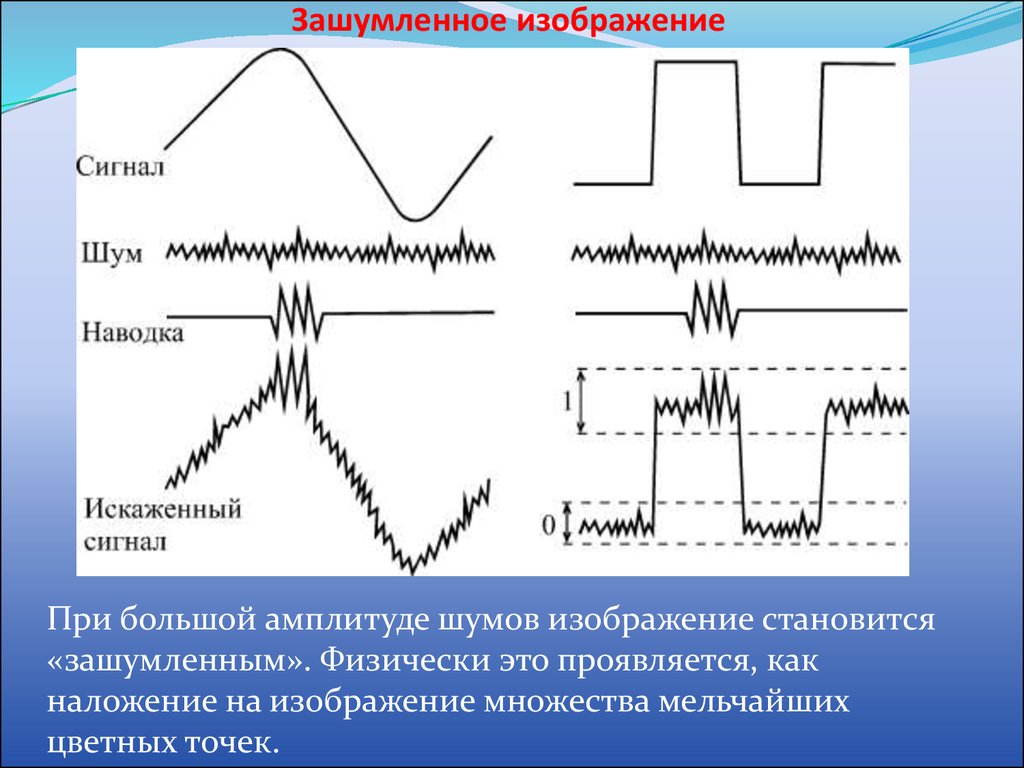
Ни одно промышленное предприятие не может быть на 100 % свободным от электрических помех. Низкий уровень шума, присутствующий на большинстве заводов, как правило, недостаточен, чтобы вызвать проблему. Когда отношение сигнал/шум становится неуправляемым, это становится проблемой. Имеются аппаратные и программные решения, помогающие бороться с сигнальным шумом в особо шумных средах, включая настройки шумовых фильтров, которые могут быть
доступны в уже установленном, но недостаточно используемом оборудовании. Покупка дорогого нового оборудования для фильтрации шума или изоляции сигналов в большинстве случаев не требуется, если в первую очередь соблюдаются надлежащие методы планирования и установки. Знание того, что такое сигнальный шум, что его вызывает и как предотвратить его влияние на сигнальные сети, должно предоставить правильный арсенал инструментов, необходимых для поддержания связи.
Шум сигнала, в самом общем смысле, — это любые нежелательные помехи, ухудшающие сигнал связи.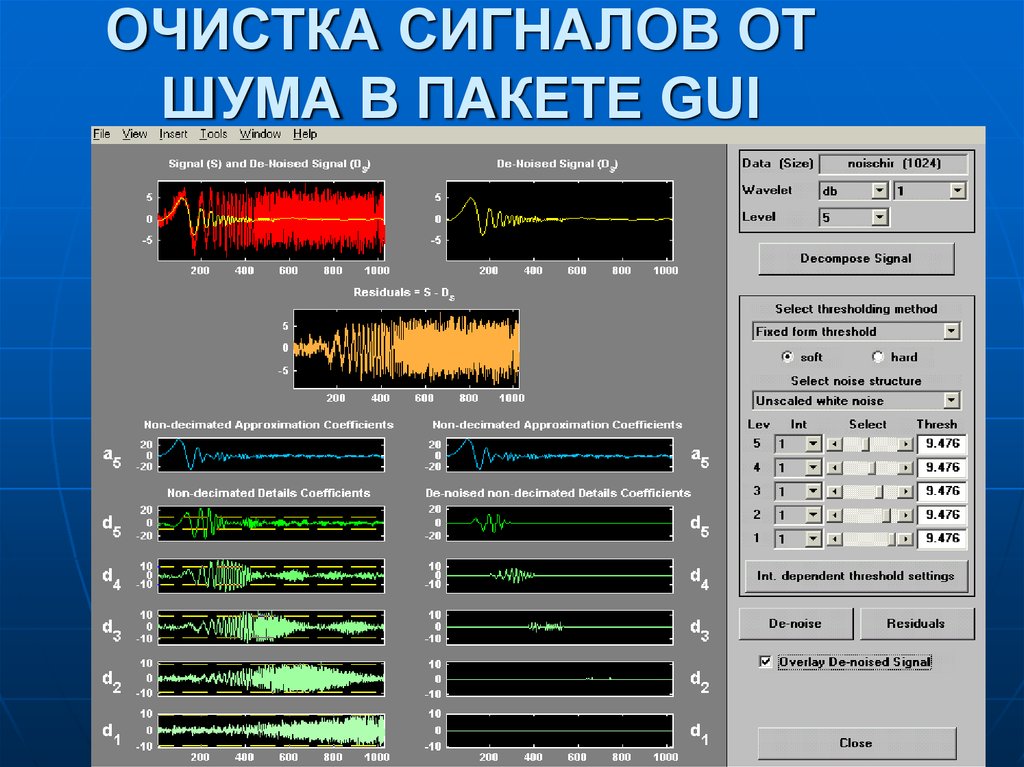
Шум сигнала может мешать как аналоговым, так и цифровым сигналам; однако количество шума, необходимого для воздействия на цифровой сигнал, намного выше. Это связано с тем, что цифровые сигналы передаются с использованием набора дискретных электрических импульсов для передачи цифровых «битов». Как видно на рисунке 1, эти электрические импульсы требуют большого количества шума, чтобы их можно было спутать друг с другом.
И наоборот, аналоговые сигналы представляют бесконечный диапазон возможных значений с использованием установленного диапазона, например, 4-20 мА или 0-10 В. В этом случае любые нежелательные скачки напряжения или тока вызовут колебания в передаваемом сообщении. Незначительные вариации аналоговых сигналов, порядка милливольт или микроампер, обычно не приводят к значительному (или даже заметному) расхождению. Однако высокие уровни электрических помех могут привести к большим колебаниям и, следовательно, к существенным расхождениям, делающим связь между устройствами управления технологическим процессом совершенно невозможной.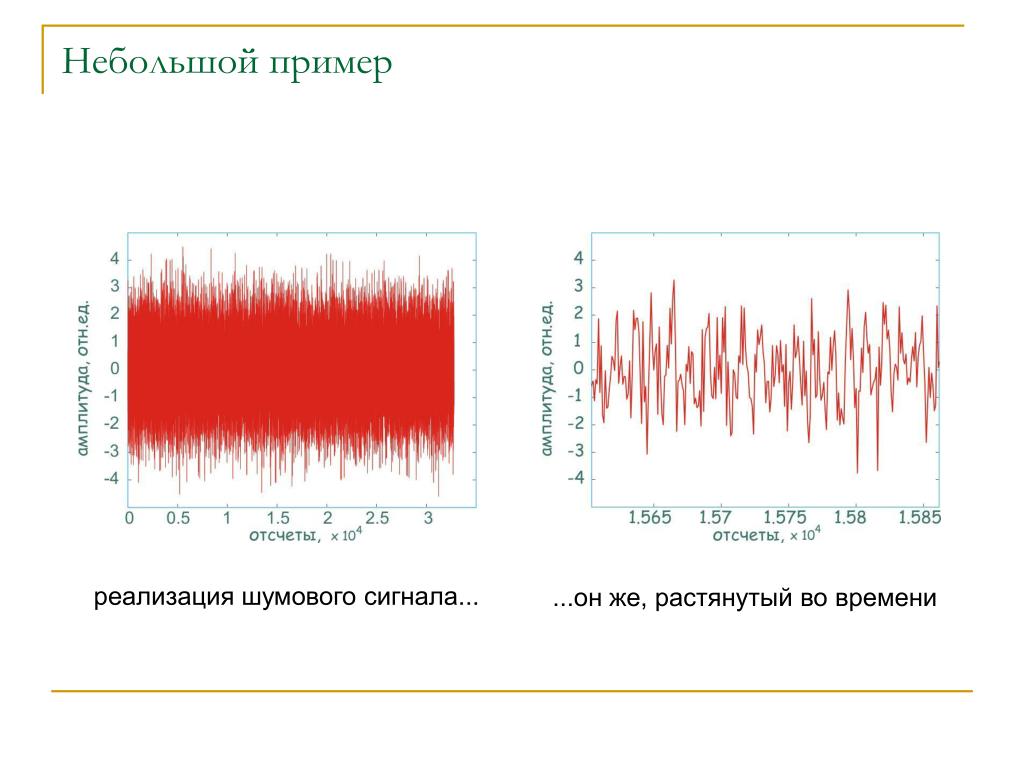
Как видно на рис. 2, сигнальный шум, введенный в электрическую связь, увеличивает или уменьшает ожидаемое значение сигнала. В производственной ситуации, когда жизненно важные процессы автоматически контролируются на основе измерения этого сигнала, любое изменение может привести к непредсказуемым и потенциально опасным результатам.
Шумовая инъекция может происходить в любом месте системы и в любом физическом месте, где сеть подвергается воздействию. Это может быть результатом действия различных факторов в любом месте сети. Устранение шумов сигнала может показаться сложной задачей; тем не менее, есть некоторые причины, которые встречаются чаще, чем другие. Эти распространенные причины составляют подавляющее большинство шумов сигналов, мешающих работе сетей управления технологическими процессами.
КОНТУРЫ ЗАЗЕМЛЕНИЯ И НЕПРАВИЛЬНОЕ ЗАЗЕМЛЕНИЕ
Как обсуждалось в предыдущем выпуске The Current Quandary, контуры заземления вводят дополнительный ток в сигнальный контур из-за перепада напряжения между двумя точками заземления в системе с несколькими заземлениями.
Эта и другие проблемы с заземлением могут привести к притоку сигнального шума в функционирующую в остальном сеть.
НЕПРАВИЛЬНАЯ ПРОВОДКА
Плохо проложенные сети, например, не использующие экранированную витую пару и кабелепровод, более восприимчивы к окружающим электрическим помехам.
ПЛОХАЯ КОНСТРУКЦИЯ ЦЕПИ ИЗДЕЛИЯ
Плохо спроектированная электронная схема в устройствах, которая не обеспечивает надлежащей защиты от внутренних и внешних источников шума, также с большей вероятностью будет иметь проблемы с сигналом.
БЛИЖАЙШАЯ БЛИЗОСТЬ К ДРУГОМУ ЭЛЕКТРИЧЕСКОМУ ОБОРУДОВАНИЮ
Устройства или провода, расположенные в непосредственной близости от электрического оборудования, генерирующего сильные магнитные поля, такого как генераторы, двигатели или линии электропередач, могут улавливать некоторые из этих помех, что может способствовать колебаниям в сигналах связи
ДЛИННЫЕ ПРОВОДА, ПОДНИМАЮЩИЕ РАДИОЧАСТОТЫ
Длинные отрезки провода (особенно неэкранированного провода) в основном действуют как антенны; они улавливают радиоволны и преобразуют их в электрические сигналы, создавая дополнительный шум в системе.
ИСКАЖЕНИЕ СИГНАЛА ПРОЦЕССА
Наиболее распространенной и очевидной проблемой, вызванной шумом сигнала, является искажение сигнала процесса, вызывающее неправильную интерпретацию или отображение состояния процесса оборудованием. Добавление и/или вычитание из сигнала процесса преобразуется в неправильную переменную процесса. Чтобы представить это в контексте, см. пример на рис. 3 ниже.
ПОЯВЛЯЕМАЯ ПОТЕРЯ СИГНАЛА
Хотя и редко, сильный шум сигнала может привести к явной потере сигнала. Большинство современных электронных устройств имеют встроенную фильтрацию шума. Однако в очень шумных условиях этого фильтра будет недостаточно, что может привести к тому, что оборудование не будет принимать сигнал и вообще не будет осуществляться связь.
НЕПРАВИЛЬНОЕ УПРАВЛЕНИЕ ПРОЦЕССОМ
В примере, показанном на рисунке 3, каждое устройство в сети работает точно так, как задумано; однако шум сигнала вызвал недопонимание между устройствами.
Следовательно, бак остался пустым. Система, испытывающая флуктуации шумового сигнала, может непреднамеренно включать и выключать реле и аварийные сигналы через нерегулярные промежутки времени, потому что шумовые сигналы неправильно интерпретируются. Подобная ситуация приводит к неправильному управлению производственным процессом.
ПРИМЕНЕНИЕ
Радарный уровнемер измеряет уровень жидкости в баке. Он выводит сигнал 4-20 мА (4 мА при пустом баке и 20 мА при полном) на механическое реле, которое при срабатывании 4,5 мА активирует насос, чтобы начать заполнение бака.
ПРОБЛЕМА
Резервуар опорожняется, и трансмиттер выдает сигнал 4 мА, но из-за сильного шума реле получает сигнал 5 мА и никогда не запускает и не активирует насос. Резервуар остается пустым, и процесс останавливается.
Как и в случае всех проблем с подключением к системе управления производственным процессом, гораздо проще следовать некоторым простым рекомендациям при планировании, проектировании и установке устройств управления технологическим процессом, чем пытаться устранять проблемы с системой после того, как она введена в эксплуатацию.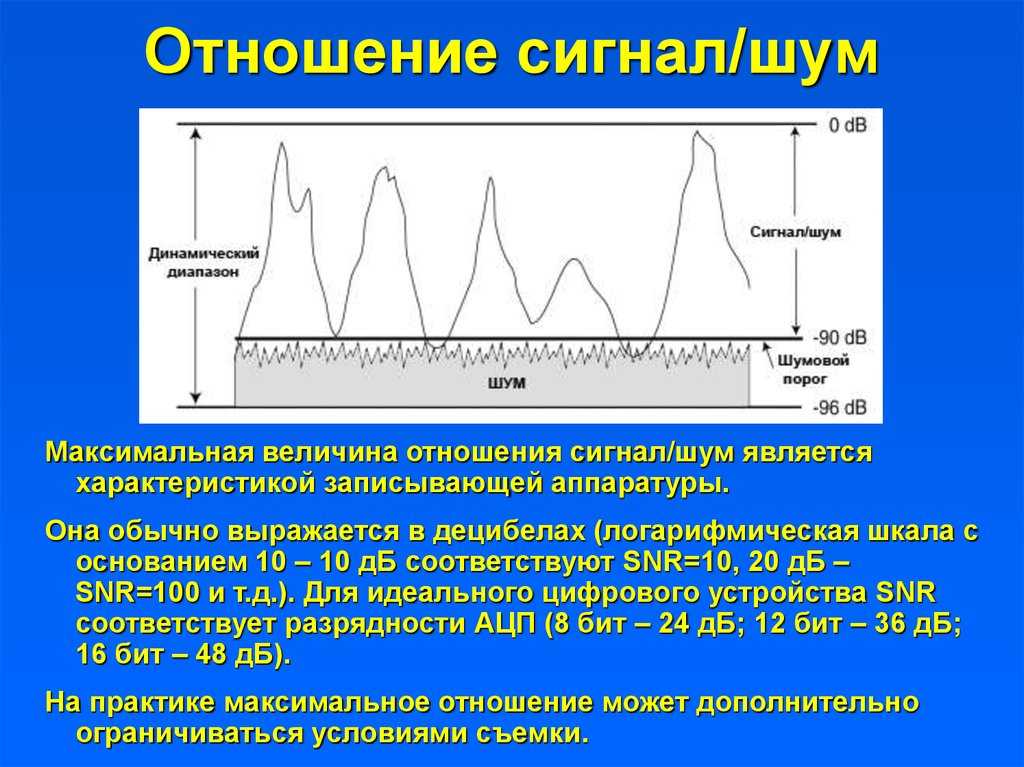
Успешное планирование может сэкономить сотни человеко-часов и неисчислимое разочарование, когда речь идет о предотвращении помех от сигнального шума в системе.
Когда речь идет о предотвращении шума сигнала, чем слабее сигнал, тем больше он подвержен шуму. Сигналы низкого уровня, такие как импульсный сигнал расходомера с магнитным датчиком или милливольтовый выход термопары, очень чувствительны к окружающему шуму. Любое количество шума, введенного в эти типы систем, обязательно окажет некоторое влияние на передаваемый сигнал.
Хотя может возникнуть соблазн просто удлинить провода от этих устройств, чтобы подключить их к устройствам отображения или управления, настоятельно рекомендуется использовать передатчик или кондиционер для усиления сигнала перед его передачей по проводу любой длины. Этот усиленный сигнал сможет выдержать большее количество шума, прежде чем его предполагаемое значение начнет искажаться. Однако более эффективным способом избежать шума является преобразование аналогового сигнала в цифровой вместо его усиления.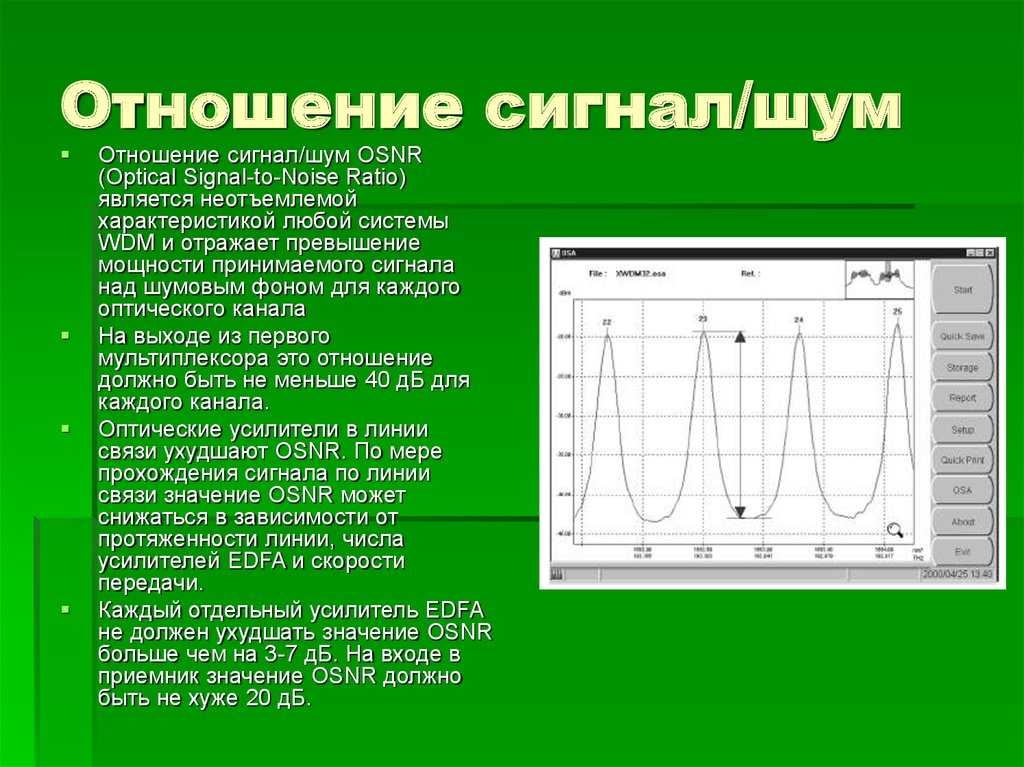
Как показано на рисунке 4, цифровые сигналы с их набором дискретных битов гораздо более устойчивы к шуму, чем аналоговые.
Если систему необходимо установить в зоне, подверженной воздействию электрических помех, установщик должен предусмотреть использование программных или аппаратных фильтров помех, которые часто входят в состав современных устройств управления технологическими процессами. Обратитесь к инструкции по эксплуатации устройства
, чтобы убедиться в наличии шумоподавляющих фильтров. Глубокое понимание среды установки и устройств может сэкономить время и нервы.
Как говорится, ни один план не выдерживает первого контакта с противником. Тем не менее, установщики должны следить за тем, чтобы непредвиденные ограничения окружающей среды или устройства не мешали процессу установки и не создавали проблем с устранением неполадок в будущем. Использование ярлыков для преодоления проблем с установкой может быть заманчивым в краткосрочной перспективе, но в будущем это решение будет стоить дорого.
Монтажники всегда должны использовать экранированную витую пару для соединения компонентов системы. Синфазный шум, или шум, общий для двух проводов витой пары, легче отфильтровать, чем шум, присутствующий только в одном проводе. Кроме того, хотя может показаться удобным прокладывать сигнальные линии через тот же кабелепровод, что и линии электропередач, этого всегда следует избегать. Шум от этих линий 120 или 240 В может легко попасть на сигнальные линии.
Провода также следует держать подальше от любого оборудования, создающего магнитные поля, такого как двигатели, трансформаторы или большие реле с индуктивными нагрузками. Провода, соединяющие разные цепи, должны быть установлены перпендикулярно друг другу, так как параллельные линии с большей вероятностью будут обмениваться помехами. Провода также должны быть как можно короче, чтобы они не действовали как антенны.
Проводка всегда должна прокладываться так, чтобы не было контуров заземления. Для этого используется только одна точка заземления для всех устройств, присутствующих в сети.
Если несколько устройств в сети требуют заземления, убедитесь, что один и тот же источник заземления подключен по всей системе к экранированному кабелю.
Помня об этих простых рекомендациях на протяжении всего процесса установки, вы сможете убедиться, что ваша реализация учитывает шум сигнала так же, как и на первоначальных этапах планирования. Если бы установщик установки, показанной на рис. 3, следовал рекомендациям во время планирования и установки, он бы знал, что линии электропередачи переменного тока всегда следует изолировать от сигнальных линий 4–20 мА, прокладывая их вдоль экранированных кабелей внутри независимого кабелепровода.
Шум сигнала — это проблема, с которой сталкиваются все промышленные предприятия из-за работающего электрического оборудования. Шум сигнала становится проблемой для этих объектов, когда он мешает сигналам процесса, передаваемым между устройствами. Это может привести к неточной передаче данных о критических переменных процесса, что может помешать работе систем управления технологическим процессом или даже привести к его остановке.
