Перевод из шестнадцатеричной в десятичную систему счисления, калькулятор

Исходное число

Направление перевода

2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Сообщить об ошибке

В избранное

Виджет

Вы можете сохранять ваши расчеты и они будут отображаться здесь.

Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.

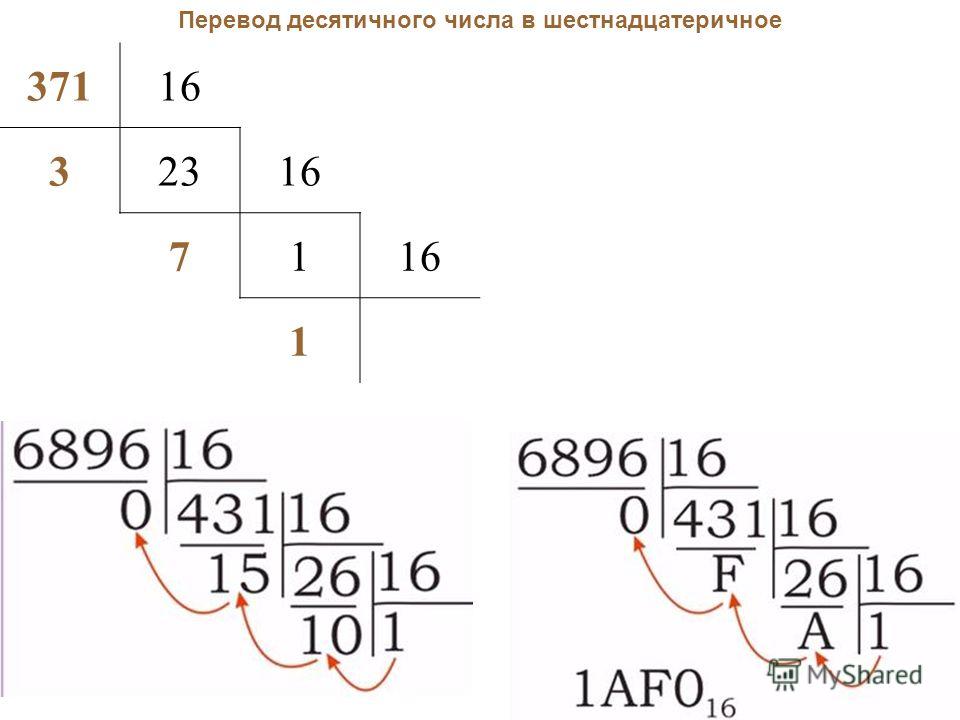
Преобразовать число из шестнадцатеричной системы счисления в десятичную можно следующим образом:

Каждый разряд числа необходимо умножить на 16ⁿ, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.

abc₂ = (a×16² + b×16¹ + c×16⁰)₁₀

5A₁₆ = (5*16

1 + 10*8⁰)₁₀ = 90₁₀

Смотрите также

• Перевод из двоичной в десятичную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в восьмеричную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в двоичную
• Перевод из восьмеричной в десятичную
• Перевод из шестнадцатеричной в двоичную

Сложение двоичных чисел онлайн

Назначение сервиса. Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.

• Решение онлайн
• Видеоинструкция
• Также решают

Число №1

Число №2

Числа представлены в 102 системе счисления.
Операция с числами СложениеВычитание Для дробных чисел использовать 2345678 знака после запятой.
Действие производить в: Прямом кодеОбратном кодеДополнительном кодеПодробнее.

Вместе с этим калькулятором также используют следующие:

Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления

Умножение двоичных чисел

Формат представления чисел с плавающей запятой

Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*10² = 1.3354*exp₁₀²
Число 1.3354*exp₁₀² состоит из двух частей: мантиссы M=1.3354 и экспоненты exp₁₀=2
Если мантисса находится в диапазоне 1 ≤ M Представление числа в денормализованном экспоненциальном виде

.
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp₁₀³

Пример №2. Представить двоичное число 101.10₂ в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности

Вычисление пределов

Арифметика в двоичной системе счисления

Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы.

В таблице представлены правила сложения и вычитания в двоичной системе счисления.

1. При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.
2. При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1. Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.

Сложение 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10

Вычитание 0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1

Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:

• преобразование исходных чисел в указанный код;
• поразрядное сложение кодов;
• анализ полученного результата.

При выполнении операции в обратном (модифицированном обратном) коде если в результате сложения в знаковом разряде возникает единица переноса, она прибавляется к младшему разряду суммы.
При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.

Пример №1.
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.

Дано: х=0,101001; y= -0,001101, сложить в дополнительном модифицированном коде.

Пример №2. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 — 10.
Решение.
Представим числа 11₂ и -10₂ в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000011 имеет обратный код 0,0000011
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000011 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.

7	6	5	4	3	2	1	0
						1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
							0

В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.

7	6	5	4	3	2	1	0
					1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
						0	0

В 2-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 3-й разряд.

7	6	5	4	3	2	1	0
				1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
					0	0	0

В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.

7	6	5	4	3	2	1	0
			1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
				0	0	0	0

В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.

7	6	5	4	3	2	1	0
		1	1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
			0	0	0	0	0

В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.

7	6	5	4	3	2	1	0
	1	1	1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
		0	0	0	0	0	0

В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
	0	0	0	0	0	0	0

В 7-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 8-й разряд.

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
0	0	0	0	0	0	0	0

В итоге получаем:

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	0	1	1
1	1	1	1	1	1	0	1
0	0	0	0	0	0	0	0

Возник перенос из знакового разряда. Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:

7	6	5	4	3	2	1	0
0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	1
0	0	0	0	0	0	0	1

Результат сложения: 00000001. Переведем в десятичное представление. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*0 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1

б) 111-010 Представим числа 111₂ и -010₂ в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.

7	6	5	4	3	2	1	0
						1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
							0

В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.

7	6	5	4	3	2	1	0
					1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
						0	0

В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.

7	6	5	4	3	2	1	0
				1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
					1	0	0

В 3-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 4-й разряд.

7	6	5	4	3	2	1	0
			1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
				0	1	0	0

В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.

7	6	5	4	3	2	1	0
		1	1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
			0	0	1	0	0

В 5-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 6-й разряд.

7	6	5	4	3	2	1	0
	1	1	1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
		0	0	0	1	0	0

В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
	0	0	0	0	1	0	0

В 7-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 8-й разряд.

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
0	0	0	0	0	1	0	0

В итоге получаем:

7	6	5	4	3	2	1	0
1	1	1	1	1	1	1
0	0	0	0	0	1	1	1
1	1	1	1	1	1	0	1
0	0	0	0	0	1	0	0

Возник перенос из знакового разряда. Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:

7	6	5	4	3	2	1	0
0	0	0	0	0	1	0	0
0	0	0	0	0	0	0	1
0	0	0	0	0	1	0	1

Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5

Сложение двоичных вещественных чисел с плавающей запятой

В компьютере любое число может быть представлено в формате с плавающей точкой. Формат с плавающей точкой показан на рисунке: Например, число 10101 в формате с плавающей точкой можно записать так: В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
b-1≤|M|<b0=1
Нормализованное число — это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2¹⁰⁰=0,101*2¹⁰
111,1001*2¹⁰=0,111001*2¹⁰¹
0,01101*2^-11=0,1101*2^-100
11,1011*2^-101=0,11011*2^-11

При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:

Алгоритм сложения чисел с плавающей точкой:

1. Выравнивание порядков;
2. Сложение мантисс в дополнительном модифицированном коде;
3. Нормализация результата.

Пример №4.
A=0,1011*2¹⁰, B=0,0001*2¹¹
1. Выравнивание порядков;
A=0,01011*2¹¹, B=0,0001*2¹¹
2. Сложение мантисс в дополнительном модифицированном коде;
MA_{доп.мод.}=00,01011
MB_{доп.мод.}=00,0001
   00,01011
+ 00,00010
=
   00,01101
A+B=0,01101*2¹¹
3. Нормализация результата.
A+B=0,1101*2¹⁰

Пример №3. Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.

Hex to Decimal (таблица, формула и преобразование)

Система счисления является важным понятием в математике, поскольку она используется для представления чисел и их классификации на основе их основных чисел. Существуют различные типы систем счисления, а именно двоичная, восьмеричная, десятичная, шестнадцатеричная и так далее. Мы можем легко преобразовать одну базовую систему в другую, используя определенные правила преобразования. В этой статье вы узнаете о шестнадцатеричной и десятичной системах, преобразовании из шестнадцатеричной в десятичную, таблице, процедуре преобразования вместе с примерами.

Содержание:

• Шестнадцатеричная система счисления
• Десятичная система счисления
• Преобразование шестнадцатеричных чисел в десятичные
• Преобразователь
• Стол
• Примеры
• Часто задаваемые вопросы

Шестнадцатеричная система счисления

Основание шестнадцатеричной системы равно 16. 16 символов, задействованных в этой системе, включают 10 десятичных цифр и первые шесть букв английского алфавита, т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Здесь можно рассматривать алфавиты 10, 11, 12, 13, 14 и 15 соответственно. Узнайте больше о шестнадцатеричной системе здесь.

Десятичная система счисления

Система счисления, в которой цифры от 0 до 9 используются для представления числа с основанием 10, называется десятичной системой счисления. Число выражается в базе 10, где каждое значение обозначается 0 или первыми девятью положительными целыми числами. Каждое значение в этой системе счисления имеет разрядное значение степени 10. Это означает, что цифра в разряде десятков в десять раз больше, чем цифра в разряде единиц.

Преобразование шестнадцатеричного формата в десятичный

Как известно, системы счисления можно переводить из одной системы счисления в другую. Таким образом, мы можем легко преобразовать шестнадцатеричные числа в десятичные. Это преобразование системы счисления можно выполнить, как показано в примере, приведенном ниже:

.

Пример:

Преобразовать 7CF (шестнадцатеричный) в десятичный.

Решение:

Задано шестнадцатеричное число 7CF.

В шестнадцатеричной системе,

7 = 7

С = 12

Ф = 15

Чтобы преобразовать это в десятичную систему счисления, умножьте каждую цифру на степени 16, начиная с разряда единиц числа.

7CF = (7 × 16 ² ) + (12 × 16 ¹ ) + (15 × 16 ⁰ )

= (7 × 256) + (12 × 16) + (15 × 1)

= 1792 + 192 + 15

= 1999

Отсюда можно определить правило преобразования шестнадцатеричных чисел в десятичные числа.

Предположим, ниже представлено шестнадцатеричное число из n цифр:

d _n-1 … d ₃ d ₂ d ₁ d ₀

Умножьте каждую цифру шестнадцатеричного числа на соответствующие степени 16 и сложите их, например:

D _N-1 × 16 ^N-1 +… + D ₃ × 16 ³ + D ₂ × 16 ² + D ₁ × 16 ¹ + D _0. × 16 ⁰

Таким образом, полученное число будет принято по основанию 10 или десятичной системе счисления.

D N-1 … D 3 D 2 D 1 D 0 (HEX) = D N-1 × 16 N-1 + +… D. 3 × 16 3 + д 2 × 16 2 + д 1 × 16 1 + д 0 × 16 90 6

Преобразователь шестнадцатеричных чисел в десятичные

Доступен инструмент для преобразования чисел из шестнадцатеричной в десятичную систему счисления.

Щелкните здесь для быстрого преобразования шестнадцатеричной системы счисления в десятичную.

Таблица преобразования шестнадцатеричных чисел в десятичную

Ниже приведена таблица преобразования чисел из шестнадцатеричных в десятичные:

Шестнадцатеричный	Десятичный (эквивалентное значение)
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
А	10
Б	11
С	12
Д	13
Е	14
Ф	15

Эта таблица поможет представить цифры и буквы по отдельности в больших числах в системе с основанием 16, как описано выше.

Кроме того, узнайте здесь о преобразовании десятичных чисел в шестнадцатеричные.

Решенные примеры

Рассмотрим примеры преобразования чисел из шестнадцатеричной системы счисления (по основанию 16) в систему счисления с основанием 10 с подробными пояснениями.

Пример 1:

Преобразование (1DA6) ₁₆ в десятичное число.

Решение:

(1DA6) ₁₆

Здесь,

1 = 1

Д = 13

А = 10

6 = 6

Таким образом,

(1DA6) ₁₆ = (1 × 16 ³ ) + (13 × 16 ² ) + (10 × 16 ¹ ) + (6 × 16 ⁰ )

= (1 × 4096) + (13 × 256) + (10 × 16) + (6 × 1)

= 4096 + 3328 + 160 + 6

= 7590

Следовательно, (1DA6) ₁₆ = (7590) ₁₀

Пример 2:

Преобразовать (E8B) ₁₆ в десятичную систему.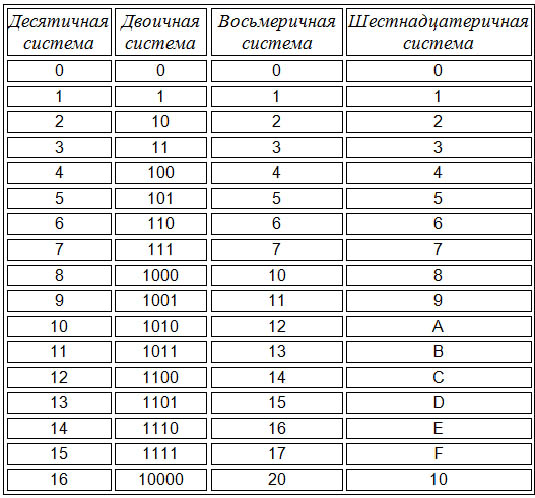

Решение:

(Е8В) ₁₆

Здесь,

Е = 14

8 = 8

Б = 11

Таким образом,

(E8B) ₁₆ = (14 × 16 ² ) + (8 × 16 ¹ ) + (11 × 16 ⁰ )

= (14 × 256) + (8 × 16) + (11 × 1)

= 3584 + 128 + 11

= 3723

Следовательно, (E8B) ₁₆ = (3723) ₁₀

Оставайтесь с нами с BYJU’S — приложением для обучения и загрузите приложение, чтобы легко изучать все понятия, связанные с математикой, просматривая больше видео.

Часто задаваемые вопросы о шестнадцатеричной системе счисления

Что такое шестнадцатеричная система счисления?

Шестнадцатеричная система счисления использует шестнадцать цифр, например 0,1, 2, 3, 4, 5, 6, 7, 8, 9и A, B, C, D, E, F с основанием 16.

Что такое десятичная система счисления?

Десятичная система счисления использует десять цифр, например 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, с основанием 10.

Как преобразовать шестнадцатеричную систему счисления в десятичную. система?

Чтобы преобразовать шестнадцатеричную систему счисления в десятичную, выполните следующие действия:
Шаг 1: Умножьте каждую цифру на степень 16, начиная с разряда единиц числа.
Шаг 2: Упростите каждый из продуктов и добавьте их.

Преобразовать 7CA (шестнадцатеричный) в десятичный.

Мы знаем, что 7 = 7, C = 12 и A = 10.
Следовательно, (7CA) ₁₆ = (7 × 16 ² ) + (12 × 16 ¹ ) + (10 × 16 ⁰ )
(7CA) ₁₆ = (7 × 256) + (12 × 16) + (10 × 1)
(7CA) ₁₆ = 1792+192+10
(7CA) ₁₆ = (199080 ) ₁₀
Следовательно, преобразование 7CA (шестнадцатеричное число) в десятичное число равно 1994.

Преобразование 5BC (шестнадцатеричное число) в десятичное число.

Мы знаем, что 5 = 5, B = 11 и C = 12.
Следовательно (5BC) ₁₆ = (5 × 16 ² ) + (11 × 16 ¹ ) + (12 × 16 ⁰ )
(5ВС) ₁₆ = (5 × 256) + (11 × 16) + (12 × 1)
(5ВС) ₁₆ = 1280+176+12
(5ВС) _{16 9080 = (146080 ) 10
Следовательно, 5BC (hex) в десятичном виде равно 1468.}

Онлайн-конвертер шестнадцатеричных чисел в десятичные

• Инструменты
• Шестнадцатеричный в десятичный

Преобразование шестнадцатеричных данных в десятичный формат.

Настройки Номер строки Перенос строки Темный режим

Преобразование шестнадцатеричных чисел в десятичные

---

Простой в использовании интерфейс

Шестнадцатеричные числа используются во многих компьютерных приложениях, но с ними может быть сложно работать. Наш инструмент для преобразования шестнадцатеричных чисел в десятичные позволяет легко преобразовывать шестнадцатеричные числа в десятичные с лучшим удобным интерфейсом.

Мгновенно сгенерировать десятичное число

Вам нужно мгновенно сгенерировать десятичное число? Не смотрите дальше! Наш бесплатный онлайн-инструмент позволяет преобразовывать шестнадцатеричные числа в десятичные, что занимает менее минуты для преобразования числа в десятичную систему счисления.

Доступен бесплатно

Когда дело доходит до преобразования десятичных чисел в восьмеричные, нет необходимости тратить деньги на конвертер. Этот бесплатный онлайн-инструмент поможет быстро и легко выполнить работу бесплатно.

Безопасный в использовании

Если вы ищете безопасный инструмент для преобразования десятичных чисел в восьмеричные, обратите внимание на наш. Мы серьезно относимся к безопасности и внедрили новейшие меры безопасности, чтобы гарантировать безопасность использования нашего инструмента.

Часто задаваемые вопросы о конвертере шестнадцатеричных чисел в десятичные

Что такое шестнадцатеричная система счисления?

Шестнадцатеричные числа представляют собой числа, представленные с основанием 16. В отличие от нашей обычной десятичной системы, в которой используется основание 10, шестнадцатеричная система использует комбинацию чисел 0-9.и буквы AF для представления значений.

Шестнадцатеричная система часто используется в компьютерных науках, поскольку она обеспечивает более лаконичный способ представления двоичных данных. В двоичном формате каждая цифра может быть только 0 или 1, поэтому четыре двоичных цифры могут представлять 16 различных комбинаций. В шестнадцатеричном формате каждая цифра может быть одним из 16 различных значений, поэтому две шестнадцатеричные цифры могут представлять 256 различных комбинаций.

Как преобразовать шестнадцатеричные числа в десятичные?

Существует два способа преобразования шестнадцатеричного числа в десятичное:

1. Преобразование шестнадцатеричной системы счисления в десятичную вручную.
2. Использование бесплатного онлайн-инструмента для преобразования шестнадцатеричных чисел в десятичные.

Как вручную преобразовать шестнадцатеричные числа в десятичные?

Используя основание числа 16, шестнадцатеричное число можно преобразовать в десятичное. Чтобы расширить шестнадцатеричные цифры, умножьте каждую цифру на 16. С увеличением мощности мощность перемещается от 0 вправо. Для того, чтобы преобразование было завершено, умноженные числа должны быть сложены вместе.

Пример:

(25)16 = 2 × (16)1 + 5 × (16)0

= 2 × 16 + 5 × 1

= 32 + 5

= 37

Следовательно, (25 )16 = (37)10

Какова формула преобразования шестнадцатеричных чисел в десятичные?

Для преобразования шестнадцатеричных формул в десятичные выполните следующие действия:

1. Числа, которые нужно преобразовать, имеют основание 16.
2. Самая правая цифра числа должна быть умножена на 16-ю степень.