Сглаживающий фильтр: Сглаживающий фильтр — Википедия – Сглаживающие фильтры :: Электроника для всех — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Сглаживающий фильтр — Википедия

Сглаживающий фильтр — устройство для сглаживания пульсаций после выпрямления переменного тока. Простейшим сглаживающим фильтром является электролитический конденсатор большой ёмкости, включённый параллельно нагрузке. Нередко параллельно электролитическому конденсатору устанавливается плёночный (или керамический) ёмкостью в доли или единицы микрофарада для устранения высокочастотных помех.

В любой схеме выпрямления на выходе выпрямленное напряжение помимо постоянной составляющей содержит переменную, называемую пульсацией напряжения^[1]. Пульсация напряжения столь значительна, что непосредственно питание нагрузки от выпрямителя возможно относительно редко (при зарядке аккумуляторных батарей, для питания цепей сигнализации, электродвигателей и т. д.) — там, где приёмник энергии не чувствителен к переменной составляющей выпрямленного напряжения. Пульсация напряжения резко ухудшает, а чаще вообще нарушает работу радиоэлектронных устройств. Для уменьшения переменной составляющей выпрямленного напряжения, то есть для ослабления пульсации, между выпрямителем и нагрузкой устанавливается сглаживающий фильтр, который обычно состоит из реактивных сопротивлений (то есть тех, которые включают в себя индуктивность и ёмкость). Данный фильтр действует как фильтр нижних частот

[2]^[3], обрезая лишние гармоники.

Переменная составляющая выпрямленного напряжения в общем случае представляет собой совокупность ряда гармоник с различными амплитудами, сдвинутых по отношению к первой на разные углы (см. Ряд Фурье). При этом первая гармоника имеет амплитуду, во много раз превосходящую амплитуды высших гармоник. В зависимости от назначения аппаратуры предъявляют различные требования к величине и характеру пульсации выпрямленного напряжения. Чаще всего для радиотехнической аппаратуры качество сглаживания характеризуется величиной максимально допустимой амплитуды переменной составляющей. В этом случае фильтры рассчитывают на максимальное подавление основной гармоники.

[4], который зависит от частоты и величина которого определяется экспериментально с учётом микротелефона и человеческого уха.

Эффективное значение псофометрического напряжения пульсации U на выходе выпрямителя будет равно:

U=0,5[(U01m⋅a1)2+(U02m⋅a2)2+…+(U0km⋅ak)2]{\displaystyle U={\sqrt {0,5[(U_{01m}\cdot a_{1})^{2}+(U_{02m}\cdot a_{2})^{2}+…+(U_{0km}\cdot a_{k})^{2}]}}}

где

a1…,ak{\displaystyle a_{1}…,a_{k}} — псофометрические коэффициенты для соответствующих гармоник;

U1…,Uk{\displaystyle U_{1}…,U_{k}} — амплитуды соответствующих гармоник выпрямленного напряжения.

Основным параметром сглаживающих фильтров является коэффициент сглаживания, которым называется отношение коэффициента пульсации на входе (KBx){\displaystyle (K_{Bx})} к коэффициенту пульсации на выходе (KH){\displaystyle (K_{H})}, то есть на нагрузке.

KC=KBx/KHa={\displaystyle K_{C}=K_{Bx}/K_{Ha}=}(U01m/U0)/(Uh2m/UH){\displaystyle (U_{01m}/U_{0})/(U_{h2m}/U_{H})}

где U01m,Uh2m{\displaystyle U_{01m},U_{h2m}} -это амплитуды первой гармоники напряжений на входе и выходе фильтра соответственно; U0,UH{\displaystyle U_{0},U_{H}} — постоянные составляющие напряжений на входе и выходе фильтра.

Индуктивный сглаживающий фильтр[править | править код]

Индуктивный фильтр состоит из дросселя, включенного последовательно с нагрузкой. Под дросселем подразумевается обычная катушка, характеризующаяся определённой индуктивностью^[5]. Сглаживающее действие такого фильтра основано на возникновении в дросселе ЭДС самоиндукции, препятствующей изменению выпрямленного тока. Дроссель выбирается так, чтобы индуктивное сопротивление его обмотки (XL=mwcL{\displaystyle X_{L}=mw_{c}L}) было больше сопротивления нагрузки RH{\displaystyle R_{H}}. При выполнении этого условия большая часть переменной составляющей падает на обмотке дросселя. На сопротивлении нагрузки выделяется в основном постоянная составляющая выпрямленного напряжения U0{\displaystyle U_{0}} и переменная составляющая, величина которой намного меньше переменной составляющей напряжения, падающего на обмотке дросселя.

Коэффициент сглаживания такого фильтра равен KC={\displaystyle K_{C}=}(RH)2+(mwcL)2RH{\displaystyle {\sqrt {(R_{H})^{2}+(mw_{c}L)^{2}}} \over R_{H}}

где у нас

RH{\displaystyle R_{H}} — сопротивление нагрузки

L{\displaystyle L} — индуктивность обмотки дросселя

wc{\displaystyle w_{c}} — угловая частота

m{\displaystyle m} — коэффициент зависящий от схемы выпрямителя и показывающий, во сколько раз частота основной гармоники выпрямленного напряжения больше частоты тока сети.

Ёмкостной сглаживающий фильтр[править | править код]

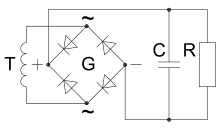Ёмкостной сглаживающий фильтр.
С — фильтрующий конденсатор, R — сопротивление нагрузки.

Ёмкостной фильтр обычно анализируют не отдельно, а совместно с выпрямителем. Его сглаживающее действие основано на накоплении электрической энергии в электрическом поле конденсатора^[6] и его разряде при отсутствии тока через выпрямитель (вентиль) в моменты времени, когда мгновенное напряжение на выходе выпрямителя ниже напряжения на конденсаторе, через сопротивление нагрузки (R){\displaystyle (R)}. Причём конденсатор подключается параллельно нагрузке.

Конденсатор имеет реактивное сопротивление:

XC=1/(ω⋅C){\displaystyle X_{C}=1/(\omega \cdot C)},

где C{\displaystyle C} — ёмкость конденсатора.

Коэффициент сглаживания такого фильтра будет следующим:

KC={\displaystyle K_{C}=}K1K2{\displaystyle K_{1} \over K_{2}}={\displaystyle =}(2m2−1{\displaystyle 2 \over m^{2}-1})/{\displaystyle /}(HrC{\displaystyle H \over rC})

где

K1{\displaystyle K_{1}} — коэффициент пульсаций на входе выпрямителя при отсутствии ёмкости

K2{\displaystyle K_{2}} — коэффициент пульсаций на выходе выпрямителя при наличии ёмкости.

При увеличении m{\displaystyle m} коэффициент сглаживания индуктивного фильтра увеличивается, а ёмкостного уменьшается. Поэтому ёмкостной фильтр выгодно применять при выпрямлении однофазных^[7], а индуктивный при выпрямлении многофазных токов.

При увеличении RH{\displaystyle R_{H}} сглаживающее действие ёмкостного фильтра увеличивается, а индуктивного уменьшается. Поэтому ёмкостной фильтр выгодно применять при малых, а индуктивный фильтр — при больших токах нагрузки.

LC-фильтр[править | править код]

Наиболее широко используют Г-образный индуктивно-ёмкостной фильтр. Для сглаживания пульсаций таким фильтром необходимо, чтобы ёмкостное сопротивление конденсатора для низшей частоты пульсации было много меньше сопротивления нагрузки, а также много меньше индуктивного сопротивления дросселя для первой гармоники.

При выполнении этих условий, пренебрегая активным сопротивлением дросселя, коэффициент сглаживания такого Г-образного фильтра будет равен

Kc=m2ωc2LC−1.{\displaystyle K_{c}=m^{2}\omega _{c}^{2}LC-1.}

Так как 1/LC=ω0{\displaystyle 1/{\sqrt {LC}}=\omega _{0}} — собственная частота фильтра, то

Kc=(mωc/ω0)2−1.{\displaystyle K_{c}=(m\omega _{c}/\omega _{0})^{2}-1.}

Одним из основных условий выбора L{\displaystyle L} и C{\displaystyle C} является обеспечение индуктивной реакции фильтра. Такая реакция необходима для большей стабильности внешней характеристики выпрямителя, а также в случаях использования в выпрямителях германиевых, кремниевых^[8] или ионных вентилей.

Для обеспечения индуктивного импеданса необходимо выполнение неравенства:

L>2RH/(m2−1)mωc.{\displaystyle L>2R_{H}/(m^{2}-1)m\omega _{c}.}

При проектировании фильтра необходимо также обеспечить такое соотношение реактивных сопротивлений дросселя и конденсатора, при которых не мог бы возникнуть резонанс на частоте пульсаций выпрямленного напряжения и частоте изменения тока нагрузки.

$L>2R_{H}/(m^{2}-1)m\omega _{c}.$

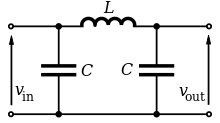П-образный LC-фильтр.

П-образный LC{\displaystyle LC} фильтр можно представить в виде двухзвенного, состоящего из ёмкостного фильтра с ёмкостью C0{\displaystyle C_{0}} и Г-образного с L{\displaystyle L} и C1{\displaystyle C_{1}}.

Коэффициент сглаживания такого фильтра будет равен:

Kc={\displaystyle K_{c}=}2rC0(m2−1)H{\displaystyle 2rC_{0} \over (m^{2}-1)H}(m2ωc2LC1−1).{\displaystyle (m^{2}\omega _{c}^{2}LC_{1}-1).}

В П-образном фильтре наибольшей величины коэффициент сглаживания достигает при равенстве ёмкостей C1=C0.{\displaystyle C_{1}=C_{0}.}

При необходимости обеспечения большого коэффициента сглаживания целесообразно применение многозвенного фильтра, — фильтра, составленного из двух и более однозвенных фильтров. Коэффициент сглаживания такого фильтра будет равен:

Kc={\displaystyle K_{c}=}Kc1⋅Kc2⋅Kc3⋅…⋅Kcn,{\displaystyle K_{c1}\cdot K_{c2}\cdot K_{c3}\cdot …\cdot K_{cn},}

то есть, общий коэффициент сглаживания будет равен произведению коэффициентов сглаживания всех последовательно соединённых фильтров.

Если все звенья фильтра состоят из одинаковых элементов (C1=C2=…=Cn{\displaystyle C_{1}=C_{2}=…=C_{n}} и L1=L2=…=Ln{\displaystyle L_{1}=L_{2}=…=L{n}}), что практически наиболее целесообразно, то:

Kc1=Kc2=…=Kcn{\displaystyle K_{c1}=K_{c2}=…=K_{cn}} и Kc=Kzvn=(mωc)2n(LzvCzv)n{\displaystyle K_{c}=K_{zv}^{n}=(m\omega _{c})^{2n}(L_{zv}C_{zv})^{n}}

где Kzv{\displaystyle K_{zv}} — коэффициент сглаживания каждого звена; Czv{\displaystyle C_{zv}},Lzv{\displaystyle L_{zv}} — соответственно индуктивность и ёмкость каждого звена; n{\displaystyle n} — число звеньев.

RC-фильтр[править | править код]

В выпрямителях^[9] малой мощности в некоторых случаях применяют фильтры, в состав которого входит активное сопротивление и ёмкость. В таком фильтре относительно велико падение напряжения и потери энергии на резисторе R{\displaystyle R}, но габариты и стоимость такого фильтра меньше, чем индуктивно-ёмкостного. Коэффициент сглаживания такого фильтра будет равен:

Kc={\displaystyle K_{c}=}mwcCR{\displaystyle mw_{c}CR}RHRH+R{\displaystyle R_{H} \over R_{H}+R}

Значение сопротивления фильтра R{\displaystyle R} определяется исходя из оптимальной величины его коэффициента полезного действия. Оптимальное значение КПД лежит в пределах от 0,6 до 0,8. Расчёт П-образного активно-ёмкостного фильтра производится так, как и в случае П-образного LC-фильтра, путём разделения этого фильтра на ёмкостной и Г-образный RC-фильтры.

Статическое электромагнитное устройство, предназначенное для использования его индуктивности в электрической цепи с целью уменьшения содержания высших гармоник (пульсаций) в выпрямленном токе. Применяется на тяговых подстанциях постоянного тока, на электроподвижном составе (электровозы, электропоезда) переменного тока. Сглаживающий реактор обычно соединяется последовательно с выпрямителем, таким образом, через него протекает весь ток нагрузки.

Китаев В. Е.,Бокуняев А. А., Колканов М. Ф. Электропитание устройств связи. — М.: «Связь», 1975. — С. 328.

Бушуев В. М., Деминский В. А., Захаров Л. Ф. Электропитание устройств и систем телекоммуникаций. — М.: «Связь», 2009. — С. 383.

Раймонд Мэк. Импульсные источники питания. — М.: Издательский дом «Додэка XXI», 2008. — С. 272.

Митрофанов А. В., Щеголев А. И. Импульсные источники вторичного электропитания в бытовой радиоаппаратуре. — М.: Радио и Связь, 1985. — С. 37.

Костиков В. Г., Парфенов Е. М., Шахнов В. А. Источники электропитания электронных средств. Схемотехника и конструирование: Учебник для ВУЗов. — 2. — М.: Горячая линия — Телеком, 2001. — 344 с. — 3000 экз. — ISBN 5-93517-052-3.

Полезные статьи

Видео

Все сглаживающие фильтры применяются в зависимости от мощности нагрузки

Сглаживающий фильтр — Википедия

Общие сведения

, обрезая лишние гармоники.

Псофометрический коэффициент помех

При оценке помех, проникающих из цепей питания в телефонные каналы, необходимо учитывать не только амплитуду напряжения данной гармоники, но и такой параметр, как частота. Это объясняется тем, что микротелефонные цепи и ухо человека обладают различной чувствительностью к колебаниям разной частоты, даже если их амплитуда одинакова. В связи с этим вводят понятие псофометрического коэффициента помех ak{\displaystyle a_{k}}^[4], который зависит от частоты и величина которого определяется экспериментально с учётом микротелефона и человеческого уха.

Эффективное значение псофометрического напряжения пульсации U на выходе выпрямителя будет равно:

U=0,5[(U01m⋅a1)2+(U02m⋅a2)2+…+(U0km⋅ak)2]{\displaystyle U={\sqrt {0,5[(U_{01m}\cdot a_{1})^{2}+(U_{02m}\cdot a_{2})^{2}+…+(U_{0km}\cdot a_{k})^{2}]}}}

где

a1…,ak{\displaystyle a_{1}…,a_{k}} — псофометрические коэффициенты для соответствующих гармоник;

U1…,Uk{\displaystyle U_{1}…,U_{k}} — амплитуды соответствующих гармоник выпрямленного напряжения.

Коэффициент сглаживания

Основным параметром сглаживающих фильтров является коэффициент сглаживания, которым называется отношение коэффициента пульсации на входе (KBx){\displaystyle (K_{Bx})} к коэффициенты пульсации на выходе (KH){\displaystyle (K_{H})}, то есть на нагрузке.

KC=KBx/KHa={\displaystyle K_{C}=K_{Bx}/K_{Ha}=}(U01m/U0)/(Uh2m/UH){\displaystyle (U_{01m}/U_{0})/(U_{h2m}/U_{H})}

Виды сглаживающих фильтров

Индуктивный сглаживающий фильтр

Коэффициент сглаживания такого фильтра равен KC={\displaystyle K_{C}=}(RH)2+(mwcL)2RH{\displaystyle {\sqrt {(R_{H})^{2}+(mw_{c}L)^{2}}} \over R_{H}}

где у нас

RH{\displaystyle R_{H}} — сопротивление нагрузки

L{\displaystyle L} — индуктивность обмотки дросселя

wc{\displaystyle w_{c}} — угловая частота

Ёмкостной сглаживающий фильтр

Ёмкостной сглаживающий фильтр.
С — фильтрующий конденсатор, R — сопротивление нагрузки.

Конденсатор имеет реактивное сопротивление:

XC=1/(ω⋅C){\displaystyle X_{C}=1/(\omega \cdot C)},

где C{\displaystyle C} — ёмкость конденсатора.

Коэффициент сглаживания такого фильтра будет следующим:

KC={\displaystyle K_{C}=}K1K2{\displaystyle K_{1} \over K_{2}}={\displaystyle =}(2m2−1{\displaystyle 2 \over m^{2}-1})/{\displaystyle /}(HrC{\displaystyle H \over rC})

где

K1{\displaystyle K_{1}} — коэффициент пульсаций на входе выпрямителя при отсутствии ёмкости

K2{\displaystyle K_{2}} — коэффициент пульсаций на выходе выпрямителя при наличии ёмкости.

LC-фильтр

Kc=m2ωc2LC−1.{\displaystyle K_{c}=m^{2}\omega _{c}^{2}LC-1.}

Так как 1/LC=ω0{\displaystyle 1/{\sqrt {LC}}=\omega _{0}} — собственная частота фильтра, то

Kc=(mωc/ω0)2−1.{\displaystyle K_{c}=(m\omega _{c}/\omega _{0})^{2}-1.}

Для обеспечения индуктивного импеданса необходимо выполнение неравенства:

L>2RH/(m2−1)mωc.{\displaystyle L>2R_{H}/(m^{2}-1)m\omega _{c}.}

П-образный LC-фильтр.

Коэффициент сглаживания такого фильтра будет равен:

Kc={\displaystyle K_{c}=}2rC0(m2−1)H{\displaystyle 2rC_{0} \over (m^{2}-1)H}(m2ωc2LC1−1).{\displaystyle (m^{2}\omega _{c}^{2}LC_{1}-1).}

Kc={\displaystyle K_{c}=}Kc1⋅Kc2⋅Kc3⋅…⋅Kcn,{\displaystyle K_{c1}\cdot K_{c2}\cdot K_{c3}\cdot …\cdot K_{cn},}

Kc1=Kc2=…=Kcn{\displaystyle K_{c1}=K_{c2}=…=K_{cn}} и Kc=Kzvn=(mωc)2n(LzvCzv)n{\displaystyle K_{c}=K_{zv}^{n}=(m\omega _{c})^{2n}(L_{zv}C_{zv})^{n}}

RC-фильтр

Kc={\displaystyle K_{c}=}mwcCR{\displaystyle mw_{c}CR}RHRH+R{\displaystyle R_{H} \over R_{H}+R}

Сглаживающий реактор

Примечания

Литература

Китаев В. Е.,Бокуняев А. А., Колканов М. Ф. Электропитание устройств связи. — М.: «Связь», 1975. — С. 328.

Бушуев В. М., Деминский В. А., Захаров Л. Ф. Электропитание устройств и систем телекоммуникаций. — М.: «Связь», 2009. — С. 383.

Раймонд Мэк. Импульсные источники питания. — М.: Издательский дом «Додэка XXI», 2008. — С. 272.

Митрофанов А. В., Щеголев А. И. Импульсные источники вторичного электропитания в бытовой радиоаппаратуре. — М.: Радио и Связь, 1985. — С. 37.

Костиков В. Г., Парфенов Е. М., Шахнов В. А. Источники электропитания электронных средств. Схемотехника и конструирование: Учебник для ВУЗов. — 2. — М.: Горячая линия — Телеком, 2001. — 344 с. — 3000 экз. — ISBN 5-93517-052-3.

См. также

Ссылки

Полезные статьи

Видео

Примечания

Все сглаживающие фильтры применяются в зависимости от мощности нагрузки

Сглаживающие фильтры | HomeElectronics

Всем доброго времени суток. Сегодня продолжение темы про выпрямители и поговорим мы о сглаживающих фильтрах выпрямителей. Сглаживающие фильтры включаются между выпрямителем и нагрузкой для уменьшения переменных составляющих (пульсаций) выпрямленного напряжения. Эти фильтры выполняются из индуктивных элементов – дросселей и из ёмкостных элементов – конденсаторов. Простейший сглаживающий фильтр может состоять только из одного элемента, например дросселя или конденсатора. В малогабаритной аппаратуре сравнительно малой мощности индуктивные элементы фильтра могут быть заменены активными (резисторами).

Сглаживающие фильтры, прежде всего, характеризуются коэффициентом сглаживания q, представляющим собой отношение коэффициентов пульсаций на входе S₀ и выходе S_0H фильтра:

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Индуктивный сглаживающий фильтр

Применяется в маломощных выпрямителях, но может входить в состав сложных многозвенных фильтров. Параметры дросселя следует выбирать так, чтобы активное сопротивление обмотки rдр было много меньше сопротивления нагрузки (r_др << R_н), а индуктивное сопротивление X_др = 2πf_пL_ф на частоте пульсаций f_п – много больше, чем R_н(X_др >> R_н). В этом случае почти вся постоянная составляющая напряжения будет приложена к нагрузке, а переменная составляющая – к дросселю.

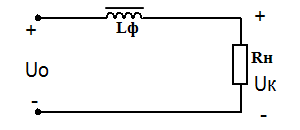
По заданному коэффициенту сглаживания q можно рассчитать необходимую индуктивность сглаживающего фильтра

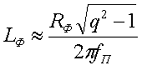
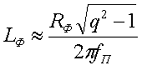
Индуктивный фильтр прост, дешев, имеет малые потери мощности; коэффициент сглаживания фильтра растёт с увеличением индуктивности дросселя, числа фаз питающего напряжения и с уменьшением сопротивления нагрузки. Поэтому индуктивные фильтры обычно применяются совместно с многофазными мощными выпрямителями. При отключении нагрузки или скачкообразном изменении ее сопротивления возможно возникновение перенапряжений; в этом случае параллельно обмотке дросселя необходимо включать защитные устройства, например разрядники. В маломощных однофазных выпрямителях индуктивный фильтр может являться звеном более сложного фильтра.

Eмкостной сглаживающий фильтр

Емкостной сглаживающий фильтр состоит из конденсатора С_ф, подключённого параллельно сопротивлению нагрузки R_н. Принцип действия заключается в накоплении электрической энергии конденсатором фильтра и последующей отдачи этой энергии в нагрузку. Заряд и разряд конденсатора фильтра происходит с частотой пульсаций f_п выпрямленного напряжения.

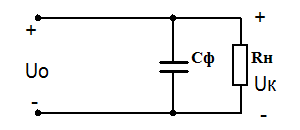
Для расчёта ёмкости конденсатора сглаживающего фильтра можно воспользоваться следующей формулой

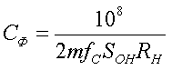
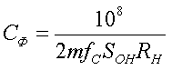, где

результируещее значение ёмкости выражено в микрофарадах,
S_OH – коэффициент пульсаций в процентах, %;
R_H – сопротивление нагрузки в омах, Ом;
f_c – частота сети в герцах, Гц;
m – число используемых при выпрямлении полупериодов за период напряжения сети,m = 1 – для однополупериодных, m = 2 – для двухполупериодных.

Емкостной фильтр целесообразней всего применять совместно с однофазными и маломощными схемами выпрямления.

Сглаживающий LC фильтр

Сглаживание пульсаций выпрямленного напряжения будет более эффективным, если в совместить два предыдущих фильтра: индуктивный и емкостной фильтры. Данные типы сглаживающих фильтров называют LC фильтрами

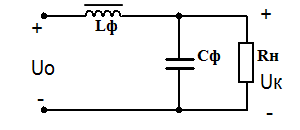
Простейший Г-образный индуктивно-емкостный фильтр рассчитывают такким образом, чтобы параметры элементов подходили под следующие условия

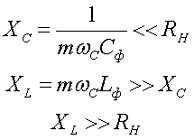
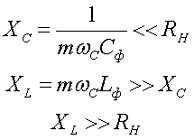
Коэффициент сглаживания Г-образного фильтра связан с произведением индуктивности и емкости следующим образом:

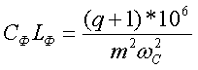
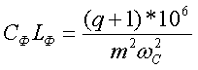
Сглаживающие RC фильтры

В схемах выпрямления малой мощности дроссель фильтра может быть заменён резистором R_Ф. Такие типы фильтров называют RC фильтрами

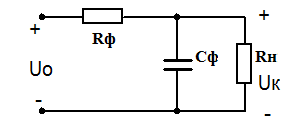
Расчёт сглаживающего RC фильтра должен вестись с учётом следующих условий

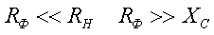
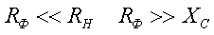
Коэффициент сглаживания фильтра

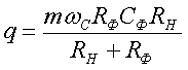
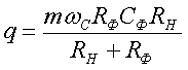
Сопротивление резистора R_Ф обычно задаются в пределах R_Ф = (0,15…0,5)R_H; КПД резистивно-емкостного фильтра сравнительно мал и обычно составляет 0,6…0,8, причем при η_ф = 0,8 R_Ф = 0,25R_H. Емкость C_ф (в микрофарадах), обеспечивает требуемый коэффициент сглаживания q при частоте сети f_C = 50 Гц, находят из выражения

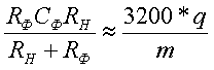
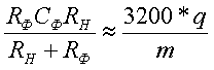
Преимущества резистивно-емкостных фильтров: малые габариты, масса и стоимость; недостаток – низкий КПД.

Многозвенные сглаживающие фильтры

Если с помощью индуктивно-емкостного фильтра необходимо обеспечить коэффициент сглаживания пульсаций более 40…50, то вместо однозвенного фильтра целесообразнее использовать двухзвенный сглаживающий фильтр.

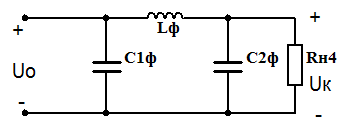
Фильтры с тремя и более звеньями на практике применяются редко. В общем случае коэффициент сглаживания многозвенного фильтра равен произведению коэффициентов сглаживания отдельных звеньев: q = q’q’’q’’’ …

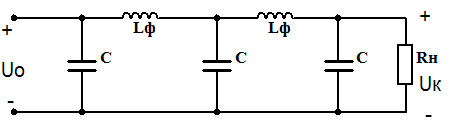
Сглаживающие индуктивно-емкостные фильтры достаточно просты и эффективны в выпрямительных устройствах средней и большой мощностей. Однако масса и габариты таких фильтров весьма значительны, коэффициент сглаживания снижается с ростом тока нагрузки, фильтры малоэффективны при появлении медленных изменений сетевого напряжения. Индуктивные элементы фильтра являются источниками магнитных полей рассеяния, а совместно с паразитными емкостными элементами создают колебательные контуры, способствующие появлению переходных процессов.

Транзисторный сглаживающий фильтр

Транзисторные фильтры по сравнению с индуктивно-емкостными сглаживающими фильтрами имеют меньшие габариты, массу и более высокий коэффициент сглаживания пульсаций.

Фильтры могут быть выполнены по схемам с последовательным или параллельным включением силового транзистора по отношению к сопротивлению нагрузки, а также с включением нагрузки R_H в цепь коллектора или эмиттера транзистора. Недостатком фильтров с нагрузкой в цепи коллектора является большое изменение выходного напряжения при изменении сопротивления нагрузки. Поэтому чаще используют фильтры, в которых сопротивление нагрузки включено в цепь эмиттера силового транзистора.

Фильтр с последовательным транзистором

Транзисторный сглаживающий фильтр с последовательным включением транзистора и нагрузкой в цепи эмиттера эквивалентен П-образному LC фильтру. Принцип действия его основан на том, что коллекторный и эмиттерный токи транзистора в режиме усиления практически не зависит от напряжения коллектор-эмиттер. Если выбрать рабочую точку транзистора на горизонтальном участке выходной вольт-амперной характеристики, то его сопротивление для переменного тока будет значительно большим, чем для постоянного тока.

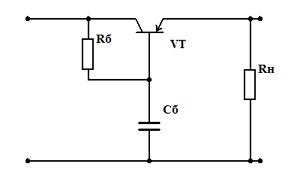
Транзисторный фильтр

В схеме базовый ток транзистора VT задается резистором R_б. Конденсатор С_б достаточно большой емкости устраняет напряжение пульсаций на переходе эмиттер-база. Поэтому переменная составляющая напряжения пульсаций прикладывается к переходу база-коллектор и выделяется на транзисторе VT. В коллекторном и эмиттерном токе переменная составляющая практически отсутствует, поэтому пульсации в нагрузке R_H также очень малы.

Коэффициент сглаживания транзисторного фильтра тем больше, чем больше коэффициент передачи тока транзистора VT и чем больше значение отношений

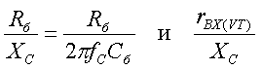
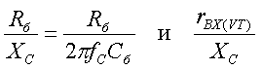
то есть чем меньше напряжение пульсаций на переходе эмиттер-база силового транзистора.

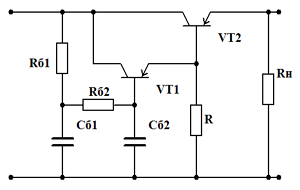
Составной транзистор

Для более успешного выполнения этих соотношений конденсатор С_б может быть заменён одно- или двухзвенным RC сглаживающим фильтром, а для увеличения коэффициента передачи тока транзистор VT можно выполнить составным

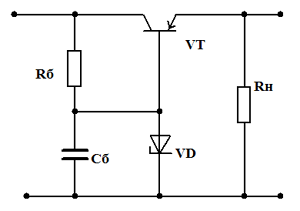
Транзисторный фильтр со стабилитроном

Еще эффективней работает транзисторный фильтр, у которого в цепь базы транзистора включен стабилитрон

Коэффициент полезного действия транзисторного фильтра будет тем больше, чем меньше падание постоянного напряжения на силовом транзисторе. Однако амплитуда переменной составляющей напряжения на транзисторе не должна превышать значение постоянного напряжения на нём, иначе фильтр потеряет свою работоспособность.

Фильтр с параллельным транзистором

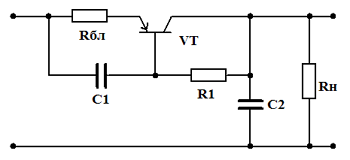
Фильтр с балластным резистором и параллельным включением транзистора

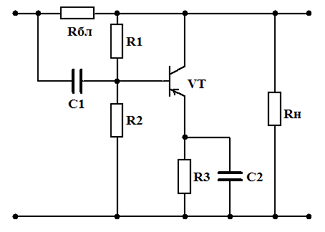
Фильтр с балластным резистором и последовательным включением транзистора

Транзисторные фильтры с балластным резистором R_бл и параллельным включением транзистора относительно нагрузки, в отличие от схем с последовательным включением, применяется при сравнительно небольшом выпрямленном напряжении (десятки вольт). Режим работы транзистора VT – минимальное значение тока I_K.min – устанавливается соответствующим выбором сопротивлений R1 и R2. Переменная составляющая напряжения в этой схеме прикладывается к переходу эмиттер-база транзистора VT, усиливается и выделяется на балластном резисторе R_бл. Эта составляющая оказывается в противофазе с переменной составляющей напряжения, выделяющейся на R_бл при непосредственном протекании тока нагрузки. Выбором R_бл и I_K.min можно добиться их полной компенсации. Амплитуда переменной составляющей тока транзистора VT должна быть меньше протекающего постоянного тока I_K.min, иначе схема будет неработоспособна. Ток I_K.min, не должен быть очень малым, так как иначе потребуется увеличение сопротивления R_бл, что приведёт к снижению КПД фильтра. Слишком большой ток также нецелесообразен, так как увеличивается мощность потерь на транзисторе и снижается КПД.

Коэффициент сглаживания параллельного транзисторного фильтра будет тем больше, чем больше сопротивление Rбл, емкость конденсаторов С1 и С2, крутизна вольт-амперной характеристики транзистора. Недостатком транзисторного фильтра с параллельным включением транзистора является значительное изменение среднего значения коллекторного тока транзистора, при изменении среднего значения выпрямленного напряжения, поступающего на вход фильтра. Это приводит к снижению КПД фильтра.

Следует помнить, что транзисторные фильтры не обеспечивают стабилизацию постоянной составляющей выпрямленного напряжения, а при изменении тока нагрузки, температуры окружающей среды и воздействия других дестабилизирующих факторов вносят дополнительную нестабильность выпрямленного напряжения.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Сглаживающие фильтры

Общие сведения

Сглаживающие фильтры включаются между выпрямителем и нагрузкой, представляет собой ФНЧ и служат для сглаживания пульсаций выпрямленного напряжения (выделения постоянной составляющей – U₀). Фильтры бывают пассивные и активные. Действие активных фильтров основано на рассеивании мощности пульсаций в виде тепла на активном элементе (транзисторе), поэтому они имеют низкий КПД. Мы будем рассматривать только пассивные фильтры. Их сглаживающее действие основано на накоплении энергии в реактивных элементах от сети в моменты её максимума и передачи в нагрузку в моменты её минимума. Основные схемы пассивных фильтров приведены на рис.3.1.

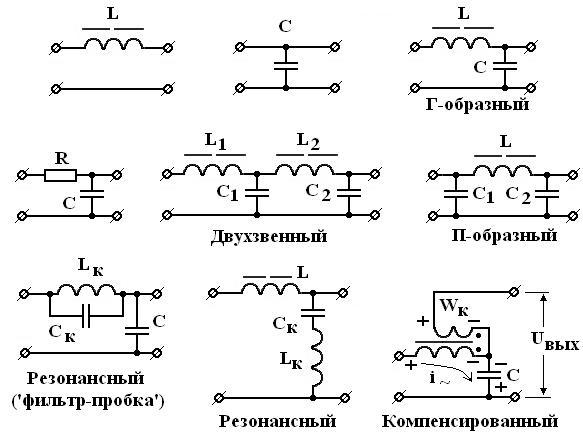
Рисунок 3.1 – Схемы пассивных сглаживающих фильтров

Критерием качества сглаживающих свойств фильтров является коэффициент сглаживания равный отношению коэффициентов пульсаций на входе и выходе фильтра

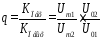(3.1)

На рис.3.2 приведена схема замещения фильтра (а) и эпюры напряжений (б).

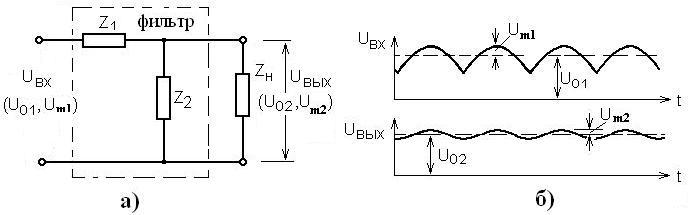
Рисунок 3.2 – Схема замещения (а) и напряжения на входе и выходе сглаживающего фильтра (б)

Выразим коэффициент сглаживания через параметры элементов фильтра:

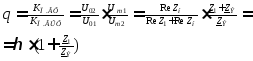(3.2)

где .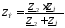

К параметрам схемы замещения предъявляются следующие требования: ; .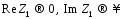

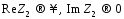Индуктивный (L) сглаживающий фильтр представляет собой катушку с ферромагнитным сердечником (дроссель), включаемую последовательно с нагрузкой (рис.3.3).

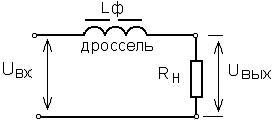
Рисунок 3.3 – Индуктивный сглаживающий фильтр

Коэффициент сглаживания фильтра равен:

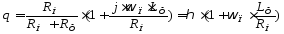(3.3)

где 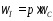— частота пульсаций,

p — пульсность схемы выпрямления,

R_Ф— сопротивление потерь дросселя.

Индуктивный фильтр является “габаритным” устройством, поэтому для уменьшения его размеров стараются повысить частоту пульсаций в звене выпрямителя. Данный фильтр используется в цепях с повышенными токами нагрузки. При возрастании тока нагрузки (уменьшении R_н) происходит увеличение энергии, накапливаемой в дросселе, увеличивается ЭДС самоиндукции, что препятствует прохождению в нагрузку переменной составляющей тока и улучшаются сглаживающие свойства фильтра.

При работе на импульсную нагрузку, а именно при “сбросе” тока нагрузки или отключении источника питания энергия, накопленная в дросселе освобождается, возникает перенапряжение, которое может привести к выходу из строя элементов схемы. Поэтому при проектировании фильтров такие перенапряжения необходимо учитывать.

Емкостный (C) сглаживающий фильтр. Представляет собой конденсатор, включаемый параллельно нагрузке (рис. 3.4).

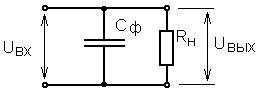
Рисунок 3.4 –Емкостный сглаживающий фильтр

Выражение для коэффициента сглаживания имеет вид:

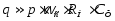(3.4)

Емкостный фильтр используются при малых токах нагрузки, так как с ростом тока уменьшается постоянная цепи разряда, что увеличивает пульсацию напряжения (из-за глубокого разряда конденсатора). К

достоинствам фильтра можно отнести: отсутствие колебаний напряжения при переходных процессах, простота, небольшие габаритные размеры. Недостатком фильтра является: воздействие на выпрямитель (угол отсечки тока меньше 180 градусов), поэтому при использовании такого фильтра с большой величиной емкости необходимо вводить в звено выпрямителя защиту по току.

Индуктивно- емкостный (LC) сглаживающий фильтр. При соблюдении условия Х_др > Х_с реакция фильтра будет индуктивного характера (рис. 3.5). Дроссель и конденсатор, используемые совместно, более эффективно выполняют функции сглаживания, чем при их раздельном включении, если выполняются неравенства: Х

др >> R_н и Х_с << R_н.

Рисунок 3.5 – Индуктивно- емкостный (LC) сглаживающий фильтр

Коэффициент сглаживания фильтра через параметры элементов схемы замещения принимает вид (R_Ф— омическое сопротивление дросселя):

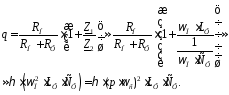(3.5)

Фильтр используется при большой мощности нагрузки. К достоинствам фильтра относятся: малые габаритные размеры, малая зависимость коэффициента сглаживания от изменений тока нагрузки (различный характер зависимости q от I

Н для реактивных элементов взаимно компенсирует это влияние). Недостатки: могут возникать резонансные переходные процессы, усложняющие работу, как потребителя, так и источника питания, дроссели фильтров имеют большие габаритные размеры и массу, а их индуктивность зависит от тока нагрузки. При включении и отключении сети, а также при резких изменениях нагрузки возникают переходные процессы, которые могут привести к перенапряжениям и броскам тока в элементах фильтра и выпрямителя. Несмотря на малую продолжительность этих процессов, они могут быть причиной выхода из строя вентилей выпрямителя по обратному напряжению или прямому току, а также пробоя конденсаторов или изоляции дросселей и силового трансформатора.

Многозвенные сглаживающие фильтры. Для получения высоких значений коэффициента сглаживания (q > 50), в выпрямительных устройствах используются многозвенные сглаживающие фильтры (рис. 3.6). Наиболее широко в выпрямительных устройствах используются двухзвенные фильтры благодаря малой зависимости коэффициента сглаживания от тока нагрузки, высоким качественным и удельным показателям. Увеличение числа звеньев более двух приводит к уменьшению области устойчивой работы (так как источник питания представляет собой замкнутую систему автоматического регулирования, то увеличение числа реактивных элементов в силовой цепи может привести к самовозбуждению) и уменьшению КПД устройства.

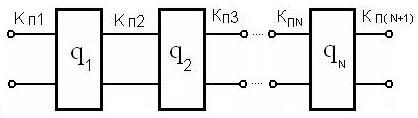
Рисунок 3.6 – Многозвенные сглаживающие фильтры

Получим выражение для коэффициента сглаживания многозвенного фильтра.

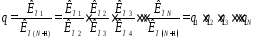(3.6)

Видно, что при каскадном включении коэффициенты сглаживания отдельных каскадов перемножаются.