Закон Ома для полной цепи. Школьный курс физики

Главная | Физика 11 класс | Закон Ома для полной цепи

Закон ома для полной цепи.

Ранее мы изучили закон Ома для участка цепи, не содержащего источник тока. Теперь рассмотрим простейшую полную (замкнутую) электрическую цепь (рис. 1.41), состоящую из источника тока (например, гальванического элемента или аккумулятора) и резистора с сопротивлением R.

Рис. 1.41

Источник тока, имеющий ЭДС , обладает сопротивлением r. Его называют внутренним сопротивлением источника, в отличие от сопротивления R цепи, называемого внешним сопротивлением.

Например, в генераторе r — это сопротивление его обмоток (медных проводов), в гальваническом элементе или аккумуляторе это сопротивление раствора электролита и электродов.

Для вывода закона Ома для полной цепи воспользуемся законом сохранения энергии.

Пусть за время Δt через поперечное сечение проводника пройдёт заряд q. Тогда, согласно формуле (см. § 7 «Электродвижущая сила. Источники тока«), работа сторонних сил при перемещении заряда q равна

А_ст = q.

Из определения силы тока I получим q = IΔt. C учётом этого

А_ст = IΔt.

Благодаря работе сторонних сил при прохождении тока в цепи на её внешнем и внутреннем участках выделяется количество теплоты, равное по закону Джоуля—Ленца

Q = I²

RΔt + I²rΔt.

Согласно закону сохранения энергии, А_ст = Q, поэтому

Произведение силы тока на сопротивление участка цепи называют падением напряжения на этом участке. Таким образом, ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи:

= U + U₀,

где U = IR — падение напряжения на внешнем участке; U₀ = Ir — падение напряжения на внутреннем участке цепи.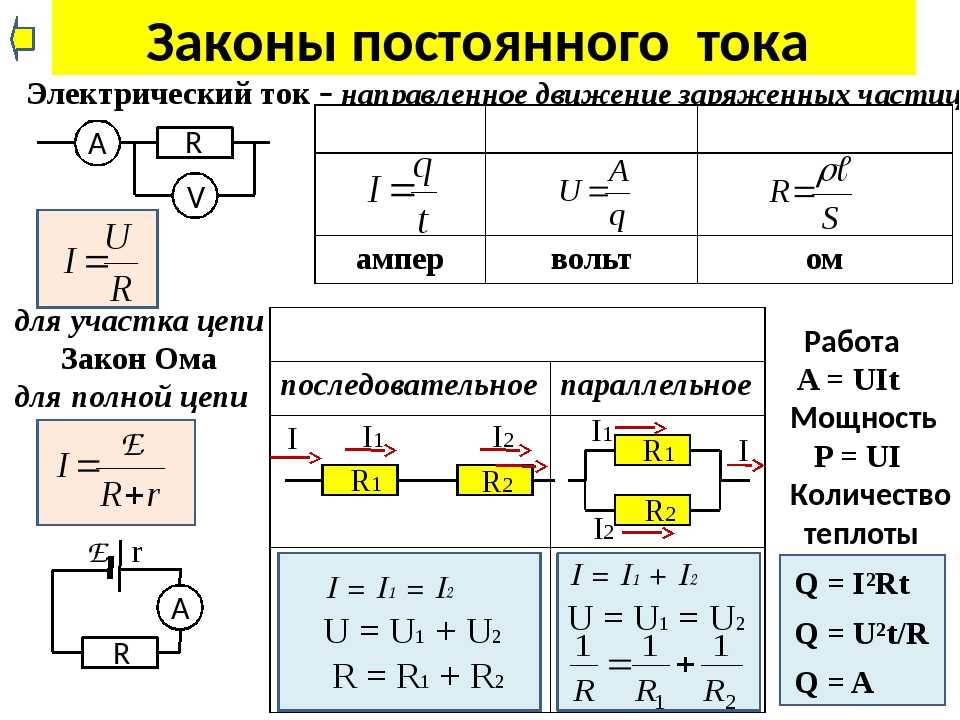

Из равенства (1) запишем:

Это и есть закон Ома для полной цепи.

Сила тока в полной цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Внутреннее сопротивление источника тока, если оно мало по сравнению с внешним сопротивлением (r << R), оказывает незначительное влияние на силу тока. Но при коротком замыкании, когда R ≈ 0, сила тока очень велика, так как r мало. Например, при = 2 В и r = 0,1 — 0,004 Ом сила тока короткого замыкания I_кз = 20 — 2000 А. При такой силе тока провода могут расплавиться, а источник тока — выйти из строя

1.

---

¹ Напомним, что при перегрузках и коротких замыканиях электрическую сеть защищает специальное устройство — предохранитель. Он состоит из проволоки, изготовленной из легкоплавкого металла. Проволока помещена в стеклянную трубку, имеющую на концах металлические наконечники, и рассчитана на определённую силу тока. Если сила тока превышает допустимое значение, то проволока плавится и цепь размыкается.

Если цепь содержит несколько последовательно соединённых источников тока (рис. 1.42),

Рис. 1.42

то полная ЭДС в цепи равна алгебраической сумме ЭДС отдельных элементов:

Определим знак ЭДС отдельных элементов. При выбранном (произвольно) направлении обхода против часовой стрелки для цепи, схема которой изображена на рисунке 1.42, ₁ > 0, ₂ < 0 и ₃ > 0, поэтому

Внутреннее сопротивление батареи, состоящей из последовательно соединённых элементов, равно сумме внутренних сопротивлений элементов:

Если батарея состоит из N одинаковых последовательно соединённых элементов с одинаковыми знаками ЭДС, то из формул (2) и (3) следует, что

где ₆ и r₆ — ЭДС и внутреннее сопротивление батареи;

э и r_э — ЭДС и внутреннее сопротивление одного элемента.

Таким образом, последовательное соединение увеличивает общую ЭДС и увеличивает внутреннее сопротивление батареи.

Если цепь содержит несколько параллельно соединённых элементов (рис. 1.43),

Рис. 1.43

то можно записать следующие формулы:

где N — число одинаковых ЭДС в цепи.

Таким образом, параллельное соединение N одинаковых источников тока не изменяет ЭДС батареи, если сравнивать с включённым в эту цепь одним источником тока с той же ЭДС. Однако при таком включении внутреннее сопротивление источника уменьшается в N раз

.

Закон Oмa для участка цепи, содержащего ЭДС.

Наиболее общую форму имеет закон Ома для участка цепи, содержащего ЭДС (иногда его называют обобщённым законом Ома).

Рассмотрим участок цепи, содержащий гальванические элементы или аккумулятор, т. е. участок, на котором действуют сторонние силы. Таким участком является, например, участок ab (рис.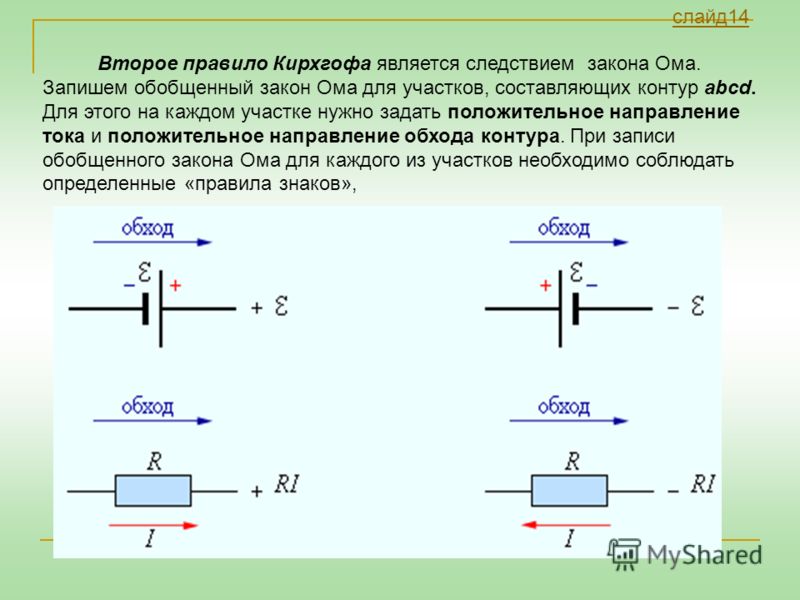 1.44).

Рис. 1.44

Внутренние сопротивления источников ₁, и ₂ равны соответственно

r₁ и r₂. Сила тока на участке равна I, ток течёт от точки а к точке b.

За время Δt через поперечное сечение проводника проходит заряд q = IΔt. При этом электрическое поле совершает работу A_π = (φ_a — φ_b)q = (φ_a — φ_b)IΔt. Источники тока совершают работу A_cт = |₁|q — |₂|q = (|₁| — |₂|)IΔt. За время Δt на участке цепи выделяется количество теплоты

Q = I²(r₁ + r₂ + R₁ + R₂)Δt. Согласно закону сохранения энергии A_п + A_ст = Q, поэтому

Сформулируем закон Ома для участка цепи, содержащего ЭДС.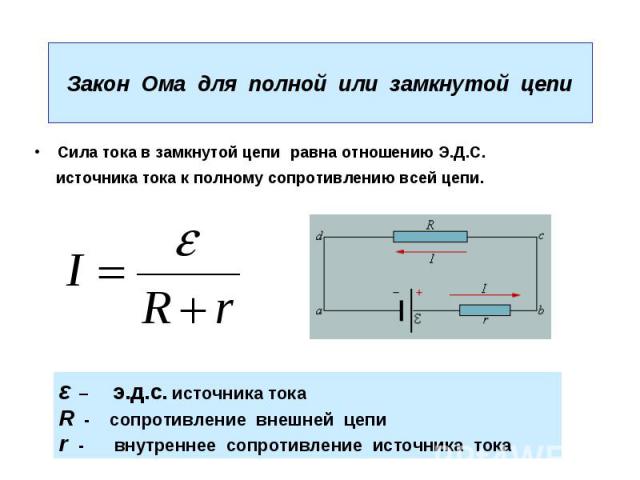

Разность потенциалов на концах участка цепи равна падению напряжения на участке минус ЭДС этого участка.

Если неразветвленный участок цепи содержит п источников тока и N резисторов, то

Применяя закон Ома для участка цепи, содержащего ЭДС, придерживаются правила знаков.

1. Сила тока в правой части уравнения (5) считается положительной, если направление тока совпадает с направлением от

a к b.

2. ЭДС считается положительной, если работа сторонних сил при перемещении единичного положительного заряда на данном участке цепи в направлении от а к Ь положительна. В случае гальванического элемента или аккумулятора ЭДС положительна, если этот заряд внутри источника перемещается от отрицательного электрода к положительному. C учётом этого в правой части уравнения (5) записывается сумма всех ЭДС по правилу знаков.

Применив закон Ома к участку 1—2 цепи, показанной на рисунке 1.

41, получим φ₁ — φ₂ = Ir — . При разомкнутой цепи I = 0 и, следовательно, = φ₂ — φ₁. Таким образом, ЭДС элемента равна разности потенциалов между его полюсами при разомкнутой цепи.

Реостат.

Реостат представляет собой резистор с регулируемым сопротивлением (рис. 1.45).

Рис. 1.45

Пусть часть цепи состоит из электрической лампы накаливания и последовательно соединённого с ней реостата (рис. 1.46).

Рис. 1.46

C помощью реостата можно изменять общее сопротивление цепи: от максимального сопротивления, равного сумме сопротивлений реостата и лампы, до минимального, равного только сопротивлению лампы.

В общем случае

Если контакт 3 совпадает с контактом /, то

Если контакт 3 совпадает с контактом 2, то

где R₁₂ — сопротивление реостата.

Таким образом, реостат позволяет плавно регулировать значение силы тока в цепи и в данном случае изменять степень накала нити лампы, включённой в цепь.

Потенциометр.

Потенциометр (делитель напряжения) — устройство, предназначенное для получения плавно изменяемого напряжения U от источника постоянного напряжения U₀: U ≤ U₀ (рис. 1.47).

Рис. 1.47

Точка D на схеме представляет собой скользящий контакт. При этом

U_Rmin = 0 (когда контакт D соединён с точкой А),

U_Rmax = U₀ (когда контакт D соединён с точкой В).

Таким образом, потенциометр позволяет получать различные значения напряжения на нагрузке, которой в данном случае является резистор с сопротивлением R.

Вопросы:

1. Какое сопротивление называют:

а) внутренним;

б) внешним?

2. Чем определяется падение напряжения на участке цепи?

3. Сформулируйте и запишите закон Ома для полной цепи.

4. Как определить ЭДС и внутреннее сопротивление батареи, содержащей несколько:

а) последовательно соединённых элементов;

б) параллельно соединённых элементов?

5. Сформулируйте и запишите закон Ома для участка цепи, содержащего ЭДС.

6. Для чего используют:

а) реостат;

б) потенциометр?

Вопросы для обсуждения:

Почему при коротком замыкании напряжение на клеммах источника тока близко к нулю, хотя сила тока в цепи имеет наибольшее значение?

Пример решения задачи

Сила тока через аккумулятор в конце зарядки I₁ = 4 А. При этом разность потенциалов на его клеммах U₁ = 12,6 В. Сила тока короткого замыкания I_кз = 305 А. В начале разрядки того же аккумулятора сила тока I₂ = 6 А. Какова при этом разность потенциалов U₂ на его клеммах?

            Рис. 1.48

Сила тока при коротком замыкании аккумулятора (рис. 1.48, б)

Схема разрядки аккумулятора на внешнюю нагрузку показана на рисунке 1.48, в. По закону Ома для участка цепи, содержащего ЭДС:

Из уравнений(1)и(2)найдём:

Подставим данные выражения в уравнение (3):

C учётом числовых данных получим

Ответ: U₂ ≈ 12,2 В.

Упражнения:

1. К источнику тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён резистор с сопротивлением 5 Ом. Найдите силу тока в цепи и напряжение на зажимах источника.

2. Чему равно внутреннее сопротивление источника тока, если его ЭДС составляет 1,2 В и при внешнем сопротивлении 5 Ом сила тока в цепи равна 0,2 А?

3. Определите разность потенциалов между точками A и B электрической цепи, схема которой приведена на рисунке 1.49. ЭДС каждого источника тока равна 1,5 В, внутреннее сопротивление каждого источника составляет 0,1 Ом.

Рис. 1.49

4. Два одинаковых источника тока с ЭДС и внутренним сопротивлением r соединены так, как показано на рисунке 1.50. Определите показания приборов. Сопротивление амперметра принять равным нулю, а сопротивление вольтметра — бесконечно большим.

Рис. 1.50

Предыдущая страницаСледующая страница

Закон Ома для полной цепи (урок-презентация)

Да, электричество – мой задушевный друг, согреет, развлечёт, прибавит света

Тема урока: Электрический ток. Закон Ома для участка цепи. Закон Ома для полной цепи

Урок — презентация

Группы взаимосвязанной информации

Тема:Электрический ток. Закон Ома для участка цепи. Закон Ома для полной цепи

Цели:обеспечить усвоение понятий электрический ток, сила тока и плотность тока, сопротивление, закон Ома для участка цепи, электрическая цепь и ее элементы, закон Ома для полной цепи;

кастинг

Заполнить таблицу

Работа с формулами

Работа над ошибками (устный счёт)

Содержание

Теория

Закрепление

Практическая работа

Условия существования постоянного тока.

Направленное, упорядоченное движение электрически заряженных частиц называется электрическим током.

Условия, необходимые для появления и существования электрического тока:

наличие в данной среде свободных носителей тока – заряженных частиц, которые могли бы в ней свободно перемещаться.

Существование в данной среде внешнего электрического поля, энергия которого должна расходоваться на упорядоченное движение электрических зарядов

Основными компонентами электрической цепи являются:

источник тока – устройство, преобразующее любой вид энергии в электрическую;

соединительные провода;

элементы, замыкающие и размыкающие цепь;

потребители тока – устройства, преобразующие электрическую энергию в тепловую, механическую и т.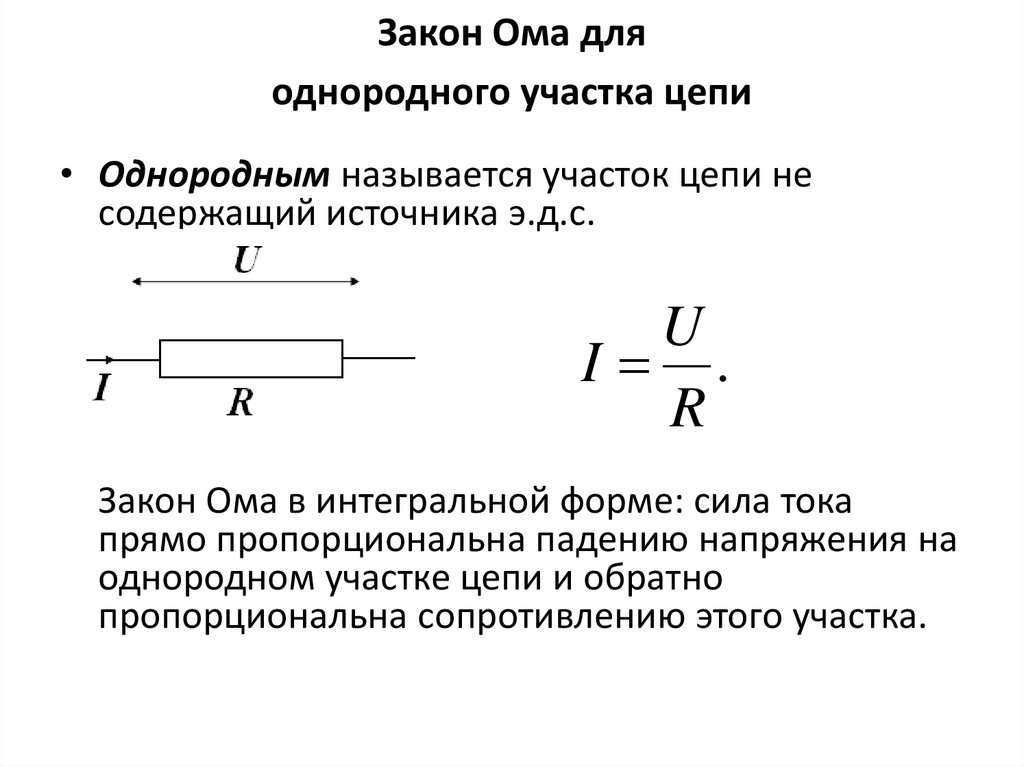 д.

Силой тока

называется величина, которая показывает, какой заряд q проходит через поперечное сечение проводника за единицу времени, т.е. I=Δq/Δt

Направлением электрического тока считается направление упорядоченного движения положительных электрических зарядов

Электродвижущая сила источника электрической энергии.

Работу электрического поля по перемещению заряда можно вычислить по формуле

A=q·U

где q-величина перемещённого заряда;

U-напряжение (разность потенциалов).

Электрическое напряжение – это физическая величина, определяемая работой электрического поля по перемещению единичного электрического заряда, т.е.

U=A/q

Величину, характеризующую зависимость электрической энергии, приобретённой зарядом в источнике от внутреннего устройства последнего, называют электродвижущей силой источника (ЭДС) и обозначают

E =A/q

Единицей ЭДС в СИ является

1B (вольт) 1B=1 Дж/Кл.

Сторонние силы имеют природу неэлектрического происхождения: в источниках тока в качестве сторонних сил могут выступать силы, возникающие за счёт энергии химической реакции (аккумуляторы, гальванические элементы), или тепловой (термопара), или световой (солнечные батареи) и т.д.

Закон Ома для участка цепи.

Немецкий физик Георг Ом в 1827 году открыл зависимость силы тока для участка электрической цепи от сопротивления:

Сила тока, текущего по участку цепи, прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

I=U/R .

ОМ (Ohm) Георг Симон (16 марта 1787, Эрланген — 6 июля 1854, Мюнхен), немецкий физик, автор одного из основных законов, определяющих электрические токи в проводниках, член Баварской АН (1845), член-корреспондент Берлинской АН, иностранный почетный член Лондонского Королевского общества (1842).

сопротивление металлического проводника

сопротивление металлического проводника зависит от его длины l , площади поперечного сечения S и рода вещества, из которого изготовлен проводник,

где ρ – удельное сопротивление проводника.

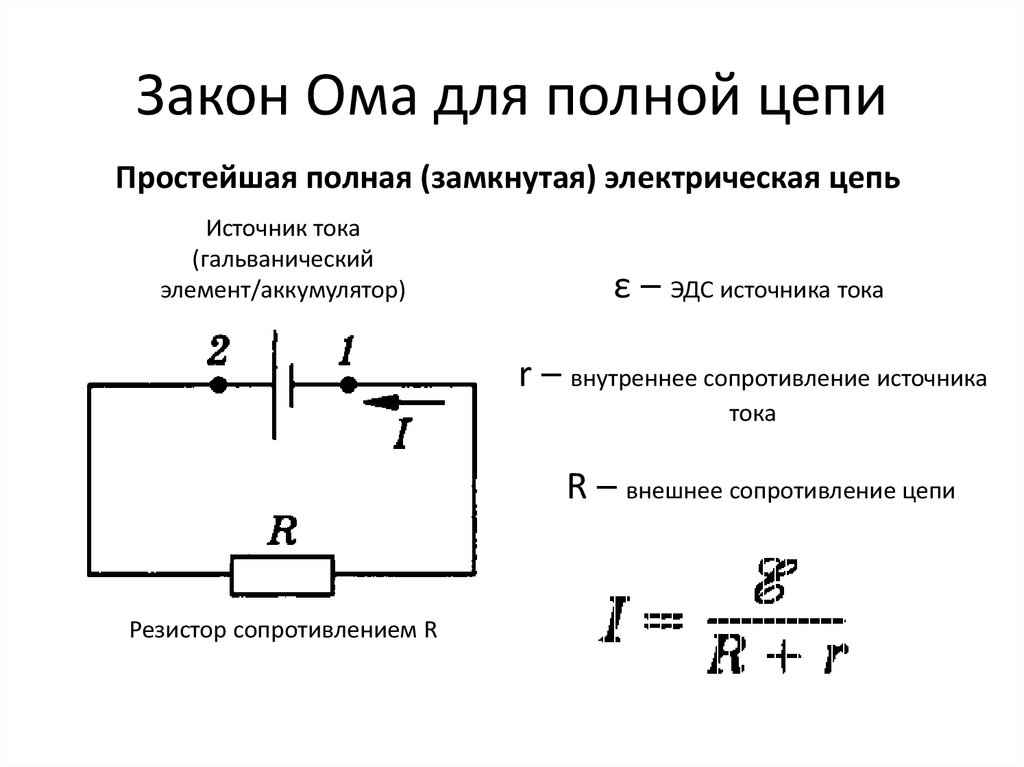
Закон Ома для полной цепи

Замкнутая цепь состоит из источника тока с ЭДС E и внутренним сопротивлением r, потребителя с сопротивлением R, и ключа К. После замыкания ключа К по цепи идёт ток силой I.

Закон Ома для полной цепи

• Сила тока в замкнутой цепи прямо пропорциональна величине электродвижущей силы источника тока и обратно пропорциональна полному сопротивлению цепи, равному сумме сопротивлений внешней и внутренней цепи. I=E/(R+r).

Давайте обсудим

Что называется электрическим током

Какая физическая величина называется силой тока?

Какие силы называются сторонними?

Какие виды источников тока вы знаете?

Сформулируйте закон Ома для участка цепи

Как зависит величина сопротивления металлического проводника от его размеров? Как это объяснить?

Какая цепь называется замкнутой или полной?

Какому закону подчиняется прохождение тока по замкнутой цепи? Сформулируйте его.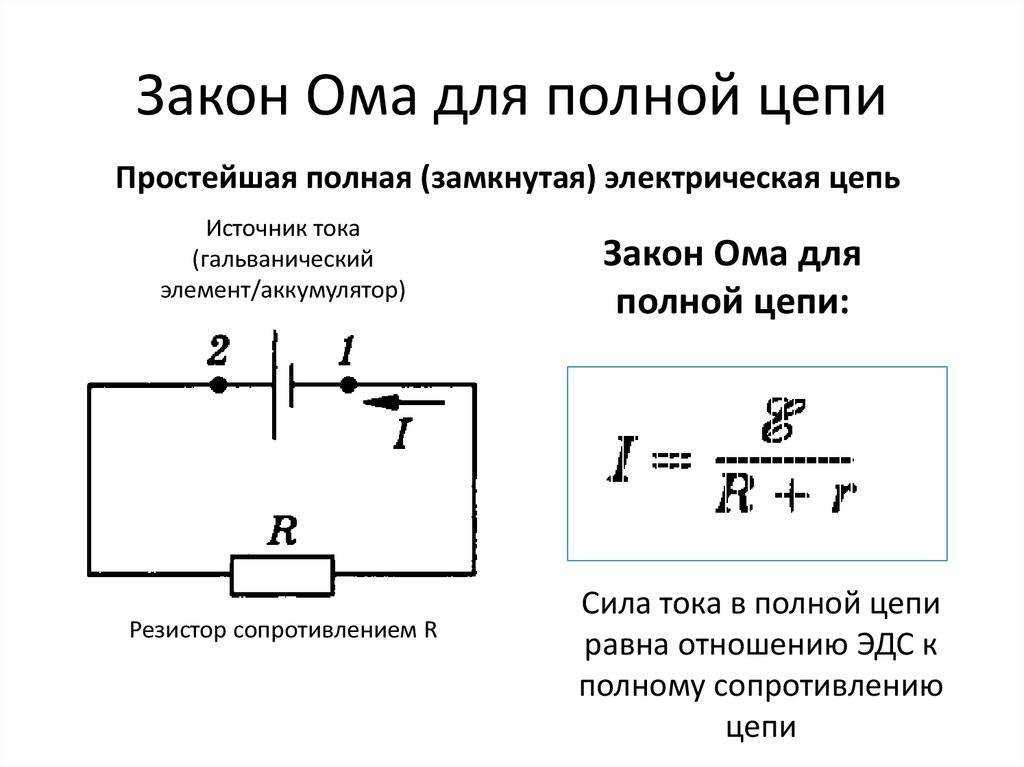

Исследовательские задания в группах Определение внутреннего сопротивления источника

• Соберите цепь по схеме
• Поместите ползунок посередине реостата
• Замкните ключ. Измерьте показания амперметра и вольтметра.
• Вычислите внешнее сопротивление по закону Ома для участка цепи
• Разомкните цепь. Снимите показания вольтметра при разомкнутом ключе, это показание примите за значение ЭДС.
• Используя формулу закона Ома для полной цепи, выведите формулу для расчёта внутреннего сопротивления. Вычислите внутреннее сопротивление источника тока.

Где допущена ошибка?

Вычислите токи короткого замыкания

Источник тока

Гальванический элемент

ε ,В

1,5

Аккумулятор

r , Ом

I к.з., А

1

6

Осветительные сети

100

0,01

0,001

1,5

600

100 000

Виды предохранителей

• Плавкие
• Автоматические
• Сетевые фильтры
• Щитки автоматические

Щиток автоматический

Решите задачу

При подключении лампочки к батарее элементов с ЭДС 4,5 В вольтметр показал напряжение на лампочке 4 В, а амперметр – силу тока 0,25 А. Каково внутреннее сопротивление батареи?

Задание на дом:§9.1;9.2;9.3;9.5; упр.19 (2)

Рефлексия:

• Визитная карточка
• Что я узнал нового на уроке
• Самооценка деятельности на уроке.

Электрические цепи: проверка закона Ома — 2133 слов

Введение

Анализ состоит из трех разделов, где первая часть использовалась для экспериментальной проверки закона Ома. Второй и третий эксперименты были проведены для оценки цепей делителя напряжения и тока. В целом, целью CEN201: Лабораторный эксперимент 1 – Электрические цепи было:

1. Экспериментальная проверка закона Ома путем поддержания постоянного напряжения и изменения сопротивления.
2. Экспериментально проверить формулу делителя напряжения.
3. Для экспериментальной проверки формулы делителя тока.

Теоретическая основа

Закон Ома определяет зависимость между напряжением и током идеального проводника.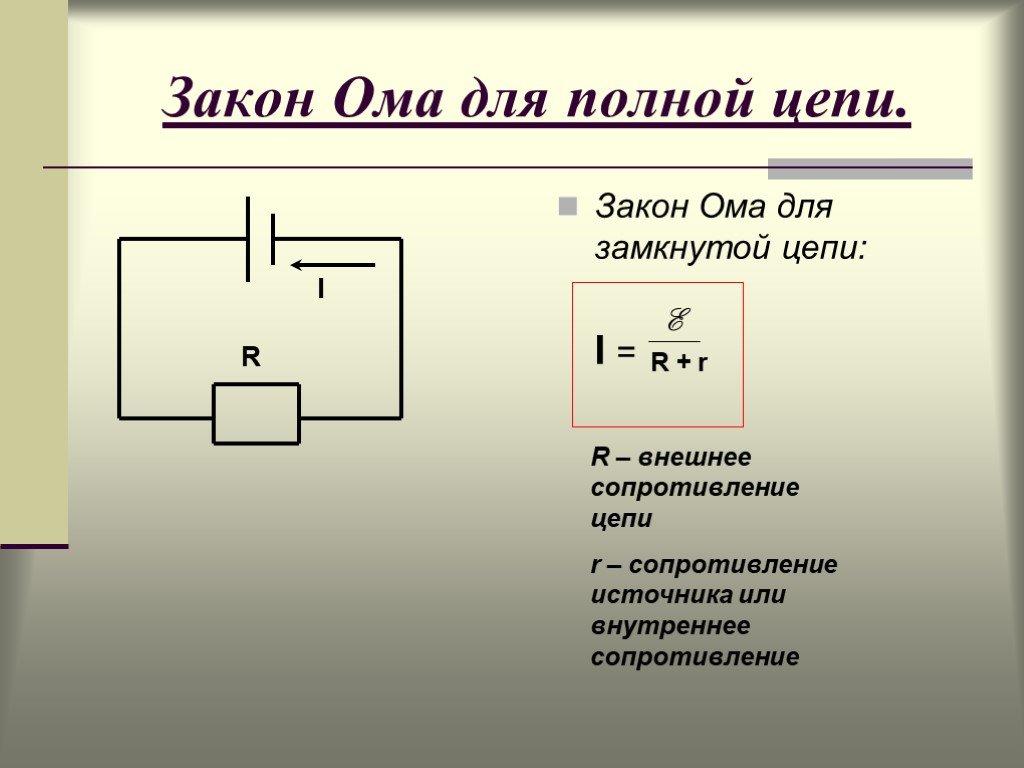 Эта взаимосвязь была впервые обнаружена немецким физиком Георгом Омом в 1826 году (Engineermaths, nd; University of Kentucky, nd). Закон гласит, что ток, проходящий через электрическую цепь, прямо пропорционален напряжению и обратно пропорционален сопротивлению системы при постоянной температуре (Engineermaths, nd; Technical Books Pdf, nd). Соотношение закона Ома представлено уравнением 1, которое иллюстрирует, что если известны два значения напряжения, тока или сопротивления, можно определить недостающую величину (Технические книги Pdf, n.d). Графическое представление закона Ома называется треугольником закона Ома, показанным на рисунке 1. На рисунке 2 показаны различные комбинации законов Ома, показывающие, как могут быть рассчитаны различные параметры.

I = V/R (уравнение 1), где

• I = ток в амперах (А)
• В = напряжение в вольтах (В)
• R = сопротивление в Омах (Ом)

Рисунок 1. Треугольник закона Ома (Technical Books Pdf, n.d). Рисунок 2. Различные комбинации законов Ома (Technical Books Pdf, nd).

Закон Ома широко используется в расчетах и ​​проектах электроники. Устройства, которые подчиняются закону Ома, называются омическими, тогда как те, которые не подчиняются, называются неомическими (Университет Кентукки, nd). Резисторы и кабели являются примерами омических устройств, тогда как диоды и транзисторы относятся к категории неомических (Университет Кентукки, nd). Взаимосвязь различных факторов закона Ома может быть установлена ​​экспериментально. В связи с этим первая часть эксперимента заключалась в проверке закона Ома путем определения тока через разное сопротивление при постоянном напряжении. В анализе использовалась простая схема, подобная той, что показана на рис. 3, где график зависимости тока от сопротивления был построен по строгому закону Ома.

Второй эксперимент использовался для исследования схемы делителя напряжения и проверки ее формул. Формула делителя напряжения показывает, как напряжение делится между последовательно соединенными резисторами. Рассмотрим схему на рисунке 3, ток, протекающий через цепь, можно рассчитать с помощью уравнения 2. Общее сопротивление цепи будет суммой номиналов резисторов 1 и 2, поскольку они соединены последовательно, как показано в уравнении 2. Напряжение на резисторе 2 можно рассчитать с помощью уравнения 4. Подставив уравнения 2 и 3 в уравнение 4, значение напряжения на резисторе 2 можно рассчитать с помощью выражения 5, которое представляет собой формулу делителя напряжения. Уравнение показывает, что напряжение на последовательных резисторах равно произведению отношения его сопротивления к суммарному значению всех резисторов, умноженному на общее напряжение (Калифорнийский университет, nd). Та же процедура может быть использована для определения напряжения на резисторе 1, которое дано в уравнении 6. Формула делителя напряжения была проверена экспериментально в этом анализе.

Рис. 3. Типичная схема с двумя последовательно соединенными резисторами (Калифорнийский университет, без даты).

I8 = Vs/Req (уравнение 2)

Req = R1 + R2 (уравнение 3)

V2 = R2I8 (уравнение 4)

/ R8 = R+R8 (Уравнение 5)

V1 = R1 / R1+R2 = V8 (Уравнение 6), где

• i _с = ток, проходящий через цепь
• v _с = напряжение в цепи
• Req = эквивалентное сопротивление (общее сопротивление системы)
• R1 = значение сопротивления резистора 1
• R2 = значение сопротивления резистора 2
• v ₂ = напряжение на резисторе 2 напряжение на резисторе 1

Третий эксперимент был использован для анализа схемы делителя тока и проверки ее формул. Формула делителя тока показывает, как делится ток при прохождении через параллельные резисторы. Рассмотрим схему на рис. 4. Общее сопротивление можно рассчитать по уравнению 7. Напряжение в точках 1 и 2 равно выражению 8. Применив законы Ома к каждому резистору, можно определить ток по уравнению 9.и 10 для резисторов 1 и 2 соответственно (Университет Саймона Фрейзера, nd). Формулы делителя показывают, что ток, проходящий через набор резисторов в параллельной конфигурации, разделяется таким образом, что большее количество течет по пути с меньшим сопротивлением. Если один из резисторов имеет нулевое сопротивление (короткое замыкание), весь ток проходит через другой. Текущая формула делителя была проверена экспериментально в исследовании.

Рис. 4. Типичная схема с двумя резисторами в параллельной конфигурации (Калифорнийский университет, без даты).

Треб. = R1R2 / R1 + R2 (уравнение 7)

V12 = I8Req (уравнение 8)

I1 = V12/R1 = Треб./R1*I8 = R1 / R1 + R2*I8 (уравнение 9) )

I2 = V12 / R2 = Req / R2 * I8 = R1 / R1 + R2 * I8 (уравнение 10) где,

• i _с = ток, проходящий через цепь
• v _с = напряжение в цепи
• Req = эквивалентное сопротивление (общее сопротивление системы)
• R1 = значение сопротивления резистора 1
• R2 = значение сопротивления резистора 2
• В ₁₂ = напряжение между точками 1 и 2
• i ₁ = ток, протекающий через резистор 1

Методика

Аппаратура

Эксперимент проводился с использованием передовой электронной экспериментальной платформы, платы электрических сетей и мультиметра, которые представлены на рисунках 5.

Рисунок 5. Перечень оборудования, использованного при анализе (усовершенствованная электронная экспериментальная платформа, плата электрических сетей и мультиметр) . Он также обеспечивает выход для различных схемных конфигураций.

Плата электрической сети представляет собой схемную платформу, которая соединяет различные компоненты цепи, такие как резисторы и кабели.

Мультиметр – портативный прибор для измерения тока, напряжения и сопротивления цепи или различных компонентов, используемых в электрической сети.

Процедура

Анализ состоит из трех частей, где первая часть использовалась для проверки закона Ома, а во второй и третьей части были исследованы цепи делителя напряжения и тока соответственно. Первый эксперимент начался с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Перемычка между розетками 1.6 и 1.7 была подключена. После этого также был подключен лид между 1.10 и 1.12. Мультиметр в режиме постоянного тока был подключен между гнездом 1. 13 (плюс) и 1.2 (общий). Схема, рассмотренная для этого эксперимента, представлена ​​на рисунке 6. Значение переменного резистора было установлено на 100 Ом. Был включен модуль питания усовершенствованной электронной экспериментальной платформы. Значение тока было измерено и записано в Таблицу 1. Эксперимент был повторен для различных значений сопротивления (200 Ом, 300 Ом, 400 Ом, 500 Ом, 600 Ом, 700 Ом и 800 Ом).

Рис. 6. Схема по закону Ома, используемая для анализа.

Вторая часть анализа была использована для исследования схемы делителя напряжения и проверки формулы. Эксперимент начался с того, что питание модуля усовершенствованной электронной экспериментальной платформы было отключено. После этого были подключены закорачивающие перемычки между розетками 3.2 и 3.3, а также между розетками 3.8 и 3.11. Напряжения на резисторах 6 и 7 были рассчитаны с использованием уравнений, аналогичных уравнениям 5 и 6, и записаны в Таблицу 2. Блок питания модуля усовершенствованной электронной экспериментальной платформы был включен, и напряжения на резисторах R6 и R7 были измерены и записаны в Таблицу 2. На Рисунке 7 показана схема делителя напряжения, рассматриваемая при анализе.

Рис. 7. Схема делителя напряжения, рассматриваемая при анализе.

Третий эксперимент был использован для исследования схемы делителя и проверки формулы. Упражнение началось с отключения питания модуля усовершенствованной электронной экспериментальной платформы. Провода между розетками 3.3 и 3.6, 3.5 и 3.13, а также между 3.2 и 3.3 были подключены, как описано в лабораторном руководстве. В анализе использовалась схема делителя тока, представленная на рис. 8. Используя аналогичные уравнения для 9и 10, ток, проходящий через R6 и R8 . После этого был включен источник питания модуля усовершенствованной электронной экспериментальной платформы, а также токи через R6 и R8 с помощью мультиметра в соответствии с подключениями, указанными в лабораторном руководстве. Расчетные и измеренные значения занесены в Таблицу 3.

Рис. 8. Схема делителя тока, рассматриваемая при анализе.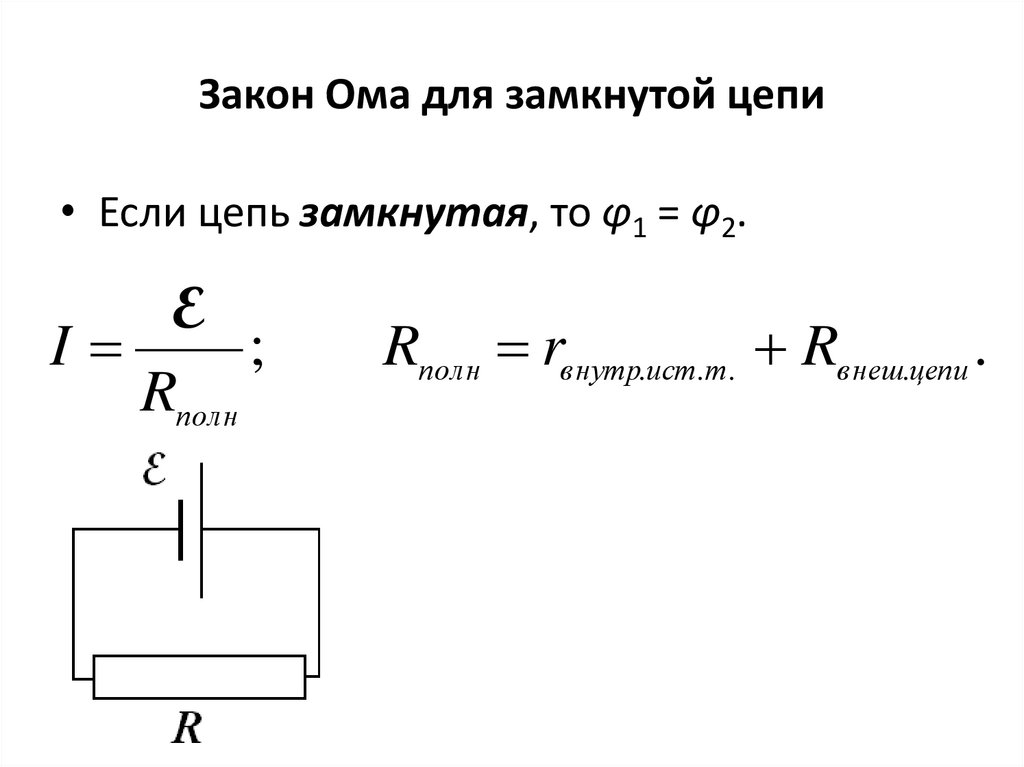

Результаты

Результаты проверки закона Ома, формулы делителя напряжения и тока были записаны в Таблицы 1, 2 и 3 соответственно.

Таблица 1. Результаты эксперимента по проверке закона Ома

Пример расчета;

Учитывая первый эксперимент с сопротивлением 100 Ом.

I = V/R

• I = ток
• V = напряжение = 12 В
• R = 100 Ом

I = V/R = 12/100 = 0,12 A = 1204 мА 9000 = погрешность Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 120 – 119,986 / 120 * 100 = 0,012%

Рисунок 9. График зависимости тока от сопротивления.

Таблица 2. Результаты были получены в результате эксперимента с делителем напряжения.

Пример расчета;

Расчетное напряжение на резисторе R6

V6 = R6 / R7 + R6 * V8 = 1000 / 1000 + 1500 * 12 = 4,8 В

Погрешность в процентах = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 4,800 – 4,900 / Теоретическое значение * 100 = 2,10%

Расчетное напряжение на R7

V7 = R7 / R6 + R7 * V8 = 1500 / 1000 + 1500 * 12 = 7,2 вольта

Процентная ошибка = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 7,200 – 7,257 / 7,200 * 100 = 0,80%

Процентная ошибка для полного напряжения;

Процентная ошибка = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 12,000 – 12,157 / 12,000 * 100 = 1,31%

Таблица 3. Результаты, полученные в ходе эксперимента с делителем тока.

Пример расчета;

Расчетный ток в R6

I6 = V12 / V6 = 12/100 = 12 мА

Погрешность в процентах = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 12,000 – 12,367 / 12,000 * 100 = 0,031%

Расчетный ток в R7

I8 = V12/R8 = 12/60 = Теоретическое значение – Экспериментальное значение / Теоретическое значение * 100 = 17,650 – 18,162 / 17,650 * 100 = 2,90%

Расчетный общий ток;

Req = R1R2 / R1+R2 = 1000 * 680 / 1000 + 680 = 404,762 Ом

V12 = IsReq = 12 v = Is * 404,762 Ом

I _S = 12 В / 404,762 Ом = 29,650 мА

Процентная ошибка = теоретическое значение — Экспериментальное значение / Thoeretication * 100 = 29,650 — 30,503 / 29,650 * 100 = 2,88%

обсуждение

. В эксперименте закон Ома определяли путем измерения тока через различные сопротивления при постоянном напряжении. Как измеренные, так и рассчитанные значения показывают, что ток уменьшается с увеличением сопротивления, как показано на рисунке 9.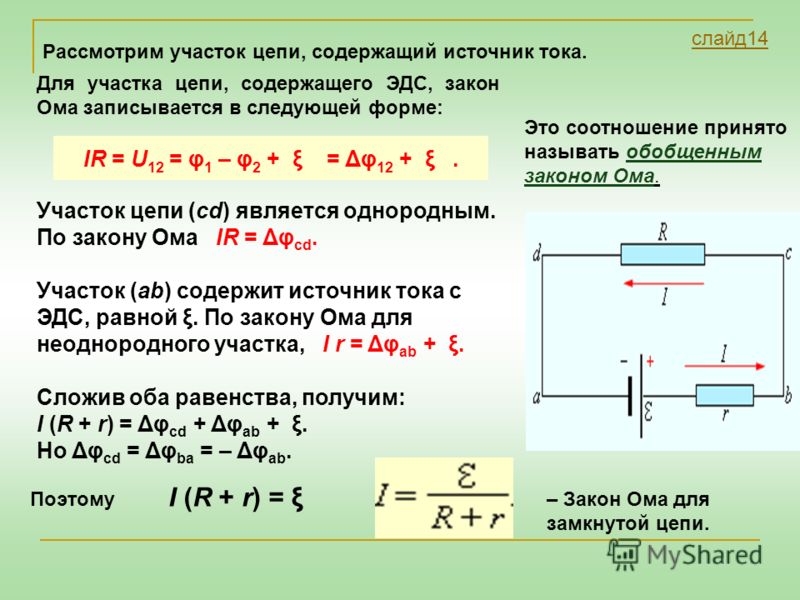 . Было обнаружено, что существует небольшая разница между измеренным и рассчитанным током, проходящим через различные сопротивления. Измеренный ток оказался выше расчетных значений, что может быть связано с некоторым сопротивлением соединительных кабелей и измерительных устройств, которое предполагается при теоретическом рассмотрении. Второй эксперимент показывает, что напряжение на резисторе R7 (7,257 вольта) было выше, чем на резисторе R6 (4,901 вольта). Результаты показывают, что напряжение разделяется в зависимости от значения сопротивления. Чем больше номинал резистора, тем больше напряжение на нем. В третьем эксперименте было обнаружено, что больший ток проходит через R8, который имеет меньшее сопротивление, чем R6. Таким образом, формула делителя тока была проверена экспериментально.

Заключение

Цели анализа были достигнуты, и в первой части эксперимента был сделан вывод, что ток, проходящий через электрическую цепь, обратно пропорционален сопротивлению системы.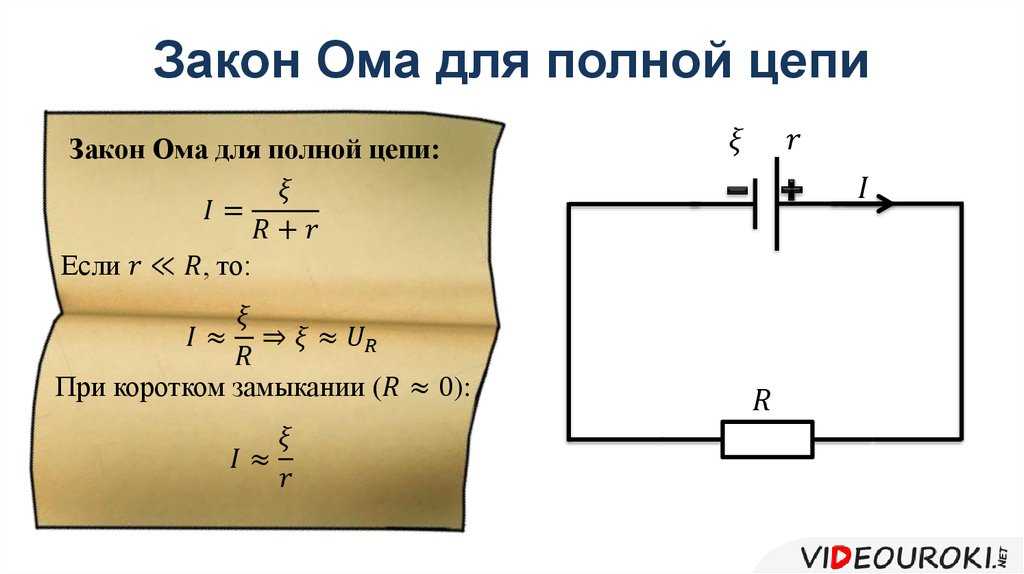 Формула делителя напряжения была проверена экспериментально, и был сделан вывод, что напряжение делится пропорционально величине сопротивления. В третьем эксперименте было установлено, что ток разделяется таким образом, что большее его количество протекает через путь с меньшим сопротивлением для резисторов, расположенных параллельно в цепи делителя.

Послелабораторные вопросы

• Вопрос 1.1: Сопротивление обратно пропорционально току для источника постоянного напряжения.
• Вопрос 1.2: Ток уменьшится, если напряжение, подаваемое на переменный резистор, уменьшится наполовину, поскольку эти два параметра прямо пропорциональны по закону Ома.
• Вопрос 2.1: Напряжение прямо пропорционально номиналу каждого резистора в цепи делителя.
• Вопрос 3.1: В цепи делителя больший ток протекает по пути с меньшим сопротивлением. Через R6 проходит меньший ток по сравнению с R7.

Ссылки

Инженерная математика, (без даты). Введение в закон Ома .

Университет Саймона Фрейзера. (н.д). КВЛ Пример резисторного делителя напряжения .

Университет Кентукки. (н.д). Закон Ома и сопротивление .

Технические книги Pdf. (н.д). Формула закона Ома .

Калифорнийский университет. (н.д). Делители напряжения и тока .

Электрическая цепь – определение, символы и формулы

Замкнутые электрические цепи или пути создают сеть электрических частей, по которым могут двигаться электроны.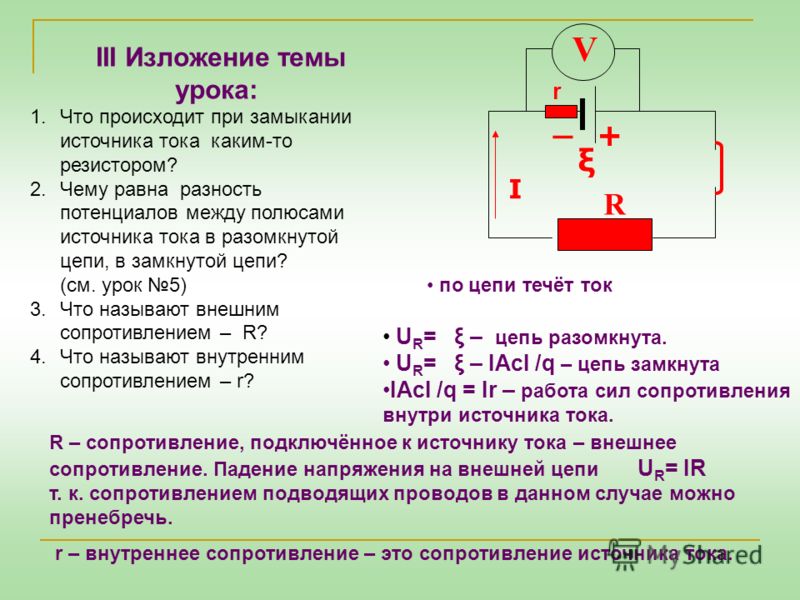 Эта дорожка построена из линий электропередач и питается от батареи или другого источника. Точка, в которой электроны входят в электрическую цепь, называется источником, а точка, откуда они выходят, известна как возврат.

Символы электрических цепей

Символ присутствует в каждом компоненте и выходе электрической цепи. На принципиальной схеме символы обозначают различные компоненты схемы. Стандартный набор символов, включенных в принципиальную схему, показан ниже.

Простая цепь

Нагрузка, переключатель, провода и источник питания образуют короткое замыкание.

• Источник питания, ячейка.
• Резистор часто называют нагрузкой. Когда цепь включена, внутри нее загорается лампочка.
• Проводники состоят из неизолированных медных проводов. Нагрузка подключается к источнику питания кабеля на одном конце, а источник питания снова подключается к блоку на другом конце.
• Переключатель: в цепи есть небольшой разрыв. Переключатели бывают разных видов. Чтобы открыть или закрыть курс, используйте элемент управления.

Как мы измеряем электрические цепи?

Простые схемы с небольшим количеством компонентов часто просты для понимания новичками. Однако, когда к вечеринке присоединяются другие элементы, все становится сложнее.

Куда пойдет ток? Это критические вопросы, которые необходимо сделать в этой ситуации. Что произойдет, если напряжение? Можно ли упростить для лучшего понимания?

При использовании цепей с наиболее фундаментальными компонентами, батареями и резисторами, первая тема для обсуждения — это различие между параллельными цепями и последовательными цепями. Разница между двумя установками, несомненно, стала бы очевидной в этой ситуации.

После этого необходимо выяснить, что происходит, когда компоненты различных типов, такие как катушки индуктивности и конденсаторы, объединяются в последовательные и параллельные цепи. Последовательная цепь — это цепь, в которой резисторы расположены в виде цепочки, требующей, чтобы ток протекал только по одному каналу. Кроме того, каждый резистор испытывает одинаковый ток. Далее, суммируя значения сопротивления каждого резистора, можно получить общее сопротивление цепи.

Параллельная цепь — это цепь, в которой резисторы расположены так, что их хвосты соединены друг с другом, а их головки соединены. Кроме того, суммируя обратные значения сопротивления, можно получить общее сопротивление группы параллельных резисторов. Сумма должна быть умножена сама на себя, чтобы получить обратное.

Формула электрической цепи

Требование определяется как Req = R1 + R2 + R3 +.

Кроме того, формула параллельной цепи 1/Req = 1/R1 + 1/R2 + 1/R3 +….

Где

Req равно суммарному сопротивлению последовательно соединенных резисторов.

R1, R2,… — резисторы, соединенные последовательно.

Вывод формулы электрической цепи

Относительно последовательных резисторов:

Ток I в цепи определяется по закону Ома, когда одиночный резистор подключен к цепи с источником напряжения V:

Закон Ома : I = V / R

Давайте теперь посмотрим, что происходит, когда мы подключаем второй резистор последовательно. Кроме того, серия подразумевает, что резисторы работают последовательно, как звенья цепи. Далее мы можем называть их резисторами R1 и R2.

Из-за соединения резисторов источник напряжения V вызывает протекание через каждый из них одинакового тока I.

Согласно закону Ома, цепь с сопротивлением R и напряжением V будет выглядеть следующим образом:

I = V / R

Следовательно, можно изменить уравнение, умножив обе части на R

V = IR

следовательно, для резистора R1

V1 = IR1

вместе с резистором R2

V2 = IR2

V – V1 – V2 = 0

организация новых договоренностей

V = V1 + V2

Кроме того, замена ранее вычисленных V1 и V2

V равно I(R1 + R2) или I(IR1 + IR2).

на I, деля обе стороны

V / I = R1 + R2

Однако теперь мы понимаем, что V / I = полное сопротивление цепи благодаря закону Ома. Кроме того, давайте назовем его Total.

Следовательно,

Итого R = R1 плюс R2

Дополнительно, Итого = R1 + R2 +…… Rn

Чтобы получить общее сопротивление последовательно соединенных резисторов, необходимо просуммировать все значения.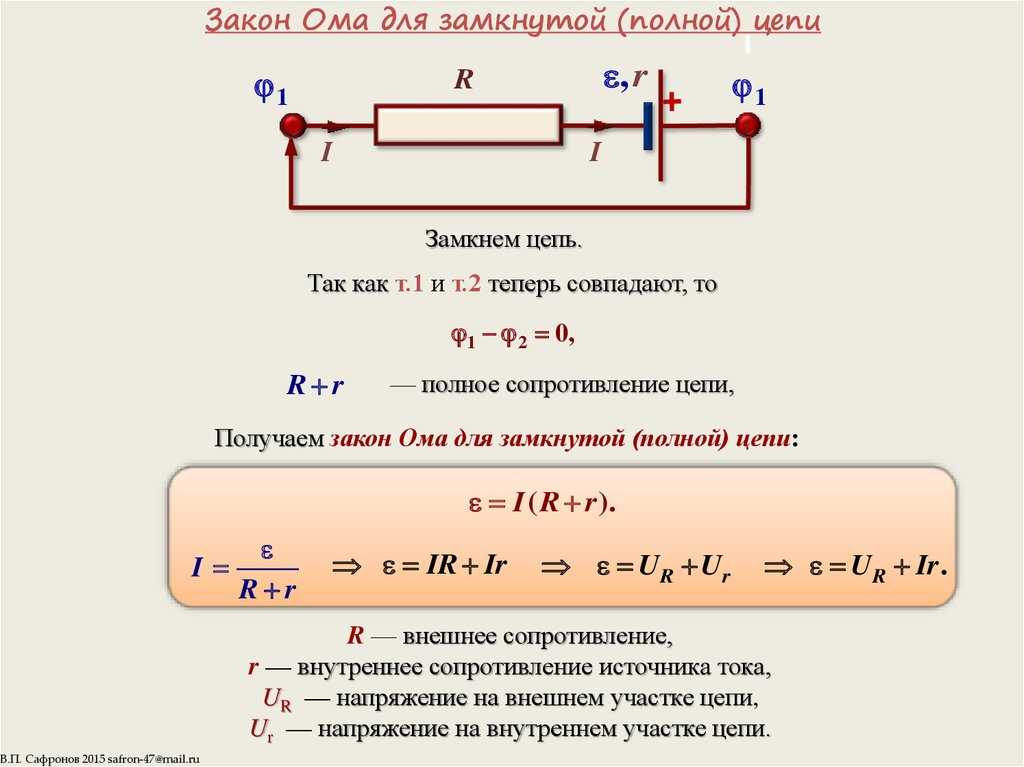

При использовании параллельных резисторов:

Все резисторы цепи содержат полное напряжение. Закон Ома гласит, что токи, протекающие через каждый резистор, равны I1 = V/R2, I2 = V/R2 и I3 = V/R3. Кроме того, сохранение заряда предполагает, что общая тяга представляет собой сумму этих отдельных токов.

I= I1 + I2 + I3.

Результаты подстановки формул для отдельных токов следующие:

I равно V/R1, R2 и R3.

Или

I = V (1/R1 + 1/R2 + 1/R3)

Отсюда следует, что общее сопротивление параллельной цепи равно сумме обратных величин ее компонентов. Следовательно, для любого хода, содержащего n параллельно соединенных резисторов,

Rn = 1/R1/R2/R3… + 1/Rn.

Серия — параллельные цепи

Однако мы не сможем применить единый набор правил к каждому участку этой цепи, если компоненты цепи соединены последовательно в серии — параллельные цепи в других. Вместо этого, чтобы понять, что происходит, мы должны сначала выяснить, что последовательно, а что параллельно. Рассмотрим курс, показанный ниже:

Серия А – Схема параллельных цепей

Мы можем исследовать цепь по фазам, рассматривая каждый компонент по одному и используя соответствующие правила для установления корреляции между напряжением, током и сопротивлением, если мы можем установить, какие элементы цепи включены последовательно, а какие — параллельно.

Электрическая распределительная коробка

Электрическая распределительная коробка, также известная как щит с выключателем, представляет собой металлический ящик с дверью, часто встроенный в стену в определенной части вашего дома, в которой находятся все выключатели вашего дома. помещается внутрь.

Кто может включить и отключить выключатель? Они предназначены для автоматического отключения, когда через них проходит слишком большой электрический ток.

Основной автоматический выключатель в распределительной коробке регулирует подачу электричества в дом. Кроме того, вы увидите различные выключатели, каждый из которых отвечает за подачу энергии в разные области вашего дома.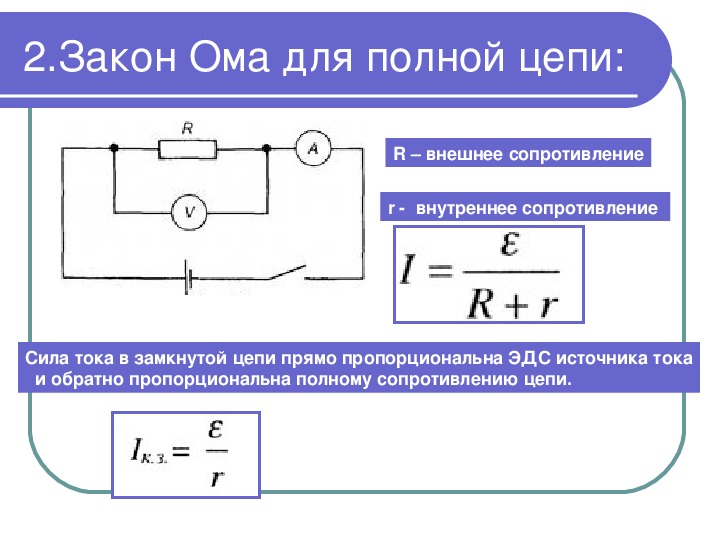 Домашняя секция, которую регулирует каждый автоматический выключатель, должна быть отмечена на этикетке устройства для постоянной проверки.

Часто задаваемые вопросы 

1. Что означает термин «электрическая цепь»?

Электрическая цепь представляет собой замкнутый контур, по которому течет ток. Канал, который позволяет передавать электрический ток, иногда называют электрической цепью.

2. Два резистора по 100 кОм соединены последовательно с пятью резисторами по 10 кОм. Общее сопротивление какое?

Мегаомы (сокращенно «М») и килоомы (сокращенно «к») часто используются для указания номиналов резисторов.

Один килоом (1 кОм) равен 1000 Ом, или 1 x 103.

Один мегаом, иногда называемый 1 МОм, равен 1 000 000 Ом, или 1 x 106.

Было бы предпочтительнее, если бы мы выразили значения в экспоненциальном представлении для дальнейшего упрощения требуемой математики.

В последовательной цепи сумма всех сопротивлений равна общему сопротивлению.

= 5 x (10k) + 2 x (100k)

= 5 x (10 x 103) + 2 x (100 x 103)

= 50 x 103 + 200 x 103

= 250 x 503 k равно 2

3. Что такое «короткое замыкание»?

«Короткое замыкание» — это ошибочное соединение с малым сопротивлением, такое как провод с почти нулевым сопротивлением, предлагающий легкий канал для электричества. Считайте, что это ярлык в электрической системе. Вместо запланированного соединения он обычно используется для обозначения ошибки или случайного соединения.

Например, мы говорим, что в батарее произошло короткое замыкание, если выводы двух батарей соприкасаются и образуют соединение с небольшим сопротивлением. Вместо прохождения правильной цепи ток будет проходить через это короткое замыкание. В результате протекания значительного тока по проводам и батареям это препятствует функционированию цепи и может привести к возгоранию.

4. Почему моя схема считает три или четыре после только одного нажатия переключателя?

Это может произойти, если переключатель подключен непосредственно к тактовому входу счетчика.