Законы Кирхгофа для цепи синусоидального тока

Законы Кирхгофа, рассмотренные ранее для цепей постоянного тока, справедливы и для мгновенных значений синусоидального тока.

Первый закон Кирхгофаприменяется к узлам электрической цепи и гласит:алгебраическая сумма мгновенных значений токов в узле электрической цепи равна нулю, т.е.

i_k = 0,

где i_k— токk-й ветви, присоединенной к данному узлу;n— число ветвей, подключенных к данному узлу.

Токи, направленные к узлу, записываются со знаком “+”, а направленные от узла — со знаком “–” (или наоборот).

Второй закон Кирхгофаприменяется к контурам электрической цепи. Контур — любой путь вдоль ветвей электрической цепи, начинающийся и заканчивающийся в одной и той же точке. Второй закон Кирхгофа формулируется следующим образом:алгебраическая сумма мгновенных значений падений напряжений на элементах контура равна алгебраической сумме мгновенных значений ЭДС, действующих

в этом контуре:

u_k = e_k,

где u_k— напряжение на к-м сопротивлении контура;e_k — к-я ЭДС, входящая в данный контур;n — число сопротивлений в контуре;m — число ЭДС в контуре.

Для составления уравнений по второму закону Кирхгофа направление обхода контура выбирается произвольно. ЭДС и падения напряжения, направления которых совпадают с направлением обхода контура, считаются положительными.

Законы Кирхгофамогут быть представлены в векторной или комплексной формах:

_k = 0, _k = _k,

Расчет электрических цепейпо законам Кирхгофа в цепях синусоидального тока проводится в том же порядке, что и для цепей постоянного тока.

Рассмотрим цепь, содержащую только резистивный элемент (резистор) с сопротивлением R. Мгновенное значение тока в цепи с резистором (рис. 3,а) определяется по закону Ома:

i_R = u_R / R,

если u_R  = U_m sin t, получимi_R= (U_m /R) sint = I_m 

sin t, гдеI_m= U_m/R, разделив левую и правую части на, получим закон Ома для цепи с резистором, выраженный через действующие значения напряжения и тока в нем:

I = U / R.

Сравнивая выражения для тока i_R и напряженияu_Rможно сделать вывод о том, чтона резистивном элементе фазы напряжения и тока совпадают. Для цепи с резистором закон Ома в комплексной форме имеет вид:

, .

Мгновенная мощность произвольного участка цепи может быть определена как произведение мгновенных значений напряжения и тока этого участка и представляет собой скорость изменения энергии в данный момент времени. Учитывая отсутствие фазового сдвига между напряжением

u_Rи токомi_Rна резистивном элементе, а также принимая значения начальных фаз напряжения и тока равными нулю, получим для мгновенной мощности резистивного элементаp_R:

p_R = u_Ri_R= U_msin(t)I_msin(t) = UI(1—cos(2t)).

Мгновенная мощность p

Rсодержит две составляющие: постоянную, равную произведению действующих значений напряжения и тока, и переменную, частота изменения которой в два раза больше, чем частота напряжения (или тока). Мгновенная мощность резистора никогда не принимает отрицательных значений. Физически это означает, что имеет место только односторонняя передача энергии: от источника энергии к резистору. В резисторе энергия не накапливается, а преобразуется в другие виды энергии (например, в тепловую).

Векторная диаграмма цепи (рис. 3, а) изображена на рис. 3,б, а графики мгновенных значений тока

i_R, напряженияu_Rи мощностиp_Rрезистивного элемента представлены на рис. 3,в.

Рис. 3

Цепи постоянного тока — Физика

ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ (СИЛЫ) ТОКА .

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике , где R — сопротивление проводника.

РЕЗИСТОРОМ называется устройство, обладающее заданным постоянным сопротивлением.

НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ

.

ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ

, где j₁ и j₂ — потенциалы концов участка Е₁₂ — э.д.с., действующая на данном участке цепи.

ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ , где Е — суммарная э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи.

РАЗВЕТВЛЕННОЙ ЦЕПЬЮ называется электрическая цепь, имеющая узлы.

УЗЛОМ называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, принято считать положительным, а ток, текущий от узла, считается отрицательным.

ПЕРВОЕ ПРАВИЛО КИРХГОФА: алгебраическая сумма токов, сходящихся в узле, равна нулю = 0.

ВТОРОЕ ПРАВИЛО КИРХГОФА: в каждом из замкнутых контуров, которые можно мысленно выделить в данной разветвленной цепи, алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с.

.

При анализе разветвленной цепи следует обозначать с одним индексом ток, протекающий по всем последовательно соединенным элементам от одного узла до другого. Направление каждого тока выбирается произвольно.

При составлении уравнений второго правила Кирхгофа токам и э.д.с. нужно приписывать знаки в соответствии с выбранным (как вам удобно) НАПРАВЛЕНИЕМ ОБХОДА:

• ток принято считать положительным, если он совпадает с направлением обхода, и отрицательным, если он направлен против этого направления;
• э.д.с. считается положительной, если ее действие (создаваемый ею ток) совпадает с направлением обхода.

КОЛИЧЕСТВО УРАВНЕНИЙ первого правила Кирхгофа должно быть на одно меньше количества узлов в данной цепи. Количество независимых уравнений второго правила Кирхгофа должно быть таким, чтобы общее количество уравнений оказалось равным количеству различных токов. Каждый новый контур при этом должен содержать хотя бы один участок цепи, не вошедший в уже рассмотренные контуры.

МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ

В данной лабораторной работе исследуется модель простейшей разветвленной электрической цепи, состоящей из трех источников э. д.с., подключенных параллельно к одному резистору (нагрузке).

Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.

Нарисуйте в конспекте эквивалентную схему цепи, расположив источники один под другим и учитывая наличие внутреннего сопротивления у каждого источника. Укажите знаки э.д.с., направления токов в каждом участке и направления обхода каждого замкнутого контура. Составьте систему уравнений для нахождения токов в каждом участке.

ИЗМЕРЕНИЯ

Соберите на экране заданную эквивалентную цепь. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Ориентируйтесь на рисунок схемы в описании к данной ЛР. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен первый источник э.д.с. Переместите маркер мыши вниз на одну клетку и снова щелкните левой кнопкой под тем местом, где расположился первый источник.

Там появится второй источник э.д.с. Аналогично разместите и третий источник.

Разместите далее последовательно с каждым источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку R в нижней части экрана) и амперметр (кнопка А там же). Затем расположите резистор нагрузки и последовательно соединенный с ним амперметр. Под нагрузкой расположите вольтметр, измеряющий напряжение на нагрузке.

Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкните левой кнопкой мыши в точке, где проходит провод.

Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, равное взятому из таблицы 1 для вашего варианта.

Установите сопротивления резистора нагрузки R = 1 Ом. Измерьте значения всех токов и напряжения на нагрузке (щелкнув мышью по кнопке «Счет») и запишите их в таблицу 2. Меняя сопротивление R, повторите измерения параметров и заполните таблицу 2.

Таблица 1. Значения э.д.с. и внутреннего сопротивления источников (не перерисовывать)

Вариат	1	2	3	4	5	6	7	8
Е1,Е2,Е3 [В]	3,7,-2	4,-3,-8	3,6,-4	6,-2,-8	-6,5,8	5,8,-4	-4,6,-7	8,-4,6
R1,R2,R3 [Ом]	2,1,1	1,3,1	2,1,2	1,1,2	2,1,1	1,2,1	1,1,2	1,3,1

Таблица 2. Результаты измерений								Таблица 3. Результаты расчета
	R[Ом]	I1 [A]	I2 [A]	I3 [A]	I [A]	U [В]		I1 [A]	I2 [A]	I3 [A]	I [A]
	1
	2
	3
	4
	5
	6

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА

Запишите для вашей цепи решение системы уравнений для всех токов в общем виде.

Рассчитайте значения всех токов для каждого сопротивления нагрузки и запишите в таблицу 3.

Постройте график экспериментальной зависимости падения напряжения на нагрузке U от тока I через нее.

Сформулируйте выводы по графику.

Вопросы и задания для самоконтроля

1. Что такое электрический ток?
2. Дайте определение величины (силы) тока.
3. Дайте определение разности потенциалов (напряжения).
4. Напишите формулу, связывающую приращение потенциалов и напряжение.
5. Что такое резистор?
6. Напишите формулу для сопротивления последовательно соединенных резисторов.
7. Напишите формулу для сопротивления параллельно соединенных резисторов.
8. Напишите закон Ома для участка цепи. Сравните его с законом Ома в дифференциальной (локальной) форме.
9. Какой участок цепи называется неоднородным?
10. Запишите закон Ома для неоднородного участка цепи.
11. Какими характеристиками описывается источник ЭДС?
12. Сформулируйте первый закон Кирхгофа. Какое свойство заряда он отражает?
13. Запишите формулу для первого закона Кирхгофа.
14. Сформулируйте второй закон Кирхгофа.
15. Запишите формулу для второго закона Кирхгофа.
16. Что такое узел электрической цепи?
17. Что такое полная электрическая цепь?

Закон Кирхгофа — Государственный закон Кирхгофа о текущем законе и законе о напряжении Для анализа любой электрической цепи закона Ома недостаточно. Тем не менее, любую электрическую цепь можно проанализировать с помощью закона Кирхгофа или комбинации закона тока Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL).

Закон Кирхгофа регулирует взаимосвязь между напряжениями и токами в электрической сети. Он был введен в 1847 году немецким физиком Густавом Робертом Кирхгофом. В статье подробно рассматриваются закон и уравнение Кирхгофа, справедливость закона Кирхгофа и некоторые примеры.

Содержание

• 1. Что такое закон Кирхгофа?
• 2. Закон тока Кирхгофа
• 3. Закон Кирхгофа о напряжении
• 4. Справедливость закона Кирхгофа
• 5. Закон Кирхгофа Формула
• 6. Примеры закона Кирхгофа

Прочитать статью полностью

Что такое закон Кирхгофа?

В 1847 году Густав Роберт Кирхгоф ввел пару законов, основанных на законе сохранения заряда и энергии в электрической цепи. Эквивалентный импеданс любой сложной сети или цепи можно легко рассчитать с помощью закона Кирхгофа.

Определение закона Кирхгофа

Ток или напряжение любой ветви цепи также можно рассчитать с помощью закона Кирхгофа. Эти законы справедливы в сетях переменного и постоянного тока на низких частотах.

Законы Кирхгофа подразделяются на два типа:

• Закон Кирхгофа для токов (KCL)
• Закон Кирхгофа для напряжений (KVL)

Закон Кирхгофа для токов

Закон Кирхгофа для токов соединение, но наиболее часто используемый термин — Текущий закон Кирхгофа или KCL. KCL основан на законе сохранения заряда.

Определение закона тока Кирхгофа

Закон тока Кирхгофа гласит, что алгебраическая сумма токов, входящих в узел или замкнутую границу, равна нулю.

Если к узлу подключено N ветвей, и это ток n-й ветви, то математически KCL утверждает, закон, ток, входящий в узел, считается положительным, а ток, выходящий из узла, принимается за отрицательный или наоборот. Предположим, что имеется набор токов ikt, где k = 1, 2, 3. . . . n текут в узел. Пусть i _T (t) будет общим током, тогда

Ток на выходе = ток на входе

Итак, альтернативное утверждение для KCL состоит в том, что сумма токов, входящих в узел, равна сумме токов, выходящих из того же узла.

Применение закона тока Кирхгофа

KCL используется для объединения источников тока, находящихся параллельно. Общий эквивалентный ток представляет собой алгебраическую сумму отдельных параллельных токов, как показано ниже:

Применение KCL в узле a,

Справедливость закона Кирхгофа о токах

Существуют некоторые условия, при которых KCL действителен, а в некоторых случаев, это недействительно. Эти условия:

• KCL не зависит от изменения температуры в контуре.
• KCL действителен для линейных, нелинейных, двусторонних, односторонних, пассивных и активных элементов.
• KCL действителен только для электрических сетей с сосредоточенными параметрами, но не для распределенных электрических сетей. На высоких частотах схема рассматривается как распределенная, а не сосредоточенная, и влияние паразитного сопротивления нельзя игнорировать, поэтому KCL недействителен на высоких частотах.
• Закон Кирхгофа недействителен для изменяющихся во времени магнитных полей.

Закон Кирхгофа о напряжении

Закон Кирхгофа о напряжении также известен как Второй закон Кирхгофа или KVL. КВЛ основан на законе сохранения энергии.

Определение закона Кирхгофа о напряжении

Закон Кирхгофа о напряжении утверждает, что алгебраическая сумма напряжений вокруг замкнутого пути или контура в цепи равна нулю. Если в петле имеется M число напряжений и V _m равно m ^th напряжению, то математически КВЛ можно записать как:

^M ∑ _n=1 v _m = 0

Знак каждого напряжения берется как полярность клеммы, встречающейся первой при движении по петле. Мы можем обходить петли как по часовой, так и против часовой стрелки. Рассмотрим приведенный ниже рисунок:

Отсюда видно, что КВЛ основан на законе сохранения энергии.

Применение закона Кирхгофа о напряжении

КВЛ используется для объединения последовательно расположенных источников напряжения. Общее эквивалентное напряжение представляет собой алгебраическую сумму отдельных напряжений, присутствующих последовательно, как показано ниже:

Справедливость закона Кирхгофа о напряжении

Существуют некоторые условия, при которых КВЛ действителен, а в некоторых случаях он недействителен. Эти условия таковы:

• КВЛ не зависит от изменения температуры в контуре.
• KVL действителен для линейных, нелинейных, двусторонних, односторонних, пассивных и активных элементов.
• KVL действителен только для сосредоточенных электрических сетей, а не для распределенных электрических сетей.

Действие закона Кирхгофа

Законы Кирхгофа действительны для сетей с сосредоточенными параметрами, а не для распределенных сетей. Есть несколько гипотетических случаев, когда KCL и KVL не выполняются.

• Два источника неодинакового напряжения расположены параллельно друг другу.

Если V ₁ ≠V ₂ , то KVL нарушается, поскольку KVL утверждает, что сумма напряжений в замкнутом контуре должна быть равна нулю.

• Два неравных источника тока расположены последовательно друг к другу.

Если I ₁ ≠I ₂ , KCL нарушается, потому что ток, входящий в узел a, не будет равен текущему выходу в узле a.

Формула закона Кирхгофа

Закон Кирхгофа состоит из KVL и KCL. КВЛ утверждает, что алгебраическая сумма напряжений вокруг замкнутого контура равна нулю. KCL утверждает, что алгебраическая сумма токов, поступающих в узел, равна нулю. Математически KCL и KVL можно записать как:

Примеры закона Кирхгофа

Пример 1 : Найти ток i ₀ и напряжение v ₀ в цепи, показанной ниже

Пример 3 : Определить ток i и напряжение v ₀ в цепи, показанной ниже

Схема Кирхгофа Законы лежат в основе анализа схемы. С помощью этих законов, наряду с законом Ома, у нас есть необходимый инструмент для анализа любых электрических цепей. Законы Кирхгофа можно разделить на KCL и KVL.

Какое значение имеет закон Кирхгофа?

Закон Кирхгофа, наряду с законом Ома, лежит в основе анализа любой первичной электрической цепи. Законы Кирхгофа используются для объяснения функции тока и напряжения в электрической цепи. Однако их также можно использовать для изучения сложных схем, которые нельзя упростить еще больше.

В чем заключается применение закона Кирхгофа?

Закон Кирхгофа в основном используется в сеточном и узловом анализе для нахождения неизвестных значений напряжения и тока в ветвях электрической цепи. KCL и KVL также полезны для определения эквивалентного сопротивления некоторых цепей, где присутствуют зависимые источники.

Что такое формула закона Кирхгофа?

Формула закона Кирхгофа основана на законе сохранения энергии и заряда.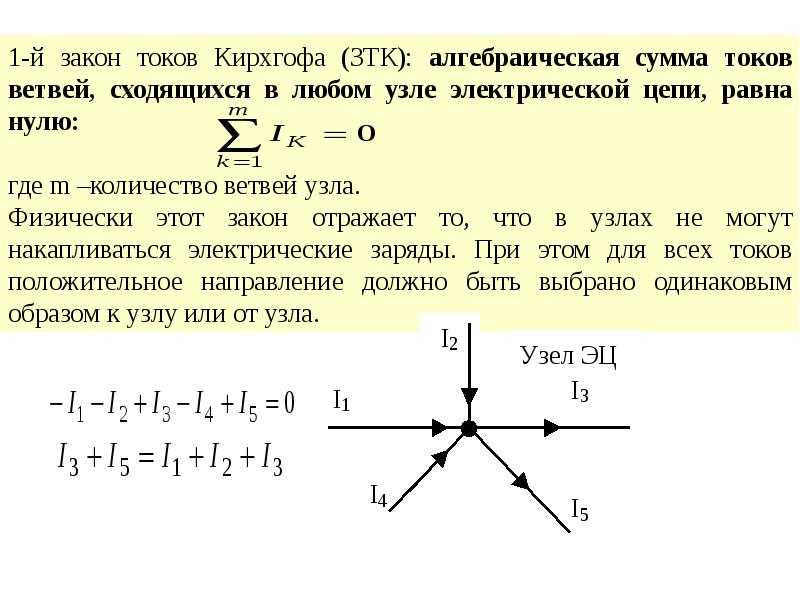 Формула, основанная на законе сохранения энергии, известна как KVL, а формула, основанная на законе сохранения заряда, известна как KCL.

Что такое первый закон Кирхгофа или текущий закон Кирхгофа?

Первый закон Кирхгофа основан на законе сохранения заряда, также известном как KCL. В нем говорится, что алгебраическая сумма токов, входящих в соединение, узел или замкнутую границу, равна нулю. В альтернативном утверждении говорится, что сумма токов, входящих в узел, всегда равна сумме токов, вытекающих из того же узла.

Что такое второй закон Кирхгофа или закон напряжения Кирхгофа?

Второй закон Кирхгофа основан на законе сохранения энергии, также известном как KVL. В нем говорится, что алгебраическая сумма напряжений в замкнутом контуре всегда равна нулю. Альтернативное утверждение утверждает, что общее падение напряжения на элементах контура равно сумме нарастаний напряжения на элементах контура.

При каких условиях закон Кирхгофа не действует?

Закон Кирхгофа недействителен для распределенных сетей и для изменяющихся во времени магнитных полей.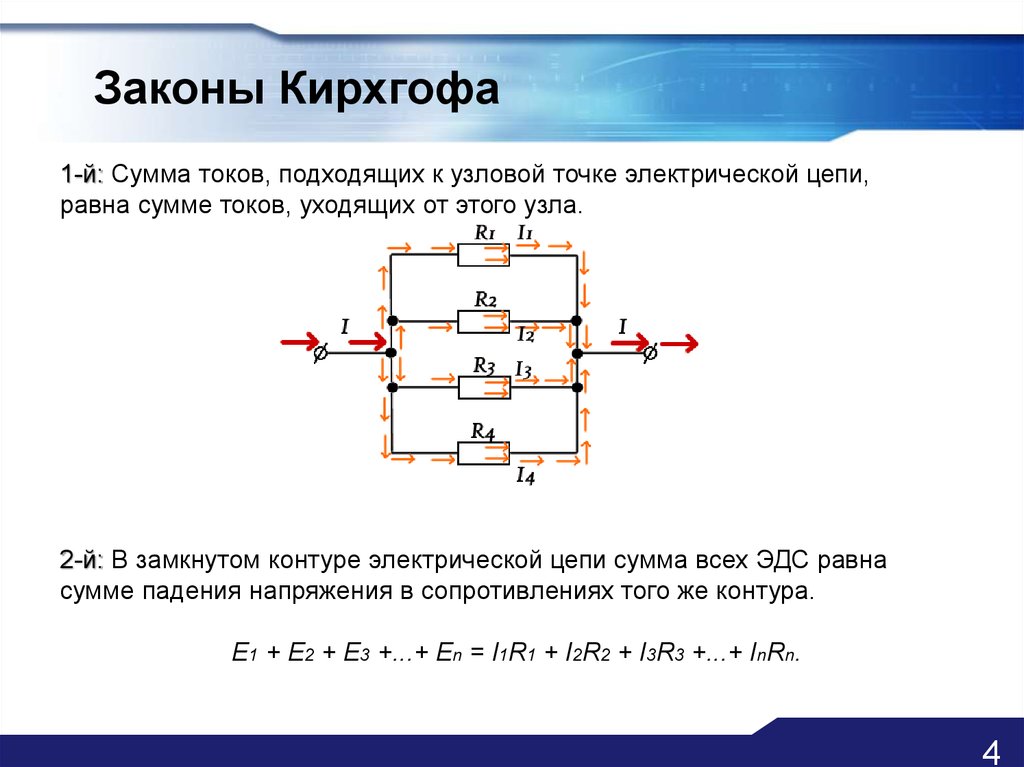 На высоких частотах закон Кирхгофа также не работает.

ESE & GATE EC

Electronic & Comm.GATEGATE ECESEESE ECOther ExamsTest Series

Featured Articles

Follow us for latest updates

Our Apps

• BYJU’S Exam Prep: The Exam Preparation Приложение

GradeStack Learning Pvt. Ltd.Windsor IT Park, Tower — A, 2-й этаж,

Sector 125, Noida,

Uttar Pradesh 201303

[email protected]

Законы Кирхгофа: первый и второй закон (с примерами) — наука

Video: How to Solve a Kirchhoff’s Rules Problem — Simple Example

Content

• Kirchhoff’s First Law
• Example
• Kirchhoff’s Second Law
• Law of conservation of charge
• Пример
• Каталожные номера

Законы Кирхгофа Они основаны на законе сохранения энергии и позволяют нам анализировать переменные, присущие электрическим цепям. Обе заповеди были сформулированы прусским физиком Густавом Робертом Кирхгофом в середине 1845 года и в настоящее время используются в электротехнике и электронной технике для расчета тока и напряжения.

Первый закон гласит, что сумма токов, входящих в узел цепи, должна быть равна сумме всех токов, выбрасываемых из узла. Второй закон гласит, что сумма всех положительных напряжений в сетке должна равняться сумме отрицательных напряжений (напряжение падает в противоположном направлении).

Законы Кирхгофа вместе с законом Ома являются основными инструментами для анализа значений электрических параметров цепи.

Путем анализа узлов (первый закон) или сеток (второй закон) можно найти значения токов и падений напряжения, которые возникают в любой точке сборки.

Вышеизложенное справедливо благодаря основанию на двух законах: законе сохранения энергии и законе сохранения электрического заряда. Оба метода дополняют друг друга и даже могут использоваться одновременно как методы взаимного тестирования одной и той же электрической цепи.

Однако для правильного использования важно следить за полярностью источников и взаимосвязанных элементов, а также за направлением тока.

Сбой в используемой системе отсчета может полностью изменить производительность вычислений и привести к неправильному разрешению анализируемой схемы.

Первый закон Кирхгофа

Первый закон Кирхгофа основан на законе сохранения энергии; более конкретно, в балансировке потока тока через узел в цепи.

Этот закон одинаково применяется в цепях постоянного и переменного тока, все они основаны на законе сохранения энергии, поскольку энергия не создается и не уничтожается, а только преобразуется.

Этот закон устанавливает, что сумма всех токов, входящих в узел, равна по величине сумме токов, выходящих из указанного узла.

Поэтому электрический ток не может возникнуть из ниоткуда, все основано на сохранении энергии. Ток, входящий в узел, должен быть распределен между ветвями этого узла. Первый закон Кирхгофа может быть выражен математически следующим образом:

То есть сумма входящих токов в узел равна сумме исходящих токов.

Узел не может производить электроны или намеренно удалять их из электрической цепи; то есть общий поток электронов остается постоянным и распределяется по узлу.

Теперь распределение токов от узла может варьироваться в зависимости от сопротивления потоку тока, которое имеет каждое отведение.

Сопротивление измеряется в омах [Ом], и чем больше сопротивление протеканию тока, тем ниже интенсивность электрического тока, протекающего через этот шунт.

В зависимости от характеристик цепи и каждого из составляющих ее электрических компонентов ток будет циркулировать по разным путям.

Поток электронов встретит большее или меньшее сопротивление на каждом пути, и это напрямую повлияет на количество электронов, которые будут циркулировать по каждой ветви.

Таким образом, величина электрического тока в каждой ветви может изменяться в зависимости от электрического сопротивления, присутствующего в каждой ветви.

Пример

Далее у нас есть простая электрическая сборка со следующей конфигурацией:

Элементы, составляющие схему:

— В: источник напряжения 10 В (постоянный ток).

— R1: сопротивление 10 Ом.

— R2: сопротивление 20 Ом.

Оба резистора включены параллельно, и ток, подаваемый в систему источником напряжения, разветвляется на резисторы R1 и R2 в узле N1.

Применяя закон Кирхгофа, получаем, что сумма всех входящих токов в узле N1 должна быть равна сумме выходящих токов; таким образом, имеем:

Заранее известно, что при заданной конфигурации схемы напряжение в обеих ветвях будет одинаковым; то есть напряжение, обеспечиваемое источником, поскольку это две параллельные сетки.

Следовательно, мы можем рассчитать значения I1 и I2, применяя закон Ома, математическое выражение которого выглядит следующим образом:

Тогда для расчета I1 значение напряжения, выдаваемого источником, необходимо разделить на значение сопротивления этой ветви. Таким образом, получается следующее:

Аналогично предыдущему расчету, для получения циркулирующего тока через второй вывод напряжение источника делится на значение сопротивления R2. Таким образом, вы должны:

Тогда общий ток, подаваемый источником (IT), представляет собой сумму ранее найденных величин:

В параллельных цепях сопротивление эквивалентной цепи определяется следующим математическим выражением:

Таким образом, эквивалентное сопротивление цепи имеет следующий вид:

Наконец, можно определить полный ток через частное между напряжением источника и полным эквивалентным сопротивлением цепи. Итак:

Результат, полученный обоими методами, совпадает, что свидетельствует о практическом использовании первого закона Кирхгофа.

Второй закон Кирхгофа

Второй закон Кирхгофа указывает, что алгебраическая сумма всех напряжений в замкнутом контуре или сетке должна равняться нулю.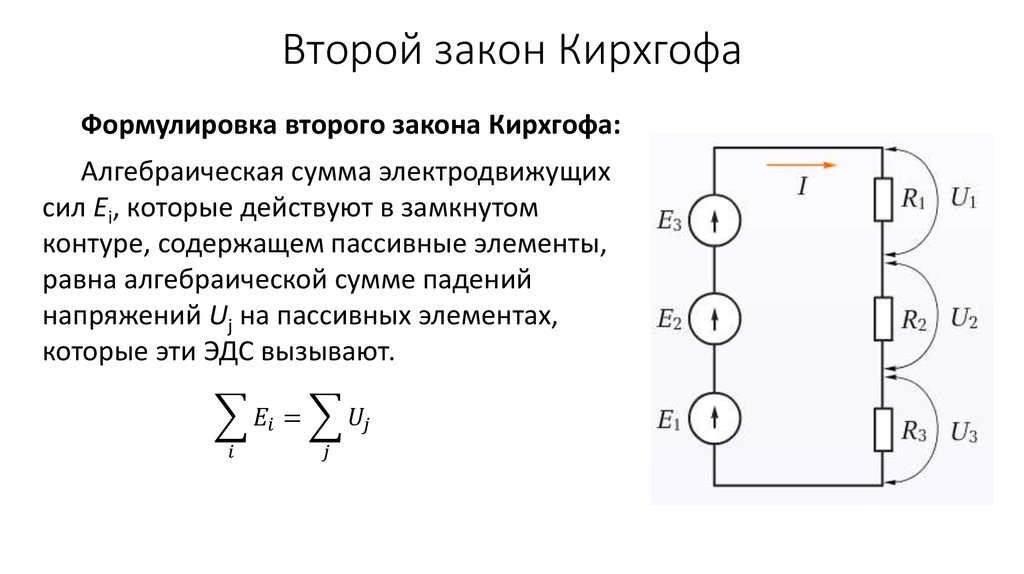 В математическом выражении второй закон Кирхгофа сводится к следующему: схема.

Поэтому при применении этого закона надо быть очень осторожным с направлением протекания тока и, следовательно, со знаками напряжений, содержащихся внутри сетки.

Этот закон также основан на законе сохранения энергии, поскольку установлено, что каждая сетка представляет собой замкнутый проводящий путь, в котором не генерируется и не теряется потенциал.

Следовательно, сумма всех напряжений на этом пути должна быть равна нулю, чтобы соблюдать энергетический баланс цепи внутри петли.

Закон сохранения заряда

Второй закон Кирхгофа также подчиняется закону сохранения заряда, поскольку электроны, протекающие по цепи, проходят через один или несколько компонентов.

Эти компоненты (резисторы, катушки индуктивности, конденсаторы и т. д.) получают или теряют энергию в зависимости от типа элемента. Это связано с совершением работы за счет действия микроскопических электрических сил.

Возникновение падения потенциала связано с выполнением работы внутри каждого компонента в ответ на энергию, подаваемую источником постоянного или переменного тока.

Эмпирическим путем, то есть благодаря результатам, полученным экспериментально, принцип сохранения электрического заряда устанавливает, что этот тип заряда не создается и не уничтожается.

Когда система подвергается взаимодействию с электромагнитными полями, соответствующий заряд сетки или замкнутого контура полностью сохраняется.

Таким образом, при сложении всех напряжений в замкнутом контуре с учетом напряжения генерирующего источника (если это так) и падения напряжения на каждом компоненте результат должен быть равен нулю.

Пример

Аналогично предыдущему примеру, у нас такая же конфигурация схемы:

Элементы, составляющие схему:

— В: источник напряжения 10 В (постоянный ток).

— R1: сопротивление 10 Ом.

— R2: сопротивление 20 Ом.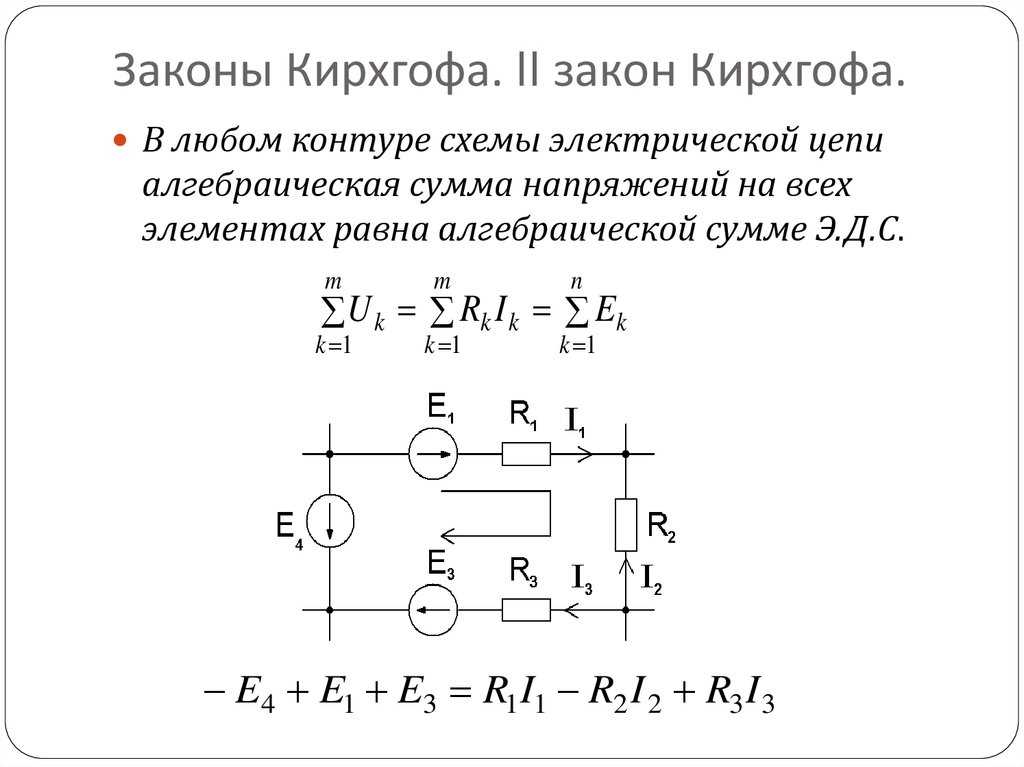

На этот раз на диаграмме выделены замкнутые контуры или ячейки цепи. Это две взаимодополняющие связи.

Первый контур (сетка 1) состоит из батареи 10 В, расположенной с левой стороны узла, параллельно резистору R1. Со своей стороны, второй контур (сетка 2) состоит из двух параллельных резисторов (R1 и R2).

По сравнению с примером первого закона Кирхгофа для целей данного анализа предполагается, что для каждой сетки существует ток.

При этом за ориентир принимается направление протекания тока, определяемое полярностью источника напряжения. То есть считается, что ток течет от отрицательного полюса источника к положительному полюсу источника.

Однако для компонентов анализ противоположный. Это означает, что мы будем считать, что ток входит через положительный полюс резисторов и выходит через отрицательный полюс резистора.

Если каждую сетку анализировать отдельно, циркулирующий ток и уравнение будут получены для каждого из замкнутых контуров в цепи.

Если исходить из того, что каждое уравнение получено из сетки, в которой сумма напряжений равна нулю, то можно уравнять оба уравнения для поиска неизвестных. Для первой сетки анализ по второму закону Кирхгофа предполагает следующее:

Вычитание между Ia и Ib представляет собой фактический ток, протекающий через ветвь. Знак отрицательный, учитывая направление течения тока. Тогда для второй сетки получается следующее выражение:

Вычитание между Ib и Ia представляет собой ток, протекающий через указанную ветвь, с учетом изменения направления циркуляции. Стоит подчеркнуть важность алгебраических знаков в этом типе операций.

Таким образом, приравнивая оба выражения (поскольку оба уравнения равны нулю), мы получаем следующее: оставшаяся переменная. Таким образом, при подстановке значения Ib в уравнение сетки 1 имеем:

При оценке результата, полученного при анализе второго закона Кирхгофа, видно, что вывод тот же.

Исходя из принципа, что ток, циркулирующий по первой ветви (I1), равен вычитанию Ia минус Ib, имеем:

законы точно такие же.