Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)
ОглавлениеТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКАГлава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.  2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17.  КОЛИЧЕСТВО ТЕПЛОТЫ18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34.  ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ.  ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. 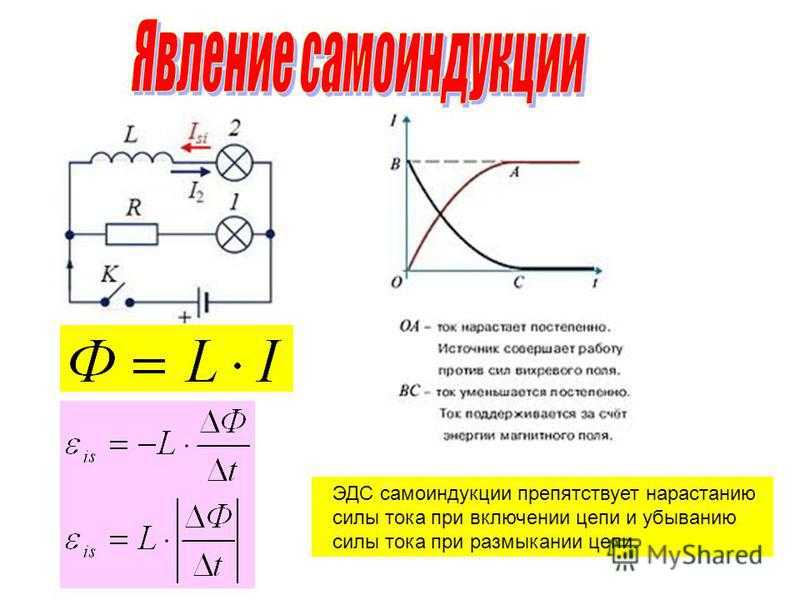 ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД.  90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ |
Самоиндукция. Индуктивность. Энергия магнитного поля тока. Школьный курс физики
Главная | Физика 11 класс | Самоиндукция. Индуктивность
Самоиндукция.
Рассмотрим частный случай явления электромагнитной индукции.
Если по катушке течёт ток, сила которого изменяется, то магнитный поток, пронизывающий катушку, изменяется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идёт такой ток.
Явление возникновения вихревого электрического поля в замкнутом проводящем контуре при изменении силы тока в нём называют самоиндукцией, а ЭДС индукции — ЭДС самоиндукции is
При самоиндукции проводящий контур играет двоякую роль: по нему протекает ток, вызывающий индукцию, и в нём же появляется ЭДС индукции. Изменяющееся магнитное поле индуцирует ЭДС в том самом проводнике, по которому течёт ток, создающий это поле.
По правилу Ленца в момент нарастания силы тока напряжённость вихревого электрического поля направлена против тока. В этот момент вихревое поле препятствует увеличению силы тока. Наоборот, в момент уменьшения силы тока вихревое поле поддерживает его.
Это приводит к тому, что при замыкании цепи, содержащей источник постоянной ЭДС, определённое значение силы тока устанавливается не сразу, а постепенно с течением времени (рис.
Рис. 4.15
При отключении источника ток в замкнутых контурах прекращается не мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника, так как изменение силы тока и его магнитного поля при отключении источника происходит очень быстро.
Исследования физических явлений опытным путём
Явление самоиндукции можно наблюдать на простых опытах. На рисунке 4.16 показана схема параллельного включения двух одинаковых электрических ламп.
Рис. 4.16
Лампу 1 подключают к источнику через резистор R, а лампу 2 — последовательно с катушкой L с железным сердечником. При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения.
Появление ЭДС самоиндукции при размыкании можно наблюдать на опыте с цепью, схематически показанной на рисунке 4.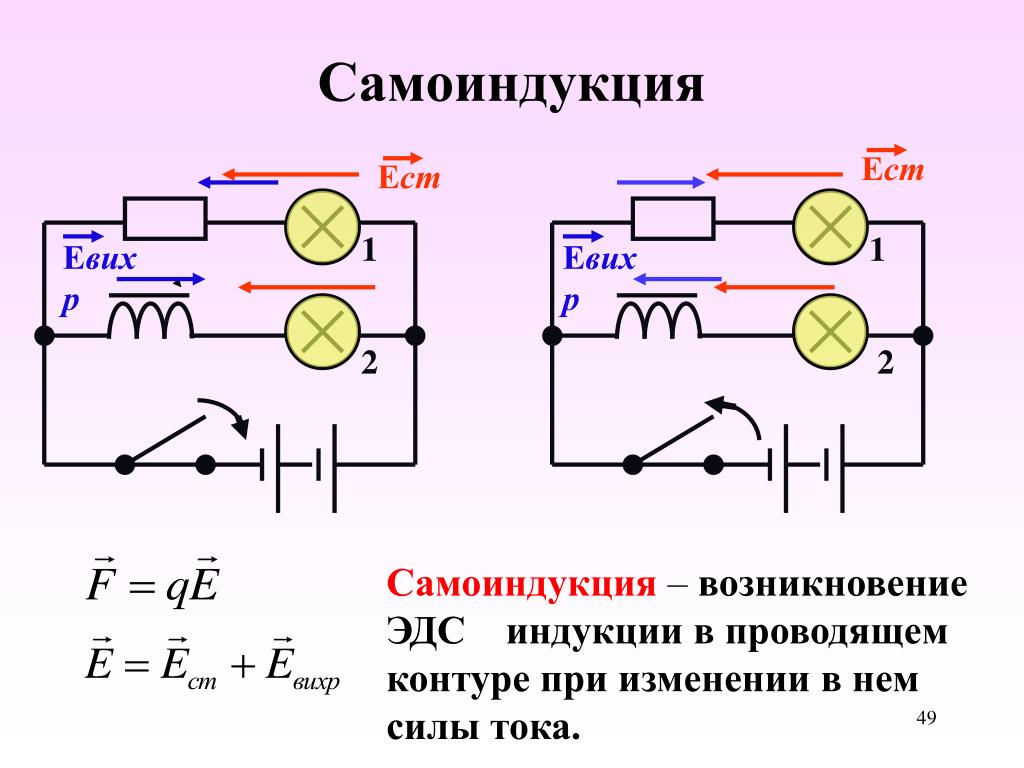
17.
Рис. 4.17
При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания ключа через гальванометр течёт ток (штриховая стрелка), направленный против начального тока до размыкания (сплошная стрелка). Причём сила тока при размыкании цепи превосходит силу тока, проходящего через гальванометр при замкнутом ключе 1. Это означает, что ЭДС самоиндукции is больше ЭДС батареи элементов.
1 Это утверждение справедливо при условии, что сопротивление катушки пренебрежимо мало.
Индуктивность контура.
Модуль индукции В магнитного поля, создаваемого током в любом замкнутом контуре, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ∼ В ∼ I.
Φ = LI,
где L — коэффициент пропорциональности (индуктивность контура, или коэффициент самоиндукции) между силой тока в проводящем контуре и созданным им магнитным потоком, пронизывающим этот контур.
Индуктивностью контура (или коэффициентом самоиндукции) называют физическую величину, равную отношению магнитного потока через поверхность, ограниченную контуром, к силе тока в этом контуре.
Используя закон электромагнитной индукции, можно записать формулу для ЭДС самоиндукции:
При этом необходимо учесть, что форма контура остаётся неизменной и магнитный поток изменяется только за счёт изменения силы тока.
Из последней формулы следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с. Индуктивность, подобно ёмкости конденсатора, зависит от размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность определяется магнитными свойствами среды, в которой находится проводник.
Единицу индуктивности в СИ называют генри (Гн). Индуктивность проводника равна 1 Гн, если в нём при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.
Энергия магнитного поля тока.
Магнитное поле тока обладает энергией. В этом можно убедиться, рассмотрев процесс спадания тока в катушке при отсоединении её от источника тока (рис. 4.18).
Рис. 4.18
До размыкания ключа в катушке течёт некоторый ток I0, который создаёт магнитное поле вокруг проводника. При размыкании цепи фактически остаётся последовательная цепь, состоящая из катушки индуктивности и резистора. Ток в катушке благодаря самоиндукции спадает постепенно, и при этом на сопротивлении R продолжает выделяться количество теплоты (в соответствии с законом Джоуля—Ленца). За счёт чего выделяется это количество теплоты, ведь источник питания уже отключён? При этом в цепи ток убывает, и индукция создаваемого им магнитного поля тоже уменьшается. Тем самым можно вполне говорить об энергии магнитного поля тока.
При замыкании цепи, когда сила тока начинает увеличиваться, в проводнике появляется вихревое электрическое ноле, действующее против того электрического поля, которое создаётся в проводнике благодаря источнику тока.
Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа идёт на увеличение энергии магнитного поля тока. Вихревое поле совершает отрицательную работу. При размыкании цепи ток исчезает, и вихревое поле совершает положительную работу. Запасённая током энергия выделяется. Это обнаруживается по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Выражение для энергии магнитного поля тока можно записать, используя аналогию между индуктивностью L в электродинамике и массой m в механике. Для того чтобы изменить скорость тела на определённую величину, требуется время. При постоянной силе это время тем больше, чем больше масса m тела. Для изменения силы тока в катушке на определённую величину также требуется время — оно тем больше, чем больше индуктивность L катушки. Согласно законам механики, для увеличения скорости тела нужно совершить работу. При торможении тело само совершает положительную работу. Для создания тока нужно совершить работу по преодолению вихревого электрического поля, а при исчезновении тока это поле само совершает работу.
Индуктивность L является аналогом массы m, а сила тока I — аналогом скорости υ (как величина, характеризующая движение электрических зарядов). Поэтому естественно предположить, что энергию магнитного поля тока Wм можно считать величиной, подобной кинетической энергии тела mυ2 / 2 в механике, и записать в виде
Именно такое выражение можно получить в результате расчётов.
При изучении электростатики мы познакомились с понятием объёмной плотности энергии электрического поля. По аналогии можно ввести понятие объёмной плотности энергии магнитного поля. Вычисления показывают, что плотность энергии магнитного поля wм (т. е. энергия единицы объёма) пропорциональна квадрату магнитной индукции, подобно тому как плотность энергии электрического ноля пропорциональна квадрату напряжённости электрического поля. Расчёты, выполненные для вакуума, приводят к следующему выражению (оно приведено в единицах СИ):
Вопросы:
1. В чём заключается явление самоиндукции?
2. В каких опытах можно наблюдать явление самоиндукции?
3. Что называют индуктивностью контура? От каких факторов она зависит?
4. От каких физических величин зависит ЭДС самоиндукции?
5. Как можно определить энергию магнитного поля тока?
Вопросы для обсуждения:
1. Объясните явления, описанные Ленцем в следующем фрагменте: «Искра при открытии цепи является сильнее тогда, когда употребляют для закрытия длинную проволоку, нежели короткую, хотя самый ток в первом случае бывает слабее по причине плохой проводимости длинной проволоки. Искра при открытии цепи будет сильнее, когда длинную соединительную проволоку наматывают на цилиндр в виде спирали, а ещё сильное, когда цилиндр будет железный».
2. К батарее аккумуляторов присоединены параллельно две цепи. Одна из них содержит лампы накаливания, а другая — большой электромагнит. Сила тока в обеих цепях одна и та же. При размыкании какой из цепей будет наблюдаться более сильная искра?
3. Объясните превращения энергии, происходящие при следующих процессах:
а) магнитная стрелка поворачивается вблизи провода, но которому пустили ток;
б) электромагнит притягивает к себе якорь;
в) от электромагнита, по обмотке которого идёт ток, отрывают якорь;
г) постоянный магнит притягивает к себе кусок железа.
Пример решения задачи
Магнитное поле создаётся протекающим ио катушке постоянным током. Магнитный поток этого поля через катушку равен 0,2 Вб, индуктивность катушки равна 0,06 Гн. Чему равна энергия магнитного поля катушки?
Ответ: Wм ≈ 0,3 Дж.
Упражнения:
1. Сила тока в катушке из 150 витков равна 7,5 Л. При этом создаётся магнитный поток 2 мВб. Чему равна индуктивность катушки?
2. При помощи реостата равномерно увеличивают силу тока в катушке со скоростью 100 А/с. Какая ЭДС самоиндукции возникает в катушке, если её индуктивность равна 200 мГн?
3. Какая ЭДС самоиндукции возникает в обмотке электромагнита индуктивностью 0,4 Гн при равномерном изменении силы тока в ней на 5 А за 0,02 с?
4. Сила тока в катушке сопротивлением 5 Ом равна 17 А, индуктивность катушки — 50 мГн. Каким будет напряжение на зажимах катушки, если сила тока в ней равномерно возрастает со скоростью 1000 А/с?
5. В катушке индуктивностью 0,6 Гн сила тока равна 20 А. Чему равна энергия магнитного поля этой катушки? Как изменится эта энергия, если сила тока уменьшится вдвое?
6. Сила тока в катушке уменьшилась с 12 А до 8 А. При этом энергия магнитного поля катушки уменьшилась на 2 Дж. Определите индуктивность катушки. Чему равна энергия её магнитного поля в обоих случаях?
Это любопытно…
Интересные факты
Сопротивление массивных проводников мало, поэтому возбуждаемая в них ЭДС индукции способна создать индукционные токи очень большой силы. Эти токи, называемые токами Фуко 1 или вихревыми токами, можно использовать для нагревания проводников.
1 По имени исследовавшего их французского физика Жана Фуко (1819—1860).
На этом принципе основано устройство индукционных электропечей. Особенно широкое применение эти печи получили для разогрева металлов перед их ковкой, штамповкой, для поверхностной закалки металлов, для их плавки в вакууме. Кроме того, созданы индукционные кухонные плиты (рис. 4.19) для приготовления и разогревания пищи.
Рис. 4.19
Во многих электротехнических устройствах возникновение токов Фуко приводит к бесполезным потерям энергии на выделение количества теплоты. Поэтому железные сердечники трансформаторов, электродвигателей делают не сплошными, а состоящими из отдельных пластин, изолированных друг от друга. Причём поверхности пластин должны быть перпендикулярны направлению вектора напряжённости вихревого электрического поля. В этом случае сопротивление пластин электрическому току будет максимальным.
Любопытные явления возникают при взаимодействии токов Фуко с вызвавшим их магнитным полем. На рисунке 4.20 изображён массивный медный маятник, колеблющийся между полюсами сильного электромагнита.
Рис. 4.20
При приближении маятника к зазору магнита в нём возникает индукционный ток, который, согласно правилу Ленца, имеет такое направление, что созданное им поле направлено против поля магнита. В результате происходит торможение маятника. При выходе маятника из зазора магнита поток, пронизывающий маятник, уменьшается и (согласно правилу Ленца) возникает притяжение маятника к магниту, и он опять тормозится. Этот эффект используют для успокоения колебаний стрелок измерительных приборов. Для этого на оси стрелки прибора закрепляют алюминиевую пластинку, движущуюся в зазоре постоянного магнита.
Предыдущая страницаСледующая страница
Собственная индуктивность
Собственная индуктивностьДалее: Энергия, хранящаяся в Вверх: Индуктивность Предыдущий: Взаимная индуктивность Нам не обязательно нужны две цепи, чтобы иметь индуктивные эффекты. Учитывать единая проводящая цепь, по которой течет ток течет. Этот ток создает магнитное поле, которое возникает магнитный поток, связывающий схема. Мы ожидаем, что поток будет прямо пропорционален к току , учитывая линейный характер законов магнитостатики, и определение магнитного потока. Таким образом, мы можем написать
| (241) |
где константа пропорциональности называется собственной индуктивностью схема.
Как и взаимная индуктивность, собственная индуктивность
цепи измеряется в генри и представляет собой
чисто геометрическая величина, зависящая только от
форма цепи и количество витков в цепи. Если ток, протекающий по цепи, изменяется на
сумма за временной интервал, то
магнитный поток, связывающий цепь, изменяется на величину
в том же интервале времени. Согласно с
Закон Фарадея, ЭДС
| (242) |
генерируется вокруг цепи. С , эту ЭДС также можно записать
| (243) |
Таким образом, ЭДС, создаваемая вокруг цепи за счет собственного тока, непосредственно пропорциональна скорости изменения тока. закон Ленца и здравый смысл требует, что если ток увеличивается, то ЭДС должна всегда действовать, чтобы уменьшить ток, и наоборот .
Это легко оценить,
так как если
ЭДС действовала на увеличение
ток, когда ток увеличивался, то мы явно получили бы нефизический
положительный отзыв
эффект, при котором ток продолжал увеличиваться без ограничений. Отсюда следует, из
уравнение (243), что
собственная индуктивность цепи обязательно равна положительному числу . Этот
это не относится к взаимным индуктивностям, которые могут быть как положительными, так и отрицательными. Рассмотрим соленоид длиной и поперечным сечением
область . Предположим, что соленоид имеет витки.
При протекании тока в соленоиде возникает однородное осевое поле величиной
| (244) |
генерируется в сердечнике соленоида. Напряженность поля вне ядра является незначительный. Магнитный поток, связывающий один виток соленоида, равен . Таким образом, магнитный поток, связывающий все витки соленоид
| (245) |
Согласно уравнению (241) собственная индуктивность соленоида определяется выражением , что сводится к
| (246) |
Заметьте, положительный.
Кроме того, является геометрической величиной, зависящей
только от размеров соленоида и количества витков в соленоиде. Инженеры нравится сводить все части электрических устройств, какими бы сложными они ни были, к эквивалентная схема , состоящая из сети всего четыре разных типа компонента. Эти четыре основных компонента ЭДС , резисторы , конденсаторы , и катушки индуктивности . Катушка индуктивности представляет собой просто чистую собственную индуктивность и обычно представлял собой маленький соленоид на принципиальных схемах. На практике катушки индуктивности обычно состоят из коротких соленоидов с воздушным сердечником, намотанных из эмалированной медной проволоки.
Далее: Энергия, хранящаяся в Вверх: Индуктивность Предыдущий: Взаимная индуктивность Ричард Фицпатрик 2007-07-14
Заметки о различиях между собственной индуктивностью и взаимной индуктивностью
Сэр Генри Джозеф дал нам первое представление о собственной индуктивности и взаимной индуктивности в 1831 году. Индуктивность является одним из наиболее уважаемых понятий в изучении физики. Единицей СИ для собственной и взаимной индуктивности является генри (Гн). Один генри определяется как взаимная индуктивность катушки для производства эквивалента одного вольта, когда скорость изменения тока составляет один ампер в секунду. Основные различия между собственной индуктивностью и взаимной индуктивностью заключаются в факторах, влияющих на индуктивность, некоторые из которых обсуждаются далее.
Введение в самоиндукцию
Известно, что:
- Катушка, по которой течет ток, создает магнитное поле (ЭДС) наводится за счет электромагнитной индукции
Таким образом, при изменении тока, протекающего через катушку или цепь, в ней создается ЭДС самоиндукции. Согласно закону известного физика Ленца, ЭДС самоиндукции пытается противостоять своей причине создания.
Это явление создания ЭДС самоиндукции, которая позже препятствует любому изменению в катушке или электрическом состоянии цепи, известно как самоиндукция.
Введение во взаимную индуктивность
Взаимная индуктивность, фундаментальное свойство в изучении физики, говорит о двух катушках, расположенных рядом друг с другом.
Предположим, две катушки названы A и B. Рассмотрим сценарий, когда ток пропускают через катушку A. В катушке, расположенной рядом с A, т. е. катушке B, индуцируется ЭДС.
- Катушка А, в которой создается ток, называется первичной катушкой
- Катушка В, в которой индуцируется ЭДС, называется вторичной катушкой
- Изменение тока, создаваемого в первичной катушке, вызывает ЭДС индуцироваться во вторичной обмотке по принципу электромагнитной индукции
- По этой причине это явление известно как взаимная индуктивность
Коэффициенты собственной и взаимной индуктивности
1. Собственная индуктивность
Магнитный поток (ɸ), связанный с катушкой, прямо пропорционален току (I), протекающему через нее в любой конкретный момент.
ɸ∝ I
Чтобы удалить знак пропорциональности, мы можем написать уравнение как:
ɸ = L I
Где L — постоянная, также известная как коэффициент собственной индуктивности.
Таким образом, коэффициент собственной индуктивности любой катушки или цепи может быть определен как магнитный поток, связанный с ней из-за протекающего через нее тока в один ампер.
- Единица СИ L определяется как Вольт/(Ампер/сек) = сек – вольт/ампер = Ом-сек
2. Взаимная индуктивность вторичная катушка будет индуцировать ЭДС.
Таким образом, магнитный поток (ɸ2) зависит от изменения тока в первичной обмотке. Он прямо пропорционален току (I1).
ɸ2 ∝ I1
Символ пропорциональности «∝» заменяется константой, обозначаемой «M». Это взаимная индуктивность двух катушек, А и В.
ɸ2 = M I1
Отсюда коэффициент взаимной индуктивности для данной пары катушек определяется следующим образом:
- Магнитный поток (ɸ), связанный с одной из катушек за счет тока в один ампер в другой катушка равна одному веберу
или
- Величина ЭДС, индуцированной в одной из катушек из-за изменения тока со скоростью один ампер в секунду в другой катушке, равна одному вольту
Факторы, влияющие на себя и Взаимная индуктивность
Ниже приведены факторы, влияющие на константу собственной индуктивности ‘L’:
- Геометрия катушек: Спиральное расположение с большей вероятностью улавливает большее количество силовых линий магнитного поля, чем прямолинейное расположение проводов
- Природа среды между двумя катушками: Если в качестве сердечника катушки используется изолированный ферромагнитный материал, это, вероятно, приведет к тому, что больше силовых линий магнитного поля свяжутся, а это, в свою очередь, повысит значение коэффициент собственной индуктивности
- Длина катушек: Магнитный поток (ɸ), индуцированный в более длинной катушке, всегда меньше, чем поток, индуцированный в более короткой катушке
Ниже приведены факторы, влияющие на постоянную взаимной индуктивности «M»:
