НОУ ИНТУИТ | Лекция | Координаты и векторы

< Лекция 15 || Лекция 3: 123

Аннотация: Рассматриваются основные математические понятия, связанные с определением положения объекта на плоскости и в пространстве, с его ориентацией и направлением, а также их обобщения на пространства большей размерности

Ключевые слова: Числовой осью, прямой, действительное число, расстояние, осью, ПО, плоскостью, значение, определение системы, прямоугольной декартовой системой координат на плоскости, осью абсцисс, осью ординат, плоскость, упорядоченные системы, прямоугольной декартовой системой координат в пространстве, осью аппликат, полярная система координат, полюсом, полярной осью, исключение, координаты, определение, сферическая система координат, связь, скалярные, векторные, словарный запас, скалярная величина, векторная величина, Геометрическим вектором, вектором, модулем, нулевым, коллинеарны, параллельны, компланарны, равны, Радиус-вектор, вектор, вектор-проекцией, проекцией, единичным вектором, ортом, орт, радиус, равенство, разложение вектора, координатой, размерностью, единичными векторами, ортами, суммой, Разностью, Произведением вектора, на скаляр, операции, аксиома, противоположный вектор, дистрибутивность, Скалярным произведением, Свойства скалярного произведения, направляющими косинусами, Произведение, алгебраические, компонент, Сумма, разность, Произведение скаляра, скалярное произведение, длина

Координаты и векторы

intuit.ru/2010/edi»> Числовой осью называется бесконечная прямая, на которой определены: точка O — начало отсчета; положительное направление, указываемое стрелкой; масштаб измерения (принцип отложения чисел на оси, часто с указанием единицы измерения). Условное изображение числовой прямой (числового луча) приведено на рис. 3.1.

Рис. 3.1. Числовая прямая

Для каждого действительного числа x на числовой оси R определена единственная точка, соответствующая его количеству (изображающая это число с учетом выбранного масштаба и отсчета) и наоборот, то есть совокупность R и множество точек числовой оси могут быть связаны общим, однозначно определяемым правилом, законом.

Пример. Числу 5 на числовой оси соответствует точка, удаленная на расстояние в 5 единиц масштаба от начальной точки (точки отсчета 0 ).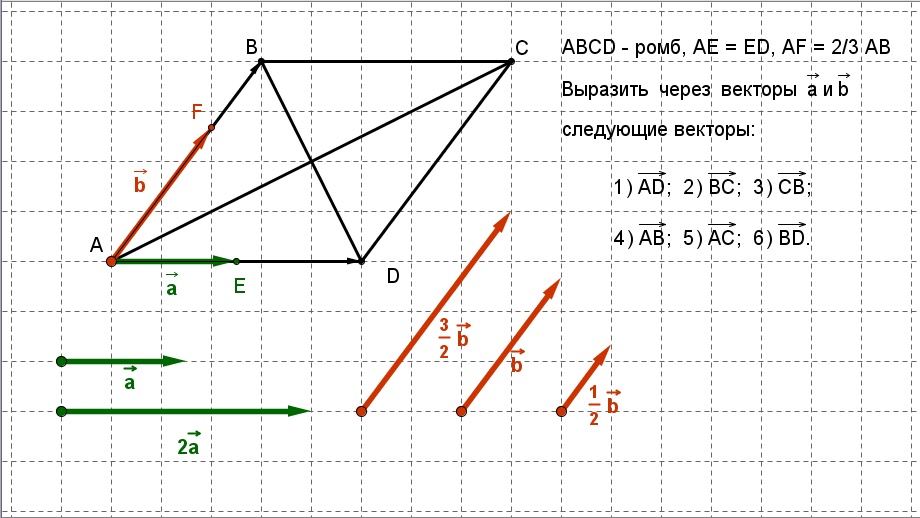

Пример. Точке A, удаленной на расстояние 3 единицы масштаба от начала координат O можно сопоставить число 3.

Числовая прямая, расположенная обычно на плоскости горизонтально к рассматривающему, называется осью x ( Ox ), а числовая прямая, расположенная обычно вертикально к нему, — осью y (Oy) .Эти прямые образуют систему ориентации каждой точки на плоскости по двум ее координатам.

Плоскость, определяемая этими двумя перпендикулярными (или, как говорят в математике, ортогональными) числовыми прямыми, называется плоскостью xy (xOy) .

Каждая пара вещественных значений (x;y) задает одну единственную точку M(x;y) на этой плоскости, которая определяется как точка пересечения перпендикулярных (ортогональных) прямых, проходящих через значения x оси Ox и значение y оси Oy. Наоборот, каждой точке (x;y) можно сопоставить пару вещественных чисел: x — на оси Ox и y — на оси Oy. Так определенная система двух перпендикулярных числовых прямых называется прямоугольной декартовой системой координат на плоскости (рис. 3.2).

Рис. 3.2. Декартова система координат на плоскости

Оси координат обычно помечаются буквами.

Ось Ox называется осью абсцисс , ось Oy — осью ординат .Эти оси делят плоскость xOy на 4 части (координатных угла или, как их еще называют, квадранта).

Упорядоченная система трех взаимно перпендикулярных осей с общим началом отсчета (началом координат) и общей единицей измерения длины (масштабом) называется прямоугольной декартовой системой координат в пространстве .Обозначается такая система Oxyz или xyz. Ось Ox называется осью абсцисс, Oy — осью ординат, Oz — осью аппликат .

ru/2010/edi»>Кроме декартовой системы координат, часто используют и другие удобные, не обязательно прямоугольные, системы координат.

Одной из наиболее часто используемых является полярная система координат, определяющая, как и в декартовой системе, однозначное положение точки на плоскости с помощью двух параметров.

Возьмем на плоскости точку O (называемую полюсом ) и выходящую из этой точки полупрямую (называемую полярной осью ). Если на этой прямой задать масштаб и положительное направление, то мы определим полярную систему координат. Положение точки M на плоскости в полярной системе координат задается двумя числовыми величинами: — расстоянием точки M от полюса, то есть и — углом, образованным отрезком OM с положительным направлением полярной оси. Обозначим точку с полярными координатами в виде . Обычно считают, что , . Эти значения называются главными значениями. Каждая точка на плоскости однозначно определяется полярными координатами.

Исключение составляет единственная точка , где угол может быть любым. Условно, в этом случае берется угол .

Найдем зависимость между координатами точки M(x;y) в прямоугольной декартовой системе координат и ее координатами в полярной системе.

Построим прямоугольную систему xOy, где ось Ox совпадает с полярной осью, O(0;0) — начала координат, а положительные направления этих осей совпадают (рис. 3.3).

Рис. 3.3. Декартова и полярная системы координат на плоскости

Используя прямоугольные треугольники и тригонометрические функции, получим следующие основные соотношения:

Таким образом, зная полярные координаты точки, можно найти прямоугольные координаты этой же точки. Кроме того, если использовать основное тригонометрическое соотношение и определение тангенса угла из школьного курса (нужно сложить квадраты x, y, а затем поделить y на x ), то справедливы следующие соотношения:

Таким образом, если мы знаем прямоугольные координаты точки, то можем определить соответствующие полярные декартовы координаты.

Пример. Если , , то по соответствующим формулам получаем

Отсюда выводим систему: y=x, x²+y²=16 или .

Пример. Уравнение окружности с центром в начале координат и радиуса r в декартовой системе координат, как известно, имеет вид: x²+y²=r². Уравнение окружности в полярных координатах будет иметь вид

Итак, это уравнение намного проще по виду: . Кроме того, это уравнение освобождено от «лишнего» параметра , который в данном случае считается любым из диапазона . Работать с объектами в полярной системе координат часто проще на практике, в геодезии, астрономии и др.

Удобной в пространстве системой координат является и так называемая сферическая система координат. В этой системе положение точки M(x;y;z) в пространстве однозначно определяется ее расстоянием r от начала координат (длиной отрезка OM ), углом между OM и положительной полуосью Oz и углом ( между проекцией OM на плоскость xOy и положительной полуосью Ox (рис.

3.4).

Выясним форму связи сферических и декартовых координат. По рис. 3.4:

Рис. 3.4. Сферическая координатная система

Отсюда получаем связь вида .

Дальше >>

< Лекция 15 || Лекция 3: 123

Правило параллелепипеда

Урок 38. Геометрия 10 класс ФГОС

На этом уроке вводится правило параллелепипеда сложения трёх некомпланарных векторов и рассматриваются примеры его применения при решении различных задач.

Конспект урока «Правило параллелепипеда»

Материал урока.

На прошлых занятиях вы познакомились с понятием компланарных векторов.

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

При этом на практике мы использовали такую формулировку: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Так же вы доказали признак компланарности векторов.

Если вектор  можно разложить по векторам  и , то векторы ,  и  компланарны.

К тому же вы убедились в справедливости и обратного утверждения.

Если векторы ,  и  компланарны, а векторы  и  не коллинеарны, то вектор  можно разложить по векторам  и , причём коэффициенты разложения определяются единственным образом.

Для сложения компланарных векторов, так как все они лежат в одной плоскости, можно использовать правила сложения известные из планиметрии, а именно: правило треугольника, правило параллелограмма и правило многоугольника.

Что же касается некомпланарных векторов, то для построения их суммы используют правило параллелепипеда.

Рассмотрим некомпланарные векторы ,  и .

От произвольной точки О пространства отложим векторы ,  и  равные векторам ,  и  соответственно.

На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.

Построим вектор суммы векторов ,  и  при этом последовательно их складывая.

Вектором суммы векторов ,  по правилу параллелограмма будет вектор .

Вектором суммы векторов  и  по тому же правилу будет вектор . Вектор  равен сумме векторов ,  и , а значит равен сумме векторов ,  и .

Отсюда правило параллелепипеда можно сформулировать так.

Если отложить некомпланарные векторы ,  и  от некоторой точки пространства О и построить на них параллелепипед, то диагональ OD параллелепипеда будет выражать вектор суммы данных векторов.

Воспользуемся сформулированным только что правилом и выполним задание.

Рассмотрим  параллелепипед и укажем вектор суммы данных векторов такой, чтобы его начало и конец совпадали с вершинами параллелепипеда.

Первым назовём вектор . Так как эти векторы отложены от одной точки и являются рёбрами данного параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда, одним из концов которой будет точка начала данных векторов А. Так мы получим вектор .

Далее назовём вектор суммы векторов .

Они также отложены от одной точки D и являются рёбрами данного параллелепипеда. Вектором их суммы будет вектор .

В следующем пункте нужно назвать вектор суммы векторов .

В данном случае векторы не имеют общего начала, а имеют общий конец.

Выразим каждый из данных векторов через противоположный.

Далее рассмотрим сумму векторов .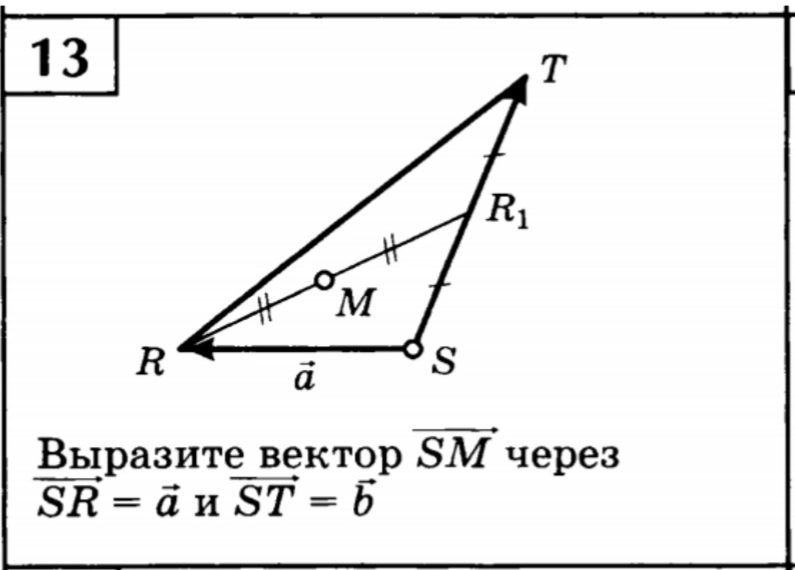 Только вектор  не берёт своё начало в точке А₁. Но вектор  равен ему, поэтому заменим вектор  в сумме на равный ему вектор .

Не трудно понять, что вектором полученной суммы будет вектор .

Последней рассмотрим сумму векторов  .

Вектор  заменим равным ему вектором . Тогда не трудно записать вектор суммы. Им будет вектор  

 

Подведём итоги урока.

Сегодня мы описали правило параллелепипеда сложения трёх некомпланарных векторов.

Если отложить некомпланарные векторы ,  и  от некоторой точки пространства О и построить на них параллелепипед, то диагональ OD параллелепипеда будет выражать вектор суммы данных векторов.

Это правило пригодится вам при изучении следующих тем курса стереометрии.

Предыдущий урок 37 Компланарные векторы

Следующий урок 39 Разложение вектора по трем некомпланарным векторам

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 10 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Стандартные единичные векторы — Mathonline

Свернуть Содержание Стандартные единичные векторы Выражение векторов с помощью стандартных единичных векторов Пример 1 Представление перекрестного произведения в стандартных единичных векторах

Определение: Векторы $\vec{i} = (1, 0, 0)$, $\vec{j} = (0, 1, 0)$ и $\vec{k} = (0, 0, 1)$ считаются стандартными единичными векторами , то есть вектор, который проходит по оси $x$, $y$ или $z$ и имеет величину 1, то есть $\mid \mid \vec{i} \mid \mid = \mid \mid \vec{j} \mid \mid= \mid \mid \vec{k} \mid \mid = 1$.

На следующем рисунке показаны три стандартных единичных вектора на плоскости $xyz$:

Стандартные единичные векторы полезны, так как фактически мы можем представить любой вектор с их помощью. Рассмотрим общий вектор $\vec{u} = (u_1, u_2, u_3)$. Мы можем представить вектор $\vec{u}$ следующим образом:

(1)

\begin{align} \vec{u} = u_1\vec{i} + u_2\vec{j} + u_3\vec{k} \end{align}

Пусть некоторый вектор u существует в 3 -Пространство. Мы знаем, что u = (u1, u2, u3). Таким образом, мы можем выразить вектор u в терминах стандартных единичных векторов с помощью свойства скалярного произведения. Например:

(2)

\begin{align} \quad \vec{u} = (u_{1}, u_{2}, u_{3}) = u_{1}\vec{i} + u_{2}\vec{j } + u_{3}\vec{k} = u_{1} \cdot (1, 0, 0) + u_{2} \cdot (0, 1, 0) + u_{3} \cdot (0, 0) , 1) \end{align}

Выразите вектор $\vec{u} = (2, -4, 5)$ через стандартные единичные векторы.

Просто подставив то, что мы знаем, в формулу, мы можем довольно легко записать $\vec{u}$ в терминах стандартных единичных векторов, то есть $\vec{u} = 2\vec{i} -4\ vec{j} + 5\vec{k}$.

Один из способов представления векторного произведения двух векторов $\vec{u} \times \vec{v}$ – это определители и единичные векторы. Во-первых, создайте матрицу $3 \times 3$ так, чтобы элементами первой строки были единичные векторы $\vec{i}$, $\vec{j}$ и $\vec{k}$. Сделайте записи второй строки компонентами $\vec{u}$, а записи третьей строки сделайте компонентами $\vec{v}$, как показано: $\begin{bmatrix}\vec{ i} & \vec{j} & \vec{k}\\ u_{1} & u_{2} & u_{3}\\ v_{1} & v_{2} & v_{3} \end{bmatrix }$.

Определитель этой матрицы равен векторному произведению $\vec{u} \times \vec{v}$. Это легко увидеть, развернув первую строку с точки зрения миноров/кофакторов:

(3)

\begin{align} \vec{u} \times \vec{v} = \begin{vmatrix}\vec{i} & \vec{j} & \vec{k}\\ u_{1} & u_ {2} & u_{3}\\ v_{1} & v_{2} & v_{3} \end{vmatrix} = \vec{i} \begin{vmatrix} u_{2} & u_{3} \ \ v_{2} & v_{2} \end{vmatrix} — \vec{j} \begin{vmatrix} u_{1} & u_{3} \\ v_{1} & v_{3} \end{vmatrix } + \vec{k} \begin{vmatrix} u_{1} & u_{2} \\ v_{1} & v_{2} \end{vmatrix} \end{align}

Линейные комбинации векторов.

Основы

В линейной алгебре мы определяем понятие линейных комбинаций в терминах векторов. Но на самом деле можно говорить о линейных комбинациях чего угодно, если вы понимаете основную идею линейной комбинации:

(скаляр)(что-то 1) + (скаляр)(что-то 2) + (скаляр)(что-то 3)

Эти «что-то» могут быть «повседневными» переменными, такими как \(x\) и \(y\) (\(3x\) + \(2y\) является линейной комбинацией \(x\) и \(y\) например) или что-то более сложное, например полиномы. В общем, линейная комбинация — это особый способ объединения вещей (переменных, векторов и т. д.) с использованием скалярного умножения и сложения.

реклама

Работа с векторами

Вернемся к векторам. Допустим, у нас есть следующие векторы:

\(\vec{v}_1 = \left[ \begin{array}{c}1\\ 2\\ 3\end{array} \right]\), \(\vec{v}_2 = \left[ \begin{array}{c}3\\ 5\\ 1\end{array} \right]\), \(\vec{v}_3 = \left[ \begin{array}{c}0\\ 0 \\ 8\конец{массив} \право]\)

Как будут выглядеть линейные комбинации этих векторов? Что ж, линейной комбинацией этих векторов будет любая их комбинация, использующая сложение и скалярное умножение. Вот несколько примеров:

Вектор \(\vec{b} = \left[ \begin{array}{c}3\\ 6\\ 9\end{array} \right]\) представляет собой линейную комбинацию \(\vec{v} _1\), \(\vec{v}_2\), \(\vec{v}_3\).

Почему это так? Этот вектор можно записать как комбинацию трех заданных векторов с помощью скалярного умножения и сложения. В частности,

\(\left[ \begin{array}{c}3\\ 6\\ 9\end{массив} \right] = 3\left[ \begin{array}{c}1\\ 2\\ 3\end {массив} \right] + 0\left[ \begin{array}{c}3\\ 5\\ 1\end{массив} \right] + 0\left[ \begin{array}{c}0\\ 0\\ 8\конец{массив} \право]\)

Или, используя имена, данные каждому вектору:

\(\vec{b} = 3\vec{v}_1 + 0\vec{v}_2 + 0\vec{v}_3\)

Вектор \(\vec{x} = \left[ \begin{array}{c}2\\ 3\\ -6\end{array} \right]\) является линейной комбинацией \(\vec{v }_1\), \(\vec{v}_2\), \(\vec{v}_3\).

Еще раз, мы можем показать, что это правда, показав, что вы можете комбинировать векторы \(\vec{v}_1\), \(\vec{v}_2\) и \(\vec{v}_3 \) с использованием сложения и скалярного умножения таким образом, чтобы результатом был вектор \(\vec{x}\).

\(\left[ \begin{array}{c}2\\ 3\\ -6\end{массив} \right] = -1\left[ \begin{array}{c}1\\ 2\\ 3 \end{массив} \right] + 1\left[ \begin{array}{c}3\\ 5\\ 1\end{массив} \right] + \left(-\dfrac{1}{2}\ вправо)\влево[ \begin{массив}{c}0\\ 0\\ 8\конец{массив} \вправо]\)

или еще раз, эквивалентно

\(\vec{x} = -1\vec{v}_1 +1\vec{v}_2 + \left(-\dfrac{1}{2}\right)\vec{v}_3\)

Конечно, мы могли бы продолжать еще долго, так как есть много разных вариантов скаляров и способов объединения трех векторов. В общем, набор ВСЕХ линейных комбинаций этих трех векторов будет называться их размахом. Это будет записано как \(\textrm{Span}\left(\vec{v}_1, \vec{v}_2, \vec{v}_3\right)\). Два приведенных выше вектора являются элементами или членами этого множества. 9{n}\) и \(c_1, c_2, \cdots , c_n\) — скаляры. Тогда вектор \(\vec{b}\), где \(\vec{b} = c_1\vec{v}_1 + c_2\vec{v}_2 + \dots + c_n\vec{v}_n\) называется линейной комбинацией из \(\vec{v}_1, \vec{v}_2, \vec{v}_3, … \vec{v}_n\).