Как на двоичном коде будет слово привет. Русский алфавит в двоичном коде. Равномерное алфавитное двоичное кодирование. Байтовый код. Понимание двоичных чисел
Термин «бинарный» по смыслу – состоящий из двух частей, компонентов. Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска.
Существуют различные возможности кодирования информации.
Двоичный код
В цифровой технике способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы ДК называют битами.
Знаки или единицы ДК называют битами.
Одним из обоснований применения ДК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства магнитного потока в данной ячейке носителя магнитной записи.
Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества битов в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный или 3-битовый код:
| числовое значение | |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Отсюда видно, что для числа больше 7 при 3-разрядном коде уже нет кодовых комбинаций из 0 и 1.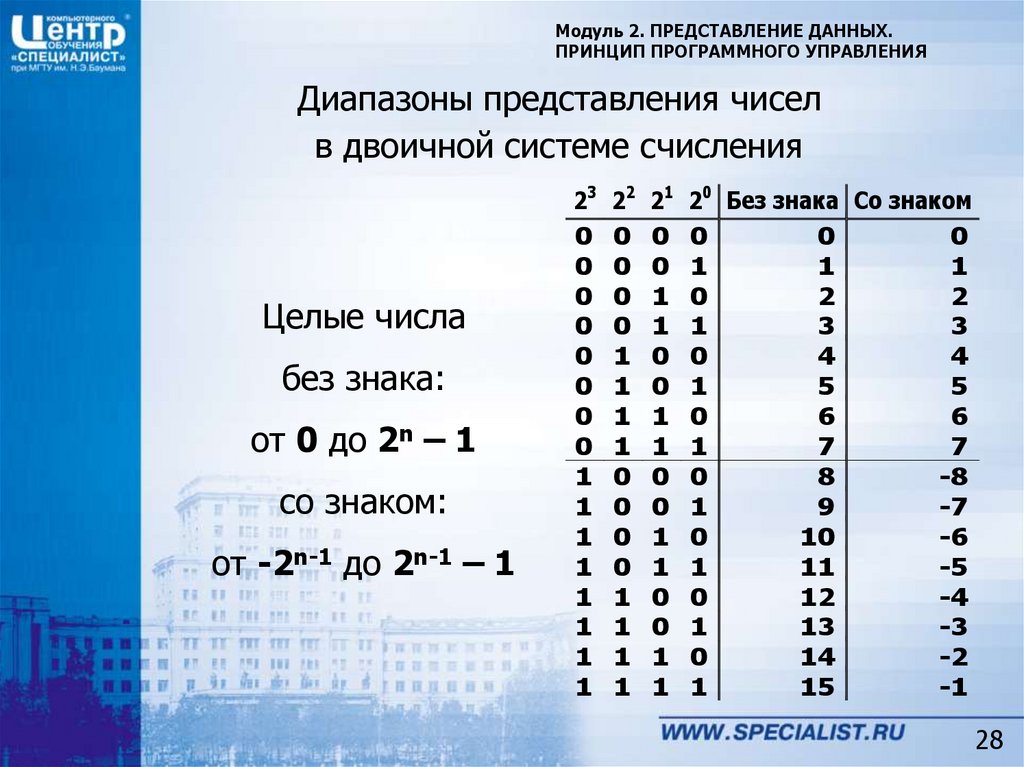
Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее количество значений m какой-либо величины (температуры, напряжения, тока и др.), которое может быть выражено двоичным кодом, зависит от числа используемых разрядов n как m=2n. Если n=3, как в рассмотренном примере, то получим 8 значений, включая ведущий 0.
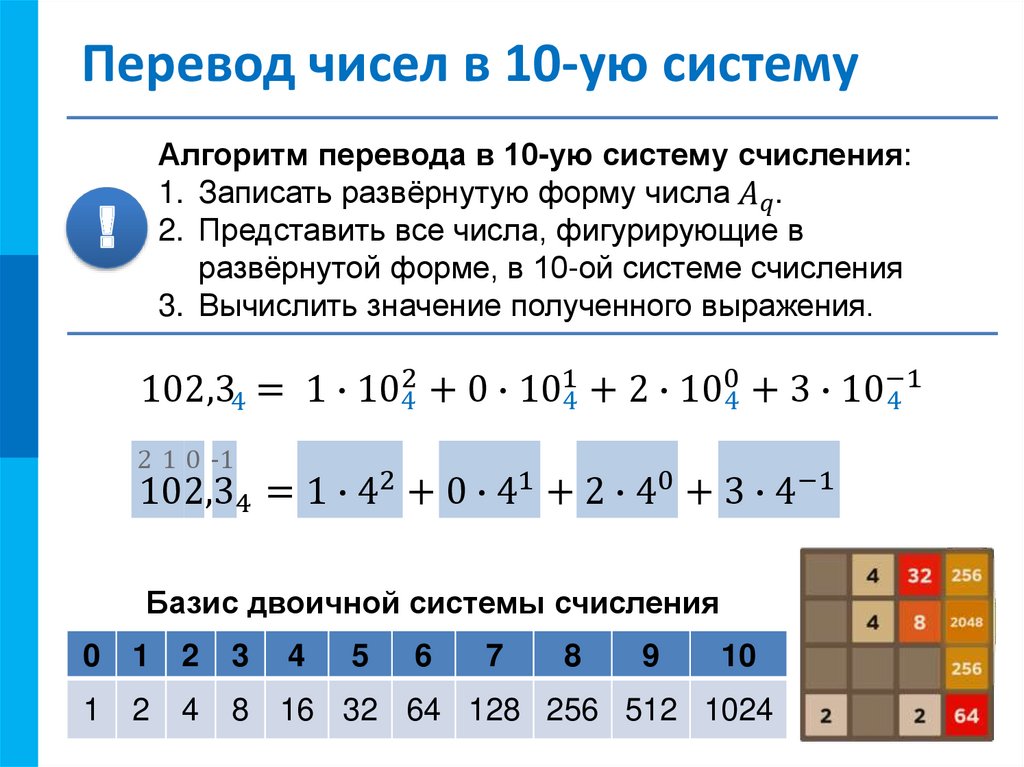
Код Грея
Грей-код является так называемым одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой-то один из всех бит информации. Погрешность при считывании информации с механического кодового диска при переходе от одного числа к другому приведет лишь к тому, что переход от одного положения к другом будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения при переходе от одного положения к другому полностью исключается.
Преимуществом Грей-кода является также его способность зеркального отображения информации. Так инвертируя старший бит можно простым образом менять направление счета и таким образом подбирать к фактическому (физическому) направлению вращения оси.
Поскольку информация выраженая в Грей-коде имеет чисто кодированный характер не несущей реальной числовой информации должен он перед дальнейшей обработкой сперва преобразован в стандартный бинарный код. Осуществляется это при помощи преобразователя кода (декодера Грей-Бинар) который к счастью легко реализируется с помощью цепи из логических элементов «исключающее или» (XOR) как програмным так и аппаратным способом.
Соответствие десятичных чисел в диапазоне от 0 до 15 двоичному коду и коду Грея
| Двоичное кодирование | Кодирование по методу Грея | ||||
| Десятичный код | Двоичное значение | Шестнадц. | Десятичный код | Двоичное значение | Шестнадц. значение |
| 0 | 0000 | 0h | 0 | 0000 | |
| 1 | 0001 | 1h | 1 | 0001 | 1h |
| 2 | 0010 | 2h | 3 | 3h | |
| 3 | 0011 | 3h | 2 | 0010 | 2h |
| 4 | 0100 | 6 | 0110 | 6h | |
| 5 | 0101 | 5h | 7 | 0111 | 7h |
| 6 | 6h | 5 | 0101 | 5h | |
| 7 | 0111 | 7h | 4 | 0100 | 4h |
| 8 | 1000 | 8h | 12 | 1100 | Ch |
| 9 | 1001 | 9h | 13 | 1101 | Dh |
| 10 | 1010 | Ah | 15 | 1111 | Fh |
| 11 | 1011 | Bh | 14 | 1110 | Eh |
| 12 | 1100 | Ch | 10 | 1010 | Ah |
| 13 | 1101 | Dh | 11 | 1011 | Bh |
| 14 | 1110 | Eh | 9 | 1001 | 9h |
| 15 | 1111 | Fh | 8 | 1000 | 8h |
Преобразование кода Грея в привычный бинарный код можно осуществить используя простую схему с инверторами и логическими элементами “исключающее или” как показано ниже:
Код Gray-Excess
Обычный одношаговый Грей-код подходит для разрешений, которые могут быть представлены в виде числа возведенного в степень 2. В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещяется на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализируются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещяется на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализируются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния : есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная . Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.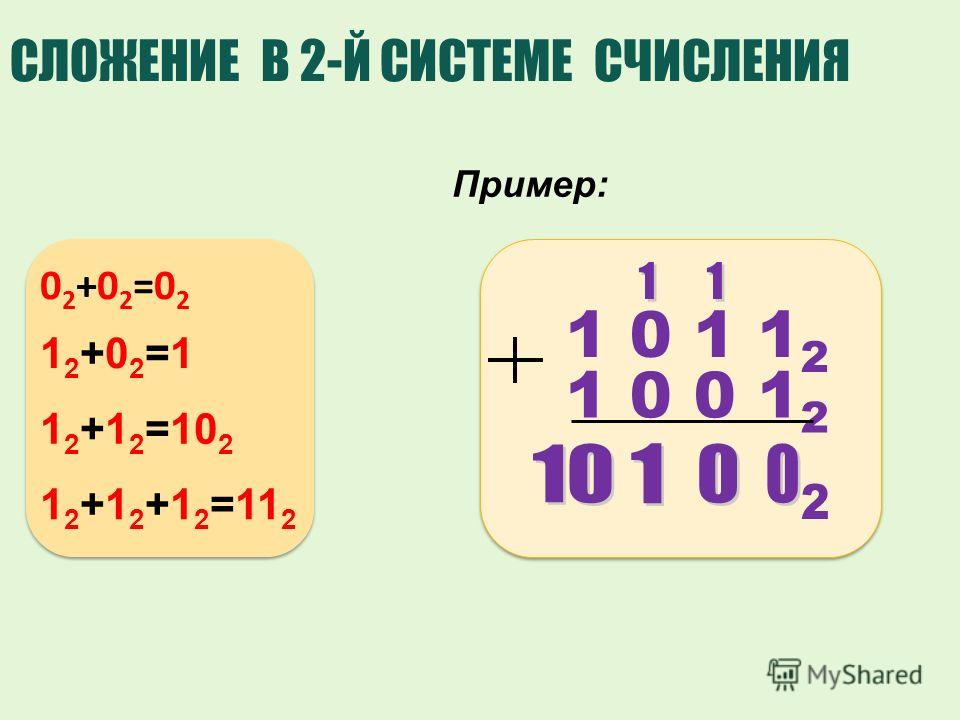
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
Вот схема типичного транзистора:
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики ).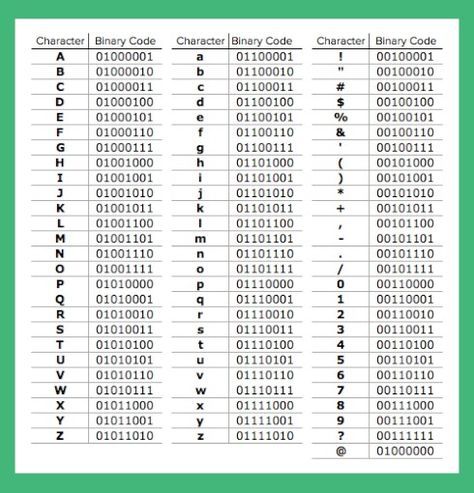
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер , разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений.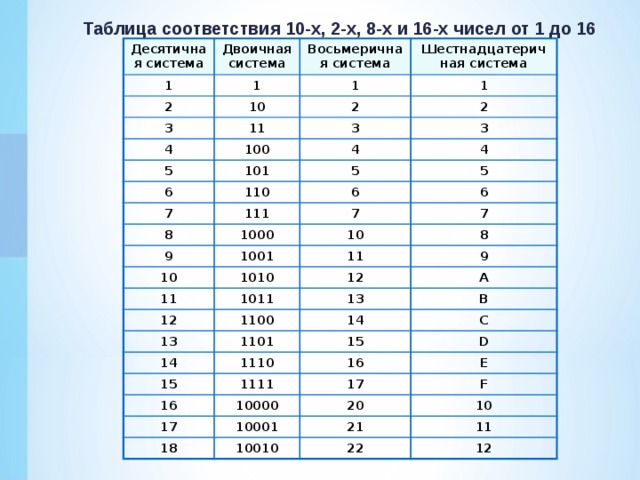 3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.
Решил сделать такой ниструмент как преобразование текста в двоичный код и обратно, такие сервисы есть, но они как правило работают с латиницей, мой же транслятор работает с кодировкой unicode формата UTF-8 , который кодирует кириллические символы двумя байтами.На данный момент возможности транслятора ограничены двухбайтными кодировками т.е. китайские иероглифы транслировать не получиться, но я собираюсь исправить это досадное недоразумение.
Для преобразования текста в бинарное представление введите текст в левое окошко и нажмите TEXT->BIN в правом окошке появится его двоичное представление.
Для преобразования бинарного кода в текст введите кода в правое окошко и нажмите BIN->TEXT в левом окошке появится его символьное представление.
В случае, если перевод бинарного кода в текст или наоборот не получился — проверьте корректность ваших данных!
Обновление!
Теперь доступно обратное преобразование текста вида:
в нормальный вид. Для этого нужно поставить галочку: «Заменить 0 пробелами, а 1 заполнителем █». Затем вставьте текст в правое окошко: «Текст в бинарном представлении» и нажмите кнопку под ним «BIN->TEXT».
При копировании таких текстов нужно быть осторожным т.к. можно запросто потерять пробелы в начале или в конце. Например строка сверху имеет вид:
██ █ █ ███████ █ ██ ██ █ █ ███ ██ █ █ ██ █ ██ █ █ ██ █ ███ █ ██ █ █ ██ █ █ ███ ██ █ █ ███ ██ █ ██
а на красном фоне:
██ █ █ ███████ █ ██ ██ █ █ ███ ██ █ █ ██ █ ██ █ █ ██ █ ███ █ ██ █ █ ██ █ █ ███ ██ █ █ ███ ██ █ ██
видите сколько пробелов в конце можно потерять?
Множество символов, с помощью которых записывается текст, называется алфавитом .
Число символов в алфавите – это его мощность .
Формула определения количества информации: N = 2 b ,
где N – мощность алфавита (количество символов),
b – количество бит (информационный вес символа).
В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным.
Т.к. 256 = 2 8 , то вес 1 символа – 8 бит.
Единице измерения 8 бит присвоили название 1 байт:
1 байт = 8 бит.
Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.
Каким же образом текстовая информация представлена в памяти компьютера?
Удобство побайтового кодирования символов очевидно, поскольку байт — наименьшая адресуемая часть памяти и, следовательно, процессор может обратиться к каждому символу отдельно, выполняя обработку текста. С другой стороны, 256 символов – это вполне достаточное количество для представления самой разнообразной символьной информации.
Теперь возникает вопрос, какой именно восьмиразрядный двоичный код поставить в соответствие каждому символу.
Понятно, что это дело условное, можно придумать множество способов кодировки.
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.
Для разных типов ЭВМ используются различные таблицы кодировки.
Международным стандартом для ПК стала таблица ASCII (читается аски) (Американский стандартный код для информационного обмена).
Таблица кодов ASCII делится на две части.
Международным стандартом является лишь первая половина таблицы, т.е. символы с номерами от 0 (00000000), до 127 (01111111).
Структура таблицы кодировки ASCII
Порядковый номер | Код | Символ |
0 — 31 | 00000000 — 00011111 | Символы с номерами от 0 до 31 принято называть управляющими. |
32 — 127 | 00100000 — 01111111 | Стандартная часть таблицы (английский). Сюда входят строчные и прописные буквы латинского алфавита, десятичные цифры, знаки препинания, всевозможные скобки, коммерческие и другие символы. |
128 — 255 | 10000000 — 11111111 | Альтернативная часть таблицы (русская). |
Первая половина таблицы кодов ASCII
Обращаю ваше внимание на то, что в таблице кодировки буквы (прописные и строчные) располагаются в алфавитном порядке, а цифры упорядочены по возрастанию значений. Такое соблюдение лексикографического порядка в расположении символов называется принципом последовательного кодирования алфавита.
Для букв русского алфавита также соблюдается принцип последовательного кодирования.
Вторая половина таблицы кодов ASCII
К сожалению, в настоящее время существуют пять различных кодировок кириллицы (КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за этого часто возникают проблемы с переносом русского текста с одного компьютера на другой, из одной программной системы в другую.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8-битный»). Эта кодировка применялась еще в 70-ые годы на компьютерах серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях операционной системы UNIX.
От начала 90-х годов, времени господства операционной системы MS DOS, остается кодировка CP866 («CP» означает «Code Page», «кодовая страница»).
Компьютеры фирмы Apple, работающие под управлением операционной системы Mac OS, используют свою собственную кодировку Mac.
Кроме того, Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка еще одну кодировку под названием ISO 8859-5.
Наиболее распространенной в настоящее время является кодировка Microsoft Windows, обозначаемая сокращением CP1251.
С конца 90-х годов проблема стандартизации символьного кодирования решается введением нового международного стандарта, который называется Unicode . Это 16-разрядная кодировка, т.е. в ней на каждый символ отводится 2 байта памяти. Конечно, при этом объем занимаемой памяти увеличивается в 2 раза. Но зато такая кодовая таблица допускает включение до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Это 16-разрядная кодировка, т.е. в ней на каждый символ отводится 2 байта памяти. Конечно, при этом объем занимаемой памяти увеличивается в 2 раза. Но зато такая кодовая таблица допускает включение до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Попробуем с помощью таблицы ASCII представить, как будут выглядеть слова в памяти компьютера.
Внутреннее представление слов в памяти компьютера
Иногда бывает так, что текст, состоящий из букв русского алфавита, полученный с другого компьютера, невозможно прочитать — на экране монитора видна какая-то «абракадабра». Это происходит оттого, что на компьютерах применяется разная кодировка символов русского языка.
Расшифровка бинарного кода применяется для перевода с машинного языка на обычный. Онлайн инструменты работают быстро, хотя и вручную это сделать несложно.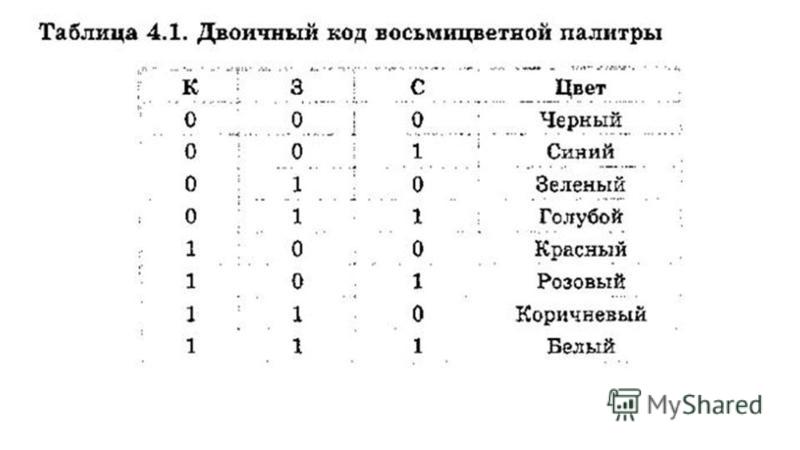
Бинарный или двоичный код используется для передачи информации в цифровом виде. Набор из всего лишь двух символов, например 1 и 0, позволяет зашифровать любую информацию, будь то текст, цифры или изображение.
Как шифровать бинарным кодом
Для ручного перевода в бинарный код любых символов используются таблицы, в которых каждому символу присвоен двоичный код в виде нулей и единиц. Наиболее распространенной системой кодировки является ASCII, в которой применяется 8-ми битная запись кода.
В базовой таблице приведены бинарные коды для латинской азбуки, цифр и некоторых символов.
В расширенную таблицу добавлена бинарная интерпретация кириллицы и дополнительных знаков.
Для перевода из двоичного кода в текст или цифры достаточно выбирать нужные коды из таблиц. Но, естественно, вручную такую работу выполнять долго. И ошибки, к тому же, неизбежны. Компьютер справляется с расшифровкой куда быстрее. И мы даже не задумываемся, набирая на экране текст, что в это момент производится перевод текста в бинарный код.
Перевод бинарного числа в десятичное
Для ручного перевода числа из бинарной системы счисления в десятичную можно использовать довольно простой алгоритм:
- Ниже бинарного числа, начиная с крайней правой цифры, написать цифру 2 в возрастающих степенях.
- Степени числа 2 умножить на соответствующую цифру бинарного числа (1 или 0).
- Получившиеся значения сложить.
Вот как этот алгоритм выглядит на бумаге:
Онлайн сервисы для бинарной расшифровки
Если все же требуется увидеть расшифрованный бинарный код, либо, наоборот, перевести текст в двоичную форму, проще всего использовать онлайн-сервисы, предназначенные для этих целей.
Два окна, привычных для онлайн-переводов позволяют практически одновременно увидеть оба варианта текста в обычной и бинарной форме. И расшифровка осуществляется в обе стороны. Ввод текста производится простым копированием и вставкой.
Двоичный код алфавит русский кодировка
С точки зрения ЭВМ текст состоит из отдельных символов.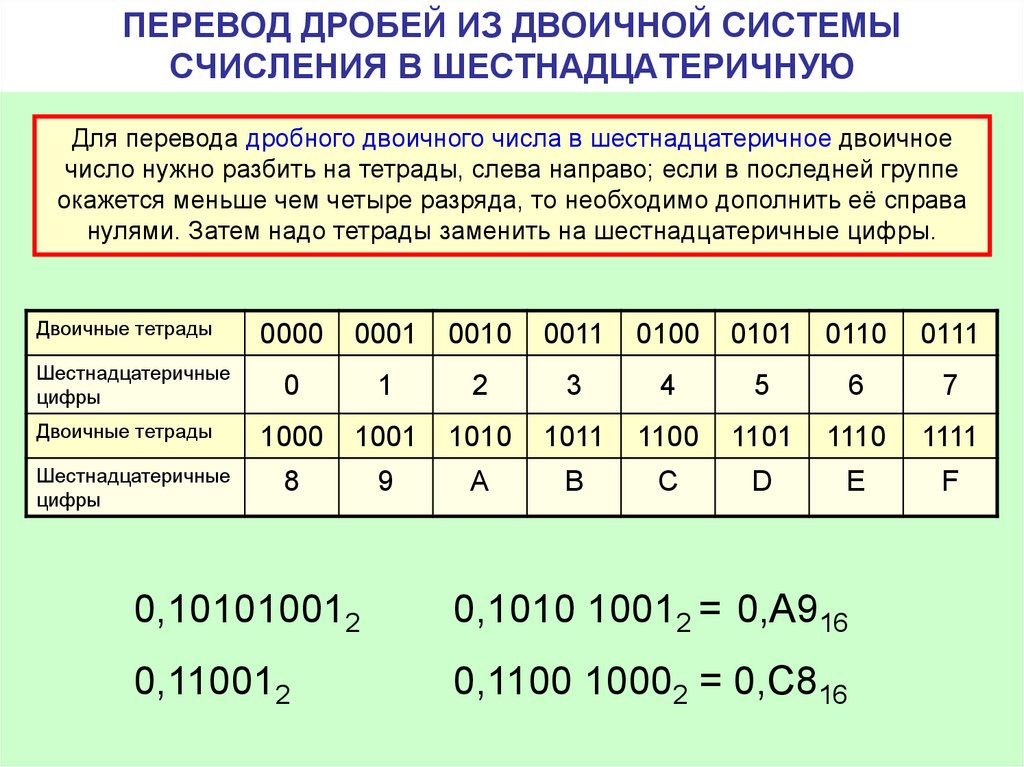 К числу символов принадлежат не только буквы (заглавные или строчные, латинские или русские), но и цифры, знаки препинания, спецсимволы типа «=», «(«, «&» и т.п. и даже (обратите особое внимание!) пробелы между словами. Да, не удивляйтесь: пустое место в тексте тоже должно иметь свое обозначение.
К числу символов принадлежат не только буквы (заглавные или строчные, латинские или русские), но и цифры, знаки препинания, спецсимволы типа «=», «(«, «&» и т.п. и даже (обратите особое внимание!) пробелы между словами. Да, не удивляйтесь: пустое место в тексте тоже должно иметь свое обозначение.
Вспомним некоторые известные нам факты:
Множество символов, с помощью которых записывается текст, называется алфавитом.
Число символов в алфавите – это его мощность.
Формула определения количества информации: N = 2 b ,
где N – мощность алфавита (количество символов),
b – количество бит (информационный вес символа).
В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным.
Т.к. 256 = 2 8 , то вес 1 символа – 8 бит.
Единице измерения 8 бит присвоили название 1 байт:
Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.
Каким же образом текстовая информация представлена в памяти компьютера?
Тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные нам буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в двоичном коде. Это значит, что каждый символ представляется 8-разрядным двоичным кодом.
Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек различает символы по их начертанию, а компьютер — по их коду.
Удобство побайтового кодирования символов очевидно, поскольку байт — наименьшая адресуемая часть памяти и, следовательно, процессор может обратиться к каждому символу отдельно, выполняя обработку текста. С другой стороны, 256 символов – это вполне достаточное количество для представления самой разнообразной символьной информации.
Теперь возникает вопрос, какой именно восьмиразрядный двоичный код поставить в соответствие каждому символу.
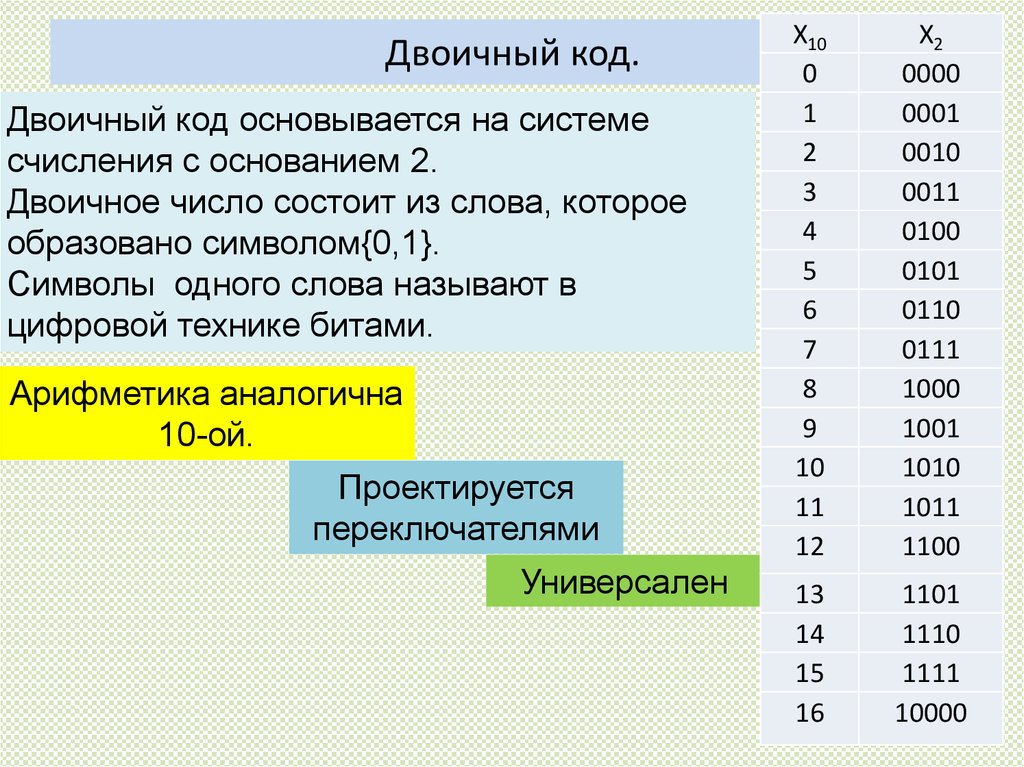
Понятно, что это дело условное, можно придумать множество способов кодировки.
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.
Для разных типов ЭВМ используются различные таблицы кодировки.
Международным стандартом для ПК стала таблица ASCII (читается аски) (Американский стандартный код для информационного обмена).
Таблица кодов ASCII делится на две части.
Международным стандартом является лишь первая половина таблицы, т.е. символы с номерами от 0 (00000000), до 127 (01111111).
Структура таблицы кодировки ASCII
Порядковый номер
Символ
0 — 31
00000000 — 00011111
Символы с номерами от 0 до 31 принято называть управляющими.
Их функция – управление процессом вывода текста на экран или печать, подача звукового сигнала, разметка текста и т.п.
32 — 127
00100000 — 01111111
Стандартная часть таблицы (английский). Сюда входят строчные и прописные буквы латинского алфавита, десятичные цифры, знаки препинания, всевозможные скобки, коммерческие и другие символы.
Символ 32 — пробел, т.е. пустая позиция в тексте.
Все остальные отражаются определенными знаками.
128 — 255
10000000 — 11111111
Альтернативная часть таблицы (русская).
Вторая половина кодовой таблицы ASCII, называемая кодовой страницей (128 кодов, начиная с 10000000 и кончая 11111111), может иметь различные варианты, каждый вариант имеет свой номер.
Кодовая страница в первую очередь используется для размещения национальных алфавитов, отличных от латинского. В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.
Первая половина таблицы кодов ASCII
Обращаю ваше внимание на то, что в таблице кодировки буквы (прописные и строчные) располагаются в алфавитном порядке, а цифры упорядочены по возрастанию значений.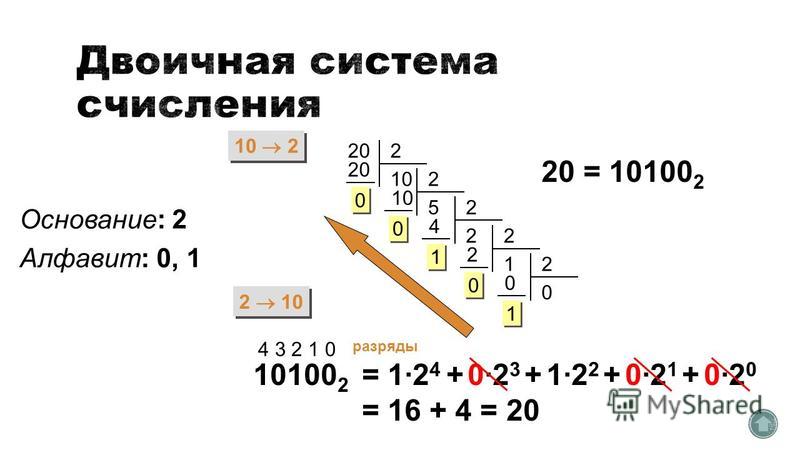 Такое соблюдение лексикографического порядка в расположении символов называется принципом последовательного кодирования алфавита.
Такое соблюдение лексикографического порядка в расположении символов называется принципом последовательного кодирования алфавита.
Для букв русского алфавита также соблюдается принцип последовательного кодирования.
Вторая половина таблицы кодов ASCII
К сожалению, в настоящее время существуют пять различных кодировок кириллицы (КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за этого часто возникают проблемы с переносом русского текста с одного компьютера на другой, из одной программной системы в другую.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8-битный»). Эта кодировка применялась еще в 70-ые годы на компьютерах серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях операционной системы UNIX.
От начала 90-х годов, времени господства операционной системы MS DOS, остается кодировка CP866 («CP» означает «Code Page», «кодовая страница»).
Компьютеры фирмы Apple, работающие под управлением операционной системы Mac OS, используют свою собственную кодировку Mac.
Кроме того, Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка еще одну кодировку под названием ISO 8859-5.
Наиболее распространенной в настоящее время является кодировка Microsoft Windows, обозначаемая сокращением CP1251.
С конца 90-х годов проблема стандартизации символьного кодирования решается введением нового международного стандарта, который называется Unicode. Это 16-разрядная кодировка, т.е. в ней на каждый символ отводится 2 байта памяти. Конечно, при этом объем занимаемой памяти увеличивается в 2 раза. Но зато такая кодовая таблица допускает включение до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
А какой минимальной длины должен быть код для кодирования символов английского алфавита, в котором 28 различных символов?
Давайте разберемся как же все таки переводить тексты в цифровой код? Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Кодирование текста.
По теории ЭВМ любой текст состоит из отдельных символов. К этим символам относятся: буквы, цифры, строчные знаки препинания, специальные символы ( «»,№, (), и т.д.), к ним, так же, относятся пробелы между словами.
Необходимый багаж знаний. Множество символов, при помощи которых записываю текст, называется АЛФАВИТОМ.
Число взятых в алфавите символов, представляет его мощность.
Количество информации можно определить по формуле : N = 2b
- N – та самая мощность ( множество символов),
- b – Бит ( вес взятого символа).
Алфавит, в котором будет 256 может вместить в себя практически все нужные символы. Такие алфавиты называют ДОСТАТОЧНЫМИ.
Если взять алфавит мощностью 256, и иметь в виду что 256 = 28
- 8 бит всегда называют 1 байт:
- 1 байт = 8 бит.
Если перевести каждый символ в двоичный код, то этот код компьютерного текста будет занимать 1 байт.
Любой текст набирают на клавиатуре, на клавишах клавиатуры, мы видим привычные для нас знаки (цифры, буквы и т. д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111.
д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111.
Поскольку, байт – это самая маленькая адресуемая частица памяти, и память обращена к каждому символу отдельно – удобство такого кодирование очевидно. Однако, 256 символов – это очень удобное количество для любой символьной информации.
Естественно, встал вопрос: Какой конкретно восьми разрядный код принадлежит каждому символу? И как осуществить перевод текста в цифровой код?
Этот процесс условный, и мы вправе придумать различные способы для кодировки символов. Каждый символ алфавита имеет свой номер от 0 до 255. И каждому номеру присвоен код от 00000000 до 11111111.
Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для различных типов ЭВМ используют разные таблицы для кодировки.
ASCII(или Аски), стала международным стандартом для персональных компьютеров. Таблица имеет две части.
Таблица имеет две части.
Таблица кода символов ASCII.
Первая половина для таблицы ASCII. (Именно первая половина, стала стандартом.)
Соблюдение лексикографического порядка, то есть, в таблице буквы (Строчные и прописные) указаны в строгом алфавитном порядке, а цифры по возрастанию, называют принципом последовального кодирования алфавита.
Для русского алфавита тоже соблюдают принцип последовательного кодирования.
Сейчас, в наше время используют целых пять систем кодировок русского алфавита(КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид.
Одним из первых стандартов для кодирования русского алфавита на персональных компьютерах считают КОИ8(«Код обмена информацией, 8-битный»). Данная кодировка использовалась в середине семидесятых годов на серии компьютеров ЕС ЭВМ, а со средины восьмидесятых, её начинают использовать в первых переведенных на русский язык операционных системах UNIX.
С начала девяностых годов, так называемого, времени, когда господствовала операционная система MS DOS, появляется система кодирования CP866 («CP» означает «Code Page», «кодовая страница»).
Гигант компьютерных фирм APPLE, со своей инновационной системой, под упралением которой они и работали (Mac OS), начинают использовать собственную систему для кодирования алфавита МАС.
Международная организация стандартизации (International Standards Organization, ISO)назначает стандартом для русского языка еще одну систему для кодирования алфавита, которая называется ISO 8859-5.
А самая распространенная, в наши дни, система для кодирования алфавита, придумана в Microsoft Windows, и называется CP1251.
С второй половины девяностых годов, была решена проблема стандарта перевода текста в цифровой код для русского языка и не только, введением в стандарт системы, под названием Unicode. Она представлена шестнадцатиразрядной кодировкой, это означает, что на каждый символ отводится ровно по два байта оперативной памяти.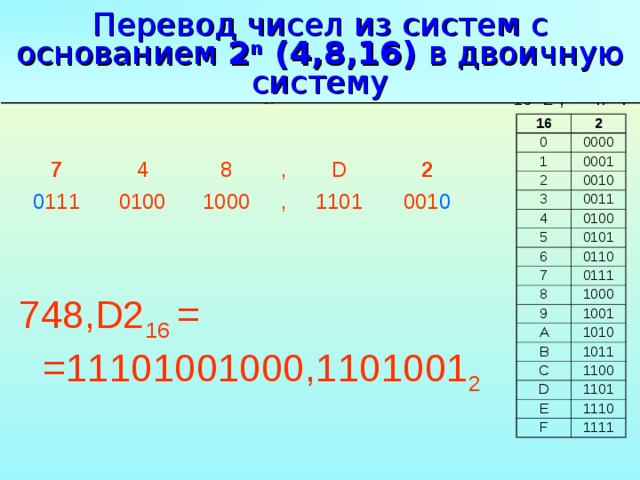 Само собой, при такой кодировке, затраты памяти увеличены в два раза. Однако, такая кодовая система позволяет переводить в электронный код до 65536 символов.
Само собой, при такой кодировке, затраты памяти увеличены в два раза. Однако, такая кодовая система позволяет переводить в электронный код до 65536 символов.
Специфика стандартной системы Unicode, является включением в себя абсолютно любого алфавита, будь он существующим, вымершим, выдуманным. В конечном счете, абсолютно любой алфавит, в добавок к этом, система Unicode, включает в себя уйму математических, химических, музыкальных и общих символов.
Давайте с помощью таблицы ASCII посмотрим, как может выглядеть слово в памяти вашего компьютера.
Очень часто случается так, что ваш текст, который написан буквами из русского алфавита, не читается, это обусловлено различием систем кодирования алфавита на компьютерах. Это очень распространенная проблема, которая довольно часто обнаруживается.
Перевод двоичной в слова. Двоичный код
Множество символов, с помощью которых записывается текст, называется алфавитом .
Число символов в алфавите – это его мощность .
Формула определения количества информации: N = 2 b ,
где N – мощность алфавита (количество символов),
b – количество бит (информационный вес символа).
В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным.
Т.к. 256 = 2 8 , то вес 1 символа – 8 бит.
Единице измерения 8 бит присвоили название 1 байт:
1 байт = 8 бит.
Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.
Каким же образом текстовая информация представлена в памяти компьютера?
Удобство побайтового кодирования символов очевидно, поскольку байт — наименьшая адресуемая часть памяти и, следовательно, процессор может обратиться к каждому символу отдельно, выполняя обработку текста. С другой стороны, 256 символов – это вполне достаточное количество для представления самой разнообразной символьной информации.
Теперь возникает вопрос, какой именно восьмиразрядный двоичный код поставить в соответствие каждому символу.

Понятно, что это дело условное, можно придумать множество способов кодировки.
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.
Для разных типов ЭВМ используются различные таблицы кодировки.
Международным стандартом для ПК стала таблица ASCII (читается аски) (Американский стандартный код для информационного обмена).
Таблица кодов ASCII делится на две части.
Международным стандартом является лишь первая половина таблицы, т.е. символы с номерами от 0 (00000000), до 127 (01111111).
Структура таблицы кодировки ASCII
Порядковый номер | Код | Символ |
0 — 31 | 00000000 — 00011111 | Символы с номерами от 0 до 31 принято называть управляющими. |
32 — 127 | 00100000 — 01111111 | Стандартная часть таблицы (английский). Сюда входят строчные и прописные буквы латинского алфавита, десятичные цифры, знаки препинания, всевозможные скобки, коммерческие и другие символы. |
128 — 255 | 10000000 — 11111111 | Альтернативная часть таблицы (русская). |
Первая половина таблицы кодов ASCII
Обращаю ваше внимание на то, что в таблице кодировки буквы (прописные и строчные) располагаются в алфавитном порядке, а цифры упорядочены по возрастанию значений. Такое соблюдение лексикографического порядка в расположении символов называется принципом последовательного кодирования алфавита.
Для букв русского алфавита также соблюдается принцип последовательного кодирования.
Вторая половина таблицы кодов ASCII
К сожалению, в настоящее время существуют пять различных кодировок кириллицы (КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за этого часто возникают проблемы с переносом русского текста с одного компьютера на другой, из одной программной системы в другую.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8-битный»). Эта кодировка применялась еще в 70-ые годы на компьютерах серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях операционной системы UNIX.
От начала 90-х годов, времени господства операционной системы MS DOS, остается кодировка CP866 («CP» означает «Code Page», «кодовая страница»).
Компьютеры фирмы Apple, работающие под управлением операционной системы Mac OS, используют свою собственную кодировку Mac.
Кроме того, Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка еще одну кодировку под названием ISO 8859-5.
Наиболее распространенной в настоящее время является кодировка Microsoft Windows, обозначаемая сокращением CP1251.
С конца 90-х годов проблема стандартизации символьного кодирования решается введением нового международного стандарта, который называется Unicode .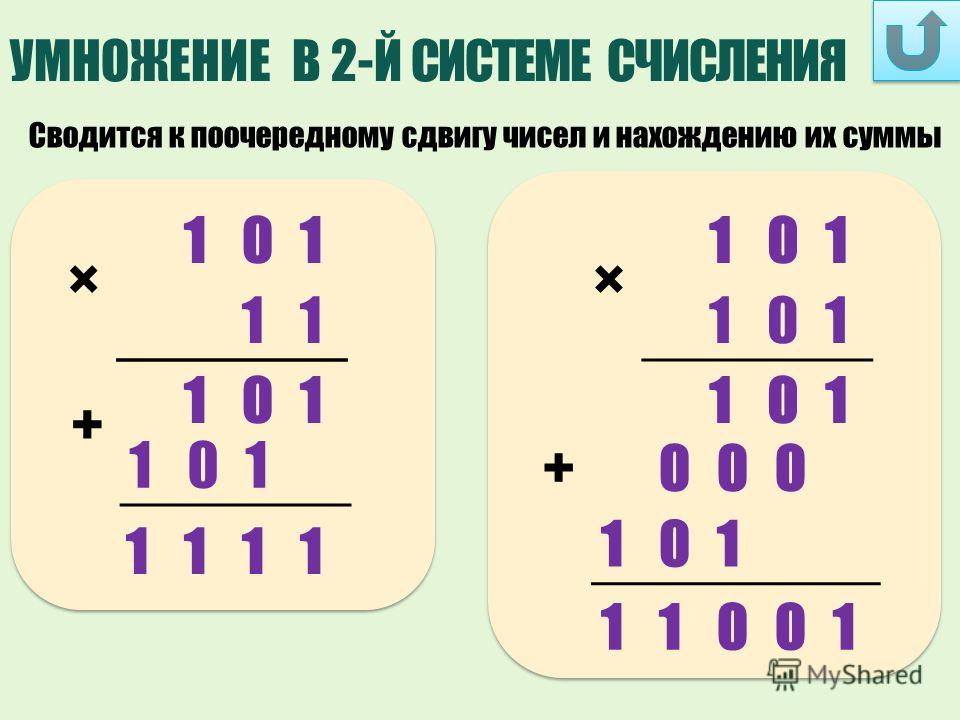 Это 16-разрядная кодировка, т.е. в ней на каждый символ отводится 2 байта памяти. Конечно, при этом объем занимаемой памяти увеличивается в 2 раза. Но зато такая кодовая таблица допускает включение до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Это 16-разрядная кодировка, т.е. в ней на каждый символ отводится 2 байта памяти. Конечно, при этом объем занимаемой памяти увеличивается в 2 раза. Но зато такая кодовая таблица допускает включение до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Попробуем с помощью таблицы ASCII представить, как будут выглядеть слова в памяти компьютера.
Внутреннее представление слов в памяти компьютера
Иногда бывает так, что текст, состоящий из букв русского алфавита, полученный с другого компьютера, невозможно прочитать — на экране монитора видна какая-то «абракадабра». Это происходит оттого, что на компьютерах применяется разная кодировка символов русского языка.
Расшифровка бинарного кода применяется для перевода с машинного языка на обычный. Онлайн инструменты работают быстро, хотя и вручную это сделать несложно.
Бинарный или двоичный код используется для передачи информации в цифровом виде. Набор из всего лишь двух символов, например 1 и 0, позволяет зашифровать любую информацию, будь то текст, цифры или изображение.
Как шифровать бинарным кодом
Для ручного перевода в бинарный код любых символов используются таблицы, в которых каждому символу присвоен двоичный код в виде нулей и единиц. Наиболее распространенной системой кодировки является ASCII, в которой применяется 8-ми битная запись кода.
В базовой таблице приведены бинарные коды для латинской азбуки, цифр и некоторых символов.
В расширенную таблицу добавлена бинарная интерпретация кириллицы и дополнительных знаков.
Для перевода из двоичного кода в текст или цифры достаточно выбирать нужные коды из таблиц. Но, естественно, вручную такую работу выполнять долго. И ошибки, к тому же, неизбежны. Компьютер справляется с расшифровкой куда быстрее. И мы даже не задумываемся, набирая на экране текст, что в это момент производится перевод текста в бинарный код.
Перевод бинарного числа в десятичное
Для ручного перевода числа из бинарной системы счисления в десятичную можно использовать довольно простой алгоритм:
- Ниже бинарного числа, начиная с крайней правой цифры, написать цифру 2 в возрастающих степенях.
- Степени числа 2 умножить на соответствующую цифру бинарного числа (1 или 0).
- Получившиеся значения сложить.
Вот как этот алгоритм выглядит на бумаге:
Онлайн сервисы для бинарной расшифровки
Если все же требуется увидеть расшифрованный бинарный код, либо, наоборот, перевести текст в двоичную форму, проще всего использовать онлайн-сервисы, предназначенные для этих целей.
Два окна, привычных для онлайн-переводов позволяют практически одновременно увидеть оба варианта текста в обычной и бинарной форме. И расшифровка осуществляется в обе стороны. Ввод текста производится простым копированием и вставкой.
Термин «бинарный» по смыслу – состоящий из двух частей, компонентов. Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска.
Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска.
Существуют различные возможности кодирования информации.
Двоичный код
В цифровой технике способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы ДК называют битами.
Одним из обоснований применения ДК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства магнитного потока в данной ячейке носителя магнитной записи.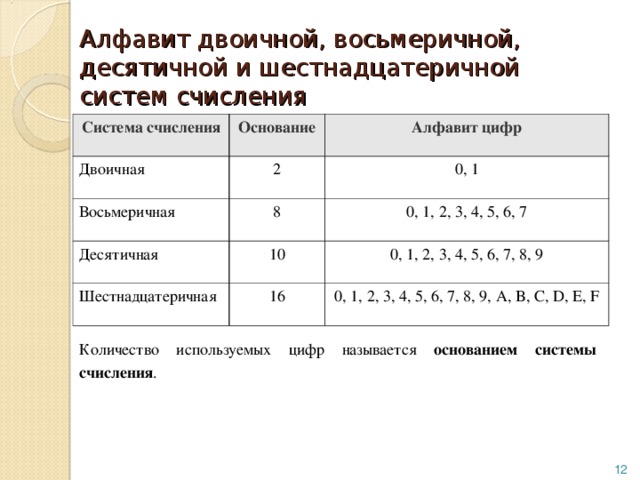
Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества битов в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный или 3-битовый код:
| числовое значение | двоичный код |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Отсюда видно, что для числа больше 7 при 3-разрядном коде уже нет кодовых комбинаций из 0 и 1.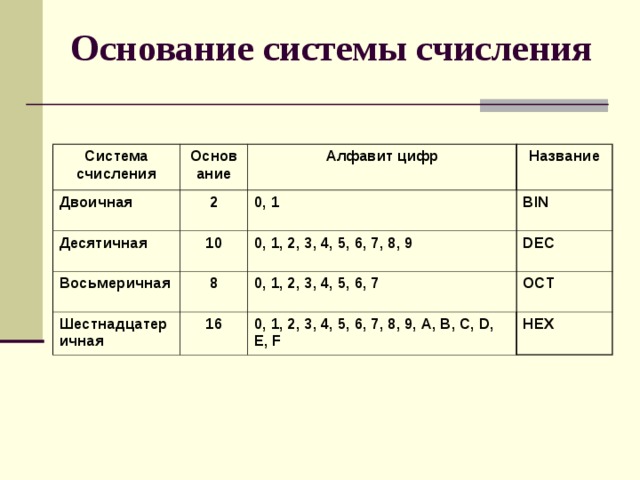
Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее количество значений m какой-либо величины (температуры, напряжения, тока и др.), которое может быть выражено двоичным кодом, зависит от числа используемых разрядов n как m=2n. Если n=3, как в рассмотренном примере, то получим 8 значений, включая ведущий 0.
Двоичный код является многошаговым кодом. Это означает, что при переходе с одного положения (значения) в другое могут изменятся несколько бит одновременно. Например число 3 в двоичном коде = 011. Число же 4 в двоичном коде = 100. Соответственно при переходе от 3 к 4 меняют свое состояние на противоположное все 3 бита одновременно. Считывание такого кода с кодового диска привело бы к тому, что из-за неизбежных отклонений (толеранцев) при производстве кодового диска изменение информации от каждой из дорожек в отдельности никогда не произойдет одновременно. Это в свою очередь привело бы к тому, что при переходе от одного числа к другому кратковременно будет выдана неверная информация. Так при вышеупомянутом переходе от числа 3 к числу 4 очень вероятна кратковременная выдача числа 7 когда, например, старший бит во время перехода поменял свое значение немного раньше чем остальные. Чтобы избежать этого, применяется так называемый одношаговый код, например так называемый Грей-код.
Так при вышеупомянутом переходе от числа 3 к числу 4 очень вероятна кратковременная выдача числа 7 когда, например, старший бит во время перехода поменял свое значение немного раньше чем остальные. Чтобы избежать этого, применяется так называемый одношаговый код, например так называемый Грей-код.
Код Грея
Грей-код является так называемым одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой-то один из всех бит информации. Погрешность при считывании информации с механического кодового диска при переходе от одного числа к другому приведет лишь к тому, что переход от одного положения к другом будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения при переходе от одного положения к другому полностью исключается.
Преимуществом Грей-кода является также его способность зеркального отображения информации. Так инвертируя старший бит можно простым образом менять направление счета и таким образом подбирать к фактическому (физическому) направлению вращения оси. Изменение направления счета таким образом может легко изменяться управляя так называемым входом ” Complement “. Выдаваемое значение может таким образом быть возврастающим или спадающим при одном и том же физическом направлении вращения оси.
Изменение направления счета таким образом может легко изменяться управляя так называемым входом ” Complement “. Выдаваемое значение может таким образом быть возврастающим или спадающим при одном и том же физическом направлении вращения оси.
Поскольку информация выраженая в Грей-коде имеет чисто кодированный характер не несущей реальной числовой информации должен он перед дальнейшей обработкой сперва преобразован в стандартный бинарный код. Осуществляется это при помощи преобразователя кода (декодера Грей-Бинар) который к счастью легко реализируется с помощью цепи из логических элементов «исключающее или» (XOR) как програмным так и аппаратным способом.
Соответствие десятичных чисел в диапазоне от 0 до 15 двоичному коду и коду Грея
| Двоичное кодирование | Кодирование по методу Грея | ||||
| Десятичный код | Двоичное значение | Шестнадц. значение значение | Десятичный код | Двоичное значение | Шестнадц. значение |
| 0 | 0000 | 0h | 0 | 0000 | 0h |
| 1 | 0001 | 1h | 1 | 0001 | 1h |
| 2 | 0010 | 2h | 3 | 0011 | 3h |
| 3 | 0011 | 3h | 2 | 0010 | 2h |
| 4 | 0100 | 4h | 6 | 0110 | 6h |
| 5 | 0101 | 5h | 7 | 0111 | 7h |
| 6 | 0110 | 6h | 5 | 0101 | 5h |
| 7 | 0111 | 7h | 4 | 0100 | 4h |
| 8 | 1000 | 8h | 12 | 1100 | Ch |
| 9 | 1001 | 9h | 13 | 1101 | Dh |
| 10 | 1010 | Ah | 15 | 1111 | Fh |
| 11 | 1011 | Bh | 14 | 1110 | Eh |
| 12 | 1100 | Ch | 10 | 1010 | Ah |
| 13 | 1101 | Dh | 11 | 1011 | Bh |
| 14 | 1110 | Eh | 9 | 1001 | 9h |
| 15 | 1111 | Fh | 8 | 1000 | 8h |
Преобразование кода Грея в привычный бинарный код можно осуществить используя простую схему с инверторами и логическими элементами “исключающее или” как показано ниже:
Код Gray-Excess
Обычный одношаговый Грей-код подходит для разрешений, которые могут быть представлены в виде числа возведенного в степень 2. В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещяется на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализируются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещяется на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализируются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
Давайте разберемся как же все таки переводить тексты в цифровой код ? Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Кодирование текста.
По теории ЭВМ любой текст состоит из отдельных символов. К этим символам относятся: буквы, цифры, строчные знаки препинания, специальные символы («»,№, (), и т.д.), к ним, так же, относятся пробелы между словами.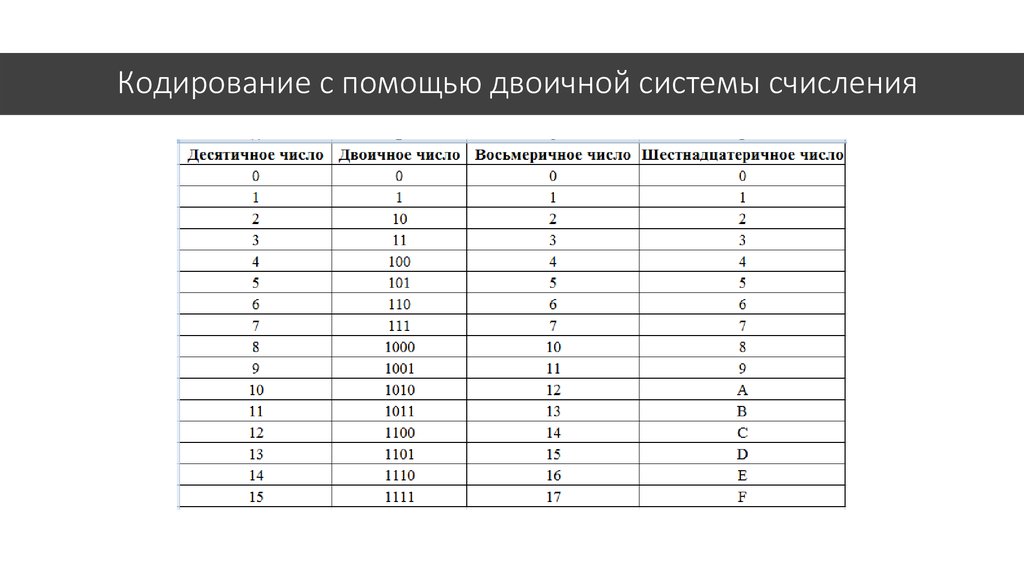
Необходимый багаж знаний. Множество символов, при помощи которых записываю текст, называется АЛФАВИТОМ.
Число взятых в алфавите символов, представляет его мощность.
Количество информации можно определить по формуле: N = 2b
- N — та самая мощность (множество символов),
- b — Бит (вес взятого символа).
Алфавит, в котором будет 256 может вместить в себя практически все нужные символы. Такие алфавиты называют ДОСТАТОЧНЫМИ.
Если взять алфавит мощностью 256, и иметь в виду что 256 = 28
- 8 бит всегда называют 1 байт:
- 1 байт = 8 бит.
Если перевести каждый символ в двоичный код, то этот код компьютерного текста будет занимать 1 байт.
Как текстовая информация может выглядеть в памяти компьютера?
Любой текст набирают на клавиатуре, на клавишах клавиатуры, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111.
Поскольку, байт — это самая маленькая адресуемая частица памяти, и память обращена к каждому символу отдельно — удобство такого кодирование очевидно. Однако, 256 символов — это очень удобное количество для любой символьной информации.
Естественно, встал вопрос: Какой конкретно восьми разрядный код принадлежит каждому символу? И как осуществить перевод текста в цифровой код?
Этот процесс условный, и мы вправе придумать различные способы для кодировки символов . Каждый символ алфавита имеет свой номер от 0 до 255. И каждому номеру присвоен код от 00000000 до 11111111.
Таблица для кодировки — это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для различных типов ЭВМ используют разные таблицы для кодировки.
ASCII(или Аски), стала международным стандартом для персональных компьютеров. Таблица имеет две части.
Первая половина для таблицы ASCII. (Именно первая половина, стала стандартом.)
Соблюдение лексикографического порядка, то есть, в таблице буквы (Строчные и прописные) указаны в строгом алфавитном порядке, а цифры по возрастанию, называют принципом последовального кодирования алфавита.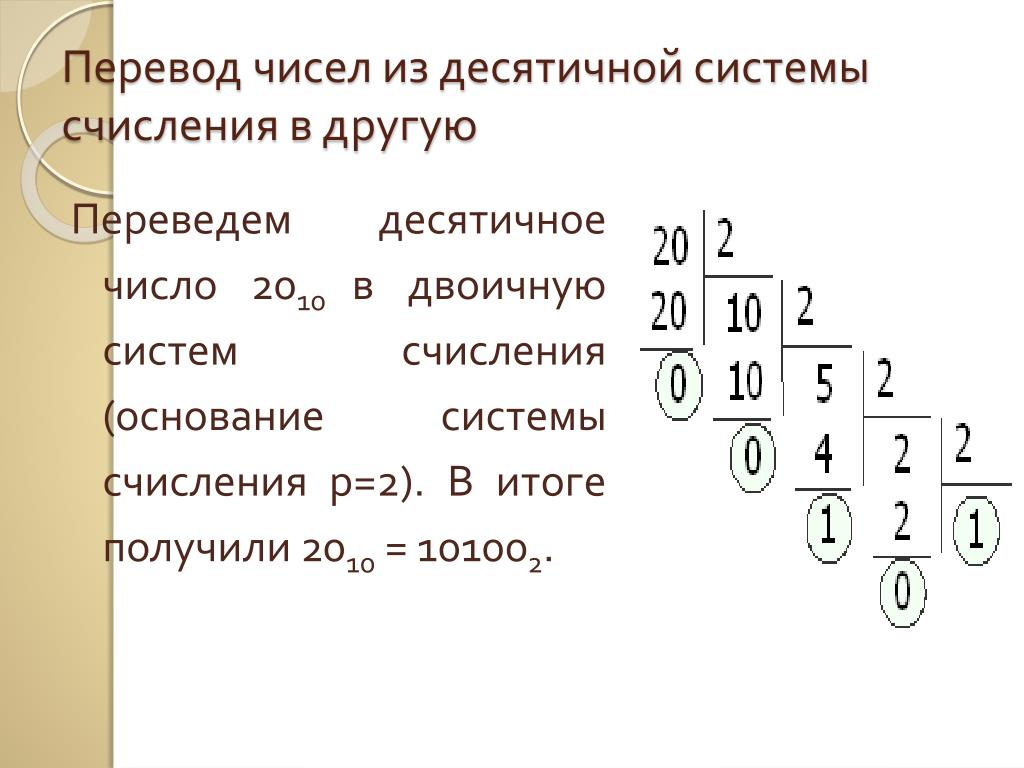
Для русского алфавита тоже соблюдают принцип последовательного кодирования .
Сейчас, в наше время используют целых пять систем кодировок русского алфавита(КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид.
Одним из первых стандартов для кодирования русского алфавит а на персональных компьютерах считают КОИ8(«Код обмена информацией, 8-битный»). Данная кодировка использовалась в середине семидесятых годов на серии компьютеров ЕС ЭВМ, а со средины восьмидесятых, её начинают использовать в первых переведенных на русский язык операционных системах UNIX.
С начала девяностых годов, так называемого, времени, когда господствовала операционная система MS DOS, появляется система кодирования CP866 («CP» означает «Code Page», «кодовая страница»).
Гигант компьютерных фирм APPLE, со своей инновационной системой, под упралением которой они и работали (Mac OS), начинают использовать собственную систему для кодирования алфавита МАС.
Международная организация стандартизации (International Standards Organization, ISO)назначает стандартом для русского языка еще одну систему для кодирования алфавита , которая называется ISO 8859-5.
А самая распространенная, в наши дни, система для кодирования алфавита, придумана в Microsoft Windows, и называется CP1251.
С второй половины девяностых годов, была решена проблема стандарта перевода текста в цифровой код для русского языка и не только, введением в стандарт системы, под названием Unicode. Она представлена шестнадцатиразрядной кодировкой, это означает, что на каждый символ отводится ровно по два байта оперативной памяти. Само собой, при такой кодировке, затраты памяти увеличены в два раза. Однако, такая кодовая система позволяет переводить в электронный код до 65536 символов.
Специфика стандартной системы Unicode, является включением в себя абсолютно любого алфавита, будь он существующим, вымершим, выдуманным. В конечном счете, абсолютно любой алфавит, в добавок к этом, система Unicode, включает в себя уйму математических, химических, музыкальных и общих символов.
Давайте с помощью таблицы ASCII посмотрим, как может выглядеть слово в памяти вашего компьютера.
Очень часто случается так, что ваш текст, который написан буквами из русского алфавита, не читается, это обусловлено различием систем кодирования алфавита на компьютерах. Это очень распространенная проблема, которая довольно часто обнаруживается.
Двоичный код — это подача информации путем сочетания символов 0 или 1. Порою бывает очень сложно понять принцип кодирования информации в виде этих двух чисел, однако мы постараемся все подробно разъяснить.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде , открывается незамысловатая истина — бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид — 01010100, E — 01000101 и буква X — 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.
К примеру, английская буква T в двоичной системе приобретет такой вид — 01010100, E — 01000101 и буква X — 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.
На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.
Перевод натурального числа десятичной системы счисления в двоичную систему.

Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:
1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет — 0.
2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.
3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя — 0.
4. В этот момент считается, что двоичный код готов.
Для примера переведем в двоичную систему число 7:
1. 7: 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.
2. 3: 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.
3. 1: 2 = 0.5. Снова выбираем 1 по тому же принципу.
4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код — 111.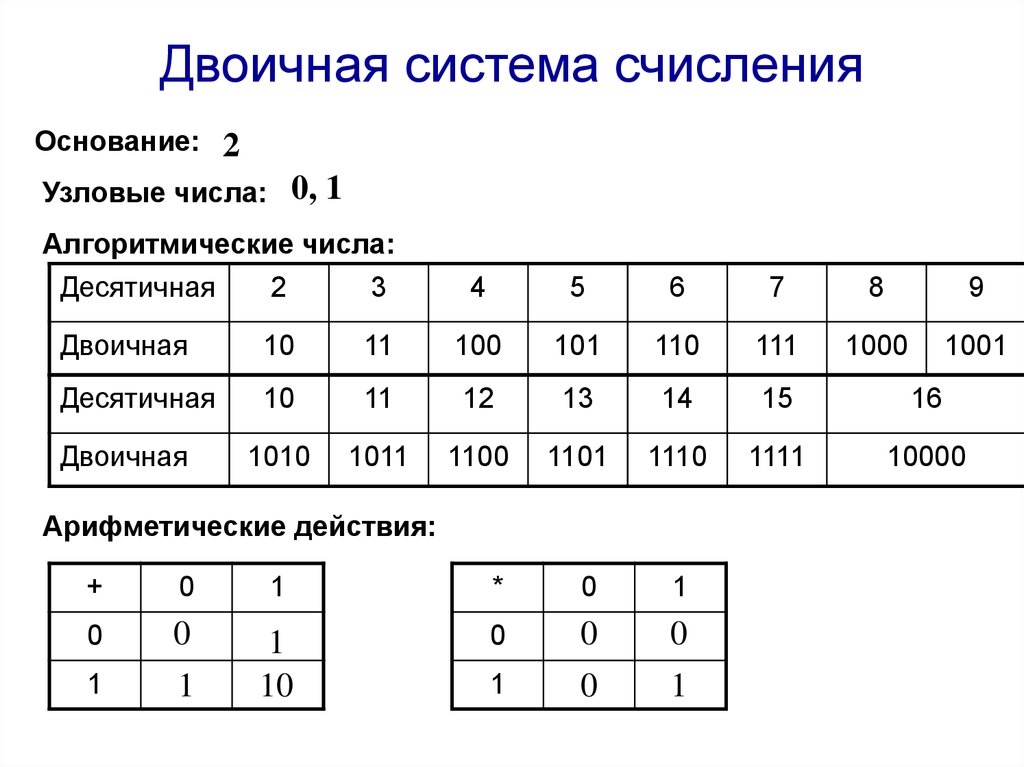 0) = 4 + 2 + 1 = 7.
0) = 4 + 2 + 1 = 7.
Немного из истории двоичной системы счисления.
Принято считать, что впервые двоичную систему предложил Готфрид Вильгельм Лейбниц, который считал систему полезной в сложных математических вычислениях и науке. Но по неким данным, до его предложения о двоичной системе счисления, в Китае появилась настенная надпись, которая расшифровывалась при использовании двоичного кода . На надписи были изображены длинные и короткие палочки. Предполагая, что длинная это 1, а короткая палочка — 0, есть доля вероятности, что в Китае идея двоичного кода существовала многим ранее его официального открытия. Расшифровка кода определила там только простое натуральное число, однако это факт, который им и остается.
Как в двоичном коде будет слово привет. Русский алфавит в двоичном коде. Единая буквенная двоичная кодировка. Байтовый код. Понимание двоичных чисел
Термин «двоичный» в том смысле — состоящий из двух частей, компонентов. Таким образом, двоичные коды — это коды, состоящие только из двух символических состояний, таких как черный или белый, светлый или темный, проводник или изолятор. Двоичный код в цифровой технике — способ представления данных (чисел, слов и др.) в виде комбинации двух знаков, которые могут обозначаться как 0 и 1. Знаки или единицы ВС называются битами. Одним из обоснований использования БК является простота и надежность накопления информации в любой среде в виде сочетания всего лишь двух ее физических состояний, например, в виде изменения или постоянства светового потока при чтение с оптического кодового диска.
Двоичный код в цифровой технике — способ представления данных (чисел, слов и др.) в виде комбинации двух знаков, которые могут обозначаться как 0 и 1. Знаки или единицы ВС называются битами. Одним из обоснований использования БК является простота и надежность накопления информации в любой среде в виде сочетания всего лишь двух ее физических состояний, например, в виде изменения или постоянства светового потока при чтение с оптического кодового диска.
Существуют различные возможности кодирования информации.
Двоичный код
В цифровой технике способ представления данных (чисел, слов и др.) в виде комбинации двух знаков, которые могут обозначаться как 0 и 1. Знаки или единицы ДК называются биты.
Одним из обоснований применения ДК является простота и надежность накопления информации в любой среде в виде комбинации всего двух ее физических состояний, например, в виде изменения или постоянства магнитного потока в данной ячейке магнитного носителя записи.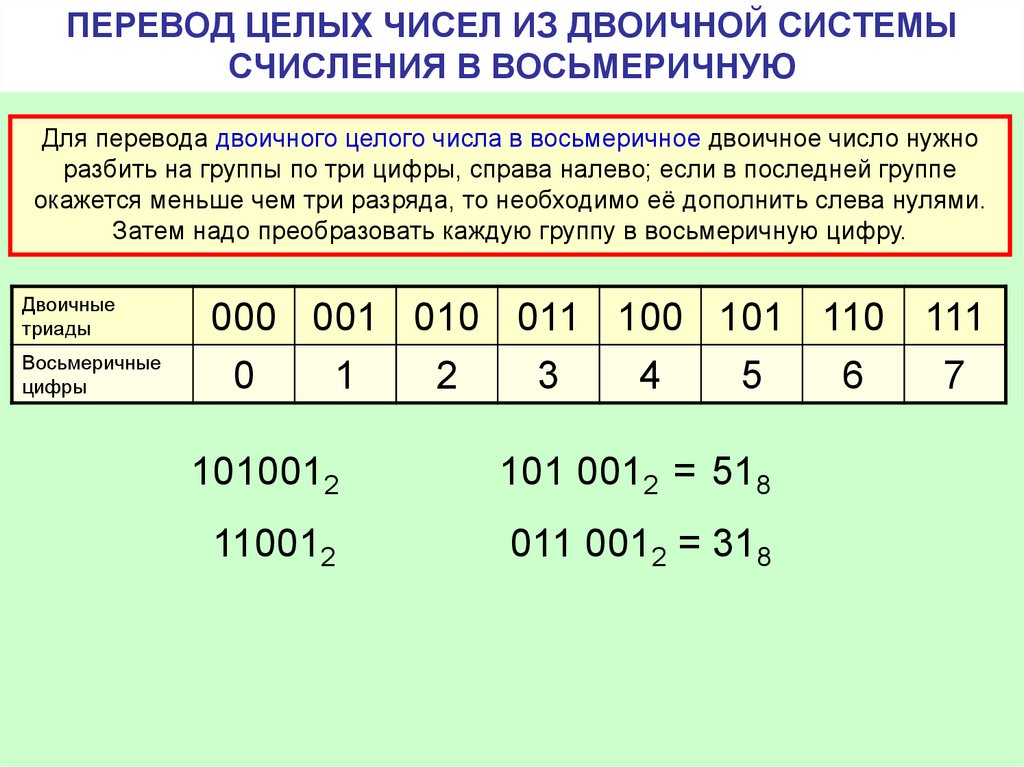
Наибольшее число, которое может быть выражено в двоичном виде, зависит от количества используемых битов, т. е. от количества битов в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-битный или 3-битный код:
| числовое значение | двоичный код |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Отсюда видно, что для числа больше 7 с 3-битным кодом больше нет кодовых комбинаций 0 и 1.
Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее число значений m любой величины (температуры, напряжения, силы тока и т. д.), которые могут быть выражены в двоичном коде, зависит от числа используемых битов n, поскольку m = 2n. Если n = 3, как в рассмотренном примере, то получаем 8 значений, включая ведущее 0,
Двоичный код — это многошаговый код. Это означает, что при переходе от одной позиции (значения) к другой одновременно может измениться несколько битов. Например, число 3 в двоичном коде = 011. Число 4 в двоичном коде = 100. Соответственно, при переходе от 3 к 4 все 3 бита одновременно меняют свое состояние на противоположное. Считывание такого кода с кодового диска привело бы к тому, что из-за неизбежных отклонений (допусков) при изготовлении кодового диска изменение информации с каждой из дорожек в отдельности никогда не будет происходить одновременно. Это, в свою очередь, привело бы к тому, что при переходе с одного номера на другой кратковременно отображалась бы неверная информация.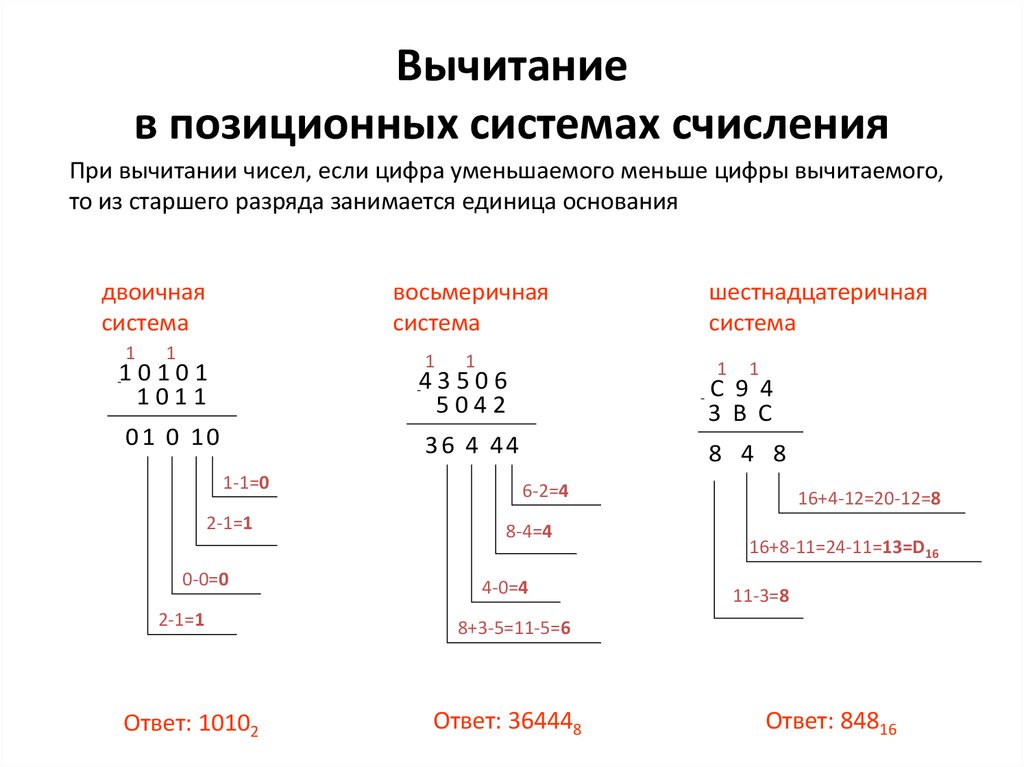 Так вот при упомянутом переходе от цифры 3 к цифре 4 очень вероятен кратковременный выход цифры 7, когда, например, старший бит при переходе изменил свое значение чуть раньше остальных. Чтобы избежать этого, используется так называемый одношаговый код, например так называемый код Грея.
Так вот при упомянутом переходе от цифры 3 к цифре 4 очень вероятен кратковременный выход цифры 7, когда, например, старший бит при переходе изменил свое значение чуть раньше остальных. Чтобы избежать этого, используется так называемый одношаговый код, например так называемый код Грея.
Код Грея
Код Грея является так называемым одношаговым кодом, т.е. при переходе от одного числа к другому всегда изменяется только один из всех битов информации. Ошибка в считывании информации с механического кодового диска при переходе от одной цифры к другой приведет лишь к тому, что переход от одной позиции к другой будет лишь незначительно сдвинут во времени, однако выдача совершенно неверного значения угловое положение при переходе из одного положения в другое полностью исключено…
Преимущество кода Грея также заключается в его способности отражать информацию. Так инвертируя старший разряд, можно просто изменить направление счета и таким образом подстроиться под фактическое (физическое) направление вращения оси. Изменение направления счета таким образом можно легко изменить, манипулируя так называемым вводом «Дополнение». Таким образом, возвращаемое значение может увеличиваться или уменьшаться для одного и того же физического направления вращения оси.
Изменение направления счета таким образом можно легко изменить, манипулируя так называемым вводом «Дополнение». Таким образом, возвращаемое значение может увеличиваться или уменьшаться для одного и того же физического направления вращения оси.
Поскольку информация, выраженная в коде Грея, является чисто закодированной, она не является реальным носителем числовой информации, ее необходимо сначала преобразовать в стандартный двоичный код перед дальнейшей обработкой. Это делается с помощью преобразователя кода (декодера Грея-Бинара), который, к счастью, легко реализуется с помощью цепочки логических элементов «исключающее ИЛИ» (XOR) как в программном, так и в аппаратном обеспечении.
Соответствие десятичных чисел в диапазоне от 0 до 15 двоичному коду и коду Грея
| Двоичное кодирование | Серый код | ||||
| Десятичный код | Двоичное значение | Шестнадцать. значение значение | Десятичный код | Двоичное значение | Шестнадцать. значение |
| 0 | 0000 | 0ч | 0 | 0000 | 0ч |
| 1 | 0001 | 1ч | 1 | 0001 | 1ч |
| 2 | 0010 | 2ч | 3 | 0011 | 3 часа |
| 3 | 0011 | 3 часа | 2 | 0010 | 2ч |
| 4 | 0100 | 4 часа | 6 | 0110 | 6ч |
| 5 | 0101 | 5ч | 7 | 0111 | 7ч |
| 6 | 0110 | 6ч | 5 | 0101 | 5ч |
| 7 | 0111 | 7ч | 4 | 0100 | 4 часа |
| 8 | 1000 | 8ч | 12 | 1100 | Ч |
| 9 | 1001 | 9ч | 13 | 1101 | дирхамов |
| 10 | 1010 | Ач | 15 | 1111 | ФХ |
| 11 | 1011 | Бх | 14 | 1110 | Эх |
| 12 | 1100 | Ч | 10 | 1010 | Ач |
| 13 | 1101 | дирхамов | 11 | 1011 | Бх |
| 14 | 1110 | Эх | 9 | 1001 | 9ч |
| 15 | 1111 | ФХ | 8 | 1000 | 8ч |
Преобразование кода Грея в привычный двоичный код можно выполнить с помощью простой схемы с инверторами и вентилями «исключающее ИЛИ», как показано ниже:
Код Грея-Избытка
Обычный одношаговый код Грея подходит для разрешений, которые можно представить в виде числа, возведенного в степень 2.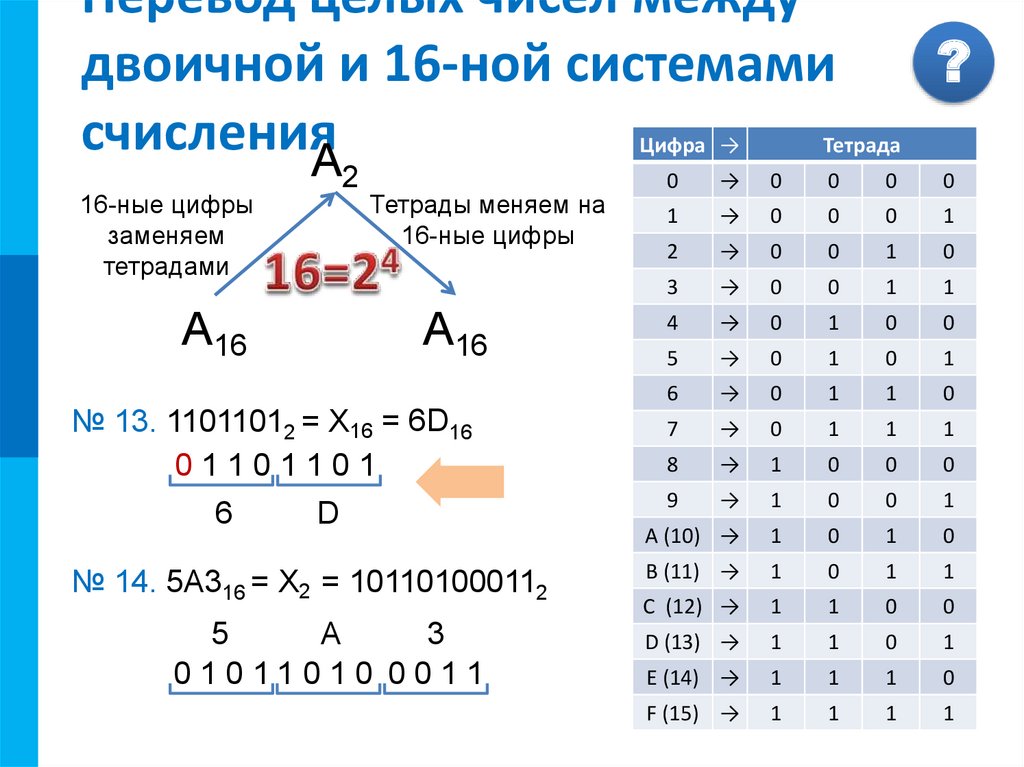 В тех случаях, когда необходимо реализовать другие разрешения из обычного кода Грея , его средняя часть вырезается и используется. Таким образом сохраняется «одношаговый» код. Однако числовой диапазон не начинается с нуля, а смещается на определенное значение. При обработке информации из сгенерированного сигнала вычитается половина разницы между исходным и уменьшенным разрешением. Разрешения типа 360? для выражения угла часто реализуются этим методом. Итак, 9-битный код Грея, равный 512 шагам, обрезанный с обеих сторон на 76 шагов, будет равен 360°.
В тех случаях, когда необходимо реализовать другие разрешения из обычного кода Грея , его средняя часть вырезается и используется. Таким образом сохраняется «одношаговый» код. Однако числовой диапазон не начинается с нуля, а смещается на определенное значение. При обработке информации из сгенерированного сигнала вычитается половина разницы между исходным и уменьшенным разрешением. Разрешения типа 360? для выражения угла часто реализуются этим методом. Итак, 9-битный код Грея, равный 512 шагам, обрезанный с обеих сторон на 76 шагов, будет равен 360°.
Компьютеры не понимают слова и числа так, как люди. Современное программное обеспечение позволяет конечному пользователю игнорировать его, но на самых низких уровнях ваш компьютер работает на двоичном электрическом сигнале, который имеет только два состояния : есть ток или нет. Чтобы «понимать» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основана на двух цифрах, 1 и 0, которые соответствуют состояниям включения и выключения, понятным вашему компьютеру. Вы, наверное, знакомы с десятичной системой. Он использует десять цифр, от 0 до 9, а затем переходит к следующему порядку для формирования двузначных чисел, причем цифра каждого следующего порядка в десять раз больше предыдущей. Двоичная система аналогична, каждая цифра в два раза больше предыдущей.
Вы, наверное, знакомы с десятичной системой. Он использует десять цифр, от 0 до 9, а затем переходит к следующему порядку для формирования двузначных чисел, причем цифра каждого следующего порядка в десять раз больше предыдущей. Двоичная система аналогична, каждая цифра в два раза больше предыдущей.
Счет в двоичном формате
В двоичном формате первая цифра — это десятичная 1. Вторая цифра — 2, третья — 4, четвертая — 8 и так далее — каждый раз она удваивается. Сложение всех этих значений даст вам десятичное число.
1111 (двоичный) = 8 + 4 + 2 + 1 = 15 (десятичный)
Счет 0 дает нам 16 возможных значений для четырех двоичных битов. Переместите 8 бит, и вы получите 256 возможных значений. Это требует гораздо больше места для представления, поскольку четыре десятичных знака дают нам 10 000 возможных значений. Конечно, двоичный код занимает больше места, но компьютеры понимают двоичный код намного лучше, чем десятичный. А для некоторых вещей, таких как логическая обработка, двоичный код лучше, чем десятичный.
Следует сказать, что есть еще одна базовая система, которая используется в программировании: шестнадцатеричный … Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют его для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть они заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует числа от 0 до 9 и буквы от A до F, чтобы дать дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: Аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере представляет собой электрический сигнал, а на заре вычислительной техники электрические сигналы было гораздо сложнее измерить. Было бы разумнее различать только состояние «включено», представленное отрицательным зарядом, и состояние «выключено», представленное положительным зарядом.
Для тех, кто не знает, почему «выкл» представлен положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов — больше ток с отрицательным зарядом.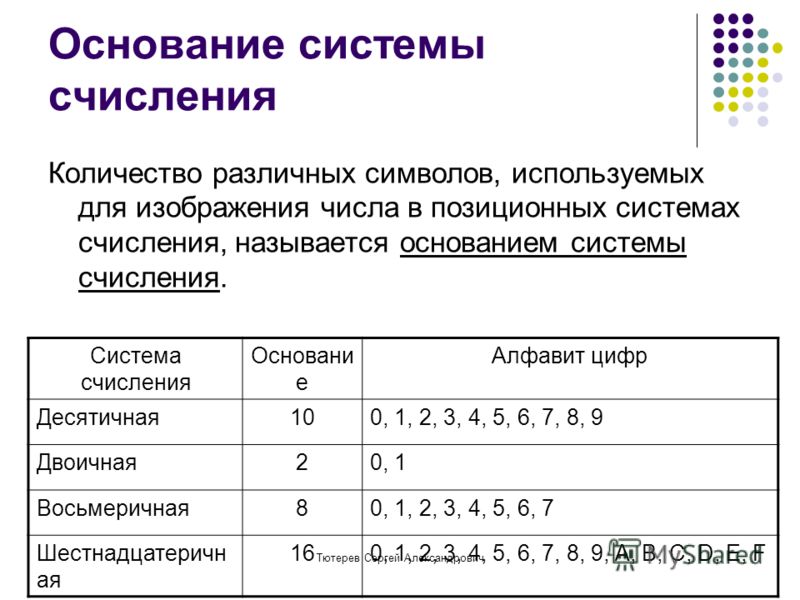
Таким образом, ранние компьютеры размером с комнату использовали двоичных файлов для построения своих систем, и хотя они использовали более старое и более громоздкое оборудование, они работали на тех же фундаментальных принципах. В современных компьютерах используется так называемый транзистор . для выполнения вычислений с двоичным кодом.
Вот схема типичного транзистора:
По сути, он позволяет току течь от истока к стоку, если в затворе есть ток. Это формирует двоичный ключ. Производители могут делать эти транзисторы невероятно маленькими — всего 5 нанометров или размером с две нити ДНК. Так работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (правда, это связано с их нереальным молекулярным размером, с учетом странности квантовой механики ).
Почему только двоичная система
Вы можете подумать: «Почему только 0 и 1? Почему бы не добавить еще один номер? «Хотя это отчасти связано с традицией создания компьютеров, добавление еще одной цифры будет означать, что будет выделено другое состояние тока, а не просто выключено или включено.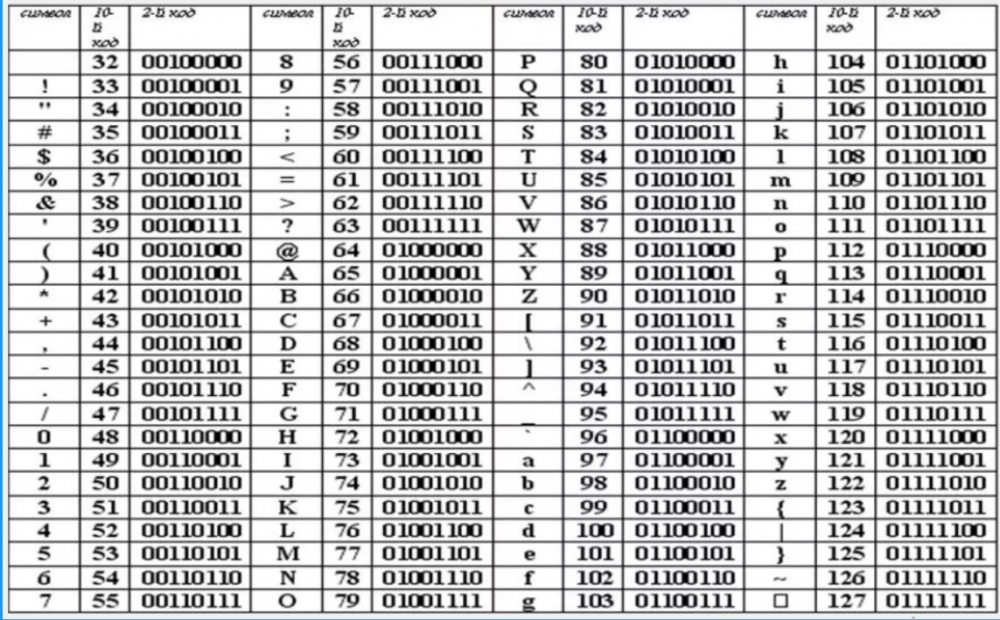
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения , вам нужен способ легкого вычисления с ними, а современное аппаратное обеспечение, способное это делать, не годится в качестве замены бинарных вычислений.Например, существует так называемый 9Тройной компьютер 0381 был разработан в 1950-х годах, но на этом разработка остановилась. Троичная логика более эффективен, чем двоичный, но эффективной замены двоичному транзистору до сих пор нет, или, по крайней мере, нет такого крошечного по масштабу транзистора, как двоичный.
Причина, по которой мы не можем использовать тройную логику, заключается в том, как транзисторы соединены в компьютере и как они используются для математических расчетов. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход. 93). Масштабирование становится проблемой, потому что, хотя троичный код более эффективен, он также экспоненциально сложнее.
Кто знает? В будущем вполне возможно, что мы увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации.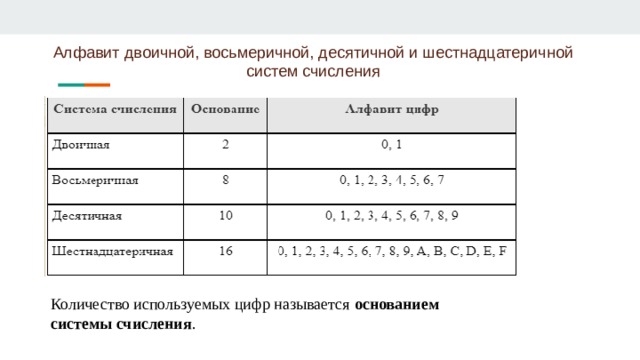 На данный момент мир будет продолжать работать в двоичном режиме.
На данный момент мир будет продолжать работать в двоичном режиме.
Решил сделать такой инструмент как преобразование текста в двоичный код и наоборот, такие сервисы есть, но они обычно работают с латиницей, у меня переводчик работает с юникод кодировкой UTF-8 формата который кодирует символы кириллицы в два байта. на данный момент возможности переводчика ограничены двухбайтными кодировками, т.е. китайские иероглифы транслировать нельзя, но я собираюсь исправить это досадное недоразумение.
Для преобразования текста в двоичный формат введите текст в левом окне и нажмите TEXT->BIN, в правом окне появится его двоичное представление.
Для преобразования двоичного кода в текст введите код в правое окно и нажмите BIN->TEXT в левом окне появится его условное обозначение.
Если перевод двоичного кода в текстовый или наоборот не получился — проверьте корректность ваших данных!
Обновление!
Теперь доступно обратное преобразование текста:
в обычный вид. Для этого поставьте галочку: «Заменить 0 на пробелы, а 1 на █». Затем вставьте текст в правое окно: «Текст в двоичном представлении» и нажмите под ним кнопку «БИН->ТЕКСТ».
Для этого поставьте галочку: «Заменить 0 на пробелы, а 1 на █». Затем вставьте текст в правое окно: «Текст в двоичном представлении» и нажмите под ним кнопку «БИН->ТЕКСТ».
При копировании таких текстов нужно быть осторожным, так как можно легко потерять пробелы в начале или в конце. Например, строка выше выглядит так:
.██ █ ███████ █ ██ ██ █ █ ███ ██ █ ██ █ ██ █ █ ██ ███ █ ██ █ ██ █ █ ██ █ ██ █ █ ███ ██ █ ██
и на красном фоне:
██ █ ███████ █ ██ ██ █ █ ███ ██ █ ██ █ ██ █ █ ██ ███ █ ██ █ ██ █ █ ██ █ ██ █ █ ███ ██ █ ██
видите, сколько пробелов в конце можно потерять?
Набор символов, которыми записывается текст, называется алфавитом .
Количество символов в алфавите равно его степени .
Формула для определения количества информации: N = 2 b ,
где N — мощность алфавита (количество символов),
b — количество бит (информационный вес символа).
256-символьный алфавит может вместить почти все необходимые вам символы.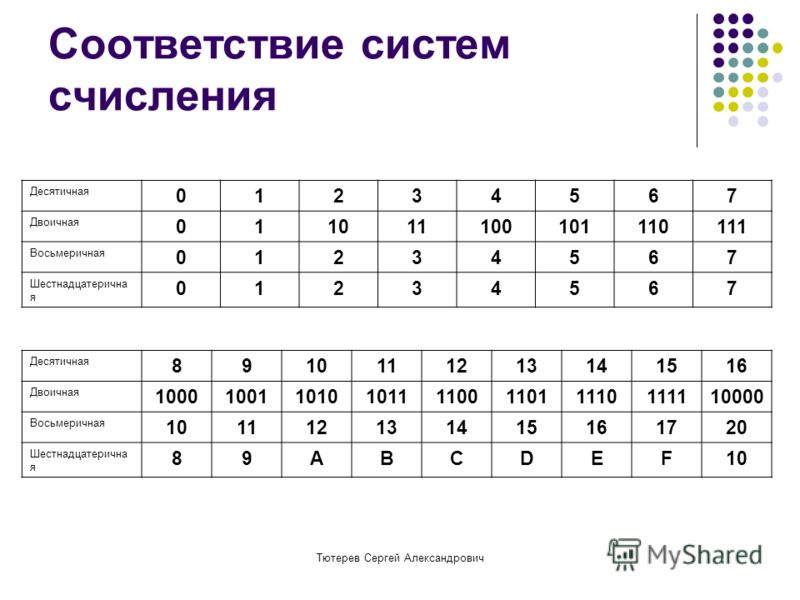 Этот алфавит называется достаточно.
Этот алфавит называется достаточно.
Поскольку 256 = 2 8, вес 1 символа равен 8 битам.
8-битный блок был назван 1 байт:
1 байт = 8 бит.
Двоичный код каждого символа компьютерного текста занимает 1 байт памяти.
Как текстовая информация представлена в памяти компьютера?
Удобство байтового кодирования символов очевидно, так как байт является наименьшей адресуемой частью памяти и, следовательно, процессор может обращаться к каждому символу отдельно, выполняя обработку текста. С другой стороны, 256 символов вполне достаточно для представления большого разнообразия символьной информации.
Теперь возникает вопрос, какой восьмибитный двоичный код присвоить каждому символу.
Понятно, что это дело условное, способов кодировки можно придумать много.
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждое число соответствует восьмизначному двоичному коду от 00000000 до 11111111.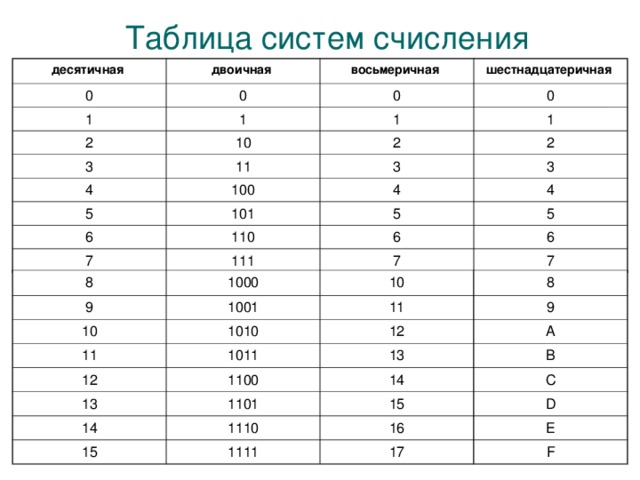 Этот код представляет собой просто порядковый номер символа в двоичной системе.
Этот код представляет собой просто порядковый номер символа в двоичной системе.
Таблица, в которой всем символам компьютерного алфавита присвоены порядковые номера, называется таблицей кодирования.
Для разных типов компьютеров используются различные таблицы кодирования.
Международным стандартом для ПК стала таблица ASCII (читается asci) (американский стандартный код для обмена информацией).
Таблица ASCII разделена на две части.
Международный стандарт — это только первая половина таблицы, т.е. символы с цифрами от 0 (00000000), до 127 (01111111).
Структура таблицы кодирования ASCII
Серийный номер | Код | Символ |
0 — 31 | 00000000 — 00011111 | Символы с номерами от 0 до 31 обычно называются управляющими символами. |
32 — 127 | 00100000 — 01111111 | Стандартная часть стола (англ.). Сюда входят строчные и прописные буквы латинского алфавита, десятичные цифры, знаки препинания, всевозможные скобки, коммерческие и другие символы. |
128 — 255 | 10000000 — 11111111 | Альтернативная часть таблицы (рус.). |
Первая половина таблицы ASCII
| |
Обращаю внимание, что в таблице кодировки буквы (прописные и строчные) расположены в алфавитном порядке, а цифры в порядке возрастания значений. Это соблюдение лексикографического порядка в расположении знаков называется принципом последовательного кодирования алфавита.
Для букв русского алфавита также соблюдается принцип последовательного кодирования.
Вторая половина таблицы ASCII
К сожалению, на данный момент существует пять различных кодировок кириллицы (KOI8-R, Windows, MS-DOS, Macintosh и ISO). Из-за этого часто возникают проблемы с переносом русского текста с одного компьютера на другой, с одной программной системы на другую.
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8-битный»). Эта кодировка использовалась еще в 70-х годах на ЭВМ серии ЕС ЭВМ, а с середины 80-х стала использоваться в первых русифицированных версиях. операционная система UNIX.
С начала 90-х, времени господства операционной системы MS DOS, сохраняется кодировка CP866 («CP» расшифровывается как «Code Page»).
Компьютеры Apple под управлением Mac OS используют собственную кодировку Mac.
Кроме того, Международная организация по стандартизации (International Standards Organization, ISO) утвердила в качестве стандарта для русского языка другую кодировку под названием ISO 8859-5.
Наиболее распространенной в настоящее время является кодировка Microsoft Windows, сокращенно CP1251.
С конца 90-х проблема стандартизации кодировки символов решается введением нового международного стандарта под названием Unicode . Это 16-битная кодировка т. е. она выделяет 2 байта памяти на каждый символ. Конечно, это удваивает объем используемой памяти. Но тогда такая кодовая таблица может включать до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и других символов.
е. она выделяет 2 байта памяти на каждый символ. Конечно, это удваивает объем используемой памяти. Но тогда такая кодовая таблица может включать до 65536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и других символов.
Давайте попробуем использовать таблицу ASCII, чтобы представить, как слова будут выглядеть в памяти компьютера.
Внутреннее представление слов в памяти компьютера
Иногда бывает так, что текст, состоящий из букв русского алфавита, полученный с другого компьютера, не читается — на экране монитора видна какая-то «тарабарщина». Это связано с тем, что в компьютерах используется разная кодировка символов русского языка.
Декодирование двоичного кода используется для перевода с машинного языка на обычный. Онлайн-инструменты работают быстро, хотя вручную это легко сделать.
Двоичный или двоичный код используется для передачи информации в цифровом виде.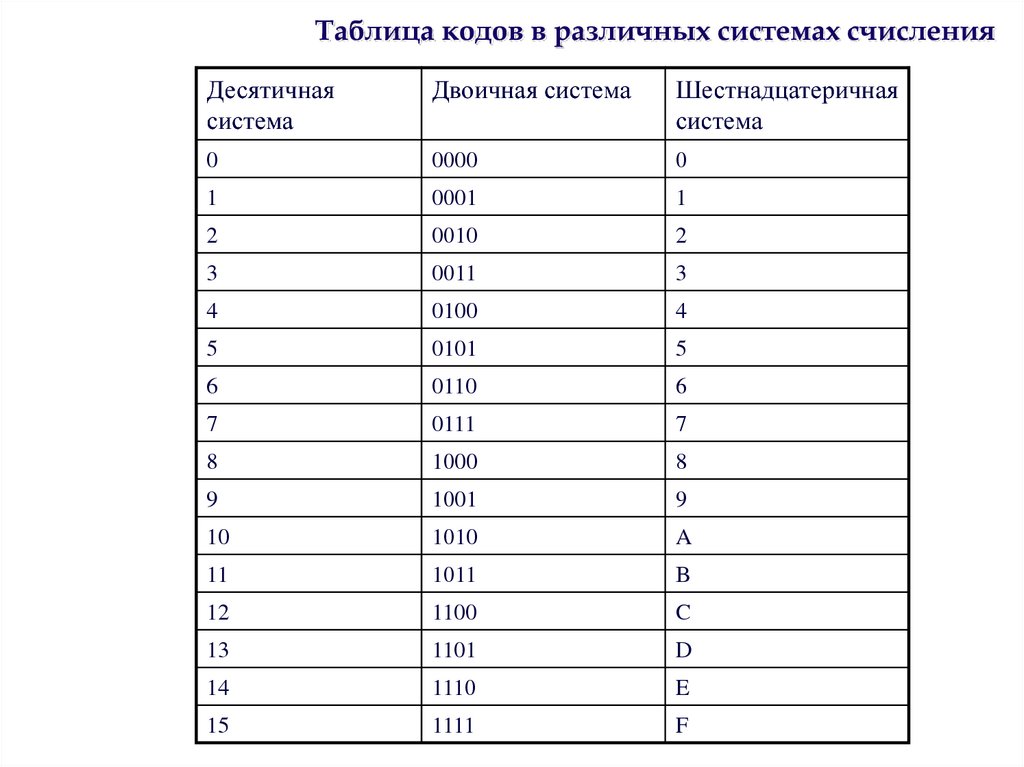 Набор всего из двух символов, например 1 и 0, позволяет зашифровать любую информацию, будь то текст, цифры или изображение.
Набор всего из двух символов, например 1 и 0, позволяет зашифровать любую информацию, будь то текст, цифры или изображение.
Как зашифровать двоичным кодом
Для ручного перевода любых символов в двоичный код используются таблицы, в которых каждому символу присвоен двоичный код в виде нулей и единиц. Наиболее распространенной системой кодирования является ASCII, в которой используется 8-битная кодовая запись.
Базовая таблица содержит двоичные коды латинского алфавита, числа и некоторые символы.
В расширенную таблицу добавлена бинарная интерпретация кириллицы и дополнительные символы.
Для перевода из двоичного кода в текст или числа достаточно выбрать нужные коды из таблиц. Но, конечно, делать такую работу вручную долго. А ошибки, к тому же, неизбежны. Компьютер гораздо быстрее справляется с расшифровкой. И мы даже не задумываемся, печатая на экране текст, что в этот момент текст переводится в двоичный код.
Преобразование двоичного числа в десятичное
Чтобы вручную преобразовать число из двоичной системы счисления в десятичную, можно воспользоваться достаточно простым алгоритмом:
- Под двоичным числом, начиная с крайней правой цифры, напишите цифру 2 в возрастающей степени.

- Умножьте степени числа 2 на соответствующую цифру двоичного числа (1 или 0).
- Добавьте полученные значения.
Так алгоритм выглядит на бумаге:
Онлайн-сервисы для бинарной расшифровки
Если вам все-таки нужно посмотреть расшифрованный бинарный код, или, наоборот, перевести текст в бинарный вид, проще всего воспользоваться онлайн-сервисами, предназначенными для этой цели.
Обычные для онлайн-переводов два окна позволяют практически одновременно видеть оба варианта текста в обычном и бинарном виде. Причем расшифровка осуществляется в обе стороны. Ввод текста осуществляется простым копированием и вставкой.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица ASCII для Cyrillic Charset (CP855)
Американский стандартный код для обмена информацией ( ASCII ) является широко используемым . , который теперь называется стандартным набором символов, изначально состоял из 128 символов (7-битный код). Первые 32 символа — это управляющие символы (также называемые непечатаемыми символами), которые используются для управления потоками данных, а также такими устройствами, как принтеры. Позже он был расширен для поддержки 256 символов (8-битный код), чтобы предоставить символы, специфичные для языка, различные символы, а также символы для рисования блоков: элементы, используемые для презентационных целей, позволяющие рисовать различные виды рамок и блоков.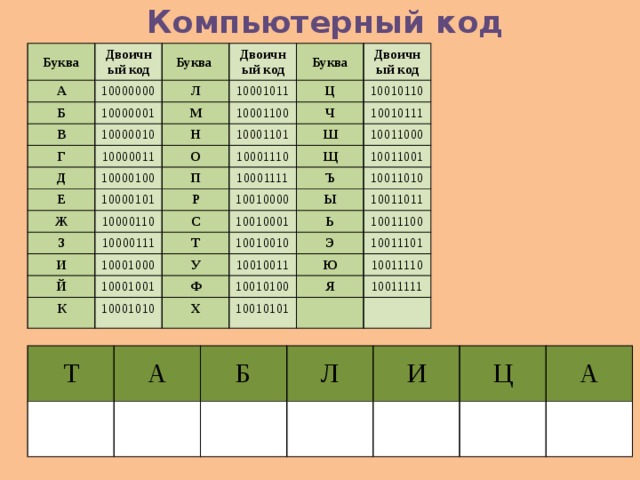 Символы в диапазоне 128-255 называются расширенным ASCII.
Символы в диапазоне 128-255 называются расширенным ASCII.
Кодовая страница 855 является альтернативной кодовой страницей , используемой для написания языков на основе кириллицы: белорусского, боснийского, болгарского, македонского, русского, сербского, украинского (славянские языки), а также казахского, киргизского, молдавского, монгольского, таджикского, узбекского. (не славянский). Он не очень популярен, кодовая страница 866 является наиболее широко используемой. Только расширенный набор символов отличается от исходной кодовой страницы, причем как управляющие символы, так и стандартный набор символов представляют собой простой ASCII.
9В приведенной ниже таблице из 1528 символов показано графическое представление каждого символа с точностью до пикселя, а также текстовое описание.
Control characters (0 — 31):
| Dec | Hex | Char | Description | Dec | Hex | Char | Description |
| 0 | 0 | NUL (Null ) | 16 | 10 | DLE (выход канала передачи данных) | ||
| 1 | 1 | SOH (Start of Header) | 17 | 11 | DC1 (Device Control 1) | ||
| 2 | 2 | STX (Start of Text) | 18 | 12 | DC2 (Device Control 2) | ||
| 3 | 3 | ETX (End of Text) | 19 | 13 | DC3 (Device Control 3) | ||
| 4 | 4 | EOT (End of Transmission) | 20 | 14 | DC4 (Device Control 4) | ||
| 5 | 5 | ENQ (Enquiry) | 21 | 15 | NAK (Negative Acknowledge) | ||
| 6 | 6 | ACK (Acknowledge) | 22 | 16 | SYN (Synchronous Idle) | ||
| 7 | 7 | Bel (Bell) | 23 | 17 | ETB (конец передачи блока) | ||
| 8 | 8 | BS (BACK SPACE) | 8 | BS (BACK SPAC | |||
| 9 | HT (горизонтальная табуляция) | 25 | 19 | EM (конец среды) | |||
| EM (конец среды) | |||||||
| EM (конец среды) | |||||||
| EM (конец среды) | 4 | EM (конец среды) | |||||
| EM (конец среды)0683 26 | 1A | SUB (Substitute) | |||||
| 11 | B | VT (Vertical Tabulation) | 27 | 1B | ESC (Escape) | ||
| 12 | C | FF (подача формы) | 28 | 1C | FS (файловый разделитель) | ||
| 13 | D | CRARIAD.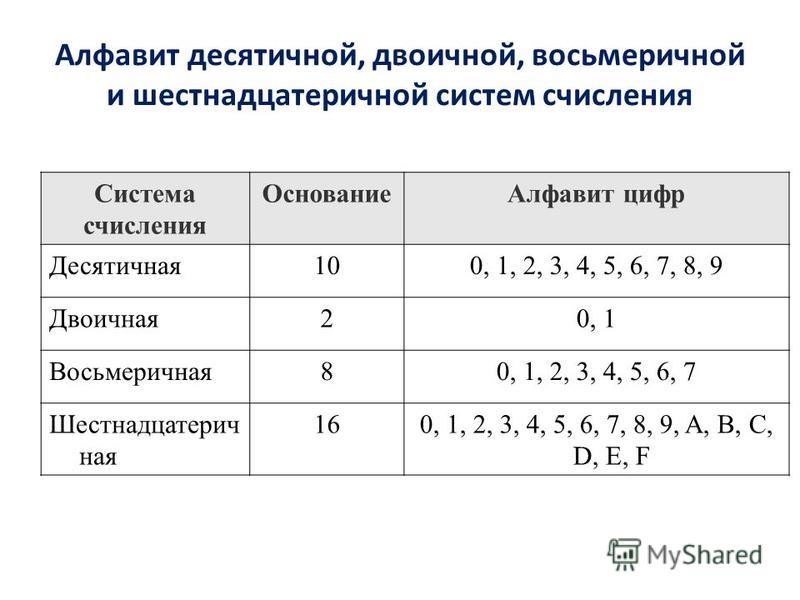 0683 GS (Group Separator) 0683 GS (Group Separator) | |||||
| 14 | E | SO (Shift Out) | 30 | 1E | RS (Record Separator) | ||
| 15 | F | SI (Shift In) | 31 | 1F | US (Unit Separator) | ||
Standard character set (32 — 127):
| Dec | Hex | Char | Description | Dec | Hex | Char | Description | |||||||||||||||||||||||
| 32 | 20 | Space | 80 | 50 | Upper case P | |||||||||||||||||||||||||
| 33 | 21 | Exclamation mark | 81 | 51 | Верхний корпус Q | |||||||||||||||||||||||||
| 34 | 22 | Цитата | 82 | 52 | 52 | 52 | 52 | 52 | 52 | .35 | 23 | Hash | 83 | 53 | Upper case S | |||||||||||||||
| 36 | 24 | Dollar | 84 | 54 | Upper case T | |||||||||||||||||||||||||
| 37 | 25 | Percent | 85 | 55 | Upper case U | |||||||||||||||||||||||||
| 38 | 26 | Ampersand | 86 | 56 | Upper case V | |||||||||||||||||||||||||
| 39 | 27 | Apostrophe | 87 | 57 | Upper case W | |||||||||||||||||||||||||
| 40 | 28 | Open bracket | 88 | 58 | Upper case X | |||||||||||||||||||||||||
| 41 | 29 | Close bracket | 89 | 59 | Upper case Y | |||||||||||||||||||||||||
| 42 | 2A | Asterisk | 90 | 5A | Upper case Z | |||||||||||||||||||||||||
| 43 | 2B | Plus | 91 | 5B | Open square bracket | |||||||||||||||||||||||||
| 44 | 2C | Запятая | 92 | 5C | БАКСЛАШ | |||||||||||||||||||||||||
| 45 | . | |||||||||||||||||||||||||||||
| 46 | 2E | Full stop | 94 | 5E | Caret | |||||||||||||||||||||||||
| 47 | 2F | Slash | 95 | 5F | Underscore | |||||||||||||||||||||||||
| 48 | 30 | ZERE | 96 | 60 | .0021 | Lower case a | ||||||||||||||||||||||||
| 50 | 32 | Two | 98 | 62 | Lower case b | |||||||||||||||||||||||||
| 51 | 33 | Three | 99 | 63 | Lower case c | |||||||||||||||||||||||||
| 52 | 34 | Four | 100 | 64 | Lower case d | |||||||||||||||||||||||||
| 53 | 35 | Five | 101 | 65 | Lower case e | |||||||||||||||||||||||||
| 54 | 36 | Six | 102 | 66 | Lower case f | |||||||||||||||||||||||||
| 55 | 37 | Seven | 103 | 67 | Lower case g | |||||||||||||||||||||||||
| 56 | 38 | Eight | 104 | 68 | Lower case h | |||||||||||||||||||||||||
| 57 | 39 | Nine | 105 | 69 | Lower case i | |||||||||||||||||||||||||
| 58 | 3A | Colon | 106 | 6A | Lower case j | |||||||||||||||||||||||||
| 59 | 3B | Semicolon | 107 | 6B | Lower case k | |||||||||||||||||||||||||
| 60 | 3C | Less than | 108 | 6C | Lower case l | |||||||||||||||||||||||||
| 61 | 3D | Equals sign | 109 | 6D | Lower case m | |||||||||||||||||||||||||
| 62 | 3E | Greater than | 110 | 6E | Lower case n | |||||||||||||||||||||||||
| 63 | 3F | Question mark | 111 | 6F | Lower case o | |||||||||||||||||||||||||
| 64 | 40 | At | 112 | 70 | Lower case p | |||||||||||||||||||||||||
| 65 | 41 | Upper case A | 113 | 71 | Lower case q | |||||||||||||||||||||||||
| 66 | 42 | Upper case B | 114 | 72 | Lower case r | |||||||||||||||||||||||||
| 67 | 43 | Upper case C | 115 | 73 | Lower case s | |||||||||||||||||||||||||
| 68 | 44 | Upper case D | 116 | 74 | Lower case t | |||||||||||||||||||||||||
| 69 | 45 | Upper case E | 117 | 75 | Lower case u | |||||||||||||||||||||||||
| 70 | 46 | Upper case F | 118 | 76 | Lower case v | |||||||||||||||||||||||||
| 71 | 47 | Upper case G | 119 | 77 | Lower case w | |||||||||||||||||||||||||
| 72 | 48 | Upper case H | 120 | 78 | Lower case x | |||||||||||||||||||||||||
| 73 | 49 | Upper case I | 121 | 79 | Lower case y | |||||||||||||||||||||||||
| 74 | 4A | Upper case J | 122 | 7A | Lower case z | |||||||||||||||||||||||||
| 75 | 4B | Upper case K | 123 | 7B | Open brace | |||||||||||||||||||||||||
| 76 | 4C | Upper case L | 124 | 7C | Pipe | |||||||||||||||||||||||||
| 77 | 4D | Upper case M | 125 | 7D | Close brace | |||||||||||||||||||||||||
| 78 | 4E | Upper case N | 126 | 7E | Tilde | |||||||||||||||||||||||||
| 79 | 4F | Upper case O | 127 | 7F | Delete | |||||||||||||||||||||||||
Extended character set ( 128 — 255):
| DEC | HEX | ChAR | Описание | DEC | HEX | .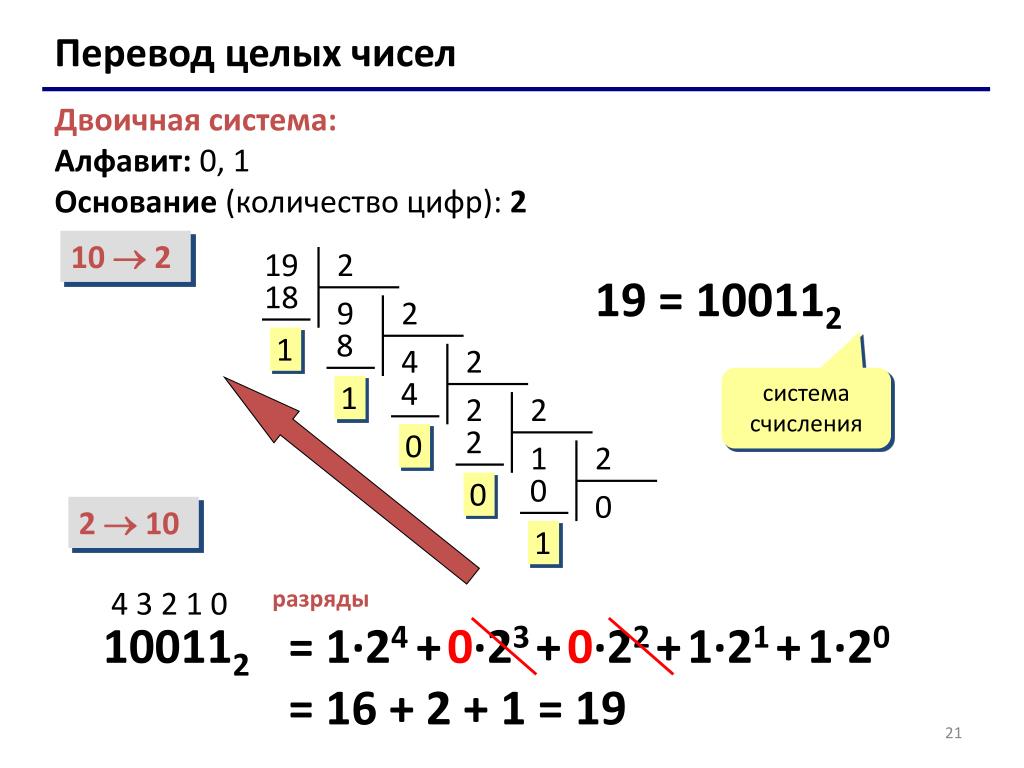 0021 0021 | 80 | Cyrillic lower case dje | 192 | C0 | Box drawings light up and right | ||
| 129 | 81 | Cyrillic upper case DJE | 193 | C1 | Box рисунки светятся вверх и горизонтально | ||||||||
| 130 | 82 | строчные буквы gje | 194 | C2 | 9 рисунков светятся вниз и горизонтально0021 | ||||||||
| 131 | 83 | Cyrillic upper case GJE | 195 | C3 | Box drawings light vertical and right | ||||||||
| 132 | 84 | Cyrillic lower case io | 196 | C4 | чертежей коробки.0021 | ||||||||
| 134 | 86 | Cyrillic lower case ukrainian ie | 198 | C6 | Cyrillic lower case ka | ||||||||
| 135 | 87 | Cyrillic upper case ukrainian IE | 199 | C7 | Cyrillic Верхний корпус KA | ||||||||
| 136 | 88 | Cyrillic Lower Case Dze | 200 | CIRILLIC | CIRILLIC | .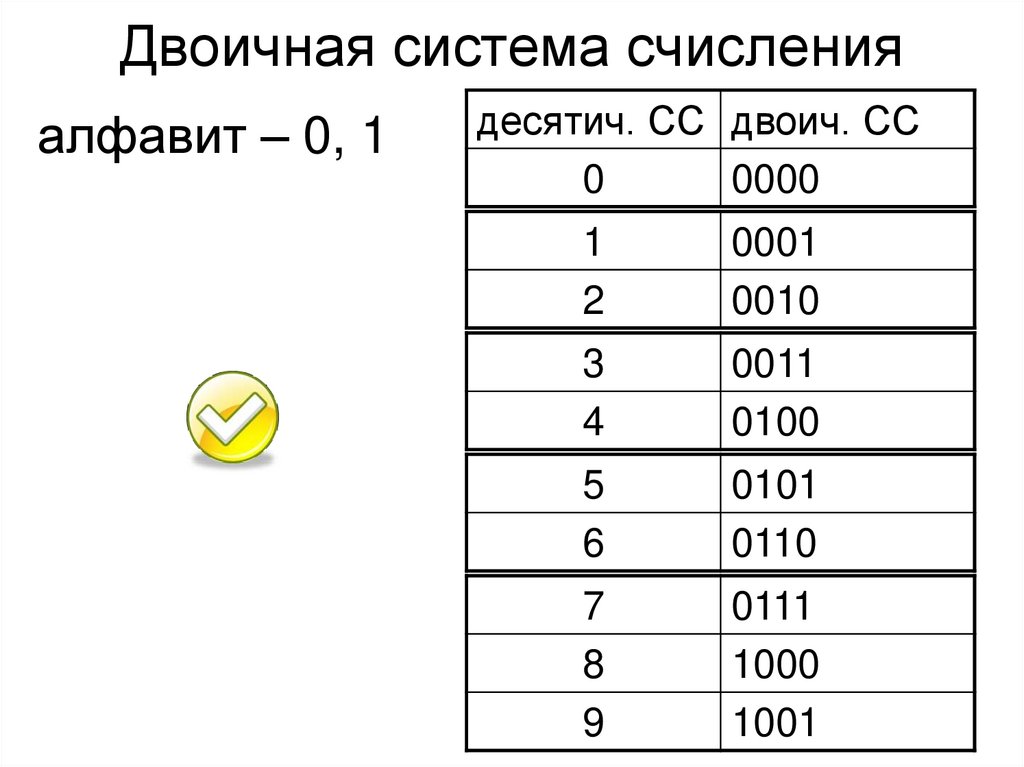 0021 0021 | |||||||
| 137 | 89 | Cyrillic upper case DZE | 201 | C9 | Box drawings double down and right | ||||||||
| 138 | 8A | Cyrillic lower case byelorussian-ukrainian i | 202 | CA | Чертежи коробок двойные и горизонтальные | ||||||||
| 139 | 8B | Кириллица заглавная белорусско-украинская I | 203 | CB | Box drawings double down and horizontal | ||||||||
| 140 | 8C | Cyrillic lower case yi | 204 | CC | Box drawings double vertical and right | ||||||||
| 141 | 8D | Заглавная кириллица YI | 205 | CD | Чертежи коробок двойные горизонтальные | ||||||||
| 142 | 142 8E0683 Cyrillic lower case je206 | CE | Box drawings double vertical and horizontal | ||||||||||
| 143 | 8F | Cyrillic upper case JE | 207 | CF | Currency sign | ||||||||
| 144 | 90 | Cyrillic lower case lje | 208 | D0 | Cyrillic lower case el | ||||||||
| 145 | 91 | Cyrillic upper case LJE | 209 | D1 | Cyrillic upper case EL | ||||||||
| 146 | 92 | Cyrillic lower case nje | 210 | D2 | Cyrillic lower case em | ||||||||
| 147 | 93 | Cyrillic upper case NJE | 211 | D3 | Cyrillic upper case EM | ||||||||
| 148 | 94 | Cyrillic lower case tshe | 212 | D4 | Cyrillic lower case en | ||||||||
| 149 | 95 | Cyrillic upper case TSHE | 213 | D5 | Cyrillic upper case EN | ||||||||
| 150 | 96 | Cyrillic lower case kje | 214 | D6 | Cyrillic lower case o | ||||||||
| 151 | 97 | Cyrillic upper case KJE | 215 | D7 | Cyrillic upper case O | ||||||||
| 152 | 98 | Cyrillic lower case short u | 216 | D8 | Cyrillic lower case pe | ||||||||
| 153 | 99 | Cyrillic Toper Case Short U | 217 | D9 | .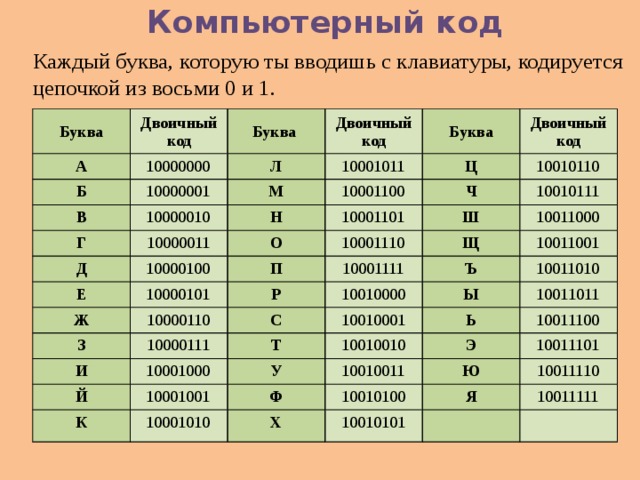 A A | Cyrillic lower case dzhe | 218 | DA | Box drawings light down and right | ||||
| 155 | 9B | Cyrillic upper case DZHE | 219 | DB | Full block | ||||||||
| 156 | 9C | Cyrillic lower case yu | 220 | DC | Lower half block | ||||||||
| 157 | 9D | Cyrillic upper case YU | 221 | DD | Cyrillic upper case PE | ||||||||
| 158 | 9E | Cyrillic lower case hard sign | 222 | DE | Cyrillic lower case ya | ||||||||
| 159 | 9F | Cyrillic upper case hard sign | 223 | DF | Upper half block | ||||||||
| 160 | A0 | Cyrillic lower case a | 224 | E0 | Cyrillic upper case YA | ||||||||
| 161 | A1 | Cyrillic upper case A | 225 | E1 | Cyrillic lower case er | ||||||||
| 162 | A2 | Cyrillic lower case be | 226 | E2 | Cyrillic upper case ER | ||||||||
| 163 | A3 | Cyrillic upper case BE | 227 | E3 | Cyrillic lower case es | ||||||||
| 164 | A4 | Cyrillic lower case tse | 228 | E4 | Cyrillic upper case ES | ||||||||
| 165 | A5 | Cyrillic upper case TSE | 229 | E5 | Cyrillic lower case te | ||||||||
| 166 | A6 | Cyrillic lower case de | 230 | E6 | Cyrillic upper case TE | ||||||||
| 167 | A7 | Cyrillic upper case DE | 231 | E7 | Cyrillic lower case u | ||||||||
| 168 | A8 | Нижний регистр кириллицы т.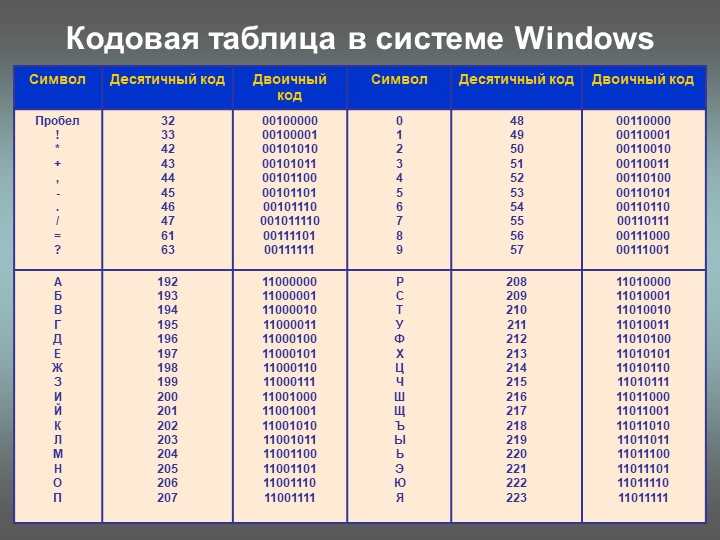 е. е. | 232 | E8 | Прописная кириллица U | ||||||||
| 169 | Прописная кириллица 90 | E9 | Cyrillic lower case zhe | ||||||||||
| 170 | AA | Cyrillic lower case ef | 234 | EA | Cyrillic upper case ZHE | ||||||||
| 171 | AB | Прописная кириллица EF | 235 | EB | Строчная кириллица ve | ||||||||
| 172 | AC | Нижняя кириллица0683 236 | EC | Cyrillic upper case VE | |||||||||
| 173 | AD | Cyrillic upper case GHE | 237 | ED | Cyrillic lower case soft sign | ||||||||
| 174 | AE | Левый указатель с двойным углами Цитата | 238 | EE | Цириллический верхний чехол.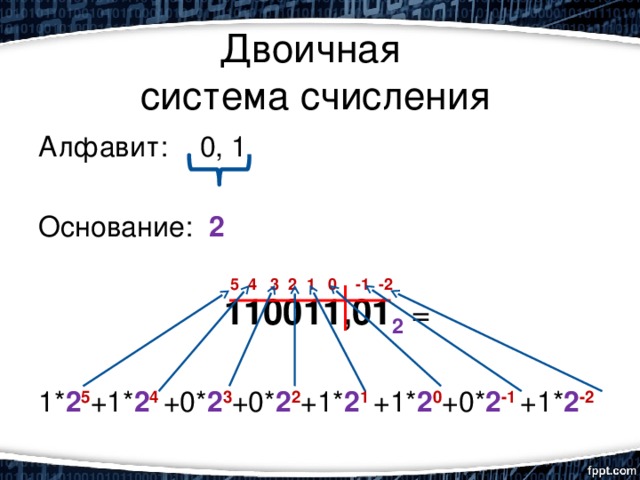 |



 В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.
В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.
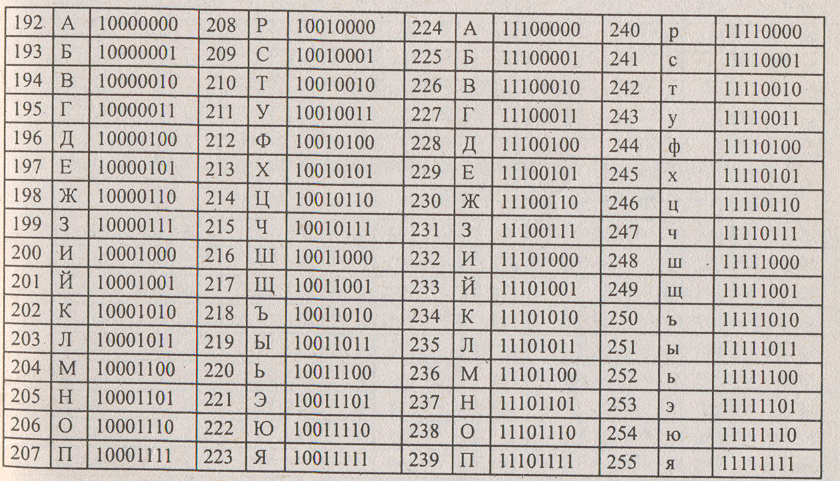 В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.
В русских национальных кодировках в этой части таблицы размещаются символы русского алфавита.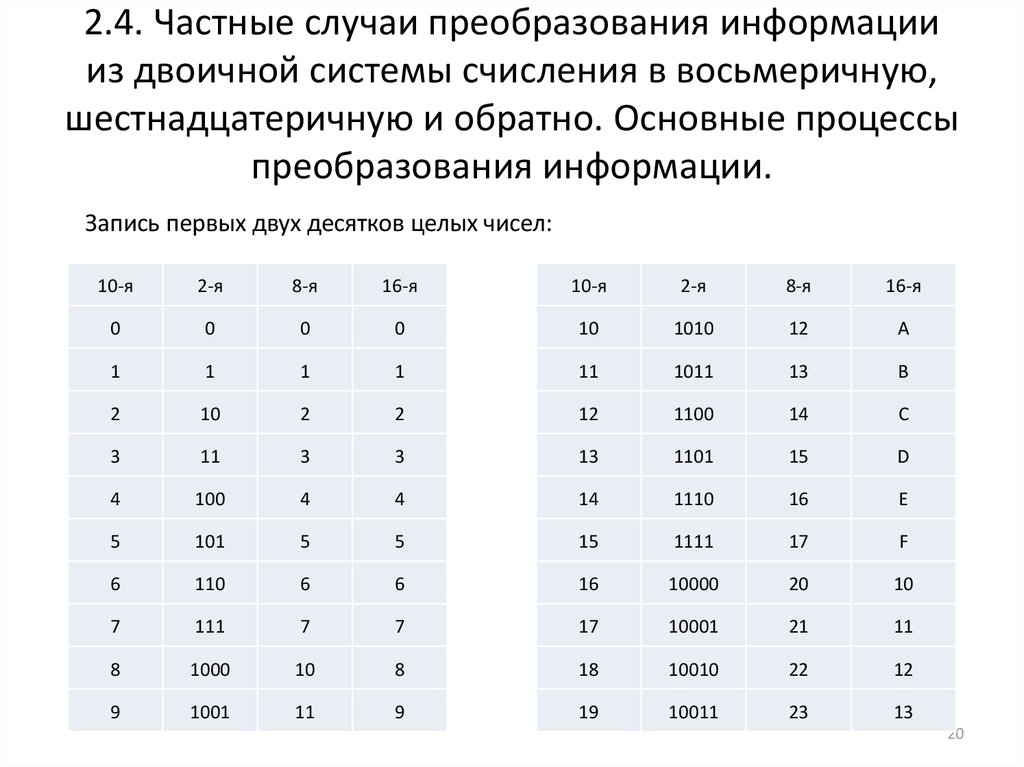
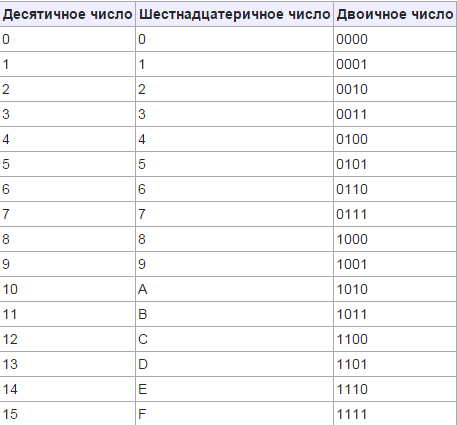

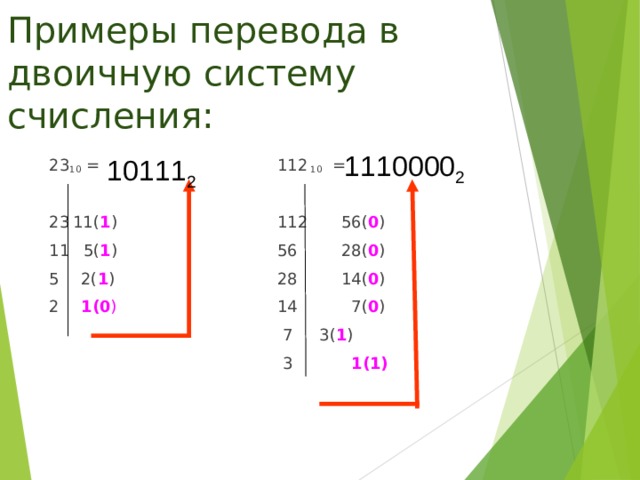 Это делается путем введения символа третьей смены «RUS».
— два других — сдвиг буквы и цифры.
Он заменяет код NULL (000·00) алфавита ITA-2, который больше не используется.
доступный.
Это делается путем введения символа третьей смены «RUS».
— два других — сдвиг буквы и цифры.
Он заменяет код NULL (000·00) алфавита ITA-2, который больше не используется.
доступный. Кириллица выбирается с прежним кодом NULL (000·00),
и отменяется нажатием FIGS (110·11) или LTRS (111·11).
CR, LF и SPACE являются общими для всех алфавитов.
Кириллица выбирается с прежним кодом NULL (000·00),
и отменяется нажатием FIGS (110·11) или LTRS (111·11).
CR, LF и SPACE являются общими для всех алфавитов.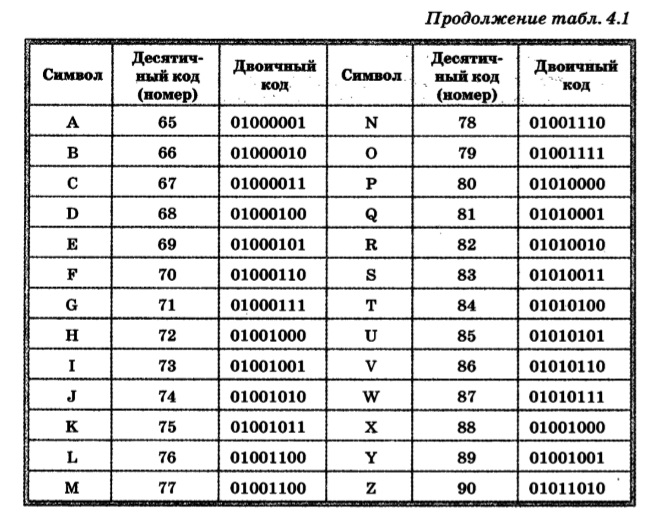
 июль 1970 года.
июль 1970 года.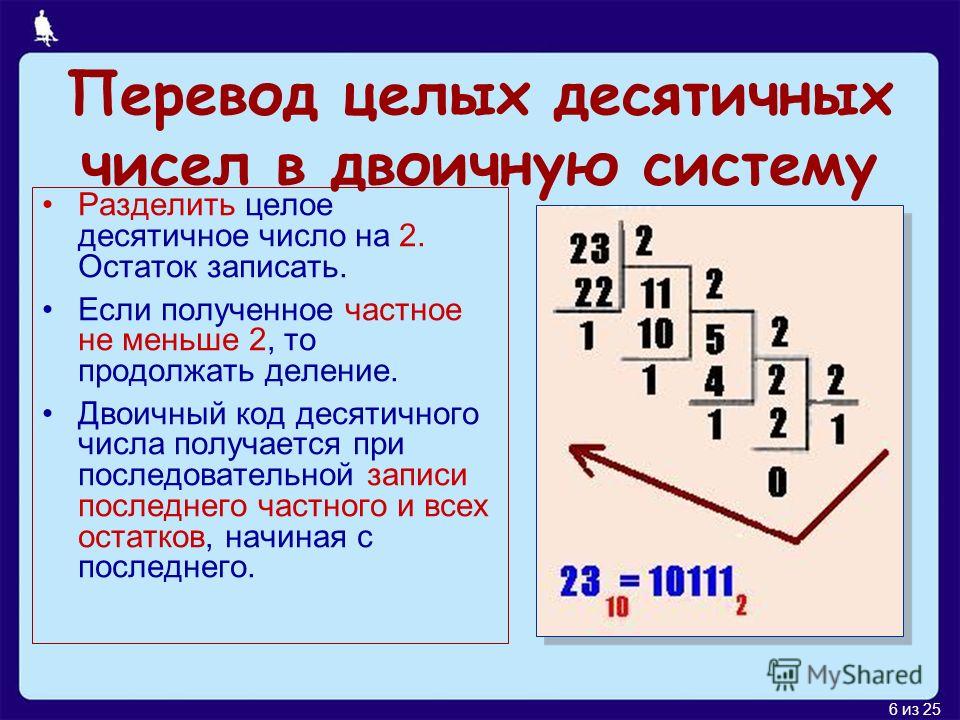 Если вам нравится информация на этом сайте, почему бы не сделать пожертвование?
Если вам нравится информация на этом сайте, почему бы не сделать пожертвование?  0094
0094 0021
0021