Ошибка 404: страница не найдена
Письмо ректору
Телефонный справочник
Электронная почта
Онлайн-обучение
Расписание
Научно-педагогические работники
Сервисы
Электронная служебная записка Электронная библиотека КалендарьГорячая линия по дистанционному обучению Тревожная кнопка Отзывы о преподавателяхПолезные ресурсы Виртуальный тур
| Министерство науки и высшего образования РФ | |
| Программа повышения конкурентоспособности | |
| Противодействие коррупции | |
Диалог науки и религии | |
| Наука и образование против террора | |
| Диссертационные советы | |
| Социальный навигатор | |
| Оформление социальной студенческой карты | |
| Study in Russia | |
| Уникальная научная установка НЕВОД | |
| Турнир «ТеМП» | |
| Международная олимпиада для студентов | |
| Олимпиада «Я — профи» |
|
Обобщенный закон фарадея для электролиза.
 Первый и второй закон фарадея
Первый и второй закон фарадеяДля описания процессов в физике и химии есть целый ряд законов и соотношений, полученных экспериментальным и расчетным путем. Ни единого исследования нельзя провести без предварительной оценки процессов по теоретическим соотношениям. Законы Фарадея применяются и в физике, и в химии, а в этой статье мы постараемся кратко и понятно рассказать о всех знаменитых открытиях этого великого ученого.
История открытия
Закон Фарадея в электродинамике был открыт двумя ученными: Майклом Фарадеем и Джозефом Генри, но Фарадей опубликовал результаты своих работ раньше – в 1831 году.
В своих демонстрационных экспериментах в августе 1831 г. он использовал железный тор, на противоположные концы которого был намотан провод (по одному проводу на стороны). На концы одного первого провода он подал питание от гальванической батареи, а на выводы второго подключил гальванометр. Конструкция была похожа на современный трансформатор. Периодически включая и выключая напряжение на первом проводе, он наблюдал всплески на гальванометре.
Гальванометр — это высокочувствительный прибор для измерения силы токов малой величины.
Таким образом было изображено влияние магнитного поля, образовавшегося в результате протекания тока в первом проводе, на состояние второго проводника. Это воздействие передавалось от первого ко второму через сердечник – металлический тор. В результате исследований было обнаружено и влияние постоянного магнита, который двигается в катушке, на её обмотку.
Тогда Фарадей объяснял явление электромагнитной индукции с точки зрения силовых линий. Еще одной была установка для генерирования постоянного тока: медный диск вращался вблизи магнита, а скользящий по нему провод был токосъёмником. Это изобретение так и называется — диск Фарадея.
Ученные того периода не признали идеи Фарадея, но Максвелл взял исследования для основы своей магнитной теории. В 1836 г. Майкл Фарадей установил соотношения для электрохимических процессов, которые назвали Законами электролиза Фарадея. Первый описывает соотношения выделенной на электроде массы вещества и протекающего тока, а второй соотношения массы вещества в растворе и выделенного на электроде, для определенного количества электричества.
Электродинамика
Первые работы применяются в физике, конкретно в описании работы электрических машин и аппаратов (трансформаторов, двигателей и пр.). Закон Фарадея гласит:
Для контура индуцированная ЭДС прямо пропорциональна величине скорости магнитного потока, который перемещается через этот контур со знаком минус.
Это можно сказать простыми словами: чем быстрее магнитный поток движется через контур, тем больше на его выводах генерируется ЭДС.
Формула выглядит следующим образом:
Здесь dФ – магнитный поток, а dt – единица времени. Известно, что первая производная по времени – это скорость. Т.е скорость перемещения магнитного потока в данном конкретном случае. Кстати перемещаться может, как и источник магнитного поля (катушка с током – электромагнит, или постоянный магнит), так и контур.
Здесь же поток можно выразить по такой формуле:
B – магнитное поле, а dS – площадь поверхности.
Если рассматривать катушку с плотнонамотанными витками, при этом в количестве витков N, то закон Фарадея выглядит следующим образом:
Магнитный поток в формуле на один виток, измеряется в Веберах. Ток, протекающий в контуре, называется индукционным.
Ток, протекающий в контуре, называется индукционным.
Электромагнитная индукция – явление протекания тока в замкнутом контуре под воздействием внешнего магнитного поля.
В формулах выше вы могли заметить знаки модуля, без них она имеет слегка иной вид, такой как было сказано в первой формулировке, со знаком минус.
Знак минус объясняет правило Ленца. Ток, возникающий в контуре, создает магнитное поле, оно направлено противоположно. Это является следствием закона сохранения энергии.
Направление индукционного тока можно определить по правилу правой руки или , мы его рассматривали на нашем сайте подробно.
Как уже было сказано, благодаря явлению электромагнитной индукции работают электрические машины трансформаторы, генераторы и двигатели. На иллюстрации показано протекание тока в обмотке якоря под воздействием магнитного поля статора. В случае с генератором, при вращении его ротора внешними силами в обмотках ротора возникает ЭДС, ток порождает магнитное поле направленное противоположно (тот самый знак минус в формуле).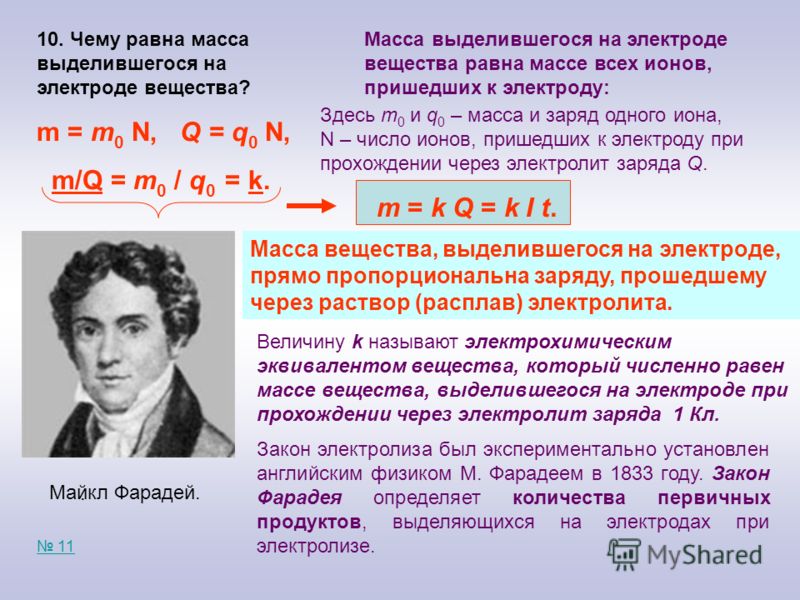 Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.
Чем больше ток, потребляемый нагрузкой генератора, тем больше это магнитное поле, и тем больше затрудняется его вращение.
И наоборот — при протекании тока в роторе возникает поле, которое взаимодействует с полем статора и ротор начинает вращаться. При нагрузке на вал ток в статоре и в роторе повышается, при этом нужно обеспечить переключение обмоток, но это уже другая тема, связанная с устройством электрических машин.
В основе работы трансформатора источником движущегося магнитного потока является переменное магнитное поле, возникающее в следствие протекания в первичной обмотке переменного тока.
Если вы желаете более подробно изучить вопрос, рекомендуем просмотреть видео, на котором легко и доступно рассказывается Закон Фарадея для электромагнитной индукции:
Электролиз
Кроме исследований ЭДС и электромагнитной индукции ученный сделал большие открытия и в других дисциплинах, в том числе химии.
При протекании тока через электролит ионы (положительные и отрицательные) начинают устремляться к электродам. Отрицательные движутся к аноду, положительные к катоду. При этом на одном из электродов выделяется определенная масса вещества, которое содержится в электролите.
Отрицательные движутся к аноду, положительные к катоду. При этом на одном из электродов выделяется определенная масса вещества, которое содержится в электролите.
Фарадей проводил эксперименты, пропуская разный ток через электролит и измеряя массу вещества отложившегося на электродах, вывел закономерности.
m – масса вещества, q – заряд, а k – зависит от состава электролита.
А заряд можно выразить через ток за промежуток времени:
I=q/t , тогда q = i*t
Теперь можно определить массу вещества, которое выделится, зная ток и время, которое он протекал. Это называется Первый закон электролиза Фарадея.
Второй закон:
Масса химического элемента, который осядет на электроде, прямо пропорциональна эквивалентной массе элемента (молярной массе разделенной на число, которое зависит от химической реакции, в которой участвует вещество).
С учетом вышесказанного эти законы объединяются в формулу:
m – масса вещества, которое выделилось в граммах, n – количество переносимых электронов в электродном процессе, F=986485 Кл/моль – число Фарадея, t – время в секундах, M молярная масса вещества г/моль.
В реальности же из-за разных причин, масса выделяемого вещества меньше чем расчетная (при расчетах с учетом протекающего тока). Отношение теоретической и реальной масс называют выходом по току:
B т = 100% * m расч /m теор
Законы Фарадея внесли существенный вклад в развитие современной науки, благодаря его работам мы имеем электродвигатели и генераторы электроэнергии (а также работам его последователей). Работа ЭДС и явления электромагнитной индукции подарили нам большую часть современного электрооборудования, в том числе и громкоговорители и микрофоны, без которых невозможно прослушивание записей и голосовая связь. Процессы электролиза применяются в гальваническом методе покрытия материалов, что несет как декоративную ценность, так и практическую.
Похожие материалы:
Нравится(0 ) Не нравится(0 )
Эти законы определяют соотношение между массой продукта, образующегося на электроде, и количеством электричества (электрическим зарядом), пропущенным через электролит.
Первый закон Фарадея гласит, что масса вещества, образующегося на электроде, пропорциональна количеству пропущенного электричества. Количественной мерой электрического заряда является единица фарадей. Фарадей — это заряд, который несет на себе один моль электронов или один моль однозарядных ионов.
Напомним, что число — это число Авогадро (см. разд. 4.2).
Разряд ионов серебра на катоде в процессе электролиза раствора нитрата серебра описывается уравнением полуреакции
Следовательно, электрический заряд в 1 фарадей (один моль электронов) разряжает 1 моль ионов серебра, в результате чего образуется 1 моль атомов серебра. Это означает, что пропускание заряда в 2 фарадея приведет к образованию 2 молей атомов серебра, пропускание 3 фарадеев заряда приведет к образованию 3 молей атомов серебра и т.д.
Второй закон Фарадея гласит, что для разряда одного моля какого-либо иона на электроде необходимо пропустить через электролит такое число фарадеев заряда, которое равно числу элементарных зарядов на этом ионе.
Моль 2 моля 1 моль Таким образом, для разряда одного моля ионов на катоде через него необходимо пропустить 2 фарадея заряда (2 моля электронов).
Моль 3 моля I моль
Для разряда одного моля ионов алюминия на катоде через него необходимо пропустить 3 фарадея заряда (3 моля электронов).
Моля 1 моль 2 моля
Для получения одного моля молекул брома в результате разряда двух молей ионов брома на аноде через него необходимо пропустить 2 фарадея заряда. Следовательно, для разряда одного моля ионов брома необходим один фарадей заряда.
Вычислим массу свинца, выделившегося на катоде в результате пропускания тока силой 2 А через расплавленный бромид в течение 30 мин
Выделение свинца на катоде происходит в результате следующей полуреакции:
Итак, 2 фарадея заряда (т. е. 2-96 500 Кл) позволяют получить 1 моль атомов РЬ (т. е. 207 г атомов РЬ). Отсюда
Учтем теперь, что ток силой 2 А, протекая в течение 30 мин, переносит заряд, равный 2-30-60 Кл. Следовательно,
Следовательно,
Майкл Фарадей (1791-1867)
Английский химик и физик Майкл Фарадей был выдающимся экспериментатором и прославился как один из первых исследователей природы электричества и магнетизма.
Фарадей не смог получить в детстве систематического образования. В возрасте 14 лет он стал помощником переплетчика. Но вскоре он заинтересовался наукой и, прослушав лекцию знаменитого химика Гемфри Дэви, написал ему и отправил свои записи лекции. Дэви принял его ассистентом в свою лабораторию в Королевском институте в Лондоне. Фарадею было в то время 21 год.
Майкл Фарадей читает рождественскую лекцию в Королевском институте (Лондон, 1955 г.) в присутствии членов королевской семьи: лицом к нему в первом ряду — муж королевы, слева от него — принц Уэльский (впоследствии Эдуард VII), справа от него — герцог Эдинбургский.
В последующие годы Фарадей открыл два новых хлорида углерода. Ему удалось также перевести в жидкое состояние хлор и другие газы. В 1825 г. он сумел выделить бензол и в том же году был назначен заведующим лабораторией. В течение нескольких лет он занимался экспериментальным изучением электролиза и в конце концов сформулировал в 1834 г. свои знаменитые законы электролиза. К этому времени он уже открыл явление электромагнитной индукции.
В течение нескольких лет он занимался экспериментальным изучением электролиза и в конце концов сформулировал в 1834 г. свои знаменитые законы электролиза. К этому времени он уже открыл явление электромагнитной индукции.
Фарадей стал президентом Королевского общества и написал несколько книг, в том числе «Экспериментальные исследования по химии и физике» (1858). В 1855 г. из-за ухудшения памяти он вынужден был прекратить исследовательскую работу. В 1867 г. Фарадей умер.
Как уже известно, при электролизе на электродах происходит выделение вещества. Попробуем выяснить, от чего будет зависеть масса это вещества. Масса выделившегося вещества m будет равна произведению массы одного иона m0i на число ионов Ni, которые достигли электрода за промежуток времени равный ∆t: m = m0i*Ni. Масса иона m0i будет вычисляться по следующей формуле:
- m0i = M/Na,
где М — молярная масса вещества, а Na — постоянная Авогадро.
Число ионов, которые достигнут электрода, вычисляется по следующей формуле:
- Ni = ∆q/q0i,
где ∆q = I*∆t — заряд, прошедший через электролит за время, равное ∆t, q0i — заряд иона.
Для того, чтобы определить заряд иона, используется следующая формула:
- q0i = n*e,
где n — валентность, e — элементарный заряд.
Собирая воедино все представленные формулы, получаем формулу для вычисления массы выделившегося на электроде вещества:
- m = (M*I*∆t)/(n*e*Na).
Теперь обозначим через k коэффициент пропорциональности между массой вещества и зарядом ∆q.
- k = M/(e*n*Na).
Этот коэффициент k будет зависеть от природы вещества. Тогда формулу массы вещества можно переписать в следующем виде:
- m = k*I*∆t.
Второй закон Фарадея
Масса вещества, выделившегося на электроде за время, равное ∆t, при прохождении электрического тока пропорциональна силе тока и времени. Коэффициент k называют электрохимическим эквивалентом данного вещества. Единицей измерения служит кг/Кл. Разберемся с физическим смыслом электрохимического эквивалента. Так как:
- M/Na = m0i,
- e*n = qi,
то формулу электрохимического эквивалента можно переписать в следующем виде:
- k = m0i/q0i.

Таким образом, k — отношение массы иона к заряду этого иона.
Для того, чтобы удостовериться в справедливости закона Фарадея, можно провести опыт. Лабораторная установка, необходимая для него, показана на следующем рисунке.
Все три емкости заполнены одинаковым электролитическим раствором. Через них будут протекать различные электрические токи, причем I1 = I2+I3. После включения установки в цепь подождем некоторое время. Потом отключим её и измерим массы веществ, выделившихся на электродах в каждом из сосудов m1, m2, m3. Можно будет убедиться, что массы веществ будут пропорциональны силам тока, которые проходили через соответствующий сосуд.
Из формулы
- m = (M*I*∆t)/(n*e*Na)
можно выразить значение заряда электрона
- e = (M*I*∆t)/(n*m*Na).
Законыэлектролиза (законыФарадея)
Поскольку прохождение электрического тока через электрохимические системы связано с химическими превращениями, между количеством протекающего электричества и количеством прореагировавших веществ должна существовать определенная зависимость. Она была открыта Фарадеем и получила свое выражение в первых количественных законах электрохимии, названных впоследствии законами Фарадея.
Она была открыта Фарадеем и получила свое выражение в первых количественных законах электрохимии, названных впоследствии законами Фарадея.
Первый закон Фарадея . Количества веществ, превращённых при электролизе, пропорциональны количеству электричества, прошедшего через электролит :
D m =k э q =k э It ,
D m – количество прореагировавшего вещества; k э – некоторый коэффициент пропорциональности; q – количество электричества, равное произведению силы тока I на время t . Еслиq = It = 1, то D m = k э, то есть коэффициент k э представляет собой количество вещества, прореагировавшего в результате протекания единицы количества электричества. Коэффициент k э называется электрохимическим эквивалентом .
Второй закон Фарадея отражает связь, существующую между количеством прореагировавшего вещества и его природой: при постоянном количестве прошедшего электричества массы различных веществ, испытывающие превращение у электродов (выделение из раствора, изменение валентности), пропорциональны химическим эквивалентам этих веществ :
D
m i /A i = const
.
Можно объединить оба закона Фарадея в виде одного общего закона : для выделения или превращения с помощью тока 1 г-экв любого вещества (1/z моля вещества) необходимо всегда одно и то же количество электричества, называемое числом Фарадея (или фарадеем ):
D m =It = It .
Точно измеренное значение числа Фарадея
F = 96484,52 ± 0,038Кл/г-экв.
Таков заряд, несомый одним грамм-эквивалентом ионов любого вида. Умножив это число на z (число элементарных зарядов иона), получим количество электричества, которое несёт 1 г-ион . Разделив число Фарадея на число Авогадро, получим заряд одного одновалентного иона, равный заряду электрона:
e = 96484,52 / (6,022035 × 10 23) = 1,6021913 × 10 –19 Кл.
Законы, открытые Фарадеем в 1833 г., строго выполняются для проводников второго рода. Наблюдаемые отклонения от законов Фарадея являются кажущимися
. Они часто связаны с наличием неучтённых параллельных электрохимических реакций. Отклонения от закона Фарадея в промышленных установках связаны с утечками тока, потерями вещества при разбрызгивании раствора и т.д. В технических установках отношение количества продукта, полученного при электролизе, к количеству, вычисленному на основе закона Фарадея, меньше единицы и называется выходом по току :
Отклонения от закона Фарадея в промышленных установках связаны с утечками тока, потерями вещества при разбрызгивании раствора и т.д. В технических установках отношение количества продукта, полученного при электролизе, к количеству, вычисленному на основе закона Фарадея, меньше единицы и называется выходом по току :
В Т = = .
При тщательных лабораторных измерениях для однозначно протекающих электрохимических реакций выход по току равен единице (в пределах ошибок опыта). Закон Фарадея точно соблюдается, поэтому он лежит в основе самого точного метода измерения количества электричества, прошедшего через цепь, по количеству выделенного на электроде вещества. Для таких измерений используюткулонометры . В качестве кулонометров используют электрохимические системы, в которых нет параллельных электрохимических и побочных химических реакций. По методам определения количества образующихся веществ кулонометры подразделяют на электрогравиметрические, газовые и титрационные
. Примером электрогравиметрических кулонометров являются серебряный и медный кулонометры. Действие серебряного кулонометра Ричардсона, представляющего собой электролизер
Примером электрогравиметрических кулонометров являются серебряный и медный кулонометры. Действие серебряного кулонометра Ричардсона, представляющего собой электролизер
(–) Ag ï AgNO 3 × aq ï Ag (+) ,
основано на взвешивании массы серебра, осевшей на катоде во время электролиза. При пропускании 96500 Кл (1 фарадея) электричества на катоде выделится 1 г-экв серебра (107 г). При пропускании n F электричества на катоде выделяется экспериментально определенная масса (D m к ). Число пропущенных фарадеев электричества определяется из соотношения
n = D m /107 .
Аналогичен принцип действия медного кулонометра.
В газовых кулонометрах продуктами электролиза являются газы, и количества выделяющихся на электродах веществ определяют измерением их объемов. Примером прибора такого типа является газовый кулонометр, основанный на реакции электролиза воды. При электролизе на катоде выделяется водород:
2Н 2 О+2е – =2ОН – +Н 2 ,
а на аноде – кислород:
Н 2 О=2Н + +½ О 2 +2е –
V
– суммарный объем выделенного газа, м 3 .
В титрационных кулонометрах количество вещества, образовавшегося в процессе электролиза, определяют титриметрически. К этому типу кулонометров относится титрационный кулонометр Кистяковского, представляющий собой электрохимическую систему
(–) Pt ï KNO 3 , HNO 3 ï Ag (+) .
В процессе электролиза серебряный анод растворяется, образуя ионы серебра, которые оттитровывают. Число фарадеев электричества определяют по формуле
n = mVc ,
где m – масса раствора, г;V – объем титранта, пошедший на титрование 1 г анодной жидкости;c –концентрация титранта, г-экв/см 3 .
Электролиз — это физико-химический процесс, осуществляемый в растворах различных веществ при помощи электродов (катода и анода). Существует множество веществ, которые химически разлагаются на составляющие при прохождении через их раствор или расплав электрического тока. Они называются электролитами. К ним относятся многие кислоты, соли и основания. Различают сильные и слабые электролиты, но это деление условно. В некоторых случаях слабые электролиты проявляют свойства сильных и наоборот.
В некоторых случаях слабые электролиты проявляют свойства сильных и наоборот.
При пропускании тока через раствор или расплав электролита на электродах оседают различные металлы (в случае кислот просто выделяется водород). Используя это свойство, можно подсчитать массу выделившегося вещества. Для подобных экспериментов используют раствор медного купороса. На угольном катоде при пропускании тока можно легко увидеть красный медный осадок. Разница между значениями его масс до и после эксперимента и будет массой осевшей меди. Она зависит от количества электричества, прошедшего через раствор.
Первый закон Фарадея можно сформулировать так: масса вещества m, выделившегося на катоде прямо пропорциональна количеству электричества (электрическому заряду q), прошедшему через раствор или расплав электролита. Этот закон выражается формулой: m=KI=Kqt, где K — коэффициент пропорциональности. Его называют электрохимическим эквивалентом вещества. Для каждого вещества он принимает различные значения. Он численно равен массе вещества, выделившегося на электроде за 1 секунду при силе тока 1 ампер.
Он численно равен массе вещества, выделившегося на электроде за 1 секунду при силе тока 1 ампер.
Второй закон Фарадея
В специальных таблицах можно посмотреть значения электрохимического для различных веществ. Вы заметите, что эти значения существенно отличаются. Объяснение такому различию дал Фарадей. Оказалось, что электрохимический эквивалент вещества прямо пропорционален его химическому эквиваленту. Это утверждение носит название второго закона Фарадея. Его истинность была подтверждена экспериментально.
Формула, выражающая второй закон Фарадея, выглядит так: K=M/F*n, где M — молярная масса, n — валентность. Отношение молярной массы к валентности называется химическим эквивалентом.
Величина 1/F имеет одно и то же значение для всех веществ. F называется постоянной Фарадея. Она равна 96,484 Кл/моль. Эта величина показывает количество электричества, которое нужно пропустить через раствор или расплав электролита, чтобы на катоде осел один моль вещества. 1/F показывает сколько моль вещества осядет на катоде при прохождении заряда в 1 Кл.
Электролиты, закон Фарадея
Электролиты
Определение 1
Явление выделения электрическим током химических составных частей проводника при прохождении тока называется электролизом.
Электролиз может протекать не во всех проводниках. К числу проводников, в которых электролиз не протекает, относят металлы, уголь и другие соединения (Это проводники первого рода). Проводники, в которых электролиз возможен, называют проводниками второго рода или электролитами. К электролитам относят большое количество водных растворов кислот, солей, некоторые жидкие и твердые соединения.
Явление электролиза часто сопровождается химическими реакциями (вторичные реакции), которые не связаны с прохождением тока. В ходе электролиза на отрицательном полюсе (катоде) всегда выделяются металлы и водород, на положительном полюсе (аноде) — остаток химического соединения. Составные части электролита выделяются только на электродах. Явление выделения составных частей электролита на электродах при прохождении электрического тока было исследовано М. Фарадеем.
Фарадеем.
Законы электролиза Фарадея не стоит путать с законом электромагнитной индукции Фарадея, рассматривающим электрический контур и силы в нём. В этом законе говорится о зависимости ЭДС от скорости изменения магнитного потока.
Явление электролиза отражает тот факт, что молекулы растворенного вещества в электролите существуют как две части: ион с положительным знаком и ион с отрицательным знаком. Под воздействием внешнего электрического поля эти ионы движутся: положительные ионы в сторону катода, отрицательные ионы в сторону анода. Таким образом, когда отрицательный ион достигнет анода, то он отдает свой заряд электроду, что ведёт к изменению его заряда. Следовательно, некоторое количество электронов проходят по внешней цепи. Ион становится нейтральным и выделяется на аноде, как атом или молекула. Положительный ион забирает у катода некоторое количество электронов (столько, сколько ему требуется для нейтрализации), что порождает его выделение на катоде.
Замечание 1
Ионы, знак заряда при которых отрицательный, выделяются на аноде, они были названы Фарадеем анионами, а положительно заряженные ионы получили название катионов.
Законы Фарадея
Фарадей установил экспериментальным путем два основных закона электролиза. В соответствии с первым законом, масса вещества $(m)$, которая выделяется на одном из электродов, прямо пропорциональна заряду $(q)$, который прошел через электролит:
$m=Kq\left(1\right),$
где $K$ — электрохимический эквивалент, который отличается для разных электролитов. $K$ равен массе электролита, которая выделяется при прохождении заряда $q=1Kл$. Основной единицей измерения электрохимического коэффициента является $\frac{кг}{Кл}$.
Кроме того, Фарадей заметил, что электрохимический эквивалент всегда пропорционален молярной массе вещества ($\mu $) и обратно пропорционален валентности $(Z)$. Отношение $\frac{\mu }{Z}$ называют химическим эквивалентом вещества.
В соответствии со вторым законом Фарадея: электрохимический эквивалент прямо пропорционален химическому эквиваленту для избранного вещества:
$K=\frac{C\mu }{Z}=\frac{\mu }{FZ}\left(2\right),$, где:
- $C=\frac{1}{F}$ — величина постоянная для всех веществ,
- $F$ — постоянная Фарадея.
 4\frac{Кл}{моль}$ — фундаментальная физическая постоянная, отражающая отношение электрохимических и физических свойств вещества. Причем известно, что:
4\frac{Кл}{моль}$ — фундаментальная физическая постоянная, отражающая отношение электрохимических и физических свойств вещества. Причем известно, что:$F=q_eN_A\left(4\right),$ где:
- $q_e$ — заряд электрона,
- $N_A$ — постоянная Авогадро.
Объяснить законы Фарадея можно с точки зрения ионной проводимости. Допустим, что количество ионов, которое выделяется на одном из электродов при электролизе равно $\nu $, заряд одного из ионов равен $q_1$. Следовательно, суммарный заряд, который прошел через электролит, на который действовало внешнее электрическое поле, равен:
$q=q_1\nu \left(5\right).$
Пусть масса одного иона равна $m_1$, тогда масса вещества, которая выделяется на электроде, равна:
$m=m_1\nu \left(6\right).$
Выразим из (5) $\nu $, получим:
$\nu =\frac{q}{q_1}\left(7\right).$
Подставим (7) в (6), имеем:
$m=\frac{m_1}{q_1}q\left(8\right).$
Выражение (8) не что иное как первый закон Фарадея, где:
$K=\frac{m_1}{q_1}=\frac{m_1N_A}{q_1N_A}=\frac{\mu }{q_1N_A}\left(9\right).
 $
$Сравним выражения (2) и (9), получим, что:
$q_1=\frac{ZF}{N_A}\left(10\right).$
В выражении (10) мы получили, что заряд иона в электролите пропорционален валентности вещества $(Z)$. Этот результат показывает, что величины электрических зарядов ионов кратны между собой. Минимальный заряд, равный заряду электрона, имеют ионы одновалентных веществ.
Пример 1
Задание: Найдите скорость $v,$ с которой увеличивается слой вещества, являющегося проводником второго рода на плоской поверхности электрода в процессе электролиза при прохождении тока, плотность которого равна $j$. Считать, что электролит имеет валентность равную $Z$, плотность $\rho ,\ молярную\ массу\ \mu .$
Решение:
В качестве основы решения задачи применим объединенный закон Фарадея:
$m=\frac{\mu }{Z}\frac{q}{F}\left(1.1\right),$
где $q=It$, $I$ — сила тока, текущего через электролит, $t$ — время, которое тек ток. Если считать, что осаждение никеля идет равномерно по поверхности металла, то массу выделившегося вещества запишем как:
$m=\rho Sh\ \left(1.
 2\right),$
2\right),$где $\rho $ — плотность никеля, $S$ — площадь поверхности металла, $h$ — толщина слоя никеля. Силу тока, выразим через его плотность:
$I=jS\left(1.3\right).$
Подставим в выражение (1.1) силу тока из (1.3) и массу из (1.2), получим:
$\rho Sh=\frac{\mu}{Z}\frac{jSt}{F}\to \rho h=\frac{\mu}{Z}\frac{jt}{F}\left(1.4\right).$
В том случае, если плотность тока постоянна, то скорость ($v=\frac{h}{t}$) увеличения слоя никеля так же постоянна. Разделим обе части выражения (1.4) на время, имеем:
$\rho \frac{h}{t}=\frac{\mu }{Z}\frac{j}{F}\to v=\frac{\mu }{Z}\frac{j}{\rho F}.$
Ответ: $v=\frac{\mu }{Z}\frac{j}{\rho F}.$
Пример 2
Задание: Через раствор электролита ток силой $I$ тек в течение времени $t$. Какое количество вещества $(\nu)$ выделится на катоде, каково число атомов $(N)$ вещества при этом, если металл имеет валентность $Z$.
Решение:
За основу решения задачи примем объединенный закон Фарадея:
$m=\frac{\mu }{Z}\frac{q}{F}\left(2.
 1\right),$
1\right),$где $q=It$, $I$ — сила тока, текущего через электролит, $t$ — время, которое тек ток. При этом нам известно, что:
$\nu =\frac{m}{\mu }\left(2.2\right).$
Разделим правую и левую части выражения (2.1) на молярную массу ($\mu $) вещества электролита, получим:
$\nu =\frac{1}{Z}\frac{q}{F}=\frac{It}{ZF}\left(2.3\right),$
где $q=It.$ Количество атомов осадка найдем, используя формулу:
$N=\nu \cdot N_A=\frac{It}{ZF}N_A.$
Ответ: $\nu =\frac{It}{ZF},\ N=\frac{It}{ZF}N_A.$
8.3: Закон Фарадея — Технические LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3946
- Стивен У.
 Эллингсон
Эллингсон - Политехнический институт Вирджинии и Государственный университет через Инициативу открытых образовательных библиотек штата Вирджиния
- Назначить клеммы «\(+\)» и «\(-\)» на напряжение промежутка \(V_T\).
- Ориентация \(\hat{\bf n}\) определяется по правилу правой руки, принимая направление \(\mathcal{C}\) за периметр цикла, начинающегося в «\(-\ )» и заканчивается на «\(+\)»
- \({\bf B}\) дает магнитный поток \(\Phi\), связанный с контуром согласно уравнению \ref{m0055_ePhi}.
 \(\mathcal{S}\) — это любая открытая поверхность, которая пересекает все силовые линии магнитного поля, проходящие через петлю (поэтому вы также можете выбрать \(\mathcal{S}\) таким образом, чтобы получить простейшую из возможных интеграция).
\(\mathcal{S}\) — это любая открытая поверхность, которая пересекает все силовые линии магнитного поля, проходящие через петлю (поэтому вы также можете выбрать \(\mathcal{S}\) таким образом, чтобы получить простейшую из возможных интеграция). - По закону Фарадея (уравнение \ref{m0055_eVT}), \(V_T\) является производной по времени от \(\Phi\) со сменой знака.
- Ток \(I\), протекающий в петле, равен \(V_T/R\), с опорным направлением (т. е. направлением положительного тока) от «\(+\)» до «\(-\)» через резистор. Думайте о контуре как об источнике напряжения, и вы получите правильное опорное направление для \(I\).
- Изменяющийся во времени \({\bf B}\) (как мы рассмотрели ранее в этом разделе). Например, \({\bf B}\) может быть связано с постоянным магнитом, который перемещается (например, перемещается или вращается) вблизи катушки, как описано в разделе 8.2. Или, что чаще, \({\bf B}\) может быть связано с другой катушкой, по которой протекает переменный во времени ток. Эти механизмы вместе именуются ЭДС трансформатора . ЭДС трансформатора лежит в основе принципа работы трансформаторов; подробнее об этом см. Раздел 8.5.
- Периметр \(\mathcal{C}\) и, следовательно, поверхность \(\mathcal{S}\), по которой определяется \(\Phi\), могут изменяться во времени. Например, проволочная петля может поворачиваться или изменять форму в присутствии постоянного магнитного поля. Этот механизм называется ЭДС движения и является основным принципом работы генераторов (раздел 8.7).
- Трансформатор и ЭДС движения могут существовать в различных комбинациях.
 С точки зрения закона Фарадея, трансформатор и ЭДС движения одинаковы в том смысле, что в любом случае \(\Phi\) изменяется во времени, а это все, что требуется для создания ЭДС.
С точки зрения закона Фарадея, трансформатор и ЭДС движения одинаковы в том смысле, что в любом случае \(\Phi\) изменяется во времени, а это все, что требуется для создания ЭДС. - Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Стивен В.
 Эллингсон
Эллингсон
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- Инициатива открытого образования технических библиотек Вирджинии
- Показать оглавление
- нет
- Теги
- Закон Фарадея
- индукция
- источник@https://doi.org/10.21061/electromagnetics-vol-1
- Определить магнитный поток через поверхность, зная напряженность магнитного поля, площадь поверхности и угол между нормалью к поверхности и магнитным полем
- Используйте закон Фарадея для определения величины ЭДС индукции в замкнутом контуре из-за изменения магнитного потока через контур
- Поток через один виток составляет
Фм=ВА=Бл2,Фм=ВА=Бл2,
поэтому мы можем рассчитать величину ЭДС по закону Фарадея. Знак ЭДС будет обсуждаться в следующем разделе, посвященном закону Ленца:
Знак ЭДС будет обсуждаться в следующем разделе, посвященном закону Ленца:|ε|=|−NdΦmdt|=Nl2dBdt=(200)(0,25 м)2(0,040 Тл/с)=0,50 В.|ε|=|−NdΦmdt|=Nl2dBdt=(200)(0,25 м)2( 0,040 Тл/с)=0,50 В.
- Величина тока, индуцируемого в катушке, составляет
I=εR=0,50 В, 5,0 Ом=0,10 A.I=εR=0,50 В, 5,0 Ом=0,10 A.
- Расчет ЭДС, силы тока и магнитного поля по закону Фарадея.
- Объясните физические результаты закона Ленца
- Составьте схему ситуации для визуализации и записи направлений.
- Определить направление магнитного поля B.
- Определите, увеличивается или уменьшается поток.
- Теперь определите направление индуцированного магнитного поля B. Оно противодействует изменению потока, добавляя или вычитая исходное поле.
- Используйте RHR-2 для определения направления индуцированного тока I, который отвечает за индуцированное магнитное поле B.
- Направление (или полярность) ЭДС индукции теперь будет управлять током в этом направлении и может быть представлено как ток, выходящий из положительной клеммы ЭДС и возвращающийся к ее отрицательной клемме.

Закон Фарадея описывает генерацию электрического потенциала изменяющимся во времени магнитным потоком. Это форма электромагнитной индукции .
Для начала рассмотрим сценарий, показанный на рисунке \(\PageIndex{1}\). Одиночная проволочная петля в присутствии приложенного магнитного поля \({\bf B}\). По причинам, объясненным позже, мы вводим небольшой зазор и определяем \(V_T\) как разность потенциалов, измеренную через зазор в соответствии с указанным соглашением о знаках. Сопротивление \(R\) может быть любым значением больше нуля, включая бесконечность; то есть буквальный разрыв.
Рисунок \(\PageIndex{1}\): Одиночная проволочная петля в присутствии приложенного магнитного поля. Пока \(R\) не бесконечно, из закона Ленца (раздел 8.2) мы знаем, что переменное во времени магнитное поле вызовет протекание тока в проводе. Закон Ленца также говорит нам, в каком направлении будет течь ток. Однако закон Ленца не говорит нам о величине тока и обходит некоторые важные физические аспекты, которые имеют большое значение для анализа и проектирования электрических устройств, включая генераторы и трансформаторы.
Закон Ленца также говорит нам, в каком направлении будет течь ток. Однако закон Ленца не говорит нам о величине тока и обходит некоторые важные физические аспекты, которые имеют большое значение для анализа и проектирования электрических устройств, включая генераторы и трансформаторы.
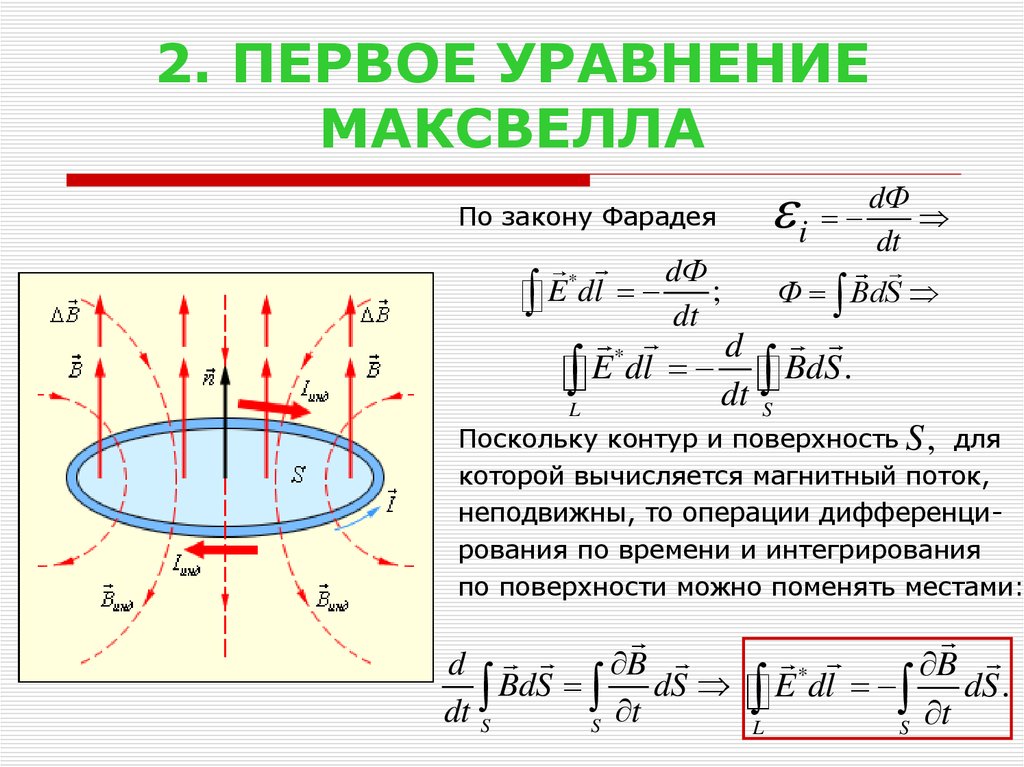
Более полную картину дает закон Фарадея. Что касается сценария на рисунке \(\PageIndex{1}\), закон Фарадея связывает потенциал \(V_T\), индуцированный изменением во времени \({\bf B}\). Затем \(V_T\) приводит к току, указанному в законе Ленца. Величина этого тока просто \(V_T/R\). Без дальнейших церемоний, вот закон Фарадея для этого сценария с одной петлей:
.\[V_T = — \frac{\partial}{\partial t} \Phi ~~\mbox{(один цикл)} \label{m0055_eVT} \] 92\)) и \(d{\bf s}\) — вектор площади дифференциальной поверхности.
Чтобы продвинуться вперед с законом Фарадея, нужно четко понимать значения \(\mathcal{S}\) и \(d{\bf s}\). Если проволочная петля в данном сценарии лежит в плоскости, то хорошим выбором для \(\mathcal{S}\) будет просто плоская область, ограниченная петлей.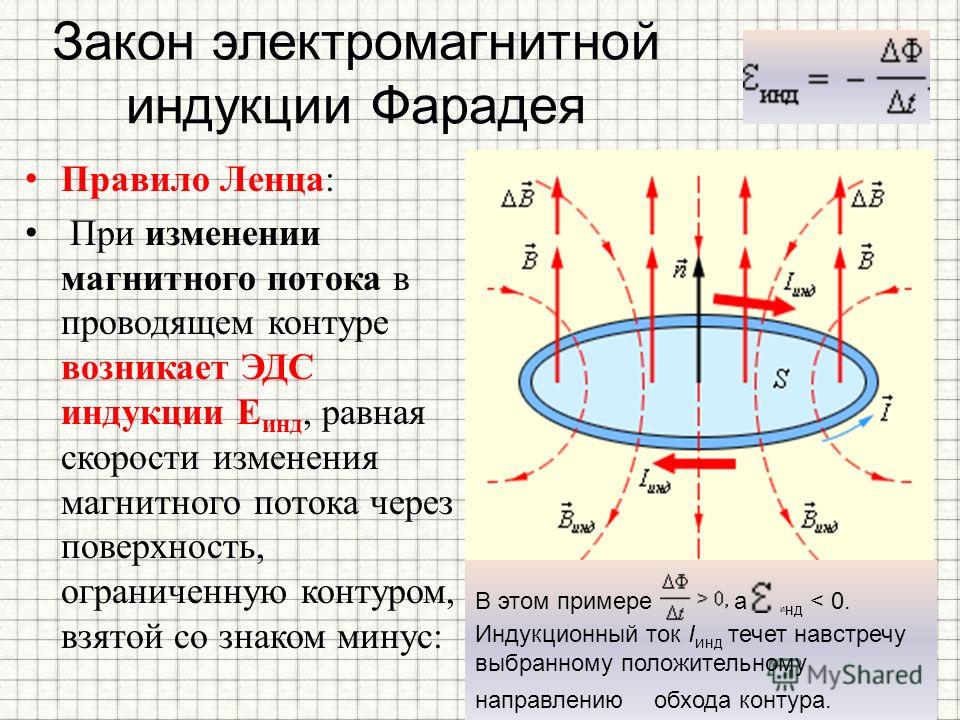 Однако любая поверхность , ограниченная петлей, будет работать, включая неплоские поверхности, которые простираются выше и/или ниже плоскости петли. Все, что требуется, это чтобы каждая линия магнитного поля, проходящая через петлю, также проходила через \(\mathcal{S}\). Это происходит автоматически, если петле соответствует кривая \(\mathcal{C}\), определяющая край открытой поверхности \(\mathcal{S}\). Следовательно, величина \(d{\bf s}\) является элементом дифференциальной поверхности \(ds\), а направление \(d{\bf s}\) является единичным вектором \(\hat{\bf n}\) перпендикулярно каждой точке на \(\mathcal{S}\), поэтому \(d{\bf s}=\hat{\bf n}ds\).
Однако любая поверхность , ограниченная петлей, будет работать, включая неплоские поверхности, которые простираются выше и/или ниже плоскости петли. Все, что требуется, это чтобы каждая линия магнитного поля, проходящая через петлю, также проходила через \(\mathcal{S}\). Это происходит автоматически, если петле соответствует кривая \(\mathcal{C}\), определяющая край открытой поверхности \(\mathcal{S}\). Следовательно, величина \(d{\bf s}\) является элементом дифференциальной поверхности \(ds\), а направление \(d{\bf s}\) является единичным вектором \(\hat{\bf n}\) перпендикулярно каждой точке на \(\mathcal{S}\), поэтому \(d{\bf s}=\hat{\bf n}ds\).
Остается только одна проблема — ориентация \(\hat{\bf n}\). Это показано на рисунке \(\PageIndex{2}\). Вектор может быть перпендикулярен поверхности двумя возможными способами, и направление, выбранное для \(\hat{\bf n}\), повлияет на знак \(V_T\). Следовательно, \(\hat{\bf n}\) должно быть как-то связано с полярностью, выбранной для \(V_T\). Рассмотрим это отношение. Пусть \(\mathcal{C}\) начинается с терминала «\(-\)» \(V_T\) и проходит по всему периметру цикла, заканчиваясь на терминале «\(+\)». Тогда \(\hat{\bf n}\) определяется следующим «правилом правой руки»: \(\hat{\bf n}\) указывает в направлении согнутых пальцев правой руки, когда большой палец правой руки выровнен в направлении \(\mathcal{C}\). Стоит отметить, что именно это соглашение используется для связи \(\hat{\bf n}\) и \(\mathcal{C}\) в теореме Стокса.
Рассмотрим это отношение. Пусть \(\mathcal{C}\) начинается с терминала «\(-\)» \(V_T\) и проходит по всему периметру цикла, заканчиваясь на терминале «\(+\)». Тогда \(\hat{\bf n}\) определяется следующим «правилом правой руки»: \(\hat{\bf n}\) указывает в направлении согнутых пальцев правой руки, когда большой палец правой руки выровнен в направлении \(\mathcal{C}\). Стоит отметить, что именно это соглашение используется для связи \(\hat{\bf n}\) и \(\mathcal{C}\) в теореме Стокса.
Теперь давайте вспомним, как закон Фарадея применяется к сценарию с одним контуром на рисунке [m0055_fFaradaySingleLoop]:
Здесь повторим, что электромагнитная индукция, описываемая законом Фарадея, индуцирует потенциала (в данном случае \(V_T\)) , а не тока . Ток в петле — это просто наведенное напряжение, деленное на сопротивление петли. Этот момент легко упустить из виду, особенно в свете закона Ленца, который, по-видимому, подразумевает, что индуцируется ток, а не потенциал.
Вас интересует значение знака минус в уравнении \ref{m0055_eVT}? В частности, это закон Ленца: ток \(I\), который в конце концов циркулирует в петле, создает собственное магнитное поле («\({\bf B}_{ind}\)» в разделе 8.2), которое отличается от приложенное магнитное поле \({\bf B}\) и которое имеет тенденцию противодействовать изменению \({\bf B}\). Таким образом, мы видим, что закон Фарадея включает в себя закон Ленца.
Часто интересуют структуры, состоящие из множества одинаковых петель. Мы имеем в виду нечто вроде катушки с \(N\ge1\) витками, плотно упакованными вместе. В этом случае закон Фарадея равен
.\[\boxed{ V_T = — N\frac{\partial}{\partial t} \Phi} \label{m0055_eVTN} \]
Обратите внимание, что разница заключается просто в том, что потенциал промежутка \(V_T\) больше на \(N\). Другими словами, каждая обмотка катушки вносит потенциал, заданный уравнением \ref{m0055_eVT}, и эти потенциалы складываются последовательно.
Закон Фарадея, представленный в общем виде уравнением \ref{m0055_eVTN}, утверждает, что потенциал, индуцированный в катушке, пропорционален производной по времени магнитного потока через катушку.
Наведенный потенциал \(V_T\) часто называют «ЭДС», что является сокращением термина электродвижущая сила – конечно, неправильное название, поскольку не подразумевается фактическая сила, а только потенциал. Тем не менее термин «ЭДС» часто используется в контексте применения закона Фарадея по историческим причинам.
Ранее в этом разделе мы рассмотрели генерацию ЭДС изменением во времени \({\bf B}\). Однако уравнение \ref{m0055_eVT} показывает, что на самом деле происходит то, что ЭДС является результатом изменения во времени магнитного потока \(\Phi\). Магнитный поток представляет собой плотность магнитного потока, проинтегрированную по площади, поэтому оказывается, что ЭДС также можно генерировать, просто изменяя \(\mathcal{S}\), независимо от любого изменения во времени \({\bf B}\). Другими словами, ЭДС может генерироваться даже тогда, когда \({\bf B}\) постоянна, вместо этого изменяя форму или ориентацию катушки. Итак, у нас есть множество схем, по которым мы можем генерировать ЭДС. Вот они:
Вот они:
Наконец, комментарий к общему закону Фарадея. Выше мы ввели закон Фарадея, как если бы он был специфичен для петель и катушек проволоки. Однако правда в том, что закон Фарадея — это фундаментальная физика. Если вы можете определить замкнутый путь — с током или без него — то вы можете вычислить разность потенциалов, полученную при пересечении этого пути, используя закон Фарадея. Значение, которое вы вычисляете, представляет собой потенциал, связанный с электромагнитной индукцией, и существует независимо и в дополнение к разности потенциалов, связанной со статическим электрическим полем (например, раздел 5.12). Другими словами:
Закон Фарадея показывает вклад электромагнитной индукции (генерация ЭДС изменяющимся во времени магнитным потоком) в разность потенциалов, достигаемую при пересечении замкнутого пути.
В разделе 8.8 это понимание используется для преобразования статической формы закона напряжения Кирхгофа (раздел 5.10), который дает разность потенциалов, связанную только с электрическим полем, в уравнение Максвелла-Фарадея (раздел 8.8), которое является общее положение о связи между мгновенным значением электрического поля и производной магнитного поля по времени.
Эта страница под названием 8.3: Закон Фарадея распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Стивеном В. Эллингсоном (Инициатива открытого образования технических библиотек штата Вирджиния) посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
13.1 Закон Фарадея — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
Первые плодотворные эксперименты, касающиеся эффектов изменяющихся во времени магнитных полей, были выполнены Майклом Фарадеем в 1831 году. Один из его ранних экспериментов представлен на рис. 13.2. ЭДС индуцируется, когда магнитное поле в катушке изменяется путем вталкивания стержневого магнита в катушку или из нее. ЭДС противоположных знаков создаются движением в противоположных направлениях, а направления ЭДС также меняются на противоположные при смене полюсов. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.
Один из его ранних экспериментов представлен на рис. 13.2. ЭДС индуцируется, когда магнитное поле в катушке изменяется путем вталкивания стержневого магнита в катушку или из нее. ЭДС противоположных знаков создаются движением в противоположных направлениях, а направления ЭДС также меняются на противоположные при смене полюсов. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.
Рисунок 13.2 Движение магнита относительно катушки создает ЭДС, как показано (а – г). Такие же ЭДС возникают, если катушку перемещать относительно магнита. Эта кратковременная ЭДС присутствует только во время движения. Чем больше скорость, тем больше величина ЭДС, а ЭДС равна нулю, когда нет движения, как показано на (е).
Фарадей также обнаружил, что аналогичный эффект можно получить, используя две цепи: изменение тока в одной цепи индуцирует ток во второй, соседней цепи. Например, когда переключатель замыкается в цепи 1 на рис. 13.3(а), стрелка амперметра в цепи 2 на мгновение отклоняется, указывая на то, что в этой цепи наведен кратковременный скачок тока. Стрелка амперметра быстро возвращается в исходное положение, где и остается. Однако если теперь внезапно разомкнуть выключатель цепи 1, то в цепи 2 наблюдается еще один кратковременный выброс тока в направлении, противоположном предыдущему.0034
Например, когда переключатель замыкается в цепи 1 на рис. 13.3(а), стрелка амперметра в цепи 2 на мгновение отклоняется, указывая на то, что в этой цепи наведен кратковременный скачок тока. Стрелка амперметра быстро возвращается в исходное положение, где и остается. Однако если теперь внезапно разомкнуть выключатель цепи 1, то в цепи 2 наблюдается еще один кратковременный выброс тока в направлении, противоположном предыдущему.0034
Рисунок 13.3 (a) Замыкание переключателя цепи 1 вызывает кратковременный скачок тока в цепи 2. (b) Если переключатель остается замкнутым, в цепи 2 ток отсутствует. (c) Повторное размыкание переключателя вызывает кратковременный ток в схеме 2, но в противоположном направлении от предыдущего.
Фарадей понял, что в обоих экспериментах ток протекал по цепи с амперметром только тогда, когда магнитное поле в области, занятой этой цепью, изменялось . При перемещении магнита фигуры сила ее магнитного поля в петле менялась; а при включении или выключении тока в цепи 1 изменялась напряженность его магнитного поля в цепи 2.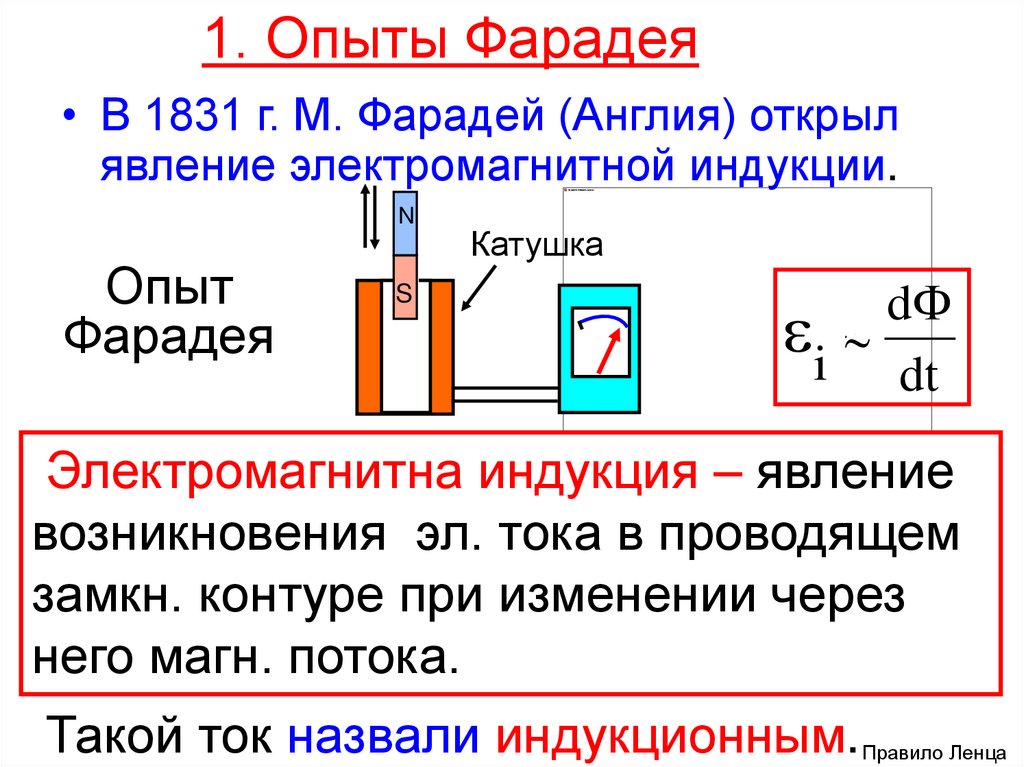 В конце концов Фарадей смог интерпретировать эти и все другие эксперименты с магнитными полями, меняющимися во времени, в соответствии со следующим законом:
В конце концов Фарадей смог интерпретировать эти и все другие эксперименты с магнитными полями, меняющимися во времени, в соответствии со следующим законом:
Закон Фарадея
Индуцированная ЭДС εε представляет собой отрицательное изменение магнитного потока ΦmΦm в единицу времени. Любое изменение магнитного поля или изменение ориентации области катушки по отношению к магнитному полю индуцирует напряжение (ЭДС). 9и вектор магнитного поля B→B→ параллельны или антипараллельны, как показано на диаграмме, магнитный поток является максимально возможным значением при заданных значениях площади и магнитного поля.
В части (а) на рис. 13.5 изображена цепь и произвольная поверхность S , которую она ограничивает. Обратите внимание, что S представляет собой открытую поверхность . Можно показать, что любая открытая поверхность, ограниченная рассматриваемой цепью, может быть использована для вычисления Φm. Φm. Например, ΦmΦm одинаково для различных поверхностей S1,S2,…S1,S2,… части (b) рисунка.
Φm. Например, ΦmΦm одинаково для различных поверхностей S1,S2,…S1,S2,… части (b) рисунка.
Рисунок 13,5 (a) Цепь, ограничивающая произвольную открытую поверхность S . Плоская область, ограниченная контуром, не является частью S . (b) Три произвольные открытые поверхности, ограниченные одним и тем же контуром. Значение ΦmΦm одинаково для всех этих поверхностей.
Единицей СИ для магнитного потока является вебер (Вб),
1Вб=1Тл·м2,1Вб=1Тл·м2.
Иногда единица измерения магнитного поля выражается в веберах на квадратный метр (Вб/м2Вб/м2) вместо тесла, исходя из этого определения. Во многих практических приложениях представляющая интерес схема состоит из числа 9.0202 Н туго намотанных витков (см. рис. 13.6). На каждый виток действует один и тот же магнитный поток. Таким образом, чистый магнитный поток через цепи в Н раз превышает поток через один виток, и закон Фарадея записывается как
ε=−ddt(NΦm)=−NdΦmdt. ε=−ddt(NΦm)=−NdΦmdt.
ε=−ddt(NΦm)=−NdΦmdt.
13,3
Пример 13.1
Квадратная катушка в изменяющемся магнитном поле
Квадратная катушка на рис. 13.6 имеет длину сторон l=0,25ml=0,25 м и плотно намотана N=200N=200 витков провода. Сопротивление катушки R=5.0Ω.R=5.0Ω. Катушка помещена в пространственно однородное магнитное поле, которое направлено перпендикулярно лицевой стороне катушки и величина которого уменьшается со скоростью дБ/dt=-0,040 Тл/с.дБ/dt=-0,040 Тл/с. а) Чему равна ЭДС индукции в катушке? б) Какова величина тока, циркулирующего по катушке? 9и что поток превращается в произведение магнитного поля на площадь. Площадь петли не меняется во времени, поэтому ее можно вычесть из производной по времени, оставив магнитное поле единственной величиной, изменяющейся во времени. Наконец, мы можем применить закон Ома, если мы знаем ЭДС индукции, чтобы найти ток в петле.
Решение
Значение
Если бы площадь петли изменялась во времени, мы бы не смогли вытащить ее из производной по времени. Поскольку петля представляет собой замкнутый путь, результатом этого тока будет небольшой нагрев проводов до тех пор, пока магнитное поле не перестанет изменяться. Это может немного увеличить площадь петли по мере нагрева проводов.
Проверьте свое понимание 13.1
Проверьте свое понимание Плотно намотанная катушка имеет радиус 4,0 см, 50 витков и общее сопротивление 40 Ом 40 Ом. С какой скоростью должно изменяться магнитное поле, перпендикулярное лицевой стороне катушки, чтобы в катушке возникал нагрев мощностью 2,0 мВт?
23.
 2 Закон индукции Фарадея: Закон Ленца – Колледж физики 2e
2 Закон индукции Фарадея: Закон Ленца – Колледж физики 2eЦели обучения
К концу этого раздела вы сможете:
Закон Фарадея и Ленца
Опыты Фарадея показали, что ЭДС, индуцируемая изменением магнитного потока, зависит лишь от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению потока ΔΦΔΦ. Во-вторых, ЭДС наибольшая, когда изменение во времени ΔtΔt наименьшее, то есть ЭДС обратно пропорциональна ΔtΔt. Наконец, если катушка имеет NN витков, будет создаваться ЭДС в NN раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна NN. Уравнение для ЭДС, индуцированной изменением магнитного потока, имеет вид
ЭДС=-NΔΦΔt.ЭДС=-NΔΦΔt.
23,2
Это соотношение известно как закон индукции Фарадея. Единицами ЭДС, как обычно, являются вольты.
Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле В, которые противодействуют изменению потока ΔΦΔΦ — это известно как закон Ленца . Направление (заданное знаком минус) эдс настолько важно, что его называют законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции. Фарадей знал об этом направлении, но Ленц сформулировал его так ясно, что ему приписывают его открытие. (См. рис. 23.7.)
Рисунок
23,7
(а) Когда этот стержневой магнит вталкивается в катушку, напряженность магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном направлению стержневого магнита, чтобы противостоять увеличению. Это один из аспектов закона Ленца — индукция противостоит любому изменению потока . (b) и (c) — две другие ситуации.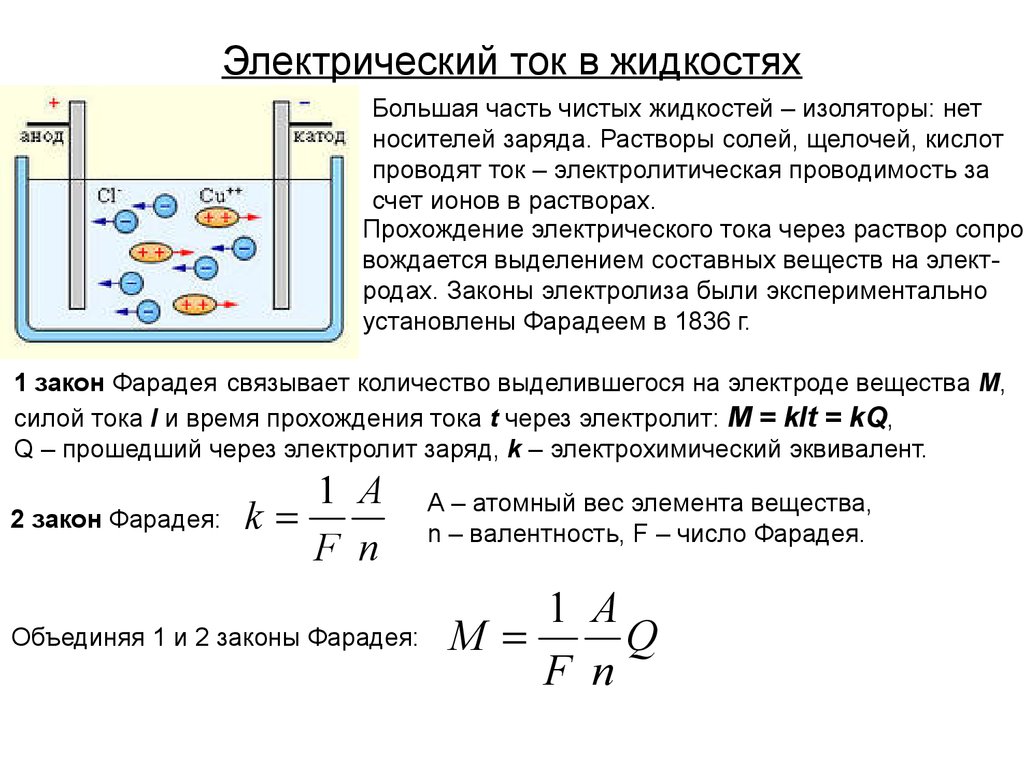 Убедитесь сами, что показанное направление индуцированного BcoilBcoil действительно противостоит изменению потока и что показанное направление тока соответствует RHR-2.
Убедитесь сами, что показанное направление индуцированного BcoilBcoil действительно противостоит изменению потока и что показанное направление тока соответствует RHR-2.
Стратегия решения проблем для закона Ленца
Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:
Для практики примените эти шаги к ситуациям, показанным на рис. 23.7, и к другим ситуациям, которые являются частью следующего текстового материала.
Применение электромагнитной индукции
Закон индукции Фарадея имеет множество применений, которые мы рассмотрим в этой и других главах. На этом этапе давайте упомянем несколько, которые связаны с хранением данных и магнитными полями. Очень важное приложение связано с аудио- и видеозаписями лент 9.0033 . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, на которое намотана катушка проволоки — электромагнит (рис. 23.8). Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые зависят от амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, что приводит к записи сигнала. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Рисунок 23,8 Головки записи и воспроизведения, используемые с аудио- и видеомагнитофонами. (кредит: Steve Jurvetson)
Аналогичные принципы применимы и к жестким дискам компьютеров, только с гораздо большей скоростью. Здесь записи на вращающемся диске с покрытием. Считывающие головки исторически заставляли работать по принципу индукции. Однако входная информация передается в цифровом, а не в аналоговом виде — на вращающемся жестком диске записывается последовательность нулей или единиц. Сегодня большинство устройств считывания с жестких дисков не работают по принципу индукции, а используют метод, известный как гигантское магнитосопротивление . (Открытие того, что слабые изменения магнитного поля в тонкой пленке железа и хрома могут вызвать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти в магнитной полосе на магнитной полосе. оборотная сторона вашей личной кредитной карты, используемой в продуктовом магазине или банкомате. Это работает по тому же принципу, что и упомянутая в последнем абзаце аудио- или видеокассета, в которой голова считывает личную информацию с вашей карты.
(Открытие того, что слабые изменения магнитного поля в тонкой пленке железа и хрома могут вызвать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти в магнитной полосе на магнитной полосе. оборотная сторона вашей личной кредитной карты, используемой в продуктовом магазине или банкомате. Это работает по тому же принципу, что и упомянутая в последнем абзаце аудио- или видеокассета, в которой голова считывает личную информацию с вашей карты.
Еще одним применением электромагнитной индукции является передача электрических сигналов через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном снаружи черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе. Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы необходимо передавать через различные среды.
Рисунок 23,9 Электромагнитная индукция используется для передачи электрических токов через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (кредит: Бьорн Кнетч)
Еще одна современная область исследований, в которой электромагнитная индукция успешно применяется (и имеет значительный потенциал), — это транскраниальное магнитное моделирование. Множество расстройств, включая депрессию и галлюцинации, можно отнести к нерегулярной локальной электрической активности в головном мозге. В транскраниальная магнитная стимуляция , быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозге. В выявленных местах индуцируются слабые электрические токи, что может привести к восстановлению электрических функций в тканях головного мозга.
Апноэ во сне («остановка дыхания») поражает как взрослых, так и младенцев (особенно недоношенных детей и может быть причиной внезапной детской смерти [SID]). У таких людей дыхание может неоднократно останавливаться во время сна. Прекращение более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль. В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
У таких людей дыхание может неоднократно останавливаться во время сна. Прекращение более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль. В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Установление связей: сохранение энергии
Закон Ленца является проявлением закона сохранения энергии. ЭДС индукции создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
ЭДС индукции создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно. Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
Пример 23.1
Расчет ЭДС: насколько велика ЭДС индукции?
Рассчитайте величину ЭДС индукции, когда магнит, показанный на рис. 23.7(а), вдавливается в катушку, учитывая следующую информацию: катушка с одним контуром имеет радиус 6,00 см и среднее значение BcosθBcosθ (это дано, поскольку поле стержневого магнита сложное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.
Стратегия
Чтобы найти величину ЭДС, мы используем закон индукции Фарадея, сформулированный как ЭДС=-NΔΦΔtemf=-NΔΦΔt, но без знака минус, указывающего направление:
ЭДС=NΔΦΔt. ЭДС=NΔΦΔt.
ЭДС=NΔΦΔt.
23,3
Решение
Нам дано, что N=1N=1 и Δt=0,100 с Δt=0,100 с, но мы должны определить изменение потока ΔΦΔΦ, прежде чем сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ).ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ).
23,4
Теперь Δ(Bcosθ)=0,200 TΔ(Bcosθ)=0,200 Тл, так как было дано, что BcosθBcosθ изменяется от 0,0500 до 0,250 Тл. Площадь петли равна A=πr2=(3,14…)( 0,060 м)2=1,13×10-2м2А=πr2=(3,14…)(0,060 м)2=1,13×10-2м2. Таким образом,
ΔΦ=(1,13×10−2 м2)(0,200 Тл).ΔΦ=(1,13×10−2 м2)(0,200 Тл).
23,5
Ввод полученных значений в выражение для ЭДС дает )(0,200Тл)0,100с=22,6мВ.
23,6
Обсуждение
Хотя это напряжение легко измерить, оно явно недостаточно велико для большинства практических приложений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.





 4\frac{Кл}{моль}$ — фундаментальная физическая постоянная, отражающая отношение электрохимических и физических свойств вещества. Причем известно, что:
4\frac{Кл}{моль}$ — фундаментальная физическая постоянная, отражающая отношение электрохимических и физических свойств вещества. Причем известно, что: $
$ 2\right),$
2\right),$ 1\right),$
1\right),$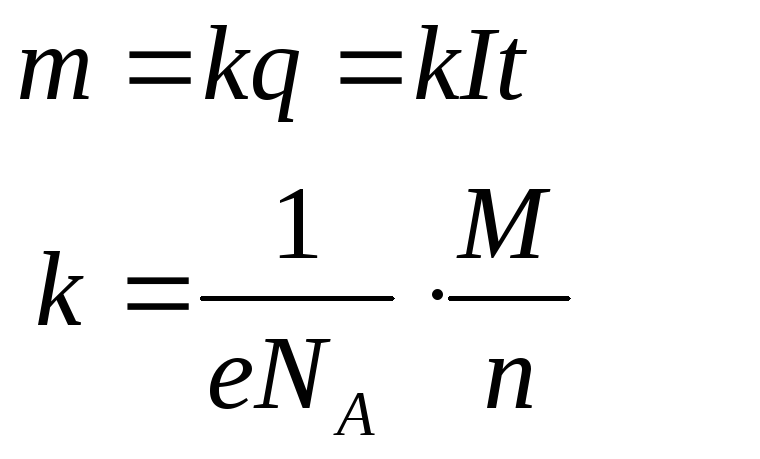 Эллингсон
Эллингсон С точки зрения закона Фарадея, трансформатор и ЭДС движения одинаковы в том смысле, что в любом случае \(\Phi\) изменяется во времени, а это все, что требуется для создания ЭДС.
С точки зрения закона Фарадея, трансформатор и ЭДС движения одинаковы в том смысле, что в любом случае \(\Phi\) изменяется во времени, а это все, что требуется для создания ЭДС. Эллингсон
Эллингсон Знак ЭДС будет обсуждаться в следующем разделе, посвященном закону Ленца:
Знак ЭДС будет обсуждаться в следующем разделе, посвященном закону Ленца: