Определение результирующий вектор общее значение и понятие. Что это такое результирующий вектор

В контексте физики величина, которая определяется его направлением, точкой приложения, количеством и значением, называется вектором . По его характеристикам можно говорить о разных видах векторов.

В латыни мы можем найти этимологическое происхождение этого термина, которое происходит именно от «vector-vectoris», что можно перевести как «тот, который ведет».

Результирующая векторная идея может появиться при выполнении операции сложения с векторами. Используя так называемый полигональный метод, вы должны поместить векторы, которые вы хотите добавить, один рядом с другим в граф, чтобы начало каждого вектора совпадало с концом следующего вектора. Результирующий вектор называется вектором, который имеет совпадающее начало с первым вектором и который заканчивается в конце вектора, расположенного в последнем месте .

VR — это аббревиатуры, которые используются для обозначения результирующего вектора, который, как и остальные векторы, при анализе требует учета трех элементов, которые придают ему форму. Мы имеем в виду следующее:

-Модуль, который используется, чтобы упомянуть, какова интенсивность его величины и который представлен тем, что является размером вектора.
Направление, которое относится к тому, что такое наклон линии.
Смысл, который имеет особенность, которая представлена ​​тем, что является вершиной стрелки рассматриваемого вектора.

Добавление векторов с помощью этого метода включает перемещение векторов, заставляя их соединяться своими концами. Итак, мы возьмем вектор и поместим его рядом с другим, чтобы начало одного связывалось с другим концом. Результирующий вектор

«рождается» в начале первого вектора, который мы взяли, и «заканчивается» в конце вектора, который мы поместили в последнее пространство.

Следует иметь в виду, что для добавления векторов с помощью полигонального метода важно не изменять свойства : векторы следует только перемещать.

Важно иметь в виду, что, когда речь заходит о возможности взять эту сумму, которая нас занимает, что нужно сделать, это прибегнуть к некоторым фундаментальным элементам в математике и алгебре. Мы имеем в виду оси координат X и Y. По сути, из них и их соответствующих сумм получается, как получить вышеупомянутый результирующий вектор.

Мы также говорим о результирующем векторе со ссылкой на тот, который в системе генерирует тот же эффект, что и векторы, составляющие его. Вектор, имеющий то же направление и величину, но противоположное направление, квалифицируется как уравновешивающий вектор.

Этот вышеупомянутый уравновешивающий вектор, который также называется VE, как мы упоминали, имеет противоположн

Определение результирующий вектор общее значение и понятие. Что это такое результирующий вектор

В контексте физики величина, которая определяется его направлением, точкой приложения, количеством и значением, называется вектором . По его характеристикам можно говорить о разных видах векторов.

В латыни мы можем найти этимологическое происхождение этого термина, которое происходит именно от «vector-vectoris», что можно перевести как «тот, который ведет».

Результирующая векторная идея может появиться при выполнении операции сложения с векторами. Используя так называемый полигональный метод, вы должны поместить векторы, которые вы хотите добавить, один рядом с другим в граф, чтобы начало каждого вектора совпадало с концом следующего вектора. Результирующий вектор называется вектором, который имеет совпадающее начало с первым вектором и который заканчивается в конце вектора, расположенного в последнем месте

.

VR — это аббревиатуры, которые используются для обозначения результирующего вектора, который, как и остальные векторы, при анализе требует учета трех элементов, которые придают ему форму. Мы имеем в виду следующее:
-Модуль, который используется, чтобы упомянуть, какова интенсивность его величины и который представлен тем, что является размером вектора.
Направление, которое относится к тому, что такое наклон линии.
Смысл, который имеет особенность, которая представлена ​​тем, что является вершиной стрелки рассматриваемого вектора.

Добавление векторов с помощью этого метода включает перемещение векторов, заставляя их соединяться своими концами. Итак, мы возьмем вектор и поместим его рядом с другим, чтобы начало одного связывалось с другим концом. Результирующий вектор

«рождается» в начале первого вектора, который мы взяли, и «заканчивается» в конце вектора, который мы поместили в последнее пространство.

Следует иметь в виду, что для добавления векторов полигональным методом важно не изменять свойства : векторы следует только перемещать.

Важно иметь в виду, что, когда речь заходит о возможности взять эту сумму, которая нас занимает, что нужно сделать, это прибегнуть к некоторым фундаментальным элементам в математике и алгебре. Мы имеем в виду оси координат X и Y. По сути, из них и их соответствующих сумм получается, как получить вышеупомянутый результирующий вектор.

Мы также говорим о результирующем векторе со ссылкой на тот, который в системе генерирует тот же эффект, что и векторы, составляющие его. Вектор, имеющий то же направление и величину, но противоположное направление, квалифицируется как уравновешивающий вектор.

Этот вышеупомянутый уравновешивающий вектор, который также называется VE, как мы

III.1. Результирующий вектор

Электрическая ось и электрическая позиция сердца неразрывно связаны с понятием результирующего вектора возбуждения желудочков во фронтальной плоскости.

Результирующий вектор возбуждения желудочков представляет собой сумму трех моментных векторов возбуждения: межжелудочковой перегородки, верхушки и основания сердца. Этот вектор имеет определенную направленность в пространстве, которое мы интерпретируем в трех плоскостях: фронтальной, горизонтальной и сагиттальной. В каждой из них результирующий вектор имеет свою проекцию.

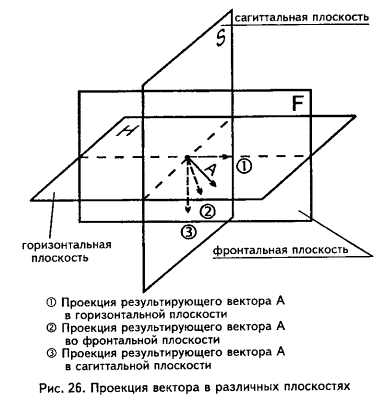
III.2. Электрическая ось сердца

Электрической осью сердца называется проекция результирующего вектора возбуждения желудочков во фронтальной плоскости.

Электрическая ось сердца может отклоняться от своего нормального положения либо влево, либо вправо.

Точное отклонение электрической оси сердца определяют по углу альфа (α).

III.3. Угол α

Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол α.

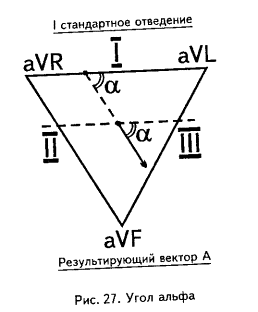
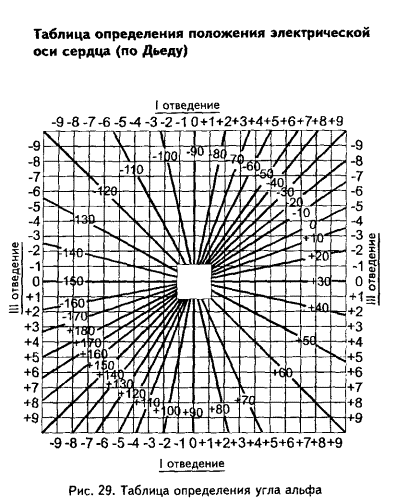
Величину угла α находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q+R+S) в T и III стандартных отведениях.

Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (-), поскольку находятся ниже изоэлектрической линии, а зубец R – знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

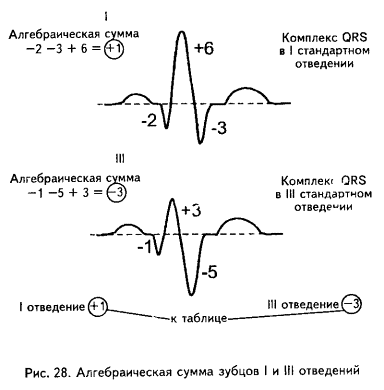
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла α. В нашем случае он равен мину с 70°.

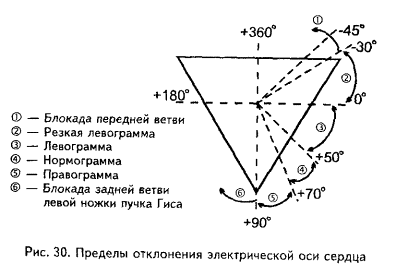
Если угол α находится в пределах 50-70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.

При отклонении электрической ось сердца вправо угол α будет определяться в пределах 70-90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол α будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.

Определяя угол α в пределах 50-0°, говорят об отклонении электрической оси сердца влево, или о левограмме.

Изменение угла α в пределах 0 – минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.

И, наконец, если значение угла α будет меньше минус 30° (например, минус 45°) – говорят о блокаде передней ветви левой ножки пучка Гиса.

Определение отклонения электрической оси сердца по углу α с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.

Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

III.4. Визуальное определение электрической оси сердца

В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса заменяют понятием «определяющий зубец» комплекса QRS, визуально сопоставляя по абсолютной величине зубцы R и S .

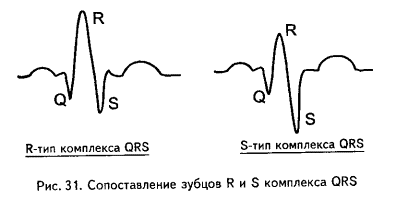
Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

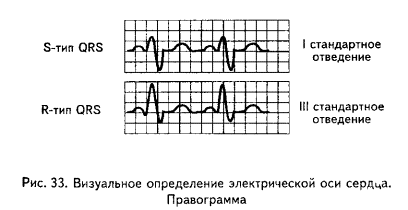
Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).

Схематично это условие записывается как RI-SIII.

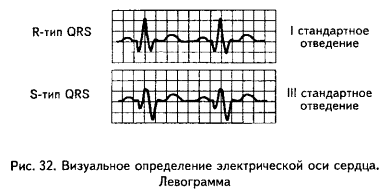
Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма).

Упрощенно это условие записывается как SI-RIII.

Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.

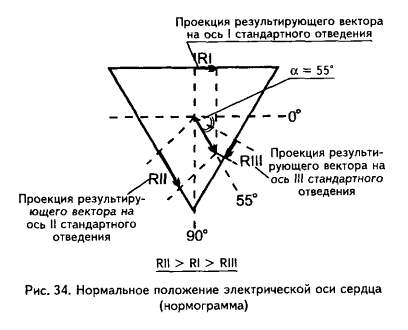
На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец R в I стандартном отведении превосходит зубец RIII.

При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена).

Краткая запись этого условия – RII>RI>RIII.

Модуль равнодействующей силы

В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.

Как найти модуль равнодействующей силы

Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.

Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.

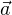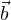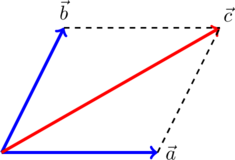
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и . Суммарный вектор есть вектор :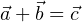

Если векторы 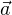и 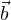не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор 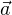заменен на равный ему вектор 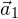, и :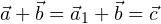

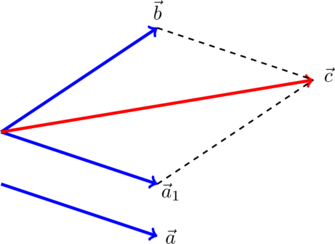
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы 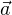и 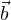. В сумме получается вектор :

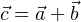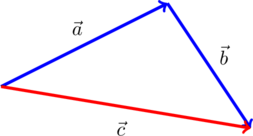
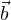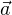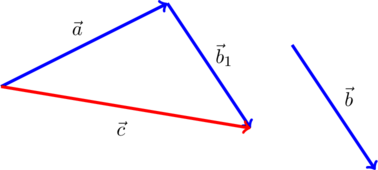
Если вектор отложен не от конца вектора , нужно заменить его равным и отложенным от конца вектора 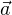, после чего воспользоваться правилом треугольника. Например, на рисунке вектор 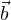заменен равным ему вектором 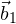, и :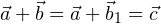

3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки 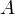отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки 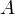в конец последнего отложенного вектора. На рисунке :

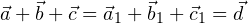Задача на нахождение модуля равнодействующей силы

Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.

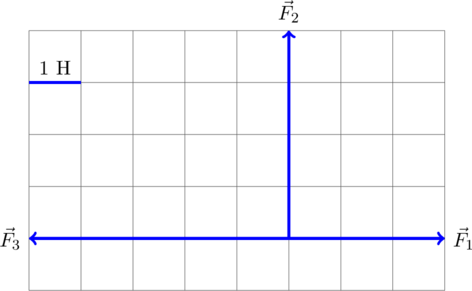
Задача 2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Чему равен модуль равнодействующей силы?

Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:

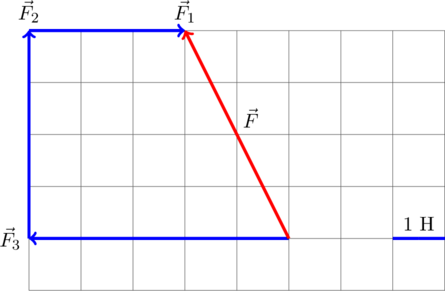
Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :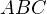

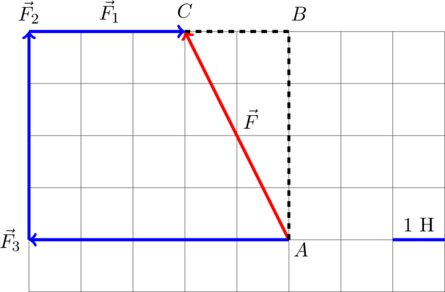
Требуется найти гипотенузу 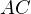этого треугольника. «По клеточкам» находим длину катетов: 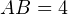Н, 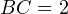Н. Тогда по теореме Пифагора для этого треугольника получаем: 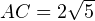Н. То есть искомый модуль равнодействующей сил раве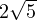н Н.

Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!

Репетитор по физике на Юго-Западной
Сергей Валерьевич