Резонансный контур | Политех в Сети

Лабораторная работа № 4

Цель работы — изучить свойства параллельного и последовательного колебательных контуров, особенности их согласования с источниками сигналов, экспериментально и теоретически определить основные параметры.

Приборы и модули: электронный осциллограф, генератор сигналов высокочастотный универсальный лабораторный стенд, модули № 1,2,6.

Сведения из теории.

Одна из важнейших задач радиоэлектроники — осуществление частотной селекции избирательности;. т. е. из множества сигналов поступающих на вход радиоприемника. необходимо выбрать узкую полосу частот сигналов интересующей нас радиостанции. Эту задачу решают при помощи частотно-избирательных цепей, например, колебательных контуров.

Колебательным контуром называется электрическая цепь, составленная из катушки индуктивности L И конденсатора C .

Свободные колебания в идеальном контуре.

Идеальный контур — цепь, состоящая из идеального конденсатора и идеальной катушки индуктивности (сопротивление потерь R=0). Если однократно зарядить конденсатор С (рис.1) до напряжения Um, то электрическая энергия, накопленная конденсатором:

За счет разряда конденсатора через индуктивность L в контуре возникает периодический колебательный процесс, при котором электрическая энергия конденсатора преобразуется в магнитную энергию катушки индуктивности и наоборот. Такие колебания называются свободными. В идеальном контуре они незатухающие (рис.2). Магнитная энергия, накопленная катушкой индуктивности

L, равна:

где – Im амплитуда тока в контуре.

Частоту свободных колебаний ω0 можно найти из равенства энергии:

Учитывая, что Um=ω0LIm, находим:

Период свободных колебаний, как известно:

Из равенства энергий найдем волновое сопротивление контура:

На резонансной частоте реактивные сопротивления конденсатора и индуктивности равны по абсолютной величине, т.е.|XL|=|XC| и:

Подставляя в последнее выражение значение:

получим:

Таким образом, на резонансной частоте сопротивления реактивных элементов равны волновому сопротивлению контура.

Свободные колебания в реальном контуре.

В реальном контуре сопротивление потерь. Сопротивление потерь контура включает омическое сопротивление провода катушки индуктивности, сопротиление потерь в диэлектрике конденсатора и потери, связанные с излучением контуром электромагнитной энергии в окружающее пространство. Из-за уменьшения запасенной в контуре энергии колебания в контуре носят затухающий характер. Физические процессы тогда описываются дифференциальным уравнением:

Решение этого уравнения дает для тока следующее выражение:

Где: — коэффициент затухания;

— частота свободных колебании в реальном контуре, характер затухающих колебаний в реальном контуре показан на рис.3.

При α=0 колебания незатухающие, что соответствует идеальному контуру без потерь. При этом частота свободных колебаний:

а период:

В реальном контуре при T→∞ Im→∞.

Период колебаний:

Если то T→∞ и колебательный процесс невозможен, т. к. имеет место апериодический разряд конденсатора через L и R (рис.4).

Колебательный процесс возможен только при:

Отсюда:

У радиотехнических контуров всегда ρ>>R. Поэтому:

По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается величиной его добротности Q=ρ/R. Для радиотехнических контуров величина

Q составляет — 10 — 100.

Величина обратная добротности, называется затуханием контура:

Ввынужденные колебания в последовательном контуре.

Эти колебания возникают под действием внешнего (вынуждающего) генератора (рис. 5). Пусть генератор является идеальным генератором гармонического напряжения.

Комплексная амплитуда тока в контуре:

Где: Ė — комплексная амплитуда напряжения внешнего генератора.

Входное сопротивление контура:

Где: R — активная составляющая входного сопротивления, характеризующая потери в контуре:

— реактивная составляющая входного сопротивления.

Модуль входного сопротивления:

Если изменять частоту внешнего генератора, то в зависимости от его частоты возможны три случая:

1. XL>XC — при этом носит XВх индуктивный характер;

2. XL<XC — при этом XВх носит емкостный характер;

3. XL=XC — при этом XВх=0 входное сопротивление контура будет чисто активным и равно R этот случай соответствует резонансу.

Векторные диаграммы для тока и напряжений при резонанса в последовательном контуре показаны на рис.6.

При резонансе:

Отсюда:

Отношение напряжений на реактивных элементах при резонансе и э. д.с. внешнего генератора:

Таким образом, при резонансе в последовательном контуре напряжения на реактивны элементах равны по абсолютной величине и в

Q раз превышаю т э. д.с. внешнего генератора. Это и есть резонанс напряжений. Для пояснения физического смысла добротности контура запишем:

Отсюда добротность контура равна умноженному на 2π отношению энергии, запасенной в контуре, к энергии, рассеиваемой в контуре за один период.

Входное сопротивление последовательного контура при резонансе мало и равно по величине сопротивлению потерь контура. Это необходимо учитывать при подключении внешнего генератора к контуру, для согласования генератора с контуром необходимо, чтобы внутреннее сопротивление генератора было мало. т. е. необходим генератор напряжения.

Амплитудно-частотная характеристика (АЧХ) последовательного контура

Зависимость тока в контуре или напряжения на реактивных элементах от частоты внешнего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой последовательного контура.

Для сравнения различных контуров резонансные кривые строят в относительном масштабе (рис.8)

В соответствии с определением выражение для АЧХ в относительном масштабе запишется:

Где: — относительная расстройка;

— обобщенная расстройка.

Характер зависимости А(ξ) говорит о том. что колебательный контур обладает свойством избирательности (селективности).

Полоса пропускания контура 2Δω0,7 оценивается па уменьшению тока в контуре или напряжения на реактивных элементах в √2 раз по сравнению с резонансным значением:

Отсюда добротность:

Где: 2ΔF0,7 — ширина полосы пропускания контура.

Параллельный колебательный контур

При параллельном соединении L, С и внешнего генератора тока получаем параллельный контур (рис.9). Физические процессы в параллельном контуре также связаны с периодическим превращением электрической энергии, накопленной конденсатором, в магнитную энергию катушки индуктивности и наоборот.

Входное сопротивление параллельного контура:

Где: R1, R2 — сопротивления потерь в катушке индуктивности и конденсаторе соответственно.

Для высокодобротных контуров в области резонансной частоты:

Поэтому:

Где: R=R1+R2.

Таким образом, Żвх зависит от частоты и носит резонансный характер. При резонансе:

Токи в ветвях контура также зависят от частоты:

На резонансной частоте токи в ветвях контура становятся равными по абсолютной величине и сдвинуты по фазе на 180° (для идеального контура ), т. к. равными по абсолютной величине становятся сопротивления реактивных элементов:

Резонансная частота как раньше:

Векторная диаграмма для токов и напряжений в идеальном параллельном контуре при резонансе приведена на рис.10.

Ток в контуре при резонансе:

Отсюда ток в контуре при резонансе:

Таким образом, токи в ветвях параллельного контура при резонансе равны по абсолютной величине, противоположны по фазе и в Q Раз превышают ток внешнего генератора. Это и есть резонанс токов.

Амплитудно-частотная характеристика параллельного контура представляет собой зависимость от частоты отношения амплитуды напряжения на контуре при любой частоте, к амплитуде напряжения на контуре при резонансной частоте:

Если, контур питается от идеального генератора тока, то:

Т. е. по форме АЧХ параллельного контура не отличается от АЧХ последовательного контура.

Так как при резонансе входное сопротивление параллельного контура велико (десятки — сотни кОм), то для согласования контура с внешним генератором необходимо большое ротивление (порядка 1ОО кОм), т. е. необходимо осуществить режим генератора тока.

Добротность параллельного контура, также как и последовательного, можно найти по АЧХ в соответствии с выражением:

Другой способ определения добротности заключается в возбуждении колебании в контуре перепадами напряжения, вырабатываемыми генератором прямоугольных импульсов (рис.11).

Добротность находят через число периодов свободных колебаний контуре, соответствующее уменьшению начальной амплитуды колебаний в «E« . раз:

Задания и методические рекомендации

1. Определите основные параметры параллельного колебательного контура в режиме вынужденных колебаний.

1.1. Соберите схему, показанную на рис.12, из элементов модуля N2, используя для согласования с генератором резистор 1ОО кОм модуля N1.

1.2.

Контролируя напряжение на контуре с помощью осциллографа, найдите резонансную частоту (в диапазоне частот гене­ратора 100 — 5ОО кГц), вращая ручку » Частота » генератора. Уровень входного сигнала и чувствительность осциллографа подберите такими, чтобы изображение сигнала на выходе коненсатора занимало всю рабочую часть экрана по вертикали. Запишите значение резонансной частоты и соответствующее ей значение напряжение на контуре в таблицу 1. Не изменяя уровня сигнала на выходе генератора, найдите и запишите в таблицу частоты, при которых отношение амплитуды напряжения на контуре U и UРез Принимает значения, приведённые в таблице.

1.3. По данным таблицы постройте резонансную кривую.

1.4. Вычислите добротность контура по резонансной кривой. Рассчитайте значение волнового сопротивления ρ, индуктивность L, сопротивление потерь R, входное сопротивлуние при резонансе ZВх рез.

1. Определите основные параметры параллельного контура в режиме свободных колебаний. Для этого в схеме на рис.12 замените высокочастотный генератор генератором прямоугольных импульсов (модуль N6). Осциллограф используйте в режимевнешней синхронизации, синхронизируя его по фронту прямоугольного импульса. По осциллограмме затухающих колебаний в контуре определите частоту свободных колебаний и добротность контура.
2. Соберите схему с последовательным контуром в соответствии с рис.13. Для согласования контура с генератором используйте резистор 2 Ом.

Настройте генератор на резонансную частоту контура. Измерьте амплитуду напряжения на выходе контура и на выходе генератора при резонансе. Вычислите добротность контура.

Оформление результатов

Отчёт должен содержать принципиальные схемы, таблицы измерений, графики, расчётные формулы результаты вычислений и выводы.

Контрольные вопросы

1.Чему равна величина входного сопротивления реального
последовательного контура, состоящего из L, C и R?

2.Чему равна величина входного сопротивления реального параллельного контура?

3.Объясните назначение резисторов, включаемых между генератором и контурам в случае параллельного и последовательного контуров.

4.Какие методы определения добротности Вам известны?

5.Какую зависимость представляет АЧХ последовательного контура?

6.Какую зависимость представляет АЧХ параллельного контура?

Литература

1.Б. Н. Ушаков. Основы радиоэлектроники и радиотехнические устройства 1976.

2.М. К. Ефимчик, С. С. Шушкевич, Основы радиоэлектроники 1981.

3.А. А. Харкевич. Основы радиотехники 1963

Резонансный контур — это… Что такое Резонансный контур?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Примечания

См. также

Ссылки

Richardson LF (1922), Weather prediction by numerical process, Cambridge.

Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.

Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.

Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.

Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.

Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.

Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.

Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука

Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.: Наука — 232 с.

Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука

Wikimedia Foundation. 2010.

РЕЗОНАНС ТОКОВ в колебательном контуре

Резонанс токов, или параллельный резонанс, получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор включен вне контура (рис.1 а). Сам же колебательный контур, рассматриваемый отвлеченно от генератора, надо по-прежнему представлять себе как последовательную цепь из L и С. Не следует считать, что в схеме резонанса токов генератор и контур соединены между собой параллельно. Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор включен последовательно, как это и бывает всегда в замкнутой цепи.

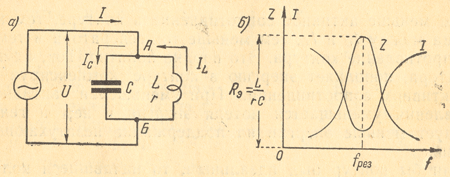
Рис.1 — Схема и резонансные кривые для резонанса токов

Условия получения резонанса токов такие же, как и для резонанса напряжений: f =fo или xL = хC. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным. Полное (эквивалентное) сопротивление контура для генератора при резонансе токов Rэ можно подсчитать по любой из следующих формул

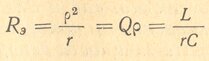
где L и С — в генри и фарадах, а Rэ, р и r — в омах.

Сопротивление Rэ, называемое резонансным сопротивлением, является чисто активным и поэтому при резонансе токов нет сдвига фаз между напряжением генератора и его током.

На (рис.1 б) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f.

В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости IL и IС можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи IL, и IC в действительности имеют сдвиг фаз несколько меньше 180° и ток IL немного( меньше Iс. Поэтому по первому закону Кирхгофа для точки разветвления можно написать

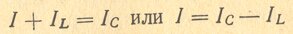
Чем меньше активное сопротивление в контуре, тем меньше разница между IC и IL, тем меньше ток генератора и тем больше сопротивление контура. Это вполне понятно. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний.
Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности.
Активная мощность, расходуемая генератором, может быть подсчитана как

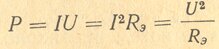
или как мощность потерь в активном сопротивлении контура

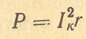
где I к — ток в контуре, равный IL или IC.

Для резонанса токов так же, как и для резонанса напряжений, характерно возникновение в контуре мощных колебаний при незначительной затрате мощности генератора.

На явление резонанса в параллельном контуре большое влияние оказывает внутреннее сопротивление Ri питающего генератора. Если это сопротивление мало, то напряжение на зажимах генератора, а следовательно, и на контуре незначительно отличается от эдс генератора и остается почти постоянным по амплитуде, несмотря на изменения тока при изменении частоты. Действительно, U = Е — IRi, но так как Ri величина малая, то потеря напряжения внутри генератора IRi также незначительна и U = Е.

Полное сопротивление цепи в этом случае приближенно равно только сопротивлению контура. При резонансе последнее сильно возрастает и ток генератора резко уменьшается. Кривая изменения тока на (рис.1 б) соответствует именно такому случаю.

Постоянство амплитуды напряжения на контуре также объясняет формула U = I * z. Для случая резонанса z велико, но I — величина малая, а если резонанса нет, то z уменьшается, но зато I увеличивается и произведение I*z остается примерно прежним.

Как видно, при малом Ri генератора параллельный контур не обладает резонансными свойствами в отношении напряжения: при резонансе напряжение на контуре почти не возрастает. Не будут заметно увеличиваться и токи IL И IС. Следовательно, при малом Ri генератора контур не имеет резонансных свойств и по отношению к токам в катушке и конденсаторе.

В радиотехнических схемах параллелыный контур обычно питается от генератора с большим внутренним сопротивлением, роль которого выполняет электронная лампа или полупроводниковый прибор. Если внутреннее сопротивление генератора значительно больше, чем сопротивление контура r, то параллельный контур приобретает резко выраженные резонансные свойства.

В этом случае полное сопротивление цепи приближенно равно одному Ri и почти неизменно при изменении частоты. Ток I, питающий контур, также почти постоянен по амплитуде:

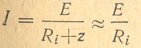
Но тогда напряжение на контуре U=I*z  при изменении частоты будет следовать за изменениями сопротивления контура z, т.е. при резонансе U резко увеличится. Соответственно возрастут токи IL и IC. Таким образом, при большом Ri генератора кривая изменения z (рис.1 б) будет в других масштабах приближенно показывать также изменение напряжения на контуре U и изменения токов IL и IC На (рис. 2) изображена подобная кривая вместе с графиком тока генератора, который в данном случае почти не меняется.

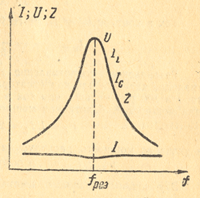
Рис.2 — Резонансные кривые параллельного контура при большом внутреннем сопротивлении генератора

Основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты.

2.9. Последовательный колебательный контур. Резонанс напряжений

Последовательным колебательным контуром называют такую цепь, в которой катушка и конденсатор соединены последовательно отно­сительно входных зажимов (рис. 2.14). В такой цепи можно наблюдать резонанс напряжений. При резонансе напряжений индуктивное и ем­костное сопротивления взаимно компенсируются и в результате этого реактивные сопротивление и мощность цепи равны нулю.

При резонансе напряжений, возни­кающем в цепи с последовательным соединением индуктивных и емкостных элементов, ток и напряжение цепи совпа­дают по фазе. В этом случае угол сдвига фаз между током и напряжением равен нулю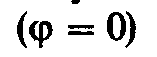и полное сопротивлениецепи равно ее активному сопротивле­нию. Если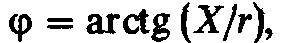то уголпри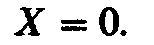

Следовательно, при резонансе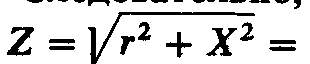

или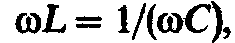откуда угловая частота при резонансе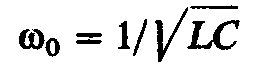и резонансная частота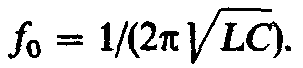

Таким образом, основным условием возникновения резонанса напря­жений в цепи является равенство реактивных сопротивлений 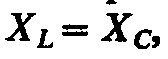так как в этом случае частота колебательного контура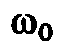равна частоте сети ω, питающей данную цепь.

Итак, индуктивное и емкостное сопротивления при резонансе равны, т. е.

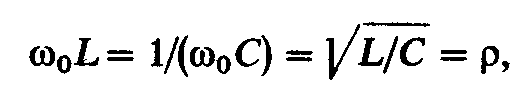(2.59)

так как

Величину ρ называют характеристическим сопротивлением контура.

Отношение напряжения на индуктивности или на емкости к напря­жению, приложенному к цепи при резонансе, называют добротностью контура или коэффициентом резонанса:

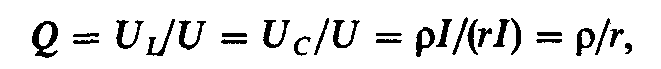(2.60)

откуда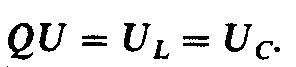

Коэффициент резонанса показывает во сколько раз напряжение на индуктивных или емкостных элементах при резонансе больше, чем напряжение, приложенное к цепи. Добротностью контура называют также отношение характеристического сопротивления контура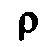к его активному сопротивлениюr. Так как характеристическое сопротивле­ние обычно составляет в среднем сотни Ом, а сопротивление r — несколько Ом, то добротность колебательных контуров, состоя­щих из индуктивных катушек и конденсаторов, находится в пределах 200-500.

Величину, обратную добротности, называют затуханием контура:

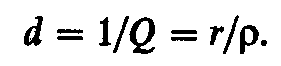(2.61)

Сопротивление r в радиотехнических контурах является, как правило, собственным сопротивлением катушек и конденсаторов. Его иногда называют сопротивлением потерь контура.

Понятие «затухание контура» связано с тем, что при отключении колебательного контура от источника питания, когда контур накоротко замкнут, колебательный процесс затухает тем быстрее, чем больше коэффициент d.

Рассмотрим схему рис. 2.14 без нагрузки (U_{C =} U_Cхх). Тогда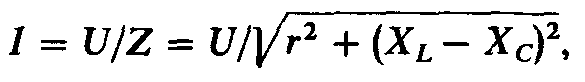

а ток при резонансе напряжений 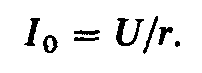(2.62)

Ток при резонансе напряжений значительно больше тока цепи в отсутствие резонанса, так как при резонансе его значение ограни­чено только сопротивлением r. При резонансе напряжение на индуктив­ности и емкости при больших по сравнению с r значениях 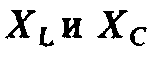может быть во много раз больше напряжения сети:

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

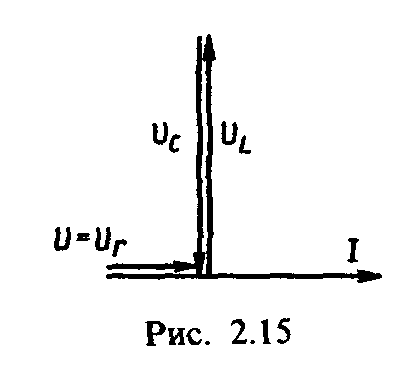
На рис. 2.15 представлена векторная диаграмма напряжений цепи рис. 2.14 при резонансе напряжений. Так как при резонансе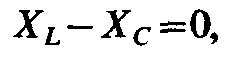то в этом случае и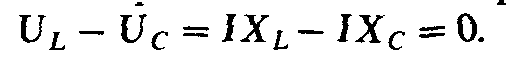

Рассмотрим энергетические процессы, наблюдаемые в данной цепи при резонансе напряжений. Для этого определим сумму мгновенных значений энергий магнитного и электрического полей цепи, т. е. Если принять при резонансе ток в контуре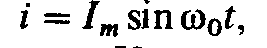то напряжение на емкости

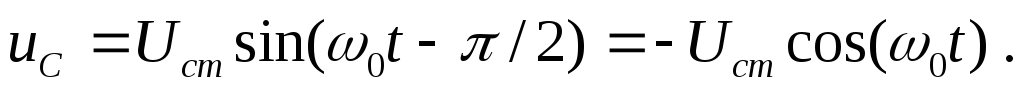
Тогда суммарная энергия

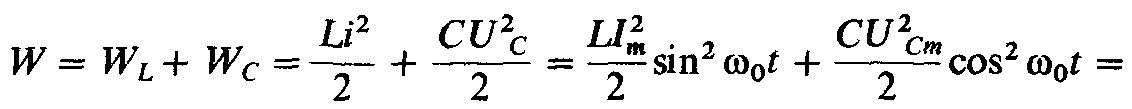
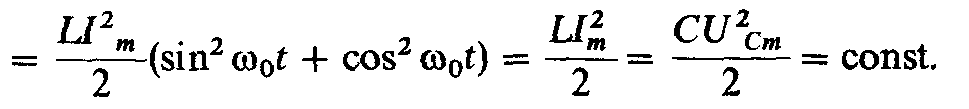(2.63)

Следовательно, при резонансе напряжений суммарная энергия магнитного и электрического полей остается постоянной, при этом непрерывно происходит перераспределение энергии магнитного и электрического полей, т. е. увеличение энергии магнитного поля сопро­вождается уменьшением энергии электрического поля и наоборот.

Таким образом, энергия, первоначально запасенная в контуре от источника (сети), колеблется при резонансе между индуктивностью и емкостью, причем без участия в этом процессе источника. Поэтому такой контур называют колебательным.

Итак, при резонансе на долю источника остается лишь покрытие расхода энергии в активном сопротивлении; следовательно, полная мощ­ность равна активной мощности

так как реактивная мощность при резонансе равна нулю:

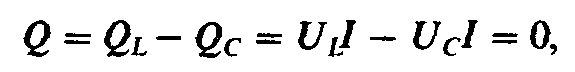где

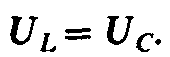
Коэффициент мощности при резонансе

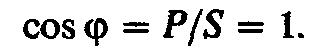
2.4. Резонансная кривая последовательного контура

Когда частота питающего генератора не равна собственной частоте контура, контур называют расстроенным.

Разность между частотой генератора и собственной частотой контура принято называть абсолютной расстройкой и обозначать :

.

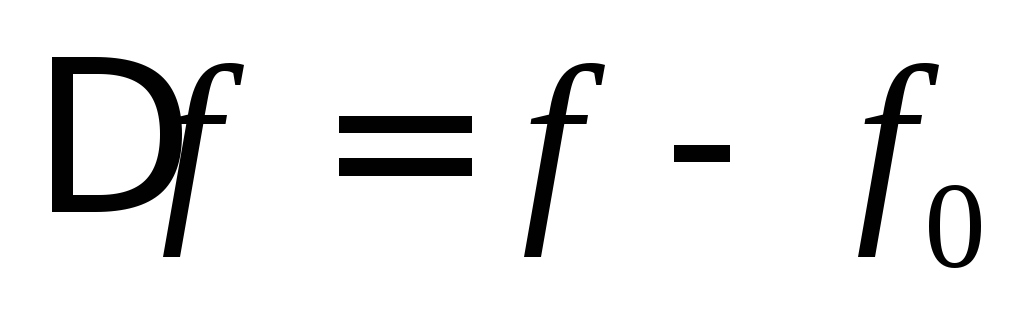Абсолютная расстройка выражается в единицах частоты. При резонансе частота генератора и собственная частота контура равны и абсолютная расстройка равна нулю.

Есличастота генератора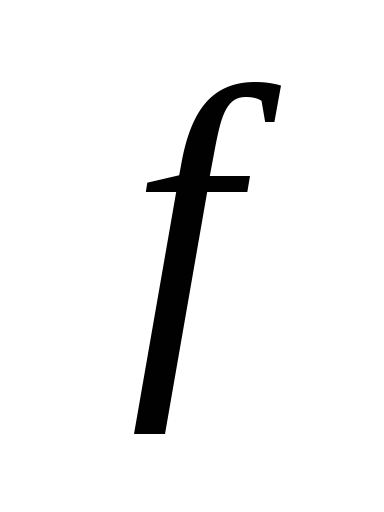больше собственной частоты 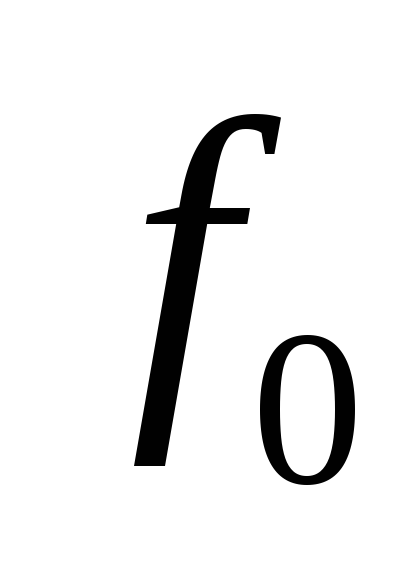контура, расстройка считается положительной (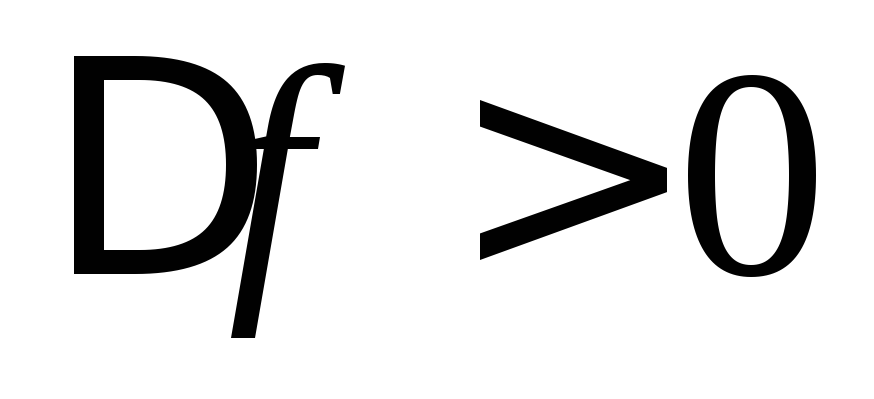). При частоте генератора меньше собственной частоты контура расстройка отрицательна ().

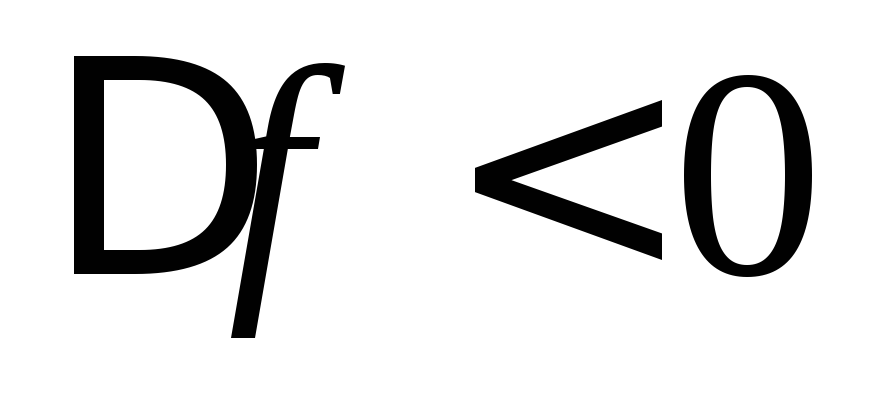Отношение абсолютной расстройки к собственной частоте контура 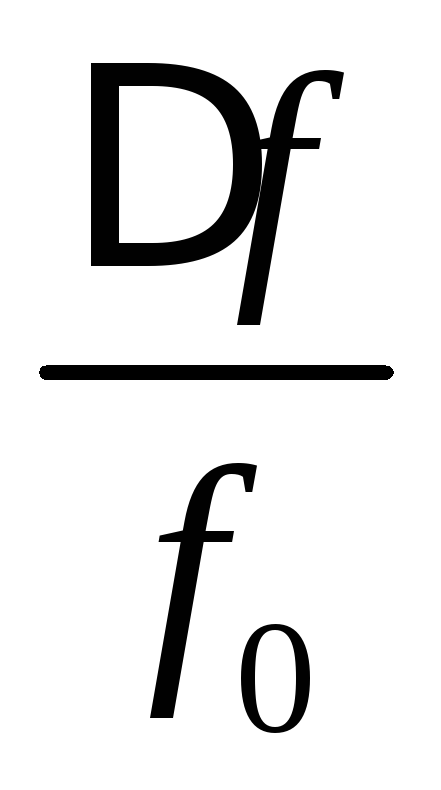называютотносительной расстройкой.

При резонансе относительная расстройка равна нулю:

.

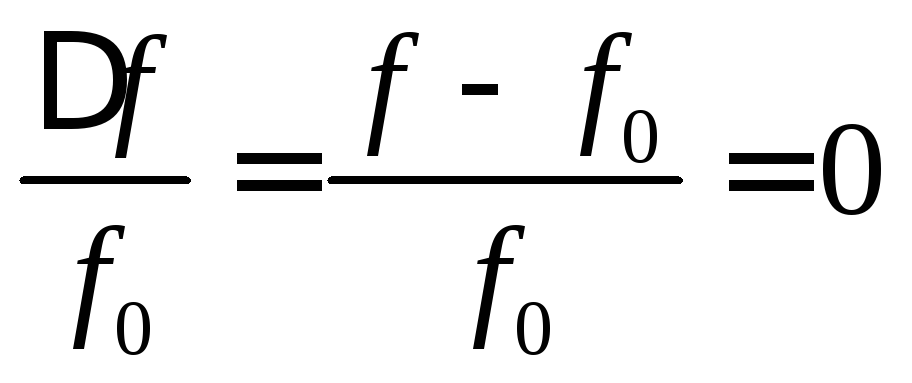Ток в контуре тем меньше, чем больше расстройка контура.

Иногда оказывается более удобной резонансная кривая, построенная в относительном масштабе. Для получения такой кривой вдоль вертикальной оси откладывается отношение тока в контурепри данной расстройке к току при резонансе 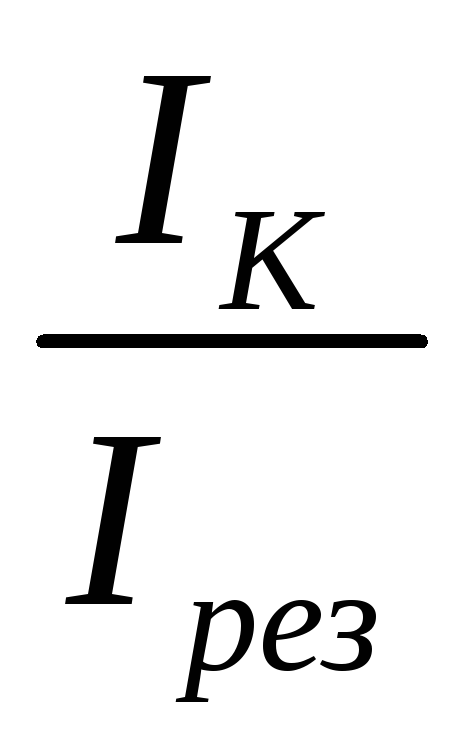, а вдоль горизонтальной оси – абсолютная или относительная расстройка (на рис.9 – абсолютная расстройка).Выведем уравнение резонансной кривой.

Ток в контуре при любой частоте равен

.

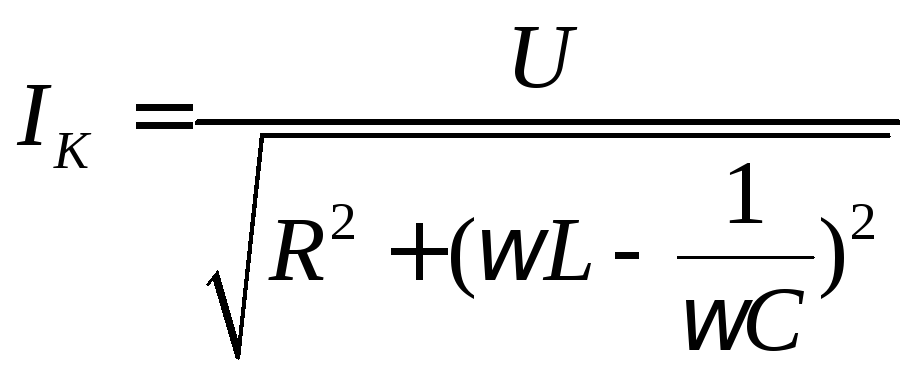Ток при резонансе

.

Отсюда получаем:

.

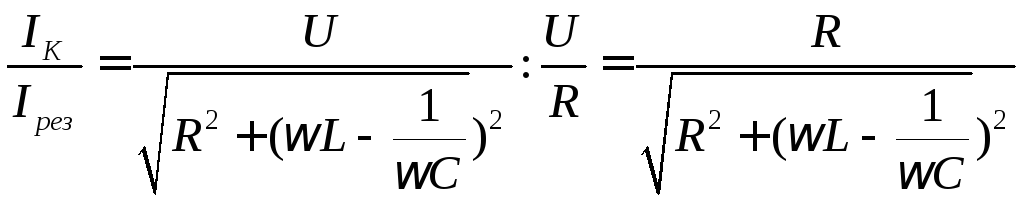Числитель и знаменатель полученной дроби сначала разделим на 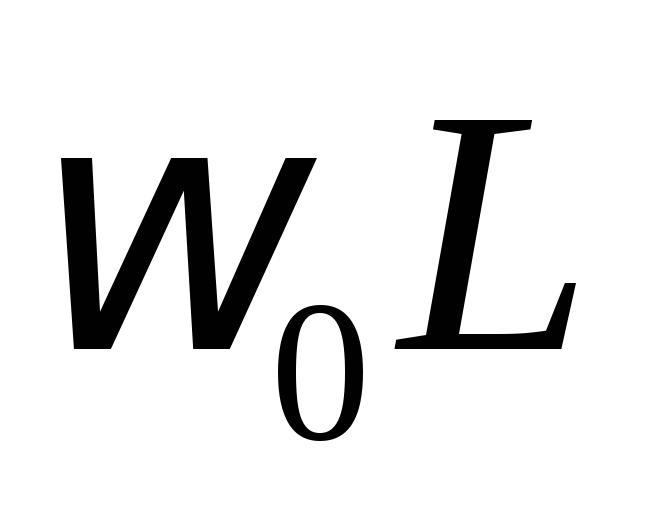, где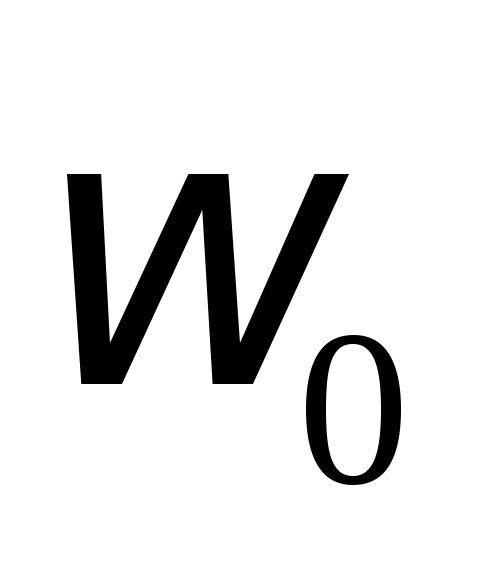– собственная частота контура, умножим на , и преобразуем выражение

.

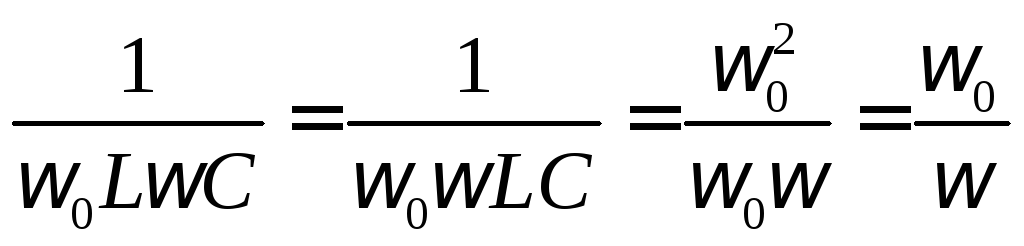Получаем следующее выражение:

.

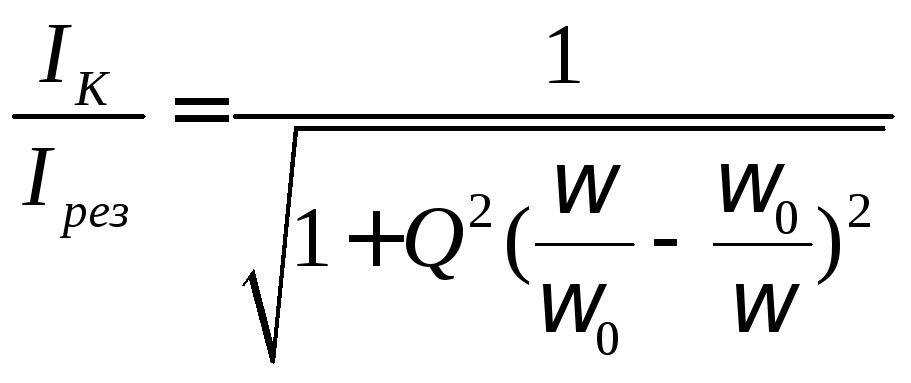Учитывая, что 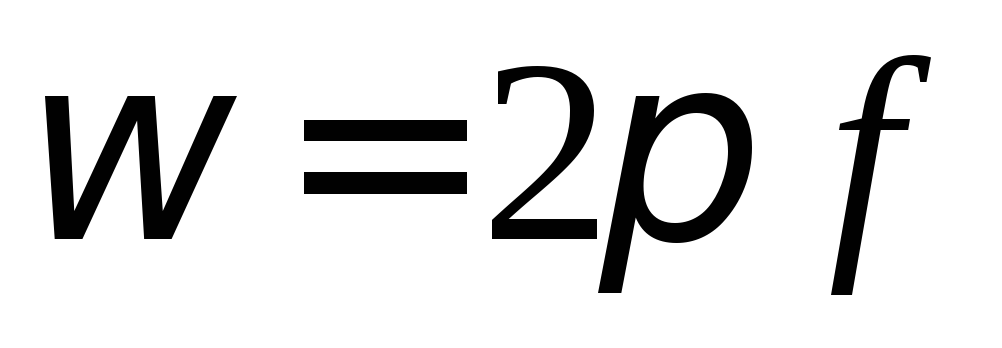, получим

.

Преобразуем выражение :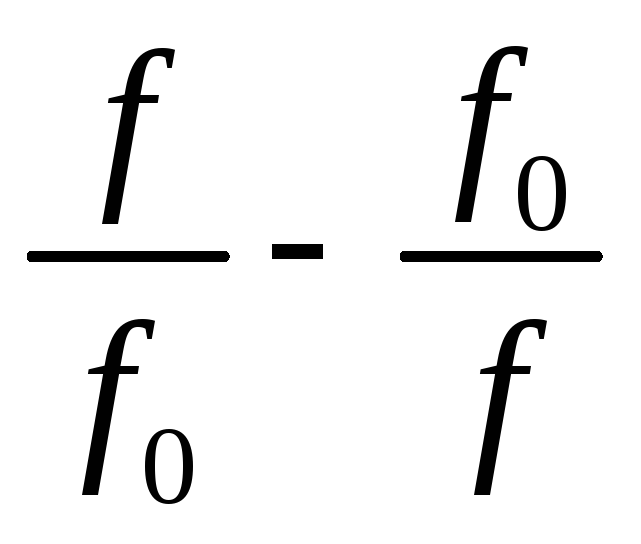

.

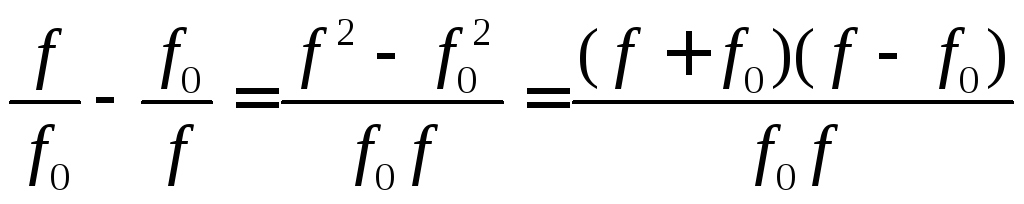Считая приближенно, что 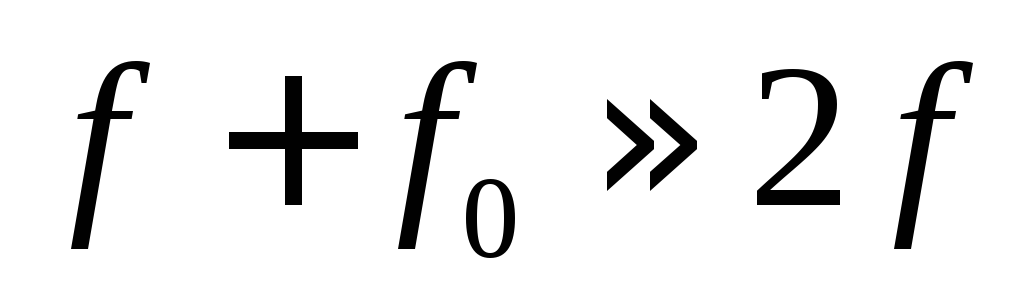и обозначив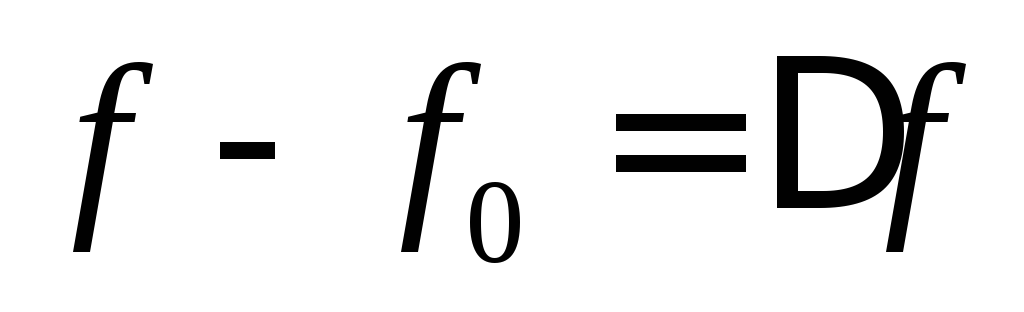(абсолютная расстройка), получим

.

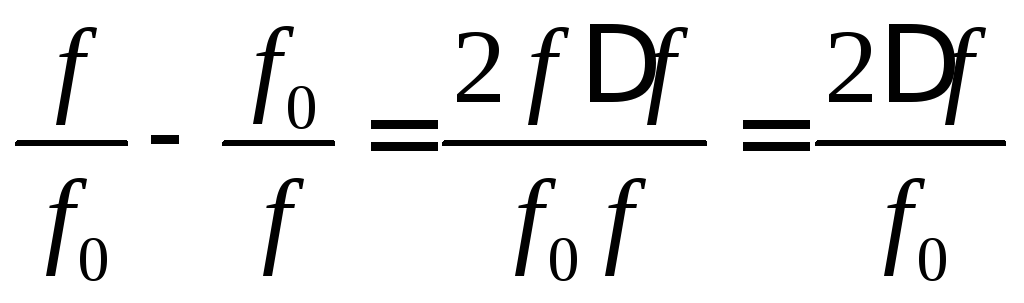Тогда

.

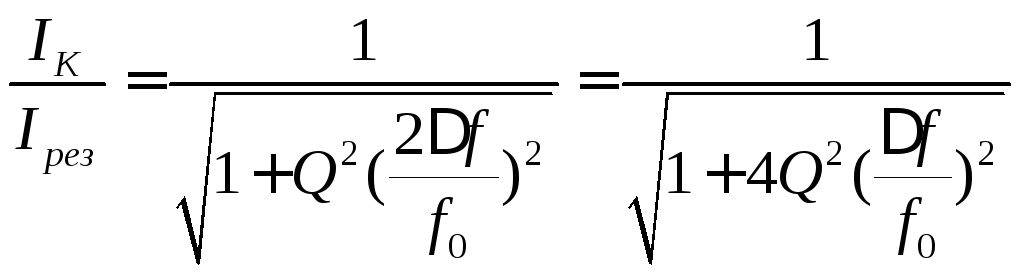Относительная расстройка

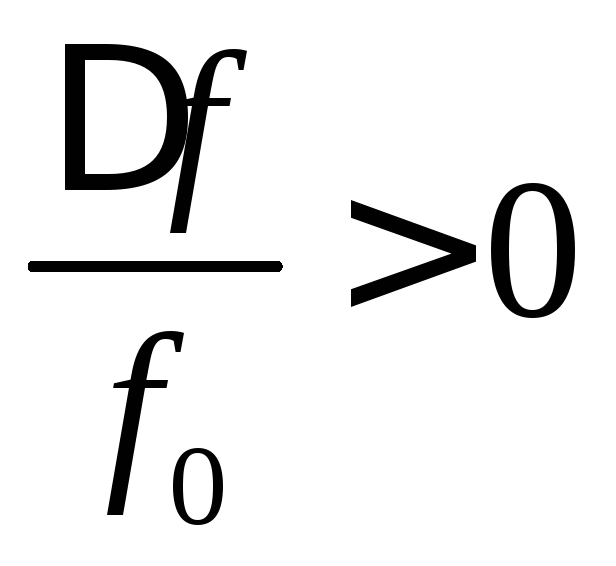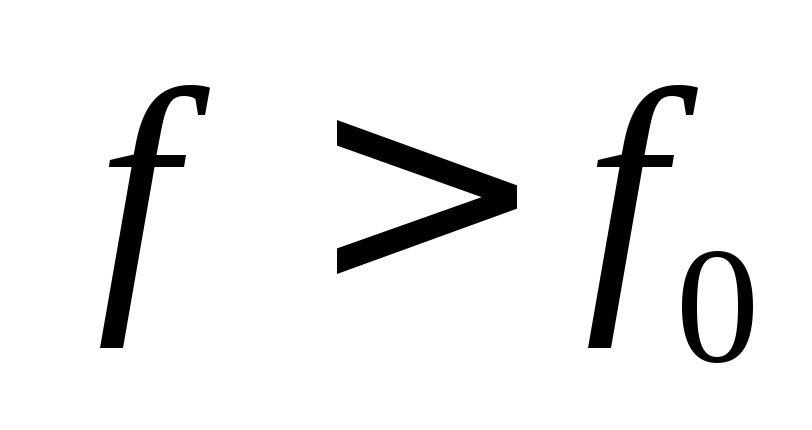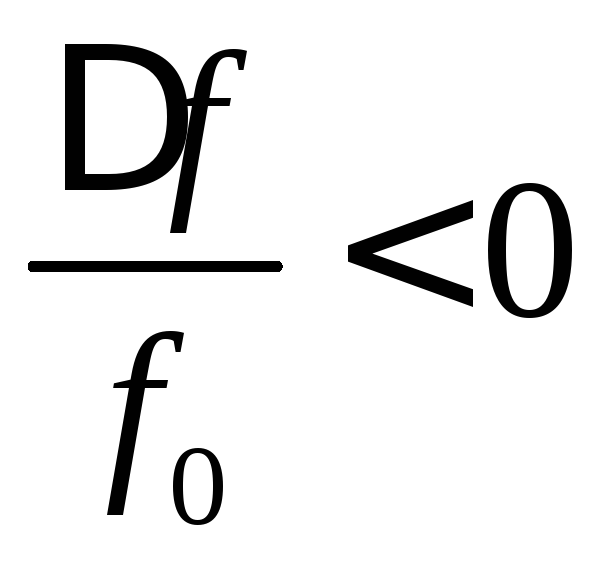если ,

,если .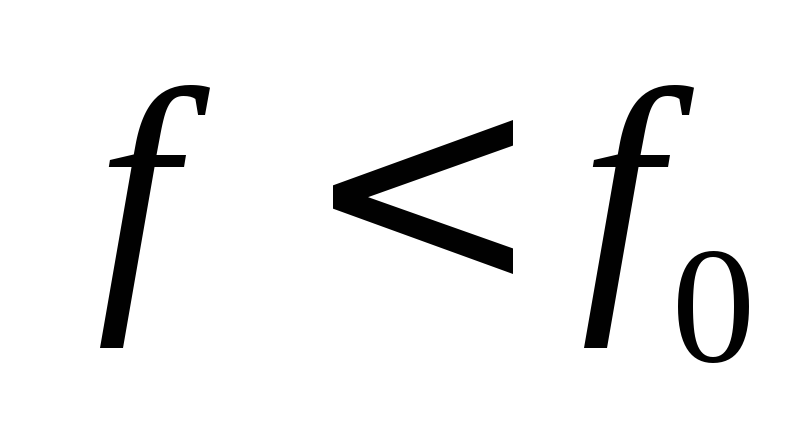

Введем обозначения:

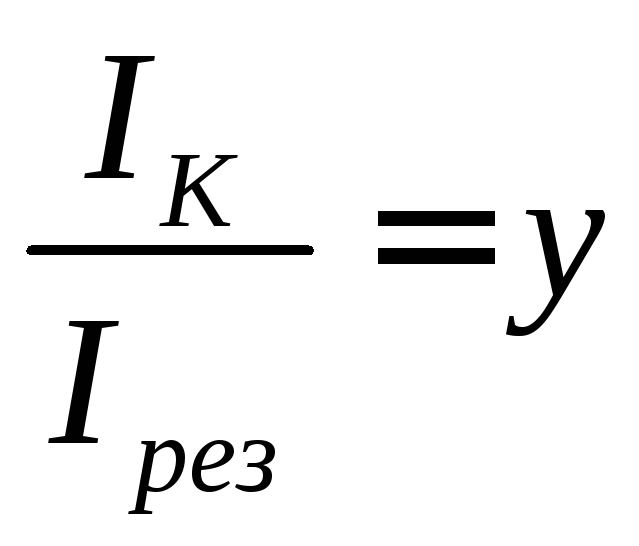и .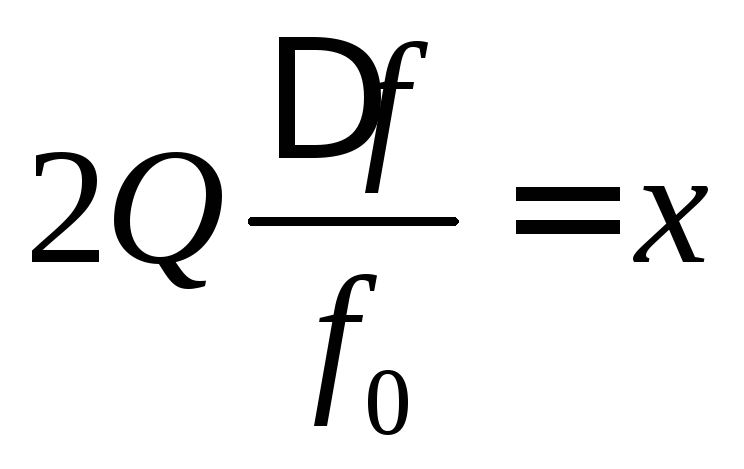

Тогда для уравнения резонансной кривой в относительном масштабе получим выражение

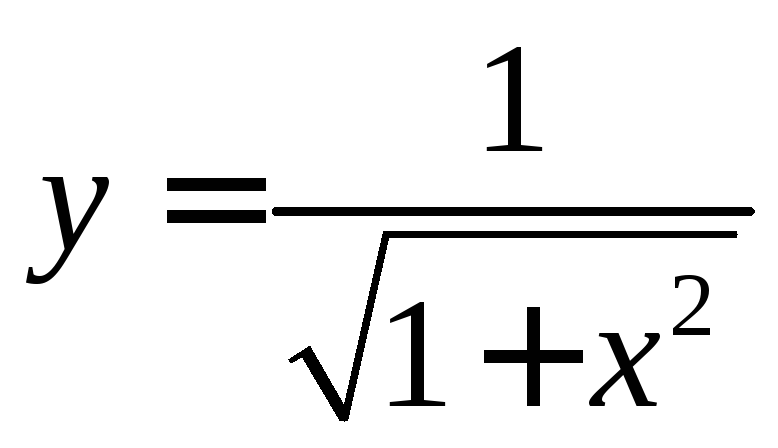
Уравнению такого вида соответствует кривая, изображенная на рис.9.

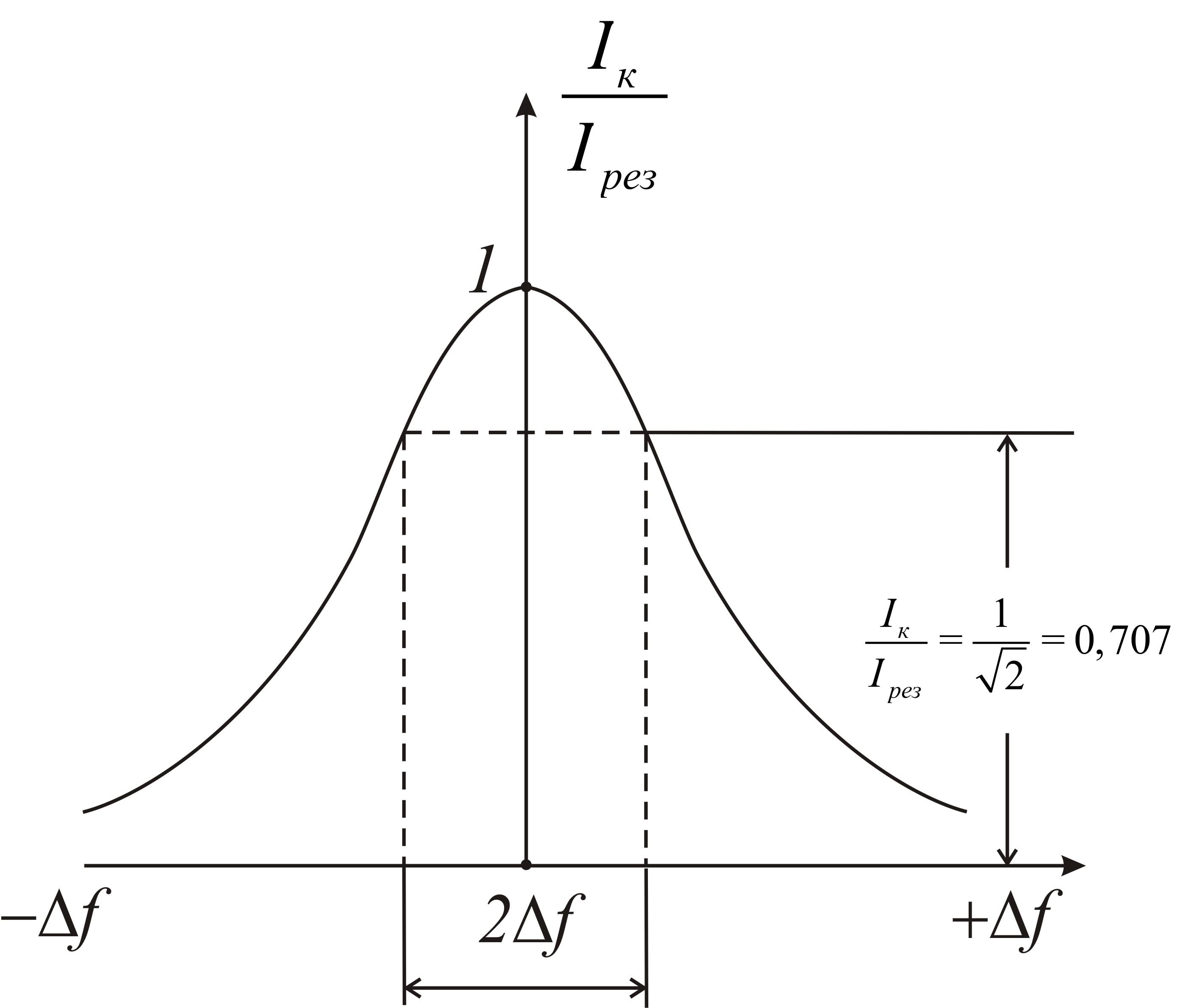
Рис.9. Резонансная кривая последовательного контура

Построение резонансных кривых в относительном масштабе дает возможность легко и удобно сравнивать между собою различные по качеству контуры, а также производить расчеты элементов радиотехнических схем

2.5. Полоса пропускания последовательного контура

Сопротивление последовательного контура вблизи резонанса резко изменяется в зависимости от частоты генератора; в соответствии с этим резко изменяется и ток в контуре. Контур по-разному ведет себя при различных значениях частоты питающего тока. Эти свойства могут быть оценены формой резонансной кривой или добротностью контура. Однако во многих случаях для такой оценки оказывается более удобным пользоваться понятием полосы пропускания контура, так как сигнал каждого передатчика представляет собой спектр частот и занимает некоторую полосу частот. Для неискаженной передачи и приема сигналов необходимо, чтобы все частоты, входящие в состав сигнала, в одинаковой степени излучались передающим устройством, а будучи приняты приемной антенной, в одинаковой степени усиливались приемником. Необходимо, чтобы колебательные контуры пропускали полосу частот, соответствующую спектру сигнала. Поэтому вопрос о полосе частот, пропускаемых контуром, имеет важное значение в радиотехнических устройствах.

Полосой пропускания контура называют полосу частот, в пределах которой ток в контуре уменьшается не более чем в 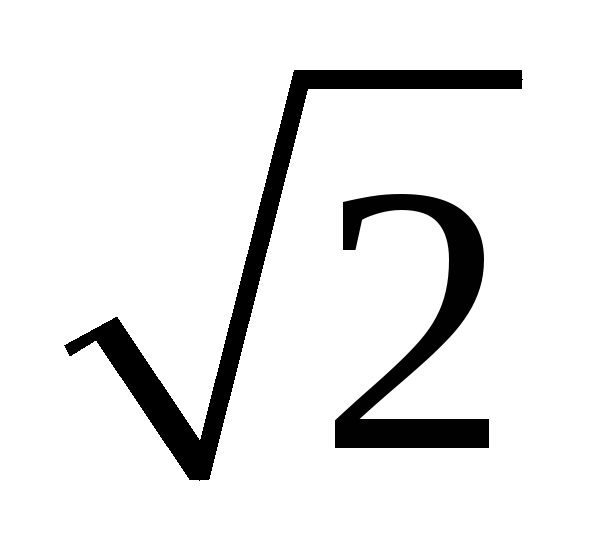раз по сравнению с током при резонансе. Иначе, полосой пропускания контура называют полосу частот, в пределах которой контурный ток составляет 0,7 или больше от тока при резонансе. На рис.10 изображена резонансная кривая последовательного контура. Полоса пропускания этого контура равна . Условно считается, что частоты в пределах от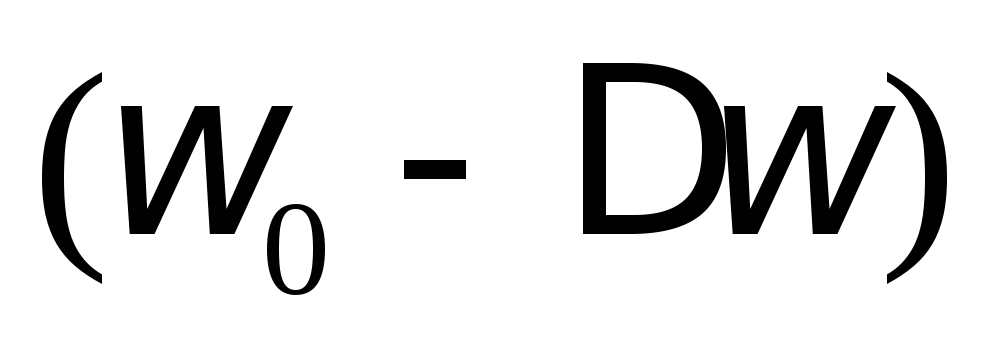 до 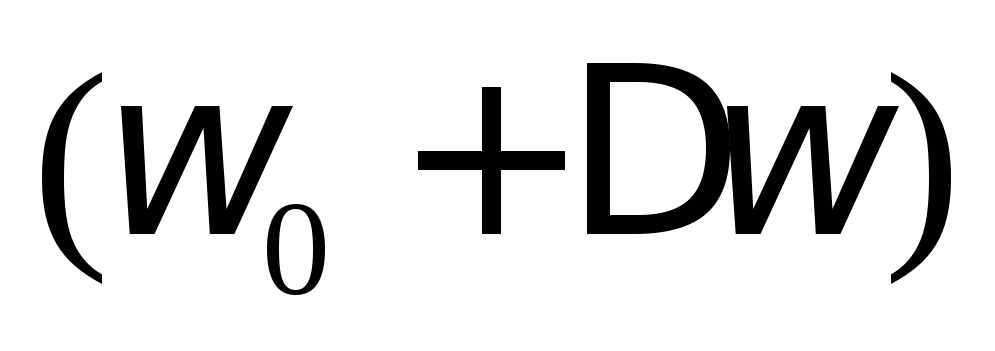контур пропускает, а частоты ниже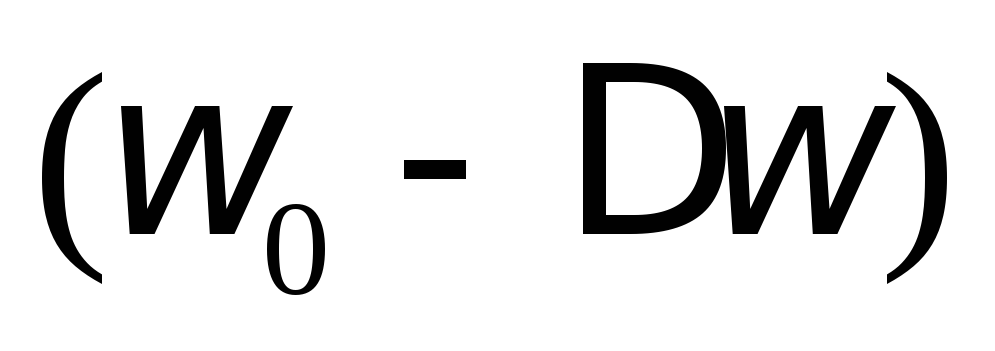и выше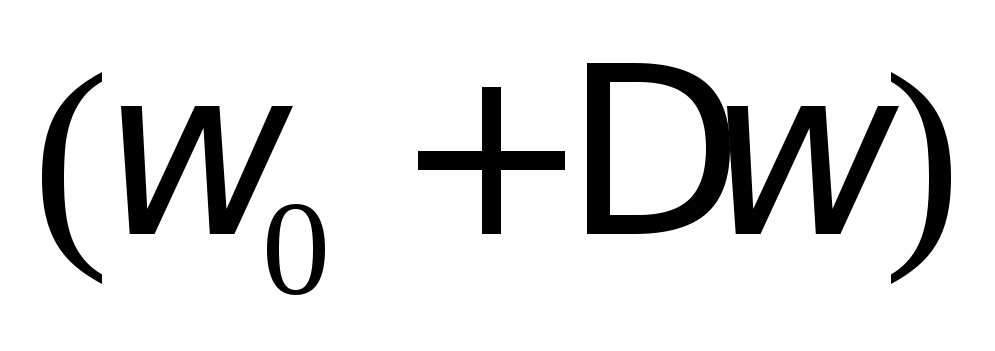не пропускает.

Ширина полосы пропускания прямо пропорциональна резонансной частоте и обратно пропорциональна добротности контура, или прямо пропорциональна затуханию при неизменной резонансной частоте.

Полоса пропускания контура зависит от его добротности: чем ниже добротность, тем «тупее» резонансная кривая и тем шире полоса пропускания контура.

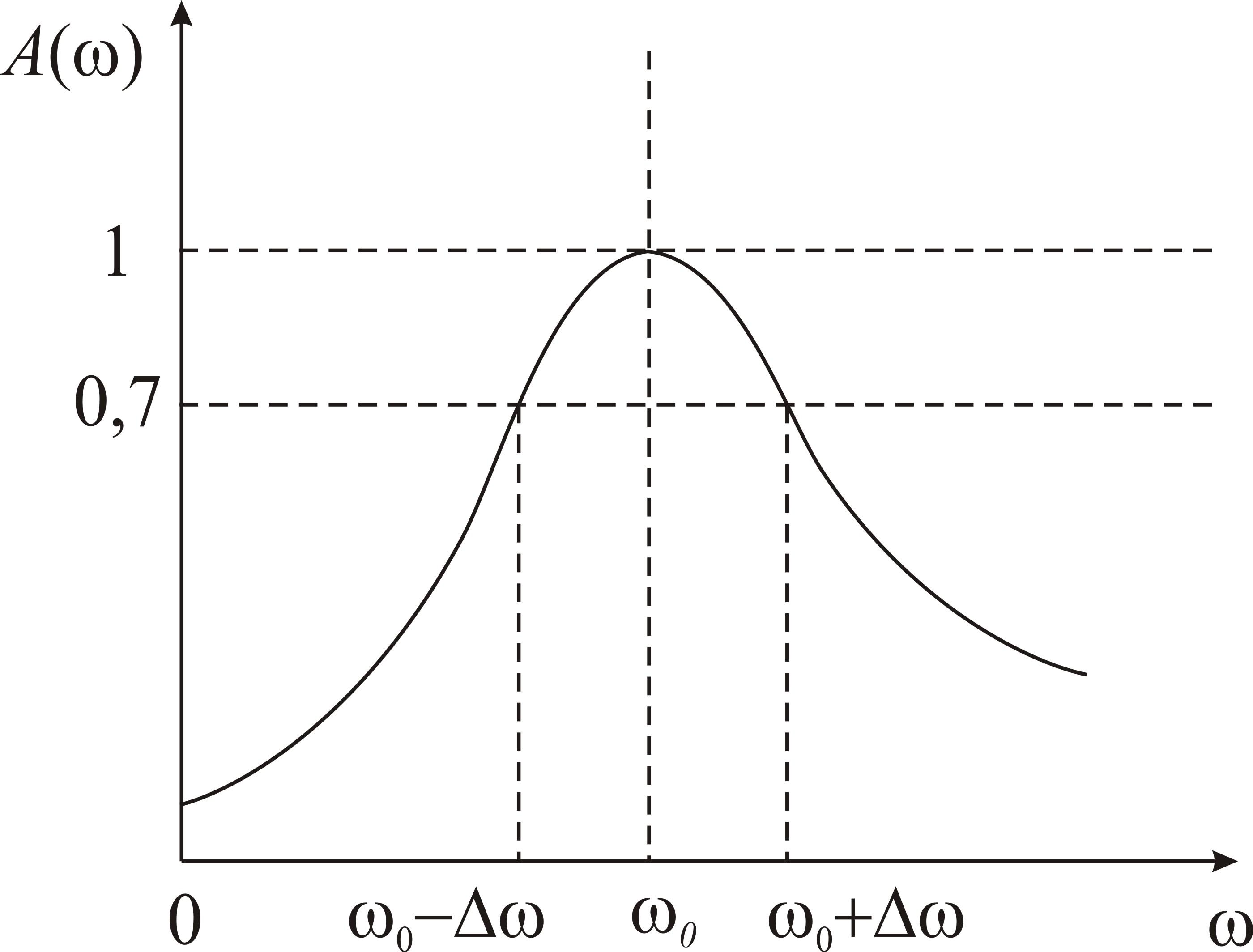
Рис.10. Полоса пропускания последовательного контура

Зависимость модуля тока от частоты, выражаемая обычно в виде отношения , носит названиерезонансной характеристики последовательного контура:

.

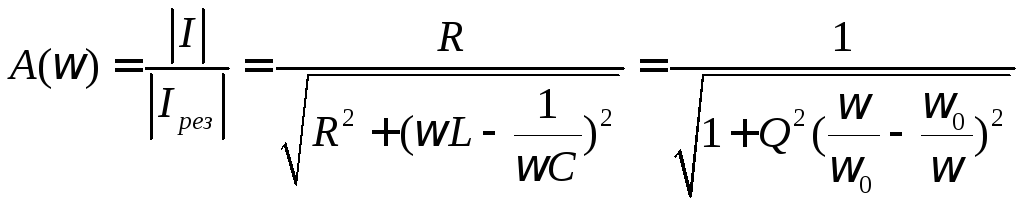На границах полосы пропускания контура 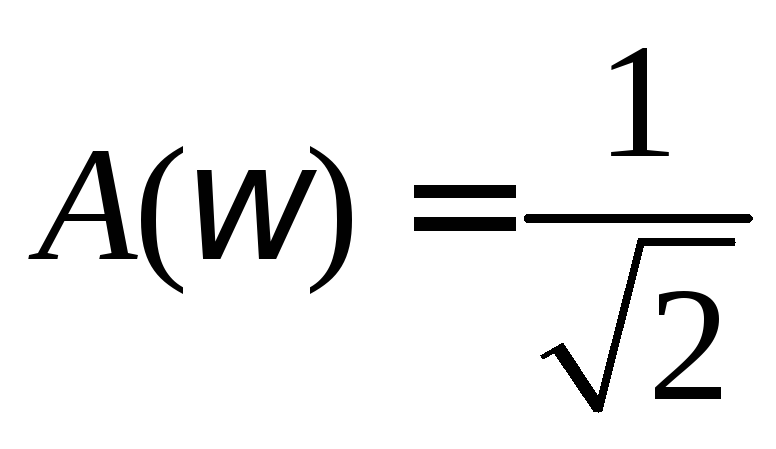, откуда следует простая формула для практического определения добротности: .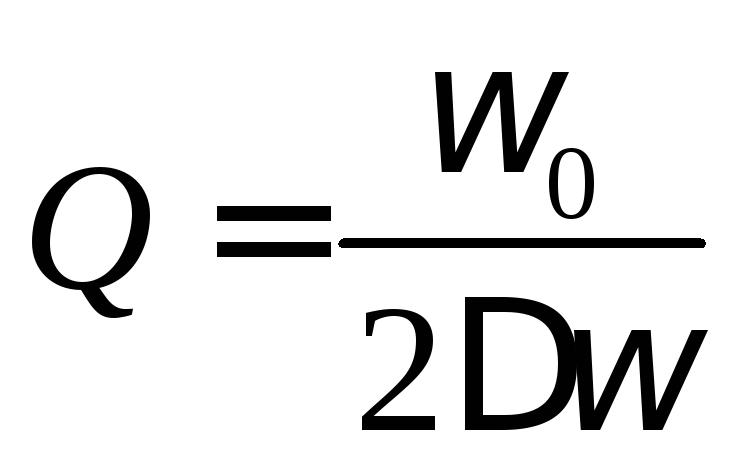

2.11. Параллельный колебательной контур. Резонанс токов

Лекция 8

Рассмотрим параллельный колебательный контур, простейшим видом которого является параллельное соединение индуктивной катушки и конденсатора (рис. 2.17, а).

Резонансом токов называют такой режим параллельного колеба­тельного контура, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением 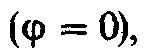а мощность, потребляемая из сети, равна активной мощности контура. Реактивная мощность при резонансе из сети не потребляется. Векторная диаграмма цепи при резонансе токов, представленная на рис. 2.17,6, выполнена согласно уравнению

Комплекс эквивалентной полной проводимости параллельного коле­бательного контура

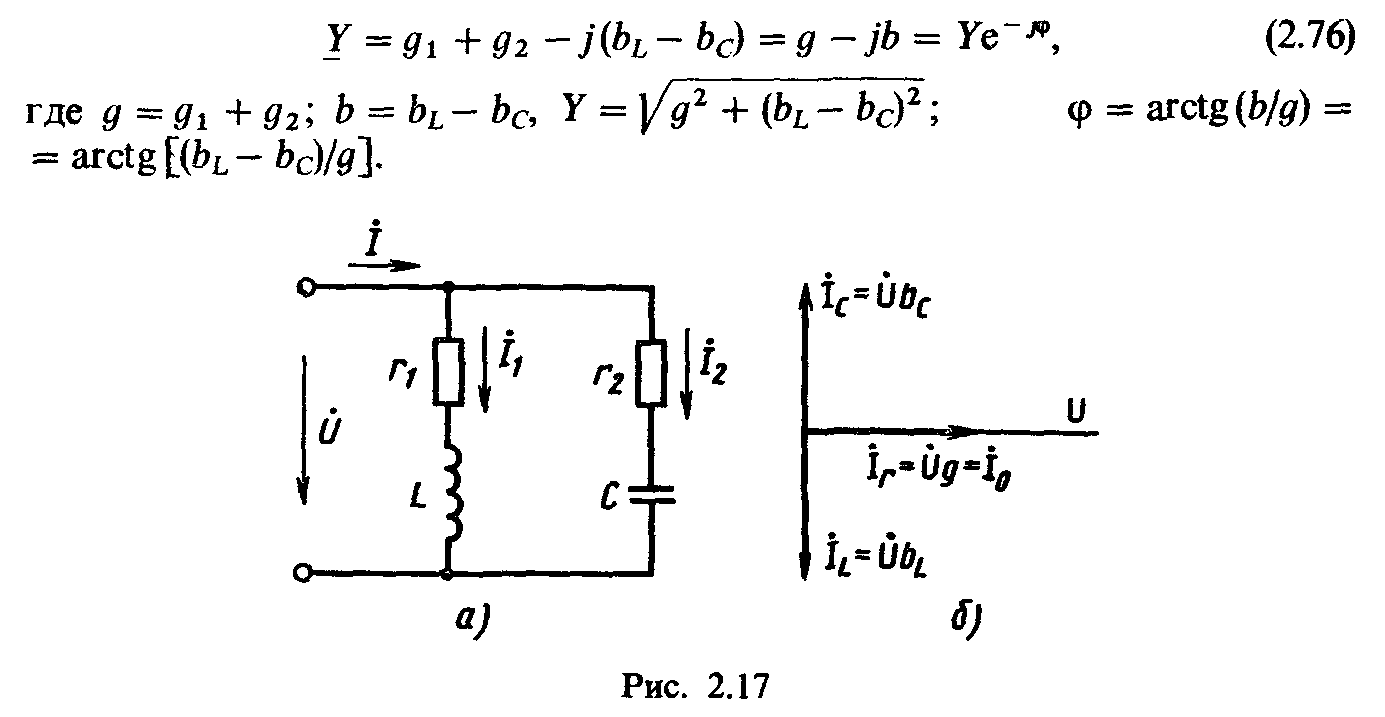
Так как при резонансе угол сдвига фаз между током I₀ и напря­жением U равен нулю, т. е. 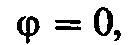то при резонансе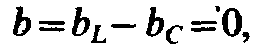или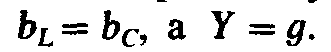Следовательно, ток при резонансе токов

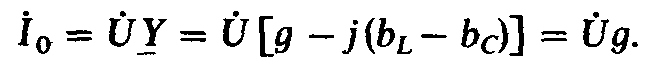(2.77)

Таким образом, резонанс токов наступает в цепи при взаимной компен­сации токов реактивных проводимостей т. е. при взаимной компенсации индуктивной и реактивной емкостной проводимостей.

При резонансе токов эквивалентная полная проводимость контура Y минимальная 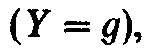т. е. входное сопротивление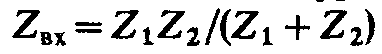достигает максимума, вследствие чего ток, идущий от сети, при резонансе токов будет минимален и равен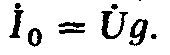

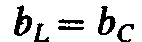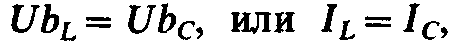При резонансе токов и, следовательно, равны между собой реактивные токикоторые находятся в этом случае в противофазе. При резонансе токов возможны ситуации, когда реактивные токи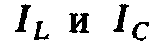намного превышают суммарный ток в цепи, вследствие чего резонанс при параллельном соединении назы­ваютрезонансом токов. Это возможно при услови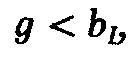и или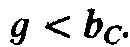

Отношение индуктивного 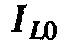или емкостного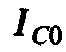токов при резонансе токов к суммарному току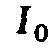называется добротностью параллельного колебательного контура:

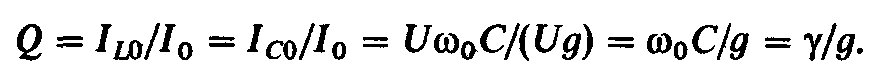(2.78)

Затухание в параллельном контуре, как и в последовательном контуре, есть величина, обратная добротности: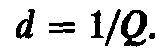

Выразивчерез параметры цепи и частоту, определим резонансную частоту контура:

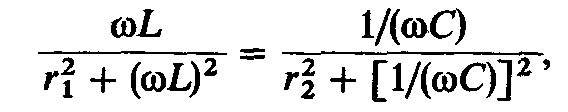
откуда найдем значение для резонансной угловой частоты:

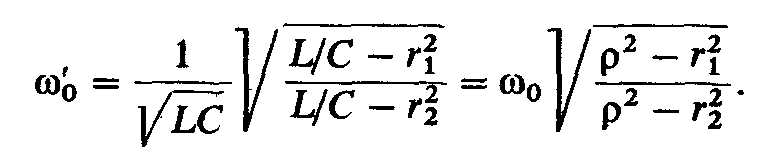(2.79)

В идеальном случае, например в радиотехнических устройствах, где применяют контуры с малыми потерями, когда практически 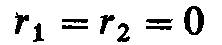(или они очень малы по сравнению с ρ), резонансную частоту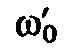можно определить, как и при резонансе в последовательном контуре, по формуле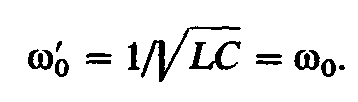

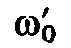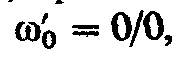Из формулы (2.79) видно, что резонанс токов возможен в цепи, если сопротивления r₁ и r₂ оба больше или оба меньше ρ, ибо при невыполнении этого условия частотаокажется мнимой и, следовательно, в этом случае не существует частоты, при которой был бы резонанс. Прирезонансная частотарезонанс токов может наблюдаться при любой частоте, так как в этом случае эквивалентное сопротивление становится активным, не зависящим от частоты.

Так как при резонансе токов 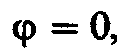а значит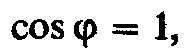то активная мощность Р равна полной мощности цепи, т. е.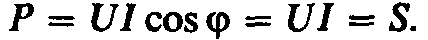Реактивная мощностьQ при резонансе токов равна нулю: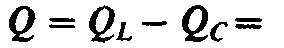

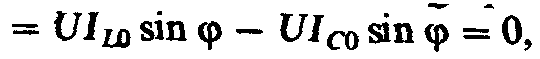так как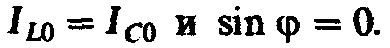

Таким образом, при резонансе токов цепь не потребляет из сети реактивной энергии. Энергетические процессы, наблюдаемые в парал­лельном колебательном контуре, в этом случае аналогичны процессам, которые протекают при резонансе напряжений. В колебательном конту­ре происходит непрерывный взаимный обмен энергиями между емкост­ным и индуктивным элементами цепи, а сеть лишь компенсирует энергию, теряемую в активных сопротивлениях контура. Если бы параллельный колебательный контур состоял только из L и С, то его входное сопро­тивление при резонансе токов было бы бесконечно большим и ток из сети не поступал бы в контур, т. е. в этом случае энергия, сообщенная контуру при включении, не расходовалась бы, а периодически перека­чивалась от магнитного к электрическому полю (и обратно), т. е. между индуктивным и емкостным элементами цепи, причем эти колебания продолжались бы неограниченное время.

46. Резонанс токов. Свойство параллельного контура на резонансной частоте.

Резонанс токов называется явление при котором общий ток в неразветвленной части цепи с параллельной части цепи с параллельным соединением L и C.

Условия возникновение:

1. Параллельная соединение индуктивности и емкости .

2. Равенство реактивных проводимостей параллельных ветвей Вl=Вс.

3. Минимальная величина активного сопротивления обеспечивающего возникновение свободных колебаний в контуре.

Свойство цепи при резонансе токов:

1. Контур оказывает току генератора макс. сопротивление , тем больше, чем меньше эквивалентное активное сопротивление контура.

2. Общий ток в неразветвленной части цепи минимальный. Этот ток значительно меньше тока в ветви с реактивным элементом и совпадает по фазе с направлением генератора питающего контур. Цепи имеет чисто активный характер.

3. Реактивные тои в параллельных ветвях равны и находятся в противофазе.

4. Как правило, активное сопротивление контура мало, меньше 2Zc, при этом ceo обмен энергией между электрическим и магнитными полями внутри контура.

5. От генератора поступает в контур энергия в небольшом количестве, которая пополняет потери энергии в контуре на активном сопротивлении и поддерживание колебания в контуре незатухающими.

F=1/2ПSqr 2С

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения,частота которого совпадает с собственной частотой контура.

Резонанс токов, или параллельный резонанс, получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор включен вне контура (рис.1 а). Сам же колебательный контур, рассматриваемый отвлеченно от генератора, надо по-прежнему представлять себе как последовательную цепь из L и С. Не следует считать, что в схеме резонанса токов генератор и контур соединены между собой параллельно. Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор

включен последовательно, как это и бывает всегда в замкнутой цепи.

47. Понятие о несинусоидальных напряжениях и токов. Причины их появления в электрических цепях.

1 Причины возникновения несинусоидальных токов

На практике зависимости ЭДС и токов от времени всегда в большей или меньшей степени отличны от синусоидальных. Например, в генераторах пере-менного тока (синхронных генераторах) из – за того, что кривая распределения магнитной индукции вдоль зазора между статором и ротором отличается от си-нусоидальной. Кроме того, в цепях, содержащих нелинейные элементы, даже при синусоидальных ЭДС источников возникают несинусоидальные токи и на-пряжения. К таким цепям можно отнести выпрямители. Графики мгновенных значений напряжения в схемах одно- и двухполупериодного выпрямителей изображены на рисунке 1.1. utTUmaxutTUmax

а) б)

Рисунок 1.1 – Графики напряжений в однополупериодном (а) и двухпо-лупериодном (б) выпрямителях

48. Разложение несинусоидального напряжения в форме тригонометрического ряда. Разложение периодических несинусоидальных кривых в тригонометрический ряд Фурье

Явления, происходящие в линейных цепях при периодических несинусоидальных напряжениях и токах, проще всего поддаются расчету и исследованию, если несинусоидальные кривые раскладывать в тригонометрический ряд Фурье. Из математики известно, что периодическая функция f(ωt), удовлетворяющая условиям Дирихле, т.е. имеющая на всяком конечном интервале времени конечное число разрывов только первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд Фурье

f(ωt)=A_o+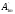sinωt+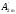sin2ωt+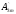sin3ωt+···+cosωt+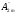cos2ωt+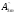cos3ωt+···=

A_o+.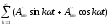

Здесь: A_o – постоянная составляющая или нулевая гармоника; 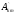— амплитуда синусной составляющей k-й гармоники; — амплитуда косинусной составляющей k-й гармоники. Они определяются по следующим формулам

Так как где как следует из векторной диаграммы (рис.6.2) 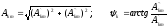, то получаем

.

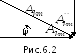
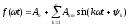Входящие в это выражение слагаемые называются гармониками. Различают четные (k – четное) и нечетные гармоники. Первую гармонику называют основной, а остальные – высшими. Последняя форма ряда Фурье удобна в том случае, когда требуется знать процентное содержание каждой гармоники. Эта же форма ряда Фурье применяется при расчете цепей несинусоидального тока.

Хотя теоретически ряд Фурье содержит бесконечно большое число слагаемых, однако он как правило быстро сходится. а сходящимся рядом можно выразить заданную функцию с любой степенью точности. На практике достаточно взять небольшое число гармоник (3-5) для получения точности расчетов в несколько процентов.
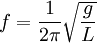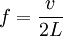
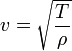
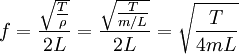