Резонанс напряжений — это… Что такое Резонанс напряжений?
Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Описание явления
Пусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f.
В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.
Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.
Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.
Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.)
Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.
Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.
Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.
В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.
Замечания
Колебательный контур, работающий в режиме резонанса напряжений, не является усилителем мощности. Повышенные напряжения, возникающие на его элементах, возникают за счет заряда конденсатора в первую четверть периода после включения и исчезают при отборе от контура большой мощности.
Явление резонанса напряжений необходимо учитывать при разработке аппаратуры. Повышенное напряжение может повредить не рассчитаные на него элементы.
Применение
При совпадении частоты генератора и собственных колебаний контура на катушке появляется напряжение, более высокое, чем на клеммах генератора. Это можно использовать в удвоителях напряжений, работающих на высокоомную нагрузку, или полосовых фильтрах, реагирующих на определенную частоту.
См. также
Резонанс токов
Колебательный контур
Литература
- Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 52.
- Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Ссылки
Резонанс напряжений — Википедия
Материал из Википедии — свободной энциклопедии
Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Описание явления
Резонанс напряжений, основанный на трансформаторе.- z^(jω0)=R+1jω0C+jω0L{\displaystyle {\hat {z}}(j\omega _{0})\;=R+{\frac {1}{j\omega _{0}C}}+j\omega _{0}L}
уменьшается, становится чисто активным и равным R{\displaystyle R} (сумма активного сопротивления катушки и соединительных проводов). В результате, согласно закону Ома: I=UR{\displaystyle I={\frac {U}{R}}}, ток в цепи достигает своего максимального значения.
Следовательно, напряжения как на катушке UL=IXL{\displaystyle U_{L}=IX_{L}}, так и на конденсаторе UC=IXC{\displaystyle U_{C}=IX_{C}} окажутся равными и будут максимально большой величины[1]. При малом активном сопротивлении цепи R{\displaystyle R} эти напряжения могут во много раз превысить общее напряжение U{\displaystyle U} на зажимах цепи, которое создаёт генератор. Это явление и называется в электротехнике резонансом напряжений.
Замечания
Колебательный контур, работающий в режиме резонанса напряжений, сам по себе не является усилителем мощности. Повышенные напряжения на его элементах возникают за счёт увеличения тока в цепи и следовательно потребляемой мощности от источника переменного напряжения.
Явление резонанса напряжений необходимо учитывать при разработке аппаратуры. Повышенное напряжение может повредить не рассчитанные на него элементы.
Если нужно повысить напряжение до безопасного уровня путем резонанса, то следует использовать комбинированный или параллельно-последовательный резонанс (описание в статье Резонанс токов).
Применение
При совпадении частоты генератора и собственных колебаний контура на катушке появляется напряжение, более высокое, чем на клеммах генератора. Это можно использовать для питания высокоомной нагрузки повышенным напряжением, или в полосовых фильтрах.
Если напряжение источника питания слишком маленькое, то можно его повысить если устроить последовательный резонанс на основе трансформатора. Если при этом полученное напряжение окажется больше расчетного для трансформатора, то первичная и вторичная обмотки соединяются последовательно чтобы трансформатор не вышел из строя.
См. также
Литература
- Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 52.
- Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Ссылки
Примечания
- ↑ Однако, точное решение задачи о максимуме напряжения на катушке и конденсаторе с учётом величины добротности Q{\displaystyle Q}, даёт несколько другой результат. Часто́ты ωC{\displaystyle \omega _{C}} и ωL{\displaystyle \omega _{L}}, на которых напряжение на катушке и конденсаторе достигает максимума, не равны между собой, и не совпадают с частотой резонанса ω0{\displaystyle \omega _{0}}: ωC=ω02Q2−12Q2{\displaystyle \omega _{C}=\omega _{0}{\sqrt {\frac {2Q^{2}-1}{2Q^{2}}}}}
ωL=ω0{\displaystyle \omega _{L}=\omega _{0}}2Q22Q2−1{\displaystyle {\sqrt {\frac {2Q^{2}}{2Q^{2}-1}}}}
Видно, что с увеличением добротности контура, часто́ты ωC{\displaystyle \omega _{C}} и ωL{\displaystyle \omega _{L}} сближаются с резонансной частотой ω0{\displaystyle \omega _{0}}.
Источник: Бакалов В. П., Дмитриков В. Ф., Крук Б. И. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова. – 3-е изд., перераб. и доп. – М.: Горячая линия – Телеком, 2007. – с.: ил. (недоступная ссылка) ISBN 5-256-01472-2, с.118
7. Резонанс напряжений и токов
Резонанс напряжений
Когда напряжения на индуктивности и емкости UL и UC , взаимно сдвинутые по фазе на 180 , равны по величине, то они полностью компенсируют друг друга (рис. 18, б). Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, а ток в цепи совпадает по фазе с напряжением. Этот случай называется резонансом напряжений.
Условием резонанса напряжений является равенство напряжений на индуктивности и емкости или равенство индуктивного и емкостного сопротивлений цепи:
xL = xC или ωL = 1/ωC (1.60)
При резонансе напряжений ток в цепи равен
I = U/√R + 0 = U/R (1.61)
то есть, цепь в данном случае имеет наименьшее возможное сопротивление, как будто в нее включено только активное сопротивление R. Ток в цепи при этом достигает максимального значения.
При резонансе напряжения на реактивных сопротивлениях xL и xC могут заметно превышать приложенное к цепи напряжение. Если мы возьмем отношение приложенного напряжения к напряжению на индуктивности (или емкости), то получим
U/ UL = IZ/I xL = Z/ xL или UL = U xL /R (1.62)
то есть напряжение на индуктивности будет больше приложенного напряжения в xL /R раз. Это значит, что при резонансе напряжений на отдельных участках цепи могут возникнуть напряжения, опасные для изоляции приборов, включенных в данную цепь. Векторная диаграмма для случая резонанса напряжений показана на рис. 18 б.
Если в последовательной цепи, содержащей активное сопротивление, индуктивность и емкость изменять величину одного из элементов цепи (например, емкости) при неизменном приложенном напряжении, то будут изменяться многие величины, характеризующих ток в цепи. Кривые, показывающие как меняются ток, напряжение, называются резонансными. Резонансные кривые при изменении емкости показаны на рисунке 20.
Резонанс токов
В отличие от последовательных цепей переменного тока, где ток, протекающий по всем элементам цепи одинаков, в параллельных цепях одинаковым будет напряжение, приложенное к параллельно включенным ветвям цепи.
Рассмотрим параллельное включение емкости и ветви, состоящей из индуктивности и активного сопротивления (рис. 21).
Обе ветви находятся под одним и тем же приложенным напряжением U. Построим векторную диаграмму для этой цепи. В качестве основного вектора выберем вектор приложенного напряжения U (рис. 22).
Затем найдем длину вектора I1 из соотношения
I1 = U/z1 = U/√R1 + xL (1.63)
и отложим этот вектор по отношению к вектору U под углом φ1 , который определяется по формуле
tg φ1 = xL/ R1 (1.64)
Полученный таким образом вектор тока I1 разложим на две составляющие: активную Iа1 = I1 cos φ1 и реактивную Ip1 = I1 sin φ1 (рис. 22).
Величину вектора тока I2 находим из соотношения
I2 = U/ xC = U/(1/ωC) = ωCU (1.65)
и откладываем этот вектор под углом 90 против часовой стрелки относительно вектора приложенного напряжения U.
Общий ток I равен геометрической сумме токов I1 и I2 или геометрической сумме реактивного тока Ip1 − I2 =IL − IC и активного тока Iа1. длина вектора I равна
I = √(IL − IC ) +( Iа1) (1.66)
Сдвиг по фазе между общим током I и приложенным напряжением U можно определить из соотношения
tgφ =(IL − IC )/ Iа1 (1.67)
Из векторной диаграммы видно, что длина и положение вектора общего тока зависят от соотношения между реактивными токами IL и IC. В частности, при IL > IC общий ток отстает по фазе от приложенного напряжения, при IL < IC ─ опережает его, а при IL = IC ─ совпадает с ним по фазе. Последний случай (IL = IC) называется резонансом токов. При резонансе токов общий ток равен активной составляющей тока в цепи, то есть происходящие в цепи процессы таковы, как будто в ней содержится только активное сопротивление (в этом случае φ = 0 и cos φ = 1). При резонансе общий ток в цепи принимает минимальное значение и становится чисто активным, тогда как реактивные токи в ветвях не равны нулю и противоположны по фазе.
Если в параллельной цепи, изображенной на рисунке 21, изменять величину емкости при неизменном приложенном напряжении, то будут изменяться многие величины, характеризующие ток в цепи. Кривые, показывающие как изменяются ток, напряжения на участках цепи и сдвиг по фазе между током и напряжением, называются резонансными.
Заключение:
Список литературы:
1
Резонанс напряжений
| Рассмотрим последовательный колебательный контур. |
Условие
резонанса: 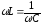 ,
при этом ток совпадает по фазе с
напряжением, угол сдвига фаз
,
при этом ток совпадает по фазе с
напряжением, угол сдвига фаз .
.
В этом случае значения противоположных по фазе напряжений на индуктивности и емкости будут равны, а вектор приложенного к цепи напряжения будет совпадать с вектором падения напряжения на активном сопротивлении. |
|
При резонансе в последовательной цепи напряжения на индуктивности и емкости могут значительно превышать приложенное напряжение. Это имеет место, когда R→ 0, а следовательно и полное сопротивлениеZ→ 0. В этом случае, при любом конечном значении приложенного напряжения, токI → ∞. Поэтому бесконечно велики могут быть напряжения на индуктивности и емкости.
Превышение
напряжения на реактивных элементах
цепи над напряжением на зажимах цепи
имеет место, если 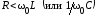
Так
как 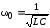 ,
то оба этих условия сводятся к одному:
,
то оба этих условия сводятся к одному: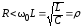 .
Эта величина имеет размерность
сопротивления и называетсяхарактеристическимиливолновым сопротивлениемконтура.
.
Эта величина имеет размерность
сопротивления и называетсяхарактеристическимиливолновым сопротивлениемконтура.
Кратность
перенапряжения на реактивном элементе,
находят из отношений:  .
.
Эта величина называется добротностьюрезонансного контура.
Величину,
обратную добротности 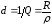 ,
называютзатуханием контура.
,
называютзатуханием контура.
Рассмотрим энергетические процессы в
последовательном контуре при резонансе.
Пусть имеем ток в контуре 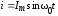 .
.
Напряжение на
емкости 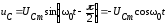 .
.
Но 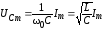 ,
тогда
,
тогда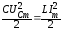
Суммарная электромагнитная энергия может быть записана в виде:
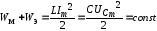 .
.
Таким образом, при резонансе сумма энергий магнитного и электрического полей с течением времени не изменяется.
Частотные характеристики последовательногоR-l-Cконтура.
Зависимости параметров цепи ( и т.д.) от частоты (
и т.д.) от частоты (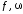 )
называютсячастотными характеристиками.
Примеры частотных характеристик
приведены на рисунках.
)
называютсячастотными характеристиками.
Примеры частотных характеристик
приведены на рисунках.
Резонансные характеристики
Действующее значение тока в последовательном резонансном контуре:
 .
.
Построим зависимости напряжений на элементах контура от частоты при поддержании на зажимах цепи постоянного напряжения.
Падение
напряжения на индуктивности: 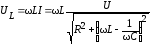 ;
;
на емкости: 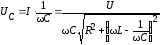 .
.
|
Имеет место
симметрия максимумов кривых напряжения
на реактивных элементах: 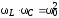 .
.
Представив 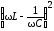 =
=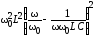 ,
после подстановки в действующее значение
для тока, получим:
,
после подстановки в действующее значение
для тока, получим:
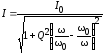 ,
где
,
где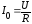 — действующий ток при резонансе.
— действующий ток при резонансе.
Из последнего выражения следует, что влияние параметров на вид резонансной кривой учитывается добротностью Q контура, причем, чем выше добротность резонансного контура, тем уже относительная ширина полосы пропускания контура. Это свойство резонансных колебательных контуров используется в практических целях, для выделения сигнала данной частоты из совокупности различных частот.
Параллельный колебательный контур. Резонанс токов.
Рассмотрим цепь, состоящую из параллельно включенных активного, индуктивного и емкостного сопротивлений.
| Для этой цепи комплексная проводимость:
Угол сдвига фаз:
Модуль проводимости: |
Из этого выражения видно, что взаимная
компенсация реактивных проводимостей
(угол 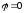 )
достигается при условии когда:
)
достигается при условии когда: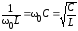 ,
притом, что
,
притом, что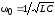 .
.
При резонансе реактивная проводимость цепи b= 0. Поэтому полная проводимостьy достигает минимального значения. Поэтому ток в общей ветви при неизменном напряжении так же минимален.
Векторная диаграмма при резонансе имеет вид:
Общий вектор тока является геометрической суммой векторов трех токов, два из которых ILиICнаходятся в противофазе. Следовательно, возможны случаи, когда токи в индуктивной катушке и конденсаторе могут значительно превосходить суммарный ток в цепи. Поэтому резонанс при параллельном соединении называютрезонансом токов. |
Энергетические процессыв параллельной цепи аналогичны соответствующим процессам в последовательной цепи, т.е. и в этом случае происходят колебания энергии в цепи. Энергия полей переходит из конденсатора в катушку и обратно. Источник энергии покрывает потери энергии в ветви с активной проводимостью.



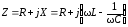 .
.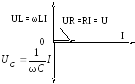


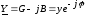 ,
, .
.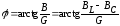 .
.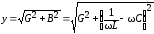 .
.