Закон Джоуля — Ленца — Википедия
Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
Определения
В словесной формулировке звучит следующим образом[2]:
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.
Математически может быть выражен в следующей форме:
- w = j → ⋅ E → = σ E 2 , {\displaystyle w={\vec {j}}\cdot {\vec {E}}=\sigma E^{2},}
где w {\displaystyle w} — мощность выделения тепла в единице объёма, j → {\displaystyle {\vec {j}}} — плотность электрического тока, E → {\displaystyle {\vec {E}}} — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.
В интегральной форме этот закон имеет вид
- d Q = I 2 R d t , {\displaystyle dQ=I^{2}Rdt,}
- Q = ∫ t 1 t 2 I 2 R d t , {\displaystyle Q=\int \limits _{t_{1}}^{t_{2}}I^{2}Rdt,}
где d Q {\displaystyle dQ} — количество теплоты, выделяемое за промежуток времени d t {\displaystyle dt} , I {\displaystyle I} — сила тока, R {\displaystyle R} — сопротивление, Q {\displaystyle Q} — полное количество теплоты, выделенное за промежуток времени от t 1 {\displaystyle t_{1}} до t 2 {\displaystyle t_{2}} . В случае постоянных силы тока и сопротивления:
- Q = I 2 R t . {\displaystyle Q=I^{2}Rt.}
Применяя закон Ома, можно получить следующие эквивалентные формулы:
- Q = U 2 t / R = I U t . {\displaystyle Q=U^{2}t/R\ =IUt.}
Практическое значение
Снижение потерь энергии
При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно, значит ток в сети I {\displaystyle I} на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами
- Q w = R w ⋅ I 2 , {\displaystyle Q_{w}=R_{w}\cdot I^{2},}
- Q c = U c ⋅ I . {\displaystyle Q_{c}=U_{c}\cdot I.}
Откуда следует, что Q w = R w ⋅ Q c 2 / U c 2 {\displaystyle Q_{w}=R_{w}\cdot Q_{c}^{2}/U_{c}^{2}} . Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение R w ⋅ Q c 2 {\displaystyle R_{w}\cdot Q_{c}^{2}} является константой, то тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.
Выбор проводов для цепей
Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.
Электронагревательные приборы
Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.
За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают
Плавкие предохранители
Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.
См. также
Примечания
Закон Джоуля-Ленца — часто используемый физический закон при расчетах потерь тепла в доме или при создании таких электроприборов как ламп. Более подробная информация о том, что это такое, какую имеет формулировку, в чем измеряется количественная величина теплового действия электротока, какой формулой выражается закон джоуля ленца далее.
Что это за закон
Закон джоуля ленца определение гласит, что это физический норматив, который определяет количественный вид меры теплового действия электротока. В девятнадцатом столетии, вне зависимости друг от друга Джоуль с российским ученым Ленцем стали изучать, как нагреваются проводники в момент прохождения электротока и нашли некую закономерность. Они узнали, что в момент прохождения электротока по проводниковому элементу получается тепло, которое равно силе тока, времени и проводниковому сопротивлению.
Обратите внимание! Это закономерность была названа законом в честь двух ученых. Стоит указать, что эта закономерность активно используется с момента открытия и по сегодняшний день и помогает решить многие вопросы, связанные с электрикой.
 История появления формулировки закона ученых
История появления формулировки закона ученыхФормулировка
Закон джоуля ленца формулировка словесно выглядит следующим образом: мощность тепла, которая выделяется в проводниковом элементе в момент протекания в нем электротока имеет пропорциональную зависимость умножения плотности электрополя на напряженность.
Его по-другому можно сформулировать так: энергия, протекая по проводнику, перемещает электрозаряд в электрополе. Так, электрополе совершает работу. Работа производится благодаря проводниковому нагреванию. Энергия превращается в тепло.
Однако, из-за чрезмерного проводникового нагрева при помощи тока и электрооборудования, может повредиться проводка и сами аппараты. Сильное перегревание опасно, когда есть короткое замыкание в проводах. Из-за этого проводники могут иметь большое токовое значение.
Что касается интегральной формы тонких проводников правило или уравнение Джоуля — Ленца звучит так: то тепло, которое выделяется за время в конкретном участке электроцепи, определяется квадратным произведением токовой силы на сопротивление участка.
Обратите внимание! Закон Джоуля-Ленца обладает достаточно общим характером, потому что не имеет зависимости от природы, силу которой генерирует электроток.
Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.
 Упрощенная формулировка
Упрощенная формулировкаВ чем измеряется
Единица теплового измерения это джоуль. Формула состоит из напряжения, измеряемого в вольтах, силы тока, измеряемого в амперах, и времени, измеряемой в секундах. Тогда выходит, что показатели будут измеряться в джоулях или одном вольте, перемноженном на ампер и секунду.
 Единица измерения тепла, выделяемого электричеством
Единица измерения тепла, выделяемого электричествомКакой формулой выражается
На данный момент существует две формулы по математическому нормативу двух ученых, в дополнение к теме, как найти джоуль формула. Согласно первой, нужно перемножить напряженность с плотностью электрического поля, а согласно второй, нужно сделать интеграл из произведения теплового эквивалента работы, количества выделяемого тепла, величины тока, активного проводникового сопротивления и времени. Величина будет определена, в зависимости от того, какая разрядность у единиц, в которых измеряются значения формулы.
 Формула выражения математического и физического закона
Формула выражения математического и физического законаГде и как используется
К примеру, благодаря нему создаются лампы накаливания и электронагревательные приборы. В них находится нагревательный элемент, выступающий в роли проводника, имеющего высокое сопротивления. Благодаря этому элементу локализовано выделяется тепло на участке. Оно будет выделяться в момент повышения сопротивления с увеличением проводниковой длины и выбором конкретного сплава.
Обратите внимание! Также используется для просчета снижения энергопотерь. Выделение тепла из тока приводит к тому, что снижается энергия. В момент ее передачи, мощность линейным образом зависит от показателя напряжения с силой тока, а нагревание зависит от токовой силы квадратичным образом. По этой причине при повышении напряжения и понижении силы тока до подачи электрической энергии, это действие будет выгодным. В момент повышения показателя напряжения снизится электробезопасность. Чтобы повысить электробезопасность, нужно повысить сопротивление нагрузки и сетевое напряжение.
Стоит указать, что он влияет на подбор проводников для электроцепей, поскольку из-за неправильного выбора может начать сильно нагреваться проводник, а также начать возгораться. Это происходит при превышении допустимых значений силы тока и выделении небольшого количества энергии. Нагрев проводников вредный, поэтому теряется энергия и передается тепло от источника к пользователю.
Чтобы уменьшить эту потерю, сила тока уменьшается и повышается напряжение источника с остатком передаваемой мощности. Во избежание изоляционного электропробоя, она поднимается на высоту на высоковольтной линии электрической передачи, которая связывает большие электрические станции с городскими и поселочными пунктами.
 Сфера применения
Сфера примененияВ целом, закон Джоуля-Ленца — норма, придуманная двумя учеными, чтобы установить, какое тепло отдает электрический ток. Данное тепло выражается через перемноженное выражение удвоенной силы тока, времени, и сопротивления проводника и измеряется в вольтах, умноженных на ампер и секунду. Используется активно как в быту, так и в промышленности, как при изучении фактора тепловой потери, так и при создании ламп накаливания и электронагревательных установок. Нередко применяется в момент выбора между проводами электроцепи.
Закон Джоуля-Ленца

При прохождении электрического тока через металлический проводник электроны сталкиваются то с нейтральными молекулами, то с молекулами, потерявшими электроны.
При столкновении электронов с молекулами расходуется энергия, которая превращается в тепло.
Любое движение, при котором преодолевается сопротивление, требует эатраты определенной энергии.
Так, например, для перемещения какого -либо тела преодолевается сопротивление трения, и работа, затраченная на это, превращается в тепло.
Таким образом, для проведения тока через проводник источник тока затрачивает некоторую энергию, которая превращается в тепло.
Переход электрической энергии в тепловую отражает закон Ленца — Джоуля
или закон теплового действия тока.
Русский ученый Ленц и английский физик Джоуль одновременно и независимо один от другого установили, что
при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.
Это положение называется законом Ленца — Джоуля.
Если обозначить количество теплоты, создаваемое током, буквой Q (Дж), ток, протекающий по проводнику — I, сопротивление проводника — R и время, в течение которого ток протекал по проводнику — t, то закону Ленца — Джоуля можно придать следующее выражение:
Q = I2Rt.
Так как I = U/R и R = U/I, то Q = (U2/R) t = UIt.
Значение мощности, при выделении определённого количества тепла
Скачать можно здесь
(Подробно и доходчиво в видеокурсе «В мир электричества — как в первый раз!»)
Работа и мощность тока. Закон Джоуля – Ленца
|
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд При этом силы электрического поля, действующего на данном участке, совершают работу: Разделив работу на время, получим выражение для мощности:
Полезно вспомнить и другие формулы для мощности и работы:
|
В 1841 г. манчестерский пивовар Джеймс Джоуль и в 1843 г. петербургский академик Эмилий Ленц установили закон теплового действия электрического тока.
| Джоуль Джеймс Пресскотт (1818 – 1889) – английский физик, один из первооткрывателей закона сохранения энергии. Первые уроки по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены электромагнетизму, кинетической теории газов. |
| Ленц Эмилий Христианович (1804 – 1865) – русский физик. Основные работы в области электромагнетизма. В 1833 г. установил правило определения электродвижущей силы индукции (закон Ленца), а в 1842 г. (независимо от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля-Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике. |
Независимо друг от друга Джоуль и Ленц показали, что при протекании тока, в проводнике выделяется количество теплоты:
| (7.7.4) |
Если ток изменяется со временем, то
.
Это закон Джоуля–Ленца в интегральной форме.
Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.
Соотношение (7.7.4) имеет интегральный характер и относится ко всему проводнику с сопротивлением R, по которому течет ток I. Получим закон Джоуля-Ленца в локальной-дифференциальной форме, характеризуя тепловыделение в произвольной точке.
Тепловая мощность тока в элементе проводника Δl, сечением ΔS, объемом равна:
.
Удельная мощность тока
.
Согласно закону Ома в дифференциальной форме . Отсюда закон Джоуля — Ленца в дифференциальной форме характеризующий плотность выделенной энергии:
| , | (7.7.5) |
Так как выделенная теплота равна работе сил электрического поля
,
то мы можем записать для мощности тока:
| . | (7.7.6) |
Мощность, выделенная в единице объема проводника .
Приведенные формулы справедливы для однородного участка цепи и для неоднородного.
Если проводник, в котором течет постоянный ток, и он при этом остается неподвижным, то работа сторонних сил расходуется на его нагревание.
Электрическая энергия, полученная от источника тока, в металлических проводниках превращается в энергию хаотического движения атомов, то есть в теплоту. Опыты полностью подтверждают данную теорию – при протекании тока по любому проводнику происходит выделение теплоты, равной работе, совершаемой электрическими силами по переносу заряда вдоль проводника.
Представим, что на концах участка проводника существует разность потенциалов φ1 – φ2 = U. Тогда на этом участке работа по переносу заряда равна:

По определению I = q/τ, откуда q = Iτ, где τ – время прохождения заряда, то есть:

Сила тока измеряется в амперах, напряжение в вольтах, время в секундах, а работа, соответственно, в джоулях: 1 Дж = 1 А·1 В·1 с.
Поскольку работа А идет на нагревание проводника, то вполне можно написать, что выделяющаяся в проводнике теплота Q равна работе А электрических сил:

Данная формула носит название закона Джоуля – Ленца. Это явление было открыто в 1841 году английским физиком Дж. Джоулем и независимо от него в 1842 году русским физиком Э. Х. Ленцем.
В системе СИ теплота и работа измеряются в джоулях.
Использовав закон Ома для участка цепи, запишем формулу (2) следующим образом:

Из формулы следует, что теплота, выделяемая в проводнике при прохождении электрического тока, зависит силы тока, времени его прохождения и сопротивления проводника.
Если измерять теплоту во внесистемных единицах – калориях, а остальные величины в единицах СИ, то в формулу (3) следует подставить коэффициент пропорциональности k = 0.24 кал/Дж, и тогда получим:

Энергия электрического тока может быть израсходована не только на нагревание проводников, но и испытывать самые разные превращения. Например, если во внешнюю цепь подключен электродвигатель, то часть электрической энергии преобразуется в механическую. Если во внешнюю цепь включены электролиты (проводники второго рода), то часть энергии превратится в химическую и так далее. Если во внешнюю цепь включены только металлические проводники, то энергия источника будет превращаться только в теплоту, а если проводники имеют высокую температуру, то будет расходоваться на излучение.
Давайте преобразуем закон Джоуля – Ленца в другой вид. Введем понятие плотность тепловой мощности ω – величину, равную энергии, выделенной за время τ прохождения тока в каждой единице объема проводника:

Где l – длина проводника, Q – теплота, а S – поперечное сечение проводника.
Приняв во внимание, что Q = I2Rτ, а R=ρl/S, получим:

Но I/S = j – это плотность тока, а ρ = l/γ, где γ – удельная проводимость, тогда:

Если учесть закон Ома в дифференциальной форме, то тогда:

Данное соотношение имеет название закон Джоуля – Ленца в дифференциальной форме. Из него делаем вывод, что плотность тепловой мощности равна произведению удельной проводимости проводника на квадрат напряженности Е электрического поля.
Формулы (3) можно применить для расчета мощности N тока, равной работе электрических сил за единицу времени:

В системе СИ мощность тока измеряется в ваттах: 1 Ватт = 1 А· 1 В.
Нагревание проводника током в одних случаях является нежелательным явлением и с ним активно борются, а в других наоборот – полезным явлением. К нежелательным тепловым явлениям относят явлениям потери электрической энергии в линиях электропередач, разрушение изоляции проводов и кабелей из-за перегрева. Также во многих случаях теплота, выделяемая электрическим током при прохождении через проводник успешно используется технике (бытовые электронагревательные приборы, электропечи в промышленности).
«Что показывает закон Джоуля-Ленца?» – Яндекс.Кью
Вообще-то Ампер, Ом, Герц — это все различные ученые-физики, но, насколько я понимаю, вас интересует не это. В Амперах (А) измеряют силу тока, в Омах (Ом) — электрическое сопротивление, а в Вольтах (В) — напряжение в электрической сети. В Герцах измеряют частоту колебаний, причем не важно каких именно. Главное, чтобы они были периодическими, т.е. не спонтанными, но даже спонтанные можно представить как сумму периодических колебаний через т.н. разложение в ряд Фурье.
Теперь немного подрбнее. Есть закон Ома, который связывает между собой три первых величины: I*R = U, где I — сила тока в электрической сети в А, R — электрическое сопротивление в Ом, а U — напряжение в В. Что же означают эти величины физически?
Начнем с напряжения, измерямеого в Вольтах, или, по-другому, разности потенциалов. Если провести работу по разделению электрических зарядов (не важно каким именно способом), то мы получим, грубо говоря, два заряженных полюса, причем один из них будет заряжен положительно (из-за недостатка отрицательно заряженных электронов), а другой отрицательно (из-за избытка электронов). Между этими полюсами возникнет электрическое поле, которое может заставить электрические заряды двигаться. Говорят, что между полюсами возникло напряжение или разность потенциалов. Это означает, что если эти полюса соединить проводником, то по нему потечет электрический ток, а если эти полюса просто поднести достаточно близко друг к другу, то даже проводника не потребуется — электроны под воздействием сильного электрического поля будут отрываться от отрицательного полюса и полетят в сторону положительного, возникнет т.н. пробой, который по сути тоже есть электрический ток, только без проводника. Способность рождать электрический ток и есть физический смысл напряжения.
Едем дальше. Что такое электрический ток? Если есть электрическое поле и в него поместить электрические заряды, то они начнут двигаться в этом поле. Это и есть электрический ток. Причем, если, например, соединить два разноименно заряженных полюса проводником, то в этом проводнике из-за напряжения между полюсами позникнет электрическое поле и электроны с отрицательного полюса устремятся к положительному. Но это еще не все. В самом проводнике тоже есть свободные электроны и они тоже начнут двигаться в направлении положительного полюса. Так возникает электрический ток в проводнике.
Ну и наконец электрическое сопротивление, измерямое в Омах. Электроны, двигаясь в проводнике, перемещаются не свободно: они время от времени сталкиваются с ядрами атомов, из которых состоит проводник, и между собой. Эти столкновения приводят к тому, что электроны теряют свою энергию, которая передается тем самым ядрам атомов, раскачивая их, что означает увеличение температуры проводника. Т.е. протекая по проводнику электрический ток испытывает сопротивление, которое приводит к нагреву этого самого проводника. Вот величина этого самого сопротивления и определяется в Омах.
Теперь закон Ома выглядит логичным, правда? Чем больше напряжение между полюсами, тем сильнее электрическое поле и тем больше электрический ток. А чем больше электрическое сопротивление, тем больше напряжения тратится на раскачку атомов проводника, т.е. на его нагрев и соответственно тем меньше энергии остается на электрический ток. При пробое или т.н. коротком замыкании, когда сопротивление стремится к нулю, ток растет неограниченно, пока все электроны с отрицательного полюса проводника не претекут на положительный. А если эта разность потенциалов поддерживается (например, если постоянно происходит разделение зарядов на полюсах засчет какой-то внешней работы), то ток может расти до тех пор, пока что-то не разрушится: проводник от перегрева или сами полюса. Если мы хотим получить электрический ток определенной заданной силы, то чем больше сопротивление проводника, тем больше напряжение нужно приложить… В общем, надеюсь, вы разобрались.
ЗАКОН ЛЕНЦА – ДЖОУЛЯ — Студопедия
При прохождении электрического тока через металлический проводник электроны сталкиваются то с нейтральными молекулами, то с молекулами, потерявшими электроны.
Движущийся электрон либо отщепляет от нейтральной молекулы новый электрон, теряя свою кинетическую энергию и образуя новый положительный ион, либо соединяется с молекулой, потерявшей электрон (с положительным ионом), образуя нейтральную молекулу.
При столкновении электронов с молекулами расходуется энергия, которая превращается в тепло.
Любое движение, при котором преодолевается сопротивление, требует эатраты определенной энергии.
Так, например, для перемещения какого -либо тела преодолевается сопротивление трения, и работа, затраченная на это, превращается в тепло.
Электрическое сопротивление проводника играет ту же роль, что и сопротивление трения.
Таким образом, для проведения тока через проводник источник тока затрачивает некоторую энергию, которая превращается в тепло.
Переход электрической энергии в тепловую отражает закон Ленца — Джоуля
или закон теплового действия тока.
Русский ученый Ленц и английский физик Джоуль одновременно и независимо один от другого установили, что при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.
Это положение называется законом Ленца — Джоуля.
Если обозначить количество теплоты, создаваемое током, буквойQ (Дж), силу тока, протекающего по проводнику — I, сопротивление проводника —Rи время, в течение которого ток протекал по проводнику —t, то закону Ленца — Джоуля можно придать следующее выражение:
Q = I 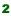 Rt.
Rt.
Так какI = U/Rи R = U/I, тоQ = (U 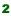 /R) t = UIt.
/R) t = UIt.
НАГРЕВАНИЕ ПРОВОДНИКОВ ЭЛЕКТРИЧЕСКИМ ТОКОМ.
РАСЧЁТ СЕЧЕНИЯ ПРОВОДОВ.
На нагревании проводников электрическим током основано устройство
электрического освещения, электронагревательных приборов, электрических печей, измерительной и медицинской аппаратуры различных типов и т. д.
Из всех видов искусственного освещения наибольшее распространение получила электрическая лампа накаливания, изобретенная А. Н. Лодыгиным в 1873 г.
В такой лампе проводник под действием тока нагревается до белого каления и вследствие этого излучает свет.
Основными частями современной лампы накаливания являются нить накала и стеклянный баллон (колба).
Материалом для изготовления нити накала осветительных ламп служит вольфрам
(с примесью оксида тория и других элементов). Этот металл обладает высокой
температурой плавления (3660°) и большой механической прочностью.
Электрическое нагревание проводников не всегда оказывает полезное влияние.
В проводах линий электропередач вследствие сильного нагрева их при больших
токах может создаваться опасность возникновения пожаров.
Во избежание чрезмерного нагрева линейных проводов, а также различных
обмоток электрических машин и аппаратов из изолированной проволоки для электрической аппаратуры установлены нормы максимальных значений сил токов, пропускаемых по данному проводу или обмотке.
Ток, при котором устанавливается наибольшая допустимая температура провода, называется допустимым током. Наибольшая допустимая температура зависит от
изоляции провода и способа его прокладки.
Расчет проводов по формулам, основанным на законах нагрева, очень сложен.
На практике допустимое для данной силы тока сечение провода определяется по
таблицам допустимых длительных токовых нагрузок на провода и кабели,
приведенным в Правилах устройства электроустановок (ПУЭ).
| Поперечное сечение провода, мм.кв | Допустимый ток в проводах, А | |
| Медные | Аллюминиевые | |
| 0.5 1 2.5 4 6 10 25 50 | 11 17 30 41 50 80 140 215 | — — 24 32 36 55 105 165 |
Провод выбирается такого сечения, чтобы допустимый ток его был равен или
больше заданного или расчетного тока.
Учтите, из ряда предпочтительных величин сечений (0,75; 1; 1,5; 2,5; 4; 6 мм? и т. д.)
для алюминиевых проводов сечение выбирают на ступень выше, чем для медных,
так как их проводимость составляет примерно 62% от проводимости медных.
Например, если по расчетам нагрузки для меди нужна величина сечения 2,5 мм?,
то для алюминия следует брать 4 мм?, если же для меди нужно 4 мм?, то для алюминия — 6 мм? и т. д.
Помимо нагрева проводов ток, проходя по ним, создает падение напряжения, так как провода обладают сопротивлением. Если расстояние между источником энергии и потребителем L, то длина двух проводов, соединяющих источник энергии с потребителем, равна2L.
Сопротивление проводов сечением S из материала с удельным сопротивлением р равно R = р(2L/S), a падение напряжения в проводах
Uпров = IR = Ip(2L/S).
Таким образом, напряжение на зажимах потребителя Uпотрокажется меньше напряжения в начале линии (источника)Uисточ.
Разность напряжений в начале и в конце линии, равная падению напряжения в проводах, называется потерей напряжения:Uисточ — Uпотр = Uпотерь = IR.
Любой приемник энергии очень чувствителен к изменениям напряжения, т. е. отклонениям его от номинального значения.
Так, например, яркость лампы накаливания примерно пропорциональна четвертой степени напряжения, т. е. при понижении напряжения на 5% световой поток лампы накаливания уменьшается на 18,5%, а при повышении напряжения на 5% сверх номинального сокращает срок службы ее вдвое.
Колебания напряжения для осветительной нагрузки не должны превышать
—2,5 +5%, а для силовой ±5 и иногда +10% номинального значения.
Следовательно, допускаемая потеря напряжения в линии не должна превышать тех же значений.
Задача расчета сводится к выбору такого сечения провода, при котором
обеспечивается нормальное рабочее напряжение на зажимах потребителей электрической энергии, т. е. необходимое сечение проводов линии
S = 2pLI/  Uпотерь.
Uпотерь.
Найденное по этой формуле сечение, округленное до ближайшего, большего стандартного, должно быть проверено на допустимый нагрев.
Для относительно коротких линий (осветительные сети промышленных предприятий, общественных и жилых зданий) сечение проводов выбирают в зависимости от допустимого нагрева, так как потеря напряжения обычно оказывается меньше допустимой.
Мощность потерь в линии электропередачи равна: Pпотерь =
Pпотерь =  Uпотерь x I = I
Uпотерь x I = I  R.
R.
Для защиты аппаратов, машин и приборов от чрезмерно больших токов устанавливают предохранительные устройства (предохранители, реле, автоматы), которые автоматически прерывают цепь тока, как только его величина превысит норму.
правило Ленца — Чтение Фейнмана
В моих двух предыдущих постах я представил все ингредиенты еды, которую мы собираемся приготовить сейчас, в частности:
- Формула для крутящего момента на контуре тока в магнитном поле и его энергии: (i) τ = μ × B и (ii) U mech = — μ · B .
- Закон Био-Савара , который дает вам магнитное поле, создаваемое проводами, несущими токи:
Оба компонента, очевидно, имеют отношение к конструкции электромагнитного двигателя , т.е.е. «двигатель, который может выполнять некоторую работу», как называет это Фейнман. Principle Его принцип показан ниже.
Две вышеупомянутые формулы объясняют, как и почему катушка вращается, и катушку можно заставить продолжать движение, договорившись о том, чтобы соединения с катушкой менялись на пол-оборота контактами, установленными на валу. Тогда крутящий момент всегда в одном направлении. Вот как сделан маленький двигатель постоянного тока (DC). Мой отец заставил меня сделать пару из них тридцать лет назад с помощью магнита, большого гвоздя и медной катушки.Я использовал скользящие контакты, и они были самой сложной вещью во всем дизайне. Но теперь я нашел на YouTube очень приятную демонстрацию парня, чья система «реверсирования» соединений удивительно проста: он не использует скользящие контакты. Он просто удаляет половину из изоляции на проводе катушки с одной стороны. Он работает как шарм, но я думаю, что он не настолько устойчив, так как вращается так быстро, что изоляция на другой стороне, вероятно, через некоторое время оторвется! 🙂
Теперь, чтобы запустить этот двигатель, вам нужен ток , и, следовательно, физики и инженеры 19-го века также задались вопросом, как можно производить токов, изменяя магнитного поля.В самом деле, они могли использовать 000 вольтового ворса Алессандро Вольта ‘для создания токов, но это было не очень удобно: он состоял из чередующихся цинковых и медных дисков, между которыми кусочки ткани были пропитаны соленой водой!
Теперь, когда Закон Био-Савара восходит к 1820 году, потребовалось еще десятилетие , чтобы выяснить, как это можно сделать. Первоначально люди думали, что магнитные поля должны вызывать какой-то ток, но это не сработало. Наконец, Фарадей однозначно установил фундаментальный принцип, согласно которому электрические эффекты присутствуют только , когда что-то меняется . Таким образом, вы получите ток в проводе с помощью , переместив его на в магнитном поле, или с помощью , переместив магнит на , или, если магнитное поле вызвано каким-либо другим током, с помощью , изменив ток в этом проводе , Это называется «правилом потока» или Закона Фарадея . Помните: мы видели закон Гаусса, затем закон Ампера, а затем этот закон Био-Савара, и теперь пришло время для закона Фарадея. Law Закон Фарадея на самом деле является третьим уравнением Максвелла, или Максвелла-Фарадея, , Закона индукции, :
.∇ × E = −∂ B / 9t
Теперь вы задаетесь вопросом: какое отношение flux имеет к этой формуле? ∇ × E — это около тиража , а не про флюс! Ну … Позвольте мне скопировать ответ Фейнмана:

Итак … Ну вот.И, да, вы правы, вместо того, чтобы писать Закон Фарадея как × × E = −∂ B / ∂t, мы должны записать его как:
Это легче понять, и с ним также легче работать, как мы увидим ниже. Итак, суть в том, что всякий раз, когда магнитный поток меняет , на провод воздействует электроны. Этот толчок называется электродвижущей силой , сокращенно эдс или ЭДС, и поэтому эта линия и / или поверхность на самом деле интегральная выше.Позвольте мне перефразировать Фейнмана, чтобы вы полностью поняли, о чем мы здесь говорим:
Когда мы перемещаем наш провод в магнитном поле, или когда мы перемещаем магнит рядом с проводом, или когда мы меняем ток в соседнем проводе, будет нетто толчок на электроны в проводе в одно направление вдоль провода . В разных местах могут быть толчки в разных направлениях, но в одном направлении будет больше толчка, чем в другом.Что важно, так это толчок, встроенный во всю цепь. Мы называем этот чистый интегрированный толчок электродвижущей силой (сокращенно ЭДС) в цепи. Точнее, ЭДС определяется как тангенциальная сила на единицу заряда в проводе, интегрированном по длине, один раз вокруг всей цепи.
Так что это неотъемлемая часть. 🙂 И вот как мы можем превратить этот двигатель выше в генератор: вместо того, чтобы подавать ток через провод, чтобы он повернулся, мы можем повернуть петлю , вручную, с помощью водяного колеса или любым другим способом.Теперь, когда катушка вращается, ее провода будут двигаться в магнитном поле, и поэтому мы обнаружим в цепи катушки эдс , и таким образом двигатель станет генератором.
Теперь позвольте мне быстро кое-что добавить сюда: когда я говорю «толчок электронов в проводе», о каких электронах мы говорим? Сколько? Что ж … Я отвечу на этот вопрос очень подробно в данный момент, но, на данный момент, просто отметьте, что ЭДС — это некоторая величина, выраженная в за кулон или, как Фейнман говорит выше, за заряд единицы .Поэтому нам нужно умножить его на ток в цепи , чтобы получить мощности нашего маленького генератора.
ОК. Давайте двигаться дальше. На самом деле, все, что я могу здесь сделать, это упомянуть лишь несколько основ, чтобы мы могли перейти к следующему. Если вы действительно хотите узнать все о мельчайших подробностях, то вам следует просто прочитать лекцию Фейнмана о наведенных токах. Это всего . И, нет, не беспокойтесь: вопреки вашим ожиданиям, мои «основы» не составляют ужасной груды формул.На самом деле, это все легко и довольно забавно, и я, вероятно, должен был бы включить намного больше. Но тогда … Ну … Мне всегда нужно двигаться дальше … Если нет, я никогда не доберусь до того, что действительно хочет понять . 😦
электродвижущая сила
Мы определили электродвижущую силу выше, включая ее формулу:
Какие единицы? Давайте посмотрим … Мы знаем, что B было измерено не в ньютонах на кулон, как электрическое поле E , но в Н · с / с · м, потому что мы должны были умножить напряженность магнитного поля на скорость заряд, чтобы найти силу на единицу заряда, ср.уравнение F / q = v × B . Теперь, в какой единице мы выражаем этот поверхностный интеграл? Мы должны умножить на m 2 , чтобы мы получили N · m · s / C. Теперь давайте упростим это, отметив, что один вольт равен 1 Н · м / с. [ вольт имеет ряд определений, но здесь применимо то, что это разность потенциалов между двумя точками, которая придаст одну единицу заряда джоулей (т.е. 1 Н · м) энергии на единицу заряда ( я.е. 1 C), который проходит между ними.] Таким образом, мы можем измерить магнитный поток в вольт-секундах , то есть V · s. Затем мы берем производную по времени, делим на s и получаем… Вольт! ЭДС измеряется в вольтах!
Это имеет смысл? Я предполагаю, что так: ЭДС вызывает ток, как разность потенциалов, то есть напряжение , и, следовательно, мы можем и должны рассматривать ЭДС как напряжение!
Но давайте еще подумаем об этом.В дифференциальной форме закон Фарадея — это просто уравнение ∇ × E = −∂ B / ∂t, так что это только одно из четырех уравнений Максвелла, и поэтому мы предпочитаем записывать его как «правило потока» , Теперь «правило потока» гласит, что электродвижущая сила (сокращенно эдс или ЭДС) на электронах в замкнутой цепи равна скорости изменения магнитного потока, который она охватывает. Как упомянуто выше, мы измеряем магнитного потока за вольт-секунд (т.е.е. V · s), поэтому его скорость изменения во времени измеряется в вольтах (потому что скорость изменения — это величина, выраженная в в секунду, ), и поэтому э.д.с. измеряется в вольтах, то есть джоулей в кулонов, , при 1 В = 1 Н · м / с = 1 Дж / с. Что это означает?
Скорость изменения магнитного потока во времени может измениться, потому что изменяется поверхность, покрытая нашей петлей, или потому что изменяется само поле, или обоими. Какой бы ни была причина, она изменит эдс или напряжение , и поэтому заставит электроны двигаться.Итак, давайте предположим, что у нас есть генератор , генерирующий ЭДС . ЭДС может использоваться для выполнения работы . Мы можем зарядить конденсатор, например. Так как это будет работать?
Увеличение заряда конденсатора приведет к увеличению напряжения V конденсатора, то есть разности потенциалов V = Φ 1 — Φ 2 между двумя пластинами. Теперь мы знаем, что увеличение напряжения V будет пропорционально увеличению заряда Q, и что константа пропорциональности равна , определенной емкостью C конденсатора: C = Q / V.[Откуда мы это знаем? Хорошо … Посмотрите на мой пост о конденсаторах.] Теперь, если у нашего конденсатора огромная емкость, его напряжение не будет расти очень быстро. Однако ясно, что независимо от того, насколько велика емкость, ее напряжение будет увеличиваться до . Это всего лишь вопрос времени. Теперь его напряжение не может быть выше, чем эдс , предоставляемых нашим «генератором», потому что тогда он захочет разрядиться по той же схеме!
Итак, мы говорим здесь о мощности и энергии, и поэтому нам нужно наложить нагрузки на наш генератор.Мощность — это скорость выполнения работы, поэтому это скорость изменения энергии, и она выражается в джоулей в секунду . Энергия нашего конденсатора составляет U = (1/2) · Q 2 / C = (1/2) · C · V 2 . [Откуда мы это знаем? Ну что ж… Посмотрите на мой пост о конденсаторах еще раз. :-)] Итак, давайте возьмем производную по времени U , предполагая некоторое постоянное напряжение V . Мы получаем: dU / dt = d [(1/2) · Q 2 / C] / dt = (Q / C) · dQ / dt = V · dQ / dt. Так что это мощность , которую генератор должен будет поставить для зарядки генератора.Как я сейчас покажу, мощность, подаваемая генератором, действительно равна эдс, раз больше тока , а ток — это скорость изменения заряда, поэтому I = dQ / dt ,
Итак, да, все работает: энергия, которая подается от нашего генератора, будет использоваться для зарядки нашего конденсатора. Теперь вы можете задаться вопросом: а как насчет тока? Где находится закон Фарадея? Ответ таков: закон Фарадея не имеет текущего. Это просто не там. ЭДС выражается в вольтах, и поэтому энергия за кулон составляет , то есть за единицу заряда.Сколько мощности генератор может и будет поставлять, зависит от его конструкции, а также от схемы и нагрузки, которые мы будем на него возлагать. Поэтому мы не можем сказать, сколько кулонов будет у нас будет. Все это зависит. Но вы можете себе представить, что если бы петля была больше или если бы у нас была катушка с большим количеством петель, то наш генератор мог бы производить больше энергии, то есть он мог бы перемещать больше электронов, поэтому упомянутый мощность = ( эдс ) × ( ток ) произведение будет больше.🙂
Наконец, в заключение отметим определение Фейнманом ЭДС : тангенциальная сила на единицу заряда в проводе, интегрированном по всей длине всей цепи. Таким образом, у нас здесь есть сила, умноженная на расстояние, но за единицу заряда. Теперь, сила, умноженная на расстояние, — это работа или энергия, и так… Да, ЭДС, — это джоул на кулон, определенно! 🙂
[…] Не беспокойтесь слишком сильно, если вы не совсем поняли это. Я вернусь к этому при обсуждении электрических цепей , что я и сделаю в своих следующих постах.
Самоиндуктивность и правило Ленца
Мы говорили о двигателях и генераторах выше. У нас также есть трансформаторов , как показано ниже. Здесь происходит то, что переменный ток (AC) генерирует непрерывно изменяющееся магнитное поле, которое генерирует переменную ЭДС во второй катушке, которая производит достаточно энергии, чтобы зажечь электрическую лампочку.
Теперь, общая эдс в катушке (b) является суммой эдс отдельных витков катушки, поэтому, если мы намотаем (б) со многими витками, мы получим большую эдс, так что мы можем «преобразовать» напряжение до некоторого другого напряжения.Из уроков старшей школы вы должны знать, как работает , то есть .
Я хочу поговорить здесь о другом. В самой катушке (а) имеется индукционный эффект. Действительно, переменный ток в катушке (а) создает переменное магнитное поле внутри себя , и поток этого поля постоянно меняется, поэтому в катушке (а) есть самоиндуцированная ЭДС . Эффект называется , , самоиндуктивность, , , и, следовательно, это , ЭДС, действующая на сам ток, когда он создает магнитное поле или, вообще, когда его поле изменяется каким-либо образом.Это самое замечательное явление, поэтому позвольте мне перефразировать Фейнмана, как он его описывает:
«Когда мы дали« правило потока », что эдс равна скорости изменения связи потока, мы не указали направление эдс. Существует простое правило, называемое , ленц-правило , для выяснения, в каком направлении движется эдс: эдс пытается противостоять любому изменению потока. То есть направление индуцированной эдс всегда таково, что если бы ток протекал в направлении эдс, он генерировал бы поток B , который противодействует изменению в B , которое производит эдс.В частности, , если есть переменный ток в одной катушке (или в любом проводе), есть «обратная» эдс в схеме . Эта эдс воздействует на заряды, протекающие в катушке, чтобы противостоять изменению магнитного поля и, таким образом, в направлении, противоположном изменению тока. Он пытается сохранить постоянный ток; он противоположен току, когда ток увеличивается, и он направлен к току, когда он уменьшается. Ток в самоиндуктивности имеет «инерцию», потому что индуктивные эффекты пытаются поддерживать постоянный поток, так же как механическая инерция пытается поддерживать постоянную скорость объекта.”
Хм … Это то, что вам нужно прочитать пару раз, чтобы полностью переварить это. На YouTube есть хорошая демонстрация, демонстрирующая физическое видео из Массачусетского технологического института, демонстрирующее этот эффект с металлическим кольцом на конце электромагнита. Вы, наверное, видели это раньше: электромагнит подключен к току, и кольцо летит в воздух. Объяснение состоит в том, что индуцированные токи в кольце создают магнитное поле , противодействующее изменению поля через него . Таким образом, кольцо и катушка отталкиваются, как два магнита с противоположными полюсами.Эффекта больше нет, когда в кольце сделан тонкий радиальный разрез, потому что тогда не может быть тока. Хорошая вещь о видео состоит в том, что он показывает, как эффект становится намного более драматичным, когда применяется переменный ток , а не постоянный ток. И это также показывает, что происходит, когда вы впервые остываете кольцо в жидком азоте. 🙂
Вы также можете заметить искры при включении электромагнита. Верьте или нет, это также связано с «обратной ЭДС».В самом деле, когда мы отключаем большой электромагнит, открывая переключатель, ток должен немедленно стремиться к нулю, но, пытаясь это сделать, он генерирует большую «обратную ЭДС»: достаточно большую, чтобы образовать дугу на разомкнутых контактах выключатель. Высокое напряжение также не подходит для изоляции катушки, так как может повредить ее. Вот почему большие электромагниты обычно содержат дополнительную цепь, которая позволяет «обратному току» разряжаться менее резко. Но я отошлю вас к Фейнману для получения более подробной информации, поскольку любая иллюстрация здесь будет загромождать разоблачения .
Вихревые токи
Мне нравятся обучающие видео, и поэтому я должен дать вам несколько ссылок здесь, но их так много, что я позволю вам Google самостоятельно. Наиболее впечатляющей демонстрацией вихревых токов являются те, которые появляются в сверхпроводнике: даже в 1970-х годах, когда Фейнман написал свои лекций , эффект магнитной левитации был хорошо известен. Фейнман иллюстрирует этот эффект с помощью простой диаграммы ниже: при приближении магнита к идеальному проводнику, такому как и ниже 3.8 ° K, вихревые токи создадут противоположные поля, так что без магнитного потока входит в сверхпроводящего материала. Этот эффект также называют эффектом Мейзнера по имени немецкого физика Вальтера Мейснера, хотя он был обнаружен гораздо раньше (в 1911 году) голландским физиком в Лейдене Хайке Камерлинг-Оннесом, который получил за него Нобелевскую премию.
Конечно, у нас есть вихревые токи и в менее драматичных ситуациях. Феномен вихревых токов обычно демонстрируется торможением листа металла, когда он качается взад и вперед между полюсами электромагнита, как показано ниже (слева).На иллюстрации справа показано, как эффект вихревых токов может быть значительно уменьшен путем вырезания пазов в пластине, что похоже на радиальный разрез в нашем прыгающем кольце. 🙂
диск Фарадея
Диск Фарадея интересен не только с исторической точки зрения — нижеприведенная иллюстрация — модель 19-го века, поэтому Майкл Фарадей мог использовать себя — но и потому, что она, кажется, противоречит «потоку правил»: как диск вращается через постоянное магнитное поле , он будет производить некоторую эдс, но так что поток не меняется.Как это возможно?
Ответ, конечно, заключается в том, что мы «обманываем» здесь: материал движется, поэтому мы фактически перемещаем «провод» или схему, если хотите, поэтому здесь нам нужно объединить с двумя уравнениями :

Если мы сделаем это, вы увидите, что все это имеет смысл. 🙂 О… Этот диск Фарадея называют гомополярным генератором, и это довольно интересно. Вы должны проверить, что случилось с концепцией в статье в Википедии об этом.Диск Фарадея, по-видимому, использовался в качестве источника мощности импульсов в 1950-х годах. Приведенная ниже вещь может хранить 500 мега- джоулей и обеспечивать токи до 2 мега- ампер, то есть 2 миллионов ампер! Увлекательно, не правда ли? 🙂
,Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:
https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторая информация на этой странице была отключена 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https: // ru.support.wordpress.com/copyright-and-the-dmca/
Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https: // ru.support.wordpress.com/copyright-and-the-dmca/
Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторое содержимое на этой странице было отключено 16 июня 2020 года в результате уведомления DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https: // ru.support.wordpress.com/copyright-and-the-dmca/
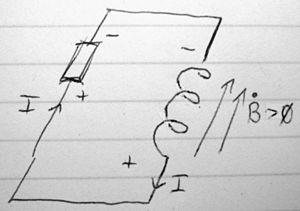
Закон Ленца — это общий способ понять, как электромагнитные цепи подчиняются третьему закону Ньютона и сохранению энергии. [1] Закон Ленца назван в честь Эмиля Ленца и гласит:
- Индуцированная электродвижущая сила (ЭДС) всегда вызывает ток, магнитное поле которого противодействует изменению исходного магнитного потока.
Закон Ленца показан с отрицательным знаком в законе индукции Фарадея:
- Е знак равно — ∂ Φ В ∂ T {\ displaystyle {\ mathcal {E}} = — {\ frac {\ частичный \ Phi _ {\ mathrm {B}}} {\ частичный t}}}
, который указывает, что индуцированная эдс (ℰ) и изменение магнитного потока (900Φ B ) имеют противоположные знаки. [2]
Индуцированная ЭДС и результирующий индуцированный ток идут против часовой стрелки, когда B направлен со страницы, а площадь цепи уменьшается. Поток через эту цепь уменьшается в направлении наружу. Теперь индуцированный ток I создает собственное магнитное поле, и мы можем использовать правило правого захвата для вычисления направления этого поля. В результате магнитное поле, вызванное наведенным током, также направлено наружу внутри цепи.Как будто природа через это индуцированное поле пыталась компенсировать уменьшение потока из-за приложенного поля B . Экспериментально это оказывается общим правилом, так что мы можем сказать, что
Направление индуцированной ЭДС всегда таково, что приводит к противодействию изменению, производящему его.
То есть закон Ленца .
В качестве другого примера применения закона Ленца рассмотрим катушку провода, к которому внезапно подключена батарея.Предположим, что батарея запускает ток, текущий по часовой стрелке, если смотреть на наблюдателя. Этот ток вызовет магнитное поле, линии которого будут пронизывать катушку и возвращаться за ее пределы. Таким образом, по мере накопления тока из-за батареи в катушке происходит изменение магнитного потока, и это должно привести к индуцированной ЭДС в катушке. Каково направление этой индуцированной ЭДС? Закон Ленца немедленно говорит нам, что он должен быть против часовой стрелки, чтобы противостоять нарастанию тока.Точно так же, когда ток в цепи обрывается, индуцированная ЭДС стремится не допустить затухания тока, и это учитывает искрение, наблюдаемое при медленном размыкании переключателей. Индуцированная ЭДС в цепи, ток которой меняется, называется противо-ЭДС , поскольку она всегда противостоит изменению тока. Это происходит из-за изменения собственного магнитного поля тока, эффект, называемый самоиндуктивностью .
Если бы закон Ленца не соответствовал действительности, увеличение тока в катушке привело бы к появлению ЭДС, которая помогла приложенному аккумулятору, увеличивая тем самым ток, вызывая большее значение ЭДС и дальнейшее увеличение тока, до до бесконечности .Это будет нестабильная ситуация, в которой принцип сохранения энергии будет нарушен.
Этот тип рассуждения может быть распространен на другие ситуации, в которых система в равновесии смещается, и принцип, к которому пришли, заключается в следующем.
Когда система в равновесии нарушается, равновесие смещается в направлении, которое стремится отменить влияние возмущения.
Это обобщение закона Ленца называется принципом Ле Шателье.
- ↑ Шмитт, Рон. Электромагнетизм объяснил . 2002 г. Получено 16 июля 2010 г.
- ↑ Джанколи, Дуглас С. (1998). Физика: принципы с приложениями (5-е изд.). п. 624.
›› Перевести петаджоули в джоули
Пожалуйста, включите Javascript использовать конвертер
›› Больше информации от конвертера
Сколько петаджоулей в 1 джоуле?
Ответ 1.0E-15.
Мы предполагаем, что вы конвертируете между петаджоулей и джоулей .
Вы можете просмотреть более подробную информацию о каждой единице измерения:
петаджоул или
Джоуль
Единица, полученная из СИ для энергии — это джоул.
1 петаджоуль равен 1,0E + 15 джоулей.
Обратите внимание, что могут возникнуть ошибки округления, поэтому всегда проверяйте результаты.
Используйте эту страницу, чтобы узнать, как переводить петаджоули в джоули.
Введите свои числа в форме для преобразования единиц!
›› Таблица быстрых конверсий петаджоулей в джоул
1 петаджоуль в джоуль = 1,0E + 15 джоулей
2 петаджоуля в джоуль = 2.0E + 15 джоулей
3 петаджоуля в джоуль = 3.0E + 15 джоулей
4 петаджоуля в джоуль = 4.0E + 15 джоулей
5 петаджоулей в джоуль = 5.0E + 15 джоулей
6 петаджоулей в джоуль = 6.0E + 15 джоулей
7 петаджоулей в джоуль = 7.0E + 15 джоулей
8 петаджоулей в джоуль = 8.0E + 15 джоулей
9 петаджоулей в джоуль = 9.0E + 15 джоулей
10 петаджоулей в джоуль = 1,0E + 16 джоулей
›› Хотите другие юниты?
Вы можете сделать обратное преобразование единиц из от джоуля до петаджоуля или введите любые две единицы ниже:
›› Общие преобразования энергии
петаджоуля в метры килограмм-сила
петаджоуля в фунт стерлингов
петаджоуля в йоттаватур
петаджоулей в тонну
петаджоулей в хартри
петаджоулей в декагорель
ватт в 9 кегаваттопараоуглерод в
000000-киловатт в тысячах кавалерийских единиц
›› Определение: Петаджоуль
Приставка СИ «peta» представляет собой фактор 10 15 , или в экспоненциальной записи, 1E15.
Итак, 1 петаджоуль = 10 15 джоулей.
Определение джоуля следующее:
Джоуль (символ J, также называемый метром ньютона, ватт-секунда или кулоновское вольт) — это единица СИ энергии и работы. Единица произносится как рифму с «инструментом», и названа в честь физика Джеймса Прескотта Джоуля (1818-1889).
›› Определение: Джоуль
Джоуль (символ J, также называемый метром ньютона, ватт-секунда или кулоновское вольт) — это единица СИ энергии и работы.Единица произносится как рифму с «инструментом», и названа в честь физика Джеймса Прескотта Джоуля (1818-1889).
›› Метрические преобразования и многое другое
ConvertUnits.com предоставляет онлайн калькулятор преобразования для всех типов единиц измерения. Вы можете найти таблицы преобразования метрик для единиц СИ, а также как английские единицы, валюта и другие данные. Введите в единицу символы, сокращения или полные имена для единиц длины, площадь, масса, давление и др. типы.Примеры включают в себя мм, дюйм, 100 кг, жидкая унция США, 6’3 «, 10 камень 4, куб. см, метров в квадрате, граммы, родинки, футы в секунду и многое другое!
,Джоулей любовь — Википедия, день рождения
Джоулей любовь годы и любовь, любовь, время, когда вы производите различные виды энергии, от идеального газа до идеального, умного и приятного времени.
Joules første lov , også kendt som Joule effekt , er er fysiklov som udtrykker sammenhængen mellem varmen udviklet af elektriske strøm der løber gennem en elektrisk leder. После смерти Джеймса Прескотта Джоул Сом Форскеде и Фёменет в 1840 году.{2} \ cdot R \ cdot t}
hvor Q er varmen udviklet af en konstant электрическая цепь I der løber geném en leder med en resistans (modstand) R , i tiden t . Når strøm, Resistans og tid udtrykkes i hhv. Ампер, Ом Секундер, Er Enheden для Q Дж. Joules første lov kaldes nogle gange Joule – Lenz lov da loven uafhængigt senere blev opdaget af Heinrich Lenz. En leders varmende virkning når den passeres af strøm kaldes Joule-varme.
Joules and lov udtrykker at den indre энергетика на идеальном газе и газе, газе, газете, газете и газе.
I sammenhængen af resistive elektriske kredsløb og i lyset af energiens bevarelse og потенциал электричества er Joules forste lov og Ohms lov vkvivalente og udledes af hinanden (som forklaret af Mascart i 1883) [1] ОГ ОЛИВЕР ХЕВИСАЙД I 1894 [2] ), вы можете получить информацию об экспериментировании, о том, что вам нужно больше электричества, что и у вас, и у вас есть потенциал.
Joules forste lov udtrykker at tilførslen at varme i from a afivent varme fra en resistiv Электронный лидер пропорциональный медицинский квадрат и современное современное здание. Эффективное сопротивление резистора, описание которого приведено ниже: [3]
- п знак равно я 2 ⋅ р {\ displaystyle P = I ^ {2} \ cdot R \} ,
Joule kom til dette resultat eksperimentielt i 1841, ved at anvende et kalorimeter to måle varme — og et galvanometer til at måle strømmen, мед. [4] [5]
Loven gælder для всех, кто занимается омом лов. Ohms Lov angiver в пропорции, пропорциональной медиуму, в том числе в Омском модном стенде. Ohms lov udtrykker at for en, с учетом затраченных U на сумму R в зависимости от: [6] [7]
- я знак равно U р {\ displaystyle I = {\ dfrac {U} {R}} \} ,
Формулирует взгляд на вещи, которые я получил. I. Состязание по замене формы для стриминга и умопомрачительного фактора в мире. Р
- п знак равно U ⋅ я знак равно U 2 р {\ displaystyle P = U \ cdot I = {\ dfrac {U ^ {2}} {R}}} ,
Реляционен п знак равно U ⋅ я {\ displaystyle P = U \ cdot I} Это просто простой пример и конец Вступление Джоулс Лов Эллер Омс Лав, да ден берёгнер ден шебликклидж эффект в течение нескольких лет U в течение года I енгесберг в эссе, США. [8] Я объединил свои взгляды с любовью к Эллеру Джоулю Лову, Кан Ден Анвендесу в Удле-ден-ден-Эллер-ден-Анден. [9]
Эффективность и эффективность в современных условиях (общая стоимость) за каждую неделю и общую сумму 9009: [10]
- Q знак равно я 2 ⋅ р ⋅ T знак равно U ⋅ я ⋅ T знак равно U 2 р ⋅ T {\ displaystyle Q = I ^ {2} \ cdot R \ cdot t = U \ cdot I \ cdot t = {\ dfrac {U ^ {2}} {R}} \ cdot t}

