Топографическая карта Московская область, высота, рельеф
Нажмите на карту, чтобы отобразить высоту.
Об этой карте
Название: Топографическая карта Московская область, высота, рельеф.
Местонахождение: Московская область, Центральный федеральный округ, Россия (54.25570 35.14850 56.95851 40.20569)
Средняя высота: 166 м
Минимальная высота: 87 м
Максимальная высота: 302 м
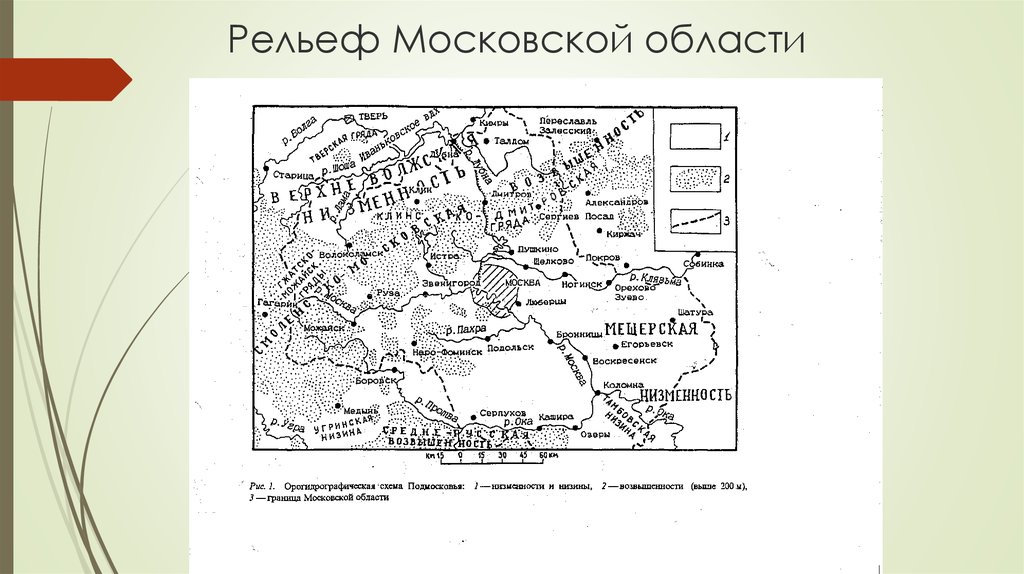
Рельеф Московской области в основном равнинный; западную часть занимают холмистые возвышенности (высоты больше 160 м), восточную — обширные низменности[14].
Другие топографические карты
Нажмите на карту, чтобы просмотреть ее топографию, ее высоту и ее рельеф.
Ленинградская область
Россия
org/Place» lang=»ru»>Ленинградская область, Северо-Западный федеральный округ, РоссияСредняя высота: 89 м
Москва
Россия
Москва, Центральный федеральный округ, Россия
Средняя высота: 163 м
Краснодарский край
Россия
Краснодарский край, Южный федеральный округ, Россия
Средняя высота: 202 м
Москва
Россия
Москва, Центральный федеральный округ, Россия
Средняя высота: 178 м
Санкт-Петербург
Россия
org/Place» lang=»ru»>Санкт-Петербург, Северо-Западный федеральный округ, РоссияСредняя высота: 17 м
Новосибирск
Россия > Новосибирская область
Новосибирск, Новосибирская область, Сибирский федеральный округ, 630000, Россия
Средняя высота: 146 м
Нижегородская область
Россия
Нижегородская область, Приволжский федеральный округ, Россия
Средняя высота: 130 м
Казань
Россия > Татарстан
Казань, Татарстан, Приволжский федеральный округ, Россия
Средняя высота: 105 м
Санкт-Петербург
Россия
org/Place» lang=»ru»>Санкт-Петербург, Северо-Западный федеральный округ, 190000, РоссияСредняя высота: 41 м
Ростов-на-Дону
Россия > Ростовская область > городской округ Ростов-на-Дону
Ростов-на-Дону, городской округ Ростов-на-Дону, Ростовская область, Южный федеральный округ, Россия
Средняя высота: 51 м
Красноярск
Россия > Красноярский край > городской округ Красноярск
Красноярск, городской округ Красноярск, Красноярский край, Сибирский федеральный округ, 660000, Россия
Средняя высота: 287 м
Екатеринбург
Россия > Свердловская область > городской округ Екатеринбург
org/Place» lang=»ru»>Екатеринбург, городской округ Екатеринбург, Свердловская область, Уральский федеральный округ, РоссияСредняя высота: 289 м
Крымский полуостров
Россия > Автономная Республика Крым
Крымский полуостров, Автономная Республика Крым, Южный федеральный округ, Россия
Средняя высота: 36 м
Свердловская область
Россия
Свердловская область, Уральский федеральный округ, Россия
Средняя высота: 175 м
Воронеж
Россия > Воронежская область > городской округ Воронеж
org/Place» lang=»ru»>Воронеж, городской округ Воронеж, Воронежская область, Центральный федеральный округ, РоссияСредняя высота: 132 м
Челябинск
Россия > Челябинская область > Челябинский городской округ
Челябинск, Челябинский городской округ, Челябинская область, Уральский федеральный округ, Россия
Средняя высота: 231 м
Уфа
Россия > Башкортостан > городской округ Уфа
Уфа, городской округ Уфа, Башкортостан, Приволжский федеральный округ, 450000, Россия
Средняя высота: 129 м
Ставрополь
Россия > Ставропольский край > городской округ Ставрополь
org/Place» lang=»ru»>Ставрополь, городской округ Ставрополь, Ставропольский край, Северо-Кавказский федеральный округ, 355000, РоссияСредняя высота: 526 м
Саратов
Россия > Саратовская область
Саратов, Саратовская область, Приволжский федеральный округ, 410000, Россия
Средняя высота: 82 м
Нижний Новгород
Россия > Нижегородская область > городской округ Нижний Новгород
Нижний Новгород, городской округ Нижний Новгород, Нижегородская область, Приволжский федеральный округ, Россия
Средняя высота: 93 м
Калининград
Россия > Калининградская область > городской округ Калининград
org/Place» lang=»ru»>Калининград, городской округ Калининград, Калининградская область, Северо-Западный федеральный округ, РоссияСредняя высота: 20 м
Краснодар
Россия > Краснодарский край > городской округ Краснодар
Краснодар, городской округ Краснодар, Краснодарский край, Южный федеральный округ, 350000, Россия
Средняя высота: 28 м
Тюмень
Россия > Тюменская область > городской округ Тюмень
Тюмень, городской округ Тюмень, Тюменская область, Уральский федеральный округ, Россия
Средняя высота: 72 м
Самарская область
Россия
org/Place» lang=»ru»>Самарская область, Приволжский федеральный округ, РоссияСредняя высота: 130 м
Ярославская область
Россия
Ярославская область, Центральный федеральный округ, Россия
Средняя высота: 139 м
Москва | История, география, население и карта
Сводка
Прочтите краткий обзор этой темы
Москва , Россия Москва , город, столица России, расположенный в крайне западной части страны. С момента первого упоминания в летописях 1147 года Москва сыграла жизненно важную роль в русской истории. Он стал столицей Московии (Великого княжества Московского) в конце 13 века; следовательно, жители Москвы известны как москвичи. Сегодня Москва — не только политический центр России, но и самый густонаселенный город страны, ее промышленная, культурная, научная и образовательная столица. Более 600 лет Москва также является духовным центром Русской Православной Церкви.
Более 600 лет Москва также является духовным центром Русской Православной Церкви.
Столица Союза Советских Социалистических Республик (СССР) до его распада в 1991 году. Москва привлекала внимание всего мира как центр коммунистической власти; действительно, название резиденции бывшего советского правительства и преемника российского правительства, Кремль (русский язык: Кремль), было синонимом советской власти. Распад СССР привел к огромным экономическим и политическим изменениям, а также к значительной концентрации российского богатства в Москве. Площадь 414 квадратных миль (1035 квадратных километров). Поп. (2010) город, 11 738 547; (оценка 2020 г.) город, 12 678 079 человек.
Если Санкт-Петербург — это российское «окно в Европу», то Москва — это сердце России. Это оптимистичный, яркий, а иногда и утомительный город. Большая часть Москвы была реконструирована после того, как она была оккупирована французами при Наполеоне I в 1812 году и почти полностью уничтожена пожаром.
Стало привычным сравнивать Москву с Санкт-Петербургом, ее соперником и бывшей (1712–1918) столицей России. В то время как Санкт-Петербург впитал в себя западноевропейские влияния, Москва считается традиционным русским городом. В отличие от своего соперника, Москва имеет четко определенный центр города, отмеченный Кремлем. Другими характеристиками Москвы являются ее физическая планировка в виде радиальных спиц и колец, которые были расширены с течением времени, ее мешанина из архитектурных стилей и ее исторические здания, которые в основном были построены русскими архитекторами. Застройка Москвы была преимущественно деревянной до 19 века.20-х годов, когда в обиход вошли кирпич и камень.
В то время как Санкт-Петербург впитал в себя западноевропейские влияния, Москва считается традиционным русским городом. В отличие от своего соперника, Москва имеет четко определенный центр города, отмеченный Кремлем. Другими характеристиками Москвы являются ее физическая планировка в виде радиальных спиц и колец, которые были расширены с течением времени, ее мешанина из архитектурных стилей и ее исторические здания, которые в основном были построены русскими архитекторами. Застройка Москвы была преимущественно деревянной до 19 века.20-х годов, когда в обиход вошли кирпич и камень.
Викторина «Британника»
Викторина «Столицы Азии»
Насколько хорошо вы знаете столицы Азии? Этот тест покажет вам название страны на азиатском континенте, и вам нужно будет определить ее столицу.
Математика | Бесплатный полнотекстовый | Взаимодействие уединенных волн с внешней периодической силой: расширенная концепция Кортевега-де Фриза
1. Введение
Взаимодействие уединенных волн с внешней силой представляет большой интерес и активно изучается в последние десятилетия. Внешняя сила обычно моделирует локализованную топографию или движущийся источник, распространяющийся вдоль свободной поверхностной волны [1]. Основной базой для изучения таких взаимодействий и, возможно, самой простой является вынужденное уравнение Кортевега-де Фриза (fKdV) [2, 3, 4, 5, 6, 7, 8]. Однако в последние годы эти взаимодействия исследовались в различных рамках, таких как уравнения Эйлера [9].], вынужденное модифицированное уравнение Кортевега-де Фриза (mKdV) [10] и неинтегрируемое вынужденное уравнение Уизема [11,12]. Интересное явление, которое происходит во время этих взаимодействий, называется захваченными волнами, которые описываются как волны, которые отскакивают назад и вперед под действием внешней силы, оставаясь захваченными в течение длительного времени. Это явление возникает, когда скорость уединенной волны и внешняя сила почти находятся в резонансе.
Внешняя сила обычно моделирует локализованную топографию или движущийся источник, распространяющийся вдоль свободной поверхностной волны [1]. Основной базой для изучения таких взаимодействий и, возможно, самой простой является вынужденное уравнение Кортевега-де Фриза (fKdV) [2, 3, 4, 5, 6, 7, 8]. Однако в последние годы эти взаимодействия исследовались в различных рамках, таких как уравнения Эйлера [9].], вынужденное модифицированное уравнение Кортевега-де Фриза (mKdV) [10] и неинтегрируемое вынужденное уравнение Уизема [11,12]. Интересное явление, которое происходит во время этих взаимодействий, называется захваченными волнами, которые описываются как волны, которые отскакивают назад и вперед под действием внешней силы, оставаясь захваченными в течение длительного времени. Это явление возникает, когда скорость уединенной волны и внешняя сила почти находятся в резонансе.
Полное асимптотическое исследование захваченных волн для уравнения фКдФ было проведено Гримшоу и его сотрудниками для локализованной внешней силы [13,14]. В асимптотике были выделены три типа режимов. Уединенная волна может отскакивать назад и вперед от внешней силы, оставаясь захваченной в течение длительного времени, она может проходить над внешней силой, не меняя своего направления, или оставаться устойчивой при внешней силе. Кроме того, в этих работах авторы обнаружили, что результаты в рамках разработанной асимптотики хорошо согласуются с численными предсказаниями. Что касается внешней периодической силы, то в отличие от локализованной внешней силы излучение спонтанно генерируется по всей области. Это поднимает естественную проблему, которая состоит в том, чтобы описать, какие волны на самом деле возникают из-за взаимодействия между уединенной волной и внешней силой или только из-за излучения из-за нелокализованной внешней силы. Для решения этого вопроса Маломед [15] предложил замену переменных для разделения этих двух типов генерируемых волн и асимптотически исследовал излучение солитонов при наличии внешней периодической силы в рамках уравнения фКдФ.
В асимптотике были выделены три типа режимов. Уединенная волна может отскакивать назад и вперед от внешней силы, оставаясь захваченной в течение длительного времени, она может проходить над внешней силой, не меняя своего направления, или оставаться устойчивой при внешней силе. Кроме того, в этих работах авторы обнаружили, что результаты в рамках разработанной асимптотики хорошо согласуются с численными предсказаниями. Что касается внешней периодической силы, то в отличие от локализованной внешней силы излучение спонтанно генерируется по всей области. Это поднимает естественную проблему, которая состоит в том, чтобы описать, какие волны на самом деле возникают из-за взаимодействия между уединенной волной и внешней силой или только из-за излучения из-за нелокализованной внешней силы. Для решения этого вопроса Маломед [15] предложил замену переменных для разделения этих двух типов генерируемых волн и асимптотически исследовал излучение солитонов при наличии внешней периодической силы в рамках уравнения фКдФ. Он показал, что внешняя сила не захватывает солитоны. В самом деле, под действием радиационных потерь солитон, двигавшийся медленнее внешней силы, дополнительно тормозится, а тот, который двигался быстрее, ускоряется. Численные результаты, подтверждающие его выводы, были представлены позже Grimshaw et al. [16].
Он показал, что внешняя сила не захватывает солитоны. В самом деле, под действием радиационных потерь солитон, двигавшийся медленнее внешней силы, дополнительно тормозится, а тот, который двигался быстрее, ускоряется. Численные результаты, подтверждающие его выводы, были представлены позже Grimshaw et al. [16].
Хотя fKdV широко используется в качестве первого приближения для изучения многих нелинейных явлений, когда солитоны имеют большую амплитуду или нелинейность преобладает в явлении распространения волн, необходимо учитывать нелинейные члены более высокого порядка. В этом случае возникает вынужденное расширенное уравнение КдФ (eKdV) или вынужденное уравнение Гарднера. Это уравнение включает в себя квадратичную и кубическую нелинейность. Среди проблем, которые могут быть исследованы в рамках этого подхода, отметим внутренние волны в двухслойных жидкостях. В данном конкретном случае знак кубического члена зависит от стратификации океана. Хотя уравнение эКдФ интегрируемо, нелинейная динамика более сложна, чем уравнение фКдФ, и знак кубической нелинейности играет фундаментальную роль в качественном поведении решений. Например, уравнение эКдФ более интересно, чем уравнение фКдФ, в том смысле, что оно описывает различные типы волновых решений, а не только солитоны. ЭКдФ допускает в качестве решений, например, солитоны обеих полярностей, бризеры (бегущие колеблющиеся движущиеся волновые пакеты) и бездиссипативные ударные волны. Сосредоточив внимание на захваченных волнах, Гримшоу и Пелиновский [17] вывели нелинейную динамическую систему второго порядка для амплитуды и положения гребня солитона для изучения взаимодействия солитона и локализованной внешней силы. Кроме того, получены условия захвата или отталкивания солитона внешней силой. Однако, насколько нам известно, нет статей с вынужденной эКдФ, изучающих захваченные волны в присутствии внешнего периодического волнового поля.
Например, уравнение эКдФ более интересно, чем уравнение фКдФ, в том смысле, что оно описывает различные типы волновых решений, а не только солитоны. ЭКдФ допускает в качестве решений, например, солитоны обеих полярностей, бризеры (бегущие колеблющиеся движущиеся волновые пакеты) и бездиссипативные ударные волны. Сосредоточив внимание на захваченных волнах, Гримшоу и Пелиновский [17] вывели нелинейную динамическую систему второго порядка для амплитуды и положения гребня солитона для изучения взаимодействия солитона и локализованной внешней силы. Кроме того, получены условия захвата или отталкивания солитона внешней силой. Однако, насколько нам известно, нет статей с вынужденной эКдФ, изучающих захваченные волны в присутствии внешнего периодического волнового поля.
В данной статье, в отличие от упомянутых выше работ, основное внимание уделяется взаимодействию уединенных волн с периодической внешней силой в рамках вынужденного уравнения эКдФ.
План настоящей статьи выглядит следующим образом. В разделе 2 вводится вынужденное уравнение эКдФ. Асимптотические и численные результаты представлены в разделе 3. Обсуждение и выводы представлены в разделе 4 и разделе 5 соответственно.
В разделе 2 вводится вынужденное уравнение эКдФ. Асимптотические и численные результаты представлены в разделе 3. Обсуждение и выводы представлены в разделе 4 и разделе 5 соответственно.
2. Принудительно расширенное уравнение Кортевега-де Фриза
Расширенное уравнение Кортевега-де Фриза в канонической форме с внешним силовым членом рассматривается как модель для изучения захваченных волн
где U(x,t) — профиль поверхностной волны, f(x+Δt) — внешняя периодическая сила, распространяющаяся с постоянной скоростью Δ, а ϵ>0 — малый параметр. Уравнение (1) удобно переписать в подвижной системе отсчета внешней силы. Следовательно,
Это уравнение сохраняет массу (M(t)), при этом
а скорость изменения импульса (P(t)) уравновешивается внешней силой как
В отсутствие внешней силы эКдФ допускает в качестве решений два семейства уединенных волн [18], которые даются выражениями
Здесь мы анализируем только уединенные волны возвышения (B>0), амплитуда которых
Внешняя периодическая сила моделируется функцией
где A — его амплитуда, q — волновое число.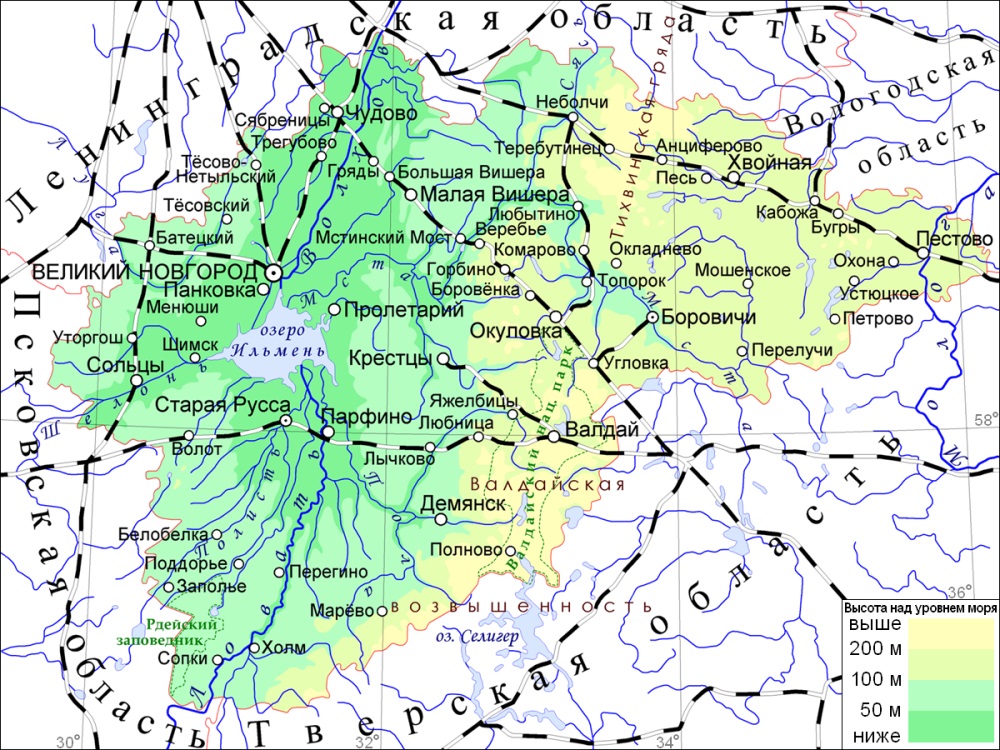 Поскольку возмущение f не локализовано, оно производит излучение по всей области, даже далеко от того места, где локализована большая часть энергии уединенной волны. Хотя это не влияет на асимптотическое исследование низших порядков, оно может вызвать затруднения при численном исследовании. По этой причине мы используем прием, аналогичный тому, который проделал Маломед [15]. Вставка в уравнение (2)
Поскольку возмущение f не локализовано, оно производит излучение по всей области, даже далеко от того места, где локализована большая часть энергии уединенной волны. Хотя это не влияет на асимптотическое исследование низших порядков, оно может вызвать затруднения при численном исследовании. По этой причине мы используем прием, аналогичный тому, который проделал Маломед [15]. Вставка в уравнение (2)
куда
является решением линеаризованного уравнения feKdV (2), имеем, что u(x,t) удовлетворяет условию
Следовательно, в первом приближении получаем новое уравнение
где возмущение теперь локализовано вдоль свободной поверхности u(x,t).
3. Результаты
3.1. Асимптотическая теория
В этом разделе мы вводим асимптотическую теорию, которая позволяет превратить исследование уравнения в частных производных (2) в динамическую систему.
Асимптотические результаты взаимодействия уединенной волны с внешней силой впервые были получены Гримшоу и Пелиновским [17]. Для полноты напомним их основные результаты, предполагая, что f(X)→0 при |X|→∞. Для слабой внешней силы (ϵ≪1) ищем медленно меняющуюся во времени уединенную волну с расширением
где X(t) — положение гребня волны. В первом порядке профиль волны определяется выражением
В частности, изменение амплитуды как функцию времени можно получить из уравнения импульса первого порядка (4)
и его скорость изменения в первом порядке, которая дается выражением
Обратите внимание, что P0 является функцией γ(t), поэтому динамическая система (10)–(12) описывает амплитуду и положение гребня решения уединенной волны.
Кроме того, в режиме слабой амплитуды уединенной волны (a ≪ 1) величины M0, P0, γ могут быть получены в явном виде
Таким образом, динамическая система для амплитуды и положения гребня имеет вид
Из уравнения (15) имеем, что положение гребня уединенной волны описывается осциллятором
Здесь мы формально считаем, что периодическая внешняя сила определяется уравнением (7). В самом деле, если внешняя сила широка по сравнению с длиной солитона, асимптотическая теория справедлива для любой функции f(X) — не только с исчезающими концами. Он работает для периодических внешних сил с малыми значениями q. Можно показать, что точками равновесия этой динамической системы являются точки x=π/2q+kπ, где k — целое число. Центры выровнены с гребнями внешней силы, а седла выровнены с впадинами внешней силы. Следовательно, при изменении знака A центры становятся седлами, и наоборот.
Решения динамической системы (15) представлены линиями тока, т. е. решениями являются линии уровня функции тока H(X,a), которая задается формулой
На рис. 1 представлены типичные фазовые портреты динамической системы (15). Напомним, что замкнутая орбита иллюстрирует уединенную волну, которая захватывается без излучения из-за ее взаимодействия с внешней силой, в то время как незамкнутая орбита представляет собой уединенную волну, которая распространяется без изменения направления.
3.2. Численные результаты
Уравнение (8) решается численно в периодической расчетной области [−L,L] с равномерной сеткой из N точек с использованием псевдоспектрального метода Фурье с интегрирующим коэффициентом [21]. Расчетная область берется достаточно большой, чтобы исключить влияние пространственной периодичности. Эволюция во времени рассчитывается методом Рунге-Кутты четвертого порядка с шагом по времени Δt. Типичные расчеты выполняются с использованием N=212 мод Фурье L=512 и Δt=10−3 в MATLAB. Чтобы проверить точность численных решений, симуляции сравниваются с использованием разного количества мод Фурье (213 и 214), и результаты совпадают.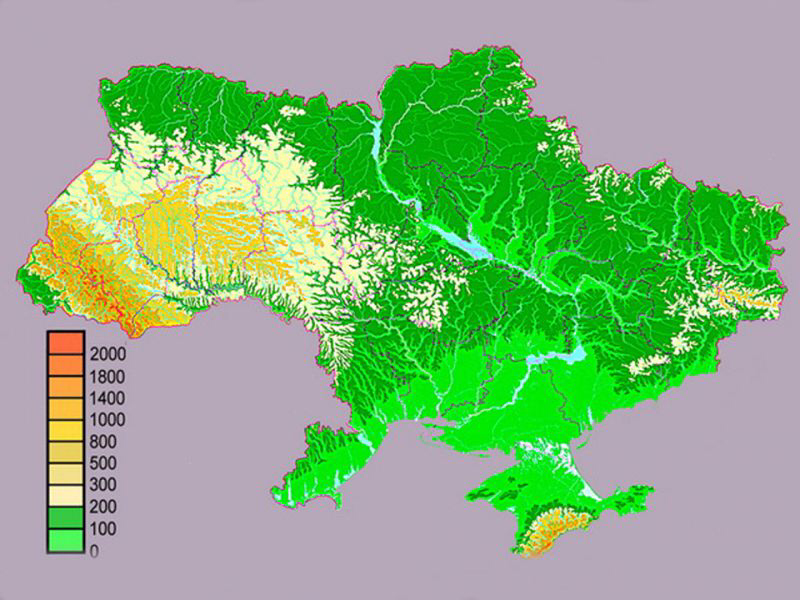 Исследование разрешающей способности аналогичного численного метода можно найти в [1]. [7].
Исследование разрешающей способности аналогичного численного метода можно найти в [1]. [7].
Чтобы сравнить численные решения с асимптотическими предсказаниями, мы проверяем, представляют ли точки равновесия динамической системы (15) качественные решения уравнения (8). Другими словами, мы проверяем, представляет ли точка рядом с седловой точкой уединенную волну, которая движется, не меняя своего направления на противоположное, и соответствует ли центральная точка захваченной уединенной волне. Поскольку существует длинный список параметров, которые необходимо учитывать при изучении взаимодействия уединенной волны с внешней силой (7), мы фиксируем несколько параметров, а именно: ϵ=0,01, A=−1, γ=1 и q=(π/L)n, где n — целое число, представляющее количество волн в интервале [−L,L]. Таким образом, большие значения n представляют высокие частоты, а малые значения n представляют низкие частоты. Обратите внимание, что при таком выборе параметров начальная уединенная волна имеет амплитуду (а), как определено в уравнении (6). Кроме того, начальные уединенные волны выбираются так, чтобы их гребни располагались в точке x=x0, где x0=±π/2q. Напомним, что согласно динамической системе (15), выбирая ∆=−2a и положение гребня x0=+π/2q, имеем седло, а выбирая ∆=−2a и положение гребня x0=−π /2q, получаем центр.
Кроме того, начальные уединенные волны выбираются так, чтобы их гребни располагались в точке x=x0, где x0=±π/2q. Напомним, что согласно динамической системе (15), выбирая ∆=−2a и положение гребня x0=+π/2q, имеем седло, а выбирая ∆=−2a и положение гребня x0=−π /2q, получаем центр.
Сначала рассмотрим простейший случай — седловые точки. С этой целью мы запускаем большое количество симуляций и наблюдаем, что уединенные волны проходят мимо внешней силы, не меняя своего направления. Однако отражение наблюдается, когда уединенная волна проходит через несколько неровностей. Отражение уменьшается с увеличением частоты внешней силы, что вызывает изменение амплитуды уединенных волн. Это типичное поведение показано на рисунке 2 для различных значений параметра n. Детали изменения амплитуды уединенной волны для случая n = 120 приведены на рис. 3. Обратите внимание, что амплитуда уединенной волны колеблется при прохождении через каждый удар внешней силы (см. рис. 3 (слева)) . Кроме того, скорость уединенной волны продолжает колебаться во времени из-за взаимодействия с внешней силой, как показано на рисунке 3 (справа). Эта динамика качественно представлена незамкнутыми орбитами динамической системы (15), см. рис. 1 (слева). На самом деле, полностью численное моделирование и динамическая система количественно хорошо согласуются при малых временах. Чтобы убедиться в этом, вспомним, что асимптотическая теория получается путем усечения членов уравнения (9).) порядка O(ϵ), который соответствует тому же порядку изменения амплитуды, что и на рисунке 3 (слева).
Эта динамика качественно представлена незамкнутыми орбитами динамической системы (15), см. рис. 1 (слева). На самом деле, полностью численное моделирование и динамическая система количественно хорошо согласуются при малых временах. Чтобы убедиться в этом, вспомним, что асимптотическая теория получается путем усечения членов уравнения (9).) порядка O(ϵ), который соответствует тому же порядку изменения амплитуды, что и на рисунке 3 (слева).
Теперь мы исследуем, определяют ли центральные точки динамической системы (15) захваченные волны для уравнения (8). Итак, мы позволяем q варьироваться и сравниваем численные результаты в рамках асимптотики. При больших значениях n уединенная волна практически не ощущает внешней силы, следовательно, уединенная волна остается практически стационарной, напоминая центральную точку равновесия динамической системы (15). Когда мы уменьшаем значения n, например, n=120, 60, 30, 15, уединенная волна отскакивает назад и вперед близко к своему начальному положению в течение больших времен с небольшим излучением. Эти результаты согласуются с результатами, предсказываемыми асимптотической теорией, и проиллюстрированы на рис. 4. Мы видим, что большие значения параметра n приводят к малым колебаниям положения гребня уединенной волны, т.е. ближе всего уединенная волна остается в исходном положении. На рисунке 5 (слева) мы отображаем зависимость амплитуды от гребня положения уединенной волны, а положение ее гребня во времени показано на рисунке 5 (справа) для n=60. Обратите внимание, что динамика амплитуды в фазе зависимости амплитуды от положения гребня напоминает неустойчивую спираль. При этом мы наблюдаем, что положение гребня колеблется, увеличиваясь во времени. Это указывает на то, что уединенная волна может удалиться от своего начального положения. Стоит отметить, что это не противоречит предсказаниям асимптотической теории, поскольку ожидается, что обе теории хорошо согласуются только на малых временах. Примечательно, что при малых возмущениях Δ=−2a уединенные волны все же остаются захваченными вблизи своих начальных положений на большие времена.
Эти результаты согласуются с результатами, предсказываемыми асимптотической теорией, и проиллюстрированы на рис. 4. Мы видим, что большие значения параметра n приводят к малым колебаниям положения гребня уединенной волны, т.е. ближе всего уединенная волна остается в исходном положении. На рисунке 5 (слева) мы отображаем зависимость амплитуды от гребня положения уединенной волны, а положение ее гребня во времени показано на рисунке 5 (справа) для n=60. Обратите внимание, что динамика амплитуды в фазе зависимости амплитуды от положения гребня напоминает неустойчивую спираль. При этом мы наблюдаем, что положение гребня колеблется, увеличиваясь во времени. Это указывает на то, что уединенная волна может удалиться от своего начального положения. Стоит отметить, что это не противоречит предсказаниям асимптотической теории, поскольку ожидается, что обе теории хорошо согласуются только на малых временах. Примечательно, что при малых возмущениях Δ=−2a уединенные волны все же остаются захваченными вблизи своих начальных положений на большие времена. В частности, он показывает, что асимптотическая теория для широкой внешней силы в слабоамплитудном режиме уединенной волны дает хорошие качественные результаты.
В частности, он показывает, что асимптотическая теория для широкой внешней силы в слабоамплитудном режиме уединенной волны дает хорошие качественные результаты.
При малом n численные результаты отличаются от асимптотической теории. Фактически асимптотический метод не работает при малых значениях q. Это происходит потому, что при слишком малых значениях q форсировка пропорциональна ϵ2. Следовательно, на уединенные волны не действует внешняя сила. На рис. 6 показана эволюция двух уединенных волн при малых значениях n. Обратите внимание, что уединенная волна распространяется влево, не меняя своего направления. Более того, изменение амплитуды этих уединенных волн невелико (см. рис. 7 (слева)) и скорость уединенной волны почти постоянна, как показано на рис. 7 (справа). Вначале амплитуда уединенной волны подстраивается под внешнюю силу, а затем изменяется незначительно. Следовательно, уединенная волна распространяется почти как классическое уединенное решение невынужденной задачи (1).
Следует отметить, что аналогичные результаты наблюдаются при положительном выборе амплитуды внешней силы (А). Чтобы проиллюстрировать это, мы ограничимся показом рис. 8. Сравнив соответствующие панели рис. 4 и рис. 8, мы увидим, что все они одинаковы, за исключением переводов.
4. Обсуждение
Представленные здесь результаты дополняют серию исследований, проведенных в литературе для локализованных внешних сил. Эта работа может быть распространена на несколько других уравнений, таких как вынужденное уравнение мКдФ, уравнение Шамеля и даже на неинтегрируемое семейство уравнений Уизема, что является тенденцией последних нескольких лет, особенно с теоретической точки зрения. Хотя мы рассмотрели только пространственные периодические внешние поля, можно также рассматривать поля, зависящие от времени, и динамика должна быть более интересной. Кроме того, хотя мы и не акцентировали внимание на применимости результатов, обсуждаемых в этой статье, они могут быть интерпретированы не только в теории волн на воде, но и в других разделах физики, например, поверхностных волнах в электрических нормальных полях и атмосферных волнах и упругих волн в твердых телах, что делает наше исследование актуальным.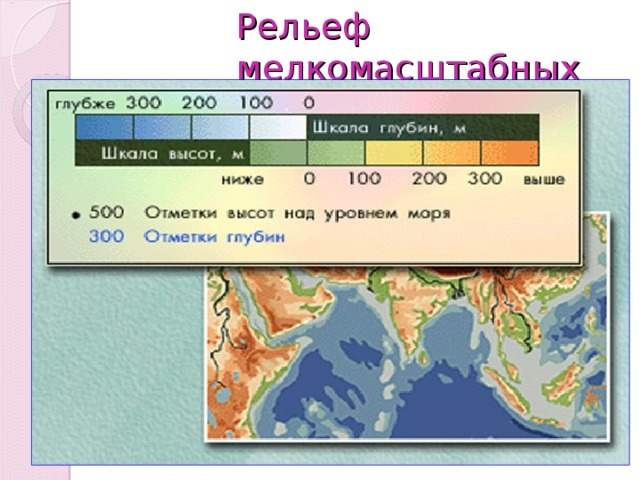
5. Выводы
В данной работе асимптотически и численно исследовано взаимодействие уединенных волн с внешней периодической силой в рамках уравнения сеКдФ. Мы обнаружили, что уединенная волна может оставаться устойчивой, если ее амплитуда и положение гребня выбраны соответствующим образом, поскольку она может отражаться взад и вперед вблизи своего начального положения или может просто удаляться от своих начальных положений. Эти результаты качественно согласуются в рамках асимптотической теории, рассматривающей широкую внешнюю силу по сравнению с длиной уединенной волны. Однако, когда волновое число периодического воздействия слишком мало, асимптотика не выполняется, поскольку уединенные волны дольше задерживаются в уравнении эКдФ.
Вклад авторов
Концептуализация, Е.П. и М.В.Ф.; методология и анализ, Е.П. и М.В.Ф.; написание М.В.Ф. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Исследование поддерживается грантом RSF 19-12-00253 (раздел 3).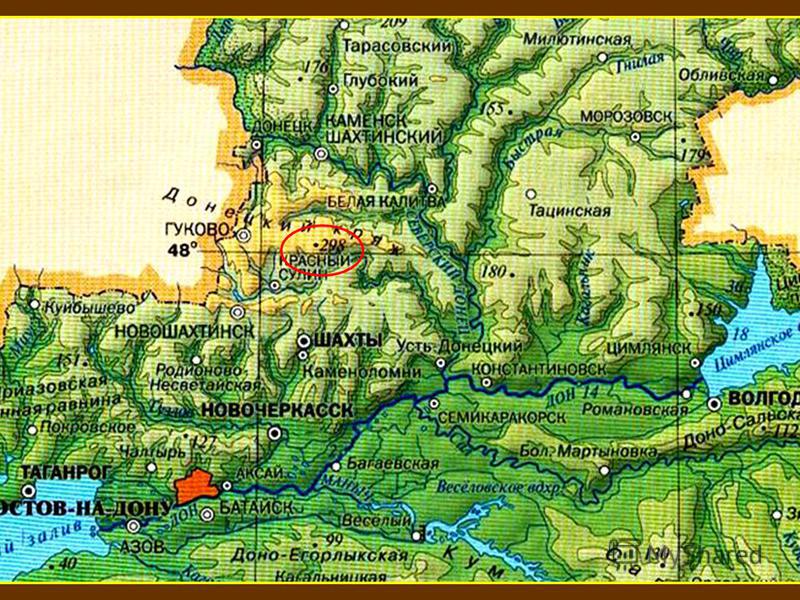
Заявление об информированном согласии
Информированное согласие было получено от всех участников исследования.
Заявление о доступности данных
Неприменимо.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Ссылки
- Бейнс, С. Топографические эффекты в стратифицированных потоках; Издательство Кембриджского университета: Кембридж, Великобритания, 1995. [Google Scholar]
- Lee, S.; Ванг, С. Захваченные сверхкритические волны для вынужденного уравнения КдФ с двумя ударами. заявл. Мат. Модель. 2015 , 39, 2649–2660. [Google Scholar] [CrossRef]
- Lee, S. Динамика захваченных уединенных волн для вынужденного уравнения КдФ. Симметрия 2018 , 10, 129. [Google Scholar] [CrossRef]
- Ким Х.; Чой, Х. Исследование захвата волны между двумя препятствиями в вынужденном уравнении Кортевега-де Фриза.
 Дж. Инж. Мат. 2018 , 108, 197–208. [Google Scholar] [CrossRef]
Дж. Инж. Мат. 2018 , 108, 197–208. [Google Scholar] [CrossRef] - Ермаков А.; Степанянц, Ю. Взаимодействие солитона с внешним воздействием в рамках уравнения Кортевега-де Фриза. Chaos 2019 , 29, 013117. [Google Scholar] [CrossRef] [PubMed]
- Flamarion, M.V.; Рибейро, Р., младший. Взаимодействие уединенных волн воды для принудительного уравнения Кортевега-де Фриза. Комп. заявл. Мат. 2021 , 40, 312. [Google Scholar] [CrossRef]
- Фламарион, М.В.; Рибейро, Р., младший. Гравитационно-капиллярные течения над препятствиями для вынужденного уравнения Кортевега-де Фриза пятого порядка. Дж. Инж. Мат. 2021 , 129, 1–17. [Google Scholar] [CrossRef]
- Flamarion, M.V. Генерация уединенных волн захваченной депрессии в гравитационно-капиллярных течениях над препятствием. Комп. заявл. Мат. 2022 , 41, 31. [Google Scholar] [CrossRef] «> Фламарион, М.В.; Рибейро, Р., младший. Взаимодействие уединенной волны в ловушке для уравнений Эйлера с областью низкого давления. Комп. заявл. Мат. 2021 , 40, 20. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Пелиновский, Э. Взаимодействие солитонов с внешним воздействием: модифицированная структура Кортевега-де Фриза. Солитоны Хаоса Фракталы 2022 , 165, 112889. [Google Scholar] [CrossRef]
- Фламарион М.В. Волны, генерируемые затопленной топографией для уравнения Уизема. Междунар. Дж. Заявл. вычисл. Мат. 2022 , 8, 257. [Google Scholar] [CrossRef]
- Фламарион, М.В. Захваченные волны, генерируемые ускоренным движущимся возмущением, для уравнения Уизема. Частичный. Отличаться. Экв. заявл. Мат. 2022 , 5, 100356. [Google Scholar] [CrossRef]
- Гримшоу, Р.; Пелиновский, Э.; Тиан, X. Взаимодействие уединенной волны с внешней силой. физ. Д 1994 , 77, 405–433.
 [Google Scholar] [CrossRef]
[Google Scholar] [CrossRef] - Гримшоу, Р.; Пелиновский, Э.; Павел С. Взаимодействие уединенной волны с внешней силой, движущейся с переменной скоростью. Стад. заявл. Мат. 1996 , 142, 433–464. [Google Scholar]
- Маломед Б.А. Эмиссия излучения солитоном КдВ при периодическом воздействии. физ. лат. А 1993 , 172, 373–377. [Google Scholar] [CrossRef]
- Гримшоу, Р.; Маломед, Б.А.; Тиан, X. Динамика солитона КдФ из-за периодического воздействия. физ. лат. А 1993 , 179, 291–298. [Google Scholar] [CrossRef]
- Гримшоу, Р.; Пелиновский Э. Взаимодействие уединенной волны с внешней силой в расширенном уравнении Кортевега-де Фриза. Междунар. Дж. Бифуркат. Хаос 2002 , 12, 2409–2419. [Google Scholar] [CrossRef]
- Гримшоу, Р.; Пелиновский, Э.; Талипова Т.; Куркина О. Внутренние уединенные волны: Распространение, деформация и распад.
 Нелинейный процесс. Геофиз. 2010 , 17, 633–649. [Google Scholar] [CrossRef]
Нелинейный процесс. Геофиз. 2010 , 17, 633–649. [Google Scholar] [CrossRef] - Frassu, S.; Viglialoro, G. Критерии ограниченности для класса непрямых (и прямых) моделей потребления хемотаксиса в больших измерениях. заявл. Мат. лат. 2022 , 132, 108108. [Google Scholar] [CrossRef]
- Frassu, S.; Гальван, Р.Р.; Вильялоро, Г. Равномерное во времени L ∞ -оценки для модели хемотаксиса притяжения-отталкивания с двойным насыщением. Дискретный. Контин. Дин. Сист.-Б 2023 , 28, 1886–1904. [Google Scholar] [CrossRef]
- Trefethen, L.N. Спектральные методы в MATLAB; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
Рис. 1. Фазовые портреты динамической системы (15) при Δ=−1. Кружки соответствуют центрам, крестики – седлам динамической системы (15).
Рисунок 1. Фазовые портреты динамической системы (15) при Δ=−1. Кружки соответствуют центрам, крестики – седлам динамической системы (15).
Рисунок 2. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=+π/2q, A=−1.
Рисунок 2. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=+π/2q, A=−1.
Рисунок 3. Слева : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рис. 2 с n=120.
Рисунок 3. Левый : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рис. 2 с n=120.
Рисунок 4. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=−π/2q, A=−1.
Рисунок 4. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=−π/2q, A=−1.
Рисунок 5. Слева : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рис. 4 с n=60.
Параметры такие же, как на рис. 4 с n=60.
Рисунок 5. Слева : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рис. 4 с n=60.
Рисунок 6. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=−π/2q, A=−1.
Рисунок 6. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=−π/2q, A=−1.
Рисунок 7. Слева : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рисунке 6 с n=1.
Рис. 7. Слева : пространственная амплитуда в зависимости от положения гребня. Справа : положение гребня во времени. Параметры такие же, как на рисунке 6 с n=1.
Рисунок 8. Уединенные волновые решения при периодическом воздействии. Параметры: Δ=−2a, x0=π/2q, A=1.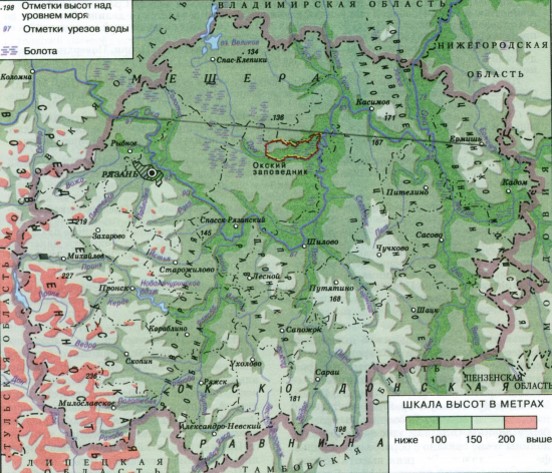


 Дж. Инж. Мат. 2018 , 108, 197–208. [Google Scholar] [CrossRef]
Дж. Инж. Мат. 2018 , 108, 197–208. [Google Scholar] [CrossRef] [Google Scholar] [CrossRef]
[Google Scholar] [CrossRef] Нелинейный процесс. Геофиз. 2010 , 17, 633–649. [Google Scholar] [CrossRef]
Нелинейный процесс. Геофиз. 2010 , 17, 633–649. [Google Scholar] [CrossRef]