Реактивное напряжение — Большая Энциклопедия Нефти и Газа, статья, страница 1
Реактивное напряжение
Cтраница 1
Реактивные напряжения могут складываться с напряжениями от внешних сил и поэтому представляют значительную опасность. [1]
Реактивные напряжения находятся в противофазе друг к другу. В этом случае говорят, что в цепи возникает резонанс напряжений. [3]
Реактивные напряжения не уравновешиваются внутри металла и поэтому при устранении закрепления они исчезают. [5]
Реактивные напряжения возникают при сварке конструкции в закреплении. [7]
Реактивные напряжения могут также снизить выносливость изделия при знакопеременной нагрузке. [8]
Реактивное напряжение Up
Рассчитанные реактивные напряжения, возникающие от заделок различных размеров ( t 40 мм), сваренных низколегированными сварочными материалами с предварительным подогревом, представлены на рис. 5.18. Реактивные напряжения, возникающие от заделок, сваренных низколегированными материалами без подогрева, ниже, чем при сварке с подогревом. [10]
Чем больше реактивное напряжение по сравнению с активным или чем больше реактивное сопротивление по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения цепи. [11]
Действие реактивных напряжений на исследуемые узлы моделировали изменением максимальных напряжений в цикле нагружения. [13]
Наличие реактивных напряжений одного знака, не урановешенных в пределах сечения и распределенных по большой площади, обусловливает накапливание в изделии больших запасов скрытой потенциальной энергии и может снизить работоспособность конструкции. Можно предполагать, что скрытая энергия способствует прежде всего процессу разрушения. Поэтому, например, при наличии в изделии различных зародышевых дефектов в виде надрывов, трещин и других накопленная скрытая энергия реактивных напряжений может приводить к их раскрытию вплоть до полного разделения деталей. Самопроизвольные разрушения, происходящие при полном отсутствии приложенных нагрузок и имеющие характер взрыва, свидетельствуют об огромных запасах энергии, которая может накопиться в конструкциях или деталях конструкции. Разрушения от действия реактивных напряжений могут происходить в процессе как изготовления, так и эксплуатации конструкции. [14]
О природе реактивной энергии / Habr
Вокруг реактивной энергии сложилось немало легенд, активно способствовала развитию околонаучного фольклора любовь нашего человека к халяве и разнообразным теориям глобального заговора.В рунете можно найти множество success story о том как простой мужичок из глубинки годами эксплуатирует халявную реактивную энергию (которую бытовой счетчик электроэнергии не регистрирует) и живет себе, не зная бед. Так же можно найти заметки людей, призывающих бросить бесполезное занятие поиска источника халявы в халявной реактивной энергии. Для того чтобы окончательно раставить точки над
Как известно, потребляемая от источника переменного тока энергия складывается из двух составляющих:
- Активной энергии
- Реактивной энергии
1. Активная энергия — та часть потребляемой энергии, которая целиком и безвозвратно преобразуется приемником в другие виды энергии.
Пример: Протекая через резистор, ток совершает активную работу, что выражается в увеличении тепловой энергии резистора. Вне зависимости от фазы протекающего тока, резистор преобразует его энергию в тепловую. Резистору не важно в каком направлении течет по нему ток, важна лишь его величина: чем он больше, тем больше тепла высвободится на резисторе (
2. Реактивная энергия — та часть потребляемой энергии, которая в следующую четверть периода будет целиком отдана обратно источнику.
Пример: Представим себе, что к источнику переменного тока подключен конденсатор. Начальный заряд на обкладках конденсатора равен нулю, начальная фаза напряжения источника так же равна нулю. Одно полное колебание состоит из четырех четвертьпериодов:
- Напряжение источника растет от 0 до максимального мгновенного значения (при действующем значении U источника 230V оно равно 230 * 1,4142 = 325V) При этом
- Напряжение источника стремительно уменьшается (движется к нулю), при этом, напряжение на заряженном конденсаторе оказывается выше чем на источнике, что вызывает течение тока в обратную сторону (ведь ток течет от большего потенциала к меньшему), то есть конденсатор разряжается, отдавая накопленную энергию обратно источнику!
- Для следующих двух четвертьпериодов вышеописанная история повторяется с тем лишь различием, что токи заряда и разряда емкости потекут в противоположных направлениях.
В случае включения вместо конденсатора катушки индуктивности, суть процесса не изменится.
В этом и состоит главный фокус реактивной энергии — в момент ‘прилива’ мы заполняем свои цистерны, в момент отлива же, мы сливаем их содержимое обратно. Как можно заметить из этой простой аналогии, мы просто туда-сюда переливаем жидкость (или ток в электроцепях). Если же мы соблазнимся слить хоть немного жидкости ‘налево’ (включить последовательно с реактивным конденсатором активный резистор), то мы станем брать ‘несколько больше’ чем возвращать, а это ‘несколько больше’ уже является активной энергией по определению (ведь мы эту часть не возвращаем обратно, не так ли?)
Или иной пример: предположим, что мы берем у кредитора некоторую сумму денег взаймы и сразу же возвращаем ему взятый только что кредит. Если мы отдадим ровно столько, сколько взяли (чистая реактивность) — мы придем к исходному состоянию и никто никому не будет ничего должен. В случае же, если мы потратим часть кредита на какую ни будь покупку и вернем то, что осталось от кредита после совершения покупки (добавим в цепь активную нагрузку и часть энергии уйдет из системы) — мы будем все еще должны. Эта потраченная часть является активной составляющей взятого нами кредита.
Теперь у вас может возникнуть один весьма резонный вопрос — если все так просто, и для того чтобы энергия считалась реактивной, ее просто нужно полностью вернуть обратно источнику, почему предприятия вынуждены платить за потребляемую
Все дело в том, что в случае чисто реактивной нагрузки, момент максимально потребляемого тока (реактивного) приходится на момент минимального значения напряжения, и наоборот, в момент максимума напряжения на клеммах нагрузки, протекающий через нее ток равен нулю.
Протекающий реактивный ток греет питающие проводники — но это активные потери, вызванные протеканием реактивного тока по проводникам с ограниченной проводимостью, что эквивалентно последовательно включенным с реактивной нагрузкой активным резистором. Так же, поскольку в момент максимума реактивного тока напряжение на полюсах реактивного элемента переходит через ноль, активная мощность подводимая к нему в этот момент
Большие предприятия сопсобны генерировать достаточно большие реактивные токи, которые отрицательно сказываются на функционировании энергосистемы. По этой причине, для них проводится учет как активной, так и реактивной составляющей потребленной энергии. Для уменьшения генерации реактивных токов
Что такое активная и реактивная электроэнергия?
Расчет электрической энергии, используемой бытовым или промышленным электротехническим прибором, производится обычно с учетом полной мощности электрического тока, проходящего через измеряемую электрическую цепь. При этом выделяются два показателя, отражающие затраты полной мощности при обслуживании потребителя. Эти показатели называются активная и реактивная энергия. Полная мощность представляет собой сумму этих двух показателей. О том, что такое активная и реактивная электроэнергия и как проверить сумму начисленных оплат, попытаемся рассказать в этой статье.
Полная мощность
По сложившейся практике потребители оплачивают не полезную мощность, которая непосредственно используется в хозяйстве, а полную, которую отпускает предприятие-поставщик. Различают эти показатели по единицам измерения – полная мощность измеряется в вольт-амперах (ВА), а полезная – в киловаттах. Активная и реактивная электроэнергия используется всеми запитанными от сети электроприборами.

Активная электроэнергия
Активная составляющая полной мощности совершает полезную работу и преобразовывается в те виды энергии, которые нужны потребителю. У части бытовых и промышленных электроприборов в расчетах активная и полная мощность совпадают. Среди таких устройств – электроплиты, лампы накаливания, электропечи, обогреватели, утюги и гладильные прессы и прочее.
Если в паспорте указана активная мощность 1 кВт, то полная мощность такого прибора будет составлять 1 кВА.

Понятие реактивной электроэнергии
Этот вид электроэнергии присущ цепям, в составе которых имеются реактивные элементы. Реактивная электроэнергия — это часть полной поступаемой мощности, которая не расходуется на полезную работу.
В электроцепях постоянного тока понятие реактивной мощности отсутствует. В цепях переменного тока реактивная составляющая возникает только в том случае, когда присутствует индуктивная или емкостная нагрузка. В таком случае наблюдается несоответствие фазы тока с фазой напряжения. Данный сдвиг фаз между напряжением и током обозначается символом «φ».
При индуктивной нагрузке в цепи наблюдается отставание фазы, при емкостной – ее опережение. Поэтому потребителю приходит только часть полной мощности, а основные потери происходят из-за бесполезного нагревания устройств и приборов в процессе эксплуатации.
Потери мощности происходят из-за наличия в электрических устройствах индуктивных катушек и конденсаторов. Из-за них в цепи в течение некоторого времени происходит накопление электроэнергии. После этого запасенная энергия поступает обратно в цепь. К приборам, в составе потребляемой мощности которых имеется реактивная составляющая электроэнергии, относятся переносные электроинструменты, электродвигатели и различная бытовая техника. Эта величина рассчитывается с учетом особого коэффициента мощности, который обозначается как cos φ.

Расчет реактивной электроэнергии
Коэффициент мощности лежит в пределах от 0,5 до 0,9; точное значение этого параметра можно узнать из паспорта электроприбора. Полная мощность должна быть определена как частное от деления активной мощности на коэффициент.
Например, если в паспорте электрической дрели указана мощность в 600 Вт и значение 0,6, тогда потребляемая устройством полная мощность будет равна 600/06, то есть 1000 ВА. При отсутствии паспортов для вычисления полной мощности прибора коэффициент можно брать равным 0,7.
Поскольку одной из основных задач действующих систем электроснабжения является доставка полезной мощности конечному потребителю, реактивные потери электроэнергии считаются негативным фактором, и возрастание этого показателя ставит под сомнение эффективность электроцепи в целом. Баланс активной и реактивной мощности в цепи может быть наглядно представлен в виде этого забавного рисунка:
Значение коэффициента при учете потерь
Чем выше значение коэффициента мощности, тем меньше будут потери активной электроэнергии – а значит конечному потребителю потребляемая электрическая энергия обойдется немного дешевле. Для того чтобы повысить значение этого коэффициента, в электротехнике используются различные приемы компенсации нецелевых потерь электроэнергии. Компенсирующие устройства представляют собой генераторы опережающего тока, сглаживающие угол сдвига фаз между током и напряжением. Для этой же цели иногда используются батареи конденсаторов. Они подключаются параллельно к рабочей цепи и используются как синхронные компенсаторы.

Расчет стоимости электроэнергии для частных клиентов
Для индивидуального пользования активная и реактивная электроэнергия в счетах не разделяется – в масштабах потребления доля реактивной энергии невелика. Поэтому частные клиенты при потреблении мощности до 63 А оплачивают один счет, в котором вся потребляемая электроэнергия считается активной. Дополнительные потери в цепи на реактивную электроэнергию отдельно не выделяются и не оплачиваются.
Учет реактивной электроэнергии для предприятий
Другое дело – предприятия и организации. В производственных помещениях и промышленных цехах установлено огромное число электрооборудования, и в общей поступаемой электроэнергии имеется значительная часть энергии реактивной, которая необходима для работы блоков питания и электродвигателей. Активная и реактивная электроэнергия, поставляемая предприятиям и организациям, нуждается в четком разделении и ином способе оплаты за нее. Основанием для регуляции отношений предприятия-поставщика электроэнергии и конечных потребителей в этом случае выступает типовой договор. Согласно правилам, установленным в этом документе, организации, потребляющие электроэнергию свыше 63 А, нуждаются в особом устройстве, предоставляющем показания реактивной энергии для учета и оплаты.
Сетевое предприятие устанавливает счетчик реактивной электроэнергии и начисляет оплату согласно его показаниям.

Коэффициент реактивной энергии
Как говорилось ранее, активная и реактивная электроэнергия в счетах на оплату выделяются отдельными строками. Если соотношение объемов реактивной и потребленной электроэнергии не превышает установленной нормы, то плата за реактивную энергию не начисляется. Коэффициент соотношения бывает прописан по-разному, его среднее значение составляет 0,15. При превышении данного порогового значения предприятию-потребителю рекомендуют установить компенсаторные устройства.
Реактивная энергия в многоквартирных домах
Типичным потребителем электроэнергии является многоквартирный дом с главным предохранителем, потребляющий электроэнергию свыше 63 А. Если в таком доме имеются исключительно жилые помещения, плата за реактивную электроэнергию не взимается. Таким образом, жильцы многоквартирного дома видят в начислениях оплату только за полную электроэнергию, поставленную в дом предприятием-поставщиком. Та же норма касается жилищных кооперативов.
Частные случаи учета реактивной мощности
Бывают случаи, когда в многоэтажном здании имеются и коммерческие организации, и квартиры. Поставка электроэнергии в такие дома регулируется отдельными Актами. Например, разделением могут служить размеры полезной площади. Если в многоквартирном доме коммерческие организации занимают менее половины полезной площади, то оплата за реактивную энергию не начисляется. Если пороговый процент был превышен, то возникают обязательства оплаты за реактивную электроэнергию.
В ряде случаев жилые дома не освобождаются от оплаты за реактивную энергию. Например, если в доме установлены пункты подключения лифтов для квартир, начисление за использование реактивной электроэнергии происходит отдельно, лишь для этого оборудования. Владельцы квартир по-прежнему оплачивают лишь активную электроэнергию.

Понимание сущности активной и реактивной энергии дает возможность грамотно рассчитать экономический эффект от установки различных компенсационных устройств, снижающих потери от реактивной нагрузки. Согласно статистике, такие устройства позволяют поднимать значение cos φ от 0.6 до 0.97. Тем самым автоматические компенсаторные устройства помогают сэкономить до трети предоставляемой потребителю электроэнергии. Значительное уменьшение тепловых потерь увеличивает срок эксплуатации приборов и механизмов на производственных участках и снижает себестоимость готовой продукции.
Активное и реактивное сопротивление | Практическая электроника
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:

Частота 285 Герц:

Частота 30 Килогерц:

Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:


Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:

Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П

Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:

Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока

Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.

100 Герц

200 Герц

Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:

Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:

Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.

Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:

Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц

34 Килогерца

17 Килогерц

10 Килогерц

Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Почему не сгорает первичная обмотка трансформатора
Ну и теперь главный вопрос, который часто задают в личке: “Почему когда я меряю первичную обмотку трансформатора, у меня выдает от 10 Ом и больше в зависимости от трансформатора. На трансформаторных сварочных аппаратах вообще пару Ом! Ведь первичная обмотка трансформатора цепляется к 220 Вольтам! Почему не сгорает обмотка, ведь сопротивление обмотки всего то десятки или сотни Ом, и может случится короткое замыкание!
А ведь и вправду, мощность равна как напряжение помноженное на ток P=IU. То есть через пару секунд от первичной обмотки трансформатора должен остаться уголек.
Дело все в том, что парные обмотки трансформатора представляют из себя катушку индуктивности с какой-то индуктивностью. Получается, что реальное сопротивление обмотки будет выражаться через формулу

поставьте сюда индуктивность, которая в трансформаторах составляет от единицы Генри и получим что-то типа от 300 и более Ом. Но это еще цветочки, ягодки впереди;-)
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:

Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или П/2.

Мощность в цепи с реактивными радиоэлементами
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:

Не знаю, какое было у вас детство, но я когда был салабоном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?

С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история для полноценной статьи.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.

В результате за весь период у нас суммарное потребление энергии равно чему?

Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESR – эквивалентное последовательное сопротивление
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле

Сопротивление конденсатора вычисляется по формуле:

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Активная, реактивная и полная мощность
В отличии от сетей постоянного тока, где мощность имеет выражение  и не изменяется во времени, в сетях переменного тока это не так.
и не изменяется во времени, в сетях переменного тока это не так.
Мощность в цепи переменного тока также есть переменной величиной. На любом участке цепи в любой момент времени t она определяется как произведение мгновенных значений напряжения и тока.
Рассмотрим, что представляет активная мощность
В цепи с чисто активным сопротивлением она равна:

Если принять  и
и  тогда выйдет:
тогда выйдет:

Где 
Исходя из выражений выше — активная энергия состоит из двух частей — постоянной  и переменной
и переменной  , которая меняется с двойной частотой. Среднее ее значение
, которая меняется с двойной частотой. Среднее ее значение 
 График Р(ωt)
График Р(ωt)Отличие реактивной мощности от активной
В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно:

Соответственно  и
и  в итоге получим:
в итоге получим:

Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю
 График q(ωt)
График q(ωt)Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C.
В таком случае полная мощность сети будет равна сумме:
 Что такое полная мощность на примере простой R-L цепи
Что такое полная мощность на примере простой R-L цепи

Графики изменения мгновенных значений u,i:
 Графики изменения мгновенных значений u,i:
Графики изменения мгновенных значений u,i:φ — фазовый сдвиг между током и напряжением
Уравнение для S примет следующий вид 
Подставим вместо  и заменим амплитудные значения на действующие:
и заменим амплитудные значения на действующие:

Значение S рассматривается как сумма двух величин  , где
, где
 и
и  — мгновенные активные и реактивные мощности на участках R-L.
— мгновенные активные и реактивные мощности на участках R-L.
 Графики p,q,s:
Графики p,q,s:Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.
Итоговые выражения для действующих значений:


Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).
Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:

Для нормальной работы генератора ток в обмотках и напряжение на зажимах не должны превышать номинальные значения Iн, Uн. Для генератора значения P и S одинаковы, однако все-таки на практике условились S выражать в вольт-амперах (ВА).
Также энергию сети можно выразить через каждую составляющую отдельно:



Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:
 Треугольник мощностей с преобладающей индуктивной нагрузкой
Треугольник мощностей с преобладающей индуктивной нагрузкойЕсли вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:

Реактивная составляющая в треугольнике является положительной (QL), когда ток отстает от напряжения, и отрицательной (QC), когда опережает:
 Треугольник мощностей с преобладающей емкостной нагрузкой
Треугольник мощностей с преобладающей емкостной нагрузкойДля реактивной составляющей сети справедливо алгебраическое выражение:

Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :
 Схема компенсации реактивной составляющей
Схема компенсации реактивной составляющейВекторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ2> cosφ1 и Iл<I.
 Векторная диаграмма
Векторная диаграммаСвязь между полной и реактивной энергии выражается:

Отсюда:

сosφ – это коэффициент мощности. он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.
Выводы о трех составляющих цепи переменного тока
В отличии от цепей постоянного тока, цепи переменного напряжения имеют три вида мощности – активная, реактивная, полная. Активная энергия, как и в цепях постоянного тока, выполняет полезную работу. Реактивная – не выполняет ничего полезного, а только снижает КПД сети, греет провода, грузит генератор. Полная – сумма активной и реактивной, она равна мощности сети. Индуктивная составляющая реактивной энергии может быть скомпенсирована емкостной. На практике в промышленности это реализовано в виде конденсаторных установок.
Что такое активная, реактивная и полная мощность нагрузки стабилизатора?
В отличии от вычисления мощности при постоянном токе, формулы для вычисления мощности в цепях переменного тока достаточно сложны. В общем случае электрическая мощность в этом случае имеет интегральные зависимости.
Для определения полной мощности нагрузки необходимо вычислить активную и реактивную мощность. Полная мощность определяется как векторное сложение этих величин.
Активная мощность — это полезная часть мощности, та часть, которая определяет прямое преобразования электрической энергии в другие необходимые виды энергии. Для каждого электрического прибора вид преобразования энергии свой: в электрической лампочке электроэнергия преобразуется в свет и тепло, в утюге электроэнергия преобразуется в тепло, в электродвигателе электроэнергия преобразуется в механическую энергию. Фактически, активная мощность определяет скорость полезного потребления энергии.
Реактивная мощность — мощность определяемая электромагнитными полями, образующимися в процессе работы приборов. Реактивная мощность, как правило, является «вредной» или «паразитной». Реактивная мощность определяется характером нагрузки. Для такого прибора как лампочка она равна нулю, в процессе горения лампы электромагнитные поля практически не образуются. В процессе работы электродвигателя реактивная мощность может достигать больших значений. Понятие реактивной мощности тесно связано с понятием «пусковые токи».
При выборе стабилизатора напряжения необходимо определять полную мощность потребителей. Самый точный способ — найти значение полной мощности прибора в его паспорте. Если такой возможности нет, то для определения полной мощности приборов с большими «пусковыми токами» принято использовать повышающий коэффициент «4».
Следует также учитывать, что номинальная мощность стабилизатора напряжения может указываться разными производителями стабилизаторов и ИБП в различных диапазонах входных параметров тока. Китайские производители часто завышают реальную мощность устройства в два и более раз.
Особое внимание при выборе подходящего стабилизатора напряжения или источника бесперебойного питания следует обратить на возможность использования стабилизатора при реактивной нагрузке. Часто производители указывают, что номинальная мощность стабилизатора или ИБП указана без учета реактивной нагрузки. В паспортных данных стабилизаторов и источников питания можно найти фразу «устройство не может использоваться для реактивной нагрузки».
Для работы с приборами, имеющими большую реактивную мощность мы рекомендуем использовать специальные стабилизаторы напряжения и ИБП компании «Бастион». Эти приборы характеризуются большой перегрузочной мощностью и хорошей защитой от помех в сети по нагрузке.
Подробные ответы вы можете найти в следующих статьях:
Сравнение реальных мощностей стабилизаторов напряжения разных марок
Сравнение стабилизаторов напряжения Ресанта, APC, Voltron, Калибри, Teplocom
Стабилизаторы напряжения для котлов отопления
Преимущества релейных стабилизаторов напряжения «Бастион»
Стабилизатор напряжения для холодильника
Стабилизаторы напряжения для насосов
Стабилизатор напряжения для кондиционера и сплит-системы
Специфика сети переменного тока приводит к тому, что в фиксированный момент времени синусоиды напряжения и тока на приемнике совпадают только в случае так называемой активной нагрузки, полностью переводящей ток в тепло или механическую работу. Практически это всевозможные электронагревательные приборы, лампы накаливания, в каком-то приближении электродвигатели и электромагниты под нагрузкой и звуковоспроизводящая аппаратура. Ситуация полностью меняется, если нагрузка, не создающая механической работы, обладает большой индуктивностью при малом сопротивлении. Это характерный случай электродвигателя или трансформатора на холостом ходу.
Подключение подобного потребителя к источнику постоянного тока привело бы к короткому замыканию, здесь же ничего особенного с сетью не случится, но мгновенный ток будет отставать от мгновенного напряжения примерно на четверть периода. В случае же чисто емкостной нагрузки (если в розетку вставить конденсатор), ток на нем будет, наоборот, на ту же четверть периода опережать напряжение. Реактивные токиПрактически такое несовпадение тока и напряжения, не производя на приемнике полезной работы, создает в проводах дополнительные, или, как принято их называть, реактивные токи, которые в особо неблагоприятных случаях могут привести к разрушительным последствиям. При меньшей величине это явление все равно требует расходовать излишний металл на более толстую проводку, повышать мощность питающих генераторов и трансформаторов электроэнергии. Поэтому экономически оправдано устранять в сети реактивную мощность всеми возможными способами. При этом следует учитывать суммарную реактивную мощность всей сети, при том, что отдельные элементы могут обладать значительными значениями реактивной мощности. Реактивная электроэнергияС количественной стороны влияние реактивной электроэнергии на работу сети оценивается Основные пути снижения реактивной мощности – взаимная компенсация сдвигов фаз, создаваемых индуктивными и емкостными приемниками и использование приемников с малым углом потерь. |


 Что такое полная мощность на примере простой R-L цепи
Что такое полная мощность на примере простой R-L цепи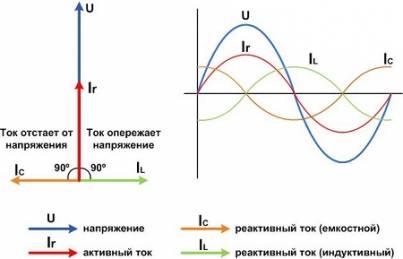
 косинусом угла потерь, который равен отношению активной мощности к полной. Полная мощность считается как векторная величина, которая зависит от сдвига фаз между током и напряжением на всех элементах сети. В отличие от активной мощности, которую, как и механическую измеряют в ваттах, полную мощность измеряют в вольт-амперах, так как эта величина присутствует только в электрической цепи. Таким образом, чем ближе косинус угла потерь к единице, тем полнее используется сечение проводов и мощность, вырабатываемая генератором.
косинусом угла потерь, который равен отношению активной мощности к полной. Полная мощность считается как векторная величина, которая зависит от сдвига фаз между током и напряжением на всех элементах сети. В отличие от активной мощности, которую, как и механическую измеряют в ваттах, полную мощность измеряют в вольт-амперах, так как эта величина присутствует только в электрической цепи. Таким образом, чем ближе косинус угла потерь к единице, тем полнее используется сечение проводов и мощность, вырабатываемая генератором.