реактивное сопротивление, что это, формулы

Индуктивный элемент L

Индуктивный элемент ( рассмотрим на примере  катушки индуктивности) представляют собой витки изолированного между собой провода. При протекании тока катушка намагничивается. Если изменить полярность  источника, катушка начнет отдавать запасенную энергию обратно, стараясь поддержать величину тока в контуре. Поэтому при протекании через нее  переменной составляющей , энергия запасенная при прохождении положительного полупериода, не успеет рассеяться и будет препятствовать прохождению отрицательного полупериода. В результате отрицательному полупериоду придется  погасить энергию запасенную катушкой. В итоге напряжение(U),  будет опережать ток (І) на какой-то угол φ. Ниже  приведен результат моделирования работы на L-R нагрузку  L=1*10-3 Гн, R=0.5 Ом. U_ист= 250 В, частота f=50 Гц.

φ – это разница фаз  между U и  I.

Реактивное сопротивление обозначается буквой X, полное  Z, активное R.

Для  индуктивности :

Где ω – циклическая  частота 

— частота питающего напряжения,  Гц;

L – индуктивность катушки;

Вывод: чем выше индуктивность L или частота , тем больше будет сопротивление катушки переменному току.

Формула расчета реактивного сопротивления

В общем случае для деталей катушечного типа применяются выражения:

X = L*w = 2* π*f*L.

Для конденсаторов применяют формулы:

X = 1/(w*C)= 1/(2* π*f*C).

Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.

Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.

Мощность в цепи с реактивными радиоэлементами

Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:

Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.

Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.

Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.

Представим себе кузнеца за работой:

Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.

А что если взять пружину от стоек ВАЗа и ударять по ней?

С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно  к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.

Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.

В третий промежуток времени  t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.

В результате за весь период у нас суммарное потребление энергии равно чему?

Правильно, нулю!

Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.

Эквивалентная схема реальной катушки индуктивности выглядит вот так:

где

R_L  — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи.  Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.

L — собственно сама индуктивность катушки

С — межвитковая емкость.

А вот и эквивалентная схема реального конденсатора:

где

r — сопротивление диэлектрика и корпуса между обкладками

С — собственно сама емкость конденсатора

ESI (ESL) — эквивалентная последовательная индуктивность

Здесь мы тоже видим такие параметры, как r  и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту.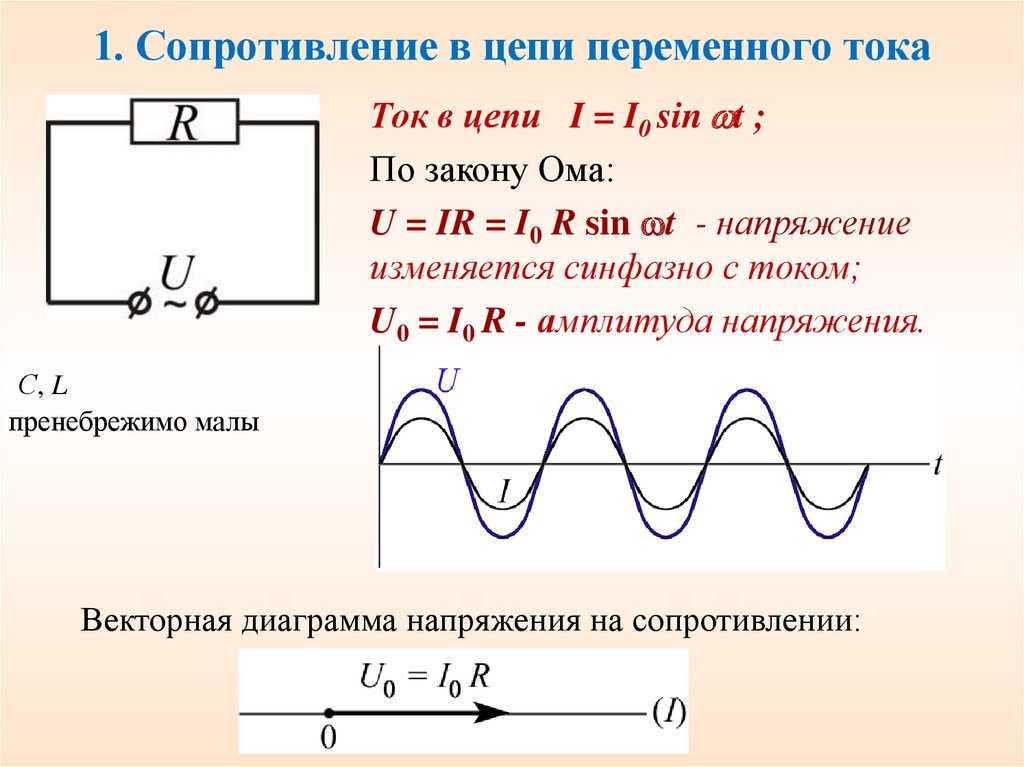 Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.

Сопротивление проводника

Так почему бы все эти свойства не применить также к проводнику? Чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Большую роль играет также материал, из которого он изготовлен.

Поэтому, окончательная формула будет принимать вид

формула сопротивления проводника

В технике до сих пор применяется устаревшая единица измерения удельного сопротивления Ом × мм2 /м.  Чтобы перевести  в Ом × м, достаточно умножить на 10-6, так как 1 мм2=10-6 м2.

удельное сопротивление веществ

Как вы видите из таблицы выше, самым маленьким удельным сопротивлением обладает серебро, поэтому провод из серебра будет наилучшим проводником. Ну а самым распространенными и дешевыми проводниками являются медь и алюминий. Именно эти два металла в основном используются во всей электронной и электротехнической промышленности.

Вещества, которые оказывают наименьшее сопротивление электрическому току и обладают очень малым сопротивлением называются проводниками, а вещества, которые обладают ну очень большим сопротивлением электрическому току и почти его не пропускают через себя, называются диэлектриками. Между ними стоит класс .

Действие индуктивного сопротивления кабельных линий

Полное сопротивление электрической цепи разделяется на активное и индуктивное сопротивление. Из них последнее является составной частью реактивного сопротивления, возникающего во время прохождения переменного тока через элементы, относящиеся к реактивным. Индуктивность считается основной характеристикой катушек, не учитывая активное сопротивление их обмоток. Как правило, реактивное сопротивление возникает под влиянием ЭДС самоиндукции. При ее росте, в зависимости от частоты тока, происходит одновременное увеличение сопротивления.

Таким образом, активное и реактивное сопротивление кабелей образуют полное сопротивление, которое есть ни что иное, как сумма квадратов каждой составляющей. Графически это отображается в виде прямоугольного треугольника, в котором гипотенуза является полным сопротивлением, а катеты – его составными элементами.

Очень быстро вычислить активное и индуктивное сопротивление кабелей помогает таблица, в которой отражаются основные характеристики наиболее распространенных проводников. Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.

В свою очередь Х определяется по другой формуле X = 0,145lg * (2Dср/d) + 0,0157 μ_т, в которой 2Dср является средним расстоянием между проводниками или центрами кабельных жил, d – диаметр этих проводников или жил, μ_т – отражает относительную магнитную проницаемость металла проводника. Таким образом, при увеличении сечения проводника реактивное сопротивление Х будет незначительно уменьшаться.

Формула индуктивного сопротивления

Активное и реактивное сопротивление

Сопротивление медного провода

Активная реактивная и полная мощность

Таблица перевода сечения кабеля AWG и GA в дюймы и миллиметры

Удельное сопротивление алюминия

Индуктивное сопротивление

Созданное в ходе передачи энергии переменное магнитное поле становится источником реактивного сопротивления подобного вида. Индуктивный вариант в основном зависит от характеристик проходящего тока, диаметра и расстояния между проводами.

Само сопротивление обычно классифицируют следующим образом:

• зависящее от параметров тока и материала — внутреннее;
• обусловленное геометрическими особенностями линии — внешнее. В этом случае данный показатель будет постоянной величиной, не зависящей от каких-либо других факторов.

Заводы по производству кабельной продукции всегда указывают в своих каталогах информацию об индуктивном сопротивлении.

Данный параметр обычно определяется следующим выражением:

в котором индуктивный показатель для 1 км провода – , а L – протяженность.

Х километрового участка рассчитывается по следующей формуле:

Где: Dср – расстояние среднее по центральной оси имеющихся проводов, мм; d – диаметр рабочего токопроводника, мм; μт –относительная магнитная проницаемость.

От чего зависит сопротивление конденсаторов цепей переменного тока

Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.

Вычисление Xc

Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

Советуем изучить — Как устроены мощные промышленные ветрогенераторы

График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.

При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной

Его электросопротивляемость является безваттной, реактивной.

Какие отличия

Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть. Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть

То есть, в окружающую среду полученная энергия не передается

Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U1=I*R1
• U2=I*R2
• Un=I*Rn
• U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу.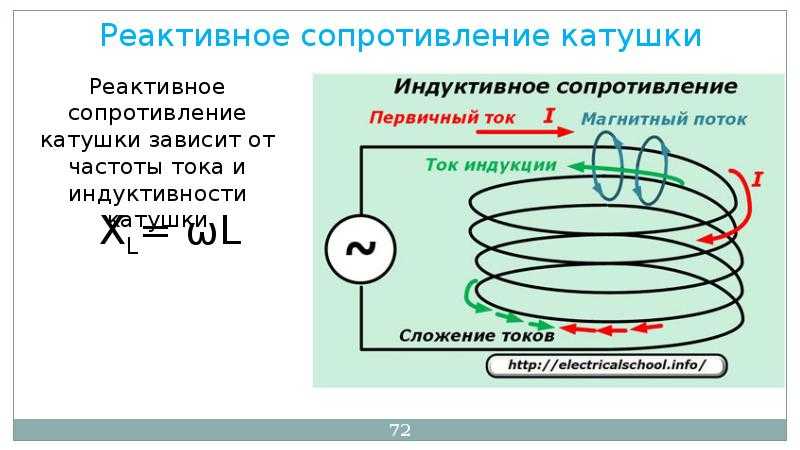 Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Треугольник сопротивлений

Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений

Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.

е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.Однако в ряде случаев относительная роль двух из трех параметров  R, L, С в электрической цепи практически незначительна.

Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r. Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.

Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?

(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части. Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:

https://youtube.com/watch?v=NSxgxMNG2fwrel%3D0%26amp%3Bcontrols%3D0%26amp%3Bshowinfo%3D0

• electrosam.ru
• electrono.ru
• electroandi.ru
• fazaa.ru

Приложения с емкостным реактивным сопротивлением

Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.

В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.

В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: X_L = 2πfL.

Емкостная проводимость

Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.

Для его определения в трехфазной линии воздушных передач применяется выражение:

Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.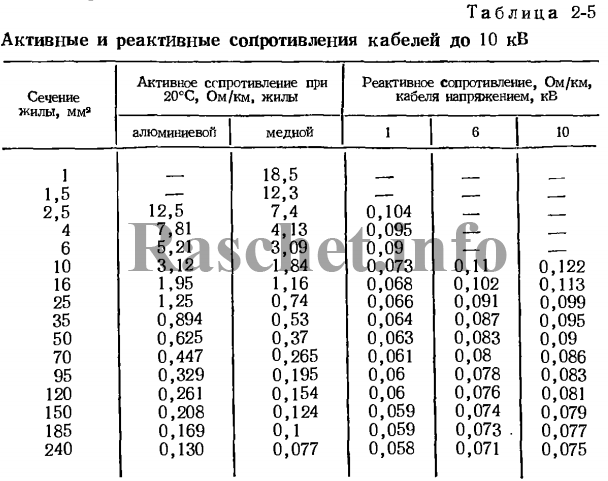

Проводимость подобного вида в воздушных линиях одноцепной конструкции рассчитывается так:Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.

Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.

Для начала линии, когда мы имеем дело с холостым ходом, емкостный ток определяется так:

Данный показатель будет объективным только при полностью обесточенных приемниках электричества.

Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.

Для воздушной линии действительна такая формула:

Для кабельных магистралей:

Области проявления

Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.

Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.

Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.

Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.

Таблица и расчет по формуле

Как показывает таблица, поверхностный эффект не критично влияет на проводники, состоящие из цветных металлов и работающие при переменном напряжении с частотой 50 Гц. Поэтому для выполнения расчетов, сопротивления таких кабелей под действием постоянного и переменного тока принимаются условно равными.

Кроме таблицы, для расчетов проводников из алюминия и меди используется специальная формула r = (l * 103)/ γ3 * S = r * l, в которой l – длина (км), γ – удельное значение проводимости конкретного материала (м/ом * мм2), r – активное сопротивление 1 км кабеля (Ом/км), S – поперечное сечение (мм2).

Значение активного сопротивления кабелей зависит также от температуры окружающей среды. Для того чтобы вычислить r при точной температуре Θ, необходимо воспользоваться еще одной формулой r = r₂₀ * = (l * 103)/ γ₂₀ * S * . Здесь α является температурным коэффициентом сопротивления, r₂₀ – активное сопротивление при t 20C, γ₂₀ – удельная проводимость при этой же температуре. Эти расчеты необходимы, когда определяется точное активное и индуктивное сопротивление какого-либо проводника.

Активное сопротивление стальных проводов существенно превышает аналогичный показатель проводников из цветных металлов. Это связано с более низкой удельной проводимостью и наличием поверхностного эффекта, выраженного намного ярче по сравнению с медными и алюминиевыми проводами. Кроме того, в линиях со стальными проводами активная энергия значительно теряется на перемагничивание и вихревые токи, поэтому такие потери становятся дополнительным компонентом активного сопротивления.

У стальных проводников существует зависимость активного сопротивления от величины протекающего тока, поэтому в расчетах неприемлемо использование постоянного значения удельной проводимости.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Формула расчета реактивного сопротивления

В общем случае для деталей катушечного типа применяются выражения:

X = L*w = 2* π*f*L.

Для конденсаторов применяют формулы:

X = 1/(w*C)= 1/(2* π*f*C).

Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.

Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.

что это, формулы, как найти

Содержание:

Что такое сопротивление

Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.

Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс.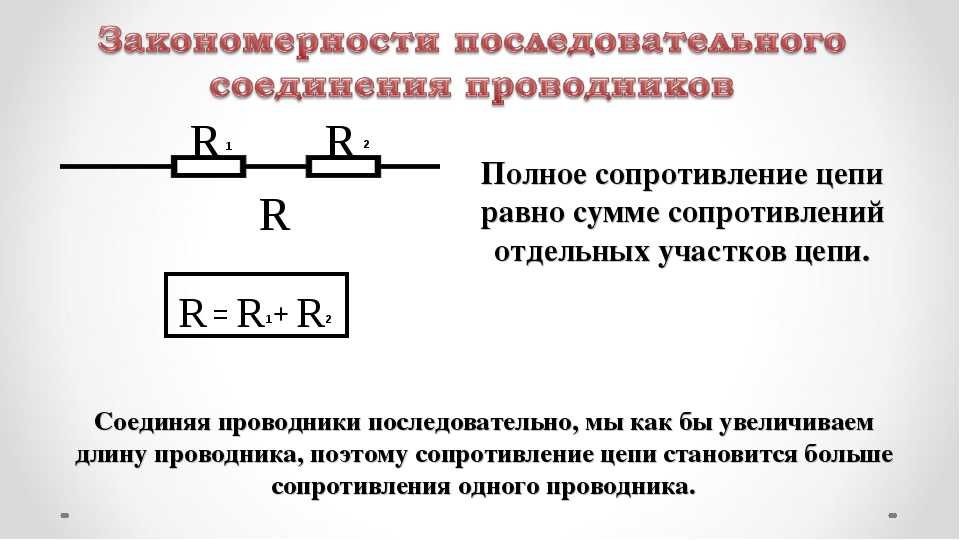 Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.

Понятие реактивного сопротивления

Данная разновидность репрезентирует взаимоотношение электротока и напряжения на определенных типах подключенных в сеть нагрузок (дросселях, конденсаторных компонентах), не сопряженное с объемами электроэнергии, используемыми потребителем. Измерительной единицей, как и для других разновидностей, выступает ом. Рассматриваемое явление обнаруживает себя только при переменном электротоке. В расчетах оно обозначается латинской литерой Х.

Активное и реактивное сопротивление

При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.

В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.

д.

В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.

С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь. В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.

Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.

В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.

После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.

Конденсатор и катушка в цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.

Если сказать простыми словами, то активное и реактивное сопротивление – это противодействие току снижения напряжения на элементе схемы. Величина снижения напряжения на активном сопротивлении имеет всегда встречное направление, а на реактивной составляющей – попутно току или навстречу, создавая сопротивление изменению тока.

Настоящие элементы цепи на практике имеют все три вида сопротивления сразу. Но иногда можно пренебречь некоторыми из них ввиду незначительных величин. Например, емкость имеет только емкостное сопротивление (при пренебрежении потерь энергии), лампы освещения имеют только активное (омическое) сопротивление, а обмотки трансформатора и электромотора – индуктивное и активное.

Активное сопротивление

В цепи действия напряжения и тока, создает противодействие, снижения напряжения на активном сопротивлении. Падение напряжения, созданное током и оказывающее противодействие ему, пропорционально активному сопротивлению.

При протекании тока по компонентам с активным сопротивлением, снижение мощности становится необратимым. Можно рассмотреть резистор, на котором выделяется тепло. Выделенное тепло не превращается обратно в электроэнергию. Активное сопротивление, также может иметь линия передачи электроэнергии, соединительные кабели, проводники, катушки трансформаторов, обмотки электромотора и т.д.

Отличительным признаком элементов цепи, которые обладают только активной составляющей сопротивления, является совпадение напряжения и тока по фазе. Это сопротивление вычисляется по формуле:

R = U/I, где R – сопротивление элемента, U – напряжение на нем, I – сила тока, протекающего через элемент цепи.

На активное сопротивление влияют свойства и параметры проводника: температура, поперечное сечение, материал, длина.

Какое сопротивление называется реактивным, какое активным

Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.

Типы рассматриваемой величины и формулы ее расчета

Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии.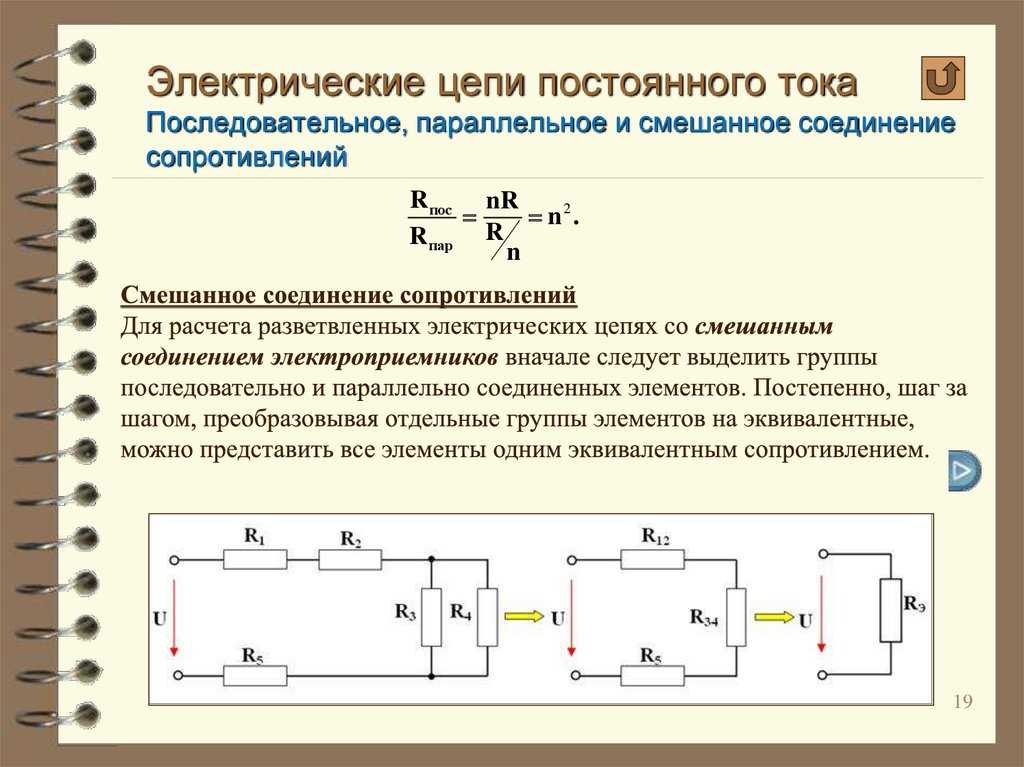 Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.

Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети

Различия между активным и реактивным сопротивлением

Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.

От чего зависит сопротивление проводника

Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.

Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.

Активное сопротивление в цепи переменного тока

Определим величину тока в цепи переменного тока с чисто активным сопротивлением.

Схема с чисто активной нагрузкой.

Для переменного тока закон, по которому меняется мгновенное значение напряжения, имеет следующий вид:

$$U=U_m sin(omega t+varphi)$$

Мгновенное значение тока через любой элемент находится по закону Ома:

$$I ={U over R}$$

Подставляя предыдущую формулу в закон Ома, получим:

$$I={U_m sin(omega t+varphi)over R}=I_m sin(omega t+varphi)$$

Из этой формулы видно, что колебания силы тока в цепи с чисто активным сопротивлением имеют ту же частоту и фазу, что и колебания напряжения. Ток в цепи в любой момент времени возрастает пропорционально напряжению. 2Rt$$

Указанные соотношения справедливы только для чисто активных сопротивлений. Для сопротивлений, которые имеют реактивную составляющую, к примеру, для катушки индуктивности, зависимость мгновенного значения тока сложнее, и закон Джоуля-Ленца в таком виде использовать нельзя.

Любой реальный проводник обладает некоторой индуктивностью, а между любыми частями реальных проводников и элементов существует некоторая электроемкость. Поэтому чисто активных сопротивлений, строго говоря, не существует. Любое реальное активное сопротивление имеет некоторую реактивную составляющую. На низких частотах она очень мала, и ею пренебрегают. На высоких же частотах ею пренебречь нельзя, и она всегда оказывает заметное влияние на поведение и параметры цепи.

Индуктивное реактивное сопротивление

Оно встречается в цепях, где есть своего рода электромагниты, влияющие на магнитное поле электрической цепи. Еще их называют катушками индуктивности. Катушки индуктивности имеют низкое полное электрическое сопротивление на низких частотах и высокое полное электрическое сопротивление на высоких частотах.

Разные катушки индуктивности. Обратите внимание на общность

конструкции – медный провод намотан на магнит, образуя катушку.

 

Как рассчитать емкостное реактивное сопротивление

Рассмотрим пример расчета емкостного реактивного сопротивления: предположим, что конденсатор 6 мкФ подключен к розетке переменного тока с напряжением 40 В и частотой F 60 Гц.

Для определения емкостного реактивного сопротивления используется определение, данное в начале. Угловая частота ω определяется как:

ω = 2πf = 2π x 60 Гц = 377 с-1

Затем этот результат подставляется в определение:

ИксC = 1 / ωC = 1 / (377 с-1х 6 х10 -6 F) = 442,1 Ом

Теперь посмотрим на амплитуду тока, циркулирующего в цепи. Поскольку источник предлагает напряжение амплитудой VC = 40 В, мы используем соотношение между емкостным реактивным сопротивлением, током и напряжением для вычисления амплитуды тока или максимального тока:

яC = VC / ИКСC = 40 В / 442,1 Ом = 0,09047 А = 90,5 м А.

Если частота становится очень большой, емкостное реактивное сопротивление становится небольшим, но если частота становится равной 0 и у нас есть постоянный ток, реактивное сопротивление стремится к бесконечности.

Приложения с емкостным реактивным сопротивлением

Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.

В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.

В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: XL = 2πfL.

Активное сопротивление проводов, кабелей и линий

Из-за того что переменный ток проходит неравномерно, то при одинаковых условиях тока переменного и постоянного R будет отличаться. Как уже было сказано, стальные электропровода имеют лучшее активное R по сравнению с проводниками из цветных металлов, которые имеют одинаковое R при любой силе тока.

Напротив, активное R электрокабелей из стали всегда зависит от электрического тока, поэтому удельную постоянную проводимость в этом случае никогда не используют. Активное R электрокабеля определяют с помощью формулы: R=l/у*s.

Определение активного сопротивления проводов

Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.

Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:

где:

• γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
• s – номинальное сечение провода(кабеля),мм2;
• l – длина линии, м;
• ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].

Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].

Предыдущая

РазноеЧто такое фазное и линейное напряжение?

Следующая

РазноеБлуждающие токи и способы борьбы с ними

Активное и реактивное сопротивления в цепи переменного тока (импеданс).

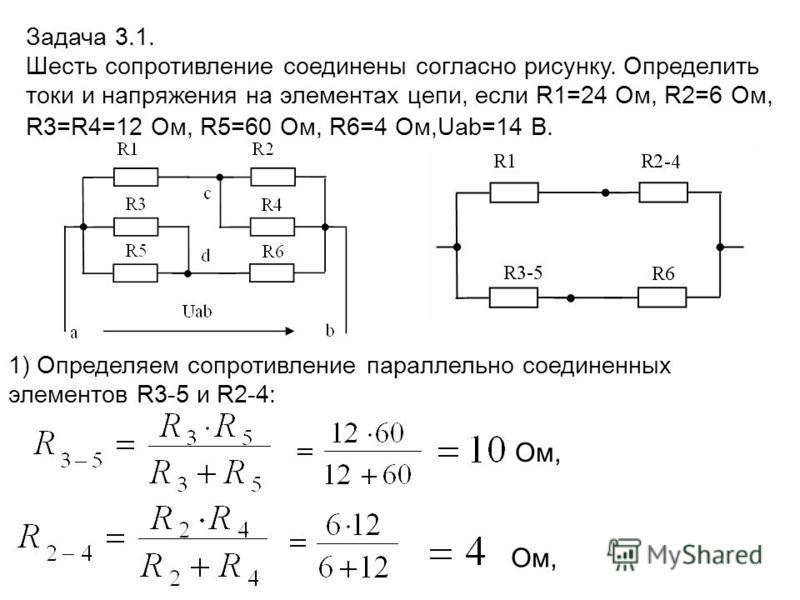Импеданс тканей организма. Частотная зависимость импеданса. Эквивалентная электрическая схема тканей организма.

В широком смысле, переменный ток – любой ток, изменяющийся со временем. Но обычно под этим термином обозначают квазистационарные токи, зависящие от времени по гармоническому закону.

Квазистационарным называют такой ток, для которого время установления одинакового значеня по всей цепи значительно меньше периода колебаний.

Импеданс ( ) – это полное сопротивление переменного тока.

Омическое сопротивление, т.е. подчиняющееся закону Ома ( ), где ток линейно зависит от напряжения, называется активным (вызывает нагревание элементов электрической цепи). В свою очередь, разность между индуктивным (величина, характеризующая сопротивление, оказываемое переменному току индуктивностью (физическая величина, характеризующая магнитные свойства электрической цепи) цепи (её участка)) и емкостным (величина, характеризующая сопротивление, оказываемое переменному току

электрической ёмкостью (характеристика проводника, количественная мера его способности удерживать электрический заряд) цепи (её участка)) сопротивлениями ( ) называют реактивным сопротивлением (НЕ вызывает нагревание элементов электрической цепи).

Ткани организма проводят не только постоянный (как в случае с токовым диполем) ток, но и переменный. Опыт показывает, что в этом случае сила тока, проходящая через биологическую ткань, опережает по фазе приложенное напряжение. Следовательно, емкостное сопротивление тканей больше индуктивного.

Из этого следует, что моделировать биологическую ткань можно с помощью резистора, обладающего активным сопротивлением, и конденсатора – носителя емкостного сопротивления. В качестве модели обычно используют эквивалентную электрическую схему тканей человека. Она представляет собой схему, состоящую из резисторов и конденстаторов, частотная зависимость (дисперсия) импеданса которых схожа с частотной зависимостью биологической ткани.

У биологической ткани существует две частотных зависимости импеданса:

1. Плавное уменьшение импеданса с увеличением частоты;

2. Наличие трех областей частот, в которых имеет место отклонение от общего хода зависимости импеданса от частоты: практически не изменяется.

   Они были названы областями .

Диагностический метод, основанный на регистрировании изменения импеданса тканей в процессе сердечной деятельности называют реографией. С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма) и др.

21. Электромагнитная волна. Уравнения электромагнитной волны. Интенсивность электромагнитной волны. Шкала электромагнитных волн.

Электромагнитная волна — это распространение единого электромагнитного поля в пространстве.

Электромагнитное поле – совокупность неразрывно связанных переменных электрических и магнитных колебаний.

Примеры ЭВМ:

— радиоволны;

— инфракрасное излучение;

— видимый свет;

— УФ-излучение;

— Рентгеновское излучение;

— .

ЭМВ — плоские волны и могут быть описаны уравнениями, подобными таковым для плоской механической волны. Плоская волна – это такая волна, у которой фронтом является плоскость, перпендикулярная направлению распространения.

В ЭМВ векторы (электрических колебаний)

и (магнитных колебаний) изменяются (колеблются) в одинаковой фазе с одинаковой частотой по гармоническому закону ( )

Уравнения ЭМВ:

Где – напряженность электрического поля, – магнитная индукция, и – амплитудные значения, – циклическая частота, – скорость распространения волны, – координата точки, – время, – фаза колебаний.

При распространении в среде ЭМВ переносят энергию (но не массу вещества). Интенсивность волны (плотность потока энергии) – энергия, которая переносится волной за единицу времени через единичную поверхность, для ЭМВ это:

Где и – амплитудные значения, – магнитная проницаемость, – магнитная проницаемость вакуума.

Шкала ЭМВ – совокупность ЭМВ, расположенных в порядке возрастания их длины волны или убывания частоты.

ЭМВ разбиты на 6 интервалов согласносвоей природе возникновения:

— радиоволны. Обусловлены (вызываются) переменными токами в проводниках или электронными потоками.

— инфракрасное излучение, видимый свет, ультрафиолетовое излучение. Обусловлены внутриатомными и молекулярными процессами.

— рентгеновское излучение. Возникает при ускоренном движении заряженных частиц и внутриатомных процессах;

— излучение. Обусловлено внутриядерными процессами.

В медицине принято следующее условное разделение ЭМ колебаний на частотные диапазоны:

Низкие (НЧ)	До 20 Гц
Звуковые (ЗЧ)	20 Гц – 20 кГц
Ультразвуковые (УЗЧ)	20 кГц – 200 кГц
Высокие (ВЧ)	200 кГц – 30 мГц
Ультравысокие (УВЧ)	30 мГц – 300 мГц
Сверхвысокие (СВЧ)	300 мГц – 300 ГГц
Крайневысокие (КВЧ)	Свыше 300 ГГц

3 направления управления сопротивлением

Возможно, в вашем браузере отключен JavaScript.

Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.

Переключить навигацию

Поиск

Изучение уровней управления изменениями

Последние публикации Физические лица Проекты и инициативы Предприятие Архивы

Prosci определяет управление изменениями как применение структурированного процесса и набора инструментов для управления человеческой стороной изменений для достижения желаемого результата. Но как часто мы видим, что управление изменениями и управление сопротивлением используются как синонимы? Если ваш ответ «довольно часто», вы не одиноки. Реальность такова, что сопротивление возникает при любых усилиях, в ходе которых люди должны изменить то, как они выполняют свою работу. Несмотря на то, что управление изменениями включает в себя множество инструментов, стратегий и методов управления изменениями, связанными с людьми, одним из основных инструментов трехэтапного процесса Prosci является разработка планов управления изменениями, включая план управления сопротивлением.

Что такое управление сопротивлением?

Не существует единого рецепта идеального управления сопротивлением. На самом деле управление сопротивлением во многом зависит от времени и обстоятельств. Вы только начинаете проект и уже слышите ворчание? Вы приближаетесь к запуску, но столкнулись с блокировкой в ​​конвейере из-за сопротивляющегося супервизора? Независимо от того, на каком этапе процесса изменений вы находитесь, вы можете предпринять шаги, чтобы смягчить негативные последствия для успеха изменений.

Вот три способа справиться с сопротивлением:

1. Предотвращение сопротивления

Предотвращение начинается с применения структурированного процесса и набора инструментов для управления изменениями, касающимися людей, для достижения бизнес-результатов. Другими словами, применение эффективного управления изменениями в первую очередь:

• Привлекайте спонсоров к общению, созданию коалиций и активному участию в изменениях
• Разработайте четкие и индивидуальные планы коммуникации, ориентированные на определенную аудиторию
• Предоставьте менеджерам возможность стать отличными сторонниками и лидерами изменений
• Обеспечить, чтобы все пострадавшие группы прошли соответствующее обучение в нужное время
• Предусмотреть полную интеграцию плана управления изменениями с планом проекта

Эти основные аспекты управления организационными изменениями представляют собой действия, предпринимаемые для поддержки сотрудников в процессе изменений.

Когда мы применяем структурированный подход к управлению изменениями, как описано выше, мы отвечаем на постоянные вопросы сотрудников, такие как: Почему происходят эти изменения? Что это значит для меня? Почему я должен попасть на борт? Когда у сотрудников есть ответы на эти вопросы, они с меньшей вероятностью будут сопротивляться, когда придет время внести изменения.

Хотя это не единственная цель, применение эффективного управления изменениями в значительной степени связано с предотвращением сопротивления.

2. Упреждающее управление резистентностью

Упреждающее управление резистентностью направлено на предполагаемые или выявленные источники резистентности. Прежде чем вы начнете реализовывать свои планы управления изменениями, необходимо выполнить несколько ключевых действий, включая необходимые оценки, чтобы адаптировать ваши планы к вашим изменениям и организации. В рамках построения этой стратегии вы определите ожидаемые точки сопротивления.

Вот несколько распространенных сценариев, в которых вы можете предвидеть сопротивление:

• Подразделение или группа в вашей организации, у которых есть история неудачных изменений, скорее всего, скептически отнесутся к новой инициативе.
• Группа старших сотрудников, приближающихся к пенсии, будет сопротивляться любой инициативе по изменению, которая даже незначительно повлияет на пенсионные планы.
• Люди, которые сильно заинтересованы в текущем состоянии и могут быть вытеснены вашими изменениями, скорее всего, будут сопротивляться этим изменениям.
• Группа, выступавшая за решение А, с большей вероятностью будет сопротивляться изменению решения Б.
• Возможно, самые важные из всех изменений, увольнения или перераспределения персонала, безусловно, вызовут сопротивление.

Упреждающее управление сопротивлением заключается в том, чтобы действовать на основе предвидения. Вместо того, чтобы ждать постфактум проекта, встройте управление сопротивлением в планы управления изменениями или решите проблему заранее. Нет причин ждать, пока сопротивление поднимет голову, прежде чем действовать. Предвидеть это. Просмотрите историю изменений в организации, определите группы с высоким риском или сильно затронутые группы и соответствующим образом спланируйте заранее.

3. Управление реактивным сопротивлением

Сопротивление – это естественная реакция на изменения. Вы можете применять превосходное управление изменениями и предвидеть потенциальные проблемы, но при этом рассчитывать на сопротивление в процессе изменений. Управление реактивным сопротивлением означает знание того, как вы будете реагировать, когда возникнет сопротивление.

1. Первым шагом является определение основной причины сопротивления. Такие инструменты, как модель Prosci ADKAR или упражнение «Пять почему», могут помочь вам определить или узнать больше об основной причине сопротивления сотрудника или группы.
2. Как только вы определите первопричину, вы сможете предпринять определенные шаги в случае сопротивления. Они включают в себя ряд действий, выполняемых разными игроками, от простого слушания и устранения барьеров до сосредоточения внимания на «что», а не на «как», и предложения четкого выбора и последствий. Вы также можете занять более жесткую позицию, продемонстрировав преимущества перемен ясным и ощутимым образом, обратив в свою веру самых сильных несогласных или, в крайнем случае, устранив сильно сопротивляющегося человека.
3. Третьим компонентом реактивного управления сопротивлением является активация и расширение прав и возможностей соответствующих менеджеров сопротивления. Хотя специалисты по управлению изменениями должны быть проводниками усилий по управлению изменениями, они редко занимают должности, связанные с сотрудниками. Наиболее эффективными менеджерами по сопротивлению являются люди, наиболее близкие к пострадавшим сотрудникам — их руководители и начальники. Важно отметить, что управление сопротивлением — это роль, с которой борются менеджеры и руководители, поэтому для лидеров изменений крайне важно дать им возможность помочь управлять сопротивлением своим сотрудникам.

Смягчение последствий сопротивления

Сопротивление не возникает в вакууме — вы должны поддерживать как личный, так и организационный контекст. Никогда не недооценивайте силу текущего состояния и удобство сотрудников при нем. Переход от текущего состояния к будущему приводит к стрессу и беспокойству для всех, кого это затрагивает. Хорошая новость заключается в том, что у вас есть возможность контролировать продолжительность, стоимость и серьезность сопротивления, а также его влияние на изменения.

Тим Кризи — директор по инновациям Prosci и признанный во всем мире лидер в области управления изменениями. Его работа формирует основу крупнейшего в отрасли свода знаний об управлении изменениями, связанными с людьми, для достижения организационных результатов.

Оставайтесь со мной в Twitter, LinkedIn

Вам также может понравиться

Подпишитесь здесь

Формула, треугольник импеданса и его работа

Как правило, мощность – это способность выполнять работу. В области электричества электрическая мощность — это количество энергии, переданной в какую-либо другую форму в единицу времени, такую ​​как свет, тепло и т. д. Математически ее можно определить как произведение напряжения и силы тока. Рассмотрим цепи постоянного тока, которые имеют только один источник напряжения либо источник напряжения, либо источник тока, поэтому конденсаторы работают как разомкнутая цепь в установившемся режиме, тогда как катушки индуктивности работают как короткое замыкание. Здесь цепь постоянного тока работает как резистивная цепь, поэтому вся электрическая мощность может рассеиваться в виде тепла. Здесь напряжение и ток находятся в одной фазе, и вся электрическая мощность может быть представлена ​​как P = V * I. Итак, в этой статье дается краткая информация о треугольнике власти.

Три элемента, составляющие мощность переменного тока, а именно активная мощность, реактивная мощность и полная мощность, могут быть выражены графически на трех сторонах прямоугольного треугольника, такого как треугольник импеданса, обсуждаемый ниже. Как показано на рисунке ниже, фактическая мощность P цепи представляет собой горизонтальную (прилегающую) сторону, реактивная мощность Q представляет собой вертикальную (противоположную) сторону, а гипотенуза представляет собой полную мощность (S), генерируемую из мощности. треугольник.

Силовой треугольник 92 в омах

Φ = фазовый угол в градусах. Больший фазовый угол дает большую реактивную мощность

Коэффициент мощности Cos(Φ) = P/S = R/Z W/VA =

Sin(Φ) = Q/S = X/Z = ВАр/ВА

Tan(Φ) = Q/P = X/R =VAr/W

полная мощность и разность фаз будут равны 0. Это называется единичным коэффициентом мощности.

Коэффициент мощности = Cos 0° = 1

Когда кривые напряжения и тока чисто реактивной цепи противофазны друг другу на угол 90 градусов, тогда разность фаз будет 90 градусов.

Коэффициент мощности = cos 90° =0

Соотношение между полной мощностью, активной мощностью и коэффициентом мощности цепи определяется как

Активная мощность P = Полная мощность (S) x коэффициент мощности

Коэффициент мощности = Вт/Вольт-ампер

В индуктивной цепи отстающий коэффициент мощности получается, потому что ток отстает от напряжения. В емкостной цепи получается опережающий коэффициент мощности, потому что ток опережает напряжение. Концепция треугольника мощности — это просто схематическое изображение фазовой диаграммы индуктивной/емкостной нагрузки, подключенной к источнику. Он получается путем умножения тока I в цепи, активного тока (IcosØ) и реактивного тока (IsinØ) на напряжение V.

Напряжение «V» и ток «I» в цепи, активный ток IcosØ и реактивный ток IsinØ дают полную мощность (S), активную мощность (P ) и реактивную мощность (Q) соответственно.

Формула треугольника мощности

Графическое изображение прямоугольного треугольника, показывающее взаимосвязь между реактивной мощностью, реальной/активной мощностью и полной мощностью, известно как треугольник мощности. Умножая каждую составляющую тока, т.е. активную составляющую (Icosϕ) или реактивную составляющую (Isinϕ) на напряжение V, мы получаем треугольник мощности, как показано на рисунке ниже.

Прямоугольный треугольник

Фактическая мощность, потребляемая или используемая в цепи переменного тока, называется истинной мощностью, реальной мощностью или активной мощностью. Измеряется в киловаттах (кВт) или МВт. Мощность, которая течет туда и обратно, то есть мощность, которая перемещается или реагирует в обоих направлениях в цепи, называется реактивной мощностью.

Реактивная мощность измеряется в реактивной мощности киловольт-ампер (кВАр) или реактивной мощности МВАР.

Произведение квадратного корня (RMS) из напряжения и тока (RMS) называется полной мощностью. Эта мощность измеряется в кВА или МВА. Следующая точка представляет взаимосвязь между следующими величинами и иллюстрируется графиком, называемым треугольником мощности, показанным выше. Умножение активной составляющей тока на напряжение цепи V дает активную мощность. Эта мощность создает крутящий момент в двигателе, тепло в нагревателе и т. д. Эта мощность измеряется с помощью устройства, называемого ваттметром. Умножьте реактивный ток на напряжение в цепи, чтобы получить реактивную мощность. Эта мощность дает коэффициент мощности, который перемещается взад и вперед по цепи.

Умножьте ток цепи на напряжение цепи, чтобы получить полную мощность. Отношение можно определить из перевернутого треугольника, изображенного на графике выше, т. е. мощность, взяв отношение активной мощности к кажущейся мощности. Коэффициент мощности рассчитывается из приведенного выше треугольника мощности, который представляет собой угол косинуса между векторами напряжения и тока, заданный как

Коэффициент мощности Cosφ = Активная мощность / Полная мощность = кВт/кВА

Как мы знаем, мощность просто известен как произведение напряжения и тока, но в цепях переменного тока, за исключением чисто резистивных цепей, обычно существует разность фаз между напряжением и током, поэтому VI не представляет фактическую мощность цепи. Соотношение между активной, реактивной и полной мощностью определяется как 92

Треугольник импеданса

Прямоугольный треугольник, основание, перпендикуляр и гипотенуза которого представляют соответственно электрическое сопротивление, реактивное сопротивление и импеданс, называется треугольником импеданса.

Это основное геометрическое представление импеданса цепи.

Импеданс состоит из двух компонентов. одно сопротивление, а другое реактивное сопротивление. Таким образом, это может быть выражено этими двумя факторами. Полное сопротивление цепи переменного тока Z = R+jX

Где «R» — сопротивление

«X» — реактивное сопротивление.

Из приведенного выше выражения Z является комплексным числом и, следовательно, может быть выражено геометрически так же, как и комплексное число. Геометрическое представление показано ниже.

Геометрическое представление

Полученный треугольник OAB называется треугольником импеданса. Значение импеданса Z можно легко определить по этому треугольнику, используя теорему Пифагора. 2 * R.

, где R — общая резистивная составляющая цепи.

Поскольку резисторы не создают разности фаз (фазового сдвига) между напряжением и током, вся полезная мощность передается непосредственно на резистор и преобразуется в тепло, свет и работу. Тогда мощность, потребляемая резистором, является фактической мощностью, которая в основном представляет собой среднюю мощность схемы. Умножьте среднеквадратичное значение напряжения и тока на косинус фазового угла (φ), как показано на рисунке, чтобы найти соответствующее фактическое значение мощности. 92*R = V*I*Cosφ в ваттах (Вт)

Поскольку в резистивной цепи нет разности фаз между напряжением и током, фазовый сдвиг между осциллограммами напряжения и тока также равен нулю.

Следовательно,

P = Vrms x Irms x Cosφ

Cos (0°) = 1

Следовательно, P = Vrms x Irms Вт

или киловатты или мегаватты

В = среднеквадратичное значение напряжения в вольтах

I= среднеквадратичное значение тока в амперах

Реактивная мощность (S)

Мощность, потребляемая в цепи переменного тока, которая не выполняет полезной задачи, но оказывает значительное влияние на фазовый сдвиг между напряжением и током, называется реактивной мощностью. . Реактивная мощность связана с реактивным сопротивлением, создаваемым катушкой и конденсатором, и противодействует действию активной мощности. В цепях постоянного тока нет реактивной мощности.

В отличие от реальной мощности (P), которая выполняет всю работу, реактивная мощность (Q) создает и ослабляет индуцированное магнитное поле и емкостное электростатическое поле для извлечения или удаления мощности из цепи, что затрудняет передачу реальной мощности напрямую подавать реальную мощность на нагрузку или цепь.

В магнитном поле энергия, накопленная катушкой индуктивности, пытается управлять током, а энергия, накопленная конденсаторами в электростатическом поле, пытается контролировать напряжение. В результате конденсатор вырабатывает реактивную мощность, а дроссель потребляет реактивную мощность. Это означает, что реальная мощность не потребляется, поскольку они одновременно потребляют энергию и отправляют ее обратно к источнику. Чтобы найти реактивную мощность, умножьте среднеквадратичное значение напряжения и тока на синус фазового угла (φ), как показано на рисунке. 92X = VIsinφ Вольт-Ампер реактивный (VAr)

Разность фаз в 90 градусов между формами тока и напряжения в чистом реактивном сопротивлении (емкостном или индуктивном), умножение VIsinφ дает перпендикулярную составляющую, которая на 90 градусов не совпадает по фазе друг с другом.

Следовательно,

Q = VRMS X IRMS X SINφ

SIN (90 °) = 1

Q = VRMS X IRMS (VAR)

, где Q = Реактивная мощность в VRM-AMPER (ВАр) или киловольт-ампер реактивный (кВАр) или мегавольт-ампер реактивный (МВАр)

Vrms = среднеквадратичное значение напряжения в вольтах

Irms = среднеквадратичное значение тока в амперах

Произведение вольт и ампер, сдвинутых по фазе друг относительно друга на 90 градусов, представляет собой реактивную мощность. В общем случае между током и напряжением может быть любой фазовый угол.

Полная мощность (S)

Мы знаем, что активная мощность рассеивается через резистор, а реактивная мощность подводится к реактивному сопротивлению. Это приводит к тому, что волны тока и напряжения не совпадают по фазе из-за разницы между резистивной и реактивной составляющими цепи. Тогда математическое соотношение между реальной мощностью (P) и реактивной мощностью (Q) называется комплексным числом. Произведение среднеквадратичного напряжения V, приложенного к цепи переменного тока, и среднеквадратичного значения тока, протекающего по этой цепи, называется произведением вольт-ампер (ВА), обозначаемым буквой «S», известным как полная мощность.

Эта комплексная мощность не равна алгебраической сумме объединенных активной и реактивной мощностей, а выражается векторной суммой P и Q в вольт-амперах (ВА), которая представляет собой комплексную мощность, представленную треугольником мощности. Среднеквадратичное значение произведения вольт-ампер обычно называют полной мощностью. Потому что «очевидно», что фактическая мощность, совершающая работу, намного меньше, но это общая мощность, потребляемая схемой.

Полная мощность генерируется двумя частями: резистивная мощность, которая представляет собой фактическую мощность или мощность в фазе или в ваттах, и другая часть, реактивная мощность, которая представляет собой фазную мощность (в противофазе) в вольт-амперах, поэтому мы можем представить векторную сумму этих двух компонентов мощности в виде треугольника мощности. Треугольник сил P, Q, S и θ.

Что такое импеданс треугольника мощности?

Импеданс треугольника мощности представляет собой геометрическую зависимость между реактивным сопротивлением, сопротивлением и импедансом. Это треугольник, образованный добавлением сопротивления к реактивному сопротивлению.

Как найти настоящую силу?

В электрической цепи активная мощность также называется активной мощностью или реальной мощностью, измеряемой в ваттах. Это полная мощность, потребляемая резистивной частью цепи. Эта мощность в цепях постоянного тока такая же, как мощность в цепях переменного тока, которую можно рассчитать по приведенной ниже формуле 9.2*R

Где «I» — ток в амперах

R — резистивная составляющая.

Или Активная мощность = VIcosφ

По какой формуле рассчитывается мощность?

Максимальная мощность, возникающая в цепи переменного тока, возникает, когда кривые тока и напряжения совпадают по фазе друг с другом. Формула для расчета мощности дается как

P = V * I

Таким образом, это все об обзоре треугольника мощности. Вот вопрос к вам: «Какие различия между активной мощностью, полной мощностью и реактивной мощностью?

Использование импеданса нагрузки в цепях и его влияние на функциональность цепи

Основные выводы

●     Получите более полное представление о концепции импеданса нагрузки.

●     Узнайте, как сопротивление нагрузки используется в цепи.

●     Узнайте больше о влиянии импеданса нагрузки на цепь.

Цифровой мультиметр

Практически во всех словарях синонимы определяются как слова, имеющие одинаковое или почти одинаковое значение друг с другом. В области электроники широко распространено использование синонимов.

Одной из таких пар синонимов является полное сопротивление (цепи переменного тока) и сопротивление (цепи постоянного тока). С технической точки зрения они оба представляют противодействие течению тока, но импеданс также включает сопротивление в свою факторизуемость. Это, конечно, включает реактивное сопротивление (конденсаторы) и индуктивность (катушки индуктивности).

Что такое импеданс?

Полное сопротивление представляет собой активное сопротивление электрической цепи или компонента переменному току, возникающее в результате комбинированного действия реактивного сопротивления и омического сопротивления. Мы также определяем его как любое препятствие или меру противодействия электрического тока потоку энергии при подаче напряжения.

Более техническое определение — это полное противодействие электрической цепи потоку переменного тока одной частоты. Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах и обозначаем символом Z. Ом. При расчете импеданса нам нужны сопротивления (импедансы) всех конденсаторов, катушек индуктивности и номиналы всех резисторов. Требование этих значений связано с тем, что каждый из этих компонентов обеспечивает различное сопротивление току. Мера, конечно, зависит от того, как ток изменяется по скорости, направлению и силе. Мы можем рассчитать импеданс, используя простую математическую формулу.

Это формулы, которые вам понадобятся для точного расчета импеданса вашей цепи

• Полное сопротивление: Z = R или XL или XC (если присутствует только один)

• Полное сопротивление только последовательно: Z = √(R2 + X2) (когда присутствуют оба R и один тип X)

• Полное сопротивление только последовательно: Z = √(R2 + (|XL — XC|)2) (при наличии R, XC и XL)

• Полное сопротивление в любой цепи = R + jX (j — мнимое число √(-1))

• Сопротивление: R = V / I

• Индуктивное сопротивление: XL = 2πƒL = ωL

• Емкостное сопротивление: XC = 1/2πƒC = 1/ωC ​​

Что такое импеданс нагрузки?

Нагрузка или импеданс нагрузки — это концепция подключения устройства или компонента к выходу функционального блока, что позволяет получать от него измеримую величину тока. Например, вы можете подключить резистор к источнику питания или подключить буферный (операционный) усилитель к генератору. Таким образом, импеданс нагрузки является входным импедансом следующего функционального блока в цепочке.

Примечание. Буферный усилитель или буфер обеспечивает преобразование электрического импеданса от одной цепи к следующей цепи в цепи. Таким образом, он обеспечивает передачу тока или напряжения из первой цепи с высоким уровнем выходного сопротивления во вторую цепь с низким уровнем входного сопротивления. Интерполированный буферный усилитель препятствует перегрузке второй схемой первой схемы и нарушению надлежащего функционирования. В общем, существует два основных типа буферов: буфер тока или буфер напряжения.

Полное сопротивление нагрузки имеет место, когда нагрузка содержит компоненты, отличные от чисто резистивных компонентов, таких как резисторы, а также реактивные компоненты, такие как катушки индуктивности и конденсаторы. Реактивные компоненты представляют собой мнимый импеданс, тогда как резистивные элементы содержат реальный импеданс.

Функционально резисторы рассеивают энергию, когда мы подаем напряжение, тогда как конденсаторы и катушки индуктивности сохраняют энергию. Поэтому мы считаем их сопротивление мнимым.

Важность импеданса нагрузки

Как и в случае с любым сопротивлением, намеренно добавленным в цепь, конечной целью является управление потоком тока и напряжения в цепи. Поскольку импеданс является просто расширением принципов сопротивления в цепях переменного тока, использование импеданса нагрузки по понятным причинам имеет решающее значение для функциональности схемы.

Полное сопротивление нагрузки также важно для оценки поведения цепи в различных условиях. Например, схема достигает максимальной передачи мощности, когда полное сопротивление нагрузки равно выходному сопротивлению схемы. Изменение импеданса нагрузки повлияет на постоянные времени зарядки и разрядки RC. Это, конечно, зависит от конструкции схемы, но также может привести к изменению времени нарастания и спада. Таким образом, поведение цепи различается в таких условиях, как индуктивные и емкостные нагрузки или даже в условиях короткого замыкания.

Импедансы нагрузки также важны, если согласование импедансов является вашей целью для конкретной цепи. Рассмотрим пример линий передачи. В идеале вы хотите, чтобы импеданс источника, импеданс линии передачи и импеданс нагрузки были равны. Достижение этих идеальных условий параметров гарантирует, что исходный сигнал 7 В будет сигналом 7 В по всей линии передачи, а выход также будет наблюдать или видеть сигнал 7 В.

Сопротивление нагрузки влияет на характеристики цепей, в частности, на выходные напряжения и токи. Эти эффекты возникают в источниках напряжения, датчиках и усилителях, и это лишь некоторые из них. Одним из лучших примеров этого являются сетевые розетки, поскольку они обеспечивают питание при постоянном напряжении. В этом случае нагрузкой является электроприбор, который вы подключаете к цепи питания. Это означает, что при включении мощного электроприбора сопротивление нагрузки значительно снижается. Однако согласование импедансов имеет решающее значение не только для линии передачи, но и для межсоединений печатных плат.

Трехфазный масляный трансформатор с высоковольтным вводом разъемного типа

К счастью, страница обзора проектирования и анализа печатных плат Cadence поможет вашим проектировщикам и производственным группам совместно работать над пониманием использования импеданс нагрузки для всех схем, применимых в вашей компании. Кроме того, выбор полнофункционального пакета для проектирования и анализа печатных плат, такого как Cadence Allegro PCB Designer, может помочь обеспечить успех проектирования вашей печатной платы с помощью полезных инструментов для обеспечения соответствующего импеданса.

Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.