Реактивная мощность | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока
Реактивная мощность связана с полной мощностью и активной :
Зная Активную мощность и Полную мощность определяем Реактивную мощность из прямоугольного треугольника
Если рассмотреть Физически «реактивная мощность» — это, энергия, затрачиваемая на перемагничивание короткозамкнутой обмотки асинхронного двигателя при его работе, то есть ЛЮБОЙ асинхронный двигатель потребляет реактивную мощность из сети независимо от момента на своем валу.
Реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Отрицательное значение активной мощности нагрузки характеризовало бы нагрузку как генератор энергии. Активное, индуктивное, ёмкостное сопротивление не могут быть источниками постоянной энергии.
Так же есть :
Полная мощность тока
Активная мощность тока
В формуле мы использовали :
— Реактивная мощность
— Напряжение в цепи
— Сила тока
— Угол сдвига фаз
— Полная мощность тока
— Активная мощность тока
как найти по формуле, в чем измеряется
Многие люди, которые изучают скалярные физические величины и такие сферы точных наук, как электродинамика, электростатика и магнитостатика, сталкиваются с понятием мощности. Каково определение активной и реактивной мощности, их источник и в чем основная разница — далее в статье.
Описание явлений
Мощностью называется скалярный вид физической величина, которая показывает, как передается или преобразуется электроэнергия. Бывает мощность постоянного и переменного тока. Что касается последнего, то делится на активную и реактивную.

Разновидности
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов.
Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значениям.

Основные понятия из учебного пособия
Зачем нужна
Электричество передает энергию в проводник для осуществления технического процесса. Чтобы процесс происходил, переданная сила должна преобразовываться в тепло и напряжение. При этом электроэнергия должна поступать постоянно, что обеспечивается обеими разновидностями мощностной характеристики. Активно действующая дает полезную силу, а реактивно действующая ее поддерживает в электродвигательных, трансформаторных, печных, сварочных, дроссельных и осветительных установках.

Значение
Источник реактивной энергии
Чтобы понять природу появления этой энергии и то, как найти реактивную мощность, нужно уточнить, что любая электромагнитная или индукционная машина, которая работает на переменном токе, преобразует электричество в тепло. Чтобы это преобразование произошло, нужно магнитное поле. Оно, соответственно, формируется безваттной энергией. Причина в поглощении энергии индукционной цепи и отдаче ее обратно при спаде магнитного поля два раза за цикл мощностной частоты.

Природа явления
Различия
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания.

Основная разница
Расчет по формуле
Представить обе разновидности можно определением из формул вычисления. Так активно действующая мощностная характеристика это соотношение напряжения с силой тока на косинус угла сдвига фаз между ними. Там, где несинусоидальный ток, она равна суммированию средних мощностных характеристик. Может быть выражена через другую формулу. Она может быть равна удвоенной силе тока на сопротивление цепи или удвоенному напряжению на проводимость. Также может быть найдена с помощью полной энергии, перемноженной на косинус угла сдвига фаз напряжения с электротоком.

Формула через полную мощностную характеристику
Возвращаясь к вопросу, в каких единицах выражается реактивная мощность потребителей, можно отметить, что она находится по двум формулам, основной из которых является умножение напряжения на силу тока и синус сдвига фаз. Также может быть найдена через квадрат вычисления удвоенной полной энергии потребления. Измерение полной происходит из умножения напряжения на токовую силу.
Обратите внимание! Обе разновидности находятся в ваттах. Один ватт равен килограмму, умноженному на соотношение квадратного метра на кубические секунды. Также он равен джоулю, поделенному на секунды, ньютону на метр/секунду, вольту на ампер.
Отыскать одну и другую силу можно не только по формулам, но и по технологически современным устройствам, таким как вольтметр, амперметр или фазометр. Для вычисления любых показателей можно воспользоваться также мультиметром.

Физические формулы нахождения величин
Мощность — то, что характеризует скорость передачи с преобразованием электроэнергии. Реактивная мощность в цепи переменного тока от активной отличается тем, что используется для передачи реальной силы источника, в то время как вторая является самой реальной электроэнергией. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне. Активно применяются в промышленности.
Реактивная мощность | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока
![Rendered by QuickLaTeX.com \[\Large Q=U*Isin\varphi \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d9a7bf843dbff57aee4c0cbb79ecf8f4_l3.png)
Реактивная мощность связана с полной мощностью и активной :

Зная Активную мощность и Полную мощность определяем Реактивную мощность из прямоугольного треугольника
Если рассмотреть Физически «реактивная мощность» — это, энергия, затрачиваемая на перемагничивание короткозамкнутой обмотки асинхронного двигателя при его работе, то есть ЛЮБОЙ асинхронный двигатель потребляет реактивную мощность из сети независимо от момента на своем валу.
Реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Отрицательное значение активной мощности нагрузки характеризовало бы нагрузку как генератор энергии. Активное, индуктивное, ёмкостное сопротивление не могут быть источниками постоянной энергии.
Так же есть :
Полная мощность тока
![Rendered by QuickLaTeX.com \[\large S=U*I\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2b1af35fb0eb8742c3ae1763ebc8f99c_l3.png)
Активная мощность тока
![Rendered by QuickLaTeX.com \[\large P=UIcos\varphi\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9d691db489cfb05743b7d52a1c77e0a3_l3.png)
В формуле мы использовали :
Q — Реактивная мощность
U — Напряжение в цепи
I — Сила тока
![Rendered by QuickLaTeX.com \[\varphi\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-727a571f244c43789846a2307f15abd5_l3.png)
— Угол сдвига фаз
S — Полная мощность тока
P — Активная мощность тока
Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)
Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:
| . | (1) |
Выражение для мгновенного значения мощности в электрических цепях имеет вид:
| . | (2) |
Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:
| . | (3) |
Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.
Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.
Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .
Среднее за период значение мгновенной мощности называется активной мощностью .
Принимая во внимание, что , из (3) получим:
| . | (4) |
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.
1. Резистор (идеальное активное сопротивление).
Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность
2. Катушка индуктивности (идеальная индуктивность)
При идеальной индуктивности ток отстает от напряжения по фазе на .
Поэтому в соответствии с (3) можно записать
.
Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
3. Конденсатор (идеальная емкость)
Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
| (5) |
Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).
В частности для катушки индуктивности имеем:
, так как .
.
Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:
.
Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
| . | (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
| . | (7) |
Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,
| . | (8) |
Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
| , | (9) |
где — комплекс, сопряженный с комплексом .
.
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:
Применение статических конденсаторов для повышения cos
Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.
Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?
Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :
| ; | (10) |
| ; | (11) |
| . | (12) |
Из (11) и (12) с учетом (10) имеем
,
но , откуда необходимая для повышения емкость:
| . | (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
| (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
| (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
| , | (16) |
где знак “+” относится к индуктивным элементам , “-” – к емкостным .
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):
или
.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему необходимо стремиться к повышению коэффициента мощности ?
- Критерием чего служит баланс мощностей?
- К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.
- В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.
- Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.
Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.
Ответ: R=30 Ом; XL=40 Ом.
Ответ: R=10 Ом; XС=7,5 Ом.
Реактивная мощность — это… Что такое Реактивная мощность?
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность
Мгновенная электрическая мощность P (t), выделяющаяся на элементе электрической цепи — произведение мгновенных значений напряжения U (t) и силы тока I (t) на этом элементе:
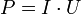 |
Если элемент цепи — резистор c электрическим сопротивлением R, то
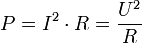 |
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам:
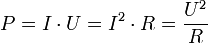 |
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: 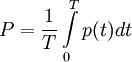 . В цепях однофазного синусоидального тока
. В цепях однофазного синусоидального тока 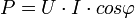 , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле
, где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле 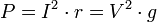 . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 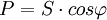 . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
. Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ. Единица реактивной мощности — вольт-ампер реактивный (var, вар). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: 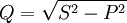 . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
. Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: 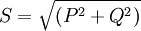 , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (VA, ВА).
, где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (VA, ВА).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: 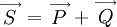
Измерения
Литература
- Бессонов Л. А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
Ссылки
См. также
Wikimedia Foundation. 2010.
Реактивная мощность — это… Что такое Реактивная мощность?
- Реактивная мощность
- величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока (См. Переменный ток). Р. м. Q равна произведению действующих значений напряжения U и тока /, умноженному на синус угла сдвига фаз (См. Сдвиг фаз) φ между ними: Q = UI sinφ. Измеряется в Варах. Р. м. связана с полной мощностью (См. Полная мощность) S и активной мощностью (См. Активная мощность) Р соотношением:
 Мощности коэффициента электрических установок осуществляется компенсация реактивной мощности (см. Компенсирующие устройства).
Мощности коэффициента электрических установок осуществляется компенсация реактивной мощности (см. Компенсирующие устройства).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Реактивная лампа
- Реактивная сила
Смотреть что такое «Реактивная мощность» в других словарях:
реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
РЕАКТИВНАЯ МОЩНОСТЬ — электр. мощность в цепи переменного тока, расходуемая на поддержание вызываемых переменным током периодических изменений: 1) магнитного поля при наличии в цепи индуктивности; 2) заряда конденсаторов при наличии конденсаторов и проводов (напр.… … Технический железнодорожный словарь
РЕАКТИВНАЯ МОЩНОСТЬ — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними: Q =… … Большой Энциклопедический словарь
РЕАКТИВНАЯ МОЩНОСТЬ — величина, характеризующая скорость обмена энергией между генератором переменного тока и магнитным (млн. электрическим) полем цепи, создаваемым электротехническими устройствами (индуктивностью и ёмкостью). Р. м. возникает в цепи при наличии сдвига … Большая политехническая энциклопедия
Реактивная мощность — Электрическая мощность физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Содержание 1 Мгновенная электрическая мощность 2 Мощность постоянного тока … Википедия
реактивная мощность — 3.1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации
реактивная мощность — reaktyvioji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Menamoji kompleksinės galios dalis, skaičiuojama pagal formulę Q² = S² – P²; čia Q – reaktyvioji galia, S – pilnutinė galia, P – aktyvioji galia. Matavimo vienetas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
реактивная мощность — reaktyvioji galia statusas T sritis fizika atitikmenys: angl. reactive power; wattless power vok. Blindleistung, f; wattlose Leistung, f rus. безваттная мощность, f; реактивная мощность, f pranc. puissance déwatée, f; puissance réactive, f … Fizikos terminų žodynas
реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь
реактивная мощность — reaktyvioji galia statusas T sritis automatika atitikmenys: angl. reactive power vok. Blindleistung, f; wattlose Leistung, f rus. реактивная мощность, f pranc. puissance réactive, f … Automatikos terminų žodynas
Реактивная мощность в электрической сети: мероприятия по компенсации
Электрическая мощность, потребляемая промышленными предприятиями и жилыми домами, бывает двух видов. Активная – затрачивается на выполнение полезной, нужной потребителю работы. Реактивная – увеличивает нагрузку на сеть и приводит к дополнительным расходам на электроэнергию.

Треугольник мощностей
Определение
Реактивная мощность не выполняет полезной работы. Она обусловлена наличием у потребителя индуктивной или ёмкостной составляющей нагрузки. На предприятиях реактивная мощность возникает при работе электрических двигателей, трансформаторов или ламп ДРЛ. В домашних условиях это моторы пылесосов, стиральных машин или компрессоров холодильников. На корпусе данных агрегатов часто можно увидеть параметр cosф, называемый коэффициентом мощности. Он количественно характеризует долю реактива.
Обратите внимание! Cosф – параметр крайне нестабильный. Он способен меняться в широком диапазоне с течением года и временем суток. Также коэффициент мощности тесно связан с будними и выходными днями.

Бирка на двигателе
Все перечисленное служит примером источников индуктивной составляющей. Гораздо реже встречается ёмкостная. К её примерам относятся мощные импульсные блоки питания и всё, что во входной части содержит конденсаторы.
Физика процесса
Для понимания процесса образования реактивной мощности следует заострить внимание на двух фактах:
- Природа переменного тока такова, что он периодически изменяет своё направление. Т.е. «+» и «-» в розетке переставляются местами 50 раз в секунду. Происходит это не рывками, а плавно по синусоидальному закону. Смена направления тока чем-то схожа с колебаниями качель.
- На создание электромагнитного поля, например, обмоткой трансформатора, требуется некоторое время.
В итоге получается следующая картина. Напряжение на выводах обмотки достигает своего пикового значения. Ток из-за индуктивного характера потребителя всё никак не может выйти на максимум. Если нагрузка ёмкостная, то эффект обратный: ток опережает напряжение.
Такое рассогласование источника и потребителя приводит к ощутимым потерям полезной мощности. Поэтому для борьбы с этими нежелательными свойствами индуктивностей и ёмкостей используют специальные устройства компенсации реактивной мощности (УКРМ).
Для чего компенсация реактивной мощности
Компенсировать реактивную составляющую мощности необходимо для повышения эффективности энергосистемы и снижения нагрузки на питающие кабеля и коммутирующие аппараты.
На производстве в основном преобладают потребители индуктивного характера. Для компенсации реактивной мощности, возникающей из-за их работы, чаще всего применяют конденсаторные установки. Их использование позволяет добиться следующих положительных эффектов:
- снизить нагрузку на сеть, избавив её от бесполезных реактивных токов;
- ощутимо уменьшить счета на электроэнергию;
- повысить качество напряжения за счёт устранения помех, шумов и высших гармоник.
Основные компоненты УКРМ
Для компенсации индуктивной составляющей реактивной мощности применяют конденсаторные установки. Иногда их объединяют в целые батареи и оснащают различной коммутирующей аппаратурой. Она необходима для автоматического переключения конденсаторов с целью повышения или понижения конечной ёмкости батареи. Дополнительно требуется к.л. измерительный прибор для отслеживания коэффициента мощности cosф и прочих параметров УКРМ. На сегодняшний день такие контроллеры выполняются на основе микропроцессоров, которые делают всю работу без вмешательства человека.

Конденсаторный компенсатор
Ёмкостная составляющая компенсируется похожим образом. Здесь уже в качестве выравнивающего cosф устройства выступают синхронные двигатели или специальные реакторы (катушки, дроссели). Ёмкостная составляющая свойственна протяжённым кабельным и воздушным линиям, а не самому промышленному оборудованию.
Виды компенсаторов и их принцип действия
Чаще всего в роли компенсирующего устройства применяется либо батареи конденсаторов, либо двигатели. При этом может использоваться как один компенсатор, так и множество подключенных параллельно.
В течение дня баланс мощности в сети может изменяться, на что УКРМ должно реагировать соответствующим образом. С этой точки зрения компенсаторы бывают:
- нерегулируемые – без возможности переключения составных элементов;
- автоматические – компенсатор сам отслеживает cosф, производит расчеты и решает, какое количество конденсаторов следует добавить в схему;
- с ручным управлением – человек сам анализирует cosф по приборам и производит соответствующие переключения.
В зависимости от условий эксплуатации выделяют следующие типы коммутирующих устройств:
- контакторные – только статические переключения;
- тиристорные – работа в реальном времени;
- вакуумные выключатели – для напряжений свыше 1 кВ.
Определение емкости конденсаторов
При проектировании УКРМ следует уделить внимание расчету ёмкости и мощности конденсаторных установок. Важно это по той причине, что в случае неправильного выбора этих параметров установка может нанести электросети больше вреда, чем пользы. Формула для расчета необходимой ёмкости конденсатора имеет следующий вид.
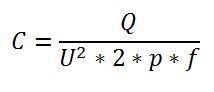
Ёмкость конденсатора
Здесь:
- C – ёмкость конденсаторной установки, Ф;
- U – сетевое напряжение, В;
- f – частота, Гц;
- Q – реактивная мощность конденсатора, вар;
- p – 3.14.
Переменная Q, в свою очередь, определяется по следующему выражению.

Реактивная мощность конденсатора
Где:
- P – активная мощность потребителя;
- К – коэффициент, подбираемый из таблицы.
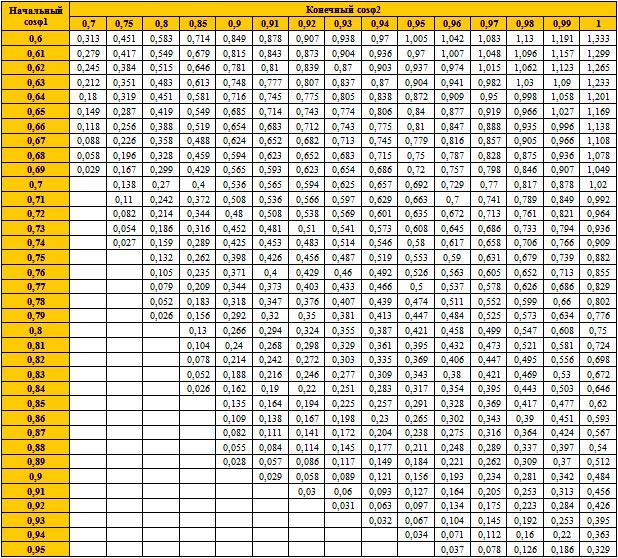
Таблица для расчёта УКРМ
Дополнительная информация. На просторах интернета полно ресурсов, содержащих в себе калькуляторы для онлайн расчета различных параметров компенсаторов.
Компенсаторы реактивной мощности в квартире
Многие промышленные предприятия, особенно крупные, применяют в целях экономии устройства компенсации реактивной мощности. Однако этот трюк не пройдёт в обычной квартире. Вытекает это из ряда причин:
- Бытовые однофазные счётчики электроэнергии, используемые в жилых домах, не способны вычислять реактивную мощность. Соответственно, никто не сможет взыскать за неё оплату. Особенно это относится к старым индукционным счётчикам.
- Организации, поставляющие электроэнергию, ведут учёт реактивной мощности только для крупных промышленных предприятий. Установка подобных устройств в жилых домах не является требованием ПУЭ.
- С технической точки зрения, проблематично и дорого будет рассчитать УКРМ для каждой квартиры или тем более поставить автоматические системы на микропроцессоре, ведь данные приборы стоят внушительных денег.
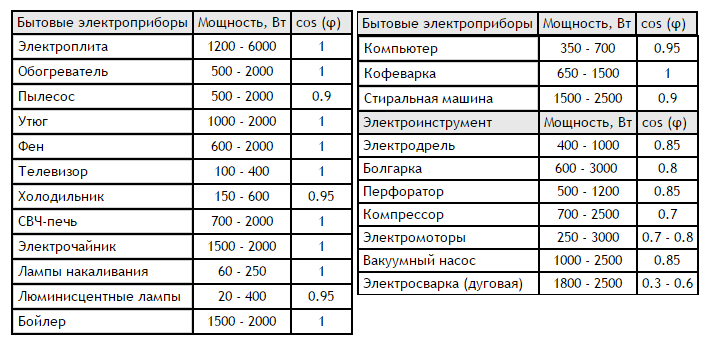
Cosф бытовых потребителей
Важно! По интернету гуляют предложения купить мошенническую чудо-коробочку. Она подключается к розетке и тем самым избавляет квартиру от излишков реактивной мощности. Как показывают обзоры, внутри этого прибора не содержится ничего, кроме светодиода. Соответственно, такое устройство никак не поможет сэкономить.
Эффективность применения конденсаторных установок
История применения метода компенсации реактивной мощности охватывает ещё советский период. Его экономическая эффективность на промышленных предприятиях доказана исследованиями и десятками лет практического использования.
Конденсаторные УКРМ предназначены в основном для компенсации реактивной мощности электрических двигателей. Энергия, потребляемая асинхронными моторами, может доходить до 40 % от всей нагрузки предприятия. Поэтому экономии на двигателях уделяют особое внимание. Масло в огонь подливает и то, что мотор, работающий с номинальной нагрузкой на валу, имеет cosф = 0,75-0,8. Это считается нормой. Однако тот же двигатель без нагрузки имеет гораздо более низкий коэффициент мощности порядка 0,3. Использование УКРМ позволяет повысить cosф до 0,99. Это хороший показатель, ведь, чем ближе этот параметр к единице, тем эффективнее расходуется электроэнергия.
Наличие устройств, компенсирующих реактивную мощность, благотворно сказывается на расходах промышленного предприятия. Помимо этого, уменьшается нагрузка на электрическую систему объекта. Это позволяет снизить сечение и конечную стоимость воздушных и кабельных линий, а также уменьшить долгосрочные затраты на их ремонт и обслуживание.


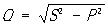 Мощности коэффициента электрических установок осуществляется компенсация реактивной мощности (см. Компенсирующие устройства).
Мощности коэффициента электрических установок осуществляется компенсация реактивной мощности (см. Компенсирующие устройства).