Фильтр верхних частот (ФВЧ) | Основы электроакустики

ФВЧ – это схема, которая передает без изменений сигналы высоких частот, а на низких обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов. Схема простого RC-фильтра верхних частот приведена на рис.3.5.

Рис.3.5. Простой ФВЧ

Частотная характеристика фильтра определяется выражением: Отсюда находим АЧХ и ФЧХ:Обе кривые представлены на рис.3.6. 

Рис.3.6. АЧХ и ФЧХ ФВЧ 

Выражение для частоты среза совпадает с соответствующим выражением для ФНЧ: 

   fСР = 1/2πRC.       Фазовый сдвиг на этой частоте составляет +45º. Как и для ФНЧ, наиболее просто составить АЧХ в двойном логарифмическом масштабе с помощью асимптот:

•  Ā = 1 = 0дБ на высоких частотах f>>fCР.
• На  низких частотах f<<fСР, согласно формуле (3.13), Ā ≈ ωRC, т.е. коэффициент усиления пропорционален частоте. Наклон асимптоты равняется + 20 дБ на декаду.
•  При f =fСР, как и для ФНЧ, Ā = 1/корень2  = –3 дБ.

Постоянная времени, как и для фильтра нижних частот, равна τ = RC. Реакция цепи на импульс напряжения описывается формулой: UВЫХ(t) = UВХ0 e–t/RC.  Для определения начального значения UВЫХ0 = UВЫХ (t=0) используем дополнительное соображение: в момент, когда входное напряжение изменяется скачкообразно, заряд конденсатора остается неизменным. Он действует как источник напряжения  Выходное напряжение повторяет скачок ΔU входного напряжения (рис. 3,7, а) от нуля до U1, а затем убывает по экспоненте, согласно равенству (3.13), снова до нуля. Если входное напряжение скачком изменяется от U1 до нуля, то UВЫХ скачком уменьшается от нуля до -U1 (рис. 3.7, б). При этом важно заметить, что выходное напряжение имеет отрицательные значения, хотя входное напряжение всегда положительно. Это обстоятельство часто используется в схемотехнике.

Фильтр верхних частот как дифференцирующее звено. Если приложено входное напряжение с частотой f<<fСР, то |UВЫХ|<<|UВХ|. Тогда  UВЫХ = RC(dUВХ / dt).  Таким образом, низкочастотные входные напряжения дифференцируются. Вид переходных характеристик ФВЧ показан на рис 3.8.

 

Рис.3.7. Реакция ФВЧ на скачок напряжения

 

Рис.3.8. Импульсный режим работы ФВЧ при различных соотношениях  частоты  и  постоянной  времени: верхняя кривая:

fВХ ≥ 10fСР; средняя кривая: fВХ = fСР; нижняя кривая: fВХ ≤ 1/10 fСР

Фильтр верхних частот как элемент RC-связи. Если на входе фильтра верхних частот приложено напряжение прямоугольной формы с периодом Т<<τ, то конденсатор в течение половины периода почти полностью перезаряжается и выходное напряжение будет равно входному с точностью до постоянной величины.

 

Рис. 3.9. Прохождение последовательности однополярных

импульсов через ФВЧ

В связи с тем, что через конденсатор не может протекать постоянный ток, среднее значение выходного напряжения равно нулю. Следовательно, постоянная составляющая входного напряжения не передается. На этом основано применение фильтра верхних частот в качестве элемента RС-связи.

 

Различные виды RC – фильтров

Фильтры ФНЧ

 

 

— для звена 1 порядка.

Если , то . Если увеличивать частоту, то коэффициент передачи будет уменьшаться, что соответствует ФНЧ. Одно звено не дает нужной крутизны характеристики, поэтому добавляют еще звенья.

Чтобы вычислить выходное напряжение, зная входное, необходимо определить входное сопротивление:

Определив ток I₁, можно узнать U₂.

Можно, применив законы Ома и Кирхгофа, рассчитать токи и напряжения на отдельных участках цепи. Можно составить систему уравнений по методу контурных токов или узловых напряжений. Есть смешанный метод. Вводятся токи и напряжения, и составляется система уравнений для каждого контура и узпа:

Затем находят определитель системы:

Используя методы решения систем уравнений с применением определителей можно найти U₂ , передаточную функцию, затем частотные и временные характеристики.

 

 

Фильтры ФВЧ

Фильтры верхних частот обратные фильтрам нижних частот:

 

Т(∞)=1.С уменьшением частоты коэффициент

передачи уменьшается.

 

 

Полосовые фильтры

Полосовой фильтр может составляется путем совмещения звеньев ФНЧ и ФВЧ.

 

На 0 частоте сигнал не проходит в нагрузку за счет продольных емкостей, а на ∞ частоте за счет поперечных.

Недостатки RC – фильтров

Основной недостаток – не очень высокая крутизна характеристик, т.е. не очень быстро нарастает ослабление в полосе непропускания, медленнее, чем у таких же LC – фильтров. Поэтому нельзя хорошо ослабить мешающий сигнал с близкой частотой.

У полосовых фильтров на средней частоте полосы пропускания ослабление не равно 0, в то время как у LC – фильтров без учета потерь ослабление на средней частоте равно 0

Активные RC – фильтры (АRC)

Общие понятия

В таких фильтрах есть RC – элементы и активный элемент. В качестве активного элемента часто выступает управляемый источник, который реализуется с использованием электронных компонентов. Одними из первых АRC – фильтров были фильтры на гираторах или имитаторах индуктивности.

Рассмотрим ФВЧ, где индуктивность подключена к общему проводу (корпусу) .

В данном ФВЧ индуктивность заменяют гиратором, нагруженным на емкость C_H, входное сопротивление которого: Гиратор имеет подключение к корпусу, да еще и источник питания. Гираторы изготавливаются в виде микросхемы

Для ФНЧ индуктивность не соединяется с корпусом и здесь для ее имитации требуется 2 гиратора и емкость, включенную между ними.

 

,

Недостатки АRC – фильтров с имитацией индуктивностей. Принцип позвенной реализации

Во-первых, необходимо много гираторов, особенно если в схеме есть продольные индуктивности. Чтобы уменьшить количество гираторов, стали применять позвенную реализацию путем каскадного соединения звеньев первого и второго порядка.

Если порядок n – четный, то все звенья второго порядка, если нечетный, то есть одно звено первого порядка.

Используя аппроксимацию по Баттерворту и Чебышеву, получаем:

— для ФНЧ. Разбиваем на звенья первого и второго порядка:

Если фильтр –верхних частот, полосовой или заграждающий, надо сделать преобразование частоты в самой передаточной функции и получить выражение для соответствующих звеньев фильтров. Передаточная функция звена ФВЧ 2 порядка Передаточная функция для полосового фильтра:

Средняя частота полосового фильтра

Чтобы коэффициент передачи на средней частоте равнялся 1, нужно, чтобы

Недостатки:

При соединении звенья влияют друг на друга. Между ними надо включать развязывающие буферные устройства типа повторителя напряжения (усилитель напряжения с единичным коэффициентом:- ИНУН, у него бесконечно большое входное сопротивление и нулевое выходное). Такое устройство позволяет перемножать коэффициенты передачи, что в данном случае и требуется. Поскольку используются усилители напряжения, решили использовать АRC – фильтры без гираторов, только на усилителях.

АRC – фильтры на усилителях

Есть усилители напряжения и усилители тока. Чаще используют усилители напряжения. Теоретически усилитель напряжения – источник напряжения. управляемый напряжением (ИНУН) или преобразователь напряжения в напряжение (ПНН).

Если коэффициент усиления – вещественный, то говорят ИНУН, если комплексный, то – ПНН.

Так как , то следующая нагрузка не влияет на передаточные функции, поэтому можно включать следующее звено.

Рассмотрим схемы различных типов фильтров, построенных на операционных усилителях.

Усилители напряжения на ОУ: не инвертирующий, единичный и инвертирующий

Коэффициент усиления полученного ИНУН определяется соотношением:

U₂ /U₁=(R₂+R₁)/R₁=K

Очевидно, что коэффициент усиления всегда больше единицы. Неинвертирующий ИНУН с единичным коэффициентом усиления можно реализовать так, как показано на рисунке. Эту схему называют обычно схемой повторителя напряжения. Инвертирующий ИНУН можно реализовать на ОУ.. Его коэффициент усиления:

U₂/U₁= — R₂/R₁ =K

ФНЧ второго порядка:

 

Емкость подключенная к корпусу шунтирует высоко частотный сигнал из-за малого сопротивления на этих частотах, а емкость в обратной связи усилителя шунтирует сам усилитель по обратной связи и он не может усиливать сигнал на этих частотах, на низких частотах сопротивления емкостей велики и они не влияют на прохождение сигнала, что и дает ФНЧ 2 порядка.

 

ФВЧ:2 порядка. Здесь емкости не пропускают сигнал с низкой частотой из-за своего большого сопротивления.

ПФ:2 порядка. Здесь первая емкость (продольная) ослабляет низкочастотный сигнал, а вторая (поперечная) ослабляет высокочастотный.

 

 

 

Сами усилители можно реализовать с помощью стандартных микросхем ОУ.

Условное обозначение операционного усилителя (ОУ) и схема замещения:

 

 

R_ВХ=∞, R_ВЫХ=0.

ФНЧ на операционном усилителе

Т_U(0)=1, Т_U(∞)=0, n=2.

Емкость С₁ шунтирует ОУ в обратной связи на высоких частотах и не дает ему усиливать, а С₂ шунтирует высоко частотный сигнал перед входом ОУ, что и дает характеристику ФНЧ 2 порядка

. Передаточная функция звена второго порядка ФНЧ имеет вид:

сравнивая соответствующие коэффициенты функций , можно составить следующую систему уравнений для определения значений элементов схемы:

В системе из трех уравнений – 5 неизвестных: R₁, R₂, R₃, C₁, C₂. Чтобы система стала определенной, значением двух любых элементов можно задаться. Положим, например, что R₂=R₃=1, тогда система уравнений примет вид:

Решая последнюю систему уравнений, получим выражения

 

для расчета значений нормированных элементов схемы:

 

; ;

;

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Исследование пассивных RC-фильтров (Отчет по лабораторной работе) | ЛАБЫ

ЛАБЫ

           

Цель работы: изучение свойств RC-фильтров низких частот, а также полосовых фильтров, приобретение навыков работы с генератором сигналов специальной формы и цифровым осциллографом.

 

1. Теоретический расчет выражений для АЧХ и ФЧХ фильтров

 

Если собрать делитель напряжения из пары пассивных двухполюсников разного типа, например из резистора и конденсатора, то возникает цепь, попадающая под понятие пассивный четырехполюсник.

Очевидно, что выходное напряжение должно зависеть от частоты входного напряжения в результате изменения емкости конденсатора.

Фаза выходного напряжения при изменении частоты также не останется неизменной, так как вклад в полное сопротивление цепи со стороны компонента (конденсатора), у которого имеется фазовый сдвиг между током и напряжением, будет разным для разных частот.

Выведем зависимости, называемые соответственно амплитудно-частотной и фазочастотной характеристиками четырехполюсника для каждого из исследованных фильтров.

 

1.1. Однозвенный фильтр нижних частот

 

Данный фильтр (рис. 1, а) является делителем напряжения, к которому не подключена никакая нагрузка. Такой делитель называют идеальным делителем напряжения (ИДН). Выходное напряжение U₂ представляет собой в данном ИДН падение напряжения на конденсаторе C и поэтому зависит от частоты.

 

 

Рис. 1. Исследуемые однозвенный (а) и двухзвенный (б) фильтры нижних частот,

фильтр Вина (в)

 

Согласно формуле делителя напряжения, отношение выходного к входному напряжений можно выразить через комплексные сопротивления, аналогично резистивному делителю напряжений:

 

.

(1)

            Произведение RC выражается в секундах, тогда единицей измерения 1/ RC как и для угловой частоты будет секунда в минус первой степени. Обозначим тогда эту величину как w₀ и подставим в формулу (1):

 

.

(2)

 

            Для устранения мнимого числа в знаменателе умножим числитель и знаменатель в (2) на сопряженное знаменателю комплексное число:

 

.

(3)

 

            Из (3) можно найти АЧХ, как модуль данного выражения, и ФЧХ как арктангенс отношения аргументов мнимой и вещественной части:

 

; .

(4)

 

            Графическое представление полученных амплитудно-частотной и фазо-частотной характеристик представлено совместно с практическими результатами на рис.

 

 

1.2. Двухзвенный фильтр нижних частот

 

Для данного фильтра (рис. 1, б) мы можем воспользоваться тем фактом, что для исследуемых синусоидальных сигналов из правила перемножения экспоненциальных зависимостей вытекают два важных свойства последовательных соединений двух и более четырехполюсников – результирующая АЧХ получается путем перемножения АЧХ отдельных четырехполюсников, а результирующая ФЧХ образуется сложением ФЧХ последовательных четырехполюсников:

 

; .

(5)

 

В предыдущем пункте мы рассчитали АЧХ и ФЧХ для одного звена. Воспользовавшись правилами (5), получим:

 

; .

(6)

 

            Стоит сказать, что поскольку в данном фильтре всего два звена, выражения (5) описывают его довольно хорошо, что подтверждают рис. 5 и 6. В случае большего числа звеньев делители напряжения еще более неидеальны, так как их выходы шунтируются выходами последующих звеньев, но на примере двухзвенного фильтра таким образом мы показали простой способ оценки усиления.

 

 

1.3. Фильтр Вина

 

Аналогично начальным выкладкам, данный фильтр (рис. 1, в) можно рассматривать как делитель напряжения с комплексными сопротивлениями, представленными последовательным и параллельным соединением резистора и конденсатора. Поэтому:

 

 

Как и ранее, произведение обозначаем величину 1/ RC как w₀ и, подставляя, получаем:

 

.

(7)

 

Из (7) можно найти АЧХ, как модуль данного выражения, и ФЧХ как арктангенс отношения аргументов мнимой и вещественной части:

 

; .

(8)

 

2.1. Характеристики однозвенного фильтра нижних частот

 

Рис. 2. Теоретическая (1) и экспериментально полученная (2) AЧХ однозвенного RC-фильтра нижних частот

Рис. 3. Теоретическая (1) и экспериментально полученная (2) ФЧХ однозвенного RC-фильтра нижних частот

 

2.2. Характеристики для двухзвенного фильтра нижних частот

Рис. 4. Теоретическая (1) и экспериментально полученная (2) AЧХ двухзвенного RC-фильтра нижних частот

Рис. 5. Теоретическая (1) и экспериментально полученная (2) ФЧХ двухзвенного RC-фильтра нижних частот

 

2.3. Характеристики фильтра Вина

Рис. 6 Теоретическая (1) и экспериментально полученная (2) AЧХ фильтра Вина

Рис. 7. Теоретическая (1) и экспериментально полученная (2) ФЧХ фильтра Вина

 

Выводы

            1. Фильтр нижних частот пропускает только низкочастотные сигналы (рис. 2 и 4). Как видно из сравнения полученных графиков, крутизну амплитудно-частотной характеристики можно увеличить за счет применения каскадного включения однозвенных фильтров, в нашем случае – двух. При этом граничная частота остается той же, а подавление высоких частот происходит лучше. Фазовый сдвиг при этом за счет вклада второй емкости увеличивается до двух раз (рис. 3 и 5).

2. Комбинации фильтров нижних и верхних частот позволяют создавать полосовые фильтры, с помощью которых их всего спектра выделяется только определенная область частот. Эта возможность продемонстрирована на приме фильтра Вина (рис. 6). Максимальный коэффициент усиления, в отличие от ФНЧ, равен 1/3.

3. Простые фильтры хорошо поддаются теоретическому описанию, как видно из полученных экспериментальных характеристик и сравнения с математическими выкладками. Неравномерность погрешностей связана с нелинейными законами распределения частот и измерительной шкалы.

Исследование ачх пассивных фильтров методические указания

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра ТС

к лабораторной работе по дисциплине «Устройства приема и обработки радиосигналов в СПРС»

УФА. 2002

Составитель: А.И.Гулин

Исследование АЧХ пассивных фильтров с использованием математического пакета МАТLАВ: Методические указания к лабораторным работам по курсу «Устройства приема и обработки радиосигналов в системах подвижной радиосвязи» Уфимский государственный авиационный технический университет; составитель: А.И.Гулин. Уфа 2002, 13 с.

Рассмотрены основные характеристики фильтров различных аппроксимаций. Описано большинство видов пассивных фильтров, даны ориентировочные АЧХ фильтров первого и второго порядков.

Предназначены для студентов направления 201200 «Средства связи с подвижными объектами», а также могут быть полезны студентам других специальностей направления «Телекоммуникации».

Рецензент: Беспалов А. И.

Уфимский государственный авиационный технический университет, 2002.

Содержание

стр.

1. Теоретическая часть………………………………………………………………4

1. Назначение, классификация и принцип работы пассивных фильтров…….4

2. Описание RC-фильтров……………………………………………………….4

3. Описание LC-фильтров……………………………………………………….7

4. Сравнение пассивных фильтров с другими видами фильтров……………..9

1. Практическая часть………………………………………………………………11

2. Варианты заданий…………………………………………………………………12

3. Контрольные вопросы……………………………………………………………12

4. Список литературы……………………………………………………………….13

Теоретическая часть

1.1. Назначение, классификация и принцип работы пассивных фильтров.

Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот. Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют. Существуют четыре типа фильтров:

1. Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.

2. Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.

3. Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.

4. Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.

1.2. Описание rc-фильтров.

Ф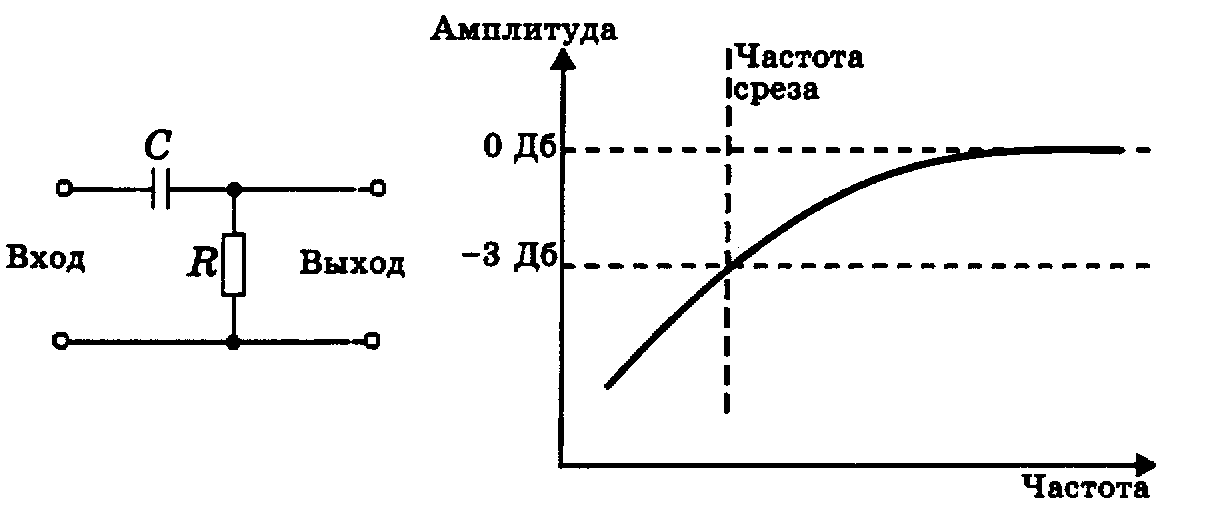ильтрация сигналов низких (звуковых) частот обычно осуществляется с помощью фильтров на основе сопротивления и емкости (RC). Схема фильтра верхних частот и его амплитудно-частотная характеристика показаны на рис. 1.

Рис. 1. Схема и амплитудно-частотная характеристика высокочастотного RC-фильтра.

В этой схеме входное напряжение прикладывается и к резистору, и к конденсатору. Выходное же напряжение снимается с сопротивления. При уменьшении частоты сигнала возрастает реактивное сопротивление конденсатора, а следовательно, и полное сопротивление цепи. Поскольку входное напряжение остается постоянным, то ток, протекающий через цепь уменьшается. Таким образом, снижается и ток через активное сопротивление, что приводит к уменьшению падения напряжения на нем.

Фильтр характеризуется затуханием, выраженным в децибелах, которое он обеспечивает на заданной частоте. RC-фильтры рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3 дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню — 3 дБ определяется по формуле:

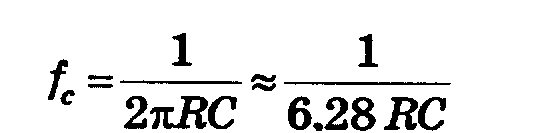
Фильтр низких частот имеет аналогичную структуру, только емкость и сопротивление там меняются местами. Амплитудно-частотную характеристику такого фильтра можно представить как зеркальное отображение АЧХ предыдущего.

В этой цепи входное напряжение также прикладывается и к резистору, и к конденсатору, но выходное напряжение снимается с конденсатора. При увеличении частоты сигнала реактивное сопротивление конденсатора, а следовательно, и полное сопротивление уменьшаются. Однако, поскольку это полное сопротивление состоит из реактивного и фиксированного активного сопротивлений, его значение уменьшается не так быстро, как реактивное сопротивление. Следовательно, при увеличении частоты снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле предыдущего фильтра.

Рассмотренные выше фильтры представляют собой RC-цепи, которые характеризуются тремя параметрами, а именно: активным, реактивным и полным сопротивлениями. Обеспечиваемая этими RC-фильтрами величина затухания зависит от отношения активного или реактивного сопротивления к полному сопротивлению.

При расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах обычно задают номинал сопротивления, поскольку он выбирается на основании других требований. Например, сопротивление фильтра является его выходным или входным полным сопротивлением.

Соединяя фильтры верхних и нижних частот, можно создать полосовой RC-фильтр, схема и амплитудно-частотная характеристика которого приведены на рис. 2.

Р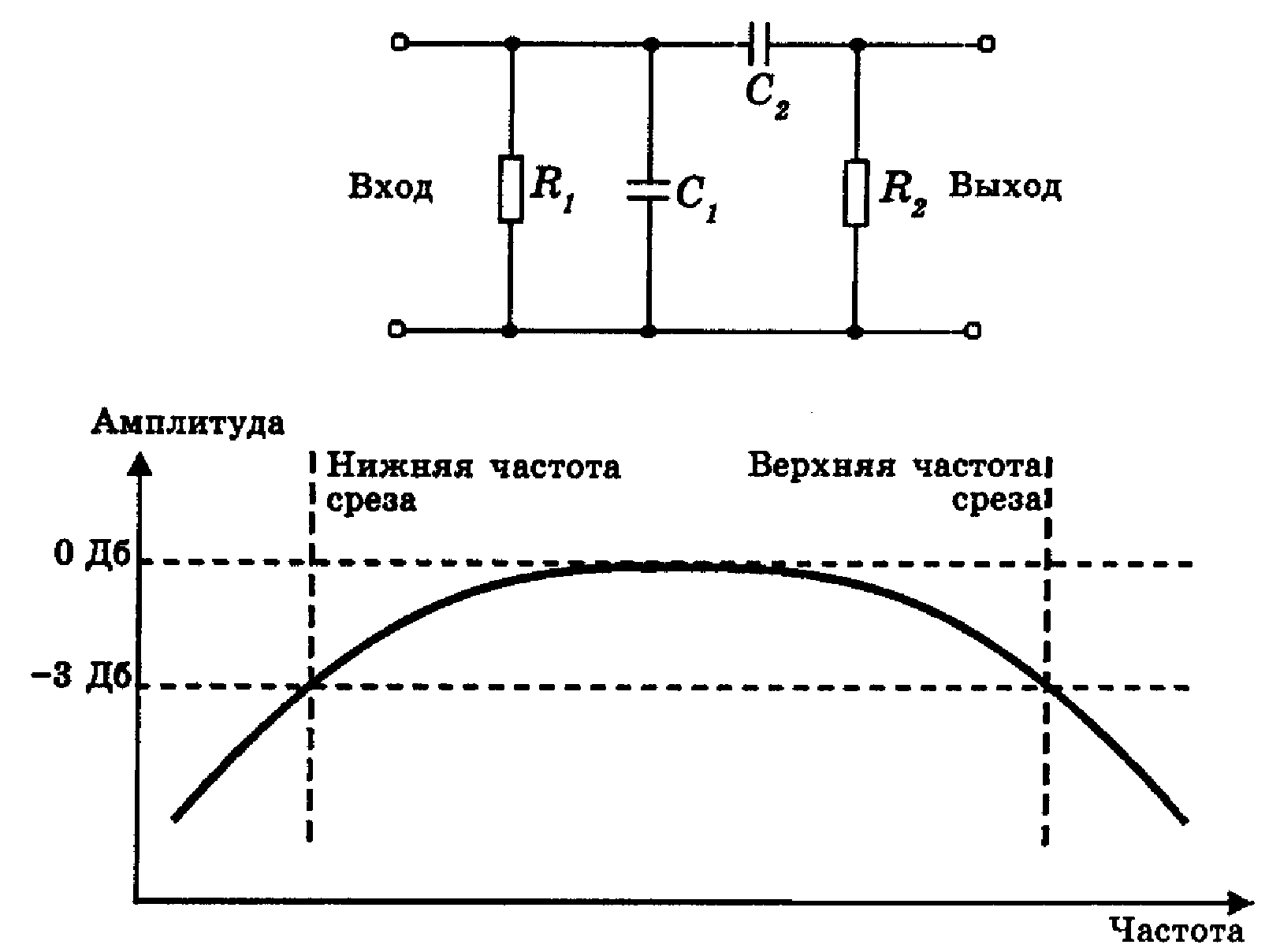ис. 2. Схема и АЧХ полосовогоRC-фильтра.

Н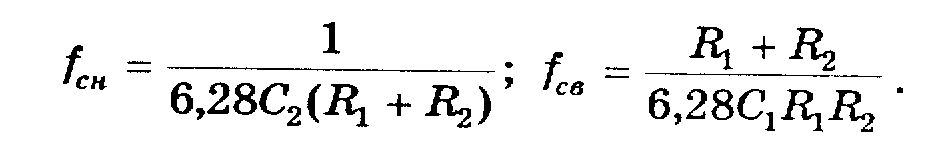а схеме рис. 2.R₁ — полное входное сопротивление; R₂ — полное выходное сопротивление, а частоты низкочастотного и высокочастотного срезов определяются по формулам:

Следует отметить, что значение верхней частоты среза (f_св) должно быть по крайней мере быть в 10 раз больше нижней частоты среза (f_сн), поскольку только в этом случае полосно-пропускающий фильтр будет работать достаточно эффективно.

Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (рис. 3.). Частота среза многозвенного фильтра определяется по формуле ВЧ,НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.

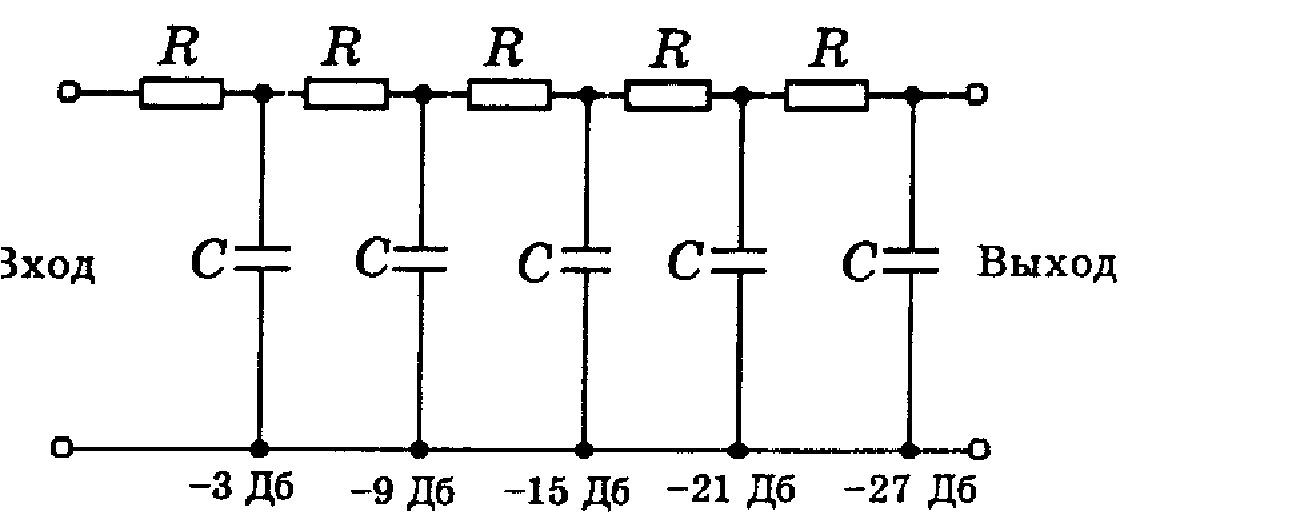
Рис. 3. Многозвенные фильтры: соответственно высокочастотный и низкочастотный.