1
Первый слайд презентации: RC-фильтры низких и высоких частот
Изображение слайда
2
Слайд 2
Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза f с
Изображение слайда
3
Слайд 3: Влияние фильтра на прямоугольный сигнал
прямоугольный сигнал представляет собой сложное колебание, состоящее из основной гармоники и бесконечного количества нечетных гармоник.
Изображение слайда
4
Слайд 4: RC- фильтры
Простейшим среди фильтров является RC -фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным.
Изображение слайда
5
Слайд 5
На схеме конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падения напряжения V c на конденсаторе будет большим, а на резисторе
V r — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: V c будет малым, а V r — большим.
При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падения напряжения V c на конденсаторе будет большим, а на резисторе
V r — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: V c будет малым, а V r — большим.
Изображение слайда
6
Слайд 6
Если теперь представить эту схему, как на рис. (б ), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора, рисунок (а), то получим фильтр верхних частот. Значения R и С определяют частоту среза фильтра.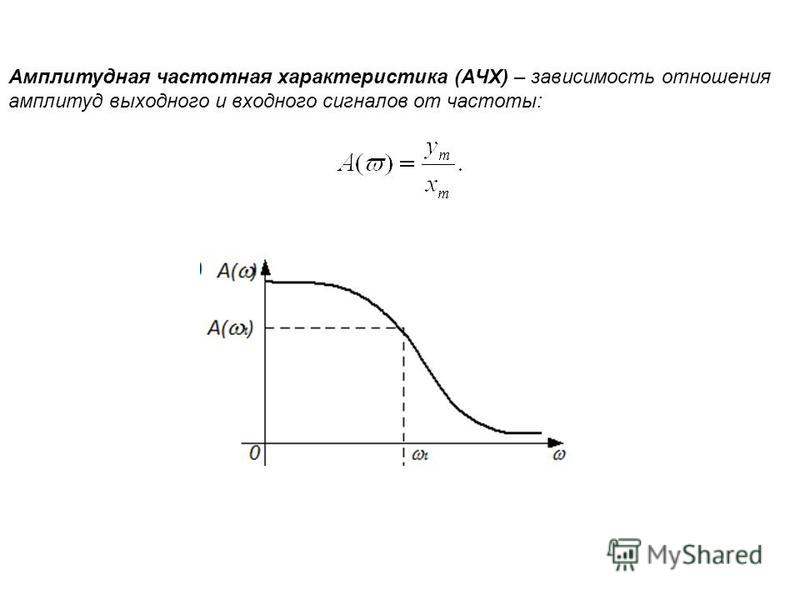
Изображение слайда
7
Слайд 7
Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или « пики ». На рисунке изображен RC -дифференциатор. Конденсатор С беспрепятственно пропускает ВЧ- составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В.
Изображение слайда
8
Слайд 8
Фильтры низких частот. Если поменять местами R и С, то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что U вых = [1/1 + ω 2 R 2 С 2 ) 1/2 ] U вх. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Изображение слайда
9
Слайд 9
для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен U вх = sinωt. Воспользуемся уравнием : U вх = RC d / dt sinωt = ωRCcosωt. Отсюда U вых « U вх, если ωRC « 1, т.е. RC « 1/ ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
Изображение слайда
10
Последний слайд презентации: RC-фильтры низких и высоких частот
Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Изображение слайда
Пассивный полосовой фильтр — принцип работы, характеристики, схемы, формулы — Кови
Пассивные полосовые фильтры можно изготовить, соединив вместе фильтр низких частот и фильтр высоких частот.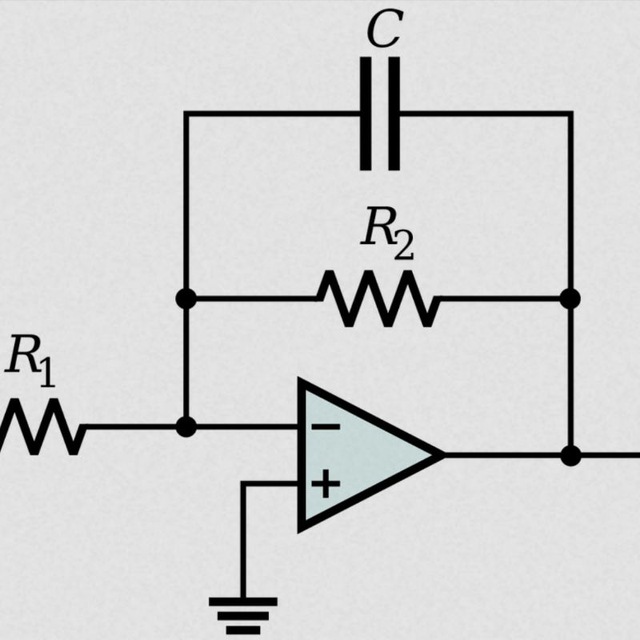
Полосно-пропускающие фильтры могут использоваться для изоляции или фильтрации определенных частот, которые находятся в определенной полосе или диапазоне частот. Частота среза или точка ƒc в простом пассивном RC-фильтре может точно контролироваться с помощью одного резистора, включенного последовательно с неполяризованным конденсатором, и в зависимости от того, как они подключены, мы видели, что получается либо низкочастотный, либо высокочастотный фильтр.
Одно из простых применений этих типов пассивных фильтров — использование в усилителях звука или схемах, например, в фильтрах кроссовера громкоговорителя или регуляторах тембра предварительного усилителя. Иногда необходимо пропускать только определенный диапазон частот, которые не начинаются с 0 Гц (постоянный ток) или заканчиваются в верхней высокочастотной точке, но находятся в определенном диапазоне или полосе частот, узкой или широкой.
Соединяя или «каскадируя» вместе одну цепь фильтра низких частот с цепью фильтра высоких частот, мы можем получить другой тип пассивного RC-фильтра, который пропускает выбранный диапазон или «полосу» частот, которые могут быть как узкими, так и широкими, при этом ослабляя все те, которые находятся за пределами этого диапазона.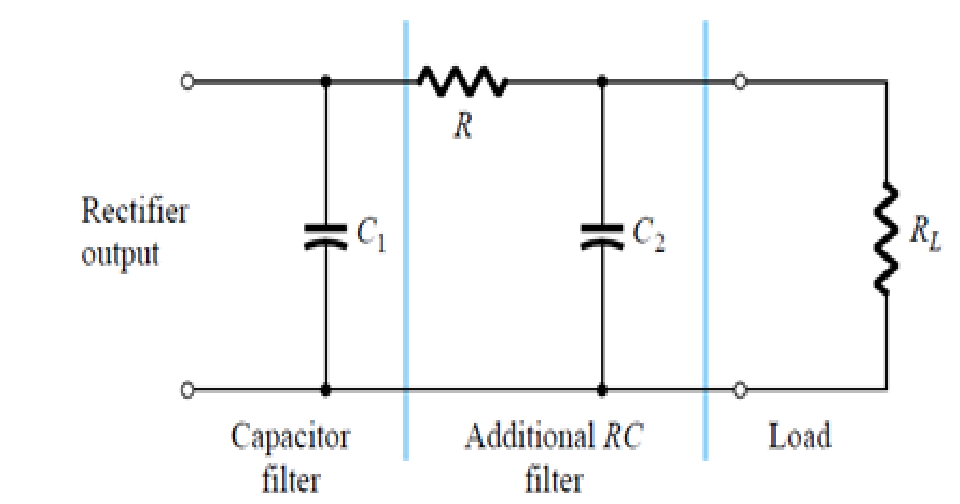 Этот новый тип пассивного фильтра создает частотно-избирательный фильтр, известный как Band Pass Filter или сокращенно BPF.
Этот новый тип пассивного фильтра создает частотно-избирательный фильтр, известный как Band Pass Filter или сокращенно BPF.
Содержание
Схема полосового фильтра
В отличие от фильтра низких частот, пропускающего только сигналы низкого диапазона частот, или фильтра высоких частот, пропускающего сигналы более высокого диапазона частот, полосовые фильтры пропускают сигналы в пределах определенной «полосы» или «разброса» частот, не искажая входной сигнал и не внося дополнительного шума. Эта полоса частот может быть любой ширины и обычно называется полосой пропускания фильтра.
Полоса пропускания обычно определяется как диапазон частот, существующий между двумя заданными точками отсечения частот ( ƒc ), которые на 3 дБ ниже максимального центра или резонансного пика, при одновременном ослаблении или затухании остальных за пределами этих двух точек.
Тогда для широко разнесенных частот мы можем просто определить термин «полоса пропускания», BW, как разницу между точками нижней частоты среза ( ƒcLOWER ) и верхней частоты среза ( ƒcHIGHER ).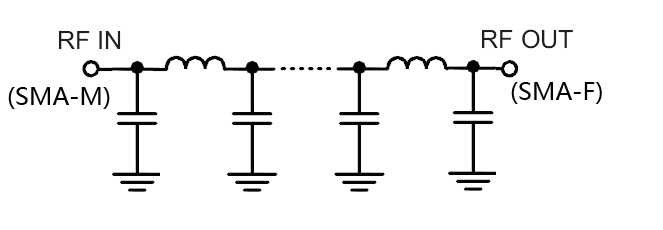 Другими словами, BW = ƒH — ƒL. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше частоты среза фильтра высоких частот.
Другими словами, BW = ƒH — ƒL. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше частоты среза фильтра высоких частот.
«Идеальный» полосовой фильтр пропускания может также использоваться для изоляции или фильтрации определенных частот, лежащих в определенной полосе частот, например, для подавления шума. Полосно-пропускающие фильтры известны как фильтры второго порядка (двухполюсные), потому что в их схеме есть «два» реактивных компонента — конденсаторы. Один конденсатор в цепи низких частот и другой конденсатор в цепи высоких частот.
Частотная характеристика полосового пропускающего фильтра 2-го порядка
Приведенный выше график Боде или кривая частотной характеристики показывает характеристики полосового фильтра. Здесь сигнал ослабляется на низких частотах, а выходное напряжение увеличивается с наклоном +20 дБ/декада (6 дБ/октава), пока частота не достигнет точки «нижней отсечки» ƒL. На этой частоте выходное напряжение снова составляет 1/√2 = 70,7% от значения входного сигнала или -3 дБ (20*log(VOUT/VIN)) от входного.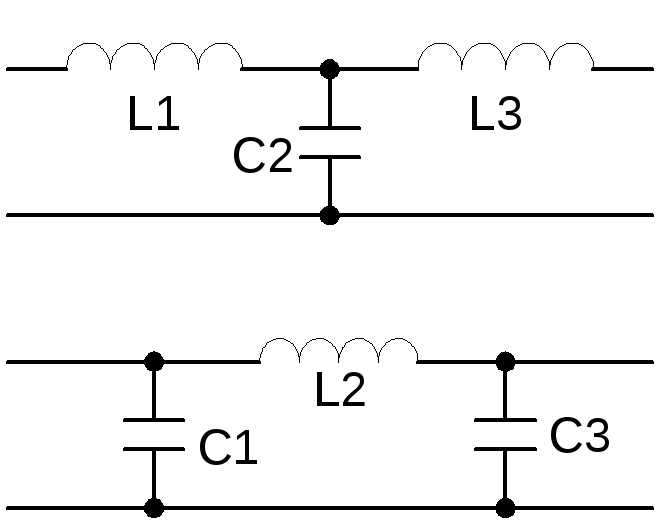
Выходной сигнал продолжает усиливаться до достижения точки «верхней отсечки» ƒH, где выходной сигнал уменьшается со скоростью -20 дБ/декада (6 дБ/октава), ослабляя любые высокочастотные сигналы. Точка максимального выходного усиления обычно является средним геометрическим двух значений -3 дБ между нижней и верхней точками отсечки и называется «центральной частотой» или «резонансным пиком» ƒr. Это среднее геометрическое значение рассчитывается как ƒr 2 = ƒ(UPPER) x ƒ(LOWER).
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку в его структуре есть «два» реактивных компонента, то фазовый угол будет в два раза больше, чем у ранее рассмотренных фильтров первого порядка, т.е. 180o. Фазовый угол выходного сигнала опережает входной на +90o до центральной или резонансной частоты, ƒr точки, где он становится «нулем» градусов (0o) или «синфазным», а затем изменяется в сторону отставания от входного на -90o по мере увеличения выходной частоты.
Верхняя и нижняя точки частоты среза для полосового фильтра могут быть найдены по той же формуле, что и для фильтров низких и высоких частот, например.
Тогда очевидно, что шириной полосы пропускания фильтра можно управлять с помощью расположения двух точек частоты среза двух фильтров.
Пример полосового фильтра No1
Необходимо построить полосовой фильтр второго порядка с использованием RC-компонентов, который будет пропускать только диапазон частот выше 1 кГц (1 000 Гц) и ниже 30 кГц (30 000 Гц). Предполагая, что оба резистора имеют значения 10kΩ, рассчитайте значения двух необходимых конденсаторов.
Этап фильтра высоких частот
Значение конденсатора C1, необходимое для получения частоты среза ƒL 1 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R1 и C1, необходимые для каскада высоких частот, чтобы обеспечить частоту среза 1,0 кГц, следующие: R1 = 10kΩ и, с точностью до предпочтительного значения, C1 = 15nF.
Этап фильтра низких частот
Значение конденсатора C2, необходимое для получения частоты среза ƒH 30 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R2 и C2, необходимые для низкочастотного каскада, чтобы обеспечить частоту среза 30 кГц, составляют R = 10 кОм и C = 530 пФ.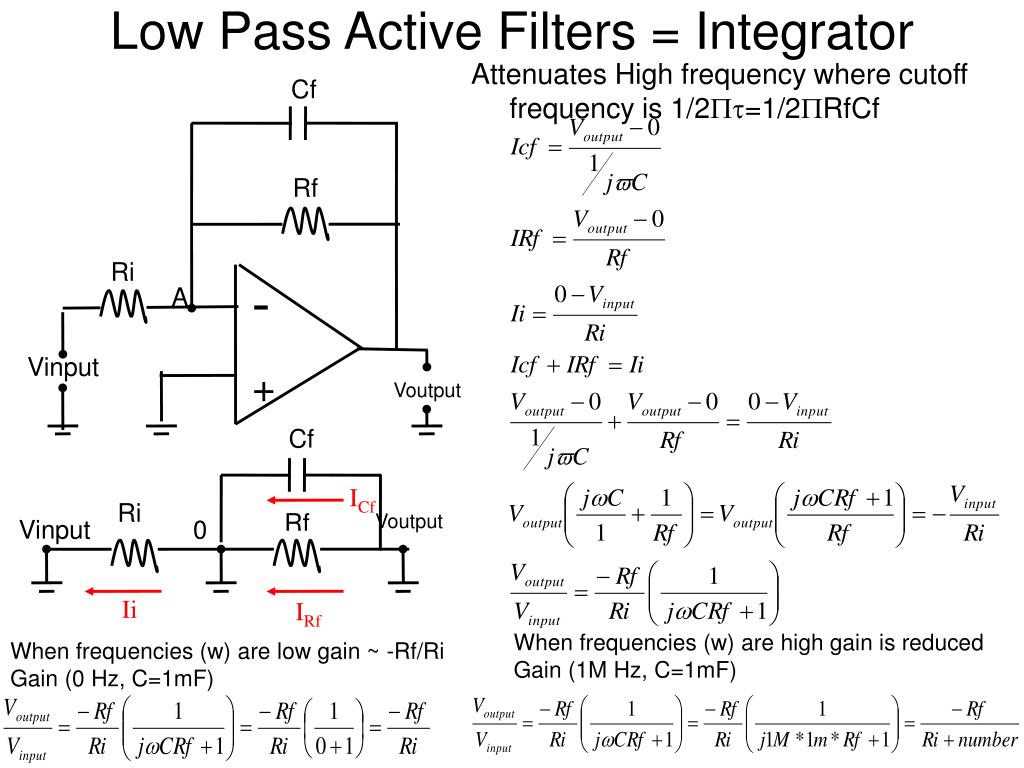 Однако ближайшим предпочтительным значением рассчитанного значения конденсатора 530пФ является 560пФ, поэтому вместо него используется это значение.
Однако ближайшим предпочтительным значением рассчитанного значения конденсатора 530пФ является 560пФ, поэтому вместо него используется это значение.
Учитывая, что значения сопротивлений R1 и R2 равны 10kΩ, а значения конденсаторов C1 и C2, найденные для фильтров высоких и низких частот, равны 15nF и 560pF соответственно, схема нашего простого пассивного полосового фильтра имеет вид.
Законченная схема полосового фильтра
Резонансная частота полосового фильтра
Мы также можем рассчитать «резонансную» или «центральную частоту» (ƒr) полосового фильтра, когда выходное усиление достигает максимального или пикового значения. Это пиковое значение не является средним арифметическим верхней и нижней точек отсечки -3 дБ, как можно было бы ожидать, а представляет собой «геометрическое» или среднее значение. Это среднее геометрическое значение рассчитывается, например, как ƒr 2 = ƒc(UPPER) x ƒc(LOWER):
Уравнение центральной частоты
Где, ƒr — резонансная или центральная частота
ƒL — нижняя точка частоты среза по уровню -3 дБ
ƒH — верхняя точка среза частоты -3 дБ
и в нашем простом примере выше, рассчитанные частоты среза составили ƒL = 1 060 Гц и ƒH = 28 420 Гц, используя значения фильтра.
Подставив эти значения в вышеприведенное уравнение, можно получить центральную резонансную частоту:
Краткое описание полосового фильтра
Простой пассивный полосовой фильтр может быть изготовлен путем каскадного соединения одного фильтра низких частот с фильтром высоких частот. Диапазон частот в герцах между нижней и верхней точками среза по уровню -3 дБ комбинации RC называется «полосой пропускания» фильтра.
Ширина или частотный диапазон полосы пропускания фильтра может быть очень маленькой и селективной или очень широкой и неселективной в зависимости от используемых значений R и C.
Точка центральной или резонансной частоты является средним геометрическим нижнего и верхнего срезов. На этой центральной частоте выходной сигнал максимален, а фазовый сдвиг выходного сигнала такой же, как и входного.
Амплитуда выходного сигнала полосового фильтра или любого другого пассивного RC-фильтра всегда будет меньше амплитуды входного сигнала. Другими словами, пассивный фильтр также является аттенюатором, дающим коэффициент усиления по напряжению менее 1 (Единство). Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, в конструкции схемы требуется некоторая форма усиления.
Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, в конструкции схемы требуется некоторая форма усиления.
Пассивный полосовой фильтр классифицируется как фильтр второго порядка, поскольку в его конструкции есть два реактивных компонента — конденсаторы. Он состоит из двух отдельных фильтрующих RC-цепей, которые сами являются фильтрами первого порядка.
При каскадном соединении нескольких фильтров результирующая схема будет называться фильтром «n-го порядка», где «n» означает количество отдельных реактивных компонентов и, следовательно, полюсов в цепи фильтра. Например, фильтры могут быть 2-го порядка, 4-го порядка, 10-го порядка и т.д.
Чем выше порядок фильтра, тем круче будет наклон при n раз -20 дБ/декада. Однако один конденсатор, полученный путем объединения двух или более отдельных конденсаторов, все равно остается одним конденсатором.
Наш пример выше показывает кривую выходной частотной характеристики для «идеального» полосового фильтра с постоянным коэффициентом усиления в полосе пропускания и нулевым коэффициентом усиления в полосе останова.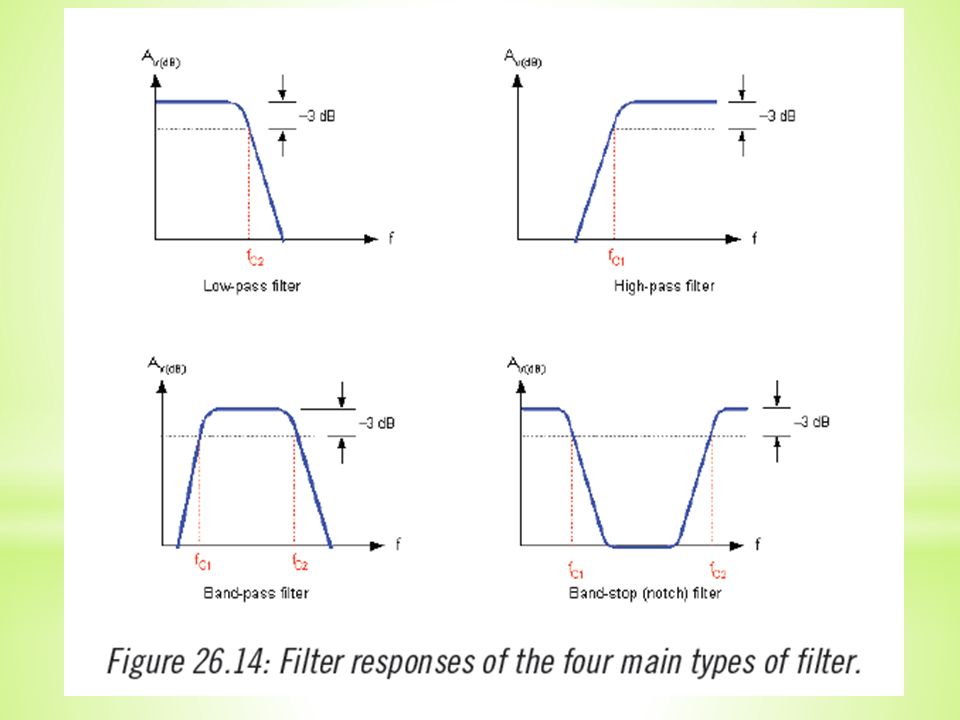 На практике частотная характеристика этой схемы полосового фильтра не будет такой же, поскольку входное реактивное сопротивление цепи высоких частот будет влиять на частотную характеристику цепи низких частот (компоненты подключены последовательно или параллельно) и наоборот. Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
На практике частотная характеристика этой схемы полосового фильтра не будет такой же, поскольку входное реактивное сопротивление цепи высоких частот будет влиять на частотную характеристику цепи низких частот (компоненты подключены последовательно или параллельно) и наоборот. Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
Буферизация отдельных ступеней фильтра
Одним из способов объединения усиления и фильтрации в одной схеме является использование операционного усилителя (Op-amp), примеры которого приведены в разделе «Операционный усилитель». В следующем уроке мы рассмотрим схемы фильтров, в которых операционный усилитель используется не только для усиления, но и для обеспечения изоляции между каскадами. Такие схемы фильтров обычно называются активными фильтрами.
Видеообзор: Пассивный полосовой фильтрФильтр высоких частот — frwiki.
 wiki
wikiДля одноименных статей см. HPF .
Изображение, к которому был применен фильтр верхних частот (результат справа)
Фильтр высоких частот (на английском языке, верхние частоты фильтр или HPF ) представляет собой фильтр , который проходит высокие частоты и ослабляет низкие частоты , то есть, что частоты ниже частоты среза . Его также можно было бы назвать фильтром низких частот.
Концепция фильтра верхних частот — это математическое преобразование, применяемое к данным (сигналу). Реализация фильтра высоких частот может быть сделана в цифровом виде или с электронными компонентами. Функция этого преобразования состоит в том, чтобы ослабить частоты ниже его частоты среза , чтобы сохранить только высокие частоты. Частота среза фильтра — это частота, разделяющая два идеальных режима работы фильтра: блокирующий или проходящий. жпротив{\ displaystyle f_ {c}}
жпротив{\ displaystyle f_ {c}}
Резюме
- 1 Идеальный фильтр
- 2 Аналоговый фильтр высоких частот
- 2.1 Фильтр высоких частот первого порядка
- 2.1.1 Пассивная схема
- 2.2 Фильтр второго порядка
- 2.2.1 Пассивная схема
- 2.1 Фильтр высоких частот первого порядка
- 3 См. Также
Идеальный фильтр
Идеальный фильтр — это теоретический фильтр, способный немедленно изменять свое усиление (от 1 до 0 или от 0 до 1 по линейной шкале) на так называемой частоте среза. В действительности фильтр имеет частоту среза при усилении Gmax -3 дБ и до того, как это усиление увеличится на декаду (фильтр порядка ). нет×20dB{\ displaystyle n \ times 20 дБ}нет{\ displaystyle n}
Аналоговый фильтр высоких частот
Фильтр высоких частот может быть реализован аналогично с электронными компонентами. Следовательно, этот вид фильтра применяется к непрерывным сигналам в реальном времени. Компоненты и конфигурация схемы будут фиксировать различные характеристики фильтра , такие как порядок, частота среза и его диаграмма Боде . Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта , Чебышева , Бесселя , эллиптические и др. Реализация фильтров одного и того же семейства обычно выполняется с использованием одной и той же конфигурации схемы, и они имеют одинаковую форму передаточной функции, но изменяются ее параметры, следовательно, значение компонентов передаточной функции. .
Обычные аналоговые фильтры бывают первого или второго порядка. Существует несколько семейств аналоговых фильтров: Баттерворта , Чебышева , Бесселя , эллиптические и др. Реализация фильтров одного и того же семейства обычно выполняется с использованием одной и той же конфигурации схемы, и они имеют одинаковую форму передаточной функции, но изменяются ее параметры, следовательно, значение компонентов передаточной функции. .
Фильтр высоких частот первого порядка
Первый порядок фильтр верхних частот характеризуются своей частотой среза и его коэффициент усиления в полосе пропускания . Передаточная функция фильтра получается денормализацией нормализованного фильтра верхних частот, замена на который дает следующую передаточную функцию: жпротив{\ displaystyle f_ {c}}K{\ displaystyle K}ωнет{\ displaystyle \ omega _ {n}}ωпротив/ω{\ displaystyle \ omega _ {c} / \ omega}
ωзнак равно2πж{\ displaystyle \ omega = 2 \ pi f}
ωпротивзнак равно2πжпротив{\ displaystyle \ omega _ {c} = 2 \ pi f_ {c}}
Модуль и фаза передаточной функции равны:
Есть несколько способов реализовать этот фильтр. Здесь представлены активная реализация и пассивная реализация. K — коэффициент усиления фильтра.
Здесь представлены активная реализация и пассивная реализация. K — коэффициент усиления фильтра.
Пассивная схема
Схема фильтра высоких частот
Самый простой способ получить этот фильтр физически — использовать RC-цепь . Как следует из названия, эта схема состоит из емкостного конденсатора и резистора . Эти два элемента размещены последовательно с источником сигнала. Выходной сигнал восстанавливается через резистор. Схема идентична схеме фильтра нижних частот, но положение резистора и конденсатора поменялось местами. Чтобы найти передаточную функцию этого фильтра, необходимо работать в области Лапласа, используя импедансы элементов. С помощью этой техники схема становится простым делителем напряжения , и мы получаем: ПРОТИВ{\ displaystyle C}р{\ displaystyle R}vя{\ displaystyle v_ {i}}vо{\ displaystyle v_ {o}}
В этом уравнении — комплексное число , такое, что j² = -1, и представляет собой пульсацию цепи или радиальную частоту, выраженную в рад / с. Поскольку частота среза RC-цепи равна:
j{\ displaystyle j}ω{\ displaystyle \ omega}
Поскольку частота среза RC-цепи равна:
j{\ displaystyle j}ω{\ displaystyle \ omega}
Здесь пульсация отсечки также является собственной пульсацией цепи, она также является обратной величиной постоянной времени цепи. Таким образом, действительно получается типичная передаточная функция фильтра верхних частот первого порядка. ωпротив{\ displaystyle \ omega _ {c}}ωо{\ displaystyle \ omega _ {o}}τ{\ Displaystyle \ тау}
Мы находим с наблюдаемыми физическими величинами, используемыми в диаграммах Боде :
График Боде фильтра высоких частот (система 1- го порядка)
- Прирост в децибелах :
- Фаза в радианах :
Тогда мы можем выделить две идеальные ситуации:
- Когда :ω≪ωпротив{\ displaystyle \ omega \ ll \ omega _ {c}}
- Когда :ω≫ωпротив{\ displaystyle \ omega \ gg \ omega _ {c}}
Обратите внимание, что для , у нас = -3 дБ. {2}}}} }
{2}}}} }
Смотрите также
- Режекторный фильтр
- Полосовой фильтр
- Фильтр низких частот
- Фильтры в электронике
- Использование фильтра высоких частот для увеличения резкости изображения (повышения резкости)
Фильтры | |
|---|---|
| Типы фильтров | Фильтр низких частот · High Pass Filter · полосовой фильтр · режекторный фильтр |
| линейные фильтры | Фильтр Бесселя · Фильтр Баттерворта · Фильтр Чебышева · Фильтр эллиптический |
| цифровые фильтры | Конечная импульсная характеристика · фильтр бесконечной импульсной характеристики |
<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Активные RC-фильтры
Пат. 2688237 Российская Федерация, МПК H03H 11/12. Полосовой ARC-фильтр на двух операционных усилителях с понижением частоты полюса и независимой подстройкой основных параметров / Денисенко Д. Ю., Бугакова А.В., Прокопенко Н.Н., Жебрун Е.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018132388/08; заявл. 11.09.2018; опубл. 21.05.2019, Бюл. № 15. – 17с.: ил. (з. 801(908))
Ю., Бугакова А.В., Прокопенко Н.Н., Жебрун Е.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018132388/08; заявл. 11.09.2018; опубл. 21.05.2019, Бюл. № 15. – 17с.: ил. (з. 801(908))
Пат. 2692967 Российская Федерация, МПК H03H 11/12, H03H 3/70. Активный RC-фильтр для обработки сигналов пьезоэлектрических датчиков / Полушкин О.О., Денисенко Д.Ю., Прокопенко Н.Н., Выродов А.С.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018132384/08; заявл. 11.09.2018; опубл. 28.06.2019, Бюл. № 19. – 16с.: ил. (829а)
Пат. 2697611 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр для обработки сигналов пьезоэлектрического преобразователя / Денисенко Д.Ю., Бутырлагин Н.В., Бугакова А.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018143801/08; заявл. 11.12.2018; опубл. 15.08.2019, Бюл. № 23. – 19с.: ил. (з. 829б)
– № 2018143801/08; заявл. 11.12.2018; опубл. 15.08.2019, Бюл. № 23. – 19с.: ил. (з. 829б)
Пат. 2694740 Российская Федерация, МПК H03H 11/12. Широкополосный избирательный RC-фильтр с дифференциальным входом / Денисенко Д.Ю., Бутырлагин Н.В., Игнашин А.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018143825/08; заявл. 11.12.2018; опубл. 16.07.2019, Бюл. № 20. – 15с.: ил. (з. 829в)
Пат. 2701095 Российская Федерация, МПК H03H 11/12. Низкочувствительный полосовой фильтр с независимой подстройкой основных параметров / Денисенко Д.Ю., Бугакова А.В., Игнашин А.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019106613/08; заявл. 11.03.2019; опубл. 24.09.2019, Бюл. № 27. – 13с.: ил. (з. 803)
Пат. 2701038 Российская Федерация, МПК H03H 11/12. Полосовой фильтр на двух операционных усилителях с независимой подстройкой основных параметров / Денисенко Д.Ю., Овсепян Е.В., Титов А.Е. Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019105489/08; заявл. 27.02.2019; опубл. 24.09.2019, Бюл. № 27. – 14с.: ил. (з. 806)
2701038 Российская Федерация, МПК H03H 11/12. Полосовой фильтр на двух операционных усилителях с независимой подстройкой основных параметров / Денисенко Д.Ю., Овсепян Е.В., Титов А.Е. Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019105489/08; заявл. 27.02.2019; опубл. 24.09.2019, Бюл. № 27. – 14с.: ил. (з. 806)
Пат. 2702499 Российская Федерация, МПК H03H 11/12. Универсальный активный RC-фильтр / Денисенко Д.Ю., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019107174/08; заявл. 14.03.2019; опубл. 08.10.2019, Бюл. № 28. – 30с.: ил. (з. 712)
Пат. 2702496 Российская Федерация, МПК H03H 11/00. Универсальный активный RC-фильтр на основе мультидифференциальных операционных усилителей / Денисенко Д.Ю., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019107341/08; заявл. 15.03.2019; опубл. 08.10.2019, Бюл. № 28. – 32с.: ил. (з. 713)
– № 2019107341/08; заявл. 15.03.2019; опубл. 08.10.2019, Бюл. № 28. – 32с.: ил. (з. 713)
Пат. 2694135 Российская Федерация, МПК H03H 11/12, H03H 7/12. ARC-фильтр верхних частот с независимой подстройкой основных параметров / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018132374/08; заявл. 11.09.2018; опубл. 09.07.2019, Бюл. № 19. – 18с.: ил. (906)
Пат. 2694134 Российская Федерация, МПК H03H 11/12. Полосовой ARC-фильтр на двух операционных усилителях с повышением частоты полюса и независимой подстройкой основных параметров / Денисенко Д.Ю., Бугакова А.В., Прокопенко Н.Н., Свизев Г.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018132364/08; заявл. 11.09.2018; опубл. 09.07.2019, Бюл. № 19. – 18с.: ил. (з. 802(907))
Пат.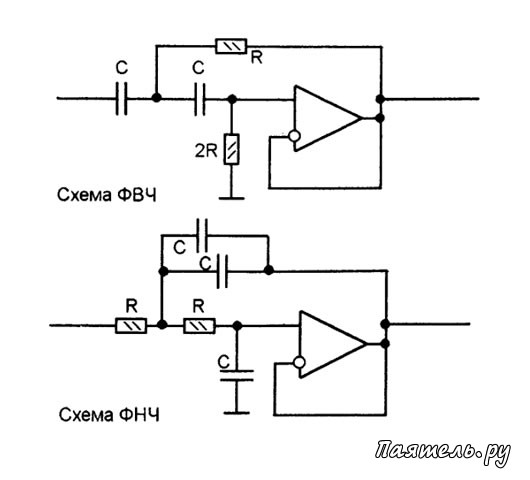 2697612 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот третьего порядка / Денисенко Д.Ю., Бутырлагин Н.В., Жебрун Е.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018143817/08; заявл. 11.12.2018; опубл. 15.08.2019, Бюл. № 23. – 12с.: ил. (з. 718)
2697612 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот третьего порядка / Денисенко Д.Ю., Бутырлагин Н.В., Жебрун Е.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2018143817/08; заявл. 11.12.2018; опубл. 15.08.2019, Бюл. № 23. – 12с.: ил. (з. 718)
Пат. 2695981 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот третьего порядка с дифференциальным входом на базе операционного усилителя с парафазным выходом / Денисенко Д.Ю., Жебрун Е.А., Бугакова А.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019106672/08; заявл. 11.03.2019; опубл. 29.07.2019, Бюл. № 22. – 13с.: ил. (з. 717а)
Пат. 2695977 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот третьего порядка на операционном усилителе с парафазным выходом / Денисенко Д. Ю., Бутырлагин Н.В., Титов А.Е., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019105508/08; заявл. 27.02.2019; опубл. 29.07.2019, Бюл. № 22. – 12с.: ил. (з. 717б)
Ю., Бутырлагин Н.В., Титов А.Е., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019105508/08; заявл. 27.02.2019; опубл. 29.07.2019, Бюл. № 22. – 12с.: ил. (з. 717б)
Пат. 2697945 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот третьего порядка на базе операционного усилителя с парафазным выходом / Денисенко Д.Ю., Бугакова А.В., Свизев Г.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019105119/08; заявл. 25.02.2019; опубл. 21.08.2019, Бюл. № 24. – 14с.: ил. (з. 716)
Пат. 2697944 Российская Федерация, МПК H03H 1/00, H03H 11/12. Полосовой фильтр второго порядка с независимой подстройкой основных параметров / Денисенко Д.Ю., Бутырлагин Н.В., Свизев Г.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет».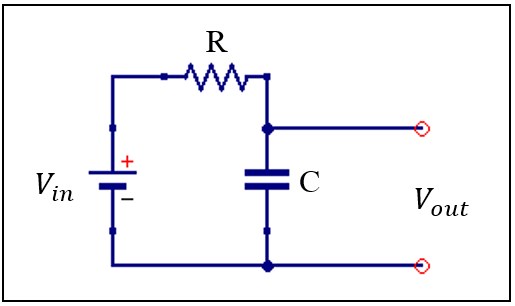 – № 2019105096/08; заявл. 25.02.2019; опубл. 21.08.2019, Бюл. № 24. – 13с.: ил. (з. 805)
– № 2019105096/08; заявл. 25.02.2019; опубл. 21.08.2019, Бюл. № 24. – 13с.: ил. (з. 805)
Пат. 2704530 Российская Федерация, МПК H03H 11/12. Широкополосный полосовой фильтр с независимой подстройкой частоты полюса, затухания полюса и коэффициента передачи / Денисенко Д.Ю., Бугакова А.В., Жебрун Е.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019106528/08; заявл. 07.03.2019; опубл. 29.10.2019, Бюл. № 31. – 14с.: ил. (з. 804)
Пат. 2707706 Российская Федерация, МПК H03H 11/12, H03H 7/12. Универсальный активный RC-фильтр второго порядка на основе мультидифференциальных операционных усилителей / Денисенко Д.Ю., Бугакова А.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019115988/08; заявл. 24.05.2019; опубл. 28.11.2019, Бюл. № 34. – 22с. : ил. (з. 831)
: ил. (з. 831)
Пат. 2710292 Российская Федерация, МПК H03H 11/12. Низкочувствительный активный RC-фильтр второго порядка на основе двух мультидифференциальных операционных усилителей / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019115651/08; заявл. 22.05.2019; опубл. 25.12.2019, Бюл. № 36. – 21с.: ил. (з. 830а)
Пат. 2710852 Российская Федерация, МПК H03H 11/12. Низкочувствительный ARC-фильтр второго порядка на основе двух мультидифференциальных операционных усилителей / Денисенко Д.Ю., Жебрун Е.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019115928/08; заявл. 23.05.2019; опубл. 14.01.2020, Бюл. № 2. – 20с.: ил. (з. 830б)
Пат. 2718212 Российская Федерация, МПК H03H 11/12.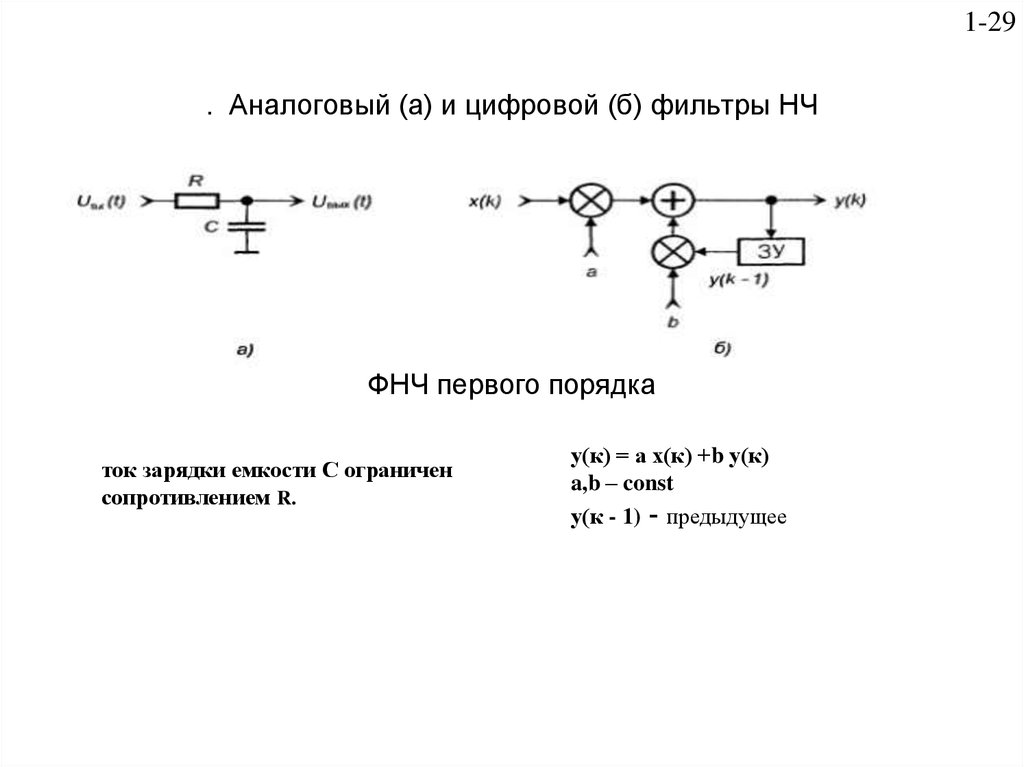 Универсальный программируемый ARC-фильтр / ДенисенкоД.Ю., Викулина Е.В., Прокопенко Н.Н., Бутырлагин Н.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137424/08; заявл. 21.11.2019; опубл. 31.03.2020, Бюл. № 10. – 14с.: ил. (з. 723б)
Универсальный программируемый ARC-фильтр / ДенисенкоД.Ю., Викулина Е.В., Прокопенко Н.Н., Бутырлагин Н.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137424/08; заявл. 21.11.2019; опубл. 31.03.2020, Бюл. № 10. – 14с.: ил. (з. 723б)
Пат. 2718210 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот с одноэлементной перестройкой частоты полюса на дифференциальных и мультидифференциальном операционных усилителях / Денисенко Д.Ю., Прокопенко Н.Н., Бутырлагин Н.В., Жебрун Е.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137425/08; заявл. 21.11.2019; опубл. 31.03.2020, Бюл. № 10. – 14с.: ил. (з. 714)
Пат. 2721155 Российская Федерация, МПК H03H 11/12. Фильтр нижних частот третьего порядка с минимальным количеством конденсаторов на порядок / Денисенко Д. Ю., Прокопенко Н.Н., Игнашин А.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137446/08; заявл. 21.11.2019; опубл. 18.05.2020, Бюл. № 14. – 11с.: ил. (з. 723а)
Ю., Прокопенко Н.Н., Игнашин А.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137446/08; заявл. 21.11.2019; опубл. 18.05.2020, Бюл. № 14. – 11с.: ил. (з. 723а)
Пат. 2720559 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр нижних частот с одноэлементной перестройкой частоты полюса на дифференциальном и двух мультидифференциальных операционных усилителях / Денисенко Д.Ю., Титов А.Е., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137553/08; заявл. 22.11.2019; опубл. 12.05.2020, Бюл. № 14. – 12с.: ил. (з. 715)
Пат. 2718709 Российская Федерация, МПК H03H 11/12. Полосовой фильтр с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137557/08; заявл. 22.11.2019; опубл. 14.04.2020, Бюл. № 11. – 12с.: ил. (з. 807)
– № 2019137557/08; заявл. 22.11.2019; опубл. 14.04.2020, Бюл. № 11. – 12с.: ил. (з. 807)
Пат. 2718830 Российская Федерация, МПК H03H 11/12. Полосовой фильтр второго порядка с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019137873/08; заявл. 25.11.2019; опубл. 14.04.2020, Бюл. № 11. – 15с.: ил. (з. 808)
Пат. 2721405 Российская Федерация, МПК H03H 11/12. Универсальный программируемый ARC-фильтр на основе матриц R-2R / Денисенко Д.Ю., Викулина Е.В., Прокопенко Н.Н., Клейменкин Д.В..; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019140625/08; заявл. 10.12.2019; опубл. 19.05.2020, Бюл. № 14. – 13с.: ил. (з. 723в)
Пат. 2720558 Российская Федерация, МПК H03H 11/12. Полосовой фильтр на двух операционных усилителях с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019140818/08; заявл. 11.12.2019; опубл. 12.05.2020, Бюл. № 14. – 14с.: ил. (з. 810)
Полосовой фильтр на двух операционных усилителях с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019140818/08; заявл. 11.12.2019; опубл. 12.05.2020, Бюл. № 14. – 14с.: ил. (з. 810)
Пат. 2721404 Российская Федерация, МПК H03H 11/12. Активный RC-фильтр с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019141018/08; заявл. 12.12.2019; опубл. 19.05.2020, Бюл. № 14. – 13с.: ил. (з. 812)
Пат. 2722602 Российская Федерация, МПК H03H 11/12. Активный полосовой фильтр второго порядка с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019140628/08; заявл. 10.12.2019; опубл. 02.06.2020, Бюл. № 16. – 14с.: ил. (з. 809)
– № 2019140628/08; заявл. 10.12.2019; опубл. 02.06.2020, Бюл. № 16. – 14с.: ил. (з. 809)
Пат. 2722752 Российская Федерация, МПК H03H 11/12. Полосовой фильтр с независимой подстройкой частоты полюса, затухания полюса и коэффициента передачи / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2019140820/08; заявл. 11.12.2019; опубл. 03.06.2020, Бюл. № 16. – 14с.: ил. (з. 811)
Пат. 2724917 Российская Федерация, МПК H03H 11/12. Универсальный активный RC-фильтр второго порядка на мультидифференциальных операционных усилителях с минимальным количеством пассивных и активных элементов / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н., Овсепян Е.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110712/08; заявл. 13.03.2020; опубл. 26. 06.2020, Бюл. № 18. – 14с.: ил. (з. 710)
06.2020, Бюл. № 18. – 14с.: ил. (з. 710)
Пат. 2737390 Российская Федерация, МПК H03H 11/00. Универсальный полосовой фильтр, фильтр низких частот и режекторный фильтр на трех мультидифференциальных операционных усилителях / Денисенко Д.Ю., Викулина Е.В., Игнатович А.А., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110709/08; заявл. 13.03.2020; опубл. 30.11.2020, Бюл. № 34 (з. 710а)
Пат. 2736239 Российская Федерация, МПК H03H 11/00. Универсальный полосовой и режекторный фильтр с регулируемой полосой пропускания / Денисенко Д.Ю., Викулина Е.В., Иванов Ю.И., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110761/08; заявл. 13.03.2020; опубл. 12.11.2020, Бюл. № 32. (з. 710б)
Пат. 2727702 Российская Федерация, МПК H03H 11/00, H03G 5/00. Графический эквалайзер на основе мультидифференциальных операционных усилителей / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110700/08; заявл. 13.03.2020; опубл. 23.07.2020, Бюл. № 21. – 14с.: ил. (з. 710в)
2727702 Российская Федерация, МПК H03H 11/00, H03G 5/00. Графический эквалайзер на основе мультидифференциальных операционных усилителей / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110700/08; заявл. 13.03.2020; опубл. 23.07.2020, Бюл. № 21. – 14с.: ил. (з. 710в)
Пат. 2730172 Российская Федерация, МПК H03H 11/12. Универсальный активный RC-фильтр второго порядка на мультидифференциальных операционных усилителях / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020110715/08; заявл. 13.03.2020; опубл. 19.08.2020, Бюл. № 23 (з. 711)
Пат. 2749400 Российская Федерация, МПК H03H 11/12. Режекторный фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Бутырлагин Н.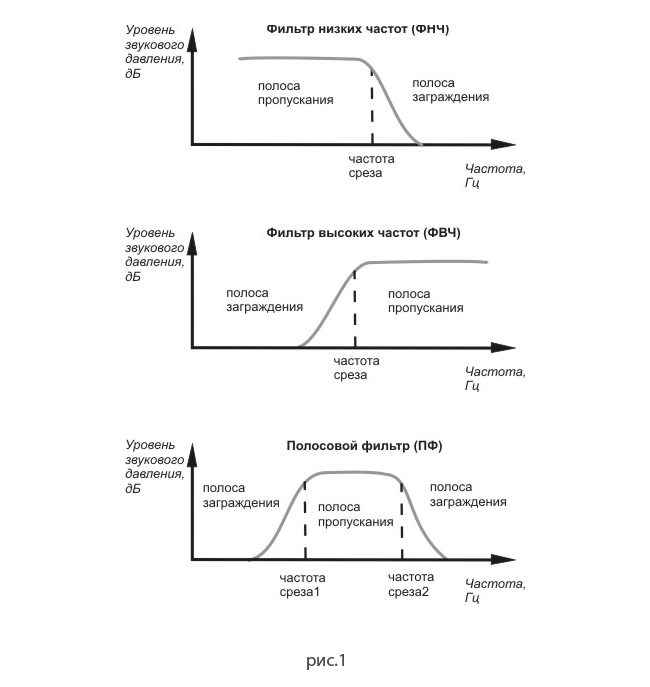 В., Клейменкин Д.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140324; заявл. 08.12.2020; опубл. 09.06.2021, Бюл. № 16. (824б)
В., Клейменкин Д.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140324; заявл. 08.12.2020; опубл. 09.06.2021, Бюл. № 16. (824б)
Пат. 2748609 Российская Федерация, МПК H03H 11/12. Фильтр низких частот четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Бутырлагин Н.В. ; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140315; заявл. 08.12.2020; опубл. 28.05.2021, Бюл. № 16. (816)
Пат. 2749605 Российская Федерация, МПК H03H 11/12. Широкополосный полосовой фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Иванов Ю.И.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140330; заявл. 08.12.2020; опубл. 16.06.2021, Бюл. № 17. (827)
Пат. 2748610 Российская Федерация, МПК H03H 11/12. Широкополосный полосовой фильтр четвертого порядка с одним входом и парафазным выходом / Денисенко Д.Ю., Прокопенко Н.Н., Жук А.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140310; заявл. 08.12.2020; опубл. 28.05.2021, Бюл. № 16. (719)
Широкополосный полосовой фильтр четвертого порядка с одним входом и парафазным выходом / Денисенко Д.Ю., Прокопенко Н.Н., Жук А.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140310; заявл. 08.12.2020; опубл. 28.05.2021, Бюл. № 16. (719)
Пат. 2748608 Российская Федерация, МПК H03H 11/12. Режекторный фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Бутырлагин Н.В., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140668; заявл. 10.12.2020; опубл. 28.05.2021, Бюл. № 16. (824а)
Пат. 2748663 Российская Федерация, МПК H03H 11/12. Широкополосный полосовой фильтр четвертого порядка с недифференциальным входом и парафазным выходом на классических операционных усилителях / Денисенко Д.Ю., Прокопенко Н.Н., Овсепян Е.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020140690; заявл. 10.12.2020; опубл. 28.05.2021, Бюл. № 16. (721)
– № 2020140690; заявл. 10.12.2020; опубл. 28.05.2021, Бюл. № 16. (721)
Пат. 2748607 Российская Федерация, МПК H03H 11/12. Широкополосный полосовой активный RC-фильтр четвертого порядка с дифференциальным входом и парафазным выходом / Денисенко Д.Ю., Прокопенко Н.Н., Чумаков В.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2020141019; заявл. 14.12.2020; опубл. 28.05.2021, Бюл. № 16. (720)
Пат. 2760930 Российская Федерация, МПК H03H 11/12. Режекторный фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Иванов Ю.И.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021102997; заявл. 09.02.2021; опубл. 01.12.2021, Бюл. № 34. (822)
Пат. 2754924 Российская Федерация, МПК H03H 11/12. Режекторный фильтр четвертого порядка / Денисенко Д.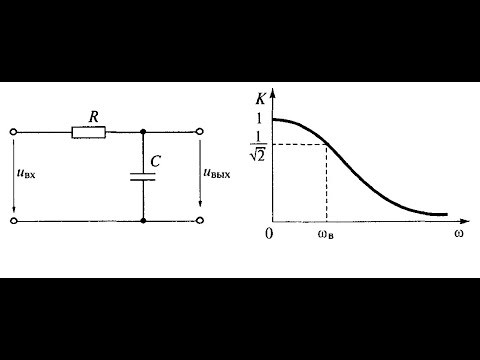 Ю., Прокопенко Н.Н., Бугакова А.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021102998; заявл. 09.02.2021; опубл. 08.09.2021, Бюл. № 25 (823)
Ю., Прокопенко Н.Н., Бугакова А.В.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021102998; заявл. 09.02.2021; опубл. 08.09.2021, Бюл. № 25 (823)
Пат. 2760871 Российская Федерация, МПК H03H 11/12. Полосовой фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021103005; заявл. 09.02.2021; опубл. 01.12.2021, Бюл. № 34. (826)
Пат. 2752254 Российская Федерация, МПК H03H 11/04. Полосовой фильтр четвертого порядка / Денисенко Д.Ю., Прокопенко Н.Н., Викулина Е.В., Игнатович А.А.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021103010; заявл. 09.02.2021; опубл. 23.07.2021, Бюл. № 21. (826в)
Пат. ______20 Российская Федерация, МПК H03H 11/12, 1/02.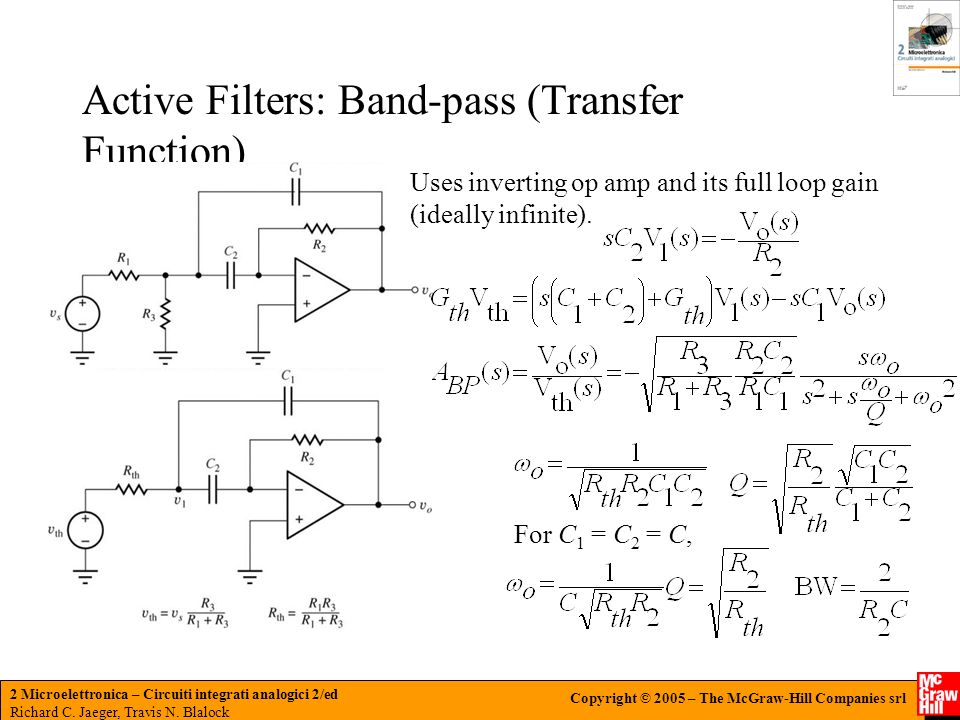 Фильтр высоких частот семейства Саллен-Ки с независимой подстройкой основных параметров / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н., Будяков П.С.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021133750; заявл. 19.11.2021; опубл. 00.00.2000, Бюл. № 00. (980)
Фильтр высоких частот семейства Саллен-Ки с независимой подстройкой основных параметров / Денисенко Д.Ю., Бутырлагин Н.В., Прокопенко Н.Н., Будяков П.С.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021133750; заявл. 19.11.2021; опубл. 00.00.2000, Бюл. № 00. (980)
Пат. ______20 Российская Федерация, МПК H03H 11/12, 1/02. Фильтр низких частот семейства Саллен-Ки с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Титов А.Е.; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021133752; заявл. 19.11.2021; опубл. 00.00.2000, Бюл. № 00. (980а)
Пат. ______20 Российская Федерация, МПК H03H 11/12, 1/02. Полосовой фильтр класса Саллен-Ки с независимой подстройкой основных параметров / Титов А.Е., Иванов Ю.И., Прокопенко Н.Н., Чумаков В.Е..; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021133749; заявл. 19.11.2021; опубл. 00.00.2000, Бюл. № 00. (980б)
– № 2021133749; заявл. 19.11.2021; опубл. 00.00.2000, Бюл. № 00. (980б)
Пат. ______20 Российская Федерация, МПК H03H 11/12, 1/02. Полосовой фильтр семейства Саллен-Ки / Пахомов И.В., Иванов Ю.И., Прокопенко Н.Н., Бугакова А.В..; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021133854; заявл. 22.11.2021; опубл. 00.00.2000, Бюл. № 00. (980в)
Пат. ______20 Российская Федерация, МПК H03H 11/12, 1/02. Полосовой фильтр семейства Саллен-Ки с независимой подстройкой основных параметров / Денисенко Д.Ю., Прокопенко Н.Н., Пахомов И.В., Будяков П.С..; заявитель и патентообладатель ФГБОУ ВО «Донской государственный технический университет». – № 2021134001; заявл. 23.11.2021; опубл. 00.00.2000, Бюл. № 00. (980г)
Пат. ______20 Российская Федерация, МПК H03H 9/00, 11/12.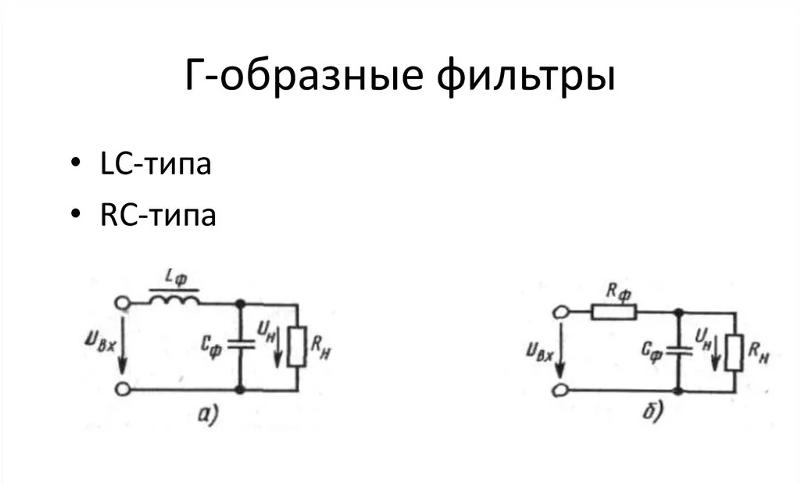 Режекторный фильтр с перестраиваемой полосой пропускания / Савченко Е.М., Прокопенко Н.Н., Любшов А.А., Денисенко Д.Ю.; заявитель и патентообладатель ООО «Инноцентр ВАО». – № 2021136533; заявл. 09.12.2021; опубл. 00.00.2000, Бюл. № 00. (1113)
Режекторный фильтр с перестраиваемой полосой пропускания / Савченко Е.М., Прокопенко Н.Н., Любшов А.А., Денисенко Д.Ю.; заявитель и патентообладатель ООО «Инноцентр ВАО». – № 2021136533; заявл. 09.12.2021; опубл. 00.00.2000, Бюл. № 00. (1113)
6. Фильтрующие цепи – В помощь студентам БНТУ – курсовые, рефераты, лабораторные !
6.1. Общие сведения об электрических фильтрах
Фильтры применяют для частотной селекции сигналов. Электрическим фильтром называется устройство (четырехполюсник), которое пропускает без ослабления или с малым ослаблением сигналы в заданном диапазоне частот (в заданной полосе), и не пропускает или пропускает с большим ослаблением сигналы других частот.
Полоса частот, в которой ослабление мало, называется полосой пропускания,(прозрачности) фильтра. Полоса частот, в которой ослабление велико, называется полосой непропускания (задержания) фильтра. Между полосами пропускания и непропускания находится переходная область.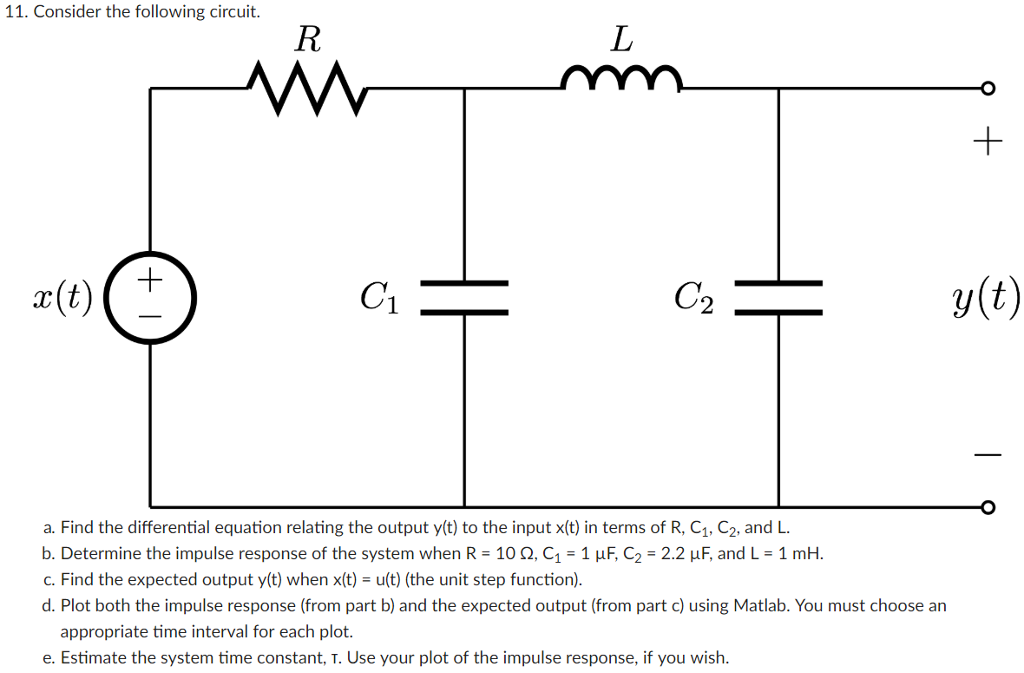 Частоты, которые соответствуют границам полос пропускания называются граничными или частотами среза и обозначаются ωгр или ωср.
Частоты, которые соответствуют границам полос пропускания называются граничными или частотами среза и обозначаются ωгр или ωср.
По частотным свойствам различают следующие фильтры (рис. 6.1): фильтры нижних частот (ФНЧ) пропускают колебания с частотами от нуля до некоторой верхней частоты ωср1, фильтры верхних частот (ФВЧ) – колебания с частотой не ниже некоторой нижней частоты ωср2. Полосовые фильтры (ПФ) имеют полосу пропускания от ωср1 до ωср2, режекторные (РФ), или заградительные (ЗФ), фильтры не пропускают колебания внутри интервала частот [ωср1, ωср2].
Рис. 6.1. Частотные характеристики идеальных (сплошная кривая) и реальных (пунктирная) фильтров нижних частот (а), верхних (б), полосового (в) и режекторного (г).
Кроме классификации фильтров по их частотным свойствам они подразделяются и по способам получения нужных частотных свойств. Фильтры создаваемые на базе реактивных четырехполюсников, в которых произведение сопротивлений продольного Z1 и поперечного Z2 плеч не зависит от частоты и для данного фильтра представляет собой некоторое постоянное число k называется k-фильтрами.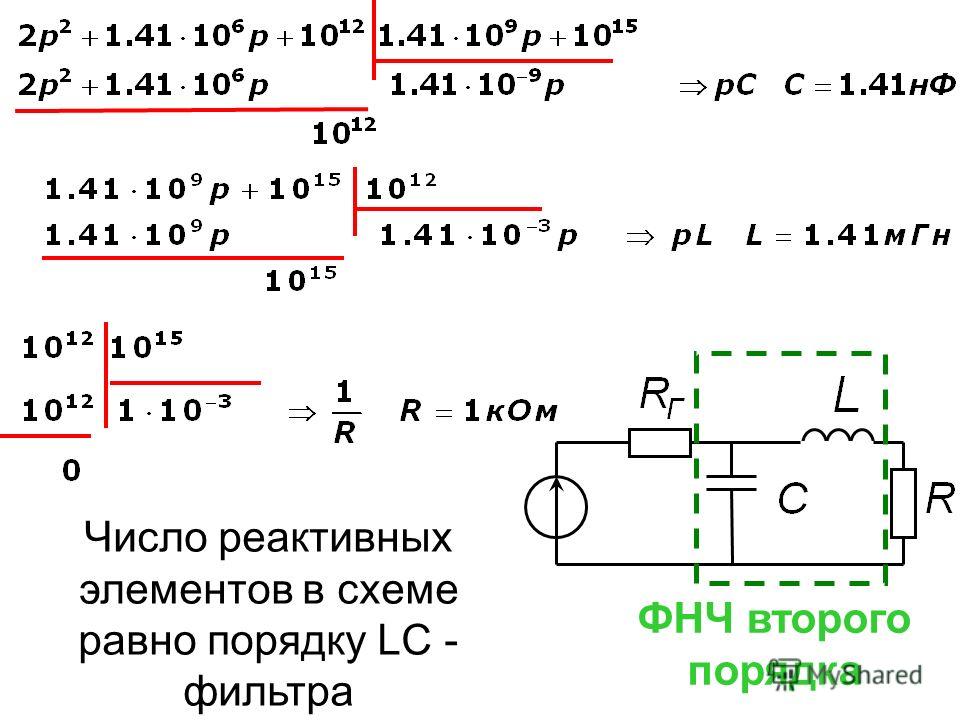
Фильтры, полученные из k–фильтров с использованием пересчетного коэффициента m и в которых произведение сопротивлений плеч зависит от частоты, называются m-фильтрами.
Фильтры, амплитудно-частотные характеристики (АЧХ), которых представляются в виде полиномов называются полиноминальными. Фильтры, АЧХ которых аппраксимируются полиномами, предложенными Чебышевым и Баттервортом называются соответственно фильтрами Чебышева и Баттерворта.
Фильтры могут быть созданы только из пассивных LC- или RC–элементов или из RC – элементов в сочетании с активными элементами (операционными усилителями). Поэтому различают пассивные LC- и RC-фильтры и активные RC–фильтры. LC- и RC–цепочки называются звеньями. Каждое звено имеет продольное и поперечное плечо. Сопротивление продольного плеча обозначается Z1, а поперечного – Z2. Если Z1 носит индуктивный характер, то Z2 должно носить емкостной характер и наоборот. Схемы Г- ,T- и П-образных звеньев LC–фильтров изображены на рис. 6.2.
Рис. 6.2. Схемы Г- (а), Т- (б) и П- (в) образных звеньев LC-фильтров.
6.2. Схемы Г- (а), Т- (б) и П- (в) образных звеньев LC-фильтров.
Фильтры могут быть однозвенные (первого порядка), двухзвенные (второго порядка) и многозвенные (n- го). Чем выше порядок фильтра, тем круче его амплитудно-частотная характеристика и тем более она похожа на его идеальную характеристику. Фильтр любого порядка можно построить путем каскадного соединения фильтров первого и второго порядков.
LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до
.
Рис. 6.3. Схема LC-фильтра нижних частот (а) и его АЧХ (б).
Это объясняется тем, что на низких частотах сопротивление индуктивного элемента XL фильтра мало, а емкостного XC – велико и электрические колебания проходят со входа на выход почти без ослабления. С увеличением частоты сопротивление индуктивного элемента возрастает, а емкостного – снижается и коэффициент передачи фильтра уменьшается (рис. 6.3,б).
LC-фильтр верхних частот (рис. 6.4,а) не пропускает нижних частот так, как XC велико, XL мало. С ростом частоты сопротивление продольного плеча (XC) уменьшается, а поперечного (XL) увеличивается, что приводит к повышению коэффициента передачи. Полоса пропускания такого фильтра лежит в диапазоне частот
6.4,а) не пропускает нижних частот так, как XC велико, XL мало. С ростом частоты сопротивление продольного плеча (XC) уменьшается, а поперечного (XL) увеличивается, что приводит к повышению коэффициента передачи. Полоса пропускания такого фильтра лежит в диапазоне частот
до ƒ = ∞ (рис. 6.4,б).
Рис. 6.4. Схема LC-фильтра верхних частот (а) и его АЧХ (б).
Принцип работы полосового фильтра (рис. 6.5,а) основан на использовании резонансов напряжений и токов в последовательных и параллельных колебательных контурах.
Рис. 6.5. Схема полосового LC-фильтра (а) и его АЧХ (б).
При совпадении частот, на которых наблюдается резонанс напряжений в последовательном контуре L1C1 и резонанс токов в параллельном колебательном контуре L2C2, сопротивление продольного плеча L1C1 оказывается минимальным, а поперечного L2C2 – максимальным. Коэффициент передачи ПФ при этом имеет наибольшее значение. При отклонении частоты входных колебаний от резонансной частоты ƒ0 коэффициент передачи ПФ уменьшается (рис.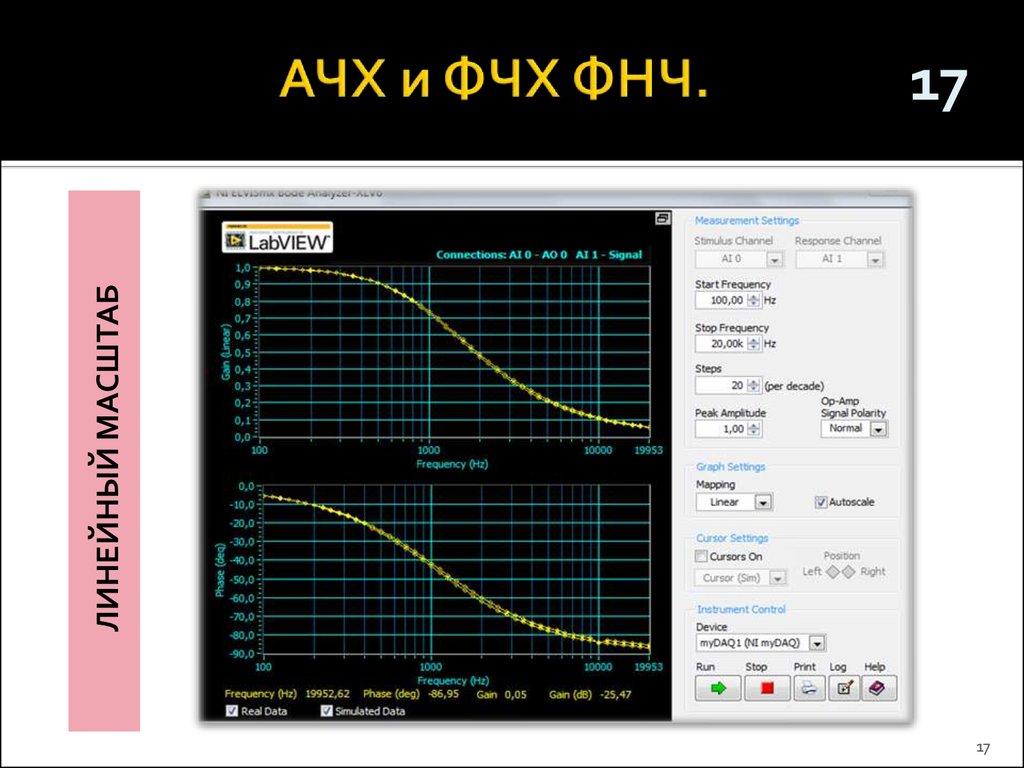 6.5,б).
6.5,б).
В заграждающих (режекторных) фильтрах (рис. 6.6,а) также используются резонансы напряжений и токов, но в отличие от ПФ параллельный колебательный контур включен в продольное плечо, а последовательный – в поперечное.
Рис. 6.6. Схема режекторного LC-фильтра (а) и его АЧХ (б).
Резонансная частота контура определяется выражением
.
При резонансе сопротивление продольного плеча оказывается максимальным, а поперечного – минимальным, что соответствует наибольшему затуханию (рис. 6.6,б). Для электрических колебаний с частотами, отличающимися от резонансной, сопротивление продольного плеча уменьшается, а поперечного – увеличивается, в результате чего происходит увеличение коэффициента передачи фильтра.
RC-фильтр нижних частот. На частотах до нескольких десятков килогерц применяются RC-фильтры, состоящие из резисторов и конденсаторов. В качестве фильтра нижних частот (ФНЧ) используется одно или несколько включённых последовательно RC-звеньев, ёмкость включается в поперечное звено (рис. 6.7,а).
6.7,а).
Рис. 6.7. Схема пассивного RC-фильтра нижних частот (а) и его АЧХ (б).
С увеличением частоты сопротивление конденсатора уменьшается, что приводит к уменьшению коэффициента передачи (рис. 6.7,б).
В RC-фильтре верхних частот (ФВЧ) конденсатор включён в продольное плечо (рис. 6.8,а). Поэтому на низких частотах его сопротивление значительно больше сопротивление резистора параллельного плеча и коэффициент передачи мал. С увеличением частоты сопротивление конденсатора уменьшается, что приводит к увеличению коэффициента передачи (рис. 6.8,б).
Рис. 6.8. Схема пассивного RC-фильтра верхних частот (а) и его АЧХ (б).
Рассмотренные ФНЧ и ФВЧ, состоящие из нескольких однотипных звеньев RC, называются цепочечными RC-фильтрами.
В качестве полосового RC-фильтра на низких частотах применяется Г-образный RC-фильтр (рис. 6.9,а).
Рис. 6.9. Схема пассивного полосового RC-фильтра (а) и его АЧХ (б).
На некоторой частоте fр, называемой квазирезонансной, коэффициент передачи такого фильтра имеет наибольшее значение, равное 1/3 , и уменьшается при отклонении частоты входного напряжения от fр (рис. 6.9,б).
6.9,б).
Роль заграждающих фильтров (ЗФ) на низких частотах выполняют Т-образные (рис. 6.10,а,б) и двойной Т-образный (рис. 6.11,а) фильтры. У этих фильтров на квазирезонансной частоте fр коэффициент передачи имеет минимальное значение и увеличивается при отклонении частоты входного напряжения от fр (рис. 6.11,б).
Рис. 6.10. Схемы заграждающих Т-образных RC-фильтров (q – коэффициент, равный целому положительному числу).
Рис. 6.11. Схема заграждающего двойного Т-образного RC-фильтра (а) и его АЧХ (б).
Материалы, изложенные в этой главе, дают общее представление об электрических фильтрах и их характеристиках, но не позволяют оценить качество их работы.
Последующие главы посвящены рассмотрению конкретных типов электрических фильтров и анализу их рабочих характеристик.
RC-фильтры низких и высоких частот
Вы можете ознакомиться и скачать презентацию на
тему RC-фильтры низких и высоких частот.
Доклад-сообщение содержит 10 слайдов. Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
RC-фильтры низких и высоких частот.
Слайд 2
Описание слайда:
Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза fс
Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и подавляют все остальные частоты.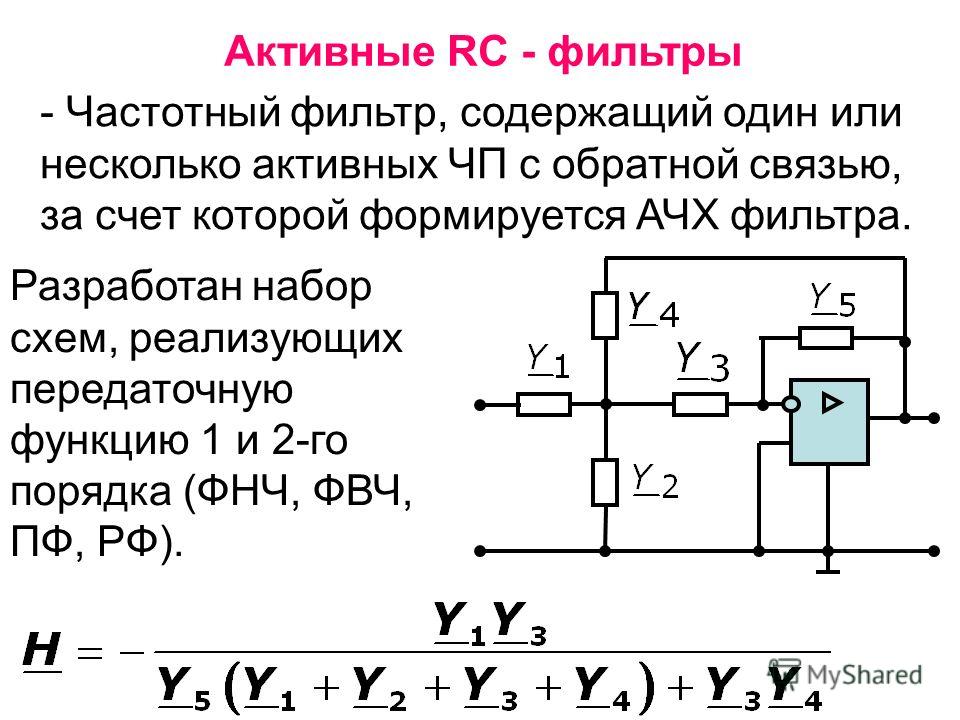 Частота, на которой начинается подавление, называется частотой среза fс
Частота, на которой начинается подавление, называется частотой среза fс
Слайд 3
Описание слайда:
Влияние фильтра на прямоугольный сигнал прямоугольный сигнал представляет собой сложное колебание, состоящее из основной гармоники и бесконечного количества нечетных гармоник. Низкочастотные составляющие формируют основание и плоскую вершину импульса, а высокочастотные — его фронт и срез. Когда прямоугольный сигнал проходит через фильтр, его форма искажается. Фильтр нижних частот (ФНЧ) будет искажать главным образом Фронты и срезы, делая их менее крутыми и скругляя углы. ФНЧ оказывает на прямоугольный сигнал такое же Действие, как усилители с недостаточной шириной полосы пропускания. Фильтр верхних частот (ФВЧ), наоборот, искажает плоскую вершину и основание прямоугольного сигнала.
Слайд 4
Описание слайда:
RC- фильтры
Простейшим среди фильтров является RC-фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным.
Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным.
Слайд 5
Описание слайда:
На схеме конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падения напряжения Vc на конденсаторе будет большим, а на резисторе
На схеме конденсатор соединен последовательно с резистором. При подаче на вход такого фильтра низкочастотного сигнала реактивное сопротивление конденсатора С будет гораздо больше, чем сопротивление резистора R. В результате падения напряжения Vc на конденсаторе будет большим, а на резисторе
Vr — малым. При подаче на вход этого фильтра высокочастотного сигнала картина будет обратная: Vc будет малым, а Vr — большим.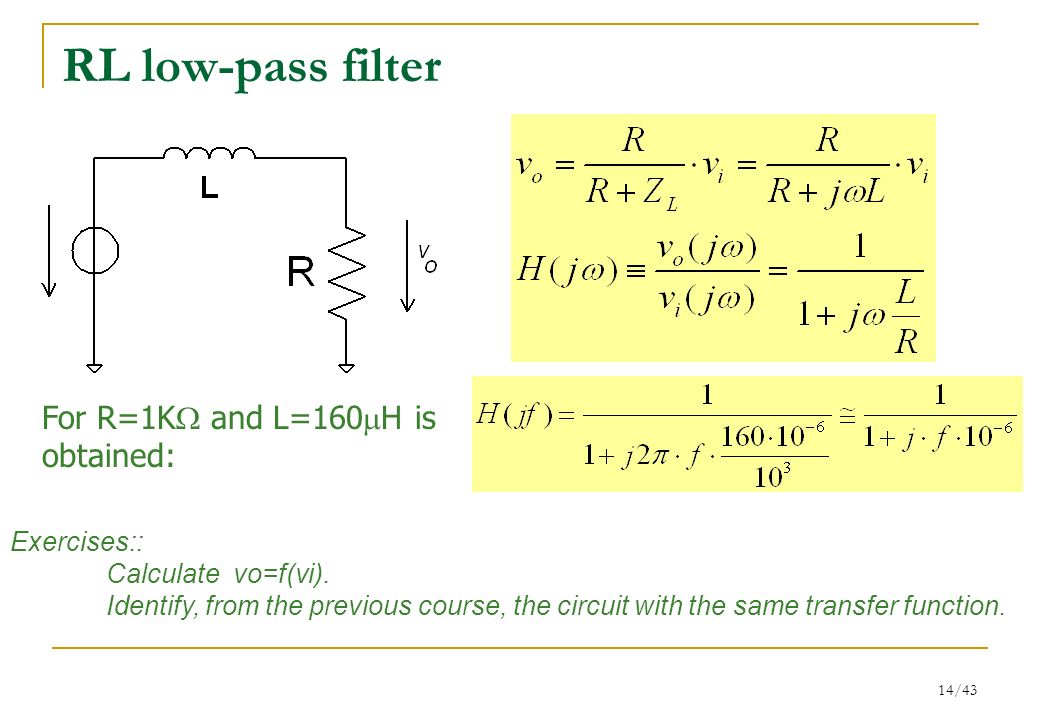
Слайд 6
Описание слайда:
Если теперь представить эту схему, как на рис.(б), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора, рисунок (а), то получим фильтр верхних частот. Значения R и С определяют частоту среза фильтра. Если теперь представить эту схему, как на рис.(б), где падение напряжения на конденсаторе является выходным, то в выходном сигнале будут преобладать НЧ-составляющие, а высокочастотные будут сильно ослабляться. Другими словами, мы получили фильтр нижних частот. И наоборот, если выходное напряжение снимать с резистора, рисунок (а), то получим фильтр верхних частот. Значения R и С определяют частоту среза фильтра.
Слайд 7
Описание слайда:
Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пики». На рисунке изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает
Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пики». На рисунке изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает
ВЧ- составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В.
Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пики». На рисунке изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает
Дифференциатор — это фильтр верхних частот. Если на вход дифференциатора подать последовательность прямоугольных импульсов, то на выходе будут получаться высокочастотные всплески, или «пики». На рисунке изображен RC-дифференциатор. Конденсатор С беспрепятственно пропускает
ВЧ- составляющие входного сигнала, образующие фронт импульса АВ, а затем начинает заряжаться до 10 В.
Слайд 8
Описание слайда:
Фильтры низких частот. Если поменять местами R и С, то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC.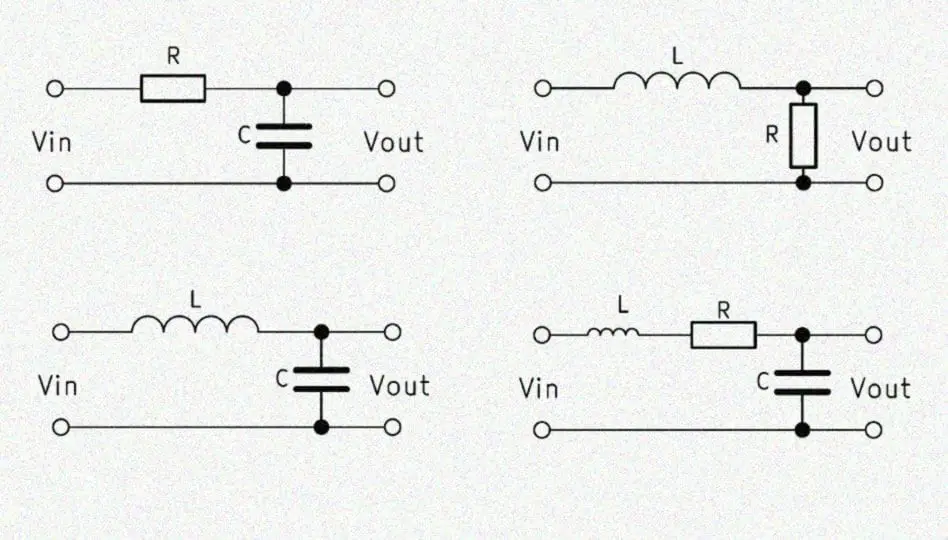 Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Фильтры низких частот. Если поменять местами R и С, то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Фильтры низких частот. Если поменять местами R и С, то фильтр будет вести себя противоположным образом в отношении частоты. Можно показать, что Uвых = [1/1 + ω2R2С2)1/2] Uвх. Такой фильтр называют фильтром низких частот. Точка -3 дБ на характеристике фильтра находится на частоте ƒ = 1/2πRC. Фильтры низких частот находят очень широкое применение. Например, их используют для устранения влияния близлежащих радио — и телевизионных станций (550 кГц — 800 МГц), на работу усилителей звуковых частот и других чувствительных электронных приборов.
Слайд 9
Описание слайда:
для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнием:
для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнием:
Uвх = RC d/dt sinωt = ωRCcosωt.
Отсюда Uвых « Uвх, если ωRC « 1, т.е. RC « 1/ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнием:
для того чтобы выходной сигнал был небольшим по сравнению с входным, частота должна быть значительно ниже, чем в точке -3 дБ. В этом легко убедиться. Допустим, что входной сигнал равен Uвх = sinωt. Воспользуемся уравнием:
Uвх = RC d/dt sinωt = ωRCcosωt.
Отсюда Uвых « Uвх, если ωRC « 1, т.е. RC « 1/ω. Если входной сигнал содержит некоторый диапазон частот, то условие должно выполняться для самых высоких частот входного диапазона.
Слайд 10
Описание слайда:
Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных).
Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Индуктивности, также как и конденсаторы, в сочетании с резисторами образуют схемы фильтров низких (или высоких) частот. Однако на практике RL — фильтры низких и высоких частот встречаются редко. Это связано с тем, что индуктивности более громоздки и дороги, а работают хуже, чем конденсаторы (их характеристики более существенно отличаются от идеальных). Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Если есть возможность выбора, то предпочтение лучше отдать конденсатору. Исключением из этой общей рекомендации являются ферритовые бусины (маленькие торроидальные сердечники) и дроссели в высокочастотных схемах. Несколько бусин нанизывают на провод, благодаря этому соединение, выполненное с помощью провода, становится в некоторой степени индуктивным; импеданс на высоких частотах увеличивается и предотвращает «колебания» в схеме, при этом в отличие от RС — фильтра активное сопротивление схемы не увеличивается. Радиочастотный дроссель — это катушка, состоящая из нескольких витков провода и ферритового сердечника и используемая с той же целью в радиочастотных схемах.
Пассивный фильтр высоких частот
Ранее мы обсуждали пассивный фильтр нижних частот, теперь пришло время взглянуть на пассивный фильтр высоких частот.
То же, что и раньше, если вы посмотрите на имя, оно покажет «Пассивный», «Высокий», «Проходной» и «Фильтр». Итак, как следует из названия, это фильтр, который блокирует низкие частоты , но пропускает высокие частоты выше заданного значения, которое будет рассчитано по формуле.
Это «пассивный» что означает отсутствие внешнего питания, отсутствие усиления входного сигнала; мы сделаем схему, используя «пассивные» компоненты, которые не требуют внешнего источника питания. Пассивные компоненты такие же, как фильтр нижних частот, но порядок подключения будет точно обратным. Пассивными компонентами являются резистор (R) и конденсатор
(C). Опять же, это конфигурация RC-фильтра.
Давайте посмотрим, что произойдет, если мы построим схему и проверим отклик или «график Боде»…
Вот схема на этом изображении:
Это RC-фильтр. Как правило, входной сигнал подается на эту комбинацию серии из неполяризованного конденсатора и резистора . Это фильтр первого порядка, так как в схеме есть только один реактивный компонент — конденсатор. Отфильтрованный выход будет доступен через резистор. Комбинация этого дуэта прямо противоположна фильтру нижних частот. Если мы сравним схему с фильтром нижних частот, то увидим, что резистор и конденсатор поменялись местами.
Как работает фильтр верхних частот?
На низких частотах реактивное сопротивление конденсатора будет очень большим, поэтому он будет действовать как разомкнутая цепь и блокировать входной сигнал ниже частоты среза (fc). Но когда достигается частота среза, реактивное сопротивление конденсатора начинает уменьшаться, позволяя сигналу проходить напрямую. Мы увидим это подробно на кривой частотной характеристики.
Вот кривая, как это выглядит на выходе конденсатора: —
Частотная характеристика и частота среза
Это кривая частотной характеристики схемы фильтра верхних частот первого порядка .
f c Частота среза фильтра. В точке -3dB сигнал проходит. Это -3dB также обозначает частоту среза. От 10 Гц до частоты среза сигнал не может проходить, так как частота низкая, в этот момент это часть полосы остановки, где сигнал не может проходить от фильтра, но выше частоты среза после -3dB часть называется позицией полосы пропускания, где сигнал может проходить.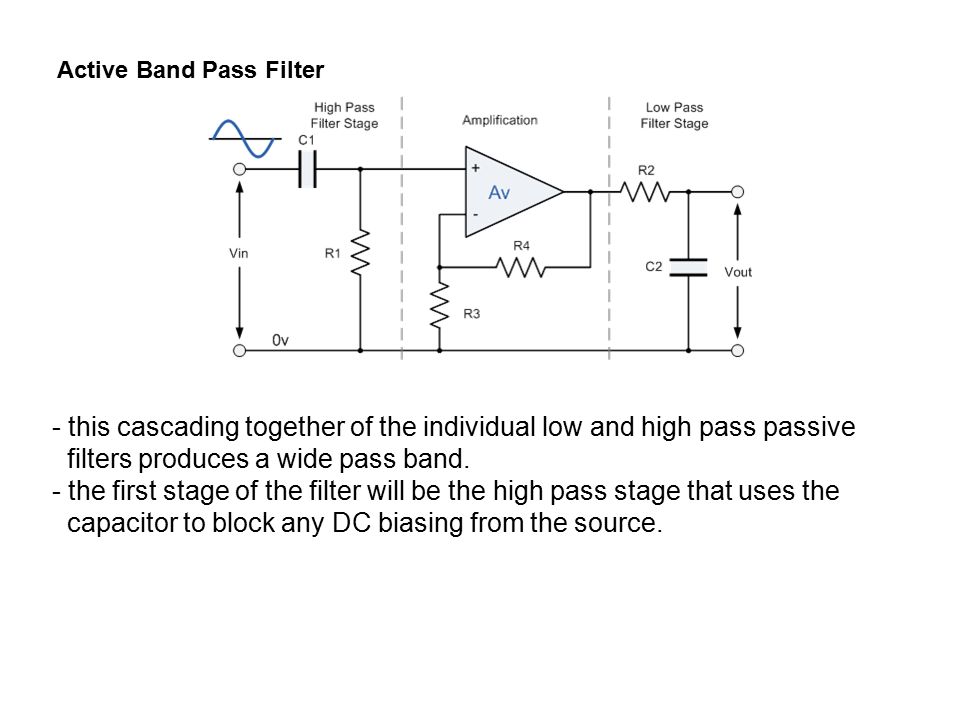 Наклон кривой составляет +20 дБ за декаду . Полная противоположность фильтру нижних частот.
Наклон кривой составляет +20 дБ за декаду . Полная противоположность фильтру нижних частот.
Формула расчета усиления такая же, как мы использовали в нашем предыдущем уроке для пассивного фильтра нижних частот.
Усиление (дБ) = 20 log (Vout / Vin)
После сигнала отсечки ответы схемы постепенно увеличиваются до Vin от 0 до , и это увеличение происходит со скоростью + 20 дБ/декада . Если мы подсчитаем увеличение на октаву, это будет 6 дБ.
Эта кривая частотной характеристики представляет собой график Боде фильтра верхних частот. Выбрав правильный конденсатор и соответствующий резистор, мы могли бы остановить низкие частоты, ограничить сигнал, проходящий через схему фильтра, не влияя на сигнал, поскольку нет активного отклика.
На изображении выше есть слово Bandwidth . Это означает, после какой частоты будет проходить сигнал. Итак, если это фильтр высоких частот 600 кГц, то полоса пропускания будет от 600 кГц до 9 кГц.0005 Бесконечность . Так как это позволит пропускать все сигналы выше частоты среза.
Итак, если это фильтр высоких частот 600 кГц, то полоса пропускания будет от 600 кГц до 9 кГц.0005 Бесконечность . Так как это позволит пропускать все сигналы выше частоты среза.
На частоте среза мы получим усиление -3дБ. В этот момент, если мы сравним амплитуду выходного сигнала с входным сигналом, мы увидим, что амплитуда выходного сигнала будет составлять 70,7% от входного сигнала. Также при усилении -3 дБ емкостное сопротивление и сопротивление будут одинаковыми. R=Хс.
Какова формула частоты среза?
Формула частоты среза точно такая же, как и у фильтра низких частот.
f c = 1/2πRC
Итак, R — сопротивление, а C — емкость. Если мы поставим значение, мы будем знать частоту среза.
Расчет выходного напряжения
Давайте посмотрим на первое изображение, схему, в которой 1 резистор и один конденсатор используются для формирования фильтра верхних частот или RC-цепи.
Когда сигнал постоянного тока подается на цепь, сопротивление цепи создает падение при протекании тока. Но в случае сигнала переменного тока не сопротивление, а импеданс отвечает за падение напряжения, которое тоже измеряется в Омах.
В RC цепи две резистивные вещи . Один — сопротивление, а другой — емкостное реактивное сопротивление конденсатора. Итак, нам нужно сначала измерить емкостное реактивное сопротивление конденсатора, так как это потребуется для расчета импеданса схемы.
Первая резистивная оппозиция равна емкостной реактивности , формула:-
Xc = 1 / 2πfC
Результат формулы будет в Омах, поскольку Ом является единицей емкостного реактивного сопротивления, потому что это сопротивление означает сопротивление.
Второй оппозицией является сам резистор . Значение резистора также является сопротивлением.
Таким образом, объединив эти две оппозиции, мы получим общее сопротивление, которое является импедансом в цепи RC (вход переменного тока).
Полное сопротивление обозначается как Z
Формула:-
конденсатор 9.0005 Бесконечность на низкой частоте значит блокирует сигнал. Выходное усиление равно 0 в это время , и из-за блокировки выходное напряжение остается равным 0 , пока не будет достигнута частота среза.
Но на высокой частоте произойдет обратное реактивное сопротивление конденсатора слишком низкое, что приведет к короткому замыканию , реактивное сопротивление конденсатора равно 0 на высокой частоте поэтому сигнал пропускается Выходное усиление в это время равно 1, то есть ситуация с единичным усилением, и из-за единичного усиления выходное напряжение такое же, как и входное напряжение после достижения частоты среза.
Пример с расчетом
Поскольку мы уже знаем, что на самом деле происходит внутри схемы и как узнать значение. Выберем практические значения.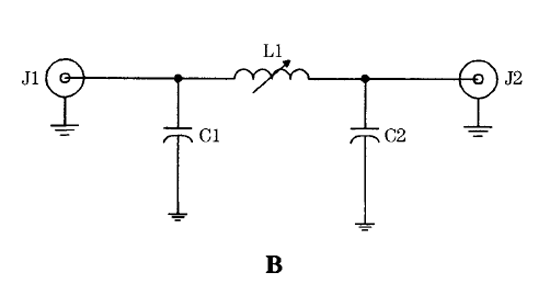
Возьмем наиболее распространенные значения резистора и конденсатора, 330k и 100pF. Мы выбрали значение, так как оно широко доступно и его легче рассчитать.
Посмотрим, какая будет частота среза и какое будет выходное напряжение.
Частота отсечки будет:-
При решении этого уравнения частота среза составляет 4825 Гц или 4,825 кГц .
Посмотрим, правда это или нет…
Это схема примера.
В соответствии с частотной характеристикой, описанной ранее, на частоте среза дБ будет
-3 дБ, независимо от частоты. Мы будем искать -3dB в выходном сигнале и посмотрим, является ли это 4825 Гц (4,825 кГц) или нет.
Вот частотная характеристика: —
Установите курсор на -3 дБ и посмотрите результат.
Поскольку мы можем видеть частотную характеристику (также называемую графиком Боде ), мы устанавливаем курсор на -3,03 дБ и получаем 4,814 кГц Полоса частот .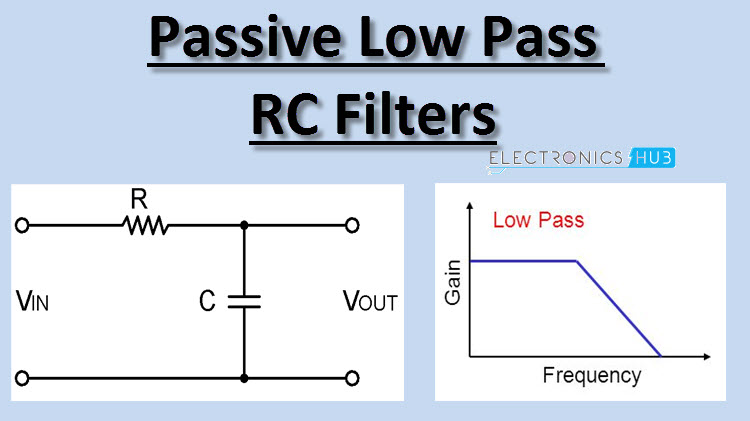
Фазовый сдвиг
Фазовый угол, обозначаемый как φ (Phi), будет на выходе равен +45 от входного сигнала при -3 дБ или частоте среза.
Как видно из АЧХ фильтра, он может пропускать все сигналы выше частоты среза до бесконечности. Это просто теоретическая практика. В практическом и реальном мире полоса пропускания ограничена ограничениями практических компонентов.
Формула фазового сдвига не такая, как у фильтра нижних частот, так как в фильтре нижних частот фаза стала отрицательной, а в фильтре верхних частот это положительный фазовый сдвиг, поэтому формула подразумевает следующее: —
Фазовый сдвиг φ = arctan (1/2πfRC)
Давайте посмотрим на кривую фазового сдвига цепи: —
Это фазовый сдвиг схемы, используемый в качестве практического примера.
Узнаем значение фазового сдвига на частоте среза:-
Устанавливаем курсор на +45 и получаем результат частоты среза 4.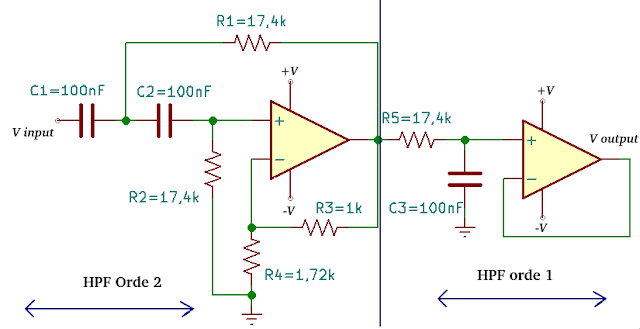 82КГц .
82КГц .
Постоянная времени
Как мы уже узнали о фазовом сдвиге и частотной характеристике, конденсатор заряжается и разряжается в зависимости от частот входного сигнала. Этот эффект зарядки и разрядки является постоянной времени и обозначается как τ (Тау). Это также связано с частотой среза.
Как?
τ = RC = 1/2π f c
Иногда нам нужно знать частоту среза, когда у нас есть значение постоянной времени, в таком случае, изменяя формулу, мы можем легко получить это: —
фк = 1/2πRC Где RC = τ fc = 1 / 2πτ
Влияние постоянной времени в фильтре верхних частот:
Фильтр верхних частот является дифференциатором. Если мы подадим прямоугольную волну и предоставим ее в идеальной временной области, форма выходной волны фильтра создаст пики или короткие импульсы. Если постоянная времени короткая, фильтр будет генерировать дифференцированную прямоугольную волну.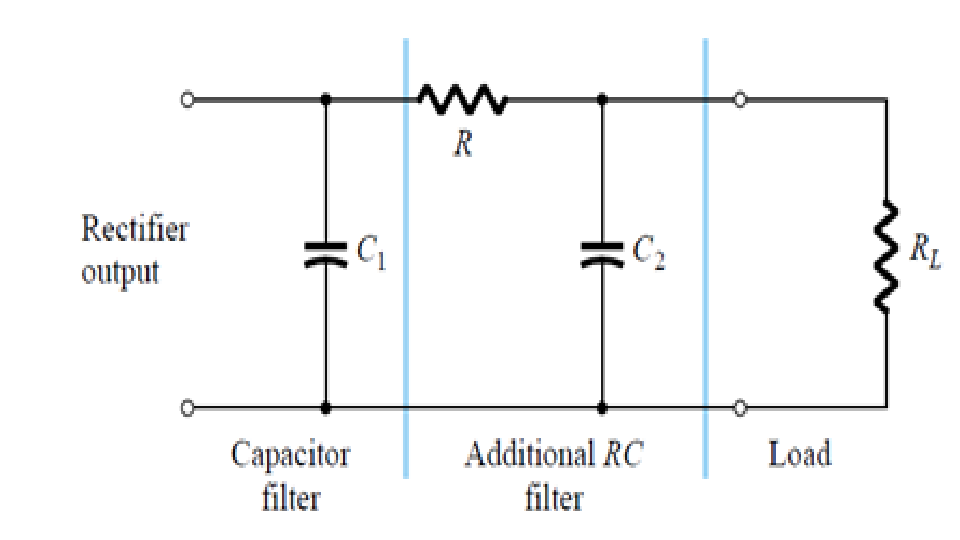 Мы можем различать сигнал, используя это свойство фильтра верхних частот.
Мы можем различать сигнал, используя это свойство фильтра верхних частот.
Фильтр нижних частот второго порядка: формулы, расчеты и частотные кривые
Когда две каскадные RC-цепи нижних частот первого порядка соединены вместе, это называется фильтром второго порядка, поскольку имеется две цепи RC-ступеней.
Вот схема:-
Это фильтр верхних частот второго порядка. КОНДЕНСАТОР и РЕЗИСТОР — это первый порядок, а КОНДЕНСАТОР1 и РЕЗИСТОР1 — второй порядок. Каскадируя вместе, они образуют фильтр верхних частот второго порядка.
Фильтр второго порядка имеет роль наклона 2 x +20 дБ/декада или +40 дБ (12 дБ/октава).
Вот кривая отклика: —
Наклон +20дБ/декада и красный на конечном выходе, который имеет наклон +40дБ/декада.
Это рассчитает частоту среза контура верхних частот второго порядка.
Как и в случае с фильтром нижних частот, не очень хорошо каскадировать два пассивных фильтра верхних частот, так как динамический импеданс каждого порядка фильтров влияет на другую цепь в той же схеме.
Применение
Фильтр нижних частот широко используется в электронике.
Вот несколько приложений:
- Аудиоресивер и эквалайзер
- Система управления музыкой и высокочастотная модуляция.
- Генератор функций
- Электронно-лучевой телевизор и осциллограф.
- Генератор прямоугольной волны из треугольной волны.
- Генераторы импульсов.
- Генераторы ступенчатого перехода.
Калькулятор фильтра высоких частот
Создано Rijk de Wet
Отзыв Стивена Вудинга
Последнее обновление: 03 октября 2022 г.
Содержание:- Как использовать калькулятор фильтра верхних частот?
- Что такое фильтр верхних частот?
- Различные фильтры верхних частот — пассивные и активные фильтры верхних частот
- RC-фильтр верхних частот
- RL-фильтр верхних частот проходной фильтр
- Часто задаваемые вопросы
Добро пожаловать в калькулятор фильтра верхних частот . Если вы хотите удалить низкочастотный шум или хотите получить больше высоких частот, вы попали по адресу. Вместе мы узнаем:
Если вы хотите удалить низкочастотный шум или хотите получить больше высоких частот, вы попали по адресу. Вместе мы узнаем:
- Что такое фильтр верхних частот ;
- различных типов схем фильтра верхних частот;
- Пассивные фильтры верхних частот и активные фильтры верхних частот ;
- Как отличить фильтры верхних и нижних частот друг от друга; и
- Как можно использовать конденсаторы в фильтрах верхних частот.
Как пользоваться калькулятором фильтра верхних частот?
Использовать вычислитель фильтра верхних частот очень просто! Вот как:
Выберите тип фильтра , который вы разрабатываете. Калькулятор фильтра верхних частот охватывает следующие типы фильтров:
RC фильтр верхних частот;
RL фильтр верхних частот;
Неинвертирующий операционный усилитель Фильтр верхних частот; и
Инвертирующий операционный усилитель Фильтр верхних частот.

Введите значения , для которых вы разрабатываете. Пассивные RC- и RL-фильтры (обе RLC-цепи) позволяют точно настроить значения компонентов и желаемую частоту среза, в то время как активные фильтры (операционные усилители) также позволяют регулировать усиление на выходе.
Продолжайте читать, если хотите узнать, как они работают!
💡 Калькулятор фильтра верхних частот позволяет вам вводить любые известные вам значения , и он рассчитает для вас другие значения. Он корректирует свои уравнения в соответствии с выбранным вами типом фильтра.
Что такое фильтр верхних частот?
Фильтр верхних частот представляет собой электронную схему, удаляющую низкочастотные компоненты из заданного сигнала переменного тока. Другими словами, он блокирует низкие частоты , а пропускает через себя высокие частоты . Вот почему мы называем это «ФВЧ» .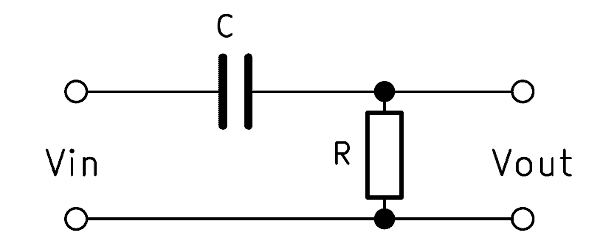
Что это означает на практике? Взгляните на график Боде для фильтров верхних частот ниже.
График Боде (частотная характеристика) фильтра верхних частот. Синяя линия представляет собой идеальный фильтр, а красная линия представляет собой реальный фильтр.График Боде (подобный приведенному выше) иллюстрирует частотную характеристику схемы , что является другим словом для обозначения того, как она усиливает сигналы одних частот и затухает другие. Частотная характеристика фильтра верхних частот подавляет низкочастотные сигналы, которые мы можем видеть вплоть до f=fcf = f_cf=fc. Эта частота называется 9.0005 частота среза , и это то, что определяет любой фильтр верхних частот:
- Частоты ниже fcf_cfc демпфируются; и
- Частоты выше fcf_cfc остаются нетронутыми.
💡 На приведенном выше графике Боде есть две линии, одна из которых представляет идеального теоретического поведения фильтра , а другая представляет реального поведения фильтра . Идеальные фильтры должны иметь прямой спад на fcf_cfc. Для реальных фильтров частота среза — это частота, при которой сигнал затухает до −3 дБ-3\ \text{дБ}-3 дБ.
Идеальные фильтры должны иметь прямой спад на fcf_cfc. Для реальных фильтров частота среза — это частота, при которой сигнал затухает до −3 дБ-3\ \text{дБ}-3 дБ.
Наклон, при котором частотная характеристика падает для все более низких частот, составляет −20 дБ/декада-20\ \text{дБ}/\text{декада}–20 дБ/декада. Это означает, что каждый раз, когда частота уменьшается в 10 раз, амплитуда уменьшается на 20 децибел . Этот наклон становится еще более крутым, если порядок фильтра увеличивается: фильтры первого порядка имеют наклон 20 децибел, фильтры второго порядка — 40 децибел, фильтры третьего порядка — 60 децибел и т. д.
Реальные сигналы редко состоят только из одной частоты, и отчасти поэтому нам нужно фильтры верхних частот в цепях обработки сигналов. Вот как фильтр верхних частот влияет на сигналы, состоящие из более чем одной частоты:
Фильтр верхних частот можно рассматривать как систему, которая удаляет низкочастотные компоненты из входных сигналов, оставляя только высокочастотные компоненты. компоненты .
компоненты .Различные фильтры верхних частот — пассивные и активные фильтры верхних частот
Существует две основные категории фильтров верхних частот:
- Пассивные фильтры верхних частот используют исключительно пассивные компоненты (резисторы, конденсаторы и катушки индуктивности). Двумя обычными пассивными фильтрами верхних частот являются фильтры верхних частот RC и фильтры верхних частот RL .
- Активные фильтры верхних частот используют некоторый активный компонент, обычно операционный усилитель (или «операционный усилитель»). Благодаря регулируемому коэффициенту усиления их можно модифицировать больше, чем пассивные фильтры.
Фильтр верхних частот RC
Фильтр верхних частот RC состоит из резистора и конденсатора в показанной ниже конфигурации.
Фильтр верхних частот RC, состоящий из резистора и конденсатора.Вероятно, это самый известный, но в то же время простой фильтр верхних частот, отчасти благодаря простой формуле для его частоты среза :
fc=12πRCf_c = \frac{1}{2\pi RC}fc=2πRC1
Фильтр высоких частот RC работает благодаря конденсатору.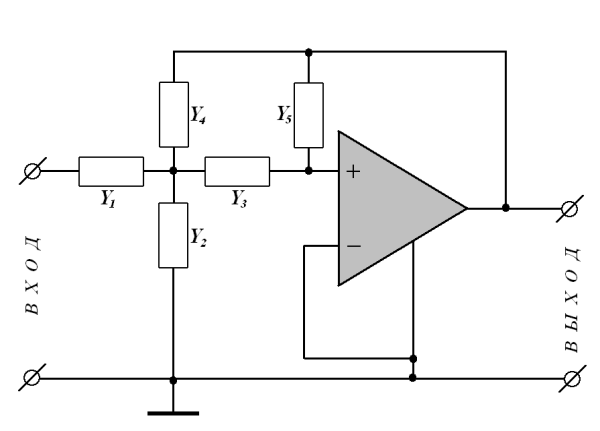 Импеданс конденсатора ZcZ_cZc уменьшается с частотой , заставляя его действовать как короткое замыкание для высокочастотных сигналов. И наоборот, конденсатор действует как разомкнутая цепь для низких частот.
Импеданс конденсатора ZcZ_cZc уменьшается с частотой , заставляя его действовать как короткое замыкание для высокочастотных сигналов. И наоборот, конденсатор действует как разомкнутая цепь для низких частот.
ZC=1j⋅(2πf)⋅CZ_C = \frac{1}{j\cdot (2\pi f)\cdot C}ZC=j⋅(2πf)⋅C1
где jjj — мнимая единица количество.
Благодаря этому импедансу, зависящему от частоты, мы можем использовать конденсаторы для фильтров верхних частот.
💡 Инженеры часто соединяют свои шины постоянного напряжения с землей с помощью конденсаторов , которые действуют как фильтры верхних частот и устранить любые шатания в подаче напряжения.
Фильтр верхних частот RL
Фильтр верхних частот RL использует катушку индуктивности и резистор в следующей конфигурации:
Фильтр верхних частот RL состоит из резистора и катушки индуктивности.Его граничную частоту также очень просто вычислить:
fc=R2πLf_c = \frac{R}{2\pi L}fc=2πLR
Дроссель LLL действует противоположно конденсатору: короткое замыкание для низкочастотных сигналов и обрыв цепи для высоких частот .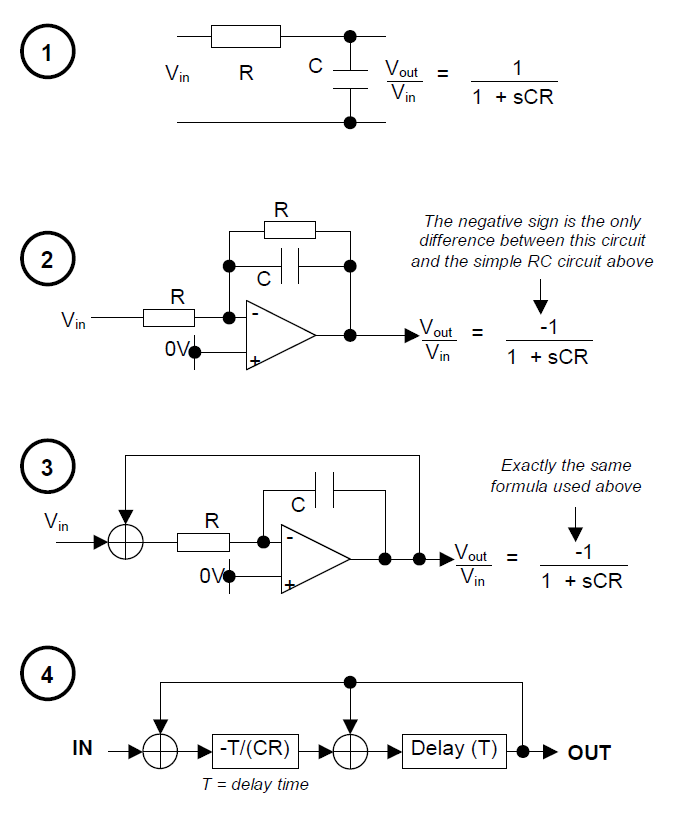 Из-за этого любые низкочастотные составляющие винв_\текст{ин}вин проходят через дроссель, а высокочастотные блокируются. Вместо этого высокочастотные компоненты должны проходить через нагрузку voutv_\text{out}vout. Вот уравнение для импеданса катушки индуктивности: фильтр верхних частот усилителя
Из-за этого любые низкочастотные составляющие винв_\текст{ин}вин проходят через дроссель, а высокочастотные блокируются. Вместо этого высокочастотные компоненты должны проходить через нагрузку voutv_\text{out}vout. Вот уравнение для импеданса катушки индуктивности: фильтр верхних частот усилителя
Фильтр верхних частот инвертирующего операционного усилителя представляет собой активный фильтр, в состав которого входит операционный усилитель (операционный усилитель). Операционный усилитель имеет обратную связь с резистором обратной связи RfR_fRf, а фильтрация верхних частот выполняется конденсатором CCC. Он устроен следующим образом:
Фильтр верхних частот инвертирующего операционного усилителя, состоящий из резисторов и конденсатора.Его частота среза рассчитывается так же, как и у RC-фильтра, но с резистором обратной связи RfR_fRf.
fc=12πRfCf_c = \frac{1}{2\pi R_f C}fc=2πRfC1
Коэффициент усиления GGG, вносимый операционным усилителем, рассчитывается как
G=−RfRivout=G⋅vin ∴vout=−RfRi⋅vin\begin{split} G &= -\tfrac{R_f}{R_i} \\ v_\text{out} &= G\cdot v_\text{in} \\ \поэтому v_\text{out} &= -\tfrac{R_f}{R_i}\cdot v_\text{in} \\ \end{split}Gvout∴vout=−RiRf=G⋅vin=-RiRf⋅vin
Видите, что минус знак в уравнении для GGG? Это означает, что мы переворачиваем сигнал по оси времени, или, говоря более технически, мы вводим фазовый сдвиг на 180° .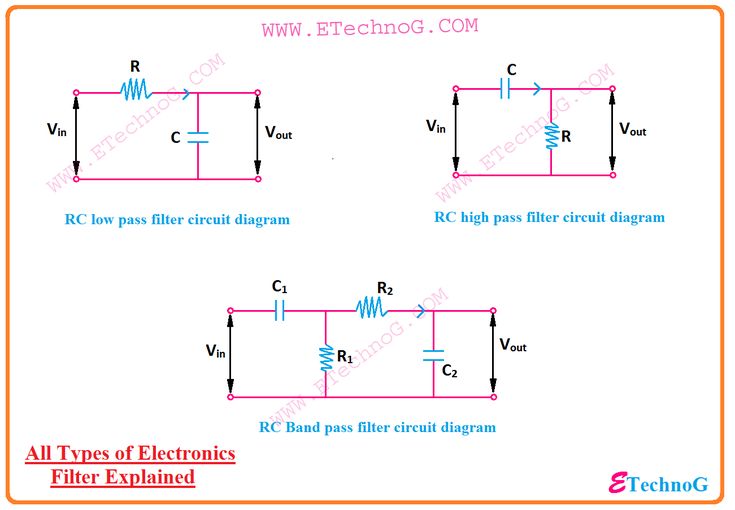 Если такое поведение нежелательно, перейдите к следующему разделу Неинвертирующих фильтров верхних частот для операционных усилителей .
Если такое поведение нежелательно, перейдите к следующему разделу Неинвертирующих фильтров верхних частот для операционных усилителей .
Фильтр верхних частот на неинвертирующем операционном усилителе
Фильтр верхних частот на неинвертирующем операционном усилителе сложнее, чем его инвертирующий аналог, но он обладает полезным свойством не инвертировать ввод . Мы подключаем RC-фильтр верхних частот к отрицательному входу операционного усилителя и создаем петлю обратной связи между выходом операционного усилителя voutv_\text{out}vout и положительным входом операционного усилителя. См. принципиальную схему ниже:
Неинвертирующий фильтр верхних частот на операционном усилителе, построенный из резисторов и конденсатора.Поскольку единственная фильтрация выполняется пассивной RC-цепью на vinv_\text{in}vin, мы можем рассчитать частоту среза фильтра по формуле:
fc=12πRiCf_c = \frac{1}{2\pi R_i C}fc =2πRiC1
И мы можем рассчитать GGG (прирост от vinv_\text{in}vin к voutv_\text{out}vout) с помощью:
G=1+RfRgvout=G⋅vin∴vout=(1+RfRg) ⋅вин\начало{раскол} G &= 1 + \tfrac{R_f}{R_g} \\ v_\text{out} &= G\cdot v_\text{in} \\ \поэтому v_\text{out} &= (1+\tfrac{R_f}{R_g})\cdot v_\text{in} \\ \end{split}Gvout∴vout=1+RgRf=G⋅vin=(1+RgRf)⋅vin
Обратите внимание, что GGG положительный, но также и то, что G ≥1G \ge 1G≥1, так как сопротивление никогда не может быть отрицательным.
Часто задаваемые вопросы
Какие компоненты мне нужны для фильтра верхних частот 1 кГц?
Для сборки фильтра верхних частот RC с частотой среза 1 кГц используйте резистор 3,3 кОм и конденсатор 47 нФ . Такая схема фильтра верхних частот будет иметь частоту среза точно .
f c = 1 / (2π × 3,3 кОм × 47 нФ) = 1,0261 кГц
Не забывайте о допусках компонентов — рассмотрите возможность их измерения с помощью мультиметра!
Как отличить фильтр верхних частот от фильтра нижних частот?
Различить фильтры верхних и нижних частот можно несколькими способами.
- Проанализируйте цепь. Используя такие методы, как преобразование Лапласа, рассчитайте частотно-зависимый импеданс каждого компонента и определите частотную характеристику фильтра.
- Проверьте с помощью сигналов. Подавайте в схему сигналы различной частоты и контролируйте амплитуды на выходах.

- Сравните схему с известными схемами фильтров. Если вы видите, что ваша схема соответствует хорошо известной конструкции фильтра, вы можете догадаться, какой это тип фильтра.
Как построить фильтр верхних частот?
Чтобы построить фильтр верхних частот , выполните следующие простые действия:
- Выберите фильтр подходящего типа (RC, RL, операционный усилитель и т. д.).
- Определите желаемую частоту среза , f c .
- Вычислите 9Значения компонентов 0005 на основе вышеуказанных вариантов. Уравнения зависят от выбранного типа фильтра.
Если вам нужна дополнительная помощь, обратитесь к калькулятора фильтра верхних частот omnicalculator.com !
RIJK DE WEE
Тип фильтра
Пассивный фильтр RC
Сопротивление (R)
емкость (C)
Частота отсечения (FC)
Проверьте 84 аналогичный электромаггнетический0003
Ускорение частицы в электрическом полеМощность переменного токаРазмер прерывателя… 81 more
Что такое фильтр верхних частот?
Ⅰ Введение Фильтр верхних частот (HPF), также называемый фильтром нижних частот или фильтром нижних частот , пропускает сигналы с частотой выше определенной частоты среза и ослабляет сигналы с частотами ниже частоты среза. То есть удаляются ненужные низкочастотные составляющие или низкочастотные помехи сигнала. В фильтрах верхних частот используются те же две топологии, что и в фильтрах нижних частот: Sallen-Key и MFB. Разница лишь в том, что изменились положения резисторов и конденсаторов. Другими словами, фильтры верхних частот дополняют фильтры нижних частот.
То есть удаляются ненужные низкочастотные составляющие или низкочастотные помехи сигнала. В фильтрах верхних частот используются те же две топологии, что и в фильтрах нижних частот: Sallen-Key и MFB. Разница лишь в том, что изменились положения резисторов и конденсаторов. Другими словами, фильтры верхних частот дополняют фильтры нижних частот.
Figure 1. High Pass RC Filter Circuit
CatalogⅠ Introduction |
Ⅱ High-pass Filter Basic 2.1 Terminology 2.2 High-pass Filter Circuit 2.2 Частота среза |
Ⅲ Типы ФВЧ 3.1 Пассивный ФВЧ и активный ФВЧ 3.2 ФВЧ первого порядка и ФВЧ второго порядка |
Ⅳ High-pass Filter Transfer Function |
Ⅴ High-pass Filter Order |
Ⅵ Difference between High-pass Filter and Low-pass Filter |
Ⅶ Приложение для фильтра с высоким проходом 7. 7.2 Ответ |
ⅱ Фильтр с высоким частотом.0005 конденсаторы , катушки индуктивности и резисторы , которые позволяют компонентам сигнала выше определенной частоты проходить и сильно подавлять компоненты сигнала ниже этой частоты. Его характеристики могут быть описаны во временной и частотной областях с помощью импульсной характеристики и частотной характеристики соответственно. Последняя представлена функцией, частота которой является независимой переменной. Последнее представляет собой функциональное представление частоты как независимой переменной, которая обычно представляет собой функцию комплексной переменной с комплексной переменной jω в качестве независимой переменной, выраженной как H (jω). H(ω) и амплитуда φ(ω) являются функциями угловой частоты ω, которые называются «амплитудно-частотной характеристикой» и «фазо-частотной характеристикой» системы соответственно. Они показывают компоненты сигнала разных частот в источнике возбуждения через изменения амплитуды и фазы, встречающиеся в этой системе.
 Можно доказать, что «частотная характеристика» системы — это «импульсная характеристика» системы, основанная на преобразовании Фурье. Когда линейная пассивная система может быть представлена линейным дифференциальным уравнением N-го порядка, частотная характеристика H (jω) представляет собой рациональную дробь, а ее числитель и знаменатель соответствуют правой и левой частям дифференциального уравнения соответственно.
Можно доказать, что «частотная характеристика» системы — это «импульсная характеристика» системы, основанная на преобразовании Фурье. Когда линейная пассивная система может быть представлена линейным дифференциальным уравнением N-го порядка, частотная характеристика H (jω) представляет собой рациональную дробь, а ее числитель и знаменатель соответствуют правой и левой частям дифференциального уравнения соответственно.Описание фильтра верхних частот RC
2.2 Фильтр верхних частот Схема
Основные фильтры верхних частот сконструированы с использованием резисторов с конденсаторами или катушками индуктивности. Фильтр верхних частот, состоящий из резисторов и конденсаторов, называется RC-фильтром верхних частот, а фильтр верхних частот с резисторами и катушками индуктивности – RL-фильтром верхних частот.
Рис. 2. Схема простого пассивного RC-фильтра верхних частот
2.2 Частота среза Обычно частота среза фильтра относится к правой частотной точке полосы пропускания фильтра нижних частот и левой частотной точке полосы пропускания фильтра верхних частот, то есть к точке частотной характеристики фильтра. Обычно определяется относительной точкой потерь 1 дБ или 3 дБ. Для ФВЧ его граничной частотой является частота, при которой выходное (нагрузочное) напряжение равно 70,7 % от входного напряжения (источника). Фильтр верхних частот основан на вносимых потерях на достаточно высокой частоте полосы пропускания без паразитной полосы задерживания.
Обычно определяется относительной точкой потерь 1 дБ или 3 дБ. Для ФВЧ его граничной частотой является частота, при которой выходное (нагрузочное) напряжение равно 70,7 % от входного напряжения (источника). Фильтр верхних частот основан на вносимых потерях на достаточно высокой частоте полосы пропускания без паразитной полосы задерживания.
Рисунок 3. Частота среза фильтра высоких частот Более распространены активные фильтры верхних частот, такие как активные фильтры верхних частот первого порядка и активные фильтры высоких частот второго порядка.
3.1 Пассивный фильтр высоких частот и активный фильтр высоких частотВ зависимости от различных устройств, его можно разделить на пассивный фильтр высоких частот и активный фильтр высоких частот.
- Пассивный фильтр высоких частот
Разновидность фильтров, состоящих из пассивных компонентов (резистор R, катушка индуктивности L и конденсатор С), построенных по принципу изменения реактивного сопротивления конденсаторов и индуктивных компонентов в зависимости от частоты. Преимущества этого типа фильтров: относительно простая схема, не требуется источник питания постоянного тока, высокая надежность. Недостатки: сигнал в полосе пропускания имеет потери энергии, эффект нагрузки более очевиден, а электромагнитная индукция легко возникает при использовании индуктивных компонентов. Когда L велико, объем и вес фильтра относительно велики, и он не подходит в области низких частот.
Преимущества этого типа фильтров: относительно простая схема, не требуется источник питания постоянного тока, высокая надежность. Недостатки: сигнал в полосе пропускания имеет потери энергии, эффект нагрузки более очевиден, а электромагнитная индукция легко возникает при использовании индуктивных компонентов. Когда L велико, объем и вес фильтра относительно велики, и он не подходит в области низких частот.
- Активный фильтр верхних частот
Фильтр состоит из пассивных компонентов (обычно R и C) и активных устройств (таких как интегральные операционные усилители). Преимущество этого типа фильтра в том, что сигнал в полосе пропускания не имеет потерь энергии, но также может быть усилен, эффект нагрузки не очевиден, а взаимное влияние мало при подключении многокаскадного каскада. Фильтр высокого порядка легко сформировать с помощью простого каскадного метода, фильтр небольшой, легкий и не требует магнитного экранирования (поскольку не используются индуктивные компоненты).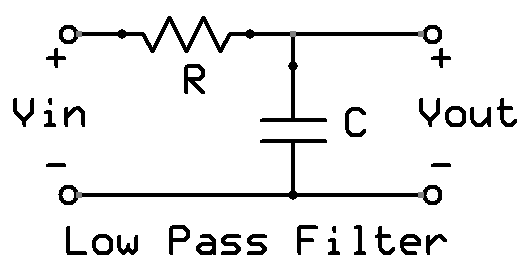 Недостатком является то, что диапазон полосы пропускания ограничен полосой пропускания активных устройств (таких как интегральные операционные усилители) и требует источника питания постоянного тока, а надежность не так высока, как у пассивных фильтров, поэтому он не подходит для высокого напряжения, высокой частоты и высокой мощности.
Недостатком является то, что диапазон полосы пропускания ограничен полосой пропускания активных устройств (таких как интегральные операционные усилители) и требует источника питания постоянного тока, а надежность не так высока, как у пассивных фильтров, поэтому он не подходит для высокого напряжения, высокой частоты и высокой мощности.
Рис. 4. Схема активного ФВЧ LM741
3.2 ФВЧ первого порядка и ФВЧ второго порядка — фильтр верхних частот и фильтр верхних частот второго порядка, фильтр верхних частот третьего порядка и так далее.
Рис. 5. Принципиальные схемы фильтра верхних частот
- Фильтр верхних частот первого порядка
Фильтр верхних частот первого порядка требует конденсатора очень большой емкости, что вызывает очень высокие основные потери, поэтому он используется редко.
Рис. 6. Фильтр высоких частот первого порядка
Преобразование Лапласа:
Дифференциальная форма:
,
- Фильтр верхних частот второго порядка
Фильтр верхних частот второго порядка имеет наилучшие характеристики, но вызывает более высокие основные потери по сравнению с другим типом. Фильтр второго порядка означает, что фильтр содержит дифференциал второго порядка в выражении во временной области, или наивысший порядок s знаменателя передаточной функции равен 2, а коэффициент усиления фильтра по постоянной составляющей равен 1.
Фильтр второго порядка означает, что фильтр содержит дифференциал второго порядка в выражении во временной области, или наивысший порядок s знаменателя передаточной функции равен 2, а коэффициент усиления фильтра по постоянной составляющей равен 1.
Секунда -порядок Цепь фильтра высоких частот (управляемая напряжением)
Рис. 5. Схема фильтра верхних частот второго порядка менее f 0 , наклон АЧХ +40дБ/дек; когда Avp больше или равно 3, схема самовозбуждается.
- Многоканальный фильтр верхних частот с обратной связью
. = С3 = С, С1 = | К | C, есть
Ⅳ Передаточная функция фильтра верхних частот
- Как определить передаточную функцию каждого фильтра верхних частот
Фильтр высокого порядка состоит из каскада секций фильтра второго порядка и секций фильтра первого порядка, и каждая секция фильтра имеет определенную передаточную функцию.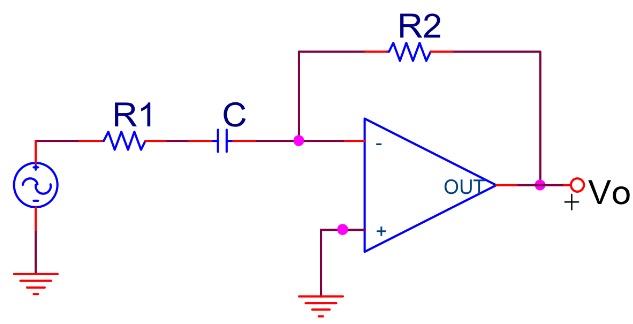 Кроме того, для секций фильтра второго порядка должны быть определены частота среза и добротность Q, а для секций первого порядка – только частота среза.
Кроме того, для секций фильтра второго порядка должны быть определены частота среза и добротность Q, а для секций первого порядка – только частота среза.
- Общий вид напряжения Передаточная функция ФВЧ второго порядка :
Wc — частота среза, а амплитудно-частотная характеристика вблизи частоты среза тесно связана с Q. K — коэффициент усиления в полосе пропускания, который представляет собой коэффициент усиления при стремлении частоты к бесконечности в области высоких частот. -проходной фильтр.
- Общий вид напряжения Передаточная функция ФВЧ первого порядка :
Значение Wc и K такое же, как и у фильтра верхних частот второго порядка, но не имеет значения Q.
При проектировании и расчете для определения этих параметров необходимо свериться с нормализованной таблицей полюсов фильтра, чтобы завершить ее через определенное преобразование. (Будь то фильтр нижних частот, верхних частот, полосовой или режекторный фильтр, его частотные характеристики могут быть получены путем преобразования частотных координат фильтра нижних частот, поэтому фильтр нижних частот также называется исходным фильтром. )
(Будь то фильтр нижних частот, верхних частот, полосовой или режекторный фильтр, его частотные характеристики могут быть получены путем преобразования частотных координат фильтра нижних частот, поэтому фильтр нижних частот также называется исходным фильтром. )
Рис. 7. Блок-схема фильтра верхних частот
В качестве примера используется обычная схема фильтра верхних частот источника напряжения, управляемого напряжением. Его принципиальная схема и передаточная функция по напряжению следующие:
Рис. 8. Цепь фильтра верхних частот, управляемого напряжением , мы можем узнать частоту среза в цепи фильтра верхних частот источника напряжения, управляемого напряжением:
Ⅴ Порядок фильтра верхних частот
Как определить порядок фильтра верхних частот
Порядок фильтра верхних частот Баттерворта равен
069, где F представляет собой 90, а порядок фильтра. C — частота среза -3 дБ, F 2 — частота заданного затухания в переходной полосе, а A 2 — затухание при F 2 .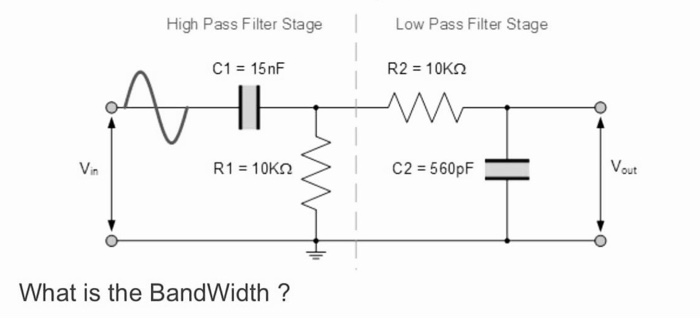
Порядок Фильтр верхних частот Чебышева :
Где n — порядок фильтра, fc — частота среза равных пульсаций, a1 — флуктуация усиления (дБ) в полосе пропускания, f2 — частота заданного затухания на переходе диапазон, а a2 — затухание на частоте f2 Volume (дБ).
fc в приведенной выше формуле представляет собой частоту отсечки равных пульсаций, то есть частоту затухания в переходной зоне при 1 . Если в конструкции используется частота среза -3 дБ, ее необходимо преобразовать в равную частоту среза пульсаций, чтобы получить приведенную выше формулу. В следующей таблице показано пропорциональное соотношение между частотой среза, такой как фильтр верхних частот Чебышева, и частотой среза -3 дБ.
Таблица 1: Отношение FC/f-3db равной ширины полосы пульсаций к ширине полосы -3dB фильтра верхних частот Чебышева
нет | 2 | 3 | 4 | 5 | 6 |
а1=0,1 дБ | 1,9432 | 1. | 1.2131 | 1.1347 | 1.0929 |
а1=0,2 дБ | 1,6743 | 1,2835 | 1.1564 | 1.0992 | 1.0685 |
а1=0,5 дБ | 1.3897 | 1.1675 | 1.0931 | 1.0593 | 1.0410 |
а1=1 дБ | 1.2176 | 1.0949 | 1.0530 | 1.0338 | 1.0234 |
Активный ФВЧ высокого порядка формируется путем каскадирования нескольких ФВЧ второго порядка (для фильтров нечетного порядка следует добавлять ФВЧ первого порядка). Каждый фильтр называется секцией фильтра, и каждый имеет свое независимое значение Q. Фильтр, сформированный после каскада, может представлять собой различные типы фильтров, такие как фильтр Баттерворта и фильтр Чебышева.
Каждый фильтр называется секцией фильтра, и каждый имеет свое независимое значение Q. Фильтр, сформированный после каскада, может представлять собой различные типы фильтров, такие как фильтр Баттерворта и фильтр Чебышева.
- Расчет секции фильтра верхних частот первого порядка:
- Расчет секции фильтра верхних частот второго порядка:
Ⅵ Разница между фильтром верхних частот и фильтром нижних частот
Разница между фильтром верхних частот и фильтром нижних частот заключается в том, Компоненты переменного тока пропускают и подавляют низкочастотные компоненты или компоненты постоянного тока. Фильтр нижних частот — это фильтр, пропускающий низкочастотные или постоянные компоненты сигнала и подавляющий высокочастотные компоненты или помехи и шум. Как правило, фильтр нижних частот задерживает сигналы, меньшие частоты среза, а фильтр верхних частот задерживает сигналы, превышающие частоту среза.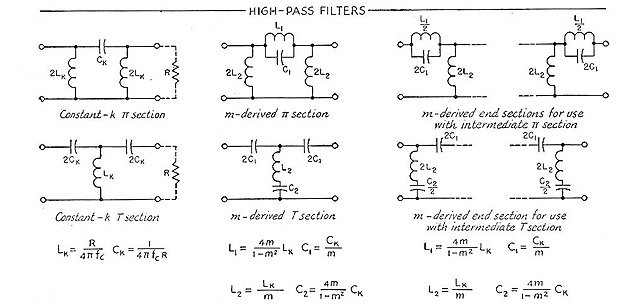
Ⅶ Применение фильтра верхних частот
1) В энергосистеме фильтр верхних частот используется для фильтрации гармоник определенного порядка и выше во время компенсации гармоник.
2) В аудиосистеме
Наиболее часто упускаемым из виду и наиболее полезным инструментом эквалайзера является фильтр верхних частот, который может удалять нежелательные низкочастотные шумы из источника звука. Фильтр верхних частот может быть частью эквалайзера эквалайзера или отдельным плагином или устройством. Обычно наши динамики, микшеры или микрофоны оснащены фильтрами верхних частот, потому что низкочастотная обрезка записанного человеческого голоса позволяет легко различить шум, хотя этот тип шума очень слабый и его трудно обнаружить. Например, в большинстве музыкальных инструментов фильтр высоких частот используется для отсекания звука ниже 100 Гц. Вы обнаружите, что звучание удивительно чистое, но это не относится к низкочастотным инструментам, таким как бочка и бас.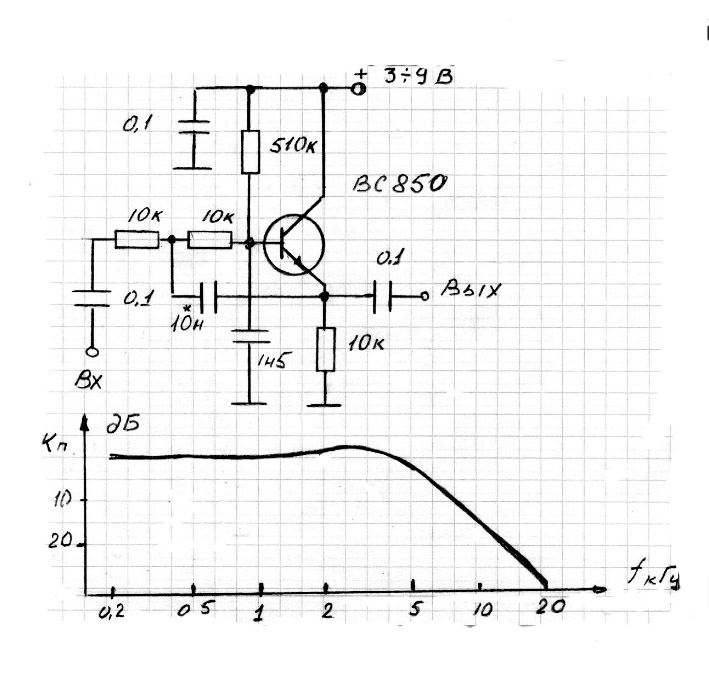
Ⅷ Вопрос, относящийся к фильтру верхних частот и дальнейшему развитию
7.1 ВопросКакова полоса пропускания фильтра верхних частот?
7.2 ОтветПолоса пропускания фильтра обозначает значение частоты, с которой разрешено проходить сигналам. Например, если полоса пропускания фильтра верхних частот задана равной 50 кГц, это означает, что разрешены только частоты от 50 кГц до бесконечности.
Часто задаваемые вопросы о фильтре верхних частот
1. Для чего используется фильтр верхних частот?
Фильтр верхних частот эффективно отсекает частотную характеристику микрофона ниже определенного заданного значения, позволяя только частотам выше этого значения «проходить» через аудиосигнал. Фильтры верхних частот удаляют нежелательную и избыточную низкочастотную энергию, которая в противном случае ухудшает качество аудиосигнала.
2.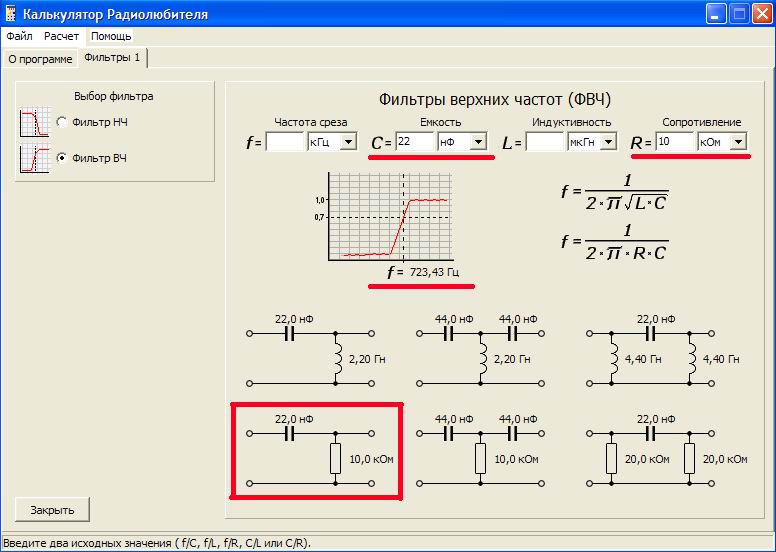 Как формируются фильтры верхних частот?
Как формируются фильтры верхних частот?
Фильтр верхних частот можно сформировать, подключив конденсатор последовательно с инвертирующим каскадом усиления.
3. Какие бывают фильтры верхних частот?
Различные типы фильтров верхних частот включают:
Цепь фильтра верхних частот R-C
Цепь фильтра верхних частот R-L
Цепь фильтра верхних частот инвертированного L-типа
Фильтр верхних частот T-типа
Фильтр верхних частот π-типа
Фильтр верхних частот с использованием операционного усилителя
Фильтр верхних частот Баттерворта
4. Когда следует использовать фильтр верхних частот?
Фильтр верхних частот — это простая, но эффективная кривая эквалайзера, которая удаляет нежелательные низкие частоты из источника звука. Как и большинство звукоинженеров, я использую их во многих моментах в своих миксах, чтобы убрать приглушенные сигналы и подтянуть аранжировки.
5. Какова частота среза фильтра верхних частот?
Частота среза фильтра верхних частот – это частота, при которой выходное (нагрузочное) напряжение составляет 70,7 % входного (источника) напряжения.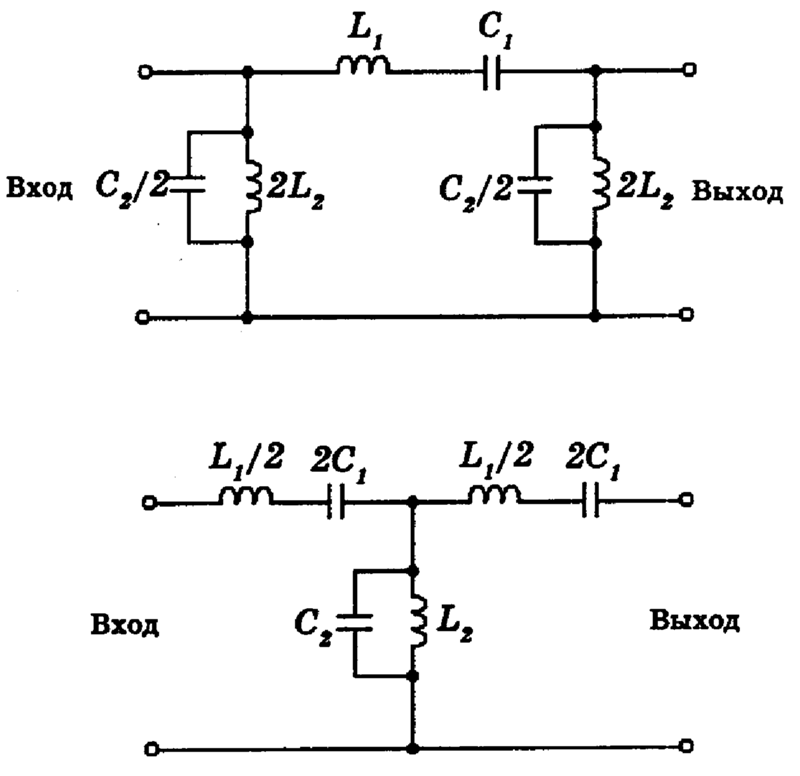 Выше частоты среза выходное напряжение превышает 70,7% от входного, и наоборот.
Выше частоты среза выходное напряжение превышает 70,7% от входного, и наоборот.
Лучшие продажи диода
| Фото | Деталь | Компания | Описание | Цены (долл. США) |
Альтернативные модели
| Деталь | Сравнить | Производители | Категория | Описание |
Заказ и качество
| Изображение | Произв.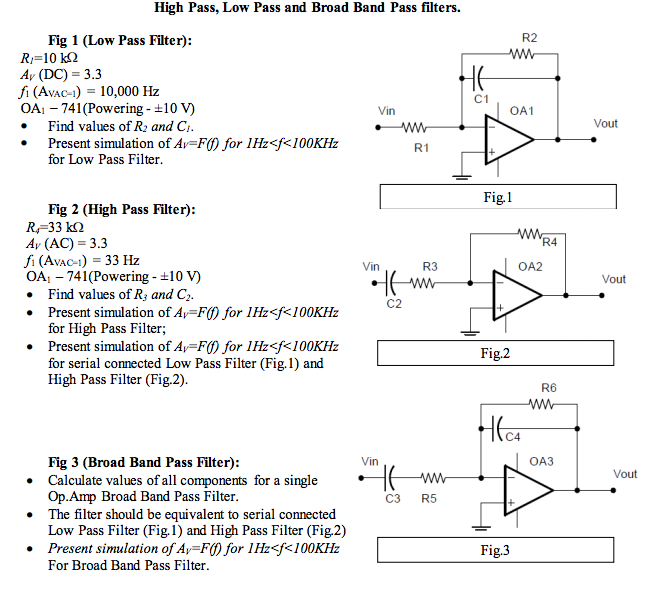 Деталь № Деталь № | Компания | Описание | Пакет | ПДФ | Кол-во | Цены (долл. США) |
Поделиться
Фильтры нижних и верхних частот | UCSC Physics Demonstration Room
Рисунок 1: Общая принципиальная схема, используемая для расчетов. Низкочастотные и высокочастотные версии цепей RL и RC можно увидеть справа и слева соответственно. Vs(w) — напряжение функционального генератора, а Vo(w) — напряжение на осциллографе.
Эта демонстрация предназначена для учащихся, которые уже изучили основы RC и RL цепей.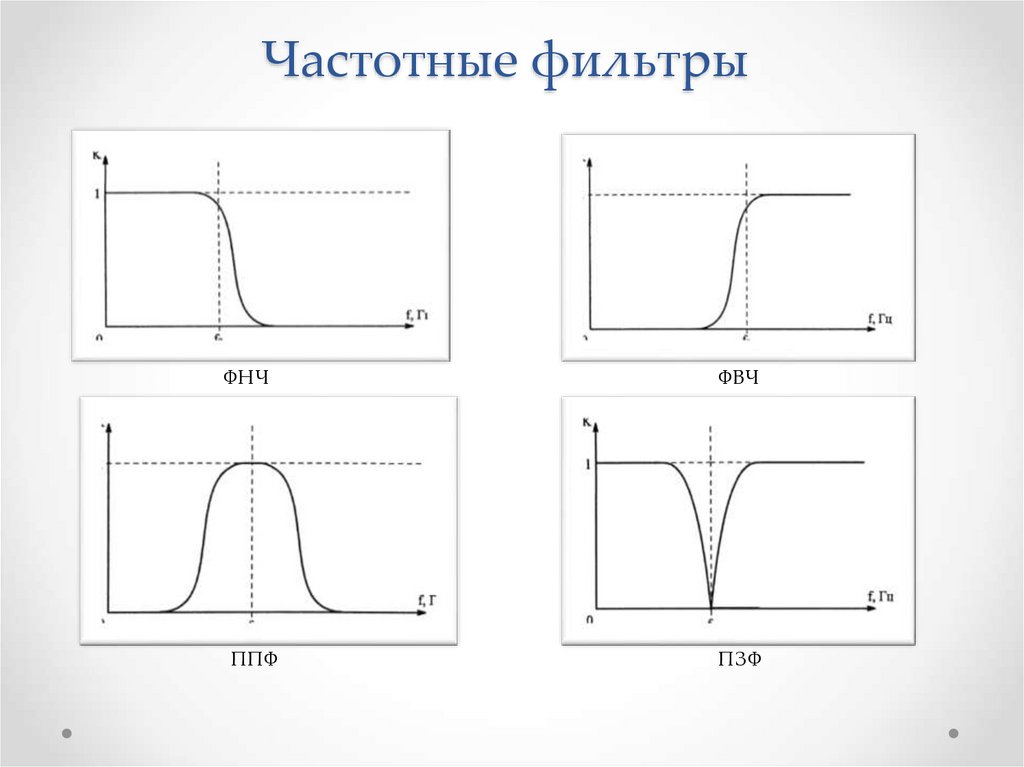 В этой демонстрации учащиеся могут увидеть одно из приложений: простые фильтры нижних и верхних частот. Студенты смогут понять, как расположение резистивных, емкостных и индуктивных нагрузок может привести к противоположным эффектам.
В этой демонстрации учащиеся могут увидеть одно из приложений: простые фильтры нижних и верхних частот. Студенты смогут понять, как расположение резистивных, емкостных и индуктивных нагрузок может привести к противоположным эффектам.
- Плата RC-фильтра. Эта плата имеет переменный резистор и конденсатор, прикрепленные к задней панели, что позволяет выполнять различные соединения между ними (рис. 2). Переменный резистор или потенциометр позволяет регулировать частоту среза фильтров. (Рисунок 3)
Рисунок 2: ПДУ
Рисунок 3: Проводка платы дистанционного управления
Функциональный генератор - : создает напряжение переменного тока для возбуждения резистивно-емкостных фильтров. (Рисунок 4)
Рис. 4: Генератор функций переменного тока
- Осциллограф: помогает визуализировать поведение выходного напряжения в зависимости от времени и сравнивается с входным напряжением от функционального генератора. (Рисунок 5)
Рисунок 5: Осциллограф
Кабели BNC - : Три кабеля BNC необходимы для подключения функционального генератора к плате RC, функционального генератора к осциллографу и осциллографа к плате RC.
 Один должен быть BNC-BNC, а два других — это кабели BNC с разъемами типа «банан».
Один должен быть BNC-BNC, а два других — это кабели BNC с разъемами типа «банан».
Плата RC (рис. 2) поддерживает как RC-фильтры нижних частот, так и RC-фильтры верхних частот. Чтобы переключиться между этими двумя настройками, нужно всего лишь изменить положение кабеля разъема типа «банан» входного и выходного напряжения. На рисунке 6 ниже показаны разъемы типа «банан», подключенные к плате в низкочастотной конфигурации. Схему для этой схемы можно увидеть выше на рисунке 1, в средней левой схеме.
Рисунок 6: Конфигурация нижних частот
Эта конфигурация нижних частот характеризуется заземлением на открытом узле конденсатора. Оба черных банановых разъема должны быть подключены к открытому концу конденсатора. Что касается красного и белого разъемов, красный разъем должен подключаться к общему узлу между резистором и конденсатором, а белый разъем должен подключаться к открытому узлу резистора. Белый разъем находится на другом конце кабеля BNC, подключенного к функциональный генератор, а красный разъем находится на другом конце разъема BNC, подключенного к осциллографу.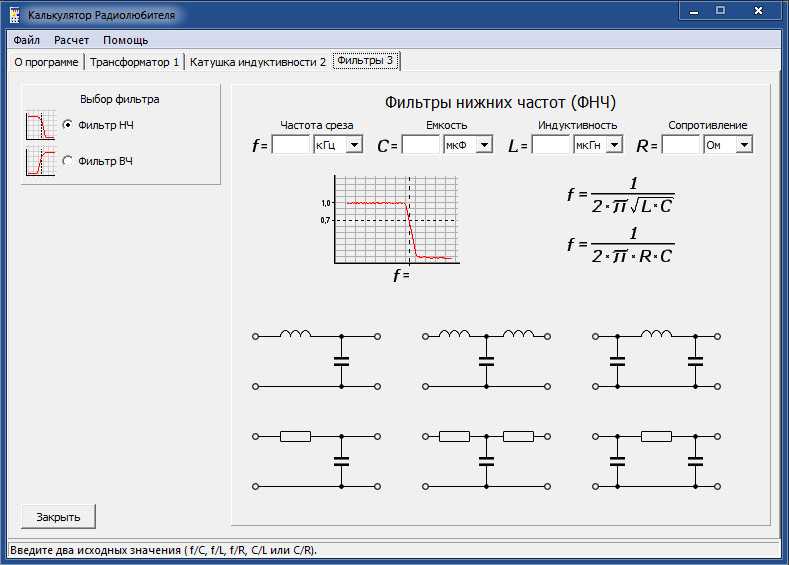 Цвет не важен, пока осциллограф измеряет выходное напряжение на конденсаторе, а функциональный генератор подает входное напряжение на открытый узел резистора. Эту конфигурацию можно увидеть в виде принципиальной схемы либо на Рисунке 1 выше, либо на Рисунке 10 ниже.
Цвет не важен, пока осциллограф измеряет выходное напряжение на конденсаторе, а функциональный генератор подает входное напряжение на открытый узел резистора. Эту конфигурацию можно увидеть в виде принципиальной схемы либо на Рисунке 1 выше, либо на Рисунке 10 ниже.
Компоновку платы можно увидеть ниже на рис. 7 для конфигурации верхних частот RC. Принципиальная схема выше на рисунке 1 в левом нижнем углу.
Рисунок 7: Конфигурация верхних частот
Заметная разница между этими двумя схемами заключается в том, что обе площадки поменялись местами с белым валетом. Теперь выходное напряжение будет измеряться на резисторе. Точнее, открытый узел резистора должен быть заземлен, а к открытому узлу конденсатора подключен белый разъем для подачи входного напряжения. Выходное напряжение по-прежнему берется из общего узла, но в этом случае оно измеряет выходное напряжение на резисторе, а не на конденсаторе, как в фильтре нижних частот.
После выполнения всех подключений можно просмотреть частоты, чтобы наблюдать затухание (уменьшение выходного сигнала по сравнению с входным) выше или ниже частоты среза. Для начала настройте функциональный генератор на создание синусоидального сигнала частотой около 500 Гц. Затем нажмите кнопку измерения на осциллографе, чтобы сравнить входное (канал 1) и выходное (канал 2) напряжения. Теперь измените потенциометр (поворотный диск на плате RC), пока выходное напряжение не будет примерно в 0,7 раза больше входного напряжения. Для этого установите входное напряжение на круглое число, такое как 10 или 1 вольт, сделав желаемое выходное напряжение равным 7 и 0,7 вольта соответственно. Варьируя сопротивление, устанавливаем критическую частоту 500 Гц. Как только это настроено, повышение или понижение частоты на функциональном генераторе приведет вас выше или ниже частоты среза, либо увеличивая, либо уменьшая затухание сигнала. С фильтром верхних частот увеличение частоты немного увеличивает выходной сигнал, а уменьшение частоты резко снижает выходной сигнал. Низкочастотный фильтр будет испытывать падение выходного сигнала при увеличении частоты и небольшое увеличение выходного сигнала при уменьшении частоты.
Для начала настройте функциональный генератор на создание синусоидального сигнала частотой около 500 Гц. Затем нажмите кнопку измерения на осциллографе, чтобы сравнить входное (канал 1) и выходное (канал 2) напряжения. Теперь измените потенциометр (поворотный диск на плате RC), пока выходное напряжение не будет примерно в 0,7 раза больше входного напряжения. Для этого установите входное напряжение на круглое число, такое как 10 или 1 вольт, сделав желаемое выходное напряжение равным 7 и 0,7 вольта соответственно. Варьируя сопротивление, устанавливаем критическую частоту 500 Гц. Как только это настроено, повышение или понижение частоты на функциональном генераторе приведет вас выше или ниже частоты среза, либо увеличивая, либо уменьшая затухание сигнала. С фильтром верхних частот увеличение частоты немного увеличивает выходной сигнал, а уменьшение частоты резко снижает выходной сигнал. Низкочастотный фильтр будет испытывать падение выходного сигнала при увеличении частоты и небольшое увеличение выходного сигнала при уменьшении частоты.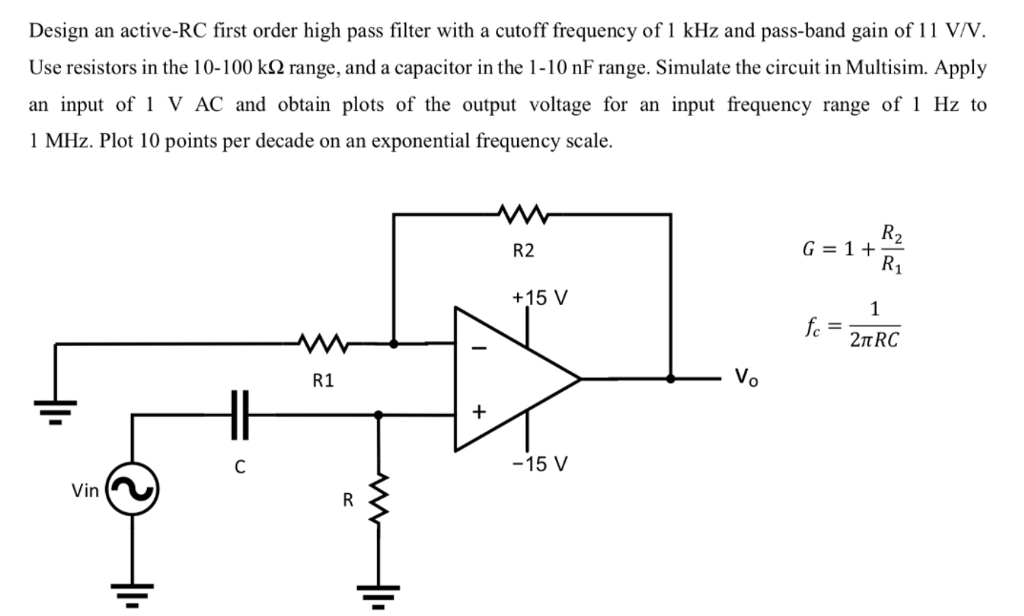 Цель этого этапа можно увидеть на рисунке 8 ниже.
Цель этого этапа можно увидеть на рисунке 8 ниже.
Рисунок 8: Неуловимая частота среза
Простое объяснение высокочастотных и низкочастотных частот RC начинается с понимания того, как конденсаторы реагируют на переменный ток, и наблюдения за крайними случаями. Ток, пропускаемый через конденсатор, равен произведению его емкости на производную по времени от его напряжения. Эта зависимость от производной его напряжения придает ему специфические свойства, которые мы наблюдаем в этой демонстрации. Изучение крайних значений частоты, таких как ноль или бесконечность, позволяет лучше понять крупномасштабные тенденции изменения напряжения, возникающие в этих фильтрах. При приближении частоты к нулю производная по времени также стремится к нулю. Это говорит нам о том, что в случае постоянного тока конденсатор становится разомкнутой цепью, через которую не будет протекать ток. Однако, когда частота приближается к бесконечности, конденсатор становится разомкнутой цепью, где весь ток может проходить без сопротивления на своем пути. Теперь мы можем сузить наше внимание до фильтра верхних частот и посмотреть, как эти крайности повлияют на поведение фильтра.
Теперь мы можем сузить наше внимание до фильтра верхних частот и посмотреть, как эти крайности повлияют на поведение фильтра.
Рис. 9: Схема высокочастотного фильтра RC, любезно предоставлена веб-сайтом Electronics Tutorials. Это говорит нам о том, что по мере уменьшения частоты ток на резисторе будет ограничен. Это ограничит ток резистора, уменьшив выходное напряжение. По мере увеличения частоты конденсатор все чаще ведет себя как короткое замыкание. Это позволяет все большему и большему току проходить от входа через резистор, вызывая более высокое выходное напряжение.
Мы также можем математически обосновать этот аргумент на основе импедансов конденсатора и резистора. Импеданс относится к аналогу комплексного числа сопротивления. Для получения фильтра верхних частот мы обращаемся к компонентам принципиальной схемы на рисунке 9 выше.
Начнем с и
Мы можем использовать закон Ома, чтобы найти соотношение для входного и выходного напряжений.
Для фильтра верхних частот мы можем объединить два приведенных выше уравнения, чтобы найти выходное напряжение как функцию частоты.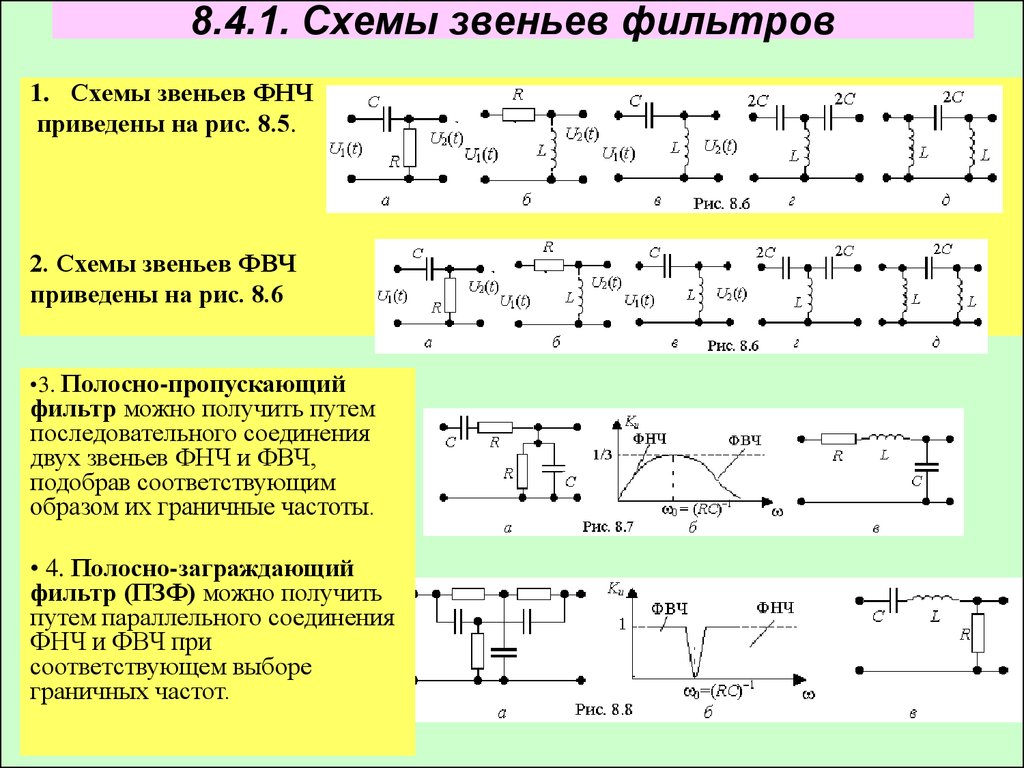
Из этого мы видим, что:
Как тогда
И так как тогда
Мы можем построить аналогичный аргумент для фильтра нижних частот, показанного ниже на рисунке 10.
Рисунок 10: RC-цепь нижних частот Диаграмма, любезно предоставленная веб-сайтом Electronics Tutorials
Мы можем использовать те же аргументы, что и выше, чтобы понять экстремальное поведение этого фильтра. Когда частота уменьшается около нуля, конденсатор действует как разомкнутая цепь, блокируя прохождение большей части тока. Блокируя большую часть тока от заземления через конденсатор, он заставляет сигнал проходить на выход. Это приводит к большому выходному напряжению для более низких частот. Когда частота увеличивается до бесконечности, конденсатор начинает действовать как короткое замыкание, позволяя всему току, подаваемому на вход, проходить через конденсатор через землю. Позволяя току течь через конденсатор с небольшим сопротивлением, конденсатор гарантирует, что на выходе не будут приниматься высокочастотные сигналы.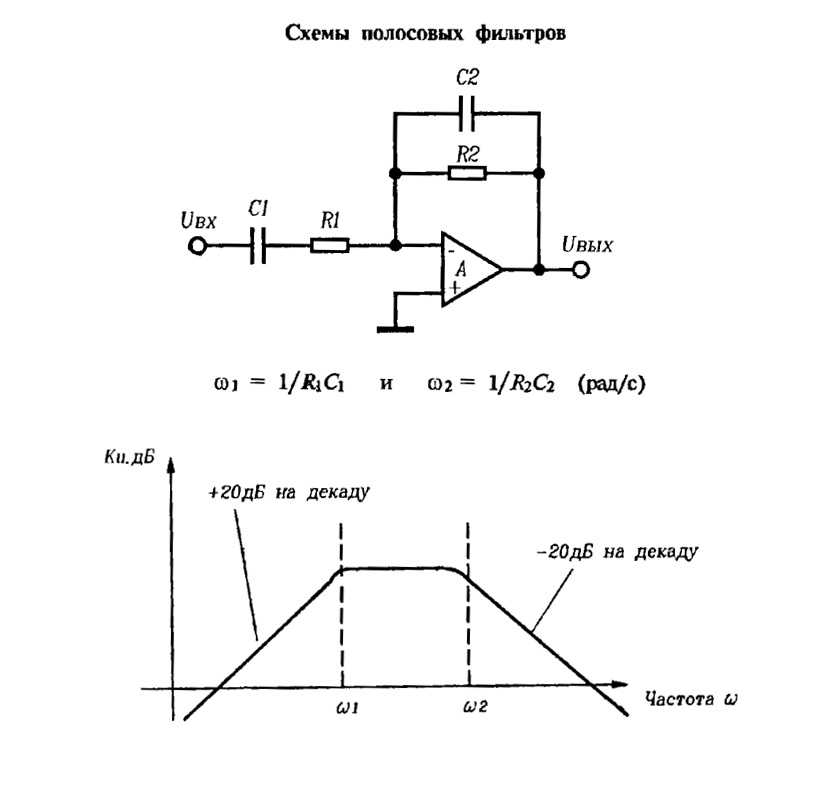
Из вывода верхних частот мы можем использовать те же импедансы и уравнение закона Ома. Однако наше выходное напряжение немного изменилось, потому что теперь оно проходит через конденсатор.
Используя тот же набор уравнений, что и для фильтра верхних частот, мы получаем окончательное уравнение выходного напряжения, зависящее от частоты.
Из этого мы видим, что:
То же, что и
И то же, что и
Чтобы определить золотую середину между этими двумя крайностями, мы определяем частоту среза, как показано ниже.
Частота среза:
или где это постоянная времени
Важно отметить, что это уравнение справедливо как для высокочастотных, так и для низкочастотных RC-фильтров с одним и тем же резистором и конденсатором. Для фильтра нижних частот увеличение частоты выше частоты среза приведет к падению выходной амплитуды. Что касается фильтра верхних частот, то уменьшение частоты ниже порога среза приведет к аналогичному снижению выходного напряжения. Эта частота разделяет область прошедших сигналов и сигналов, ослабленных на выходе.
Эта частота разделяет область прошедших сигналов и сигналов, ослабленных на выходе.
Также может быть любопытно, как быстро падает каждое из этих выходных напряжений при изменении частоты. Чтобы понять это, наиболее эффективна зависимость частоты развертки от коэффициента усиления. Усиление относится к логарифму отношения выходного напряжения к входному напряжению: мы определяем эту новую величину, чтобы сравнить выходное и входное напряжения в масштабе, изменяющемся в 10 раз. Умножение на 20 является просто условным. Единицами усиления являются децибелы, которые масштабируются с коэффициентом 10, а не линейно.
Одним из важных примеров усиления является -3 дБ. Для справки, усиление -3 дБ соответствует коэффициенту Это значение усиления очень важно, потому что оно часто отмечает поворотную точку в фильтре. Как в фильтрах высоких, так и в нижних частотах усиление на -3 дБ происходит на частоте среза, после которой усиление уменьшается с постоянной скоростью. Еще одна часто используемая метрика — децибелы за десятилетие.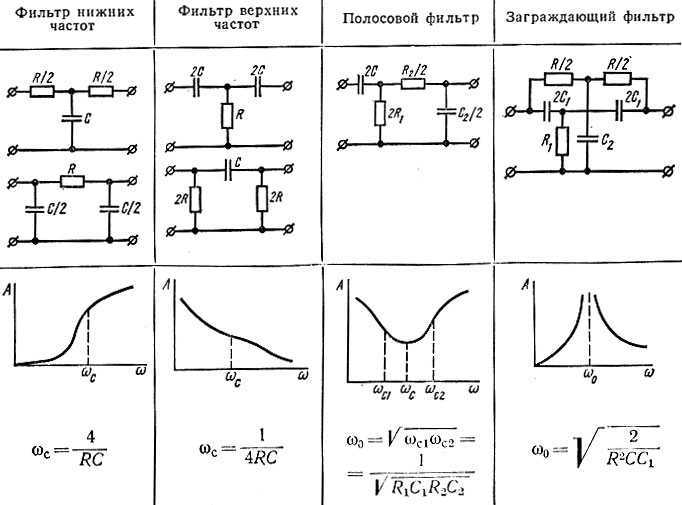 Это измерение относится к затуханию на частоту, где затухание дается как усиление, а частота выражается в 10 Гц или одной декаде. Затухание в RC-фильтрах верхних и нижних частот составляет 20 дБ на декаду, что соответствует 10 Гц.
Это измерение относится к затуханию на частоту, где затухание дается как усиление, а частота выражается в 10 Гц или одной декаде. Затухание в RC-фильтрах верхних и нижних частот составляет 20 дБ на декаду, что соответствует 10 Гц.
Имея в виду эту информацию, теперь мы можем понять график зависимости выходного сигнала от частоты для фильтров верхних и нижних частот. Ниже приведены два таких графика, один для верхних частот (рис. 11), а другой для нижних частот (рис. 12).
Рисунок 11. Развертка частоты RC-фильтра верхних частот, предоставлено веб-сайтом Electronics Tutorials
Рисунок 12. Развертка частоты RC-фильтра нижних частот, предоставлено веб-сайтом Electronics Tutorials
Фильтры, которые мы обсуждали, будут реагировать на широкий диапазон частот. Чтобы пояснить некоторые термины, используемые на этих графиках, полоса пропускания относится к частотному диапазону, в котором входной сигнал переменного тока может проходить к выходу, а полоса заграждения относится к частоте, в которой вход остановлен или заблокирован.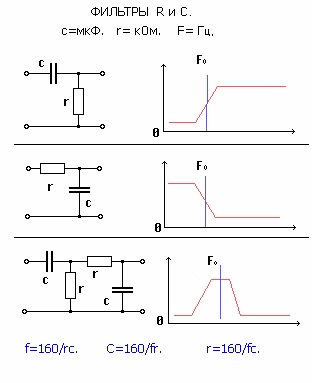 Упомянутая угловая частота — это другое название частоты среза, которую мы рассчитали выше. Выход, нанесенный на оси y, представляет собой значение усиления на каждой частоте по оси x.
Упомянутая угловая частота — это другое название частоты среза, которую мы рассчитали выше. Выход, нанесенный на оси y, представляет собой значение усиления на каждой частоте по оси x.
Графики подтверждают предыдущие расчеты, сделанные для экстремальных случаев, но также заполняют области, которые мы не смогли количественно определить с помощью элементарного анализа пределов. Важно понимать, что при выполнении описанной выше демонстрации RC-фильтра аудитории будет показана одна точка на этих графиках. Частота будет установлена на одно конкретное значение, а осциллограф покажет входное и выходное переменные напряжения фильтра. Чтобы визуализировать это поведение, необходимо просмотреть частоты и наблюдать за результирующими выходными амплитудами. Выходное и входное напряжения будут следовать этим графикам, повышаясь или понижаясь в зависимости от того, где они находятся на кривой. Лучшей областью для выборки будет частота среза или точка 3 дБ, которая находится на частоте среза.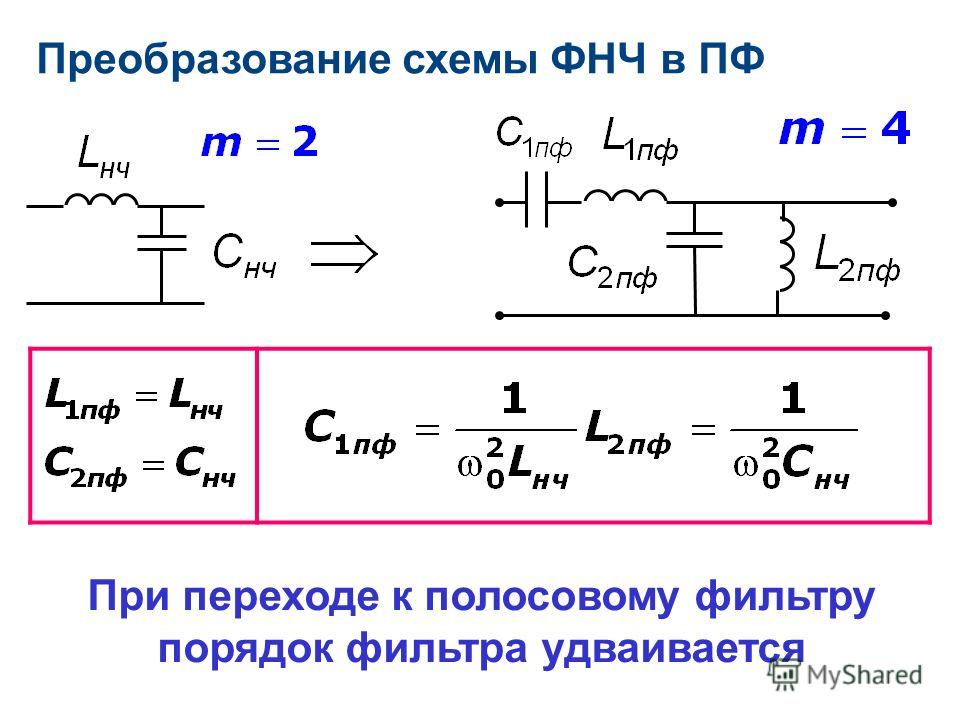
Разделение концепции выходного сигнала в зависимости от времени, как показано на осциллографе, и выходного сигнала в зависимости от частоты, как показано на графиках выше, является трудным, но необходимым процессом для полного понимания. Графики частоты показывают нам общую тенденцию, которой следует фильтр, описывая его общие характеристики. Временной график показывает нам один снимок частотного графика. При неизменной частоте мы наблюдаем изменения выходной амплитуды в течение некоторого времени.
Автор: Ной Пик
Типы пассивных фильтров высоких частот
Типы активных фильтров высоких частотТипы пассивных фильтров высоких частот – пассивные фильтры 1-го порядка и 2-го порядка сигнал & разрешить только высокочастотные сигналы. Он блокирует частоту ниже выбранной частоты, известной как частота среза или частота среза.
Существует два основных типа фильтра верхних частот ;
- Пассивный фильтр высоких частот
- Активный фильтр высоких частот
В этой статье мы сосредоточимся на пассивном фильтре верхних частот и подробно обсудим его с примерами. Пассивные фильтры высоких частот будут рассмотрены в следующем посте.
Пассивные фильтры высоких частот будут рассмотрены в следующем посте.
Содержание
Пассивный фильтр верхних частот:
Фильтр, состоящий только из пассивных компонентов, таких как резистор, конденсатор и катушка индуктивности, называется пассивным фильтром. Пассивные фильтры не нуждаются в каком-либо внешнем источнике, поэтому они не имеют усиления, т. е. амплитуда выходного сигнала всегда равна или меньше амплитуды входного сигнала.
Конструкция пассивного фильтра очень проста, а используемые компоненты очень дешевы.
Простой фильтр высоких частот состоит из резистора с конденсатором (известного как RC-цепь) и катушки индуктивности (известной как RL-цепь). В этой статье мы обсудим фильтры верхних частот RC и RL с примерами.
- Запись по теме: Типы активных фильтров нижних частот
Пассивный фильтр верхних частот первого порядка:
Фильтры первого порядка содержат только один реактивный компонент, т.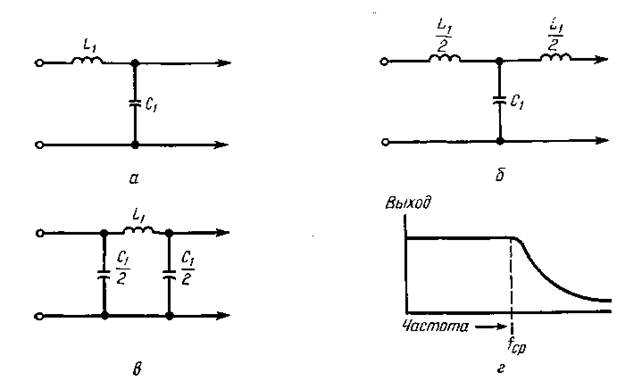 е. либо конденсатор, либо катушку индуктивности. Это простейшая форма фильтра, состоящего всего из двух компонентов, причем резистор используется в обеих конструкциях, то есть в RC и RL.
е. либо конденсатор, либо катушку индуктивности. Это простейшая форма фильтра, состоящего всего из двух компонентов, причем резистор используется в обеих конструкциях, то есть в RC и RL.
Частотная характеристика и используемые в ней термины:
Чтобы понять фильтр, необходимо изучить его частотную характеристику. Частотная характеристика или диаграмма Боде представляет собой график схемы, который показывает ее коэффициент усиления по вертикальной оси относительно частоты по горизонтальной оси.
Однако частотная характеристика содержит некоторые ключевые термины, которые необходимо обсудить, чтобы полностью понять ее. Вот частотная характеристика фильтра верхних частот первого порядка.
Эта частотная характеристика четко показывает усиление фильтра верхних частот, которое увеличивается с увеличением частоты.
Частота среза или угловая частота:
Частота, при которой усиление фильтра составляет ½ или -3 дБ или выходная амплитуда составляет 70,7% (1/√2) от входного сигнала, называется угловой частотой и обозначается на f с . Это граница между полосой пропускания и полосой задерживания фильтра.
Это граница между полосой пропускания и полосой задерживания фильтра.
Полоса заграждения:
Полоса заграждения — это полоса частот, блокируемая фильтром. в фильтре верхних частот частота, которая ниже частоты среза f c , является частотой полосы задерживания.
Как показано на графике, усиление фильтра в полосе заграждения очень низкое.
Полоса пропускания:
Полоса частот, проходящая через фильтр без затухания, называется полосой пропускания. Частота выше частоты среза f c — частота полосы пропускания фильтра верхних частот. Это хорошо видно на графике АЧХ выше.
Полоса пропускания Фильтра;
Ширина полосы пропускания фильтра называется полосой пропускания фильтра. Согласно этому определению полоса пропускания ФВЧ бесконечна, т.е. частота от точки среза f c до бесконечности.
Коэффициент усиления фильтра:
Коэффициент усиления фильтра определяется выражением;
Усиление = В вых / В вх
Усиление в дБ = 20 log (V out /V in )
Усиление на частоте среза:
Мы установили, что выходная амплитуда на частоте среза составляет 70,7% или (1/√2).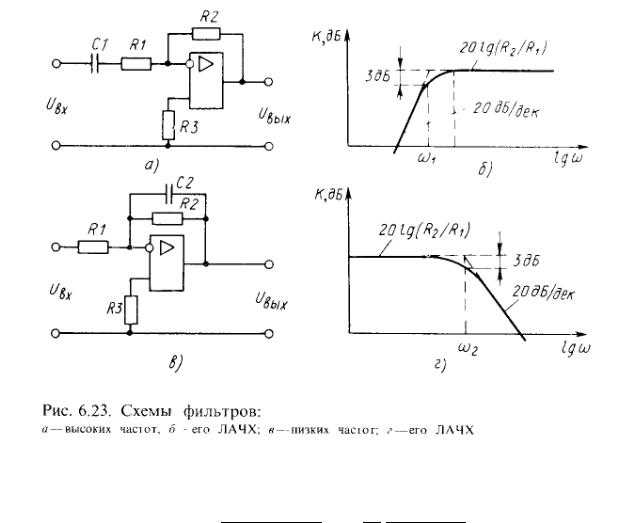 ) его входной максимальной амплитуды.
) его входной максимальной амплитуды.
Преобразование усиления в дБ;
Скорость спада:
Скорость спада — это скорость изменения усиления или крутизны кривой в полосе задерживания фильтра. Это зависит от порядка фильтра и задается;
20n дБ/декада или 6n дБ/октава
Где n — порядок фильтра.
Декада означает увеличение частоты в 10 раз, тогда как октава означает увеличение частоты в 2 раза.
- Запись по теме: Типы пассивных фильтров нижних частот
В этой конструкции фильтра верхних частот последовательно соединены конденсатор и резистор. Входной сигнал подается через конденсатор. Выход снимается через резистор, как показано на рисунке.
Его конструкция такая же, как у RC-фильтра нижних частот с небольшим изменением местами конденсатора и резистора.
- Сообщение по теме: Резистор и типы резисторов | Фиксированный, переменный, линейный и нелинейный
Реактивное сопротивление конденсатора очень велико на низкой частоте. Он действует как разомкнутая цепь для низкочастотных сигналов. Таким образом, низкочастотный входной сигнал блокируется и никогда не попадает на выходную клемму, поскольку весь сигнал проходит через конденсатор.
Реактивное сопротивление конденсатора уменьшается с увеличением частоты. Поэтому он начинает разрешать входной сигнал, когда он достигает определенной частоты.
Реактивное сопротивление конденсатора играет важную роль в характеристиках этого фильтра. Это зависит только от частоты сигнала.
Общее сопротивление этой цепи составляет;
- Запись по теме: Типы выпрямителей и их работа
На частоте среза сопротивление и емкостное сопротивление цепи эквивалентны.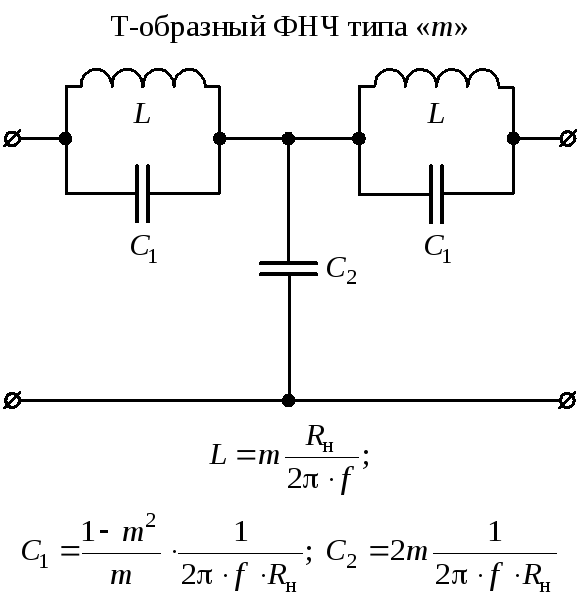 то есть
то есть
Фазовый сдвиг φ(phi) этого фильтра определяется выражением;
Таким образом, фазовый сдвиг на частоте среза будет всегда;
Выходное напряжение;
Выходное напряжение для этой схемы определяется с помощью правила делителя напряжения;
- Связанный пост:Типы реле SSR – конструкция и эксплуатация
Допустим, резистор R = 10 кОм и конденсатор C = 10 нФ.
Расчет частоты среза для этого фильтра;
Давайте проверим эту частоту среза, смоделировав данный пример с помощью Proteus. Частотная характеристика этого примера приведена ниже;
Частота отображается в левом нижнем углу, а соответствующий коэффициент усиления — в правом нижнем углу для выбранной точки на графике. Он ясно показывает усиление -3 дБ на частоте 1,59 кГц , которая является частотой среза этого фильтра .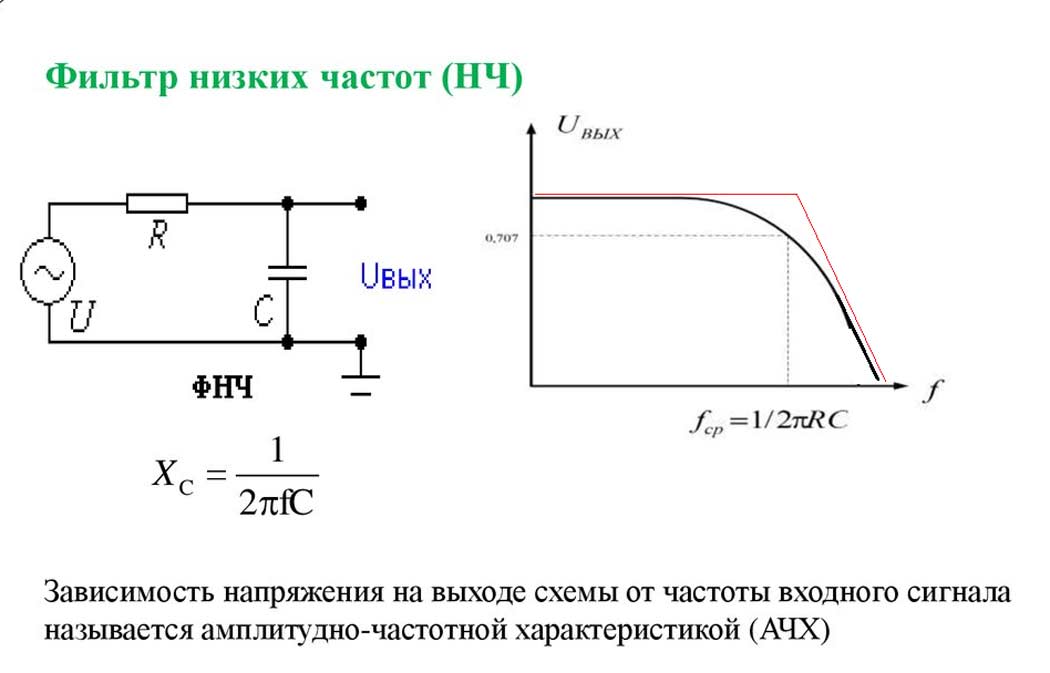
- Запись по теме: Типы диодов и их применение
Этот фильтр представляет собой комбинацию резистора и катушки индуктивности. Вход подается на резистор, а выход — на индуктор, как показано на рисунке внизу;
Операция:Реактивное сопротивление катушки индуктивности зависит от частоты сигнала. Он прямо пропорционален частоте. При подаче низкочастотного сигнала реактивное сопротивление катушки индуктивности становится очень низким, и она начинает вести себя как короткое замыкание. Тогда как сопротивление резистора относительно очень велико. Таким образом, сигнал развивается только через резистор, оставляя небольшое напряжение на выходной клемме.
При увеличении частоты реактивное сопротивление катушки индуктивности также увеличивается. В конце концов, он преодолевает сопротивление резистора и начинает вырабатывать большую часть входного сигнала на своих клеммах.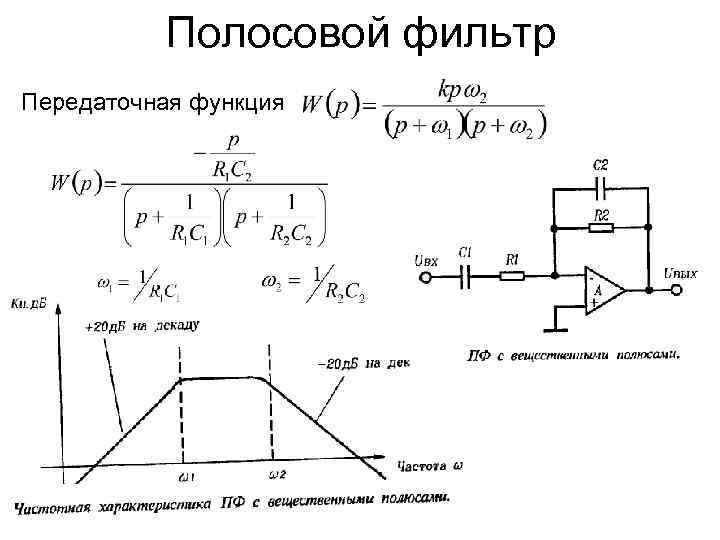
Так низкочастотный сигнал отфильтровывается через фильтр верхних частот RL.
Индуктивное реактивное сопротивление определяется по формуле;
Полное сопротивление этой цепи RL определяется выражением;
- Запись по теме: Счетчик и типы электронных счетчиков
Точно так же, как и RC-фильтры, фильтры RL имеют такое же условие для частоты среза, т. е. частоты, при которой индуктивное реактивное сопротивление становится эквивалентным сопротивлению резистора.
Фазовый сдвиг φ определяется выражением;
Выходное напряжение:Применяя правило делителя напряжения, выходное напряжение схемы определяется выражением;
Пример фильтра верхних частот RL первого порядка:Предположим, резистор R = 2,2 кОм с конденсатором C = 10 мГн.
Найдем его граничную частоту по формуле;
мы собираемся проверить этот результат с помощью инструмента моделирования Proteus.
Как показано на частотном графике выше, усиление на частоте 35 кГц составляет -3 дБ, что является усилением на частоте среза.
- Запись по теме: Типы цифровых защелок — защелки SR D
Фильтры второго порядка содержат два реактивных компонента. Пассивный фильтр порядка 2 и состоит из каскада двух фильтров порядка 1 st . Эта конфигурация может быть применена как к фильтрам верхних частот RC, так и к RL.
Основные характеристики фильтров второго порядка:- Скорость спада :
Скорость спада фильтра определяется выражением;
Скорость спада = 20n дБ/декада или 6n дБ/октава
Где n — порядок фильтра
Таким образом, скорость спада фильтра порядка 2 nd составляет 40 дБ/декаду или 12 дБ/октаву. Это означает, что кривая фильтра порядка 2 и круче, чем кривая фильтра порядка 1 st .
- Коэффициент усиления на частоте среза;
Коэффициент усиления частоты среза фильтра n-й ступени определяется выражением;
Таким образом, прирост 2 -й заказ фильтр есть;
Преобразование усиления в дБ;
Следовательно, усиление фильтра верхних частот 2 -го порядка на частоте среза составляет -6b. Это также имеет смысл, потому что усиление каждого каскада суммируется при их каскадировании.
- -3 дБ Частота
Мы знаем, что коэффициент усиления на частоте среза составляет -6b, что не соответствует истинной частоте полосы пропускания. Частота полосы пропускания любого фильтра находится на уровне усиления -3 дБ. Таким образом, частота -3 дБ фильтра верхних частот n-го порядка рассчитывается по формуле;
Где n — порядок фильтра верхних частот.
Определяет частоты полосы задерживания и полосы пропускания фильтра. Таким образом, становится частота -3 дБ фильтра верхних частот -го порядка -го порядка.
Таким образом, становится частота -3 дБ фильтра верхних частот -го порядка -го порядка.
Мы будем использовать эти термины в примере, обсуждаемом ниже;
- Эффект нагрузки:
Это явление низкого падения сигнала в цепи нагрузки из-за его более низкого импеданса, чем в цепи источника.
В идеале при оценке производительности многокаскадного фильтра мы не учитываем входное и выходное сопротивление каждого каскада. На практике, если последующий каскад имеет такое же или более низкое входное сопротивление, чем предыдущий каскад, падение сигнала на последующем каскаде будет небольшим. Это вызывает ошибочный вывод.
Чтобы уменьшить влияние нагрузки, импеданс последующего каскада должен быть как минимум в 10 раз выше, чем у предыдущего каскада. Это делается путем масштабирования резистора, конденсатора и катушки индуктивности в обоих каскадах многокаскадных фильтров.
- Связанная запись: Типы конденсаторов | Фиксированный, переменный, полярный и неполярный
RC Пассивный фильтр верхних частот второго порядка:
Каскадирование двух 1 st порядка RC фильтров дает фильтр 2 nd порядка RC фильтр верхних частот, как показано на рисунке внизу.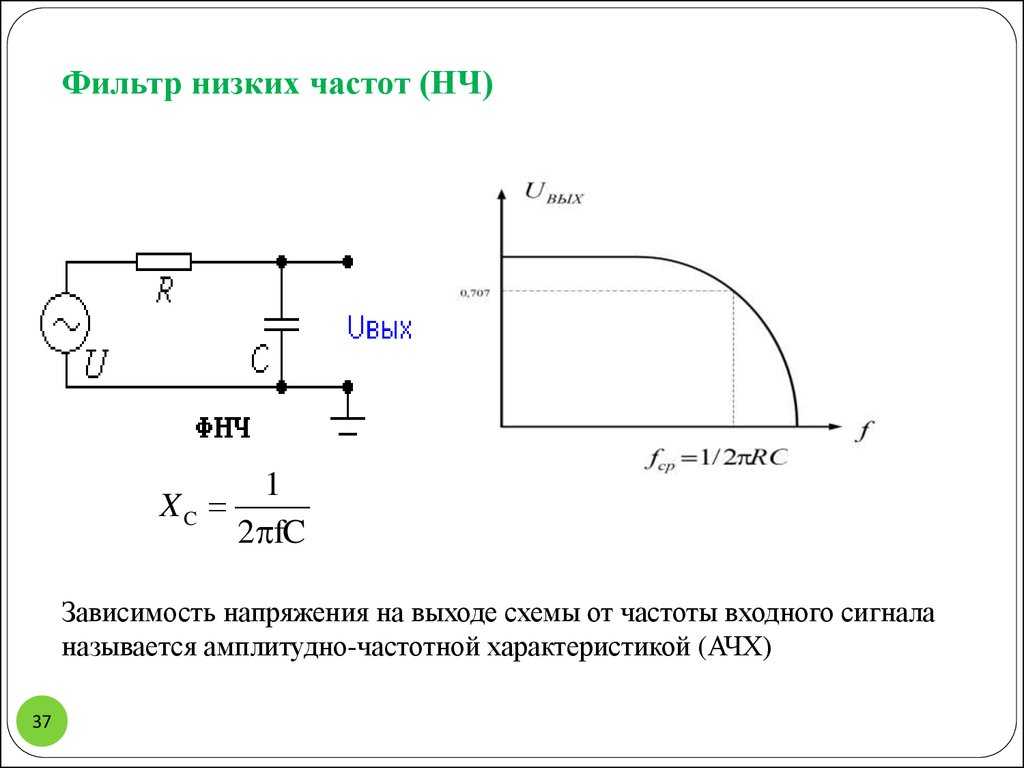
Частота среза 2
nd Заказ фильтра высоких частот RC:Частота среза каскадных фильтров зависит от обоих каскадов и определяется по формуле;
, но если резистор R 1 = R 2 и конденсатор C 1 = C 2 , то частота среза становится равной;
Пример RC 2
nd Закажите пассивный фильтр верхних частот:Предположим, резистор R 1 = R 2 = 10 кОм и конденсатор C 1 = 901 9 C 90
Масштабирование резистора и конденсаторов для увеличения импеданса второго каскада;
Increasing the impedance of the 2 nd stage by the scale of 10
Decreasing the impedance of 1 st stage by 10
The R 1 ‘ , R 2 ‘ , C 1 ‘ , C 2 ‘ — масштабированный резистор и конденсаторы. Помните, масштабирование выполняется для практической реализации. Коэффициент масштабирования должен быть одинаковым для обоих этапов, чтобы получить одинаковую реакцию. Теоретически частота среза для обеих конфигураций остается одинаковой.
Помните, масштабирование выполняется для практической реализации. Коэффициент масштабирования должен быть одинаковым для обоих этапов, чтобы получить одинаковую реакцию. Теоретически частота среза для обеих конфигураций остается одинаковой.
Теперь рассчитаем частоту среза f c ;
Теперь мы рассчитаем его частоту -3 дБ, которая является фактической частотой среза.
Таким образом, частота среза этого фильтра составляет 2,47 кГц, что соответствует коэффициенту усиления -3 дБ. Подтвердим это, смоделировав схему в Proteus.
Он ясно показывает усиление -3 дБ на частоте 2,47 кГц, а также выделена точка -6 дБ, которая находится на частоте 1,59 кГц.
- Связанная запись: Различные типы датчиков с приложениями
Так же, как и фильтр RC, каскадирование двух фильтров верхних частот 1 -го порядка создаст фильтр верхних частот RL 2-го порядка -го порядка , как показано на рисунке ниже.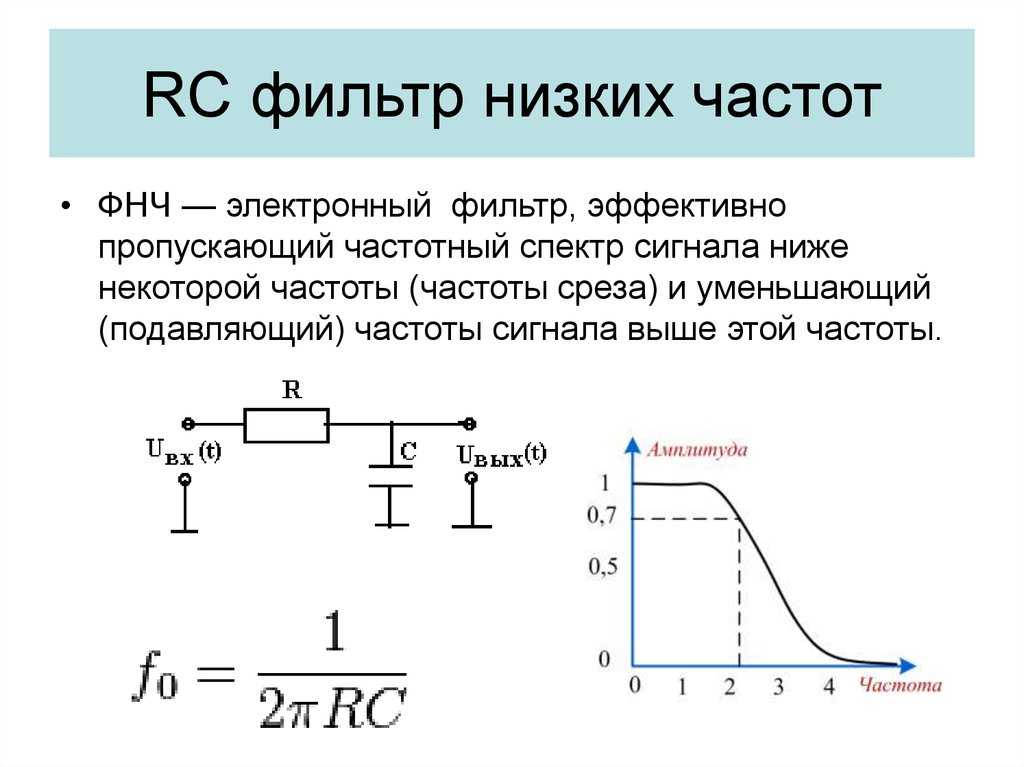
Частота среза или частота среза f c из 2 nd заказать RL Фильтр высоких частот.
Или, если индуктор и резисторы имеют одинаковое значение, тогда угловая частота становится;
Пример 2 nd Заказ RL Фильтр высоких частот:
Предположим, что номиналы резистора и индуктивности в обоих каскадах одинаковы, т.е. = 2,2 кОм и катушка индуктивности L 1 = L 2 = 10 мГн
Мы взяли резистор одинакового номинала для простоты расчета. На практике вам придется увеличить импеданс каскада 2 и путем масштабирования резисторов и катушек индуктивности, как показано ниже;
Увеличение импеданса 2-й -й -й ступени на 10
Уменьшение импеданса 1-й -й -й ступени на 10
Рассчитаем частоту среза фильтра;
Но это частота -6 дБ, и нам нужна частота фильтра -3 дБ, которая является фактической частотой среза.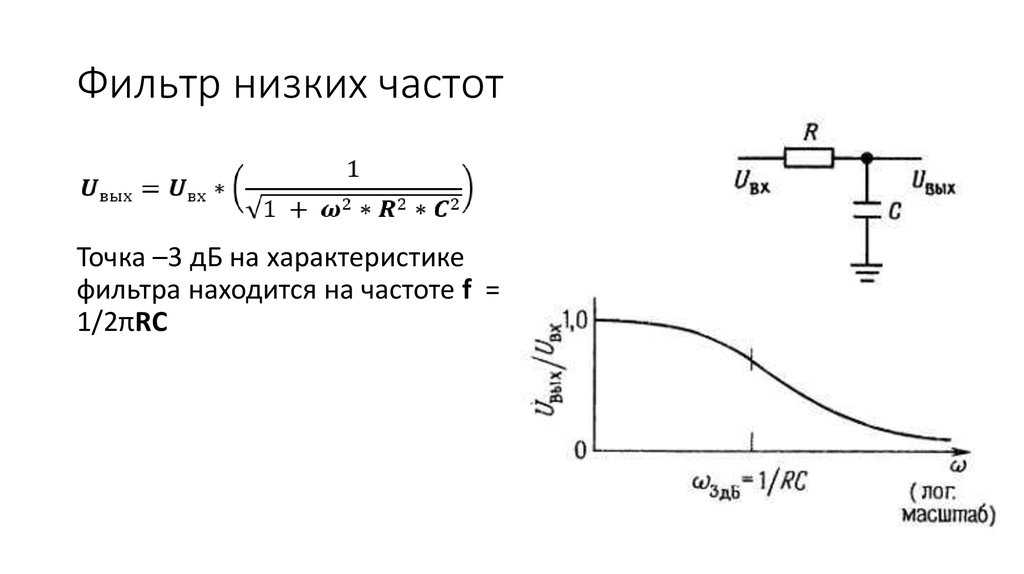 Это дается;
Это дается;
мы собираемся смоделировать данный пример, чтобы проверить наши результаты с помощью инструмента Proteus.
Вы видите частоту 54,4 кГц при усилении -3db . Кроме того, обратите внимание на кривую, она намного круче, чем фильтр порядка 1 st , и имеет скорость спада 40 дБ/декаду.
Related Posts:
- Типы амплитудной модуляции (AM) – преимущества и недостатки
- Типы методов модуляции, используемые в системах связи
- Типы резистивных датчиков — преобразователь, потенциометр и тензодатчик
Частотная характеристика фильтра нижних и верхних частот
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
Существует множество практических применений, в которых используются фильтры того или иного типа. Современные солнцезащитные очки отфильтровывают вредное для глаз ультрафиолетовое излучение и уменьшают интенсивность солнечного света, попадающего в глаза. Система подвески автомобиля отфильтровывает дорожный шум и снижает воздействие выбоин на пассажиров. Аналогичная концепция применима к электрическим цепям: можно ослабить (т. е. уменьшить амплитуду) или полностью исключить сигналы нежелательных частот, например те, которые могут быть вызваны электромагнитными помехами (ЭМП).
Система подвески автомобиля отфильтровывает дорожный шум и снижает воздействие выбоин на пассажиров. Аналогичная концепция применима к электрическим цепям: можно ослабить (т. е. уменьшить амплитуду) или полностью исключить сигналы нежелательных частот, например те, которые могут быть вызваны электромагнитными помехами (ЭМП).
На рис. 1 изображен простой RC-фильтр , а его входное и выходное напряжения обозначены соответственно В i и В 90
Рис. 1 RC Фильтр нижних частот
Частотную характеристику фильтра можно получить, рассмотрев функцию }}{{{V}_{i}}}\left( j\omega \right)\begin{matrix}{} & (1) \\\end{matrix}\]
и отметив, что выходное напряжение может быть выражено как функция входного напряжения с помощью делителя напряжения следующим образом
\[{{V}_{0}}(j\omega )={{V} _{i}}(j\omega)\frac{1/j\omega C}{R+1/j\omega C}={{V}_{i}}(j\omega)\frac{1} {1+j\omega RC}\begin{matrix}{} & (2) \\\end{matrix}\]
Таким образом, частотная характеристика фильтра RC равна
\[\frac{{ {V}_{0}}}{{{V}_{i}}}(j\omega )=\frac{1}{1+j\omega CR}\begin{matrix}{} & (3) \\\конец{матрица}\]
Непосредственное наблюдение при изучении этой частотной характеристики заключается в том, что если частота сигнала ω равна нулю, значение функции частотной характеристики равно 1.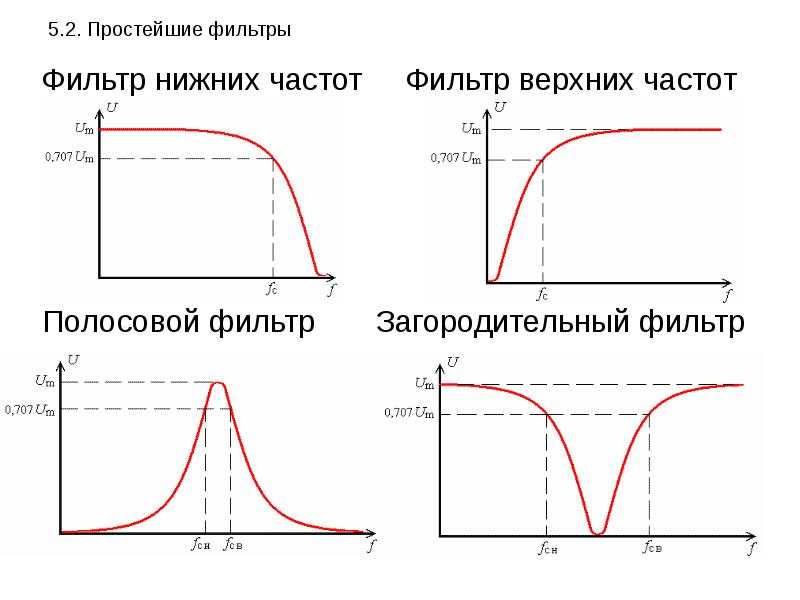 {-j \arctan (\omega CR)}} & {} & {} \\\end{matrix}\] 9{2}}}}\begin{matrix}{} & (7) \\\end{matrix}\]
{-j \arctan (\omega CR)}} & {} & {} \\\end{matrix}\] 9{2}}}}\begin{matrix}{} & (7) \\\end{matrix}\]
И
\[\угол H (j\omega )=-\arctan (\omega CR) =-\arctan \frac{\omega}{{{\omega}_{0}}}\begin{matrix}{} & (8) \\\end{matrix}\]
С
\[{ {\omega }_{0}}=\frac{1}{RC}\begin{matrix}{} & (9) \\\end{matrix}\]
Самый простой способ представить эффект фильтра состоит в том, чтобы думать о векторном напряжении, масштабированном с коэффициентом | Н | и сдвигается на фазовый угол ∠ H фильтром на каждой частоте, так что результирующий выходной сигнал определяется вектором с
\[\begin{matrix}{{V}_{0}}=\left| H \right|.{{V}_{i}} & {} & {} \\{} & {} & (10) \\{{\phi }_{0}}=\угол H +{{ \phi }_{i}} & {} & {} \\\end{matrix}\]
и где | Н | и ∠ H являются функциями частоты. Частота ω 0 называется частотой среза фильтра и, как будет показано ниже, дает представление о характеристиках фильтрации схемы.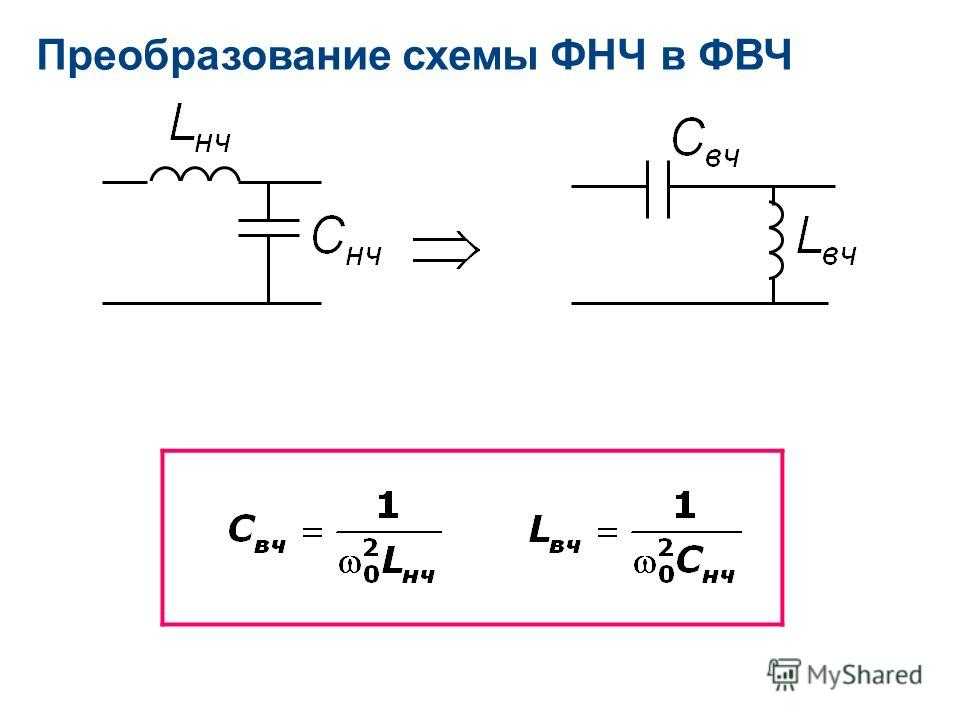
Принято представлять H ( jω ) на двух отдельных участках, представляющих | Н | и ∠ H как функции ω . Они показаны на Рис. 2 в нормализованной форме, то есть с | Н | и ∠ H в зависимости от ω/ω o , что соответствует частоте среза ω 0 = 1 рад/с.
Обратите внимание, что на графике ось частот масштабирована логарифмически. Это обычная практика в электротехнике, поскольку она позволяет просматривать очень широкий диапазон частот на одном и том же графике без чрезмерного сжатия низкочастотного конца графика.
Графики частотной характеристики Рис. 2 обычно используются для описания частотной характеристики цепи, поскольку они могут с первого взгляда дать четкое представление о влиянии фильтра на сигнал возбуждения. Частота среза ω = 1/ RC имеет особое значение, поскольку она примерно представляет собой точку, в которой фильтр начинает отфильтровывать высокочастотные сигналы.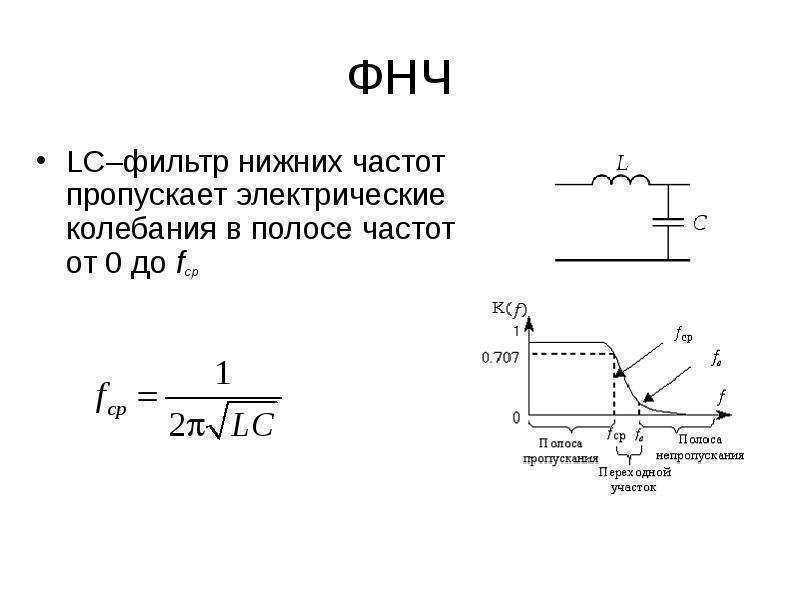 {1}/{}_{\sqrt{2}}=0,707$ . Обратите внимание, что частота среза зависит исключительно от значений R и C . Таким образом, можно настроить отклик фильтра по желанию, просто выбрав соответствующие значения для C и R , и, следовательно, можно выбрать желаемые характеристики фильтрации.
{1}/{}_{\sqrt{2}}=0,707$ . Обратите внимание, что частота среза зависит исключительно от значений R и C . Таким образом, можно настроить отклик фильтра по желанию, просто выбрав соответствующие значения для C и R , и, следовательно, можно выбрать желаемые характеристики фильтрации.
Рис. 2 Частотная характеристика RC-фильтра нижних частот
Частотная характеристика фильтра верхних частотТочно так же, как фильтр нижних частот сохраняет низкочастотные сигналы и ослабляет более высокие частоты, a 9Фильтр верхних частот 0005
ослабляет низкочастотные сигналы и сохраняет сигналы на частотах выше частоты среза. Рассмотрим схему фильтра верхних частот, показанную на рис. 3 .Рис. 3 RC Фильтр верхних частот
Частотная характеристика определяется как: }_{i}}}(j\omega )\]
Деление напряжения дает:
\[{{V}_{0}}(j\omega )={{V}_{i}}(j \omega)\frac{R}{R+1/j\omega C}={{V}_{i}}(j\omega)\frac{j\omega CR}{1+j\omega CR}\ begin{matrix}{} & (11) \\\end{matrix}\] 9{o}}-\arctan (\omega CR) & {} & {} \\\end{matrix}\]
Вы можете проверить, проверив, что амплитудная характеристика фильтра верхних частот будет равна нулю при ω = 0 и будет асимптотически приближаться к 1 по мере того, как ω приближается к бесконечности, в то время как фазовый сдвиг составляет π /2 при ω = 0 и стремится к нулю при увеличении ω.


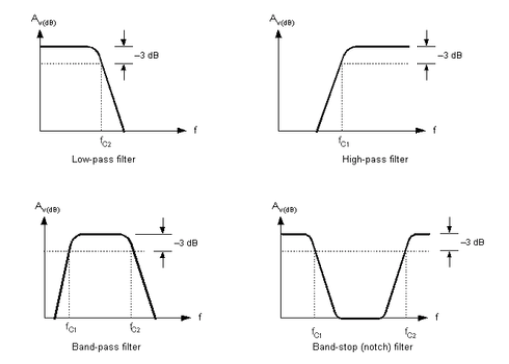
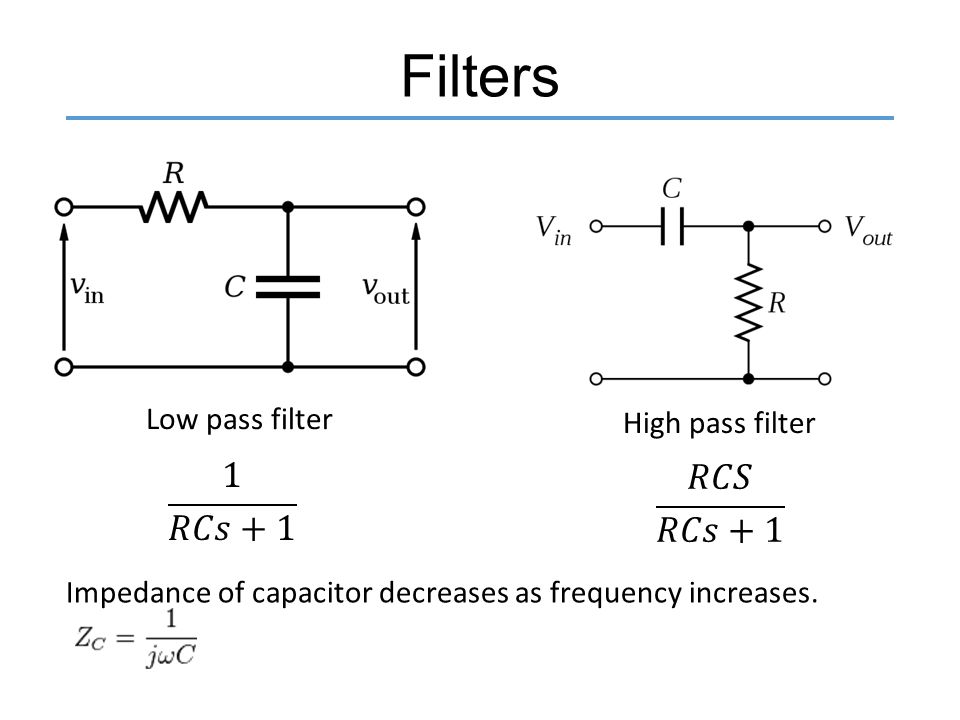
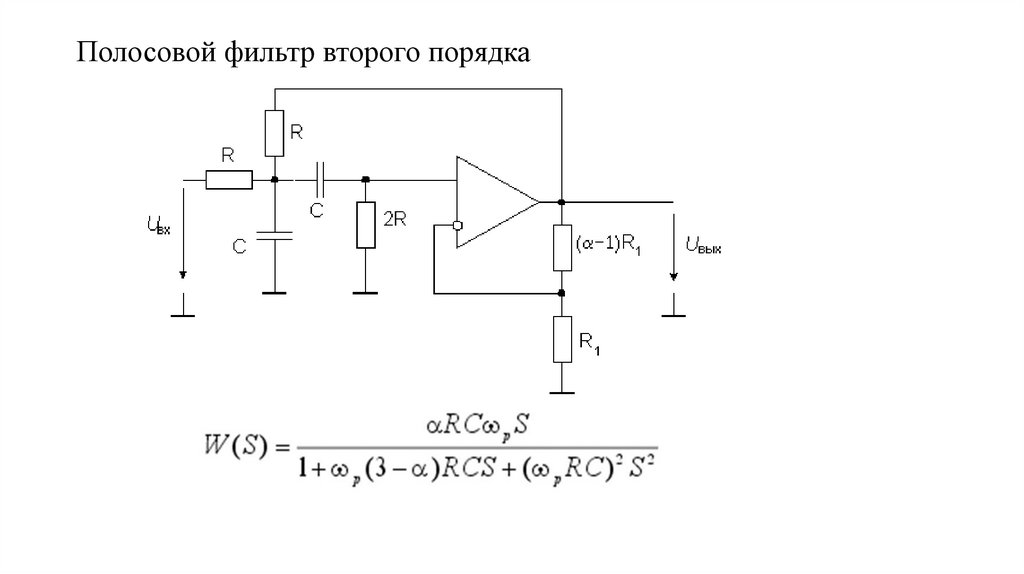 1 Вопрос
1 Вопрос 3690
3690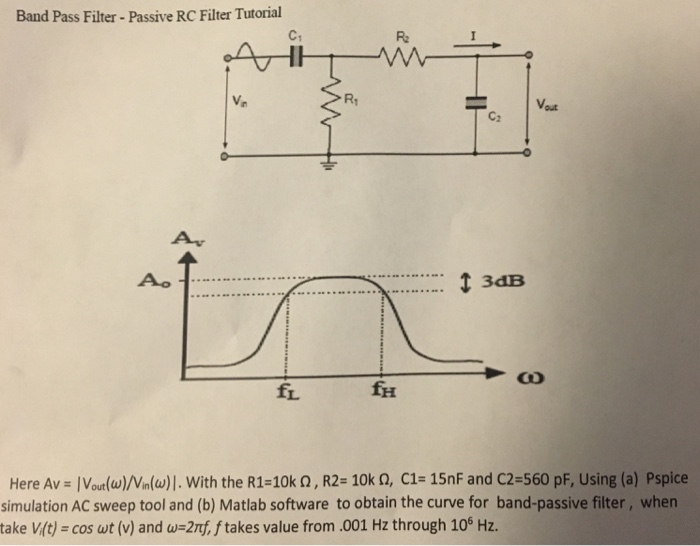 Один должен быть BNC-BNC, а два других — это кабели BNC с разъемами типа «банан».
Один должен быть BNC-BNC, а два других — это кабели BNC с разъемами типа «банан».