Сложение и вычитание векторов
Материал урока.
Вспомним, как мы вводили понятие суммы двух векторов в планиметрии.
Сначала мы рассматривали такой пример.
Под действием воздушных масс воздушный шар сначала двигался из точки А в точку B, а затем из точки B переместился в точку C.
Каждое из этих двух перемещений можно представить в виде вектора. и .
Но можно ведь сказать, что в результате воздушный шар из точки А попал в точку C. И это перемещение задает вектор .
Так как перемещение из точки А в C складывается из перемещений из точки А в B и из B в C, то можно записать, что вектор .
Этот пример подводит нас к понятию суммы двух векторов.
Рассмотрим два ненулевых вектора: и .
Отметим произвольную точку А и отложим от неё вектор , равный вектору . Далее от точки B отложим вектор , равный вектору .
Можем
изобразить вектор ,
который называется суммой векторов и
.
Данное правило сложения векторов в пространстве, так же, как и в планиметрии, будем называть правилом треугольника.
Нужно отметить, что сумма векторов и не зависит от выбора точки А, от которой будет отложен вектор .
Докажем это.
Найдём сумму векторов и , но начнём откладывать их от некоторой точки А1.
Нам необходимо доказать, что полученный вектор равен вектору .
Из
построений очевидно, что векторы и
равны.
А значит, они сонаправлены и равны по длине. То есть стороны AB
и A
Стороны AA1 и BB1 данного параллелограмма также равны и параллельны. Тогда получаем, равны векторы и .
Аналогично,
из равенства векторов и
следует,
что четырёхугольник BCC1B1
также является параллелограммом.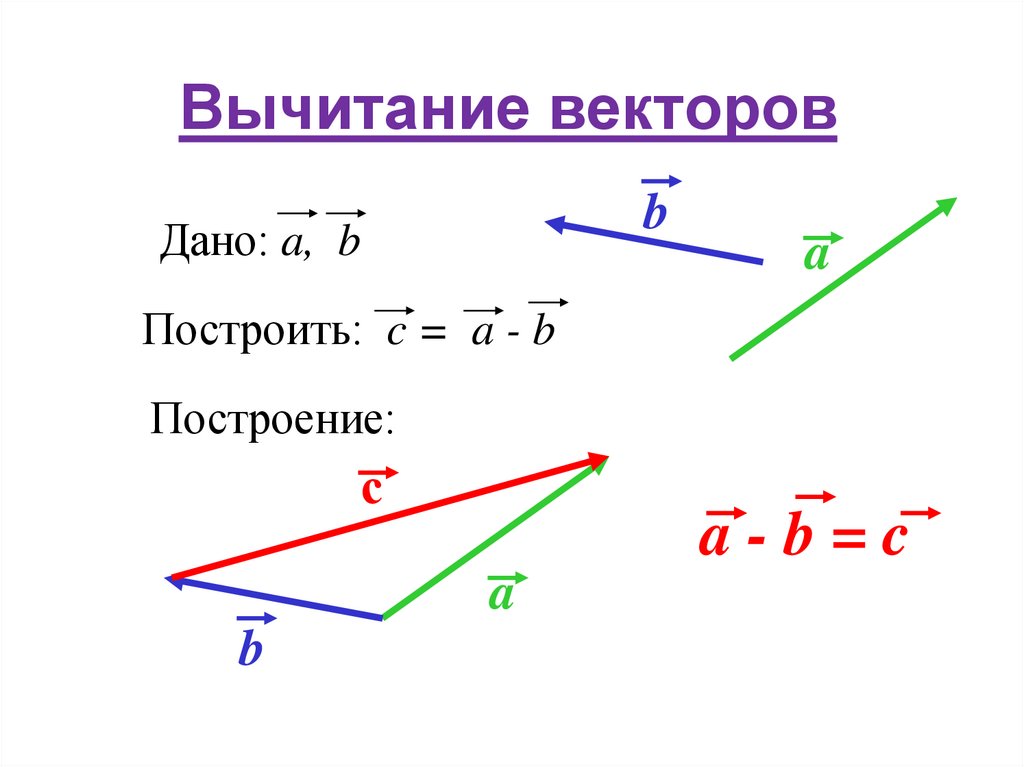 А значит, равны векторы и
.
А значит, равны векторы и
.
Из полученных равенств получаем, что равны векторы и .
Поэтому четырёхугольник AA1C1C — параллелограмм. Его стороны AC и A1C1 параллельны и равны. А значит, равны векторы и .
Что и требовалось доказать.
Итак, в точности так же, как и на плоскости, мы ввели правило треугольника сложения двух векторов в пространстве. И доказали, что сумма векторов и не зависит от выбора точки А, от которой будет отложен вектор .
Для любых трёх точек пространства А, B и C правило треугольника можно сформулировать так: сумма векторов и равна вектору
То
есть даже не строя вектор суммы можно его найти. Если конец вектора,
являющегося первым слагаемым, совпадаем с началом вектора, являющегося вторым
слагаемым, то началом вектора суммы является начало первого вектора, а концом —
конец второго вектора.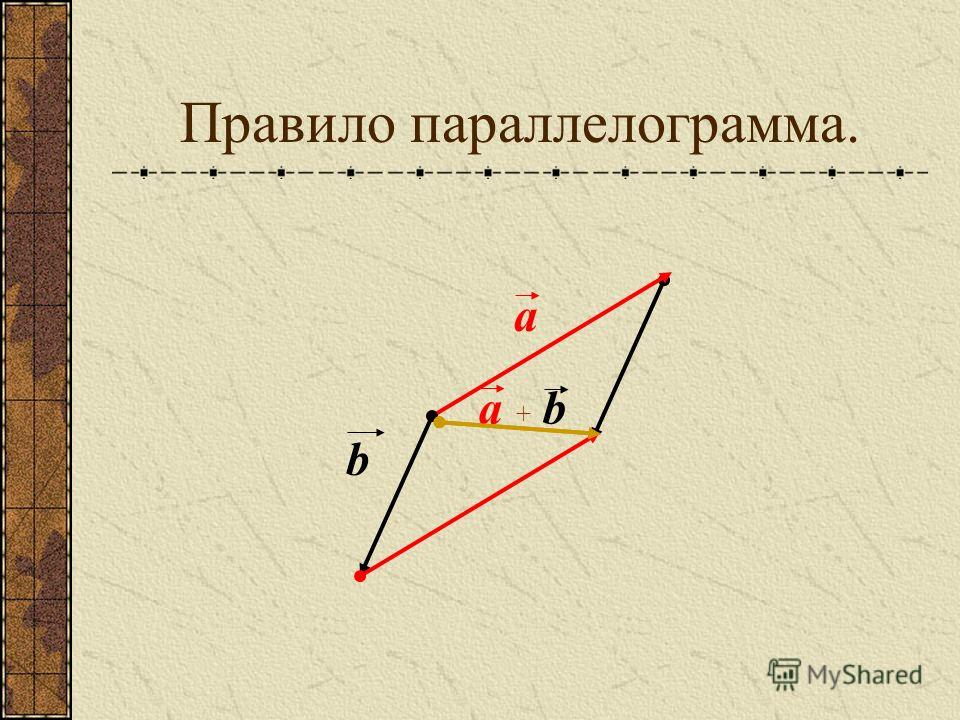
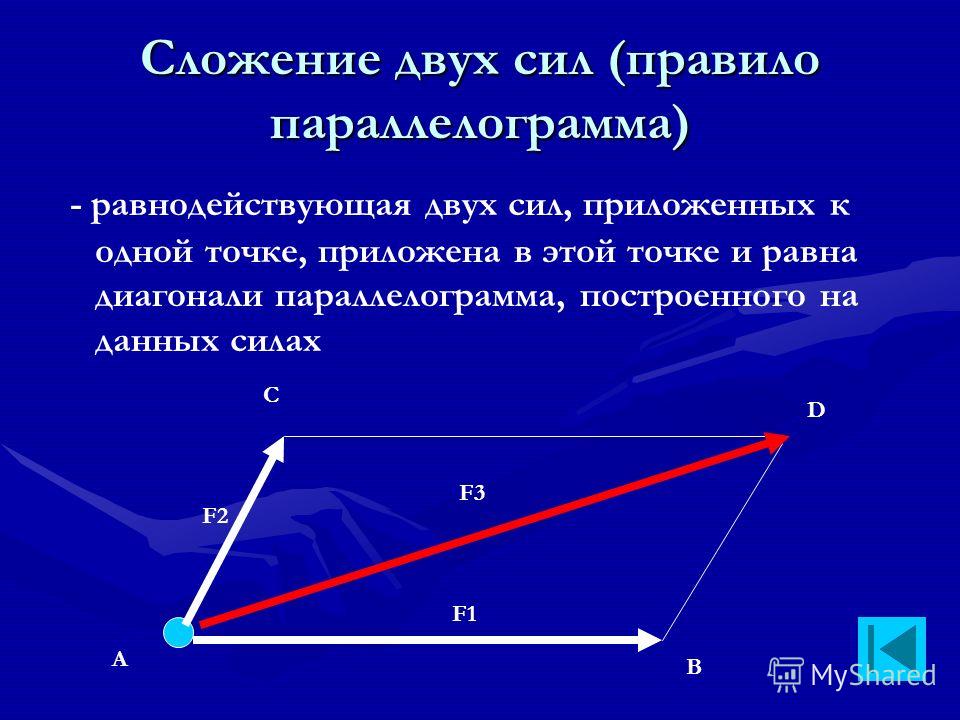
Так же для сложения двух векторов можно применять правило параллелограмма, которое мы уже формулировали в планиметрии. Вспомним его. От произвольной точки А отложим векторы и , равные векторам и соответственно.
Теперь на этих векторах построим параллелограмм ABCD. Вектор является вектором суммы векторов и .
Для любых векторов , и действуют переместительный и сочетательный законы сложения векторов.
Эти законы мы уже записывали и доказывали для векторов на плоскости.
Выполним задание.
На экране изображён параллелепипед ABCDA1B1C1D1.
Требуется назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей сумме векторов.
Первой рассмотрим сумму векторов и
Чтобы
сложить векторы по правилу треугольника, они должны быть отложены друг за
другом, а чтобы воспользоваться правилом параллелограмма, они должны быть
отложены от одной точки.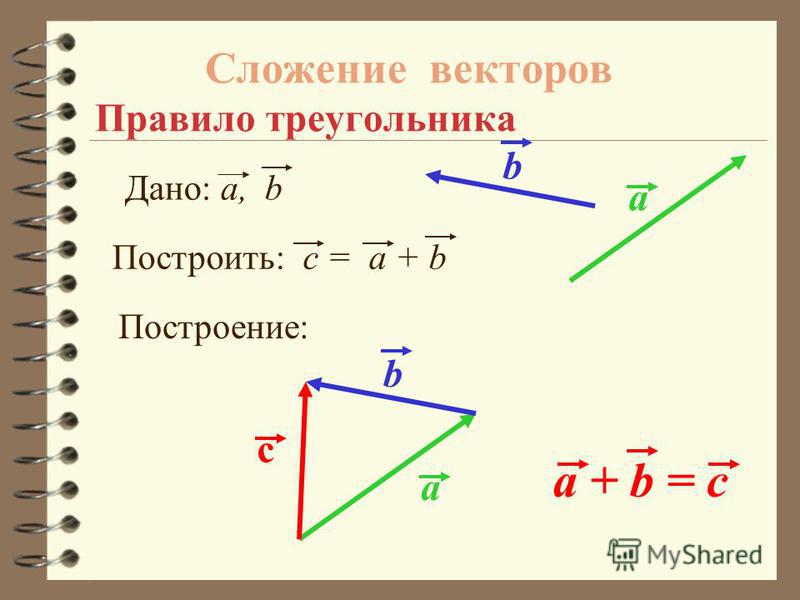
Данные векторы не подходят ни к одному правилу.
Но здесь нам поможет знание о том, что от любой точки пространства можно отложить вектор равный данному, и притом только один.
Так как перед нами параллелепипед и все его грани являются параллелограммами, то можно сказать, что есть вектор, который отложен от точки А и равен вектору Напомним, что равными называются сонаправленные векторы, длины которых равны.
Вектор Ведь эти векторы лежат на противоположных сторонах параллелограмма, которые равны и параллельны.
От данной нам суммы перейдём к сумме векторов и . Они отложены от одной точки, поэтому воспользуемся правилом параллелограмма. Если построить параллелограмм на этих векторах, то мы получим грань ABCD.
Диагональ AC и будет вектором суммы данных векторов.
Следующей рассмотрим сумму векторов и .
Они
уже отложены от одной точки, и на этих векторах можно построить параллелограмм ABC1D1. Диагональ AC1
и будет являться вектором суммы.
Диагональ AC1
и будет являться вектором суммы.
Далее рассмотрим сумму векторов и .
Вектор равен вектору . И перейдя к сумме векторов и , не трудно заметить, что они отложены друг за другом, и именно поэтому можно применить правило треугольника. Вектор — искомый.
Обратите внимание, пользуясь переместительным законом, можно записать, что сумма векторов и , равна сумме векторов , и . Тогда по правилу треугольника сложения векторов для трёх произвольных точек пространства, можно сразу записать вектор суммы — . Так мы получили тот же вектор.
Теперь рассмотрим сумму векторов и . Вектор равен вектору . Векторы полученной суммы отложены друг за другом, поэтому вектором их суммы будет вектор .
Последней
рассмотрим сумму векторов и
.
Видим, что конец первого вектора в сумме совпадает с началом второго вектора.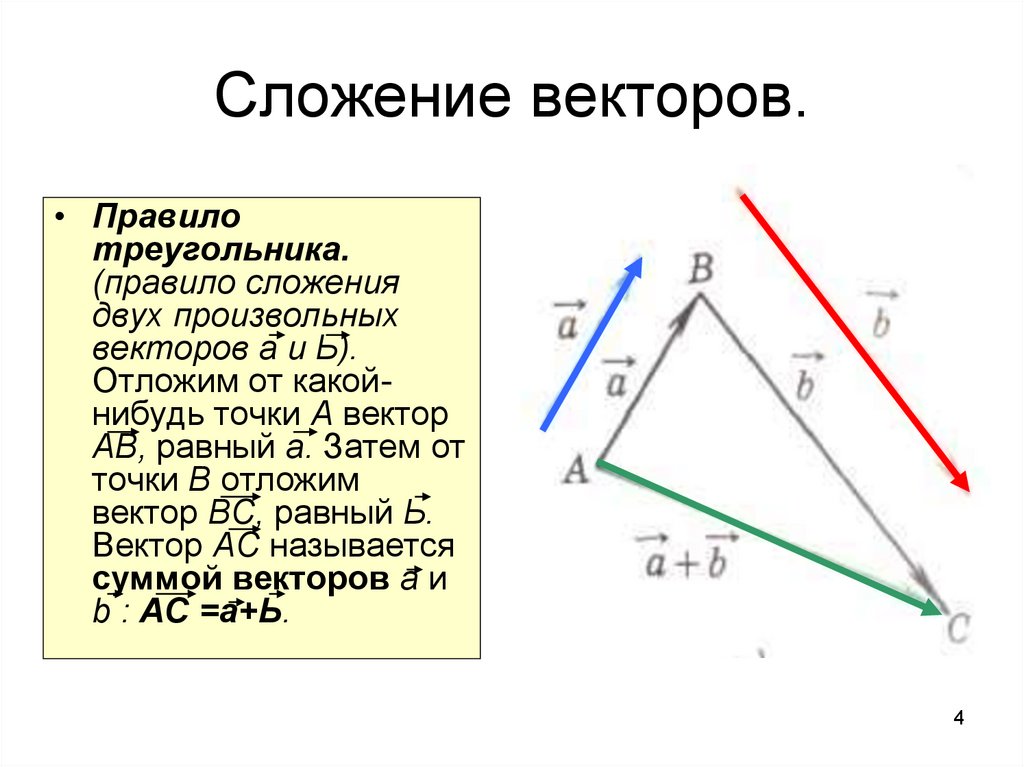 Тогда можно сразу сказать, что вектором суммы является вектор .
Этот же результат мы получим, пользуясь рисунком.
Тогда можно сразу сказать, что вектором суммы является вектор .
Этот же результат мы получим, пользуясь рисунком.
Далее поговорим о разности векторов и . Это такой вектор, сумма которого с вектором равна вектору .
Проиллюстрируем это определение для данных векторов и .
Итак, вектор должен являться суммой векторов и . Тогда, отложив вектор от начала вектора , мы без труда проведём вектор из конца вектора к концу вектора .
Действительно, плюс равно . А значит, вектор равен разности векторов и .
Таким образом, можно откладывать векторы уменьшаемое и вычитаемое от одной точки, а вектором разности будет являться вектор, направленный из конца вектора вычитаемого к концу вектора уменьшаемого.
Вы помните, что векторы называются противоположными, если их длины равны, а направления противоположны
Так
вот если в данной иллюстрации у вектора сменить
направление, то есть заменить его на «»,
то мы получим, что вектор равен
разности векторов и
,
а также, по правилу треугольника, сумме векторов и
«».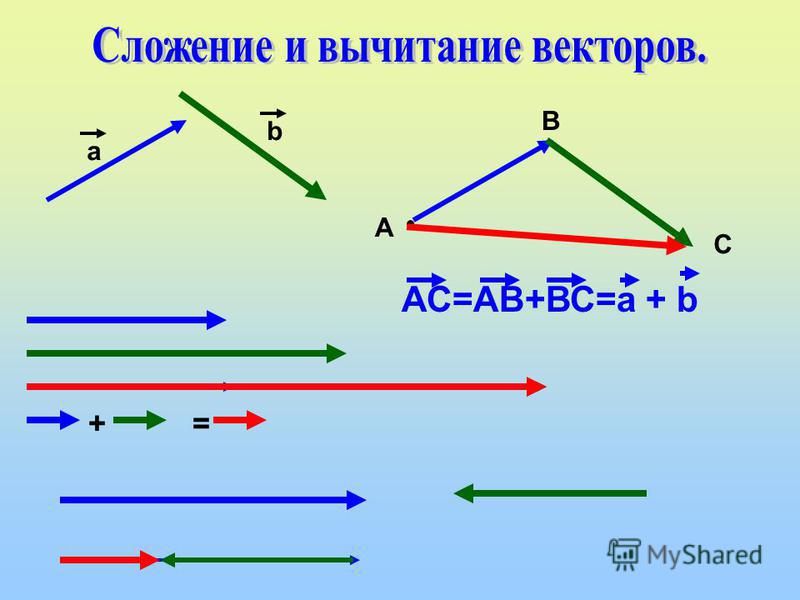
Так мы получили два способа построения вектора разности.
Рассмотрим тот же параллелепипед, что и в предыдущей задаче.
Нужно назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей разности векторов.
Найдём вектор разности векторов и .
Они отложены от одной точки, поэтому вектором разности будет являться вектор, направленный из конца вектора-вычитаемого к концу вектора-уменьшаемого . Так получаем вектор .
Применим второй способ построения вектора разности.
Нам известно, что разность векторов можно представить в виде суммы вектора уменьшаемого и вектора, противоположного вектору вычитаемому. Вектором противоположным вектору является вектор . По правилу треугольника сложения двух векторов мы также получим вектор .
Далее рассмотрим разность векторов и .
Они
отложены от одной точки. и поэтому вектор разности будет направлен из конца
вектора-вычитаемого к
концу вектора-уменьшаемого .
Таким образом мы получим вектор .
и поэтому вектор разности будет направлен из конца
вектора-вычитаемого к
концу вектора-уменьшаемого .
Таким образом мы получим вектор .
Последней рассмотрим разность векторов и . Вектор заменим равным ему вектором . А разностью векторов и будет вектор . В результате и разность векторов и равна вектору .
Подведём итоги нашего урока.
В точности так же, как и на плоскости, на этом уроке мы с вами сформулировали правило треугольника и правило параллелограмма сложения двух векторов в пространстве, а также записали переместительный и сочетательный законы сложения векторов.
Убедившись в том, что разность векторов и равна сумме вектора и вектора, противоположного вектору , мы получили два способа построения вектора разности двух векторов.
Так мы рассмотрели сложение и вычитание векторов в пространстве.
Как производят сложение и вычитание вектора?.
 .. -reshimne.ru
.. -reshimne.ruНовые вопросы
Ответы
Сумма двух векторов.
Дан вектор а и вектор b. Еслиот произвольной точки А отложить вектор АВ, равный вектору а, затем отточки В отложим вектор ВС, равный вектору b. Полученный вектор АС — этосумма векторов а и b. Это правило сложения векторов называется правиломтреугольника.
Сумма векторов обозначается вектор а + вектор b.
Для любого вектора а справедливо равенство вектор а + нулевой вектор=вектор а.
Правило треугольника можно сформулировать и по другому, если А, В, С — произвольные точки, то вектор АВ + вектор ВС = вектор АС.
Законы сложения векторов. Правило параллелограмма.
Для любых векторов а, b и с справедливы равенства:
1. вектор а + вектор b = вектор b + вектор а (переместительный закон)
2. (вектор а + вектор b)+вектор с = вектор а + (вектор b+ вектор с) (сочетательный закон).
Правилопараллелограмма: чтобы сложить неколлинеарные векторы а и b, нужноотложить от какой — нибудь точки А вектор АВ=вектору а и векторAD=вектору b и построить параллелограмм.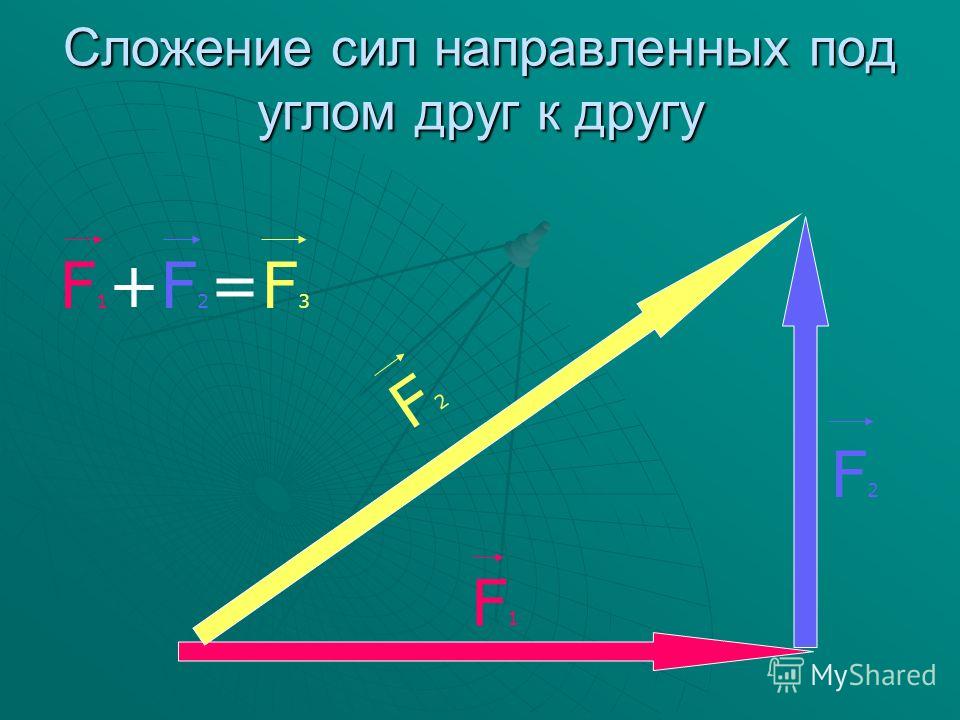 Тогда вектор АС = вектор а +вектор b.
Тогда вектор АС = вектор а +вектор b.
Сумма нескольких векторов.
Сложениенескольких векторов производится следующим образом: первый векторскладывается со вторым, затем их сумма складывается с третьим вектором ит. д. Сумма нескольких векторов не зависит от того, в каком порядке онискладываются.
Правило многоугольника: если А1,А2,…,Аn -произвольные точки плоскости, то вектор А1А2+векторА2А3+…+векторАn-1An=вектор А1Аn
Вычитание векторов.
разностьювекторов а и b называется такой вектор, сумма которого с вектором bравна вектору а. Таким образом, вектор а — вектор b = вектор а + вектор(-b).
Вектор -b — противоположный вектор, вектору b. Противоположныевектора — это вектора, которые имеют равные длины, но противоположнонаправленные.
Обозначается разность: вектор а — вектор b.
Похожие вопросы
Помогите решить!Скорость тела при вылите из пружинного пистолета 1,2 м/с за секунду,масса тела 200 гр,опр жесткость пружины,если ее сжатие 30 мм. ..
..
Физика 7 приведите примеры тел обладающих одновременно и потенциальной и кинетической энергией…
Заn time закон Гей-Люссака. Какой процесс он описывает?…
Помогите с 4 задачей!)) Очень нужно, срочно!!! 15 баллов Срочно ооооооочень!!!!!!!…
Помогите пожалуйста, буду очень благодарен……
Чему равна сила тяжести действующая на слона массой 2 т…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Что такое вектор, как найти длину? Координаты? Формулы
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Виды векторов
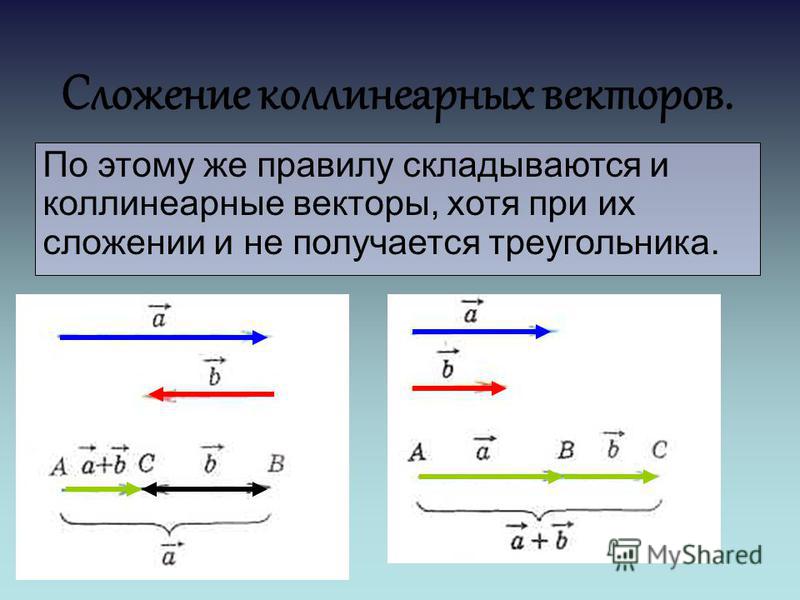
Во-первых, векторы бывают коллинеарными и неколлинеарными.
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке и и являются коллинеарными, а и относительно друг друга — нет.
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так:
Если же они противоположно направлены, мы можем записать это следующим образом:
Сонаправленные векторы обозначаются так:
Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).
Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.

Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.
Сложение: метод треугольника
Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
Отложить начало одного вектора от конца другого.
Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
Сложить векторы можно и по-другому, используя метод параллелограмма:
Совместим между собой концы и
Отложим от конца вектор, равный
Отложим от конца вектор, равный
Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).

Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Задача решена, вы великолепны!
Обратите внимание
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их концы, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:
Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание.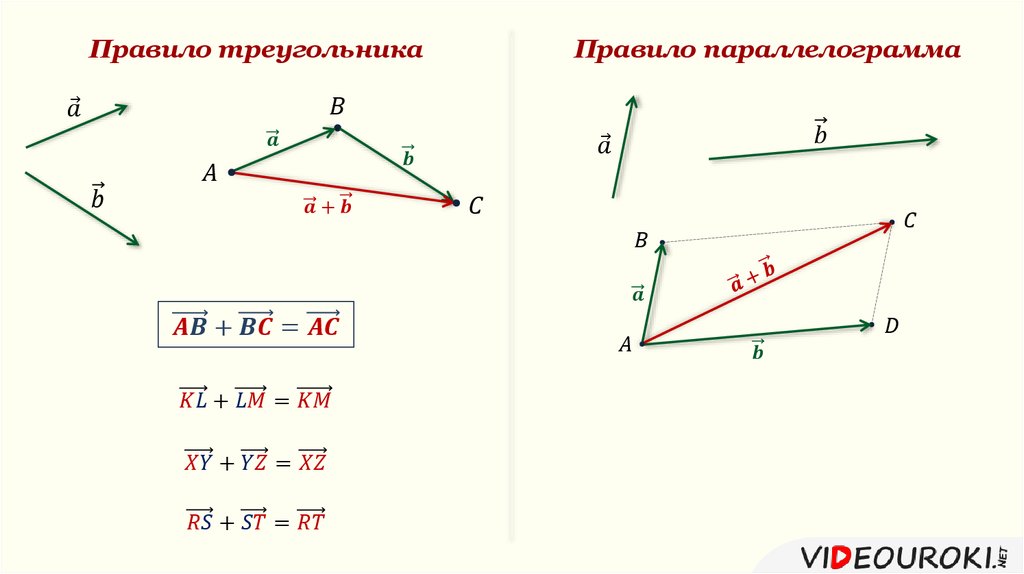 Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:
Отложим один вектор от начала другого.
Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.
Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно пользоваться как на плоскости с осями X и Y, так и в пространстве с осями X, Y, Z.
Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает
одна простая задача: умножение вектора на число.
За все эти действия отвечает
одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.
Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.
Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:
Длину вектора можно найти разными способами, вот основные:
через координаты вектора;
через координаты точек начала и конца вектора;
через теорему косинусов.

Давайте вместе разберём все методы!
Длина вектора через его координаты
Если задан через координаты то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как
Рассчитаем длину через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль , если его координаты
Решение:
Модуль вектора — это его длина, а значит,
Задача 2
Длина Чему равна координата по оси , если координата по оси
Решение:
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.
Рассмотрим где и Тогда координаты вектора можно выразить так:
Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:
Задача 3
Найдите длину если и
Решение:
Задача 4
Рассчитайте координату по точки вектора , если его длина равна а
Решение:
Остановимся здесь и подставим известные числа в формулу:
или
Длина вектора через теорему косинуса
К сожалению, в задачах не всегда даны координаты точек вектора или его самого.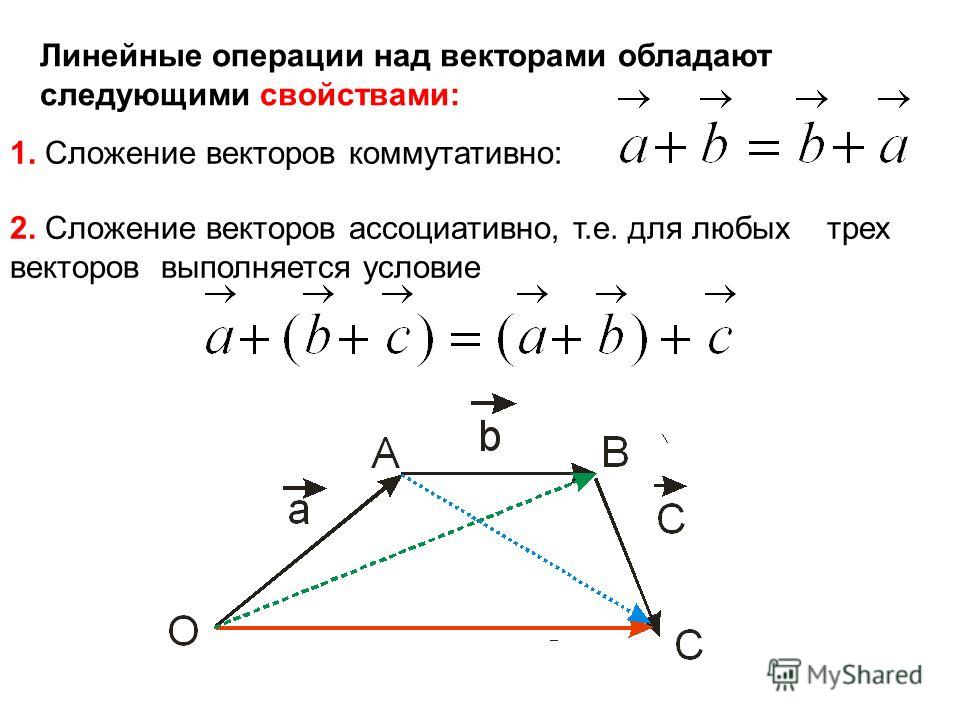 В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.
В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:
Тогда, чтобы найти длину , необходимо знать (или иметь возможность вычислить) длины и , знать угол между ними, а также уметь рассчитать произведение длин этих векторов.
Задача 5
Длины и равны 4 и 6 соответственно, а угол между ними равен Вычислите длину
Решение:
Задача 6
Рассчитайте модуль вектора в треугольнике, если длина = 8, длина = 10, а угол между ними равен
Решение:
Скалярное произведение векторов
Мы практически дошли до финала нашего путешествия по царству векторов. 👑 Нам осталось изучить только скалярное
произведение векторов. Что это?
👑 Нам осталось изучить только скалярное
произведение векторов. Что это?
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Скалярным произведением и будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные (имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.
Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:
Скалярное произведение вектора на само себя равно квадрату его модуля: В данном случае значение скалярного произведения является наибольшим из возможных.

Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как
Если угол между векторами прямой, то скалярное произведение равно 0, так как
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как
Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их длин . В данном случае значение скалярного произведения является наименьшим из возможных.
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные
вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное
произведение — просто, особенно если рассмотреть его через координаты.
Если выражен координатами а то скалярное произведение этих векторов описывается формулой: В пространстве скалярное произведение через координаты векторов будет задаваться так:
Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой раз. 🙂
Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.
Интегрированный урок по физике и математике «Векторы».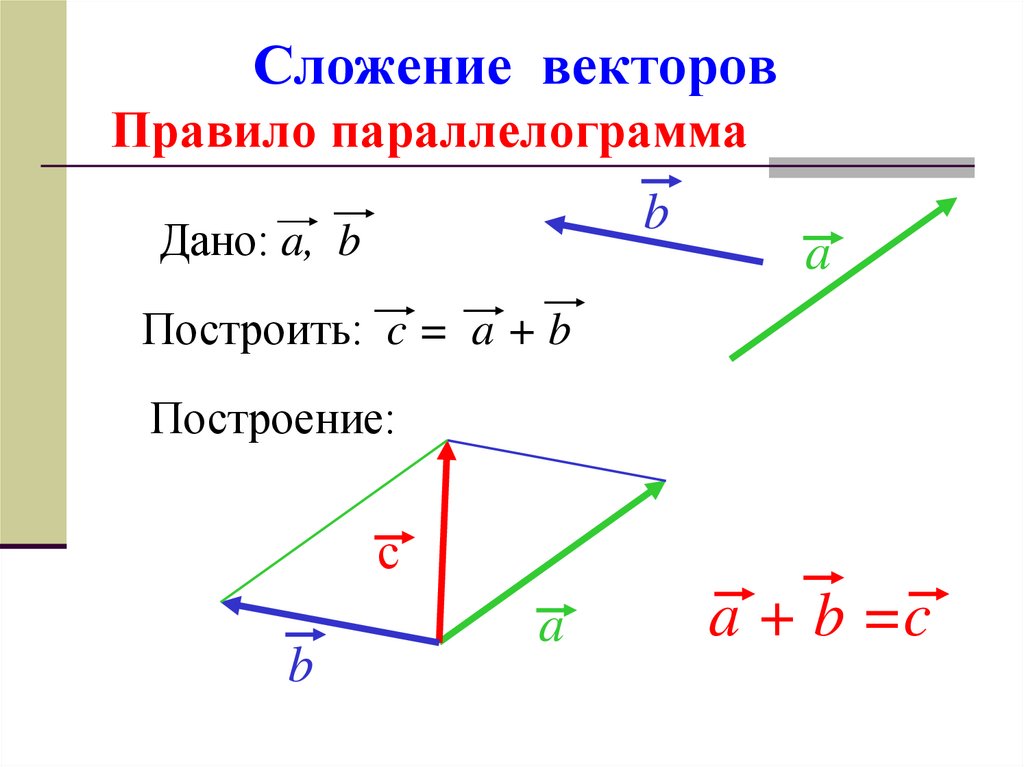 9 класс Повторение и закрепление основных понятий в математике и физике, связанных с векторами. Повторить и закрепить основные понятия, связанные с векторами, закрепить умение решать задачи, применяя теоретический материал геометрии и физики. Применение темы «Векторы» при решении задач практического содержания. Цель урока:
Задачи урока:
Ученик должен знать:
Ученик должен уметь:
Тип урока: Личностно-ориентированная, информационно-коммуникативная. КЭС: векторы, сумма, разность, умножение вектора на число, координаты вектора, скалярное произведение двух векторов, вычисление значений угла между векторами, радиус-вектор, практическая значимость понятия «вектор».
Сценарий урока: 1. Подготовка к восприятию материала: Вступительное слово учителя математики: «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.Лобачевский -Мы изучаем векторы. А где это применяется? Векторная история это пограничная история, между математикой и физикой. Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию «направление», смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. Прежде, чем говорить об использовании векторов при решении физических задач, вспомним действия, которые можно выполнять с векторами. (Задавая вопросы, учитель может использовать игровой компонент: бросая мячик, формулировать вопрос, принимая его, получать ответ). — Какие способы сложения векторов вам известны? (Правило треугольника и правило параллелограмма) — В чем принципиальное отличие этих правил? ( При сложении по правилу треугольника начало второго вектора совмещается с концом первого (слайд 2), а при сложении по правилу параллелограмма начала обоих векторов совпадают (слайд 3).) — Что будет вектором суммы при сложении векторов по правилу треугольника? (Вектор, берущий начало в начале первого и заканчивающийся в конце второго вектора.) — Что будет вектором суммы при сложении векторов по правилу параллелограмма? (Вектор, являющийся диагональю параллелограмма, построенного на исходных векторах, исходящий из общего начала слагаемых векторов.) — Что будет вектором разности двух векторов? (Вектор, соединяющий концы векторов и идущий в направлении уменьшаемого (слайд 4)). — А если нужно выполнить действие с векторами, которые не выходят из одной точки? (Один из векторов параллельным переносом перенести так, чтобы начала их совпали.) — Что происходит при умножении вектора на положительное число? (Длина вектора изменяется во столько раз, на какое число выполняется умножение, а направление не изменяется). — А если выполняем умножение на отрицательное число? (Направление меняется на противоположное (слайд 5)). — Как называются получившиеся векторы? (Коллинеарные (сонаправленные и противоположно направленные)). Задача 1. Построить вектор , равный сумме трех заданных векторов (слайд 6). Решение (слайд 7): Задача 2. Построить вектор . (слайд 8). Решение (слайд 9). Задача 3 (слайд 10). Решение (слайд 11). Задача 4 (слайд 12). Решение (слайд 13). — Как найти координаты вектора, зная координаты его начала и его конца (слайд 14)? (Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала вектора (слайд 15)). — Как найти длину вектора, зная координаты его начала и его конца (слайд 16)? ( Длина вектора равна корню из суммы квадратов разностей соответствующих координат начала и конца вектора) . Задача 5(слайд 17). Решение (слайд 18). — Как найти координаты суммы двух векторов? (Найти сумму соответствующих координат (слайд 19)). — Как найти координаты разности двух векторов? (Найти разность соответствующих координат (слайд 20)). — Что называют «скаляром»? (Скаляр – это физический термин, обозначающий число). -Почему умножение векторов называется скалярным? (Потому что в результате умножения двух векторов получается число). — А что получается при умножении вектора на число (скаляр)? (Вектор). — Как найти в этой ситуации координаты нового вектора? (Координаты исходного вектора умножить на скаляр (слайд 21)). — Модуль вектора – это скаляр или вектор? (Скаляр, так как модуль – это длина вектора). — Чему равен модуль вектора? (Корню из квадрата этого вектора (слайд 22)). — Как найти модуль вектора, если нам известны его координаты? (Извлечь корень из суммы квадратов координат этого вектора (слайд 23)). — Как найти скалярное произведение векторов, зная их координаты? (Сложить произведения соответствующих координат этих векторов (слайд 24)). — Как найти скалярное произведение векторов другим способом? (Умножить произведение длин этих векторов на косинус угла между ними (слайд 25)). В физике дается определение радиус-вектора. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Если противоречие между двумя определениями, сформулированными в математике и физике? (В любом случае, сделать акцент на идею направления в обоих определениях) Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например: скорость, перемещение, импульс, напряженность электрического поля, сила и др. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов мы будем использовать с вами на уроках физики неоднократно, изучая разные темы. Сейчас мы рассматриваем задачи по теме «Относительность механического движения, законы сложения скоростей и перемещений». Данные задачи обязательно встретятся вам на ГИА в этом году и при сдаче ЕГЭ по физике в 11 классе. Рассмотрим сегодня на уроке задачи практического содержания по этой теме. Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2км? Работа над задачей.
Задача 2. Штурман пытается провести судно в тумане через узкий проход между рифами. Представьте себе, что проход между рифами идет в северном направлении, Скорость океанского течения равна 5м/с, направлено оно на восток, а скорость, сообщаемая винтом судну 9 м/с. Идет аналогичная работа над задачей. (Слайды 30 – 32) Задача 3. Скорость лодки 4 м/с, скорость течения 2 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж. (Слайды 33 – 35) В конце урока предлагается тест по материалам урока. Вопросы теста по карточкам, которые выдают каждому обучающемуся. Тест на тему «Векторы» ученика 9 класса гимназии №1799 «Экополис» _______________________________________________.
3. Лодка должна попасть на противоположный берег реки кратчайшим путем в системе отсчета, связанной с берегом. 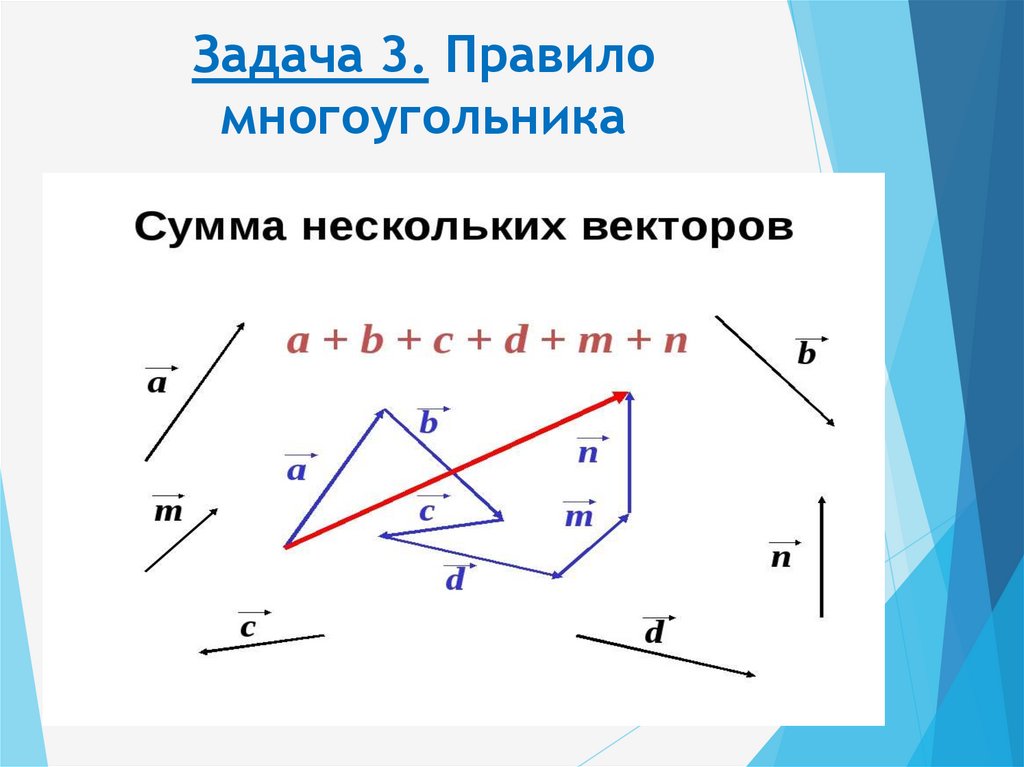 Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен1) 2) 3) 4) Ответ: 4 4. Два автомобиля движутся по прямой дороге: один — со скоростью (–10 м/с), другой – со скоростью (–25 м/с). Скорость второго автомобиля относительно первого равна 1) –35 м/с 2) –15 м/с 3) –20 м/с 4) 35 м/с Ответ: 2 5. Пилот поднялся на воздушном шаре на высоту 800м, за это время шар был отнесен ветром в горизонтальном направлении на 600м. Найдите перемещение шара относительно земли? 1) 1400м 2)200м 3)1000м 4) 800м Ответ: 3 Заключительная часть урока. Подводится итог. Выставляются оценки за урок. Идет обобщение материала. Домашнее задание. 1. Лодка с туристами потерпела крушение в 40 м от берега, налетев на пороги. Туристы поплыли к берегу со скоростью 2 м/с, относительно воды перпендикулярно линии берега, но быстрое течение со скоростью 10 м/с сносило их в сторону. 2. Вертолет летел на юг со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует восточный ветер со скоростью 10 м/с? 3. Задачник Степановой Г.Н. №№ 61, 60,59. Интегрированные уроки имеют огромное значение для создания предметных, метапредметных и личностных компетенции обучающихся, являются мощным мотивом к интеллектуальному труду, способствуют более глубокому усвоению материала, расширению границ изученного материала, развитию творческих способностей учащихся, которые развиваются в рамках двух дисциплин, умению логично, научно и доступно излагать свои мысли, математически грамотно говорить. Литература:
|
Перемещение | 9 класс | Физика
Содержание
Решая задачи, связанные с движением тел, мы использовали такие величины, как скорость или средняя скорость, время движения и пройденный путь. Но дело в том, что знание пройденного телом пути не всегда дает нам возможность определить конечное положение тела в пространстве.
Поэтому в физике используется специальная векторная величина — перемещение. На данном уроке вы узнаете, чем перемещение отличается от пути и как его найти, если для этого требуется произвести сложение или вычитание нескольких перемещений.
Путь
Вспомним уже знакомые нам определения (рисунок 1).
Рисунок 1. Траектория и путьПуть — это длина траектории, по которой двигалось тело в течение определенного промежутка времени.
Траектория — это воображаемая линия в пространстве, по которой движется тело.
Мы обозначали путь буквами $s$ или иногда $l$. При этом путь всегда был для нас скалярной величиной. То есть эта величина не указывала нам никакое направление, а просто давала нам информацию численного характера — сколько метров прошло тело при его движении.
Зачем же теперь нам понадобилось вводить еще одну величину? Давайте рассмотрим на примере, почему знания пройденного телом пути может быть недостаточно для определения его положения в пространстве в какой-то определенный момент времени.
Итак, пусть нашим рассматриваемым телом (материальной точкой) будет автомобиль. Он выезжает из точки O. За $1 \space ч$ он проехал путь, равный $60 \space км$. И где же он теперь? На рисунке 2 показаны разные точки (A, B, C, D), где он может оказаться. Длины траекторий OA, OB, OC и OD равны между собой ($l = 60 \space км$).
Рисунок 2. Различные пути одинаковой длиныКак вы видите, мы не можем ответить на вопрос, где же находится автомобиль в конце своего движения.
{"questions":[{"content":"Путь — это[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["скалярная величина","векторная величина","величина, которая может быть как векторной, так и скалярной"],"answer":[0]}}}]}Перемещение
Чтобы избежать неопределенности, показанной выше, мы вводим новую физическую величину — перемещение.
Что называют перемещением тела (материальной точки)?
Перемещение — это вектор, соединяющий начальное положение тела с его последующим положением в пространстве.
Обратите внимание, что перемещение — это векторная величина. То есть она имеет некоторое направление.
Обозначается перемещение той же буквой, что и путь, но со стрелочкой — $\vec s$. В СИ модуль перемещения $|\vec s|$ измеряется в метрах ($м$).
Как тогда будет выглядеть векторы перемещений для автомобиля, который мы рассматривали ранее? Взгляните на рисунок 3.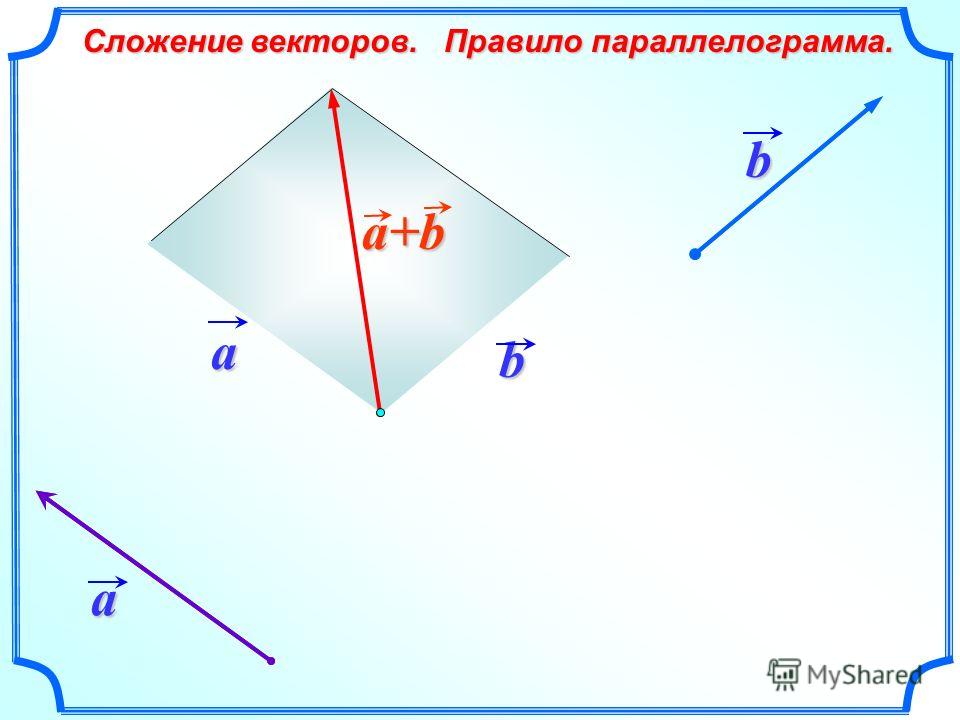
- Если бы автомобиль прямолинейно поехал на север — вектор был бы $\vec s_{OA}$;
- При прямолинейном движении на юго-восток — вектор $\vec s_{OC}$;
- По криволинейной траектории OD — вектор $\vec s_{OD}$;
- Движение до точки B и обратно в точку O (по кругу) — вектор перемещения $\vec s_{OB}$ будет равен нулю.
Зная начальное положение тела и вектор перемещения, мы можем однозначно определить, где это тело находится.
{"questions":[{"content":"Как обозначается перемещение материальной точки?[[choice-4]]","widgets":{"choice-4":{"type":"choice","options":["$\\vec s$","$s$","$\\vec l$","$l$","$|\\vec s|$"],"explanations":["","Так обозначается путь.","","Так обозначается длина или путь в некоторых случаях.","Так обозначается модуль перемещения."],"answer":[0]}}}]}Сложение путей
Рассмотрим, как мы можем найти суммарный путь, если он складывается из нескольких.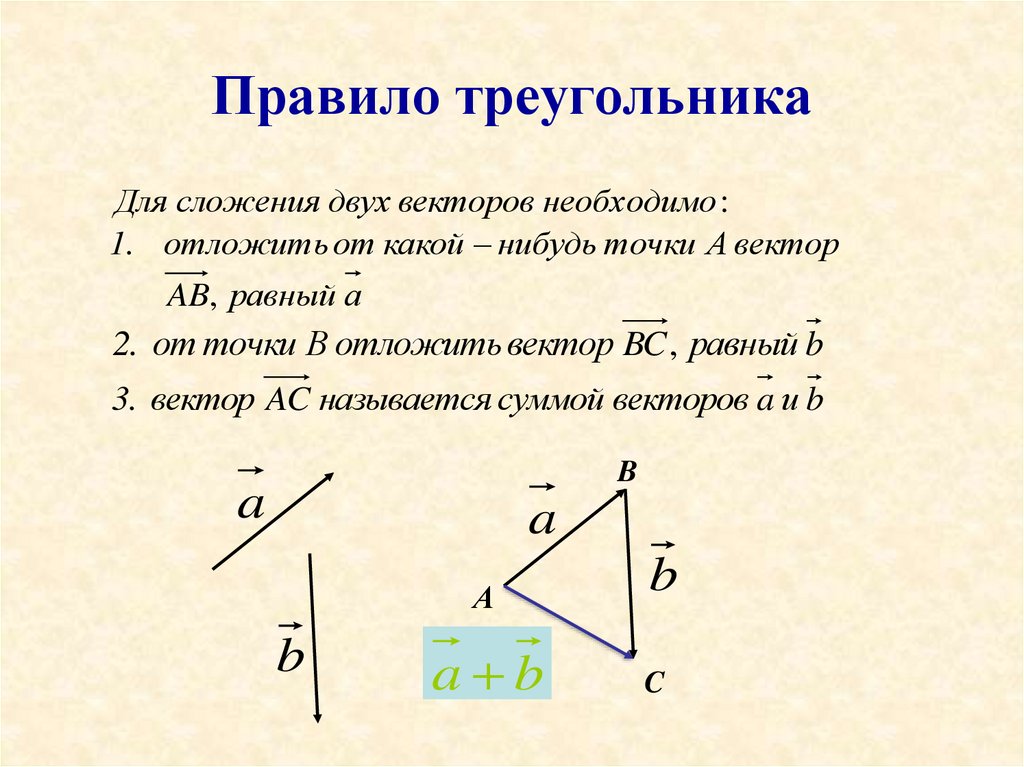
Например, самолет движется на север и пролетает $100 \space км$. Затем $150 \space км$ на запад и еще $300 \space км$ на юго-запад (рисунок 4).
Рисунок 4. Сложение путей, пройденных движущимся теломПуть — скалярная величина. Значит, складывать пути мы будем арифметически:
$s = s_1 + s_2 + s_3 = 100 \space км + 150 \space км + 300 \space км = 550 \space км$.
{"questions":[{"content":"Какой путь проехал автобус, если сначала он прошел $30 \\space км$ в северном направлении, а затем еще $20 \\space км$ в восточном?[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["$50 \\space км$","$10 \\space км$","$40 \\space км$","$60 \\space км$"],"explanations":["$s = s_1 + s_2 = 30 \\space км + 20 \\space км = 50 \\space км$.","","",""],"answer":[0]}}}]}Вычитание и сложение перемещений
Если мы рассматриваем подобные операции с перемещениями, то здесь у нас будут действовать правила сложения и вычитания векторов.
Если два вектора $\vec a$ и $\vec b$ имеют одинаковое направление, то их сумма — это вектор $\vec c$ того же направления. Его модуль будет равен сумме модулей двух данных векторов: $|\vec c| = |\vec a| + |\vec b|$ (рисунок 5).
Его модуль будет равен сумме модулей двух данных векторов: $|\vec c| = |\vec a| + |\vec b|$ (рисунок 5).
Если направления векторов $\vec a$ и $\vec b$ противоположны, то их сумма — это вектор $\vec c$, одинаковый по направлению с тем вектором, модуль которого больше ($\vec a$). Модуль итогового вектора будет равен разности модулей слагаемых векторов: $|\vec c| = |\vec a| − |\vec b|$ (рисунок 6).
Рисунок 6. Сложение параллельных векторов разных направленийПравило параллелограмма
Если векторы расположены под некоторым углом друг к другу, то мы можем использовать правило параллелограмма.
Для этого мы совмещаем начала векторов $\vec a$ и $\vec b$, которые нужно сложить друг с другом, и достраиваем параллелограмм на их основе (рисунок 7).
Рисунок 7. Сложение векторов по правилу параллелограммаСуммой данных векторов является вектор $\vec c$, выходящий из точки, в которой расположены начала слагаемых векторов $\vec a$ и $\vec b$, и совпадающий с большей диагональю параллелограмма.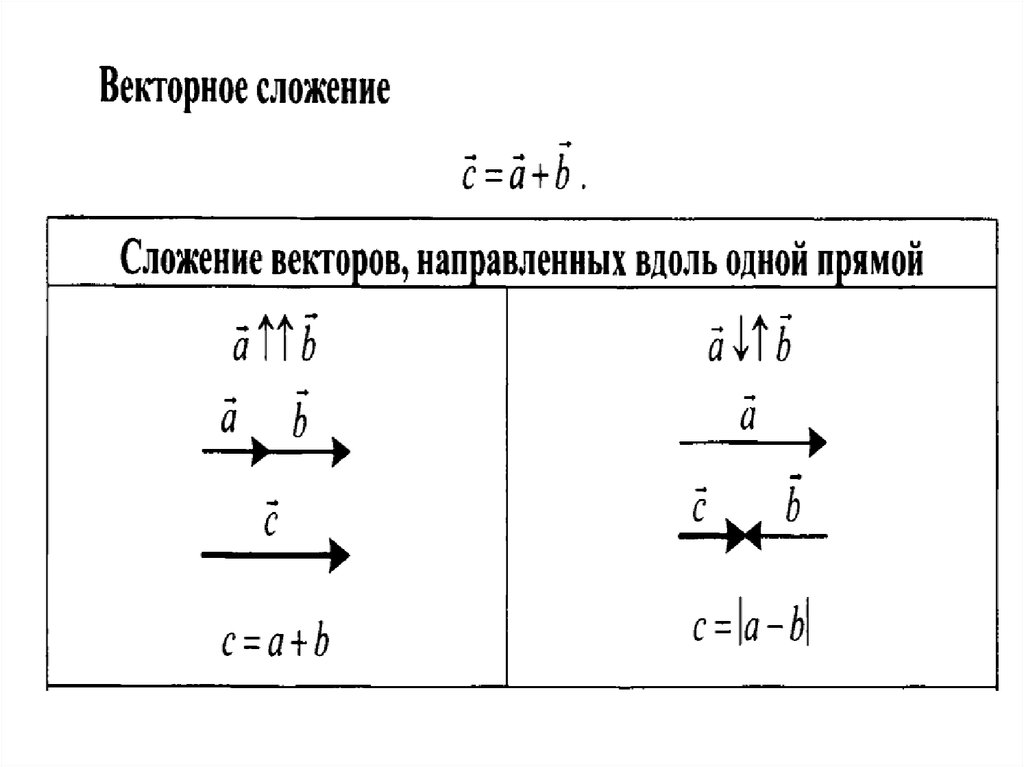
{"questions":[{"content":"При использовании правила параллелограмма суммарный вектор $\\vec c$ является[[choice-17]]","widgets":{"choice-17":{"type":"choice","options":["большей диагональю параллелограмма","меньшей диагональю параллелограмма","большей стороной параллелограмма","меньшей стороной параллелограмма"],"answer":[0]}}}]}Правило треугольника
Также при работе с векторами вы можете использовать правило треугольника. Для этого нужно совместить конец одного вектора с началом другого (рисунок 8). Так мы получим вектор $\vec c$, равный сумме $\vec a$ и $\vec b$.
Рисунок 8. Сложение векторов по правилу треугольникаПравило многоугольника
Если нам потребуется найти сумму более, чем двух векторов, то мы используем правило многоугольника.
Например, нам нужно сложить четыре вектора $\vec a$, $\vec b$, $\vec c$ и $\vec d$. Для этого мы совмещаем векторы так, чтобы каждый следующий выходил из конца предыдущего (рисунок 9).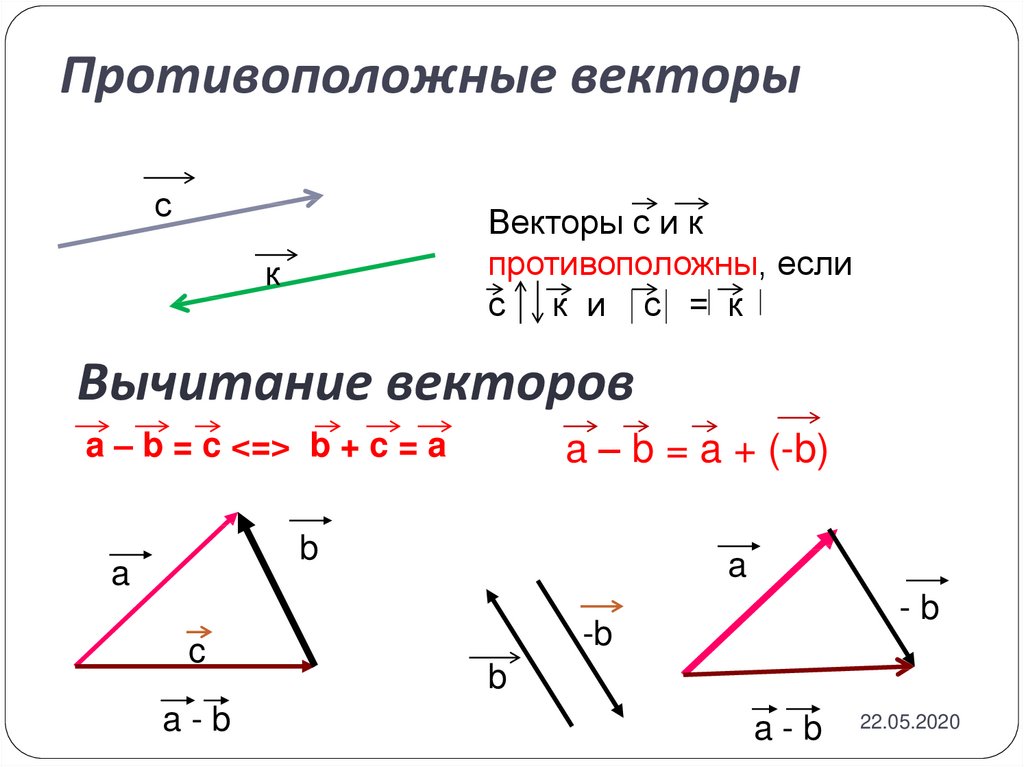 Затем соединяем начало первого вектора $\vec a$ и конец последнего $\vec d$ и получаем суммарный вектор $\vec e$.
Затем соединяем начало первого вектора $\vec a$ и конец последнего $\vec d$ и получаем суммарный вектор $\vec e$.
Вычитание векторов
Наконец, если нам потребуется найти разность двух векторов $\vec a$ и $\vec b$, нужно совместить их начала. Затем мы проводим вектор $\vec c$ ($\vec c = \vec a \space − \space \vec b$) из конца вычитаемого вектора $\vec b$ в конец уменьшаемого вектора $\vec a$ (рисунок 10).
Рисунок 10. Вычитание векторовУпражнения
Упражнение №1
Какую физическую величину определяет водитель автомобиля по счетчику спидометра — пройденный путь или перемещение?
Рисунок 11. Спидометр автомобиляПосмотреть ответ
Скрыть
Ответ:
Счетчик, расположенный под спидометром, по которому смотрят так называемый «пробег» автомобиля называется одометром (рисунок 11). Этот прибор считает количество оборотов колеса. Каждый оборот колеса соответствует определенному пройденному пути, поэтому показания прибора выводятся в километрах.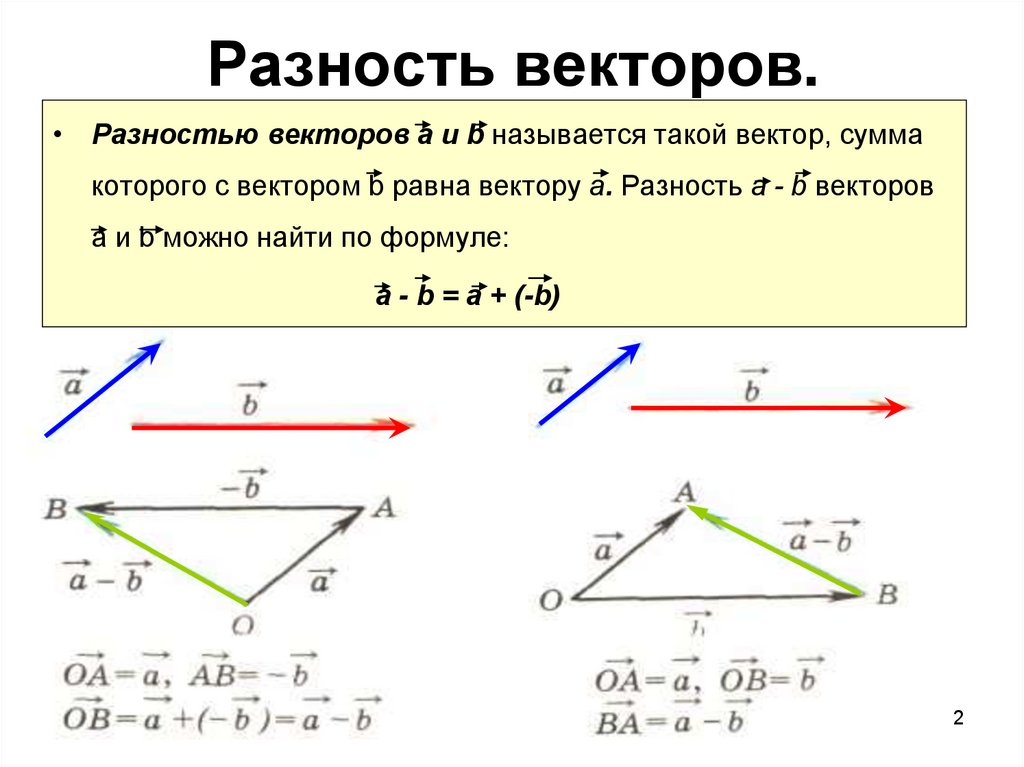
Соответственно, одометр показывает пройденный автомобилем путь, а не его перемещение.
Упражнение №2
Как должен двигаться автомобиль в течение некоторого промежутка времени, чтобы по спидометру можно было определить модуль перемещения, совершенного автомобилем за этот промежуток времени?
Посмотреть ответ
Скрыть
Ответ:
Автомобиль должен двигаться прямолинейно. Тогда пройденный им путь будет равен модулю перемещения.
Сложение и вычитание векторов: аналитические методы · Физика
Сложение и вычитание векторов: аналитические методы · Физика- Понимать правила сложения и вычитания векторов с использованием аналитических методов.
- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
- Применение аналитических методов для определения величины и направления результирующего вектора.

Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Разложение вектора на перпендикулярные компоненты
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, для вектора типа A size 12{A} {}
в [ссылка], мы можем захотеть найти, какие два перпендикулярных вектора, Ax size 12{A rSub { size 8{x} } } {}
и Ay размер 12{A rSub { размер 8{y} } } {}
, добавьте, чтобы произвести его.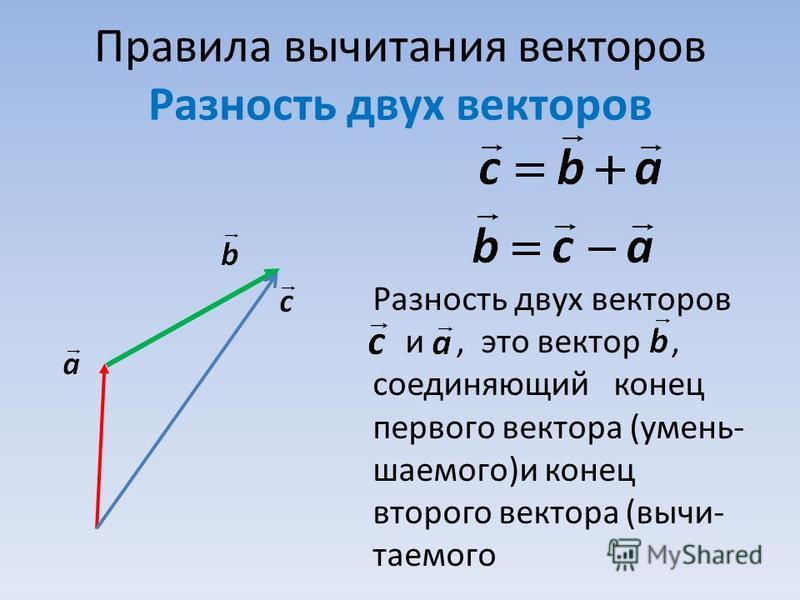
и размер Ay 12 {A rSub { размер 8 {y} } } {}
определяются как компоненты **A размера 12{A} {}
по осям x — и y -. Три вектора A размера 12{A} {}
, Размер оси 12 {A rSub { размер 8 {x} } } {}
и Ay size 12{A rSub { size 8{y} } } {}
образуют прямоугольный треугольник:
Ax + Ay = A. размер 12{A rSub { размер 8{x}} жирный » + A» rSub { размер 8{y} } жирный «= A.»} {}
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если Ax=3 м размер 12{A rSub { размер 8{x} } } {}
восток, Ay=4 м размер 12{A rSub { размер 8{y} } } {}
север, и A=5 м размер 12{A} {}
северо-восток, то верно, что векторы Ax + Ay = A размер 12{A rSub { размер 8{x} } жирный » + A» rSub { размер 8{y} } жирный » = A»} {}
. Однако не верно, что сумма модулей векторов также равна. То есть
Однако не верно, что сумма модулей векторов также равна. То есть
3 м+4 м ≠ 5 malignl { стопка { размер 12 {«3 м + 4 м » <> » 5 м»} {} # {} } } {}
Таким образом,
Ax+Ay≠A размер 12{A rSub {размер 8{x}} +A rSub {размер 8{y}} <> A} {}
Если размер вектора A 12{A} {}
известно, то его величина A size 12{A} {}
(его длина) и его угол θ размер 12{θ} {}
(его направление) известны. Чтобы найти размер оси 12 {A rSub { размер 8 {x} } } {}
** и **Ay размер 12{A rSub { размер 8{y} } } {}
, его x — и {::} y**-компонент, мы используем следующие отношения для прямоугольного треугольника.
Ax=Acosθ размер 12{A rSub { размер 8{x} } =A»cos»θ} {}
и
Ay=Asinθ. размер 12{A rSub { размер 8{y} } =A»sin»θ».»} {}
Предположим, например, что размер A 12{A} {}
— это вектор, представляющий общее перемещение человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение и сложение и вычитание векторов: графические методы».
Тогда A=10,3 размер 12{A} {}
блоков и θ=29,1º размер 12{«29,1º»}
, так что
Ax=Acosθ=(10,3 блоков)(cos29,1º)=9,0 блоков размером 12{}
Ay=Asinθ=(10,3 блоков)(sin29,1º)=5,0 блоков. размер 12{«»}
Вычисление результирующего вектора
Если перпендикулярные компоненты Ax размер 12{A rSub { размер 8{x} } } {}
и Ay размер 12{A rSub { размер 8{y} } } {}
вектора A размера 12{A} {}
известны, то размер A 12{A} {}
также можно найти аналитически. Чтобы найти величину A size 12{A} {}
и направление θ размер 12{θ} {}
вектора из его перпендикулярных компонент Ax size 12{A rSub { size 8{x} } } {}
и Ay размер 12{A rSub { размер 8{y} } } {}
, мы используем следующие отношения:
A=Ax2+Ay2 размер 12{A= sqrt {A rSub { размер 8{x} rSup { размер 8{2} } } +A rSub { размер 8{y} rSup {размер 8{2} } } } } {}
θ=tan−1(Ay/Ax). размер 12{θ=»tan» rSup { размер 8 {- 1} } \( A rSub { размер 8 {y} } /A rSub { размер 8 {x} } \) } {}
Обратите внимание, что уравнение A=Ax2+Ay2 размер 12{A= sqrt {A rSub { размер 8{x} rSup { размер 8{2} } } +A rSub { размер 8{y} rSup { размер 8{2} } } } } {}
— это всего лишь теорема Пифагора, связывающая катеты прямоугольного треугольника с длиной гипотенузы.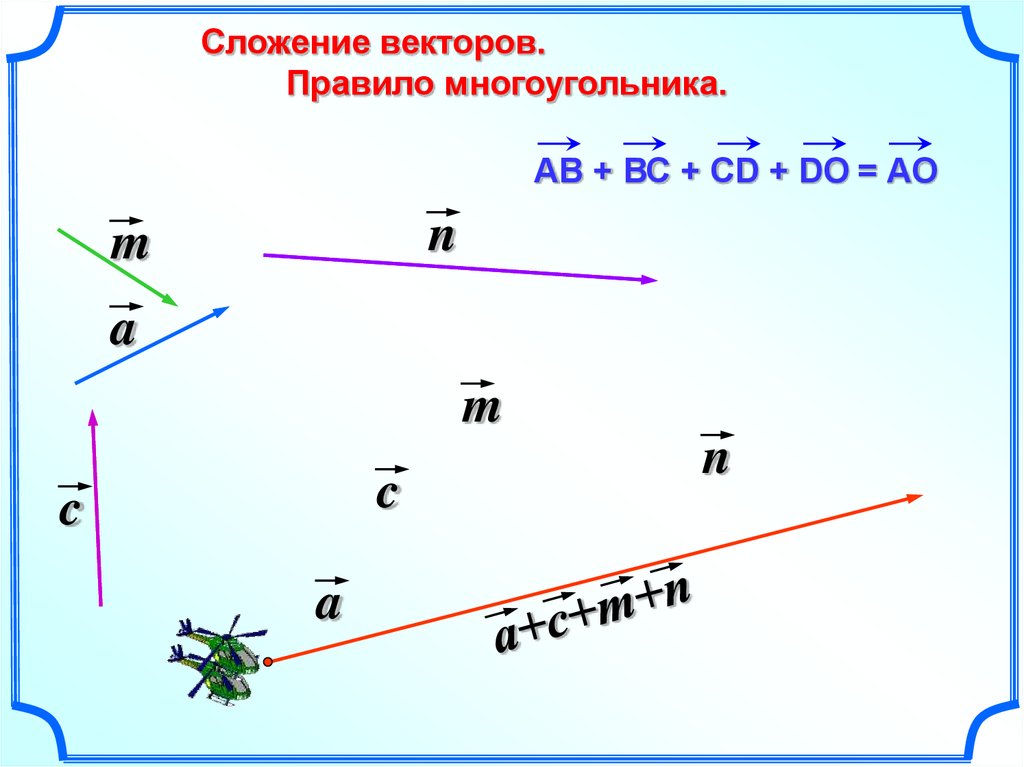 Например, если Ax size 12{A rSub { size 8{x} } } {}
Например, если Ax size 12{A rSub { size 8{x} } } {}
и Ay размер 12{A rSub { размер 8{y} } } {}
— это 9 и 5 блоков соответственно, тогда A=92+52=10,3 size 12{A= sqrt {9 rSup { size 8{2} } «+5» rSup { size 8{2} } } «=10» «.» 3} {}
блоков, что опять же соответствует примеру человека, идущего по городу. Наконец, направление равно θ=tan–1(5/9)=29,1º size 12{θ=»tan» rSup { size 8{–1} } \(«5/9″ \)»=29» «. » 1 rSup {размер 8{o} } } {}
, как и раньше.
Определение векторов и компонентов векторов с помощью аналитических методов
Уравнения Ax=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}
и Ay=Asinθ размер 12{A rSub { размер 8{y} } =A»sin»θ} {}
используются для нахождения перпендикулярных компонент вектора, то есть для перехода от A размера 12{ A} {}
и θ размера 12{θ} {}
до Ax размера 12{A rSub {размер 8{x}} } {}
и Ay размера 12{A rSub {размер 8{y}} } {}
. Уравнения A=Ax2+Ay2 размер 12{A= sqrt {A rSub { размер 8{x} rSup { размер 8{2} } } +A rSub { размер 8{y} rSup { размер 8{2} } } } } {}
и θ=tan–1(Ay/Ax)
используются для нахождения вектора по его перпендикулярным компонентам, т. е. для перехода от Ax
е. для перехода от Ax
и Ay
до A
и θ
. Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Добавление векторов с использованием аналитических методов
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрим [ссылка], в которой векторы A размером 12{A} {}
и размер B 12{B} {}
добавляются для получения результирующего размера R 12{R} {}
.
Если А
и Б
обозначают два этапа ходьбы (два перемещения), затем R
— полное водоизмещение. Человек, совершающий прогулку, оказывается на кончике R.
.Есть много способов добраться до одной и той же точки. В частности, человек мог пройти сначала в направлении x , а затем в направлении y . Эти пути являются x — и y -компонентами результирующего, Rx
и Ry размер 12{R rSub { размер 8{y} } } {}
. Если мы знаем Rx
Если мы знаем Rx
и Ry размер 12{R rSub { размер 8{y} } } {}
, мы можем найти R
и θ
с использованием уравнений A=Ax2+Ay2
и θ=tan–1(Ay/Ax) размер 12{θ=»tan» rSup { размер 8{–1} } \( A rSub { размер 8{y} } /A rSub { размер 8{x}} \) } {}
. Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей . Используйте уравнения Ax=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}
и Ay=Asinθ размер 12{A rSub {размер 8{y}} =A»sin»θ} {}
, чтобы найти компоненты. В [ссылке] эти компоненты имеют размер 12 {A rSub { размер 8 {x} } } {}
., Ay size 12{A rSub {size 8{y}} } {}
, Bx размер 12{B rSub {размер 8{x}} } {}
и По размеру 12{B rSub {размер 8{y}} } {}
. Углы векторов A размером 12{A} {}
Углы векторов A размером 12{A} {}
и размер B 12{B} {}
делают с осью x θA размер 12{θ rSub { размер 8{A} } } {}
и θB размер 12{θ rSub {размер 8{B} } } {}
соответственно.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано в [ссылка],
Rx=Ax+Bx размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8{x} } } {}
и
Ry=Ay+By. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}
Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси y . (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток, а вторые 6 кварталов на восток, всего 9 кварталов.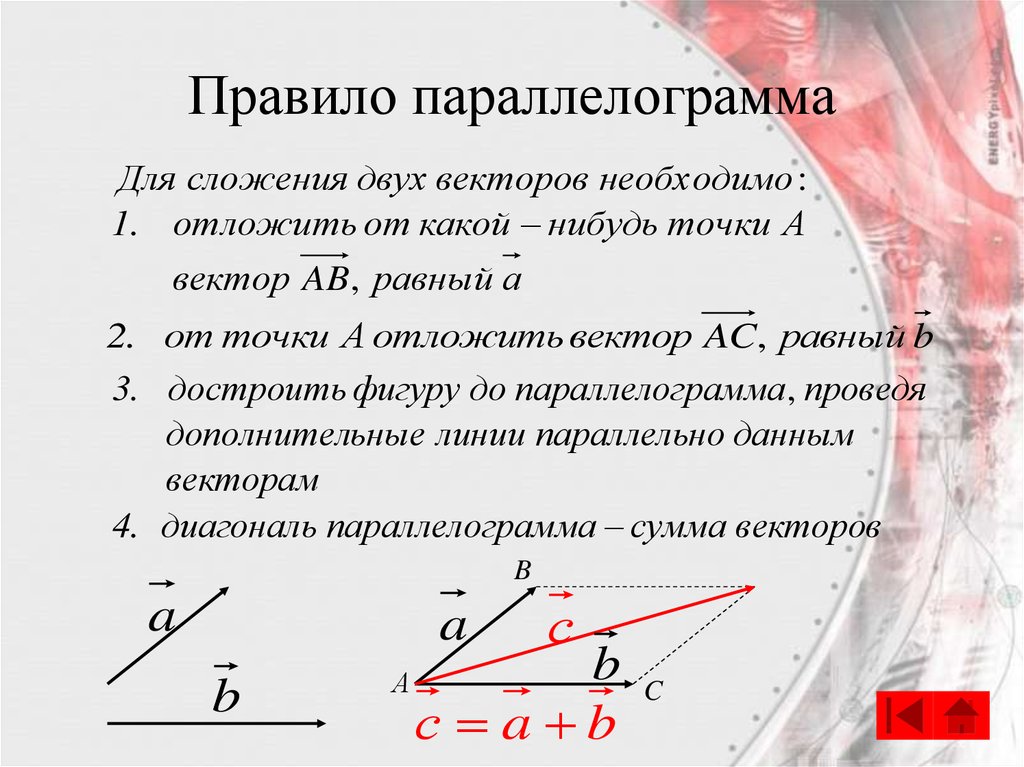 , потому что они расположены в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общих осей упрощает их сложение. Теперь, когда компоненты размера R 12{R} {}
, потому что они расположены в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общих осей упрощает их сложение. Теперь, когда компоненты размера R 12{R} {}
известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину R size 12{R } {} равнодействующей, используйте теорему Пифагора:
R=Rx2+Ry2. размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup { размер 8{2} } } «.»} {}
Шаг 4. Чтобы получить направление равнодействующей:
θ=tan-1(Ry/Rx). size 12{θ=»tan» rSup { size 8{- 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «.»} {}
В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.
Добавление векторов с использованием аналитических методов
Добавьте вектор A размера 12{A} {}
к вектору B размера 12{B} {}
, показанному в [ссылка], используя перпендикулярные компоненты вдоль х — и у — оси.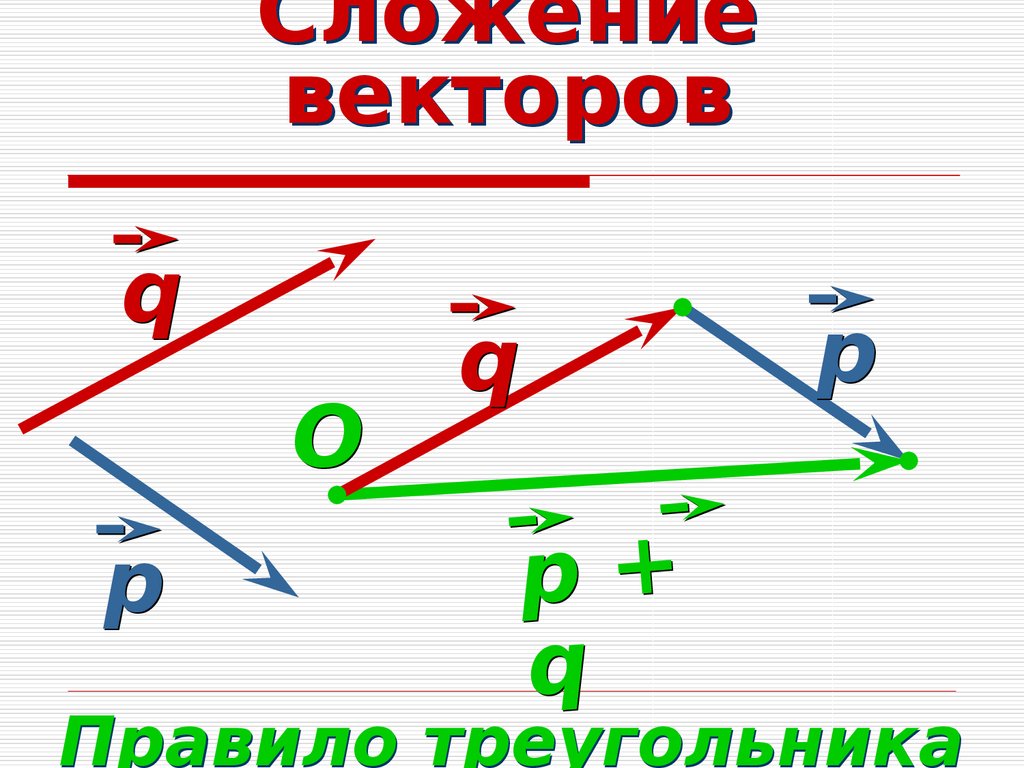 Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор A размера 12{A} {}
Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор A размера 12{A} {}
представляет собой первый этап ходьбы, на котором человек проходит 53,0 м размера 12{«53» «.» «0 м»} {}
в направлении 20,0º размер 12{«20» «.» 0º } {}
к северу от востока. Вектор B размером 12{B} {}
представляет вторую ветвь, смещением 34,0 м, размером 12{«34» «.» «0 м»} {}
в направлении 63,0º размер 12{«63» «.» 0º } {}
к северу от востока.
Стратегия
Компоненты размера A 12{A} {}
и размера B 12{B} {}
вдоль осей x — и на восток — 2 y 9001 на север, чтобы добраться до той же конечной точки. После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты размера A 12{A} {}
и размера B 12{B} {}
по осям x — и y -. Обратите внимание, что A=53,0 м размер 12{«A» «=» «53,0 м»} {}
Обратите внимание, что A=53,0 м размер 12{«A» «=» «53,0 м»} {}
, θA=20,0º размер 12{«θ» «subA» «=» «20,0°» } {}
, B=34,0 м размер 12{«B» «=» «34,0» «м»} {}
, и θB=63,0º размер 12{θ rSub { размер 8{B} } } {}
. Мы находим x -компоненты, используя Ax=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}
, что дает
Ax=AcosθA=(53,0 м)( cos 20,0º) = (53,0 м) (0,940) = 49,8 malignl { stack { размер 12 {A rSub { размер 8 {x} } = A «cos» θ rSub { размер 8 {A} } = \ («53» «.» 0″ m» \) \( «cos» «20» «.» 0 { size 12{ circ } } \) } {} # » «= \( «53» «.» 0″ m» \ ) \( 0 «.» «940» \) =»49″ «.» 8″ м» {} } } {}
и
Bx=BcosθB=(34,0 м)(cos 63,0º)=(34,0 м)(0,454)=15,4 м .alignl {стек {размер 12{B rSub {размер 8{x}} =B»cos»θ rSub {размер 8{B}} = \(«34» «.» 0″ m» \) \( «cos «»63» «.» 0 { size 12{ circ } } \) } {} # » «= \( «34» «.» 0″ m» \) \( 0 «.» «454» \) = «15» «.» 4″ m» {} } } {}
Аналогично, y -компоненты находятся с использованием Ay=AsinθA size 12{A rSub { size 8{y} } =A»sin»θ rSub { размер 8{A} } } {}
:
Ay=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 malignl { stack { размер 12{A rSub { размер 8{y} } =A»sin»θ rSub { size 8{A} } = \(«53» «. 0″ m» \) \( «sin»»20» «.» 0 { size 12{ circ } } \) } {} # » «= \( «53» «.» 0″ м» \) \( 0 «.» «342» \) =»18″ «.» 1″ м» {} } } {}
0″ m» \) \( «sin»»20» «.» 0 { size 12{ circ } } \) } {} # » «= \( «53» «.» 0″ м» \) \( 0 «.» «342» \) =»18″ «.» 1″ м» {} } } {}
и
By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891)=30,3 м.alignl {stack {размер 12{B rSub {размер 8{y}} =B»sin «θ rSub { size 8{B} } = \( «34» «. 0″ m» \) \( «sin» «63» «.» 0 { size 12{ circ } } \) } {} # » «= \( «34» «. 0″ м» \) \( 0 «.» «891» \) =»30″ «.» 3″ м» «.» {} } } {}
Таким образом, x — и y -компоненты равнодействующей
Rx=Ax+Bx=49,8 м+15,4 м=65,2 м size 12{R rSub { size 8{x } } =A rSub {размер 8{x}} +B rSub {размер 8{x}} =»49″ «.» 8″ м»+»15″ «.» 4″ м»=»65″ «.» 2″ м»} {}
и
Ry=Ay+By=18,1 м+30,3 м= 48,4 м. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y}} =»18″ «.» 1″ м»+»30″ «.» 3″ m»=»48″ «. 4″ m.»} {}
Теперь мы можем найти величину равнодействующей по теореме Пифагора:
R=Rx2+Ry2=(65.2) 2+(48,4)2 м размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup { размер 8{2} } } = sqrt { \(«65» «. » 2 \) rSup { размер 8{2} } + \(«48» «.» 4 \) rSup { размер 8{2} } } «m»} {}
» 2 \) rSup { размер 8{2} } + \(«48» «.» 4 \) rSup { размер 8{2} } } «m»} {}
, так что
R=81,2 м. size 12{R =»81,2″ «m.»} {}
Наконец, мы находим направление равнодействующей:
θ=tan−1(Ry/Rx)=+tan−1(48,4/65,2). size 12{θ=»tan» rSup { size 8{ — 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «=+»»tan» rSup { size 8{ — 1} } \(«48» «.» 4/»65″ «.» 2 \) «.»} {}
Таким образом,
θ=tan−1(0,742)=36,6º. size 12{θ=»tan» rSup { size 8{ — 1} } \( 0 «.» «742» \) =»36″ «.» 6 {размер 12{круг} } «.»} {}
Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A−B≡A+(–B) размер 12{A – B эквивалент A+ \( — B \) } {}
. Таким образом, способ вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения 9. 0190 . Компоненты –B
0190 . Компоненты –B
являются негативами компонентов размера B 12{B} {}
. Таким образом, x — и y -компоненты результирующего A−B = R размера 12{A- жирным шрифтом «B = R»} {}
равны
Rx=Ax+(–Bx) размера 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +-B rSub { размер 8{x} } } {}
и
Ry=Ay+(–By) размер 12{R rSub { size 8{y} } =A rSub { size 8{y} } +-B rSub { size 8{y} } } {}
, а остальная часть метода, описанного выше, идентична методу добавления. (См. [ссылка].)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль Projectile Motion — один из многих, в котором использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
PhET Explorations: Сложение векторов
Узнайте, как складывать векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах. * * *
Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах. * * *
Резюме
- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги по добавлению векторов
Размер 12 {A} {}
и
Размер B 12{B} {}с использованием аналитического метода выглядит следующим образом: Шаг 1: Определите систему координат для векторов. Затем определите горизонтальную и вертикальную составляющие каждого вектора, используя уравнения
Ax=AcosθBx=Bcosθalignl {стек {размер 12{A rSub {размер 8{x}} =A»cos»θ} {} # B rSub {размер 8{x} } =B»cos»θ {} } } {}
и
Ay=A sinθBy=B sin θ.alignl { stack { size 12{A rSub { size 8{y} } =A» sin»θ} {} # B=B suby » sin «θ {} } } {}
Шаг 2. Сложите горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты Rx size 12{R rSub { size 8{x} } } {}
и Ry размер 12{R rSub { размер 8{y} } } {}
результирующего вектора, размер R 12{R} {}
:
Rx=Ax+Bx размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8{x} } } {}
и
Ry=Ay+By.
 размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}
размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}Шаг 3: Используйте теорему Пифагора для определения магнитуды, размер R 12{R} {}
результирующего вектора R размера 12{R} {}
:
R=Rx2+Ry2. размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup {размер 8{2} } } } {}
Шаг 4. Используйте тригонометрическую идентичность для определения направления, размер θ 12{θ} {}
, размер R 12 {R} {}
:
θ=tan-1(Ry/Rx). размер 12{θ=»tan» rSup { размер 8 {- 1} } \( R rSub { размер 8 {y} } /R rSub { размер 8 {x} } \) } {}
Концептуальные вопросы
Предположим, вы добавили два вектора размера A 12{A} {}
и размера B 12{B} {}
. Какое относительное направление между ними дает равнодействующую с наибольшей величиной? Какова максимальная величина? Какое относительное направление между ними дает равнодействующую с наименьшей величиной? Какова минимальная величина?
Приведите пример ненулевого вектора, у которого есть нулевая компонента.
Объясните, почему вектор не может иметь компонент, превышающий его собственную величину.
Если векторы A размера 12{A} {}
и B размера 12{B} {}
перпендикулярны, какова составляющая A размера 12{A} {}
вдоль направления B размера 12 {B} {}
? Какова составляющая размера B 12{B} {}
вдоль направления размера A 12{A} {}
?
Задачи и упражнения
Найдите следующее для пути C в [ссылка]: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
(а) 1,56 км
(б) 120 м на восток
Найдите следующее для пути D в [ссылка]: (а) общее пройденное расстояние и (б) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
Найдите северную и восточную составляющие смещения из Сан-Франциско в Сакраменто, показанные в [ссылка].
Северный компонент 87,0 км, восточный компонент 87,0 км
Решите следующую задачу, используя аналитические методы: Предположим, вы прошли 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы в виде векторных смещений A размером 12{A} {}
и размер B 12{B} {}
, как в [ссылка], то эта задача просит вас найти их сумму R=A+B размера 12{R=A+B} {}
.)
Обратите внимание, что вы также можете решить это графически. Обсудите, почему аналитический метод решения этой задачи потенциально более точен, чем графический метод.
Повторите [ссылка], используя аналитические методы, но поменяйте порядок двух этапов ходьбы и покажите, что вы получаете тот же конечный результат. (Эта задача показывает, что сложение их в обратном порядке дает тот же результат, то есть B + A = A + B
. ) Обсудите, как использование другого пути для достижения той же точки может помочь преодолеть препятствие, блокирующее другой путь.
) Обсудите, как использование другого пути для достижения той же точки может помочь преодолеть препятствие, блокирующее другой путь.
30,8 м, 35,8 к западу от севера
Вы проезжаете 7,50 км размером 12{7 «.» «50 км»} {}
по прямой в направлении 15º размера 12{«15º»} {}
к востоку от севера. а) Найдите расстояние, которое вам пришлось бы проехать прямо на восток, а затем прямо на север, чтобы оказаться в той же точке. (Это определение эквивалентно нахождению компонентов смещения вдоль восточного и северного направлений.) (b) Покажите, что вы все равно прибудете в ту же точку, если восточный и северный участки поменялись местами.
Сделайте [ссылка] еще раз, используя аналитические методы, и измените второй этап ходьбы на 25,0 м
прямо на юг. (Это эквивалентно вычитанию размера B 12{B} {}
из размера A 12{A} {}
, то есть получению R’=A – B
) (b) Повторите еще раз, но теперь вы первая прогулка 25,0 м размер 12{«25» «. » «0 м»} {}
» «0 м»} {}
север, а затем 18,0 м размер 12{«18» «.» «0 м»} {}
восток. (Это эквивалентно вычитанию размера A 12{A} {}
из размера B 12{B} {}
— то есть найти A=B+C размера 12{A=B+C} {}
. Это соответствует вашему результату?)
(a) 30,8 м размер 12{«30» «.» «8 м»} {}
, 54,2º размер 12{«54» «.» 2°} {}
к югу от запада
(b) 30,8 м размер 12{«30» «.» «8 м»} {}
, 54,2º размер 12{«54» «.» 2°} {}
к северу от востока
У нового землевладельца есть треугольный участок ровной земли, который она хочет огородить. Начиная с западного угла, она измеряет первую сторону длиной 80,0 м, а следующую — 105 м. Эти стороны представлены в виде векторов смещения A размера 12{A} {}
от размера B 12{B} {}
в [ссылка]. Затем она правильно вычисляет длину и ориентацию третьей стороны C size 12{C} {}
. Каков ее результат?
Вы летите 32,0 км размером 12{«32» «.» «0 км»} {}
по прямой в штиль в направлении 35,0º размера 12{«35″°} {}
к юго-западу.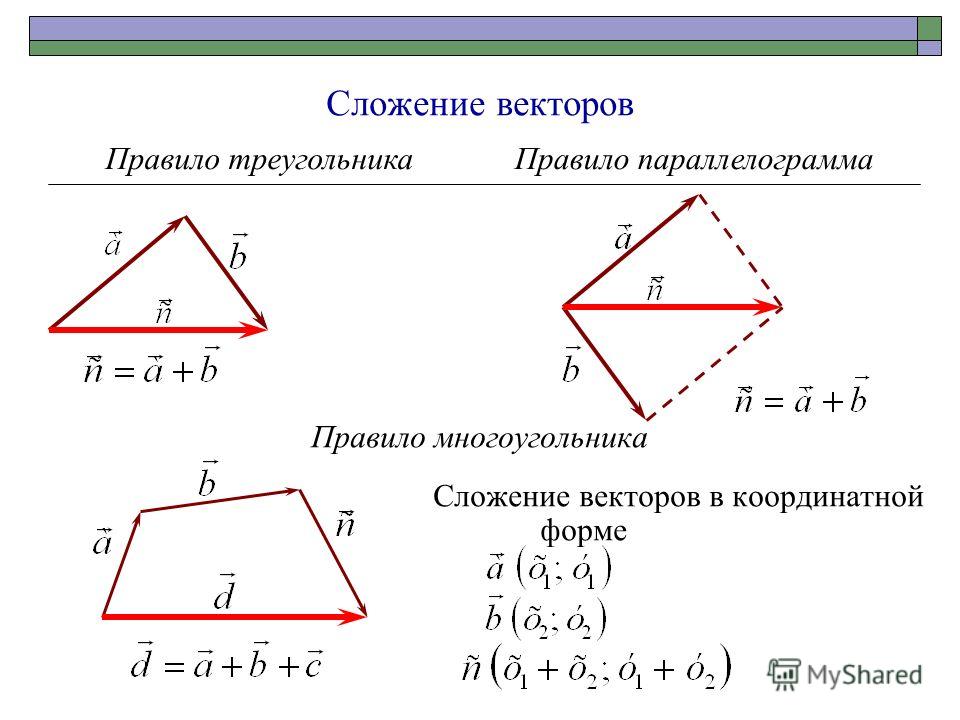 а) Найдите расстояние, которое вам пришлось бы пролететь прямо на юг, а затем прямо на запад, чтобы оказаться в той же точке. (Это определение эквивалентно нахождению компонентов смещения вдоль южного и западного направлений.) (b) Найдите расстояния, которые вам придется пролететь сначала в направлении 45,0º size 12{«45,0º»} {}
а) Найдите расстояние, которое вам пришлось бы пролететь прямо на юг, а затем прямо на запад, чтобы оказаться в той же точке. (Это определение эквивалентно нахождению компонентов смещения вдоль южного и западного направлений.) (b) Найдите расстояния, которые вам придется пролететь сначала в направлении 45,0º size 12{«45,0º»} {}
к югу от запада, а затем в направлении 45,0º размер 12{«45,0º»} {}
к западу от севера. Это компоненты смещения по другому набору осей — одна повернута на 45º размером 12{«45″°} {}
.
18,4 км к югу, затем 26,2 км к западу(b) 31,5 км по 45,0º, размер 12{«45,0º»} {}
к югу от запада, затем 5,56 км по 45,0º, размер 12{«45,0º»} {}
к западу от севера
Фермер хочет отгородить свой четырехсторонний участок плоской земли. Он измеряет первые три стороны, обозначенные как A, размером 12{A,} {}
B, размер 12{B,} {}
и C размер 12{C} {}
в [ссылка], а затем правильно вычисляет длину и ориентацию четвертой стороны D размера 12{D} {}
. Каков его результат?
Каков его результат?
Пытаясь сбежать со своего острова, Гиллиган строит плот и отправляется в море. Ветер в течение дня сильно меняет направление и дует по следующим прямым линиям: 2,50 км размером 12{2″». «50 км»} {}
45,0º размер 12 {«45,0º»} {}
к северу от запада; затем 4,70 км размером 12{4″». «70 км»} {}
60,0º размер 12{«60″°} {}
к югу от востока; затем 1,30 км размер 12{«1,30″ » км»} {}
25,0º размер 12{«25″°} {}
к югу от запада; затем 5,10 км размером 12{5″». «10 км»} {}
прямо на восток; затем 1,70 км размер 12{«1,70» «км»} {}
5,00º размер 12{5 rSup { размер 8{ круговой } } } {}
к востоку от севера; затем 7,20 км размером 12{7″». «20 км»} {}
55,0º размер 12{«55″°} {}
к югу от запада; и, наконец, 2,80 км размером 12{2″».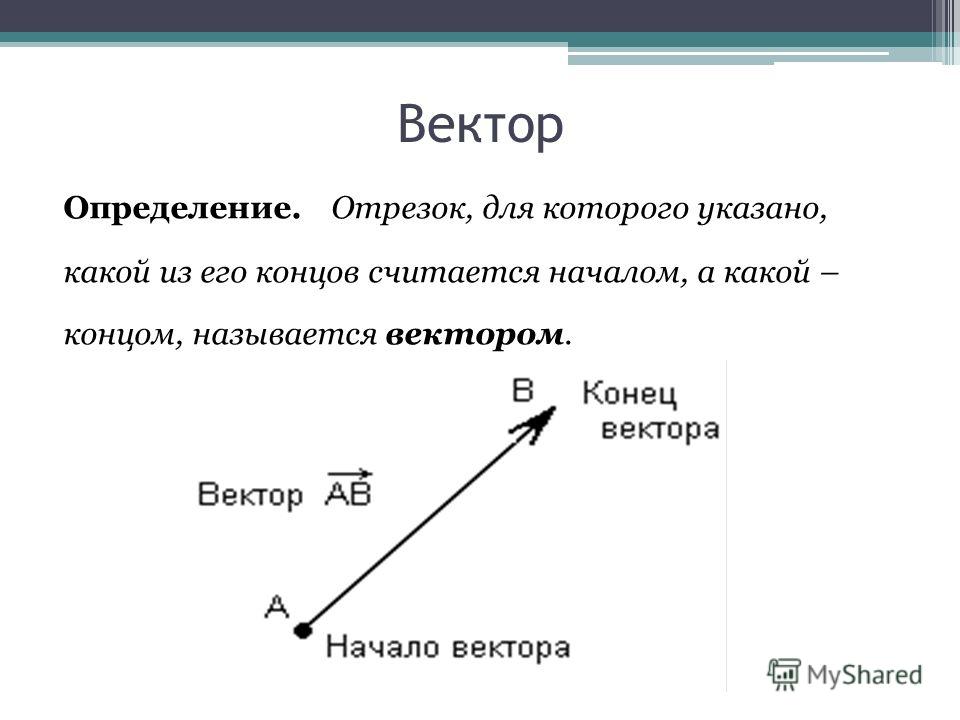 «80 км»} {}
«80 км»} {}
10,0º размер 12{«10″°} {}
к северу от востока. Каково его конечное положение относительно острова?
7,34 км размер 12{2 «.» «97 км»} {}
, 63,5º размер 12{«22» «.» 2°} {}
к югу от востока
Предположим, пилот пролетает 40,0 км размером 12{«40» «.» «0 км»} {}
в направлении 60º размер 12{«60″°} {}
к северу от востока, а затем летит 30,0 км размер 12{«30» «.» «0 км»} {}
в направлении 15º размера 12{«15″°} {}
к северу от востока, как показано на [ссылка]. Найдите ее общее расстояние R size 12{R} {}
от начальной точки и направление θ размер 12{θ} {}
прямолинейного пути до конечного положения. Обсудите качественно, как этот полет будет изменен северным ветром и как влияние ветра будет зависеть как от скорости ветра, так и от скорости самолета относительно воздушной массы.
Глоссарий
- аналитический метод
- метод определения величины и направления результирующего вектора с помощью теоремы Пифагора и тригонометрических тождеств
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, физика. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]».
- Если вы распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Скачать бесплатно на http://cnx.
 org/contents/[email protected].»
org/contents/[email protected].»
Диаграммы сложения векторов силы (или компонентов больше нет!) — Физика! Блог!
Баг с графическим решением меня в этом году сильно достал (и в лучшем виде). Очевидно, я проделал такую хорошую работу по продвижению графических решений, что один из моих классов остановил меня, пока я показывал им, как решать проблемы сил, разбивая силы на компоненты и выполняя 2 перпендикулярных анализа N2L.
«Почему мы не можем просто использовать диаграмму сложения векторов, которую мы уже нарисовали?»
«Ага! Мы можем вычислить длину этой стороны, а затем вычислить, насколько большим должен быть разрыв. Это не так сложно».
Не так уж сложно? Этот навык (решение двухмерных силовых задач, особенно когда силы неуравновешены) обычно был одним из самых сложных за весь год обучения физике! классы (старшеклассники, как правило, Precalculus), хотя это не имело (и не имеет) большого значения в классах с отличием по физике (второкурсники и младшие школьники, как правило, с отличием по алгебре 2 или выше).
Итак, когда мы впервые начинаем рассматривать проблемы несбалансированной силы и мою обычную физику! студенты говорят мне расслабиться, потому что они уже видят очевидный способ решить их, кто я такой, чтобы вмешиваться?
Что такое диаграммы сложения векторов силы?
Диаграммы сложения векторов сил (многие студенты заканчивают тем, что пишут «VAD», хотя я никогда этого не делаю) возьмите диаграмму свободного тела (FBD) и сложите все силы в виде векторов (так, голова к хвосту с размер и направление каждой стрелки очень важны). Если силы уравновешены, то у вас ничего не должно остаться, когда вы сложите их все вместе (). То есть, когда вы суммируете все силы вместе, вы должны вернуться в то же место, откуда начали. Таким образом, при уравновешенных силах диаграмма сложения векторов имеет замкнутую форму.
Если силы неуравновешены, на диаграмме будет пробел, так как сумма векторов не будет равна нулю. Размер разрыва показывает, насколько неуравновешены силы. Направление зазора представляет собой направление ускорения (так же, как и направление чистой силы). Обычно мы рисуем вектор результирующей силы в виде более крупной контурной стрелки, чтобы отличить его от сил, действующих на объект.
Направление зазора представляет собой направление ускорения (так же, как и направление чистой силы). Обычно мы рисуем вектор результирующей силы в виде более крупной контурной стрелки, чтобы отличить его от сил, действующих на объект.
Порядок сложения не имеет значения (так же, как и при «обычном» сложении). Таким образом, может быть несколько правильных ответов на задачу на сложение, которые (для детей) не выглядят одинаково. Результат будет таким же, но форма, созданная векторами, может выглядеть иначе. Некоторые студенты уже давно это поняли, а некоторые только начинают осознавать тонкости этого.
Обе эти диаграммы показывают правильное сложение векторов из одних и тех же правильных FBD (у второй были некоторые проблемы с числами, но форма была правильной).
Разбивка транспортиров: использование диаграмм сложения векторов для решения задач
Сначала мы всегда рисуем диаграммы в масштабе. Пока вы знаете достаточно о направлениях и/или длинах векторов, вы можете вычислить направление(я) и/или длину(я), которые вам не известны.
Вот отличное решение для учащихся из викторины. Это было на раннем этапе нашего опыта рисования векторных диаграмм сложения, поэтому она записала много своих мыслей, когда говорила сама с собой, как настроить свою работу. В светлых карандашных пометках вверху (справа) вы можете увидеть набросок общей формы, которую она сделала, прежде чем пытаться нарисовать ее в масштабе. Она записывает свои преобразования между своими измерениями в сантиметрах и значениями в ньютонах.
Рисование схемы (особенно в масштабе) может помочь отстающим учащимся проверить, имеют ли смысл их ответы.
Вы можете увидеть стертые строки предыдущих попыток решения задачи. Как только она нарисовала углы, она поняла, что, должно быть, что-то не так с тем, что она сделала. Она упорствовала в выяснении того, что было неправильным, пока все ее решение не было правильным.
По мере того, как они привыкали к диаграммам, многие ученики начали рисовать только эскиз, обозначая углы, разбивая фигуру на более мелкие фигуры (треугольники, прямоугольники) и используя тригонометрию прямого угла для нахождения неизвестных длин и направлений. Они увидели возможность использовать триггер без моего предложения, и в то время как у них уже был другой, вполне допустимый способ решения проблемы. Мне это нравится гораздо больше, чем кормить их компонентами, пока я обучаю их алгоритму.
Они увидели возможность использовать триггер без моего предложения, и в то время как у них уже был другой, вполне допустимый способ решения проблемы. Мне это нравится гораздо больше, чем кормить их компонентами, пока я обучаю их алгоритму.
Некоторые ученики (особенно младшие школьники по Алгебре 2) еще не изучили синус/косинус/и т.д. Было бы достаточно просто показать им, как использовать кнопку на калькуляторе, но они (пока что) более чем счастливы продолжать использовать транспортир и чертеж в масштабе для решения задач. У них уже есть метод, который имеет для них смысл.
Теперь, когда мы находимся в новом семестре и два раздела (скоро будет три) удалены из того, когда мы узнали о несбалансированных силах, я начинаю видеть, как несколько студентов «изобретают» идею смотреть на x- и y-компоненты сил и выполнение анализа 2-го закона Ньютона в компонентной форме. Проведя так много времени с диаграммами сложения векторов, они начали видеть закономерность в определении размера горизонтальных сторон и размера вертикальных сторон практически на любой диаграмме, которую они рисовали.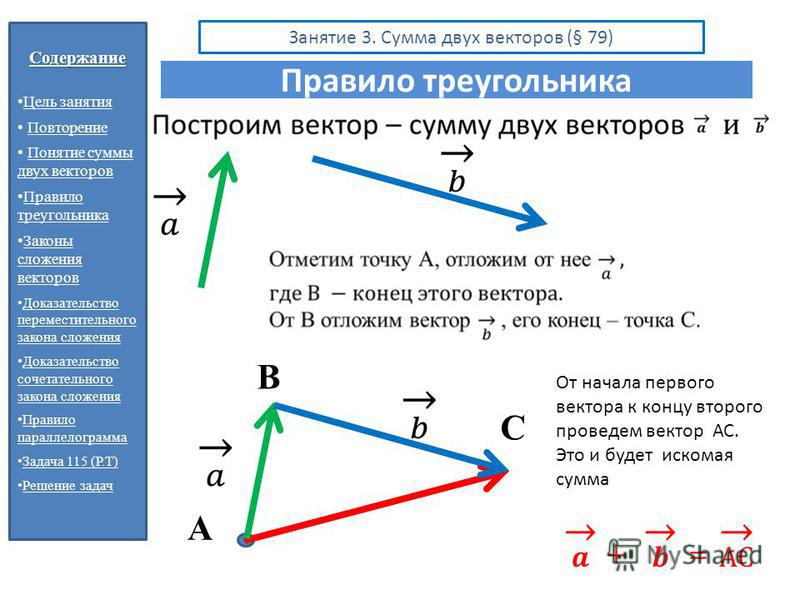
Использование этих диаграмм в качестве «исключительного» (пока они не поймут, что это не так) способа решения силовых задач было отличным решением для моих студентов в этом году. По сравнению с прошлыми годами, многие из них находят успех в ситуациях с неуравновешенными силами и уровень понимания (у всех учеников, включая самых сильных) более глубокий. Использование одной из этих диаграмм для решения задачи показывает гораздо большее понимание того, как связаны величины, чем взбалтывание алгоритма и запись множества уравнений. Итак, беспроигрышный вариант.
Нравится:
Нравится Загрузка…
Kelly O’Sheaphysicsdiagrams, Modeling Instruction, физика, студенческая работа
Аналитические методы — Колледж физики
Резюме
- Понимание правил сложения и вычитания векторов с использованием аналитических методов.
- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.

- Применение аналитических методов для определения величины и направления результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, имея вектор, как на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора и , добавить, чтобы получить его.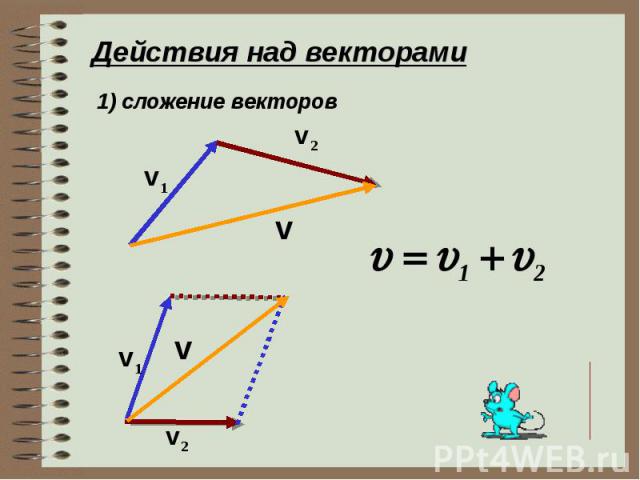
и определяются как компоненты осей x и y. Три вектора и образуют прямоугольный треугольник:
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если восток, север и северо-восток, то верно, что векторы Однако это не правда, что сумма модулей векторов тоже равна. То есть
Таким образом,
Если известен вектор, то известны его модуль и угол (его направление). Чтобы найти его x- и y-компоненты, мы используем следующие соотношения для прямоугольного треугольника.
и
Рисунок 2. Величины компонент вектора A x и A y можно отнести к результирующему вектору A и угол θ с тригонометрическими тождествами. Здесь мы видим, что A x =A cos θ и A y =A sinθ .Предположим, например, что это вектор, представляющий полное перемещение человека, идущего по городу, который рассматривался в главе 3.1 «Кинематика в двух измерениях: введение» и главе 3.2 «Сложение и вычитание векторов: графические методы».
Рисунок 3. Мы можем использовать отношения A x =A cos θ и A y =A sinθ для определения величины векторов горизонтальной и вертикальной составляющих в этом примере.Тогда и так
Если известны перпендикулярные компоненты и вектора, то их можно найти и аналитически.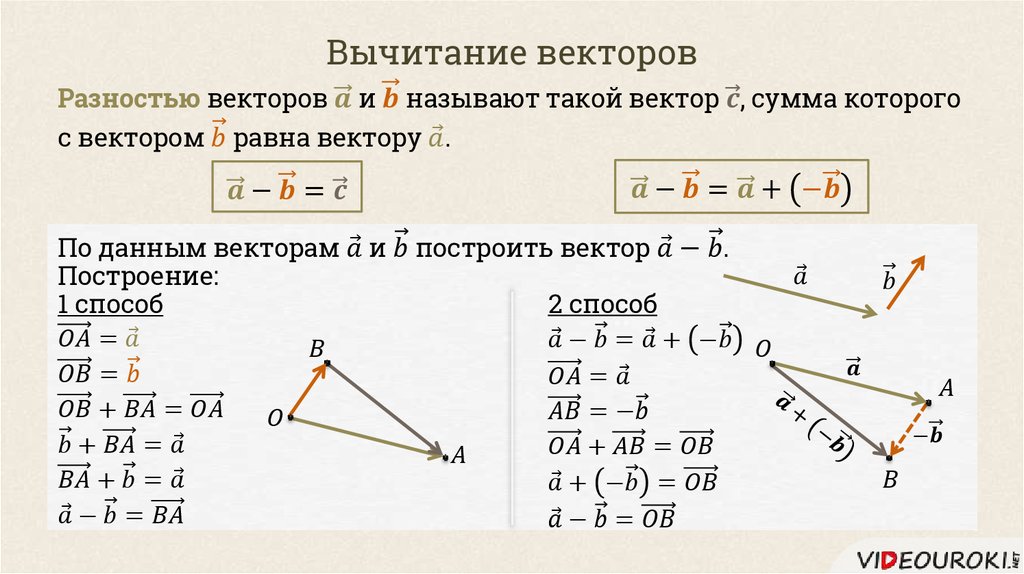 Чтобы найти величину и направление вектора по его перпендикулярным компонентам, мы используем следующие соотношения:
Чтобы найти величину и направление вектора по его перпендикулярным компонентам, мы используем следующие соотношения:
Обратите внимание, что это уравнение — всего лишь теорема Пифагора, связывающая катеты прямоугольного треугольника с длиной гипотенузы. Например, если и составляют 9 и 5 кварталов соответственно, то кварталы, опять же, соответствуют примеру человека, идущего по городу. Наконец, направление прежнее.
ОПРЕДЕЛЕНИЕ ВЕКТОРОВ И КОМПОНЕНТОВ ВЕКТОРОВ С ПОМОЩЬЮ АНАЛИТИЧЕСКИХ МЕТОДОВ
Уравнения и используются для нахождения перпендикулярных компонентов вектора, то есть для перехода от и к и Уравнения и используются для нахождения вектора по его перпендикулярным компонентам, то есть для перехода от и к и Оба процесса имеют решающее значение для аналитические методы сложения и вычитания векторов.
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рисунок 5, на котором векторы и складываются для получения результирующего числа
. Рисунок 5. Векторы A и B — две ноги прогулки, а R — результирующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления R . Если и представляют собой два этапа ходьбы (два перемещения), то это общее перемещение. Человек, совершающий прогулку, оказывается на вершине. Есть много способов добраться до одной и той же точки. В частности, человек мог пройти сначала в направлении x , а затем в направлении y 9.0190 -направление. Этими путями являются x — и y -компоненты равнодействующей, и Если мы знаем и можем найти и используя уравнения и Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.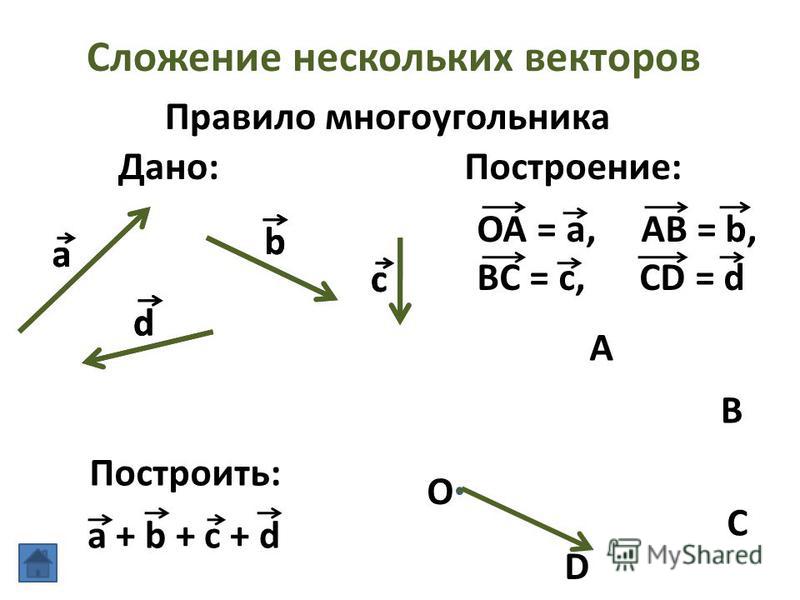
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей . Используйте уравнения и, чтобы найти компоненты. На рисунке 6 эти компоненты равны и Углы, которые векторы и образуют с осью x , равны и соответственно.
Рисунок 6. Чтобы сложить векторы A и B , сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это вектора, обозначенные пунктиром0012 и B y показаны на изображении.Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано на рисунке 7,
и
Рисунок 7. Величина векторов A x и B x суммируйте, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Точно так же величины векторов A y и B y складываются, чтобы получить величину R y
Точно так же величины векторов A y и B y складываются, чтобы получить величину R y в вертикальном направлении результирующего вектора.
Компоненты вдоль одной оси, скажем, оси x , являются векторами вдоль одной линии и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль и -ось. (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину равнодействующей, используйте теорему Пифагора:
Шаг 4. Чтобы получить направление равнодействующей:
В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.
Пример 1. Добавление векторов с помощью аналитических методов
Добавьте вектор к вектору, показанному на рисунке 8, используя перпендикулярные компоненты вдоль осей x и y . Оси x и y проходят соответственно с востока на запад и с севера на юг. Вектор представляет собой первый этап прогулки, когда человек идет в направлении к северу от востока. Вектор представляет второй отрезок, смещение направления к северу от востока.
Рисунок 8. Вектор A имеет звездную величину 53,0 м и направление 20,0 0 к северу от оси x. Вектор B имеет величину 34,0 м и направление 63,0 0 к северу от оси x. Вы можете использовать аналитические методы для определения величины и направления R .Стратегия
Компоненты осей x и y и вдоль них представляют ходьбу строго на восток и строго на север, чтобы добраться до одной и той же конечной точки.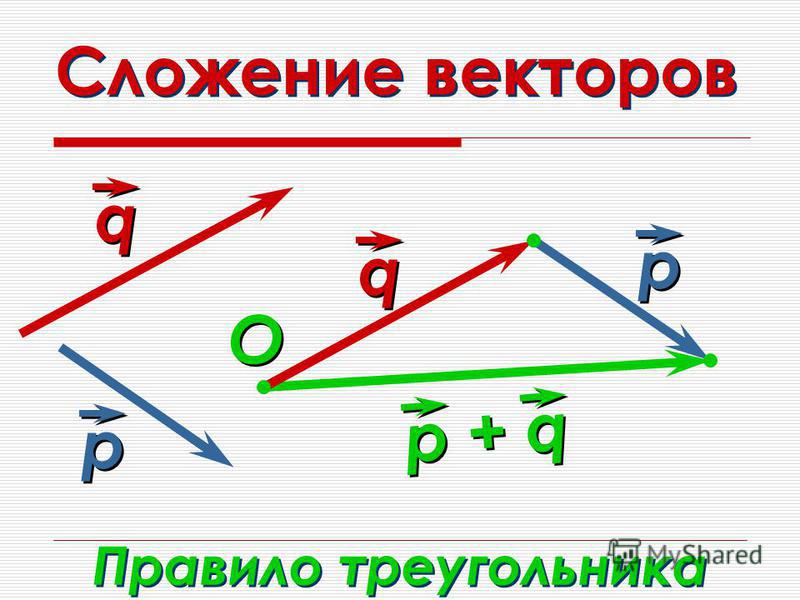 После обнаружения они объединяются для получения результирующего.
После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты и вдоль осей x и y . Обратите внимание, что и Мы находим x -компоненты, используя которые дает
и
Аналогично, y -компоненты находятся с использованием
и
x – и y -компоненты результатов таким образом,
и
Теперь мы можем найти величину равнодействующей, используя теорему Пифагора:
так что
Наконец, находим направление равнодействующей:
Таким образом,
Рис. 0 к северу от востока.Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора.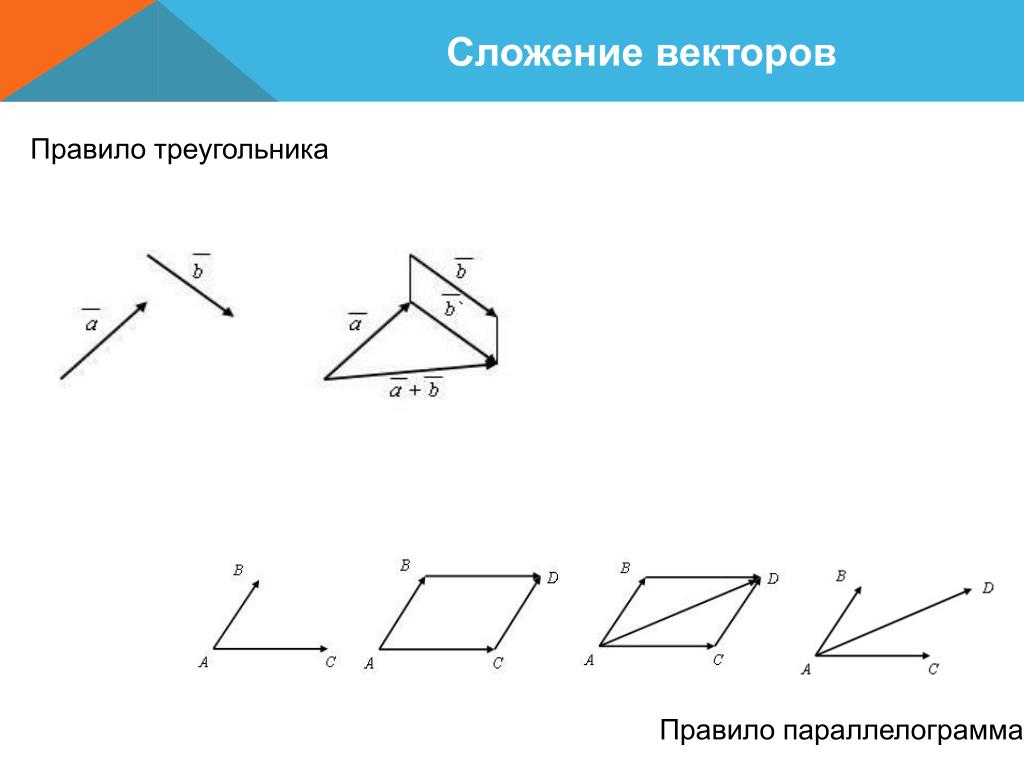 Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты являются минусами компонентов x — и y -компоненты равнодействующей, таким образом,
Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты являются минусами компонентов x — и y -компоненты равнодействующей, таким образом,
и
, а остальная часть метода, описанного выше, идентична методу сложения. (См. рис. 10.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль, Глава 3.4 Движение снаряда, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
Рисунок 10. Вычитание двух векторов, показанных на рисунке 5. Компоненты -B являются минусами компонентов B . Метод вычитания такой же, как и для сложения.ИССЛЕДОВАНИЯ PHET: ДОБАВЛЕНИЕ ВЕКТОРОВ
Узнайте, как добавлять векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги для добавления векторов и использования аналитического метода следующие:
Шаг 1: Определите систему координат для векторов. Затем определите горизонтальную и вертикальную составляющие каждого вектора, используя уравнения
.и
Шаг 2: Сложите горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты и результирующий вектор,
и
Шаг 3: Используйте теорему Пифагора, чтобы определить величину результирующего вектора
Шаг 4: Используйте тригонометрическую идентичность для определения направления
- аналитический метод
- метод определения величины и направления результирующего вектора с использованием теоремы Пифагора и тригонометрических тождеств
ВЕКТОРОВ И СЛОЖЕНИЯ ВЕКТОРОВ Помощь с домашними заданиями по физике, Помощь с заданиями и проектами по физике, Задания Репетиторы онлайн
Некоторые физические величины, такие как время, температура, масса, плотность и электрический заряд, могут быть полностью описаны одним числом с единицей измерения. Но многие другие важные величины имеют связанное с ними направление и не могут быть описаны одним числом. Такие величины играют важную роль во многих центральных темах физики, включая движение и его причины, а также явления электричества и магнетизма. Простым примером количества с направлением является движение самолета. Чтобы полностью описать это движение, мы должны сказать не только, с какой скоростью движется самолет, но и в каком направлении. Чтобы лететь из Чикаго в Нью-Йорк, самолет должен лететь на восток, а не на юг. Скорость самолета в сочетании с направлением его движения вместе составляют величину, называемую скоростью. Другим примером является сила, которая в физике означает толчок или притяжение, действующее на тело. Дать полное описание силы означает описать как силу, с которой сила давит или тянет на тело, так и направление толчка или притяжения.
Но многие другие важные величины имеют связанное с ними направление и не могут быть описаны одним числом. Такие величины играют важную роль во многих центральных темах физики, включая движение и его причины, а также явления электричества и магнетизма. Простым примером количества с направлением является движение самолета. Чтобы полностью описать это движение, мы должны сказать не только, с какой скоростью движется самолет, но и в каком направлении. Чтобы лететь из Чикаго в Нью-Йорк, самолет должен лететь на восток, а не на юг. Скорость самолета в сочетании с направлением его движения вместе составляют величину, называемую скоростью. Другим примером является сила, которая в физике означает толчок или притяжение, действующее на тело. Дать полное описание силы означает описать как силу, с которой сила давит или тянет на тело, так и направление толчка или притяжения.
Когда физическая величина описывается одним числом, мы называем ее скалярной величиной. Напротив, векторная величина имеет как величину (часть «сколько» или «насколько большая»), так и направление в пространстве.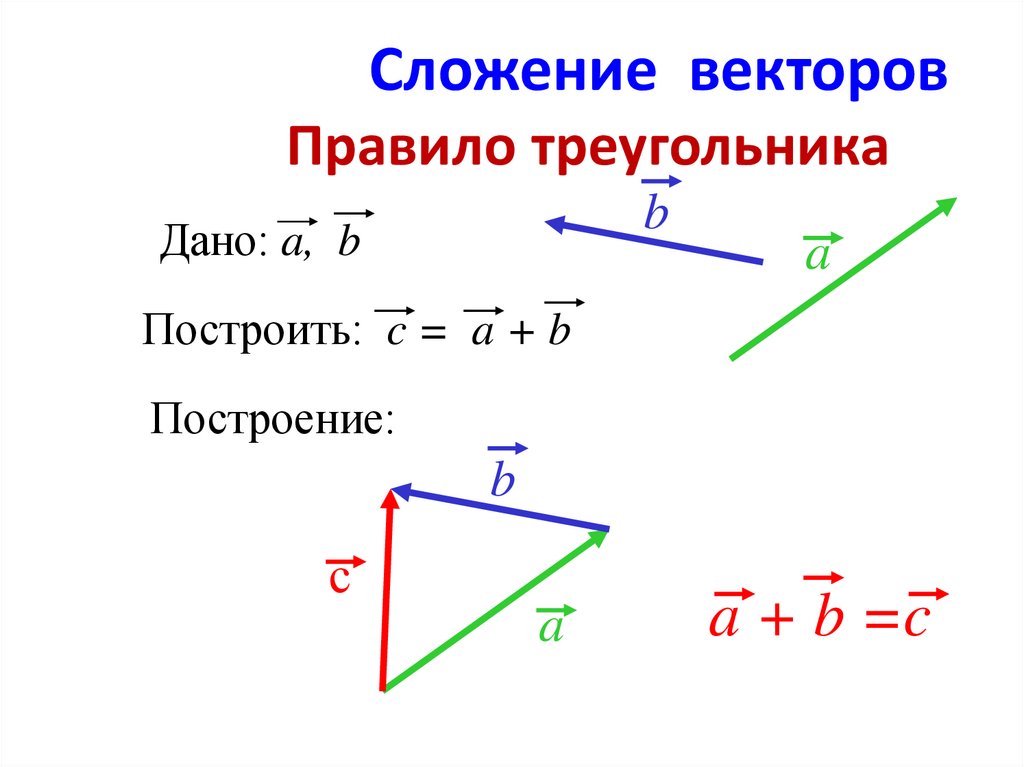 Расчеты со скалярными величинами используют операции
Расчеты со скалярными величинами используют операции
обычной арифметики. Например, 6 кг + 3 кг = 9 кг или 4 х 2 с = 8 с. Однако для объединения векторов требуется другой набор операций. Чтобы больше узнать о векторах и о том, как они комбинируются, мы начнем с простейшей векторной величины — смещения. Смещение — это просто изменение положения точки. (Точка может представлять собой частицу или маленькое тело.) На рис. 1-4а мы представляем изменение положения от точки p. до точки Pz линией от PI до ~ со стрелкой в Pz, обозначающей направление движения, Смещение является векторной величиной, потому что мы должны указать не только, как далеко движется частица, но и в каком направлении. Пройдя 3 км на север от входной двери, вы не окажетесь в том же месте, что и пройдя 3 км на юго-восток; эти два смещения имеют одинаковую величину, но разные направления.
Обычно мы представляем векторную величину, такую как смещение, одной буквой, например, A на рис. 1-4a. В этой книге мы всегда печатаем векторные символы полужирным курсивом со стрелкой над ними. Мы делаем это, чтобы напомнить вам, что свойства векторных величин отличаются от свойств скалярных величин; стрелка напоминает, что векторы имеют направление. В рукописном вводе векторные символы обычно подчеркиваются или пишутся со стрелкой над ними (рис. 1-4). Когда вы пишете символ для вектора, всегда записывайте его в одном из этих
Мы делаем это, чтобы напомнить вам, что свойства векторных величин отличаются от свойств скалярных величин; стрелка напоминает, что векторы имеют направление. В рукописном вводе векторные символы обычно подчеркиваются или пишутся со стрелкой над ними (рис. 1-4). Когда вы пишете символ для вектора, всегда записывайте его в одном из этих
способов. Если вы не различаете скалярные и векторные величины в своих обозначениях, вы, вероятно, не будете различать их и в своем мышлении, что приведет к безнадежной путанице.
При рисовании любого вектора мы всегда рисуем линию со стрелкой на конце. Длина линии показывает величину вектора, а направление линии показывает направление вектора. Смещение всегда представляет собой прямолинейный отрезок, направленный от начальной точки
к конечной точке, даже если фактический путь частицы может быть искривлен. На рис. 1-4b частица движется по криволинейной траектории, показанной от PI к Pz, но смещение по-прежнему является вектором A.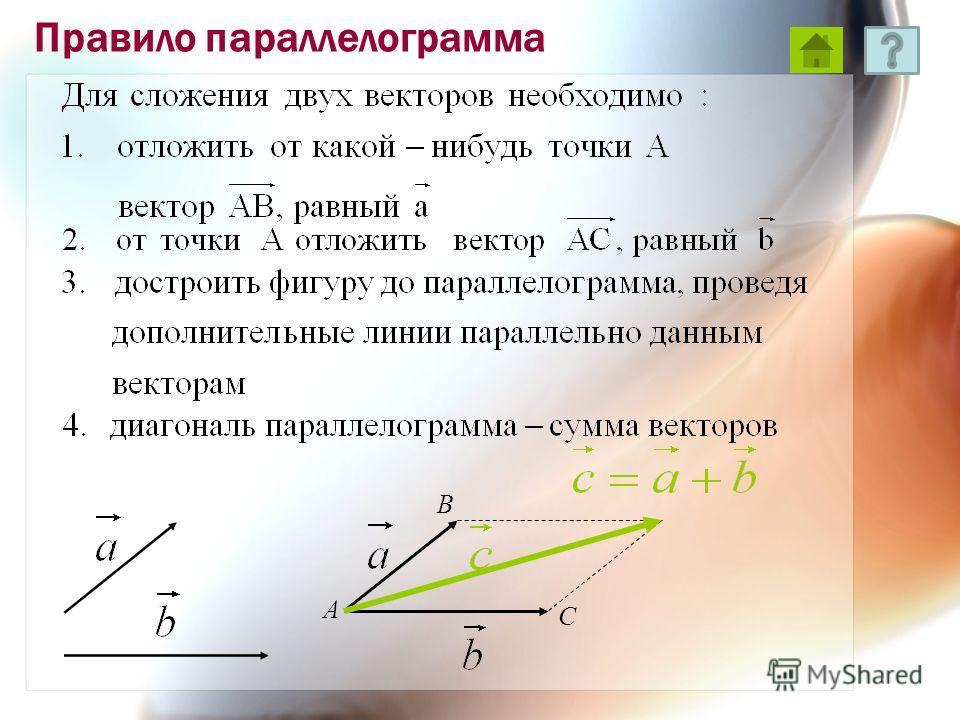 Обратите внимание, что смещение не связано напрямую с полным. Если бы частица продолжила движение до l’:! а затем вернуться к PI’ dis-:’:’=:z::z: f,X», вся поездка будет равна нулю. имеют одинаковое направление, они параллельны.
Обратите внимание, что смещение не связано напрямую с полным. Если бы частица продолжила движение до l’:! а затем вернуться к PI’ dis-:’:’=:z::z: f,X», вся поездка будет равна нулю. имеют одинаковое направление, они параллельны.
Если они имеют одинаковое направление, они равны, независимо от того, где они расположены в пространстве. от точки р) до точки ~ на рис. 1-5 имеет одинаковую длину и направление. Они равны, даже несмотря на то, что они начинаются с того, что мы пишем это как A на рис. 1-5, использование полужирного знака равенства для равенства двух векторных величин не является тем же отношением, что и равенство «количеств». Две векторные величины равны только тогда, когда они имеют одно и то же направление.
Вектор на рис. 1-5, однако, не равен A, потому что его направление противоположно e определяют отрицательное значение вектора как вектор, имеющий ту же величину. вектор, но в противоположном направлении. Отрицательное значение векторной величины A равно , и мы используем полужирный знак минус, чтобы подчеркнуть векторный характер X в 87 м к югу, тогда -1 означает 87 м к северу.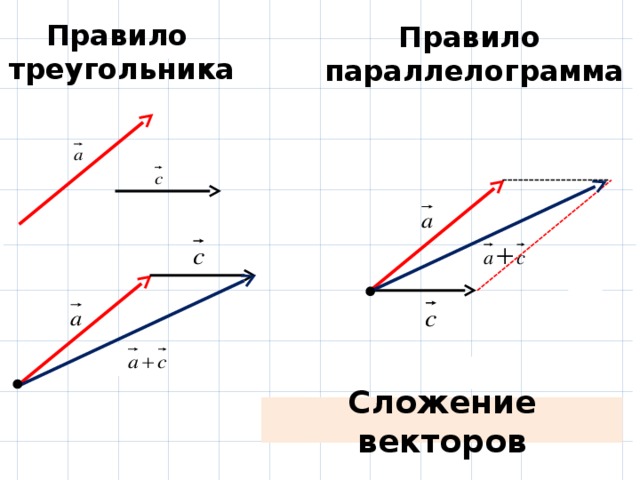
Таким образом, отношение между и будет записано как. та же буква, используемая для вектора, но выделенная светлым курсивом сверху, а не полужирным курсивом со стрелкой (которая зарезервирована для векторов). I. (1-2) z J o модуль векторной величины является скалярной величиной (числом). Отметим также, что вектор никогда не может быть равен скаляру, потому что они виды величин.
Выражение «1 = 6 м» так же неверно, как и «на 2 меньше» или «6 1 b = 7 км на диаграммах с векторами, мы обычно будем использовать масштаб, аналогичный используемому — расстояние на диаграмме равно пропорционально величине примера, смещение в 5 км может быть представлено на диаграмме с помощью vecg, поскольку диаграмма в реальном размере непрактична. Когда мы работаем с 2 с единицами измерения, отличными от смещения, такими как сила или скорость, мы должны На диаграмме для векторов силы мы могли бы использовать шкалу, в которой вектор, равный _, представляет силу величиной 5 Н.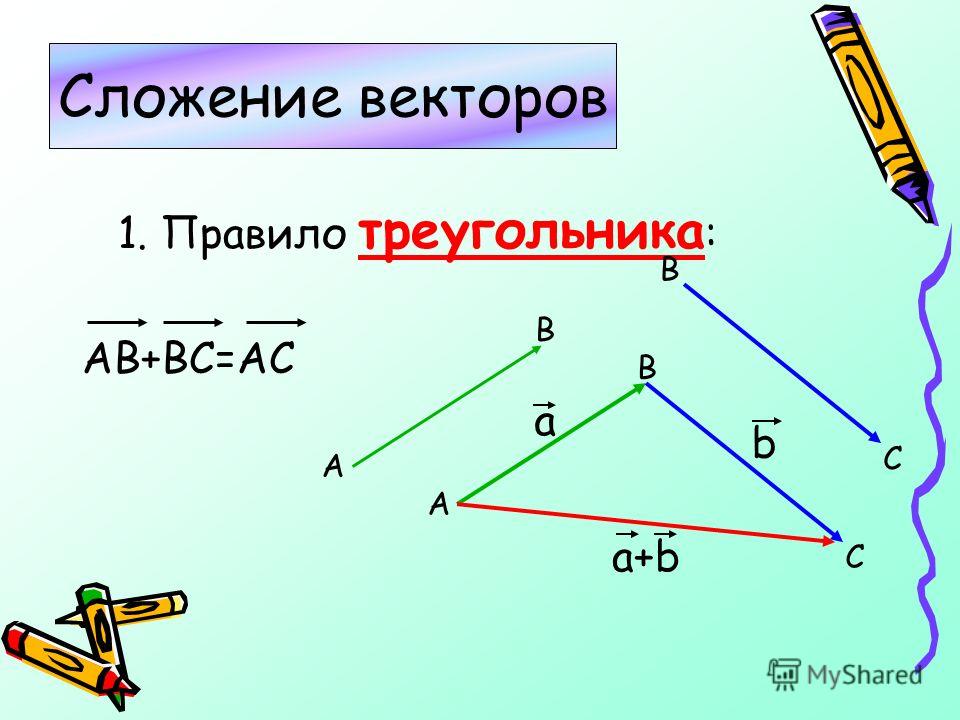 Сила 20 Н будет представлен 4 em в длину с соответствующим направлением.
Сила 20 Н будет представлен 4 em в длину с соответствующим направлением.
ВЕКТОРНОЕ СЛОЖЕНИЕ
Теперь предположим, что частица испытывает смещение 1, за которым следует второе смещение -6a), Окончательный результат такой же, как если бы частица стартовала в том же начальном состоянии претерпела единственное смещение C, как показано. Мы называем смещение C результирующим вектором смещений 1 и ii. Мы выражаем эту связь символически.
Жирный знак плюса подчеркивает, что добавление двух векторных величин требует геометрической операции – это не то же самое, что добавление двух скалярных величин, таких как . При сложении векторов мы обычно помещаем хвост второго вектора в головной вектор (рис. 1-6а). произвести перемещения 1 и ii в обратном порядке, причем ii сначала то же самое (рис. 1-6б),
Как решать задачи кинематики: руководство по векторам
Эта статья является третьей главой в серии о том, как понимать задачи кинематики и подходить к ним. В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.
В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.
Есть много способов думать о векторах, но основное определение — это величина (число) и направление. Так что «четыре метра на восток» — это просто вектор в словесной форме. Вы также можете думать о векторе как о стрелке; он указывает определенное расстояние в определенном направлении.
Все это векторы, причем красивые векторы.
Добавление векторовДобавление векторов работает не так, как добавление чисел. Мы не можем просто суммировать величины (это распространенная ошибка), потому что это не учитывает направление. В конце концов, если вы пройдете 8 метров на восток, а затем 5 метров на запад, вы не окажетесь в 13 метрах от того места, откуда начали; вам будет всего 3 года (мы видели вариант этой идеи в главе 1, посвященной перемещению)
При сложении векторов вместо суммирования величин мы наклеиваем один на конец другого и смотрим, где они окажутся.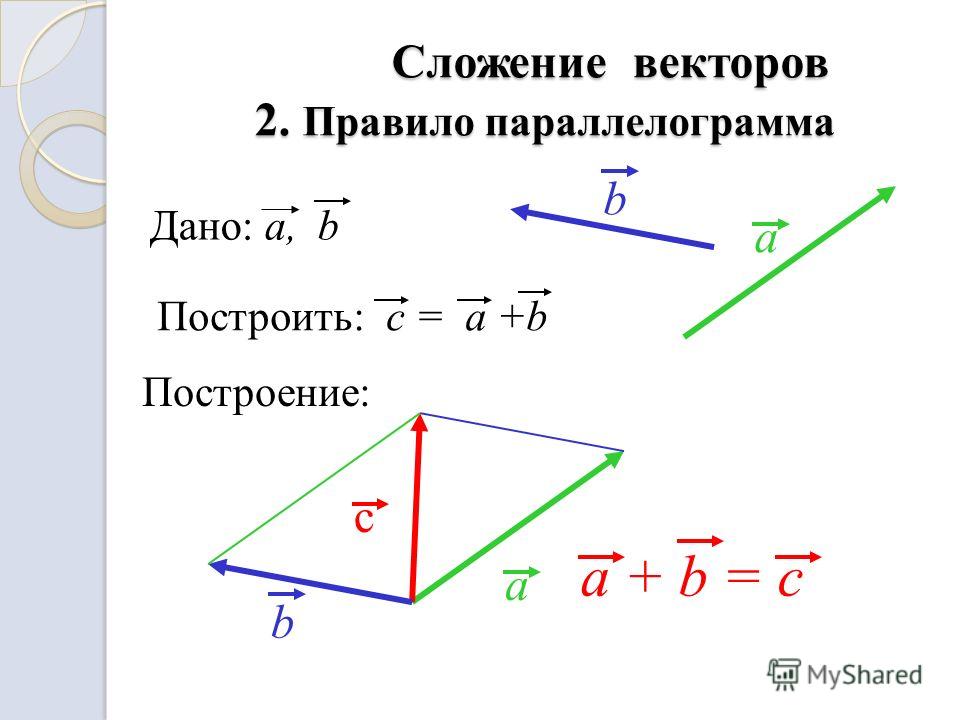
Итак, если я хочу добавить этот вектор к этому вектору
, я могу соединить их вместе, чтобы получить:
Мы называем красный вектор «результирующим», потому что он является результирующим. от сложения двух векторов вместе
Компоненты вектораЧтобы прояснить векторы, мы часто записываем их как сумму их «компонентов». Каждый компонент сообщает, как далеко заходят векторы в определенном направлении. Обычно согласованный набор направлений составляет x̂, ŷ , ẑ . В книгах по физике эти направления иногда называют х , х , k̂ , потому что они глупы (на самом деле это делается для упрощения векторных полей, когда дело доходит до продвинутого уровня).
Почему это работает? Добавление вектора! Поскольку векторы складываются, мы можем думать о каждом векторе как о сумме 2 (в 2D) или 3 (в 3D) векторов, которые движутся только в направлениях x, y или z.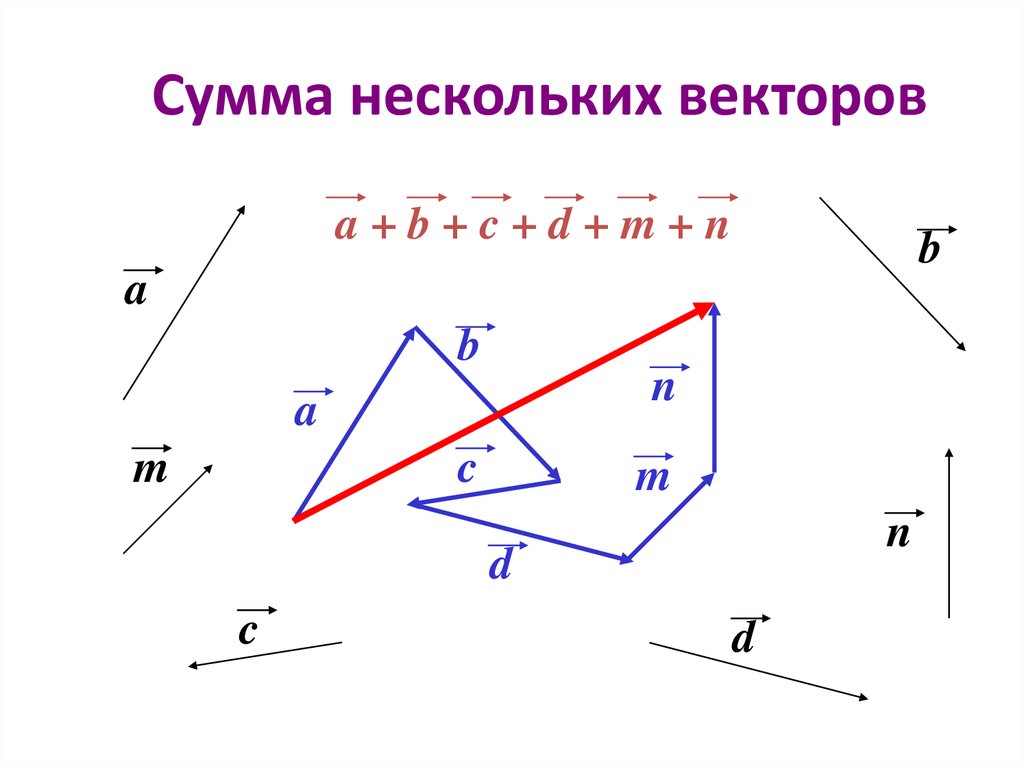
Допустим, вы получили вектор с определенной величиной и углом от горизонтали (также известный как ось x) и хотите найти компоненты векторов. Это очень распространено в кинематике и за ее пределами, но как вы это делаете? Ответ тот же, что и у любой успешной фолк-рок группы: правильное использование треугольников.
Помните, мы разделили наш вектор на компоненты? Вы могли заметить, что компоненты и исходный вектор образуют прямоугольный треугольник. Это связано с тем, что оси x и y по определению всегда расположены под углом 90° друг к другу. Вы также можете помнить из геометрии, что если у нас есть угол и гипотенуза прямоугольного треугольника, то мы можем найти другие стороны (называемые катетами) с помощью SOH-CAH-TOA.
Вы можете найти более подробные обзоры в Интернете, но основная идея SOH-CAH-TOA заключается в том, что синус угла равен стороне, противоположной углу деленная на гипотенузу (таким образом, S=O/H или SOH). Точно так же косинус равен прилежащей стороне относительно гипотенузы (C=A/H), а тангенс равен противолежащей стороне прилежащей стороны (T=O/A). Используя это, легко доказать, что вертикальный катет, направление y, нашего составного треугольника будет гипотенузой*sin(угол). Или, поскольку гипотенуза — это исходный вектор, векторная величина*sin(угол). Точно так же направление x будет просто векторной величиной * cos (угол).
Пример: Нахождение компонентов вектораУ меня есть вектор величиной 5 метров, который направлен вверх и вправо под углом 37 градусов к оси x. Я хочу знать форму компонента. Давайте проработаем это.
Шаги:
- Нарисуйте вектор.

- Добавьте треугольные ножки.
- Математика
Y-направление = величина * sin(угол) = 5 метров * sin (37) = 3 метра
x-направление = величина * cos(угол) = 5 метров * cos (37) = 4 метра
- Подставьте решения в определение вектора
Вектор = 3x̂ + 4 х
Тада, просто как π!
Иногда вам могут быть заданы компоненты вектора, и вы хотите найти общую величину и угловое направление этого вектора. И снова на помощь приходят треугольники.
Величину вектора легко вычислить по теореме Пифагора. Из теоремы Пифагора a 2 +b 2 =c 2 , поэтому, когда мы применим это к векторам: компонент) 2 .
Чтобы найти угловое направление вектора, мы можем использовать арктангенс. Поскольку тангенс равен стороне, противоположной прилежащей стороне (T=O/A):
tan(угол вектора)=(y-компонента)/(x-компонента)
Затем используйте функцию invtan на вашем калькуляторе, чтобы найти обратную сторону этого тангенса, которая дает вам угол.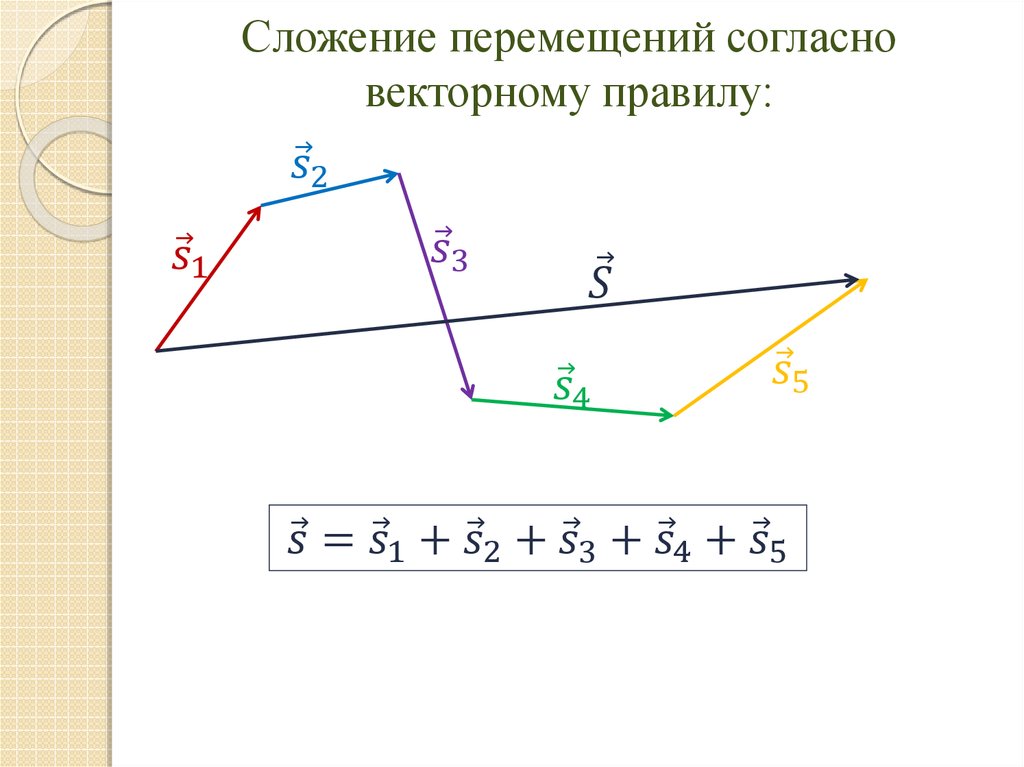
Самое лучшее в векторных компонентах то, что они упрощают добавление векторов. Пока мы сохраняем компоненты x, y и z разными, мы можем просто добавлять компоненты. Таким образом, если V 1 = (x 1 , y 1 , z 1 ) и V 2 = (x 2 , y 2 , z 0797 2 ), то вектор их суммы равен V 1 +V 2 =(x 1 +x 2 , y 1 +y 7 2 90 1 , 7 9 0 9 9 z 9 2 ). Когда у вас есть этот новый вектор, вы можете использовать предыдущий раздел, чтобы найти величину и угловое направление.
ЗаключениеТеперь мы знаем, что такое вектор, как разделить его на компоненты, как сложить эти компоненты и как рекомбинировать его по величине и углу. В нашем следующем блоге мы обсудим, как использовать эти векторы для кинематики в двух измерениях.
Физика колледжа: сложение и вычитание векторов: графические методы
Смещение можно определить графически, используя масштабную карту, такую как карта Гавайских островов.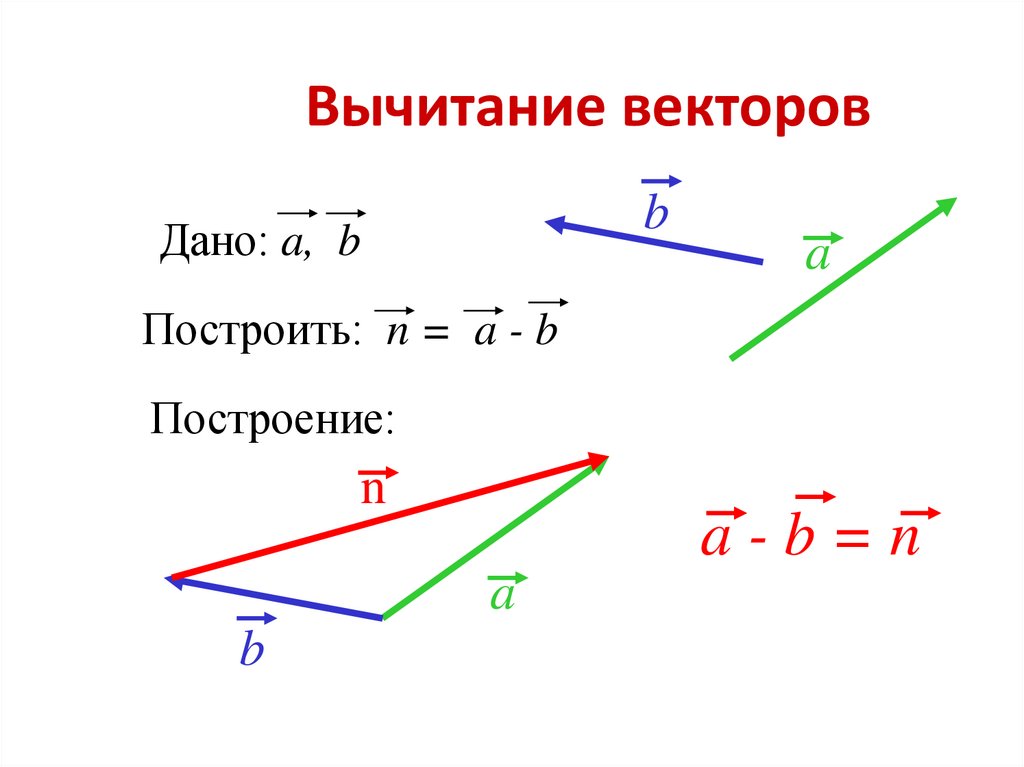 Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США)
Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США)Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
[ссылка] показывает такое графическое представление вектора , используя в качестве примера полное перемещение человека, идущего по городу, рассмотренное в Кинематике в двух измерениях: введение. Мы будем использовать обозначение, что жирный шрифт, такой как D size 12{D} {}, обозначает вектор. Его величина представлена символом, выделенным курсивом, размером D 12{D} {}, а его направление размером θ 12{θ} {}.
Его величина представлена символом, выделенным курсивом, размером D 12{D} {}, а его направление размером θ 12{θ} {}.
Векторы в этом тексте
В этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором F size 12{F} {}, который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например, F размером 12{F} {}, а направление переменной будет задано углом θ размером 12{θ} {}.
Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29,1º размером 12{«29» «.» «1º»} {} к северу от востока. Чтобы графически описать результирующий вектор для человека, идущего по городу, рассматриваемому в [ссылка], нарисуйте стрелку, чтобы представить вектор полного смещения D размером 12{D} {}. С помощью транспортира начертите линию под углом θ размером 12{θ} {} относительно оси восток-запад. Длина D size 12{D} {} стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки.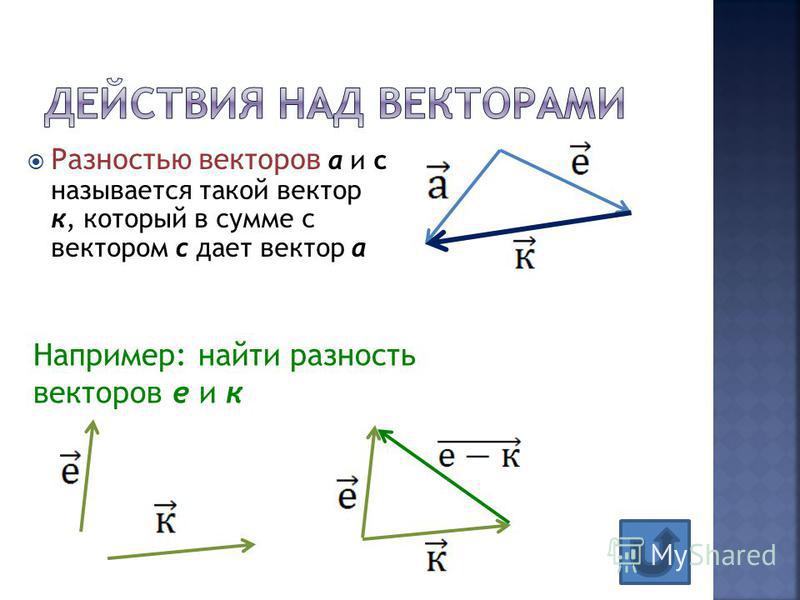 В этом примере величина D размера 12{D} {} вектора составляет 10,3 единицы, а направление θ размера 12{θ} {} равно 29.1º размер 12{«29» «.» 1 rSup { размер 12{º} } } {} к северу от востока.
В этом примере величина D размера 12{D} {} вектора составляет 10,3 единицы, а направление θ размера 12{θ} {} равно 29.1º размер 12{«29» «.» 1 rSup { размер 12{º} } } {} к северу от востока.Метод «голова к хвосту» — это графический способ добавления векторов, описанный в [ссылка] ниже и в следующих шагах. Хвост вектора — это начальная точка вектора, а начало (или кончик) вектора — это конечный заостренный конец стрелки.
Метод «голова к хвосту»: Метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного в [ссылка]. (a) Нарисуйте вектор, представляющий смещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Нарисуйте линию от конца вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы сформировать сумму или результирующий вектор D размера 12{A} {}. Длина стрелки D size 12{A} {} пропорциональна величине вектора и составляет 10,3 единицы. Его направление, описываемое как угол по отношению к востоку (или горизонтальной оси) θ размером 12{θ} {}, измеряется с помощью транспортира и составляет 29.1º размер 12{«29» «.» 1°} {}.
Длина стрелки D size 12{A} {} пропорциональна величине вектора и составляет 10,3 единицы. Его направление, описываемое как угол по отношению к востоку (или горизонтальной оси) θ размером 12{θ} {}, измеряется с помощью транспортира и составляет 29.1º размер 12{«29» «.» 1°} {}.Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 блоков на север). Поместите конец второго вектора в начало первого вектора .
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от кончика до хвоста 9.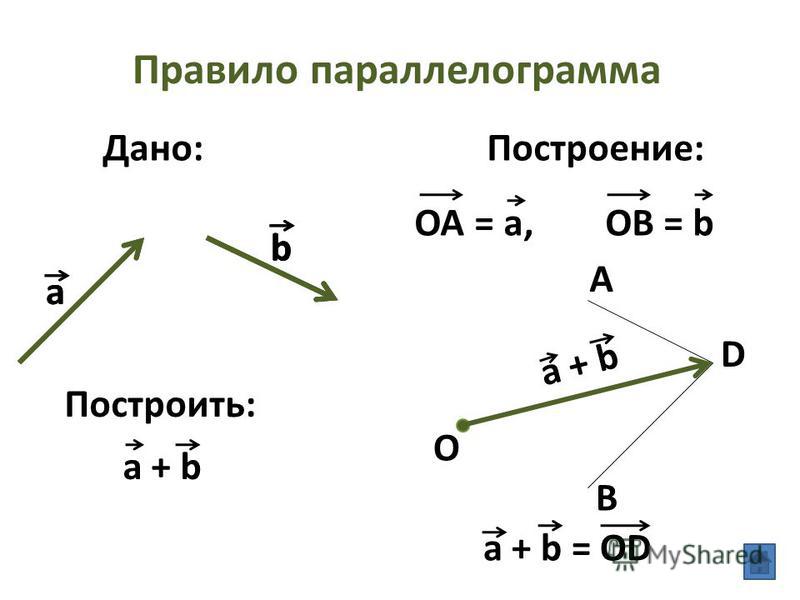 0190 .
0190 .
Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который он образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть сделаны чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Это справедливо для любого количества векторов.
Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке
Используйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по плоскому полю. Сначала она проходит 25,0 м в направлении 49,0º размера 12{«49» «.» «0º»} {} к северу от востока. Затем она проходит 23,0 м курсом 15,0º размером 12{«15» «.» «º°»} {} к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, пометив первый размер A 12{A} {}, второй размер B 12{B} {} и третий размер C 12{C} {} , делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначенного как R size 12{R} {}.
Решение
(1) Нарисуйте три вектора смещения.
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
(3) Нарисуйте результирующий вектор размером R 12{R} {}.
(4) Используйте линейку для измерения величины R размера 12{R} {} и транспортир для измерения направления R размера 12{R} {}. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
В этом случае видно, что полное смещение R размером 12{R} {} имеет величину 50,0 м и лежит в направлении 7,0º размера 12{7 «.» 0°} {} к югу от востока. Используя его величину и направление, этот вектор можно выразить как R=50,0 м, размер 12{R» = 50″ «.» «0 м»} {} и θ=7,0º размер 12{θ=7 «. » «0°»} {} к югу от востока.
» «0°»} {} к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на [ссылка], и все равно получим то же решение.
Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно. Векторы можно добавлять в любом порядке.
А+В=В+А. size 12{«A+B=B+A»} {}
(Это верно и для сложения обычных чисел — вы получите тот же результат, если сложите 2+3 size 12{«2+3»} {} или же 3+2 размер 12{«3+2»} {}, например).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть размер B 12{B} {} из
Размер 12 {А} {}
, пишется A–B размер 12{ «A» «-B»} {}
, мы должны сначала определить, что мы подразумеваем под вычитанием. минус вектора B
определяется как –B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано в [ссылка]. Другими словами, размер B 12{B} {} имеет ту же длину, что и размер –B 12{«-» «B»} {}, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
минус вектора B
определяется как –B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано в [ссылка]. Другими словами, размер B 12{B} {} имеет ту же длину, что и размер –B 12{«-» «B»} {}, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора B из вектора A просто определяется как добавление –B к A. Обратите внимание, что вычитание вектора – это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
А – В = А + (–В).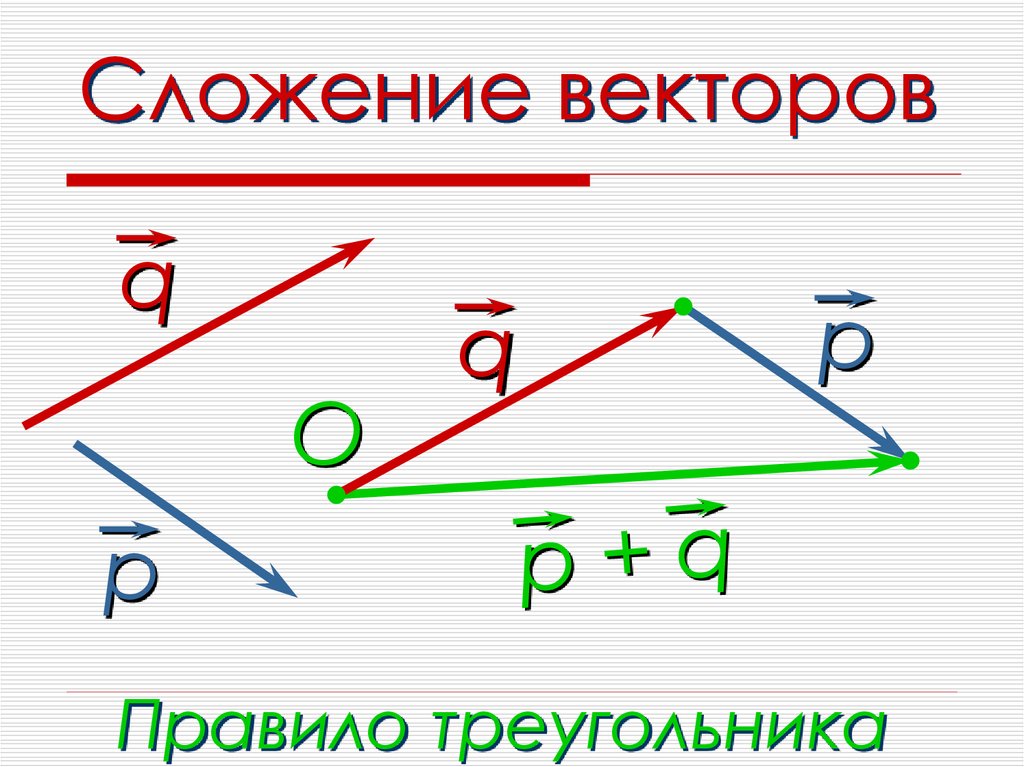 размер 12{ жирный «A – B = A + » \( жирный «–B» \) } {}
размер 12{ жирный «A – B = A + » \( жирный «–B» \) } {}
Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2) size 12{«5 – 2 = 5 + » \( «–2» \) } {}). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Графическое вычитание векторов: женщина, плывущая на лодке
Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласят, что сначала нужно пройти 27,5 м в направлении 66,0º размера 12{«66» «.» 0º} {} к северу-востоку от ее текущего местоположения, а затем пройдите 30,0 м в направлении 112º размера 12{«112″º} {} к северу от востока (или 22,0º размера 12{«22» «.» 0º} { } к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на второй этап поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап поездки с помощью вектора A, а второй этап поездки с помощью вектора
Размер B 12 {B} {}.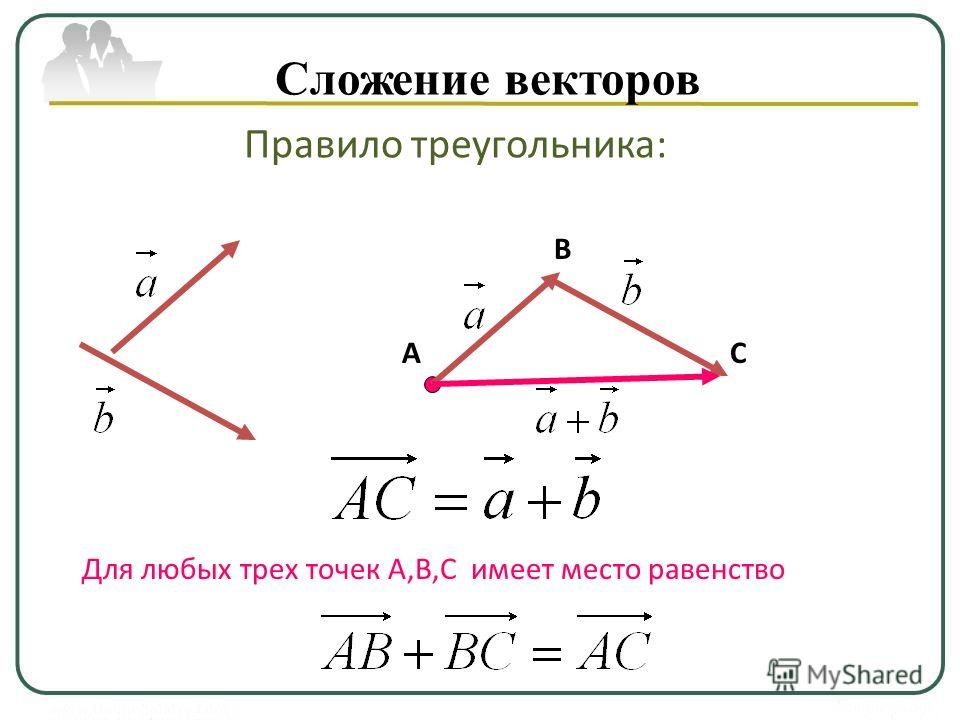 Пристань расположена в точке A + B. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от восток. Мы представляем это как –B, как показано ниже. Вектор –B имеет ту же величину, что и B, но направлен в противоположную сторону. Таким образом, она окажется в точке A+(–B) или A–B.
Пристань расположена в точке A + B. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от восток. Мы представляем это как –B, как показано ниже. Вектор –B имеет ту же величину, что и B, но направлен в противоположную сторону. Таким образом, она окажется в точке A+(–B) или A–B.
Мы выполним сложение векторов, чтобы сравнить местоположение причала, размер A + B 12{ ital «A «»+ «B} {}, с местом, в которое по ошибке прибыла женщина, размер A + (–B) 12{жирный «A + » \(жирный «–B» \) } {}.
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы A размером 12{A} {} и –B.
(2) Разместите векторы лицом к хвосту.
(3) Нарисуйте результирующий вектор R размером 12{R} {}.
(4) С помощью линейки и транспортира измерьте величину и направление размера R 12{R} {}.
В данном случае R=23,0 м размер 12{R»=23″ «.» «0 м»} {} а также θ=7,5º размер 12{θ=7 «.» «5° к югу от востока»} {} к югу от востока.
(5) Чтобы определить местоположение дока, мы повторяем этот метод, чтобы добавить векторы размера A 12{A} {} и размера B 12{B} {}. Получаем результирующий вектор R’ размер 12{R’} {}:
В этом случае R = 52,9 м размер 12{R» = 52″ «.» «9 м»} {} и θ=90,1º размер 12{θ=»90″ «.» «1° к северу от востока»} {} к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м размером 12{«3 » раз » 27″ «.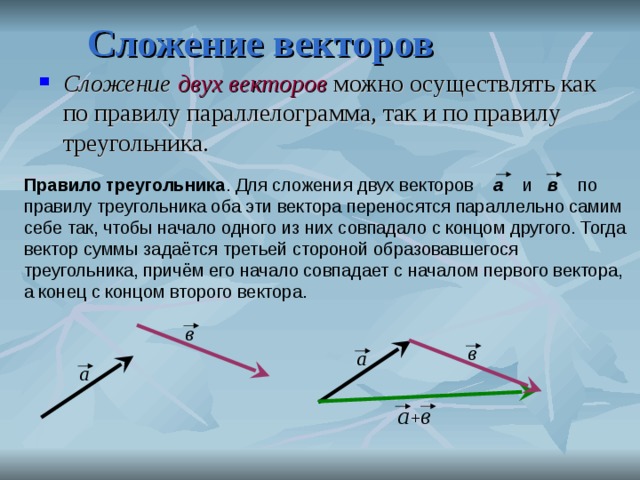 » «5 м»} {}, или 82,5 м, в направлении 66,0º размер 12{«66» «.» 0 { размер 12 {º} } } {} к северу от востока. Это пример умножения вектора на положительную скалярную величину. Обратите внимание, что величина меняется, но направление остается прежним.
» «5 м»} {}, или 82,5 м, в направлении 66,0º размер 12{«66» «.» 0 { размер 12 {º} } } {} к северу от востока. Это пример умножения вектора на положительную скалярную величину. Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор A размера 12{A} {} умножается на скаляр c размера 12{c} {},
- , величина вектора становится абсолютной величиной c размера 12. {c} {}A размер 12{A} {},
- , если c size 12{A} {} положителен, направление вектора не меняется,
- , если c size 12{A} {} является отрицательным, направление меняется на противоположное.
В нашем случае c=3размер 12{c=3} и A=27,5 mразмер 12{«A= 27,5 м»}.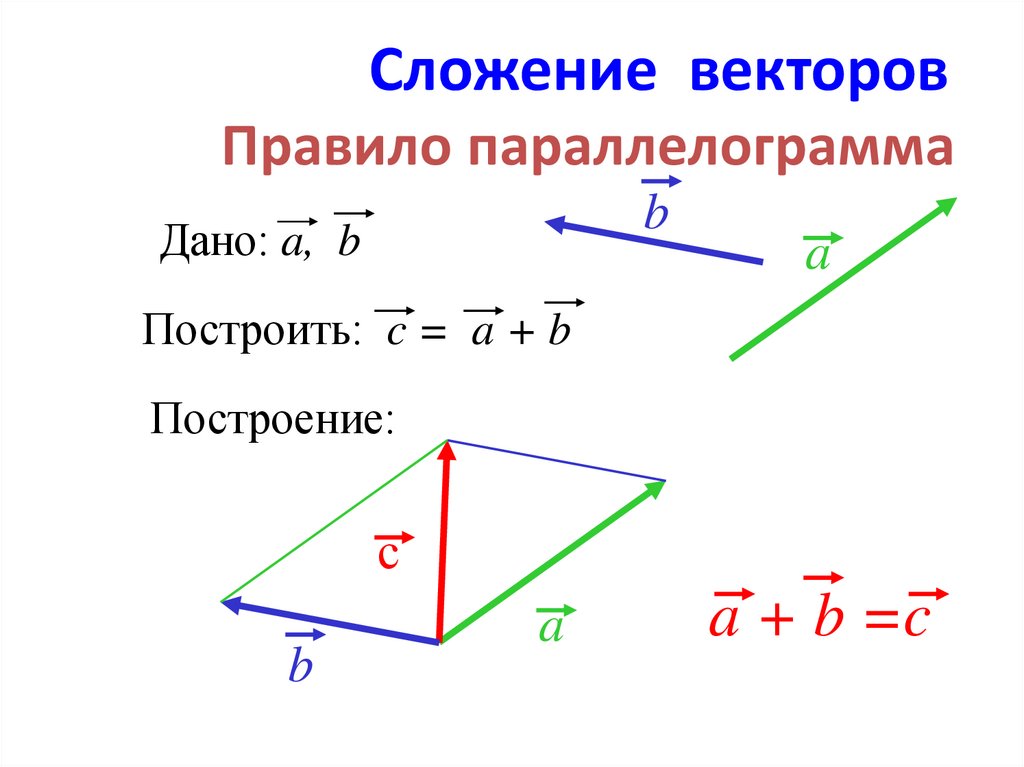 Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x — и y или компонентов север-юг и восток-запад.
Например, мы можем знать, что полное перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29.0º размер 12{«29» «.» 0º} } {} к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и север.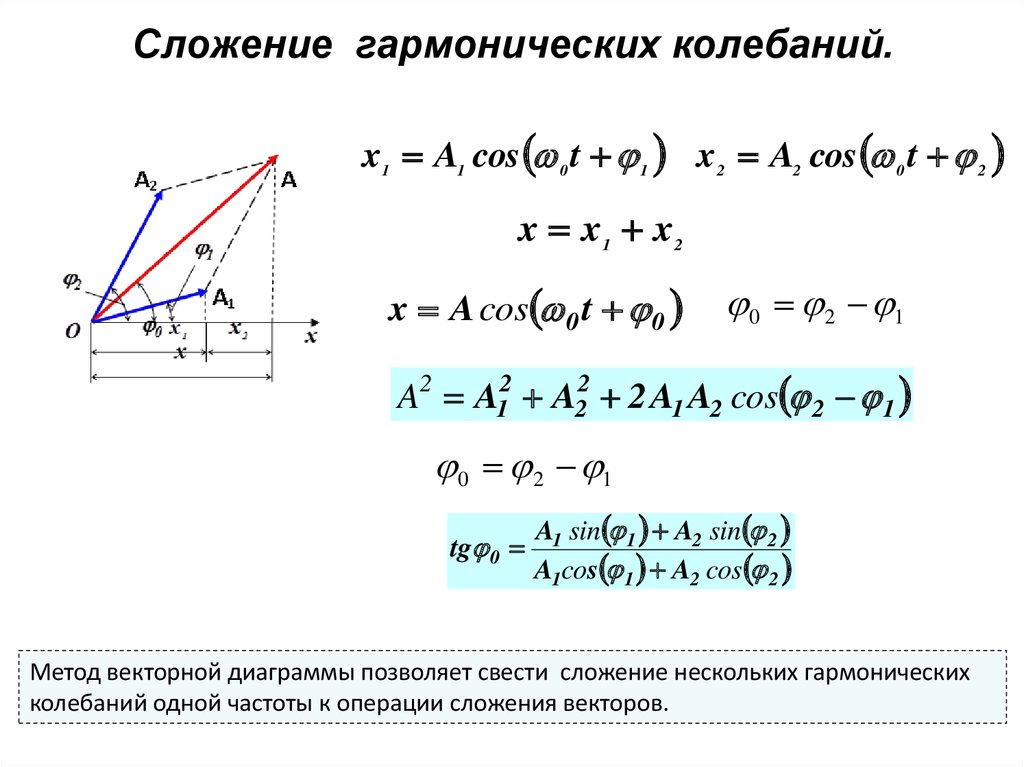 Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
PhET Explorations: Maze Game
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Постарайтесь достичь цели как можно быстрее.
- Графический метод сложения векторов размера A 12{A} {} и размера B 12{B} {} включает в себя рисование векторов на графике и их сложение с использованием метода «голова к хвосту». Результирующий вектор Размер R 12{A} {} определяется таким образом, что А+В=Р. Величина и направление размера R 12{A} {} затем определяются с помощью линейки и транспортира соответственно.
- Графический метод вычитания вектора B из A включает добавление противоположного вектора B, который определяется как -B size 12{ — B} {}. В этом случае A–B=A+(–B)=R. Затем обычным образом применяется метод сложения «голова к хвосту» для получения результирующего вектора R.
- Сложение векторов коммутативно, так что A+B=B+A size 12{«A + B = B + A»} {} .
- Метод сложения векторов «голова к хвосту» заключается в том, что первый вектор рисуется на графике, а хвост каждого последующего вектора помещается в начало предыдущего вектора.
 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора. - Если вектор A size 12{A} {} умножить на скалярную величину c size 12{A} {}, величина произведения будет равна cA size 12{ ital «cA»} {}. Если размер c 12{c} {} положительный, направление произведения указывает в том же направлении, что и размер A 12{A} {}; если c size 12{c} {} является отрицательным, направление произведения указывает в направлении, противоположном A size 12{A} {}.
Что из следующего является вектором: рост человека, высота на Эвересте, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?
Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.
Что общего между векторами и скалярами? Чем они отличаются?
Два отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый из которых идет своим путем, как показано ниже.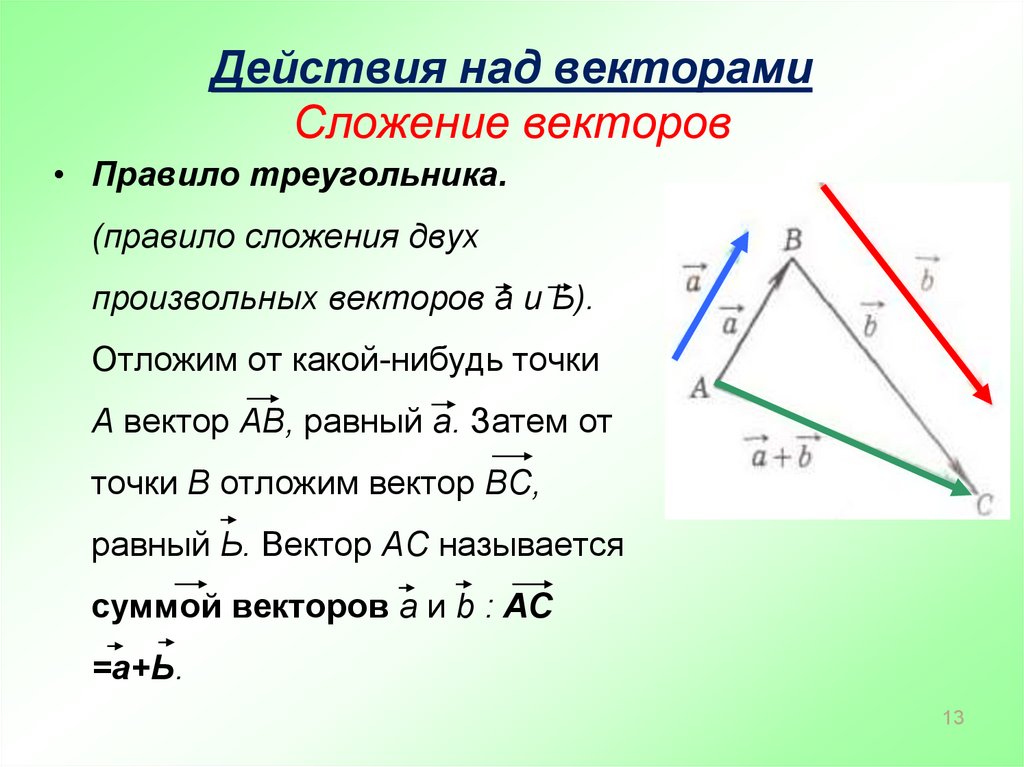 Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?
Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?
Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на [ссылка]. Какая еще информация ему понадобится, чтобы добраться до Сакраменто?
Предположим, вы делаете два шага A и B (то есть два ненулевых перемещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить нуль? Максимальное расстояние, которое вы можете пройти от начальной точки A+B, равно сумме длин двух шагов?
Объясните, почему невозможно добавить скаляр к вектору.
Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше?
0″ fo:font-weight=»bold»> Используйте графические методы для решения этих задач. Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр.Найдите следующее для пути A в [link]: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
Различные линии представляют пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м.(a) 480 м размер 12{«480 м»} {}
(b) 379 м размер 12{«379 м»} {}, 18,4º размер 12{«18» «.» «4º к востоку от севера»} {} к востоку от севера
Найдите следующее для пути B в [link]: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
Найдите северную и восточную составляющие смещения для туристов, показанных на [ссылка].
северная составляющая 3,21 км, восточная составляющая 3,83 км
Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A размером 12{A} {} и B размером 12{B} {}, как в [ссылка], то эта задача просит вас найти их сумму R = A + Размер B 12{«R = A + B»} {}. )
)
Предположим, вы сначала прошли 12,0 м в направлении 20º размер 12{«20» { размер 12{°} } } {} к западу от севера, а затем 20,0 м в направлении 40,0º размер 12{«40» { размер 12{° } } } {} к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A размера 12{A} {} и B размера 12{B} {}, как в [link], то эта задача находит их сумму R = A + B размер 12 {жирный «R = A + B»} {}.)
19,5 м размер 12{«19» «.» «5 м»} {}, 4,65º размер 12{4 «.» «65°»} {} к югу от запада
Повторите задачу, описанную выше, но поменяйте порядок двух этапов ходьбы; показать, что вы получаете тот же конечный результат. То есть сначала вы проходите участок B размера 12{B} {}, который составляет 20,0 м в направлении точно на 40º размера 12{«20» { размер 12{°} } } {} к югу от запада, а затем участок A размера 12{A} {}, что составляет 12,0 м в направлении точно на 20º размер 12{«20» { размер 12{°} } } {} к западу от севера. (Эта задача показывает, что размер A+B=B+A 12{A+B=B+A} {}.)
(Эта задача показывает, что размер A+B=B+A 12{A+B=B+A} {}.)
(a) Повторите задачу двумя предыдущими задачами, но для второго этапа вы пройдете 20,0 м в направлении 40,0º размера 12{«40,0» { размера 12{°} } } к северу от востока (что эквивалентно вычитанию B размер 12{B} {} от размера A 12{A} {}, то есть до нахождения R′=A−B размера 12{жирный шрифт «R'»=A — B} {}). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала проходите 20,0 м в направлении 40,0º размера 12{«40,0» {размера 12{°} } } к югу от запада, а затем 12,0 м в направлении 20,0º размера 12. {«20.0″ { размер 12{ ° } } } {} к востоку от юга (что эквивалентно вычитанию Размер 12{A} {} от размера B 12{B} {} — то есть до нахождения R»=B-A=-R’ размер 12{R»= B – A = -R’ } {}). Покажите, что это так.
(а) 26,6 м размер 12{«26» «.» «6 м»} {}, 65,1º размер 12{«65» «.» «1º»} {} к северу от востока
(b) 26,6 м размер 12{«26» «.» «6 м»} {}, 65,1º размер 12{«65» «.» «1º»} {} к югу от запада
Показать, что порядок сложения трех векторов не влияет на их сумму.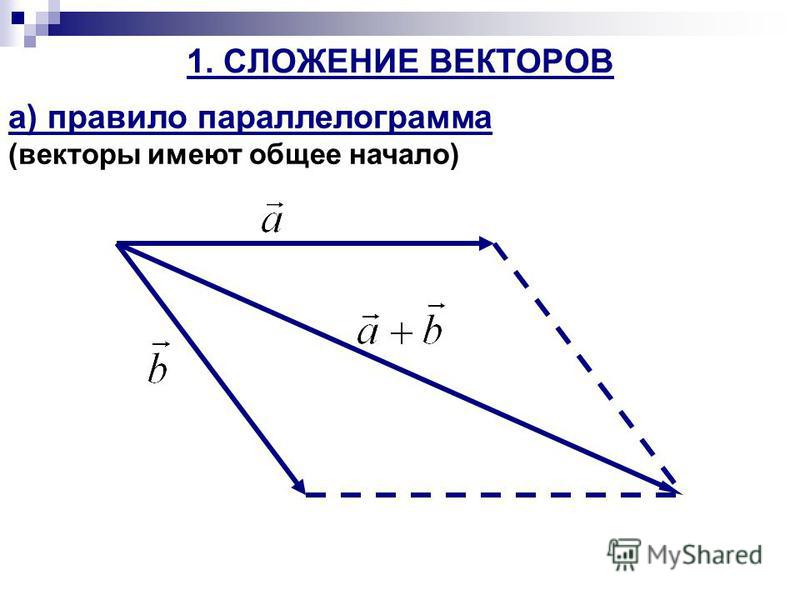


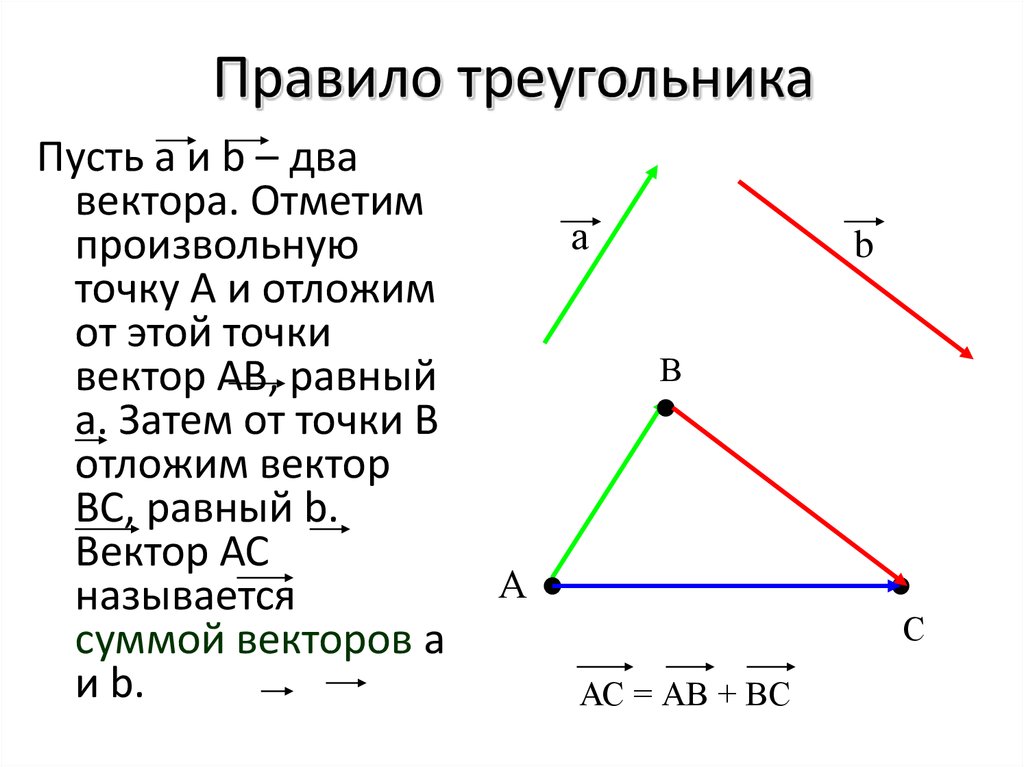
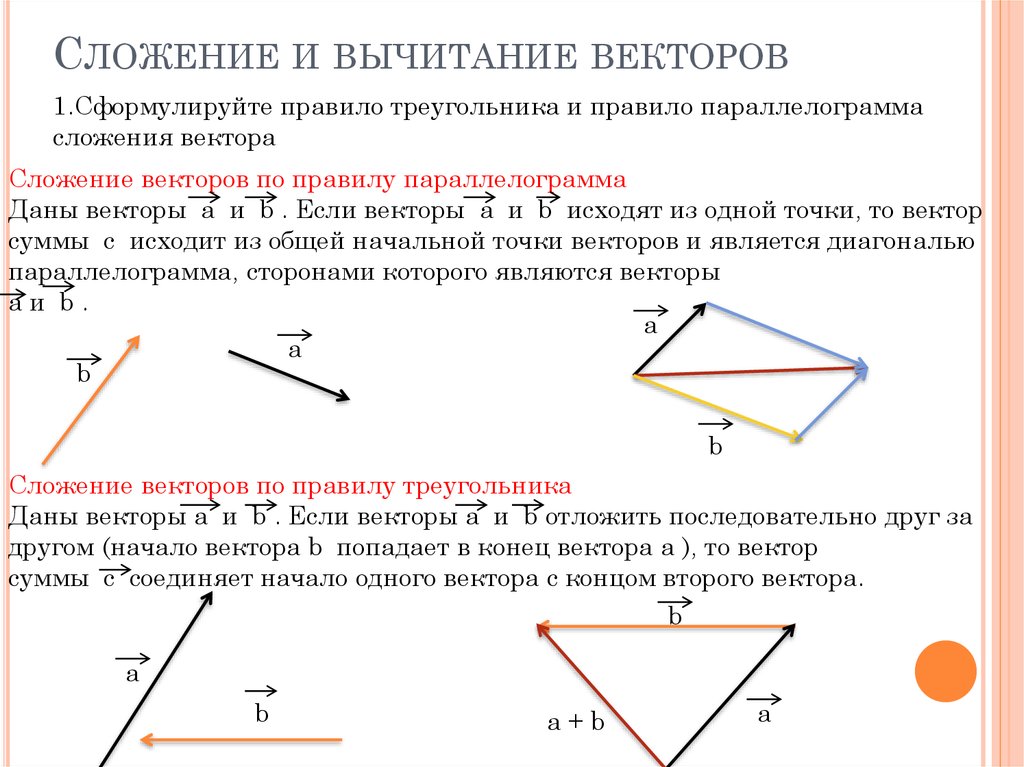
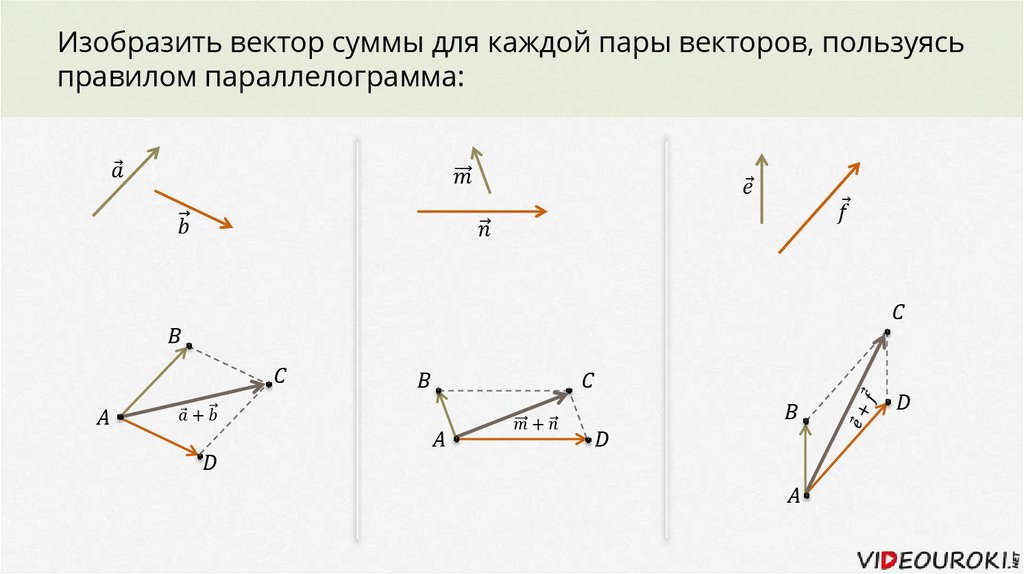


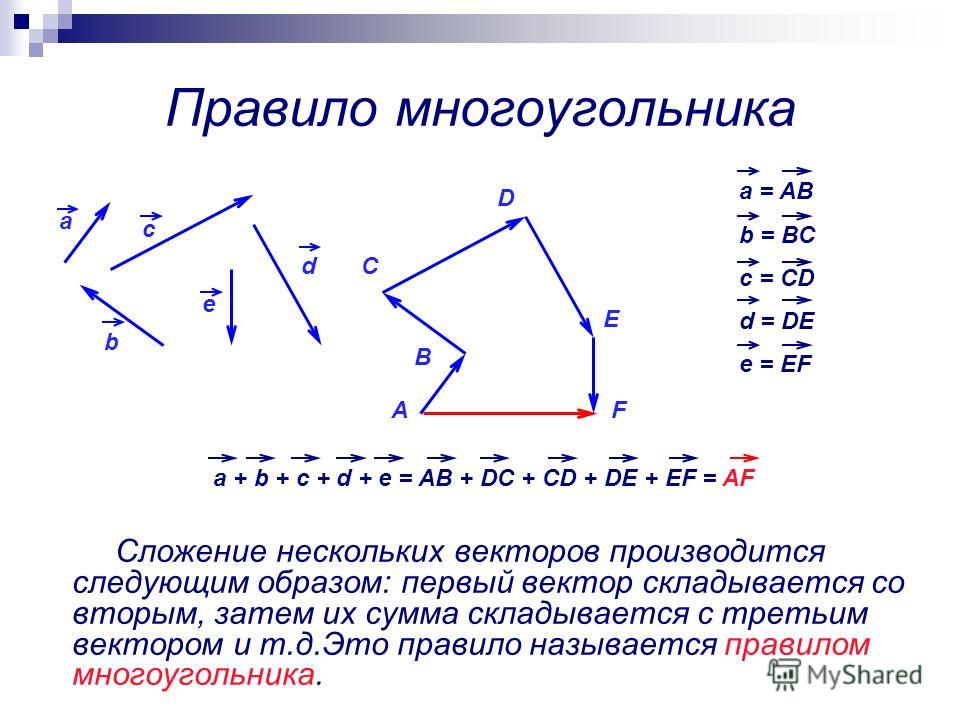
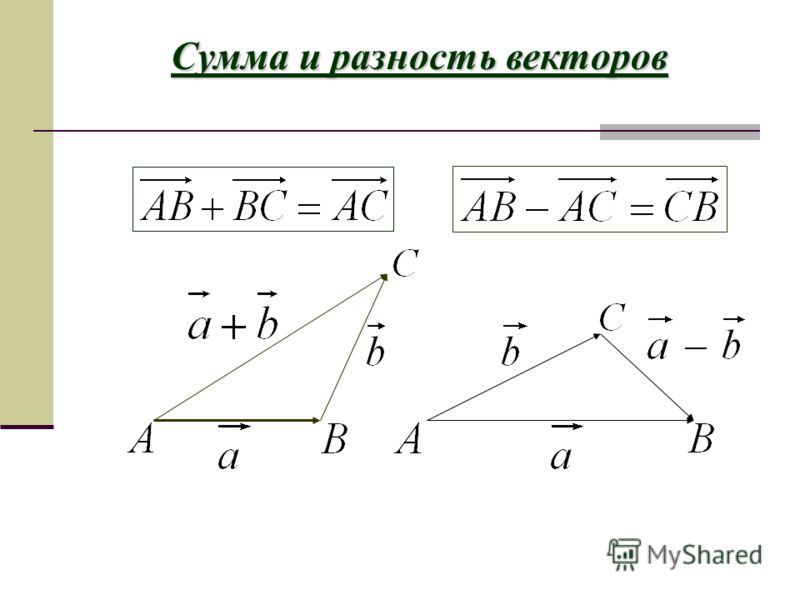
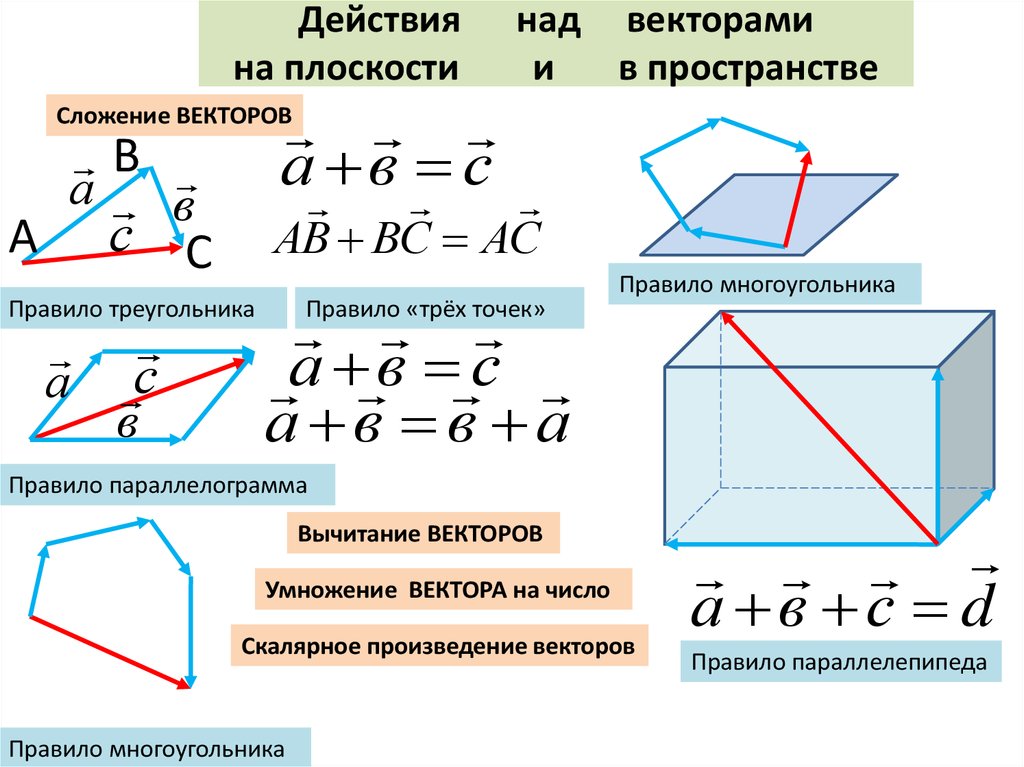

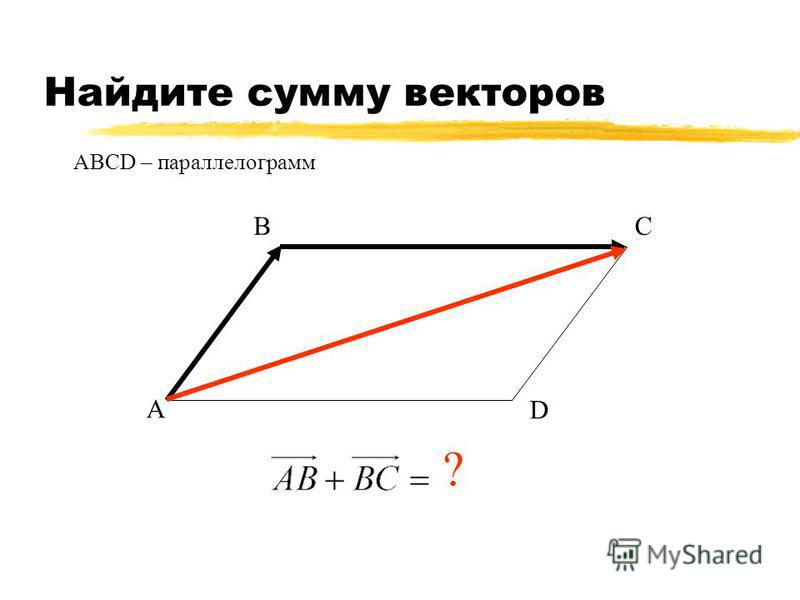

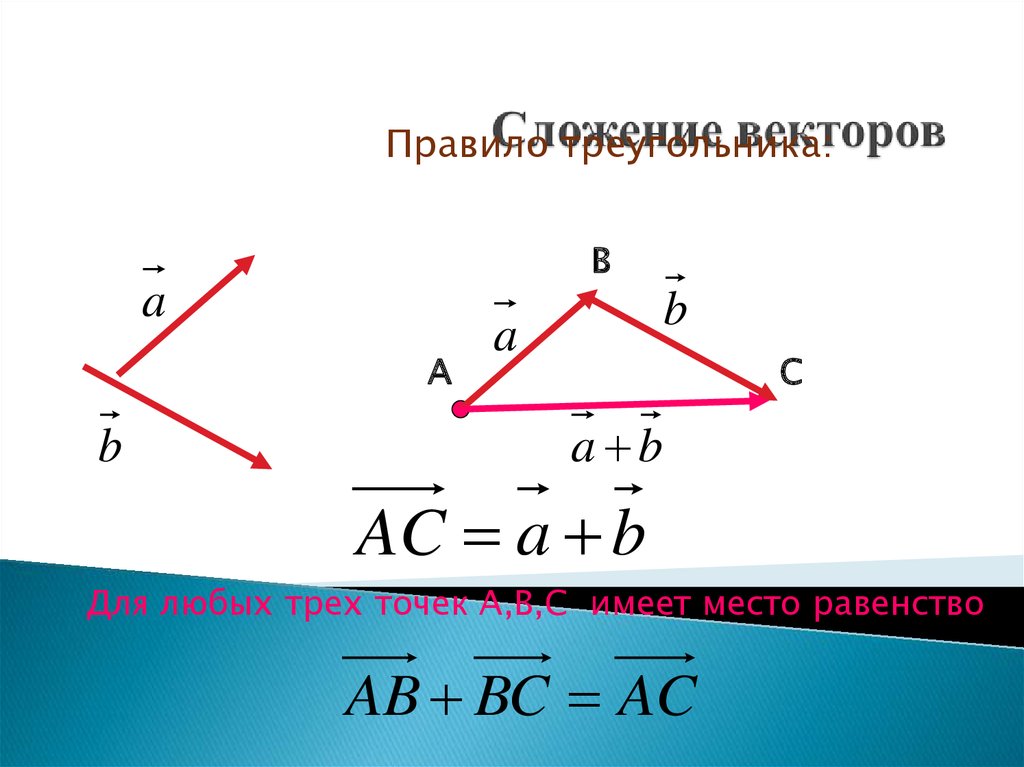 Выполните построение и покажите в каком направлении штурман должен вести судно по компасу.
Выполните построение и покажите в каком направлении штурман должен вести судно по компасу.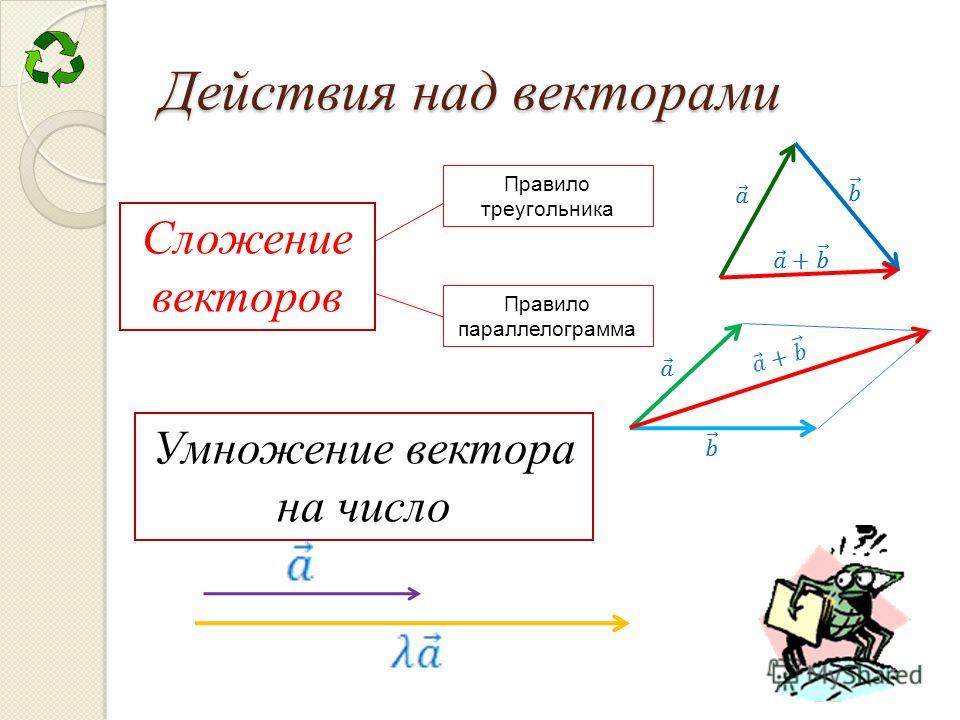 С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.
С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.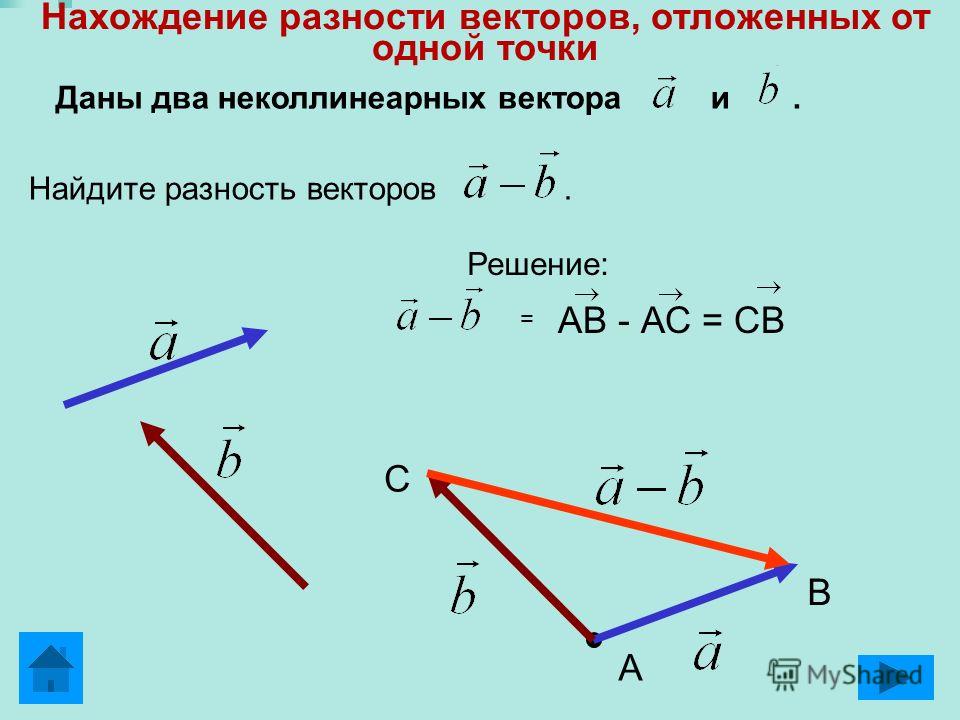 Дидактические материалы для 8 класса. Просвещение,2006
Дидактические материалы для 8 класса. Просвещение,2006
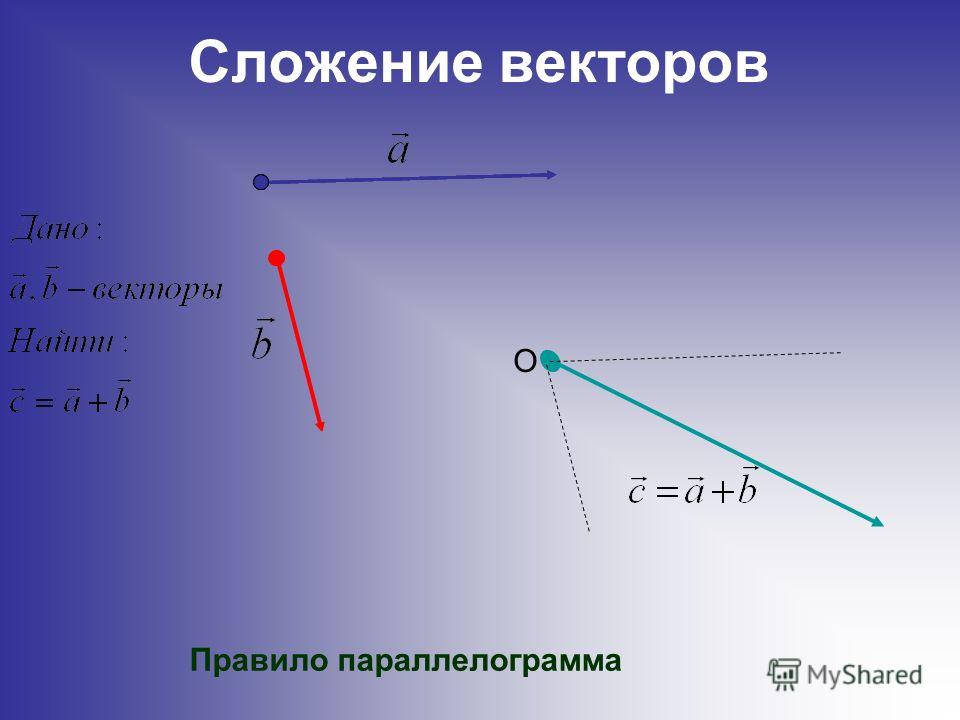
 размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}
размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {} org/contents/
org/contents/
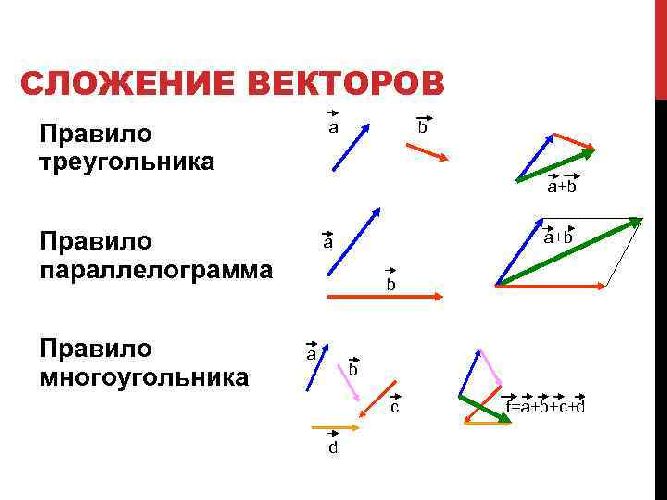
 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.