«Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций. Практическая работа №1. Кодирование информации»
Тема урока: «Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций.
Практическая работа №1. Кодирование информации»
Цели: сформировать у учащихся понимание процесса обмена информацией; показать различные виды кодирования информации; выявить преимущества двоичного кодирования различных видов информации.
Требования к знаниям и умениям:
Учащиеся должны знать:
что такое «код», «кодирование», «двоичное кодирование», бит;
почему в вычислительной технике используется двоичное кодирование информации;
как кодируются различные виды информации в вычислительной технике.

Учащиеся должны уметь:
— кодировать информацию;
— восстанавливать информацию по ее кодовому представлению.
Ход урока
Орг. Момент
Актуализация
Визуальная проверка выполнения домашнего задания.
Опрос по теме знаковая система
Заполнить таблицы
Естественные языки (носят национальный характер): речь и письменность | Формальные языки (интернациональны, понятны всем) | |||||
Примеры | -русский язык; — английский язык; -и т.д. | — язык математики; — язык химии; — языки программирования — командные языки опера — и т. | ||||
Алфавит — набор основных символов, различимых по их начертанию | — кириллица — 33 буквы; — латиница — 26 букв; — иероглифы и др | Алфавит жестко зафиксирован. — арабские цифры; — ноты; — дорожные знаки; — точки и тире; — изображения элементов | ||||
Синтаксис — правила для образования предложений языка | Формируется из большого числа правил, из которых существуют исключения | Наличие строгих правил | ||||
Грамматика — правила правописания | ||||||
Физическая природа знаков | Изображения на бумаге, звуки (фонемы), электрические импульсы и т. | |||||
Информация | Естественный язык | Формальный язык | ||||
Нахождение площади прямоугольника | ||||||
Правило дорожного движения | ||||||
Призыв о помощи | ||||||
3. Изложение нового материала
1. Кодирование информации
Когда человек или какой-либо другой живой организм или какое-то устройство участвуют в информационном процессе, то все они представляют информацию в той или иной форме. При выполнении домашнего задания вы также представляли информацию в различных формах.
Когда мы представляем информацию в разных формах или преобразуем ее из одной формы в другую, мы информацию кодируем.
Код — это система условных знаков для представления информации.
Кодирование — это операция преобразования символов или группы символов одного кода в символы или группы символов другого кода.
Человек кодирует информацию с помощью языка.
Язык — это знаковая форма представления информации.
В процессе обмена информацией кроме кодирования информации происходит и ее декодирование.
Теоретически и экспериментально было показано, что с технической точки зрения самым удобным и эффективным является использование двоичного кода, то есть набора символов, алфавита, состоящего из пары чисел {0,1}. Поскольку двоичный код используется для хранения информации в вычислительных машинах, его еще называют машинным кодом.
Цифры 0 и 1, образующие набор {0,1}, обычно называют двоичными цифрами, потому что они используются как алфавит в так называемой двоичной системе счисления.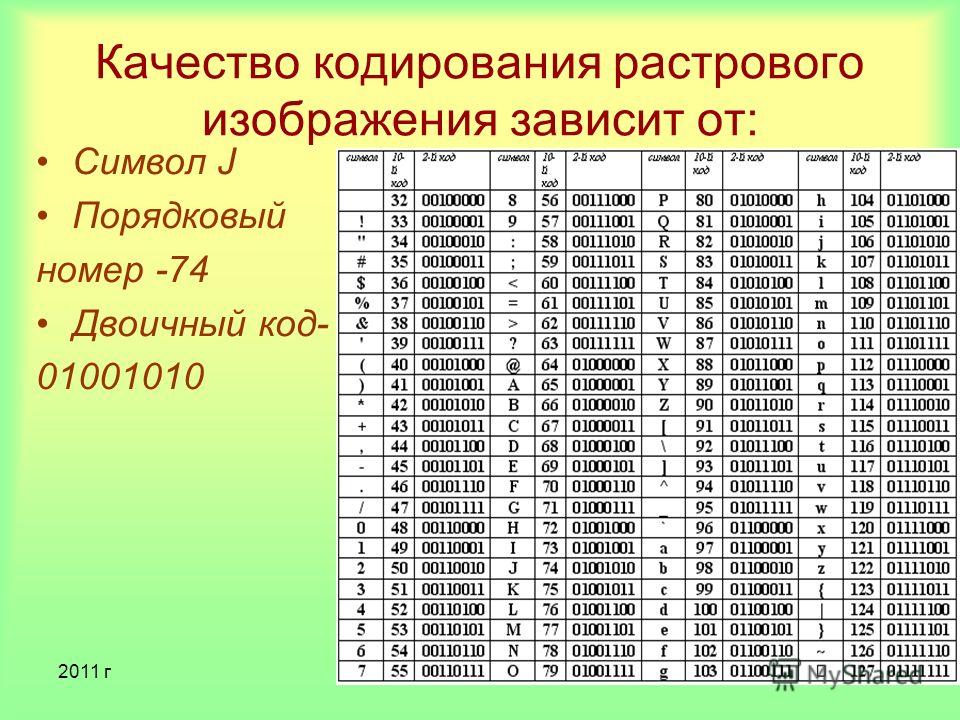 Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Элементарное устройство памяти компьютера, которое применяется для изображения одной двоичной цифры, называется двоичным разрядом или битом.
Слово «бит» произошло от английского термина bit, представляющего собой сокращение словосочетания Binary digit – двоичная цифра.
1 бит кодирует 2 понятия или сообщения (0 или 1).
2 бита — 4 разных сообщения (11 или 00 или 01 или 10).
3 бита — 8 разных сообщений.
4 бита — 16 сообщений и т.д.
Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 — есть сигнал, 0 — нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Как разные виды информации кодируются в компьютере?
2. Кодирование чисел
В двоичной системе счисления для записи чисел используется всего две цифры — 1 и 0. С их помощью можно записать любое число. Во всем остальном эта система счисления не отличается от привычной для вас десятичной системы. Она обладает всеми теми же свойствами, в ней соблюдаются все основные законы выполнения арифметических операций.
3. Кодирование текстовой информации
Для кодирования текстовой информации в компьютере также применяется двоичное кодирование, т.е. представление текста в виде последовательности 0 и 1. Каждому символу алфавита сопоставили определенное целое число, которое и принято считать кодом этого символа.
Бит – это очень маленькая порция информации. Поэтому, так же как и при записи десятичных чисел, используется несколько десятичных разрядов – разряд единиц, разряд десятков, сотен и т. д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
Для хранения двоичных чисел в компьютере используется устройство, которое принято называть ячейкой памяти. / Память компьютера можно образно представить себе как автоматическую камеру хранения, состоящую из отдельных ячеек, в каждую из которых можно положить некоторое число./
Ячейки образуются из нескольких битов, так же как двоичные числа образуются из двоичных разрядов. В общем случае ячейки различных компьютеров могут состоять из различного количества битов. Поэтому, начиная с машин третьего поколения, стандартными являются те ячейки, которые состоят из восьми битов.
Элемент памяти компьютера, состоящий из восьми битов, называется байтом.
1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
а) б)
Сколько же бит необходимо для кодирования символов?
Чтобы ответить на этот вопрос, нужно определить их количество. Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Запись двоичного кода легко спутать с аналогичным по записи десятичным числом. В таких случаях справа от двоичного числа записывают индекс 2, а около десятичного числа указывают индекс 10. Например: 101100112 – двоичное число, 1011001110 – десятичное.
Так как байт состоит из восьми двоичных разрядов, то количество различных кодов, различных комбинаций из восьми нулей и единиц, записываемых в один байт, равно 28=256. (00000001, 00000010,…, 11111111).
С помощью 1 байта можно закодировать 256 различных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Система счисления | Основание | Алфавит цифр |
Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Двоичная | 2 | 0, 1 |
Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.
Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.
Переведем десятичное число 20 в двоичную систем счисления (основание системы счисления p=2).
В итоге получили 2010 = 101002.
Обратный перевод осуществляется операцией умножение. Умножаем на p в n-1 степени
1*24+0*23+1*22+0*21+0*20=20
4. Закрепление пройденного
1. Каким образом информация добирается от источника информации до приемника
2. Как информация кодируется в компьютере. Почему?
Практическая работа №1. Кодирование информации
Перевести
ИЗ 10-ной в 2-ную
27, 48, 64, 115, 57
ИЗ 2-ной в 10-ную
1011, 11011,1111, 10000
5. Итоги урока
Выставление оценок.
Беседа: что понятно, что – нет, что нового…
Домашнее задание
Уровень знания: выучить, что такое код, кодирование, бит, байт и формулу, связывающую количество разных сообщений и количество бит.
§ 1.5 чит.
Уровень понимания:
Перевести
ИЗ 10-ной в 2-ную
47, 28, 92, 18, 103
ИЗ 2-ной в 10-ную
1001, 111,1100, 1110
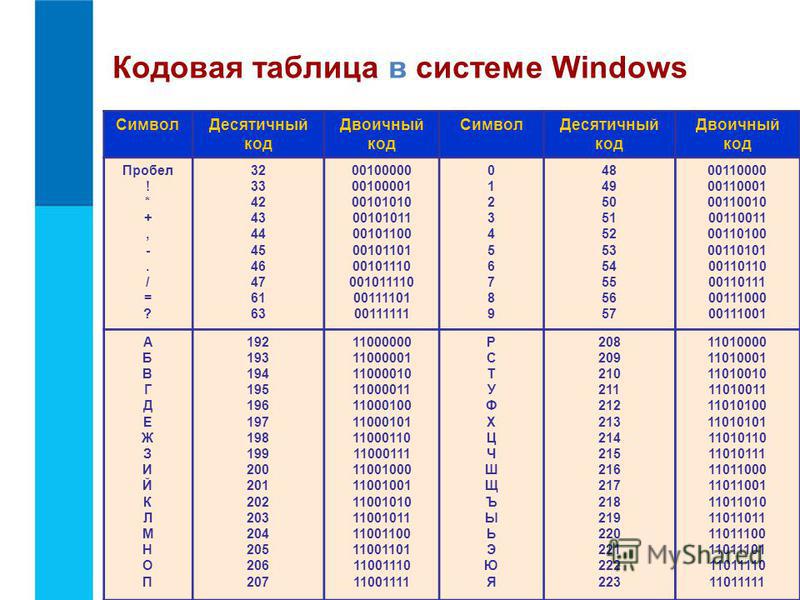
Двоичное кодирование текстовой информации и таблица кодов ASCII
Минимальные единицы измерения информации – это бит и байт.
Один бит позволяет закодировать 2 значения (0 или 1).
Используя два бита, можно закодировать 4 значения: 00, 01, 10, 11.
Тремя битами кодируются 8 разных значений: 000, 001, 010, 011, 100, 101, 110, 111.
Сколько значений можно закодировать с помощью нуля и единицы
Из приведенных примеров видно, что добавление одного бита увеличивает в 2 раза то количество значений, которое можно закодировать:
1 бит кодирует —> 2 разных значения (21 = 2),
2 бита кодируют —> 4 разных значения (22 = 4),
3 бита кодируют —> 8 разных значений (23 = 8),
4 бита кодируют —> 16 разных значений (24 = 16),
5 бит кодируют —> 32 разных значения (2
6 бит кодируют —> 64 разных значения (26 = 64),
7 бит кодируют —> 128 разных значения (27 = 128),
8 бит кодируют —> 256 разных значений (28 = 256),
9 бит кодируют —> 512 разных значений (29 = 512),
10 бит кодируют —> 1024 разных значений (210 = 1024).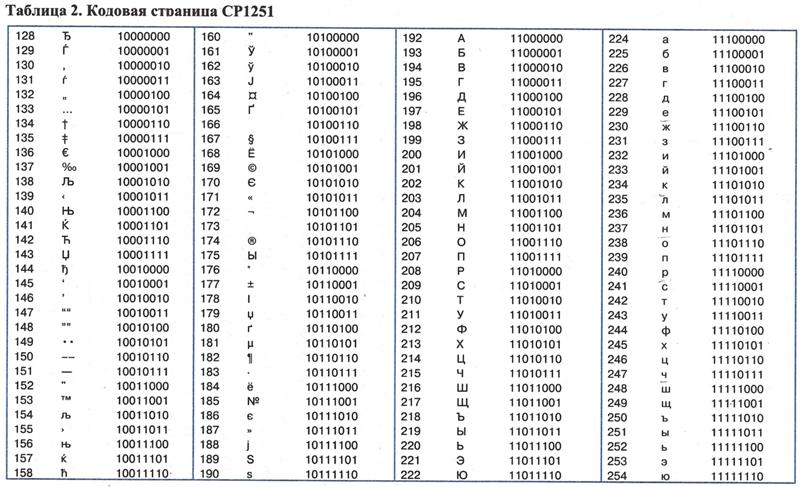
Мы помним, что в одном байте не 9 и не 10 бит, а всего 8. Следовательно, с помощью одного байта можно закодировать 256 разных символов. Как Вы думаете, много это или мало? Давайте посмотрим на примере кодирования текстовой информации.
Как происходит кодирование текстовой информации
В русском языке 33 буквы и, значит, для их кодирования надо 33 байта. Компьютер различает большие (заглавные) и маленькие (строчные) буквы, только если они кодируются различными кодами. Значит, чтобы закодировать большие и маленькие буквы русского алфавита, потребуется 66 байт.
Для больших и маленьких букв английского алфавита потребуется ещё 52 байта. В итоге получается 66 + 52 = 118 байт. Сюда надо ещё добавить цифры (от 0 до 9), символ «пробел», все знаки препинания: точку, запятую, тире, восклицательный и вопросительный знаки, скобки: круглые, фигурные и квадратные, а также знаки математических операций: +, –, =, / (это деление), * (это умножение). Добавим также специальные символы: %, $, &, @, #, № и др. Все это вместе взятое как раз и составляет около 256 различных символов.
Все это вместе взятое как раз и составляет около 256 различных символов.
А дальше дело осталось за малым. Надо сделать так, чтобы все люди на Земле договорились между собой о том, какие именно коды (с 0 до 255, т.е. всего 256) присвоить символам. Допустим, все люди договорились, что код 33 означает восклицательный знак (!), а код 63 – вопросительный знак (?). И так же – для всех применяемых символов. Тогда это будет означать, что текст, набранный одним человеком на своем компьютере, всегда можно будет прочитать и распечатать другому человеку на другом компьютере.
Таблица ASCII
Такая всеобщая договоренность об одинаковом использовании чего-либо называется стандартом. В нашем случае стандарт должен представлять из себя таблицу, в которой зафиксировано соответствие кодов (с 0 до 255) и символов. Подобная таблица называется таблицей кодировки.
Но не всё так просто. Ведь символы, которые хороши, например, для Греции, не подойдут для Турции потому, что там используются другие буквы. Аналогично то, что хорошо для США, не подойдет для России, а то, что подойдет для России, не годится для Германии.
Аналогично то, что хорошо для США, не подойдет для России, а то, что подойдет для России, не годится для Германии.
Поэтому приняли решение разделить таблицу кодов пополам.
Первые 128 кодов (с 0 до 127) должны быть стандартными и обязательными для всех стран и для всех компьютеров, это – международный стандарт.
А со второй половиной таблицы кодов (с 128 до 255) каждая страна может делать все, что угодно, и создавать в этой половине свой стандарт – национальный.
Первую (международную) половину таблицы кодов называют таблицей ASCII, которую создали в США и приняли во всем мире.
За вторую половину кодовой таблицы (с 128 до 255) стандарт ASCII не отвечает. Разные страны создают здесь свои национальные таблицы кодов.
Может быть и так, что в пределах одной страны действуют разные стандарты, предназначенные для различных компьютерных систем, но только в пределах второй половины таблицы кодов.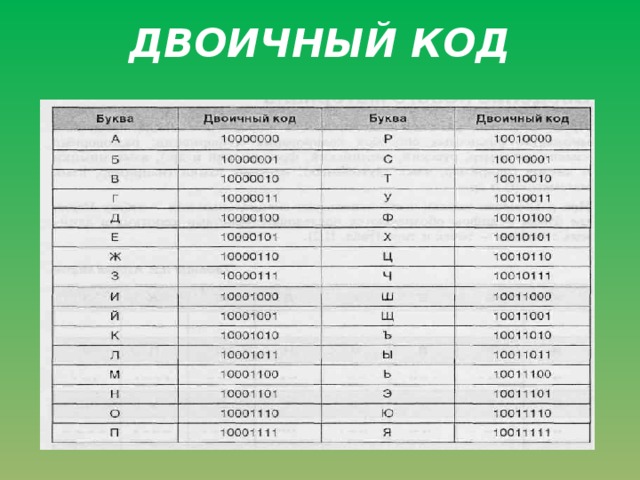
Коды из международной таблицы ASCII
0-31 – Особые символы, которые не распечатываются на экране или на принтере. Они служат для выполнения специальных действий, например, для «перевода каретки» – перехода текста на новую строку, или для «табуляции» – установки курсора на специальные позиции в строке текста и т.п.
32 – Пробел, который является разделителем между словами. Это тоже символ, подлежащий кодировке, хоть он и отображается в виде «пустого места» между словами и символами.
33-47 – Специальные символы (круглые скобки и пр.) и знаки препинания (точка, запятая и пр.).
48-57 – Цифры от 0 до 9.
58-64 – Математические символы: плюс (+), минус (-), умножить (*), разделить (/) и пр., а также знаки препинания: двоеточие, точка с запятой и пр.
65-90 – Заглавные (прописные) английские буквы.
91-96 – Специальные символы (квадратные скобки и пр.).
97-122 – Маленькие (строчные) английские буквы.
123-127 – Специальные символы (фигурные скобки и пр.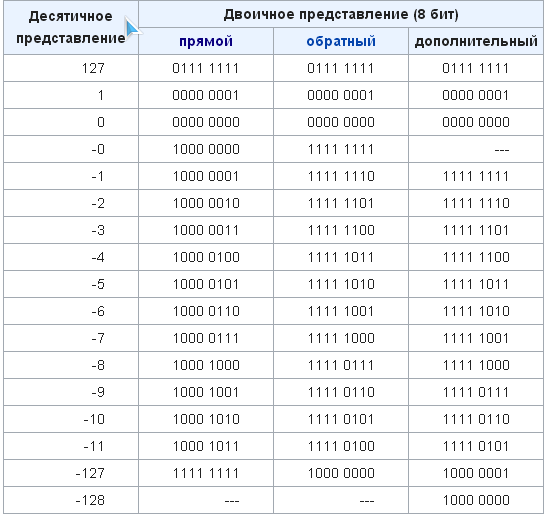 ).
).
За пределами таблицы ASCII, начиная с цифры 128 по 159, идут заглавные (прописные) русские буквы. А с цифры 160 по 170 и с 224 по 239 – маленькие (строчные) русские буквы.
Кодировка слова МИР
Пользуясь показанной кодировкой, мы можем представить себе, как компьютер кодирует и затем воспроизводит. Например, рассмотрим слово МИР (заглавными буквами). Это слово представляется тремя кодами:
букве М соответствует код 140 (по национальной российской системе кодировки),
для буквы И – это код 136 и
буква Р – это 144.
Но как уже говорилось ранее, компьютер воспринимает информацию только в двоичном виде, т.е. в виде последовательности нулей и единиц. Каждый байт, соответствующий каждой букве слова МИР, содержит последовательность из восьми нулей и единиц. Используя правила перевода десятичной информации в двоичную, можно заменить десятичные значения кодов букв на их двоичные аналоги.
Десятичной цифре 140 соответствует двоичное число 10001100. Это можно проверить, если сделать следующие вычисления: 27 + 23 +22 = 140.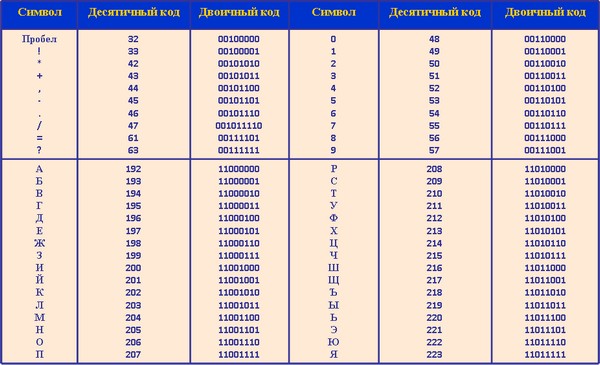 Степень, в которую возводится каждая «двойка» – это номер позиции двоичного числа 10001100, в которой стоит «1». Причем позиции нумеруются справа налево, начиная с нулевого номера позиции: 0, 1, 2 и т.д.
Степень, в которую возводится каждая «двойка» – это номер позиции двоичного числа 10001100, в которой стоит «1». Причем позиции нумеруются справа налево, начиная с нулевого номера позиции: 0, 1, 2 и т.д.
Более подробно о переводе чисел из одной системы счисления в другую можно узнать, например, из учебников по информатике или через Интернет.
Аналогичным образом можно убедиться, что цифре 136 соответствует двоичное число 10001000 (проверка: 27 + 23 = 136). А цифре 144 соответствует двоичное число 10010000 (проверка: 27 + 24 = 144).
Таким образом, в компьютере слово МИР будет храниться в виде следующей последовательности нулей и единиц (бит): 10001100 10001000 10010000.
Разумеется, что все показанные выше преобразования данных производятся с помощью компьютерных программ, и они не видны пользователям. Они лишь наблюдают результаты работы этих программ, как при вводе информации с помощью клавиатуры, так и при ее выводе на экран монитора или на принтер.
Неужели нужно знать все коды?
Следует отметить, что на уровне изучения компьютерной грамотности пользователям компьютеров не обязательно знать двоичную систему счисления. Достаточно иметь представление о десятичных кодах символов.
Только системные программисты на практике используют двоичную, шестнадцатеричную, восьмеричную и иные системы счисления. Особенно это важно для них, когда компьютеры выводят сообщения об ошибках в программном обеспечении, в которых указываются ошибочные значения без преобразования в десятичную систему.
Упражнения по компьютерной грамотности, позволяющие самостоятельно увидеть и почувствовать описанные системы кодировок, приведены в статье «Проверяем, кодирует ли компьютер текст?»
P.S. Статья закончилась, но можно еще прочитать:
Представление информации в компьютере
Что такое переменная в программировании и чем она отличается от константы
Смотрим на кодировку цвета
Получайте новые статьи по компьютерной грамотности на ваш почтовый ящик:
Необходимо подтвердить подписку в своей почте. Спасибо!
Спасибо!
Битовая глубина
Битовая глубина количественно определяет, сколько уникальных цветов доступно в цветовой палитре изображения с точки зрения количества нулей и единиц, или «битов», которые используются для указания каждого цвета. Это не означает, что изображение обязательно использует все эти цвета, но вместо этого оно может задавать цвета с таким уровнем точности. Для изображения в градациях серого глубина цвета определяет количество доступных уникальных оттенков. Изображения с более высокой битовой глубиной могут кодировать больше оттенков или цветов, поскольку доступно больше комбинаций 0 и 1.
ТЕРМИНОЛОГИЯ
Каждый цветовой пиксель в цифровом изображении создается комбинацией трех основных цветов: красного, зеленого и синего. Каждый основной цвет часто называют «цветовым каналом» и может иметь любой диапазон значений интенсивности, определяемый его битовой глубиной. Битовая глубина для каждого основного цвета называется «бит на канал».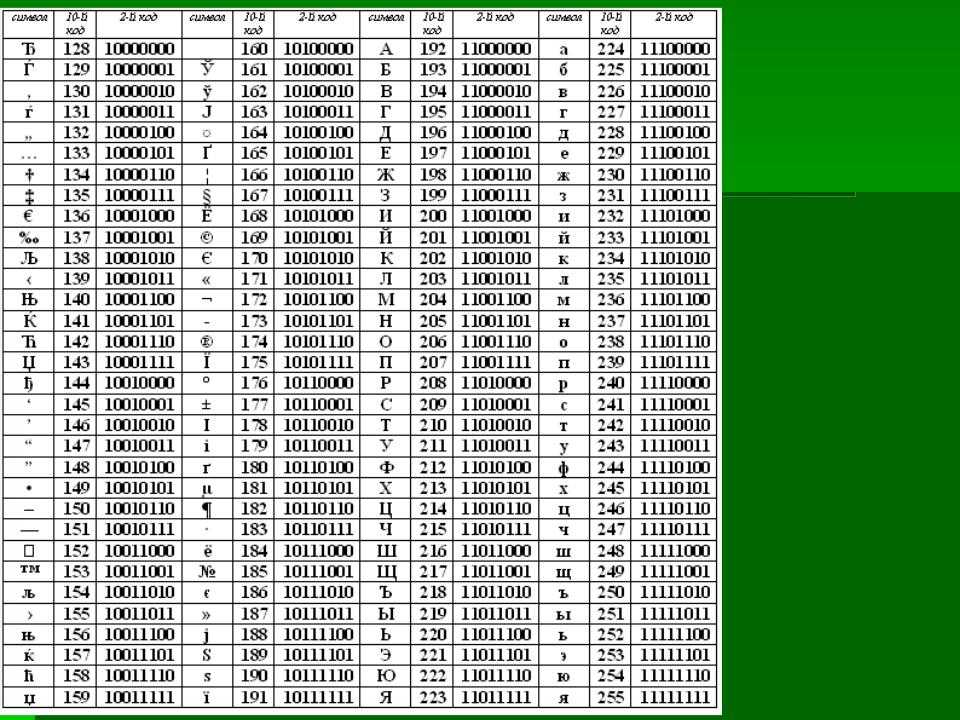 «Бит на пиксель» (bpp) относится к сумме битов во всех трех цветовых каналах и представляет общее количество цветов, доступных для каждого пикселя. С цветными изображениями часто возникает путаница, потому что может быть неясно, относится ли указанное число к битам на пиксель или к битам на канал. Использование «bpp» в качестве суффикса помогает различать эти два термина.
«Бит на пиксель» (bpp) относится к сумме битов во всех трех цветовых каналах и представляет общее количество цветов, доступных для каждого пикселя. С цветными изображениями часто возникает путаница, потому что может быть неясно, относится ли указанное число к битам на пиксель или к битам на канал. Использование «bpp» в качестве суффикса помогает различать эти два термина.
ПРИМЕР
Большинство цветных изображений с цифровых камер имеют 8 бит на канал, поэтому они могут использовать в общей сложности восемь нулей и единиц. Это позволяет использовать 2 8 или 256 различных комбинаций, что соответствует 256 различным значениям интенсивности для каждого основного цвета. Когда все три основных цвета объединяются в каждом пикселе, это позволяет использовать до 2 8 * 3 или 16 777 216 различных цветов, или «истинный цвет». Это называется 24 битами на пиксель, поскольку каждый пиксель состоит из трех 8-битных цветовых каналов. Количество цветов, доступных для любого X-битного изображения, составляет всего 2 9. 0011 X , если X относится к битам на пиксель, и 2 3X , если X относится к битам на канал.
0011 X , если X относится к битам на пиксель, и 2 3X , если X относится к битам на канал.
СРАВНЕНИЕ
В следующей таблице показаны различные типы изображений с точки зрения количества бит (битовая глубина), общего количества доступных цветов и общих имен.
| Бит на пиксель | Количество доступных цветов | Общее имя(а) |
|---|---|---|
| 1 | 2 | Монохромный |
| 2 | 4 | СГА |
| 4 | 16 | ЭГА |
| 8 | 256 | VGA |
| 16 | 65536 | XGA, High Color |
| 24 | 16777216 | SVGA, истинный цвет |
| 32 | 16777216 + Прозрачность | |
| 48 | 281 трлн |
ВИЗУАЛИЗАЦИЯ БИТОВОЙ ГЛУБИНЫ
При наведении курсора мыши на любую из меток ниже изображение будет повторно отображаться с использованием выбранного количества цветов. Разница между 24 битами на пиксель и 16 битами на пиксель незначительна, но будет четко видна, если ваш дисплей настроен на истинный цвет или выше (24 или 32 бита на пиксель).
Разница между 24 битами на пиксель и 16 битами на пиксель незначительна, но будет четко видна, если ваш дисплей настроен на истинный цвет или выше (24 или 32 бита на пиксель).
| 24 бита на пиксель | 16 бит на пиксель | 12 бит на пиксель | 10 бит/п | 8 бит на пиксель |
ПОЛЕЗНЫЕ СОВЕТЫ
- Человеческий глаз может различать только около 10 миллионов различных цветов, поэтому сохранение изображения с разрешением более 24 бит на пиксель является излишним, если оно предназначено только для просмотра. С другой стороны, изображения с битрейтом более 24 бит на пиксель по-прежнему весьма полезны, поскольку они лучше сохраняются при постобработке (см. «Учебник по постеризации»).
- Цветовые градации изображений с менее чем 8 битами на цветовой канал хорошо видны на гистограмме изображения.
- Доступные настройки битовой глубины зависят от типа файла. Стандартные файлы JPEG и TIFF могут использовать только 8 и 16 бит на канал соответственно.

Хотите узнать больше?
— Вернуться к урокам по фотографии —
Объяснение битовой глубины: все, что вам нужно знать
В современную эпоху аудио нельзя не упомянуть о Hi-Res и 24-битной музыке студийного качества. Если вы еще не заметили тенденцию в смартфонах высокого класса — кодек Sony LDAC Bluetooth — и потоковые сервисы, такие как Qobuz, вам действительно нужно больше читать этот сайт.
Обещание простое — превосходное качество прослушивания благодаря большему объему данных, также известному как битовая глубина. Это 24 бита цифровых единиц и нулей по сравнению с жалким 16-битным пережитком эпохи компакт-дисков. Конечно, вам придется доплачивать за эти продукты и услуги более высокого качества, но чем больше битов, тем лучше, верно?
Звук в низком разрешении часто отображается в виде лестничного сигнала. Это не то, как работает сэмплирование звука, и это не то, как выглядит звук, выходящий из устройства.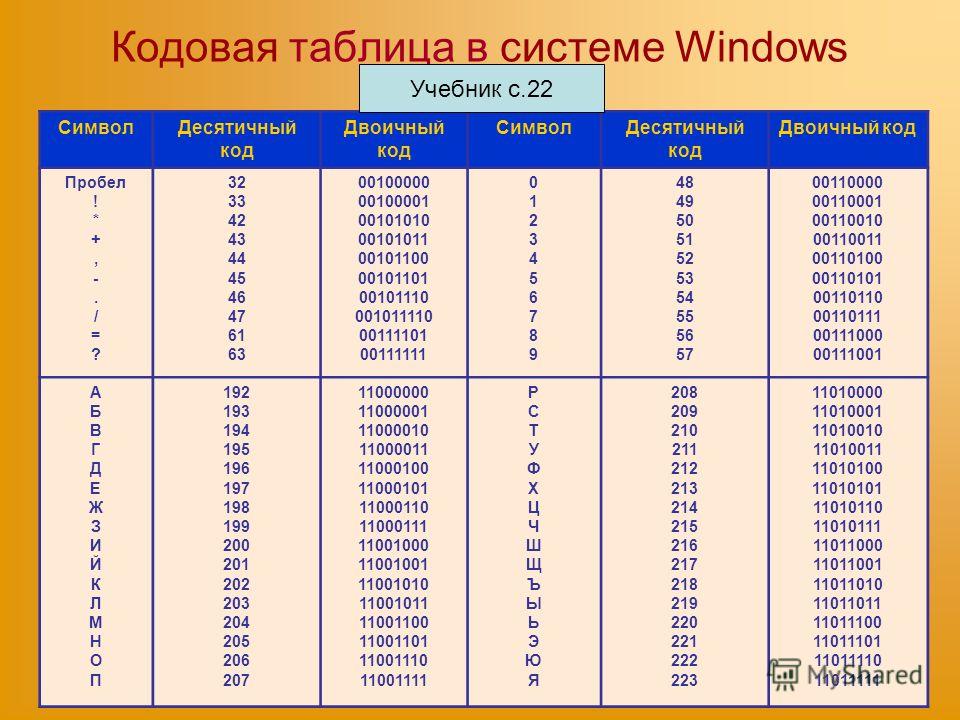
Не обязательно. Потребность во все большей и большей битовой глубине основана не на научной реальности, а скорее на искажении правды и использовании неосведомленности потребителей о науке о звуке. В конечном счете, компании, продающие 24-битное аудио, могут получить гораздо больше прибыли, чем вы от превосходного качества воспроизведения.
Примечание редактора: эта статья была обновлена 13 июля 2021 г., чтобы обновить некоторые технические формулировки и добавить меню содержания.
Битовая глубина и качество звука: шагать по лестнице не проблема качественная лестница в небо. 16-битный пример всегда показывает неровное, зубчатое воспроизведение синусоиды или другого сигнала, в то время как 24-битный эквивалент выглядит красиво и с более высоким разрешением. Это простое наглядное пособие, но оно опирается на незнание темы и науки, чтобы привести потребителей к неверным выводам.
Прежде чем кто-нибудь откусит мне голову, технически говоря, эти ступенчатые примеры довольно точно отображают звук в цифровой области.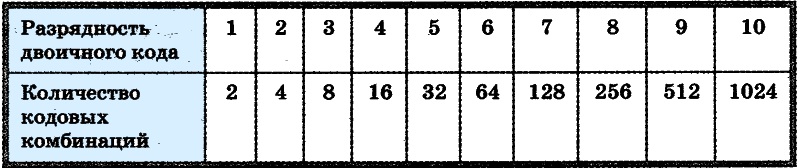 Тем не менее, диаграмма основы/леденец-диаграмма является более точным графическим изображением для визуального аудиосемплирования, чем эти ступенчатые ступени. Подумайте об этом так: сэмпл содержит амплитуду в определенный момент времени, а не амплитуду, удерживаемую в течение определенного промежутка времени.
Тем не менее, диаграмма основы/леденец-диаграмма является более точным графическим изображением для визуального аудиосемплирования, чем эти ступенчатые ступени. Подумайте об этом так: сэмпл содержит амплитуду в определенный момент времени, а не амплитуду, удерживаемую в течение определенного промежутка времени.
Использование ступенчатых диаграмм намеренно вводит в заблуждение, когда стержневые диаграммы обеспечивают более точное представление цифрового звука. Эти два графика отображают одни и те же точки данных, но ступенчатый график выглядит гораздо менее точным.
Однако верно то, что аналого-цифровой преобразователь (АЦП) должен умещать бесконечно переменный аналоговый аудиосигнал в конечное число битов. Бит, попадающий между двумя уровнями, должен быть округлен до ближайшего приближения, которое известно как ошибка квантования или шум квантования . (Запомните это, мы еще вернемся к этому.)
Однако, если вы посмотрите на аудиовыход любого цифро-аналогового преобразователя (ЦАП), построенного в этом столетии, вы не увидите никаких ступенек.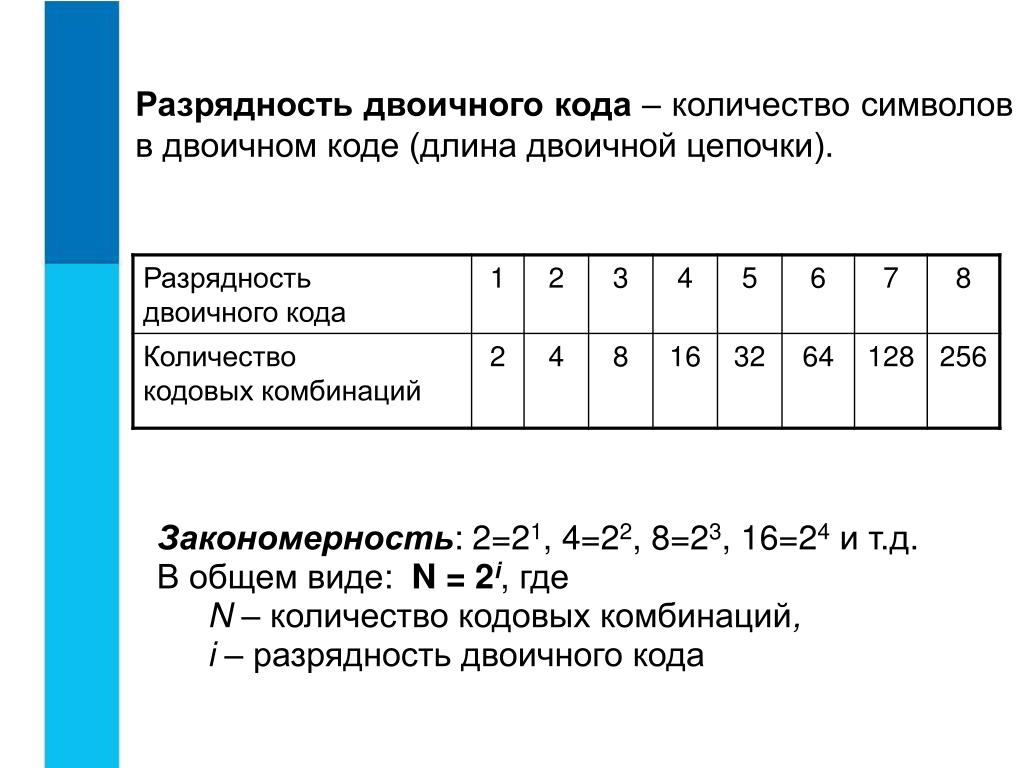 Даже если вы выводите 8-битный сигнал. Так что дает?
Даже если вы выводите 8-битный сигнал. Так что дает?
8-битный синусоидальный сигнал с частотой 10 кГц, полученный с недорогого смартфона Pixel 3a. Мы можем видеть некоторый шум, но никаких заметных ступенек, которые так часто изображают аудиокомпании.
Во-первых, то, что описывают эти ступенчатые диаграммы, если мы применим их к аудиовыходу, называется ЦАП нулевого порядка. Это очень простая и дешевая технология ЦАП, в которой сигнал переключается между различными уровнями каждый новый семпл для получения выходного сигнала. Это не используется ни в каких профессиональных или полуприличных потребительских аудиопродуктах. Вы можете найти его в микроконтроллере за 5 долларов, но уж точно не где-либо еще. Искажение аудиовыхода таким образом подразумевает искаженную, неточную форму волны, но это не то, что вы получаете.
На самом деле выход современного ∆Σ ЦАП представляет собой 1-битный сигнал PDM с передискретизацией (справа), а не сигнал удержания нуля (слева). Последний производит более низкий уровень шума на аналоговом выходе при фильтрации.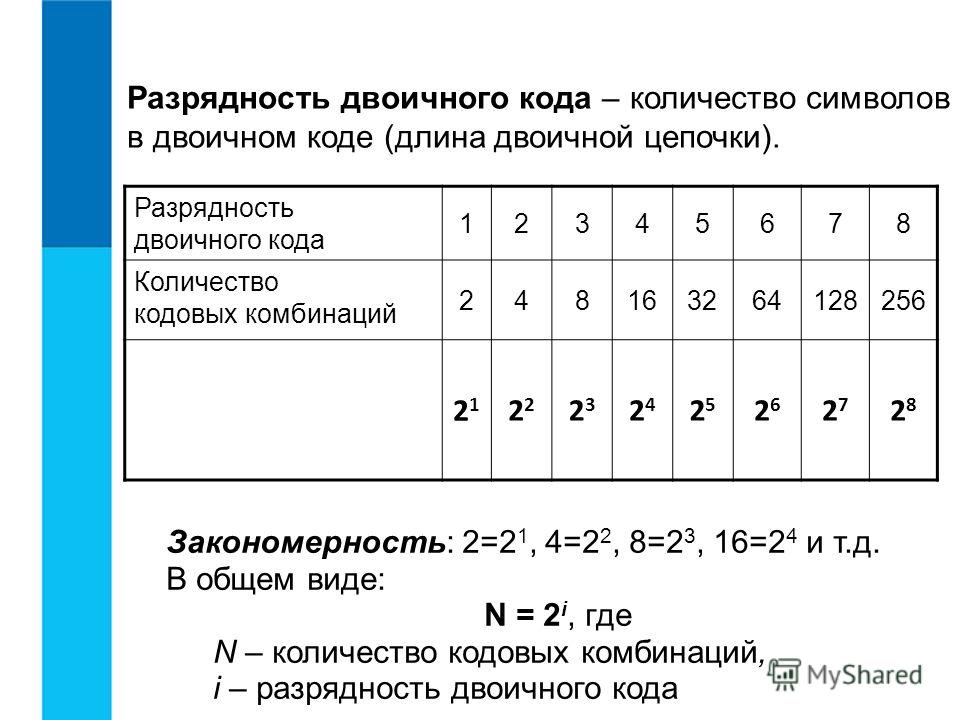
АЦП и ЦАП звукового класса преимущественно основаны на дельта-сигма (∆Σ) модуляции. Компоненты этого калибра включают интерполяцию и передискретизацию, формирование шума и фильтрацию для сглаживания и уменьшения шума. Дельта-сигма ЦАП преобразуют аудиосэмплы в 1-битный поток (модуляция плотности импульсов) с очень высокой частотой дискретизации. При фильтрации это дает гладкий выходной сигнал с шумом, далеко выходящим за пределы слышимых частот.
В двух словах: современные ЦАП не выводят грубые зубчатые аудиосэмплы — они выводят битовый поток, который фильтруется шумом, в очень точный, гладкий выходной сигнал. Эта ступенчатая визуализация неверна из-за так называемого «шума квантования».
Понимание шума квантования
В любой конечной системе случаются ошибки округления. Это правда, что 24-битный АЦП или ЦАП будет иметь меньшую ошибку округления, чем 16-битный эквивалент, но что это на самом деле означает? Что еще более важно, что мы на самом деле слышим? Это искажение или пух, детали потеряны навсегда?
На самом деле это немного и то, и другое, в зависимости от того, находитесь ли вы в цифровой или аналоговой сферах. Но ключевой концепцией для понимания обоих является понимание минимального уровня шума и того, как он улучшается по мере увеличения битовой глубины. Чтобы продемонстрировать, давайте отойдем от 16 и 24 бит и посмотрим на примеры с очень маленькой битовой глубиной.
Но ключевой концепцией для понимания обоих является понимание минимального уровня шума и того, как он улучшается по мере увеличения битовой глубины. Чтобы продемонстрировать, давайте отойдем от 16 и 24 бит и посмотрим на примеры с очень маленькой битовой глубиной.
Разница между глубиной 16 и 24 бита заключается не в точности формы волны, а в доступном пределе до того, как цифровой шум будет мешать нашему сигналу.
В приведенном ниже примере есть несколько вещей, которые нужно проверить, поэтому сначала краткое объяснение того, что мы рассматриваем. У нас есть входные (синие) и квантованные (оранжевые) сигналы на верхних диаграммах с разрядностью 2, 4 и 8 бит. Мы также добавили к нашему сигналу небольшое количество шума, чтобы лучше имитировать реальный мир. Внизу у нас есть график ошибки квантования или шума округления, который вычисляется путем вычитания квантованного сигнала из входного сигнала.
Шум квантования увеличивается, чем меньше битовая глубина, из-за ошибок округления.
Очевидно, что увеличение разрядности делает квантованный сигнал более подходящим для входного сигнала. Однако это не главное, обратите внимание на гораздо больший сигнал ошибки/шума для более низких разрядностей. Квантованный сигнал не удаляет данные из нашего ввода, они фактически добавляются в этот сигнал ошибки. Аддитивный синтез говорит нам, что сигнал может быть воспроизведен суммой любых двух других сигналов, включая несовпадающие по фазе сигналы, которые действуют как вычитание. Так работает шумоподавление. Таким образом, эти ошибки округления вносят новый шумовой сигнал.
Это не просто теория, вы можете услышать все больше и больше шума в аудиофайлах с более низкой битовой глубиной. Чтобы понять почему, изучите, что происходит в 2-битном примере с очень маленькими сигналами, например, до 0,2 секунды. Щелкните здесь для увеличения изображения. Очень небольшие изменения во входном сигнале вызывают большие изменения в квантованной версии. Это ошибка округления в действии, которая приводит к усилению шума слабого сигнала. Таким образом, шум снова становится громче по мере уменьшения битовой глубины.
Таким образом, шум снова становится громче по мере уменьшения битовой глубины.
Квантование не удаляет данные из нашего ввода, оно фактически добавляет зашумленный сигнал ошибки.
Подумайте об этом и в обратном порядке: невозможно захватить сигнал, меньший размера шага квантования — по иронии судьбы известного как младший значащий бит. Небольшие изменения сигнала должны переходить к ближайшему уровню квантования. Большие битовые глубины имеют меньшие шаги квантования и, следовательно, меньшие уровни усиления шума.
Самое главное, обратите внимание, что амплитуда шума квантования остается неизменной, независимо от амплитуды входных сигналов. Это демонстрирует, что шум возникает на всех различных уровнях квантования, поэтому существует постоянный уровень шума для любой заданной битовой глубины. Большая битовая глубина производит меньше шума. Поэтому мы должны думать о различиях между 16- и 24-битной глубиной не как о точности формы сигнала, а как о доступном пределе до того, как цифровой шум начнет мешать нашему сигналу.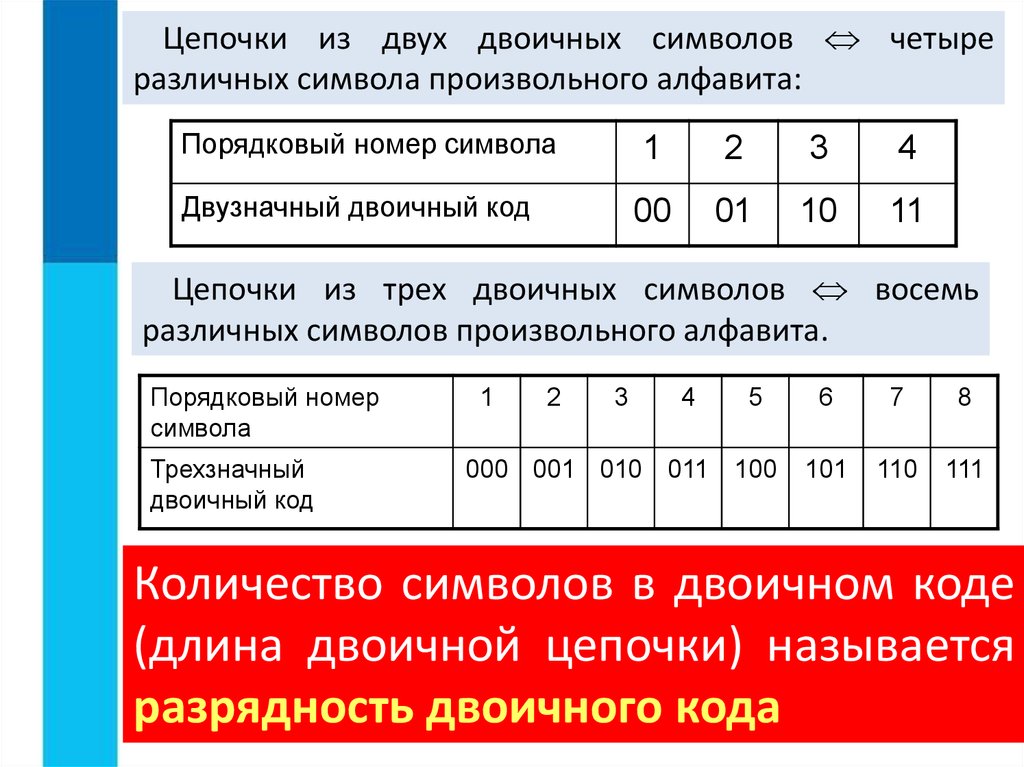
Битовая глубина зависит от шума
Келли Сиккема Нам нужна битовая глубина с достаточным соотношением сигнал-шум, чтобы приспособиться к нашему фоновому шуму, чтобы записать наш звук так же идеально, как он звучит в реальном мире.
Теперь, когда мы говорим о битовой глубине с точки зрения шума, давайте в последний раз вернемся к нашему графику выше. Обратите внимание, как 8-битный пример выглядит почти идеально для нашего зашумленного входного сигнала. Это связано с тем, что его 8-битного разрешения на самом деле достаточно для захвата уровня фонового шума. Другими словами: размер шага квантования меньше, чем амплитуда шума, или отношение сигнал/шум (SNR) лучше, чем уровень фонового шума.
Уравнение 20log(2 n ) , где n — битовая глубина, дает нам SNR. 8-битный сигнал имеет SNR 48 дБ, 12-битный — 72 дБ, 16-битный — 96 дБ, а 24-битный — колоссальные 144 дБ. Это важно, потому что теперь мы знаем, что нам нужна только битовая глубина с достаточным SNR, чтобы согласовать динамический диапазон между нашим фоновым шумом и самым громким сигналом, который мы хотим захватить, чтобы воспроизвести звук так же идеально, как он выглядит в реальном мире.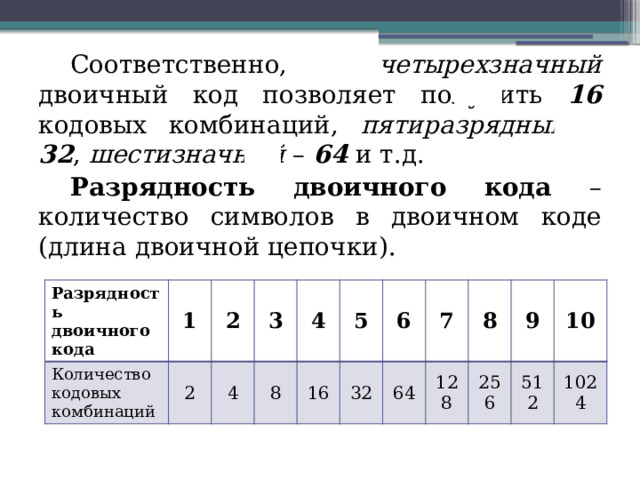 Немного сложно перейти от относительных масштабов цифрового царства к масштабам физического мира, основанным на звуковом давлении, поэтому мы постараемся сделать это проще.
Немного сложно перейти от относительных масштабов цифрового царства к масштабам физического мира, основанным на звуковом давлении, поэтому мы постараемся сделать это проще.
CD-качество может быть «всего» 16-битным, но это слишком много для качества.
Чувствительность вашего уха варьируется от 0 дБ (тишина) до примерно 120 дБ (мучительно громкий звук), а теоретическая способность (в зависимости от нескольких факторов) различать громкость составляет всего 1 дБ. Таким образом, динамический диапазон вашего уха составляет около 120 дБ или около 20 бит.
Однако вы не можете услышать все это сразу, так как барабанная перепонка , или барабанная перепонка, сжимается, чтобы уменьшить объем звука, фактически достигающего внутреннего уха в шумных условиях. Вы также не будете слушать музыку на такой громкости, , потому что ты оглохнешь . Кроме того, среда, в которой вы и я слушаем музыку, не такая тихая, как может слышать здоровое ухо. В хорошо оборудованной студии звукозаписи уровень фонового шума может быть ниже 20 дБ, но прослушивание в шумной гостиной или в автобусе, очевидно, ухудшит условия, и r демонстрируют полезность широкого динамического диапазона.
Человеческое ухо имеет огромный динамический диапазон, но не весь одновременно. Маскировка и собственная защита слуха нашего уха снижает ее эффективность.
Вдобавок ко всему: по мере увеличения громкости в вашем ухе начинает действовать маскировка более высоких частот. При низкой громкости от 20 до 40 дБ маскировка не происходит, за исключением звуков близкой по высоте. Однако при 80 дБ звуки ниже 40 дБ будут маскироваться, а при 100 дБ звуки ниже 70 дБ услышать невозможно. Динамический характер уха и материала для прослушивания затрудняет определение точного числа, но реальный динамический диапазон вашего слуха, вероятно, находится в районе 70 дБ в среднем окружении и всего до 40 дБ в очень громком окружении. Битовая глубина всего 12 бит, вероятно, охватила бы большинство людей, поэтому 16-битные компакт-диски дают нам достаточно места.
гиперфизика Маскировка высоких частот происходит при высокой громкости прослушивания, что ограничивает наше восприятие более тихих звуков.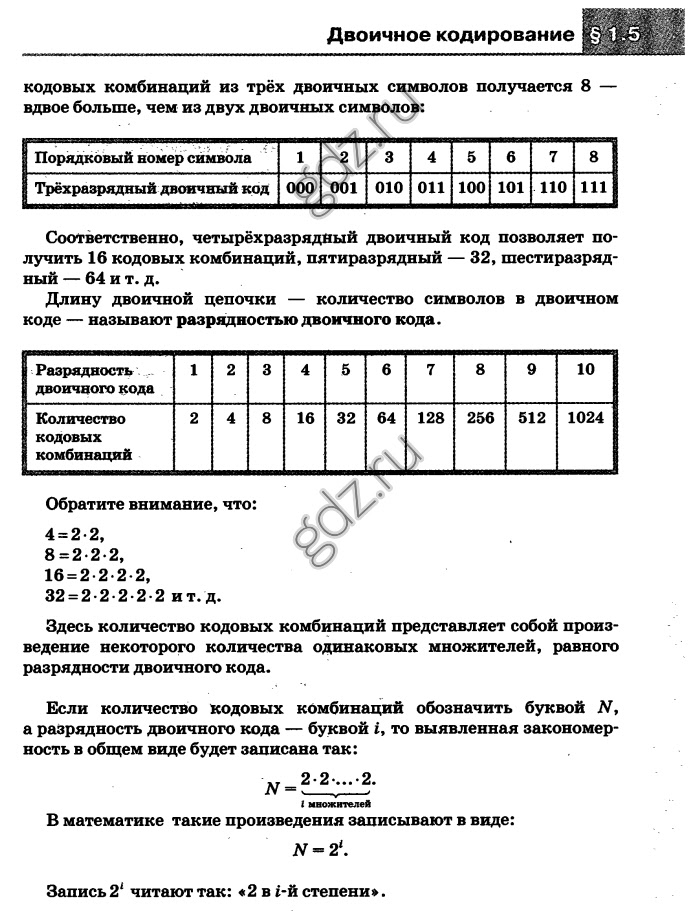
Инструменты и записывающее оборудование также создают шум (особенно гитарные усилители) даже в очень тихих студиях звукозаписи. Также было проведено несколько исследований динамического диапазона различных жанров, включая это, которое показывает типичный динамический диапазон 60 дБ. Неудивительно, что жанры с большей близостью к тихим партиям, такие как хор, опера и фортепиано, показали максимальный динамический диапазон около 70 дБ, в то время как «более громкие» жанры рок, поп и рэп имели тенденцию к 60 дБ и ниже. В конечном счете, музыка создается и записывается только с такой точностью.
Возможно, вы знакомы с «войнами громкости» в музыкальной индустрии, что, безусловно, противоречит цели современных аудиоформатов Hi-Res. Интенсивное использование сжатия (которое усиливает шум и ослабляет пики) уменьшает динамический диапазон. У современной музыки значительно меньший динамический диапазон, чем у альбомов 30-летней давности. Теоретически современная музыка может распространяться с более низким битрейтом, чем старая музыка. Вы можете проверить динамический диапазон многих альбомов здесь.
Вы можете проверить динамический диапазон многих альбомов здесь.
16 бит — это все, что вам нужно
Это было довольно сложное путешествие, но, надеюсь, вы получили гораздо более детализированную картину битовой глубины, шума и динамического диапазона, чем те вводящие в заблуждение примеры лестницы, которые вы так часто часто вижу.
Битовая глубина полностью связана с шумом, и чем больше битов данных у вас есть для хранения звука, тем меньше шума квантования будет внесено в вашу запись. Кроме того, вы также сможете более точно захватывать меньшие сигналы, помогая снизить уровень цифрового шума ниже уровня записи или прослушивания. Это все, для чего нам нужна битовая глубина. Нет никакой пользы в использовании огромной битовой глубины для мастер-аудио.
Алексей Рубан Из-за того, что шум суммируется в процессе микширования, имеет смысл записывать звук в 24-битном формате. Это не обязательно для окончательного мастер-стерео.
Удивительно, но 12 бит, вероятно, достаточно для приличного звучания музыкального мастера и для соответствия динамическому диапазону большинства условий прослушивания.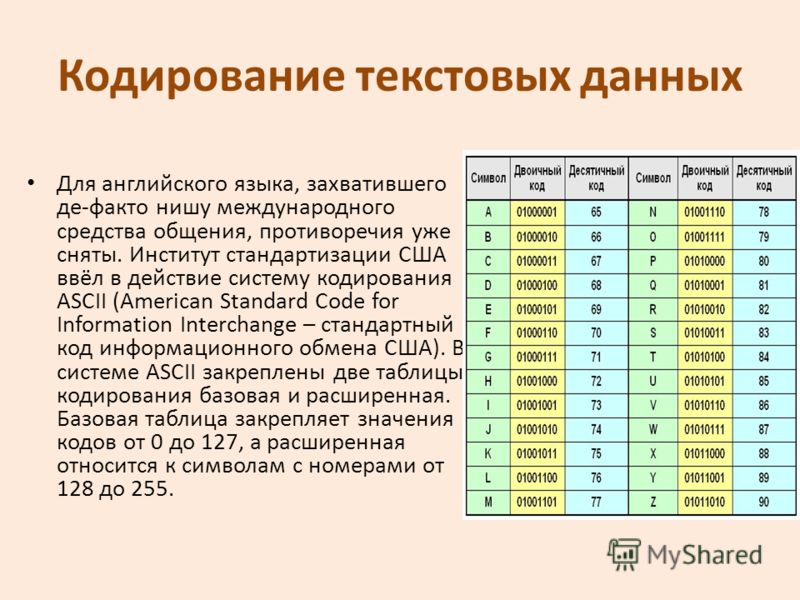



 д.
д. д.
д.