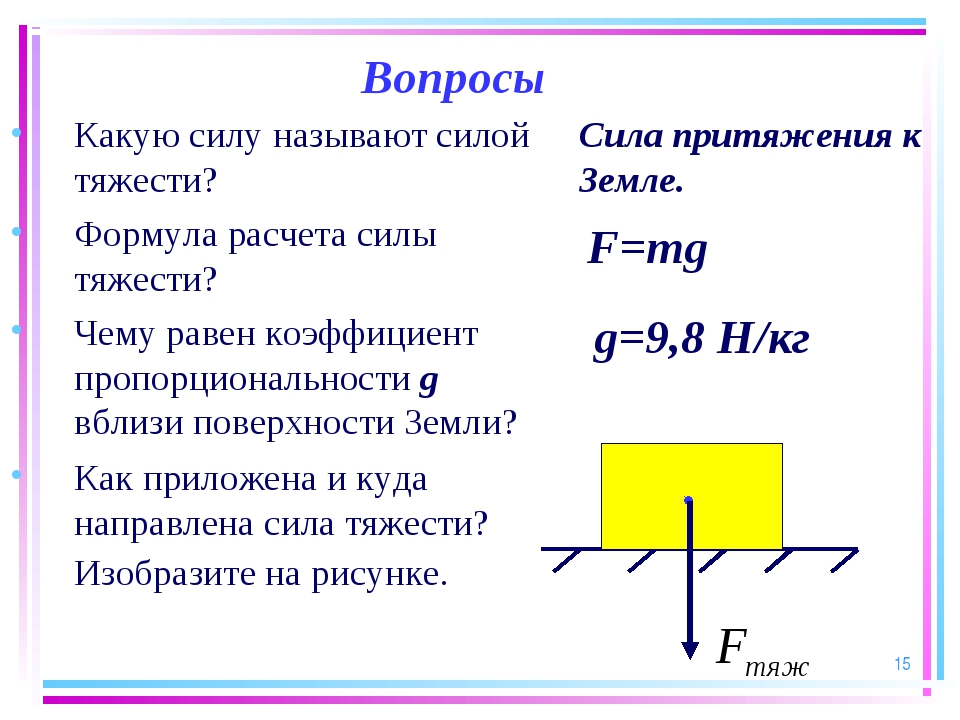
4.6.1.1. Размерность силы
,
1 ньютон (1Н) — это сила, которая массе 1 кг сообщает ускорение 1 м/с.
4.7. Третий закон Ньютона
Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример — взаимодействие двух электрических зарядов:
Из третьего закона Ньютона следует, что для каждой силы можно указать тело, являющееся причиной этой силы. Если же указать такое тело — причину возникшей силы — не удается, то тогда причина «силы» — неинерциальность системы отсчета. Напомним, что законы Ньютона справедливы только в инерциальных системах отсчета.
5. Законы сохранения
5.1. Механическая система — это совокупность тел, выделенных нами для рассмотрения 5.1.1. Внутренние и внешние силы
Внутренние
силы — силы, с которыми взаимодействуют
тела системы между собой. Внешние силы действуют со стороны тел, не входящих в систему. |
5.1.2. Замкнутая система Замкнутая система — это система, на которую внешние силы не действуют.
5.1.3. Импульс системы материальных точек — это векторная сумма импульсов всех материальных точек, входящих в систему
, (см. 4.5).
5.2. Закон сохранения импульса
Импульс замкнутой системы сохраняется, т.е. не изменяется со временем.
На рисунке изображена замкнутая система, состоящая из трех тел.
По II закону Ньютона (4.6), примененному к каждому телу рассматриваемой замкнутой системы, имеем:
Сложим
эти уравнения. Справа, по III закону
Ньютона (4.7),
получим ноль. Слева — производную по
времени от полного импульса системы (5.1.3).
Производная — ноль, значит, сама величина — константа.
если нет внешних сил (система замкнута).
рх = const, если Fx = 0, рy = const, если Fy = 0, рz = const, если Fz = 0. |
| |
Если система не замкнута, но внешние силы не действуют на неЈ вдоль каких-либо осей, то соответствующие компоненты импульса сохраняются, например:
рх = const, если Fx=
0,
рy≠
const, если Fy ≠ 0,
р |
| |
5.
3.1.
Работа постоянной силы
5.3.2. Элементарная работа
5.3.3.Работа переменной силы
5.3.4. Единица измерения работы
[A]=[F].[s]= H.м = джоуль, Дж
5.4. Мощность P — это скорость совершения работы, т.е.
Используя (5.3.2) и
Здесь v — скорость материальной точки, к которой приложена сила .
5.4.1. Единица мощности
5.5. Кинетическая энергия
Применим II закон Ньютона для материальной точки m, движущейся под действием результирующей силы : |
Помножим скалярно: слева на — справа на
.
Используя (5.3.2) справа и преобразуя левую часть,
получим
.
Половина произведения массы частицы на квадрат ее скорости названа ее кинетической энергией
Таким образом элементарная работа, совершаемая над телом, равна элементарному приращению его кинетической энергии. При интегрировании вдоль траектории частицы, от точки 1 до точки 2, мы получим:
Работа результирующей силы идет на приращение кинетической энергии материальной точки.
5.6. Консервативные и неконсервативные силы Консервативные (conservativus — охранительный) — такие силы, РАБОТА которых не зависит от траектории, а определяются только начальным и конечным положением материальной точки. Силы, не обладающие только что названным свойством, называют
Применение размерности для проверки правильности решения физических задач
Цели:
- шире использовать полученные теоретические знания по физике;
- вооружить учащихся большим набором способов решения задач.
1. Понятие размерности
Для начала упорядочим некоторые понятия, с
которыми мы имели дело раньше и с теми, которые
встретятся нам в будущем. К таким физическим
понятиям относятся: наименование, название
физической величины, в выбранной системе единиц,
размерность, обозначение и определяющее
уравнение.
| Название физ. величины | Обозначение | Определяющее уравнение | Наименование |
Размерность | |
| Площадь | S |
S = a3 |
м2 |
кв. |
L2 |
| Объём | V |
м3 |
куб. метр |
L3 |
|
| Скорость | V |
V = S/t |
м/с; м с–1 |
метр в сек. |
L T–1 |
| Ускорение | а |
а = | м/с2; м с–2 |
метр в секунду |
L T–2 |
| Плотность | кг/м3; кг м–3 |
кг на куб. |
M L–3 |
||
метр
метрЭто простые и часто встречающиеся понятия, причём название физической величины вытекает из определяющего её уравнения. Но ряд физических величин имеют «клички». Название величины не следует прямо, как прежде, из определяющего уравнения.
Например.
Наименование величины – сила. Название единицы
измерения – Ньютон. Вспомним материал 7-го
класса. Что такое Ньютон? Это такая сила, которая
за 1 секунду изменяет скорость тела массой 1 кг на
1 метр в секунду. Примером одной из сил является
вес тела. Мы знаем, что вес тела равен Р = mg,
где m – масса тела , а g – ускорение
свободного падения.
Из физики 8-го класса мы знаем, что ускорение
измеряется в м/с2. Значит, если речь идёт о
весе тела 
Отсюда можно сделать вывод,
что и любая другая сила F равна произведению
массы тела на полученное в результате действия
силы ускорение, т.е. F = ma.
Обратим внимание на то, что, если масса тела
равна 1 кг и полученное ускорение равно 1 м/с2,
то и сила будет равна единице силы, то есть 1-му
Ньютону. Тогда размерность Ньютона будет
[ F ] = кг = кг м /с2
= M L T–2. Заметим, что определяющим
уравнением будет уравнение F = ma. Обратите
внимание, что название единицы силы не кг м/с2,
а Ньютон – «кличка». Просто громоздкое
наименование единицы заменили на «Ньютон» в
честь знаменитого английского учёного Ньютона.
Таких имён «кличек» которые носят единицы
измерения физических величин много. В механике
это Джоуль, Герц, Ватт.
Каждой такой единице присуща ей размерность,
которая показывает, из каких основных единиц
системы СИ «приготовлена», «сделана» такая
единица, в какой степени входят в состав этой
величины основные единицы и где они находятся в
числителе или в знаменателе.
Что такое определяющее уравнение? Это уравнение,
которое следует из определения физической
величины.
Например.
1. Скорость – это физическая величина равная
отношению пути, пройденного телом, ко времени за
которое этот путь пройден. Отсюда следует
определяющее уравнение V = S/t.
2. Работа – это физическая величина равная
произведению силы, приложенной к телу на путь,
который прошло тело под действием этой силы.
Отсюда следует определяющее уравнение: A = F S.
До введения интернациональной системы единиц
(СИ), существовал несколько систем единиц.
Так в одной из них основными единицами были:
единица массы – грамм; единица длины –
сантиметр; единица времени – секунда. Эта
система единиц называлась СГС.
Были и другие системы единиц. Но масса есть масса
в любой системе. Будь она в кг, или в г, или в мг.
Поэтому, независимо от выбранной системы единиц,
принято размерность выражать в символах.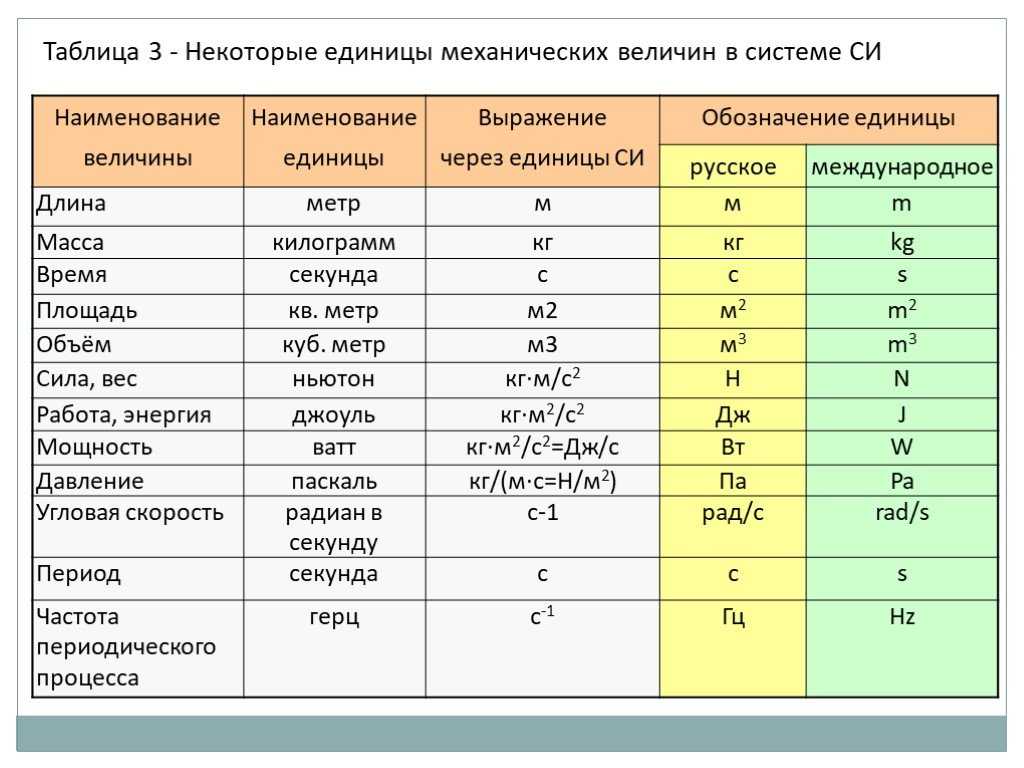
Масса –
М. Длина – L. Время – Т.
В таблице выше соответствующая колонка называется просто размерность.
Задачи для самостоятельного решения.
1. Определить размерность Джоуля. Определяющее
уравнение A = F S
2. Определить размерность Ватта. Определяющее
уравнение N = A / t
3. Определить размерность Герца. Определяющее
уравнение = 1 / Т
4. Определить размерность Паскаля. Определяющее
уравнение р = F/S
5. Определить размерность момента силы.
Определяющее уравнение М = F L.
2. Проверка правильности решения задач по размерности
«Видкиль воно взялось и на щоб воно сдалось» Украинская пословица.
Откуда взялась размерность мы рассмотрели.
Рассмотрим где, и как она может быть применена и
её особенности.
Рассмотрим решение нескольких задач:
1. Определить расстояние между Землёй и Солнцем,
если луч света, двигаясь со скоростью 3 х 108 м/с,
проходит это расстояние примерно за 8,5 минут?
2.
Какое расстояние по прямой может пройти ракета
за 1 минуту, двигаясь от места старта с ускорением
20 м/с2?
3. Автомобиль, двигаясь со скоростью 54 км/ч, пошел
на обгон и в течение 10 секунд двигался с
ускорением 2 м/с2. Какой путь прошел
автомобиль за это время?
4. Автомобиль, двигаясь со скоростью 54 км/ч, перед
поворотом в течение 10 секунд двигался
равнозамедленно с ускорением – 2 м/с2. Какой
путь прошел автомобиль за это время?
Решения:
Проанализируем решение этих задач.
1. Что общего было в этих задачах? (Определялся
путь S)
2. В чём различие в этих задачах? (В каждой
задаче описывается различное движение, а значит,
применяются различные уравнения для определения
пути)
То есть различие в том, что одна и та же величина
(путь) определяется через различные величины. В №
1 через V и t. В № 2 через а и t.
В
№ 3 и № 4 через Vо, a, t.
Эти величины имеют различные размерности, а в
результате произведенных действий получается во
всех случаях одна и та же размерность – метр.
Произведём, не используя модулей этих величин,
предлагаемые действия только с размерностями.
1. S = V t = 2. S = . 3.4. S = V0t ± = ± =L±L= L
Отсюда следует закономерность: В правильно
составленном уравнении, размерность правой его
части равна размерности его левой части.
Эту закономерность можно применить для проверки
правильности решения задач.
Допустим, задачу №3 решили с ошибкой (она очень
часто встречается), записав
уравнение так S = Vо + at2/2
, тогда S = 15 + 2 х 102 /2 = 65 (м). Так как
правильный ответ неизвестен, то неясно, как
проверить правильность решения, и найти причину
ошибки.
То ли ошибка в вычислениях, то ли в
преобразованиях, то ли в неправильном написании
правильно выбранного уравнения?
Проверяя правильность решения по наименованию
можно найти причину ошибки.
Как это сделать? Вместо модулей величин
подставить размерности величин и сравнить
размерности левой и правой части уравнения.
(использовать, указанную выше, закономерность )
Отсюда следует, L =/= 1 + Т. Задача решена
неверно. Где ошибка? В правой части уравнение
представляет двучлен. Одна его часть имеет
размерность L, а другая L/T. Как из
этого выражения L/T получить L? Нужно
умножить его на Т. Тогда получим размерность
первого члена L. Первый член и второй член правой
части уравнения будут иметь размерность L,
то есть L + L = L. Левая и правая части будут
иметь одинаковую размерность. Значит, первый
член правой части уравнения должен иметь вид не Vо,
а Vоt.
Теперь, предположим, решающий допустил другую
ошибку. В уравнении S = Vоt +at2/2
вместо знака «+» поставил знак «–». Поможет ли
здесь метод размерности указать на ошибку?
Решение задачи № 4 говорит о том, что задача
решена правильно. L = L – L = L, но модуль
величины другой.
Отсюда следует второй вывод: метод
размерностей может подсказать ошибочность
физического направления решения, но не может
подсказать ошибочность математического
действия.
Решим несколько задач по кинематике и сделаем
проверку их правильности решения, применив метод
размерности.
Задача № 1.
За время равное 2 с, тело, двигаясь прямолинейно и равноускоренно, прошло путь 20 м. Его скорость при этом увеличилась в 3 раза. Определить ускорение тела.
Сделаем проверку решения методом размерности.
Размерности левой и правой части уравнения
совпадают, значит, задача решена правильно.
Задача №2.
Тело, двигаясь от остановки равноускоренно, за первые 5 секунд движения прошло путь 10 м. Какой путь пройдёт это тело за 10 секунд от начала движения?
Задача № 3. Тело, двигаясь равноускоренно, за 5 секунд движения прошло путь 100 м , а за 10 сек. – 300 м. Определить начальную скорость движения тела.
Мы проделали громоздкие преобразования. Не
допустили ли мы ошибку? Воспользуемся знанием
закономерности размерности и проверим свою
работу.
L T–1 =
Следовательно, задача решена верно.
Подставим числовое значение входящих величин и
получим числовой ответ задачи.
V0 = (м/с)
Задача №4. Во сколько раз скорость пули при вылете её из ствола винтовки больше скорости этой пули при прохождении ею 1/3 ствола?
Размерности кинематических, механических и тепловых величин
Библиографическое описание: Улямаев, К.
С. Размерности кинематических, механических и тепловых величин / К. С. Улямаев, М. А. Безгин, А. А. Симонова, А. В. Левин. — Текст : непосредственный // Молодой ученый. — 2019. — № 48 (286). — С. 8-12. — URL: https://moluch.ru/archive/286/64457/ (дата обращения: 21.10.2022).
Физические величины. Все они тем или иным образом связаны друг с другом и составляют глобальную систему природных постулатов. Эти положения признаются большинством деятелей науки. Постижение и использование всей совокупности вселенских взаимосвязей вряд ли доступно человечеству — даже если рассматривать в контексте истории человеческого рода. Однако физическую сущность и определенную системность в закономерных взаимосвязях известных нам на сегодня физических величин можно постичь уже сегодня, применяя системный размерностный анализ, то есть изучая используемые размерности физических величин и их соотношения. Многие из них выражают природные закономерности.
Обнаружение системности в расположении и взаимосвязях физических величин по аналогии с системой химических элементов Д. И. Менделеева позволяет многие факторы. Во-первых, уточнить характер или принцип строения структуры и взаимосвязей системных элементов. Во-вторых, правильная расстановка элементов системы позволяет выявить «белые пятна» и целенаправленно искать недостающие элементы системы. В-третьих, исходя из общих свойств системы, имеется возможность априори выявлять некоторые характерные свойства и признаки этих, еще не обнаруженных элементов, поскольку их свойства, как правило, определяются местоположением в системе. И, самое примечательное, что подтверждено на практике, правильно найденная система физических величин содержит в себе и систему природных закономерностей.
Размерность физической величины иее обозначение
Под физической величиной понимают качественную характеристику того или иного физического объекта материального мира, существующую как бы сама по себе (например, время и пространство).
Допустим, что мы договорились обозначать длину в любых уравнениях символом L (англ. length), а время- символом T (англ. time). Будем называть эти символы размерностями длины и времени, причем независимо от размера длины и времени.
Тогда размерность объема любого тела (газа, жидкости или твердого тела) всегда будет обозначаться символом , независимо ни от какого числового коэффициента, стоящего в уравнении расчета объема. Точно так же размерность скорости будет обозначаться символом . Теперь пусть на любой другой обитаемой планете длину и время обозначат другими символами. Заменить эти символы на L и T совсем не сложно. Но размерности объема и скорости и на Земле, и на другой планете будут одинаковыми.
Имеется еще несколько величин, считающихся в системе единиц СИ основными, их размерности имеют свои символы, например, размерность массы имеет символ М (англ. mass). Поэтому размерность такой величины, как сила, будет обозначаться в СИ выражением , чему соответствует в СИ единица , которая названа сокращенно Ньютоном (Н).
Следует всегда помнить, что формула размерности не является произведением размерностей, как это может показаться, судя по форме записи. Ведь символы M, L и T сами по себе не являются обозначениями каких-либо физических величин. Это такие же операторы как div, rot и (набла) в векторном анализе, как условные значки, обозначающие логические операции в булевой алгебре, как дифференциальный оператор s=d/dt, заменяющий условно операцию дифференцирования и т. д.
Запись — это просто последовательная запись символов размерностей в определенном установленном стандартном порядке, а вовсе не из произведения. Поэтому, в частности, лишена какого-нибудь смысла запись M+L+T, так как никто не станет записывать «кг+м+с».
Размерность физической величины — одна из важнейших ее характеристик, которую можно определить, как буквенное выражение, показывающее связь данной величины с величинами, принятыми за основные в рассматриваемой системе единиц. Для обозначения размерности основных величин системы СИ приняты большие буквы латинского алфавита: для длины — L, массы — М, времени — Т, силы электрического тока — I, термодинамической температуры — Θ, количества вещества — N и силы света — J.
Размерности записывают прописными буквами и печатают прямым шрифтом. Кроме основных величин в системе СИ имеются две дополнительные: плоский угол и телесный угол. Единицами их измерения установлены радиан и стерадиан, они признаются безразмерными (таблица1).
Таблица 1
Основные идополнительные величины системы СИ
Все величины, не входящие в основные, называются производными. Единицы измерения производных физических величин устанавливаются строго определенным образом — по так называемым уравнениям связи. Например, скорость есть путь (длина), деленный на время. Уравнение связи для скорости v l / t. Поскольку длина и время входят в основные величины и их единицы измерения уже установлены, то единицей измерения скорости в системе СИ будет м/с, а в системе СГС см/с и никак не иначе. Размерности всех производных величин по форме представляют собой одночлен из обозначения размерности основных величин, имеющих определенные степени.
Обозначение основной величины в степени 0 обычно используется. Например, размерность скорости имеет вид LT–1, размерность силы — МLT–2. Показатель степени, в которую возведена размерность основной величины, входящей в степенной одночлен, называют показателем размерности. Примеры обозначения в СИ размерностей других наиболее часто используемых величин приведены в таблице 2.
Таблица 2
Наиболее широко используемые кинематические, механические итепловые физические величины
Размерности тепловых величин
В измерении тепловых величин в системе СИ используют метр [м], килограмм [кг], секунда [с] и Кельвин [К]. В качестве основных температурных шкал приняты абсолютная термодинамическая шкала температуры, которая измеряется в градусах Кельвина и стоградусная международная температурная шкала, измеряемая в градусах Цельсия. В данных температурных системах реперной точкой, то есть точкой отсчета, являются:
– тройная точка воды для термодинамической шкалы;
– температура плавления льда (0 ℃) и температура кипения воды (100 ℃) при нормальном давлении для международной шкалы.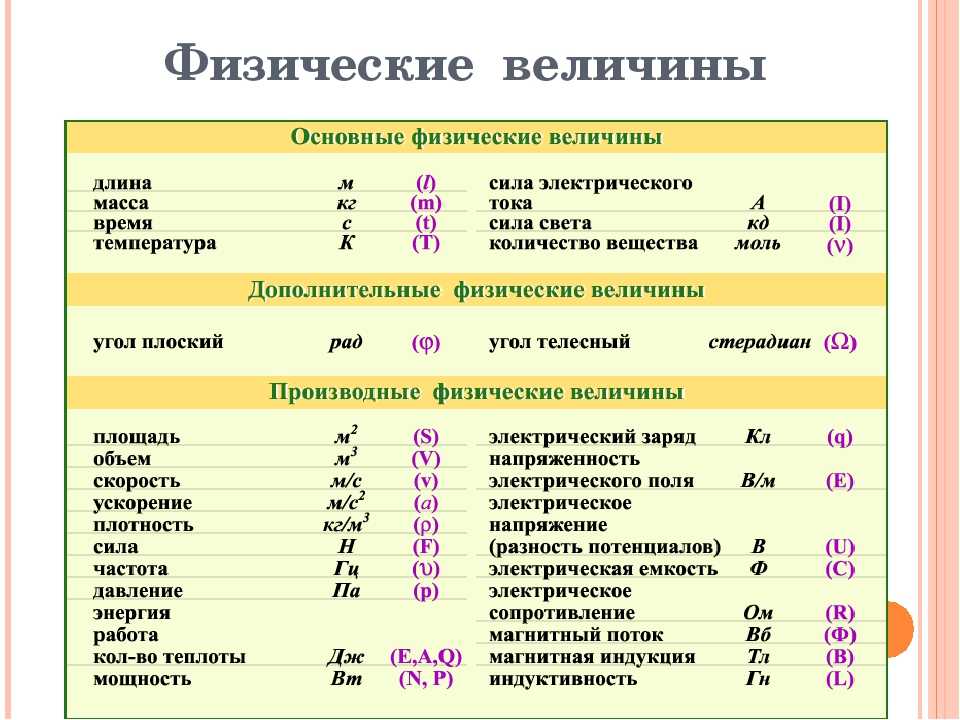
Если международной системой все просто, то термодинамическая шкала требует пояснения. Под тройной точкой воды подразумевают точку с определенными значениями давления и температуры, при которых вода находится одновременно в трех состояниях. Значение давление равно 0,006 атм=611,657 Па, а значение температуры — 0,01 ℃=273,16 К (рисунок 1).
Рис. 1. Фазовая диаграмма воды
Понятие теплоты характеризует процесс теплообмена, определяемая количеством энергии, которое получает или отдает тело в процессе теплообмена. В СИ теплота измеряется в джоулях (1 Дж=1 кг·м2/с2=1 Н·м). Так же пользуются внесистемной единицей — калорией, которая равна 4,187 Дж. На практике с некоторым допущением за калорию принимают количество теплоты, необходимое для нагревания 1 г воды на 1°С при атмосферном давлении.
Теплоемкость — количество теплоты, поглощаемой или выделяемой телом в процессе нагревания или остывания на 1 кельвин, находится, как отношение изменения количества теплоты и изменению температуры:
.
Различают теплоемкость массовую [ккал/(кг·°С)], мольную [ккал/(кмоль·°С)] и объемную [ккал/(м3·°С)].
Энтальпия, тепловая функция состояния тела, которая определяется как сумма внутренней энергии тела и произведения давления на объем:
Размерность данной величины будет Дж/моль. По своему физическому смыслу энтальпия представляет собой энергию, которая доступна для преобразования в теплоту при определенных значениях температуры и давления.
Литература:
- Чертов А. Г. Единицы физический величин. — М.: Высшая школа, 1977. — 287 с.
- Чуев А. С., Задорожный Н. А. Введение в размерностное и системное представление физических величин. Учебное пособие. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2016. — 18 с.
- Кононюк А. Е. Обобщенная количественные характеристики моделей. К.3. Ч. 2 Физические величины (Начало). — Киев: «Освіта України», 2012. — 476 с.
- Основные тепловые величины // ООО Свой Мастер & PoliStyle.
URL: http://svoymaster.com/santehnika/osnovnye-teplovye-velichiny.html - Кузнецов А. М., Муравлева Л. В. Введение в физику. Механика: Учебно-методическое пособие к семинарским и практическим занятиям для студентов инженерных специальностей. Тула: 2014. — 188 с.
URL: http://svoymaster.com/santehnika/osnovnye-teplovye-velichiny.htmlОсновные термины (генерируются автоматически): величина, размерность, система СИ, физическая величина, значение температуры, обозначение размерности, основная величина, процесс теплообмена, размерность скорости, термодинамическая шкала.
Force Dimension — Тактильные устройства
omega.3
Семейство тактильных устройств omega.x сочетает в себе производительность и дизайн в одном из самых совершенных и модульных тактильных интерфейсов, когда-либо созданных. Устройство может быть отклонено в трех версиях, обеспечивающих возможности перемещения, вращения и захвата.
Модель omega.3 с тонко отполированными кинематическими звеньями и рамой из анодированного алюминия демонстрирует непревзойденную надежность, простоту и стиль.
Его тонко текстурированный сферический рабочий орган обеспечивает универсальный интерфейс как для левшей, так и для правшей. Этот очень эргономичный и отличительный дизайн делает omega.3 Устройство выбора при выполнении ловких роботизированных задач телеманипуляции или для инстинктивного взаимодействия со сложными виртуальными средами, требующими удобных интерфейсов с оптимальным удобством использования.
Спецификация omega.3
omega.6
Тактильное устройство omega.6 оснащено конечным эффектором в форме ручки с широким диапазоном движений запястья. Основанный на базе omega.x , его конструкция обеспечивает идеальное разделение поступательных и вращательных движений.
Haptic SDK обеспечивает полный доступ к ориентации запястья либо в виде значений угла сустава, либо в виде матрицы вращения, выраженной в декартовом пространстве. Положение рабочего органа устройства указано в декартовых координатах.
Сочетание полной компенсации силы тяжести и калибровки без дрейфа способствует большему удобству пользователя и точности прибора.
omega.6 поставляется как в левосторонней, так и в правосторонней конфигурации и использует все возможности обратной связи поступательного усилия омега.3 .
omega.6 спецификация
omega.7
Благодаря уникальному активному удлинителю для захвата, omega.7 является самым универсальным из доступных тактильных устройств. Его рабочий орган охватывает естественный диапазон движений руки человека и совместим с конструкцией двуручной консоли дистанционного управления.
Сочетание полной компенсации силы тяжести и калибровки без дрейфа способствует большему удобству и точности для пользователя. Активный захват может создавать усилие захвата до 8 ньютонов в обоих направлениях.
omega.7 выпускается как в левосторонней, так и в правосторонней конфигурации и использует все возможности обратной связи поступательного усилия omega.3 .
omega.7 specsheet
- omega. 3
- omega.6
- omega.7
3| workspace | translation | ∅ 160 x 110 mm | forces | translation | 12,0 N | разрешение | translation | < 0.01 mm | interface | standard rate | USB 2.0 up to 4 KHz | power | universal | 100V — 240V | platforms | Microsoft Linux Apple Blackberry WindRiver | Windows все дистрибутивы macOS QNX VxWorks | программное обеспечение | SDK Haptics SDK Robotics CHAI3D | Эргономика | Устройство может использоваться как с левой, так и с правой рукой | Структура | DELTA DELTA.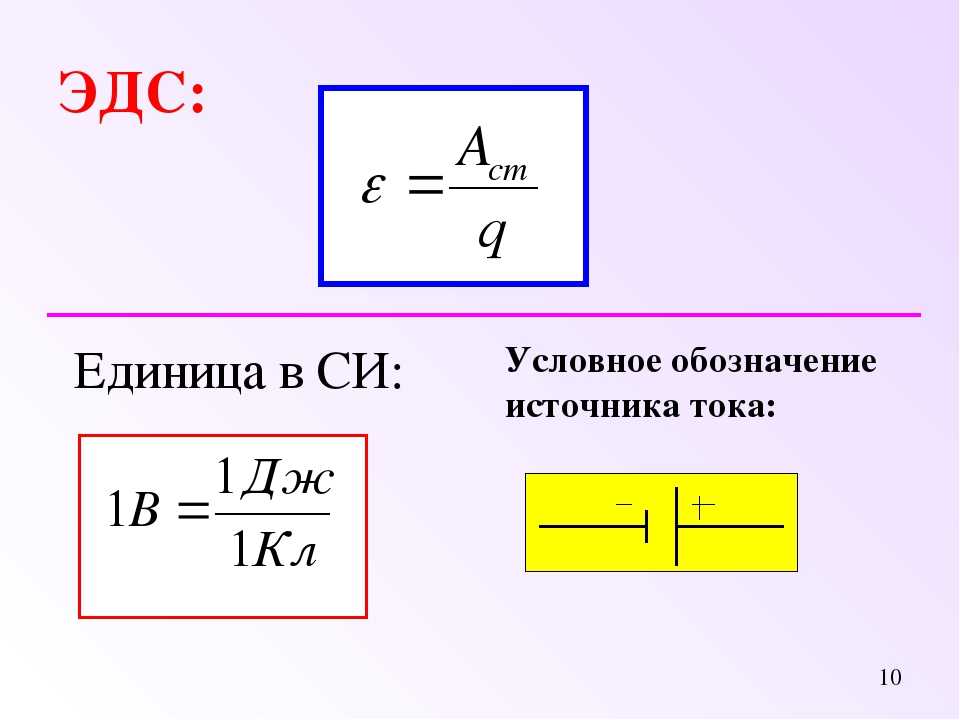 бездрейфовая | ввод данных пользователем | 1 кнопка пользователя | безопасность | контроль скорости электромагнитное демпфирование |
| workspace | translation rotation | ∅ 160 x 110 mm 240 x 140 x 320 deg | forces | translation rotation | 12.0 N not actuated | разрешение | перемещение вращение | < 0,01 мм 0,09 град | интерфейс | стандарт скорость | USB 2.0 до 9 9009K0064 | power | universal | 100V — 240V | platforms | Microsoft Linux Apple Blackberry WindRiver | Windows all distributions macOS QNX VxWorks | software | SDK Haptics SDK Robotics CHAI3D | Эргономика | доступны в лево- и правосторонней конфигурации | Структура | delta-based parallel kinematics hand-centered rotation movements decoupling between translation and rotation movements active gravity compensation | calibration | automatic driftless | user input | 1 user button | safety | контроль скорости электромагнитное демпфирование |
| рабочее пространство | translation rotation gripper | ∅ 160 x 110 mm 240 x 140 x 320 deg 25 mm | forces | translation rotation gripper | 12. 0 N not actuated 8.0 N | resolution | Перевод Вращение GRIPPER | <0,01 мм 0,09 DEG 0,006 мм | раз интерфейс | Стандарт | USB 2,0909.0064 | power | universal | 100V — 240V | platforms | Microsoft Linux Apple Blackberry WindRiver | Windows all distributions macOS QNX VxWorks | software | SDK Haptics SDK Robotics CHAI3D | Эргономика | доступны в лево- и правосторонней конфигурации | Структура | delta-based parallel kinematics hand-centered rotation movements decoupling between translation and rotation movements active gravity compensation | calibration | automatic driftless | user input | 1 simulated button using the force gripper | Безопасность | Контроль скорости Электромагнитное демпфирование |
Фотогалерея
Force Dimension — Компания | О нас
Справочная информация
Компания Force Dimension, основанная в 2001 году как дочерняя компания Швейцарского федерального технологического института в Лозанне (EPFL), является ведущим новатором в области высокоточных тактильных технологий.
Компания завоевала международную репутацию за разработку и производство уникального дизайна и усовершенствованных интерфейсов с силовой обратной связью для робототехники, промышленности, аэрокосмической, медицинской и бытовой электроники.
Компания Force Dimension, занимающаяся разработкой продуктов, также лицензирует и разрабатывает индивидуальные роботизированные и VR-решения для широкого спектра областей применения. На протяжении многих лет Force Dimension также тесно сотрудничает с академическими учреждениями, такими как EPFL и Стэнфордский университет, а также со школами дизайна, включая ECAL и Швейцарский центр дизайна.
Хронология
Ноябрь 2021
Международная космическая станция (МКС)
Астронавты Томас Песке (ЕКА) и Меган Макартур (НАСА) используют sigma.7 на борту МКС в рамках эксперимента PILOTE, воссоздающего ощущение давления и коснитесь при дистанционном управлении манипулятором. Sigma.7 празднует два года пребывания в космосе, совершив более 10 000 оборотов вокруг Земли и преодолев расстояние в 420 миллионов километров.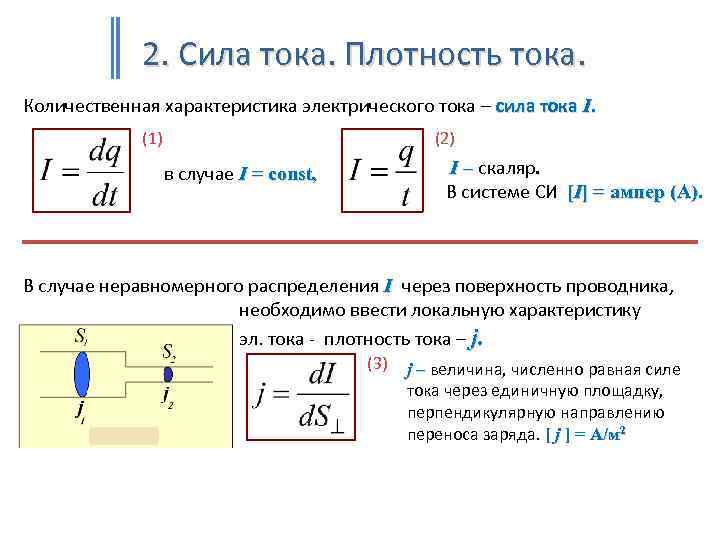
ноябрь 2021 г.
август 2020 г.
Consumer Entertainment
Force Dimension запускает технологию тактильного управления и рендеринга высокой четкости для развлечений. Эта новая технология позволяет студиям разработки игр легко включать в свои приложения сверхреалистичные возможности силовой обратной связи.
ноябрь 2019 г.
Международная космическая станция (МКС)
В сотрудничестве с Европейским космическим агентством (ЕКА) Force Dimension сертифицирует тактильное устройство sigma.7 для использования в космосе и запускает устройство на Международную космическую станцию (МКС). Впервые астронавт ЕКА Лука Пармитано успешно дистанционно управляет роботом-манипулятором, расположенным на Земле, с трехмерным интерфейсом силовой обратной связи.
ноябрь 2019 г.
июнь 2018 г.
Искусство часового дела
В сотрудничестве со швейцарским производителем роскошных часов Audemars Piguet компания Force Dimension представляет ChronoSim, первый тактильный симулятор для дизайнеров часов.
Сентябрь 2017 г.
Лямбда-тактильное устройство
«Титан Медикал» представляет систему SPORT, в которую интегрированы новейшие лямбда-тактильные устройства Force Dimension.
Сентябрь 2017 г.
Апрель 2016 г.
OceanOne
Force Dimension поставляет тактильные устройства для OceanOne, подводного робота, разработанного Стэнфордским университетом и Google и оснащенного искусственным интеллектом и системами тактильной обратной связи. Система дает археологам беспрецедентную возможность исследовать глубины океанов с высокой точностью.
ноябрь 2014 г.
Hansen Medical
Медицинские тактильные устройства Force Dimension насчитывают в общей сложности более 15 000 клинических случаев использования хирургами устройств для хирургических вмешательств.
ноябрь 2014 г.
март 2013 г.
Тактильные и промышленные роботы
Компания Vulcan Engineering представляет VTS, большого промышленного робота, который управляется вручную с помощью тактильного устройства омега.
3 для операций отрезания и шлифования.
Июль 2015
Medical Robotics
Компания Medrobotics получила разрешение CE и FDA на роботизированную систему Flex® для ЛОР-приложений. Хирургическая система включает в себя тактильное устройство omega.3 Force Dimension.
Июль 2015 г.
Июнь 2012 г.
Медицинское моделирование
Force Dimension разрабатывает и производит первый ScanTrainer TAS для Medaphor.
Март 2012 г.
Тактильная консоль Sigma.7
Force Dimension выпускает консоль sigma.7, двуручный интерфейс, предназначенный для управления робототехникой.
Март 2012 г.
Ноябрь 2011 г.
Медицинская робототехника
Компания Magnetecs включает тактильное устройство omega.3 в свою роботизированную систему управления наведением катетера и визуализации (CGCI) для минимально инвазивной хирургии.
Январь 2013 г.
NeuroArm
IMRIS и Университет Калгари проводят первые клинические испытания на людях NeuroArm, совместимого с МРТ робота для операций на головном мозге, управляемого двумя тактильными устройствами омега.
7.
Январь 2013 г.
Январь 2009
Тактильное устройство Delta.3
Force Dimension выпускает обновленную версию тактильных устройств delta.3.
Август 2008 г.
Hansen Medical
Роботизированная система Hansen Medical Sensei®, включающая в себя медицинское тактильное устройство omega.3 Force Dimension, получила разрешение FDA и маркировку CE. Отгружены первые системы.
Август 2008 г.
Сентябрь 2007 г.
Первые полеты в условиях микрогравитации
В сотрудничестве с SRI International и NASA компания Force Dimension проводит первые экспериментальные испытания тактильных устройств Omega.7 в условиях микрогравитации на борту C9самолет.
Июнь 2007 г.
Novint Falcon
Force Dimension передает лицензию на свою тактильную технологию компании Novint Technologies. Запуск первого в мире потребительского тактильного 3D-устройства, разработанного для рынка развлечений.
Июнь 2007 г.
Март 2007 г.
Тактильное устройство Omega.7
Force Dimension представляет тактильное устройство omega.7, первое коммерческое тактильное устройство с 7 степенями свободы и технологией обратной связи по силе.
Май 2010 г.
Тактильное устройство Sigma.7
Force Dimension представляет тактильное устройство sigma.7, первое коммерческое тактильное устройство, сочетающее в себе высокие силы, крутящие моменты и возможности захвата. Устройство интегрировано в хирургическую роботизированную систему MIRO, разработанную Немецким аэрокосмическим центром (DLR).
Май 2010 г.
Январь 2005 г.
Сеть продаж
Force Dimension расширяет свою торговую деятельность в Японии, Корее и Китае.
Август 2006 г.
Сертификация FDA
Force Dimension выпускает свой первый тактильный интерфейс, сертифицированный с медицинской точки зрения. Система интегрирована в роботизированную систему Sensei, разработанную и выпущенную на рынок компанией Hansen Medical.
