Температурные воздействия на конструкции – Часть 2: Термомеханика
См. начало: Температурные воздействия на конструкции – Часть 1: Нормы проектирования
Введение
В этой части рассмотрены теоретические основы температурных воздействий на конструкции с точки зрения классической механики материалов.
В предыдущей части 1 рассмотрены особенности учета температурных воздействий при проектировании конструкций зданий по российскому своду правил СП 20.13330.2011 (СНиП 2.01.07-85).
В части 3 представлены примеры температурных воздействий на простые конструкции – балки с различными условиями закрепления.
1. Теоретические основы температурных воздействий на материалы
1.1. Температурное расширение-сокращение
Изменения температуры вызывают расширение или сокращение конструкционных материалов, в результате чего в них возникают температурные деформации и температурные напряжения. Простая иллюстрация температурного расширения показана на рисунке 2. 1, где брусок материала не закреплен и поэтому имеет возможность свободно расширяться [1].
1, где брусок материала не закреплен и поэтому имеет возможность свободно расширяться [1].
Рисунок 2.1 – Брусок материала под воздействием увеличения температуры [1]
Когда этот брусок нагревается, каждый элемент материала подвергается температурным деформациям по всем направлениям, и, соответственно, размеры бруска увеличиваются также во всех направлениях. Если взять угол А за точку отсчета и дать стороне АВ возможность сохранять свое исходное направление, то брусок примет форму, которая показана штриховыми линиями.
Для большинства конструкционных материалов температурная деформация εTявляется пропорциональной изменению температуры ΔT, то есть
εT = α·ΔT, (1)
где α – свойство материала, которое называется коэффициентом температурного расширения. Согласно принятому в мире «знаковому соглашению» температурное расширение считается положительным, а температурное сокращение – отрицательным [1, 2].
1.2. Коэффициент температурного расширения конструкционных материалов
Поскольку деформация является безразмерной величиной, этот коэффициент температурного расширения имеет размерность, обратную изменению температуры. В системе СИ размерность αТ может выражаться как 1/К (величина обратная единице СИ Кельвин) или 1/ºС (величина обратная градусу Цельсия). Величина αТ является одинаковой в обоих случаях, так как изменение температуры является численно одинаковым как в градусах Кельвина, так и в градусах Цельсия.
Удобно представлять величину коэффициента температурного расширения в единицах 10-6/ºС или мкм/м·ºС. Последний вид особенно удобен – он наглядно показывает насколько микрометров удлиняется один метр материала при увеличении температуры на один градус температуры.
Информация о коэффициентах температурного расширения некоторых конструкционных материалов представлена в таблице 1.
Таблица 2.1 — Коэффициент температурного расширения конструкционных материалов [1]
1.3. Коэффициент температурного расширения алюминиевых сплавов
Коэффициенты температурного расширения основных алюминиевых сплавов, которые применяются в строительстве, показаны в таблице 2.
Таблица 2.2 — Коэффициент температурного расширения строительных алюминиевых сплавов [3]
Из таблицы 2.2 видно, что коэффициенты температурного расширения различных алюминиевых сплавов различаются незначительно. Поэтому в своде правил СП 128.13330.2012 (СНИП 2.03.06-85) для расчетов алюминиевых конструкций в интервале температуры от минус 70 ºС до 100 ºС для всех применяемых в строительстве алюминиевых сплавов применяется коэффициент температурного расширения 0,23·10-4 1/ºС [4]. В европейском стандарте EN 1991-1-5 величина расчетного коэффициента температурного расширения составляет 24·10-6 1/ºС [5].
1.4. Температурные напряжения
Чтобы продемонстрировать относительную важность температурных напряжений, можно сравнить температурные напряжения с напряжениями, которые возникают при силовом нагружении [1]. Предположим, что мы имеем брус, который нагружен силами в осевом направлении с продольными деформациями, которые даются равенством
Предположим, что мы имеем брус, который нагружен силами в осевом направлении с продольными деформациями, которые даются равенством
ε = σ/Е, (2)
где σ – напряжение, а Е – модуль упругости. Далее предположим, что мы имеем идентичный брусок, которые подвержен изменению температуры ΔT. Это означает, что этот брусок имеет температурные деформации согласно равенства (1). Приравнивание этих двух видов деформаций дает уравнение
σ = Е·α·ΔT (3)
Пример.
Вычислим осевое напряжение σ, которое дает такие же деформации, как и изменение температуры ΔT в стержнях из алюминиевого сплава и строительной (малоуглеродистой) стали при увеличении их температуры на 50 ºС.
Для алюминиевого стержня (α = 23·106, Е = 70000 Н/мм2):
σ = 70000·23·10-6·50 = 80,5 Н/мм2
Для стержня из малоуглеродистой стали (α = 12·106, Е = 210000 Н/мм2):
σ = 210000·12·10-6·50 = 126 Н/мм2
Отметим известный факт, что при одинаковом изменении температуры температурные напряжения в алюминиевом стержне составляют только 2/3 от величины температурных напряжений в стальном стержне. Так происходит потому, что величина температурных напряжений зависит от произведения модуля упругости и коэффициента температурного расширения (см. формулу (3)). Поэтому, хотя коэффициент температурного расширения алюминия в два раза больше, чем у стали, но модуль упругости алюминия в три раза меньше, чем у стали.
Так происходит потому, что величина температурных напряжений зависит от произведения модуля упругости и коэффициента температурного расширения (см. формулу (3)). Поэтому, хотя коэффициент температурного расширения алюминия в два раза больше, чем у стали, но модуль упругости алюминия в три раза меньше, чем у стали.
Как видно из приведенных выше расчетов, температурные напряжения могут достигать величин, сравнимых с напряжениями от механических нагрузок. Поэтому термические воздействия на конструкции зданий необходимо учитывать наряду с другими нагрузками, как того и требуют нормативные документы [4, 5].
1.5. Температурные перемещения
Вернемся к бруску материала, показанного на рисунке 1 [1]. Предполагаем, что материал бруска является гомогенным и изотропным, то есть механические свойства материала бруска являются одинаковыми во всем его объеме. Кроме того, предполагаем, что изменение температуры ΔT является однородным, то есть одинаковым, по всему бруску. При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину
При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину
δТ = εT·L= α·ΔT·L (4)
Уравнение (4) можно применять для вычисления изменений длин элементов конструкций после однородного нагрева, например, удлинение призматического стержня на рисунке 2.2. Поперечные размеры стержня также изменятся, но эти изменения не показаны на рисунке 2.2, так как обычно они не оказывают влияния на осевые силы, которые передаются этим стержнем.
Рисунок 2.2 – Увеличение длины призматического стрежня
в результате однородного увеличения температуры (уравнение (4)) [1]
Пример.
Оценим удлинение незакрепленных алюминиевого и стального стержней длиной 3 м при увеличении их температуры на 50 ºС.
Для алюминиевого стержня:
δТ = α·ΔT·L = 23·10-6·50·3000 = 3,5 мм
Для стержня из малоуглеродистой стали:
δТ = α·ΔT·L = 12·10-6·50·3000 = 1,8 мм
При рассмотрении выше температурных деформаций предполагалось, что конструкция не имеет ограничений для своих перемещений, что позволяло ей расширяться или сокращаться совершенно свободно. Такие условия возникают, например, когда объект лежит на гладкой поверхности, на которой не возникает трения [1]. В таких случаях при однородном нагреве всего объекта в целом не возникает напряжений, хотя неоднородные изменения температуры могут вызывать внутренние температурные напряжения. Однако многие конструкции имеют опоры, которые препятствуют свободному расширению и сокращению их размеров. Поэтому в них развиваются температурные напряжения даже, если изменение температуры является однородным по всей конструкции.
1.6. Температурные деформации в статически определимых конструкциях
Рассмотрим ферму АВС из двух стержней, показанную на рисунке 2.3. Предположим, что температура стержня АВ изменилась на ΔТ1, а стержня ВС – на ΔТ2. Поскольку эта ферма является статически определимой, то оба стержня могут свободно удлиняться или укорачиваться, давая в результате перемещение соединения В. Однако в этом случае температурные напряжения в стержнях, а также реакции в опорах, отсутствуют.
Рисунок 2.3 – Статически определимая ферма
с однородным изменением температуры в каждом элементе
Это заключение справедливо в целом для всех статически определимых конструкций, а именно: однородное изменение температуры в элементах конструкции вызывают температурные деформации (и соответствующие изменения длин элементов) без возникновения соответствующих температурных напряжений [1, 2].
1.7. Температурные деформации в статически неопределимых конструкциях
Статически неопределимыми конструкциями называются конструкции, у которых число реакций превышает число уравнений статического равновесия. В отличие от статически определимых конструкций при расчете таких конструкций принимаются во внимание прогибы [1, 2].
В отличие от статически определимых конструкций при расчете таких конструкций принимаются во внимание прогибы [1, 2].
В статически неопределимой конструкции температурные напряжения могут возникать или не возникать в зависимости от особенностей конструкции и особенностей температурных изменений. Чтобы проиллюстрировать некоторые из таких возможностей, рассмотрим статически неопределимую ферму, показанную на рисунке 2.4.
Рисунок 2.4 — Статически неопределимая ферма
под воздействием изменений температуры
Опоры этой конструкции позволяют узлу D двигаться горизонтально. Поэтому, когда вся ферма однородно нагревается, в ней не возникает температурных напряжений. Все элементы увеличиваются в длине пропорционально своим первоначальным длинам, а вся ферма в целом становится немного больше в размерах.
Однако, если некоторые из стержней нагреваются, а другие – нет, то возникают температурные напряжения, так как статически неопределимое расположение стержней препятствует их свободному расширению.
Заключение
1) Изменение температуры элементов конструкции вызывает в них температурные деформации. Температурные напряжения возникают только в статически неопределимых конструкциях.
2) Однородный нагрев алюминиевого стержня на 50 ºС способен при жестком закреплении концов стержня вызывать значительные температурные напряжения. При таком нагреве удлинение стержня со свободными концами составляет 3,5 мм.
См. окончание:
Температурные воздействия на конструкции – Часть 3: Теория и примеры
Источники:
1. James M. Gere & Barry J. Goodno — Mechanics of Materials, 2009
2. Тимошенко С.П., Гере Дж. – Механика материалов, М.: Мир, 1976
3. Aluminum and Aluminum Alloys / ed. J.R. Davis, ASM International, 1993
4. СП 128.13330.2012 (СНИП 2.03.06-85) Алюминиевые конструкции
5. EN 1991-1-5 Еврокод 1: Воздействия на сооружения. Часть 1-5. Основные воздействия. Температурные воздействия
Подготовлено сотрудниками Алюком
Теория электрических цепей — Википедия
(перенаправлено с «Узел (теория электрических цепей)»)
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июля 2018 года; проверки требуют 8 правок.
Теория электрических цепей (ТЭЦ) — совокупность наиболее общих закономерностей, описывающих процессы в электрических цепях. Теория электрических цепей основана на двух постулатах:
- Исходное предположение теории электрических цепей. Все процессы в любых электротехнических устройствах можно описать с помощью двух понятий: тока и напряжения.
- Исходное допущение теории электрических цепей. Сила тока в любой точке сечения любого проводника одна и та же, а напряжение между любыми двумя точками пространства изменяется по линейному закону[источник не указан 2268 дней]
Электрическое напряжение
Сила тока
Электрическая мощность
Электрическое сопротивление
Содержание
- 1 Основные понятия
- 1.1 Электрическая цепь
- 1.2 Ветвь
- 1.3 Узел
- 1.4 Контур
- 1.5 Двухполюсник
- 1.6 Четырёхполюсник
- 2 См. также
- 3 Литература
Основные понятияПравить
Сила тока — количество заряда (q, в Кулонах), перемещаемое через поперечное сечение проводника в единицу времени (t, в секундах).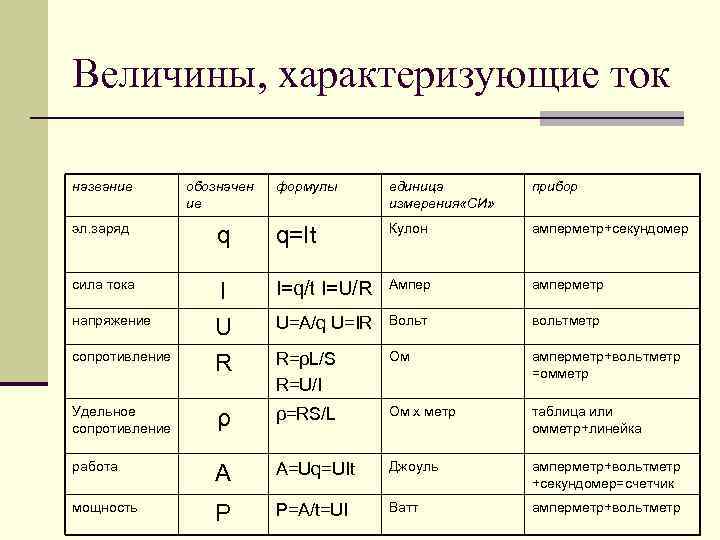
- i(t) = dq/dt или I = q/t , измеряется в Амперах =
Напряжение — предел отношения количества энергии, необходимой для переноса некоторого количества электричества из одной точки пространства в другую, к этому количеству электричества, когда оно стремится к нулю. Последнее равенство написано в предположении, что энергия и заряд — величины непрерывные. Размерность напряжения:
- В = Дж • Кл−1
Из основных понятий как следствие вытекают определения:
Энергия — мера способности объекта совершать работу. Её размерность:
- Дж = В • А • с
Мощность — скорость изменения энергии во времени. Размерность мощности:
- Вт = Дж • с−1 = В • А
Электрическая цепьПравить
Электрическая цепь — совокупность элементов и источников, предназначенных для генерации, приема и преобразования токов и напряжений (электрических сигналов). Те участки цепи, куда поступают или для которых генерируются сигналы, называют входами; те участки, на которых регистрируют токи или напряжения в результате их генерации или преобразования, — выходами.
Те участки цепи, куда поступают или для которых генерируются сигналы, называют входами; те участки, на которых регистрируют токи или напряжения в результате их генерации или преобразования, — выходами.
Элементы электрической цепи — идеализированные устройства с двумя или более зажимами, все электромагнитные процессы в которых с достаточной для практики точностью могут быть описаны только в основных понятиях (тока и напряжения).
Элементы бывают: линейные и нелинейные, пассивные и активные, стационарные и нестационарные, непрерывные и дискретные, с сосредоточенными и распределенными параметрами. Из дальнейшего рассмотрения исключим нестационарные элементы и элементы с распределенными параметрами. Источники электромагнитной энергии — идеализированные устройства, имеющие два или более зажимов и предназначенные для генерации или преобразования электромагнитной энергии. Источники бывают: независимые, зависимые и управляемые.
ВетвьПравить
Ветвью называется участок электрической цепи с одним и тем же током.
УзелПравить
Основная статья: Узел цепи
Узлом называется место соединения ветвей. Различают понятия геометрического и потенциального узлов. Геометрические узлы, имеющие одинаковые потенциалы, могут быть объединены в один потенциальный узел.
КонтурПравить
Контуром называется замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи.
ДвухполюсникПравить
Основная статья: Двухполюсник
Двухполюсником называют часть электрической цепи с двумя выделенными зажимами-полюсами.
ЧетырёхполюсникПравить
Четырёхполюсником называют часть электрической цепи, имеющую две пары зажимов, которые называются входными и выходными.
- Медиафайлы на Викискладе
- Теоретические основы электротехники
- Линейные электрические цепи
- Нелинейные электрические цепи
- Переходные процессы
- Добротворский И.
 Н. Теория электрических цепей. Учебник. — М.: Радио и связь, 1989.
Н. Теория электрических цепей. Учебник. — М.: Радио и связь, 1989. - В. Г. Герасимов, Э. В. Кузнецов, О. В. Николаева. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. —
- Андреев В. С. Теория нелинейных электрических цепей: Учебное пособие для вузов.. — «Радио и связь», 1982. — 280 с.
Dimensions Of Stress — Infinity Learn
Напряжение, обозначаемое σ, представляет собой внешнюю восстанавливающую силу, действующую на единицу площади. Выражается в Н/м². . Он используется для расчета напряжения, приложенного к любому данному телу, когда сила и площадь, на которую оно действует, заданы в задаче. В результате σ = F/A
σ – это величина напряжения, приложенного к объекту
Зарегистрируйтесь, чтобы получить бесплатные пробные тестовые и учебные материалы
+91
Подтвердите код OTP (обязательно)
Я согласен с условиями и политикой конфиденциальности.
F обозначает силу, действующую на объект.
Площадь поперечного сечения обозначается буквой A.
Напряжение также можно определить как силу, приложенную к объекту, которая вызывает его полную деформацию. Мы обнаружили, как формула напряжения выводится в физической терминологии. Известно, что более крупные объекты более устойчивы к широкому диапазону сил. Мы можем использовать один и тот же предел текучести для одного и того же материала, независимо от того, насколько велик объект, используя напряжение вместо силы. Более того, стресс и напряжение неразрывно связаны, и по мере того, как увеличивается одно, вместе с ним растет и другое. И чем больше напряжение в объекте, тем большую деформацию он испытывает.
Типы напряженияНормальное напряжение
Нормальное напряжение возникает, когда объект нагружен осевой силой. Когда осевая сила делится на площадь поперечного сечения, представляется нормальное напряжение. Это произойдет, когда объект сжат.
Это произойдет, когда объект сжат.
Продольное напряжение возникает, когда длина тела изменяется из-за приложения нормального напряжения. Продольное напряжение представлено делением деформирующей силы на площадь поперечного сечения.
Объемный и объемный стрессЭто тип стресса, при котором объем тела изменяется в результате стресса. Нормальное напряжение на объекте вызывает изменение его длины или объема, тогда как касательное напряжение вызывает изменение формы тела, известное как объем.
Деформация при растяжении Напряжение при растяжении определяется как сила на единицу площади и напряжение, возникающее при приложении силы и увеличивающее длину тела в результате действия силы. Наблюдается при растяжении стержня в соответствии с третьим законом движения. Резина является распространенным примером растягивающего напряжения, и растяжение является величиной, связанной с ним.
Когда мы прикладываем к телу касательную силу, форма и объем объекта изменяются. Длина объекта уменьшается в результате напряжения сжатия. Это обратное напряжение растяжения.
Прежде чем обсуждать стресс, необходимо рассмотреть несколько концепций. Кроме того, напряжение определяется как количество силы (силы или энергии), приложенной к объекту, деленное на площадь его поперечного сечения. Более крупные объекты также могут выдерживать большие силы. Кроме того, используя напряжение, а не силу, мы можем использовать один и тот же предел текучести для одного и того же материала независимо от размера объекта. Самое главное, стресс и напряжение неразрывно связаны, и по мере того, как растет одно, растет и другое. Кроме того, поскольку объект подвергается большему напряжению, он деформируется до тех пор, пока не выйдет из строя.
Размерная формула напряженияОпределенная формула напряжения приведена, [M 1 L -1 T -2 ]
, где
- M = MASS
- L = LINE,
- M = MASS
- L = LINE L = LINE
L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE L = LINE 9007 - T = Время
Напряжение = Сила [Площадь]-1. ., , (1)
., , (1)
Формула измерения площади = [M 0 L 2 T 0 ] . . . . (2)
Поскольку Сила = M × a = [M] × [M 0 L 1 T -2 ]
Формула измерения силы = [M 1 L 1 T -2 ] . . . . (3)
Когда мы подставляем уравнения (2) и (3) в уравнение (1), мы получаем
Напряжение = [Площадь]-1 Сила Альтернативно, Напряжение = [M 1 L 1 T — 2 ] × [M 0 L 2 T 0 ] -1 = [M 1 L -1 T -2 ] 9000 [M 1 L -1 T -2 ].
Часто задаваемые вопросыВ. Каковы единица измерения и формула измерения напряжения?
Ответ: Сила, действующая на «маленькую» границу на единицу площади этой границы, определяется как напряжение. Как известно, сила, действующая на единицу площади, называется давлением. Потому что стресс и давление — это одно и то же. В результате единицей стресса в СИ является Паскаль. Он имеет ту же размерную формулу, что и давление, которая равна 9.0150 M¹L⁻¹T⁻² .
Как известно, сила, действующая на единицу площади, называется давлением. Потому что стресс и давление — это одно и то же. В результате единицей стресса в СИ является Паскаль. Он имеет ту же размерную формулу, что и давление, которая равна 9.0150 M¹L⁻¹T⁻² .
В. Одинаковы ли размеры давления и напряжения?
Ответ : Размеры напряжения и давления одинаковы, но давление не то же самое, что напряжение.
Сопутствующая информация
Соотношения напряжение-размер-укорочение левого желудочка до и после коррекции хронической аортальной и митральной недостаточности
. 1985 г., 1 июля; 56 (1): 99–105.
дои: 10.1016/0002-9149(85)90574-0.
М. Р. Зиле, В. Х. Гааш, Х. Дж. Левин
- PMID: 3160230
- DOI:
10.

М. Р. Зиле и др. Ам Джей Кардиол. .
. 1985 г., 1 июля; 56 (1): 99–105.
doi: 10.1016/0002-9149(85)90574-0.
Авторы
М. Р. Зиле, В. Х. Гааш, Х. Дж. Левин
- PMID:
- DOI: 10.1016/0002-9149(85)90574-0
Абстрактный
Механические характеристики левого желудочка при хронической аортальной недостаточности (АР) отличаются от таковых при хронической митральной недостаточности (МР). Считается, что эти различия частично ответственны за изменения функции левого желудочка (ЛЖ), наблюдаемые после хирургической коррекции АР или МР. Для проверки этой гипотезы определяли отношения нагрузки, размера и укорочения ЛЖ до и после протезирования клапана у пациентов с компенсированными и декомпенсированными хроническими АР и МР. Использованы эхокардиографические данные 32 больных с АР и 20 больных с МР; до операции у всех 52 пациентов было увеличение ЛЖ. На основании послеоперационных данных для каждого поражения были выделены 2 подгруппы: у пациентов группы А был достигнут нормальный конечно-диастолический размер (менее 3,3 см/м2), а у пациентов группы В имелось стойкое увеличение ЛЖ. До операции у пациентов группы А с АР было повышено пиковое систолическое напряжение, но конечно-систолическое напряжение и фракционное укорочение были нормальными; у пациентов в группе В с АР было повышено пиковое систолическое напряжение, повышено конечно-систолическое напряжение и снижено укорочение.
Считается, что эти различия частично ответственны за изменения функции левого желудочка (ЛЖ), наблюдаемые после хирургической коррекции АР или МР. Для проверки этой гипотезы определяли отношения нагрузки, размера и укорочения ЛЖ до и после протезирования клапана у пациентов с компенсированными и декомпенсированными хроническими АР и МР. Использованы эхокардиографические данные 32 больных с АР и 20 больных с МР; до операции у всех 52 пациентов было увеличение ЛЖ. На основании послеоперационных данных для каждого поражения были выделены 2 подгруппы: у пациентов группы А был достигнут нормальный конечно-диастолический размер (менее 3,3 см/м2), а у пациентов группы В имелось стойкое увеличение ЛЖ. До операции у пациентов группы А с АР было повышено пиковое систолическое напряжение, но конечно-систолическое напряжение и фракционное укорочение были нормальными; у пациентов в группе В с АР было повышено пиковое систолическое напряжение, повышено конечно-систолическое напряжение и снижено укорочение.
Похожие статьи
Значение предоперационной гипертрофии, напряжения стенки и конечного систолического размера как эхокардиографических предикторов нормализации дилатации левого желудочка после протезирования клапана при хронической аортальной недостаточности.
Kumpuris AG, Quinones MA, Wagoner AD, Kanon DJ, Nelson JG, Miller RR.

Несоответствие постнагрузки при заболеваниях аортального и митрального клапанов: значение для хирургического лечения.
Росс Дж. Мл. Росс Дж. Мл. J Am Coll Кардиол. 1985 г., апрель 5(4):811-26. doi: 10.1016/s0735-1097(85)80418-6. J Am Coll Кардиол. 1985. PMID: 3882814 Обзор.
Соотношения длина-сила-укорочение левого желудочка до и после хирургической коррекции хронической митральной недостаточности.
Goldfine H, Aurigemma GP, Zile MR, Gaasch WH. Голдфайн Х. и др. J Am Coll Кардиол. 1998 янв.; 31(1):180-5. doi: 10.1016/s0735-1097(97)00453-1.
 J Am Coll Кардиол. 1998.
PMID: 9426038
J Am Coll Кардиол. 1998.
PMID: 9426038[Эхокардиография с упражнениями для оценки функции левого желудочка при митральной и аортальной недостаточности].
Нисида К., Китамура Х., Хигами М., Кода М., Накагава Х., Йошига М., Сугихара Х., Фурукава К., Кацумэ Х., Иджичи Х. Нисида К. и др. J Кардиогр. 1985 март; 15(1):123-33. J Кардиогр. 1985. PMID: 4067339 Японский язык.
Функция левого желудочка после хирургической коррекции хронической митральной недостаточности.
Gaasch WH, Zile MR. Гааш В.Х. и др. Европейское сердце J. 1991 июля; 12 Приложение B: 48-51. doi: 10.1093/eurheartj/12.suppl_b.48. Европейское Сердце Дж. 1991. PMID: 1936024 Обзор.
Посмотреть все похожие статьи
Цитируется
Оценка отношений стимул-эффект при росте левого желудочка с использованием простой многомасштабной модели.

Ронданина Э., Бовендерд PHM. Ронданина Э. и др. Биомех Модель Механобиол. 2020 фев;19(1): 263-273. doi: 10.1007/s10237-019-01209-2. Epub 2019 6 августа. Биомех Модель Механобиол. 2020. PMID: 31388869 Бесплатная статья ЧВК.
Взаимосвязь между функцией почек и чрескожными вмешательствами на митральном клапане: всесторонний обзор.
Ло К.Б., Даянанд С., Рам П., Даянанд П., Слипчук Л.Н., Фигередо В.М., Рангасвами Дж. Ло К.Б. и др. Curr Cardiol Rev. 2019;15(2):76-82. дои: 10.2174/1573403X14666181024155247. Curr Cardiol Rev. 2019. PMID: 30360746 Бесплатная статья ЧВК. Обзор.
Использование тканевой допплерэхокардиографии для раннего выявления систолической дисфункции левого желудочка у больных с митральной недостаточностью.



 Н. Теория электрических цепей. Учебник. — М.: Радио и связь, 1989.
Н. Теория электрических цепей. Учебник. — М.: Радио и связь, 1989.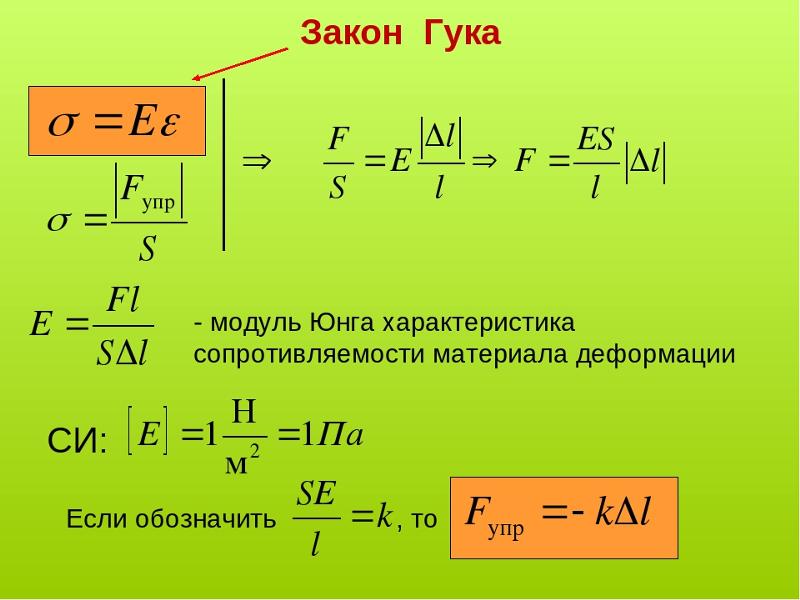

 J Am Coll Кардиол. 1998.
PMID: 9426038
J Am Coll Кардиол. 1998.
PMID: 9426038