Разложение сигнала на гармоники | MATHCAD
Сигнал прямоугольной формы можно описать следующим аналитическим выражением
|
|
(1) |
Спектр такого сигнала s(t) с помощью ряда Фурье в тригонометрической форме имеет следующий вид:
|
s(t) = (2)
|
где ω = 2π/T – угловая частота; n – номер гармоники; t – время; A0, Bn, Bn – коэффициенты разложения ряда Фурье |
Коэффициенты разложения ряда Фурье вычисляются по формулам:
где x(t) – периодический сигнал.
Полученное аналитическое выражение сигнала x(t) в среде MathCAD будет иметь вид:
|
|
(6) |
Для построения графика сигнала x = f(t) необходимо выбрать в главном меню программы MathCAD «Вид – Панели инструментов – График», далее на появившейся панели «Graph» выбрать элемент «Декартов график», после чего на рабочей области программы MathCAD появится область построения графика. По оси ординат области построения графика необходимо ввести «
Рис. График сигнала прямоугольной формы в среде MathCAD: A = 1, T = 50, τ = 25
Для записи разложения сигнала в тригонометрический ряд Фурье потребуется вызвать панель «Calculus» или в главном меню выбрать «Вид – Панели инструментов – Калькуляция». На этой панели есть элементы «Определённый интеграл» и «Суммирование по дискретному элементу». Они необходимы для записи ряда Фурье и его коэффициентов разложения.
Полученное выражение для спектрального показания сигнала в общем виде для заданного числа гармоник N = 3 запишем следующим образом:
|
N := 3 n := 1, 2, … N ω := 2,
|
(7) |
|
|
(8) |
|
An := ,
|
(9) |
|
Bn := ,
|
(10) |
|
s(t) := + (Aпcos(tnω) + Bnsin(tnω)).
|
(11) |
Чтобы добавить на график x = f(t) спектральную форму сигнала s = f(t), нужно выделить указателем мыши на оси ординат поле, где записана функция исходного сигнала x(t) и справа от неё ввести запятую, после этого ниже появится поле для ввода ещё одной функции, куда следует ввести s(t). Графики сигнала прямоугольной формы и его спектральное показание по первым трём гармоникам показаны на рисунке ниже.
Рис. Графики исходного сигнала прямоугольной формы
и его спектральное показание s(t) для числа гармоник N = 3
Аналогично строят графики для пяти и семи гармоник. Для этого в программе расчёта гармоник нужно лишь присвоить числу гармоник N новое значение, а программа автоматически пересчитает спектр сигнала. При этом автоматически обновится график зависимости s = f(t).
Рис. Графики исходного сигнала прямоугольной формы x(t)
и его спектральное показание s(t) для числа гармоник
Рис. Графики исходного сигнала прямоугольной формы x(t)
и его спектральное показание s(t) для числа гармоник N = 7
Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
(1), где:
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
(2),
где , k-я комплексная амплитуда.
или
(3)
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени , т.е. с частотой Fd ≥ 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
2. Разложение периодического сигнала на гармоники. Анализ и синтез электрических фильтров
Похожие главы из других работ:
Анализ линейной электрической цепи во временной и частотной областях. Расчет и построение отклика аналогового фильтра на сигнал
1.2 Разложение непериодического сигнала на типовые составляющие
Рисунок 1.2 — Временное представление аналогового непериодического сигнала Представление исходного сигнала с помощью элементарных составляющих, т.е. через функции Хевисайда (единичных скачков) Рисунок 1…
Анализ линейной электрической цепи во временной и частотной областях. Расчет и построение отклика аналогового фильтра на сигнал
3.1 Расчет прохождения периодического сигнала через ЛЭЦ
Периодический сигнал, проходя через ЛЭЦ, не теряет своей периодической природы, поэтому сигналы на входе и выходе линейной цепи можно представить бесконечной суммой непериодических сигналов, сдвинутых друг относительно друга на период…
Анализ сигналов в радиотехнических цепях
3. Спектральный анализ периодического сигнала (Период T=20мс)
…
Анализ сигналов в радиотехнических цепях
3.2 Средняя мощность периодического сигнала
По определению под средней мощностью периодического сигнала понимается средняя мощность за один период Средняя мощность за период равна 2.827(стр.18 приложения). 4. Расчет передаточной, амплитудно-частотной…
Анализ сигналов и их прохождение через линейные цепи
3. Получение аналитического выражение (модели) периодического сигнала
Периодический видеосигнал выразим через одиночную функцию Эрмита третьей степени, длительностью 3 миллисекунды: Рис.3…
Анализ функций и моделирование сигналов в приложении Simulink
4. Моделирование периодического сигнала
Смоделировать периодический сигнал. Форма сигнала задана графически (рис. 4.1). Определить все временные характеристики сигнала, построить структурную схему для моделирования заданного сигнала, выполнить моделирование…
Исследование искажений сигналов на выходе фильтра нижних частот
10. Определение спектра периодического входного сигнала
I1(s) = — e-Stu/2+ e-Stu = (1 — 2e-Stu/2 + e-Stu) Еk = * (1 — e-jk2рtu/2tu + e-jk2рtu/tu) = (1 — 2e-jkр + e-jk2р) = e-jkр sin2 Aмплитудный спектр входного периодического сигнала Ak = | Еk| = sin2 Фазовый спектр входного периодического сигнала Фk = arg Еk = — kр + Запишем отрезок ряда Фурье…
Исследование радиотехнических сигналов
3.1 Построение АЧХ и ФЧХ спектра периодического сигнала
Для анализа сигналов и их обработки важное значение имеет разложение заданной функции по различным ортогональным системам. Бесконечная система действительных функций называется ортогональной на отрезке , если При этом предполагается, что , т…
Исследование радиотехнических сигналов
3.3 Энергия и средняя мощность периодического сигнала
Средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Таким образом, средняя мощность периодического сигнала При использовании тригонометрической формы ряда Фурье, учитывая, что С0=а0/2…
Преобразование сигналов
6. Зависимости энергии сигнала от номера гармоники
Построение зависимости энергии сигнала от номера гармоники производится после просчета энергии сигнала по…
Преобразование сигналов
6.1 Построение графика зависимости энергии сигнала от номера гармоники
По полученным данным строим, при помощи программы «MathCad 15»…
Разработка эквивалентных и принципиальных схем электрического фильтра и усилителя напряжения
4 Анализ спектра сложного периодического сигнала
…
Спектральный анализ аналоговых сигналов и расчет откликов на выходе линейной цепи
1.2 Разложение непериодического сигнала на типовые составляющие
Рисунок 1.2 — Временное представление аналогового непериодического сигнала Представление исходного сигнала с помощью элементарных составляющих, т.е. через функции Хевисайда (единичных скачков) где Рисунок 1…
Спектральный анализ аналоговых сигналов и расчет откликов на выходе линейной цепи
1.6 Расчет ширины спектра периодического сигнала по пороговому критерию
Для ограничения спектра сигнала необходимо задаться пороговым критерием. Порог определим как десятую часть гармоники с максимальной амплитудой Так как последний коэффициент превышающий , где то сигнал соберем по 20 гармоникам, т.е…
Спектральный анализ аналоговых сигналов и расчет откликов на выходе линейной цепи
3.1 Расчет прохождения периодического сигнала через ЛЭЦ
Периодический сигнал, проходя через ЛЭЦ, не теряет своей периодической природы, поэтому сигналы на входе и выходе линейной цепи можно представить бесконечной суммой непериодических сигналов, сдвинутых друг относительно друга на период…
2.4. Разложение сигнала на элементарные составляющие. 2. Сигналы и помехи. Теория передачи сигналов
В общем случае сигнал представляет собой сложное колебание, поэтому возникает необходимость представить сложную функцию s(t), определяющую сигнал, через простые функции. Простейшей с практической точки зрения формой выражения сигнала является линейная комбинация некоторых элементарных функций
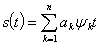 (2.51)
(2.51)
При изучении линейных систем такое представление сигнала весьма удобно. Оно позволяет решение многих задач расчленить на части, применяя принцип суперпозиции. Например, чтобы определить сигнал на выходе линейной системы, вычисляется реакция системы на каждое элементарное воздействие 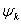 (t), а затем результаты, умноженные на соответствующие коэффициенты ak складываются.
(t), а затем результаты, умноженные на соответствующие коэффициенты ak складываются.
Функции 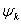 (t) выбираются таким образом, чтобы любой сигнал можно было представить сходящейся суммой вида (2.51). Далее требуется, чтобы коэффициенты ak легко вычислялись и не зависели от числа членов суммы (2.51). Указанным требованиям наиболее полно удовлетворяет совокупность ортогональных функций.
(t) выбираются таким образом, чтобы любой сигнал можно было представить сходящейся суммой вида (2.51). Далее требуется, чтобы коэффициенты ak легко вычислялись и не зависели от числа членов суммы (2.51). Указанным требованиям наиболее полно удовлетворяет совокупность ортогональных функций.
Функции
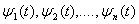 (2.52)
(2.52)
заданные на интервале 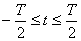 называются ортогональными, если
называются ортогональными, если
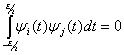 при
при 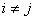 (2.53)
(2.53)
Интеграл от квадрата каждой функции семейства (2.52) равняется некоторой постоянной
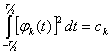 (2.54)
(2.54)
Семейство функций
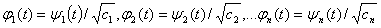
в силу (2.53) и (2.54) будет удовлетворять не только условию ортогональности, но и интеграл от квадрата каждой функции будет равен единице, т. е.
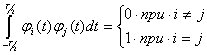 (2.55)
(2.55)
Говорят, что функции семейства
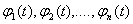 (2.56)
(2.56)
ортогональны и нормированы (ортонормированны), если выполняются условия (2.55).
Пусть сигнал s(t) представлен в виде ряда по ортонормированным функциям (2.56):
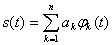 (2.57)
(2.57)
где 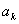 — некоторые числовые коэффициенты. Для определения коэффициентов
— некоторые числовые коэффициенты. Для определения коэффициентов 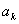 умножим обе части равенства (2.57) на
умножим обе части равенства (2.57) на 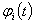 проинтегрируем по промежутку
проинтегрируем по промежутку
(-T/2,T/2):
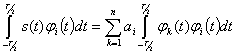
Принимая во внимание (2.55), получим
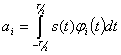 (2.58)
(2.58)
Коэффициенты 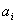 , определяемые по этим формулам, называются обобщенными коэффициентами Фурье, а ряд (2.57) при этом называют обобщенным рядом Фурье.
, определяемые по этим формулам, называются обобщенными коэффициентами Фурье, а ряд (2.57) при этом называют обобщенным рядом Фурье.
В теории связи для представления сигналов широко используются два частных случая разложения функций в ортогональные ряды: разложение по тригонометрическим функциям и разложение по функциям вида sinx/x. В первом случае получаем спектральное представление сигнала в виде обычного ряда Фурье, а во втором случае — временное представление в виде ряда В. А. Котельникова. Очевидно, оба эти представления адекватны (равносильны).
Для достаточной идентивности (точности) представления сигнала суммой (2.57) необходимо потребовать, чтобы
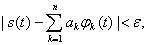 где ε — произвольная сколь угодно малая
где ε — произвольная сколь угодно малая
положительная величина. Погрешность представления сигнала удобно оценивать средней квадратичной ошибкой
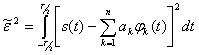 (2.59)
(2.59)
Можно показать, что 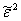 имеет наименьшее значение, если
имеет наименьшее значение, если 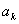 равны коэффициентам Фурье. В этом случае
равны коэффициентам Фурье. В этом случае
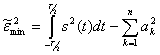 (2.60)
(2.60)
Отсюда получаем неравенство
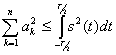 (2.61)
(2.61)
При 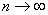 величина
величина 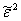 стремится к нулю и неравенство (2.61) превращается в известное равенство Парсеваля
стремится к нулю и неравенство (2.61) превращается в известное равенство Парсеваля
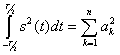 (2.62)
(2.62)
-Г/2
Система ортонормированных функций (2.56) называется замкнутой, если справедливо равенство (2.62). Эта система будет называться полной, если к ней нельзя присоединить ни одной функции, ортогональной одновременно всем функциям (2.56) и не равной тождественно нулю. Из условия замкнутости функции следует и их полнота. Поэтому можно сказать, что равенство (2.62) является необходимым и достаточным условием полного представления некоторого класса сигналов совокупностью ортогональных функций {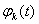 }
}
Случайный сигнал (или помеха), заданный на интервале (-Т/2,Т/2), может быть также представлен рядом (2.51) или (2.57). При этом коэффициенты 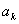 будут случайными величинами, принимающими с определенной вероятностью значения, соответствующие различным реализациям сигнала (помехи).
будут случайными величинами, принимающими с определенной вероятностью значения, соответствующие различным реализациям сигнала (помехи).
Простыми словами о преобразовании Фурье / Habr
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.(с) xkcd
Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
- FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
- Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
- Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
- Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
- Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
- Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
- Как по цифровой последовательности восстанавливают исходный сигнал
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi…pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:
Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.
Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T…1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)
То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.
Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.
Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:
Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.
На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.
Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0…1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.
До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.
Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):
В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для бесконечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.
Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.
Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).
Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:
Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.
Как интерпретировать получившийся результат? С учетом всего вышеизложенного,
- Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
- Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
- Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
- Для действительнозначного входного сигнала, спектр в диапазоне 1/2T…1/T просто зеркально повторяет спектр 0…1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
- Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
- В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
- Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
- Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)
Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.
2. Прямоугольные сигналы | 7. Смешивание частот | Часть2
2. Прямоугольные сигналы
Прямоугольные сигналы
Было установлено, что любой повторяющийся, несинусоидальный сигнал может быть приравнен к комбинации постоянного напряжения, синусоидальной волны, и (или) косиносуидальной волны (синусоидальная волна с фазовым сдвигом 90 градусов) с различными амплитудами и частотами. Это верно в независимости от того, насколько странной или замысловатой будет рассматриваемая форма волны. Пока такой сигнал повторяется в течение долгого времени, он может быть сведен к последовательности синусоидальных волн. В частности, было обнаружено, что прямоугольные сигналы математически эквивалентны сумме синусоидальной волны на этой же частоте, а так же бесконечной последовательности нечетнократных частот синусоидальных волн с уменьшающейся амплитудой:
Такая правда о сигналах на первый взгляд может показаться слишком странной, чтобы в нее поверить. Однако, если прямоугольный сигнал представляет собой смесь бесконечной последовательности гармоник синусоидальных волн, мы в состоянии это доказать, сложив вместе несколько гармоник синусоидальных волн для получения приближенного прямоугольного сигнала. Данное рассуждение не просто пустой звук, оно легко проверяется при помощи программы SPICE.
Схема, которую мы будем моделировать, состоит из нескольких источников синусоидальных переменных напряжений (соответствующих амплитуд и частот), соединенных последовательно:
В данном моделировании мы суммировали последовательные источники напряжений 1, 3, 5, 7 и 9 гармоник. Основная частота составляет 50 Гц, а каждая гармоника — целое число, кратное этой частоте. Значения амплитуд (напряжений) не случайны; они были получены из уравнений, приведенных в начале статьи (4/π помноженное на 1, 1/3, 1/5, 1/7 и т.д. для каждой из возрастающих нечетных гармоник).
building a squarewave v1 1 0 sin (0 1.27324 50 0 0) 1-я гармоника (50 Гц) v3 2 1 sin (0 424.413m 150 0 0) 3-я гармоника v5 3 2 sin (0 254.648m 250 0 0) 5-я гармоника v7 4 3 sin (0 181.891m 350 0 0) 7-я гармоника v9 5 4 sin (0 141.471m 450 0 0) 9-я гармоника r1 5 0 10k .tran 1m 20m .plot tran v(1,0) Построение графика 1 гармоники .plot tran v(2,0) Построение графика 1 + 3 гармоники .plot tran v(3,0) Построение графика 1 + 3 + 5 гармоники .plot tran v(4,0) Построение графика 1 + 3 + 5 + 7 гармоники .plot tran v(5,0) Построение графика 1 + . . . + 9 гармоники .end
Теперь мы объясним вам проведенный SPICE анализ шаг за шагом. На первом графике вы можете видеть основной синусоидальный сигнал частотой 50 Гц. Он представляет собой чистую синусоидальную волну без дополнительного гармонического содержания. Такой сигнал производится идеальным источником переменного напряжения:
Следующий график покажет нам что произойдет, когда чистый сигнал объединится с третьей гармоникой (три раза по 50 Гц, или 150 Гц). Он больше не будет похож на чистую синусоиду:
Взлеты и падения волны между положительными и отрицательными циклами сейчас гораздо круче, а гребни волны становятся более плоскими. Давайте посмотрим, что произойдет, если мы добавим следующую нечетную гармоническую частоту:
На этом графике мы видим еще большее сглаживание гребней волны. Несмотря на то, что на каждом из гребней существуют провалы, их амплитуда стала меньше, чем была прежде. Теперь посмотрим, что произойдет, если мы добавим еще одну нечетную гармоническую частоту:
Здесь мы видим, что волна становится еще более плоской на каждом из своих пиков. И наконец, добавив 9-ю гармонику (пятый источник синусоидального напряжения нашей схемы), мы получим следующий результат:
Конечным результатом сложения пяти нечетных гармонических частот является весьма близкое подобие прямоугольной волны. Рассмотренный пример показывает нам, как можно создать прямоугольный сигнал из нескольких синусоидальных сигналов с разными частотами. Все это доказывает, что чистая прямоугольная волна фактически эквивалентна последовательности синусоидальных волн. Когда переменное напряжение прямоугольной формы воздействует на цепь с реактивными компонентами (конденсаторами и катушками индуктивности), эти компоненты реагируют так, как будто на них воздействует несколько синусоидальных напряжений с разными частотами.
фундаментальным свойством всех явлений связанных с волнами (электрическими или иными), является то, что повторяющиеся несинусоидальные волны эквивалентны определенной последовательности смешения постоянного напряжения, синусоидальных волн и (или) косинусоидальных волн. Математический процесс разбивки несинусоидальной волны на составляющие ее частоты называется анализом Фурье. Детали этого анализа выходят далеко за рамки данной статьи. Однако, существуют компьютерные алгоритмы, способные быстро выполнить анализ Фурье для реальных сигналов.
Программа SPICE умеет работать с сигналами, и разбивать их на составные гармоники синусоидальных волн посредством алгоритма быстрого преобразования Фурье, выводя частотный анализ в виде таблицы чисел. Давайте испробуем эту способность программы на прямоугольном сигнале, который как вы знаете состоит из нечетных гармоник синусоидальных волн:
squarewave analysis netlist v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .tran 1m 40m .plot tran v(1,0) .four 50 v(1,0) .end
Параметр «pulse» в списке соединений, описывающем источник напряжения V1, дает команду на моделирование сигнала (импульса) прямоугольной формы. В нашем случае он является симметричным (равное время для каждого полупериода) и имеет максимальную амплитуду 1 вольт. В ходе своей работы программа сначала «нарисует» прямоугольный сигнал, который будет анализироваться ….
… а затем, она распечатает анализ Фурье для этого сигнала:
fourier components of transient response v(1) dc component = -2.439E-02 harmonic frequency fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 5.000E+01 1.274E+00 1.000000 -2.195 0.000 2 1.000E+02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E+02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E+02 4.936E-02 0.038757 -98.780 -96.585 5 2.500E+02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E+02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E+02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E+02 5.116E-02 0.040175 -107.561 -105.366 9 4.500E+02 1.443E-01 0.113316 -19.756 -17.561 total harmonic distortion = 43.805747 percent
Как видите, программа разложила прямоугольный сигнал на спектр синусоидальных частот (до девятой гармоники), и на небольшое постоянное напряжение, обозначенное как «dc component». Мы сообщили программе SPICE значение основной частоты (для прямоугольной волны с периодом 20 мс, эта частота равна 50 Гц), чтобы она знала, как классифицировать гармоники. Обратите внимание, насколько малы значения всех четных гармоник (2-й, 4-й, 6-й, 8-й), и как уменьшаются амплитуды нечетных гармоник (1 является самой большой, а 9 — самой маленькой).
Этот же самый метод «Преобразования Фурье» используется в компьютеризированной аппаратуре питания, которая «отбирает пробы» сигналов переменного напряжения и определяет их гармоническое содержание. Общим компьютерным алгоритмом для выполнения данной задачи выступает алгоритм быстрого преобразования Фурье. Вам не нужно знать, как эти компьютерные программы работают, но вы должны быть в курсе их существования и применения.
Такие же математические методы (которые используются в программе SPICE для анализа гармонического содержания сигналов) могут быть применены к анализу музыки. Вы наверное видели устройство, называемое графическим эквалайзером. Это устройство является частью высококачественного стерео оборудования, которое контролирует (а иногда и отображает) характер содержания гармоник в музыке. Эквалайзер, оснащенный несколькими кнопками или ползунками, позволяет выборочно ослаблять (уменьшать) амплитуду определенных частот, настраивая звук для удобства слушателя. Рядом с каждым ползунком, как правило, отображается «гистограмма» соответствующей частоты.
Устройство, предназначенное для отображения амплитуд частотных составляющих какого либо сигнала, называется анализатором спектра. Анализаторы спектра могут быть как простыми устройствами, состоящими из набора «фильтрующих» схем (предназначенных для «отделения» разных частот друг от друга), так и сложными, представляющими собой компьютер под управлением алгоритма быстрого преобразования Фурье, который математически «раскладывает» сигнал на составляющие гармоники. Анализаторы спектра широко применяются для анализа высокочастотных сигналов, производимых радиопередатчиками или компьютерными сетями. Отображаемая ими информация очень похожа на осциллограмму:
Как и в осциллографе, в анализаторе спектра для отображения графика сигнала используется электронно-лучевая трубка или жидкокристаллический дисплей. Анализатор спектра, в отличии от осциллографа, показывает график зависимости амплитуды от частоты (осциллограф отображает график зависимости амплитуды от времени). Иначе говоря, анализатор спектра производит анализ сигнала в частотной области, а не во временной.
А сейчас обратите внимание на то, что анализ Фурье последнего SPICE моделирования далек от совершенства. В идеале, амплитуды всех четных гармоник и значение постоянного напряжения должны иметь нулевое значение. Такое положение дел не является особенностью программы SPICE — это свойство сигналов в целом. Сигнал неограниченной продолжительности (бесконечное количество циклов) может быть проанализирован с абсолютной точностью. Анализ сигнала с небольшим количеством циклов менее точен. Только тогда, когда мы имеем уравнение, описывающее сигнал в полном объеме, анализ Фурье может свести его к определенной последовательности синусоидальных волн. Чем меньше циклов имеет сигнал, тем меньше мы уверены в его частоте. Принимая эту концепцию за основу можно сделать вывод, что короткий импульс сигнала, который даже не завершает цикл, на самом деле не имеет частоты, а выступает в качестве бесконечного диапазона частот. Этот принцип характерен для всех волновых явлений, а не только для переменных напряжений и токов.
Достаточно сказать, что количество циклов и достоверность частотной составляющей сигнала непосредственно связаны между собой. Мы можем улучшить точность нашего анализа, позволив волне колебаться на протяжении многих циклов. В этом случае результат будет более близок к идеалу:
squarewave v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .option limpts=1001 .tran 1m 1 .plot tran v(1,0) .four 50 v(1,0) .end
fourier components of transient response v(1) dc component = 9.999E-03 harmonic frequency fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 5.000E+01 1.273E+00 1.000000 -1.800 0.000 2 1.000E+02 1.999E-02 0.015704 86.382 88.182 3 1.500E+02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E+02 1.997E-02 0.015688 82.764 84.564 5 2.500E+02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E+02 1.994E-02 0.015663 79.146 80.946 7 3.500E+02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E+02 1.989E-02 0.015627 75.529 77.329 9 4.500E+02 1.396E-01 0.109662 -16.199 -14.399
Обратите внимание, этот анализ показывает меньшее значение постоянной составляющей напряжения и низкие амплитуды каждой из четных гармоник. Все это произошло потому, что мы позволили программе использовать большее количество циклов волны.
Примеры разложения в ряд Фурье реальных сигналов. — Студопедия.Нет
Nbsp; Лабораторная работа № 8
Аппроксимация периодического сигнала рядом Фурье.
| Цель работы: | Изучение представления различных периодических сигналов рядом ортогональной системе тригонометрических функций |
1. ВВЕДЕНИЕ
В электроэнергетике и электротехнике предъявляются достаточно жёсткие требования к строго синусоидальному закону изменения токов и напряжений во времени. Но во многих областях радиотехники, автоматики, связи, электротехники, несинусоидальные, периодические сигналы (тока и напряжения) соответствуют нормальному режиму работы цепей и устройств. Нередко даже при синусоидальном входном воздействии выходная величина существенно отличается от гармонической, если в цепи содержатся наименьшие элементы (электронные или полупроводниковые приборы, катушки с ферромагнитным сердечником и др.). Поэтому методы анализа цепей с периодическими негармоническими воздействиями имеют большое значение при, разработке устройств весьма широкого применения.
Поскольку разновидностей периодических негармонических сигналов, в принципе, неограниченное множество, важнейшей задачей становится выбор такого метода анализа, который был бы применим к любой форме сигнала. Таковым оказался метод, основанный на использовании тригонометрического ряда Фурье и принципа суперпозиции, применимого к линейным энергетическим цепям.
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Представление периодических функций рядом Фурье.
Все периодические сигналы (напряжения, токи), отличаемые от гармонических, называются негармоническими. Они характеризуются периодом Т, формой и размахом напряжения или тока (Up или Ip_). Математически такой сигнал, как функция времени, удовлетворяет условию:

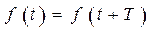

Если эта функция удовлетворяет ряду условий, называемых условиями Дирихле, (в пределах периода Т функция f ( x ) непрерывна, либо имеет конечное число разрывов первого рода и конечное число максимумов и минимумов), то такая функция может быть представлена в виде бесконечного гармонического ряда Фурье. Сумма этого ряда совпадает со значениями f ( t ) во всех точках непрерывности, а в точках разрыва дает среднее арифметическое предельных значений функции при приближении к точке разрыва слева f ( t -) и справа f ( t +).
Если обозначить w =2 p /Т (частота основной или первой гармоники), то ряд Фурье в тригонометрической форме можно записать:
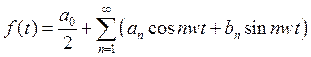 (1)
(1)
где

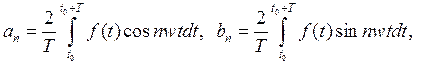 (2)
(2)

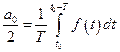
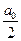 — постоянная составляющая, an, в n — амплитуды косинусоидальных и синусоидальных членов ряда. Как следует из (1), ряд Фурье содержит только кратные основной частоте гармонические слагаемые, поскольку n принимает только целые значения, и называется номером гармоники. Все гармоники, кроме первой, называются высшими гармониками.
— постоянная составляющая, an, в n — амплитуды косинусоидальных и синусоидальных членов ряда. Как следует из (1), ряд Фурье содержит только кратные основной частоте гармонические слагаемые, поскольку n принимает только целые значения, и называется номером гармоники. Все гармоники, кроме первой, называются высшими гармониками.
Можно показать, что значения anи в n не зависят от выбора t 0. Поэтому, положив t 0.=0. Поэтому, положив t 0.=0 и введя новую переменную 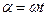 с учетом, что
с учетом, что 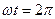 и
и 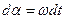 , формулы (1) и (2) можно переписать:
, формулы (1) и (2) можно переписать:
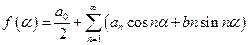 (3)
(3)
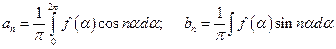 (4).
(4).
Если вспомнить соотношение из тригонометрии:
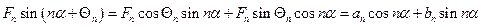 (5)
(5)
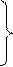 откуда
откуда 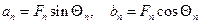 и
и
(6)
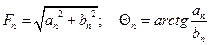 ,
,
то ряд Фурье запишется в виде:
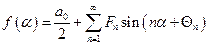 . (7)
. (7)
либо 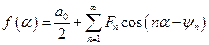 , (8)
, (8)
где 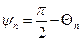 (9)
(9)
Очень часто периодические функции электрических или магнитных величин обладают некоторым видом симметрии, что значительно укрощает разложение такой функции в ряд Фурье. Отметим некоторые виды симметрии:
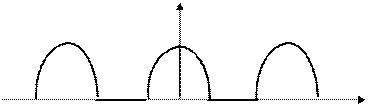
1. Функция f ( a ) симметрична относительно оси ординат (рис.1).
 f( a )
f( a )

 t
t
-2p
Рис. 1.
В этом случае 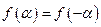 , т.е. функция четная. Из тригонометрических функций четной является только косинус, а синус – нечетная. Поэтому синусоиды не входят в состав ряда Фурье таких функций, т.е.
, т.е. функция четная. Из тригонометрических функций четной является только косинус, а синус – нечетная. Поэтому синусоиды не входят в состав ряда Фурье таких функций, т.е.
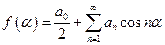 , (10)
, (10)
т.е. четная функция может содержать только косинусоиды и постоянную составляющую. Важное свойство четных функций: для определения коэффициентов а n достаточно пользоваться кривой f ( a ) за половину периода, т.е.
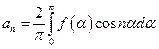 (11)
(11)
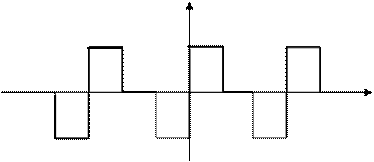 2. Функция f ( a ) симметрична относительно начала координат (рис.2).
2. Функция f ( a ) симметрична относительно начала координат (рис.2).
f ( a )

 0 a
0 a
2p
 |  | ||
Рис. 2
В этом случае выполняется условие f (- a )= — f ( a ). Такие функции называются нечетными. Этому условию не удовлетворяют постоянная составляющая и косинусоиды, поэтому при данном виде симметрии ряд содержит только синусоиды.
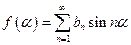 , (12)
, (12)
т.е. нечетная функция может содержать только синусоиды. Здесь также для определения коэффициентов bn достаточно пользоваться кривой f ( a ) за половину периода, т.е.
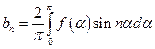 (13)
(13)
3. Функция f ( a ) симметрична относительно оси абсцисс, если её дополнить той же функцией, смещенной на полпериода (рис. 3).
Такая функция удовлетворяет условию: f ( a )= — f ( a + p ). Заменив f ( a ) по формуле (3), получим:
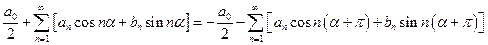 ,
,
откуда для четных n получим:
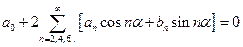 .
.
Это условие выполняется при произвольных значениях a только в том случае, когда a 0 =0 и an = bn =0 для четных n. То есть, при данном виде симметрии
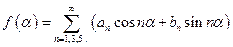 . (14)
. (14)
Поэтому, функция с данным видом симметрии содержит только нечетные гармоники. Коэффициенты anи bn можно вычислять по формулам (11) и (13).
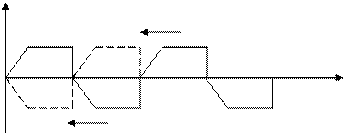
p 2p a
Рис. 3
При разложении периодической функции в ряд Фурье следует сначала проанализировать её на наличие каких-либо видов симметрии. Если они имеются, то этот факт позволяет предсказать, какие гармоники не войдут в разложение. Если, например, одновременно выполняются условия симметрии по п.п. 1 и 3, то в разложении будут только нечетные синусоиды.
Часто для придания функции симметрии относительно оси ординат бывает необходимо перенести начало отсчета. На рис. 4 показана однополупериодная синусоида. Если сместить начало отсчета на отрезок b, то кривая становится симметричной относительно оси абсцисс.
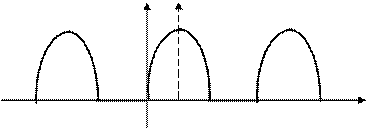 f( a )
f( a )
 0 0’ a
0 0’ a
b
Рис. 4.
Пусть для некоторой функции f ( a ) известно разложение в ряд Фурье, т.е. заданы коэффициенты anи bn:
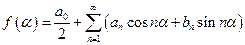 .
.
Если сместить начало отсчета на отрезок b вправо или налево относительно исходного положения, то разложение функции в новой координатной системе получается заменой a на a 1 +b 1, где a 1 – абсцисса в новой системе координат; b >0 – соответствует смещению нового начала координат вправо, b <0 – влево.
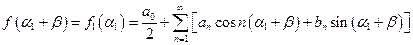 (15)
(15)
Используя известные соотношения для тригонометрических функций:
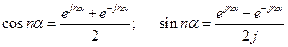 ,
,
выражение под знаком суммы формулы (3) можно переписать:
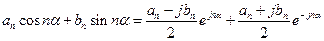
Из формул (4) нетрудно определить, что an – четная функция n, а bn – нечетная, т.е. an = a —n; bn = — b —n. Кроме того, 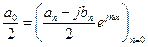 .
.
Поэтому ряд Фурье можно записать в следующем виде:
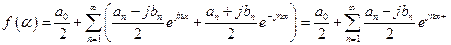
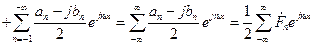 , (16)
, (16)
где 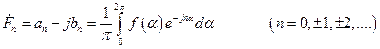 (17)
(17)
называется комплексной амплитудой n-ой гармоники. Формула (16) – ряд Фурье в комплексной форме.
Примеры разложения в ряд Фурье реальных сигналов.
Приведем разложения в ряд Фурье некоторых, наиболее часто встречающихся периодических сигналов.
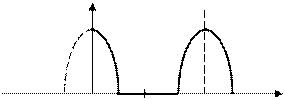
а). Сигнал на выходе однополупериодного выпрямителя (рис. 5)
 U
U
Um
t
0 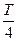
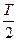
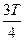 T
T
Рис. 5
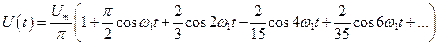 (18)
(18)
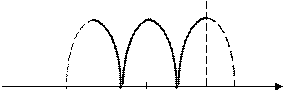
б). Сигнал на выходе двухполупериодного выпрямителя (рис. 6)
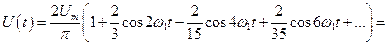
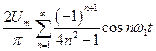 (19)
(19)
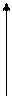 U
U
Um
t
0 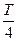
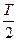
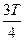 T
T
Рис. 6
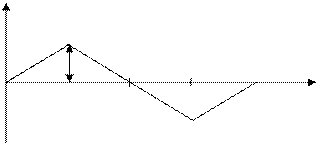
в). Сигнал треугольной формы (рис. 7а, б)
 U
U
T
 T/2 t
T/2 t
Рис. 7а
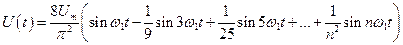 (20)
(20)
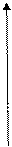 U
U

 Um
Um

 -T/2 T/2
-T/2 T/2



 t
t
-T/4 0 T/4
Рис. 7б
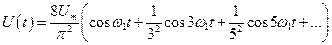 (21)
(21)
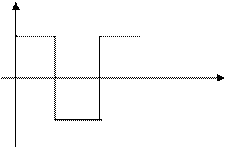
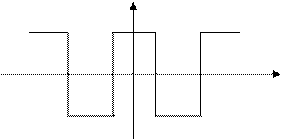
г). Сигнал прямоугольной формы со скважностью 2 (меандр) (рис.8 а,б)
 |  | ||
U U Um
Um


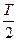 T t —
T t — 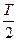
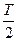 t
t
а) б)
Рис. 8
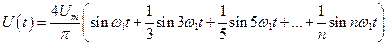 (n – целое, нечетное) (22)
(n – целое, нечетное) (22)
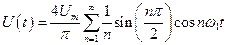 (23)
(23)
Сигналы рис. 8 а, б идеализированы, т.к. имеют фронты бесконечно малой длительности. Практически такие сигналы не существуют, в точках разрыва, как отмечалось, ряды (22) и (23) не сходятся, но в среднем сходимость ряда обеспечивается.
д). Сигналы трапецеидальной формы (рис. 9).
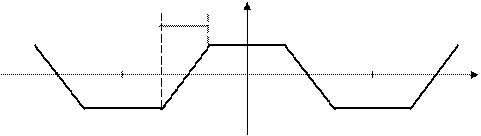 U(t)
U(t)
tф

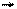 Um
Um
-T/2 T/2
t
-T/4 T/4
Рис. 9
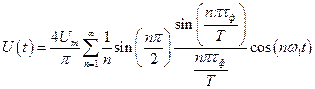 (24)
(24)
обычно t ф << Т, поэтому при малых n множитель 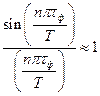 . При этом амплитуды нескольких первых гармоник рядов (23) и (24) почти одинаковы. Нос ростом n амплитуды гармоник ряда (24) убывают быстрее, чем у ряда (23). Ряд Фурье для реального сигнала рис. 9 сходится быстрее.
. При этом амплитуды нескольких первых гармоник рядов (23) и (24) почти одинаковы. Нос ростом n амплитуды гармоник ряда (24) убывают быстрее, чем у ряда (23). Ряд Фурье для реального сигнала рис. 9 сходится быстрее.
е). Пилообразный сигнал (рис. 10).
Такой формы напряжение используется в схемах развертки осциллографа, телевизора, монитора. Ряд Фурье этого сигнала:
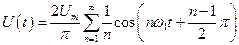 (25)
(25)
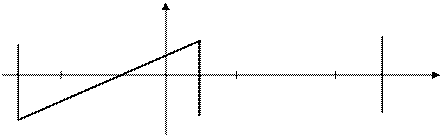 U
U

 Um
Um
-T/2 -T/4 T/4 T/2
t
Рис. 10
ж). Последовательность коротких прямоугольных видеоимпульсов (рис.11)
 U
U
Um
-T/2 T/2
 t
t
-T — 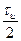
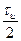 T
T
рис. 11
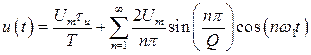 (26)
(26)
здесь 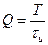 — скважность импульса.
— скважность импульса.
з). Амплитудно-модулированный (АМ) сигнал при гармоническом законе модуляции.
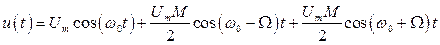 , (26/)
, (26/)
где 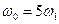 — частота несущего колебания,
— частота несущего колебания, 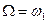 — частота гармонического сообщения.
— частота гармонического сообщения.

