Постоянная времени для RC-цепи Калькулятор
✖Сопротивление является мерой сопротивления току, протекающему в электрической цепи. Сопротивление измеряется в омах, что обозначается греческой буквой омега (Ом).ⓘ Сопротивление [R] | AbohmEMU сопротивленияESU сопротивленияExaohmГигаомкилооммегаоммикроомМиллиомНаномомПетаомПланка сопротивлениеКвантованная Hall СопротивлениеВзаимный СименсStatohmВольт на АмперYottaohmZettaohm | +10% -10% | |
✖Емкость — это способность материального объекта или устройства накапливать электрический заряд. Он измеряется изменением заряда в ответ на разность электрических потенциалов.ⓘ Емкость [C] | AbfaradАттофарадсантифарадаКл / вольтдекафарадДецифарадEMU конденсаторнойESU конденсаторнойэксафарадафарадафемтофарадагигафарадагектофарадкилофарадМегафарадаМикрофарадМиллифараднанофарадапетафарадапикофарадаStatfaradтерафарада | +10% -10% |
✖Постоянная времени — это отклик, представляющий прошедшее время, необходимое для того, чтобы отклик системы затухал до нуля, если бы система продолжала затухать с начальной скоростью. |
АттосекундаМиллиард летсантисекундаВекаЦикл переменного тока 60 ГцЦикл переменного токаДеньДесятилетиеДекасекундаДецисекундаExasecondФемтосекундаГигасекундагектосекундаЧаскилосекундаМегасекундамикросекундаМиллениумМиллион летМиллисекундаминутМесяцНаносекундаПетасекундаПикосекундаВторойСведбергТерасекундаТысяча летНеделюГодYoctosecondЙоттасекундаЗептосекундаЗеттасекунда |
⎘ копия |
👎
Формула
сбросить
👍
Постоянная времени для RC-цепи Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.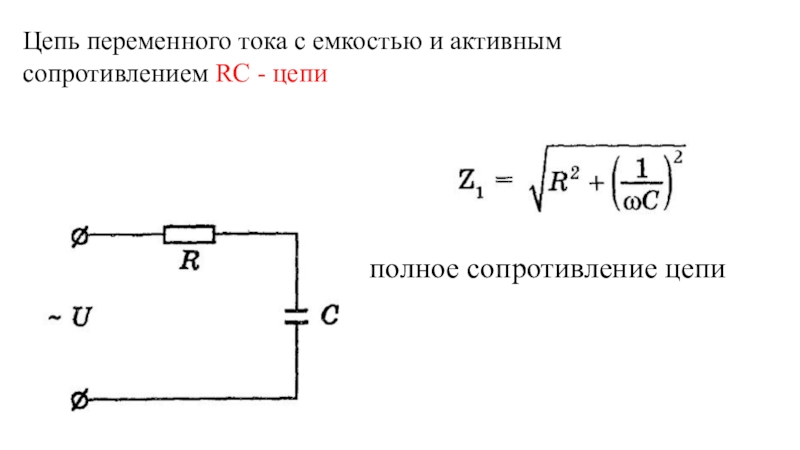 Преобразование входов в базовый блок
Преобразование входов в базовый блок
Сопротивление: 60 ом —> 60 ом Конверсия не требуется
Емкость: 350 Микрофарад —> 0.00035 фарада (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.021 Второй —>21 Миллисекунда (Проверьте преобразование здесь)
< 3 Постоянная времени Калькуляторы
Постоянная времени для RC-цепи формула
Постоянная времени = Сопротивление*Емкость
Что такое постоянная времени τ?
Время, которое представляет скорость, с которой конкретная система может реагировать на изменение, обычно равное времени, необходимому для изменения указанного параметра с коэффициентом 1-1 / е (приблизительно 0,6321).
Share
Copied!2.
 6 Примеры расчета в цепях переменного тока
6 Примеры расчета в цепях переменного тока2.6.1 Последовательная r-c цепь
Рассмотрим R—C цепь на примере задачи.
Дана цепь из последовательно соединенных R и C элементов (рис. 2.11) , Напряжение на входе
Найти ток , падения напряжений на каждом из элементов, мощности , построить векторную диаграмму токов и напряжений.
Рис. 2.11 – Цепь последовательно соединенных R и C элементов
Решение:
Записываем комплексы сопротивлений: , .
Сопротивление всей цепи равно сумме комплексных сопротивлений .
Модуль полного сопротивления .
По закону Ома:
.
Модуль тока: ,
Модуль тока можно определить так же следующим способом:
Комплексное падение напряжения на резистивном элементе
.
Комплексное падение напряжения на емкостном элементе С по закону Ома:
.
Измерительные приборы (вольтметр, амперметр, ваттметр) показывает модуль комплекса измеряемой величины.
Модуль (то, что покажет вольтметр):
;
.
Проверка:
По второму закону Кирхгофа:
,
или из прямоугольного треугольника (рис. 2.10):
.
Рассчитываем мощности:
Активная: ;
Реактивная: ;
Полная: ;
.
Коэффициент мощности: .
Угол φ определяем по тангенсу угла или из векторной диаграммы. Угол положительный.
Ток I опережает напряжение на входе на угол .
Строим векторную диаграмму по точкам
(координатам) в соответствии с выбранным
масштабом.
Рис. 2.12 – Векторная диаграмма
2.6.2 Последовательная r-l цепь
Рассмотрим R—L цепь на примере задачи.
Дана цепь из последовательно соединенных R и L элементов (рис. 2.13) б, Напряжение на входе
Найти ток I, падения напряжений на каждом из элементов, мощности , построить векторную диаграмму токов и напряжений.
Рис. 2.13 – Цепь последовательно соединенных R и L элементов
Решение:
1) Записываем комплексы сопротивлений: , ;
2) Общее сопротивление цепи равно сумме комплексов сопротивлений ;
3) Модуль ;
4) Рассчитаем комплексный ток в цепи по закону Ома:
;
5) Модуль тока: .
Модуль тока можно определить и стандартным способом:
6) Комплексное падение напряжения на резистивном элементе R по закону Ома:
;
7) Комплексное падение напряжения индуктивном элементе L по закону Ома:
.
Измерительные приборы (вольтметр, амперметр, ваттметр) показывает модуль комплекса измеряемой величины;
8) Рассчитаем модули падений напряжений:
;
;
9) Проверка:
По второму закону Кирхгофа:
,
или из прямоугольного треугольника (рис. 2.10):
;
10) Рассчитываем мощности:
Активная: ;
Реактивная: ;
Полная : ;
;
11) Коэффициент мощности: ;
12) Знак угла φ определяем по тангенсу угла или из векторной диаграммы. Угол положительный.
Ток в цепи отстает от входного напряжения на угол 360.
Строим векторную диаграмму по точкам
(координатам) в соответствии с выбранным
масштабом.
Рис. 2.14 – Векторная диаграмма
2.7 Частотные свойства цепей переменного тока
Частотной характеристикой называется зависимость параметров цепи от частоты (например ). Активное сопротивление устройств от частоты не зависит. Зависимость индуктивного и емкостного сопротивлений от частоты определяется формулами:
и . Графики зависимости реактивных сопротивлений от частоты представлены на рис. 2.15.
Рис. 2.15 – Графики зависимости реактивных сопротивлений
от частоты
Рассмотрим цепь из последовательно соединенных R, L, C элементов (рис. 2.15). На участке цепи с последовательно соединенными R, L, C элементами найдется такая частота (резонансная) при которой сопротивления и окажутся равными.
При этом, и полное сопротивление Z окажется чисто активным и равным R.
Пример: Дана цепь из последовательно соединенных R, L, C элементов . Определить токи , напряжения, мощности и и изучить их зависимости от частоты.
Рис. 2.16
1) Согласно второго закона Кирхгофа:
ЭДС источника отсутствует, Е = 0, контур К обходим по часовой стрелке
Так как цепь последовательная, то ток один и тот же, поэтому:
.
Рассчитаем ток в цепи: .
Если
,
то то есть сопротивление цепи становиться
чисто омическим, при этом ток в цепи
максимальный
,
а падения напряжений на емкости и
индуктивности будут по величине
одинаковыми: , но фазы напряжений
,
,
сдвинуты на 180 градусов, то есть направления
векторов
,
,
противоположны. Или говорят, что
напряжения на индуктивности и на емкости
находятся в противофазе.
Или говорят, что
напряжения на индуктивности и на емкости
находятся в противофазе.
Сдвиг фаз между током и входным напряжением:
,
так как при резонансе .
Вывод:
1) При резонансе напряжений величина напряжения на конденсаторе равна величине напряжения на индуктивности.
2) Напряжения на всех элементах схемы максимальны:
.
3) При резонансе напряжений сдвиг фаз между входным напряжением и током в цепи равен нулю.
4) Резонансная частота рассчитывается из условия равенства величин реактивных сопротивлений: или .
5) Суммарное напряжение на реактивных элементах при резонансе равно нулю. Между точками б и г напряжение равно нулю. Вольтметр, включенный между точками б и г покажет 0 (ноль) вольт.
6) Падение напряжения на сопротивлении равно входному напряжению
.
7) Полная мощность в цепи будет чисто активной. , так как .
Активная мощность в цепи будет максимальной: .
8) Реактивные мощности на каждом из реактивных элементов так же максимальны и равны соответственно:
;
.
Суммарная реактивная мощность при резонансе равна нулю, .
Рис. 2.17 – Векторная диаграмма токов и напряжений при резонансе при последовательномсоединении R, L, C элементов
Вероятные вопросы при тестировании по теме 2.7:
1.Резонансная частота в цепи при последовательном соединении R,L,C элементов равна :
(а)
(б)
(в)
(г)
(Ответ (в)
1. При резонансе в цепи при последовательном соединении R,L,C элементов максимальный ток равен:
(а)
(б)
(в)
(г)
(Ответ (б)
3. При
резонансе коэффициент мощности cos
φ
равен:
При
резонансе коэффициент мощности cos
φ
равен:
(а)- 0;
(б)- 0,5;
(в)- 0,865;
(г)- 1.0
(Ответ (г)
4.При резонансе напряжение на конденсаторе UC сдвинуто относительно напряжения на индуктивности UL на угол:
(а)- 0 ˚;
(б)- минус180˚;
(в)- плюс90˚;
(г)- плюс 45˚
(Ответ( б)
4.При резонансе потребляемая мощность :
(а)- чисто активная;
(б)- чисто реактивная ;
(в)- ;
(г )-
(Ответ( а)
3
3.1 Трехфазные цепи. Основные понятия. Элементы трехфазных цепей
Определения
Трехфазной цепью называют электрическую цепь образованной из источника трехфазной ЭДС и трехфазного приемника.
Трехфазный
генератор, принцип действия и устройство.
Трехфазный генератор состоит из трех однофазных генераторов расположенных в одном корпусе. Оси обмоток каждого из генераторов геометрически смещены относительно друг друга на или на 1/3 оборота.
На рис. 3.1 (а) схематично показано устройство трех фазного генератора.
Рис. 3.1 –Трехфазный генератор
а – схематичное изображение устройства генератора, b – схема соединения обмоток генератора по схеме звезда без нейтрального провода, c – схема замещения (идеального) трехфазного генератора
На статоре расположены 3 пары обмоток AX, BY, CZ. Ротор (электромагнит
или постоянный магнит) при равномерном
вращении возбуждает в каждой из обмоток
(фазах) переменную (синусоидальную) ЭДС
(согласно закону электромагнитной
индукции). Так как оси обмоток геометрически
смещены на
,
(1/3 оборота), то время наступления
максимума ЭДС в каждой обмотке будет
сдвинуто на 1/3 периода вращения ротора. Говорят, что фазы ЭДС в каждой из обмоток
сдвинуты на 1200.
Говорят, что фазы ЭДС в каждой из обмоток
сдвинуты на 1200.
Закон изменения и соответствующие графики мгновенных значений фазных ЭДС на клеммах генераторов можно представить в виде уравнений и графиков на рис. 3.2:
Рис. 3.2 – Эпюры мгновенных значений фазных напряжений трех фазного генератора
Большими буквами А, В, С и X, Y, Z обозначают начала и концы обмоток генератора. Концы и начала сопротивлений нагрузки обозначают малыми буквами a, b, с и x, y, z соответственно.
Обмотки генератора могут соединяться по схеме звезда (с выводом и без вывода нейтрального провода) или по схеме треугольник. Внутренне сопротивление генератора мало и в дальнейшем будем считать его равным нулю ().
а б
Рис. 3.3 – Схемы замещения и условные
обозначение схем соединения трех фазных
обмоток генератора по схеме звезда (а)
и по схеме треугольник (б)
3.3 – Схемы замещения и условные
обозначение схем соединения трех фазных
обмоток генератора по схеме звезда (а)
и по схеме треугольник (б)
На электрических схемах они обозначаются следующим образом:
Рис. 3.4 – Условные обозначения схем соединений обмоток генератора: звезда, звезда с нейтральным проводом, треугольник
Комплексные ЭДС генератора представляются в виде:
Напряжение на клеммах генератора , , (при ) равно соответственно ЭДС генератора , , .
Для симметричного генератора выполняется соотношение:
.
Соединение генератора и приемника по схеме звезда – звезда
Соединение генератора и приемника по схеме звезда –звезда приведены на рис. 3.5.
Рис. 3.5 – Соединение приемника и генератора звездой
Определения и обозначения
– фазные напряжения генератора;
При соединении звездой фазные напряжения генератора обозначают: ;
– фазное напряжение нагрузки;
– линейные напряжения генератора;
– линейные напряжения нагрузки;
– фазный ток нагрузки фазы А;
– линейный ток в проводе Аа;
Обычно вместо
,
, пишут
,
()
или
.
Если все фазные напряжения равны, то генератор называется симметричным.
Приемник соединен по схеме звезда аналогичным образом. Точка соединения концов нагрузок фаз приемника обозначают буквой n.
Если нейтрального провода нет, то при неравномерной нагрузке () между точками и появляется напряжение . называют напряжением смещения нейтрали.
Для симметричного приемника:
;
. (3.5д)
Для несимметричного приемника с нейтральным проводом в нейтральном проводе появляется ток:
.
Для симметричного генератора линейные и фазные напряжения связаны соотношением:
.
Соединение генератора и приемника по схеме звезда –треугольник
Соединение генератора звездой и приемника
треугольником представлено на рис. 3.6.
3.6.
Рис. 3.6 – Соединение генератора звездой и приемника треугольником
По первому закона Кирхгофа для приемника:
.
Линейные напряжения генератора равны напряжениям на фазных нагрузках приемника:
; ; . (3.7в)
Вектор линейного напряжения генератора равен разности векторов фазных напряжений генераторов:
; ; .
RC Circuit: определение, уравнения и примеры
Таймеры являются жизненно важным инструментом практически во всех повседневных делах. Будь то на кухне, чтобы отслеживать, как долго индейка находится в духовке, или в физической лаборатории при проведении экспериментов по измерению скорости звука. Электрические устройства, которые позволяют нам отслеживать, сколько времени прошло за период, состоят из крошечных цепей, содержащих массив резисторов и конденсаторов, также называемых резисторно-конденсаторными (RC) цепями.
Рис. 1. Электрическая система за светофором обслуживается RC-цепью.
Особенно важной ролью этих цепей является техническое обслуживание и синхронизация светофоров. Эти устройства, которые указывают водителям, когда им безопасно продолжать движение, имеют жизненно важное значение для безопасности дорожного движения во всем мире. Изменяя количество резисторов и заряд конденсатора в RC-цепях, инженеры могут использовать их для изменения времени, отведенного на красный или зеленый свет. Чтобы узнать больше о RC-цепях и о том, как они работают, продолжайте читать!
Определение RC-цепи
Сначала давайте определим RC-цепь и принцип ее работы. Ссылаясь на рисунок ниже, у нас есть простая схема, соединяющая заряженный конденсатор с емкостью \(C\) с резистором с сопротивлением \(R\).
Рис. 2 – Схема RC-цепи.
Когда заряженный конденсатор подключен к резистору, он разряжает накопленную электрическую энергию через электрический ток в цепи.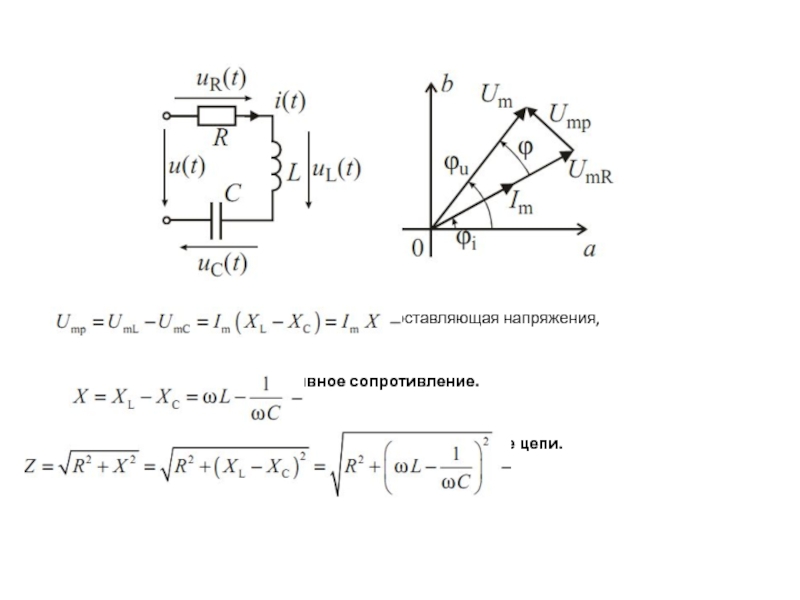 Однако значение тока определяется сопротивлением резистора; добавление большего количества резисторов последовательно и параллельно изменит результирующий ток и напряжение в цепи. Со временем электрическая энергия, хранящаяся в конденсаторе, будет исчерпана, что приведет к нулевому току. Применение RC-цепей с несколькими резисторами включает фильтры нижних частот, которые будут обсуждаться в последующих разделах этой статьи.
Однако значение тока определяется сопротивлением резистора; добавление большего количества резисторов последовательно и параллельно изменит результирующий ток и напряжение в цепи. Со временем электрическая энергия, хранящаяся в конденсаторе, будет исчерпана, что приведет к нулевому току. Применение RC-цепей с несколькими резисторами включает фильтры нижних частот, которые будут обсуждаться в последующих разделах этой статьи.
Уравнения RC-цепей
Теперь, когда мы поняли устройство RC-цепи, давайте посмотрим, как мы можем описать происходящее математически. Во-первых, давайте подумаем о токе, протекающем через оба компонента. Согласно закону тока Кирхгофа, ток, протекающий через конденсатор, должен быть равен и противоположен току, протекающему через резистор. Мы можем записать это как
\[ I_{\text{C}} + I_{\text{R}} = 0 ,\]
, где \(I_{\text{C}}\) — текущий текущий через конденсатор и \(I_{\text{R}}\) — ток, протекающий через резистор, оба из которых измеряются в амперах \(\mathrm{A}\). Теперь мы можем подставить в наши уравнения, связывающие ток, с напряжением на компоненте, которое для конденсатора равно
Теперь мы можем подставить в наши уравнения, связывающие ток, с напряжением на компоненте, которое для конденсатора равно
\[ I_{\text{C}} = C \frac{\mathrm{d} V}{\mathrm{d} t} ,\]
где \(C\) — емкость, измеренная в фарадах \ (\mathrm{F}\), \(V\) — напряжение, измеренное в вольтах, \(\mathrm{V}\), а \(t\) — время, измеренное в секундах, \(\mathrm{s}\ ). Для резистора это определяется законом Ома: \Омега\).
Теперь мы можем подставить эти выражения в уравнение текущего закона, чтобы получить
\[ C \frac{\mathrm{d} V}{\mathrm{d} t} + \frac{V}{R} = 0,\]
, которое является дифференциальным уравнением первого порядка.
Решив это, мы получим выражение напряжения в цепи по отношению ко времени. Во-первых, мы немного изменим уравнение как
\[ \frac{\mathrm{d}V}{\mathrm{d}t} = — \frac{1}{CR} V ,\]
, где мы разделили дифференциалы от постоянных и переменных с обеих сторон. Вы можете решить это дифференциальное уравнение любым удобным для вас способом. В этой статье мы будем использовать метод разделения переменных, в результате чего 9{\ гидроразрыва {-t} {CR}} . \end{align} \]
В этой статье мы будем использовать метод разделения переменных, в результате чего 9{\ гидроразрыва {-t} {CR}} . \end{align} \]
Таким образом, получается уравнение напряжения в RC-цепи.
Постоянная времени в RC-цепи
Важной характеристикой RC-цепи является ее постоянная времени.
Постоянная времени RC-цепи — это время, за которое конденсатор увеличивает или уменьшает напряжение до доли \(\frac{1}{e}\приблизительно 0,632\) (где \(e \) — знаменитое число Эйлера) его начального или конечного значения в зависимости от того, заряжается система или разряжается. 9{\frac{-\tau}{CR}} \\ -1 &= \frac{-\tau}{CR} \\ \tau &= CR , \end{align} \]
где мы обозначили постоянная времени как \(\tau\), измеренная в секундах \(\mathrm{s}\). В результате мы видим, что характеристическая постоянная времени цепи зависит от общего сопротивления и общей емкости в цепи.
Разрядка RC-цепи
RC-цепь может быть двух ориентаций: зарядка и разрядка.
A RC-цепь зарядки — это когда конденсатор и резистор подключены к источнику питания, что позволяет накапливать противоположные заряды на пластинах конденсатора.
С другой стороны, у нас также есть разряжающийся конденсатор.
Разрядная RC-цепь представляет собой заряженный конденсатор, подключенный к резистору, при этом электрическая энергия конденсаторов течет по цепи в виде тока.
Мы уже видели, как получить напряжение в разряжающейся RC-цепи, поэтому мы можем представить это графически на рисунке ниже.
Рис. 3 – Напряжение на конденсаторе в разряжающейся RC цепи.
Таким образом, мы можем видеть экспоненциальный спад величины напряжения, присутствующего в цепи. Через некоторое время, когда в конденсаторе закончится электрическая энергия, напряжение в цепи установится и приблизится к нулю.
Стационарное состояние определяется как состояние, в котором система в среднем не испытывает значительных колебаний.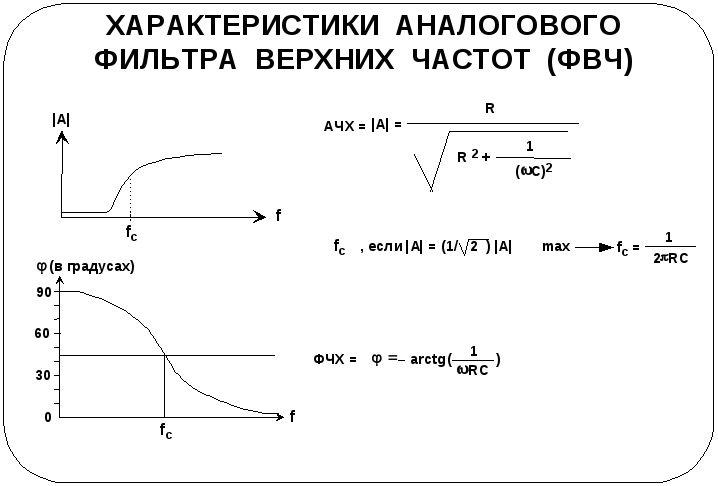
С другой стороны, зарядная RC-цепь будет следовать обратной схеме, что приводит к графику ниже. 9{\frac{-t}{CR}} \right) .\]
Частота среза RC-цепи
Применение RC-цепи — фильтр нижних частот .
Фильтр нижних частот представляет собой схему, которая пропускает более низкие частоты сигнала, отфильтровывая и удаляя более высокие частоты в сигнале.
Чтобы полностью понять, как работает фильтр нижних частот, мы должны понять импеданс и его сходство с сопротивлением.
Импеданс электрического компонента измеряет, насколько компонент сопротивляется переменному току.
Это действительно похоже на определение сопротивления, и импеданс даже имеет те же единицы сопротивления, ом \(\Омега\). Импеданс — это более обобщенное понятие сопротивления, в то время как сопротивление конкретно определяется как \(R = \frac{V}{I}\).
Рис. 5 – Схема фильтра нижних частот с использованием RC-цепи.
На рисунке выше показана схема фильтра нижних частот, в котором используется RC-цепочка. \(V_{\text{in}}\) представляет входной сигнал в схему. Затем он проходит через резистор, а затем в конденсатор и нагрузку, которые расположены параллельно друг другу. Нагрузка в этом случае представляет собой выходной сигнал \(V_{\text{out}}\).
Если бы у нас был входной сигнал с высокой частотой, импеданс на резисторе был бы выше, чем на конденсаторе, что привело бы к более высокой разности потенциалов на резисторе, чем на конденсаторе. Поскольку конденсатор подключен параллельно нагрузке, это также приводит к низкой разности потенциалов на нагрузке, уменьшая количество выходного сигнала от схемы.
С другой стороны, если бы наш сигнал состоял из более низких частот, импеданс конденсатора был бы выше, чем сопротивление резистора. Таким образом, у нас будет более высокая разность потенциалов между конденсатором и нагрузкой, что приведет к большему выходному сигналу.
Частота среза — это точка, в которой сигнал с частотами ниже этого значения удаляется из выходного сигнала.
Мы также можем математически определить частоту среза как
\[ f_{\text{C}} = \frac{1}{2\pi RC} ,\]
где C}}\) — частота среза, измеренная в герцах, \(\mathrm{Hz}\), \(R\) — сопротивление резистора, измеренное в омах, \(\Omega\), и \(C\ ) — емкость конденсатора, измеренная в фарадах \(\mathrm{F}\). 9{\ гидроразрыва {-t} {CR}} \).
Ссылки
- Рис. 1 — Светофор, Wikimedia Commons (https://commons.wikimedia.org/wiki/File:Traffic_Light,_Vienna.
 jpg) Лицензия CC BY-SA 4.0 (https:// creativecommons.org/licenses/by-sa/4.0/)
jpg) Лицензия CC BY-SA 4.0 (https:// creativecommons.org/licenses/by-sa/4.0/) - Рис. 2 — RC-схема, StudySmarter Originals.
- Рис. 3 – График напряжения разряда, StudySmarter Originals.
- Рис. 4 – График зарядного напряжения, StudySmarter Originals.
- Рис. 5 — Фильтр нижних частот, StudySmarter Originals.
Как рассчитать изменение частоты цепи RC/IC?
Изменение частоты цепи RC/IC определяется как частота сигналов, которые могут проходить по цепи. Она также известна как характеристическая частота. Резистивно-емкостная цепь состоит из резистора и конденсатора, соединенных последовательно. Он подавляет частоты ниже f, позволяя свободно протекать сигналам с частотами выше f. Однако сигналы с частотами, близкими к f, тем не менее частично передаются. В зависимости от конструкции RC-фильтр может использоваться для фильтрации низких или высоких частот. Интегральная схема (ИС) — это полупроводник, содержащий сотни миллионов небольших конденсаторов, резисторов и транзисторов.
Формула
Формула изменения частоты дается обратной величиной удвоенного произведения пи, сопротивления и емкости цепи. Обозначается символом f. Его стандартной единицей измерения является герц или секунда (Гц или с -1 ), а его размерная формула определяется как [M 0 L 0 T -1 ].
f = 1/(2πRC)
Где,
- f – изменение частоты,
- π — константа со значением 3,14,
- R — сопротивление,
- Кл — емкость цепи.
Примеры задач
Задача 1. Рассчитать изменение частоты для цепи с сопротивлением 2 Ом и емкостью 3 Ф.
Решение:
Имеем,
R = 2
C = 3
Используя формулу, которую мы имеем,
f = 1/(2πRC)
= 1 / (2 × 3,14 × 2 × 3)
= 0,0265 Гц
Задача 2. Рассчитать изменение частоты для цепи с сопротивлением 4 Ом и емкостью 5 Ф.
Решение:
9000 2 Задача 3: вычислить частоту вариант для цепи с сопротивлением 2,5 Ом и емкостью 6 Ф.Имеем,
R = 4
C = 5
Используя формулу, которую мы имеем,
f = 1/(2πRC)
= 1 / (2 × 3,14 × 4 × 5)
= 0,007958 Гц
Решение:
Имеем,
R = 2,5
C = 6
Используя полученную формулу,
f = 1/( 2πRC)
= 1 / (2 × 3,14 × 2,5 × 6)
= 0,01061 Гц
Задача 4. Рассчитать сопротивление цепи с изменением частоты 0,2 Гц и емкостью 1 Ф.
Решение: 9 0005
У нас есть,
f = 0,2
С = 1
Используя полученную формулу,
f = 1/(2πRC)
=> R = 1/(2πfC)
= 1 / (2 × 3,14 × 0,2 × 1)
= 0,7958 Ом
Задача 5. Рассчитать сопротивление цепи с изменением частоты 0,06 Гц и емкостью 3,5 Ф.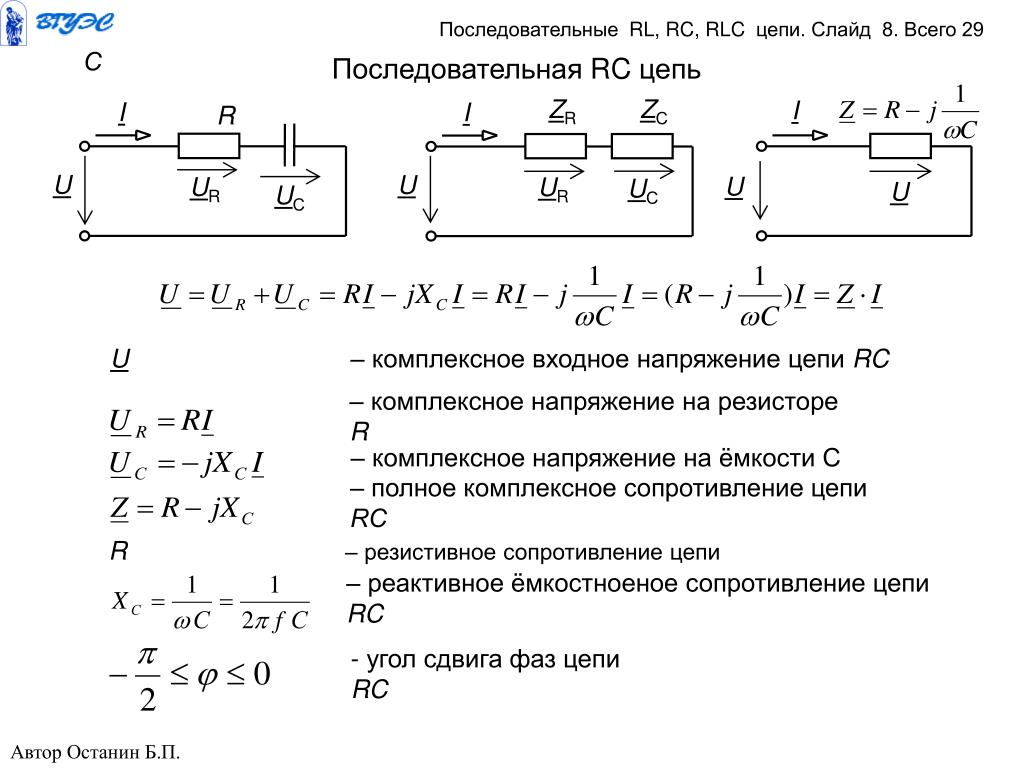


 ⓘ Постоянная времени для RC-цепи [τ]
ⓘ Постоянная времени для RC-цепи [τ]
 jpg) Лицензия CC BY-SA 4.0 (https:// creativecommons.org/licenses/by-sa/4.0/)
jpg) Лицензия CC BY-SA 4.0 (https:// creativecommons.org/licenses/by-sa/4.0/)