Расчет крутящего момента на валу гидронасоса | Мир гидравлики
Инженерно-проектный центр
- О нас
- Наши проекты
- Формы заказа
- Выбор гидроагрегата
- Гидроагрегат, Гидростанция, Маслонапорная установка, Насосная станция или Насосная установка
- Выбор пресса
- Гидравлические прессы
- Выбор вулканизационного пресса
- Вулканизационные пресса
- Выбор гидроцилиндра
- Гидравлические цилиндры
- Выбор гидроагрегата
- Модернизация оборудования
- Проектирование гидравлических систем
- Услуги оказываемые нашей компанией
- Опросные листы
- Сотрудничество
- Техническая информация
- Руководство по эксплуатации БГ12-4 РЭ
- Паспорт. П-КРМ.000 ПС
- Паспорт. Пневмораспределитель 5Р2.00.000 ПС
- ГОСТ 6911-71
- Паспорт на станцию смазочную СДР
- Таблица аналогов гидравлических схем для гидрораспределителей Российского и зарубежного производства
- Калькуляторы
- Расчет гидропривода
- Расчет мощности, расхода и давления гидропривода
- Расчет подачи насоса
- Расчет крутящего момента на валу гидронасоса
- Расчет оборотов гидромотора
- Расчет крутящего момента гидромотора
- Расчет параметров гидравлического цилиндра по размерным характеристикам
- Расчет размеров гидравлического цилиндра по техническим параметрам
- Расчет диаметра трубопровода, скорости потока рабочей жидкости
- Литература
- Станочные гидроприводы.
 В.К. Свешников, А.А. Усов
В.К. Свешников, А.А. Усов - Станочные гидроприводы. В.К. Свешников
- Гидрооборудование. Международный справочник. В.К. Свешников
- Гидравлика. Гидромашины и гидроприводы. Т.М. Башта
- Объёмные гидравлические и пневматические приводы. Никитин
- Металлорежущие станки. Тепинкичиев В.К
- Учебный курс по гидравлике. Том 1. Rexroth Bosch Group
- Гидравлические системы станков и автоматических линий. М.М. Кузнецов
- Гидравлическое оборудование металлорежущих станков
- Рекомендуемые рабочие жидкости для гидросистем
- Гидронасосы и гидромоторы
- ГОСТ 15150-69
- Станочные гидроприводы.
- Контакты
Для проведения расчeта и получения параметров крутящего момента-значение М (ед. измерения, Нм), который при проектировании необходимо передать гидронасосу от выходного вала асинхронного эл. двигателя необходимо использовать следующие данные: 1) Силовой показатель (Мощность) асинхронного эл. 2) Частота (скорость) вращения выходного вала гидравлического насоса n, (при проектировании гидроагрегатов в основном используют асинхронные эл.двигателей переменного тока с 960 и 1450 реже 1370 и 2850 об. мин.) Далее нажмите » Вычислить М «, для получения рассчитываемого параметра. Заполните формыПримечание, для разделения разрядов используйте «.»(точка) | |||||||||
| |||||||||
Вы можете ознакомиться с перечнем жидкостей, рекомендуемых для использования в гидросистемах. |
Расчет момента прокатки
Как видно из уравнения (13.1), на каждый валок действует половина момента прокатки — произведение силы прокатки на её плечо (кратчайшее расстояние от оси вращения валка до линии действия этой силы). Чтобы найти плечо силы прокатки, надо знать её направление.
При простом процессе прокатки направление силы прокатки Р можно определить из уравнения равновесия полосы в очаге деформации (см. рис. 13.1):
, (13.6)
где Хi– проекции всех сил, действующих на полосу.
При простом процессе прокатки на полосу действуют силы только со стороны валков в очаге деформации, другие внешние силы (натяжений, подпора) отсутствуют.
Если предположить, что сила R,
действующая со стороны каждого валка
на полосу (равнодействующая сил прокатки
и трения), отклонена от вертикали на
угол , то уравнение
(13.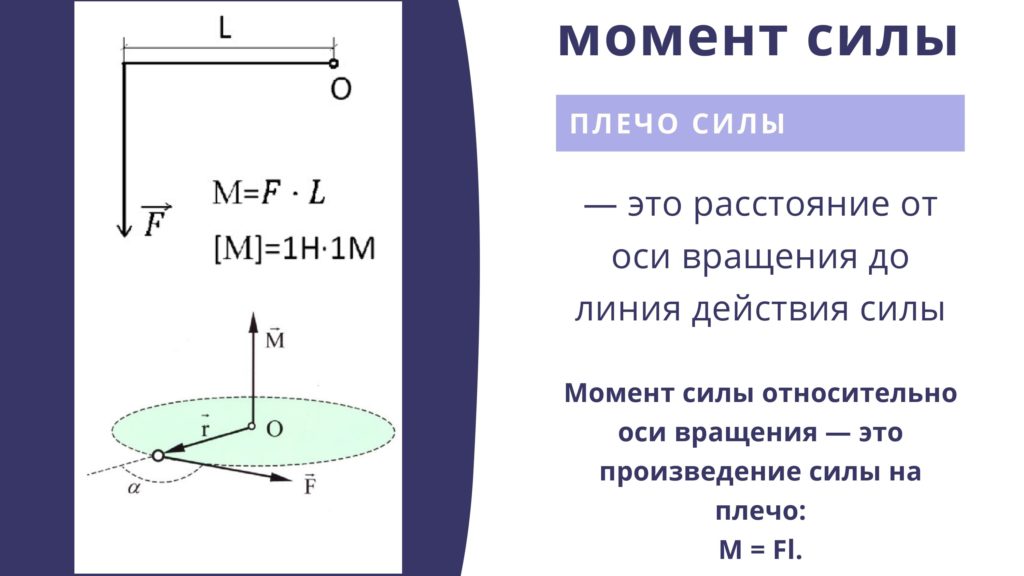
, (13.7)
где Rx– проекция на ось х силы R.
Поскольку сила R заведомо не равна нулю, из выражения (13.7) следует, что sin =0, что возможно только в случае, когда угол =0.
Отсюда следует, что при простом процессе прокатки равнодействующая всех сил, действующих в контакте полосы и валка, направлена вертикально. Но эта равнодействующая и является силой прокатки Р (см. главу 11). Таким образом, можно сделать окончательный вывод: если на полосу не действуют другие силы, кроме сил со стороны валков в очаге деформации, то сила, действующая между каждым валком и полосой, направлена перпендикулярно оси прокатки и равна силе прокатки.
Необходимо сделать одну оговорку: этот
вывод можно распространить на следующий
частный случай отступления от простого
процесса прокатки: если к полосе приложены
силы переднего и заднего натяжения,
равные по величине, то в уравнении
равновесия полосы (13.
Поэтому, силы прокатки останутся вертикальными (перпендикулярными оси х), если на полосу действуют вдоль оси х силы переднего и заднего натяжения, равные по величине.
Установив направление сил Р, можно определить момент прокатки по формуле (см. рис.13.1):
, (13.8)
где а – плечо силы прокатки относительно оси вращения валка (кратчайшее расстояние от этой оси до линии действия силы).
В формуле (13.8) учитываются силы Р, которые действуют со стороны полосы на каждый валок. Они, согласно 3-ему закону Ньютона, равны по величине силам, действующим со стороны каждого валка на полосу, но противоположно направлены.
Чтобы использовать формулу (13. 8) в
практических расчетах, надо знать
величину а, определяющую координату
точки
8) в
практических расчетах, надо знать
величину а, определяющую координату
точки
В большинстве известных методик, разработанных в 20 веке, для расчета величины а рекомендуется следующая эмпирическая формула [13.1…13.5]:
, (13.9)
где l – длина очага деформации (см. рис. 13.1), — эмпирический коэффициент, называемый коэффициентом плеча силы прокатки.
В указанных литературных источниках приводятся многочисленные эмпирические выражения или числовые значения этого коэффициента, согласно которым, он может изменяться в широком диапазоне:
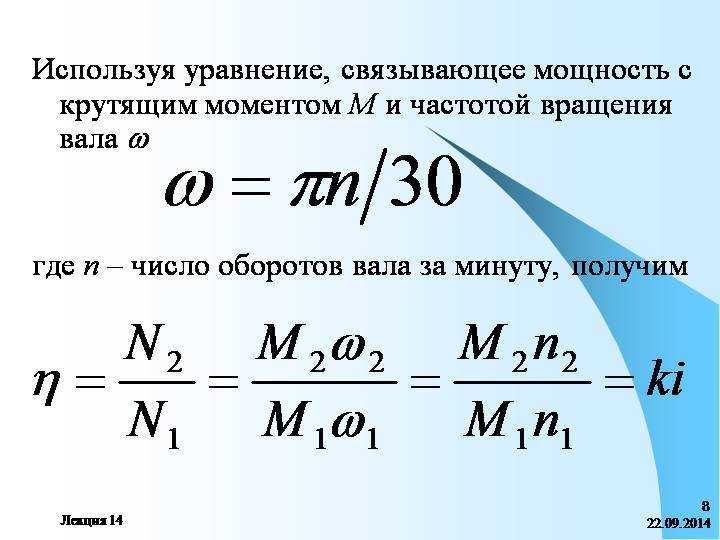 9) вносит существенную погрешность в
расчет момента и мощности главного
привода рабочей клети, достигающую
30-40% и более от фактических значений.
9) вносит существенную погрешность в
расчет момента и мощности главного
привода рабочей клети, достигающую
30-40% и более от фактических значений.В современных условиях, когда задачи повышения энергоэффективности и экономии энергии в металлургическом производстве приобрели большую актуальность, требуется более точный метод расчета плеча силы прокатки, не использующий эмпирический коэффициент
Такой метод разработан и опубликован в работах [13.6…13.8].
Сущность его в том, что сначала определяют мощность прокатки в i—й клети Nпрiпо методике, изложенной в разделе 12 данного учебника, а затем, используют связь между моментом и мощностью прокатки:
, (13.10)
Мпрi– момент прокатки вi—й
клети, — угловая скорость прокатных (рабочих)
валков i—й клети, npi – число оборотов этих валков
в минуту.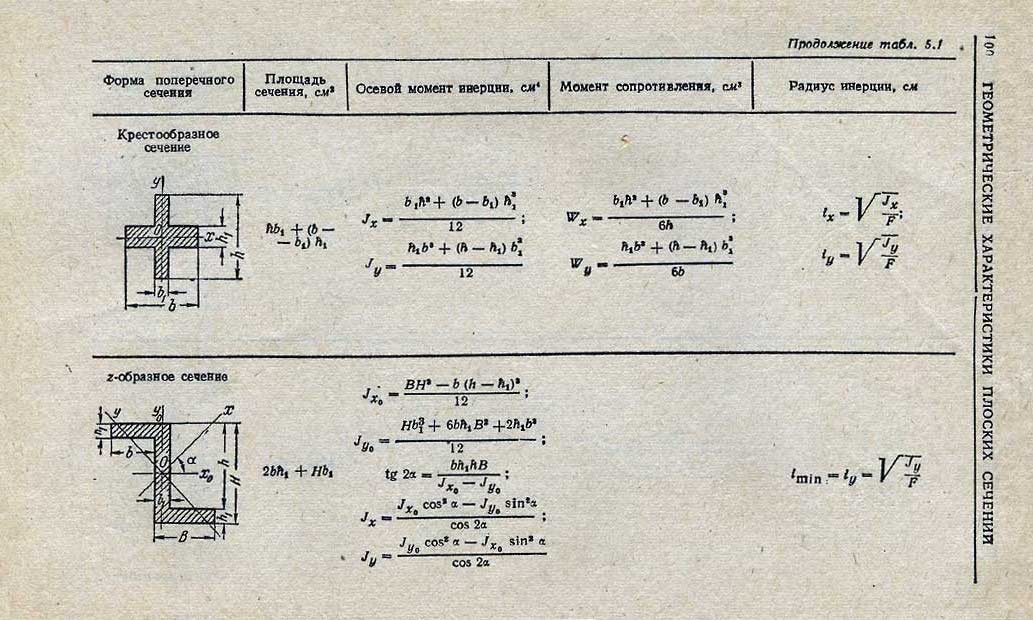
Подставив в (13.10) выражение Мпрiпо формуле (13.8), получают искомую величину плеча силы прокатки:
, (13.11)
Формула (13.11) не содержит эмпирических коэффициентов, а входящие в нее величины Nпрi и Pi, вычисляемые по методикам, изложенным в разделах 11 и 12, имеют наименьшие погрешности, по сравнению с другими известными методиками.
При их расчете не используются никакие эмпирические величины, кроме общепринятых: коэффициента трения в очаге деформации и сопротивления деформации прокатываемого металла.
Вычислив величину а по формуле
(13.11), легко найти угол ,
определяющий точку приложения силы
прокатки на дуге захвата (см.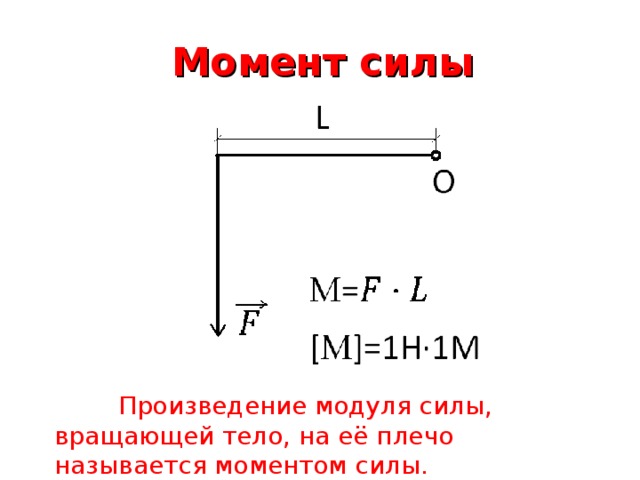 рис. 13.1):
рис. 13.1):
, (13.12)
где D – диаметр бочки прокатного валка.
Что такое момент и как его рассчитать?
Когда я обучаю своих студентов-физиков, я хочу, чтобы они понимали основы концепции, а не только то, как подставлять числа в уравнение. Когда я изучал физику, мне хотелось, чтобы мои учителя больше использовали реальные жизненные приложения, вещи, которые мы уже знаем о мире, чтобы помочь нам действительно получить его .
Я надеюсь, что этот пример понравится всем моим заядлым лыжникам.
Когда я был молод и учился кататься на лыжах, я боялся кресельных подъемников (немного до сих пор). Висеть высоко на открытом воздухе было страшно. Когда кресельный подъемник был полным, когда я сидел на нем со всей семьей — все казалось сбалансированным, меня там благополучно придавливало. Но если бы я был на кресельном подъемнике один, если бы я сел на один край, кресельный подъемник сильно бы наклонился в эту сторону.
Или, если бы я (маленький ребенок) сидел с папой (намного тяжелее ребенка), кресельный подъемник опрокинулся бы в его сторону.
За годы катания на кресельном подъемнике я понял, как мне удерживать кресельный подъемник в равновесии. Если бы я был один, я бы сидел посередине. Если бы я был со своим папой, он мог бы сидеть чуть не по центру с одной стороны, а я мог бы сесть полностью к одному краю с другой стороны. Это позволит кресельному подъемнику оставаться в горизонтальном положении.
Кто-нибудь из вас замечал такое, когда сидел на кресельном подъемнике с кем-то, кто намного легче или тяжелее вас?
Вот несколько правил, касающихся сидения на кресельном подъемнике. Подумайте, имеют ли они смысл для вас.
- Один человек, сидящий посередине, сделает кресельный подъемник горизонтальным.
- Более тяжелый человек будет опрокидывать кресельный подъемник сильнее, чем легкий, если он сидит на одинаковом расстоянии от центра.

- Есть способ достичь равновесия двумя людьми разного веса, сидящими на рассчитанном расстоянии от центра.
Это фундаментальное понятие физики называется моментом .
МОМЕНТ силы является мерой ее стремления заставить тело вращаться вокруг определенной точки или оси.
Когда я сижу на кресельном подъемнике, я создаю момент, который заставляет кресельный подъемник вращаться вокруг оси.
Как рассчитать момент?Момент равен приложенной силе, умноженной на расстояние от оси вращения:
Момент = Сила x Расстояние
Давайте рассмотрим пример: A взвешивание 2 фута от центра кресельного подъемника. На каком расстоянии от центра на противоположной стороне кресельного подъемника должен сидеть ее отец (который весит 180 фунтов), чтобы кресельный подъемник был горизонтальным («уравновешенным»)?
Сначала вычислите момент, создаваемый ребенком:
ПРИМЕЧАНИЕ.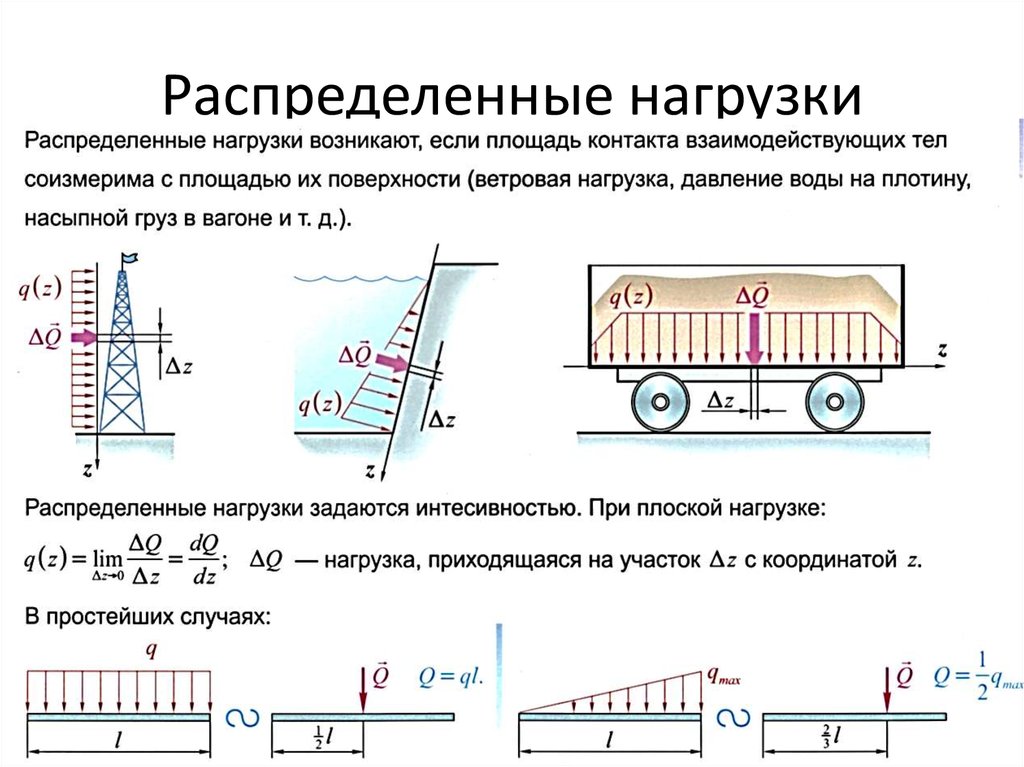 Мы можем смоделировать кресельный подъемник как невесомую балку = 120 ft-lbs
Мы можем смоделировать кресельный подъемник как невесомую балку = 120 ft-lbs
Если ребенок сидит слева от точки поворота, в какую сторону наклоняется кресельный подъемник?
Она поворачивает кресельный подъемник против часовой стрелки .
Правило: моменты против часовой стрелки считаются отрицательными значениями.Чтобы кресельный подъемник находился в равновесии, момент, действующий на ось со стороны Отца, должен быть равен и противоположен ребенку.
Ребенок создал момент -120 ft-lbs, поэтому ее отцу необходимо создать момент +120 ft-lbs.
120 ft-lbs = (180 фунтов)(x футов)
x = ⅔ футов = 8 дюймов.
С какой стороны от точки опоры должен сидеть Отец, чтобы уравновесить ребенка
С правой стороны!
Когда Отец сидит с правой стороны, он заставляет кресельный подъемник наклониться по часовой стрелке .
Правило: моменты по часовой стрелке считаются положительными величинами.
Когда Отец сидит в 8 дюймах слева от оси вращения, он создает момент +120 ft-lbs вокруг оси. Равный и противоположный момент ребенку. Следовательно, кресельный подъемник находится в равновесии.
Какие еще приложения в реальной жизни, связанные с моментами, вы можете придумать?- Если гайку трудно открутить коротким ключом, поможет более длинный ключ. Это связано с тем, что на гайку будет действовать больший момент, когда та же сила будет приложена дальше от оси.
- Попробуйте толкнуть дверь очень близко к петле. Чем ближе к точке шарнира, тем сильнее придется давить. Если дверь очень тяжелая, толкните дверь в сторону, которая находится дальше всего от петли. Это еще одно реальное применение момента.
Физика может показаться абстрактной и запутанной, когда вы рисуете балки и диаграммы свободного тела. Но физика есть везде. Когда вы изучаете новую концепцию в физике, попросите своих наставников привести примеры из реальной жизни и объяснить, как теория применяется на практике!
Метод расчета моментных нагрузок на линейные приводы
Загрузить PDF
Электрический линейный привод представляет собой комбинированный продукт, состоящий из линейного механизма и электродвигателя, который в предварительно собранном виде имеет более простую конструкцию, более короткое время установки, и высокое качество.
При работе привода моментные нагрузки возникают не только от силы тяжести, но и от ускорения и торможения груза. Поскольку моментные нагрузки могут повредить приводы, крайне важно убедиться, что они соответствуют техническим требованиям. Однако расчет моментных нагрузок на линейные приводы может быть сложным и трудоемким.
В этом документе описывается простой метод расчета моментных нагрузок и упрощается выбор привода.
1. Введение
Комбинируя двигатель с линейными механическими компонентами, электрические линейные приводы приносят пользу инженерам-проектировщикам, сокращая время на проектирование, установку и настройку оборудования (см. рис. 1).
При работе электрических линейных приводов моментные нагрузки возникают из-за силы тяжести, приложенной к нагрузке, и ускорения груза. Поскольку крутящие моменты сильно влияют на срок службы приводов, важно убедиться, что они находятся в пределах технических характеристик привода. Однако расчет моментных нагрузок электрических линейных приводов может быть сложным и трудоемким, поскольку для линейных приводов обычно учитываются направления установки и движения.
Однако расчет моментных нагрузок электрических линейных приводов может быть сложным и трудоемким, поскольку для линейных приводов обычно учитываются направления установки и движения.
2. Выбор линейных приводов (концепция опережения по моменту)
На рис. 2 показан процесс выбора линейного привода. Во-первых, проверьте размер и транспортируемую массу линейного привода. Затем проверьте время позиционирования, чтобы определить рабочие условия, соответствующие требуемому времени позиционирования. Наконец, проверьте, находится ли момент, приложенный к приводу, в пределах допустимого диапазона.
3. Структура электрических линейных приводов
На примере серии EAS конструкция электрического линейного привода показана на рис. 3. Кроме того, на рис. 4 показана его конструкция в поперечном сечении.
Нагрузка, приложенная к столу, и мгновенные нагрузки поддерживаются линейной направляющей, состоящей из направляющего рельса и направляющего блока.
Эти нагрузки влияют на срок службы линейной направляющей, поэтому их важно учитывать при выборе.
4. Момент, приложенный к приводу
Момент, приложенный к электрическому линейному приводу, объясняется в следующем разделе.
4.1. Момент, приложенный к электрическому линейному приводу
Как показано на рис. 5, когда центр тяжести переносимого груза свисает над центром стола электрического линейного привода, момент прикладывается от центра стола как опоры. точка. Момент, приложенный к электрическому линейному приводу, можно получить по следующей формуле.
С этого момента гравитационное ускорение в этой статье считается равным 9,807 м/с² .
4.2. Moment Direction
Существует три разных направления моментов, действующих на электрический линейный привод: направление тангажа, направление рыскания и направление качения (см. рис. 6). Точки опоры момента находятся на нижней грани (установочной поверхности) линейного привода и в центре стола.
4.3. Направление момента определяется направлением установки
Направление моментов, действующих на электрические линейные приводы, может изменяться в зависимости от условий установки нагрузки и направления установки самого привода. На рис. 7 показано, как изменяется направление момента при изменении направления установки привода при тех же условиях установки нагрузки.
4.4. Допустимый статический момент и допустимый динамический момент
4.4.1. Статический допустимый момент
Момент, приложенный к остановленному линейному приводу, называется статическим моментом. Допустимое значение статического момента линейного привода называется допустимым статическим моментом и определяется коэффициентами механической прочности линейной направляющей и стола. Когда при остановленном линейном приводе прикладывается внешняя сила, необходимо убедиться, что статический момент находится в пределах допустимого диапазона в каждом направлении.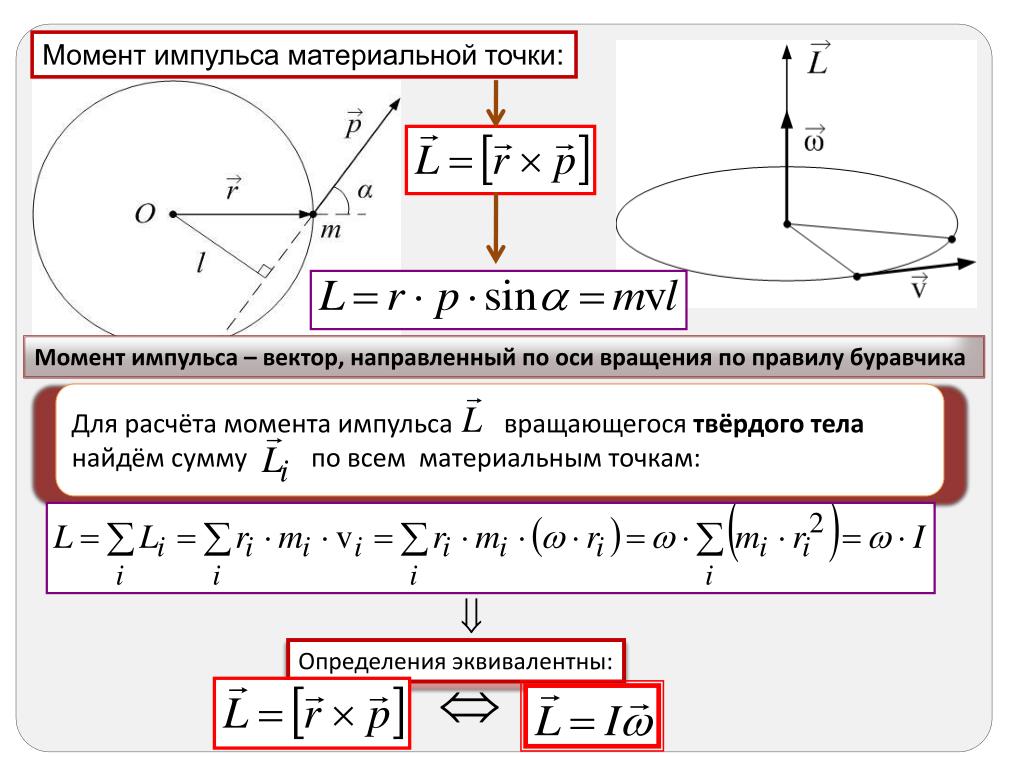
4.4.2. Динамический допустимый момент
Момент, прилагаемый к линейному приводу при транспортировке груза, называется динамическим моментом. Поскольку во время работы применяется ускорение, момент применяется в зависимости от расстояния вылета от стола.
Методы расчета момента в каждом направлении при транспортировке груза линейным приводом, как показано на рис. 8, показаны в следующих формулах.
Каждое обозначение на рисунке 8 означает следующее:
Масса руки и положение центра тяжести на этом рисунке не указаны.
Формула 2 вычисляет момент направления тангажа; формула 3 вычисляет момент направления рыскания; а формула 4 вычисляет момент направления качения.
Рассчитайте коэффициент, разделив значения моментов, рассчитанных по этим формулам (2), (3) и (4), на допустимые динамические моменты в каждом направлении, которые являются спецификациями продукта. Затем добавьте все рассчитанные соотношения моментов в каждом направлении. Если общая сумма меньше 1, как показано в формуле момента (5), то ее можно использовать.
Если общая сумма меньше 1, как показано в формуле момента (5), то ее можно использовать.
5. Пример расчета моментных нагрузок для одновального линейного привода
В этом разделе приведены примеры расчета моментных нагрузок в зависимости от направления установки. В качестве примера используется линейный привод с одним валом. Ниже показан пример расчета моментных нагрузок при выборе электрического линейного привода EASM4XD020ARAC с шириной направляющей 45 мм (1,771 дюйма) и высотой стола 60 мм (2,362 дюйма):
5.1. При установке в горизонтальном направлении
На рис. 9 показан электрический линейный привод, установленный горизонтально с грузом, подвешенным в направлении оси Y. Динамический допустимый момент электрического линейного привода показан ниже:
Центр тяжести нагрузки от привода и вылет центра тяжести рычага показаны ниже:
Масса нагрузки, масса рычага, и ускорение показаны ниже:
Исходя из результатов, момент находится в пределах допустимого динамического момента и, таким образом, его можно использовать.
5.2. При установке в вертикальном направлении
На рис. 10 показан пример расчета динамического момента при установке линейного привода в вертикальном направлении. Установочные размеры, нагрузки и условия эксплуатации точно такие же, как в 5.1.
Момент MR направления качения не применяется, поэтому он равен 0 [Н·м]. Из формулы допустимого момента (5):
Исходя из результатов, момент находится в пределах динамического допустимого момента и, следовательно, его можно использовать.
6. 2 Метод расчета моментных нагрузок при объединении двух осей
Далее, в качестве примера объединения двух осей, поясняется расчет моментных нагрузок комбинации X-Y электрических линейных приводов.
При использовании комбинации X-Y сначала рассчитывается единственная ось Y, которая передает нагрузку, чтобы определить, можно ли использовать ось Y. Затем для расчета моментных нагрузок по оси X к расчету добавляются моментная нагрузка от общей массы оси Y и моментная нагрузка, возникающая при ускорении оси Y для передачи нагрузки.
На рис. 11 показан пример комбинации X-Y электрических линейных приводов. EASM6XD030ARAK фиксируется на салазках оси X, а EASM4YD020ARAK комбинируется на оси Y. Ось Y фиксируется на фиксирующей пластине оси Y, а затем фиксируется на столе оси X.
1) Расчет моментной нагрузки для оси Y
Сначала рассчитывается моментная нагрузка, приложенная к оси Y (см. рис. 12). Динамические допустимые моменты привода оси Y EASM4YD020ARAK указаны ниже.
Расстояние вылета центра тяжести груза от оси Y, масса груза и ускорение оси Y указаны следующим образом.
Поскольку момент MY не применяется к направлению рыскания, он равен 0 [Н·м].
Из формулы допустимого момента (5):
Момент ползуна оси Y находится в допустимом диапазоне, поэтому его можно использовать.
2) Расчет моментных нагрузок для оси X
Затем вычисляется момент нагрузки, приложенный к салазкам оси X. Ниже указаны допустимые динамические моменты салазок оси X EASM6XD030ARAK .
Ниже указаны допустимые динамические моменты салазок оси X EASM6XD030ARAK .
Нагрузка от оси X, центр тяжести нагрузки по оси Y и расстояние вылета центра тяжести нагрузки неподвижной пластины скольжения оси Y указаны следующим образом.
Масса неподвижной пластины оси Y, масса ползуна оси Y и рабочее ускорение оси X указаны следующим образом.
На рис. 13 показана стрелка A на рис. 11, а на рис. 14 показана стрелка B на рис. 11. , и рассчитать при условии, что Y1 находится на пике.
Момент, приложенный к оси X, ниже заданного значения, поэтому его можно использовать. На основании полученных данных обе оси X и Y соответствуют соответствующим допустимым динамическим моментам, и, следовательно, определено, что они пригодны для использования. Те же этапы вычислений выполняются для комбинации X–Y–Z с добавлением оси Z; начните вычислять момент с крайней оси, то есть оси Z, затем перейдите к оси Y и оси X.
7. Отклонение при приложении момента к столу
Отклонение при приложении момента к столу
Когда момент приложен к салазкам, стол наклоняется в направлении момента. Этот наклон приводит к смещению в выступающее положение. В таблице 1 показана величина отклонения при приложении допустимых динамических моментов в каждом направлении к подвижному столу серии EAS, как показано на рис. 15. и значения только для справки.
8. Расчет моментных нагрузок для электрических цилиндров
При использовании электрического цилиндра необходимо снаружи установить направляющую для поддержки штока, чтобы он мог воспринимать моментные нагрузки. Также доступна серия электроцилиндра с направляющей (направляющей вала), которую можно использовать при приложении нагрузки к штоку (см. рис. 16). В этом разделе поясняются примеры расчета моментных нагрузок для электроцилиндра с направляющей.
8.1. При приложении момента к электрическому цилиндру с направляющей
Для электрического цилиндра с направляющей существуют направления, в которых действуют моменты, как и в линейном электрическом приводе. На рис. 17 показаны направления моментов, действующих на цилиндр с направляющей.
На рис. 17 показаны направления моментов, действующих на цилиндр с направляющей.
8.2. Расчет моментных нагрузок электроцилиндра с направляющей
8.2.1. Передача нагрузок в вертикальном направлении
Ниже показан пример расчета моментных нагрузок, действующих на шариковую втулку, когда цилиндр с направляющей передает нагрузки в вертикальном направлении. На рисунке 18 показано следующее.
Как показано на рисунке 18, при указании момента направления тангажа в виде Mp, приложенного к вертикально установленной линейной втулке, его можно рассчитать по следующей формуле (6).
Это необходимо для подтверждения того, что расчетное значение момента направления тангажа находится в пределах допустимого динамического момента.
8.2.2. Передача нагрузки в горизонтальном направлении
Далее, с цилиндром с направляющей вала, как показано на рис. 18, исходное положение устанавливается, когда шток вставлен до упора.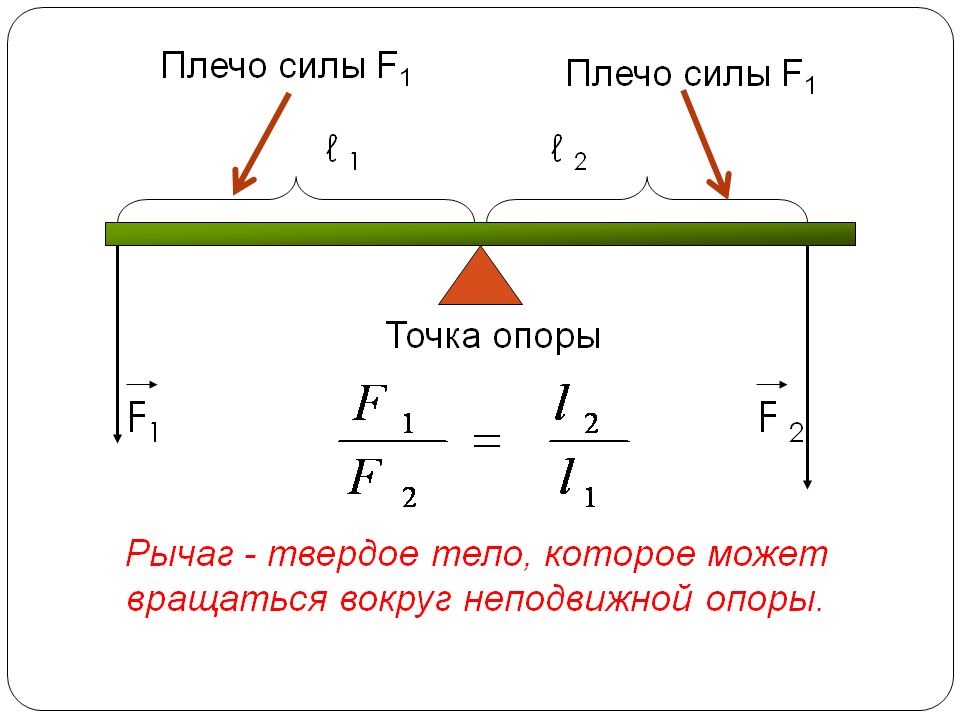


 В.К. Свешников, А.А. Усов
В.К. Свешников, А.А. Усов двигателя N (единица измерения, кВт).
двигателя N (единица измерения, кВт). (Здесь)
(Здесь)