Пример расчёта сердечника трансформатора | HomeElectronics

Всем доброго времени суток! В прошлой статье я рассказал о выборе сердечника трансформатора и определении его основных размеров. Сегодня я приведу примеры расчётов сердечников нескольких типов трансформаторов.

Следует отметить, что все расчёты основаны на оптимально-компромиссной геометрии сердечника, а у промышленных образцов геометрия другая. Поэтому под рассчитанные параметры сердечника (a, b, c, h) необходимо подобрать унифицированный магнитопровод, применяя следующее правило: произведение линейных размеров рассчитанного сердечника и такое же произведение размеров унифицированного сердечника не должны значительно различаться, причем отличие каждого из размеров не должно превышать ± 15 %. В противном случае будут закладываться изначально плохие удельно-экономические показатели.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

При этих условиях электромагнитные режимы и необходимая мощность трансформатора обеспечивается, даже если фактические и расчётные размеры существенно отличаются.

При расчёте магнитной индукции для трансформаторов ТЕР необходимо придерживаться следующего правила, что расчётная индукция В_P не должна быть меньше, чем 0,8B_S для данного вида материала сердечника. В случае меньшего значения можно вернуться к выбору материала магнитопровода, либо изменить значения режимов работы трансформатора, наиболее эффективно: перегрев τ_М, площадь охлаждения сердечника П_С.

Расчёт сердечника трансформатора ТВР

Необходимо найти основные размеры сердечника наименьшей стоимости со входным напряжением U₁ = 220 B при частоте f = 50 Гц, допустимым перегревом τ_M = 50 ºС, выходные обмотки со следующими параметрами: одна вторичная обмотка нагружена на мостовой выпрямитель, U₂₁ = 50 B, I₂₁ = 0,7 А, вторая обмотка – на двухполупериодный выпрямитель со средней точкой, U₂₂ = 5 B, I₂₂ = 2,5 А. Обмотки выполнить из меди, остальные условия типовые.

1. Определяем габаритную мощность трансформатора.

— мощности

— коэффициент коррекции типа выпрямителя k_B1 = 1, k_B2 = 0,71;

— требуемая габаритная мощность

-коэффициент увеличения электромагнитной мощности с_P

Зависимость коэффициента увеличения габаритной мощности с_P от габаритной мощности Р_Г.

Определим с_P = 1,075.

2. Выбираем тип сердечника – броневой шихтованный сердечник из пластин толщиной – 0,35 мм, коэффициент заполнения сердечника k_C = 0,93, коэффициент заполнения окна для начала выберем типовой k_OK = 0,3. Данный трансформатор отнесём к трансформаторам с вынужденным режимом работы ТВР, поэтому рабочую индукцию ограничим предельной B = B_S. При условии наименьшей стоимости выберем горячекатаную сталь 1512 (Э42), электромагнитные параметры которой представлены ниже

Кривая намагничивания стали 1512.

Удельные потери в стали 1512.

Для данной стали определяем B_S = 1,15 Тл, удельные потери в магнитном материале р^/ = 1,55 Вт/кг. В готовом сердечнике удельные потери будут выше из-за влияния технологии изготовления, вида сердечника, частоты которые корректируются коэффициентом k_P = 1,5, тогда удельные потери р₁ готового сердечника составят

Параметры оптимальной геометрии для трансформатора наименьшей стоимости с заданным перегревом (τ = const) будут равны

3. Определяем дополнительные параметры:

— соотношение плотностей тока в обмотках ε, для БТ х_k = x

— относительный ток первичной обмотки i₁ = 1,1;

— функции геометрии φ_i

— соотношение поверхностей охлаждения β

— оптимальное соотношение потерь в данном типе трансформатора ν₀

— определим соотношение потерь в трансформаторе ν, для ТВР ν < ν₀

Так как ν = 0,314 < ν₀, то трансформатор правильно отнесён к ТВР.

4. Определяем электромагнитные нагрузки трансформатора.

Определим дополнительные параметры:

— расчётный параметр Б

— определим плотность тока вторичных обмоток j₂

5.Определим основные размеры трансформатора:

— базовый размер а

— расчётные размеры трансформатора

6. Выбираем унифицированный сердечник:

— произведение сечений окна и стержня рассчитываемого трансформатора

— выбор унифицированного сердечника. В данном случае можно взять сердечник типа Ш20х40 со следующими размерами

Данный сердечник больше расчётного, что немного утяжелит трансформатор, однако за счёт неполного заполнения окна сердечника будет улучшено его охлаждение и снижен перегрев.

Расчёт сердечника трансформатора ТЕР

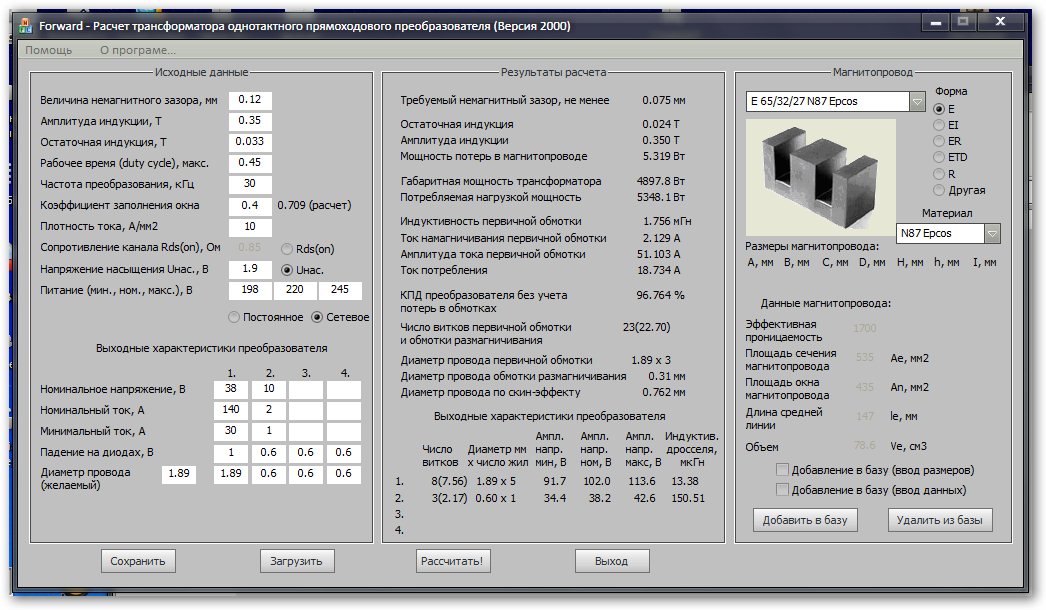
Необходимо рассчитать трансформатор наименьшей массы со входным напряжением U₁ = 310 В, частотой f = 60 кГц, форма напряжения прямоугольная со скважностью Q = 0,7. Трансформатор рассчитывается на максимальный перегрев τ_M = 30 ºС и имеет две выходные обмотки: первая с напряжением U₂₁ = 12 В, выходным током I₂₁ = 2 А, нагружена на двухполупериодный выпрямитель со средней точкой, вторая обмотка с напряжением U₂₂ = 5 В, с действующим током обмотки I₂₂ = 0,5 А, нагруженная на мостовой выпрямитель. Остальные условия типовые.

1. Определяем габаритную мощность трансформатора

— выходная мощность трансформатора

— коэффициент коррекции типа выпрямителя

— требуемая габаритная мощность

2. Выбираем тип сердечника. Для данного трансформатора выбираем Ш-образный сердечник из феррита N27, коэффициент заполнения сердечника k_C = 1, коэффициент заполнения окна для начала выберем типовой k_OK = 0,15. Трансформатор отнесём к ТЕР типу. Электромагнитные параметры данного феррита приведены ниже

Динамическая кривая намагничивания для N27.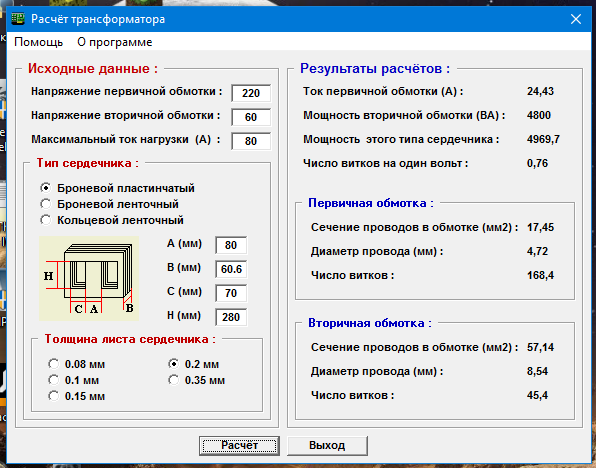

Относительные потери в сердечнике в зависимости от частоты для N27.

Предельная рабочая индукция для N27 B_S = 0,5 Тл, потери в сердечнике при данной индукции

-коэффициент увеличения электромагнитной мощности с_P

Зависимость коэффициента увеличения габаритной мощности с_P от габаритной мощности Р_Г

Определим для ТЕР с_P^* = 1,035, тогда

Для трансформатора наименьшей массы с ограничением по перегреву параметры оптимальной геометрии составят

3. Определяем дополнительные параметры

— соотношение плотностей тока в обмотках ε, для БТ х_k = x

— относительный ток первичной обмотки i₁ = 1,1;

— функции геометрии φ_i

— соотношение поверхностей охлаждения β

— оптимальное соотношение потерь в данном типе трансформатора ν₀

— определим соотношение потерь в трансформаторе ν, для ТЕР ν = ν₀ = 2,19.

4. Определяем электромагнитные нагрузки трансформатора.

Определим дополнительные параметры:

— расчётный параметр Б

— плотность тока вторичных обмоток j₂

— магнитная индукция в сердечнике

Магнитная индукция в данном сердечнике меньше индукции насыщения B = 0,28 < B_S, поэтому трансформатор правильно отнесён к ТЕР типу. В противном случае его надо было бы пересчитать как ТВР с ограничением индукции. Так при перегреве уже в 50 ºС магнитная индукция составила бы В = 0,44 Тл, что находится на пределе для данного типа сердечника.

5.Определим основные размеры трансформатора:

— коэффициент формы напряжения

— базовый размер а

— расчётные размеры трансформатора

6. Выбираем унифицированный сердечник:

— произведение сечений окна и стержня рассчитываемого трансформатора

— выбор унифицированного сердечника. В данном случае можно взять сердечник типа EE19 со следующими размерами

Данный сердечник больше расчётного, что немного утяжелит трансформатор, однако за счёт неполного заполнения окна сердечника будет улучшено его охлаждение и снижен перегрев.

В следующей статье я рассмотрю, как выполнить электрический расчёт трансформатора.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Расчет импульсного трансформатора для двухтактного преобразователя и согласующих устройств / Хабр

В правильно сконструированном двухтактном преобразователе постоянный ток через обмотку и подмагничивание сердечника отсутствуют. Это позволяет использовать полный цикл перемагничивания и получить максимальную мощность. Поскольку трансформатор имеет много взаимозависимых параметров, расчет ведут по шагам, уточняя при необходимости исходные данные.

1. Как определить число витков и мощность?

Габаритная мощность, полученная из условия не перегрева обмотки, равна [1]:

Pгаб = So ⋅ Sc ⋅ f ⋅ Bm / 150           (1)

Где: Pгаб — мощность, Вт;
Sc — площадь поперечного сечения магнитопровода, см² ;
So — площадь окна сердечника, см²;
f — частота колебаний, Гц;
Bm = 0,25 Тл — допустимое значение индукции для отечественных никель-марганцевых ферритов на частотах до 100 кГц.  

Максимальную мощность трансформатора выбираем 80% от габаритной:

Pmax = 0,8 ⋅ Pгаб           (2)

Минимальное число витков первичной обмотки n1 определяется максимальным напряжением на обмотке Um и допустимой индукцией сердечника Bm:

n1 = ( 0,25 ⋅ 10⁴ ⋅ Um ) / ( f ⋅ Bm ⋅ Sc )           (3)

Размерности единиц здесь те же, что и в формуле (1).

Плотность тока в обмотке j для трансформаторов мощностью до 300 Вт принимаем 3..5 А/мм² (большей мощности соответствует меньшее значение). Диаметр провода в мм рассчитываем по формуле:

d = 1,13 ⋅ ( I / j )^1/2           (4)

Где I — эффективный ток обмотки в А.

Пример 1:

Для ультразвуковой установки нужен повышающий трансформатор мощностью 30..40 Вт. Напряжение на первичной обмотке синусоидальное, с эффективным значением Uэфф = 100 В и частотой 30 кГц.

Выберем ферритовое кольцо К28x16x9.

Площадь его сечения: Sc = ( D — d ) ⋅ h / 2 = ( 2,8 — 1,6 ) ⋅ 0,9 / 2 = 0,54 см²
Площадь окна: So = π ⋅ ( d / 2 )² = π⋅ ( 1,6 / 2 )² = 2 см²
Габаритная мощность: Pгаб = 0,54 ⋅ 2 ⋅ 30 ⋅ 10³ ⋅ 0,25 / 150 = 54 Вт
Максимальная мощность: Pmax = 0,8 ⋅ 54 = 43,2 Вт
Максимальное напряжение на обмотке: Um = 1,41 ⋅ 100 = 141 В
Число витков: n1 = 0,25 ⋅10⁴ ⋅ 141 / ( 30 ⋅ 10³ ⋅ 0,25 ⋅ 0,54 ) = 87
Число витков на вольт: n0 = 87 / 100 = 0,87
Эффективное значение тока первичной обмотки: I = P / U = 40 / 100 = 0,4 A
Плотность тока выберем 5 А/мм².
Тогда диаметр провода по меди: d = 1,13 ⋅ ( 0,4 / 5 )^1/2 = 0,31 мм

2. Как уточнить плотность тока?

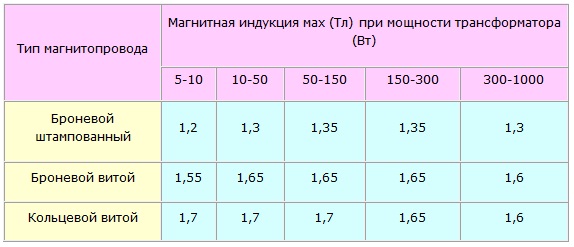
Если мы делаем маломощный трансформатор, то можем поиграть с плотностью тока и выбрать более тонкие провода, не опасаясь их перегрева. В книге Эраносяна [2, Стр.109] дана такая табличка:

Pн, Вт	1 .. 7	8 .. 15	16 .. 40	41 .. 100	101 .. 200
j, А/мм2	7 .. 12	6 .. 8	5 .. 6	4 .. 5	4 .. 4,5

Почему плотность тока зависит от мощности трансформатора?

Выделяемое количество теплоты равно произведению удельных потерь на объем провода. Рассеиваемое количество теплоты пропорционально площади обмотки и перепаду температур между ней и средой. С увеличением размера трансформатора объем растет быстрее площади и для одинакового перегрева удельные потери и плотность тока надо уменьшать. Для трансформаторов мощностью 4..5 кВА плотность тока не превышает 1..2 А/мм² [3].

3. Как уточнить число витков первичной обмотки?

Зная число витков первичной обмотки n вычислим ее индуктивность. Для тороида она определяется по формуле:

L = μ0 ⋅ μ ⋅ Sс ⋅ n² / la        (5)

Где:
Площадь Sс  дана в м²; 
средняя длина магнитной линии la в м;
индуктивность в Гн;
μ0 = 4π ⋅ 10^-7 Гн/м — магнитная постоянная.

В инженерном виде эта формула выглядит так:

L = A_L n²        (5А)    ,     n = ( L / A_L )^1/2        (5Б)

Коэффициент A_L и параметр мощности Sо ⋅ Sc для некоторых типов колец приведены в Таблице 2 [4,5,6]:

Кольцо	К7х4х2	К10х6х3	К10х6х4,5	К16х10х4,5	К20х12х6	К32х20х6	К38х24х7	К40х25х11
AL , нГн/вит2 ± 25%	224	310	460	430	620	570	650	1050
Sо ⋅ Sc , см4	0,004	0,017	0,025	0,106	0,271	1,131	2,217	4,050

Для работы трансформатора в качестве согласующего устройства должно выполняться условие:

L > ( 4 . . 10 ) ⋅ R / ( 2 ⋅ π ⋅ fmin )         (6)

Где L — индуктивность в Гн;
R = U²эфф / Pн приведенное к первичной обмотке сопротивление нагрузки Ом;
fmin — минимальная частота, Гц.

В ключевых преобразователях в первичной обмотке трансформатора текут два тока: прямоугольный ток нагрузки Iпр = Um / R и треугольный ток намагничивания обмотки I_T:

Для нормальной работы преобразователя величина треугольной составляющей не должна превышать 10% от прямоугольной, т.е индуктивность обмотки должна удовлетворять неравенству:

L > 5 R / f         (7)

При необходимости число витков увеличивают или применяют феррит с большей μ. Чрезмерно завышать число витков в обмотке не желательно. Из-за роста межвитковой емкости на рабочей частоте могут возникнуть резонансные колебания.

Выбранный феррит должен иметь достаточную максимальную индукцию и малые потери в рабочей полосе частот. Как правило, на низких частотах (до 1 МГц) применяют феррит с μ = 1000 .. 6000 , а на радиочастотах приходиться использовать материалы с μ = 50 .. 400.

Пример 2:

Трансформатор из Примера 1 намотан на кольце К28х16х9 из никель-марганцевого феррита 2000НМ с магнитной проницаемостью μ = 2000.
Мощность нагрузки P = 40 Вт , эффективное напряжение первичной обмотки Uэфф = 100 В , частота f = 30 кГц. Уточним число его витков.

Приведенное сопротивление нагрузки:  R = 100² / 40 = 250 Ом
Площадь поперечного сечения магнитопровода:  Sc = 0,54 см² = 0,54 ⋅ 10 ^-4 м²
Средняя длина магнитной линии: la = π ( D +d ) / 2 = π ( 2,8 + 1,6 ) ⋅ 10 ^-2 / 2 = 6,9 ⋅ 10 ^-2 м
Коэффициент индуктивности: A_L = 4π ⋅ 10^-7 ⋅ 2000 ⋅ 0,54 ⋅ 10 ^-4 / 6,9⋅10^-2 = 1966 нГн / вит²

Минимальная индуктивность первичной обмотки по формуле (6): 
L = 10 ⋅ 250 / ( 2π ⋅ 3 ⋅ 10⁴ ) = 13,3 мГн
Число витков: n = (13,3 ⋅ 10 ^-3 / 1,963 ⋅ 10 ^-6 ) ^1/2 = 82      

Оно даже меньше, чем рассчитанное ранее в Примере 1  nmin = 87.
Таким образом, условие достаточной индуктивности выполнено и число витков первичной обмотки n = 87.

4. Какие ферриты можно применить и почему?

Как известно, сердечник в трансформаторе выполняет функции концентратора электромагнитной энергии. Чем выше допустимая индукция B и магнитная проницаемость μ , тем больше плотность передаваемой энергии и компактнее трансформатор. Наибольшей магнитной проницаемостью обладают т.н. ферромагнетики — различные соединения железа, никеля и некоторых других металлов.

Магнитное поле описывают две величины: напряженность Н (пропорциональна току обмотки) и магнитная индукция В (характеризует силовое действие поля в материале). Связь В и H называют кривой намагничивания вещества. У ферромагнетиков она имеет интересную особенность — гистерезис (греч. отстающий) — когда мгновенный отклик на воздействие зависит от его предыстории.

После выхода из нулевой точки (этот участок называют основной кривой намагничивания) поля начинают бегать по некой замкнутой кривой (называемой петлей гистерезиса). На кривой отмечают характерные точки — индукцию насыщения Bs, остаточную индукцию Br и коэрцитивную силу Нс.

Рис.1. Магнитные свойства ферритов. Слева форма петли гистерезиса и ее параметры. Справа основная кривая намагничивания феррита 1500НМ3 при различных температурах и частотах: 1 — 20кГц, 2 — 50кГц, 3 — 100 кГц.

По значениям этих величин ферромагнетики условно делят на жесткие и мягкие. Первые имеют широкую, почти прямоугольную петлю гистерезиса и хороши для постоянных магнитов. А материалы с узкой петлей используют в трансформаторах. Дело в том, что в сердечнике трансформатора есть два вида потерь — электрические, и магнитные. Электрические (на возбуждение вихревых токов Фуко) пропорциональны проводимости материала и частоте, а вот магнитные тем меньше, чем меньше площадь петли гистерезиса.

Ферриты это пресс порошки окисей железа или других ферромагнетиков спеченные с керамическим связующим. Такая смесь сочетает два противоположных свойства — высокую магнитную проницаемость железа и плохую проводимость окислов. Это минимизирует как электрические, так и магнитные потери и позволяет делать трансформаторы, работающие на высоких частотах. Частотные свойства ферритов характеризует критическая частота fc , при которой тангенс потерь достигает 0,1. Тепловые — температура Кюри Тс , при которой μ скачком уменьшается до 1.

Отечественные ферриты маркируются цифрами, указывающими начальную магнитную проницаемость, и буквами, обозначающими диапазон частот и вид материала.

Наиболее распространен низкочастотный никель-цинковый феррит, обозначаемый буквами НН. Имеет низкую проводимость и сравнительно высокую частоту fc. Но у него большие магнитные потери и невысокая температура Кюри.

Никель-марганцевый феррит имеет обозначение НМ. Проводимость его больше, поэтому fc низкая. Зато малы магнитные потери, температура Кюри выше, он меньше боится механических ударов.

Иногда в маркировке ферритов ставят дополнительную цифру 1, 2 или 3. Обычно, чем она выше, тем более температурно стабилен феррит.

Какие марки ферритов нам наиболее интересны?

Для преобразовательной техники хорош термостабильный феррит 1500НМ3 с fc=1,5 МГц, Bs=0,35..0,4 Тл и Tc=200 ℃.

Для спец применений выпускают феррит 2000НМ3 с нормируемой дезакаммодацией (временной стабильностью магнитной проницаемости). У него fc=0,5 МГц, Bs=0,35..0,4 Тл и Tc=200 ℃.

Для мощных и компактных трансформаторов разработаны ферриты серии НМС. Например 2500НМС1 с Bs=0,45 Тл и 2500НМС2 c Bs=0,47 Тл. Их критическая частота fc=0,4 МГц, а температура Кюри Tc>200 ℃.

Что касается допустимой индукции Bm, этот параметр подгоночный и в литературе не нормируется. Ориентировочно можно считать Bm = 0,75 Вsmin. Для никель-марганцевых ферритов это дает примерно 0,25 Тл. С учетом падения Bs при повышенных температурах и за счет старения в ответственных случаях лучше подстраховаться и снизить Bm до 0,2 Тл.

Основные параметры распространенных ферритов сведены в Таблицу 3:

Марка	100НН	400НН	600НН	1000 НН	2000 НН	2000 НМ	1000 НМ3	1500 НМ1	1500 НМ3
μнач	80. .120	350.. 500	500.. 800	800.. 1200	1800.. 2400	1700.. 2500	800.. 1200	1200.. 1800	1200.. 1800
fc, МГц	7	3,5	1,5	0,4	0,1	0,5	1,8	0,7	1,5
Tc, ℃	120	110	110	110	70	200	200	200	200
Bs, Тл	0,44	0,25	0,31	0,27	0,25	0,38.. 0,4	0,33	0,35.. 0,4	0,35.. 0,4

5. Насколько нагреется сердечник?

Потери в магнетике.

При частоте менее критической fс потери энергии в магнетике складываются в основном из потерь на перемагничивание, а вихретоковыми можно пренебречь.

Опыт и теория показывают, что потери энергии в единице объема (или массы) на одном цикле перемагничивания прямо пропорциональны площади петли гистерезиса. Следовательно мощность магнитных потерь:

P_H = P₀ ⋅ V ⋅ f      (8)

Где:
P₀ – удельные потери в единице объема (измеренные на частоте f₀ при индукции B₀ ) ;
V – объем образца.

Таблица 4. Удельные объемные потери в ферритах 2500НМС при f₀ =16 кГц ; B₀=0,2 Тл:

T , oC	P0 , мкВт / ( см 3 ⋅ Гц )
	2500НМС1	2500НМС2
25	10,5	8,5
100	8,7	6

Однако, с ростом частоты индукция насыщения уменьшается, петля гистерезиса деформируется, а потери растут. Для учета этих факторов Штейнмец (C. P. Steinmetz, 1890-1892) предложил эмпирическую формулу:

PH = P1 ⋅ m ⋅ ( f / f1 ) ^α ( B / B1) ^β      (9)

Условились [7, Стр.54], что f1 = 1 кГц, B1 = 1 Тл.
Величины P1, α, β и массу сердечника m указывают в справочнике.

Таблица 5. Удельные потери в некоторых ферритах

Марка	1500НМ3	2000НМ1-А,Б		2000НМ3	2000НМ-17		3000 НМ-А	6000НМ-1
f	—	0,4..100 кГц	0,1..1 МГц	—	0,4..100 кГц	0,1..1 МГц	0,4..200 кГц	20..50 кГц	50..100 кГц
P1, Вт / кг	23,2	32±7	13±3	44,6	63±10	25±4	48±8	11±2	38±0,8
α	1,2	1,2	1,4	1,3	1,2	1,4	1,2	1,35	1,6
β	2,2	2,4		2,7	2,85		2,76	2,69	2,6

Потери в меди.

Омические потери в первичной обмотке при комнатной температуре и без учета скин-эффекта:

P_M1 = I² эфф ( ρ / Sm ) ( ( D — d ) + 2h ) ⋅ n1      (10)

Где:
Iэфф — эффективный ток,
D — внешний, d — внутренний диаметр кольца, h — его высота в метрах;
n1 — число витков; Sm — поперечное сечение провода, в мм² ;
ρ = 0,018 Ом ⋅ мм² / м — удельное сопротивление меди.

Суммарные потери во всех обмотках при повышенной температуре окружающей среды:

P_M = ( P_M1 + P_M2 + .. )⋅ ( 1 + 0,004⋅ ( T — 25^oC ) )      (11)

Общие потери в трансформаторе.

Потери в магнетике и меди:

P_Σ = P_H + P_M      (12)

Предполагаемая температура перегрева при естественной конвекции:

ΔT = P_Σ / ( α_m Sохл )      (13)

Где α_m = (10. .15) ^-4 Вт/(см^2oС)     ,     Sохл = π /2 ( D2 — d2 ) + π h ( D + d )

Пример 3:

Найдем потери в трансформаторе из Примеров 1 и 2. Для простоты считаем, что вторичная и первичная обмотка одинаковые. 

Эффективный ток первичной обмотки Iэфф = 0,4 А.

Потери в меди первичной обмотки:
P_M1 = 0,42 ⋅ ( 0,018 / 0,08 ) ⋅ ( 28 — 16 + 18 ) ⋅ 10 ^-3 ⋅ 87 ≈ 0,1 Вт.

Потери в меди обеих обмоток: P_M = 0,2 Вт.

Согласно справочным данным для феррита 2000НМ P1 = 32 Вт / кг ; α = 1,2 ; β = 2,4 ; масса сердечника К28х16х9 равна 20 грамм.

Потери в феррите: P_H = 32 ⋅ ( 30 / 1 ) ⋅ 1,2 ⋅ ( 0,25 / 1 ) ⋅ 2,4 ⋅ 20 ⋅ 10 ^-3= 1,36 Вт

Суммарные потери в трансформаторе:   P_Σ = 1,56 Вт.     

Ориентировочный КПД = ( 40 — 1,56 ) / 40 ⋅ 100% ≈ 96%

6. Как учесть инерционные свойства трансформатора?

На Рис.2. показана T-схема замещения трансформатора.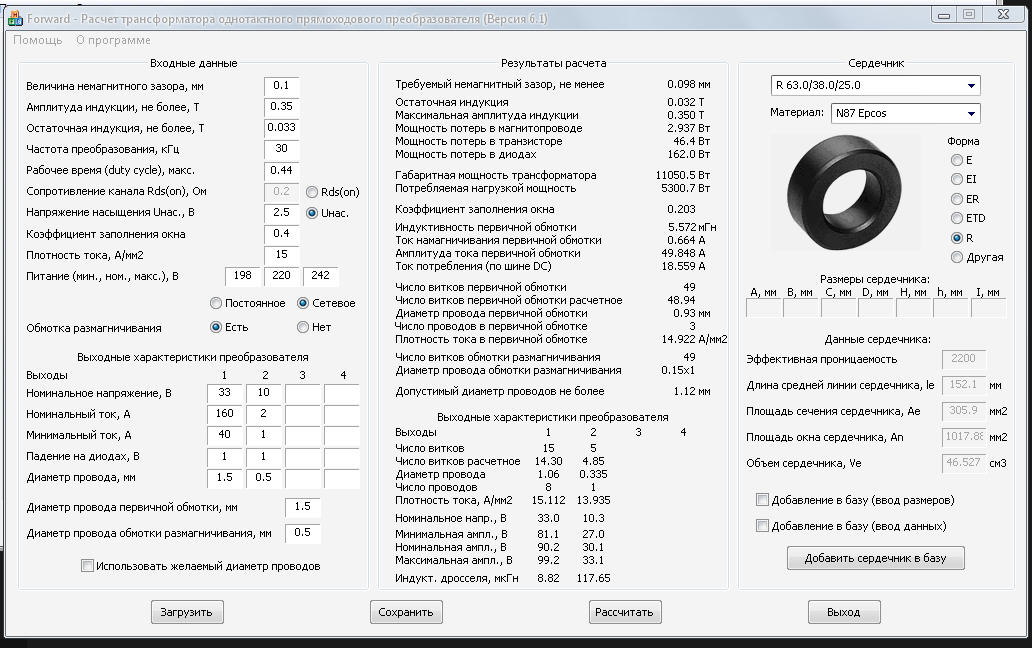 В нее входят сопротивление источника r_i , приведенное сопротивление нагрузки R = n² Rн   или R = Pн / U²эфф   ,     где n = U1 / U2 — коэффициент трансформации, Uэфф — эффективное напряжение первичной обмотки.

Рис.2. Эквивалентная схема трансформатора.

Инерционные свойства трансформатора определяют малые индуктивности рассеяния Ls, индуктивность намагничивания Lμ (почти равна индуктивности первичной обмотки L1), параллельная емкость обмотки Сp (т.н. динамическая емкость) и последовательная емкость между обмотками Сп.

Как оценить индуктивности и емкости?

L1 рассчитывают по формуле (5) или измеряют экспериментально.
Согласно [8] индуктивность рассеивания по порядку величины равна Ls ~ L1 / μ.
Емкость Ср составляет примерно 1 пФ на виток.

Трансформатор работает подобно полосовому фильтру. На малых частотах он представляет собой ФВЧ с частотой среза ωн = R / Lμ.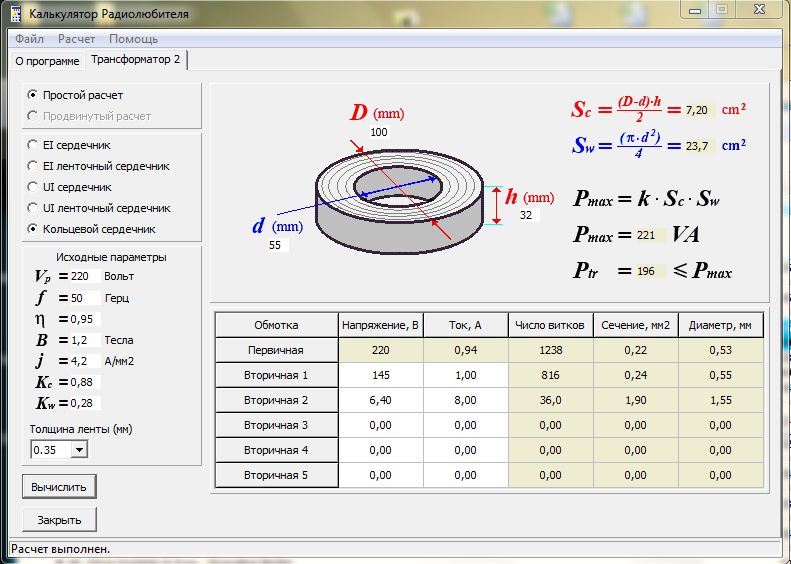
На высоких частотах элементы Ls и Cp образуют ФНЧ с частотой среза ωв ≈ ( Ls Cp )^-1/2
Последовательная емкость Сп невелика и на работу практически не влияет.

В модели есть два характерных резонанса:

Низкочастотный (резонанс намагничивания) в параллельном контуре Lμ Ср.
Его частота   fμ ≈ ( 1/ 2 π ) ⋅ (Lμ Cp )^-1/2  , а добротность
Qμ ≈ ( r_i || R ) ⋅ ( Lμ / Cp)^-1/2      (14)

Высокочастотный (резонанс рассеивания) в контуре, образованном Ls и Cр.
Его частота fs ≈ ( 1/ 2 π ) ⋅ (Ls Cp )^-1/2   , а добротность   Qs ≈ ( Ls / Cp)^1/2 / r_i         (15)

Как влияют резонансы обмотки?

Амплитудно-частотная характеристика трансформатора похожа на АЧХ полосового фильтра, но на ее верхнем краю резонанс fs дает характерный пик.

Реакция же на импульсы напряжения зависит от способа включения источника и величин сопротивлений схемы.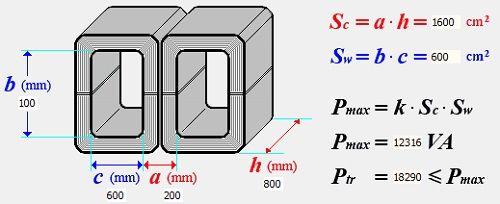

При малом внутреннем сопротивлении источника r_iпроявляется лишь резонанс fs в виде характерного «звона» на фронтах импульсов.
Если же источник подключается через ключ, то при его размыкании могут возникать интенсивные колебания с частотой  fμ.

Рис.3. Пример АЧХ и переходного процесса в трансформаторе. Его эквивалентная схема дана ниже на рисунке 4.

7. Экспериментальное измерение параметров импульсного трансформатора.

Для пробы было взято кольцо из феррита 3000НМ размера К10х6х2. Первичная обмотка составляла 21 виток; вторичная 14; коэффициент трансформации n = 1,5 ; сопротивление нагрузки равнялось 4,7 кОм; источником служил генератор прямоугольных импульсов на TTL микросхемах с уровнем 6В, частотой 1 МГц и внутренним сопротивлением r_i ≈ 200 Ом.

Рассчитаем теоретические параметры:

Sc = 4 ⋅ 10 ^-6 м² , la = 25,13 ⋅ 10 ^-3 м , A_Lтеор = 600 нГн / вит² , L1_теор = 0,6 ⋅ 212 = 265 мкГн, Ls _теор ≈ 265/3000 = 0,09 мкГн , Сp _теор ≈ 21+14 = 35 пФ.
Приведенное сопротивление нагрузки R = n² Rн = 2,25 ⋅ 4,7 ~ 10 кОм.

Результаты измерений индуктивностей прибором АКИП-6107:

L1 = 269 мкГн ,   L2 = 118 мкГн , закоротив вторичную обмотку получим 2Ls = 6,8 мкГн, что на два порядка выше ее теор оценки.

Динамическую емкость Cp можно оценить по формуле (15), подав на трансформатор прямоугольные импульсы и измерив при помощи осциллографа период колебаний «звона» на фронтах импульсов на выходе вторичной обмотки. Частота «звона» fs оказалась 18,5 МГц , что дает Ср ≈ 21 пФ и неплохо согласуется с теор оценкой.

Для сравнения с опытом эквивалентная схема с измеренными параметрами моделировалась в программе LT Spice.

Рис.4. Модель трансформатора. Vout — приведенное напряжение, фактическое будет в n раз меньше.Рис.5. Результаты эксперимента. Масштаб вертикальной шкалы 1 вольт на деление.

Итак, модель, построенная на основе измеренных Lμ , Ls и Cp вполне согласуется с экспериментом.

Теоретическая оценка [8] емкости 1 пФ на виток для малых колец приемлема, но оценка индуктивности рассеяния на два порядка расходится с фактической. Ее проще определять на опыте.

Приложение 1. Вывод формулы для числа витков.

При подаче напряжения U на обмотку в ней возникнет ЭДС индукции E:
U = -E = n Sc dB / dt

Для синусоидального напряжения с амплитудой Um:
Um = n Sc ω Bm
Откуда число витков: n = Um / ( Sc ω Bm )

Выразив круговую частоту через обычную, а площадь в см² получим инженерную формулу:

n = 0,16 ⋅ 10⁴ / ( f ⋅ Bm⋅ Sc )

Для прямоугольного напряжения величиной Um приращение индукции: 
dB = dt Um / ( n Sc )
Интегрируя ее по времени от 0 до T/2 и учитывая, что за половину периода поле изменится от -Bm до +Bm получим:     2Bm = ( T / 2) Um / ( n Sc )

Выразив период через частоту, а площадь в см² получим инженерную формулу:

n = 0,25 ⋅10⁴ / ( f ⋅ Bm ⋅ Sc )

Она пригодна для обоих случаев.

Приложение 2. Вывод формулы для габаритной мощности трансформатора.

Согласно закону электромагнитной индукции Фарадея связь напряжения на катушке с изменением магнитной индукции в ней:  

U dt = n Sc dB

За время от 0 до T/2 индукция изменится от -Bm до +Bm.  Интегрируя в этих пределах получим среднее напряжение:

Uср = 4n  ⋅  Sc ⋅  Bm ⋅  f

Где:

Но приборы измеряют не среднее, а действующее напряжение, которое эквивалентно постоянному по энергии. Связь среднего и действующего напряжения дает коэффициент формы кф = Uэфф / Uср . Для меандра он равен 1, для синуса 1,11.

Отсюда эффективное напряжение на катушке:
Uэфф = 4 ⋅  кф ⋅  n ⋅  Sc ⋅  Bm ⋅  f

Габаритную мощность оценим из следующих соображений. Частота f не велика, потери на вихревые токи и перемагничивания малы и мощность ограничена лишь перегревом обмотки. Его определяет максимальная плотность тока j , одинаковая для обоих обмоток.

Определим габаритную мощность как полусумму мощностей первичной и вторичной обмоток.

Pгаб = ( P1+P2 ) / 2 = ( U_эфф1⋅ I1 + U_эфф2 ⋅ I2 ) / 2 = j ( S1 n1 + S2 n2 ) 4 кф Sc Bm f / 2       

Где S1 и S2 площади витка первичной и вторичной обмоток.

Это соотношение можно записать через площадь меди Sm: 

Pгаб = 2⋅  кф ⋅ f ⋅ Sc ⋅ Sm ⋅ Bm ⋅ j

Площадь меди связывают с коэффициентом заполнения окна σ = Sm / Sо.

Сигма это некий эмпирический коэффициент, равен минимум 0,15 для однослойной обмотки и максимум 0,4 для многослойной (больше не поместится).

В итоге наша формула имеет вид:

Pгаб = 2 ⋅ кф ⋅ σ⋅  f ⋅ Sc⋅  Sо ⋅ Bm ⋅ j 

Все величины здесь в СИ.

Допустим, что напряжение имеет форму меандра, кф = 1. Выбирая плотность тока j = 2,2 А / мм² ; коэффициент заполнения σ = 0,15 ; выразив площади в см² ; Bm в Тл ; частоту в Гц получим расчетную формулу:

Pгаб = Sc ⋅ So ⋅ f ⋅ Bm / 150

Как видно, эта формула выведена с большим запасом, реально можно получить с трансформатора и большую мощность.

Литература.

1. Косенко С. “Расчёт импульсного трансформатора двухтактного преобразователя” // Радио, №4, 2005, с. 35 — 37, 44.

2. Эраносян С. А. Сетевые блоки питания с высокочастотными преобразователями. — Л.: Энергоатомиздат. Ленингр. отд-ние, 1991,— 176 с: ил.

3. С. В. Котенёв, А. Н. Евсеев. Расчет и оптимизация тороидальных трансформаторов и дросселей. — М.: Горячая линия-Телеком, 2013. — 359 с.: ил.

4. А. Петров «Индуктивности, дроссели, трансформаторы «// Радиолюбитель, №12, 1995, с.10-11.

5. Михайлова М.М., Филиппов В.В., Муслаков В.П. Магнитомягкие ферриты для радиоэлектронной аппаратуры. Справочник. — М.: Радио и связь, 1983. — 200 с., ил.

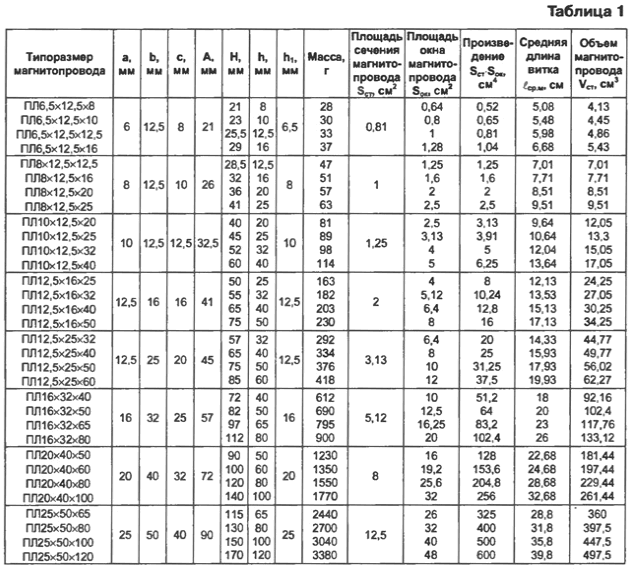
6. Расчетные геометрические параметры кольцевых сердечников.

7. Б.Ю.Семенов. Силовая электроника для любителей и профессионалов. М. : Солон-Р, 2001. — 327 с. : ил

8. Курс лекций «Импульсная техника» для студентов 4-го курса кафедры Радиофизики. Глава 3.

Как выбрать трансформатор

Рисунок 1: Трансформатор

Трансформатор — это пассивное электрическое устройство, использующее электромагнитную индукцию для передачи электроэнергии из одной цепи в другую. Выбор подходящего трансформатора для приложения требует тщательного рассмотрения нескольких факторов, таких как напряжение, ток, тип нагрузки, эффективность, окружающая среда и стоимость. В этой статье дается пошаговое руководство по выбору трансформатора и анализу различных мощностей в трансформаторе. Прочтите нашу обзорную статью о трансформаторах для получения дополнительной информации о том, как они работают, их конструкции и типах.

Содержание

• Выбор трансформатора
• Калькулятор номинальной нагрузки трансформатора
• Нагрузочная способность трансформатора
• Расчет КПД трансформатора
• Калькулятор мощности трансформатора
• Потери трансформатора
• Как уменьшить потери трансформатора
• Часто задаваемые вопросы

Выбор трансформатора

Доступны трансформаторы различных конструкций, спецификаций и размеров. Важно учитывать следующее:

• Повышающий или понижающий трансформатор: Выберите повышающий или понижающий трансформатор в зависимости от конкретных требований применения. Например, при работе на выпрямителе для снижения питающего напряжения с 230 до 12 вольт выберите понижающий трансформатор на 230-12 вольт.

Примечание: Напряжение и частота основного источника питания различаются в зависимости от страны. Такие страны, как США, используют основной источник питания 120 вольт, работающий на частоте 60 Гц, тогда как страны Европы, такие как Великобритания, Нидерланды и Германия, работают на 230 вольт и 50 Гц. Соответственно выбирайте трансформатор. Для получения более подробной информации см. полный список стран с соответствующими напряжениями питания и рабочими частотами.

Рис. 2: Понижение (слева) и повышение (справа)

• Характеристики напряжения и тока: Следующий шаг при выборе трансформатора включает определение требований к току и напряжению нагрузки.
  • Если в здании имеется сеть переменного тока 240 В, а для электрооборудования требуется 120 В, выберите трансформатор на 240–120 В.

Примечание: Как правило, первичное и вторичное напряжения указаны в технических характеристиках трансформатора. Но в исключительных случаях, таких как трансформатор тока, вместо этого указываются первичный и вторичный токи.

• ВА: Определите мощность, требуемую нагрузкой (ВА), при выборе трансформатора, так как трансформаторы обычно определяются первичным и вторичным напряжением и значениями ВА. Заранее определить эти значения необходимо для выбора подходящего трансформатора для конкретного применения.

Калькулятор номинальной нагрузки трансформатора

Номинальная нагрузка (полная мощность) трансформатора измеряется в ВА (вольт-ампер). Номинальная мощность представляет собой общую мощность, которую трансформатор может передать в нагрузку. Для расчета номинальной нагрузки необходимо:

1. Определите требования к току и напряжению нагрузки.
2. Умножьте ток нагрузки в амперах (I) и значения напряжения (V), чтобы получить ВА (или номинальную нагрузку) трансформатора.

1. Для однофазного трансформатора,

2. Для трехфазного трансформатора,

Примечание: Небольшие трансформаторы оценивают свою отдаваемую мощность в вольт-амперах, но гораздо более крупные силовые трансформаторы оцениваются в киловольт-амперах (кВА) и мегавольт-амперах (МВА). Таким образом, ВА, кВА и МВА являются аналогичными единицами. Например, 6 ВА равно 0,006 кВА.

Прочтите наши статьи об однофазных и трехфазных трансформаторах, чтобы получить дополнительную информацию об их работе и конструкции.

Нагрузочная способность трансформатора

Нагрузочная способность трансформатора — это максимальное количество электроэнергии, с которым трансформатор может безопасно и эффективно работать без перегрева или повреждения.

Например, трансформатор мощностью 200 ВА может выдерживать 200 вольт при силе тока в один ампер или 100 вольт при силе тока в два ампера.

Зная значение ВА трансформатора, можно определить ток через нагрузку, изменив уравнение для ВА.

1. Узнайте мощность трансформатора в ВА.
2. Определите требуемое напряжение нагрузки.
3. Измените уравнение для ВА, чтобы решить его для тока. Например, для однофазного трансформатора.

Примечание: Не рекомендуется нагружать трансформатор выше 80 % его номинальной мощности ВА. После расчета ВА разделите значение на 0,8, чтобы получить минимальное необходимое значение ВА. Электрик или инженер-электрик должен проверить и подтвердить все значения из соображений безопасности.

Пример

Рассчитайте номинальную мощность однофазного трансформатора при напряжении нагрузки 24 вольта и максимальном фазном токе нагрузки 5 ампер.

Номинальная мощность трансформатора в ВА = (В × I)= (24 × 5) = 120 ВА

Разделив ВА на 0,8, пересмотренное значение ВА = 150

Выберите трансформатор с номинальной мощностью примерно 150 ВА для нагрузка.

Расчет эффективности трансформатора

Эффективность трансформатора определяется по формуле:

При работе с трансформаторами первичная мощность обычно обозначается как вольт-ампер (ВА), чтобы отличить ее от вторичной мощности. Таким образом, КПД определяется как:

Трансформаторы имеют высокий КПД из-за отсутствия движущихся частей. Трансформаторы также называют статическими машинами переменного тока. КПД хорошо спроектированного силового трансформатора очень высок, в среднем более 98 процентов. Единственные потери связаны с потерями в сердечнике, поддержанием переменного магнитного поля, потерями сопротивления в катушках и мощностью, используемой для охлаждения.

Калькулятор мощности трансформатора

Коэффициент мощности

В цепи переменного тока коэффициент мощности равен косинусу разности фаз между напряжением и током. Коэффициент мощности представляет собой долю номинальной мощности (полной мощности), которая потребляется (действительная мощность) цепью.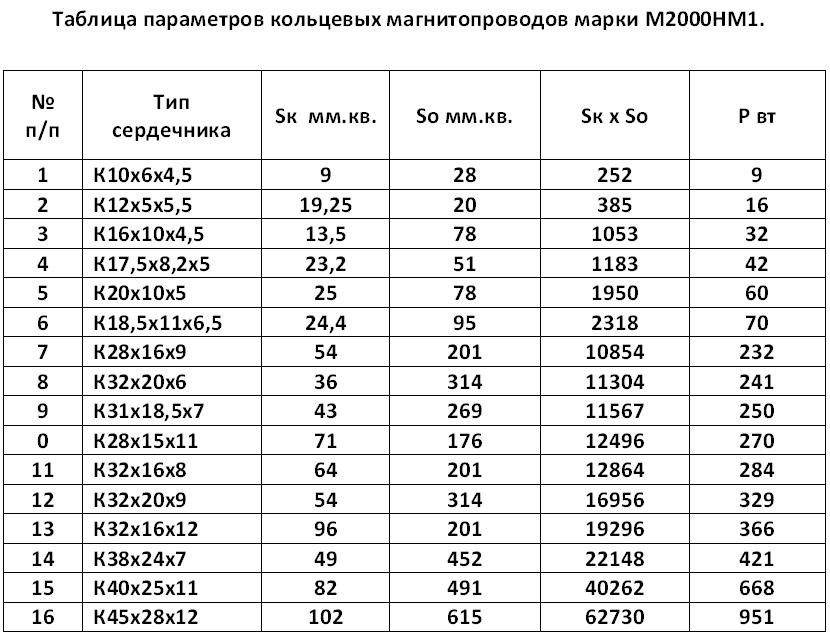

• PF: Коэффициент мощности
• 𝛷: Разность фаз между напряжением и током в цепи

Низкий коэффициент мощности означает, что для подачи заданного количества активной мощности на нагрузку требуется более высокий ток, что приводит к более высоким потерям энергии и снижению эффективности. Коэффициент мощности также может помочь рассчитать общую мощность, с которой трансформатор может работать без перегрузки.

Треугольник мощности

Полная мощность, активная мощность и активная мощность могут быть представлены в прямоугольном треугольнике, известном как треугольник мощности (рис. 4).

• S: Полная мощность (номинальная мощность), измеренная в ВА
• Q: Реактивная мощность измеряется в ВАр. Реактивная мощность потребляется при подключении индуктивной нагрузки, такой как двигатель, что создает разность фаз между напряжением и током
• P: Активная мощность в ваттах. Активная мощность — это мощность, которая производит реальную работу.
• 𝛷: Разность фаз между напряжением и током в цепи

Рис. 3. Треугольник мощностей, показывающий активную мощность (P), полную мощность (S) и реактивную мощность (Q) в магнитной цепи.

Используйте рис. 3, чтобы вывести соотношение между различными типами мощности в трансформаторе.

• Реактивная мощность

• Активная мощность

• Полная мощность

• Коэффициент мощности

Потери в трансформаторе

В трансформаторе имеется несколько источников потерь мощности.

• Потери в меди: Потери в меди вызваны циркулирующими токами вокруг медных обмоток трансформатора.
• Потери в сердечнике (потери в стали): Потери в стали вызваны вихревыми токами и гистерезисом, которые возникают в сердечнике из-за переменного потока.
• Диэлектрические потери: В изоляционном материале трансформатора наблюдаются диэлектрические потери. Если масло портится или твердая изоляция повреждается, это снижает качество системы, влияя на общий КПД трансформатора.

Как уменьшить потери в трансформаторе

Различные потери в трансформаторе могут вызвать перегрев устройства, что приведет к повреждению и сокращению срока службы трансформатора. Необходимо уменьшить эти потери, чтобы повысить КПД трансформатора и обеспечить оптимальную работу электрической системы. Общие меры:

1. Используйте медный провод большего диаметра в обмотках трансформатора, чтобы уменьшить потери в меди.
2. Используйте высококачественный магнитный материал, такой как кремнистая сталь, с наименьшей площадью петли гистерезиса, чтобы уменьшить потери в железе или сердечнике.
3. Сложите вместе тонкие листы при изготовлении сердечника трансформатора; это снижает потери на вихревые токи.
4. Регулярно проверяйте масло и поддерживайте качество изоляции для снижения диэлектрических потерь.

Часто задаваемые вопросы

Как подобрать трансформатор?

Чтобы определить размер трансформатора, определите требования к нагрузке электрической системы по напряжению и току, а затем выберите трансформатор с подходящей номинальной мощностью в кВА на основе требований к нагрузке.

Как рассчитать ВА трансформатора?

Чтобы рассчитать номинальную мощность трансформатора в ВА (вольт-ампер), необходимо рассчитать произведение номинальных значений напряжения и тока трансформатора.

Каковы размеры однофазных трансформаторов в кВА?

Стандартные размеры кВА для однофазных трансформаторов: 1, 1,5, 2, 3, 5, 7,5, 10, 15, 25, 37,5, 50, 75, 100, 167, 200, 250 и 333 (кВА)

КПД трансформатора 100%?

КПД трансформатора составляет менее 100 % из-за различных типов потерь внутри устройства, таких как потери в сердечнике, потери в меди и диэлектрические потери.

Расчетные данные — EILOR MAGNETIC CORES

ХАРАКТЕРИСТИКИ ГЕОМЕТРИЧЕСКИЕ ДАННЫЕ

Характеристические геометрические данные

Тип сердечника	Средняя длина пути потока Lm, мм	Эффективная площадь поперечного сечения, Ac, мм2	Масса сердечника, Вт, г
С-жила	Amax+Bmax+Fmin+Gmin-1,72*(Rmax+Emax/2) 902 66	Дмин *Emin*S	Ac min*Lm*g*10-3
E-core		Dmin*Emin*S	г*Acmin*(Amax+Bmax+2Fmin+2Gmin-0 .074Emax- 2,58Rmax)* 10-3
Тороид	(p/2)* (ODmax+IDmin)	Dmin*Emin*S	Ac min*Lm*g*10-3

 

Примечания:

• A, B, D, E, F, G, R, OD, ID
• г-плотность материала (7,65 г/см³),
• Коэффициент S-пространства

Численные значения Lm, A _c и W _t , рассчитанные на основании вышеизложенного для наших стандартных сердечников, можно увидеть  в разделе C.

Уравнение трансформатора (возбуждение синусоидальным напряжением)

 V=4,44*f*B _m *A _c *N*10 ^-6

Где:

В = R.M.S. Напряжение;
f   = Частота (Гц),
B _{м = Максимальная магнитная индукция (Тесла),}
A _{с мин}  = Эффективная площадь поперечного сечения (мм ² ),
Н = Количество витков.

ВОЗБУЖДЕНИЕ И ПОТЕРИ В ОСНОВЕ

Всего захватывающих VA 9где :

ВА = Общее среднеквадратичное значение вольт-ампер возбуждения ( ВА ),
Вт = Суммарные потери в сердечнике (в железе) (Вт),
ВА·м = Суммарная реактивная мощность металла
ВА·р _г

Примечание:

Общая мощность возбуждения (ВА) может быть кратко рассчитана путем умножения веса ядра на 9. 0333 гарантированная удельная мощность возбуждения (ВА/кг).

Общие потери в активной зоне (железо)

P=Вт/кг*Вт _{т мин} *10 ^-3

Где:

P = общие потери в активной зоне (железо) (Вт),
Вт /кг   = Удельные потери в сердечнике,
Вт _т мин = Вес сердечника (г).

Общая VAR металла

вар _м =вар _м /кг*Вт _{т мин} *10 ^-3

Где:

вар 903 09 м /кг = Удельная реактивная мощность металла
Вт _{t   мин}   = Вес ядра (г).

Суммарная VAR воздушного зазора

VAR _г = VAR _г /кг*Вт _{т мин} *10 ^-3

Где:

ВАр _г /кг = Удельная реактивная мощность воздушного зазора,
Вт _{т   мин}   = Масса активной зоны (г).

Удельная VAR воздушного зазора — C-core

VAR г /кг =

Bm2*f*a*104 90 506 4*г*лм

Удельная VAR Air-Gap-E-core

Где:

ВАр _г /кг = Удельная реактивная мощность воздушного зазора,
Б _м   = Максимальная индукция (Тесла),
f   = Частота (Гц),
А _{c min} = частота (Гц),
a   = средняя длина пути потока через два зазора (мм),
g   = плотность материала (7,65 г/см ³ ),
Ш _t.min   = Вес сердечника (г).

МОЩНОСТЬ ГРУЗОВАЯ МОЩНОСТЬ

Общие

Допустимая мощность магнитных сердечников зависит от требуемых нормативных требований, коэффициента площади медных проводников и предельного повышения температуры. Допустимое повышение температуры зависит от плотности тока, плотности потока, частоты, класса изоляции, рабочего цикла и способности трансформатора рассеивать тепло. Поэтому нельзя точно указать номинальную мощность. Допустимая мощность магнитных сердечников может быть определена из уравнений B.5.4.2-B.5.4.3 с использованием следующих значений:

Масса ядра, грамм	Плотность тока, А/мм²
0-3500	3,1
3500-10000	2,0
10000-50000	1,5
50000-60000	1,0

 

Примечания:

• A, B, D, E, F, G, R, OD, ID
• г-плотность материала (7,65 гр/см³),
• S-пространство, коэффициент

Числовые значения Lm, A _c и W _t , рассчитанные выше для наших стандартных сердечников, можно увидеть  в разделе C.

Допустимая мощность-тороид

ВА=5,0*J*B _м *f*A _{с мин.} *ID²*10 ^-7

32 ВА

= допустимая мощность (ВА ),
Дж   = Плотность тока (А/мм ²⁾ ,
B _м = Максимальная магнитная индукция (Тесла),
f = Частота (Гц),
ID = Внутренний диаметр (мм),
B _{c min} = Эффективная площадь поперечного сечения ( мм ² )

Допустимая мощность-C-core

ВА=7,0*J*B _м *f*GF*A _{c min} *10 ^-7

Где:

9003 2 ВА = допустимая мощность (Вирджиния),
Дж   = Плотность тока (А/мм ²⁾ ,
B _м = Максимальная индукция (Тесла),
f = Частота (Гц),
9 0695 GF = площадь окна (мм ² ),
A _{c min} = Эффективное сечение жилы) (мм ² ).

Допустимая мощность-E-core

ВАР г /кг=

2.5*B m 2 *f*a*A cmin W tmin 9003 3

Нестандартные сердечники

Модификация намотанных сердечников (разрезанных или неразрезанных) в соответствии с особыми требованиями к размеру и форме намного проще по сравнению с дорогостоящим процессом штамповки новых форм ламинирования. Определите размеры сердечника, используя уравнение B.5.4. или по другим соображениям. Обратите внимание, что квадратное сечение жилы (D=E) дает минимальную среднюю длину витка медного провода. Следует, однако, отметить, что поскольку индукция обратно пропорциональна длине пути (B _м »1/L _м ), большая разница между внутренней (оконной) длиной пути сердечника и внешней (общей) длиной пути приведет к преждевременному насыщению внутренних витков сердечника. Поэтому желательно свести к минимуму разницу между внешней и внутренней длинами пути.

ТОРОИДЫ

Общее

Нескрепленный неразрезанный тороид представляет собой почти идеальную магнитную петлю. Он сохраняет практически все основные свойства материала. Это сводит к минимуму потери и уменьшает силу намагничивания, необходимую для создания заданного потока внутри материала. В узле тороид и катушка весь магнитный путь находится внутри электрической обмотки, что дополнительно минимизирует поток рассеяния и увеличивает сцепление между обмотками. Тороид также обеспечивает хорошую степень самозащиты от внешних магнитных полей. Единственный однородный магнитный путь заставляет любое входящее магнитное поле разделяться на два и индуцировать одинаковое, но противоположное напряжение в двух половинах равномерно распределенной обмотки. Таким образом, они, как правило, не являются напряжением, явно индуцированным в общей обмотке.

Механические допуски

Внешний диаметр OD (мм)	Допустимые допуски (мм)
	Внешний диаметр OD	Внутренний диаметр ID	Ширина полосы H
35÷50	± 1,0	± 0,5	+ 0,6
50÷80	± 1,25	± 0,75	+ 0,8
80÷100	± 1,5	± 1,0	+ 1,0
100÷160	± 2,0 902 66	± 1,3	+ 1,5
160÷200	± 2,5	± 1,5	+ 1,5
200÷340	± 3,0	± 2,0	+ 2,0

ИМПУЛЬСНЫЕ СЕРДЕЧНИКИ

General

Типичная импульсная проницаемость при использовании сброса постоянного тока и изменении потока ΔB=2,2 Тесла для материала толщиной 0,05 мм и ΔB=2,8 Тесла для материала толщиной 0,10 мм показана на D.