«Расчет электрических фильтров»
Федеральное агентство связи
Государственное образовательное учреждение
Высшего профессионального образования
«Сибирский государственный университет
телекоммуникаций и информатики»
(ГОУ ВПО «СибГУТИ»)
Курсовая работа по дисциплине
«Основы теории цепей»
На тему:
Вариант №36
Выполнил: Черепенин А. В.
Группа: ЗТ-02
Кафедра: ТЭЦ
Проверила: Булатова Г. И.
Новосибирск 2011
Содержание:
Введение. 1 стр.
1. Задание на курсовую работу.
2 стр.
Задание на курсовую работу.
2 стр.
2. Расчет полосового LC-фильтра. 4 стр.
2.1. Расчет амплитудного спектра радиоимпульсов. 4 стр.
2.2. Формирование требований к полосовому фильтру. 9 стр.
2.3. Формирование передаточной функции НЧ-прототипа. 11 стр.
2.4. Реализация LC-прототипа. 14 стр.
2.5. Реализация пассивного полосового фильтра. 17 стр.
3.
Расчет активного полосового фильтра.
19 стр.
3.1. Расчет полюсов ARC-фильтра. 19 стр.
3.2. Формирование передаточной функции. 21 стр.
3.3. Расчет элементов схемы фильтра. 23 стр.
4. Проверка результатов расчета. 26 стр.
Заключение. 30 стр.
Литература. 31 стр.
Электрические
фильтры – это линейные четырехполюсники,
обладающие избирательными свойствами:
они предназначены для выделения из
состава сложного электрического
колебания частотных составляющих
определенного спектра частот, лежащего
в полосе пропускания (ПП), и подавления
тех составляющих, частоты которых лежат
за пределами ПП, т. е. в полосе непропускания
(ПН) или полосе задерживания (ПЗ). Между
этими полосами находится переходная
область.
е. в полосе непропускания
(ПН) или полосе задерживания (ПЗ). Между
этими полосами находится переходная
область.
Обычно выделяют следующие четыре типа фильтра:
—
фильтр нижних частот (ФНЧ), пропускающий
все частоты ниже выбранного значения
w
— фильтр верхних частот (ФВЧ), пропускающий все частоты выше выбранного значения и подавляющий нижние частоты;
— режекторный или заграждающий фильтр, подавляющий выбранную полосу частот и пропускающий нижние и верхние частоты;
— полосовой фильтр (ПФ), пропускающий выбранную полосу частот и подавляющий нижние и верхние частоты.
В соответствии с элементной базой можно выделить различные типы фильтров. Пассивные фильтры, содержащие элементы L и C. Они носят название LC-фильтры.
Требования
микроминиатюризации аппаратуры заставили
отказаться от использования индуктивностей,
которые имеют большие габаритные
размеры, особенно на низких частотах.
Расчет активного фильтра включает в себя два этапа – этап аппроксимации и этап реализации. На первом этапе по заданному максимальному и минимальному ослаблению в полосе пропускания и в полосе непропускания формируется передаточная функция фильтра, т.е. математическое описание цепи. На втором этапе создают схему цепи и определяют значение ее элементов по полученной передаточной функции.
Мостовые электрические фильтры. Теорема о мостовых фильтрах. Расчет фильтров по характеристическим параметрам
Лекция № 8
Мостовые электрические фильтры
Мостовые фильтры конструктивно представляются в виде мостового четырехполюсника:
– характеристическое сопротивление
, .
Последние соотношения рекомендуется доказать самостоятельно.
Известно, что , с другой стороны .
Таким образом:.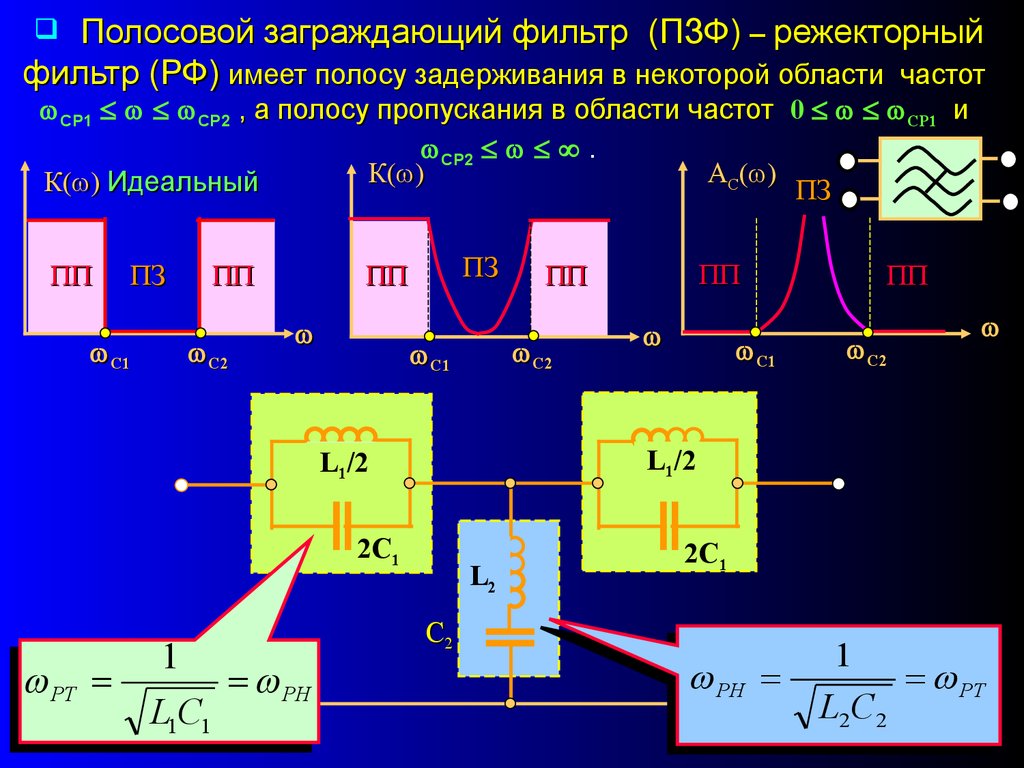 Полоса пропускания фильтра имеет
место при мнимых значениях корня и
действительных значениях корня . При этом и имеют
разные знаки.
Полоса пропускания фильтра имеет
место при мнимых значениях корня и
действительных значениях корня . При этом и имеют
разные знаки.
При , затухание бесконечно, и напряжение на выходе мостовой схемы равно нулю!
Теорема о мостовых фильтрах
Основываясь на том, что в полосе пропускания и имеют разные знаки, а в точке пересечения кривых и затухание бесконечно, можно легко найти частоты среза и бесконечно большого затухания. Покажем это на примере ФНЧ.
Расчет фильтров по характеристическим параметрам
Задачей расчета электрического фильтра по характеристическим параметрам
состоит в построении фильтра, составленного путем каскадного соединения
минимального числа согласованных звеньев
(полузвеньев) и удовлетворяющего заданным техническим
требованиям.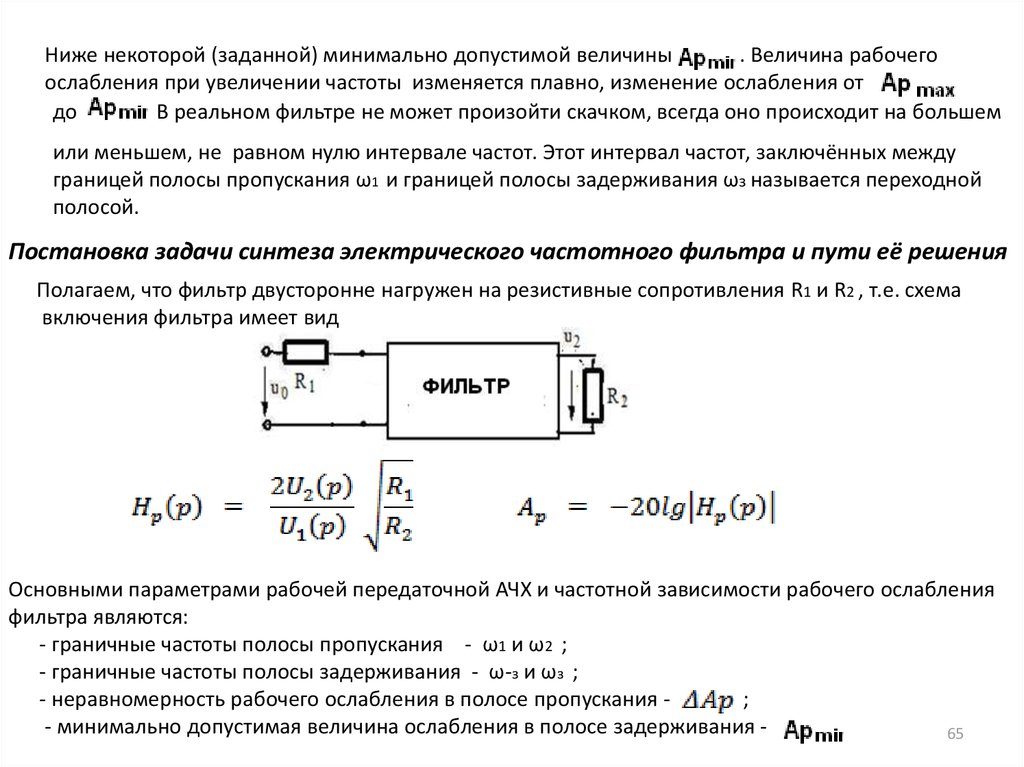
Поскольку полное согласование генератора с входом фильтра и нагрузки с выходом фильтра невозможно, то рабочее затухание:
, где – ослабление отражения, обусловленное несогласованностью.
В частотной характеристике рабочего затухания различают три полосы:
1. ПЭП – полоса эффективного пропускания.
2. ПО – переходная область.
3. ПЭЗ – полоса эффективного задерживания.
Представим график частотной зависимости рабочего ослабления для ФНЧ «к».
Amin – минимально допустимое ослабление в ПЭЗ.
∆A – максимально допустимое ослабление в ПЭП.
fe1 – граничная частота ПЭП.
fe2 – граничная частота ПЭЗ.
Введем степень использования ПЭП:
, следовательно .
Собственные сопротивления фильтра:
, .
Сопротивление генератора и нагрузки выбирают как среднее геометрическое:
– со стороны Т-входа.
– со стороны П-входа.
Классы фильтров по сопротивлению и ослаблению
Особую роль отводят определению класса фильтра. Различают класс по сопротивлению (NZ) и класс по ослаблению (NA).
NA – определяется количеством звеньев и полузвеньев. К фильтрам 1 класса по ослаблению (NA = 1) относятся звенья ФНЧ и ФВЧ типа «к» и типа «m», а также звенья ЗФ типа «к».
Полузвеньям перечисленных фильтров присвоен класс по ослаблению 0.5 (NA = 0.5).
Звено полосового фильтра типа «к» имеет класс NA = 2, а его полузвено NA = 1.
NZ – определяется количеством частот согласования. К
фильтрам 1 класса по сопротивлению (NZ = 1)
относят все звенья и полузвенья ФНЧ и ФВЧ типа «k». К
фильтрам 2 класса по сопротивлению (NZ = 2)
относят звенья ФНЧ и ФВЧ типа «m», ПФ и ЗФ типа «k».
Определим класс
следующего фильтра: NZ = 2, N
График частотной зависимости характеристического ослабления данного фильтра:
Здесь – резонансные частоты параллельного и последовательного колебательных контуров, располагающихся на входе и выходе фильтра.
Расчет электрических фильтров по рабочим параметрам. Основные понятия и определения
Основные преимущества:
1. Электрический фильтр с меньшим числом элементов
2. Точность вычислений
3. Разработана общая методика расчета
Рассмотрим реактивный двусторонне нагруженный электрический фильтр:
Рабочая мера передачи данного фильтра определяется соотношением:
, [Нп],
[дБ].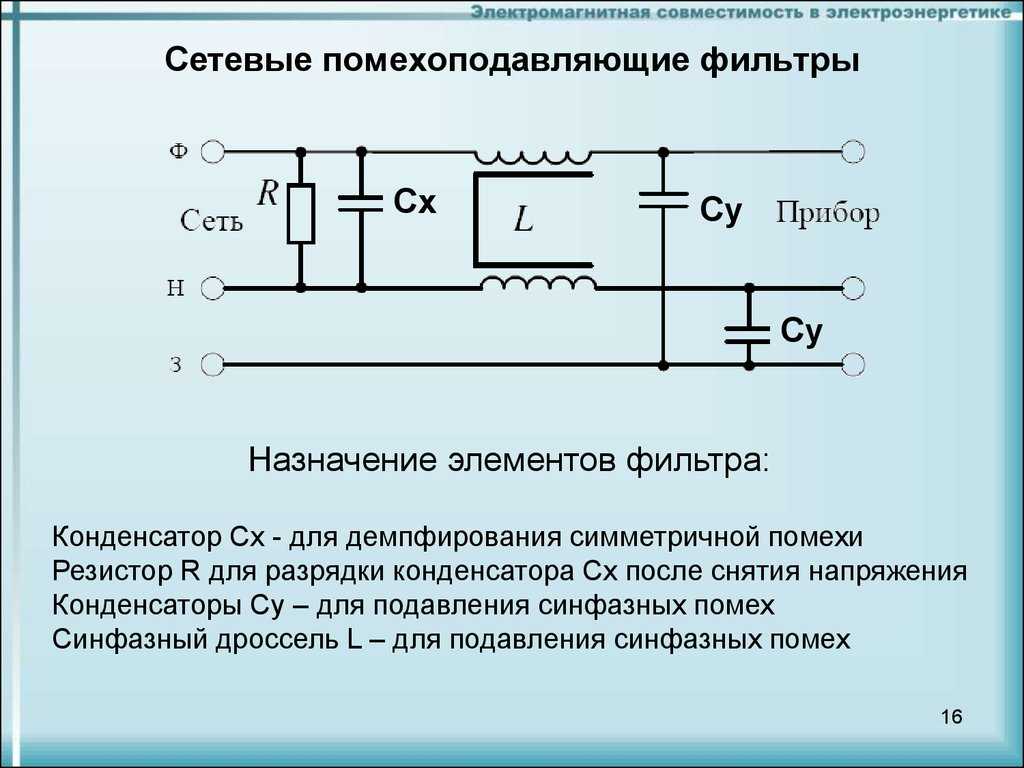
– активная максимальная мощность источника.
– активная мощность, передаваемая от источника в нагрузку.
Из-за несогласованности входного сопротивления с внутренним
Активные и пассивные частотные фильтры
Содержание
Частотные фильтры: Пассивные фильтрыТип цепей выбора частоты, состоящих только из пассивных компонентов, таких как резистор, конденсатор и катушка индуктивности.
Фильтр нижних частот:Пропускает низкие входные частоты без ослабления и блокирует высокие частоты после фиксированной точки, известной как частота среза.
Выход берется через C и R в цепи RC и RL соответственно.
Related Posts:
- Типы активных фильтров нижних частот
- Типы пассивных фильтров нижних частот — Пассивные фильтры RL и RC
Частота, при которой выходной сигнал становится равным 70,7% входного сигнала, называется частотой отсечки, угловой или контрольной точки и определяется как;
Передаточная функция:Передаточная функция для обеих цепей RC и RL одинакова;
Постоянная времени: Постоянная времени играет важную роль в определении частоты среза цепи.
- τ = 1 / ω c Для обеих цепей
- τ = L / R Для цепи RL
- τ = RC Для RC-цепи
Этот тип фильтра пропускает высокочастотную составляющую из входного сигнала. Схема, используемая для HPF, такая же, как и для LPF, но выход берется через R и L в цепи RC и RL соответственно.
Related Posts:
- Типы активных фильтров верхних частот
- Типы пассивных фильтров верхних частот
Аналогично фильтру нижних частот.
Передаточная функция:
Из-за изменения выходного элемента изменяется только передаточная функция.
Постоянная времени:Она также останется прежней.
- τ = 1 / ω c Для обеих цепей
- τ = L / R Для цепи RL
- τ = RC Для RC-цепи
разрешает фиксированный диапазон частот и блокирует все остальные частотные компоненты до или после этого допустимого диапазона.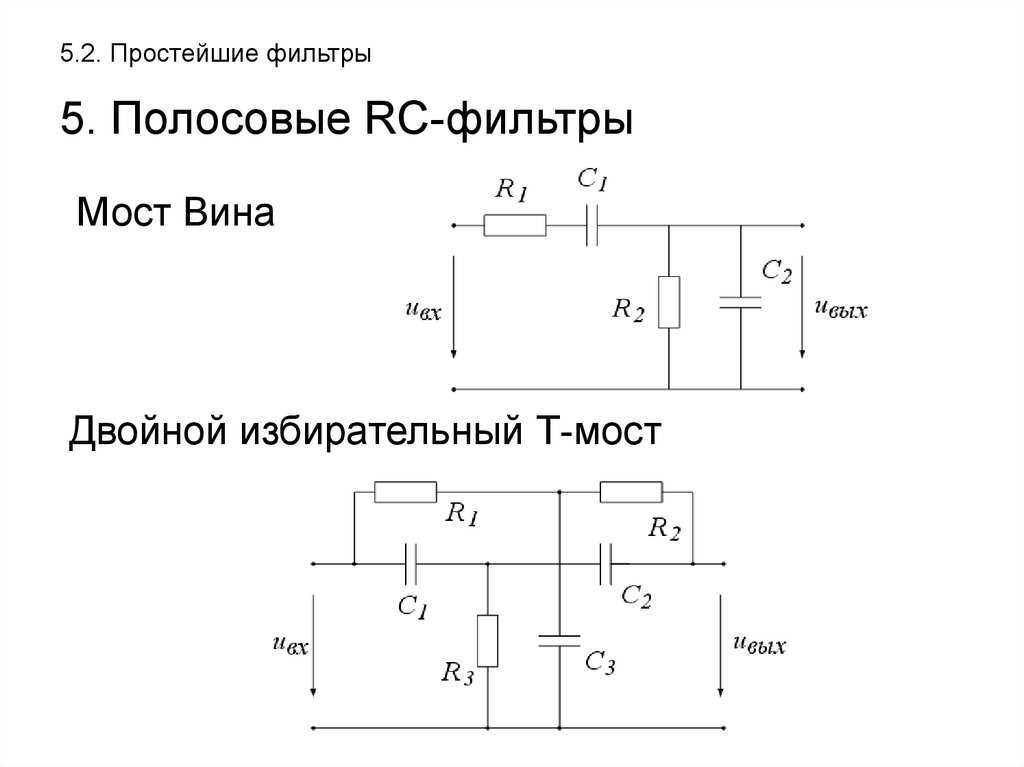
центр допустимой полосы частот f c определяется по формуле;
Частота отсечения:Существуют две частоты отсечения в полосовых фильтрах проходов, т.е. блокируется фильтром.
Полоса пропускания:
Полный диапазон допустимой частоты называется полосой пропускания, от нижней до верхней частоты среза.
β = ω c2 – ω c1
- β = R/L Для серии RLC
- β = 1/RC Для параллельного RLC
Связанные сообщения:
- Символы электронных фильтров
- Символы индуктора — символы соленоида, блока и катушек
Они допускают определенные частоты с коэффициентом усиления, который можно изменить с помощью сети резисторов.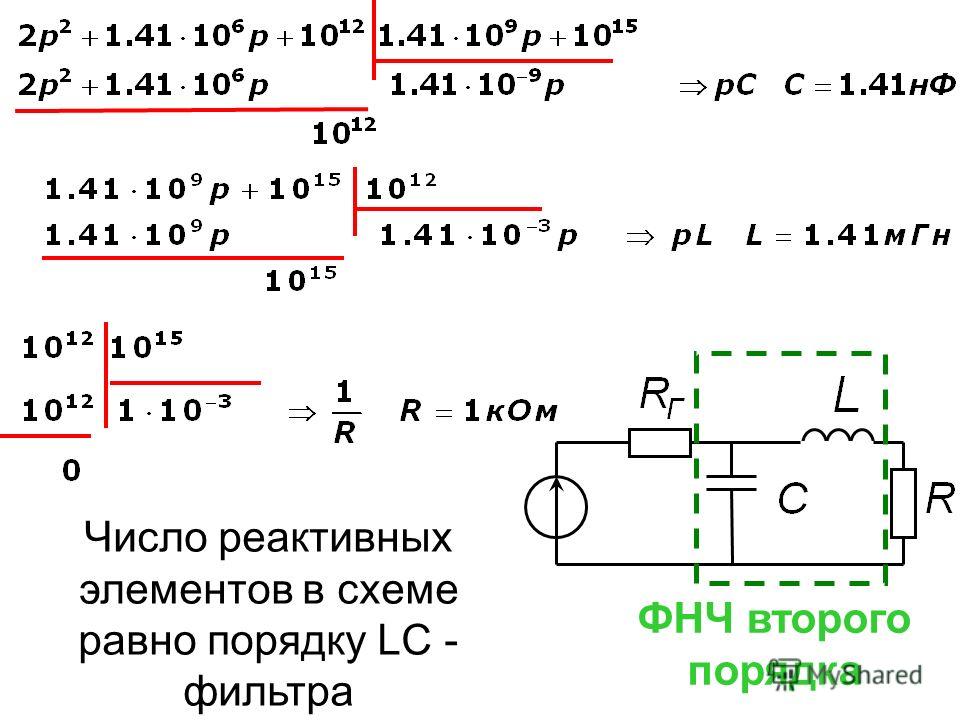
Фильтр первого порядка содержит только один реактивный компонент.
Частота среза:Частота среза для активного фильтра верхних и нижних частот;
Коэффициент усиления:Суммарный коэффициент усиления выходного напряжения для этого фильтра определяется выражением;
K = R 2 / R 1
Передаточная функция:Передаточная функция для активного фильтра нижних и верхних частот с коэффициентом усиления K определяется выражением;
Масштабирование: Масштабирование позволяет нам использовать более реалистичные значения резисторов, катушек индуктивности и конденсаторов, сохраняя при этом качество фильтра. Его можно использовать как в пассивных, так и в активных фильтрах. Существует два типа масштабирования: масштабирование амплитуды и масштабирование частоты.
Масштабирование величины
, если вы хотите масштабировать только величину фильтра.
- R’ = k м R
- L’ = k м L
- C’ = C / k м
Масштабирование частоты
Если вы хотите масштабировать только частоту фильтра
- R’ = R
- L’ = L/k f
- С’ = С / k f
Одновременное масштабирование
Если вы хотите масштабировать как частоту, так и амплитуду фильтра;
- R’ = k м R
- L’ = (k m /k f ) L
- C’ = (1/k m k f ) C
- R’ = масштабированное сопротивление
- L’ = масштабированная индуктивность
- Кл’ = емкость в масштабе
- k m = Масштабный коэффициент магнитуды
- k f = масштабный коэффициент частоты
Связанные формулы и уравнения Посты:
- Основные формулы и уравнения электротехники
- Сопротивление, емкость и индуктивность в последовательно-параллельном соединении – уравнения и формулы
- Формулы сопротивления, проводимости, импеданса и проводимости
- Основные формулы электрических величин
- Правила делителя напряжения и тока (VDR и CDR) Уравнения
- Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
- Магнитные термины, используемые в магнитных цепях – определения и формулы
- Постоянная времени τ «Тау» формулы для цепей RC, RL и RLC
- Операционный усилитель (OP-AMP) – формулы и уравнения
- Транзистор с биполярным переходом (BJT) – формулы и уравнения
- Диодные формулы и уравнения – Zenner, Schockley & Rectifier
- Формулы электрического и магнитного потока, плотности и напряженности поля
- Формула и уравнения для законов Ома, Кирхгофа и Кулона
- Уравнения и формулы для цепей RLC (последовательные и параллельные)
- Формула и уравнения для индуктора и индуктивности
- Формула и уравнения для конденсатора и емкости
- Потери в электрических машинах – формулы и уравнения
- Формулы и уравнения генератора постоянного тока
- Уравнение мощности, напряжения и ЭДС двигателя постоянного тока – формулы
- Формулы и уравнения синхронного генератора и генератора переменного тока
- Формулы и уравнения синхронных, шаговых и двигателей переменного тока
- Асинхронный двигатель и линейные асинхронные двигатели Формулы и уравнения
- Трансформаторные формулы и уравнения
- Формулы и уравнения в области электротехники и электроники
- Электрические и электронные элементы и символы
Показать полную статью
Статьи по теме
Расчеты и тестирование базовых фильтров
Рассмотрение проектирования фильтров нижних и верхних частот и их тестирование с помощью Analog Discovery 2.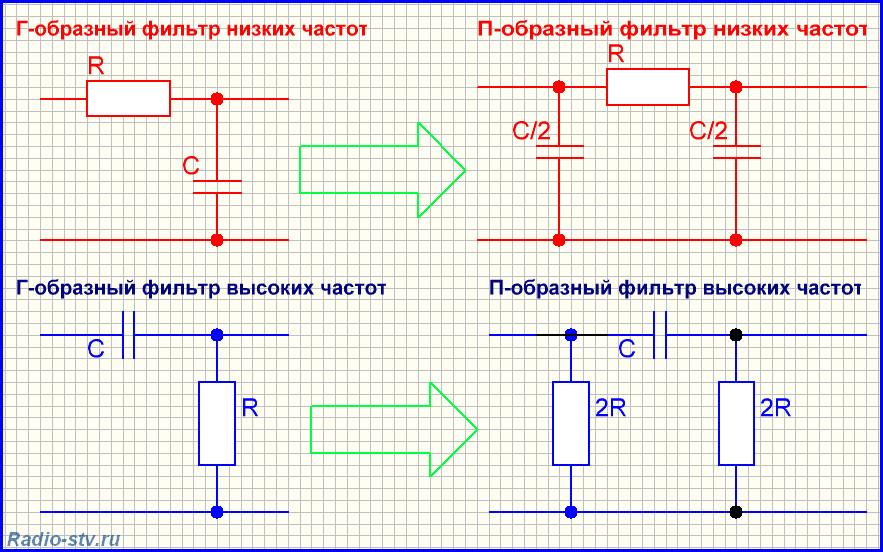
В предыдущем посте Знакомство с фильтрами. Я рассмотрел некоторые из различных типов электронных фильтров, их функции и области их применения. Это включало как базовые фильтры нижних частот, так и фильтры высоких частот. Чтобы лучше понять их конструкцию и то, как они работают, в этом посте я рассмотрю расчеты, лежащие в основе определения их частот среза, прежде чем приступить к тестированию.
Фильтры нижних частот
Для начала я собираюсь рассмотреть фильтр нижних частот. Фильтр нижних частот пропускает все частоты ниже определенной точки среза и блокирует частоты выше нее.
Это пассивный фильтр, состоящий только из последовательно соединенных резистора и конденсатора. Чтобы определить значения компонентов, необходимые для достижения определенной частоты среза, мы используем формулу:
Fc = 1 / 2PiRC
Есть несколько способов, которыми эта формула может быть изменена, чтобы сделать либо C, либо R субъектом, следующее что я буду использовать:
Fc2PiR = 1/C
Допустим, для этого приложения мы хотим оценить частоту среза 1 кГц (1000 Гц) и примем значение резистора 10 кОм. Подставляя эти значения в формулу, мы получаем:
Подставляя эти значения в формулу, мы получаем:
1000 x 2 x Pi x 10 000 = 1/C
1000 x 2 x Pi x 10 000 = 1/62831835,07
Это приводит к емкости конденсатора 15,9×10-9 Ф или просто 15,9 nF
Поскольку у меня нет доступного конденсатора на 15,9 нФ, я буду использовать конденсатор с ближайшим значением, которое я могу найти, это 15 нФ. Поскольку это не точное значение конденсатора, необходимое для частоты среза 1 кГц, я собираюсь использовать исходное уравнение с этим значением конденсатора и резистором 10 кОм, чтобы определить, какой должна быть фактическая расчетная частота среза.
Fc = 1 / 2PiRC
Fc = 1 / 2 x Pi x 10,000 x 15×10-9
Fc = 1061.03Hz or 1.06KHz
Здесь этот фильтр должен пропускать примерно все частоты ниже 1,06 кГц и останавливать выше него, с учетом колена данной конструкции фильтра.
Чтобы проверить это, я подключил Analog Discovery 2 к цепи. Зонд Wavegen был подключен к входу резистора, а зонд осциллографа подключен к соединению резистора и конденсатора, а затем заземлен к другой стороне конденсатора.
Я установил Wavegen на источник синусоидальной волны с амплитудой 1 В (2 В PP) в диапазоне частот, начиная с 1 Гц и заканчивая 500 кГц. Результаты следующие:
Затем я построил зависимость усиления от частоты, чтобы визуализировать кривую отклика
Здесь мы можем посмотреть на меньший диапазон показаний вокруг частоты среза, чтобы получить более четкое представление кривой колена.
Затем это повторялось с меньшими и меньшими диапазонами показаний, пока колено кривой частотной характеристики не стало достаточно четким, чтобы его можно было увидеть.
Глядя на графики АЧХ и таблицу разработанного ФНЧ, мы видим, что пропускаются частоты до 200 Гц и что где-то между частотами 200 Гц и 500 Гц начинается затухание.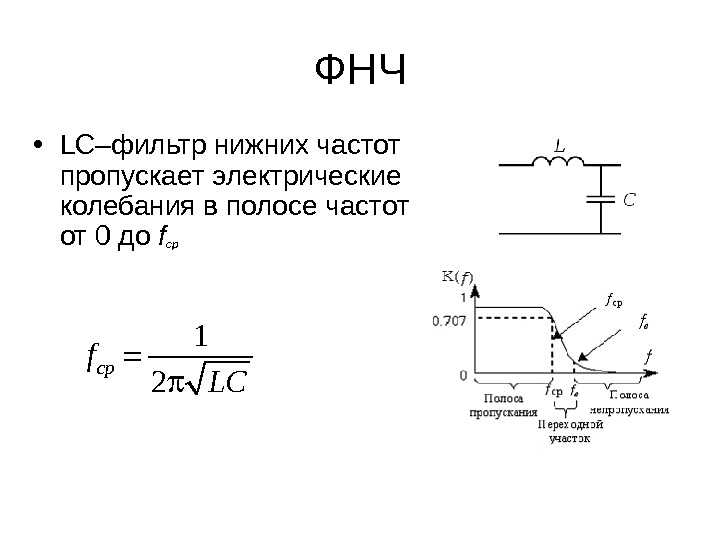 Таким образом, этот фильтр действует так, как должен, и работает как фильтр нижних частот, пропуская частоты ниже своей частоты среза и блокируя частоты выше нее.
Таким образом, этот фильтр действует так, как должен, и работает как фильтр нижних частот, пропуская частоты ниже своей частоты среза и блокируя частоты выше нее.
Фильтры верхних частот
Как и фильтр нижних частот, который мы только что рассмотрели, простой фильтр верхних частот, который я собираюсь разработать, также является пассивным и состоит только из последовательно соединенных конденсатора и резистивного конденсатора.
Чтобы определить значения компонентов, необходимых для достижения определенной частоты среза, мы используем формулу, как и для фильтра нижних частот:
Fc = 1 / 2PiRC сделать емкость (C) объектом:
Fc2PiR = 1/C
Поскольку это фильтр высоких частот, скажем, мы хотим пропустить все частоты выше приблизительно 2 кГц, это заблокирует все частоты ниже этой частоты среза. Подставив эту частоту и еще раз приняв номинал резистора 10K, мы получим:
2000 x 2 x Pi x 10 000 = 1/C
2000 x 2 x Pi x 10 000 = 1/125663706,1
Это дает значение конденсатора 7,9577×10-9 Ф или просто 7,9 нФ.
Поскольку у меня нет доступного конденсатора на 7,9 нФ, я снова буду использовать конденсатор с ближайшим номиналом. Ближайшие значения, которые у меня есть в наличии, это 6,8 нФ или 10 нФ, для целей этого фильтра я буду использовать конденсатор 6,8 нФ, так как это наиболее близко к расчетному значению, необходимому для приблизительной частоты 2 кГц.
Как и раньше, я снова вернусь к этим значениям компонентов, чтобы определить фактическую расчетную частоту среза. Используя резистор 10 кОм и конденсатор 6,8 нФ, это должно быть:
Fc = 1/2PiRC
Fc = 1/2 x Pi x 10 000 x 6,8×10-9
Fc = 2340,51 Гц или 2,34 кГц
Зная это, я должен ожидать этот фильтр пропускает частоты выше отметки 2,34 кГц и блокирует частоты ниже этой отметки.
После того, как эта схема была построена на ранее, я повторил, что я закончил подключенный к входу конденсатора, щуп прицела был подключен к соединению резистора и конденсатора, а затем он был заземлен с другой стороны резистора.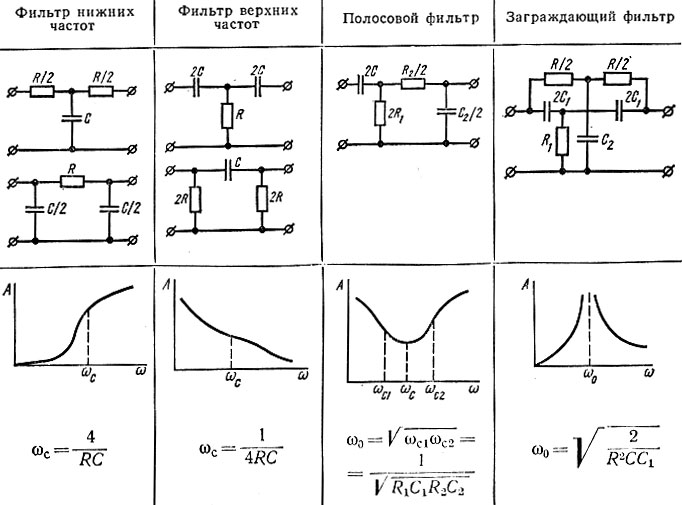 Снова Wavegen был настроен на источник синусоидальной волны с амплитудой 1 В (2 В PP) в диапазоне частот от 1 Гц до 500 кГц. Результаты следующие:
Снова Wavegen был настроен на источник синусоидальной волны с амплитудой 1 В (2 В PP) в диапазоне частот от 1 Гц до 500 кГц. Результаты следующие:
Ниже мы видим график зависимости выходного усиления от подаваемой частоты.
Еще раз мы можем посмотреть на меньшую выборку результатов около частоты среза, чтобы получить лучшее представление о колене кривой.
Мгновенно мы получаем лучшее представление о колене кривой частотной характеристики, но, взглянув на еще меньшую выборку, мы можем увидеть это более подробно из протестированного диапазона частот.
Глядя на графики частотных характеристик и таблицу, мы видим, что частоты выше 5 кГц пропускаются, а частоты ниже этой точки в некоторой степени блокируются. Здесь мы знаем, что частота среза этого фильтра верхних частот должна быть около 2,34 кГц, в то время как некоторые частоты в этой точке и выше ослабляются, это находится в пределах нормального диапазона для частоты среза, равной -3 дБ, что около.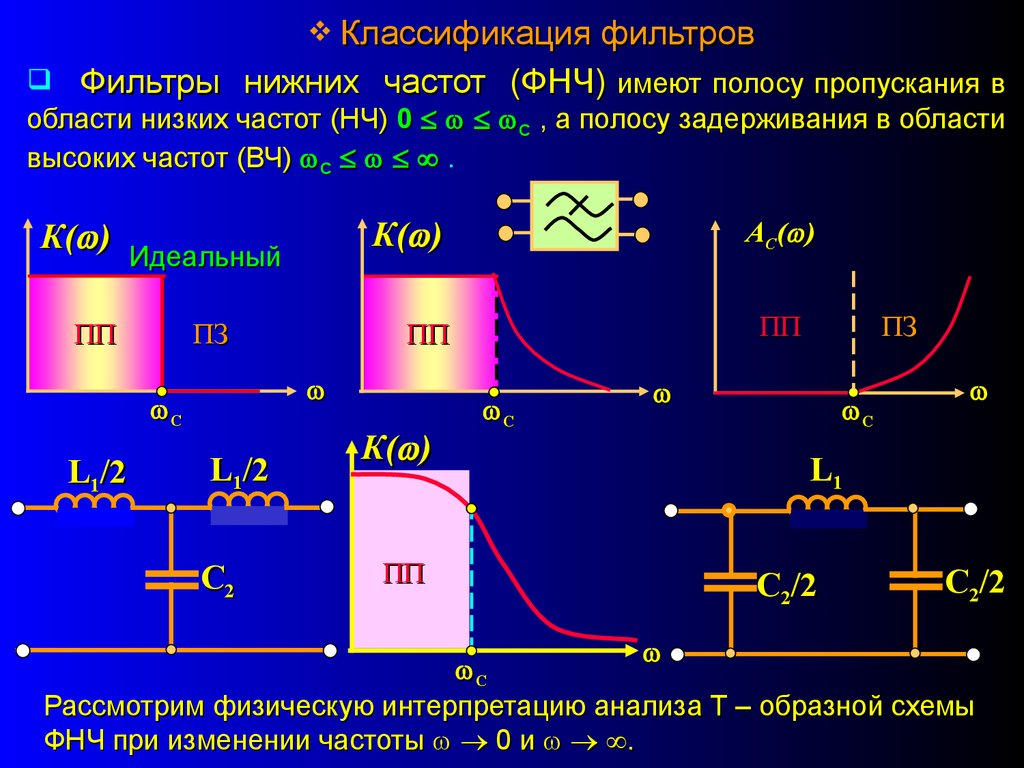
Генератор свипирующих сигналов
Когда я играл с программным обеспечением WaveForms, я заметил, что функция Wavegen заключается в том, что вы можете установить ее для развертки, а затем вы можете использовать анализатор спектра для просмотра графика отклика. Я хотел попробовать развернуть частоту по диапазону, чтобы увидеть кривую частотной характеристики, не беря много ручных показаний, а затем строя их самостоятельно. Это означает, что теоретически график будет намного четче, так как это также позволит проверить промежуточные частоты точек, измеренных вручную.
Сначала я подключил фильтр нижних частот к Analog Discovery 2, при этом генератор сигналов был подключен к входу резистора, а щуп осциллографа — к соединению резистора и конденсатора. Затем другая сторона конденсатора была подключена к GND, и сюда же был подключен отрицательный канал 1 осциллографа.
Я настроил Wavegen на развертку в диапазоне от 1 Гц до 500 кГц, и ниже мы можем увидеть график этого на анализаторе спектра.

